Modeling Parallel Transport

Abstract

In 1918, the Dutch geometer Jan Arnoldus Schouten used plaster models of standard curved surfaces to illustrate a novel geometric concept of the geodesic transport of reference frames in curved spaces. This paper discusses Schouten’s use of material modeling in the context of an emerging abstract geometric concept of parallel transport.

Introduction

This paper is about one particular set of models, a set of three material models of simple curved surfaces dating from 1918. What makes these three surface models special in the context of a history of mathematical modeling is that they carry an additional layer of information, i.e. these plain surface models serve to illustrate a new concept that was painted onto the model surfaces. The basic models were most likely purchased from a standard collection of models that had been commercially available for a long time. The interesting feature is what was painted onto them, and this embellishment happened in 1918. These models were turned into illustrations of a new abstract concept by the Dutch geometer Jan Arnoldus Schouten (1883–1971). He wanted to illustrate or visualize the new geometric concept of parallel transport. Photographs of his illustrated models were included in a paper that introduced this new concept. Identical copies of these photographs appeared in four different publications up until 1924, but it appears that they have never been republished or referenced again after that.

I will argue that these three illustrative models represent a certain transitional stage in a process of conceptual development of differential geometry and it is this transitional nature that makes this case interesting. We also see here that there were two levels to these models at work because Schouten took existing geometric models and added a visual layer, so as to illustrate and visualize an emerging new abstract concept. Such a two-layered use of models was not unusual, but here we see the significance of using the basic models as background for more abstract concepts very clearly.

Historical Context: Localization of the Models in Space and Time

The models were first referenced and depicted in Schouten’s monograph-length contribution to the Verhandelingen der Koninklijke Akademie van Wetenschapen, entitled Die direkte Analysis zur neueren Relativitätstheorie. Photographs of the models were reproduced in the paper.¹ Max von Laue (1879–1960) then reproduced the same pictures in the second volume of his textbook on relativity that was one of the first textbook expositions in Germany of the new general theory of relativity.² Dirk Struik (1894–2000) then reproduced them again in his 1922 monograph on Grundzüge der mehrdimensionalen Differentialgeometrie in direkter Darstellung³ (see Figs. 1 and 2). The very same photographs were reproduced once more in an introduction to modern differential geometry jointly authored by Schouten and Struik.⁴

Fig. 1

Jan A. Schouten’s model for geodesic motion of a frame over a spherical cap as an example of a surface of positive curvature. From Dirk J. Struik, Grundzüge der mehrdimensionalen Differentialgeometrie in direkter Darstellung (Berlin: Springer, 1922), 47. © Springer, all rights reserved

Fig. 2

Jan A. Schouten’s model for geodesic motion of a frame over two examples of surfaces of negative curvature. From Dirk J. Struik, Grundzüge der mehrdimensionalen Differentialgeometrie in direkter Darstellung (Berlin: Springer, 1922), 48. © Springer, all rights reserved

When Laue republished Schouten’s photographs in his textbook, he did not give any information about the origin and creator of these models. In fact, Struik found it necessary to pass on proper credit for his teacher Schouten and through this comment we learn about the origin and original location of these models. He added in a footnote: “These models were made first by Prof. J. A. Schouten and are part of the model collection of the Technical University Delft.”⁵ We do have, in fact, accounts of that larger collection which appears to have been used intensely also in later times: Fig. 3 shows David van Dantzig (1900–1959) during one of his lectures at Delft Polytechnic in 1937 engaged with a geometric thread model.

Fig. 3

David van Dantzig during one of his lectures at Delft Polytechnic with geometric models in 1938 (Photo: Archiv Gerard Alberts; reproduced in Irene Polo Blanco, “Physical models for the learning of geometry,” Nieuwe Wiskrant 31, no.1 (September 2011), 36; also reproduced in Irene Polo-Banco, “Theory and history of geometric models,” (Ph.D. diss., Groningen, 2007, 8). © Archiv Gerard Alberts, all rights reserved

The specific interest of these three models derives from the combination of the material geometric surface together with the inscription on them, painted onto the surface with white on black.

The geometric model surfaces were, in fact, rather standard and not in any way exotic shapes, a segment of a sphere, a hyperbolic paraboloid and a pseudosphere, i.e. the rotational surface of a tractrix. Interest in the shape of a sphere and a pseudosphere derived from the properties that they display constant positive or constant negative curvature. Plaster models of these shapes could have been ordered readily from Schilling’s catalogue (see also Fig. 4).⁶ Spheres were available in different sizes “with black board paint and a wooden stand” (“mit schwarzem Tafelanstrich und Holzuntersatz”) so that they could be drawn on with chalk as on a regular blackboard.⁷

Fig. 4

The basic shapes of Jan A. Schouten’s models could be purchased from Schilling's catalogue. From Martin Schilling, ed., Catalog mathematischer Modelle für den höheren mathematischen Unterricht, 7th ed. (Leipzig: Martin Schilling, 1911), 115, 114, 144. Similar pictures can be found in Walther Dyck, ed., Katalog mathematischer und mathematisch-physikalischer Modelle, Apparate und Instrumente (Munich: C. Wolf und Sohn, 1892), 259, 292

Spheres were available with diameters of 35, 14, and 10 cm, with price tags of Mk. 43.20, 12.20, or 9.50, respectively. The size of the paraboloid was 15 by 13 cm and its cost was Mk. 4.50 or 8.00 depending on whether it had the lines of horizontal cuts, i.e. equilateral hyperbolas imprinted on them or not. The production of the pseudosphere was credited to “stud. math. Bacharach” from Munich, its size was given as 25 by 18 cm and its price tag was Mk. 11.00.⁸ Examples of the hyperbolic paraboloid and of the pseudosphere are depicted also in Gerd Fischer’s Mathematische Modelle⁹ (see Fig. 5a, b) and in Digitales Archiv mathematischer Modelle.¹⁰

Fig. 5

Photographs of typical specimens of models of the hyperbolic paraboloid and the pseudosphere. Reprinted by permission from Springer Nature: Gerd Fischer, ed., Mathematical Models, vol. 1, 2nd ed. (Wiesbaden: Springer Spektrum, 2017), 8, photo 7; 77, photo 82. © Springer Nature, all rights reserved

The materiality of the models reflects a culture of preparing modeling clay of a kind especially suitable for the making of geometric models. Fischer cites a contemporary recipe for making modeling clay, an elaborate procedure involving various ingredients, specific temperatures, kneading, and patience.¹¹

The Notion of Parallel Transport

The completion of the general theory of relativity in late 1915 triggered a renewed interest in higher-dimensional differential geometry. Thus, Struik wrote in a 1922 monograph: “Einstein’s theory of relativity, which had made use of the Ricci Calculus since 1913, has kindled an interest in this method of calculation and in the differential geometry of higher manifolds in broader circles of society and has stimulated new investigations.”¹² As an example he mentions the “geometric meaning of covariant differentiation.”

Similarly, Ludwig Berwald (1883–1942) wrote in his chapter on differential invariants for the Encyklopädie der mathematischen Wissenschaften (Encyclopedia of Mathematical Sciences):

In recent years the interest in Riemannian manifolds has been given new incentive from Einstein’s gravitation theory, a boost that has also resulted in an important principal theoretical advance: the introduction of the concept of parallelism in a [Riemannian manifold] V_n by Levi-Civita.¹³

Einstein had worked out the general theory of relativity in the years prior to its completion in late 1915 in a purely analytic way using only concepts from invariant theory. The transition from a scalar theory of gravitation to a metric one was taken in 1912 and involved the introduction of a metric tensor and a differential line element defined by it. The theory of differential invariants was the main resource for Einstein and his collaborator Marcel Grossmann (1878–1936) when they began developing a relativistic theory of gravitation. In the analytic tradition, the field had been established by Elwin Bruno Christoffel (1829–1900) and others. To be sure, there was an implicit geometric meaning, which was more explicit in Riemann’s work and the tradition based on his work¹⁴ and which came to the fore when the general theory was restricted to binary forms in two variables that could then be interpreted in terms of Gaussian surface coordinates. But Christoffel did not emphasize this geometric implication nor did Einstein and Grossmann make any use of it. Instead, Grossmann explicitly denied the advantage of geometric conceptualization in their endeavor, writing: “I have purposely not employed geometrical aids because, in my opinion, they contribute very little to an intuitive understanding of the conceptions of vector analysis.”¹⁵

When Einstein and Grossmann were searching for field equations of generalized covariance, the geometric intuition of the two-dimensional case may have been distracting from the general case of a four-dimensional space–time with the added complication of a Lorentz signature metric or an imaginary time coordinate. But with the establishment of the general theory, and especially after the publication of Einstein’s gravitational field equations in November 1915, mathematicians and physicists began to explore the geometric implications introduced by the new theory. General Relativity had introduced a curvature in space–time, a consequence that was only by and by extracted from the differential equations.

In the course of this early elaboration of Einstein’s new theory, a conceptual distinction between the metric and the affine connection was introduced.¹⁶ The introduction of the related concept of parallel transport allowed the geometric interpretation of the new theory of space–time in terms of parallel transport of vectors, etc. After the introduction of general relativity, it was Tullio Levi-Civita (1873–1941), Jan Arnoldus Schouten, Gerhard Hessenberg (1874–1925), Hermann Weyl (1885–1955), and others who realized the implications.¹⁷

The Context of the History of Mathematics

The notion of a covariant derivative generalizes the notion of ordinary differentiation for the case when invariance of a differential form was required for arbitrary (smoothly differentiable) transformations of the basic variables. This concept was readily available to Einstein and Grossmann in the so-called absolute differential calculus of Gregorio Ricci-Curbastro and Tullio Levi-Civita.¹⁸ That calculus was designed and presented from the outset for manifolds of an arbitrary number of dimensions.

From the outset, the problem of parallel transport, therefore, was one of interpreting an analytical concept for an arbitrary number of dimensions. It was only when the geometric meaning of the generalized n-dimensional algebraic concept became an object of study that the geometric interpretation for the case of a two-dimensional manifold (a surface) embedded in Euclidean three-dimensional space was reconsidered.

Gauss, indeed, had introduced the notion of the intrinsic curvature of a surface, a notion of curvature that was independent of the specific way the surface was embedded in space. Riemann had begun to generalize this notion of intrinsic curvature from surfaces to n-dimensional spaces.

For spaces with intrinsic curvature, the notion of parallelism needs to be generalized: how can one define a notion of parallelism or equivalently of the transport of a vector such that the transported vectors remain parallel to each other in a curved space, especially if the notion of the parallelism of the embedding space can no longer be drawn upon? The answer is provided by the concept of an affine connection and its associated notion of parallel transport.

The Levi-Civita Connection

Nowadays, we call a Levi-Civita connection the uniquely defined affine connection that is symmetric and compatible with the metric. For most practical purposes, it is the affine connection used routinely in standard applications of general relativity. At the time, however, it was a pioneering concept that established the link between the algebraic formulation of field equations in Einstein’s original formulation with a geometric interpretation.

Let me briefly recapitulate the early history of the notion of an affine connection.¹⁹ Levi-Civita’s notion of affine connection was presented in a paper entitled “Nozione di parallelismo in una varietà qualunque e conseguente specificazione geometrica della curvature Riemanniana” that was published in Rendiconti del Circolo Matematico di Palermo, presented on 24 December 1916.²⁰ In it, Levi-Civita explicitly stated his motivation to further develop what he called the “embryo” of Riemann’s ideas.²¹ In the sequel, Levi-Civita argued very explicitly in geometric language and with the notion of parallelism. The latter concept was established by way of embedding the manifold in a Euclidean reference space, which can always be obtained by increasing the number of dimensions (at most you need n(n + 1)/2 according to a theorem going back to Ludwig Schläfli (1814–1895) if n is the dimension of the original manifold). Nevertheless, in Levi-Civita’s original paper the reference to the embedding space is only for convenience, it is not a conceptual necessity.²²

Another relevant paper that even predates Levi-Civita’s “Nozione” paper, although it was published later, was written by Gerhard Hessenberg and is entitled “Vektorielle Begründung der Differentialgeometrie.” It is dated “June 1916” but apparently was issued only later. This paper of 32 pages begins with a general remark on the relevance of differential forms for relativity theory. It states that the aim of the paper was to establish a “connection between the theory of differential forms and differential geometry.” Hessenberg explicitly refers to Christoffel’s 1869 paper and to the 1901 paper by Ricci and Levi-Civita. He further mentioned work by Knoblauch, Maschke, Wright, Gauss, Riemann, Grassmann, Pfaff, and Beltrami.

Although Hessenberg wants to give a geometric formulation, the word ‘parallel’ does not appear in the paper. Instead, his program is captured by the following quote:

The path we shall follow will lead us to Christoffel’s three index expressions via the equations (12) and (13) [i.e. the vanishing of the covariant derivative of the metric and the symmetry of the Christoffel symbols]. It will become clear that for the invariant relations that we will get, also for the curvature tensor, only the equations (12) are relevant, while the Christoffel symmetry (13) can be discarded. Their meaning can be summarized by saying that in the geometry of an n-dimensional manifold the ‘straightest’ lines are also the ‘shortest.’²³

Let us now look at Schouten’s work. His so-called “direct analysis” aimed at giving a formulation of geometric quantities that was explicitly independent of coordinates and already in its form displayed the relevant geometric characteristics. Schouten’s 1918 paper, in this sense, extended earlier work of his from 1914 which had been motivated by the wish to look at geometric quantities from an engineer’s point of view.²⁴

Schouten’s notion of a geodesically transported frame was constituted in a technically elaborate way, a detailed discussion that would go beyond the framework of this paper. Schouten relied on a so-called ‘symbolic method’ which was widely used in invariant theory at the time and which allowed an algebraic handling of invariance and transformation properties. The method introduced so-called ideal vectors, which do not have a simple interpretation from a modern understanding, for the representation of the metric tensor and other invariant objects. In more modern terms, the basic presuppositions here were a manifold with a differentiability structure and a metric field defined on it that allows the intrinsic determination of distances within the manifold. It therefore also allowed the definition of the notion of shortest lines, i.e. lines between two points A and B along which the integrated distance is minimal. Schouten then looked at infinitesimally small rigid frames, i.e. linearly independent, small vectors at each point of the manifold. Since a notion of parallel transport was not available, a clear distinction between the manifold and its tangent space in a point was only emerging and was not made explicit. Geodesic transport of frames was then defined in terms of ideal vectors which were introduced in such a way that the resulting relations did not depend on them explicitly.

Schouten then developed the notion of parallel transport by arguing that one needs a geodesically co-moving coordinate system that follows a geodesic line and at each point of the geodesic line is uniquely determined in its orientation. At this point, he illustrated this idea with the above-mentioned models of surfaces of positive and negative curvature. The illustration consists, on the one hand, in drawing frames of reference onto the curved surfaces, i.e. by depicting the moving frames in this curved two-dimensional manifold directly as a pair of orthogonal vectors in the local tangent spaces. For the case of the sphere, he also showed a piece of paper that can be laid out, without tearing or wrinkling, onto the sphere along the connecting line (not the geodesic) where we follow the rigid frame. The picture thus illustrated the ability to develop the notion of geodesic transport.²⁵ Schouten also created two examples of parallel transport on surfaces with negative curvature (Fig. 2): he painted geodesically moving frames onto models of a hyperbolic paraboloid and on a model of a pseudosphere, i.e. a rotated tractrix. Together with the illustration of the geodesic transport on the spherical surface (Fig. 1), these models seem to be the first visual illustration of the concept of parallel transport, i.e. a two-dimensional illustration of a vector parallel transported along a path in a two-dimensional curved space. If the transport is done along a closed loop, e.g. along a closing parallelogram, the difference between the initial and the final orientation of the frame is a measure of the integrated curvature of the enclosed area. Such a loop is nowadays often referred to as a Levi-Civita parallelogram.

Before continuing with our story, we should mention also Hermann Weyl’s concept of infinitesimal geometry. His work was published together with the first edition of his highly influential book entitled Space-Time-Matter, the preface of which was dated “Easter, 1918.” In this preface Weyl wrote that he could make use of Levi-Civita’s paper, but that Hessenberg’s paper had appeared only just before his book was going to press. Weyl clearly formulated the problem in terms of his philosophy of a “pure near geometry” (“reine Nahegeometrie”). Perhaps more importantly, Weyl realized very clearly in this context that the affine connection is an independent concept that can be defined without recourse or reference to the notion of a metric. Schouten listed and discussed Hessenberg’s paper, and he also refers to Levi-Civita’s work. However, it appears that Schouten’s creation of the notion of geodesic transport was an independent discovery. In fact, Dirk Struik, who was a collaborator of Schouten at the time, later reminisced:

Schouten and Levi-Civita had thus obtained the same result, but there were differences in the way each of them introduced parallelism. Schouten’s method was entirely intrinsic, whereas that of Levi-Civita utilized a surface embedded in space. He also had derived his result only for the case n = 2, although it was clear that it was intrinsic and valid for all values of n. The main difference, however, insofar as influence was concerned, was that Levi-Civita’s text was elegant and employed his absolute differential calculus (the tensor calculus with which mathematicians all over the world were becoming familiar) whereas Schouten’s work was difficult to read due to its unfamiliar notation. And, of course, Levi-Civita also had priority of publication, so that the discovery has since become known as the ‘parallelism of Levi-Civita.’²⁶

As to the question of priority, Struik remarked:

Schouten published this work in 1918. Although he translated some of his formulas into the language of the Ricci-Einstein tensor calculus, his theory was so overloaded with symbols that it proved next to impossible to follow. Direct analysis is fine for vectors, when only two multiplications · and x are involved, but for higher systems one gets lost in the maze of the dots, hooks, and crosses necessary to perform the various multiplications.

Despite all this, Schouten had succeeded in giving a geometrical interpretation of the covariant derivative, an important accomplishment. Circumstances conspired against him, however, preventing him from being credited with a major mathematical achievement. It was nearing the climax of the war, so that communications with Italy were most difficult.

Thus Schouten was totally unaware of Levi-Civita’s work. I still remember how Schouten came running into my office one day waving a reprint he had just received of Levi-Civita’s paper. ‘He has it, too!’ he cried out.²⁷

Struik’s recollection many years later may be subject to the skepticism that all such reminiscences should evoke. But we do have contemporary evidence to back up some of Struik’s claims. Schouten refers to Levi-Civita’s “Nozione” paper in his 1918 article. In a footnote, he wrote:

T. Levi-Civita conceived of the concept of parallelism in a general space already in 1917 in a work of which I only received an offprint by friendly mediation after finalizing this manuscript due to the political circumstances. The geodesically comoving frame successively takes on positions, which are parallel in the sense of Levi-Civita, and the notion of geodesic motion therefore is contained in the notion of parallelism. The relationship between the covariant differential and the geodesically co-moving frame, and the fundamental importance, which the motion of such a system carries for the geometric properties of space [...] Levi-Civita, however, has not yet been made aware of.²⁸

A Mechanical Model of Parallel Transport

It is interesting to note that Schouten, perhaps due to his engineering background, also thought about other ways of illustrating his concept of geodesic transport. In a footnote to his 1918 paper, he wrote:

For surfaces the geodesically transported frame can sometimes be realized by a three-dimensional mechanism. A Foucault pendulum which travels around any line of constant latitude along the earth thought to be at rest and perfectly spherical, will always remain oriented with respect to the geodesically co-moving coordinate system, and the same will hold when the pendulum runs along any arbitrary curve on the surface. We can also construct a two-wheeled mechanism by means of a differential wheel, which rolled over the surface will show at each point the geodesically co-moving system.²⁹

Schouten’s reference to the Foucault pendulum references a discussion about realizing what he called a Kompaszkörper, i.e. a rigid solid whose motion realizes the geodesic transport of a frame. The question whether an extended rigid solid has enough degrees of freedom to realize geodesic motion in an arbitrary curved manifold was clarified in discussion with Adriaan D. Fokker (1887–1972). The problem is whether different points of a rigid frame can each follow the geodesic trajectories of curved space while at the same time preserving their mutual distances, a more detailed discussion of this problem by Fokker³⁰ was communicated to the Amsterdam Academy a year later. The problem was still relevant for the well-known Gravity Probe B experiment of the early twenty-first century.³¹

In our context, the other reference is equally interesting. Schouten did not explicate his idea any further than this, but it seems clear that what he refers to is the same as what was and is known as a south-pointing chariot.³² Such a mechanical device is said to have been known already in ancient China and to have been built in that period, although the documentary evidence is thin. Later reconstructions and rebuilds nevertheless abound. Figure 6 shows a picture of a reconstruction of such a device that was erected in front of the National Museum in Taipeh. Figure 7 shows a model built using Fischer-Technik and was designed by Thomas Püttmann.

Fig. 6

Model of a south-pointing chariot in front of the National Museum in Taipeh. From Dierck-E. Liebscher, “Mit dem Kompasswagen über den Globus,” Der mathematisch-naturwissenschaftliche Unterricht 52 (1999): 140–144, Fig. 4. All rights reserved

Fig. 7

Model of a south-pointing chariot realized with Fischer-Technik according to a design by Thomas Püttmann. © Photo: Tilman Sauer, all rights reserved

The idea is to create a mechanism that is devised in such a way that on a plane surface any difference in path length between the left and the right wheels is compensated by a differential gear mechanism such that a flag or pointer connected to the mechanism will always point in the same direction, even if the carriage is pushed along curved paths. Naturally, the device works on curved surfaces as well and will then indicate the path difference between the two wheels on the curved ground. Pushing the carriage along a closed loop, i.e. along a Levi-Civita loop, the difference between the initial and final position of the pointer will not in general coincide and will instead be a measure of the local curvature integrated over the loop.

It is unclear whether Schouten had anything like this in mind when he added his footnote about the mechanical device, but it appears quite possible, if not likely given his intellectual background as an engineer.

Later History

It seems a notable fact that the very same photographic images of Schouten’s models for geodesic frame transport were reproduced three more times between 1921 and 1924 after the initial publication in 1918. I have not seen later instances of reproduction. In fact, I have not come across later instances of material models of curved surfaces for the purpose of illustrating the notion of parallel transport of vectors. But I cannot claim that such material models do not exist.

Graphical representations of parallel transport of vectors or connections of tangent spaces to two-dimensional surfaces embedded in three-dimensional space, however, have become rather common, both in textbooks on general relativity as on differential geometry, although they by no means accompany each and every analytical discussion.

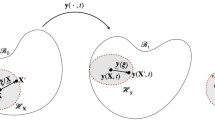
As an example of such common illustrations of parallel transport, Fig. 8 illustrates the definition of the covariant derivative of a vector field v along a curve P(λ) in an abstract sense. Figure 9 then illustrates the notion of connection coefficients by geodesic transport of two-dimensional frames over a spherical surface.

Fig. 8

Graphical Representation of the covariant derivative of a vector field along a curve. From Charles W. Misner, Kip S. Thorne, and John A. Wheeler, Gravitation (New York: Freeman, 1973), 209, Fig. 8.2. © Freeman, all rights reserved

Fig. 9

Graphical Representation of geodesic transport of a frame over a curved spherical surface. From Charles W. Misner, Kip S. Thorne, and John A. Wheeler, Gravitation (New York: Freeman, 1973), Fig. 8.3. © Freeman, all rights reserved

These illustrations appear in the widely used, highly influential textbook on relativity and gravitation published by Charles W. Misner, Kip S. Thorne, and John A. Wheeler in 1973, a textbook that became a standard source of reference for generations of physicists for many reasons, one of them being its emphasis on physical intuition and visual illustration. In fact, the authors quite explicitly reflected on the necessity of what they called a “pictorial treatment” of geometry: “Gain the power […] to discuss tangent vectors, 1-forms, tensors in curved spacetime; gain the power […] to parallel-transport vectors, to differentiate them, to discuss geodesics; use this power […] to discuss geodesic deviation, to define curvature, […] But full power this will be only if it can be exercised in three ways: in pictures, in abstract notation, and in component notation.”³³

Another example of how Schouten’s illustrative model of parallel transport has found its way onto modern textbooks is shown in Fig. 10, taken from V.I. Arnold’s, Mathematical Methods of Classical Mechanics.³⁴ Although the vector that is being parallel-transported here points off the surface, the illustration almost looks like a graphical representation of Schouten’s original model.

Fig. 10

Graphical representation of parallel transport on the sphere as shown in Vladimir I. Arnold, Mathematical Methods of Classical Mechanics (New York: Springer, 1989), 302, Fig. 231. © Springer, all rights reserved

Concluding Remarks

The transitional nature of Schouten’s model of parallel transport is indicative of the primacy of the ideal in mathematics. Parallel transport, even though it can be regarded as a genuine geometric concept, is defined and represented exclusively in analytic terms for an arbitrary number of dimensions. Geometric intuition is derived from finite objects and their properties in three-dimensional Euclidean space. Our intuition for higher dimensions, curvature, or extensions to infinity, even though genuinely geometrical, must be assisted by and eventually based on other means. Schouten’s model for geodesic transport was mostly and from the beginning merely illustrative. It built on a well-established tradition of models that were used for teaching. Yet it was illustrative for a conceptual problem that was at the time still in the process of being explored and discovered. It investigated a notion that is inherently n-dimensional and associated with curvature, and it helps our understanding of the abstract concept by providing an interpretation of the special and intuitive case of a curved two-dimensional surface embedded in three-dimensional Euclidean space. His mechanical devices, like the Foucault pendulum or the south-pointing chariot are also illustrative but in a different sense. Their physical properties help us understand the necessary implications of the abstract concept and may indeed have played an important role in Schouten’s heuristics of concept development.