Abstract
We first define the real matrix-variate gamma function, the gamma integral and the gamma density, wherefrom their counterparts in the complex domain are developed. An important particular case of the real matrix-variate gamma density known as the Wishart density is widely utilized in multivariate statistical analysis. Additionally, real and complex matrix-variate type-1 and type-2 beta density functions are defined. Various results pertaining to each of these distributions are then provided. More general structures are considered as well.
You have full access to this open access chapter, Download chapter PDF
Similar content being viewed by others
5.1. Introduction
The notations introduced in the preceding chapters will still be followed in this one. Lower-case letters such as x, y will be utilized to represent real scalar variables, whether mathematical or random. Capital letters such as X, Y will be used to denote vector/matrix random or mathematical variables. A tilde placed on top of a letter will indicate that the variables are in the complex domain. However, the tilde will be omitted in the case of constant matrices such as A, B. The determinant of a square matrix A will be denoted as |A| or det(A) and, in the complex domain, the absolute value or modulus of the determinant of B will be denoted as |det(B)|. Square matrices appearing in this chapter will be assumed to be of dimension p × p unless otherwise specified.
We will first define the real matrix-variate gamma function, gamma integral and gamma density, wherefrom their counterparts in the complex domain will be developed. A particular case of the real matrix-variate gamma density known as the Wishart density is widely utilized in multivariate statistical analysis. Actually, the formulation of this distribution in 1928 constituted a significant advance in the early days of the discipline. A real matrix-variate gamma function, denoted by Γ p(α), will be defined in terms of a matrix-variate integral over a real positive definite matrix X > O. This integral representation of Γ p(α) will be explicitly evaluated with the help of the transformation of a real positive definite matrix in terms of a lower triangular matrix having positive diagonal elements in the form X = TT ′ where T = (t ij) is a lower triangular matrix with positive diagonal elements, that is, t ij = 0, i < j and t jj > 0, j = 1, …, p. When the diagonal elements are positive, it can be shown that the transformation X = TT ′ is unique. Its associated Jacobian is provided in Theorem 1.6.7. This result is now restated for ready reference: For a p × p real positive definite matrix X = (x ij) > O,
where T = (t ij), t ij = 0, i < j and t jj > 0, j = 1, …, p. Consider the following integral representation of Γ p(α) where the integral is over a real positive definite matrix X and the integrand is a real-valued scalar function of X:
Under the transformation in (5.1.1),
Observe that tr(X) = tr(TT′) = the sum of the squares of all the elements in T, which is \(\sum _{j=1}^pt_{jj}^2+\sum _{i>j}t_{ij}^2\). By letting \(t_{jj}^2=y_j\Rightarrow \text{d}t_{jj}=\frac {1}{2}y_j^{\frac {1}{2}-1}\text{d}y_j\), noting that t jj > 0, the integral over t jj gives
the final condition being \(\Re (\alpha )>\frac {p-1}{2}\). Thus, we have the gamma product \(\varGamma (\alpha )\varGamma (\alpha -\frac {1}{2})\cdots \varGamma (\alpha -\frac {p-1}{2})\). Now for i > j, the integral over t ij gives
Therefore
For example,
This Γ p(α) is known by different names in the literature. The first author calls it the real matrix-variate gamma function because of its association with a real matrix-variate gamma integral.
5.1a. The Complex Matrix-variate Gamma
In the complex case, consider a p × p Hermitian positive definite matrix \(\tilde {X}=\tilde {X}^{*}>O\), where \(\tilde {X}^{*}\) denotes the conjugate transpose of \(\tilde {X}\). Let \(\tilde {T}=(\tilde {t}_{ij})\) be a lower triangular matrix with the diagonal elements being real and positive. In this case, it can be shown that the transformation \(\tilde {X}=\tilde {T}\tilde {T}^{*}\) is one-to-one. Then, as stated in Theorem 1.6a.7, the Jacobian is
With the help of (5.1a.1), we can evaluate the following integral over p × p Hermitian positive definite matrices where the integrand is a real-valued scalar function of \(\tilde {X}\). We will denote the integral by \(\tilde {\varGamma }_p(\alpha )\), that is,
Let us evaluate the integral in (5.1a.2) by making use of (5.1a.1). Parallel to the real case, we have
As well,
Since t jj is real and positive, the integral over t jj gives the following:
the final condition being \(\Re (\alpha )>p-1\). Note that the absolute value of \(\tilde {t}_{ij}\), namely, \(|\tilde {t}_{ij}|\) is such that \(|\tilde {t}_{ij}|{ }^2=t_{ij1}^2+t_{ij2}^2\) where \(\tilde {t}_{ij}=t_{ij1}+it_{ij2}\) with t ij1, t ij2 real and \(i=\sqrt {(-1)}\). Thus,
Then
We will refer to \(\tilde {\varGamma }_p(\alpha )\) as the complex matrix-variate gamma because of its association with a complex matrix-variate gamma integral. As an example, consider
5.2. The Real Matrix-variate Gamma Density
In view of (5.1.3), we can define a real matrix-variate gamma density with shape parameter α as follows, where X is p × p real positive definite matrix:
Example 5.2.1
Let

where x 11, x 12, x 22, x 1, x 2, y 2, x 3 are all real scalar variables, \(i=\sqrt {(-1)}\), \(x_{22}>0,~ x_{11}x_{22}-x_{12}^2>0\). While these are the conditions for the positive definiteness of the real matrix X, \(x_1>0,~x_3>0,~ x_1x_3-(x_2^2+y_2^2)>0\) are the conditions for the Hermitian positive definiteness of \(\tilde {X}\). Let us evaluate the following integrals, subject to the previously specified conditions on the elements of the matrix:
Solution 5.2.1
(1): Observe that δ 1 can be evaluated by treating the integral as a real matrix-variate integral, namely,
and hence the integral is
This result can also be obtained by direct integration as a multiple integral. In this case, the integration has to be done under the conditions \(x_{11}>0,~x_{22}>0,~ x_{11}x_{22}-x_{12}^2>0\), that is, \(x_{12}^2<x_{11}x_{22}\) or \(-\sqrt {x_{11}x_{22}}<x_{12}<\sqrt {x_{11}x_{22}}\). The integral over x 12 yields \(\int _{-\sqrt {x_{11}x_{22}}}^{\sqrt {x_{11}x_{22}}}\text{d}x_{12}=2\sqrt {x_{11}x_{22}}\), that over x 11 then gives
and on integrating with respect to x 22, we have
so that \(\delta _1=\frac {1}{2}\sqrt {\pi }\sqrt {\pi }=\frac {\pi }{2}\).
(2): On observing that δ 2 can be viewed as a complex matrix-variate integral, it is seen that
This answer can also be obtained by evaluating the multiple integral. Since \(\tilde {X}>O\), we have \(x_1>0,~x_3>0,~ x_1x_3-(x_2^2+y_2^2)>0\), that is, \(x_1>\frac {(x_2^2+y_2^2)}{x_3}\). Integrating first with respect to x 1 and letting \(y=x_1-\frac {(x_2^2+y_2^2)}{x_3}\), we have
Now, the integrals over x 2 and y 2 give
that with respect to x 3 then yielding
so that \(\delta _2=(1)\sqrt {\pi }\sqrt {\pi }=\pi .\)
(3): Observe that δ 3 can be evaluated as a real matrix-variate integral. Then
Let us proceed by direct integration:
letting \(y=x_{11}-\frac {x_{12}^2}{x_{22}}\), the integral over x 11 yields
Now, the integral over x 12 gives \(\sqrt {x_{22}}\sqrt {\pi }\) and finally, that over x 22 yields
(4): Noting that we can treat δ 4 as a complex matrix-variate integral, we have
Direct evaluation will be challenging in this case as the integrand involves \(|\text{det}(\tilde {X})|{ }^2\).
If a scale parameter matrix B > O is to be introduced in (5.2.1), then consider \(\text{tr}(BX)=\text{tr}(B^{\frac {1}{2}}XB^{\frac {1}{2}})\) where \(B^{\frac {1}{2}}\) is the positive definite square root of the real positive definite constant matrix B. On applying the transformation \(Y=B^{\frac {1}{2}}XB^{\frac {1}{2}}\Rightarrow \text{d}X=|B|{ }^{-\frac {(p+1)}{2}}\text{d}Y\), as stated in Theorem 1.6.5, we have
This equality brings about two results. First, the following identity which will turn out to be very handy in many of the computations:
As well, the following two-parameter real matrix-variate gamma density with shape parameter α and scale parameter matrix B > O can be constructed from (5.2.2):
5.2.1. The mgf of the real matrix-variate gamma distribution
Let us determine the mgf associated with the density given in (5.2.4), that is, the two-parameter real matrix-variate gamma density. Observing that X = X ′, let T be a symmetric p × p real positive definite parameter matrix. Then, noting that
it is seen that the non-diagonal elements in X multiplied by the corresponding parameters will have twice the weight of the diagonal elements multiplied by the corresponding parameters. For instance, consider the 2 × 2 case:

where α 1 and α 2 represent elements that are not involved in the evaluation of the trace. Note that due to the symmetry of T and X, t 21 = t 12 and x 21 = x 12, so that the cross product term t 12 x 12 in (ii) appears twice whereas each of the terms t 11 x 11 and t 22 x 22 appear only once.
However, in order to be consistent with the mgf in a real multivariate case, each variable need only be multiplied once by the corresponding parameter, the mgf being then obtained by taking the expected value of the resulting exponential sum. Accordingly, the parameter matrix has to be modified as follows: let ∗ T = (∗ t ij) where \({{ }_{*}t_{jj}}=t_{jj},~ {{ }_{*}t_{ij}}=\frac {1}{2}t_{ij},~ i\ne j,\) and t ij = t ji for all i and j or, in other words, the non-diagonal elements of the symmetric matrix T are weighted by \(\frac {1}{2}\), such a matrix being denoted as ∗ T. Then,
and the mgf in the real matrix-variate two-parameter gamma density, denoted by M X(∗ T), is the following:
Now, since
for (B −∗ T) > O, that is, \(~ (B-{{ }_{*}T})^{\frac {1}{2}}>O,\) which means that \(Y=(B-{{ }_{*}T})^{\frac {1}{2}}X(B-{{ }_{*}T})^{\frac {1}{2}}\Rightarrow \text{ d}X=|B-{{ }_{*}T})|{ }^{-(\frac {p+1}{2})}\text{d}Y\), we have
When ∗ T is replaced by −∗ T, (5.2.5) gives the Laplace transform of the two-parameter gamma density in the real matrix-variate case as specified by (5.2.4), which is denoted by L f(∗ T), that is,
For example, if

then |B| = 5 and

If ∗ T is partitioned into sub-matrices and X is partitioned accordingly as

where ∗ T 11 and X 11 are r × r, r ≤ p, then what can be said about the densities of the diagonal blocks X 11 and X 22? The mgf of X 11 is available from the definition by letting ∗ T 12 = O,∗ T 21 = O and ∗ T 22 = O, as then \(E[\text{e}^{\text{tr}({{ }_{*}T}X)}]=E[\text{ e}^{\text{tr}({{ }_{*}T}_{11}X_{11})}].\) However, B −1 ∗ T is not positive definite since B −1 ∗ T is not symmetric, and thereby I − B −1 ∗ T cannot be positive definite when ∗ T 12 = O,∗ T 21 = O,∗ T 22 = O. Consequently, the mgf of X 11 cannot be determined from (5.2.6). As an alternative, we could rewrite (5.2.6) in the symmetric format and then try to evaluate the density of X 11. As it turns out, the densities of X 11 and X 22 can be readily obtained from the mgf in two situations: either when B = I or B is a block diagonal matrix, that is,

Hence we have the following results:
Theorem 5.2.1
Let the p × p matrices X > O and ∗ T > O be partitioned as in (iii). Let X have a p × p real matrix-variate gamma density with shape parameter α and scale parameter matrix I p . Then X 11 has an r × r real matrix-variate gamma density and X 22 has a (p − r) × (p − r) real matrix-variate gamma density with shape parameter α and scale parameters I r and I p−r, respectively.
Theorem 5.2.2
Let X be partitioned as in (iii). Let the p × p real positive definite parameter matrix B > O be partitioned as in (iv). Then X 11 has an r × r real matrix-variate gamma density with the parameters (α and B 11 > O) and X 22 has a (p − r) × (p − r) real matrix-variate gamma density with the parameters (α and B 22 > O).
Theorem 5.2.3
Let X be partitioned as in (iii). Then X 11 and X 22 are statistically independently distributed under the restrictions specified in Theorems 5.2.1 and 5.2.2.
In the general case of B, write the mgf as M
X(∗
T) = |B|α|B −∗
T|−α, which corresponds to a symmetric format. Then, when  ,
,

which is obtained by making use of the representations of the determinant of a partitioned matrix, which are available from Sect. 1.3. Now, on comparing the last line with the first one, it is seen that X 11 has a real matrix-variate gamma distribution with shape parameter α and scale parameter matrix \(B_{11}-B_{12}B_{22}^{-1}B_{21}\). Hence, the following result:
Theorem 5.2.4
If the p × p real positive definite matrix has a real matrix-variate gamma density with the shape parameter α and scale parameter matrix B and if X and B are partitioned as in (iii), then X 11 has a real matrix-variate gamma density with shape parameter α and scale parameter matrix \(B_{11}-B_{12}B_{22}^{-1}B_{21}\) , and the sub-matrix X 22 has a real matrix-variate gamma density with shape parameter α and scale parameter matrix \(B_{22}-B_{21}B_{11}^{-1}B_{12}\).
5.2a. The Matrix-variate Gamma Function and Density, Complex Case
Let \(\tilde {X}=\tilde {X}^{*}>O\) be a p × p Hermitian positive definite matrix. When \(\tilde {X}\) is Hermitian, all its diagonal elements are real and hence \(\text{ tr}(\tilde {X})\) is real. Let \(\text{det}(\tilde {X})\) denote the determinant and \(|\text{det}(\tilde {X})|\) denote the absolute value of the determinant of \(\tilde {X}\). As a result, \(|\text{det}(\tilde {X})|{ }^{\alpha -p}\,\text{e}^{-\text{tr}(\tilde {X})}\) is a real-valued scalar function of \(\tilde {X}\). Let us consider the following integral, denoted by \(\tilde {\varGamma }_p(\alpha )\):
which was evaluated in Sect. 5.1a. In fact, (5.1a.3) provides two representations of the complex matrix-variate gamma function \(\tilde {\varGamma }_p(\alpha )\). With the help of (5.1a.3), we can define the complex p × p matrix-variate gamma density as follows:
For example, let us examine the 2 × 2 complex matrix-variate case. Let \(\tilde {X}\) be a matrix in the complex domain, \(\bar {\tilde {X}}\) denoting its complex conjugate and \(\tilde {X}^{*},\) its conjugate transpose. When \(\tilde {X}=\tilde {X}^{*},\) the matrix is Hermitian and its diagonal elements are real. In the 2 × 2 Hermitian case, let

Then, the determinants are
due to Hermitian positive definiteness of \(\tilde {X}\). As well,
Note that \(\text{tr}(\tilde {X})=x_1+x_3\) and \(\tilde {\varGamma }_2(\alpha )=\pi ^{\frac {2(1)}{2}}\varGamma (\alpha )\varGamma (\alpha -1),~ \Re (\alpha )>1,~ p=2\). The density is then of the following form:
for \(x_1>0,~x_3>0,~ x_1x_3-(x_2^2+y_2^2)>0,~ \Re (\alpha )>1\), and \(f_1(\tilde {X})=0\) elsewhere.
Now, consider a p × p parameter matrix \(\tilde {B}>O\). We can obtain the following identity corresponding to the identity in the real case:
A two-parameter gamma density in the complex domain can then be derived by proceeding as in the real case; it is given by
5.2a.1. The mgf of the complex matrix-variate gamma distribution
The moment generating function in the complex domain is slightly different from that in the real case. Let \(\tilde {T}>O\) be a p × p parameter matrix and let \(\tilde {X}\) be p × p two-parameter gamma distributed as in (5.2a.4). Then \(\tilde {T}=T_1+iT_2\) and \(\tilde {X}=X_1+iX_2\), with T 1, T 2, X 1, X 2 real and \(i=\sqrt {(-1)}\). When \(\tilde {T}\) and \(\tilde {X}\) are Hermitian positive definite, T 1 and X 1 are real symmetric and T 2 and X 2 are real skew symmetric. Then consider
Note that tr(T 1 X 1) + tr(T 2 X 2) contains all the real variables involved multiplied by the corresponding parameters, where the diagonal elements appear once and the off-diagonal elements each appear twice. Thus, as in the real case, \(\tilde {T}\) has to be replaced by \({{ }_{*}\tilde {T}}={{ }_{*}T}_1+i{{ }_{*}T}_2\). A term containing i still remains; however, as a result of the following properties, this term will disappear.
Lemma 5.2a.1
Let \(\tilde {T},~ \tilde {X},~ T_1,~T_2,~X_1,~X_2\) be as defined above. Then, tr(T 1 X 2) = 0, tr(T 2 X 1) = 0, tr(∗ T 1 X 2) = 0, tr(∗ T 2 X 1) = 0.
Proof
For any real square matrix A, tr(A) = tr(A′) and for any two matrices A and B where AB and BA are defined, tr(AB) = tr(BA). With the help of these two results, we have the following:
as T 1 is symmetric and X 2 is skew symmetric. Now, tr(T 1 X 2) = −tr(T 1 X 2) ⇒tr(T 1 X 2) = 0 since it is a real quantity. It can be similarly established that the other results stated in the lemma hold.
We may now define the mgf in the complex case, denoted by \(M_{\tilde {X}}({ }_{*}T)\), as follows:
Since \(\text{tr}(\tilde {X}(\tilde {B}-{{ }_{*}\tilde {T}}^{*}))=\text{ tr}(C\tilde {X}C^{*})\) for \(C=(\tilde {B}-{{ }_{*}\tilde {T}}^{*})^{\frac {1}{2}}\) and C > O, it follows from Theorem 1:6a.5 that \(\tilde {Y}=C\tilde {X}C^{*} \Rightarrow \text{d}\tilde {Y}=|\text{det}(CC^{*})|{ }^{p}\,\text{d}\tilde {X}\), that is, \(\text{d}\tilde {X}=|\text{det}(\tilde {B}-{{ }_{*}\tilde {T}}^{*})|{ }^{-p}\text{ d}\tilde {Y}\) for \(\tilde {B}-{{ }_{*}\tilde {T}}^{*}>O\). Then,
For example, let p = 2 and

with \(\tilde {x}_{21}=\tilde {x}_{12}^{*}\) and \( {{{ }_{*}\tilde t}}_{21}={{{ }_{*}\tilde t}}_{12}^{\,*}\). In this case, the conjugate transpose is only the conjugate since the quantities are scalar. Note that B = B ∗ and hence B is Hermitian. The leading minors of B being |(3)| = 3 > 0 and |B| = (3)(2) − (−i)(i) = 5 > 0, B is Hermitian positive definite. Accordingly,
Now, consider the partitioning of the following p × p matrices:

where \(\tilde {X}_{11}\) and \({{ }_{*}\tilde {T}}_{11}\) are r × r, r ≤ p. Then, proceeding as in the real case, we have the following results:
Theorem 5.2a.1
Let \(\tilde {X}\) have a p × p complex matrix-variate gamma density with shape parameter α and scale parameter I p , and \(\tilde {X}\) be partitioned as in (i). Then, \(\tilde {X}_{11}\) has an r × r complex matrix-variate gamma density with shape parameter α and scale parameter I r and \(\tilde {X}_{22}\) has a (p − r) × (p − r) complex matrix-variate gamma density with shape parameter α and scale parameter I p−r.
Theorem 5.2a.2
Let the p × p complex matrix \(\tilde {X}\) have a p × p complex matrix-variate gamma density with the parameters ( \(\alpha ,\tilde {B}>O)\) and let \(\tilde {X}\) and \(\tilde {B}\) be partitioned as in (i) and \(\tilde {B}_{12}=O,~\tilde {B}_{21}=O\) . Then \(\tilde {X}_{11}\) and \(\tilde {X}_{22}\) have r × r and (p − r) × (p − r) complex matrix-variate gamma densities with shape parameter α and scale parameters \(\tilde {B}_{11}\) and \(\tilde {B}_{22},\) respectively.
Theorem 5.2a.3
Let \(\tilde {X},\ \tilde {X}_{11},\ \tilde {X}_{22}\) and \(\tilde {B}\) be as specified in Theorems 5.2a.1 or 5.2a.2 . Then, \(\tilde {X}_{11}\) and \(\tilde {X}_{22}\) are statistically independently distributed as complex matrix-variate gamma random variables on r × r and (p − r) × (p − r) matrices, respectively.
For a general matrix B where the sub-matrices B 12 and B 21 are not assumed to be null, the marginal densities of \(\tilde {X}_{11}\) and \(\tilde {X}_{22}\) being given in the next result can be determined by proceeding as in the real case.
Theorem 5.2a.4
Let \(\tilde {X}\) have a complex matrix-variate gamma density with shape parameter α and scale parameter matrix B = B ∗ > O. Letting \(\tilde {X}\) and B be partitioned as in (i), then the sub-matrix \(\tilde {X}_{11}\) has a complex matrix-variate gamma density with shape parameter α and scale parameter matrix \(B_{11}-B_{12}B_{22}^{-1}B_{21}\) , and the sub-matrix \(\tilde {X}_{22}\) has a complex matrix-variate gamma density with shape parameter α and scale parameter matrix \(B_{22}-B_{21}B_{11}^{-1}B_{12}\).
Exercises 5.2
5.2.1
Show that
5.2.2
Show that \(\varGamma _r(\alpha )\varGamma _{p-r}(\alpha -\frac {r}{2})=\varGamma _p(\alpha ).\)
5.2.3
Evaluate (1): ∫X>Oe−tr(X)dX, (2): ∫X>O|X| e−tr(X)dX.
5.2.4
Write down (1): Γ 3(α), (2): Γ 4(α) explicitly in the real and complex cases.
5.2.5
Evaluate the integrals in Exercise 5.2.3 for the complex case. In (2) replace det(X) by |det(X)|.
5.3. Matrix-variate Type-1 Beta and Type-2 Beta Densities, Real Case
The p × p matrix-variate beta function denoted by B p(α, β) is defined as follows in the real case:
This function has the following integral representations in the real case where it is assumed that \(\Re (\alpha )>\frac {p-1}{2}\) and \(\Re (\beta )>\frac {p-1}{2}\):
For example, for p = 2, let

Then for example, (5.3.2) will be of the following form:
We will derive two of the integrals (5.3.2)–(5.3.5), the other ones being then directly obtained. Let us begin with the integral representations of Γ p(α) and Γ p(β) for \(\Re (\alpha )>\frac {p-1}{2},~\Re (\beta )>\frac {p-1}{2}\):
Making the transformation U = X + Y, X = V , whose Jacobian is 1, taking out U from \(|U-V|=|U|~|I-U^{-\frac {1}{2}}VU^{-\frac {1}{2}}|\), and then letting \(W= U^{-\frac {1}{2}}VU^{-\frac {1}{2}}\Rightarrow \text{d}V=|U|{ }^{\frac {p+1}{2}}\text{d}W\), we have
Thus, on dividing both sides by Γ p(α, β), we have
This establishes (5.3.2). The initial conditions \(\Re (\alpha )>\frac {p-1}{2},~\Re (\beta )>\frac {p-1}{2}\) are sufficient to justify all the steps above, and hence no conditions are listed at each stage. Now, take Y = I − W to obtain (5.3.3). Let us take the W of (i) above and consider the transformation
which gives
Taking determinants and substituting in (ii) we have
On expressing W, I − W and dW in terms of Z, we have the result (5.3.4). Now, let T = Z −1 with the Jacobian dT = |Z|−(p+1)dZ, then (5.3.4) transforms into the integral (5.3.5). These establish all four integral representations of the real matrix-variate beta function. We may also observe that B p(α, β) = B p(β, α) or α and β can be interchanged in the beta function. Consider the function
for \(O<X<I,~\Re (\alpha )>\frac {p-1}{2},~\Re (\beta )>\frac {p-1}{2}\), and f 3(X) = 0 elsewhere. This is a type-1 real matrix-variate beta density with the parameters (α, β), where O < X < I means X > O, I − X > O so that all the eigenvalues of X are in the open interval (0, 1). As for
whenever \(Z>O,~ \Re (\alpha )>\frac {p-1}{2},~\Re (\beta )>\frac {p-1}{2}\), and f 4(Z) = 0 elsewhere, this is a p × p real matrix-variate type-2 beta density with the parameters (α, β).
5.3.1. Some properties of real matrix-variate type-1 and type-2 beta densities
In the course of the above derivations, it was shown that the following results hold. If X is a p × p real positive definite matrix having a real matrix-variate type-1 beta density with the parameters (α, β), then: (1): Y 1 = I − X is real type-1 beta distributed with the parameters (β, α); (2): \(Y_2=(I-X)^{-\frac {1}{2}}X(I-X)^{-\frac {1}{2}}\) is real type-2 beta distributed with the parameters (α, β); (3): \(Y_3=(I-X)^{\frac {1}{2}}X^{-1}(I-X)^{\frac {1}{2}}\) is real type-2 beta distributed with the parameters (β, α). If Y is real type-2 beta distributed with the parameters (α, β) then: (4): Z 1 = Y −1 is real type-2 beta distributed with the parameters (β, α); (5): \(Z_2=(I+Y)^{-\frac {1}{2}}Y(I+Y)^{-\frac {1}{2}}\) is real type-1 beta distributed with the parameters (α, β); (6): \(Z_3=I-(I+Y)^{-\frac {1}{2}}Y(I+Y)^{-\frac {1}{2}}=(I+Y)^{-1}\) is real type-1 beta distributed with the parameters (β, α).
5.3a. Matrix-variate Type-1 and Type-2 Beta Densities, Complex Case
A matrix-variate beta function in the complex domain is defined as
with a tilde over B. As \(\tilde {B}_p(\alpha ,\beta )=\tilde {B}_p(\beta ,\alpha ),\) clearly α and β can be interchanged. Then, \(\tilde {B}_p(\alpha ,\beta )\) has the following integral representations, where \(\Re (\alpha )>p-1, \Re (\beta )>p-1\):
For instance, consider the integrand in (5.3a.2) for the case p = 2. Let

the diagonal elements of \(\tilde {X}\) being real; since \(\tilde {X}\) is Hermitian positive definite, we have \(x_1>0,~x_3>0,~x_1x_2-(x_2^2+y_2^2)>0\), \(\text{ det}(\tilde {X})=x_1x_3-(x_2^2+y_2^2)>0\) and \(\text{det}(I-\tilde {X})=(1-x_1)(1-x_3)-(x_2^2+y_2^2)>0\). The integrand in (5.3a.2) is then
The derivations of (5.3a.2)–(5.3a.5) being parallel to those provided in the real case, they are omitted. We will list one case for each of a type-1 and a type-2 beta density in the complex p × p matrix-variate case:
for \(O<\tilde {X}<I,~\Re (\alpha )>p-1,~ \Re (\beta )>p-1\) and \(\tilde {f}_3(\tilde {X})=0\) elsewhere;
for \(\tilde {Z}>O,~ \Re (\alpha )>p-1,~ \Re (\beta )>p-1\) and \(\tilde {f}_4(\tilde {Z})=0\) elsewhere.
Properties parallel to (1) to (6) which are listed in Sect. 5.3.1 also hold in the complex case.
5.3.2. Explicit evaluation of type-1 matrix-variate beta integrals, real case
A detailed evaluation of a type-1 matrix-variate beta integral as a multiple integral is presented in this section as the steps will prove useful in connection with other computations; the reader may also refer to Mathai (2014,b). The real matrix-variate type-1 beta function which is denoted by
has the following type-1 beta integral representation:
for \(\Re (\alpha )>\frac {p-1}{2},~\Re (\beta )>\frac {p-1}{2}\) where X is a real p × p symmetric positive definite matrix. The standard derivation of this integral relies on the properties of real matrix-variate gamma integrals after making suitable transformations, as was previously done. It is also possible to evaluate the integral directly and show that it is equal to Γ p(α)Γ p(β)∕Γ p(α + β) where, for example,
A convenient technique for evaluating a real matrix-variate gamma integral consists of making the transformation X = TT ′ where T is a lower triangular matrix whose diagonal elements are positive. However, on applying this transformation, the type-1 beta integral does not simplify due to the presence of the factor \(|I-X|{ }^{\beta -\frac {p+1}{2}}\). Hence, we will attempt to evaluate this integral by appropriately partitioning the matrices and then, successively integrating out the variables. Letting X = (x ij) be a p × p real matrix, x pp can then be extracted from the determinants of |X| and |I − X| after partitioning the matrices. Thus, let

where X 11 is the (p − 1) × (p − 1) leading sub-matrix, X 21 is 1 × (p − 1), X 22 = x pp and \(X_{12}=X_{21}^{\prime }\). Then \(|X|=|X_{11}||x_{pp}-X_{21}X_{11}^{-1}X_{12}|\) so that
and
It follows from (i) that \(x_{pp}>X_{21}X_{11}^{-1}X_{12}\) and, from (ii) that x pp < 1 − X 21(I − X 11)−1 X 12; thus, we have \(X_{21}X_{11}^{-1}X_{12}<x_{pp}<1-X_{21}(I-X_{11})^{-1}X_{12}\). Let \(y=x_{pp}-X_{21}X_{11}^{-1}X_{12}\Rightarrow \text{d}y=\text{d}x_{pp}\) for fixed X 21, X 11, so that 0 < y < b where
The second factor on the right-hand side of (ii) then becomes
Now letting \(u=\frac {y}{b}\) for fixed b, the terms containing u and b become \(b^{\alpha +\beta -(p+1)+1}u^{\alpha -\frac {p+1}{2}}\) \((1-u)^{\beta -\frac {p+1}{2}}\). Integration over u then gives
for \(~\Re (\alpha )>\frac {p-1}{2}, ~\Re (\beta )>\frac {p-1}{2}.\) Letting \(W=X_{21}X_{11}^{-\frac {1}{2}}(I-X_{11})^{-\frac {1}{2}}\) for fixed X 11, \(\text{d}X_{21}=|X_{11}|{ }^{\frac {1}{2}}|I-X_{11}|{ }^{\frac {1}{2}}\text{d}W\) from Theorem 1.6.1 of Chap. 1 or Theorem 1.18 of Mathai (1997), where X 11 is a (p − 1) × (p − 1) matrix. Now, letting v = WW ′ and integrating out over the Stiefel manifold by applying Theorem 4.2.3 of Chap. 4 or Theorem 2.16 and Remark 2.13 of Mathai (1997), we have
Thus, the integral over b becomes
Then, on multiplying all the factors together, we have
whenever \(\Re (\alpha )>\frac {p-1}{2},~\Re (\beta )>\frac {p-1}{2}\). In this case, \(X_{11}^{(1)}\) represents the (p − 1) × (p − 1) leading sub-matrix at the end of the first set of operations. At the end of the second set of operations, we will denote the (p − 2) × (p − 2) leading sub-matrix by \(X_{11}^{(2)}\), and so on. The second step of the operations begins by extracting x p−1,p−1 and writing
where \(X_{21}^{(2)}\) is a 1 × (p − 2) vector. We then proceed as in the first sequence of steps to obtain the final factors in the following form:
for \(\Re (\alpha )>\frac {p-2}{2},~\Re (\beta )>\frac {p-2}{2}\). Proceeding in such a manner, in the end, the exponent of π will be
and the gamma product will be
These gamma products, along with \(\pi ^{\frac {p(p-1)}{4}},\) can be written as \(\frac {\varGamma _p(\alpha )\varGamma _p(\beta )}{\varGamma _p(\alpha +\beta )}=B_p(\alpha ,~\beta )\); hence the result. It is thus possible to obtain the beta function in the real matrix-variate case by direct evaluation of a type-1 real matrix-variate beta integral.
A similar approach can yield the real matrix-variate beta function from a type-2 real matrix-variate beta integral of the form
where X is a p × p positive definite symmetric matrix and it is assumed that \(\Re (\alpha )>\frac {p-1}{2}\) and \(\Re (\beta )>\frac {p-1}{2}\), the evaluation procedure being parallel.
Example 5.3.1
By direct evaluation as a multiple integral, show that
for p = 2.
Solution 5.3.1
The integral to be evaluated will be denoted by δ. Let
It is seen from (i) that
Letting \(y=x_{22}-\frac {x_{12}^2}{x_{11}}\) so that \(0\le y\le b,\ \mbox{and}\ b=1-\frac {x_{12}^2}{x_{11}}-\frac {x_{12}^2}{1-x_{11}}=1-\frac {x_{12}^2}{x_{11}(1-x_{11})},\) we have
Now, integrating out y, we have
whenever \(\Re (\alpha )>\frac {1}{2}\) and \(\Re (\beta )>\frac {1}{2},\) b being as previously defined. Letting \(w=\frac {x_{12}}{[x(1-x)]^{\frac {1}{2}}}\), \(\text{d}x_{12}=[x_{11}(1-x_{11}]^{\frac {1}{2}}\text{d}w\) for fixed x 11. The exponents of x 11 and (1 − x 11) then become \(\alpha -\frac {3}{2}+\frac {1}{2}\) and \(\beta -\frac {3}{2}+\frac {1}{2}\), and the integral over w gives the following:
Now, integrating out x 11, we obtain
Then, on collecting the factors from (i) to (iv), we have
Finally, noting that for \(p=2,~\pi ^{\frac {p(p-1)}{4}}=\pi ^{\frac {1}{2}}=\frac {\pi ^{\frac {1}{2}}\pi ^{\frac {1}{2}}}{\pi ^{\frac {1}{2}}}\), the desired result is obtained, that is,
This completes the computations.
5.3a.1. Evaluation of matrix-variate type-1 beta integrals, complex case
The integral representation for B p(α, β) in the complex case is
whenever \(\Re (\alpha )>p-1,~\Re (\beta )>p-1\) where det(⋅) denotes the determinant of (⋅) and |det(⋅)|, the absolute value (or modulus) of the determinant of (⋅). In this case, \(\tilde {X}=(\tilde {x}_{ij})\) is a p × p Hermitian positive definite matrix and accordingly, all of its diagonal elements are real and positive. As in the real case, let us extract x pp by partitioning \(\tilde {X}\) as follows:

where \(\tilde {X}_{22}\equiv x_{pp}\) is a real scalar. Then, the absolute value of the determinants have the following representations:
where * indicates conjugate transpose, and
Note that whenever \(\tilde {X}\) and \(I-\tilde {X}\) are Hermitian positive definite, \(\tilde {X}_{11}^{-1}\) and \((I-\tilde {X}_{11})^{-1}\) are too Hermitian positive definite. Further, the Hermitian forms \(\tilde {X}_{21}\tilde {X}_{11}^{-1}\tilde {X}_{12}^{*}\) and \(\tilde {X}_{21}(I-\tilde {X}_{11})^{-1}\tilde {X}_{12}^{*}\) remain real and positive. It follows from (i) and (ii) that
Since the traces of Hermitian forms are real, the lower and upper bounds of x pp are real as well. Let
for fixed \(\tilde {X}_{11}\). Then
and \(|\text{det}(\tilde {X})|{ }^{\alpha -p},~ |\text{det}(I-\tilde {X}_{11})|{ }^{\beta -p}\) will become \(|\text{det}(\tilde {X}_{11})|{ }^{\alpha +1-p},~ |\text{ det}(I-\tilde {X}_{11})|{ }^{\beta +1-p},\) respectively. Then, we can write
Now, letting u = y∕b, the factors containing u and b will be of the form u α−p (1 − u)β−p b α+β−2p+1; the integral over u then gives
for \(\Re (\alpha )>p-1,~\Re (\beta )>p-1\). Letting \(v=\tilde {W}\tilde {W}^{*}\) and integrating out over the Stiefel manifold by making use of Theorem 4.2a.3 of Chap. 4 or Corollaries 4.5.2 and 4.5.3 of Mathai (1997), we have
The integral over b gives
for \(\Re (\alpha )>p-1,~\Re (\beta )>p-1\). Now, taking the product of all the factors yields
for \(\Re (\alpha )>p-1,~\Re (\beta )>p-1\). On extracting x p−1,p−1 from \(|\tilde {X}_{11}|\) and \(|I-\tilde {X}_{11}|\) and continuing this process, in the end, the exponent of π will be \((p-1)+(p-2)+\cdots +1=\frac {p(p-1)}{2}\) and the gamma product will be
These factors, along with \(\pi ^{\frac {p(p-1)}{2}}\) give
The procedure for evaluating a type-2 matrix-variate beta integral by partitioning matrices is parallel and hence will not be detailed here.
Example 5.31
For p = 2, evaluate the integral
as a multiple integral and show that it evaluates out to \(\tilde {B}_2(\alpha ,\beta )\), the beta function in the complex domain.
Solution 5.31
For p = 2, \(\pi ^{\frac {p(p-1)}{2}}=\pi ^{\frac {2(1)}{2}}=\pi \), and
whenever \(\Re (\alpha )>1 \) and \(\Re (\beta )>1\). For p = 2, our matrix and the relevant determinants are

where \(\tilde {x}_{12}^{*}\) is only the conjugate of \(\tilde {x}_{12}\) as it is a scalar quantity. By expanding the determinants of the partitioned matrices as explained in Sect. 1.3, we have the following:
From (i) and (ii), it is seen that
Note that when \(\tilde {X}\) is Hermitian, \(\tilde {x}_{11}\) and \(\tilde {x}_{22}\) are real and hence we may not place a tilde on these variables. Let \(\tilde {y}=x_{22}-{\tilde {x}_{12}\tilde {x}_{12}^{*}}/{x_{11}}.\) Note that \(\tilde {y}\) is also real since \(\tilde {x}_{12}\tilde {x}_{12}^{*}\) is real. As well, 0 ≤ y ≤ b, where
Further, b is a real scalar of the form \(b=1-\tilde {w}\tilde {w}^{*}\) where \(\tilde {w}=\frac {\tilde {x}_{12}}{[x_{11}(1-x_{11})]^{\frac {1}{2}}}\Rightarrow \text{d}\tilde {x}_{12}=x_{11}(1-x_{11})\text{d}\tilde {w}\). This will make the exponents of x 11 and (1 − x 11) as α − p + 1 = α − 1 and β − 1, respectively. Now, on integrating out y, we have
Integrating out \(\tilde {w}\), we have the following:
This integral is evaluated by writing \(z=\tilde {w}\tilde {w}^{*}\). Then, it follows from Theorem 4.2a.3 that
Now, collecting all relevant factors from (i) to (iv), the required representation of the initial integral, denoted by δ, is obtained:
whenever \(\Re (\alpha )>1\) and \(\Re (\beta )>1\). This completes the computations.
5.3.3. General partitions, real case
In Sect. 5.3.2, we have considered integrating one variable at a time by suitably partitioning the matrices. Would it also be possible to have a general partitioning and integrate a block of variables at a time, rather than integrating out individual variables? We will consider the real matrix-variate gamma integral first. Let the p × p positive definite matrix X be partitioned as follows:

so that X 12 is p 1 × p 2 with \(X_{21}=X_{12}^{\prime }\) and p 1 + p 2 = p. Without any loss of generality, let us assume that p 1 ≥ p 2. The determinant can be partitioned as follows:
Letting
for fixed X 11 and X 22 by making use of Theorem 1.6.4 of Chap. 1 or Theorem 1.18 of Mathai (1997),
Letting S = Y Y ′ and integrating out over the Stiefel manifold, we have
refer to Theorem 2.16 and Remark 2.13 of Mathai (1997) or Theorem 4.2.3 of Chap. 4. Now, the integral over S gives
for \(\Re (\alpha )>\frac {p_1-1}{2}\). Collecting all the factors, we have
One can observe from this result that the original determinant splits into functions of X 11 and X 22. This also shows that if we are considering a real matrix-variate gamma density, then the diagonal blocks X 11 and X 22 are statistically independently distributed, where X 11 will have a p 1-variate gamma distribution and X 22, a p 2-variate gamma distribution. Note that tr(X) = tr(X 11) + tr(X 22) and hence, the integral over X 22 gives \(\varGamma _{p_2}(\alpha )\) and the integral over X 11, \(\varGamma _{p_1}(\alpha )\). Thus, the total integral is available as
since \(\pi ^{\frac {p_1p_2}{2}}\varGamma _{p_1}(\alpha )\varGamma _{p_2}(\alpha -\frac {p_1}{2})=\varGamma _p(\alpha )\).
Hence, it is seen that instead of integrating out variables one at a time, we could have also integrated out blocks of variables at a time and verified the result. A similar procedure works for real matrix-variate type-1 and type-2 beta distributions, as well as the matrix-variate gamma and type-1 and type-2 beta distributions in the complex domain.
5.3.4. Methods avoiding integration over the Stiefel manifold
The general method of partitioning matrices previously described involves the integration over the Stiefel manifold as an intermediate step and relies on Theorem 4.2.3. We will consider another procedure whereby integration over the Stiefel manifold is not required. Let us consider the real gamma case first. Again, we begin with the decomposition
Instead of integrating out X 21 or X 12, let us integrate out X 22. Let X 11 be a p 1 × p 1 matrix and X 22 be a p 2 × p 2 matrix, with p 1 + p 2 = p. In the above partitioning, we require that X 11 be nonsingular. However, when X is positive definite, both X 11 and X 22 will be positive definite, and thereby nonsingular. From the second factor in (5.3.8), \(X_{22}>X_{21}X_{11}^{-1}X_{12}\) as \(X_{22}-X_{21}X_{11}^{-1}X_{12}\) is positive definite. We will attempt to integrate out X 22 first. Let \(U=X_{22}-X_{21}X_{11}^{-1}X_{12}\) so that dU = dX 22 for fixed X 11 and X 12. Since tr(X) = tr(X 11) + tr(X 22), we have
On integrating out U, we obtain
since \(\alpha -\frac {p+1}{2}=\alpha -\frac {p_1}{2}-\frac {p_2+1}{2}\). Letting
for fixed X 11 (Theorem 1.6.1), we have
But tr(Y Y ′) is the sum of the squares of the p 1 p 2 elements of Y and each integral is of the form \(\int _{-\infty }^{\infty }\text{e}^{-z^2}\text{ d}z=\sqrt {\pi }\). Hence,
We may now integrate out X 11:
Thus, we have the following factors:
since
and
Hence the result. This procedure avoids integration over the Stiefel manifold and does not require that p 1 ≥ p 2. We could have integrated out X 11 first, if needed. In that case, we would have used the following expansion:
We would have then proceeded as before by integrating out X 11 first and would have ended up with
Note 5.3.1: If we are considering a real matrix-variate gamma density, such as the Wishart density, then from the above procedure, observe that after integrating out X 22, the only factor containing X 21 is the exponential function, which has the structure of a matrix-variate Gaussian density. Hence, for a given X 11, X 21 is matrix-variate Gaussian distributed. Similarly, for a given X 22, X 12 is matrix-variate Gaussian distributed. Further, the diagonal blocks X 11 and X 22 are independently distributed.
The same procedure also applies for the evaluation of the gamma integrals in the complex domain. Since the steps are parallel, they will not be detailed here.
5.3.5. Arbitrary moments of the determinants, real gamma and beta matrices
Let the p × p real positive definite matrix X have a real matrix-variate gamma density with the parameters (α, B > O). Then for an arbitrary h, we can evaluate the h-th moment of the determinant of X with the help of the matrix-variate gamma integral, namely,
By making use of (i), we can evaluate the h-th moment in a real matrix-variate gamma density with the parameters (α, B > O) by considering the associated normalizing constant. Let u 1 = |X|. Then, the moments of u 1 can be obtained by integrating out over the density of X:
Thus,
This is evaluated by observing that when E[u 1]h is taken, α is replaced by α + h in the integrand and hence, the answer is obtained from equation (i). The same procedure enables one to evaluate the h-th moment of the determinants of type-1 beta and type-2 beta matrices. Let Y be a p × p real positive definite matrix having a real matrix-variate type-1 beta density with the parameters (α, β) and u 2 = |Y |. Then, the h-th moment of Y is obtained as follows:
In a similar manner, let u 3 = |Z| where Z has a p × p real matrix-variate type-2 beta density with the parameters (α, β). In this case, take α + β = (α + h) + (β − h), replacing α by α + h and β by β − h. Then, considering the normalizing constant of a real matrix-variate type-2 beta density, we obtain the h-th moment of u 3 as follows:
Relatively few moments will exist in this case, as \(\Re (\alpha +h)>\frac {p-1}{2}\) implies that \(\Re (h)>-\Re (\alpha )+\frac {p-1}{2}\) and \(\Re (\beta -h)>\frac {p-1}{2}\) means that \(\Re (h)<\Re (\beta )-\frac {p-1}{2}\). Accordingly, only moments in the range \(-\Re (\alpha )+\frac {p-1}{2}<\Re (h)<\Re (\beta )-\frac {p-1}{2}\) will exist. We can summarize the above results as follows: When X is distributed as a real p × p matrix-variate gamma with the parameters (α, B > O),
When Y has a p × p real matrix-variate type-1 beta density with the parameters (α, β) and if u 2 = |Y | then
When the p × p real positive definite matrix Z has a real matrix-variate type-2 beta density with the parameters (α, β), then letting u 3 = |Z|,
Let us examine (5.3.9):
where x j is a real scalar gamma random variable with shape parameter \(\alpha -\frac {j-1}{2}\) and scale parameter λ j where λ j > 0, j = 1, …, p are the eigenvalues of B > O by observing that the determinant is the product and trace is the sum of the eigenvalues λ 1, …, λ p. Further, x 1, .., x p, are independently distributed. Hence, structurally, we have the following representation:
where x j has the density
for \(\Re (\alpha )>\frac {j-1}{2},~ \lambda _j>0\) and zero otherwise. Similarly, when the p × p real positive definite matrix Y has a real matrix-variate type-1 beta density with the parameters (α, β), the determinant, |Y |, has the structural representation
where y j is a real scalar type-1 beta random variable with the parameter \((\alpha -\frac {j-1}{2},~\beta )\) for j = 1, …, p. When the p × p real positive definite matrix Z has a real matrix-variate type-2 beta density, then |Z|, the determinant of Z, has the following structural representation:
where z j has a real scalar type-2 beta density with the parameters \((\alpha -\frac {j-1}{2},~\beta -\frac {j-1}{2})\) for j = 1, …, p.
Example 5.3.2
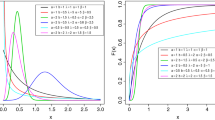
Consider a real 2 × 2 matrix X having a real matrix-variate distribution. Derive the density of the determinant |X| if X has (a) a gamma distribution with the parameters (α, B = I); (b) a real type-1 beta distribution with the parameters \((\alpha =\frac {3}{2},~\beta =\frac {3}{2})\); (c) a real type-2 beta distribution with the parameters \((\alpha =\frac {3}{2},~\beta =\frac {3}{2})\).
Solution 5.3.2
We will derive the density in these three cases by using three different methods to illustrate the possibility of making use of various approaches for solving such problems. (a) Let u 1 = |X| in the gamma case. Then for an arbitrary h,
Since the gammas differ by \(\frac {1}{2}\), they can be combined by utilizing the following identity:
which is the multiplication formula for gamma functions. For m = 2, we have the duplication formula:
Thus,
Now, by taking \(z=\alpha -\frac {1}{2}+h\) in the numerator and \(z=\alpha -\frac {1}{2}\) in the denominator, we can write
Accordingly,
This shows that \(v=2u_1^{\frac {1}{2}}\) has a real scalar gamma distribution with the parameters (2α − 1, 1) whose density is
Hence the density of u 1, denoted by f 1(u 1), is the following:
and zero elsewhere. It can easily be verified that f 1(u 1) is a density.
(b) Let u 2 = |X|. Then for an arbitrary h, \(\alpha =\frac {3}{2}\) and \(\beta =\frac {3}{2}\),
the last expression resulting from an application of the partial fraction technique. This results from h-th moment of the distribution of u 2, whose density which is
and zero elsewhere, is readily seen to be bona fide.
(c) Let the density u 3 = |X| be denoted by f 3(u 3). The Mellin transform of f 3(u 3), with Mellin parameter s, is
the corresponding density being available by taking the inverse Mellin transform, namely,
where \(i=\sqrt {(-1)}\) and c in the integration contour is such that 0 < c < 2. The integral in (i) is available as the sum of residues at the poles of \(\varGamma (s)\varGamma (s+\frac {1}{2})\) for 0 ≤ u 3 ≤ 1 and the sum of residues at the poles of \(\varGamma (2-s)\varGamma (\frac {5}{2}-s)\) for 1 < u 3 < ∞. We can also combine Γ(s) and \(\varGamma (s+\frac {1}{2})\) as well as Γ(2 − s) and \(\varGamma (\frac {5}{2}-s)\) by making use of the duplication formula for gamma functions. We will then be able to identify the functions in each of the sectors, 0 ≤ u 3 ≤ 1 and 1 < u 3 < ∞. These will be functions of \(u_3^{\frac {1}{2}}\) as done in the case (a). In order to illustrate the method relying on the inverse Mellin transform, we will evaluate the density f 3(u 3) as a sum of residues. The poles of \(\varGamma (s)\varGamma (s+\frac {1}{2})\) are simple and hence two sums of residues are obtained for 0 ≤ u 3 ≤ 1. The poles of Γ(s) occur at s = −ν, ν = 0, 1, …, and those of \(\varGamma (s+\frac {1}{2})\) occur at \(s=-\frac {1}{2}-\nu ,~\nu =0,1,\ldots \). The residues and the sum thereof will be evaluated with the help of the following two lemmas.
Lemma 5.3.1
Consider a function Γ(γ + s)ϕ(s)u −s whose poles are simple. The residue at the pole s = −γ − ν, ν = 0, 1, …, denoted by R ν , is given by
Lemma 5.3.2
When Γ(δ) and Γ(δ − ν) are defined
where, for example, (a)ν = a(a + 1)⋯(a + ν − 1), (a)0 = 1, a≠0, is the Pochhammer symbol.
Observe that Γ(α) is defined for all α≠0, −1, −2, …, and that an integral representation requires \(\Re (\alpha )>0\). As well, Γ(α + k) = Γ(α)(α)k, k = 1, 2, ….. With the help of Lemmas 5.3.1 and 5.3.2, the sum of the residues at the poles of Γ(s) in the integral in (i), excluding the constant \(\frac {4}{\pi }\), is the following:
where the 2 F 1(⋅) is Gauss’ hypergeometric function. The same procedure consisting of taking the sum of the residues at the poles \(s=-\frac {1}{2}-\nu ,~ \nu =0,1,\ldots , \) gives
The inverse Mellin transform for the sector 1 < u 3 < ∞ is available as the sum of residues at the poles of \(\varGamma (\frac {5}{2}-s)\) and Γ(2 − s) which occur at \(s=\frac {5}{2}+\nu \) and s = 2 + ν for ν = 0, 1, … . The sum of residues at the poles of \(\varGamma (\frac {5}{2}-s)\) is the following:
and the sum of the residues at the poles of Γ(2 − s) is given by
Now, on combining all the hypergeometric series and multiplying the result by the constant \(\frac {4}{\pi },\) the final representation of the required density is obtained as
This completes the computations.
5.3a.2. Arbitrary moments of the determinants in the complex case
In the complex matrix-variate case, one can consider the absolute value of the determinant, which will be real; however, the parameters will be different from those in the real case. For example, consider the complex matrix-variate gamma density. If \(\tilde {X}\) has a p × p complex matrix-variate gamma density with the parameters \((\alpha ,~\tilde {B}>O)\), then the h-th moment of the absolute value of the determinant of \(\tilde {X}\) is the following:
that is, \(|\text{ det}(\tilde {X})|\) has the structural representation
where the \(\tilde {x}_j\) is a real scalar gamma random variable with the parameters (α − (j − 1), λ j), j = 1, …, p, and the \(\tilde {x}_j\)’s are independently distributed. Similarly, when \(\tilde {Y}\) is a p × p complex Hermitian positive definite matrix having a complex matrix-variate type-1 beta density with the parameters (α, β), the absolute value of the determinant of \(\tilde {Y}\), \(|{\text{det}(\tilde {Y})}|\), has the structural representation
where the \(\tilde {y}_j\)’s are independently distributed, \(\tilde {y}_j\) being a real scalar type-1 beta random variable with the parameters (α − (j − 1), β), j = 1, …, p. When \(\tilde {Z}\) is a p × p Hermitian positive definite matrix having a complex matrix-variate type-2 beta density with the parameters (α, β), then for arbitrary h, the h-th moment of the absolute value of the determinant is given by
so that the absolute value of the determinant of \(\tilde {Z}\) has the following structural representation:
where the \(\tilde {z}_j\)’s are independently distributed real scalar type-2 beta random variables with the parameters (α − (j − 1), β − (j − 1)) for j = 1, …, p. Thus, in the real case, the determinant and, in the complex case, the absolute value of the determinant have structural representations in terms of products of independently distributed real scalar random variables. The following is the summary of what has been discussed so far:
Distribution | Parameters, real case | Parameters, complex case |
gamma | \((\alpha -\frac {j-1}{2},~\lambda _j)\) | (α − (j − 1), λ j) |
type-1 beta | \((\alpha -\frac {j-1}{2},~\beta )\) | (α − (j − 1), β) |
type-2 beta | \((\alpha -\frac {j-1}{2},~\beta -\frac {j-1}{2})\) | (α − (j − 1), β − (j − 1)) |
for j = 1, …, p. When we consider the determinant in the real case, the parameters differ by \(\frac {1}{2}\) whereas the parameters differ by 1 in the complex domain. Whether in the real or complex cases, the individual variables appearing in the structural representations are real scalar variables that are independently distributed.
Example 5.3a.2
Even when p = 2, some of the poles will be of order 2 since the gammas differ by integers in the complex case, and hence a numerical example will not be provided for such an instance. Actually, when poles of order 2 or more are present, the series representation will contain logarithms as well as psi and zeta functions. A simple illustrative example is now considered. Let \(\tilde {X}\) be 2 × 2 matrix having a complex matrix-variate type-1 beta distribution with the parameters (α = 2, β = 2). Evaluate the density of \(\tilde {u}=|\text{det}(\tilde {X})|\).
Solution 5.3a.2
Let us take the (s − 1)th moment of \(\tilde {u}\) which corresponds to the Mellin transform of the density of \(\tilde {u}\), with Mellin parameter s:
The inverse Mellin transform then yields the density of \(\tilde {u}\), denoted by \(\tilde {g}(\tilde {u})\), which is
where the c in the contour is any real number c > 0. There is a pole of order 1 at s = 0 and another pole of order 1 at s = −2, the residues at these poles being obtained as follows:
The pole at s = −1 is of order 2 and hence the residue is given by
Hence the density is the following:
and zero elsewhere, where u is real. It can readily be shown that \(\tilde {g}(\tilde {u})\ge 0\) and \(\int _0^1\tilde {g}(\tilde {u})\text{d}u=1\). This completes the computations.
Exercises 5.3
5.3.1
Evaluate the real p × p matrix-variate type-2 beta integral from first principles or by direct evaluation by partitioning the matrix as in Sect. 5.3.3 (general partitioning).
5.3.2
Repeat Exercise 5.3.6 for the complex case.
5.3.3
In the 2 × 2 partitioning of a p × p real matrix-variate gamma density with shape parameter α and scale parameter I, where the first diagonal block X 11 is r × r, r < p, compute the density of the rectangular block X 12.
5.3.4
Repeat Exercise 5.3.8 for the complex case.
5.3.5
Let the p × p real matrices X 1 and X 2 have real matrix-variate gamma densities with the parameters (α 1, B > O) and (α 2, B > O), respectively, B being the same for both distributions. Compute the density of (1): \(U_1=X_2^{-\frac {1}{2}}X_1X_2^{-\frac {1}{2}}\), (2): \(U_2=X_1^{\frac {1}{2}}X_2^{-1}X_1^{\frac {1}{2}}\), (3): \(U_3=(X_1+X_2)^{-\frac {1}{2}}X_2(X_1+X_2)^{-\frac {1}{2}}\), when X 1 and X 2 are independently distributed.
5.3.6
Repeat Exercise 5.3.10 for the complex case.
5.3.7
In the transformation Y = I − X that was used in Sect. 5.3.1, the Jacobian is \(\text{d}Y=(-1)^{\frac {p(p+1)}{2}}\text{d}X\). What happened to the factor \((-1)^{\frac {p(p+1)}{2}}\)?
5.3.8
Consider X in the (a) 2 × 2, (b) 3 × 3 real matrix-variate case. If X is real matrix-variate gamma distributed, then derive the densities of the determinant of X in (a) and (b) if the parameters are \(\alpha =\frac {5}{2},~B=I\). Consider \(\tilde {X}\) in the (a) 2 × 2, (b) 3 × 3 complex matrix-variate case. Derive the distributions of \(|\text{det}(\tilde {X})|\) in (a) and (b) if \(\tilde {X}\) is complex matrix-variate gamma distributed with parameters (α = 2 + i, B = I).
5.3.9
Consider the real cases (a) and (b) in Exercise 5.3.13 except that the distribution is type-1 beta with the parameters \((\alpha =\frac {5}{2},~\beta =\frac {5}{2})\). Derive the density of the determinant of X.
5.3.10
Consider \(\tilde {X}\), (a) 2 × 2, (b) 3 × 3 complex matrix-variate type-1 beta distributed with parameters \(\alpha =\frac {5}{2}+i,~\beta =\frac {5}{2}-i)\). Then derive the density of \(|\text{det}(\tilde {X})|\) in the cases (a) and (b).
5.3.11
Consider X, (a) 2 × 2, (b) 3 × 3 real matrix-variate type-2 beta distributed with the parameters \((\alpha =\frac {3}{2},~\beta =\frac {3}{2})\). Derive the density of |X| in the cases (a) and (b).
5.3.12
Consider \(\tilde {X},\) (a) 2 × 2, (b) 3 × 3 complex matrix-variate type-2 beta distributed with the parameters \((\alpha =\frac {3}{2},~\beta =\frac {3}{2})\). Derive the density of \(|\text{det}(\tilde {X})|\) in the cases (a) and (b).
5.4. The Densities of Some General Structures
Three cases were examined in Section 5.3: the product of real scalar gamma variables, the product of real scalar type-1 beta variables and the product of real scalar type-2 beta variables, where in all these instances, the individual variables were mutually independently distributed. Let us now consider the corresponding general structures. Let x j be a real scalar gamma variable with shape parameter α j and scale parameter 1 for convenience and let the x j’s be independently distributed for j = 1, …, p. Then, letting v 1 = x 1⋯x p,
Now, let y 1, …, y p be independently distributed real scalar type-1 beta random variables with the parameters \((\alpha _j,~\beta _j), ~ \Re (\alpha _j)>0,~\Re (\beta _j)>0,~j=1,\ldots ,p,\) and v 2 = y 1⋯y p,
for \(\Re (\alpha _j)>0,~\Re (\beta _j)>0,~ \Re (\alpha _j+h)>0,~j=1,\ldots ,p\). Similarly, let z 1, …, z p, be independently distributed real scalar type-2 beta random variables with the parameters (α j, β j), j = 1, …, p, and let v 3 = z 1⋯z p. Then, we have
for \(\Re (\alpha _j)>0,~ \Re (\beta _j)>0,~ \Re (\alpha _j+h)>0,~ \Re (\beta _j-h)>0,~j=1,\ldots ,p\). The corresponding densities of v 1, v 2, v 3, respectively denoted by g 1(v 1), g 2(v 2), g 3(v 3), are available from the inverse Mellin transforms by taking (5.4.1) to (5.4.3) as the Mellin transforms of g 1, g 2, g 3 with h = s − 1 for a complex variable s where s is the Mellin parameter. Then, for suitable contours L, the densities can be determined as follows:
where \(\Re (\alpha _j+s-1)>0,~ j=1,\ldots ,p,\) and g 1(v 1) = 0 elsewhere. This last representation is expressed in terms of a G-function, which will be defined in Sect. 5.4.1.
where \(G_{p,p}^{p,0}\) is a G-function, \(\Re (\alpha _j+s-1)>0,~\Re (\alpha _j)>0,~ \Re (\beta _j)>0,~j=1,\ldots ,p,\) and g 2(v 2) = 0 elsewhere.
where \(\Re (\alpha _j)>0,~\Re (\beta _j)>0,~\Re (\alpha _j+s-1)>0,~\Re (\beta _j-s+1)>0,~ j=1,\ldots ,p,\) and g 3(v 3) = 0 elsewhere.
5.4.1. The G-function
The G-function is defined in terms of the following Mellin-Barnes integral:
where the parameters a j, j = 1, …, p, b j, j = 1, …, q, can be complex numbers. There are three general contours L, say L 1, L 2, L 3 where L 1 is a loop starting and ending at −∞ that contains all the poles of Γ(b j + s), j = 1, …, m, and none of those of Γ(1 − a j − s), j = 1, …, n. In general L will separate the poles of Γ(b j + s), j = 1, …, m, from those of Γ(1 − a j − s), j = 1, …, n, which lie on either side of the contour. L 2 is a loop starting and ending at + ∞, which encloses all the poles of Γ(1 − a j − s), j = 1, …, n. L 3 is the straight line contour c − i∞ to c + i∞. The existence of the contours, convergence conditions, explicit series forms for general parameters as well as applications are available in Mathai (1993). G-functions can readily be evaluated with symbolic computing packages such as MAPLE and Mathematica.
Example 5.4.1
Let x 1, x 2, x 3 be independently distributed real scalar random variables, x 1 being real gamma distributed with the parameters (α 1 = 3, β 1 = 2), x 2, real type-1 beta distributed with the parameters \((\alpha _2=\frac {3}{2}+2i,~\beta _2=\frac {1}{2})\) and x 3, real type-2 beta distributed with the parameters \((\alpha _3=\frac {5}{2}+i,~\beta _3=2-i)\). Let \(u_1=x_1x_2x_3,~ u_2=\frac {x_1}{x_2x_3}\) and \( u_3=\frac {x_2}{x_1x_3}\) with densities g j(u j), j = 1, 2, 3, respectively. Derive the densities g j(u j), j = 1, 2, 3, and represent them in terms of G-functions.
Solution 5.4.1
Observe that \(E\big [\frac {1}{x_j}\big ]^{s-1}\!\!\!\!=\!E[x_j^{-s+1}],~j=1,2,3\), and that g 1(u 1), g 2(u 2) and g 3(u 3) will share the same ‘normalizing constant’, say c, which is the product of the parts of the normalizing constants in the densities of x 1, x 2 and x 3 that do not cancel out when determining the moments, respectively denoted by c 1, c 2 and c 3, that is, c = c 1 c 2 c 3. Thus,
The following are \(E[x_j^{s-1}]\) and \(E[x_j^{-s+1}]\) for j = 1, 2, 3:
Then from (i)-(iv),
Taking the inverse Mellin transform and writing the density g 1(u 1) in terms of a G-function, we have
Using (i)-(iv) and rearranging the gamma functions so that those involving + s appear together in the numerator, we have the following:
Taking the inverse Mellin transform and expressing the result in terms of a G-function, we obtain the density g 2(u 2) as
Using (i)-(iv) and conveniently rearranging the gamma functions involving + s, we have
On taking the inverse Mellin transform, the following density is obtained:
This completes the computations.
5.4.2. Some special cases of the G-function
Certain special cases of the G-function can be written in terms of elementary functions. Here are some of them:
for p ≤ q or p = q + 1 and |z| < 1.
5.4.3. The H-function
If we have a general structure corresponding to v 1, v 2 and v 3 of Sect. 5.4, say w 1, w 2 and w 3 of the form
for some δ j > 0, j = 1, …, p the densities of w 1, w 2 and w 3 are then available in terms of a more general function known as the H-function. It is again a Mellin-Barnes type integral defined and denoted as follows:
where α j > 0, j = 1, …, p, β j > 0, j = 1, …, q, are real and positive, a j, j = 1, …, p, and b j, j = 1, …, q, are complex numbers. Three main contours L 1, L 2, L 3 are utilized, similarly to those described in connection with the G-function. Existence conditions, properties and applications of this generalized hypergeometric function are available from Mathai et al. (2010) among other monographs. Numerous special cases can be expressed in terms of known elementary functions.
Example 5.4.2
Let x 1 and x 2 be independently distributed real type-1 beta random variables with the parameters (α j > 0, β j > 0), j = 1, 2, respectively. Let \(y_1=x_1^{\delta _1},~\delta _1>0,\) and \(y_2=x_2^{\delta _2},~\delta _2>0\). Compute the density of u = y 1 y 2.
Solution 5.4.2
Arbitrary moments of y 1 and y 2 are available from those of x 1 and
x 2.
Accordingly, the density of u, denoted by g(u), is the following:
where 0 ≤ u ≤ 1, \(\Re (\alpha _j-\delta _j+\delta _js)>0,~ \Re (\alpha _j)>0,~\Re (\beta _j)>0,~j=1,2\) and g(u) = 0 elsewhere.
When α 1 = 1 = ⋯ = α p, β 1 = 1 = ⋯ = β q, the H-function reduces to a G-function. This G-function is frequently referred to as Meijer’s G-function and the H-function, as Fox’s H-function.
5.4.4. Some special cases of the H-function
Certain special cases of the H-function are listed next.
where the Bessel function
where the generalized Mittag-Leffler function
where Γ(γ) is defined. For γ = 1, we have \(E_{\alpha ,\beta }^1(z)=E_{\alpha ,\beta }(z)\); when γ = 1, β = 1, \(E_{\alpha ,1}^1(z)=E_{\alpha }(z)\) and when γ = 1 = β = α, we have E 1(z) = ez.
where \(K_{\rho }^{\nu }(z)\) is Krätzel function
Exercises 5.4
5.4.1
Show that
5.4.2
Show that
5.4.3
Show that
5.4.4
Show that
5.4.5
Show that
5.5,5.5a. The Wishart Density
A particular case of the real p × p matrix-variate gamma distribution, known as the Wishart distribution, is the preeminent distribution in multivariate statistical analysis. In the general p × p real matrix-variate gamma density with parameters (α, B > O), let \(\alpha =\frac {m}{2},~ B=\frac {1}{2}\varSigma ^{-1}\) and Σ > O; the resulting density is called a Wishart density with degrees of freedom m and parameter matrix Σ > O. This density, denoted by f w(W), is given by
for m ≥ p, and f w(W) = 0 elsewhere. This will be denoted as W ∼ W p(m, Σ). Clearly, all the properties discussed in connection with the real matrix-variate gamma density still hold in this case. Algebraic evaluations of the marginal densities and explicit evaluations of the densities of sub-matrices will be considered, some aspects having already been discussed in Sects. 5.2 and 5.2.1.
In the complex case, the density is the following, denoted by \(\tilde {f}_w(\tilde {W})\):
and \(\tilde {f}_w(\tilde {W})=0\) elsewhere. This will be denoted as \(\tilde {W}\sim \tilde {W}_p(m,\varSigma )\).
5.5.1. Explicit evaluations of the matrix-variate gamma integral, real case
Is it possible to evaluate the matrix-variate gamma integral explicitly by using conventional integration? We will now investigate some aspects of this question.
When the Wishart density is derived from samples coming from a Gaussian population, the basic technique relies on the triangularization process. When Σ = I, that is, W ∼ W p(m, I), can the integral of the right-hand side of (5.5.1) be evaluated by resorting to conventional methods or by direct evaluation? We will address this problem by making use of the technique of partitioning matrices. Let us partition

where let X 22 = x pp so that \(X_{21}=(x_{p1},\ldots ,x_{p\,p-1}), ~X_{12}=X_{21}^{\prime }\). Then, on applying a result from Sect. 1.3, we have
Note that when X is positive definite, X 11 > O and x pp > 0, and the quadratic form \(X_{21}X_{11}^{-1}X_{12}>0\). As well,
Letting \(Y=x_{pp}^{-\frac {1}{2}}X_{21}X_{11}^{-\frac {1}{2}},\) then referring to Mathai (1997, Theorem 1.18) or Theorem 1.6.4 of Chap. 1, \(\text{d}Y=x_{pp}^{-\frac {p-1}{2}}|X_{11}|{ }^{-\frac {1}{2}}\text{d}X_{21}\) for fixed X 11 and x pp, . The integral over x pp gives
If we let u = Y Y ′, then from Theorem 2.16 and Remark 2.13 of Mathai (1997) or using Theorem 4.2.3, after integrating out over the Stiefel manifold, we have
(Note that n in Theorem 2.16 of Mathai (1997) corresponds to p − 1 and p is 1). Then, the integral over u gives
Now, collecting all the factors, we have
for \(\Re (\alpha )>\frac {p-1}{2}\). Note that \(|X_{11}^{(1)}|\) is (p − 1) × (p − 1) and |X 11|, after the completion of the first part of the operations, is denoted by \(|X_{11}^{(1)}|\), the exponent being changed to \(\alpha +\frac {1}{2}-\frac {p+1}{2}\). Now repeat the process by separating x p−1,p−1, that is, by writing

Here, \(X_{11}^{(2)}\) is of order (p − 2) × (p − 2) and \(X_{21}^{(2)}\) is of order 1 × (p − 2). As before, letting u = Y Y ′ with \(Y=x_{p-1,p-1}^{-\frac {1}{2}}X_{21}^{(2)}[X_{11}^{(2)}]^{-\frac {1}{2}},\) \(\text{d}Y=x_{p-1,p-1}^{-\frac {p-2}{2}}|X_{11}^{(2)}|{ }^{-\frac {1}{2}}\text{d}X_{21}^{(2)}.\) The integral over the Stiefel manifold gives \(\frac {\pi ^{\frac {p-2}{2}}}{\varGamma (\frac {p-2}{2})}u^{\frac {p-2}{2}-1}\text{d}u\) and the factor containing (1 − u) is \((1-u)^{\alpha +\frac {1}{2}-\frac {p+1}{2}}\), the integral over u yielding
and that over v = x p−1,p−1 giving
The product of these factors is then
Successive evaluations carried out by employing the same procedure yield the exponent of π as \(\frac {p-1}{2}+\frac {p-2}{2}+\cdots +\frac {1}{2}=\frac {p(p-1)}{4}\) and the gamma product, \(\varGamma (\alpha -\frac {p-1}{2})\varGamma (\alpha -\frac {p-2}{2})\cdots \varGamma (\alpha ),\) the final result being Γ p(α). The result is thus verified.
5.5a.1. Evaluation of matrix-variate gamma integrals in the complex case
The matrices and gamma functions belonging to the complex domain will be denoted with a tilde. As well, in the complex case, all matrices appearing in the integrals will be p × p Hermitian positive definite unless otherwise stated; as an example, for such a matrix X, this will be denoted by \(\tilde {X}>O\). The integral of interest is
A standard procedure for evaluating the integral in (5.5a.2) consists of expressing the positive definite Hermitian matrix as \(\tilde {X}=\tilde {T}\tilde {T}^{*}\) where \(\tilde {T}\) is a lower triangular matrix with real and positive diagonal elements t jj > 0, j = 1, …, p, where an asterisk indicates the conjugate transpose. Then, referring to (Mathai (1997, Theorem 3.7) or Theorem 1.6.7 of Chap. 1, the Jacobian is seen to be as follows:
and then
and
Now. integrating out over \(\tilde {t}_{jk}\) for j > k,
and
As well,
for j = 1, …, p. Taking the product of all these factors then gives
and hence the result is verified.
An alternative method based on partitioned matrix, complex case
The approach discussed in this section relies on the successive extraction of the diagonal elements of \(\tilde {X}\), a p × p positive definite Hermitian matrix, all of these elements being necessarily real and positive, that is, x jj > 0, j = 1, …, p. Let

where \(\tilde {X}_{11}\) is (p − 1) × (p − 1) and
and
Then,
Let
referring to Theorem 1.6a.4 or Mathai (1997, Theorem 3.2(c)) for fixed x pp and X 11. Now, the integral over x pp gives
Letting \(u=\tilde {Y}\tilde {Y}^{*}\), \(\text{ d}\tilde {Y}=u^{p-2}\frac {\pi ^{p-1}}{\varGamma (p-1)}\text{d}u\) by applying Theorem 4.2a.3 or Corollaries 4.5.2 and 4.5.3 of Mathai (1997), and noting that u is real and positive, the integral over u gives
Taking the product, we obtain
where \(\tilde {X}_{11}^{(1)}\) stands for \(\tilde {X}_{11}\) after having completed the first set of integrations. In the second stage, we extract x p−1,p−1, the first (p − 2) × (p − 2) submatrix being denoted by \(\tilde {X}_{11}^{(2)}\) and we continue as previously explained to obtain \(|\text{det}(\tilde {X}_{11}^{(2)})|{ }^{\alpha +2-p}\pi ^{p-2}\varGamma (\alpha -(p-2))\). Proceeding successively in this manner, we have the exponent of π as (p − 1) + (p − 2) + ⋯ + 1 = p(p − 1)∕2 and the gamma product as Γ(α − (p − 1))Γ(α − (p − 2))⋯Γ(α) for \(\Re (\alpha )>p-1\). That is,
5.5.2. Triangularization of the Wishart matrix in the real case
Let W ∼ W p(m, Σ), Σ > O be a p × p matrix having a Wishart distribution with m degrees of freedom and parameter matrix Σ > O, that is, let W have a density of the following form for Σ = I:
and f w(W) = 0 elsewhere. Let us consider the transformation W = TT ′ where T is a lower triangular matrix with positive diagonal elements. Since W > O, the transformation W = TT ′ with the diagonal elements of T being positive is one-to-one. We have already evaluated the associated Jacobian in Theorem 1.6.7, namely,
Under this transformation,
In view of (5.5.6), it is evident that t jj, j = 1, …, p and the t ij’s, i > j are mutually independently distributed. The form of the function containing t ij, i > j, is \(\text{e}^{-\frac {1}{2}t_{ij}^2},\) and hence the t ij’s for i > j are mutually independently distributed real standard normal variables. It is also seen from (5.5.6) that the density of \(t_{jj}^2\) is of the form
which is the density of a real chisquare variable having m − (j − 1) degrees of freedom for j = 1, …, p, where c j is the normalizing constant. Hence, the following result:
Theorem 5.5.1
Let the real p × p positive definite matrix W have a real Wishart density as specified in (5.5.4) and let W = TT ′ where T = (t ij) is a lower triangular matrix whose diagonal elements are positive. Then, the non-diagonal elements t ij such that i > j are mutually independently distributed as real standard normal variables, the diagonal elements \(t_{jj}^2,~ j=1,\ldots ,p,\) are independently distributed as a real chisquare variables having m − (j − 1) degrees of freedom for j = 1, …, p, and the \(t_{jj}^2\) ’s and t ij ’s are mutually independently distributed.
Corollary 5.5.1
Let W ∼ W p(n, σ 2 I), where σ 2 > 0 is a real scalar quantity. Let W = TT ′ where T = (t ij) is a lower triangular matrix whose diagonal elements are positive. Then, the t jj ’s are independently distributed for j = 1, …, p, the t ij ’s, i > j, are independently distributed, and all t jj ’s and t ij ’s are mutually independently distributed, where \(t_{jj}^2/{\sigma ^2}\) has a real chisquare distribution with m − (j − 1) degrees of freedom for j = 1, …, p, and t ij, i > j, has a real scalar Gaussian distribution with mean value zero and variance σ 2 , that is, \(t_{ij} \overset {iid}{\sim } N(0,\sigma ^2)\) for all i > j.
5.5a.2. Triangularization of the Wishart matrix in the complex domain
Let \(\tilde {W}\) have the following Wishart density in the complex domain:
and \(\tilde {f}_w(\tilde {W})=0\) elsewhere, which is denoted \(\tilde {W}\sim \tilde {W}_p(m,I)\). Consider the transformation \(\tilde {W}=\tilde {T}\tilde {T}^{*}\) where \(\tilde {T}\) is lower triangular whose diagonal elements are real and positive. The transformation \(\tilde {W}=\tilde {T}\tilde {T}^{*}\) is then one-to-one and its associated Jacobian, as given in Theorem 1.6a.7, is the following:
Then we have
In light of (5.5a.6), it is clear that all the t jj’s and \(\tilde {t}_{ij}\)’s are mutually independently distributed where \(\tilde {t}_{ij},~i>j,\) has a complex standard Gaussian density and \(t_{jj}^2\) has a complex chisquare density with degrees of freedom m − (j − 1) or a real gamma density with the parameters (α = m − (j − 1), β = 1), for j = 1, …, p. Hence, we have the following result:
Theorem 5.5a.1
Let the complex Wishart density be as specified in (5.5a.4), that is, \(\tilde {W}\sim \tilde {W}_p(m,I)\) . Consider the transformation \(\tilde {W}=\tilde {T}\tilde {T}^{*}\) where \(\tilde {T}=(\tilde {t}_{ij})\) is a lower triangular matrix in the complex domain whose diagonal elements are real and positive. Then, for i > j, the \(\tilde {t}_{ij}\) ’s are standard Gaussian distributed in the complex domain, that is, \(\tilde {t}_{ij}\sim \tilde {N}_1(0,1),~i>j\), \(t_{jj}^2\) is real gamma distributed with the parameters (α = m − (j − 1), β = 1) for j = 1, …, p, and all the t jj ’s and \(\tilde {t}_{ij}\) ’s, i > j, are mutually independently distributed.
Corollary 5.5a.1
Let \(\tilde {W}\sim \tilde {W}_p(m,\sigma ^2I)\) where σ 2 > 0 is a real positive scalar. Let \(\tilde {T},~ t_{jj},~ \tilde {t}_{ij},~i>j\) , be as defined in Theorem 5.5a.1 . Then, \(t_{jj}^2/{\sigma ^2}\) is a real gamma variable with the parameters (α = m − (j − 1), β = 1) for j = 1, …, p, \(\tilde {t}_{ij}\sim \tilde {N}_1(0,\sigma ^2)\) for all i > j, and the t jj ’s and \(\tilde {t}_{ij}\) ’s are mutually independently distributed.
5.5.3. Samples from a p-variate Gaussian population and the Wishart density
Let the p × 1 real vector X j be normally distributed, X j ∼ N p(μ, Σ), Σ > O. Let X 1, …, X n be a simple random sample of size n from this normal population and the p × n sample matrix be denoted in bold face lettering as X = (X 1, X 2, …, X n) where \(X_j^{\prime }=(x_{1j},x_{2j},\ldots ,x_{pj})\). Let the sample mean be \(\bar {X}=\frac {1}{n}(X_1+\cdots +X_n)\) and the matrix of sample means be denoted by the bold face \({\bar {\mathbf {X}}}=(\bar {X},\ldots ,\bar {X})\). Then, the p × p sample sum of products matrix S is given by
where \(\bar {x}_r=\sum _{k=1}^nx_{rk}/n,~ r=1,\ldots ,p,\) are the averages on the components. It has already been shown in Sect. 3.5 for instance that the joint density of the sample values X 1, …, X n, denoted by L, can be written as
But \((\mathbf {X}-{\bar {\mathbf {X}}})J=O,~ J^{\prime }=(1,\ldots ,1),\) which implies that the columns of \((\mathbf {X}-{\bar {\mathbf {X}}})\) are linearly related, and hence the elements in \((\mathbf {X}-{\bar {\mathbf {X}}})\) are not distinct. In light of equation (4.5.17), one can write the sample sum of products matrix S in terms of a p × (n − 1) matrix Z n−1 of distinct elements so that \(S=Z_{n-1}Z_{n-1}^{\prime }\). As well, according to Theorem 3.5.3 of Chap. 3, S and \(\bar {X}\) are independently distributed. The p × n matrix Z is obtained through the orthonormal transformation X P = Z, PP ′ = I, P′P = I where P is n × n. Then dX = dZ, ignoring the sign. Let the last column of P be p n. We can specify p n to be \(\frac {1}{\sqrt {n}}J\) so that \(\mathbf {X}p_n=\sqrt {n}\bar {\mathbf {X}}\). Note that in light of (4.5.17), the deleted column in Z corresponds to \(\sqrt {n}\bar {\mathbf {X}}\). The following considerations will be helpful to those who might need further confirmation of the validity of the above statement. Observe that \(\mathbf {X} -{\bar {\mathbf {X}}}=\mathbf {X}(I-B),\) with \(B=\frac {1}{n}JJ^{\prime }\) where J is a n × 1 vector of unities. Since I − B is idempotent and of rank n − 1, the eigenvalues are 1 repeated n − 1 times and a zero. An eigenvector, corresponding to the eigenvalue zero, is J normalized or \(\frac {1}{\sqrt {n}}J\). Taking this as the last column p n of P, we have \(\mathbf {X}p_n=\sqrt {n}\bar {\mathbf {X}}\). Note that the other columns of P, namely p 1, …, p n−1, correspond to the n − 1 orthonormal solutions coming from the equation BY = Y where Y is a n × 1 non-null vector. Hence we can write \(\text{d}Z=\text{d}Z_{n-1}\wedge \text{d}\bar {X}\). Now, integrating out \(\bar {X}\) from (5.5.7), we have
where c is a constant. Since Z n−1 contains p(n − 1) distinct real variables, we may apply Theorems 4.2.1, 4.2.2 and 4.2.3, and write dZ n−1 in terms of dS as
Then, if the density of S is denoted by f(S),
where c 1 is a constant. From a real matrix-variate gamma density, we have the normalizing constant, thereby the value of c 1. Hence
for S > O, Σ > O, n − 1 ≥ p and f(X) = 0 elsewhere, Γ p(⋅) being the real matrix-variate gamma given by
Usually the sample size is taken as N so that N − 1 = n the number of degrees of freedom associated with the Wishart density in (5.5.10). Since we have taken the sample size as n, the number of degrees of freedom is n − 1 and the parameter matrix is Σ > O. Then S in (5.5.10) is written as S ∼ W p(m, Σ), with m = n − 1 ≥ p. Thus, the following result:
Theorem 5.5.2
Let X 1, …, X n be a simple random sample of size n from a N p(μ, Σ), Σ > O. Let \(X_j,~\mathbf {X},~\bar {X},~{\bar {\mathbf {X}}},~S\) be as defined in Sect. 5.5.3 . Then, the density of S is a real Wishart density with m = n − 1 degrees of freedom and parameter matrix Σ > O, as given in (5.5.10).
5.5a.3. Sample from a complex Gaussian population and the Wishart density
Let \(\tilde {X}_j\sim \tilde {N}_p(\tilde {\mu },\varSigma ),~ \varSigma >O,~ j=1,\ldots ,n\) be independently distributed. Let \(\tilde {\mathbf {X}}=(\tilde {X}_1,\ldots ,\tilde {X}_n),~ \bar {\tilde {X}}=\frac {1}{n}(\tilde {X}_1+\cdots +\tilde {X}_n),~ {\bar {\tilde {\mathbf {X}}}}=(\bar {\tilde {X}},\ldots ,\bar {\tilde {X}})\) and let \(\tilde {S}=(\tilde {\mathbf {X}}-{\bar {\tilde {\mathbf {X}}}})(\tilde {\mathbf {X}}-{\bar {\tilde {\mathbf {X}}}})^{*}\) where a * indicates the conjugate transpose. We have already shown in Sect. 3.5a that the joint density of \(\tilde {X}_1,\ldots ,\tilde {X}_n\), denoted by \(\tilde {L}\), can be written as
Then, following steps parallel to (5.5.7) to (5.5.10), we obtain the density of \(\tilde {S}\), denoted by \(\tilde {f}(\tilde {S})\), as the following:
for \(\tilde {S}>O,~\varSigma >O,~ n-1\ge p,\) and \(\tilde {f}(\tilde {S})=0\) elsewhere, where the complex matrix-variate gamma function being given by
Hence, we have the following result:
Theorem 5.5a.2
Let \(\tilde {X}_j\sim \tilde {N}_p(\mu ,\varSigma ),~\varSigma >O,~j=1,\ldots ,n\) , be independently and identically distributed. Let \(\tilde {\mathbf {X}},~ \bar {\tilde {X}}, ~{\bar {\tilde {\mathbf {X}}}},~\tilde {S}\) be as previously defined. Then, \(\tilde {S}\) has a complex matrix-variate Wishart density with m = n − 1 degrees of freedom and parameter matrix Σ > O, as given in (5.5a.8).
5.5.4. Some properties of the Wishart distribution, real case
If we have statistically independently distributed Wishart matrices with the same parameter matrix Σ, then it is easy to see that the sum is again a Wishart matrix. This can be noted by considering the Laplace transform of matrix-variate random variables discussed in Sect. 5.2. If S j ∼ W p(m j, Σ), j = 1, …, k, with the same parameter matrix Σ > O and the S j’s are statistically independently distributed, then from equation (5.2.6), the Laplace transform of the density of S j is
where ∗ T is a symmetric parameter matrix T = (t ij) = T′ > O with off-diagonal elements weighted by \(\frac {1}{2}\). When S j’s are independently distributed, then the Laplace transform of the sum S = S 1 + ⋯ + S k is the product of the Laplace transforms:
Hence, the following result:
Theorems 5.5.3, 5.5a.3
Let S j ∼ W p(m j, Σ), Σ > O, j = 1, …, k, be statistically independently distributed real Wishart matrices with m 1, …, m k degrees of freedoms and the same parameter matrix Σ > O. Then the sum S = S 1 + ⋯ + S k is real Wishart distributed with degrees of freedom m 1 + ⋯ + m k and the same parameter matrix Σ > O, that is, S ∼ W p(m 1 + ⋯ + m k, Σ), Σ > O. In the complex case, let \(\tilde {S}_j\sim \tilde {W}_p(m,\tilde {\varSigma }),~ \tilde {\varSigma }=\tilde {\varSigma }^{*}>O,~ j=1,\ldots ,k\) , be independently distributed with the same \(\tilde {\varSigma }\) . Then, the sum \(\tilde {S}=\tilde {S}_1+\cdots +\tilde {S}_k\sim \tilde {W}_p(m_1+\cdots +m_k,\tilde {\varSigma })\).
We now consider linear functions of independent Wishart matrices. Let S j ∼ W p(m j, Σ), Σ > O, j = 1, …k, be independently distributed and S a = a 1 S 1 + ⋯ + a k S k where a 1, …, a k are real scalar constants, then the Laplace transform of the density of S a is
The inverse is quite complicated and the corresponding density cannot be easily determined; moreover, the density is not a Wishart density unless a 1 = ⋯ = a k. The types of complications occurring can be apprehended from the real scalar case p = 1 which is discussed in Mathai and Provost (1992). Instead of real scalars, we can also consider p × p constant matrices as coefficients, in which case the inversion of the Laplace transform will be more complicated. We can also consider Wishart matrices with different parameter matrices. Let U j ∼ W p(m j, Σ j), Σ j > O, j = 1, …, k, be independently distributed and U = U 1 + ⋯ + U k. Then, the Laplace transform of the density of U, denoted by L U(∗ T), is the following:
This case does not yield a Wishart density as an inverse Laplace transform either, unless Σ 1 = ⋯ = Σ k. In both (i) and (ii), we have linear functions of independent Wishart matrices; however, these linear functions do not have Wishart distributions.
Let us consider a symmetric transformation on a Wishart matrix S. Let S ∼ W p(m, Σ), Σ > O and U = ASA ′ where A is a p × p nonsingular constant matrix. Let us take the Laplace transform of the density of U:
Hence we have the following result:
Theorems 5.5.4, 5.5a.4
Let S ∼ W p(m, Σ > O) and U = ASA′, |A|≠0. Then, U ∼ W p(m, AΣA′), Σ > O, |A|≠0, that is, when U = ASA ′ where A is a nonsingular p × p constant matrix, then U is Wishart distributed with degrees of freedom m and parameter matrix AΣA ′ . In the complex case, the constant p × p nonsingular matrix A can be real or in the complex domain. Let \(\tilde {S}\sim \tilde {W}_p(m,\tilde {\varSigma }),~ \tilde {\varSigma }=\tilde {\varSigma }^{*}>O\) . Then \(\tilde {U}=A\tilde {S}A^{*}\sim \tilde {W}_p(m, A\tilde {\varSigma }A^{*}).\)
If A is not a nonsingular matrix, is there a corresponding result? Let B be a constant q × p matrix, q ≤ p, which is of full rank q. Let X j ∼ N p(μ, Σ), Σ > O, j = 1, …, n, be iid so that we have a simple random sample of size n from a real p-variate Gaussian population. Let the q × 1 vectors Y j = BX j, j = 1, …, n, be iid. Then E[Y j] = Bμ, Cov(Y j) = E[(Y j−E(Y j))(Y j−E(Y j))′] = BE[(X j−E(X j))(X j−E(X j))′B′ = BΣB ′ which is q × q. As well, Y j ∼ N q(Bμ, BΣB′), BΣB′ > O. Consider the sample matrix formed from the Y j’s, namely the q × n matrix Y = (Y 1, …, Y n) = (BX 1, …, BX n) = B(X 1, …, X n) = B X where X is the p × n sample matrix from X j. Then, the sample sum of products matrix in Y is \((\mathbf {Y}-{\bar {\mathbf {Y}}})(\mathbf {Y}-{\bar {\mathbf {Y}}})'=S_y\), say, where the usual notation is utilized, namely, \(\bar {Y}=\frac {1}{n}(Y_1+\cdots +Y_n)\) and \({\bar {\mathbf {Y}}}=(\bar {Y},\ldots ,\bar {Y})\). Now, the problem is equivalent to taking a simple random sample of size n from a q-variate real Gaussian population with mean value vector Bμ and positive definite covariance matrix BΣB′ > O. Hence, the following result:
Theorems 5.5.5, 5.5a.5
Let X j ∼ N p(μ, Σ), Σ > O, j = 1, …, n, be iid, and S be the sample sum of products matrix in this p-variate real Gaussian population. Let B be a q × p constant matrix, q ≤ p, which has full rank q. Then BSB ′ is real Wishart distributed with degrees of freedom m = n − 1, n being equal to the sample size, and parameter matrix BΣB′ > O, that is, BSB ∼ W q(m, BΣB′). Similarly, in the complex case, let B be a q × p, q ≤ p, constant matrix of full rank q, where B may be in the real or complex domain. Then, \(B\tilde {S}B^{*}\) is Wishart distributed with degrees of freedom m and parameter matrix \(B\tilde {\varSigma }B^{*}\) , that is, \(B\tilde {S}B^{*}\sim \tilde {W}_q(m, B\tilde {\varSigma }B^{*}).\)
5.5.5. The generalized variance
Let \(X_j,~ X_j^{\prime }=(x_{1j},\ldots ,x_{pj}),\) be a real p × 1 vector random variable for j = 1, …, n, and the X j’s be iid (independently and identically distributed) as X j. Let the covariance matrix associated with X j be Cov(X j) = E[(X j − E(X j))(X j − E(X j))′] = Σ, Σ ≥ O, for j = 1, …, n in the real case and \(\tilde {\varSigma }=E[(\tilde {X}_j-E(\tilde {X}_j))(\tilde {X}_j-E(\tilde {X}_j))^{*}]\) in the complex case, where an asterisk indicates the conjugate transpose. Then, the diagonal elements in Σ represent the squares of a measure of scatter or variances associated with the elements x 1j, …, x pj and the off-diagonal elements in Σ provide the corresponding measure of joint dispersion or joint scatter in the pair (x rj, x sj) for all r≠s. Thus, Σ gives a configuration of individual and joint squared scatter in all the elements x 1j, …, x pj. If we wish to have a single number or single scalar quantity representing this configuration of individual and joint scatter in the elements x 1j, …, x pj what should be that measure? Wilks had taken the determinant of Σ, |Σ|, as that measure and called it the generalized variance or square of the scatter representing the whole configuration of scatter in all the elements x 1j, …, x pj. If there is no scatter in one or in a few elements but there is scatter or dispersion in all other elements, then the determinant is zero. If the matrix is singular then the determinant is zero, but this does not mean that there is no scatter in these elements. Thus, determinant as a measure of scatter or dispersion, violates a very basic condition that if the proposed measure is zero then there should not be any scatter in any of the elements or Σ should be a null matrix. Hence, the first author suggested to take a norm of Σ, ∥Σ∥, as a single measure of scatter in the whole configuration, such as ∥Σ∥1 =maxi∑j|σ ij| or ∥Σ∥2 = largest eigenvalue of Σ since Σ is at least positive semi-definite. Note that normality is not assumed in the above discussion.
If S ∼ W p(m, Σ), Σ > O, what is then the distribution of Wilks’ generalized variance in S, namely |S|, which can be referred to as the sample generalized variance? Let us determine the h-th moment of the sample generalized variance |S| for an arbitrary h. This has already been discussed for real and complex matrix-variate gamma distributions in Sect. 5.4.1 and can be obtained from the normalizing constant in the Wishart density:
Then
where y 1, ⋯ , y p are independently distributed real scalar gamma random variables with the parameters \((\frac {m}{2}-\frac {j-1}{2},~ 1),~ j=1,\ldots ,p\). In the complex case
where \(\tilde {y}_1,\ldots ,\tilde {y}_p\) and independently distributed real scalar gamma random variables with the parameters (m − (j − 1), 1), j = 1, …, p. Note that if we consider E[|Σ −1 S|h] instead of E[|(2Σ)−1 S|h] in (5.5.14), then the y j’s are independently distributed as real chisquare random variables having m − (j − 1) degrees of freedom for j = 1, …, p. This can be stated as a result.
Theorems 5.5.6, 5.5a.6
Let S ∼ W p(m, Σ), Σ > O, and |S| be the generalized variance associated with this Wishart matrix or the sample generalized variance in the corresponding p-variate real Gaussian population. Then, \(E[|(2\varSigma )^{-1}S|{ }^h]=E[y_1^h]\cdots E[y_p^h]\) so that |(2Σ)−1 S| has the structural representation |(2Σ)−1 S| = y 1⋯y p where the y j ’s are independently distributed real gamma random variables with the parameters \((\frac {m}{2}-\frac {j-1}{2},~ 1),~ j=1,\ldots ,p\) . Equivalently, \(E[|\varSigma ^{-1}S|{ }^h]=E[z_1^h] \cdots E[z_p]^h]\) where the z j ’s are independently distributed real chisquare random variables having m − (j − 1), j = 1, …, p, degrees of freedom. In the complex case, if we let \(\tilde {S}\sim \tilde {W}_p(m,\tilde {\varSigma }),~ \tilde {\varSigma }=\tilde {\varSigma }^{*}>O,\) and \(|\mathit{\text{det}}(\tilde {S})|\) be the generalized variance, then \(|\mathit{\text{ det}}((\tilde {\varSigma })^{-1}\tilde {S})|\) has the structural representation \(|\mathit{\text{det}}((\tilde {\varSigma })^{-1}\tilde {S})|=\tilde {y}_1\cdots \tilde {y}_p\) where the \(\tilde {y}_j\) ’s are independently distributed real scalar gamma random variables with the parameters (m − (j − 1), 1), j = 1, …, p or chisquare random variables in the complex domain having m − (j − 1), j = 1, …, p, degrees of freedom.
5.5.6. Inverse Wishart distribution
When S ∼ W p(m, Σ), Σ > O, what is then the distribution of S −1? Since S has a real matrix-variate gamma distribution, that of its inverse is directly available from the transformation U = S −1. In light of Theorem 1.6.6, we have dS = |U|−(p+1)dU for the real case and \(\text{ d}\tilde {X}=|\text{det}(\tilde {U}\tilde {U}^{*})|{ }^{-p}\text{d}\tilde {U}\) in the complex domain. Thus, denoting the density of U by g(U), we have the following result:
Theorems 5.5.7, 5.5a.7
Let the real Wishart matrix S ∼ W p(m, Σ), Σ > O, and the Wishart matrix in the complex domain \(\tilde {S}\sim \tilde {W}_p(m,~\tilde {\varSigma }),~ \tilde {\varSigma }=\tilde {\varSigma }^{*}>O\) . Let U = S −1 and \(\tilde {U}=\tilde {S}^{-1}\) . Letting the density of S be denoted by g(U) and that of \(\tilde {U}\) be denoted by \(\tilde {g}(\tilde {U})\),
and zero elsewhere, and
and zero elsewhere.
5.5.7. Marginal distributions of a Wishart matrix
At the beginning of this chapter, we had explicitly evaluated real and complex matrix-variate gamma integrals and determined that the diagonal blocks are again real and complex matrix-variate gamma integrals. Hence, the following results are already available from the discussion on the matrix-variate gamma distribution. We will now establish the results via Laplace transforms. Let S be Wishart distributed with degrees of freedom m and parameter matrix Σ > O, that is, S ∼ W p(m, Σ), Σ > O, m ≥ p. Let us partition S and Σ as follows:

(referred to as a 2 × 2 partitioning) S 11, Σ 11 being r × r and S 22, Σ 22 being (p − r) × (p − r) – refer to Sect. 1.3 for results on partitioned matrices. Let ∗ T be a similarly partitioned p × p parameter matrix with ∗ T 11 being r × r where

Observe that ∗ T is a slightly modified parameter matrix T = (t ij) = T ′ where the t ij’s are weighted with \(\frac {1}{2}\) for i≠j to obtain ∗ T. Noting that \(\text{tr}({{ }_{*}T}'S)=\text{tr}({{ }_{*}T}_{11}^{\prime }S_{11})\), the Laplace transform of the Wishart density W p(m, Σ), Σ > O, with ∗ T as defined above, is given by

Thus, S 11 has a Wishart distribution with m degrees of freedom and parameter matrix Σ 11. It can be similarly established that S 22 is Wishart distributed with degrees of freedom m and parameter matrix Σ 22. Hence, the following result:
Theorems 5.5.8, 5.5a.8
Let S ∼ W p(m, Σ), Σ > O. Let S and Σ be partitioned into a 2 × 2 partitioning as above. Then, the sub-matrices S 11 ∼ W r(m, Σ 11), Σ 11 > O, and S 22 ∼ W p−r(m, Σ 22), Σ 22 > O. In the complex case, let \(\tilde {S}\sim \tilde {W}_p(m,~\tilde {\varSigma }),~ \tilde {\varSigma }=\tilde {\varSigma }^{*}>O\) . Letting \(\tilde {S}\) be partitioned as in the real case, \(\tilde {S}_{11}\sim \tilde {W}_r(m,~\tilde {\varSigma }_{11})\) and \(\tilde {S}_{22}\sim \tilde {W}_{p-r}(m,~\tilde {\varSigma }_{22}).\)
Corollaries 5.5.2, 5.5a.2
Let S ∼ W p(m, Σ), Σ > O. Suppose that Σ 12 = O in the 2 × 2 partitioning of Σ. Then S 11 and S 22 are independently distributed with S 11 ∼ W r(m, Σ 11) and S 22 ∼ W p−r(m, Σ 22). Consider a k × k partitioning of S and Σ, the order of the diagonal blocks S jj and Σ jj being p j × p j , p 1 + ⋯ + p k = p. If Σ ij = O for all i≠j, then the S jj ’s are independently distributed as Wishart matrices on p j components, with degrees of freedom m and parameter matrices Σ jj > O, j = 1, …, k. In the complex case, consider the same type of partitioning as in the real case. Then, if \(\tilde {\varSigma }_{ij}=O\) for all i≠j, \(\tilde {S}_{jj}, ~ j=1,\ldots ,k,\) are independently distributed as \(\tilde {S}_{jj}\sim \tilde {W}_{p_j}(m,~\tilde {\varSigma }_{jj}),~ j=1,\ldots ,k,~ p_1+\cdots +p_k=p\).
Let S be a p × p real Wishart matrix with m degrees of freedom and parameter matrix Σ > O. Consider the following 2 × 2 partitioning of S and Σ −1:

Then, the density, denoted by f(S), can be written as
In this case, dS = dS 11 ∧dS 22 ∧dS 12. Let \(U_2=S_{22}-S_{21}S_{11}^{-1}S_{12}\). Referring to Sect. 1.3, the coefficient of S 11 in the exponent is \(\varSigma ^{11}=(\varSigma _{11}-\varSigma _{12}\varSigma _{22}^{-1}\varSigma _{21})^{-1}\). Let \(U_2=S_{22}-S_{21}S_{11}^{-1}S_{12}\) so that \(S_{22}=U_2+S_{21}S_{11}^{-1}S_{12}\) and dS 22 = dU 2 for fixed S 11 and S 12. Then, the function of U 2 is of the form
However, U 2 is (p − r) × (p − r) and we can write \(\frac {m}{2}-\frac {p+1}{2}=\frac {m-r}{2}-\frac {p-r+1}{2}\). Therefore \(U_2\sim W_{p-r}(m-r,~\varSigma _{22}-\varSigma _{21}\varSigma _{11}^{-1}\varSigma _{12})\) as \(\varSigma ^{22}=(\varSigma _{22}-\varSigma _{21}\varSigma _{11}^{-1}\varSigma _{12})^{-1}\). From symmetry, \(U_1=S_{11}-S_{12}S_{22}^{-1}S_{21}\sim W_r(m-(p-r),~\varSigma _{11}-\varSigma _{12}\varSigma _{22}^{-1}\varSigma _{21})\). After replacing S 22 in the exponent by \(U_2+S_{21}S_{11}^{-1}S_{12}\), the exponent, excluding \(-\frac {1}{2}\), can be written as \(\text{tr}[\varSigma ^{11}S_{11}]+\text{ tr}[\varSigma ^{22}S_{12}S_{22}^{-1}S_{21}]+\text{tr}[\varSigma ^{12}S_{21}]+\text{tr}[\varSigma ^{21}S_{12}]\). Let us try to integrate out S 12. To this end, let \(V=S_{11}^{-\frac {1}{2}}S_{12}\Rightarrow \text{d}S_{12}=|S_{11}|{ }^{\frac {p-r}{2}}\text{d}V\) for fixed S 11. Then the determinant of S 11 in f(X) becomes \(|S_{11}|{ }^{\frac {m}{2}-\frac {p+1}{2}}\times |S_{11}|{ }^{\frac {p-r}{2}}=|S_{11}|{ }^{\frac {m}{2}-\frac {r+1}{2}}\). The exponent, excluding \(-\frac {1}{2}\) becomes the following, denoting it by ρ:
Note that tr(Σ 22 V ′V ) = tr(V Σ 22 V ′) and
On comparing (i) and (ii), we have \(C'=(\varSigma ^{22})^{-1}\varSigma ^{21}S_{11}^{\frac {1}{2}}\). Substituting for C and C ′ in ρ, the term containing S 11 in the exponent becomes \(-\frac {1}{2}\text{tr}(S_{11}(\varSigma ^{11}-\varSigma ^{12}(\varSigma ^{22})^{-1}\varSigma ^{21})=-\frac {1}{2}\text{ tr}(S_{11}\varSigma _{11}^{-1})\). Collecting the factors containing S 11, we have S 11 ∼ W r(m, Σ 11) and from symmetry, S 22 ∼ W p−r(m, Σ 22). Since the density f(S) splits into a function of U 2, S 11 and \(S_{11}^{-\frac {1}{2}}S_{12}\), these quantities are independently distributed. Similarly, U 1, S 22 and \( S_{22}^{-\frac {1}{2}}S_{21}\) are independently distributed. The exponent of |U 1| is \(\frac {m}{2}-\frac {p+1}{2}=(\frac {m}{2}-\frac {p-r}{2})-\frac {r+1}{2}\). Observing that U 1 is r × r, we have the density of \(U_1=S_{11}-S_{12}S_{22}^{-1}S_{21}\) as a real Wishart density on r components, with degrees of freedom m − (p − r) and parameter matrix \(\varSigma _{11}-\varSigma _{12}\varSigma _{22}^{-1}\varSigma _{21}\) whose the density, denoted by f 1(U), is the following:
A similar expression can be obtained for the density of U 2. Thus, the following result:
Theorems 5.5.9, 5.5a.9
Let S ∼ W p(m, Σ), Σ > O, m ≥ p. Consider the 2 × 2 partitioning of S as specified above, S 11 being r × r. Let \(U_1=S_{11}-S_{12}S_{22}^{-1}S_{21}\) . Then,
In the complex case, let \(\tilde {S}\sim \tilde {W}_p(m,~\tilde {\varSigma }),~ \tilde {\varSigma }=\tilde {\varSigma }^{*}>O\) . Consider the same partitioning as in the real case and let \(\tilde {S}_{11}\) be r × r. Then, letting \(\tilde {U}_1=\tilde {S}_{11}-\tilde {S}_{12}\tilde {S}_{22}^{-1}\tilde {S}_{21}\), \(\tilde {U}_1\) is Wishart distributed as
A similar density is obtained for \(\tilde {U}_2=\tilde {S}_{22}-\tilde {S}_{21}\tilde {S}_{11}^{-1}\tilde {S}_{12}\).
Example 5.5.1
Let the 3 × 3 matrix S ∼ W 3(5, Σ), Σ > O. Determine the distributions of \(Y_1=S_{22}-S_{21}S_{11}^{-1}S_{12},~ Y_2=S_{22}\) and Y 3 = S 11 where

with S 11 being 2 × 2.
Solution 5.5.1
Let the densities of Y j be denoted by f j(Y j), j = 1, 2, 3. We need the following matrix, denoted by B:

From our usual notations, Y 1 ∼ W p−r(m − r, B). Observing that Y 1 is a real scalar, we denote it by y 1, its density being given by
and zero elsewhere. Now, consider Y 2 which is also a real scalar that will be denoted by y 2. As per our notation, Y 2 = S 22 ∼ W p−r(m, Σ 22). Its density is then as follows, observing that Σ 22 = (3), |Σ 22| = 3 and \(\varSigma _{22}^{-1}=(\frac {1}{3})\):
and zero elsewhere. Note that Y 3 = S 11 is 2 × 2. With our usual notations, p = 3, r = 2, m = 5 and |Σ 11| = 5; as well,

Thus, the density of Y 3 is
and zero elsewhere. This completes the calculations.
Example 5.5a.1
Let the 3 × 3 Hermitian positive definite matrix \(\tilde {S}\) have a complex Wishart density with degrees of freedom m = 5 and parameter matrix Σ > O. Determine the densities of \(\tilde {Y}_1=\tilde {S}_{22}-\tilde {S}_{21}\tilde {S}_{11}^{-1}\tilde {S}_{12}, \ \tilde {Y}_2=\tilde {S}_{22}\) and \(\tilde {Y}_3=\tilde {S}_{11}\) where

with S 11 and Σ 11 being 2 × 2.
Solution 5.5a.1
Observe that Σ is Hermitian positive definite. We need the following numerical results:


Note that \(\tilde {Y}_1\) and \(\tilde {Y}_2\) are real scalar quantities which will be denoted as y 1 and y 2, respectively. Let the densities of y 1 and y 2 be f j(y j), j = 1, 2. Then, with our usual notations, f 1(y 1) is
and zero elsewhere, and the density of \(\tilde {y}_2\), is
and zero elsewhere. Note that \(\tilde {Y}_3=\tilde {S}_{11}\) is 2 × 2. Letting

and \(|\text{det}(\tilde {Y}_3)|=[s_{11}s_{22}-\tilde {s}_{12}^{*}\tilde {s}_{12}]\). With our usual notations, the density of \(\tilde {Y}_3\), denoted by \(\tilde {f}_3(\tilde {Y}_3)\), is the following:
and zero elsewhere, where \(5^5\tilde {\varGamma }_2(5)=3125(144)\pi \). This completes the computations.
5.5.8. Connections to geometrical probability problems
Consider the representation of the Wishart matrix \(S=Z_{n-1}Z_{n-1}^{\prime }\) given in (5.5.8) where the p rows are linearly independent 1 × (n − 1) vectors. Then, these p linearly independent rows, taken in order, form a convex hull and determine a p-parallelotope in that hull, which is determined by the p points in the (n − 1)-dimensional Euclidean space, n − 1 ≥ p. Then, as explained in Mathai (1999), the volume content of this parallelotope is \(v=|Z_{n-1}Z_{n-1}^{\prime }|{ }^{\frac {1}{2}}=|S|{ }^{\frac {1}{2}}\), where S ∼ W p(n − 1, Σ), Σ > O. Thus, the volume content of this parallelotope is the positive square root of the generalized variance |S|. The distributions of this random volume when the p random points are uniformly, type-1 beta, type-2 beta and gamma distributed are provided in Chap. 4 of Mathai (1999).
5.6. The Distribution of the Sample Correlation Coefficient
Consider the real Wishart density or matrix-variate gamma in (5.5.10) for p = 2. For convenience, let us take the degrees of freedom parameter n − 1 = m. Then for p = 2, f(S) in (5.5.10), denoted by f 2(S), is the following, observing that |S| = s 11 s 22(1 − r 2) where r is the sample correlation coefficient:
where ρ = the population correlation coefficient, \(|\varSigma |=\sigma _{11}\sigma _{22}-\sigma _{12}^2=\sigma _{11}\sigma _{22}(1-\rho ^2)\), \(\varGamma _2(\frac {m}{2})=\pi ^{\frac {1}{2}}\varGamma (\frac {m}{2})\varGamma (\frac {m-1}{2}), ~-1<\rho <1\),

Let us make the substitution \(x_1=\frac {s_{11}}{\sigma _{11}},~ x_2=\frac {s_{22}}{\sigma _{22}}\). Note that dS = ds 11 ∧ds 22 ∧ ds 12. But \(\text{d}s_{12}=\sqrt {s_{11}s_{22}}\,\text{d}r\) for fixed s 11 and s 22. In order to obtain the density of r, we must integrate out x 1 and x 2, observing that \(\sqrt {s_{11}s_{22}}\) is coming from ds 12:
For convenience, let us expand
Then the part containing x 1 gives the integral
By symmetry, the integral over x 2 gives \([2(1-\rho ^2)]^{\frac {m}{2}+\frac {k}{2}}\varGamma (\frac {m+k}{2}),~ m\ge 2.\) Collecting all the constants we have
We can simplify \(\varGamma (\frac {m}{2})\varGamma (\frac {m}{2}-\frac {1}{2})\) by using the duplication formula for gamma functions, namely
Then,
Hence the density of r, denoted by f r(r), is the following:
and zero elsewhere, m = n − 1, n being the sample size.
5.6.1. The special case ρ = 0
In this case, (5.6.3) becomes
zero elsewhere, m = n − 1 ≥ 2, n being the sample size. The simplification is made by using the duplication formula and writing \(\varGamma (m-1)=\pi ^{-\frac {1}{2}}2^{m-2}\varGamma (\frac {m-1}{2})\varGamma (\frac {m}{2})\). For testing the hypothesis H o : ρ = 0, the test statistic is r and the null distribution, that is, the distribution under the null hypothesis H o is given in (5.6.5). Numerical tables of percentage points obtained from (5.6.5) are available. If ρ≠0, the non-null distribution is available from (5.6.3); so, if we wish to test the hypothesis H o : ρ = ρ o where ρ o is a given quantity, we can compute the percentage points from (5.6.3). It can be shown from (5.6.5) that for ρ = 0, \( t_m=\sqrt {m}\frac {r}{\sqrt {1-r^2}}\) is distributed as a Student-t with m degrees of freedom, and hence for testing H o : ρ = 0 against H 1 : ρ≠0, the null hypothesis can be rejected if \(|t_m|=\sqrt {m}\big |\frac {r}{\sqrt {1-r^2}}\big |\ge t_{m,\frac {\alpha }{2}}\) where \(Pr\{|t_m|\ge t_{m,\frac {\alpha }{2}}\}=\alpha \). For tests that make use of the Student-t statistic, refer to Mathai and Haubold (2017b). Since the density given in (5.6.5) is an even function, when ρ = 0, all odd order moments are equal to zero and the even order moments can easily be evaluated from type-1 beta integrals.
5.6.2. The multiple and partial correlation coefficients
Let the p × 1 real vector X j with \(X_j^{\prime }=(x_{1j},\ldots ,x_{pj})\) have a p-variate distribution whose mean value E(X j) = μ and covariance matrix Cov(X j) = Σ, Σ > O, where μ is p × 1 and Σ is p × p, for j = 1, …, n, the X j’s being iid (independently and identically distributed). Consider the following partitioning of Σ:

Let
Then, ρ 1.(2…p) is called the multiple correlation coefficient of x 1j on x 2j, …, x pj. The sample value corresponding to \(\rho _{1.(2\ldots p)}^2\) which is denoted by \(r_{1.(2\ldots p)}^2\) and referred to as the square of the sample multiple correlation coefficient, is given by

where s 11 is 1 × 1, S 22 is (p − 1) × (p − 1), \(S=(\mathbf {X}-{\bar {\mathbf {X}}})(\mathbf {X}-{\bar {\mathbf {X}}})'\), X = (X 1, …, X n) is the p × n sample matrix, n being the sample size, \(\bar {X}=\frac {1}{n}(X_1+\cdots +X_n),~ {\bar {\mathbf {X}}}=(\bar {X},\ldots ,\bar {X})\) is p × n, the X j’s, j = 1, …, n, being iid according to a given p-variate population having mean value vector μ and covariance matrix Σ > O, which need not be Gaussian.
5.6.3. Different derivations of ρ 1.(2…p)
Consider a prediction problem involving real scalar variables where x 1 is predicted by making use of x 2, …, x p or linear functions thereof. Let \(A_2^{\prime }=(a_2,\ldots ,a_p)\) be a constant vector where a j, j = 2, …, p are real scalar constants. Letting \(X_{(2)}^{\prime }=(x_2,\ldots ,x_p)\), a linear function of X (2) is \(u=A_2^{\prime }X_{(2)}=a_2x_2+\cdots +a_px_p\). Then, the mean value and variance of this linear function are \(E[u]=E[A_2^{\prime }X_{(2)}]=A_2^{\prime }\mu _{(2)}\) and \(\text{Var}(u)=\text{Var}(A_2^{\prime }X_{(2)})=A_2^{\prime }\varSigma _{22}A_2\) where \(\mu _{(2)}^{\prime }=(\mu _2,\ldots ,\mu _p)=E[X_{(2)}]\) and Σ 22 is the covariance matrix associated with X (2), which is available from the partitioning of Σ specified in the previous subsection. Let us determine the correlation between x 1, the variable being predicted, and u, a linear function of the variables being utilized to predict x 1, denoted by ρ 1,u, that is,
where Cov(x 1, u) = E[(x 1−E(x 1))(u−E(u))] = E[(x 1−E(x 1))(X (2)−E(X (2)))′A 2] = Cov(x 1, X (2))A 2 = Σ 12 A 2, Var(x 1) = σ 11, \(\text{Var}(u)=A_2^{\prime }\varSigma _{22}A_2>O\). Letting \(\varSigma _{22}^{-\frac {1}{2}}\) be the positive definite square root of Σ 22, we can write \(\varSigma _{12}A_2=(\varSigma _{12}\varSigma _{22}^{-\frac {1}{2}})(\varSigma _{22}^{\frac {1}{2}}A_2)\). Then, on applying Cauchy-Schwartz’ inequality, we may write \(\varSigma _{12}A_2=(\varSigma _{12}\varSigma _{22}^{-\frac {1}{2}})\) \((\varSigma _{22}^{\frac {1}{2}}A_2)\le \sqrt {(\varSigma _{12}\varSigma _{22}^{-1}\varSigma _{21})(A_2^{\prime }\varSigma _{22}A_2)}\). Thus,
This establishes the following result:
Theorem 5.6.1
The multiple correlation coefficient ρ 1.(2…p) of x 1 on x 2, …, x p represents the maximum correlation between x 1 and an arbitrary linear function of x 2, …, x p.
This shows that if we consider the joint variation of x 1 and (x 2, …, x p), this scale-free joint variation, namely the correlation, is maximum when the scale-free covariance, which constitutes a scale-free measure of joint variation, is the multiple correlation coefficient. Correlation measures a scale-free joint scatter in the variables involved, in this case x 1 and (x 2, …, x p). Correlation does not measure general relationships between the variables; counterexamples are provided in Mathai and Haubold (2017b). Hence “maximum correlation” should be interpreted as maximum joint scale-free variation or joint scatter in the variables.
For the next property, we will use the following two basic results on conditional expectations, referring also to Mathai and Haubold (2017b). Let x and y be two real scalar random variables having a joint distribution. Then,
whenever the expected values exist, where the inside expectation is taken in the conditional space of y, given x, for all x, that is, E y|x(y|x), and the outside expectation is taken in the marginal space of x, that is E x(x). The other result states that
where it is assumed that the expected value of the conditional variance and the variance of the conditional expectation exist. Situations where the results stated in (i) and (ii) are applicable or not applicable are described and illustrated in Mathai and Haubold (2017b). In result (i), x can be a scalar, vector or matrix variable. Now, let us examine the problem of predicting x 1 on the basis of x 2, …, x p. What is the “best” predictor function of x 2, …, x p for predicting x 1, “best” being construed as in the minimum mean square sense. If ϕ(x 2, …, x p) is an arbitrary predictor, then at given values of x 2, …, x p, ϕ is a constant. Consider the squared distance (x 1 − b)2 between x 1 and b = ϕ(x 2, …, x p|x 2, …, x p) or b is ϕ at given values of x 2, …, x p. Then, “minimum in the mean square sense” means to minimize the expected value of (x 1 − b)2 over all b or \(\min E(x_1-b)^2\). We have already established in Mathai and Haubold (2017b) that the minimizing value of b is b = E[x 1] at given x 2, …, x p or the conditional expectation of x 1, given x 2, …, x p or b = E[x 1|x 2, …, x p]. Hence, this “best” predictor is also called the regression of x 1 on (x 2, …, x p) or E[x 1|x 2, …, x p] = the regression of x 1 on x 2, …, x p, or the best predictor of x 1 based on x 2, …, x p. Note that, in general, for any scalar variable y and a constant a,
As the only term on the right-hand side containing a is [E(y) − a]2, the minimum is attained when this term is zero since it is a non-negative constant, zero occurring when a = E[y]. Thus, E[y − a]2 is minimized when a = E[y]. If a = ϕ(X (2)) at given value of X (2), then the best predictor of x 1, based on X (2) is E[x 1|X (2)] or the regression of x 1 on X (2). Let us determine what happens when E[x 1|X (2)] is a linear function in X (2). Let the linear function be \(b_0+b_2x_2+\cdots +b_px_p=b_0+B_2^{\prime }X_{(2)},\ B_2^{\prime }=(b_2,\ldots ,b_p),\) where b 0, b 2, …, b p are real constants [Note that only real variables and real constants are considered in this section]. That is, for some constant b 0,
Taking expectation with respect to x 1, x 2, …, x p in (iv), it follows from (i) that the left-hand side becomes E[x 1], the right side being b 0 + b 2 E[x 2] + ⋯ + b p E[x p]; subtracting this from (iv), we have
Multiplying both sides of (v) by x j − E[x j] and taking expectations throughout, the right-hand side becomes b 2 σ 2j + ⋯ + b p σ pj where σ ij = Cov(x i, x j), i≠j, and it is the variance of x j when i = j. The left-hand side is E[(x j−E(x j))(E[x 1|x (2)]−E(x 1))] = E[E(x 1 x j|X (2))]−E(x j)E(x 1) = E[x 1 x j]−E(x 1)E(x j) = Cov(x 1, x j). Three properties were utilized in the derivation, namely (i), the fact that Cov(u, v) = E[(u − E(u))(v − E(v))] = E[u(v − E(v))] = E[v(u − E(u))] and Cov(u, v) = E(uv) − E(u)E(v). As well, Var(u) = E[u − E(u)]2 = E[u(u − E(u))] as long as the second order moments exist. Thus, we have the following by combining all the linear equations for j = 2, …, p:
when Σ 22 is nonsingular, which is the case as it was assumed that Σ 22 > O. Now, the best predictor of x 1 based on a linear function of X (2) or the best predictor in the class of all linear functions of X (2) is
Let us consider the correlation between x 1 and its best linear predictor based on X (2) or the correlation between x 1 and the linear regression of x 1 on X (2). Observe that \(\text{Cov}(x_1,\varSigma _{12}\varSigma _{22}^{-1}X_{(2)})= \varSigma _{12}\varSigma _{22}^{-1}\text{ Cov}(X_{(2)},~x_1)=\varSigma _{12}\varSigma _{22}^{-1}\varSigma _{21},~ \varSigma _{21}=\varSigma _{12}^{\prime }\). Consider the variance of the best linear predictor: \(\text{ Var}(b'X_{(2)})=b'\text{Cov}(X_{(2)})b=\varSigma _{12}\varSigma _{22}^{-1}\varSigma _{22}\varSigma _{22}^{-1}\varSigma _{21}=\varSigma _{12}\varSigma _{22}^{-1}\varSigma _{21}\). Thus, the square of the correlation between x 1 and its best linear predictor or the linear regression on X (2), denoted by \(\rho ^2_{x_1,b'X_{(2)}}\), is the following:
Hence, the following result:
Theorem 5.6.2
The multiple correlation ρ 1.(2…p) between x 1 and x 2, …, x p is also the correlation between x 1 and its best linear predictor or x 1 and its linear regression on x 2, …, x p.
Observe that normality has not been assumed for obtaining all of the above properties. Thus, the results hold for any population for which moments of order two exist. However, in the case of a nonsingular normal population, that is, X j ∼ N p(μ, Σ), Σ > O, it follows from equation (3.3.5), that for r = 1, \(E[x_1|X_{(2)}]=\varSigma _{12}\varSigma _{22}^{-1}X_{(2)}\) when E[X (2)] = μ (2) = O and E(x 1) = μ 1 = 0; otherwise, \(E[x_1|X_{(2)}]=\mu _{1}+\varSigma _{12}\varSigma _{22}^{-1}(X_{(2)}-\mu _{(2)})\).
5.6.4. Distributional aspects of the sample multiple correlation coefficient
From (5.6.7), we have
which can be established from the expansion of the determinant \(|S|=|S_{22}|~|S_{11}-S_{12}S_{22}^{-1}S_{21}|\), which is available from Sect. 1.3. In our case S 11 is 1 × 1 and hence we denote it as s 11 and then \(|S_{11}-S_{12}S_{22}^{-1}S_{21}|\) is \(s_{11}-S_{12}S_{22}^{-1}S_{21}\) which is 1 × 1. Let \(u=1-r_{1.(2\ldots p)}^2=\frac {|S|}{|S_{22}|s_{11}}\). We can compute arbitrary moments of u by integrating out over the density of S, namely the Wishart density with m = n − 1 degrees of freedom when the population is Gaussian, where n is the sample size. That is, for arbitrary h,
Note that \(u^h=|S|{ }^h|S_{22}|{ }^{-h}s_{11}^{-h}\). Among the three factors |S|h, |S 22|−h and \(s_{11}^{-h}\), |S 22|−h and \(s_{11}^{-h}\) are creating problems. We will replace these by equivalent integrals so that the problematic part be shifted to the exponent. Consider the identities
for \(X_2>O,~ S_{22}>O,~\Re (h)>\frac {p_2-1}{2}\) where X 2 > O is a p 2 × p 2 real positive definite matrix, p 2 = p − 1, p 1 = 1, p 1 + p 2 = p. Then, excluding \(-\frac {1}{2}\), the exponent in (i) becomes the following:

Noting that (Σ −1 + 2Z) = Σ −1(I + 2ΣZ), we are now in a position to integrate out S from (i) by using a real matrix-variate gamma integral, denoting the constant part in (i) as c 1:
The integral in (5.6.13) can be evaluated for a general Σ, which will produce the non-null density of \(1-r_{1.(2\ldots p)}^2\)—non-null in the sense that the population multiple correlation ρ 1.(2…p)≠0. However, if ρ 1.(2…p) = 0, which we call the null case, the determinant part in (5.6.13) splits into two factors, one depending only on x and the other only involving X 2. So letting H o: ρ 1.(2…p) = 0,
But the x-integral gives \(\frac {\varGamma (h)\varGamma (\frac {m}{2})}{\varGamma (\frac {m}{2}+h)}(2\sigma _{11})^{-h}\) for \(\Re (h)>0\) and the X 2-integral gives \(\frac {\varGamma _{p_2}(h)\varGamma _{p_2}(\frac {m}{2})}{\varGamma _{p_2}(\frac {m}{2}+h)}|2\varSigma _{22}|{ }^{-h}\) for \(\Re (h)>\frac {p_2-1}{2}\). Substituting all these in (v), we note that all the factors containing 2 and Σ, σ 11, Σ 22 cancel out, and then by using the fact that
we have the following expression for the h-th null moment of u:
which happens to be the h-th moment of a real scalar type-1 beta random variable with the parameters \((\frac {m}{2}-\frac {p-1}{2},~ \frac {p-1}{2})\). Since h is arbitrary, this h-th moment uniquely determines the distribution, thus the following result:
Theorem 5.6.3
When the population has a p-variate Gaussian distribution with the parameters μ and Σ > O, and the population multiple correlation coefficient ρ 1.(2…p) = 0, the sample multiple correlation coefficient r 1.(2…p) is such that \(u=1-r^2_{1.(2\ldots p)}\) is distributed as a real scalar type-1 beta random variable with the parameters \((\frac {m}{2}-\frac {p-1}{2},~ \frac {p-1}{2})\) , and thereby \(v=\frac {u}{1-u}=\frac {1-r^2_{1.(2\ldots p)}}{r^2_{1.(2\ldots p)}}\) is distributed as a real scalar type-2 beta random variable with the parameters \((\frac {m}{2}-\frac {p-1}{2},~ \frac {p-1}{2})\) and \(w=\frac {1-u}{u}=\frac {r^2_{1.(2\ldots p)}}{1-r^2_{1.(2\ldots p)}}\) is distributed as a real scalar type-2 beta random variable with the parameters \((\frac {p-1}{2},~ \frac {m}{2}-\frac {p-1}{2})\) whose density is
and zero elsewhere.
As F-tables are available, we may conveniently express the above real scalar type-2 beta density in terms of an F-density. It suffices to make the substitution \(w=\frac {p-1}{m-p+1}F\) where F is a real F random variable having p − 1 and m − p + 1 degrees of freedom, that is, an F p−1,m−p+1 random variable, with m = n − 1, n being the sample size. The density of this F random variable, denoted by f F(F), is the following:
whenever 0 ≤ F < ∞, and zero elsewhere. In the above simplification, observe that \(\frac {(p-1)/2}{(\frac {m}{2}-\frac {p-1}{2})}=\frac {p-1}{m-p+1}\). Then, for taking a decision with respect to testing the hypothesis H o : ρ 1.(2…p) = 0, first compute \(F_{p-1,m-p+1}=\frac {m-p+1}{p-1}w,~ w=\frac {r^2_{1.(2\ldots p)}}{1-r^2_{1.(2\ldots p)}}\). Then, reject H o if the observed F p−1,m−p+1 ≥ F p−1,m−p+1,α for a given α. This will be a test at significance level α or, equivalently, a test whose critical region’s size is α. The non-null distribution for evaluating the power of this likelihood ratio test can be determined by evaluating the integral in (5.6.13) and identifying the distribution through the uniqueness property of arbitrary moments.
Note 5.6.1
By making use of Theorem 5.6.3 as a starting point and exploiting various results connecting real scalar type-1 beta, type-2 beta, F and gamma variables, one can obtain numerous results on the distributional aspects of certain functions involving the sample multiple correlation coefficient.
5.6.5. The partial correlation coefficient
Partial correlation is a concept associated with the correlation between residuals in two variables after removing the effects of linear regression on a set of other variables. Consider the real vector \(X'=(x_1,x_2,x_3,\ldots ,x_p)=(x_1,x_2,X_3^{\prime }), ~X_3^{\prime }=(x_3,\ldots ,x_p)\) where x 1, …, x p are all real scalar variables. Let the covariance matrix of X be Σ > O and let it be partitioned as follows:

where σ 11, σ 12, σ 21, σ 22 are 1 × 1, Σ 13 and Σ 23 are 1 × (p − 2), \(\varSigma _{31}=\varSigma _{13}^{\prime },~\varSigma _{32}=\varSigma _{23}^{\prime }\) and Σ 33 is (p − 2) × (p − 2). Let E[X] = O without any loss of generality. Consider the problem of predicting x 1 by using a linear function of X (3). Then, the regression of x 1 on X (3) is \(E[x_1|X_{(3)}]=\varSigma _{13}\varSigma _{33}^{-1}X_{(3)}\) from (5.6.10), and the residual part, after removing this regression from x 1 is \(e_1=x_1-\varSigma _{13}\varSigma _{33}^{-1}X_{(3)}\). Similarly, the linear regression of x 2 on X (3) is \(E[x_2|X_{(3)}]=\varSigma _{23}\varSigma _{33}^{-1}X_{(3)}\) and the residual in x 2 after removing the effect of X (3) is \(e_2=x_2-\varSigma _{13}\varSigma _{33}^{-1}X_{(3)}\). What are then the variances of e 1 and e 2, the covariance between e 1 and e 2, and the scale-free covariance, namely the correlation between e 1 and e 2? Since e 1 and e 2 are all linear functions of the variables involved, we can utilize the expressions for variances of linear functions and covariance between linear functions, a basic discussion of such results being given in Mathai and Haubold (2017b). Thus,
It can be similarly shown that
Then, the correlation between the residuals e 1 and e 2, which is called the partial correlation between x 1 and x 2 after removing the effects of linear regression on X (3) and is denoted by ρ 12.(3…p), is such that
In the above simplifications, we have for instance used the fact that \(\varSigma _{13}\varSigma _{33}^{-1}\varSigma _{32}=\varSigma _{23}\varSigma _{33}^{-1}\varSigma _{31}\) since both are real 1 × 1 and one is the transpose of the other.
The corresponding sample partial correlation coefficient between x 1 and x 2 after removing the effects of linear regression on X (3), denoted by r 12.(3…p), is such that:
where the sample sum of products matrix S is partitioned correspondingly, that is,

and s 11, s 12, s 21, s 22 being 1 × 1. In all the above derivations, we did not use any assumption of an underlying Gaussian population. The results hold for any general population as long as product moments up to second order exist. However, if we assume a p-variate nonsingular Gaussian population, then we can obtain some interesting results on the distributional aspects of the sample partial correlation, as was done in the case of the sample multiple correlation. Such results will not be herein considered.
Exercises 5.6
5.6.1
Let the p × p real positive definite matrix W be distributed as W ∼ W
p(m, Σ) with Σ = I. Consider the partitioning  where W
11 is r × r, r < p. Evaluate explicitly the normalizing constant in the density of W by first integrating out (1): W
11, (2): W
22, (3): W
12.
where W
11 is r × r, r < p. Evaluate explicitly the normalizing constant in the density of W by first integrating out (1): W
11, (2): W
22, (3): W
12.
5.6.2
Repeat Exercise 5.6.1 for the complex case.
5.6.3
Let the p × p real positive definite matrix W have a real Wishart density with degrees of freedom m ≥ p and parameter matrix Σ > O. Consider the transformation W = TT ′ where T is lower triangular with positive diagonal elements. Evaluate the densities of the t jj’s and the t ij’s, i > j if (1): Σ = diag(σ 11, …, σ pp), (2): Σ > O is a general matrix.
5.6.4
Repeat Exercise 5.6.3 for the complex case. In the complex case, the diagonal elements in T are real and positive.
5.6.5
Let S ∼ W p(m, Σ), Σ > O. Compute the density of S −1 in the real case, and repeat for the complex case.
5.7. Distributions of Products and Ratios of Matrix-variate Random Variables
In the real scalar case, one can easily interpret products and ratios of real scalar variables, whether these are random or mathematical variables. However, when it comes to matrices, products and ratios are to be carefully defined. Let X 1 and X 2 be independently distributed p × p real symmetric and positive definite matrix-variate random variables with density functions f 1(X 1) and f 2(X 2), respectively. By definition, f 1 and f 2 are respectively real-valued scalar functions of the matrices X 1 and X 2. Due to statistical independence of X 1 and X 2, their joint density, denoted by f(X 1, X 2), is the product of the marginal densities, that is, f(X 1, X 2) = f 1(X 1)f 2(X 2). Let us define a ratio and a product of matrices. Let \(U_2=X_2^{\frac {1}{2}}X_1X_2^{\frac {1}{2}}\) and \(U_1=X_2^{\frac {1}{2}}X_1^{-1}X_2^{\frac {1}{2}}\) be called the symmetric product and symmetric ratio of the matrices X 1 and X 2, where \(X_2^{\frac {1}{2}}\) denotes the positive definite square root of the positive definite matrix X 2. Let us consider the product U 2 first. We could have also defined a product by interchanging X 1 and X 2. When it comes to ratios, we could have considered the ratios X 1 to X 2 as well as X 2 to X 1. Nonetheless, we will start with U 1 and U 2 as defined above.
5.7.1. The density of a product of real matrices
Consider the transformation \(U_2=X_2^{\frac {1}{2}}X_1X_2^{\frac {1}{2}},~V=X_2\). Then, it follows from Theorem 1.6.5 that:
Letting the joint density of U 2 and V be denoted by g(U 2, V ) and the marginal density of U 2, by g 2(U 2), we have
g 2(U 2) being referred to as the density of the symmetric product U 2 of the matrices X 1 and X 2. For example, letting X 1 and X 2 be independently distributed two-parameter matrix-variate gamma random variables with the densities
for \(B_j>O,~ X_j>O,~ \Re (\alpha _j)>\frac {p-1}{2},~j=1,2\), and zero elsewhere, we have
where c is the product of the normalizing constants of the densities specified in (i). On comparing (5.7.3) with the Krätzel integral defined in the real scalar case in Chap. 2, as well as in Mathai (2012) and Mathai and Haubold (1988, 2011a, 2017,a), it is seen that (5.7.3) can be regarded as a real matrix-variate analogue of Krätzel’s integral. One could also obtain the real matrix-variate version of the inverse Gaussian density from the integrand.
As another example, let f 1(X 1) be a real matrix-variate type-1 beta density as previously defined in this chapter, whose parameters are \((\gamma +\frac {p+1}{2},~\alpha )\) with \(\Re (\alpha )>\frac {p-1}{2},~ \Re (\gamma )>-1\), its density being given by
for \(O<X_1<I,~ \Re (\gamma )>-1,~\Re (\alpha )>\frac {p-1}{2}\), and zero elsewhere. Letting f 2(X 2) = f(X 2) be any other density, the density of U 2 is then
where
is called the real matrix-variate Erdélyi-Kober right-sided or second kind fractional integral of order α and parameter γ as for p = 1, that is, in the real scalar case, (5.7.5) corresponds to the Erdélyi-Kober fractional integral of the second kind of order α and parameter γ. This connection of the density of a symmetric product of matrices to a fractional integral of the second kind was established by Mathai (2009, 2010) and further papers.
5.7.2. M-convolution and fractional integral of the second kind
Mathai (1997) referred to the structure in (5.7.2) as the M-convolution of a product where f 1 and f 2 need not be statistical densities. Actually, they could be any function provided the integral exists. However, if f 1 and f 2 are statistical densities, this M-convolution of a product can be interpreted as the density of a symmetric product. Thus, a physical interpretation to an M-convolution of a product is provided in terms of statistical densities. We have seen that (5.7.2) is connected to a fractional integral when f 1 is a real matrix-variate type-1 beta density and f 2 is an arbitrary density. From this observation, one can introduce a general definition for a fractional integral of the second kind in the real matrix-variate case. Let
and f 2(X 2) = ϕ 2(X 2)f(X 2) where ϕ 1 and ϕ 2 are specified functions and f is an arbitrary function. Then, consider the M-convolution of a product, again denoted by g 2(U 2):
The right-hand side (5.7.6) will be called a fractional integral of the second kind of order α in the real matrix-variate case. By letting p = 1 and specifying ϕ 1 and ϕ 2, one can obtain all the fractional integrals of the second kind of order α that have previously been defined by various authors. Hence, for a general p, one has the corresponding real matrix-variate cases. For example, on letting ϕ 1(X 1) = |X 1|γ and ϕ 2(X 2) = 1, one has Erdélyi-Kober fractional integral of the second kind of (5.7.5) in the real matrix-variate case as for p = 1, it is the Erdélyi-Kober fractional integral of the second kind of order α. Letting ϕ 1(X 1) = 1 and ϕ 2(X 2) = |X 2|α, (5.7.6) simplifies to the following integral, again denoted by g 2(U 2):
For p = 1, (5.7.7) is Weyl fractional integral of the second kind of order α. Accordingly, (5.7.7) is Weyl fractional integral of the second kind in the real matrix-variate case. For p = 1, (5.7.7) is also the Riemann-Liouville fractional integral of the second kind of order α in the real scalar case, if there exists a finite upper bound for V . If V is bounded above by a real positive definite constant matrix B > O in the integral in (5.7.7), then (5.7.7) is Riemann-Liouville fractional integral of the second kind of order α for the real matrix-variate case. Connections to other fractional integrals of the second kind can be established by referring to Mathai and Haubold (2017).
The appeal of fractional integrals of the second kind resides in the fact that they can be given physical interpretations as the density of a symmetric product when f 1 and f 2 are densities or as an M-convolution of products, whether in the scalar variable case or the matrix-variate case, and that in both the real and complex domains.
5.7.3. A pathway extension of fractional integrals
Consider the following modification to the general definition of a fractional integral of the second kind of order α in the real matrix-variate case given in (5.7.6). Let
where \(\Re (\alpha )>\frac {p-1}{2}\) and q < 1, and a > 0, η > 0 are real scalar constants. For all q < 1, g 2(U 2) corresponding to f 1(X 1) and f 2(X 2) of (iv) will define a family of fractional integrals of the second kind. Observe that when X 1 and I − a(1 − q)X 1 > O, then \(O<X_1<\frac {1}{a(1-q)}I\). However, by writing (1 − q) = −(q − 1) for q > 1, one can switch into a type-2 beta form, namely, I + a(q − 1)X 1 > O for q > 1, which implies that X 1 > O and the fractional nature is lost. As well, when q → 1,
which is the exponential form or gamma density form. In this case too, the fractional nature is lost. Thus, through q, one can obtain matrix-variate type-1 and type-2 beta families and a gamma family of functions from (iv). Then q is called the pathway parameter which generates three families of functions. However, the fractional nature of the integrals is lost for the cases q > 1 and q → 1. In the real scalar case, x 1 may have an exponent and making use of \([1-(1-q)x_1^{\delta }]^{\alpha -1}\) can lead to interesting fractional integrals for q < 1. However, raising X 1 to an exponent δ in the matrix-variate case will fail to produce results of interest as Jacobians will then take inconvenient forms that cannot be expressed in terms of the original matrices; this is for example explained in detail in Mathai (1997) for the case of a squared real symmetric matrix.
5.7.4. The density of a ratio of real matrices
One can define a symmetric ratio in four different ways: \(X_2^{\frac {1}{2}}X_1^{-1}X_2^{\frac {1}{2}}\) with V = X 2 or V = X 1 and \(X_1^{\frac {1}{2}}X_2^{-1}X_1^{\frac {1}{2}}\) with V = X 2 or V = X 1. All these four forms will produce different structures on f 1(X 1)f 2(X 2). Since the form U 1 that was specified in Sect. 5.7 in terms of \(X_2^{\frac {1}{2}}X_1^{-1}X_2^{\frac {1}{2}}\) with V = X 2 provides connections to fractional integrals of the first kind, we will consider this one whose density, denoted by g 1(U 1), is the following observing that \(\text{d}X_1\wedge \text{ d}X_2=|V|{ }^{\frac {p+1}{2}}|U_1|{ }^{-(p+1)}\text{d}U_1\wedge \text{d}V\):
provided the integral exists. As in the fractional integral of the second kind in real matrix-variate case, we can give a general definition for a fractional integral of the first kind in the real matrix-variate case as follows: Let f 1(X 1) and f 2(X 2) be taken as in the case of fractional integral of the second kind with ϕ 1 and ϕ 2 as preassigned functions. Then
As an example, letting
we have
for \(\Re (\alpha )>\frac {p-1}{2}, ~ \Re (\gamma )>\frac {p-1}{2}\), where
for \(\Re (\alpha )>\frac {p-1}{2},~ \Re (\gamma )>\frac {p-1}{2},\) is Erdélyi-Kober fractional integral of the first kind of order α and parameter γ in the real matrix-variate case. Since for p = 1 or in the real scalar case, \(K_{1,u_1,\gamma }^{-\alpha }f\) is Erdélyi-Kober fractional integral of order α and parameter γ, the first author referred to \(K_{1,u_1,\gamma }^{-\alpha }f\) in (5.7.11) as Erdélyi-Kober fractional integral of the first kind of order α in the real matrix-variate case.
By specializing ϕ 1 and ϕ 2 in the real scalar case, that is, for p = 1, one can obtain all the fractional integrals of the first kind of order α that have been previously introduced in the literature by various authors. One can similarly derive the corresponding results on fractional integrals of the first kind in the real matrix-variate case. Before concluding this section, we will consider one more special case. Let
In this case, g 1(U 1) is not a statistical density but it is the M-convolution of a ratio. Under the above substitutions, g 1(U 1) of (5.7.9) becomes
For p = 1, (5.7.12) is Weyl fractional integral of the first kind of order α; accordingly the first author refers to (5.7.12) as Weyl fractional integral of the first kind of order α in the real matrix-variate case. Since we are considering only real positive definite matrices here, there is a natural lower bound for the integral or the integral is over O < V < U 1. When there is a specific lower bound, such as O < V , then for p = 1, (5.7.12) is called the Riemann-Liouville fractional integral of the first kind of order α. Hence (5.7.12) will be referred to as the Riemann-Liouville fractional integral of the first kind of order α in the real matrix-variate case.
Example 5.7.1
Let X 1 and X 2 be independently distributed p × p real positive definite gamma matrix-variate random variables whose densities are
and zero elsewhere. Show that the densities of the symmetric ratios of matrices \(U_1=X_1^{-\frac {1}{2}}X_2X_1^{-\frac {1}{2}}\) and \(U_2=X_2^{\frac {1}{2}}X_1^{-1}X_2^{\frac {1}{2}}\) are identical.
Solution 5.7.1
Observe that for p = 1 that is, in the real scalar case, both U 1 and U 2 are the ratio of real scalar variables \(\frac {x_2}{x_1}\) but in the matrix-variate case U 1 and U 2 are different matrices. Hence, we cannot expect the densities of U 1 and U 2 to be the same. They will happen to be identical because of a property called functional symmetry of the gamma densities. Consider U 1 and let V = X 1. Then, \(X_2=V^{\frac {1}{2}}U_1V^{\frac {1}{2}}\) and \(\text{ d}X_1\wedge \text{d}X_2=|V|{ }^{\frac {p+1}{2}}\text{d}V\wedge \text{d}U_1\). Due to the statistical independence of X 1 and X 2, their joint density is f 1(X 1)f 2(X 2) and the joint density of U 1 and V is \(|V|{ }^{\frac {p+1}{2}}f_1(V)f_2(V^{\frac {1}{2}}U_1V^{\frac {1}{2}})\), the marginal density of U 1, denoted by g 1(U 1), being the following:
The exponent of e can be written as follows:
Letting \(Y=(I+U_1)^{\frac {1}{2}}V(I+U_1)^{\frac {1}{2}}\Rightarrow \text{d}Y=|I+U_1|{ }^{\frac {p+1}{2}}\text{d}V.\) Then carrying out the integration in g 1(U 1), we obtain the following density function:
which is a real matrix-variate type-2 beta density with the parameters (α 2, α 1). The original conditions \(\Re (\alpha _j)>\frac {p-1}{2},~j=1,2,\) remain the same, no additional conditions being needed. Now, consider U 2 and let V = X 2 so that \(X_1=V^{\frac {1}{2}}U_2^{-1}V^{\frac {1}{2}}\Rightarrow \text{ d}X_1\wedge \text{d}X_2=|V|{ }^{\frac {p+1}{2}}|U_2|{ }^{-(p+1)}\text{d}V\wedge \text{d}U_2\). The marginal density of U 2 is then:
As previously explained, the exponent in (ii) can be simplified to \(-\text{tr}[(I+U_2^{-1})^{\frac {1}{2}}V\) \((I+U_2^{-1})^{\frac {1}{2}}]\), which once integrated out yields \(\varGamma _p(\alpha _1+\alpha _2)|I+U_2^{-1}|{ }^{-(\alpha _1+\alpha _2)}\). Then,
It follows from (i),(ii) and (iii) that g 1(U 1) = g 2(U 2). Thus, the densities of U 1 and U 2 are indeed one and the same, as had to be proved.
5.7.5. A pathway extension of first kind integrals, real matrix-variate case
As in the case of fractional integral of the second kind, we can also construct a pathway extension of the first kind integrals in the real matrix-variate case. Let
and f 2(X 2) = ϕ 2(X 2)f(X 2) for the scalar parameters a > 0, η > 0, q < 1. When q < 1, (5.7.13) remains in the generalized type-1 beta family of functions. However, when q > 1, f 1 switches to the generalized type-2 beta family of functions and when q → 1, (5.6.13) goes into a gamma family of functions. Since X 1 > O for q > 1 and q → 1, the fractional nature is lost in those instances. Hence, only the case q < 1 is relevant in this subsection. For various values of q < 1, one has a family of fractional integrals of the first kind coming from (5.7.13). For details on the concept of pathway, the reader may refer to Mathai (2005) and later papers. With the function f 1(X 1) as specified in (5.7.13) and the corresponding f 2(X 2) = ϕ 2(X 2)f(X 2), one can write down the M-convolution of a ratio, g 1(U 1), corresponding to (5.7.8). Thus, we have the pathway extended form of g 1(U 1).
5.7a. Density of a Product and Integrals of the Second Kind
The discussion in this section parallels that in the real matrix-variate case. Hence, only a summarized treatment will be provided. With respect to the density of a product when \(\tilde {f}_1\) and \(\tilde {f}_2\) are matrix-variate gamma densities in the complex domain, the results are parallel to those obtained in the real matrix-variate case. Hence, we will consider an extension of fractional integrals to the complex matrix-variate cases. Matrices in the complex domain will be denoted with a tilde. Let \(\tilde {X}_1\) and \(\tilde {X}_2\) be independently distributed Hermitian positive definite complex matrix-variate random variables whose densities are \(\tilde {f}_1(\tilde {X}_1)\) and \(\tilde {f}_2(\tilde {X}_2),\) respectively. Let \(\tilde {U}_2=\tilde {X}_2^{\frac {1}{2}}\tilde {X}_1\tilde {X}_2^{\frac {1}{2}}\) and \(\tilde {U}_1=\tilde {X}_2^{\frac {1}{2}}\tilde {X}_1^{-1}\tilde {X}_2^{\frac {1}{2}}\) where \(\tilde {X}_2^{\frac {1}{2}}\) denotes the Hermitian positive definite square root of the Hermitian positive definite matrix \(\tilde {X}_2\). Statistical densities are real-valued scalar functions whether the argument matrix is in the real or complex domain.
5.7a.1. Density of a product and fractional integral of the second kind, complex case
Let us consider the transformation \((\tilde {X}_1,~\tilde {X}_2)\to (\tilde {U}_2,~\tilde {V})\) and \((\tilde {X}_1,~\tilde {X}_2)\to (\tilde {U}_1,~\tilde {V})\), the Jacobians being available from Chap. 1 or Mathai (1997). Then,
When f 1 and f 2 are statistical densities, the density of the product, denoted by \(\tilde {g}_2(\tilde {U}_2)\), is the following:
where |det(⋅)| is the absolute value of the determinant of (⋅). If f 1 and f 2 are not statistical densities, (5.7a.1) will be called the M-convolution of the product. As in the real matrix-variate case, we will give a general definition of a fractional integral of order α of the second kind in the complex matrix-variate case. Let
and \(f_2(\tilde {X}_2)=\phi _2(\tilde {X}_2)\tilde {f}(\tilde {X}_2)\) where ϕ 1 and ϕ 2 are specified functions and f is an arbitrary function. Then, (5.7a.2) becomes
for \(\Re (\alpha )>p-1\). As an example, let
Observe that \(\tilde {f}_1(\tilde {X}_1)\) has now become a complex matrix-variate type-1 beta density with the parameters (γ + p, α) so that (5.7a.3) can be expressed as follows:
where
is Erdélyi-Kober fractional integral of the second kind of order α in the complex matrix-variate case, which is defined for \(\Re (\alpha )>p-1,~\Re (\gamma )>-1\). The extension of fractional integrals to complex matrix-variate cases was introduced in Mathai (2013). As a second example, let
In that case, (5.7a.3) becomes
The integral (5.7a.6) is Weyl fractional integral of the second kind of order α in the complex matrix-variate case. If V is bounded above by a Hermitian positive definite constant matrix B > O, then (5.7a.6) is a Riemann-Liouville fractional integral of the second kind of order α in the complex matrix-variate case.
A pathway extension parallel to that developed in the real matrix-variate case can be similarly obtained. Accordingly, the details of the derivation are omitted.
5.7a.2. Density of a ratio and fractional integrals of the first kind, complex case
We will now derive the density of the symmetric ratio \(\tilde {U}_1\) defined in Sect. 5.7a. If \(\tilde {f}_1\) and \(\tilde {f}_2\) are statistical densities, then the density of \(\tilde {U}_1\), denoted by \(\tilde {g}_1(\tilde {U}_1)\), is given by
provided the integral is convergent. For the general definition, let us take
and \(\tilde {f}_2(\tilde {X}_2)=\phi _2(\tilde {X}_2)\tilde {f}(\tilde {X}_2)\) where ϕ 1 and ϕ 2 are specified functions and \(\tilde {f}\) is an arbitrary function. Then \(\tilde {g}_1(\tilde {U}_1)\) is the following:
As an example, let
and ϕ 2 = 1. Then,
where
for \(\Re (\alpha )>p-1\), is the Erdélyi-Kober fractional integral of the first kind of order α and parameter γ in the complex matrix-variate case. We now consider a second example. On letting \(\phi _1(\tilde {X}_1)=|\text{det}(\tilde {X}_1)|{ }^{-\alpha -p}\) and \(\phi _2(\tilde {X}_2)=|\text{det}(\tilde {X}_2)|{ }^{\alpha }\), the density of \(\tilde {U}_1\) is
The integral in (5.7a.11) is Weyl’s fractional integral of the first kind of order α in the complex matrix-variate case, denoted by \(\tilde {W}_{1,\tilde {U}_1}^{-\alpha }f\). Observe that we are considering only Hermitian positive definite matrices. Thus, there is a lower bound, the integral being over \(O<\tilde {V}<\tilde {U}_1\). Hence (5.7a.11) can also represent a Riemann-Liouville fractional integral of the first kind of order α in the complex matrix-variate case with a null matrix as its lower bound. For fractional integrals involving several matrices and fractional differential operators for functions of matrix argument, refer to Mathai (2014a, 2015); for pathway extensions, see Mathai and Haubold (2008, 2011).
Exercises 5.7
All the matrices appearing herein are p × p real positive definite, when real, and Hermitian positive definite, when in the complex domain. The M-transform of a real-valued scalar function f(X) of the p × p real matrix X, with the M-transform parameter ρ, is defined as
whenever the integral is convergent. In the real case, the M-convolution of a product \(U_2=X_2^{\frac {1}{2}}X_1X_2^{\frac {1}{2}}\) with the corresponding functions f 1(X 1) and f 2(X 2), respectively, is
whenever the integral is convergent. The M-convolution of a ratio in the real case is g 1(U 1). The M-convolution of a product and a ratio in the complex case are \(\tilde {g}_2(\tilde {U}_2)\) and \( \tilde {g}_1(\tilde {U}_1)\), respectively, as defined earlier in this section. If α is the order of a fractional integral operator operating on f, denoted by A −α f, then the semigroup property is that A −α A −β f = A −(α+β) f = A −β A −α f.
5.7.1
Show that the M-transform of the M-convolution of a product is the product of the M-transforms of the individual functions f 1 and f 2, both in the real and complex cases.
5.7.2
What are the M-transforms of the M-convolution of a ratio in the real and complex cases? Establish your assertions.
5.7.3
Show that the semigroup property holds for Weyl’s fractional integral of the (1): first kind, (2): second kind, in the real matrix-variate case.
5.7.4
Do (1) and (2) of Exercise 5.7.3 hold in the complex matrix-variate case? Prove your assertion.
5.7.5
Evaluate the M-transforms of the Erdélyi-Kober fractional integral of order α of (1): the first kind, (2): the second kind and state the conditions for their existence.
5.7.6
Repeat Exercise 5.7.5 for (1) Weyl’s fractional integral of order α, (2) the Riemann-Liouville fractional integral of order α.
5.7.7
Evaluate the Weyl fractional integral of order α of (a): the first kind, (b): the second kind, in the real matrix-variate case, if possible, if the arbitrary function is (1): e−tr(X), (2): etr(X) and write down the conditions wherever it is evaluated.
5.7.8
Repeat Exercise 5.7.7 for the complex matrix-variate case.
5.7.9
Evaluate the Erdélyi-Kober fractional integral of order α and parameter γ of the (a): first kind, (b): second kind, in the real matrix-variate case, if the arbitrary function is (1): |X|δ, (2): |X|−δ, wherever possible, and write down the necessary conditions.
5.7.10
Repeat Exercise 5.7.9 for the complex case. In the complex case, |X| = determinant of X, is to be replaced by \(|\text{ det}(\tilde {X})|\), the absolute value of the determinant of \(\tilde {X}\).
5.8. Densities Involving Several Matrix-variate Random Variables, Real Case
We will start with real scalar variables. The most popular multivariate distribution, apart from the normal distribution, is the Dirichlet distribution, which is a generalization of the type-1 and type-2 beta distributions.
5.8.1. The type-1 Dirichlet density, real scalar case
Let x 1, …, x k be real scalar random variables having a joint density of the form
for ω = {(x 1, …, x k)|0 ≤ x j ≤ 1, j = 1, …, k, 0 ≤ x 1 + ⋯ + x k ≤ 1}, \(\Re (\alpha _j)>0,~j=1,\ldots ,k+1\) and f 1 = 0 elsewhere. This is type-1 Dirichlet density where c k is the normalizing constant. Note that ω describes a simplex and hence the support of f 1 is the simplex ω. Evaluation of the normalizing constant can be achieved in differing ways. One method relies on the direct integration of the variables, one at a time. For example, integration over x 1 involves two factors \(x_1^{\alpha _1-1}\) and \((1-x_1-\cdots -x_k)^{\alpha _{k+1}-1}\). Let I 1 be the integral over x 1. Observe that x 1 varies from 0 to 1 − x 2 −⋯ − x k. Then
But
Make the substitution \(y=\frac {x_1}{1-x_2-\cdots -x_k}\Rightarrow \text{d}x_1=(1-x_2-\cdots -x_k)\text{d}y\), which enable one to integrate out y by making use of a real scalar type-1 beta integral giving
for \(\Re (\alpha _1)>0,~\Re (\alpha _{k+1})>0\). Now, proceed similarly by integrating out x 2 from \(\,x_2^{\alpha _2-1}(1-x_2-\cdots -x_k)^{\alpha _1+\alpha _{k+1}}\), and continue in this manner until x k is reached. Finally, after canceling out all common gamma factors, one has Γ(α 1)⋯Γ(α k+1)∕Γ(α 1 + ⋯ + α k+1) for \(\Re (\alpha _j)>0,~ j=1,\ldots ,k+1\). Thus, the normalizing constant is given by
Another method for evaluating the normalizing constant c k consists of making the following transformation:
It is then easily seen that
Under this transformation, one has
Then, we have
Now, all the y j’s are separated and each one can be integrated out by making use of a type-1 beta integral. For example, the integrals over y 1, y 2, …, y k give the following:
for \(\Re (\alpha _j)>0,~j=1,\ldots ,k+1\). Taking the product produces \(c_k^{-1}\).
5.8.2. The type-2 Dirichlet density, real scalar case
Let x 1 > 0, …, x k > 0 be real scalar random variables having the joint density
for \(x_j>0,~ j=1,\ldots ,k,~ \Re (\alpha _j)>0,~ j=1,\ldots ,k+1\) and f 2 = 0 elsewhere, where c k is the normalizing constant. This density is known as a type-2 Dirichlet density. It can be shown that the normalizing constant c k is the same as the one obtained in (5.8.2) for the type-1 Dirichlet distribution. This can be established by integrating out the variables one at a time, starting with x k or x 1. This constant can also be evaluated with the help of the following transformation:
whose Jacobian is given by
5.8.3. Some properties of Dirichlet densities in the real scalar case
Let us determine the h-th moment of (1 − x 1 −⋯ − x k) in a type-1 Dirichlet density:
In comparison with the total integral, the only change is that the parameter α k+1 is replaced by α k+1 + h; thus the result is available from the normalizing constant. That is,
The additional condition needed is \(\Re (\alpha _{k+1}+h)>0\). Considering the structure of the moment in (5.8.8), u = 1 − x 1 −⋯ − x k is manifestly a real scalar type-1 beta variable with the parameters (α k+1, α 1 + ⋯ + α k). This is stated in the following result:
Theorem 5.8.1
Let x 1, …, x k have a real scalar type-1 Dirichlet density with the parameters (α 1, …, α k;α k+1). Then, u = 1 − x 1 −⋯ − x k has a real scalar type-1 beta distribution with the parameters (α k+1, α 1 + ⋯ + α k), and 1 − u = x 1 + ⋯ + x k has a real scalar type-1 beta distribution with the parameters (α 1 + ⋯ + α k, α k+1).
Some parallel results can also be obtained for type-2 Dirichlet variables. Consider a real scalar type-2 Dirichlet density with the parameters (α 1, …, α k;α k+1). Let v = (1 + x 1 + ⋯ + x k)−1. Then, when taking the h-th moment of v, that is E[v h], we see that the only change is that α k+1 becomes α k+1 + h. Accordingly, v has a real scalar type-1 beta distribution with the parameters (α k+1, α 1 + ⋯ + α k). Thus, \(1-v=\frac {x_1+\cdots +x_k}{1+x_1+\cdots +x_k}\) is a type-1 beta random variables with the parameters interchanged. Hence the following result:
Theorem 5.8.2
Let x 1, …, x k have a real scalar type-2 Dirichlet density with the parameters (α 1, …, α k;α k+1). Then v = (1 + x 1 + ⋯ + x k)−1 has a real scalar type-1 beta distribution with the parameters (α k+1, α 1 + ⋯ + α k) and \(1-v=\frac {x_1+\cdots +x_k}{1+x_1+\cdots +x_k}\) has a real scalar type-1 beta distribution with the parameters (α 1 + ⋯ + α k, α k+1).
Observe that the joint product moments \(E[x_1^{h_1}\cdots x_k^{h_k}]\) can be determined both in the cases of real scalar type-1 Dirichlet and type-2 Dirichlet densities. This can be achieved by considering the corresponding normalizing constants. Since an arbitrary product moment will uniquely determine the corresponding distribution, one can show that all subsets of variables from the set {x 1, …, x k} are again real scalar type-1 Dirichlet and real scalar type-2 Dirichlet distributed, respectively; to identify the marginal joint density of a subset under consideration, it suffices to set the complementary set of h j’s equal to zero. Type-1 and type-2 Dirichlet densities enjoy many properties, some of which are mentioned in the exercises. As well, there exist several types of generalizations of the type-1 and type-2 Dirichlet models. The first author and his coworkers have developed several such models, one of which was introduced in connection with certain reliability problems.
5.8.4. Some generalizations of the Dirichlet models
Let the real scalar variables x 1, …, x k have a joint density of the following type, which is a generalization of the type-1 Dirichlet density:
for (x 1, …, x k) ∈ ω, \(\Re (\alpha _j)>0,~j=1,\ldots ,k+1,\) as well as other necessary conditions to be stated later, and g 1 = 0 elsewhere, where b k denotes the normalizing constant. This normalizing constant can be evaluated by integrating out the variables one at a time or by making the transformation (5.8.3) and taking into account its associated Jacobian as specified in (5.8.4). Under the transformation (5.8.3), y 1, …, y k will be independently distributed with y j having a type-1 beta density with the parameters (α j, γ j), γ j = α j+1 + ⋯ + α k+1 + β j + ⋯ + β k, j = 1, …, k, which yields the normalizing constant
for \(\Re (\alpha _j)>0,~ j=1,\ldots ,k+1,~ \Re (\gamma _j)>0,~ j=1,\ldots ,k,\) where
Arbitrary moments \(E[x_1^{h_1}\cdots x_k^{h_k}]\) are available from the normalizing constant b k by replacing α j by α j + h j for j = 1, …, k and then taking the ratio. It can be observed from this arbitrary moment that all subsets of the type (x 1, …, x j) have a density of the type specified in (5.8.9). For other types of subsets, one has initially to rearrange the variables and the corresponding parameters by bringing them to the first j positions and then utilize the previous result on subsets.
The following model corresponding to (5.8.9) for the type-2 Dirichlet model was introduced by the first author:
for \(x_j>0,~j=1,\ldots ,k,~ \Re (\alpha _j)>0,~ j=1,\ldots ,k+1,\) as well as other necessary conditions to be stated later, and g 2 = 0 elsewhere. In order to evaluate the normalizing constant a k, one can use the transformation (5.8.6) and its associated Jacobian given in (5.8.7). Then, y 1, …, y k become independently distributed real scalar type-2 beta variables with the parameters (α j, δ j), where
for \(\Re (\alpha _j)>0,~j=1,\ldots ,k+1,~ \Re (\delta _j)>0,~j=1,\ldots ,k\). Other generalizations are available in the literature.
5.8.5. A pseudo Dirichlet model
In the type-1 Dirichlet model, the support is the previously described simplex ω. We will now consider a model, which was recently introduced by the first author, wherein the variables can vary freely in a hypercube. Let us begin with the case k = 2. Consider the model
for \(\Re (\alpha _j)>0,~j=1,2,\) and g 12 = 0 elsewhere. In this case, the variables are free to vary within the unit square. Let us evaluate the normalizing constant c 12. For this purpose, let us expand the last factor by making use of the binomial expansion since 0 < x 1 x 2 < 1. Then,
where for example the Pochhmmer symbol (a)k stands for
Integral over x 1 gives
and the integral over x 2 yields
Taking the product of the right-hand side expressions in (ii) and (iii) and observing that Γ(α 1 + α 2 + k + 1) = Γ(α 1 + α 2 + 1)(α 1 + α 2 + 1)k and Γ(k + 1) = (1)k, we obtain the following total integral:
where the 2 F 1 hypergeometric function with argument 1 is evaluated with the following identity:
whenever the gamma functions are defined. Observe that (5.8.15) is a surprising result as it is the total integral coming from a type-1 real beta density with the parameters (α 1, α 2). Now, consider the general model
Proceeding exactly as in the case of k = 2, one obtains the total integral as
This is the total integral coming from a (k − 1)-variate real type-1 Dirichlet model. Some properties of this distribution are pointed out in some of the assigned problems.
5.8.6. The type-1 Dirichlet model in real matrix-variate case
Direct generalizations of the real scalar variable Dirichlet models to real as well as complex matrix-variate cases are possible. The type-1 model will be considered first. Let the p × p real positive definite matrices X 1, …, X k be such that X j > O, I − X j > O, that is X j as well as I − X j are positive definite, for j = 1, …, k, and, in addition, I − X 1 −⋯ − X k > O. Let Ω = {(X 1, …, X k)| O < X j < I, j = 1, …, k, I − X 1 −⋯ − X k > O}. Consider the model
for \(\Re (\alpha _j)>\frac {p-1}{2},~ j=1,\ldots ,k+1,\) and G 1 = 0 elsewhere. The normalizing constant C k can be determined by using real matrix-variate type-1 beta integrals to integrate the matrices one at the time. We can also evaluate the total integral by means of the following transformation:
The associated Jacobian can then be determined by making use of results on matrix transformations that are provided in Sect. 1.6. Then,
It can be seen that the Y j’s are independently distributed as real matrix-variate type-1 beta random variables and the product of the integrals gives the following final result:
By integrating out the variables one at a time, we can show that the marginal densities of all subsets of {X 1, …, X k} also belong to the same real matrix-variate type-1 Dirichlet distribution and single matrices are real matrix-variate type-1 beta distributed. By taking the product moment of the determinants, \(E[|X_1|{ }^{h_1}\cdots |X_k|{ }^{h_k}],\) one can anticipate the results; however, arbitrary moments of determinants need not uniquely determine the densities of the corresponding matrices. In the real scalar case, one can uniquely identify the density from arbitrary moments, very often under very mild conditions. The result I − X 1 −⋯ − X k has a real matrix-variate type-1 beta distribution can be seen by taking arbitrary moments of the determinant, that is, E[|I − X 1 −⋯ − X k|h], but evaluating the h-moment of a determinant and then identifying it as the h-th moment of the determinant from a real matrix-variate type-1 beta density is not valid in this case. If one makes a transformation of the type Y 1 = X 1, …, Y k−1 = X k−1, Y k = I − X 1 −⋯ − X k, it is seen that X k = I − Y 1 −⋯ − Y k and that the Jacobian in absolute value is 1. Hence, we end up with a real matrix-variate type-1 Dirichlet density of the same format but whose parameters α k and α k+1 are interchanged. Then, integrating out Y 1, …, Y k−1, we obtain a real matrix-variate type-1 beta density with the parameters (α k+1, α 1 + ⋯ + α k). Hence the result. When Y k has a real matrix-variate type-1 beta distribution, we have that I − Y k = X 1 + ⋯ + X k is also a type-1 beta random variable with the parameters interchanged.
The first author and his coworkers have proposed various types of generalizations to the matrix-variate type-1 and type-2 Dirichlet models in the real and complex cases. One of those extensions which is defined in the real domain, is the following:
for (X 1, …, X k) ∈ Ω, \(\Re (\alpha _j)>\frac {p-1}{2},~ j=1,\ldots ,k+1\), and G 2 = 0 elsewhere. The normalizing constant C 1k can be evaluated by integrating variables one at a time or by using the transformation (5.8.20). Under this transformation, the real matrices Y j’s are independently distributed as real matrix-variate type-1 beta variables with the parameters (α j, γ j), γ j = α j+1 + ⋯ + α k+1 + β j + ⋯ + β k. The conditions will then be \(\Re (\alpha _j)>\frac {p-1}{2},~ j=1,\ldots ,k+1,\) and \( \Re (\gamma _j)>\frac {p-1}{2},~j=1,\ldots ,k\). Hence
5.8.7. The type-2 Dirichlet model in the real matrix-variate case
The type-2 Dirichlet density in the real matrix-variate case is the following:
for \(\Re (\alpha _j)>\frac {p-1}{2},~j=1,\ldots ,k+1\) and G 3 = 0 elsewhere, the normalizing constant C k being the same as that appearing in the type-1 Dirichlet case. This can be verified, either by integrating matrices one at a time from (5.8.25) or by making the following transformation:
Under this transformation, the Jacobian is as follows:
Thus, the Y j’s are independently distributed real matrix-variate type-2 beta variables and the product of the integrals produces [C k]−1. By integrating matrices one at a time, we can see that all subsets of matrices belonging to {X 1, …, X k} will have densities of the type specified in (5.8.25). Several properties can also be established for the model (5.8.25); some of them are included in the exercises.
Example 5.8.1
Evaluate the normalizing constant c explicitly if the function f(X 1, X 2) is a statistical density where the p × p real matrices X j > O, I − X j > O, j = 1, 2, and I − X 1 − X 2 > O where
Solution 5.8.1
Note that
Now, letting \(Y=(I-X_1)^{-\frac {1}{2}}X_2(I-X_1)^{-\frac {1}{2}}\Rightarrow \text{d}Y=|I-X_1|{ }^{-\frac {p+1}{2}}\text{d}X_2\), and the integral over X 2 gives the following:
for \(\Re (\alpha _2)>\frac {p-1}{2},~\Re (\beta _2)>\frac {p-1}{2}\). Then, the integral over X 1 can be evaluated as follows:
for \(\Re (\alpha _1)>\frac {p-1}{2},~ \Re (\beta _1+\beta _2+\alpha _2)>\frac {p-1}{2}\). Collecting the results from the integrals over X 2 and X 1 and using the fact that the total integral is 1, we have
for \(\Re (\alpha _j)>\frac {p-1}{2},~j=1,2,~\Re (\beta _2)>\frac {p-1}{2},\) and \(\Re (\beta _1+\beta _2+\alpha _2)>\frac {p-1}{2}\).
The first author and his coworkers have established several generalizations to the type-2 Dirichlet model in (5.8.25). One such model is the following:
for \(\Re (\alpha _j)>\frac {p-1}{2},~ j=1,\ldots ,k+1,~ X_j>O,~ j=1,\ldots ,k\), as well as other necessary conditions to be stated later, and G 4 = 0 elsewhere. The normalizing constant C 2k can be evaluated by integrating matrices one at a time or by making the transformation (5.8.26). Under this transformation, the Y j’s are independently distributed real matrix-variate type-2 beta variables with the parameters (α j, δ j), where
The normalizing constant is then
where the δ j is given in (5.8.29). The marginal densities of the subsets, if taken in the order X 1, {X 1, X 2}, and so on, will belong to the same family of densities as that specified by (5.8.28). Several properties of the model (5.8.28) are available in the literature.
5.8.8. A pseudo Dirichlet model
We will now discuss the generalization of the model introduced in Sect. 5.8.5. Consider the density
Then, by following steps parallel to those used in the real scalar variable case, one can show that the normalizing constant is given by
The binomial expansion of the last factor determinant in (5.8.31) is somewhat complicated as it involves zonal polynomials; this expansion is given in Mathai (1997). Compared to the real scalar case, the only change is the appearance of the constant \(\frac {\varGamma _p(p+1)}{[\varGamma _p(\frac {p+1}{2})]^2}\) which is 1 when p = 1. Apart from this constant, the rest is the normalizing constant in a real matrix-variate type-1 Dirichlet model in k − 1 variables instead of k variables.
5.8a. Dirichlet Models in the Complex Domain
All the matrices appearing in the remainder of this chapter are p × p Hermitian positive definite, that is, \(\tilde {X}_j=\tilde {X}_j^{*}\) where an asterisk indicates the conjugate transpose. Complex matrix-variate random variables will be denoted with a tilde. For a complex matrix \(\tilde {X}\), the determinant will be denoted by \(\text{det}(\tilde {X})\) and the absolute value of the determinant, by \(|\text{det}(\tilde {X})|\). For example, if \(\text{det}(\tilde {X})=a+ib, \ a\) and b being real and \(i=\sqrt {(-1)}\), the absolute value is \(|\text{det}(\tilde {X})|=+(a^2+b^2)^{\frac {1}{2}}\). The type-1 Dirichlet model in the complex domain, denoted by \(\tilde {G}_1\), is the following:
for \((\tilde {X}_1,\ldots ,\tilde {X}_k)\in \tilde {\varOmega },\ \tilde {\varOmega }=\{(\tilde {X}_1,\ldots ,\tilde {X}_k)|\,O<\tilde {X}_j<I,~ j=1,\ldots ,k,~O<\tilde {X}_1+\cdots +\tilde {X}_k<I\},~ \Re (\alpha _j)>p-1,~j=1,\ldots ,k+1,\) and \(\tilde {G}_1=0\) elsewhere. The normalizing constant \(\tilde {C}_k\) can be evaluated by integrating out matrices one at a time with the help of complex matrix-variate type-1 beta integrals. One can also employ a transformation of the type given in (5.8.20) where the real matrices are replaced by matrices in the complex domain and Hermitian positive definite square roots are used. The Jacobian is then as follows:
Then \(\tilde {Y}_j\)’s are independently distributed as complex matrix-variate type-1 beta variables. On taking the product of the total integrals, one can verify that
where for example \(\tilde {\varGamma }_p(\alpha )\) is the complex matrix-variate gamma given by
The first author and his coworkers have also discussed various types of generalizations to Dirichlet models in complex domain.
5.8a.1. A type-2 Dirichlet model in the complex domain
One can have a model parallel to the type-2 Dirichlet model in the real matrix-variate case. Consider the model
for \(\tilde {X}_j>O,~ j=1,\ldots ,k,~ \Re (\alpha _j)>p-1,~j=1,\ldots ,k+1,\) and \(\tilde {G}_2=0\) elsewhere. By integrating out matrices one at a time with the help of complex matrix-variate type-2 integrals or by using a transformation parallel to that provided in (5.7.26) and then integrating out the independently distributed complex type-2 beta variables \(\tilde {Y}_j\)’s, we can show that the normalizing constant \(\tilde {C}_k\) is the same as that obtained in the complex type-1 Dirichlet case. The first author and his coworkers have given various types of generalizations to the complex type-2 Dirichlet density as well.
Exercises 5.8
5.8.1
By integrating out variables one at a time derive the normalizing constant in the real scalar type-2 Dirichlet case.
5.8.2
By using the transformation (5.8.3), derive the normalizing constant in the real scalar type-1 Dirichlet case.
5.8.3
By using the transformation in (5.8.6), derive the normalizing constant in the real scalar type-2 Dirichlet case.
5.8.4
Derive the normalizing constants for the extended Dirichlet models in (5.8.9) and (5.8.12).
5.8.5
Evaluate \(E[x_1^{h_1}\cdots x_k^{h_k}]\) for the model specified in (5.8.12) and state the conditions for its existence.
5.8.6
Derive the normalizing constant given in (5.8.18).
5.8.7
With respect to the pseudo Dirichlet model in (5.8.17), show that the product u = x 1⋯x k is uniformly distributed.
5.8.8
Derive the marginal distribution of (1): x 1; (2): (x 1, x 2); (3): (x 1, …, x r), r < k, and the conditional distribution of (x 1, …, x r) given (x r+1, …, x k) in the pseudo Dirichlet model in (5.8.17).
5.8.9
Derive the normalizing constant in (5.8.22) by completing the steps in (5.8.22) and then by integrating out matrices one by one.
5.8.10
From the outline given after equation (5.8.22), derive the density of I − X 1 −⋯ − X k and therefrom the density of X 1 + ⋯ + X k when (X 1, …, X k) has a type-1 Dirichlet distribution.
5.8.11
Complete the derivation of C 1k in (5.8.24) and verify it by integrating out matrices one at a time from the density given in (5.8.23).
5.8.12
Show that U = (I + X 1 + ⋯ + X k)−1 in the type-2 Dirichlet model in (5.8.25) is a real matrix-variate type-1 beta distributed. As well, specify its parameters.
5.8.13
Evaluate the normalizing constant C k in (5.8.25) by using the transformation provided in (5.8.26) as well as by integrating out matrices one at a time.
5.8.14
Derive the δ j in (5.8.29) and thus the normalizing constant C 2k in (5.8.28).
5.8.15
For the following model in the complex domain, evaluate C:
5.8.16
Evaluate the normalizing constant in the pseudo Dirichlet model in (5.8.31).
5.8.17
In the pseudo Dirichlet model specified in (5.8.31), show that \(U=X_k^{\frac {1}{2}}\cdots X_2^{\frac {1}{2}}\) \(X_1X_2^{\frac {1}{2}}\cdots X_k^{\frac {1}{2}}\) is uniformly distributed.
5.8.18
Show that the normalizing constant in the complex type-2 Dirichlet model specified in (5.8a.5) is the same as the one in the type-1 Dirichlet case. Establish the result by integrating out matrices one by one.
5.8.19
Show that the normalizing constant in the type-2 Dirichlet case in (5.8a.5) is the same as that in the type-1 case. Establish this by using a transformation parallel to (5.8.26) in the complex domain.
5.8.20
Construct a generalized model for the type-2 Dirichlet case for k = 3 parallel to the case in (5.8.28) in the complex domain.
References
Mathai, A.M. (1993): A Handbook of Generalized Special Functions for Statistical and Physical Sciences, Oxford University Press, Oxford.
Mathai, A.M. (1997): Jacobians of Matrix Transformations and Functions of Matrix Argument, World Scientific Publishing, New York.
Mathai, A.M. (1999): Introduction to Geometrical Probabilities: Distributional Aspects and Applications, Gordon and Breach, Amsterdam.
Mathai, A.M. (2005): A pathway to matrix-variate gamma and normal densities, Linear Algebra and its Applications, 396, 317–328.
Mathai, A.M. (2009): Fractional integrals in the matrix-variate case and connection to statistical distributions, Integral Transforms and Special Functions, 20(12), 871–882.
Mathai, A.M. (2010): Some properties of Mittag-Leffler functions and matrix-variate analogues: A statistical perspective, Fractional Calculus & Applied Analysis, 13(2), 113–132.
Mathai, A.M. (2012): Generalized Krätzel integral and associated statistical densities, International Journal of Mathematical Analysis, 6(51), 2501–2510.
Mathai, A.M. (2013): Fractional integral operators in the complex matrix-variate case, Linear Algebra and its Applications, 439, 2901–2913.
Mathai, A.M. (2014): Evaluation of matrix-variate gamma and beta integrals, Applied Mathematics and computations, 247, 312–318.
Mathai, A.M. (2014a): Fractional integral operators involving many matrix variables, Linear Algebra and its Applications, 446, 196–215.
Mathai, A.M. (2014b): Explicit evaluations of gamma and beta integrals in the matrix-variate case, Journal of the Indian Mathematical Society, 81(3), 259–271.
Mathai, A.M. (2015): Fractional differential operators in the complex matrix-variate case, Linear Algebra and its Applications, 478, 200–217.
Mathai, A.M. and H.J. Haubold, H.J. (1988) Modern Problems in Nuclear and Neutrino Astrophysics, Akademie-Verlag, Berlin.
Mathai, A.M. and Haubold, H.J. (2008): Special Functions for Applied Scientists, Springer, New York.
Mathai, A.M. and Haubold, H.J. (2011): A pathway from Bayesian statistical analysis to superstatistics, Applied Mathematics and Computations, 218, 799–804.
Mathai, A.M. and Haubold, H.J. (2011a): Matrix-variate statistical distributions and fractional calculus, Fractional Calculus & Applied Analysis, 24(1), 138–155.
Mathai, A.M. and Haubold, H.J. (2017): Introduction to Fractional Calculus, Nova Science Publishers, New York.
Mathai, A.M. and Haubold, H.J. (2017a): Fractional and Multivariable Calculus: Model Building and Optimization, Springer, New York.
Mathai, A.M. and Haubold, H. J. (2017b): Probability and Statistics, De Gruyter, Germany.
Author information
Authors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2022 The Author(s)
About this chapter
Cite this chapter
Mathai, A., Provost, S., Haubold, H. (2022). Chapter 5: Matrix-Variate Gamma and Beta Distributions. In: Multivariate Statistical Analysis in the Real and Complex Domains. Springer, Cham. https://doi.org/10.1007/978-3-030-95864-0_5
Download citation
DOI: https://doi.org/10.1007/978-3-030-95864-0_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-95863-3
Online ISBN: 978-3-030-95864-0
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)