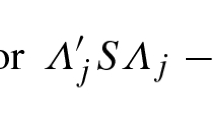Chapter 11: Factor Analysis

Abstract

Factor analysis is a statistical method aiming at identifying a relatively small number of underlying (unobserved) factors that could explain certain interdependencies among a larger set of observed variables. Factor analysis proves useful for analyzing causal mechanisms. A suitable general linear model is posited and the maximum likelihood estimates of its parameters are derived. As well, the likelihood ratio statistic is determined and its asymptotic distribution, specified.

11.1. Introduction

We will utilize the same notations as in the previous chapters. Lower-case letters x, y, … will denote real scalar variables, whether mathematical or random. Capital letters X, Y, … will be used to denote real matrix-variate mathematical or random variables, whether square or rectangular matrices are involved. A tilde will be placed on top of letters such as $\tilde {x},\tilde {y},\tilde {X},\tilde {Y}$ to denote variables in the complex domain. Constant matrices will for instance be denoted by A, B, C. A tilde will not be used on constant matrices unless the point is to be stressed that the matrix is in the complex domain. In the real and complex cases, the determinant of a square matrix A will be denoted by |A| or det(A) and, in the complex case, the absolute value or modulus of the determinant of A will be denoted as |det(A)|. When matrices are square, their order will be taken as p × p, unless specified otherwise. When A is a full rank matrix in the complex domain, then AA ^∗ is Hermitian positive definite where an asterisk designates the complex conjugate transpose of a matrix. Additionally, dX will indicate the wedge product of all the distinct differentials of the elements of the matrix X. Thus, letting the p × q matrix X = (x _ij) where the x _ij’s are distinct real scalar variables, $\mathrm {d}X=\wedge _{i=1}^p\wedge _{j=1}^q\mathrm {d}x_{ij}$. For the complex matrix $\tilde {X}=X_1+iX_2,\ i=\sqrt {(-1)}$, where X ₁ and X ₂ are real, $\mathrm {d}\tilde {X}=\mathrm {d}X_1\wedge \mathrm {d}X_2$.

Factor analysis is a statistical method aiming to identify a relatively small number of underlying (unobserved) factors that could explain certain interdependencies among a larger set of observed variables. Factor analysis also proves useful for analyzing causal mechanisms. As a statistical technique, Factor Analysis was originally developed in connection with psychometrics. It has since been utilized in operations research, finance and biology, among other disciplines. For instance, a score available on an intelligence test will often assess several intellectual faculties and cognitive abilities. It is assumed that a certain linear function of the contributions from these various mental factors is producing the final score. Hence, there is a parallel to be made with analysis of variance as well as design of experiments and linear regression models.

11.2. Linear Models from Different Disciplines

In order to introduce the current topic, we will first examine a linear regression model and an experimental design model.

11.2.1. A linear regression model

Let x be a real scalar random variable and let t ₁, …, t _r be either r real fixed numbers or given values of r real random variables. Let the conditional expectation of x, given t ₁, …, t _r, be of the form

$$\displaystyle \begin{aligned} E[x|t_1,\ldots ,t_r]=a_o+a_1t_1+\cdots +a_rt_r \end{aligned}$$

or the corresponding model be

$$\displaystyle \begin{aligned} x=a_o+a_1t_1+\cdots +a_rt_r+e \end{aligned}$$

where a _o, a ₁, …, a _r are unknown constants, t ₁, …, t _r are given values and e is the error component or the sum total of contributions coming from unknown or uncontrolled factors plus the experimental error. For example, x might be an inflation index with respect to a particular base year, say 2010. In this instance, t ₁ may be the change or deviation in the average price per kilogram of certain staple vegetables from the base year 2010, t ₂ may be the change or deviation in the average price of a kilogram of rice compared to the base year, t ₃ may be the change or deviation in the average price of flour per kilogram with respect to the base year, and so on, and t _r may be the change or deviation in the average price of milk per liter compared to the base year 2010. The notation t _j, j = 1, …, r, is utilized to designate the given values as well as the corresponding random variables. Since we are taking deviations from the base values, we may assume without any loss of generality that the expected value of t _j is zero, that is, E[t _j] = 0, j = 1, …, r. We may also take the expected value of the error term e to be zero, that is, E[e] = 0. Now, let x ₁ be the inflation index, x ₂ be the caloric intake index per person, x ₃ be the general health index and so on. In all these cases, the same t ₁, …, t _r can act as the independent variables in a regression set up. Thus, in such a situation, a multivariate linear regression model will have the following format:

(11.2.1)

and we may write this model as

$$\displaystyle \begin{aligned} X=M+\varLambda F+{\boldsymbol{\epsilon}} \end{aligned}$$

where Λ = (λ _ij) is a p × r, r ≤ p, matrix of full rank r, 𝜖 is p × 1 and F is r × 1. In (11.2.1), λ _ij = a _ij and f _j = t _j. Then, E[X] = M + Λ E[F] + E[𝜖] = M since we have assumed that E[F] = O (a null matrix) and E[𝜖] = O. When F and 𝜖 are uncorrelated, the covariance matrix associated with X, denoted by Cov(X) = Σ, is the following:

$$\displaystyle \begin{aligned} \varSigma&=\mathrm{Cov}(X)=E\{(X-M)(X-M)'\}=E\{(\varLambda F+{\boldsymbol{\epsilon}})(\varLambda F+{\boldsymbol{\epsilon}})'\} \\ &=\varLambda\ \mathrm{Cov}(F)\ \varLambda'+\mathrm{Cov}({\boldsymbol{\epsilon}})+O\\ &=\varLambda\,\varPhi\, \varLambda'+\varPsi{} \end{aligned} $$

(11.2.2)

where the covariance matrices of F and 𝜖 are respectively denoted by Φ > O (positive definite) and Ψ > O. In the above formulation, F is taken to be a real vector random variable. In a simple linear model, the covariance matrix of 𝜖, namely Ψ, is usually taken as σ ² I where σ ² > 0 is a real scalar quantity and I is the identity matrix. In a more general setting, Ψ can be taken to be a diagonal matrix whose diagonal elements are positive; in such a model, the e _j’s are uncorrelated and their variances need not be equal. It will be assumed that the covariance matrix Ψ in (11.2.2) is a diagonal matrix having positive diagonal elements.

11.2.2. A design of experiment model

Consider a completely randomized experiment where one set of treatments are undertaken. In this instance, the experimental plots are assumed to be fully homogeneous with respect to all the known factors of variation that may affect the response. For example, the observed value may be the yield of a particular variety of corn grown in an experimental plot. Let the set of treatments be r different fertilizers F ₁, …, F _r, the effects of these fertilizers being denoted by α ₁, …, α _r. If no fertilizer is applied, the yield from a test plot need not be zero. Let μ ₁ be a general effect when F ₁ is applied so that we may regard α ₁ as a deviation from this effect μ ₁ due to F ₁. Let e ₁ be the sum total of the contributions coming from all unknown or uncontrolled factors plus the experimental error, if any, when F ₁ is applied. Then a simple linear one-way classification model for F ₁ is

$$\displaystyle \begin{aligned} x_1=\mu_1+\alpha_1+e_1, \end{aligned}$$

with x ₁ representing the yield from the test plot where F ₁ was applied. Then, corresponding to F ₁, …, F _r, r = p we have the following system:

$$\displaystyle \begin{aligned} \begin{array}{ll} x_1 &=\mu_1+\alpha_1+e_1\\ \ \, &\, \vdots\qquad \ \\ x_p &=\mu_p+\alpha_p+e_p\end{array} \end{aligned}$$

or, in matrix notation,

$$\displaystyle \begin{aligned} X=M+\varLambda F+{\boldsymbol{\epsilon}}{} \end{aligned} $$

(11.2.3)

where

In this case, the elements of Λ are dictated by the design itself. If the vector F is fixed, we call the model specified by (11.2.3), the fixed effect model, whereas if F is assumed to be random, then it is referred to as the random effect model. With a single observation per cell, as stated in (11.2.3), we will not be able to estimate the parameters or test hypotheses. Thus, the experiment will have to be replicated. So, let the j-th replicated observation vector be

Σ, Φ, and Ψ remaining the same for each replicate within the random effect model. Similarly, for the regression model given in (11.2.1), the j-th replication or repetition vector will be $X_j^{\prime }=(x_{1j},\ldots ,x_{pj})$ with Σ, Φ and Ψ therein remaining the same for each sample.

We will consider a general linear model encompassing those specified in (11.2.1) and (11.2.3) and carry out a complete analysis that will involve verifying the existence and uniqueness of such a model, estimating its parameters and testing various types of hypotheses. The resulting technique is referred to as Factor Analysis.

11.3. A General Linear Model for Factor Analysis

Consider the following general linear model:

$$\displaystyle \begin{aligned} X=M+\varLambda F+{\boldsymbol{\epsilon}}{} \end{aligned} $$

(11.3.1)

where

with the μ _j’s, λ _ij’s, f _j’s being real scalar parameters, the x _j’s, j = 1, …, p, being real scalar quantities, and Λ being of dimension p × r, r ≤ p, and of full rank r. When considering expected values, variances, covariances, etc., X, F, and 𝜖 will be assumed to be random quantities; however, when dealing with estimates, X will represent a vector of observations. This convention will be employed throughout this chapter so as to avoid a multiplicity of symbols for the variables and the corresponding observations.

From a geometrical perspective, the r columns of Λ, which are linarly independent, span an r-dimensional subspace in the p-dimensional Euclidean space. In this case, the r × 1 vector F is a point in this r-subspace and this subspace is usually called the factor space. Then, right-multiplying the p × r matrix Λ by a matrix will correspond to employing a new set of coordinate axes for the factor space.

Factor Analysis is a subject dealing with the identification or unique determination of a model of the type specified in (11.3.1), as well as the estimation of its parameters and the testing of various related hypotheses. The subject matter was originally developed in connection with intelligence testing. Suppose that a test is administered to an individual to evaluate his/her mathematical skills, spatial perception, language abilities, etc., and that the score obtained is recorded. There will be a component in the model representing the expected score. If the test is administered to 10th graders belonging to a particular school, the grand average of such test scores among all 10th graders across the nation could be taken as the expected score. Then, inputs associated to various intellectual faculties or combinations thereof will come about. All such factors may be contributing towards the observed test score. If f ₁, …, f _r, are the contributions coming from r factors corresponding to specific intellectual abilities, then, when a linear model is assumed, a certain linear combination of these inputs will constitute the final quantity accounting for the observed test score. A test score, x ₁, may then result from a linear model of the following form:

$$\displaystyle \begin{aligned} x_1=\mu_1+\lambda_{11}f_1+\lambda_{12}f_2+\cdots +\lambda_{1r}f_r+e_1 \end{aligned}$$

with λ ₁₁, …, λ _1r being the coefficients of f ₁, …, f _r, where f ₁, …, f _r, are contributions from r factors toward x ₁; these factors may be called the main intellectual factors in this case, and the coefficients λ ₁₁, …, λ _1r may be referred to as the factor loadings for these main factors. In this context, μ ₁ is the general expected value and e ₁ is the error component or the sum total of contributions originating from all unknown factors plus the experimental error, if any. Note that the contributions f ₁, …, f _r due to the main intellectual factors can vary from individual to individual, and hence it is appropriate to treat f ₁, …, f _r as random variables rather than fixed unknown quantities. These f ₁, …, f _r are not observable as in the case of the design model in (11.2.3), whereas in the regression type model specified by (11.2.1), they may take on the recorded values of the observable variables which are called the independent variables. Thus, the model displayed in (11.3.1) may be analyzed either by treating f ₁, …, f _r as fixed quantities or as random variables. If they are treated as random variables, we can assume that f ₁, …, f _r follow some joint distribution. Usually, joint normality is presupposed for f ₁, …, f _r. Since f ₁, …, f _r are deviations from the general effect μ ₁ due to certain main intellectual faculties under consideration, it may be assumed that the expected value is a null vector, that is, E[F] = O. We will denote the covariance matrix associated with F as Φ: Cov(F) = Φ > O (real positive definite). Note that the model’s error term e _j is always a random variable. Letting x ₁, …, x _p be the test scores on p individuals, we have the error vector 𝜖 ′ = (e ₁, …, e _p). Without any loss of generality, we may take the expected value of 𝜖 as being a null vector, that is, E[𝜖] = O. For a very simple situation, we may assume the covariance matrix associated with 𝜖 to be Cov(𝜖) = σ ² I where σ ² > 0 is a real positive scalar quantity and I is the identity matrix. For a somewhat more general situation, we may take Cov(𝜖) = Ψ where Ψ is a real positive definite diagonal matrix, or a diagonal matrix with positive diagonal elements. In the most general case, we may take Ψ to be a real positive definite matrix. It will be assumed that Ψ is diagonal with positive diagonal elements in the model (11.3.1), and that F and 𝜖 are uncorrelated. Thus, letting Σ be the covariance matrix of X, we have

$$\displaystyle \begin{aligned} \varSigma &=E[(X-M)(X-M)']=E[(\varLambda F+{\boldsymbol{\epsilon}})(\varLambda F+{\boldsymbol{\epsilon}})']\\ &=\varLambda E(FF')\varLambda'+E(\boldsymbol{\epsilon\epsilon}')+O\\ &=\varLambda \varPhi\varLambda'+\varPsi{}\end{aligned} $$

(11.3.2)

where Σ, Φ and Ψ, with Σ =  ΛΦΛ′ + Ψ, are all assumed to be real positive definite matrices.

11.3.1. The identification problem

Is the model specified by (11.3.1) unique or could it represent different situations? In other words, does it make sense as a model as stated? Given any r × r nonsingular matrix A, let AF = F ^∗ and ΛA ⁻¹ = Λ ^∗. Then, Λ ^∗ F ^∗ = ΛA ⁻¹ AF = ΛF. In other words,

$$\displaystyle \begin{aligned} X=M+\varLambda F+{\boldsymbol{\epsilon}}=M+\varLambda^{*}F^{*}+{\boldsymbol{\epsilon}}.{} \end{aligned} $$

(11.3.3)

Consequently, the model in (11.3.1) is not identified, that is, it is not uniquely determined.

The identification problem can also be stated as follows: Does there exist a real positive definite p × p matrix Σ > O containing p(p + 1)∕2 distinct elements, which can be uniquely represented as ΛΦΛ′ + Ψ where Λ has p r distinct elements, Φ > O has r(r + 1)∕2 distinct elements and Ψ is a diagonal matrix having p distinct elements? There is clearly no such matrices as can be inferred from (11.3.3). Note that an r × r arbitrary matrix A represents r ² distinct elements. It can be observed from (11.3.3) that we can impose r ² conditions on the parameters in Λ, Φ and Ψ. The question could also be posed as follows: Can the p(p + 1)∕2 distinct elements in Σ plus the r ² elements in A (r ² conditions) uniquely determine all the elements of Λ, Ψ and Φ? Let us determine how many elements there are in total. Λ, Ψ and Φ have a total of pr + p + r(r + 1)∕2 elements while A and Σ have a total of r ² + p(p + 1)∕2 elements. Hence, the difference, denoted by δ, is

$$\displaystyle \begin{aligned} \delta=\frac{p(p+1)}{2}+r^2-\Big[pr+\frac{r(r+1)}{2}+p\Big]=\frac{1}{2}[(p-r)^2-(p+r)].{} \end{aligned} $$

(11.3.4)

Observe that the right-hand side of (11.3.2) is not a linear function of Λ, Φ and Ψ. Thus, if δ > 0, we can anticipate that existence and uniqueness will hold although these properties cannot be guaranteed, whereas if δ < 0, then existence can be expected but uniqueness may be in question. Given (11.3.2), note that

$$\displaystyle \begin{aligned} \varSigma=\varPsi +\varLambda \varPhi\varLambda'\Rightarrow \varSigma-\varPsi=\varLambda \varPhi\varLambda' \end{aligned}$$

where ΛΦΛ′ is positive semi-definite of rank r, since the p × r, r ≤ p, matrix Λ has full rank r and Φ > O (positive definite). Then, the existence question can also be stated as follows: Given a p × p real positive definite matrix Σ > O, can we find a diagonal matrix Ψ with positive diagonal elements such that Σ − Ψ is a real positive semi-definite matrix of a specified rank r, which is expressible in the form BB′ for some p × r matrix B of rank r where r ≤ p? For the most part, the available results on this question of existence can be found in Anderson (2003) and Anderson and Rubin (1956). If a set of parameters exist and if the model is uniquely determined, then we say that the model is identified, or alternatively, identifiable. The concept of identification or identifiability within the context of Factor Analysis has been studied by Ihara and Kano (1995), Wegge (1996), Allman et al. (2009) and Chen et al. (2020), among others.

Assuming that Φ = I will impose r(r + 1)∕2 conditions. However, $r^2=\frac {r(r+1)}{2}+\frac {r(r-1)}{2}$. Thus, we may impose r(r − 1)∕2 additional conditions after requiring that Φ = I. Observe that when Φ = I, Λ ^∗ ΦΛ′ ^∗ = Λ ^∗ Λ′ ^∗ = ΛA ⁻¹ A′ ⁻¹ Λ′, and if this is equal to ΛΛ′ assuming that Φ = I, this means that (A′A)⁻¹ = I or A′A = I, that is, A is an orthonormal matrix. Thus, under the condition Φ = I, the arbitrary r × r matrix A becomes an orthonormal matrix. In this case, the transformation Y = ΛA is an orthonormal transformation or a rotation of the coordinate axes. The following r × r symmetric matrix of r(r + 1)∕2 distinct elements

$$\displaystyle \begin{aligned} \varDelta=\varLambda'\varPsi^{-1}\varLambda{} \end{aligned} $$

(11.3.5)

is needed for solving estimation and hypothesis testing problems; accordingly, we can impose r(r − 1)∕2 conditions by requiring Δ to be diagonal with distinct diagonal elements, that is, Δ = diag(η ₁, …, η _r), η _j > 0, j = 1, …, r. This imposes $\frac {r(r+1)}{2}-r=\frac {r(r-1)}{2}$ conditions. Thus, for the model to be identifiable or for all the parameters in Λ, Φ, Ψ to be uniquely determined, we can impose the condition Φ = I and require that Δ = Λ′Ψ ⁻¹ Λ be diagonal with positive diagonal elements. These two conditions will provide $\frac {r(r+1)}{2}+\frac {r(r-1)}{2}=r^2$ restrictions on the model which will then be identified.

When Φ = I, the main factors are orthogonal. If Φ is a diagonal matrix (including the identity matrix), the covariances are zeros and it is an orthogonal situation, in which case we say that the main factors are orthogonal. If Φ is not diagonal, then we say that the main factors are oblique.

One can also impose r(r − 1)∕2 conditions on the p × r matrix Λ. Consider the first r × r block, that is, the leading r × r submatrix or the upper r × r block in the p × r matrix, which we will denote by B. Imposing the condition that this r × r block B is lower triangular will result in $r^2-\frac {r(r+1)}{2}=\frac {r(r-1)}{2}$ conditions. Hence, Φ = I and the condition that this leading r × r block B is lower triangular will guarantee r ² restrictions, and the model will then be identified. One can also take a preselected r × r matrix B ₁ and then impose the condition that B ₁ B be lower triangular. This will, as well, produce $\frac {r(r-1)}{2}$ conditions. Thus, Φ = I and B ₁ B being lower triangular will ensure the identification of the model.

When we impose conditions on Φ and Ψ, the unknown covariance matrices must assume certain formats. Such conditions can be justified. However, could conditions be put on Λ, the factor loadings? Letting the first r × r block B in the p × r matrix Λ be lower triangular is tantamount to assuming that λ ₁₂ = 0 = λ ₁₃ = ⋯ = λ _1r or, equivalently, that f ₂, …, f _r do not contribute to the model for determining x ₁ in X′ = (x ₁, x ₂, …, x _p). Such restrictions are justified if we can design the experiment in such a way that x ₁ depends on f ₁ alone and not on f ₂, …, f _r. In psychological tests, it is possible to design tests in such a way that only certain main factors affect the scores. Thus, in such instances, we are justified to utilize a triangular format such that, in general, there are no contributions from f _i+1, …, f _r, toward x _i or, equivalently, the factor loadings λ _{i i+1}, …, λ _ir equal zero for i = 1, …, r − 1. For example, suppose that the first r tests are designed in such a way that only f ₁, …, f _i and no other factors contribute to x _i or, equivalently, x _i = μ _i + λ _i1 f ₁ + ⋯ + λ _ii f _i + e _i, i = 1, …, r. We can also measure the contribution from f _i in λ _ii units or we can take λ _ii = 1. By taking B = I _r, we can impose r ² conditions without requiring that Φ = I. This means that the first r tests are specifically designed so that x ₁ only has a one unit contribution from f ₁, x ₂ only has a one unit contribution from f ₂, and so on, x _r receiving a one unit contribution from f _r. When B is taken to be diagonal, the factor loadings are λ ₁₁, λ ₂₂, …, λ _rr, respectively, so that only f _i contributes to x _i for i = 1, …, r. Accordingly, the following are certain model identification conditions: (1): Φ = I and Λ′Ψ ⁻¹ Λ is diagonal with distinct diagonal elements; (2): Φ = I and the leading r × r submatrix B in the p × r matrix Λ is triangular; (3): Φ = I and B ₁ B is lower triangular where B ₁ is a preselected matrix; (4): The leading r × r submatrix B in the p × r matrix Λ is an identity matrix. Observe that when r = p, condition (4) corresponds to the design model considered in (11.2.3).

11.3.2. Scaling or units of measurement

A shortcoming of any analysis being based on a covariance matrix Σ is that the covariances depend on the units of measurement of the individual variables. Thus, modifying the units will affect the covariances. If we let y _i and y _j be two real scalar random variables with variances σ _ii and σ _jj and associated covariance σ _ij, the effect of scaling or changes in the measurement units may be eliminated by considering the variables $z_i=y_i/\sqrt {\sigma _{ii}}$ and $z_j=y_j/\sqrt {\sigma _{jj}}$ whose covariance Cov(z _i, z _j) ≡ r _ij is actually the correlation between y _i and y _j, which is free of the units of measurement. Letting Y ′ = (y ₁, …, y _p) and $D=\mathrm {diag}(\frac {1}{\sqrt {\sigma _{11}}},\ldots ,\frac {1}{\sqrt {\sigma _{pp}}}),$ consider Z = DY . We note that Cov(Y ) = Σ ⇒Cov(Z) = DΣD = R which is the correlation matrix associated with Y .

In psychological testing situations or referring to the model (11.3.1), when a test score x _j is multiplied by a scalar quantity c _j, then the factor loadings λ _j1, …, λ _jr, the error term e _j and the general effect μ _j are all multiplied by c _j, that is, c _j x _j = c _j μ _j + c _j(λ _j1 f ₁ + ⋯ + λ _jr f _r) + c _j e _j. Let Cov(X) = Σ = (σ _ij), that is, Cov(x _i, x _j) = σ _ij, X′ = (x ₁, …, x _p) and $D=\mathrm {diag}(\frac {1}{\sqrt {\sigma _{11}}},\ldots ,\frac {1}{\sqrt {\sigma _{pp}}})$. Consider the model

$$\displaystyle \begin{aligned} DX=DM+D\varLambda F+D{\boldsymbol{\epsilon}}\Rightarrow \mathrm{Cov}(DX)= D\varSigma D=D\varLambda\varPhi \varLambda'D+D\varPsi D.{} \end{aligned} $$

(11.3.6)

If X ^∗ = DX, M ^∗ = DM, Λ ^∗ = DΛ, and 𝜖 ^∗ = D 𝜖, then we obtain the following model and the resulting covariance matrix:

$$\displaystyle \begin{aligned} X^{*}=M^{*}+\varLambda^{*}F+{\boldsymbol{\epsilon}}^{*}&\Rightarrow \varSigma^{*}=\mathrm{Cov}(X^{*})=\varLambda^{*}\mathrm{Cov}(F){\varLambda^{*}}'+\varPsi^{*} \\ &\Rightarrow D\varSigma D=D\varLambda\varPhi \varLambda' D+D\varPsi D \\ &\Rightarrow R=\varLambda^{*}\varPhi {\varLambda^{*}}'+\varPsi^{*}{}\end{aligned} $$

(11.3.7)

where R = (r _ij) is the correlation matrix in X. An interesting point to be noted is that the identification conditions Φ = I and Λ ^∗ ′Ψ ^{∗ −1} Λ ^∗ being diagonal become the following: Φ = I and Λ ^∗ ′Ψ ^{∗ −1} Λ ^∗ = Λ′DD ⁻¹ Ψ ⁻¹ D ⁻¹ DΛ = Λ′Ψ ⁻¹ Λ which is diagonal, that is, Λ′Ψ ⁻¹ Λ is invariant under scaling transformations on the model or under X ^∗ = DX and Ψ ^∗ = DΨD.

11.4. Maximum Likelihood Estimators of the Parameters

A simple random sample of size n from the model X = M + ΛF + 𝜖 specified in (11.3.1) is understood to be constituted of independently and identically distributed (iid) X _j’s, j = 1, …, n, where

(11.4.1)

and the X _j’s are iid. Let f _j and E _j be independently normally distributed. Let E _j ∼ N _p(O, Ψ) and X _j ∼ N _p(μ, Σ), Σ = ΛΦΛ′ + Ψ where Φ = Cov(F) > O, Ψ = Cov(𝜖) > O and Σ > O, Ψ being a diagonal matrix with positive diagonal elements. Then, the likelihood function is the following:

$$\displaystyle \begin{aligned} L&=\prod_{j=1}^n\frac{1}{(2\pi)^{\frac{p}{2}}|\varSigma|{}^{\frac{1}{2}}}\mathrm{e}^{-\frac{1}{2}(X_j-M)'\varSigma^{-1}(X_j-M)} \\ &=\frac{1}{(2\pi)^{\frac{np}{2}}|\varSigma|{}^{\frac{n}{2}}}\mathrm{e}^{-\frac{1}{2}\sum_{j=1}^n(X_j-M)'\varSigma^{-1}(X_j-M)}.{}\end{aligned} $$

(11.4.2)

The sample matrix will be denoted by a boldface X = (X ₁, …, X _n). Let J be the n × 1 vector of unities, that is, J = (1, 1, …, 1)′. Then,

where $\bar {X}$ is the sample average vector or the sample mean vector. Let the boldface $\bar {\mathbf {X}}$ be the p × n matrix $\bar {\mathbf {X}}=(\bar {X},\bar {X},\ldots ,\bar {X})$. Then,

$$\displaystyle \begin{aligned} (\mathbf{X}-\bar{\mathbf{X}})(\mathbf{X}-\bar{\mathbf{X}})'=S=(s_{ij}),~ s_{ij}=\sum_{k=1}^n(x_{ik}-\bar{x_i})(x_{jk}-\bar{x_j}),{} \end{aligned} $$

(11.4.3)

where S is the sample sum of products matrix or the “corrected” sample sum of squares and cross products matrix. Note that

$$\displaystyle \begin{aligned} \bar{X}&=\frac{1}{n}\mathbf{X}J\\ &\Rightarrow \bar{\mathbf{X}}=(\bar{X},\ldots ,\bar{X})=\mathbf{X}\Big(\frac{1}{n}JJ'\Big)\\ &\Rightarrow \mathbf{X}-\bar{\mathbf{X}}=\mathbf{X}\Big(I-\frac{1}{n}JJ'\Big).\end{aligned} $$

Thus,

$$\displaystyle \begin{aligned} S=\mathbf{X}\Big(I-\frac{1}{n}JJ'\Big)\Big(I-\frac{1}{n}JJ'\Big)'\mathbf{X}'=\mathbf{X}\Big(I-\frac{1}{n}JJ'\Big)\mathbf{X}'.{} \end{aligned} $$

(11.4.4)

Since (X _j − M)′Σ ⁻¹(X _j − M) is a real scalar quantity, we have the following:

$$\displaystyle \begin{aligned} \sum_{j=1}^n(X_j-M)'\varSigma^{-1}(X_j-M)&=\sum_{j=1}^n\mathrm{tr}(X_j-M)'\varSigma^{-1}(X_j-M)\\ &=\sum_{j=1}^n\mathrm{tr}[\varSigma^{-1}(X_j-M)(X_j-M)']\\ &=\mathrm{tr}[\varSigma^{-1}\sum_{j=1}^n(X_j-\bar{X}+\bar{X}-M)(X_j-\bar{X}+\bar{X}-M)']\\ &=\mathrm{tr}[\varSigma^{-1}\sum_{j=1}^n(X_j-\bar{X})(X_j-\bar{X})']\\ &\ \ \ +n\,\mathrm{tr}[\varSigma^{-1}(\bar{X}-M)(\bar{X}-M)']\\ &=\mathrm{tr}(\varSigma^{-1}S)+n(\bar{X}-M)'\varSigma^{-1}(\bar{X}-M).{} \end{aligned} $$

(11.4.5)

Hence,

$$\displaystyle \begin{aligned} L=(2\pi)^{-\frac{np}{2}}|\varSigma|{}^{-\frac{n}{2}}\mathrm{e}^{-\frac{1}{2}\{\mathrm{tr}(\varSigma^{-1}S)+n(\bar{X}-M)'\varSigma^{-1}(\bar{X}-M)\}}.{} \end{aligned} $$

(11.4.6)

Differentiating (11.4.6) with respect to M, equating the result to a null vector and solving, we obtain an estimator for M, denoted by $\hat {M}$, as $\hat {M}=\bar {X}$. Then, $\ln L$ evaluated at $M=\bar {X}$ is

$$\displaystyle \begin{aligned} \ln L&=-\frac{np}{2}\ln (2\pi)-\frac{n}{2}\ln |\varSigma|-\frac{1}{2}\mathrm{tr}(\varSigma^{-1}S)\\ &=-\frac{np}{2}\ln (2\pi)-\frac{n}{2}\ln |\varLambda\varPhi \varLambda'+\varPsi|-\frac{1}{2}\mathrm{tr}[(\varLambda\varPhi \varLambda'+\varPsi)^{-1}S].{} \end{aligned} $$

(11.4.7)

11.4.1. Maximum likelihood estimators under identification conditions

The derivations in the following sections parallel to those found in Mathai (2021). One of the conditions for identification of the model is Φ = I and Λ′Ψ ⁻¹ Λ being a diagonal matrix with positive diagonal elements. We will examine the maximum likelihood estimators (MLE)/maximum likelihood estimates (MLE) under this identification condition. In this case, it follows from (11.4.7) that

$$\displaystyle \begin{aligned} \ln L=-\frac{np}{2}\ln (2\pi)-\frac{n}{2}\ln |\varLambda\varLambda'+\varPsi|-\frac{1}{2}\mathrm{tr}[(\varLambda\varLambda'+\varPsi)^{-1}S].{} \end{aligned} $$

(11.4.8)

By expanding the following determinant in two different ways by applying properties of partitioned determinants that are stated in Sect. 1.3, we have the following identities:

(11.4.9)

Hence, letting

$$\displaystyle \begin{aligned} \varDelta&= \varLambda'\varPsi^{-1}\varLambda=\mathrm{diag}(\delta_1^{\prime}\delta_1,\delta_2^{\prime}\delta_2,\ldots ,\delta_r^{\prime}\delta_r),\end{aligned} $$

we have

$$\displaystyle \begin{aligned} \ln |\varLambda\varLambda'+\varPsi|&=\ln |\varPsi|+\ln |I+\varLambda'\varPsi^{-1}\varLambda|\\ &=\sum_{j=1}^p\ln \psi_{jj}+\sum_{j=1}^r\ln(1+\delta_j^{\prime}\delta_j), {}\end{aligned} $$

(11.4.10)

where $\delta _j^{\prime }=\varLambda _j^{\prime }\varPsi ^{-\frac {1}{2}},~ \varLambda _j$ is the j-th column of Λ and ψ _jj, j = 1, …, p, is the j-th diagonal element of the diagonal matrix Ψ, the identification condition being that Φ = I and $\varLambda '\varPsi ^{-1}\varLambda =\varDelta =\mathrm {diag}(\delta _1^{\prime }\delta _1,\ldots ,\delta _r^{\prime }\delta _r)$. Accordingly, if we can write tr(Σ ⁻¹ S) = tr[(ΛΛ′ + Ψ)⁻¹ S] in terms of ψ _jj, j = 1, …, p, and $\delta _j^{\prime }\delta _j,~j=1,\ldots ,r,$ then the likelihood equation can be directly evaluated from (11.4.8) and (11.4.10), and the estimators can be determined. The following result will be helpful in this connection.

Theorem 11.4.1

Whenever ΛΛ′ + Ψ is nonsingular, which in this case, means real positive definite, the inverse is given by

$$\displaystyle \begin{aligned} (\varLambda\varLambda'+\varPsi)^{-1}=\varPsi^{-1}-\varPsi^{-1}\varLambda(\varDelta+I)^{-1}\varLambda'\varPsi^{-1}{} \end{aligned} $$

(11.4.11)

where the Δ is defined in (11.4.10).

It can be readily verified that pre and post multiplications of Ψ ⁻¹ − Ψ ⁻¹ Λ(Δ + I)⁻¹ Λ′Ψ ⁻¹ by ΛΛ′ + Ψ yield the identity matrix I _p.

11.4.2. Simplifications of |Σ| and tr(Σ ⁻¹ S)

In light of (11.4.9) and (11.4.10), we have

$$\displaystyle \begin{aligned} |\varSigma|&=|\varLambda\varLambda'+\varPsi|=|\varPsi|~|\varLambda'\varPsi^{-1}\varLambda+I|\\ &=|\varPsi|~|I+\varDelta|=\Big\{\prod_{j=1}^p\psi_{jj}\Big\}\Big\{\prod_{j=1}^r (1+\delta_j^{\prime}\delta_j)\Big\}.\end{aligned} $$

Now, observe the following: In $\varLambda (\varDelta +I)^{-1}=\varLambda \, \mathrm {diag}(\frac {1}{1+\delta _1^{\prime }\delta _1},\ldots ,\frac {1}{1+\delta _r^{\prime }\delta _r}),$ the j-th column of Λ is multiplied by $\frac {1}{1+\delta _j^{\prime }\delta _j}$, j = 1, …, r, and

$$\displaystyle \begin{aligned} \varLambda (\varDelta+I)^{-1}\varLambda' = \sum_{j=1}^r\frac{1}{1+\delta_j^{\prime}\delta_j}\varLambda_j\varLambda_j^{\prime} \end{aligned}$$

where Λ _j is the j-th column of Λ and the δ _j’s are specified in (11.4.10). Thus,

$$\displaystyle \begin{aligned} \ln |\varSigma|&=\sum_{j=1}^p\ln \psi_{jj}+\sum_{j=1}^r\ln (1+\delta_j^{\prime}\delta_j){} \end{aligned} $$

(11.4.12)

and, on applying Theorem 11.4.1,

$$\displaystyle \begin{aligned} \mathrm{tr}(\varSigma^{-1}S)&=\mathrm{tr}[(\varLambda\varLambda'+\varPsi)^{-1}S]=\mathrm{tr}[(\varPsi^{-1}S)]-\mathrm{tr}[\varPsi^{-1}\varLambda (\varDelta+I)^{-1}\varLambda'\varPsi^{-1}S]\\ &=\mathrm{tr}(\varPsi^{-1}S)-\sum_{j=1}^r\frac{1}{1+\delta_j^{\prime}\delta_j}\mathrm{tr}(\varLambda_{j}\varLambda_{j}^{\prime}(\varPsi^{-1}S\varPsi^{-1}))\\ &=\mathrm{tr}(\varPsi^{-1}S)-\sum_{j=1}^r\frac{1}{1+\delta_j^{\prime}\delta_j}\mathrm{tr}(\varLambda_{j}^{\prime}(\varPsi^{-1}S\varPsi^{-1})\varLambda_{j})\\ &=\mathrm{tr}(\varPsi^{-1}S)-\sum_{j=1}^r\frac{1}{1+\delta_j^{\prime}\delta_j}\varLambda_{j}^{\prime}(\varPsi^{-1}S\varPsi^{-1}) \varLambda_{j}{}\end{aligned} $$

(11.4.13)

where Λ _j is the j-th column of Λ, which follows by making use of the property tr(AB) = tr(BA) and observing that $\varLambda _{j}^{\prime }(\varPsi ^{-1}S\varPsi ^{-1})\varLambda _{j}$ is a quadratic form.

11.4.3. Special case Ψ = σ ² I _p

Letting Ψ = σ ² I where σ ² is a real scalar, Ψ ⁻¹ = σ ⁻² I _p = θI _p where θ = σ ⁻², and the log-likelihood function can be simplified as

$$\displaystyle \begin{aligned} \ln L &=-\frac{np}{2}\ln (2\pi)+\frac{np}{2}\ln \theta-\frac{n}{2}\sum_{j=1}^r\ln (1+\delta_j^{\prime}\delta_j)\\ &\ \ \ \ -\frac{\theta}{2}\mathrm{tr}(S)+\frac{\theta^2}{2}\sum_{j=1}^r\frac{1}{1+\delta_j^{\prime}\delta_j}\varLambda_{j}^{\prime}S\varLambda_{j}\end{aligned} $$

where $1+\delta _j^{\prime }\delta _j=1+\theta \varLambda _j^{\prime }\varLambda _j$ with Λ _j being the j-th column of Λ. Consider the equation

$$\displaystyle \begin{aligned} \frac{\partial}{\partial\theta}\ln L&=0\Rightarrow\\ \frac{np}{\theta}&-n\sum_{j=1}^r\frac{\varLambda_{j}^{\prime}\varLambda_{j}}{1+\theta \varLambda_{j}^{\prime}\varLambda_{j}}-\mathrm{tr}(S)\\ &+2\theta\sum_{j=1}^r\frac{\varLambda_{j}^{\prime}S\varLambda_{j}}{1+\theta \varLambda_{j}^{\prime}\varLambda_{j}}-\theta^2\sum_{j=1}^r\frac{\varLambda_{j}^{\prime}\varLambda_{j}}{(1+\theta \varLambda_{j}^{\prime}\varLambda_{j})^2}\varLambda_{j}^{\prime}S\varLambda_{j}=0.{}\end{aligned} $$

(11.4.14)

For a specific j, we have

$$\displaystyle \begin{aligned} \frac{\partial}{\partial \varLambda_{j}}\ln L &=O\Rightarrow\\ -\frac{n}{2}\frac{2\theta\varLambda_{j}}{1+\theta \varLambda_{j}^{\prime}\varLambda_{j}}+\frac{\theta^2}{2}\frac{2S\varLambda_{j}}{1+\theta \varLambda_{j}^{\prime}\varLambda_{j}} &-\frac{\theta^2}{2}\frac{\varLambda_{j}^{\prime}S\varLambda_{j}}{[1+\theta\varLambda_{j}^{\prime}\varLambda_{j}]^2}(2\theta) \varLambda_{j}=O.{}\end{aligned} $$

(11.4.15)

Pre-multiplying (11.4.15) by $\varLambda _j^{\prime }$ yields

$$\displaystyle \begin{aligned} -\frac{n\theta \varLambda_j^{\prime}\varLambda_j}{1+\theta\varLambda_j^{\prime}\varLambda_j}+\frac{\theta^2\varLambda_j^{\prime}S\varLambda_j}{1+\theta\varLambda_j^{\prime}\varLambda_j} -\frac{\theta^3(\varLambda_j^{\prime}S\varLambda_j)(\varLambda_j^{\prime}\varLambda_j)}{(1+\theta\varLambda_j^{\prime}\varLambda_j)^2}=0.{} \end{aligned} $$

(11.4.16)

Now, on comparing (11.4.16) with (11.4.14) after multiplying (11.4.14) by θ, we have

$$\displaystyle \begin{aligned} np-\theta\,\mathrm{tr}(S)+\theta^2\sum_{j=1}^r\frac{\varLambda_j^{\prime}S\varLambda_j}{1+\theta\varLambda_j^{\prime}\varLambda_j}=0.{} \end{aligned} $$

(11.4.17)

Multiplying the left-hand side of (11.4.15) by $[1+\theta \varLambda _{j}^{\prime }\varLambda _{j}]^2/\theta$ gives

$$\displaystyle \begin{aligned} -n(1+\theta\varLambda_{j}^{\prime}\varLambda_{j})\varLambda_{j}+\theta(1+\theta\varLambda_{j}^{\prime}\varLambda_{j})S\varLambda_{j} -\theta^2(\varLambda_{j}^{\prime}S\varLambda_{j})\varLambda_{j}=O.{} \end{aligned} $$

(11.4.18)

Then, by pre-multiplying (11.4.18) by $\varLambda _{j}^{\prime }$, we obtain

$$\displaystyle \begin{aligned} -n(1+\theta\varLambda_{j}^{\prime}\varLambda_{j})\varLambda_{j}^{\prime}\varLambda_{j}&+\theta[(1+\theta\varLambda_{j}^{\prime}\varLambda_{j})\varLambda_{j}^{\prime}S\varLambda_{j} -\theta^2(\varLambda_{j}^{\prime}S\varLambda_{j})\varLambda_{j}^{\prime}\varLambda_{j}=0\Rightarrow\\ \theta(\varLambda_j^{\prime}S\varLambda_j)&=n(1+\theta\varLambda_j^{\prime}\varLambda_j)(\varLambda_j^{\prime}\varLambda_j), {} \end{aligned} $$

(11.4.19)

which provides the following representation of θ:

$$\displaystyle \begin{aligned} \theta=\frac{n\varLambda_j^{\prime}\varLambda_j}{\varLambda_j^{\prime}S\varLambda_j-n(\varLambda_j^{\prime}\varLambda_j)^2}\ \mbox{ for }\varLambda_j^{\prime}S\varLambda_j-n(\varLambda_j^{\prime}\varLambda_j)^2>0 \end{aligned}$$

(i)

since θ must be positive. Further, on substituting $\theta \varLambda _j^{\prime }S\varLambda _j\overset {\mbox{(11.4.19)}}{=}n(1+\theta \varLambda _j^{\prime }\varLambda _j)(\varLambda _j^{\prime }\varLambda _j)$ in (11.4.18), we have

$$\displaystyle \begin{aligned} -n\varLambda_j+\theta[S-n(\varLambda_j^{\prime}\varLambda_j)I]\varLambda_j=O, \end{aligned}$$

(ii)

which, on replacing θ by the right-hand side of (i) yields

$$\displaystyle \begin{aligned} -(\varLambda_j^{\prime}S\varLambda_j)\varLambda_j+(\varLambda_j^{\prime}\varLambda_j)S\varLambda_j=O \end{aligned}$$

or, equivalently,

$$\displaystyle \begin{aligned} \left[S-\frac{\varLambda_{j}^{\prime}S\varLambda_{j}}{\varLambda_{j}^{\prime}\varLambda_{j}}I\right]\varLambda_{j}&=O\Rightarrow {} \end{aligned} $$

(11.4.20)

$$\displaystyle \begin{aligned}{}[S-\lambda_jI]\varLambda_j&=O{}\end{aligned} $$

(11.4.21)

where $\lambda _j=\frac {\varLambda _j^{\prime }S\varLambda _j}{\varLambda _j^{\prime }\varLambda _j}$. Observe that Λ _j in (11.4.20) is an eigenvector of S for j = 1, …, p. Substituting the value of $\varLambda _j^{\prime }S\varLambda _j$ from (11.4.19) into (11.4.17) gives the following estimate of θ:

$$\displaystyle \begin{aligned} \hat{\theta}=\frac{np}{\mathrm{tr}(S)-n\sum_{j=1}^p\hat{\varLambda}_j^{\prime}\hat{\varLambda}_j}{} \end{aligned} $$

(11.4.22)

whenever the denominator is positive as θ is by definition positive. Now, in light of (11.4.18) and (11.4.19), we can also obtain the following result for each j:

$$\displaystyle \begin{aligned} \hat{\theta}=\frac{n\hat{\varLambda}_{j}^{\prime}\hat{\varLambda}_{j}}{\hat{\varLambda}_{j}^{\prime}S\hat{\varLambda}_{j}-n(\hat{\varLambda}_{j}^{\prime}\hat{\varLambda}_{j})^2}, ~j=1,\ldots ,p,{} \end{aligned} $$

(11.4.23)

requiring again that the denominator be positive. In this case, $\hat {\varLambda }_j$ is an eigenvector of S for j = 1, …, p. Let us conveniently normalize the $\hat {\varLambda }_j$’s so that the denominator in (11.4.22) and (11.4.23) remain positive.

Thus, $\hat {\varLambda }_j$ is an eigenvector of S with the corresponding eigenvalue λ _j for each j, j = 1, …, p. Out of these, the first r of them, corresponding to the r largest eigenvalues, will also be estimates for the factor loadings Λ _j, j = 1, …, r. Observe that we can multiply $\hat {\varLambda }_j$ by any constant c ₁ without affecting equations (11.4.20) or (11.4.21). This constant c ₁ may become necessary to keep the denominators in (11.4.22) and (11.4.23) positive. Hence we have the following result:

Theorem 11.4.2

The sum of all the eigenvalues of S from Eq.(11.4.20), including the estimates of the r factor loadings $\hat {\varLambda }_1,\ldots ,\hat {\varLambda }_p,$ is given by

$$\displaystyle \begin{aligned} \sum_{j=1}^p\frac{\hat{\varLambda}_{j}^{\prime}S\hat{\varLambda}_{j}}{\hat{\varLambda}_{j}^{\prime}\hat{\varLambda}_{j}}=\mathrm{tr}(S).{} \end{aligned} $$

(11.4.24)

It can be established that the representations of $\hat {\theta }$ given by (11.4.22) and (11.4.23) are one and the same. The equation giving rise to (11.4.23) is

$$\displaystyle \begin{aligned} \theta[\varLambda_j^{\prime}S\varLambda_j-n(\varLambda_j^{\prime}\varLambda_j)^2]=n\varLambda_j^{\prime}\varLambda_j\mbox{ for each }j. \end{aligned}$$

(iii)

Let us divide both sides of (iii) by $\varLambda _j^{\prime }\varLambda _j$. Observe that $\frac {\varLambda _j^{\prime }S\varLambda _j}{\varLambda _j^{\prime }\varLambda _j}=\lambda _j$ is an eigenvalue of S for j = 1, …, p, treating Λ _j as an eigenvector of S. Now, taking the sum over j = 1, …, p, on both sides of (iii) after dividing by $\varLambda _j^{\prime }\varLambda _j$, we have

$$\displaystyle \begin{aligned} \theta\Big[\sum_{j=1}^p\lambda_j-n\sum_{j=1}^p(\varLambda_j^{\prime}\varLambda_j)\Big]&=np\Rightarrow\\ \theta\Big[\mathrm{tr}(S)-n\sum_{j=1}^p\varLambda_j^{\prime}\varLambda_j\Big]&=np,\end{aligned} $$

(iv)

which is Eq. (11.4.22). This proves the claim.

Hence the procedure is the following: Compute the eigenvalues and the corresponding eigenvectors of the sample sum of products matrix S. The estimates for the factor loadings, denoted by $\hat {\varLambda }_{j}$, are available from the eigenvectors $\hat {\varLambda }_j$ of S after appropriate normalization to make the denominators in (11.4.22) and (1.4.23) positive. Take the first r largest eigenvalues of S and then compute the corresponding eigenvectors to obtain estimates for all the factor loadings. This methodology is clearly related to that utilized in Principal Component Analysis, the estimates of the variances of the principal components being $\hat {\varLambda }_{j}^{\prime }S\hat {\varLambda }_{j}/{\hat {\varLambda }_{j}^{\prime }\hat {\varLambda }_j}$ for j = 1, …, r. Verification

Does the representation of θ given in (11.4.22) and (11.4.23) satisfy the likelihood Eq. (11.4.14)? Since θ is estimated through Λ _j for each j = 1, …, p, we may replace θ in (11.4.14) by θ _j and insert the summation symbol. Equation (11.4.14) will then be

$$\displaystyle \begin{aligned} n\sum_j\frac{1}{\theta_j}&-n\sum_j\frac{\varLambda_{j}^{\prime}\varLambda_{j}}{1+\theta_j\varLambda_{j}^{\prime}\varLambda_{j}}-\mathrm{tr}(S)\\ &+2\sum_j\theta_j\frac{\varLambda_{j}^{\prime}S\varLambda_{j}}{1+\theta_j\varLambda_{j}^{\prime}\varLambda_{j}}-\sum_j\theta_j^2 \frac{\varLambda_{j}^{\prime}\varLambda_{j}(\varLambda_j^{\prime}S\varLambda_j)}{(1+\theta_j\varLambda_{j}^{\prime}\varLambda_{j})^2}=0.{} \end{aligned} $$

(11.4.25)

Now, substituting the value of θ _j specified in (11.4.23) into (11.4.14), the left-hand side of (11.4.14) reduces to the following:

$$\displaystyle \begin{aligned} &\ n\sum_j\frac{[\varLambda_{j}^{\prime}S\varLambda_{j}-n(\varLambda_{j}^{\prime}\varLambda_{j})^2]}{n\varLambda_{j}^{\prime}\varLambda_{j}} -n\sum_j\frac{\varLambda_{j}^{\prime}\varLambda_{j}}{\varLambda_{j}^{\prime}S\varLambda_{j}}[\varLambda_{j}^{\prime}S\varLambda_{j}-n(\varLambda_{j}^{\prime}\varLambda_{j})^2]-\mathrm{tr}(S)\\ & +2\sum_jn\varLambda_{j}^{\prime}\varLambda_{j}-\sum_j\frac{\varLambda_{j}^{\prime}\varLambda_{j}}{\varLambda_{j}S\varLambda_{j}}(n\varLambda_{j}^{\prime}\varLambda_{j})^2\\ =&\ \sum_j\frac{\varLambda_{j}^{\prime}S\varLambda_{j}}{\varLambda_{j}^{\prime}\varLambda_{j}}-\mathrm{tr}(S)=0,\end{aligned} $$

owing to Theorem 11.4.2. Hence, Eq. (11.4.14) holds for the value of θ given in (11.4.23) and the value of Λ _j specified in (11.4.20).

Since the basic estimating equation for $\hat {\theta }$ arises from (11.4.23) as

$$\displaystyle \begin{aligned} \theta[\varLambda_{j}^{\prime}S\varLambda_{j}-n(\varLambda_{j}^{\prime}\varLambda_{j})^2]=n\varLambda_{j}^{\prime}\varLambda_{j}, \end{aligned}$$

(v)

a combined estimate for θ can be secured. On dividing both sides of (v) by $\varLambda _j^{\prime }\varLambda _j$ and summing up over j, j = 1, …, p, it is seen that the resulting estimate of θ agrees with that given in (11.4.22).

11.4.4. Maximum value of the exponent

We have the estimate $\hat {\theta }$ of θ provided in (11.4.23) at the estimated value $\hat {\varLambda }_j$ of Λ _j for each j, where $\hat {\varLambda }_j$ is an eigenvector of S resulting from (11.4.20). The exponent of the likelihood function is $-\frac {1}{2}\mathrm {tr}(\varSigma ^{-1}S)$ and, in the current context, Σ = ΛΦΛ′ + Ψ, the identification conditions being that Φ = I _p and Λ′Ψ ⁻¹ Λ be a diagonal matrix with positive diagonal elements. Under these conditions and for the special case Ψ = σ ² I _p with σ ⁻² = θ, we have shown that the exponent in the log-likelihood function reduces to $-\frac {1}{2}\theta \,\mathrm {tr}(S)+\frac {1}{2}\theta ^2\sum _{j=1}^r\frac {\varLambda _j^{\prime }S\varLambda _j}{1+\theta \varLambda _j^{\prime }\varLambda _j}$. Now, consider $\theta \,\mathrm {tr}(S)-\sum _{j=1}^r\theta ^2\frac {\varLambda _j^{\prime }S\varLambda _j}{1+\theta \varLambda _j^{\prime }\varLambda _j}\equiv \delta$. Then,

$$\displaystyle \begin{aligned} \delta&=\theta\,\mathrm{tr}(S)-\theta\sum_{j=1}^r\theta\frac{\varLambda_j^{\prime}S\varLambda_j}{1+\theta\varLambda_j^{\prime}\varLambda_j}\\ &=\theta\,\Big[\mathrm{tr}(S)-\sum_{j=1}^p\theta\frac{\varLambda_j^{\prime}S\varLambda_j}{1+\theta\varLambda_j^{\prime}\varLambda_j}\Big]\\ &=\theta\,\Big[\mathrm{tr}(S)-\sum_{j=1}^pn\varLambda_j^{\prime}\varLambda_j\Big]\mbox{ from (11.4.19)}\\ &=np\mbox{ from (11.4.22)}.\end{aligned} $$

Hence the result.

Example 11.4.1

Tests are conducted to evaluate x ₁  :  verbal-linguistic skills, x ₂  :  spatial visualization ability, and x ₃  :  mathematical abilities. Test scores on x ₁, x ₂, and x ₃ are available. It is known that these abilities are governed by two intellectual faculties that will be identified as f ₁ and f ₂, and that linear functions of f ₁ and f ₂ are contributing to x ₁, x ₂, x ₃. These coefficients in the linear functions, known as factor loadings, are unknown. Let Λ = (λ _ij) be the matrix of factor loadings. Then, we have the model

$$\displaystyle \begin{aligned} x_1&=\lambda_{11}f_1+\lambda_{12}f_2+\mu_1+e_1\\ x_2&=\lambda_{21}f_1+\lambda_{22}f_2+\mu_2+e_2\\ x_3&=\lambda_{31}f_1+\lambda_{32}f_2+\mu_3+e_3.\end{aligned} $$

Let

where M is some general effect, 𝜖 is the error vector or the sum total of the contributions from unknown factors, F represents the vector of contributing factors and Λ, the levels of the contributions. Let Cov(X) = Σ, Cov(F) = Φ and Cov(𝜖) = Ψ. Under the assumptions Φ = I, Ψ = σ ² I where σ ² is a real scalar quantity, and I is the identity matrix, and Λ′Ψ ⁻¹ Λ is diagonal, estimate the factor loadings λ _ij’s and σ ² in Ψ. A battery of tests are conducted on a random sample of six individuals and the following are the data, where our notations are X: the matrix of sample values, $\bar {X}$: the sample average, $\bar {\mathbf {X}}$: the matrix of sample averages, and S: the sample sum of products matrix. So, letting

estimate the factor loadings λ _ij’s and the variance σ ².

Solution 11.4.1

We begin with the computations of the various quantities required to arrive at a solution. Observe that since the matrix of factor loadings Λ is 3 × 2 and a random sample of 6 observation vectors is available, n = 6, p = 3 and r = 2 in our notation.

In this case,

$$\displaystyle \begin{aligned}{}[\mathbf{X}-\bar{\mathbf{X}}][\mathbf{X}-\bar{\mathbf{X}}]'=S=\left[\begin{array}{rrr}6&0&-2\\ 0&6&-2\\ -2&-2&6\end{array}\right]. \end{aligned}$$

An estimator/estimate of Σ is $\hat {\varSigma }=\frac {S}{n}$ whereas an unbiased estimator/estimate of Σ is $\frac {S}{n-1}$. An eigenvalue of $\frac {S}{\alpha }$ is $\frac {1}{\alpha }$ times the corresponding eigenvalue of S. Moreover, constant multiples of eigenvectors are also eigenvectors for a given eigenvalue. Accordingly, we will work with S instead of $\hat {\varSigma }$ or an unbiased estimate of Σ. Since

the eigenvalues are $\lambda _1=6+\sqrt {8},~ \lambda _2=6,~\lambda _3=6-\sqrt {8}$, the two largest ones being $\lambda _1=6+\sqrt {8}$ and λ ₂ = 6. Let us evaluate the eigenvectors U ₁, U ₂ and U ₃ associated with these three eigenvalues. An eigenvector U ₁ corresponding to $\lambda _1=6+\sqrt {8}$ will be a solution of the equation

For λ ₂ = 6, the equation to be solved is

As for the eigenvalue $\lambda _3=6-\sqrt {8}$, it is seen from the derivation of U ₁ that $U_3^{\prime }=[\frac {1}{\sqrt {2}},~\frac {1}{\sqrt {2}},~1]$. Let us now examine the denominator of $\hat {\theta }$ in (11.4.22). Observe that $U_1^{\prime }U_1=2,~U_2^{\prime }U_2=2,~U_3^{\prime }U_3=2$ and $n\sum _{j=1}^pU_j^{\prime }U_j=6(2+2+2)=36$. However, $\mathrm {tr}(S)=(6+\sqrt {8})+(6)+(6-\sqrt {8})=18$. So, let us multiply each vector by $\frac {1}{\sqrt {3}}$ so that $n(\sum _{j=1}^pU_j^{\prime }U_j=6(\frac {2}{3}+\frac {2}{3}+\frac {2}{3})=12$ and $\mathrm {tr}(S)-n\sum _{j=1}^pU_j^{\prime }U_j=18-12>0$. Thus, the estimate of θ is given by

$$\displaystyle \begin{aligned}\hat{\theta}=\frac{np}{\mathrm{tr}(S)-n\sum_{j=1}^pU_j^{\prime}U_j}=\frac{(6)(3)}{18-12}=3\Rightarrow \hat{\sigma}^2=\frac{1}{3} \end{aligned}$$

In light of (11.4.20), the factor loadings are estimated by U ₁ and U ₂ scaled by $\frac {1}{\sqrt {3}}$. Hence, the estimates of the factor loadings, denoted with a hat, are the following: $\hat {\lambda }_{11}=(\frac {1}{\sqrt {3}})(-\frac {1}{\sqrt {2}})=-\frac {1}{\sqrt {6}}$, $\hat {\lambda }_{21}=(\frac {1}{\sqrt {3}})(-\frac {1}{\sqrt {2}})=-\frac {1}{\sqrt {6}},~ \hat {\lambda }_{31}=(\frac {1}{\sqrt {3}})(1)=\frac {1}{\sqrt {3}}$, $\hat {\lambda }_{12}=(\frac {1}{\sqrt {3}})(1)=\frac {1}{\sqrt {3}},~\hat {\lambda }_{22}=(\frac {1}{\sqrt {3}})(-1)=-\frac {1}{\sqrt {3}},~ \hat {\lambda }_{32}=0$.

11.5. General Case

Let

We will take δ _j, j = 1, …, r, and Θ = diag(θ ₁, θ ₂, …, θ _p) as the parameters. Expressed in terms of the δ _j’s and Θ, the log-likelihood function is the following:

$$\displaystyle \begin{aligned} \ln L&=-\frac{np}{2}\ln (2\pi)+n\sum_{j=1}^p\ln\theta_j-\frac{n}{2}\sum_{j=1}^r\ln (1+\delta_j^{\prime}\delta_j)\\ &\ \ \ \, -\frac{1}{2}\mathrm{tr}(\varTheta^2 S)+\frac{1}{2}\sum_{j=1}^r\frac{1}{1+\delta_j^{\prime}\delta_j}(\delta_j^{\prime}\varTheta S\varTheta\, \delta_j).{}\end{aligned} $$

(11.5.1)

Let us take δ _j, j = 1, …, r, and Θ as the parameters. Differentiating $\ln L$ partially with respect to the vector δ _j, for a specific j, and equating the result to a null vector, we have the following (referring to Chap. 1 for vector/matrix derivatives):

$$\displaystyle \begin{aligned}-\frac{n}{2}\frac{2\delta_j}{1+\delta_j^{\prime}\delta_j}-\frac{1}{2}(\delta_j^{\prime}\varTheta S\varTheta \,\delta_j)\frac{2\delta_j}{(1+\delta_j^{\prime}\delta_j)^2}+\frac{1}{2}\frac{2\,\varTheta S\varTheta\, \delta_j}{1+\delta_j^{\prime}\delta_j}=O, \end{aligned}$$

(i)

which multiplied by $1+\delta _j^{\prime }\delta _j>0$, yields

$$\displaystyle \begin{aligned} -n\delta_j-\frac{(\delta_j^{\prime}\varTheta S\varTheta\delta_j)}{1+\delta_j^{\prime}\delta_j}\delta_j+(\varTheta S\varTheta)\delta_j=O.{} \end{aligned} $$

(11.5.2)

On premultiplying (11.5.2) by $\delta _j^{\prime }$ and then by $1+\delta _j^{\prime }\delta _j$, and simplifying, we then have

$$\displaystyle \begin{aligned} -n(1+\delta_j^{\prime}\delta_j)(\delta_j^{\prime}\delta_j)&+(\delta_j^{\prime}\varTheta S\varTheta\delta_j)=O\Rightarrow \\ \frac{\delta_j^{\prime}\varTheta S\varTheta\delta_j}{1+\delta_j^{\prime}\delta_j}&=n\delta_j^{\prime}\delta_j.{} \end{aligned} $$

(11.5.3)

Let us differentiate $\ln L$ as given in (11.5.1) partially with respect to θ _j for a specific j such as j = 1. Then,

$$\displaystyle \begin{aligned}\frac{n}{\theta_j}-\frac{1}{2}2\theta_j s_{jj}+\frac{1}{2}\sum_{j=1}^r\frac{1}{1+\delta_j^{\prime}\delta_j}\frac{\partial}{\partial \theta_j}(\delta_j^{\prime}\varTheta S\varTheta\delta_j),\end{aligned}$$

where

so that

$$\displaystyle \begin{aligned}\Big[\theta_1\frac{\partial}{\partial\theta_1}+\cdots +\theta_p\frac{\partial}{\partial \theta_p}\Big]\varTheta =\varTheta. \end{aligned}$$

(ii)

Hence,

$$\displaystyle \begin{aligned}\Big[\sum_{j=1}^p\theta_j\frac{\partial}{\partial \theta_j}\Big]\sum_{j=1}^r\frac{\delta_j^{\prime}\varTheta S\varTheta\delta_j}{1+\delta_j^{\prime}\delta_j}=2\sum_{j=1}^r\frac{\delta_j^{\prime}\varTheta S\varTheta\delta_j}{1+\delta_j^{\prime}\delta_j}, \end{aligned}$$

and then,

$$\displaystyle \begin{aligned} \Big[\sum_{j=1}^p&\theta_j\frac{\partial}{\partial \theta_j}\Big]L=0\Rightarrow \\ np-\sum_{j=1}^p&\theta_j^2s_{jj}+\sum_{j=1}^r\frac{\delta_j^{\prime}\varTheta S\varTheta\delta_j}{1+\delta_j^{\prime}\delta_j}=0.{}\end{aligned} $$

(11.5.4)

However, given (11.5.3), we have $n\delta _j^{\prime }\delta _j=\delta _j^{\prime }\varTheta S\varTheta \delta _j/(1+\delta _j^{\prime }\delta _j),~j=1,\ldots ,r,$ and therefore (11.5.4) can be expressed as

$$\displaystyle \begin{aligned} np-\sum_{j=1}^p\theta_j^2s_{jj}+\sum_{j=1}^rn\delta_j^{\prime}\delta_j=0. \end{aligned}$$

(iii)

Letting

$$\displaystyle \begin{aligned} c=\frac{1}{p}\sum_{j=1}^r\delta_j^{\prime}\delta_j,{} \end{aligned} $$

(11.5.5)

equation(iii) can be written as

$$\displaystyle \begin{aligned}\sum_{j=1}^p[n(1+c)-\theta_j^2s_{jj}]=0, ~~ c=0, ~j=r+1,\ldots,p, \end{aligned}$$

so that a solution for θ _j is

$$\displaystyle \begin{aligned} \hat{\theta}_j^2=\frac{n(1+c)}{s_{jj}}\ \mbox{ or }\ \hat{\sigma}_j^2=\frac{s_{jj}}{n(1+c)},{} \end{aligned} $$

(11.5.6)

with the proviso that c = 0 for $\hat {\theta }^2_j$ and $\hat {\sigma }^2_j,~j=r+1,\ldots ,p$. Then, an estimate of ΘSΘ is given by

(11.5.7)

where R is the sample correlation matrix, and on applying the identities (11.5.3) and (11.5.7), (11.5.2) becomes

$$\displaystyle \begin{aligned} -n\delta_j&-n(\delta_j^{\prime}\delta_j)\delta_j+(n(1+c)R)\delta_j=0\Rightarrow \\ &\Big[R-\frac{1+\hat{\delta}_j^{\prime}\hat{\delta}_j}{1+c}I\Big]\delta_j=O.{} \end{aligned} $$

(11.5.8)

This shows that δ _j is an eigenvector of R. If ν _j is an eigenvalue of R, then the largest r eigenvalues are of the form

$$\displaystyle \begin{aligned} \nu_j=\frac{1+\hat{\delta}_j^{\prime}\hat{\delta}_j}{1+c},~j=1,\ldots ,r,{} \end{aligned} $$

(11.5.9)

and the remaining ones are ν _r+1, …, ν _p, where c is as specified in (11.5.5). Thus, the procedure is the following: Compute the eigenvalues ν _j, j = 1, …, p, of R and determine the corresponding eigenvectors, denoted by δ _j, j = 1, …, p. The first r of them which correspond to the r largest ν _j’s, are $\hat {\delta }_j=\hat {\varTheta }\hat {\varLambda }_j\Rightarrow \hat {\varLambda }_j=\hat {\varTheta }^{-1}\hat {\delta }_j,~j=1,\ldots ,r$. Let

(11.5.10)

Then,

$$\displaystyle \begin{aligned} \hat{\lambda}_{ij}=\frac{\sqrt{s_{jj}}}{\sqrt{n(1+c)}}\,\hat{\delta}_{ij},~i=1,\ldots ,p,~ j=1,\ldots ,r,{} \end{aligned} $$

(11.5.11)

and $\hat {\varTheta }$ is available from (11.5.10). All the model parameters have now been estimated.

11.5.1. The exponent in the likelihood function

Given the MLE’s of the parameters which are available from (11.5.6), (11.5.8), (11.5.10) and (11.5.11), what will be the maximum value of the likelihood function? Let us examine its exponent:

$$\displaystyle \begin{aligned} -\frac{1}{2}\mathrm{tr}(\hat{\varTheta}^2S)&+\frac{n}{2}\sum_{j=1}^r\hat{\delta}_j^{\prime}\hat{\delta}_j=-\frac{1}{2}n(1+c)\mathrm{tr}(R)+\frac{n}{2}pc\\ &=-\frac{1}{2}n(1+c)p+\frac{1}{2}npc=-\frac{np}{2},\end{aligned} $$

that is, the same value of the exponent that is obtained under a general Σ. The estimates were derived under the assumptions that Σ = Ψ + ΛΛ′, Λ′Ψ ⁻¹ Λ is diagonal with the diagonal elements $\delta _j^{\prime }\delta _j,~j=1,\ldots ,r,$ and Ψ = Θ ⁻².

Example 11.5.1

Using the data set provided in Example 11.4.1, estimate the factor loadings and the diagonal elements of Cov(𝜖) = Ψ = diag(ψ ₁₁, …, ψ _pp). In this example, p = 3, n = 6, r = 2.

Solution 11.5.1

We will adopt the same notations and make use of some of the computational results already obtained in the previous solution. First, we need to compute the eigenvalues of the sample correlation matrix R. The sample sum of products matrix S is given by

$$\displaystyle \begin{aligned}S=\left[\begin{array}{rrr}6&0&-2\\ 0&6&-2\\ \!\!-2&-2&6\end{array}\right]\Rightarrow R=\left[\begin{array}{rrr}1&0&-\frac{2}{6}\\ 0&1&-\frac{2}{6}\\ \!\! -\frac{2}{6}&-\frac{2}{6}&1\end{array}\right]=\frac{1}{6}S. \end{aligned}$$

Hence, the eigenvalues of R are $\frac {1}{6}$ times the eigenvalues of S, that is, $\nu _1=\frac {1}{6}(6+\sqrt {8})=1+\frac {\sqrt {2}}{3},~ \nu _2=\frac {1}{6}(6)=1$ and $\nu _3=1-\frac {\sqrt {2}}{3}$. Since $\frac {1}{6}$ will be canceled when determining the eigenvectors, the eigenvectors of S will coincide with those of R. They are the following, denoted again by δ _j, j = 1, 2, 3:

Therefore, $\delta _1^{\prime }\delta _1=2,~ \delta _2^{\prime }\delta _2=2,~\delta _3^{\prime }\delta _3=2$ and c as defined in (11.5.5) is $c=\frac {1}{3}(2+2)=\frac {4}{3}\Rightarrow n(1+c)=6(1+\frac {4}{3})=14$. Then, in light of (11.5.10), the estimates of ψ _jj, j = 1, 2, 3, are available as $\hat {\psi }_{jj}=\hat {\theta }_j^{-2}=\frac {s_{jj}}{n(1+c)}$ or $\hat {\psi }_{11}=\hat {\theta }_{1}^{-2}=\frac {6}{14}=\frac {3}{7}=\hat {\psi }_{22}=\hat {\psi }_{33}$, denoting the estimates with a hat. Therefore, the diagonal matrix $\hat {\varPsi }=\mathrm {diag}(\frac {3}{7},~\frac {3}{7},~\frac {3}{7})$. Hence, the matrix $\varTheta ^{-1}=\varPsi ^{\frac {1}{2}}$ is estimated by $\hat {\varTheta }^{-1}=\mathrm {diag}(\frac {\sqrt {3}}{\sqrt {7}},~\frac {\sqrt {3}}{\sqrt {7}},~\frac {\sqrt {3}}{\sqrt {7}})$. From (11.5.11), $\hat {\varLambda }_j=\hat {\varTheta }^{-1}\delta _j=\mathrm {diag}(\frac {\sqrt {3}}{\sqrt {7}},~\frac {\sqrt {3}}{\sqrt {7}},~\frac {\sqrt {3}}{\sqrt {7}})\,\delta _j$, that is, δ _j is pre-multiplied by $\frac {\sqrt {3}}{\sqrt {7}}$. Therefore, the estimates of the factor loadings are: $\hat {\lambda }_{11}=-(\frac {\sqrt {3}}{\sqrt {7}})(\frac {1}{\sqrt {2}})=\hat {\lambda }_{21}=-\hat {\lambda }_{13}=-\hat {\lambda }_{23},~ \hat {\lambda }_{31}=\frac {\sqrt {3}}{\sqrt {7}}=\hat {\lambda }_{33}=\hat {\lambda }_{12}=-\hat {\lambda }_{22}$, and $\hat {\lambda }_{32}=0$.

11.6. Tests of Hypotheses

The usual test in connection with the current topic consists of assessing identifiability, that is, testing the hypothesis H ₀ that the population covariance matrix Σ > O can be represented as Σ = ΛΦΛ′ + Ψ when Φ = I, Λ′Ψ ⁻¹ Λ is a diagonal matrix with positive diagonal elements, Ψ > O is a diagonal matrix and Λ = (λ _ij) is a p × r, r ≤ p, matrix of full rank r, whose elements are the factor loadings. That is,

$$\displaystyle \begin{aligned} H_0:~ \varSigma = \varLambda\varLambda'+\varPsi.{} \end{aligned} $$

(11.6.1)

In this instance, a crucial aspect of the hypothesis H _o consisting of determining whether “the model fits”, is that the number r be designated since the other quantities n, the sample size, and p, the order of the observation vector, are preassigned. Thus, the phrase “model fits” means that for a given r, Σ can be expressed in the form Σ = Ψ + ΛΛ′, in addition to satisfying the identification conditions. The assumed model has the representation: X = M + ΛF + 𝜖 where X′ = (x ₁, …, x _p) stands for the p × 1 vector of observed scores on p tests or p batteries of tests, M is a p × 1 vector of general effect, F is an r × 1 vector of unknown factors, Λ = (λ _ij) is the unknown p × r matrix of factor loadings and 𝜖 is the p × 1 error vector. When 𝜖 and F are uncorrelated, the covariance matrix of X is given by

$$\displaystyle \begin{aligned}\varSigma=\varLambda\varPhi\varLambda'+\varPsi \end{aligned}$$

where Φ = Cov(F) > O and Ψ = Cov(𝜖) > O with Φ being r × r and Ψ being p × p and diagonal. A simple random sample from X will be taken to mean a sample of independently and identically distributed (iid) p × 1 vectors $X_j^{\prime }=(x_{1j},x_{2j},\ldots ,x_{pj}),~j=1,\ldots ,n,$ with n denoting the sample size. The sample sum of products matrix or “corrected” sample sum of squares and cross products matrix is $S=(s_{ij}),~s_{ij}=\sum _{k=1}^n(x_{ik}-\bar {x}_i)(x_{jk}-\bar {x}_j)$, where, for example, the average of the x _i’s comprising the i-th row of X = [X ₁, …, X _n], namely, $\bar {x}_i$, is $\bar {x}_i=\sum _{k=1}^nx_{ik}/n$. If 𝜖 and F are independently normally distributed, then the likelihood ratio criterion or λ-criterion is

$$\displaystyle \begin{aligned} \lambda = \frac{\max_{H_0}L}{\max L}=\frac{|\hat{\varSigma}|{}^{\frac{n}{2}}}{|\hat{\varLambda}\hat{\varLambda}'+\hat{\varPsi}|{}^{\frac{n}{2}}}\ \,\Rightarrow\ \, w=\lambda^{\frac{2}{n}}=\frac{|\hat{\varSigma}|}{|\hat{\varLambda}\hat{\varLambda}'+\hat{\varPsi}|}{} \end{aligned} $$

(11.6.2)

where $\hat {\varSigma }=\frac {1}{n}S$ and the covariance matrix Σ = ΛΛ′ + Ψ under H ₀, with Φ = Cov(F) assumed to be an identity matrix and the r × r matrix $\varLambda '\varPsi ^{-1}\varLambda =\mathrm {diag}(\delta _1^{\prime }\delta _1,\ldots ,\delta _r^{\prime }\delta _r)$ having positive diagonal elements $\delta _j^{\prime }\delta _j,~j=1,\ldots ,r$. Referring to Sect. 11.4.2, we have

$$\displaystyle \begin{aligned} |\varLambda\varLambda'+\varPsi|=|\varPsi|~|\varLambda'\varPsi^{-1}\varLambda+I|{} \end{aligned} $$

(11.6.3)

and $1+\delta _j^{\prime }\delta _j=1+\varLambda _j^{\prime }\varPsi ^{-1}\varLambda _j=1+\varLambda _j^{\prime }\varTheta ^2\varLambda _j$ where $\delta _j=\varPsi ^{-\frac {1}{2}}\varLambda _j=\varTheta \varLambda _j$ and Λ _j is the j-th column of Λ for j = 1, …, r. It was shown in (11.5.8) that δ _j is an eigenvector of the sample correlation matrix R and

$$\displaystyle \begin{aligned}\prod_{j=1}^r(1+\delta_j^{\prime}\delta_j)=|\varLambda'\varPsi^{-1}\varLambda +I|.\end{aligned}$$

However, in view of the discussion following (11.5.8), an eigenvalue of R is of the form $\nu _j=\frac {1+\delta _j^{\prime }\delta _j}{(1+c)},~ j=1,\ldots ,r$. Let ν ₁, …ν _p be the eigenvalues of R and let the largest r of them be ν ₁, …, ν _r. It also follows from (11.5.8) that $\hat {\varTheta }^2=n(1+c)\mathrm {diag}(\frac {1}{s_{11}},\ldots ,\frac {1}{s_{pp}})$ with $\varTheta =\varPsi ^{-\frac {1}{2}}$. Thus,

$$\displaystyle \begin{aligned} \frac{|\hat{\varSigma}|}{|\hat{\varPsi}|}&=\Big|\hat{\varTheta}\Big(\frac{S}{n}\Big)\hat{\varTheta}\Big|=|(1+c)R| =\Big\{\prod_{j=1}^r(1+c)\nu_j\Big\}(1+0)^{p-r}\nu_{r+1}\cdots\nu_p \\ &=\Big\{\prod_{j=1}^r (1+\hat{\delta}_j^{\prime}\hat{\delta}_j)\Big\}\nu_{r+1}\cdots\nu_p \\ &\Rightarrow \frac{|\frac{1}{n}S|}{|\hat{\varPsi}|~|\hat{\varLambda}'\hat{\varPsi}^{-1}\hat{\varLambda}+I|} =\frac{\{\prod_{j=1}^r(1+\hat{\delta}_j^{\prime}\hat{\delta}_j)\} \nu_{r+1}\cdots\nu_p} {\{\prod_{j=1}^r(1+\hat{\delta}_j^{\prime}\hat{\delta}_j)\}} \\ &=\nu_{r+1}\cdots\nu_p=w=\lambda^{\frac{2}{n}}.{}\end{aligned} $$

(11.6.4)

Hence, we reject the null hypothesis for small values of the product ν _r+1⋯ν _p, that is, the product of the smallest p − r eigenvalues of the sample correlation matrix R. In order to evaluate critical points, one would require the null distribution of the product of the eigenvalues, ν _r+1⋯ν _p, which is difficult to determine for a general p. How can rejecting the null hypothesis that the “model fits” be interpreted? Since, in the whole structure, the decisive quantity is r, we are actually rejecting the hypothesis that a given r is the number of main factors contributing to the observations. Hence, we may seek a larger or smaller r, keeping the structure unchanged and testing the same hypothesis again until the hypothesis is not rejected. We may then assume that the r specified at the last stage is the number of main factors contributing to the observation or we may assert that, with that particular r, there is evidence that the model fits.

We will now determine conditions ensuring that the likelihood ratio criterion λ be less than or equal to one. While, assuming that Λ′Ψ ⁻¹ Λ is diagonal, the left-hand side of the deciding equation, Σ = ΛΛ′ + Ψ, has p(p + 1)∕2 parameters, there are p r + p − r(r − 1)∕2 conditions on the right-hand side where r(r − 1)∕2 arises from the diagonality condition. The difference is then

$$\displaystyle \begin{aligned} \frac{p(p+1)}{2}-\Big[p\,r+p-\frac{r(r-1)}{2}\Big]=\frac{1}{2}[(p-r)^2-(p+r)]\equiv\rho.{} \end{aligned} $$

(11.6.5)

This ρ depends upon the parameters p and r, whereas λ depends upon p, r and c. Thus, λ may not be ≤ 1. In order to make λ ≤ 1, we can make c close to 0 by multiplying the $\hat {\delta }_j$’s by a constant, observing that this is always possible because the $\hat {\delta }_j$’s are the eigenvectors of R. By selecting a constant m and taking the new $\hat {\delta }_j$ as $\frac {1}{\sqrt {m}}\delta _j$, c can be made close to 0 and λ will be ≤ 1, so that rejecting the null hypothesis for small values of λ will make sense. It may so happen that there will not be any parameter left to be restricted by the hypothesis H _o that “model fits”. The quantity ρ appearing in (11.6.5) could then be ≤ 0, and in such an instance, the hypothesis would not make sense and could not be tested.

The density of the sample correlation matrix R is provided in Example 1.25 of Mathai (1997, p. 58). Denoting this density by f(R), it is the following for the population covariance matrix Σ in a parent N _p(μ, Σ) population with Σ being a positive definite diagonal matrix, as was assumed in Sect. 11.6:

$$\displaystyle \begin{aligned} f(R)=\frac{[\varGamma(\frac{m}{2})]^p}{\varGamma_p(\frac{m}{2})}|R|{}^{\frac{m}{2}-\frac{p+1}{2}},~R>O,~ m=n-1,~n>p,{} \end{aligned} $$

(11.6.6)

and zero elsewhere, where n is the sample size.

11.6.1. Asymptotic distribution of the likelihood ratio statistic

For a large sample size n, $-2\ln \lambda$ is approximately distributed as a chisquare random variable having k degrees of freedom where λ is the likelihood ratio criterion and k is the number of parameters restricted by the hypothesis H ₀. This approximation holds whenever the sample size n is large and k ≥ 1. With ρ as defined in (11.6.5), we have

$$\displaystyle \begin{aligned} k=\rho=\frac{1}{2}[(p-r)^2-(p+r)].{} \end{aligned} $$

(11.6.7)

However, p − r = 1 and p + r = 5 in the illustrative example, so that k = −2. Accordingly, even if the sample size n were large, this asymptotic result would not be applicable.

11.6.2. How to decide on the number r of main factors?

The structure of the population covariance matrix Σ under the model X _j = M + ΛF + E _j, j = 1, …, n, is

$$\displaystyle \begin{aligned} \varSigma=\varLambda\varPhi\varLambda'+\varPsi\ \Rightarrow\ \varSigma=\varLambda\varLambda'+\varPsi\ \mbox{ for }\ \varPhi=I,{} \end{aligned} $$

(11.6.8)

where it is assumed that E _j and F are uncorrelated, Σ = Cov(X _j) > O is p × p, Φ = Cov(F) = I, the r × r identity matrix, Ψ = Cov(E _j) is a p × p diagonal matrix and Λ = (λ _ij) is a full rank p × r, r ≤ p, matrix whose elements are the factor loadings. Under the orthogonal factor model, Φ = I. Moreover, to ensure the identification of the model, we assume that Λ′Ψ ⁻¹ Λ is a diagonal matrix. Before initiating any data analysis, we have to assign a value to r on the basis of the data set at hand in order to set up the model. Thus, the matter of initially setting the number of main factors has to be addressed. Given

$$\displaystyle \begin{aligned} R=\varLambda \varLambda'+\varPsi{} \end{aligned} $$

(11.6.9)

where Λ = (λ _ij) is a p × r matrix and Ψ is a p × p diagonal matrix, does a solution that is expressible in terms of the elements of R (or those of S if S is used), exist for all λ _ij’s and ψ _jj’s? In general

$$\displaystyle \begin{aligned} R=\lambda_1U_1U_1^{\prime}+\cdots +\lambda_pU_pU_p^{\prime}{} \end{aligned} $$

(11.6.10)

where the λ _j’s are the eigenvalues of R and the U _j’s are the corresponding normalized eigenvectors. Observe that $U_jU_j^{\prime }$ is p × p whereas $U_j^{\prime }U_j=1,\ j=1,\ldots ,p$. If r = p, then a solution always exists for (11.6.9). When taking Ψ = O, we can always let R = BB′ for some p × p matrix B, which can be achieved for example via a triangular decomposition. Accordingly, the relevant aspects are r < p and the diagonal elements in Ψ, namely, the ψ _jj’s being positive. Can we then solve for all the λ _ij’s and ψ _jj’s involved in (11.6.9) in terms of the elements in R? The answer is that a solution exists, but only when certain conditions are satisfied. Our objective is to select a value of r that is as small as possible and then, to obtain a solution to (11.6.9) in terms of the elements in R.

The analysis is to be carried out by utilizing either the sample sum of products matrix S or the sample correlation matrix R. The following are some of the guidelines for selecting r in order to set up the model. (i): Compute all the eigenvalues of R (or S). Let r be the number of eigenvalues ≥ 1 if the sample correlation matrix R is used. If S is used, then determine all the eigenvalues, calculate the average of these eigenvalues, and count the number of eigenvalues that are greater than or equal to this average. Take that number to be r. (2): Carry out a Principal Component Analysis on R (or S). If S is used, ensure that the units of measurements are not creating discrepancies. Compute the variances of these Principal Components, which are the eigenvalues of R (or S). Let λ _j, j = 1, …, p, denote these eigenvalues. Compute the ratios

$$\displaystyle \begin{aligned}\frac{\lambda_1+\cdots +\lambda_m}{\lambda_1+\cdots +\lambda_p},\ m=1,2,\ldots,\end{aligned}$$

and stop with that m for which the desired fraction of the total variation in the data is accounted for. Take that m as r. When implementing the principal component approach, the factor loadings λ _ij’s and the ψ _jj’s can be estimated as follows: From (11.6.10), write

$$\displaystyle \begin{aligned}R=A+B\, \ {\mathrm{with }} \ \ A=\sum_{j=1}^r\lambda_jU_jU_j^{\prime}\ \,{\mathrm{and }} \ \,B=\sum_{j=r+1}^p\lambda_jU_jU_j^{\prime}, \end{aligned}$$

where A can be expressed as V V ′ with $V=[\sqrt {\lambda _j}U_1,\ldots ,\sqrt {\lambda _j}U_r]$. Then, V  is taken as an approximate estimate of Λ or as $\hat {\varLambda }$. Observe that λ _j > 0, j = 1, …, p. The sum over j of the i-th diagonal elements of $\lambda _jU_jU_j^{\prime },\ j=r+1,\ldots ,p,$ will provide an estimate for ψ _ii, i = 1, …, p. These estimates can also be obtained as follows: Consider the estimate of σ _ii denoted by $\hat {\sigma }_{ii}$ which is equal to the sum of all the i-th diagonal elements in A + B; it will be 1 if R is used and $\hat {\sigma }_{ii}$ if S is utilized in the analysis; then, $\hat {\psi }_{ii}=\hat {\sigma }_{ii}-\sum _{j=1}^r\hat {\lambda }_{ij}$ and $\hat {\psi }_{ii}$ is now the sum of the i-th diagonal elements in B. (iii): Consider the individual correlations in the sample correlation matrix R. Identify the largest ones in absolute value. If the largest ones occur at the (1,3)-th and (2,3)-th positions, then the factor f ₃ will be deemed influential. Start with r = 1 (factor f ₃) and carry out the analysis. Then, assess the proportion of the total variation accounted for by $\hat {\sigma }_{33}$. Should the proportion not be satisfactory, we may continue with r = 2. If the (2,3)-th position value is larger in absolute value than the value at the (1,3)-th position, then f ₂ may be the next significant factor. Compute $\hat {\sigma }_{33}+\hat {\sigma }_{22}$ and determine the proportion to the total variation. If the resulting model is rejected, then take r = 3, and continue in this fashion until an acceptable proportion of the total variation is accounted for. (iv): The maximum likelihood method. With this approach, we begin with a preselected r and test the hypothesis that, when comprising r factors, the model fits. If the hypothesis is rejected, then we let number of influential factors be r − 1 or r + 1 and continue the process of testing and deciding until the hypothesis is not rejected. That final r is to be taken as the number of main factors contributing towards the observations. The initial value of r may be determined by employing one of the methods described in (i) or (ii) or (iii).

Exercises

11.1

For the following data, where the 6 columns of the matrix represent the 6 observation vectors, verify whether r = 2 provides a good fit to the data. The proposed model is the Factor Analysis model X = M + ΛF + 𝜖, F′ = (f ₁, f ₂), Λ is 3 × 2 and of rank 2, Cov(𝜖) = Ψ is diagonal, Cov(F) = Φ = I, and Cov(X) = Σ > O. The data set is

$$\displaystyle \begin{aligned}\left[\begin{array}{rrrrrr}0&1&-1&0&1&-1\\ 1&1&0&2&2&0\\ \!\! -1&-1&0&-1&-1&-2\end{array}\right].\end{aligned}$$

11.2

For the model X = M + ΛF + 𝜖 with the conditions as specified in Exercise 11.1, verify whether the model with r = 2 or r = 3 gives a good fit on the basis of the following data, where the columns in the matrix represent five observation vectors:

$$\displaystyle \begin{aligned}\left[\begin{array}{rrrrrr}1&0&\!\!-1&1&0\\ \!\!-1&1&1&0&\!\!-1\\ 1&0&1&2&1\\ 1&1&2&1&0\end{array}\right].\end{aligned}$$

11.3

Do a Principal Component Analysis in Exercise 11.1 to assess what percentage of the total variation in the data is accounted for by r = 2.

11.4

Do a Principal Component Analysis in Exercise 11.2 to determine what percentages of the total variation in the data are accounted for by r = 2 and r = 3.

11.5

Even though the sample sizes are not large, perform tests based on the asymptotic chisquare to assess whether the two tests there agree with the findings in Exercises 11.1 and 11.2.

11.6

Four model identification conditions are stated at the end of Sect 11.3.1. Develop λ-criteria under the conditions stated in (i): case (2); (ii): case (3), selecting your own B ₁; (iii): case (4).