Dark Matter Radios

Abstract

Many theories predict that ultralight bosonic dark matter (UBDM) can couple to photons and thus generate electromagnetic signals. In such scenarios, UBDM can be searched for using a radio: an antenna connected to a tunable LC circuit that is in turn connected to an amplifier. Such “dark matter radios” are particularly useful tools to search the broad range of UBDM wavelengths where resonant cavity dimensions are too large to be practical. In this chapter, we discuss how dark matter radios can be used to search for UBDM, focusing on the case of hidden photons.

7.1 Hidden Photons

Chapters 4 and 5 of this text have described searches for UBDM in the form of axions or axionlike particles (ALPs) that utilize techniques based on their coupling to electromagnetic fields. In this chapter, we describe another technique that can be used to look for electromagnetic couplings of UBDM (including axions and ALPs), but instead focus on a different class of ultralight bosons known as hidden photons [1].

Hidden sectors described by extra $\mathbb {U}(1)$ symmetries¹ are a common feature in theories going beyond the Standard Model such as string theory [2]. Even though such hidden sectors may be quite complicated [3, 4], their observable effects can be parameterized by the effective operators coupling them to Standard Model particles and fields [5]. One possibility is direct couplings: Standard Model particles and fields can be “charged” with respect to the hidden sector [6]. It turns out that the only other generic possibility is a kinetic mixing between the new $\mathbb {U}(1)$ symmetry and electromagnetism [1]: this is the origin of the hidden photon.

The effects of this hidden photon can be understood in particularly simple terms: it behaves exactly like a photon except that

• It has a nonzero mass $m_{\gamma '}$.

• It interacts with charged particles primarily through its mixing into a “real” photon field, parameterized by a kinetic mixing parameter κ.

The Lagrangian describing photons and hidden photons can be written in what is known as the “mass basis” as follows:

$$\displaystyle \begin{aligned} \mathcal{L} = -\frac{1}{16\pi} \left( F_{\mu\nu}F^{\mu\nu} + \mathcal{F}_{\mu\nu}\mathcal{F}^{\mu\nu} \right) + \frac{m_{\gamma'}^2c^2}{2\hbar^2} \mathcal{X}_\mu \mathcal{X}^\mu - \frac{1}{c}J^\mu {\left( A_\mu + \kappa \mathcal{X}_\mu \right)}, {} \end{aligned} $$

(7.1)

where A_μ and F_μν are the gauge potential and field strength tensor of electromagnetism (the ordinary photon field), $\mathcal {X}_\mu$ and $\mathcal {F}_{\mu \nu }$ are the gauge potential and field strength of the hidden photon field, J^μ is the ordinary electromagnetic current, and here and throughout this chapter we use Gaussian (cgs) units. Notice that in the limit where $m_{\gamma '} \rightarrow 0$, because of the symmetry between the photon and hidden photon fields, one can redefine a linear combination $A_\mu + \kappa \mathcal {X}_\mu$ that couples to the electromagnetic current J^μ and a sterile component $\mathcal {X}_\mu - \kappa A_\mu$ that does not interact at all electromagnetically. Essentially, this means that all hidden photon interactions are suppressed by powers of $m_{\gamma '}^2$ in the small mass limit. This is the argument that significantly reduces many astrophysical bounds on hidden photons [7].

In vacuum, the hidden photon field obeys the wave equation

$$\displaystyle \begin{aligned} {\left(\frac{1}{c^2}{\frac{\partial ^2}{\partial t^2}} - \nabla^2 + \frac{m_{\gamma'}^2c^2}{\hbar^2}\right)} \mathcal{X}_\mu = 0~, {} \end{aligned} $$

(7.2)

and the constraint $\partial _\mu \mathcal {X}^\mu = 0$ is assumed (equivalent to the Lorenz gauge condition).

The two key features of hidden photons, that they have nonzero mass and only weakly interact with SM particles via the kinetic mixing with photons, have three important consequences: (1) their nonzero mass means that hidden photons can have the right characteristics to behave as cold dark matter [8], (2) their kinetic mixing with photons means that hidden photons can weakly excite electromagnetic systems, and (3) their weak coupling with SM particles and macroscopic Compton wavelength allow hidden photons to have a long penetration depth in conductors and superconductors.

7.2 Hidden Photon Electrodynamics

A useful way to understand the effect of the hidden photon on electrodynamics is to rewrite the Lagrangian given in Eq. (7.1) in the “interaction basis” by making the substitutions:

$$\displaystyle \begin{aligned} \bar{A}_\mu & = A_\mu + \kappa\mathcal{X}_\mu~, {} \end{aligned} $$

(7.3)

$$\displaystyle \begin{aligned} \bar{\mathcal{X}}_\mu & = \mathcal{X}_\mu - \kappa A_\mu~, {} \end{aligned} $$

(7.4)

which yields for the Lagrangian

$$\displaystyle \begin{aligned} \mathcal{L} = -\frac{1}{16\pi} &\left( \bar{F}_{\mu\nu}\bar{F}^{\mu\nu} + \bar{\mathcal{F}}_{\mu\nu}\bar{\mathcal{F}}^{\mu\nu} \right) + \frac{m_{\gamma'}^2c^2}{2\hbar^2} \bar{\mathcal{X}}_\mu \bar{\mathcal{X}}^\mu \\ & - \frac{1}{c}J^\mu \bar{A}_\mu + \kappa \frac{m_{\gamma'}^2c^2}{\hbar^2} \bar{\mathcal{X}}^\mu \bar{A}_\mu~. {} \end{aligned} $$

(7.5)

From Eq. (7.5), we can see that the effect of hidden photons on Standard Model particles can be derived from the existence of an effective current density:

$$\displaystyle \begin{aligned} \bar{\mathcal{J}}^\mu = -\kappa \frac{m_{\gamma'}^2c^3}{\hbar^2} \bar{\mathcal{X}}^\mu~, {} \end{aligned} $$

(7.6)

since the last term in Eq. (7.5) describes the coupling to SM particles.

This gives us

$$\displaystyle \begin{aligned} \mathcal{L} = -\frac{1}{16\pi} \left( \bar{F}_{\mu\nu}\bar{F}^{\mu\nu} + \bar{\mathcal{F}}_{\mu\nu}\bar{\mathcal{F}}^{\mu\nu} \right) + \frac{m_{\gamma'}^2c^2}{2\hbar^2} \bar{\mathcal{X}}_\mu \bar{\mathcal{X}}^\mu - \frac{1}{c}{\left( J^\mu + \bar{\mathcal{J}}^\mu \right)} \bar{A}_\mu~. {} \end{aligned} $$

(7.7)

Note that the timelike component of the four-potential, $\bar {\mathcal {X}}^0$, is suppressed compared to the spacelike component, i.e., the vector potential $\boldsymbol {\mathcal {X}}$. The relationship between $\bar {\mathcal {X}}^0$ and $\boldsymbol {\mathcal {X}}$ is derived from the equivalent of the Lorenz gauge condition,

$$\displaystyle \begin{aligned} \frac{1}{c}{\frac{\partial \bar{\mathcal{X}}^0}{\partial t}} = \nabla \cdot \boldsymbol{\mathcal{X}}~. {} \end{aligned} $$

(7.8)

Assuming a plane wave solution for $\bar {\mathcal {X}}^\mu \propto e^{i(\mathbf {k}\cdot \mathbf {r} - \omega t)}$, Eq. (7.8) yields

$$\displaystyle \begin{aligned} \bar{\mathcal{X}}^0 = -\frac{c}{\omega}\mathbf{k} \cdot \boldsymbol{\mathcal{X}}~. {} \end{aligned} $$

(7.9)

Using the relationship between the wavevector k and the hidden photon’s velocity,

$$\displaystyle \begin{aligned} \mathbf{k} = m_{\gamma'}\mathbf{v}/\hbar~, {} \end{aligned} $$

(7.10)

and the fact that $\hbar \omega \approx m_{\gamma '}c^2$, we find that

$$\displaystyle \begin{aligned} \bar{\mathcal{X}}^0 \approx -\frac{\mathbf{v}}{c} \cdot \boldsymbol{\mathcal{X}}~. {} \end{aligned} $$

(7.11)

Therefore, the timelike component of the hidden photon four-potential is suppressed by a factor ≈ v∕c ≈ 10⁻³ as compared to the spacelike component. For the same reason, the spacelike component of the hidden photon four-current (i.e., the effective charge density) is suppressed by ≈ v∕c compared to the hidden photon current density, $\boldsymbol {\mathcal {J}}$, see Eq. (7.6).

7.3 Hidden Electric and Magnetic Fields as Dark Matter

If hidden photons comprise the majority of dark matter, they must be nonrelativistic and the energy of the hidden photon field is stored primarily in the hidden-electric field $\mathcal {E}'$. This can be understood by analogy with the relativistic properties of ordinary electric and magnetic fields. If an observer is in the rest frame of a static charge distribution, they will measure a static electric field E sourced by the charges but no magnetic field. If the observer moves at a constant velocity v with respect to the charge distribution, they will measure a motional magnetic field of magnitude $B \sim {\left (v/c\right )} E$. In the case where v ≪ c, the observer measures that most of the energy is stored in the electric field. This contrasts with the case of electromagnetic waves propagating in vacuum, where there is equal energy stored in both E and B. Because hidden photons have a nonzero rest mass, there exists a hidden photon rest frame in which the hidden photon energy is stored entirely in the oscillating hidden electric field $\mathcal {E}'$—analogous to the rest frame of a static charge distribution. If the hidden photons are the dark matter, they must be nonrelativistic (see Chaps. 1 and 3), and so the vast majority of the hidden photon energy density is associated with $\mathcal {E}'$.

The dark matter energy density in our local region of the Milky Way galaxy, ρ_dm ≈ 0.4 GeV∕cm³, can thus be estimated using the hidden electric field analog of the usual formula from electromagnetism

$$\displaystyle \begin{aligned} \rho{{}_{\mbox{ dm}}} = \frac{1}{8\pi} {\left( \mathcal{E}' \right)}^2~, {} \end{aligned} $$

(7.12)

from which we find that

$$\displaystyle \begin{aligned} \mathcal{E}' \approx 40~\mathrm{V/cm}~. {} \end{aligned} $$

(7.13)

The associated hidden magnetic field is

$$\displaystyle \begin{aligned} \mathcal{B}' \approx \frac{v}{c}\mathcal{E}' \approx 10^{-4}~\mathrm{G}~. {} \end{aligned} $$

(7.14)

The hidden fields $\mathcal {E}'$ and $\mathcal {B}'$ result from the interference of a large number of virialized hidden photons having high mode occupation number, and thus the hidden field properties have a stochastic nature [9, 10]. The stochastic behavior of virialized UBDM fields is analogous to that of thermal (chaotic) light [11]. The finite coherence time τ_coh and coherence length λ_coh of $\mathcal {E}'$ and $\mathcal {B}'$ result from the velocity spread of the hidden photons (δv ≈ v ≈ 10⁻³c, see Chap. 1):

$$\displaystyle \begin{aligned} \tau{{}_{\mbox{ coh}}} \approx 4000~\mathrm{s} \times \frac{10^{-12}~\mathrm{eV}}{m_{\gamma'}c^2}~, {} \end{aligned} $$

(7.15)

and

$$\displaystyle \begin{aligned} \lambda{{}_{\mbox{ coh}}} \approx 10^6~\mathrm{km} \times \frac{10^{-12}~\mathrm{ eV}}{m_{\gamma'}c^2}~. {} \end{aligned} $$

(7.16)

The amplitude, phase, and polarization of $\mathcal {E}'$ and $\mathcal {B}'$ remain roughly constant over τ_coh and λ_coh.

Also of note is the fact that due to the nonzero rest mass of hidden photons, hidden photon fields can possess longitudinal modes unlike photon fields in vacuum [12]. The existence of longitudinal modes of the hidden fields affects both astrophysical constraints and experimental strategies [12].

7.4 Dark Matter Radio Experimental Scheme

Because the coupling of the hidden photon field to Standard Model particles is entirely through kinetic mixing into real electromagnetic fields, it can be difficult to distinguish hidden photon dark matter signals from electromagnetic noise. Therefore, in order to achieve the highest possible sensitivity to hidden photon dark matter, it is generally advantageous to enclose the detector within electromagnetic shielding (for example, a superconducting shield). The hidden photon dark matter will penetrate the shield and can produce a signal in the detector. As noted above, however, the hidden photon field also affects charges within the shield and generates a real electromagnetic field inside the shield that can interfere with the signal from the hidden photons. Therefore, careful consideration of the “hidden photon electrodynamics” is needed to understand the measurable signal inside the shield.

Consider a cylindrical superconducting shield of radius R and length ℓ with axis along z. Working in the interaction basis, let us consider a single mode of the hidden photon field described by the vector potential $\boldsymbol {\mathcal {X}}$ which we assume points along $\hat {\mathbf {z}}$, parallel to the shield axis. The effective current density can be described by

$$\displaystyle \begin{aligned} \boldsymbol{\mathcal{J}}(\mathbf{r},t) = - \kappa \frac{m_{\gamma'}^2c^3}{\hbar^2} X_0 e^{i(\mathbf{k}\cdot\mathbf{r} - \omega t)} \hat{\mathbf{z}}~, {} \end{aligned} $$

(7.17)

where X₀ is the amplitude of the vector potential. As discussed above, the spacelike components of the effective four-current (the charge density) and four-potential (the scalar potential) are suppressed by ≈ v∕c and can be neglected in the following considerations.

7.4.1 Electric Field Due to Hidden Photons Within Shields

To solve for the electric field E inside the cylindrical shield, we start from Maxwell’s equations for E, namely Gauss’s Law and Faraday’s Law:

$$\displaystyle \begin{aligned} \nabla \cdot \mathbf{E} = 4 \pi \rho \approx 0~, {} \end{aligned} $$

(7.18)

$$\displaystyle \begin{aligned} \nabla \times \mathbf{E} = - \frac{1}{c} {\frac{\partial \mathbf{B}}{\partial t}}~. {} \end{aligned} $$

(7.19)

Taking the curl of Eq. (7.19), we find

$$\displaystyle \begin{aligned} \nabla \times {\left( \nabla \times \mathbf{E} \right)} = - \frac{1}{c} \nabla \times {\frac{\partial \mathbf{B}}{\partial t}} = - \frac{1}{c} {\frac{\partial }{\partial t}} {\left( \nabla \times \mathbf{B} \right)}~. {} \end{aligned} $$

(7.20)

The left-hand side of Eq. (7.20) can be simplified by using the identity

$$\displaystyle \begin{aligned} \nabla \times {\left( \nabla \times \mathbf{E} \right)} & = \nabla {\left( \nabla \cdot \mathbf{E} \right)} - \nabla^2 \mathbf{E} \approx - \nabla^2 \mathbf{E}~, {} \end{aligned} $$

(7.21)

where the right-hand side follows from Eq. (7.18). The right-hand side of Eq. (7.20) can be rewritten in terms of E and $\boldsymbol {\mathcal {J}}$ using another of Maxwell’s equations, Ampère’s Law,

$$\displaystyle \begin{aligned} \nabla \times \mathbf{B} = \frac{1}{c} {\left( 4 \pi \boldsymbol{\mathcal{J}} + {\frac{\partial \mathbf{E}}{\partial t}} \right)}~, {} \end{aligned} $$

(7.22)

yielding

$$\displaystyle \begin{aligned} - \frac{1}{c} {\frac{\partial }{\partial t}} {\left( \nabla \times \mathbf{B} \right)} = -\frac{4\pi}{c^2} {\frac{\partial \boldsymbol{\mathcal{J}}}{\partial t}} - \frac{1}{c^2} {\frac{\partial ^2 \mathbf{E}}{\partial t^2}}~. {} \end{aligned} $$

(7.23)

Combining Eqs. (7.21) and (7.23), we obtain

$$\displaystyle \begin{aligned} {\left( \frac{1}{c^2} {\frac{\partial ^2}{\partial t^2}} - \nabla^2 \right)} \mathbf{E} = -\frac{4\pi}{c^2} {\frac{\partial \boldsymbol{\mathcal{J}}}{\partial t}}~. {} \end{aligned} $$

(7.24)

So far the analysis has been quite general. Now, let us assume the z-polarized current density of Eq. (7.17), giving us a more specific form of the wave equation for E, namely

$$\displaystyle \begin{aligned} {\left( \frac{1}{c^2} {\frac{\partial ^2}{\partial t^2}} - \nabla^2 \right)} \mathbf{E} &= 4 \pi i \frac{\omega}{c^2}\boldsymbol{\mathcal{J}}(\mathbf{r},t)~. \\ & = -4 \pi i \kappa \frac{m_{\gamma'}^2 \omega c}{\hbar^2} X_0 e^{i(\mathbf{k}\cdot\mathbf{r} - \omega t)} \hat{\mathbf{z}}~. {} \end{aligned} $$

(7.25)

It can be seen from Eq. (7.25) that E is aligned with $\boldsymbol {\mathcal {J}}$. Because the electric field arising from the hidden photon field generates forces on charges within the cylindrical superconducting shields, the charges will rearrange themselves so as to cancel the field parallel to the surface of the shield (r = R), resulting in the boundary condition $\mathbf {E}(R)\cdot \hat {\mathbf {z}} = 0$. Furthermore, based on Eq. (7.25), the time dependence of E must match the time dependence of $\boldsymbol {\mathcal {J}}$, and so the time derivative in Eq. (7.25) can be resolved:

$$\displaystyle \begin{aligned} {\left( -\frac{\omega^2}{c^2} - \nabla^2 \right)} \mathbf{E} = -4 \pi i \kappa \frac{m_{\gamma'}^2 \omega c}{\hbar^2} X_0 e^{i(\mathbf{k}\cdot\mathbf{r} - \omega t)} \hat{\mathbf{z}}~. {} \end{aligned} $$

(7.26)

Next, let us take the limit where kR ≪ 1; in other words, the de Broglie wavelength (approximately equal to the coherence length for virialized dark matter) of the hidden photon field is far larger than the dimensions of the shield. In practical terms, this is the scenario for which dark matter radios have an advantage compared to resonant cavities. The kR ≪ 1 limit allows us to assume e^ik⋅r ≈ 1, further simplifying our equation for the spatial dependence of E:

$$\displaystyle \begin{aligned} {\left(\frac{\omega^2}{c^2} + \nabla^2 \right)} \mathbf{E} = 4 \pi i \kappa \frac{m_{\gamma'}^2 \omega c}{\hbar^2} X_0 e^{-i\omega t} \hat{\mathbf{z}}~. {} \end{aligned} $$

(7.27)

Since we ignore edge effects based on taking the ℓ ≫ R limit for the shield and have cylindrical symmetry, E can be assumed to be independent of z and the angular variable ϕ. Equation (7.27) is solved by assuming a spatial dependence for the electric field of

$$\displaystyle \begin{aligned} E(r) = E_0 {\left( 1 - \frac{J_0(\omega r / c)}{J_0(\omega R / c)} \right)}~, {} \end{aligned} $$

(7.28)

where J_n(x) is the nth order Bessel function of the first kind [13, 14]. Note that E(R) = 0, thus satisfying the boundary condition imposed by the shield. Substituting Eq. (7.28) into Eq. (7.27) enables us to solve for E₀, and we find that

$$\displaystyle \begin{aligned} E_0 = 4 \pi i \kappa \frac{m_{\gamma'}^2 c^3}{\hbar^2\omega}X_0~. {} \end{aligned} $$

(7.29)

Since $\omega \approx m_{\gamma '}c^2/\hbar$,

$$\displaystyle \begin{aligned} E_0 = 4 \pi i \kappa \frac{m_{\gamma'}c}{\hbar}X_0~. {} \end{aligned} $$

(7.30)

Thus, the full description of the electric field generated inside the shield by the hidden photon field is

$$\displaystyle \begin{aligned} \mathbf{E}(\mathbf{r},t) = 4 \pi i \kappa \frac{m_{\gamma'}c}{\hbar}X_0 {\left( 1 - \frac{J_0(\omega r / c)}{J_0(\omega R / c)} \right)} e^{-i \omega t} \hat{\mathbf{z}}~. {} \end{aligned} $$

(7.31)

For ωR∕c ≪ 1, we can Taylor expand the Bessel functions and find that

$$\displaystyle \begin{aligned} \mathbf{E}(\mathbf{r},t) &\approx 4 \pi i \kappa \frac{m_{\gamma'}c}{\hbar}X_0 \frac{\omega^2}{c^2} {\left( R^2 - r^2 \right)} e^{-i \omega t} \hat{\mathbf{z}}~, \\ &\approx 4 \pi i \kappa \frac{X_0}{\lambda_{\gamma'}^3} {\left( R^2 - r^2 \right)} e^{-i \omega t} \hat{\mathbf{z}}~, {} \end{aligned} $$

(7.32)

which shows that the electric field at the center of the shield is suppressed by a factor $\approx R^2/\lambda _{\gamma '}^2$ in comparison to the field in the absence of a shield, where $\lambda _{\gamma '} = \hbar /(m_{\gamma '}c)$ is the hidden photon Compton wavelength.

7.4.2 Magnetic Field Due to Hidden Photons Within Shields

The magnetic field induced within the shield by the hidden photons can be derived from Faraday’s Law [Eq. (7.19)],

$$\displaystyle \begin{aligned} \nabla \times \mathbf{E} = \frac{i\omega}{c} \mathbf{B}~, {} \end{aligned} $$

(7.33)

where we have used the fact that the time dependence of B is described by e^−iωt. Taking the curl of the E described by Eq. (7.31), we obtain

$$\displaystyle \begin{aligned} \mathbf{B}(\mathbf{r},t) = 4 \pi \kappa \frac{m_{\gamma'} c}{\hbar}X_0 {\left(\frac{J_1(\omega r / c)}{J_0(\omega R / c)} \right)} e^{-i \omega t} \hat{\boldsymbol{\phi}}~. {} \end{aligned} $$

(7.34)

Taylor expansion of the Bessel functions for ωR∕c ≪ 1 yields

$$\displaystyle \begin{aligned} \mathbf{B}(\mathbf{r},t) &\approx 4 \pi \kappa \frac{m_{\gamma'} c}{\hbar}X_0 {\left(\frac{\omega r}{c} \right)} e^{-i \omega t} \hat{\boldsymbol{\phi}}~, \\ &\approx 4 \pi \kappa \frac{X_0}{\lambda_{\gamma'}^2} r e^{-i \omega t} \hat{\boldsymbol{\phi}}~. {} \end{aligned} $$

(7.35)

The relative amplitudes of the electric and magnetic fields can be compared by taking the ratio:

$$\displaystyle \begin{aligned} \frac{\left|\mathbf{B}\right|}{\left|\mathbf{E}\right|} \approx \frac{r \lambda_{\gamma'}}{R^2 - r^2}~, \end{aligned} $$

(7.36)

and therefore the measurable magnetic field is $\sim \lambda _{\gamma '} / R$ larger than the electric field. For this reason, dark matter radios are designed to detect B.

7.4.3 DM Radio Inside a Cylindrical Shield

Essentially, a dark matter radio is an antenna readout by a tunable LC circuit connected to an amplifier. This methodology is complementary to microwave cavity searches as discussed in Chap. 4. A crucial difference between a microwave cavity and a dark matter radio is the frequency range that can be probed. The resonant frequency of a microwave cavity is inversely proportional to its size, which creates a practical limit on the lowest Compton frequencies that can be probed. On the other hand, the resonant frequency of an LC circuit is $\omega _0 = 1/\sqrt { LC }$, and thus large inductors and capacitors enable searches for hidden photons with much lower Compton frequencies.

Let us consider a schematic design of a dark matter radio as proposed in Ref. [15]. Figure 7.1 shows the schematic diagram of the DM Radio experiment. A hollow cylindrical superconducting sheath is housed within a superconducting shield. External electromagnetic fields are screened by the superconductors, but the hidden photon field penetrates inside. This gives rise to the circumferential magnetic field as described by Eqs. (7.34), (7.35), and (7.37), as shown in Fig. 7.2.

Fig. 7.1

Top left: schematic diagram of the DM Radio setup discussed in Ref. [15], showing the hollow superconducting sheath housed within a superconducting shield. Bottom left: cross-section of the hollow superconducting sheath. Top right: outer superconducting shield of the first generation “DM Radio Pathfinder” experiment. Bottom right: hollow superconducting sheath for DM Radio Pathfinder

Fig. 7.2

The oscillating effective current due to the hidden photon field $\boldsymbol {\mathcal {J}}(\mathbf {r},t)$ (pale violet arrows) induces a circumferential magnetic field B(r, t) (green arrows) inside the hollow superconducting sheath. The screening currents (yellow arrows) induced in the superconductor cancel B(r, t) within the bulk of the superconductor. A concentric circular slit is cut in the bottom of the superconducting sheath. The two sides of the slit are connected through an inductive loop, and the current through the loop is measured by a SQUID

The next step is to measure the field B generated within the superconducting sheath using a resonant LC circuit. The DM Radio approach is to use the superconducting sheath as the “pick-up loop” for detection, and thus the sheath acts as the inductor in the circuit. The current through the inductor is read out by cutting a concentric circular slit in the bottom of the sheath and connecting the two sides of the slit through an inductive loop that siphons off the screening current. The field from the inductive loop can be measured with a SQUID.

A slitted sheath of inner radius r₁, outer radius r₂, and height h has an approximate inductance of

$$\displaystyle \begin{aligned} L \approx \frac{2}{c^2} h \ln{\left(\frac{r_2}{r_1}\right)}~. {} \end{aligned} $$

(7.38)

The resonant circuit also needs a capacitor. Since the mass and, therefore, the Compton frequency of the hidden photon are unknown, the resonant frequency of the circuit needs to be scanned, for example, with a tunable capacitor. The tunable capacitor in the approach of DM Radio is a set of concentric hexagonal niobium “cylinders” between which sapphire plates are inserted (Fig. 7.3). The sapphire plates are a dielectric material, and by adjusting how far they extend into the hexagonal capacitor, the capacitance can be adjusted.

Fig. 7.3

Tunable concentric hexagonal capacitor used in the DM Radio experiment

Combining these elements, we have all the essential components of a dark matter radio. A schematic circuit diagram is shown in Fig. 7.4; note that the LC circuit naturally has nonzero resistance R due to loss mechanisms. (For the DM Radio Pathfinder experiment, R ≈ 5 × 10⁻³  Ω.) The induced electromotive force (EMF), $\mathcal {V}_{\gamma '}$, in the dark matter radio is due to the changing magnetic flux through the inductor induced by the hidden photon field. For conceptual simplicity, here let us model the concentric cylindrical slitted sheath as an N-turn toroidal solenoid with equivalent inductance, as discussed in Problem 7.4 (in fact, for the DM Radio Pathfinder experiment, such a solenoid is used as the resonator). The field is given by Eq. (7.37) from which we derive

$$\displaystyle \begin{aligned} \mathcal{V}_{\gamma'} \approx 4 i \kappa \sqrt{2\pi \rho{{}_{\mbox{ dm}}}} \frac{NV}{\lambda_{\gamma'}^2}e^{-i \omega t}~. {} \end{aligned} $$

(7.39)

Fig. 7.4

Schematic diagram of a dark matter radio circuit

The EMF $\mathcal {V}_{\gamma '}$ induced by the hidden photon field drives a current through the resonant RLC circuit. The advantage of the resonant RLC circuit is that when the resonance frequency is tuned near the hidden photon Compton frequency, the circuit will “ring up” and enhance the measurable signal. This enhancement is described by the Q-factor of the circuit, given by the ratio of the energy stored in the inductor to the energy lost per cycle due to dissipation (equivalent to the ratio of the resonant frequency to the linewidth)

$$\displaystyle \begin{aligned} Q = \frac{\omega_0}{\Delta \omega} = \frac{\omega_0 L}{R}~. {} \end{aligned} $$

(7.40)

The magnetic flux Φ through a cross-sectional area of the sheath, i.e., the flux through one loop of the equivalent N-turn toroidal solenoid, is given by (see solution to Problem 7.5):

$$\displaystyle \begin{aligned} \Phi = 4 \kappa \sqrt{2\pi \rho{{}_{\mbox{ dm}}}} \frac{V}{\lambda_{\gamma'}}e^{-i \omega t}~, {} \end{aligned} $$

(7.41)

and the flux through the solenoid due to the hidden photon field is N Φ. Because the RLC circuit rings up, on resonance this translates to a total flux of QN Φ due to the current accumulated in the inductor due to the hidden photon-induced EMF $\mathcal {V}_{\gamma '}$.

The magnetic flux in the inductor can be measured with a SQUID. The flux through the SQUID is scaled by its area (A_s) relative to the cross-sectional area of the inductor A = h(r₂ − r₁),

$$\displaystyle \begin{aligned} \Phi{{}_{\mbox{ SQUID}}} \approx {\left( \frac{A_s}{A} \right)} QN\Phi~, {} \end{aligned} $$

(7.42)

and SQUIDs can have areas of A_s ≈ 1 cm². A typical commercial DC SQUID has a noise floor of $\delta \Phi \approx 10^{-6} \Phi _0 / \sqrt {\mathrm {Hz}}$, where Φ₀ ≈ 2 × 10⁻⁷ G ⋅cm² is the magnetic flux quantum and, as argued in Ref. [15], is an efficient detector for frequencies below about 100 MHz. To evaluate the sensitivity of a DM Radio experiment, the SQUID sensitivity must be compared to other sources of noise. A main source of noise comes from the circuit itself: the Johnson noise δV_th from the resistance. This thermal noise can be estimated by considering the current noise δI_th generated in the inductor:

$$\displaystyle \begin{aligned} \delta I{{}_{\mbox{ th}}} & = \frac{\delta V{{}_{\mbox{ th}}}}{R} = \sqrt{\frac{2 k_B T \Delta \omega}{\pi R}} = \sqrt{\frac{2 k_B T Q \Delta\omega}{\pi \omega_0 L}} = \sqrt{\frac{2 k_B T}{\pi L}}~, {} \end{aligned} $$

(7.43)

where T is the temperature of the circuit, k_B is Boltzmann’s constant, and we assume for the bandwidth of the measurement Δω = ω₀∕Q. This thermal current generates noise in the magnetic flux measured by the SQUID:

$$\displaystyle \begin{aligned} \delta \Phi{{}_{\mbox{ th}}} \approx c L \delta I{{}_{\mbox{ th}}} \approx c \sqrt{\frac{2 k_B T L}{\pi}}~. {} \end{aligned} $$

(7.44)

It turns out that under typical conditions, even for a cryogenic system with T ≪ 1 K, δ Φ_th is much greater than the SQUID noise floor.

From these properties and Eq. (7.41), we can estimate the sensitivity (on resonance) of a prototypical DM Radio experiment to κ:

$$\displaystyle \begin{aligned} \delta \kappa \approx \frac{1}{m_{\gamma'}c^2} \frac{\delta \Phi{{}_{\mbox{ th}}}}{QNV} \frac{A}{A_s} \frac{\hbar c}{4 \sqrt{ 2 \pi \rho{{}_{\mbox{ dm}}} }}~,\end{aligned} $$

(7.45)

and integrating for a time τ would improve the sensitivity by a factor of $\approx \sqrt {1/(\tau \Delta \omega )} \approx \sqrt {Q/(\omega _0 \tau )}$. Choosing V ≈ 3 × 10⁶ cm³, A ≈ 10⁴ cm², N ≈ 2, Q ≈ 10⁶, and T = 1 K, we obtain the relationship:

$$\displaystyle \begin{aligned} \delta \kappa \approx ~ {\left( 5 \times 10^{-8} \right)} \times {\left( \frac{10^{-12}~\mathrm{eV}}{m_{\gamma'}c^2} \right)}.\end{aligned} $$

(7.46)

7.5 Out-of-Band Sensitivity

Consider a DM Radio-style resonator operating at a fixed frequency. It is unlikely that the resonant frequency is exactly matched to the oscillation frequency of the hidden photons. The farther detuned the dark matter frequency is from resonance, the weaker the resonant enhancement of the signal. A large mismatch will result in very little signal power, but for small detunings the degradation is mild. With this in mind, over what frequency range does the resonator have sensitivity to a dark matter signal? A reasonable choice might be to assert that the sensitivity should be limited to the standard half-power bandwidth of the resonator: Δf = f₀∕Q.

Note, however, that the ability to detect a dark matter signal actually depends on the signal-to-noise ratio. A relatively weaker signal due to detuning can be detected just as easily if the noise power has also decreased by the same amount. It was previously shown that the dark matter signal manifests as an effective voltage source in series with the resonator. The degradation of signal power due to detuning follows the Lorentzian line shape of the resonator. The thermal noise due to loss mechanisms (the resistor R in the circuit model) also appears as a series voltage source, and its power also follows the Lorentzian line shape at detuned frequencies. Thus, the ratio of signal power to thermal noise power remains unchanged even away from the LC resonance.

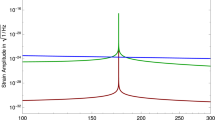
Since the total noise power is the sum of the frequency-dependent thermal noise power and the frequency-independent white noise of the amplifier, there is still some degradation in detection ability with detuning, but the effective sensitivity bandwidth can be much greater than the intrinsic resonator bandwidth and depends on the noise properties of the readout amplifier. This concept is shown in Fig. 7.5.

Fig. 7.5

Total noise, thermal noise, and amplifier noise as a function of detuning from the LC oscillator resonant frequency. The signal-to-noise ratio is only slightly degraded away from resonance, resulting in a much greater sensitivity bandwidth compared to the intrinsic resonator bandwidth

The out-of-band sensitivity offers several advantages. First, the total time required to scan a range of frequencies to a particular level of dark matter coupling is reduced as each frequency step of the resonator covers a greater bandwidth than the resonator bandwidth alone. Second, the larger frequency steps of the resonator during a scan relax the engineering requirements of the detector tuning system. Finally, it makes the use of quantum-limited amplifiers for dark matter radios desirable in order to maximize the sensitivity bandwidth. A detailed analysis of the quantum limits on dark matter radios, including amplifier back-action, can be found in Ref. [16]. While this same analysis applies to microwave cavity detectors, their total noise tends to be dominated by the readout amplifier and the sensitivity bandwidth is about the same as the resonator bandwidth. The out-of-band sensitivity is a consequence of the lower operating frequency, resulting in a higher thermal occupation of the resonator.

7.6 Sensitivity of Dark Matter Radio Experiments

There are a number of DM Radio experiments proposed, planned, or underway aimed at exploring unconstrained parameter space for UBDM [15, 17,18,19], and several have reported initial results [20,21,22]. These experiments employ a variety of tools and techniques going beyond the basic scheme described in Sect. 7.4 and target axion and ALPs as well as hidden photons.

The sensitivity of DM Radio experiments can be compared to astrophysical constraints (see Chap. 3). In contrast to axions and ALPs, there are no strong constraints on hidden photons from supernovae for any parameters [7]. Constraints from star-cooling fall off rapidly for smaller values of $m_{\gamma '}$, and so the dominant constraint on κ comes from measurements of the cosmic microwave background (CMB). The idea of the CMB limits is that there can be resonant conversion of CMB photons into hidden photons when the “effective mass” of the photon due to interactions with the primordial plasma matches $m_{\gamma '}$ [23]. (This resonant conversion effect is similar to the Mikheyev–Smirnov–Wolfenstein (MSW) effect for neutrinos [24, 25].) Therefore, the constraints from the CMB have a sharp cutoff at around $m_{\gamma '}c^2 \approx 10^{-14}~\mathrm {eV}$ [23, 26]. Constraints below $m_{\gamma '}c^2 \approx 10^{-14}~\mathrm {eV}$ come from limits on heating of the ionized interstellar medium by hidden photon dark matter [27].

A wide view of the hidden photon parameter space is shown in Fig. 7.6. The green areas show regions of parameter space excluded by a reinterpretation of published ADMX and precursor experiment axion limits applied to hidden photons [28]. The thin red line shows the first exclusion limit produced by a dark matter radio—the DM Radio Fixed Resonator [22]. Shown in blue is the expected exclusion limit for a 1-year scan of the DM Radio Pathfinder, a larger detector currently operating at Stanford University. These prototype dark matter detectors have served as stepping-stones for two future axion-focused detectors being constructed by the DM Radio collaboration: DM-Radio-50L and DM-Radio-m³. The DM-Radio-50L detector will use a 50 liter, ∼1T toroidal magnet to probe axionlike particles between 5 kHz and 5 MHz, corresponding to the 20 peV–20 neV axion mass range. The DM-Radio-m³ detector will use a cubic meter, 4T magnet to probe the QCD axion between 5 MHz and 300 MHz (∼20 neV–800 neV) with sensitivity to the DFSZ QCD axion above 30 MHz. Both of these detectors may also be modified to search for hidden photons over the same span of frequencies. Interestingly, it has recently been realized that the Earth itself can be used as a transducer for a DM-Radio-like experiment at much lower frequencies [29].

Fig. 7.6

Current exclusion limits for the hidden photon parameter space. Plot adapted from Ref. [22]