1 Introduction

The nature of Dark Matter (DM) is one of the very important issues in fundamental physics. It affects particle physics, astrophysics and cosmology all at once. In fact, particle physicists for a long time suggested candidates with a mass in the \(\hbox {GeV/c}^2\) to \(\hbox {TeV/c}^2\) range motivated by the hierarchy problem. This can be solved elegantly by adding new particles in this mass range, some of which can play the role of DM.

So far direct searches in dedicated DM experiments and the LHC did not provide any conclusive evidence for any DM candidates around the weak scale. That is one of the reasons, why recently there have been stronger efforts to increase the sensitivity towards lighter and heavier DM masses, see, e.g., the community report [1].

On the other hand, with the discovery of gravitational waves (GWs) by LIGO and VIRGO in 2016 [2] particle physicists also developed a growing interest in this technology. One of the authors discussed with other collaborators the prospects for the discovery of the Cosmic Neutrino Background using laser interferometers also briefly mentioning DM in [3]. Scattering of DM particles in GW detectors and interferometers in general can lead to an effect similar to Brownian motion which was discussed from a particle physicist’s point of view in [4]. Shortly after, a similar idea was discussed in [5], which employs a more common language in the GW community. The main motivation of this paper is to build a framework which realistically models a DM scattering signal in an optomechanical setup like a GW detector. Within this framework we can then compare a potential DM signal to common backgrounds in GW detectors in the language of the GW community. As an explicit and realistic example we will consider KAGRA [6] and also briefly comment on other technologies.

Actually, the aforementioned works have not been the only proposals to search for DM at GW detectors or interferometers in general, see, for instance [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32]. Nevertheless, our approach here differs from these works. They usually focus on very light DM which has wave-like properties or very heavy DM which produces a GW signal itself. We instead focus here on light DM in the mass range between 1 \(\hbox {keV/c}^2\) and 1 \(\hbox {GeV/c}^2\) where DM has a particle nature and our DM signal is modelled as an elastic scattering event with components of the interferometer.

Our paper is organised as follows: In Sect. 2 we first discuss a damped harmonic oscillator as a simplified toy model for the mirror system in realistic GW detectors. For that model we discuss the most important sources of noise and a potential DM signal, from which we can also derive simple formulas for the signal-to-noise ratio (SNR) which allows to provide a rough estimate for the DM sensitivity of any terrestrial GW detector. In Sect. 3 we generalise the formulas derived in Sect. 2 and apply them to the concrete case of the KAGRA detector. In Sect. 4 we briefly comment on space-based experiments and atomic interferometers before we summarise and conclude in Sect. 5.

2 Simplified setup: damped harmonic oscillator

Before we discuss KAGRA as a realistic example we would like to first study how a potential DM signal compares to thermal and quantum noise for a toy model of a damped harmonic oscillator in one dimension. The calculations here can later be easily extended to the KAGRA case.

We base our discussion on the complex differential equation

$$\begin{aligned} m \, \ddot{x}_c + k_{c} \, (1+ {{\,\mathrm{\text {i}}\,}}\phi ) \, x_c = \frac{F_{\text {ext},c}}{L} , \end{aligned}$$
(2.1)

where \(x_c(t)\) is the dimensionless relative displacement in complex form, L is the interferometer arm length, m is the mass of the oscillator (the test mirror (TM)) and \(k_c\) is the equivalent to a spring constant of the suspension system. The suspension loss angle, \(0 < \phi \ll 1\), describes the damping of the system. \(F_{\text {ext},c}\) is an external force applied to the system which will be adjusted depending on which physics aspect we are discussing. This equation has the form of how KAGRA published the parameters describing their suspension system.

This differential equation has only complex solutions due to its complex coefficients, which has advantages and disadvantages. One of the big advantages is that it describes the damping induced by internal friction well, cf. [33]. This internal friction is frequency dependent which makes it difficult to write down explicitly for a system of coupled oscillators as in KAGRA. A disadvantage is, that the displacement \(x_c\) does not correspond immediately to an observable quantity which makes the modelling of the external force less intuitive.

If we would want to describe the same system instead in terms of a more intuitive real differential equation describing a real displacement we can use

$$\begin{aligned} m \, \ddot{x}_{r} + 2 \, m \, \omega _r \, \xi \, \dot{x}_{r} + m\, \omega _r^2 (1 + \xi ^2 ) x_{r} = \frac{F_{\text {ext},r}}{L} , \end{aligned}$$
(2.2)

and we will discuss later how we match the quantities in this equation with the quantities in Eq. (2.1).

In our analysis we follow a standard approach for GW detectors described in [34]. In this reference, the measured output of the detector is split into a noise and a signal part. For the toy model considered here, the total displacement

$$\begin{aligned} x_{\text {tot},c}(t) = x_{\text {th},c}(t) + x_{\text {qu},c}(t) + x_{\text {DM},c}(t) \end{aligned}$$
(2.3)

is given by the superposition of thermal noise \(x_{\text {th},c}(t)\), quantum noise \(x_{\text {qu},c}(t)\) and the signal displacement induced by DM scattering \(x_{\text {DM},c}(t)\) and similarly for the real displacement. In a realistic experiment there are other sources of noise but here we want to focus on the most sensitive region of GW detectors, KAGRA in particular, where the suspension thermal noise and quantum noise are mostly dominant, cf. [35].

2.1 Noise

First, we discuss the suspension thermal noise, following closely the approach described in [36, 37] based on the fluctuation-dissipation theorem [38, 39]. Accordingly, the one-sided power spectral density (PSD) of the thermal noise \(S_{\text {th}}\), is given by

$$\begin{aligned} S_{\text {th}}(\omega )=\frac{4 \, k_B \, T}{L^2 \, \omega ^2} \mathfrak {R}[Y(\omega )] , \end{aligned}$$
(2.4)

where \(k_B\) is Boltzmann’s constant, T the temperature of the system, L the interferometer arm length as before, \(\omega \) the frequency of the external force, and \(\mathfrak {R}[Y(\omega )]\) is the real part of the complex admittance in the frequency domain.

The admittance is defined for periodic external forces. For a given frequency, \(\omega \), of the external force, i.e. \(F_{\text {ext}} \sim \text {exp}({{\,\mathrm{\text {i}}\,}}\omega \, t)\), the time dependence of the steady state solution would be of the form \(x_{\text {th},c}(t) \sim \text {exp}({{\,\mathrm{\text {i}}\,}}\omega \, t)\) as well. The admittance for the complex case is then given by

$$\begin{aligned}&Y_c(\omega ) \equiv \frac{\dot{x}_{\text {th},c}}{F_{\text {ext}}/( m \, L)} = \text {i} \, \omega \, D_c^{-1}(\omega )\nonumber \\&\quad =\frac{{{\,\mathrm{\text {i}}\,}}\omega }{ (- m \, \omega ^2 + k_c (1 + {{\,\mathrm{\text {i}}\,}}\phi ) ) } , \end{aligned}$$
(2.5)

where we have introduced \(D_c(\omega )\) as the Fourier transform of the differential operator, in this case \(D_c(\omega ) = - m \,\omega ^2 + k_c (1 + {{\,\mathrm{\text {i}}\,}}\phi )\). The real part of the associated admittance is

$$\begin{aligned} \mathfrak {R}[Y_c(\omega )]= & {} \mathfrak {R}\left[ \frac{{{\,\mathrm{\text {i}}\,}}\omega (- m \, \omega ^2 + k_c - {{\,\mathrm{\text {i}}\,}}k_c \, \phi ) }{ (k_c - m \, \omega ^2)^2 + k_c^2 \phi ^2 } \right] \nonumber \\= & {} \frac{k_c \, \omega \, \phi }{(k_c - m \, \omega ^2)^2 + k_c^2 \phi ^2 } . \end{aligned}$$
(2.6)

The corresponding thermal noise PSD originated from the internal damping of the system is therefore given by

$$\begin{aligned} S_{\text {th},c}(\omega )= & {} \frac{4 \, k_{B} \, T}{L^2} \frac{k_c \, \phi /\omega }{ (k_c - m \, \omega ^2)^{2} + \, k_c^2 \, \phi ^2 }\nonumber \\= & {} \frac{4 \, k_B \, T \,}{L^2} \frac{ \phi \, \omega _c^2/(m \,\omega )}{ (\omega ^2 - \omega _c^2)^2 + \omega _c^4 \phi ^2 } , \end{aligned}$$
(2.7)

where we have introduced \(\omega _c^2 \equiv k_c/m\). Notice that the PSD vanishes when the loss angle \(\phi \) equals to zero. Following the same procedure, one obtains the thermal noise PSD from the real differential Eq. (2.2), cf. [36], as

$$\begin{aligned} S_{\text {th},r}(\omega )&= \frac{4 \, k_{B} \, T}{L^2} \frac{2 \, \omega _r \, \xi /m }{ (\omega ^2 - \omega _r^2 \left( 1 + \xi ^2 \right) )^2 + (2 \, \omega _r \, \xi )^2 \omega ^2 } \nonumber \\&= \frac{4 \, k_{B} \, T}{L^2} \frac{2 \, \omega _r \, \xi /m }{ (\omega ^2 - \omega _r^2 \left( 1 - \xi ^2 \right) )^2 + 4 \, \omega _r^4 \, \xi ^2 } . \end{aligned}$$
(2.8)

Now one can argue that since both equations describe the same physical system the thermal noise spectra \(S_{\text {th},c}\) and \(S_{\text {th},r}\) should be identical, i.e. \(S_{\text {th},c} = S_{\text {th},r}\). From this we derive relations between the parameters in Eqs. (2.1) and (2.2) as

$$\begin{aligned} \begin{aligned} \omega _r^2&= \omega _c^2 \left( 1 - \frac{\omega _c^2}{\omega ^2} \frac{\phi ^2}{4} \right) , \\ \xi&= \frac{\omega _c}{ \omega } \left( 1 - \frac{\omega _c^2}{\omega ^2} \frac{\phi ^2}{4} \right) ^{-1/2} \frac{\phi }{2} \approx \frac{\omega _c}{ \omega } \frac{\phi }{2} \left( 1 + \frac{\omega _c^2}{\omega ^2} \frac{\phi ^2}{8} \right) . \end{aligned} \end{aligned}$$
(2.9)

Here we see the forementioned dependence of \(\xi \) on the frequency of the driving force explicitly which has been observed in systems with internal damping. On a side-note, in KAGRA and LIGO ordinary viscous damping with a constant \(\xi \) induced by surrounding gas is negligible, cf. [36].

In the next subsection, we present an alternative way to determine \(\omega _r\) and \(\xi \) which is more immediately related to the physical situation where we need them. For that reason we will not use the matching from Eq. (2.9) explicitly later on. Nevertheless, both matchings differ only in \({\mathcal {O}}(\phi ^2)\) which is negligibly small for KAGRA. Indeed, it is long known that it is not possible to match a complex and a real differential equation for a system with internal damping in a uniquely consistent way [40].

In the following discussion, we always refer to the thermal noise derived from the complex equation: \(S_{\text {th}} \equiv S_{\text {th},c}\). The readout of the GW experiment is expressed in terms of the strain amplitude which is related to the PSD as [34]

$$\begin{aligned} h_{\text {th}}(\omega ) = \sqrt{ S_{\text {th}}(\omega ) } . \end{aligned}$$
(2.10)

Next, for the quantum noise induced by the uncertainty principle of the measurement we use in the toy model the so-called standard quantum limit (SQL) [41]

$$\begin{aligned} S_{\text {qu}} = \frac{8 \, \hbar }{ m \, \omega ^2 \, L^2 } . \end{aligned}$$
(2.11)

Modern GW detectors can do better than this in certain frequency ranges, see, e.g., [42, 43]. The quantum noise in such setups depends on a lot of parameters though and we want to keep things simple and transparent here.

The strain of the quantum noise is again related to the PSD via the standard relation [34]

$$\begin{aligned} h_{\text {qu}}(\omega ) = \sqrt{ S_{\text {qu}}(\omega ) } . \end{aligned}$$
(2.12)

Finally, the total noise PSD of the toy model is given by the thermal noise and quantum noise

$$\begin{aligned} S_n = S_{\text {th}} + S_{\text {qu}} , \end{aligned}$$
(2.13)

with the corresponding strain amplitude

$$\begin{aligned} h_n = \sqrt{ h_{\text {th}}^2 + h_{\text {qu}}^2 } . \end{aligned}$$
(2.14)

2.2 DM signal

In this subsection, we focus on the signal part of the output induced by the DM hit. We consider the situation where the TM is being hit by a DM particle at \(t=0\) transferring a recoil momentum \(q_R\) to it. This picture can be straightforwardly implemented into the real differential Eq. (2.2) setting the external DM force to \(F_{\text {ext},r} = q_R \, \delta (t)\), cf. [5].

The mechanical loss of the KAGRA components were actually tested using a pulse-like force [44] exactly what we assume for the DM signal. The response of the system was fitted to a function

$$\begin{aligned} x_{r}(t) \sim \text {exp}\left( - \omega _r \, \xi \, t \right) \sin (\omega _r \, t) , \end{aligned}$$
(2.15)

where we have slightly adapted the notation of Chapter 5 of [44] to our notation such that it solves the free version of Eq. (2.2) with no external force.

We now compare this solution to the free solution of Eq. (2.1) which has the form

$$\begin{aligned}&x_{\text {DM},c}(t) \sim \exp \left( - \omega _c \, \mathfrak {I}\left( \sqrt{1 + {{\,\mathrm{\text {i}}\,}}\phi }\right) \, t \right) \nonumber \\&\quad \exp \left( {{\,\mathrm{\text {i}}\,}}\omega _c \, \mathfrak {R}\left( \sqrt{1 + {{\,\mathrm{\text {i}}\,}}\phi }\right) \, t\right) . \end{aligned}$$
(2.16)

Since both Eqs. (2.1) and (2.2) should describe the same (free) physical system we demand that the damping of the amplitude and the oscillation frequency in both cases are identical. From that we determine the relations between the parameters in both cases as

$$\begin{aligned} \begin{aligned} \omega _r&= \omega _c \, \mathfrak {R}\left( \sqrt{1 + {{\,\mathrm{\text {i}}\,}}\phi }\right) = \omega _c \left( 1 + \phi ^2 \right) ^{1/4} \cos \left( \frac{1}{2} \arctan \phi \right) \\&\approx \omega _c \left( 1 + \frac{\phi ^2}{8} \right) ,\\ \xi&= \frac{\mathfrak {I}\left( \sqrt{1 + {{\,\mathrm{\text {i}}\,}}\phi }\right) }{\mathfrak {R}\left( \sqrt{1 + {{\,\mathrm{\text {i}}\,}}\phi }\right) } = \tan \left( \frac{1}{2} \arctan \phi \right) \approx \frac{\phi }{2} \left( 1 - \frac{\phi ^2}{4} \right) . \end{aligned} \end{aligned}$$
(2.17)

We see that up to \({\mathcal {O}}(\phi ^2)\) this solution is identical to the leading order one from the matching of the thermal spectra in Eqs. (2.9) after setting \(\omega = \omega _r\). In fact, this is the only available choice for \(\omega \) since we consider here a free oscillator where the only available physical frequency is the oscillation frequency \(\omega _r\).

Fig. 1
figure 1

The strain amplitudes in our toy model for the thermal suspension noise (green line), the quantum noise (blue line) and a hypothetical DM signal (maroon line). For more details, see main text

Full size image

We further assume the initial condition \(x_{\text {DM},r}(t) = 0\) for \(t \le 0\) and we model only one hit at \(t=0\). For a given recoil momentum \(q_R\), the dimensionless displacement due to the DM hit is then given by

$$\begin{aligned} x_{\text {DM}}(t)&= \theta (t) \frac{q_R}{ m \, \omega _r \, L} \text {exp}\left( - \omega _r \, \xi \, t \right) \sin (\omega _r \, t) , \end{aligned}$$
(2.18)

where we have dropped the index r from the displacement.

In order to calculate the strain amplitude, we need the Fourier transform of the displacement and its respective modulus squared

$$\begin{aligned}&{\tilde{x}}_{\text {DM}}(\omega ) = \int {{\,\mathrm{\text {d}}\,}}t \, x_{\text {DM}}(t) \, \text {e}^{-{{\,\mathrm{\text {i}}\,}}\omega \, t} = \frac{q_R}{ m \, L} \frac{1}{\omega _r^2 - (\omega - {{\,\mathrm{\text {i}}\,}}\omega _r \, \xi )^2} , \end{aligned}$$
(2.19)
$$\begin{aligned}&| {\tilde{x}}_{\text {DM}}(\omega ) |^2 = \frac{q_R^2}{ m^2 \, L^2} \frac{1}{ \left( \omega ^2 - \omega _r^2 (1 - \xi ^2) \right) ^2 + 4 \, \omega _r^4 \, \xi ^2 } . \end{aligned}$$
(2.20)

It is easy to see here that if we would have multiple hits in the observed time window the result would be simply

$$\begin{aligned} {\tilde{x}}_{\text {DM}}(\omega )&= \frac{1}{ m \, L} \frac{1}{\omega _r^2 - (\omega - {{\,\mathrm{\text {i}}\,}}\omega _r \, \xi )^2} \sum _i q_R^{(i)} \text {e}^{-{{\,\mathrm{\text {i}}\,}}\omega \, t_i} , \end{aligned}$$
(2.21)

where \(q_R^{(i)}\) is the recoil momentum (with either sign) of the i-th hit at time \(t_i\). In the analysis, it would then be recommended to choose different time intervals for the Fourier transform to determine the times when a hit occurred. In fact, random hits as we study them here are more easily studied and analysed in the time-domain, cf. [4]. The advantage of using the frequency-domain approach is the comparability to the results from GW detectors where everything is presented in this way. To keep things simple, we will in the following only consider the case of one hit at \(t=0\).

The DM induced strain amplitude is given by [34]

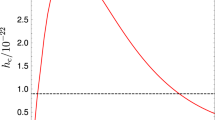
$$\begin{aligned} h_{\text {DM}}(\omega ) = \sqrt{\frac{2 \, \omega }{\pi }} \, |{\tilde{x}}_{\text {DM}}(\omega )| . \end{aligned}$$
(2.22)

In Fig. 1, we plot the strain amplitudes for the DM signal and the noise for the toy model. The noise input parameters are specified as: \(f_0 = \omega _c/(2 \, \pi ) = 175.4\) Hz, \(\phi = 6.32 \times 10^{-12}\), \(m = 22.8\) kg, \(T = 19\) K, \(L = 3\) km. The frequency \(f_0\) corresponds to one of the peaks in the thermal suspension noise of KAGRA and the loss angle \(\phi \) was chosen to correspond to the width of that peak. The other parameters are chosen to agree with KAGRA as well. The DM recoil momentum is roughly approximated by the DM momentum \(q_R = m_{\text {DM}} \, |\vec {v}_{\text {DM}}|\), where we use \(m_{\text {DM}}= 1\) \(\hbox {GeV}/\text {c}^2\) and \(|\vec {v}_{\text {DM}}|=220\) km/s. From Fig. 1 we see that a potential light DM signal at KAGRA is pretty much hidden behind the noise, the thermal suspension noise in particular. The peak of the thermal noise nevertheless coincides with the peak of the DM signal, while off-resonance they behave differently. For smaller frequencies the DM signal falls faster while for large frequencies the thermal noise falls faster. To give a more quantitative statement regarding the DM signal, we will discuss the SNR in the next subsection.

But before we discuss this, we present an alternative approach to derive \(|{\tilde{x}}_{\text {DM}}(\omega )|^2\) directly from the complex differential Eq. (2.1) without having to go through the matching to a real differential equation as in Eq. (2.2) making the realistic considerations for KAGRA much easier.

We start with the Fourier expansion of the dimensionless displacement induced by DM as

$$\begin{aligned} x_{\text {DM}} (t) \equiv \int {{\,\mathrm{\text {d}}\,}}\omega \, {\tilde{x}}_{\text {DM}} (\omega ) \exp ({{\,\mathrm{\text {i}}\,}}\omega \, t) , \end{aligned}$$
(2.23)

and we set the external force for the complex case equal to the external force for the real case

$$\begin{aligned} F_{\text {ext},c} = F_{\text {ext},r} = q_R \, \delta (t) = q_{R} \, \int {{\,\mathrm{\text {d}}\,}}\omega \, \exp ({{\,\mathrm{\text {i}}\,}}\omega \, t) . \end{aligned}$$
(2.24)

The Fourier transformed displacement \({\tilde{x}}_{\text {DM}}(\omega )\) can then be obtained easily after taking the Fourier transform of Eq. (2.1)

$$\begin{aligned} ( - \omega ^2 + \omega _c^2 (1 + {{\,\mathrm{\text {i}}\,}}\phi ) ){\tilde{x}}_{\text {DM}}(\omega ) = \frac{q_R}{m \, L} . \end{aligned}$$
(2.25)

The corresponding absolute square of \({\tilde{x}}_{\text {DM}}(\omega )\) is then

$$\begin{aligned} |{\tilde{x}}_{\text {DM}}(\omega )|^2 = \frac{q_R^2}{m^2 \, L^2} \frac{1}{ (\omega ^2 - \omega _c^2)^2 + \omega _c^4 \phi ^2} . \end{aligned}$$
(2.26)

This result is identical to the result in Eq. (2.20) taking into account the exact matching in Eqs. (2.17). This method is particularly useful since KAGRA presents their experimental parameters in a form identical to Eq. (2.1).

There is also an important lesson, which we can draw from this equation in comparison to Eq. (2.7). Whenever we have a mode excited by a DM hit, the same mode will also be excited by thermal energy. This was not taken properly into account in the ThinET proposal in [5] and we think that it would reduce their SNR significantly.

2.3 SNR

To better quantify under which circumstances a potential DM signal could be seen in a common earth-bound GW detector setup, we discuss the signal-to-noise ratio (SNR), \(\varrho ^2\). Simply speaking this is defined as the integral of signal over noise in the frequency domain. Ideally we should also apply some kind of filter to enhance the SNR. This is discussed in [34] and references therein. The optimal SNR is given by

$$\begin{aligned} \varrho ^2 = \int _{f_\text {min}}^{f_\text {max}} {{\,\mathrm{\text {d}}\,}}f \frac{4 \, |{\tilde{x}}_{\text {DM}}(2 \, \pi \, f)|^{2}}{S_n(2 \, \pi \, f)} . \end{aligned}$$
(2.27)

In fact, in [34] the integration is chosen from zero to infinity. In a realistic setup this is nevertheless not recommended, since at small and large frequencies the background levels are very high suppressing any signal component. We also did not take them into account in our toy setup.

Looking at Fig. 1 it is suggestive to just integrate around the expected signal peak. The signal spectrum has the shape of a Lorentzian with the peak frequency \(\omega _r (1 - \xi ^2)\) and the full-width at half maximum (FWHM) is at the frequencies

$$\begin{aligned} \begin{aligned} \omega _{\text {max}}^2&= \omega _r^2 (1 - \xi ^2) + 2 \, \omega _r^2 \, \xi = \omega ^{2}_{c} (1 + \phi ),\\ \omega _{\text {min}}^2&= \omega _r^2 (1 - \xi ^2) - 2 \, \omega _r^2 \, \xi = \omega ^{2}_{c} (1 - \phi ), \end{aligned} \end{aligned}$$
(2.28)

where we have used the exact result for \(\omega _r\) and \(\xi \) from Eqs. (2.17).

Let us assume first that we have a situation at hand as in Fig. 1, where the quantum noise can be neglected compared to the thermal noise. Then the SNR is

$$\begin{aligned} \varrho _{\text {th}}^2&= \frac{1}{2 \pi } \int _{\omega _\text {min}}^{\omega _\text {max}} {{\,\mathrm{\text {d}}\,}}\omega \frac{4 \, |{\tilde{x}}_{\text {DM}}(\omega )|^{2}}{S_n(\omega )}\nonumber \\&\approx \frac{1}{4 \pi } \int _{\omega _\text {min}^2}^{\omega _\text {max}^2} \frac{{{\,\mathrm{\text {d}}\,}}\omega ^2}{\omega } \frac{4 \, |{\tilde{x}}_{\text {DM}}(\omega )|^{2}}{S_{\text {th}}(\omega )} \nonumber \\&= \frac{q_R^2}{4 \, \pi \, m \, k_B \, T} \int _{\omega _\text {min}^2}^{\omega _\text {max}^2} \frac{{{\,\mathrm{\text {d}}\,}}\omega ^2}{\omega _c^2 \, \phi }\nonumber \\&= \frac{1}{4 \pi } \frac{q_R^2}{m \, k_B \, T } \frac{ \omega _\text {max}^2 - \omega _\text {min}^2 }{\omega _c^2 \, \phi } = \frac{1}{4 \pi } \frac{E_R}{ E_{\text {th}} } \frac{ \omega _\text {max}^2 - \omega _\text {min}^2 }{\omega _c^2 \, \phi } \nonumber \\&= \frac{1}{2 \pi } \frac{q_R^2}{m \, k_B \, T } = \frac{1}{2 \pi } \frac{E_R}{E_{\text {th}} } , \end{aligned}$$
(2.29)

where we have again used the exact result for \(\omega _r\) and \(\xi \) from Eqs. (2.17) and we have introduced the recoil energy \(E_R \equiv q_R^2/(2 \, m)\) and the thermal energy \(E_{\text {th}} \equiv k_B \, T/2\) for one degree of freedom. The integration limits are based on Eq. (2.28). As one might have guessed naively, the SNR is proportional to the ratio of DM scattering recoil energy and thermal energy. For our example the SNR would be very small \(\varrho ^{2}_{\text {th}} = 4.09 \times 10^{-24}\). Mainly because the recoil energy is so tiny compared to the thermal energy (\(E_R = 3.37 \times 10^{-45}~\text {J}\) and \(E_{\text {th}} = 1.31 \times 10^{-22}~\text {J}\)). If we would follow the suggestion of [4] instead and use \(m = 10^{-6}\) kg with the other parameters kept the same the SNR would be much larger, but still small \(\varrho ^{2}_{\text {th}} = 9.33 \times 10^{-17}\). So we would need not only much lighter mirrors but also very low temperatures, to enhance the SNR and make the signal actually observable.

At this point we would like to give a disclaimer. The approximate formula presented here is good for our toy model near the resonance. In the realistic case of KAGRA the ratio \(|{\tilde{x}}_{\text {DM}}|^2/(\omega \, S_{\text {th}})\) is a complicated function of \(\omega \) and not just a constant even near the peak. We will come back to this point later.

Let us now have a closer look at the quantum noise. Actually, to have a peak in the DM signal can help to overcome the quantum noise even though it is just in a narrow frequency window, cf. Fig. 1. In the experimentally difficult limit, where \(T \approx 0\) and \(S_\text {th} \ll S_{\text {qu}}\) even at the peak, we can approximate the SNR as

$$\begin{aligned} \varrho _{\text {qu}}^2&= \frac{1}{2 \pi } \int _{\omega _\text {min}}^{\omega _\text {max}} {{\,\mathrm{\text {d}}\,}}\omega \frac{4 \, |{\tilde{x}}_{\text {DM}}(\omega )|^{2}}{S_n(\omega )}\nonumber \\&\approx \frac{1}{2 \pi } \int _{\omega _\text {min}}^{\omega _\text {max}} {{\,\mathrm{\text {d}}\,}}\omega \frac{4 \, |{\tilde{x}}_{\text {DM}}(\omega )|^{2}}{S_{\text {qu}}(\omega )} \nonumber \\&\approx \frac{q_R^2}{16 \, m \, \hbar \, \omega _c \, \phi } \left( 1 + \frac{\pi - 8}{8 \, \pi } \phi ^2 \right) \nonumber \\&= \frac{1}{16 \, \phi } \frac{E_R}{E_0} \left( 1 + \frac{\pi - 8}{8 \, \pi } \phi ^2 \right) , \end{aligned}$$
(2.30)

where we have expanded in the small damping parameter \(\phi \) and we have introduced the zero energy of the quantum mechanical oscillator \(E_0 \equiv \hbar \, \omega _c/2\).

In our example the peak of the DM signal actually overcomes the quantum noise in a tiny frequency window, but we would still find a rather small SNR \(\varrho ^{2}_{\text {qu}} = 5.74 \times 10^{-4}\). However, with the hypothetical smaller target mass as suggested in [4] where \(m = 10^{-6}\) kg, the SNR value could be raised significantly to \(\varrho ^{2}_{\text {qu}} = 1.31 \times 10^{4}\) which is actually observable if we could suppress the suspension thermal noise without suppressing the DM signal.

In summary, from this simple toy model we have already learned that conventional gravitational wave detectors are not suited as detectors for light DM although they are extremely sensitive. We have shown that the test mass m and the temperature T of the detector are two of the most crucial properties affecting the sensitivity. Just reducing the test mass, the SNR increases since \(\varrho ^2 \sim 1/m\). It is clear from Eqs. (2.7), (2.11) and (2.26), that the DM signal and noises are proportional to \(1/m^2\) and 1/m, respectively. Therefore, we can see there is a factor of 1/m enhancement of the SNR, see Eqs. (2.29) and (2.30). Besides, lower temperatures could further suppress the thermal noise. Hence, to make this idea work one would need ideally light and ultracold targets to increase the recoil energy and reduce the thermal noise. Quantum sensing technologies which fulfill these criteria are currently being investigated as DM detectors, for a recent overview see [57]. In [32] results for a DM search have been presented using an optically levitated nanogram test mass cooled down to \({\mathcal {O}}(100)~\upmu \hbox {K}\) which is able to detect momentum transfers as low as 200 MeV/c but much higher than what we consider here. These experiments are nevertheless rather new and small compared to KAGRA and other gravitational wave detectors. Their noise is therefore still dominated by technical limitations and not fundamental physics backgrounds as thermal or quantum noise. In the future that will improve, but we refrain from providing a projection here, what their ultimate sensitivity will be.

To reduce suspension thermal noise in gravitational wave detectors there are actually proposals, i.e. one where the noise is being filtered out from the data by actively monitoring the suspension system [45]. This idea is not being implemented so far as we know so we will not discuss it in great detail here. Even if such a filter could distinguish between thermal noise and a potential DM signal exploiting, for instance, cancellations in the spectrum as we discuss them in the next subsection, one would still have to overcome the quantum noise, which is challenging in a conventional GW detector setup.

To distinguish a DM signal from thermal noise one could also change the temperature and see if there is a noise component, which looks similar to thermal suspension noise but is not affected by the temperature. Based on Eqs. (2.7) and (2.26), if the detector’s temperature is lowered, the suspension thermal noise would be suppressed as mentioned before while a DM signal would remain unchanged.

2.4 Cancellations in the DM signal spectrum

Before we apply what we learned from the above toy model to KAGRA, we would like to extend our toy model a bit.

KAGRA and other earth-bound GW detectors consist of a set of coupled damped harmonic oscillators. Therefore the motion of the target mirrors cannot be described in terms of a single resonance frequency. As the simplest generalization, we study the case of a free motion with two eigenfrequencies and two damping factors,

$$\begin{aligned} x(t)= & {} \theta (t) A ( \text {exp}(- \omega _1 \, \xi _1 \, t ) \sin (\omega _1 t)\nonumber \\&+ r \, \text {exp}(- \omega _2 \, \xi _2 \, t ) \sin (\omega _2 t)), \end{aligned}$$
(2.31)

where A and r are real coefficients. The frequencies \(\omega _1\), \(\omega _2\) and the damping factors \(\xi _1\) and \(\xi _2\) are all positive. The Fourier transform squared in this case is, cf. Eq. (2.19),

$$\begin{aligned} | {\tilde{x}}(\omega ) |^2&= A^2 \left| \frac{1}{\omega _1^2 (1 + \xi _1^2) - \omega ^2 + 2 \, {{\,\mathrm{\text {i}}\,}}\omega \, \omega _1 \, \xi _1}\right. \nonumber \\&\quad \left. + r \frac{1}{\omega _2^2 (1 + \xi _2^2) - \omega ^2 + 2 \, {{\,\mathrm{\text {i}}\,}}\omega \, \omega _2 \, \xi _2} \right| ^2 \end{aligned}$$
(2.32)
$$\begin{aligned}&\equiv A^2 \left| {\hat{x}}_1 + r \, {\hat{x}}_2 \right| ^2 . \end{aligned}$$
(2.33)

The two terms proportional to \(|{\hat{x}}_1|^2\) and \(|{\hat{x}}_2|^2\) just give two resonance-like peaks in the Fourier spectrum similar to what we discussed before. On the other hand, for certain parameters, the interference term

$$\begin{aligned} \begin{aligned} {\hat{x}}_{12}^2&\equiv 2 \,r\, \mathfrak {R}( {\hat{x}}_1 {\hat{x}}_2^\star ) \\&= \frac{2 \, r \, [ (\omega ^2 - \omega _1^2 (1 + \xi _1^2) ) ( \omega ^2 - \omega _2^2 (1 + \xi _2^2) ) + 4 \, \omega ^2 \omega _1 \omega _2 \xi _1 \xi _2 ] }{ ( (\omega - \omega _1)^2 + \omega _1^2 \xi _1^2 )((\omega + \omega _1)^2 + \omega _1^2 \xi _1^2 )( (\omega - \omega _2)^2 + \omega _2^2 \xi _2^2 )((\omega + \omega _2)^2 + \omega _2^2 \xi _2^2 ) } , \end{aligned} \end{aligned}$$
(2.34)

can significantly suppress the total \(| {\tilde{x}}(\omega ) |^2\) for certain frequencies. In the case of driven oscillators this phenomenon is well known as anti-resonance. In our previous toy setup, when we calculated the SNR, we focused on the frequency range around the resonance peaks. Therefore, our objective here is to investigate under which conditions such an anti-resonance-like behaviour can occur near a peak.

Inspired by the KAGRA parameters, we assume that \(\xi _1\), \(\xi _2 \ll 1\) and \(|\omega _i - \omega _j|/\omega _i \gg \xi _{i,j}\), where \(i,j = 1\), 2. Based on these assumptions and looking at the above expression for \({\hat{x}}_{12}^2\) we have to consider the interference term at \(\omega \approx \omega _1\) or \(\omega \approx \omega _2\). Since the problem is basically symmetric under exchange of the labels, it is sufficient to consider only one case. Taking the latter case as an example

$$\begin{aligned}&{\hat{x}}_{12}^2(\omega _2)\nonumber \\&= \frac{2 \, r \, [ - \xi _2 (\omega _2^2 - \omega _1^2 (1 + \xi _1^2) ) + 4 \, \omega _1 \omega _2 \xi _1 ]}{\omega _2^2 \xi _2 (4 + \xi _2^2) ( (\omega _2 - \omega _1)^2 + \omega _1^2 \xi _1^2 )((\omega _2 + \omega _1)^2 + \omega _1^2 \xi _1^2 )} \end{aligned}$$
(2.35)
$$\begin{aligned}&\approx \frac{r \, [ - \xi _2 (\omega _2^2 - \omega _1^2 ) + 4 \, \omega _1 \omega _2 \xi _1 ]}{2 \, \omega _2^2 \xi _2 (\omega _2^2 - \omega _1^2)^2 }. \end{aligned}$$
(2.36)

The denominator of Eq. (2.35) is always positive and a cancellation with the other (positive) terms in \(|{\tilde{x}}(\omega )|^2\) can only occur if the nominator is negative, i.e. if \(r \, [ - \xi _2 (\omega _2^2 - \omega _1^2 (1 + \xi _1^2) ) + 4 \, \omega _1 \omega _2 \xi _1 ] < 0\). Furthermore, to be noticeable the interference term should be similar in size as the other two terms. Let us assume that we can neglect the contribution from the first resonance compared to the second term for simplicity, i.e.

$$\begin{aligned} |{\hat{x}}_1(\omega _2)|^2 \ll r^2 |{\hat{x}}_2(\omega _2)|^2 = \frac{r^2}{ \omega _2^4 \xi _2^2 (4 + \xi _2^2) } . \end{aligned}$$
(2.37)

Therefore, under these assumptions a cancellation occurs if \({\hat{x}}_{12}^2(\omega _2) \approx - r^2 |{\hat{x}}_2(\omega _2)|^2\), i.e.

$$\begin{aligned} \begin{aligned} - \frac{r}{2 }&\approx \frac{ - \omega _2^2 \xi _2 (\omega _2^2 - \omega _1^2 (1 + \xi _1^2) ) + 4 \, \omega _1 \omega _2^3 \xi _1 }{ ( (\omega _2 - \omega _1)^2 + \omega _1^2 \xi _1^2 )((\omega _2 + \omega _1)^2 + \omega _1^2 \xi _1^2 )} \\&\approx \frac{-\omega _2^2 \xi _2}{( \omega _1^2 - \omega _2^2 )} + \frac{4 \, \omega _1 \, \omega _2^3 \, \xi _1}{( \omega _1^2 - \omega _2^2 )^2} . \end{aligned} \end{aligned}$$
(2.38)

That means that r must be small of the order of \({\mathcal {O}}(\xi _{i,j})\). If we would look at the other case, where a cancellation occurs near \(\omega \approx \omega _1\) then 1/r must be small, \({\mathcal {O}}(\xi _{i,j})\).

For the calculation of the SNR we also assume that we only need to take into account the thermal noise from the second mode and we neglect quantum noise

$$\begin{aligned} S_n \approx S_{\text {th},2}(\omega ) = \frac{4\, k_{B} \, T}{L^{2}} \, \frac{2\, \omega _{2}\, \xi _{2}/m}{(\omega ^{2}-\omega ^{2}_{2}(1-\xi ^{2}_{2}))^{2}+4\, \omega ^{4}_{2}\, \xi ^{2}_{2}} , \end{aligned}$$
(2.39)

which is consistent with our previous assumptions. We also use the FWHM boundaries for the integration as if there was no cancellation or second resonance peak. The peak we consider here is at \(\omega _2^2 (1 - \xi _2^2)\) and the FWHM is located at \(\pm 2 \, \omega _2^2 \xi _2\) around the peak. The interference term has an extremum at \(\omega _2\) meaning that it is situated within this FWHM range.

The SNR is then given by

$$\begin{aligned} \varrho ^2&\approx \frac{2 \, A^2}{\pi } \int _{\omega _\text {min}}^{\omega _\text {max}} {{\,\mathrm{\text {d}}\,}}\omega \frac{ r^2 \, |{\hat{x}}_{2}(\omega )|^{2} + {\hat{x}}_{12}^2(\omega ) }{S_{\text {th},2}(\omega )} \nonumber \\&= \frac{A^2 r^2 m L^2}{2 \, \pi \, k_B \, T} \left( 1- \frac{4 \,\xi _2^2}{3} \frac{\omega _2^2 (5 \, \omega _2^2 - 3 \, \omega _1^2) }{ r\, (\omega _2^2 - \omega _1^2)^2 }\right) + {\mathcal {O}}(\xi _2^4,\xi _1). \end{aligned}$$
(2.40)

Thus, given that \(\xi _2 \ll 1\) we expect the correction to the SNR to be very small. Even in the case of a strong cancellation, i.e. \({\hat{x}}_{12}^2(\omega _2) \approx - r^2 |{\hat{x}}_2(\omega _2)|^2\), this would still be true since then r is \({\mathcal {O}}(\xi _1,\xi _2)\), cf. Eq. (2.38). Based on this, we conclude that the occurrence of cancellations in the signal spectrum does not significantly reduce the expected SNR.

At this point, we already want to point out, that these cancellations in the spectrum are characteristic for the DM noise, but not the thermal suspension noise. We will see this very clearly, when we compare a potential DM signal with the noise spectrum in KAGRA. The DM signal features many prominent dips while the noise does not. In a dedicated DM experiment these differences could be optimised to allow a better distinction of signal and noises.

3 A realistic example: KAGRA

After having discussed some essential features using a simple toy model, we now want to turn to the concrete example of KAGRA [35]. The results for other earth-bound GW detectors based on laser interferometers, like LIGO or VIRGO, would be qualitatively very similar. Due to the cryogenic system KAGRA is actually better for our purposes since thermal noise is smaller then.

Let us briefly provide some essential details about the experimental setup in KAGRA. KAGRA consists of a double pendulum connected by blade springs (BSs). The first pendulum is represented by the suspended intermediate mass (IM) connected by 4 CuBe wires to the upper part of the system. The second pendulum corresponds to the TM suspended by 4 sapphire wires attached to the BSs. Mathematically this corresponds to a triple oscillator system. The three kinds of masses relevant here are the IM, \(m_1\), the BS, \(m_2\), and the TM, \(m_3\), where we closely follow the notation and labelling as in [35] with only minor modifications. The relative positions of the four TMs are probed by the interferometer system. We will also use \(i=1\), 2, 3 for the relative coordinates of the three kinds of masses. To be precise, we are only concerned with the vertical (horizontal) dimensionless, relative displacements, which we label as \(x_{iv}(t)\) (\(x_{ih}(t)\)), \(i=1\), 2, 3. These two sets of coordinates are orthogonal to each other and can be treated independently. It should be noted that in Komori’s code from [35] the displacements are not dimensionless which leads to some differences in the appearance of factors of L.

We split our discussion again into two parts. First, we discuss the noise which is completely based on [35] and we use the detuned resonant side-band extraction (DRSE) configuration to be precise. We then describe DM scattering in KAGRA and compare it to the noise and also briefly comment on the SNR.

3.1 Noise

Terrestrial GW detectors generically suffer from seismic noise at low frequencies below 10 Hz and at large frequencies above 1 kHz other sources of noise dominate. For KAGRA in this region actually quantum noise gets dominant, cf., for instance, [35, 42]. In the region in between, the KAGRA noise budget is mostly dominated by suspension thermal noise and quantum noise. For that reason we have focused on these two sources of noise in our toy model and we also focus on these two here.

3.1.1 Vertical suspension thermal noise

We begin our discussion of the thermal noise with the vertical direction which is easier compared to the horizontal one as we will see later. As we mentioned already the KAGRA detector can be modelled as three coupled (damped) harmonic oscillators in terms of the coupled differential equation [35]

$$\begin{aligned} \left( M \frac{{{\,\mathrm{\text {d}}\,}}^{2}}{{{\,\mathrm{\text {d}}\,}}t^{2}} + K_{v} \right) \vec {x}_{v}(t) = \frac{\vec {F}_{\text {ext},v}(t)}{L} , \end{aligned}$$
(3.1)

where

$$\begin{aligned}&M =\begin{pmatrix} m_{1} &{} 0 &{} 0 \\ 0 &{} m_{2} &{} 0 \\ 0 &{} 0 &{} m_{3} \end{pmatrix},\;&\nonumber \\ \quad&K_{v} = \begin{pmatrix} K_{1v}+K_{2v} &{} -K_{2v} &{} 0 \\ -K_{2v} &{} K_{2v}+K_{3v} &{} -K_{3v} \\ 0 &{} -K_{3v} &{} K_{3v} \end{pmatrix} , \end{aligned}$$
(3.2)
$$\begin{aligned}&\vec {x}_{v}(t) = \begin{pmatrix} x_{1v}(t) \\ x_{2v}(t) \\ x_{3v}(t) \end{pmatrix} \text { and } \vec {F}_{\text {ext},v}(t) = \begin{pmatrix} F_{\text {ext},1v}(t) \\ F_{\text {ext},2v}(t) \\ F_{\text {ext},3v}(t) \end{pmatrix} . \end{aligned}$$
(3.3)

The spring constants \(K_{iv} \equiv k_{iv}(1+\text {i} \, \phi _{iv})\) are complex. As we have discussed in our toy model the imaginary parts damp the oscillations. The numerical values of the parameters in Eq. (3.2) are for the convenience of the reader taken from [35] and collected in Table 1.

Here, we can see the advantage of the complex spring constant notation compared to a real notation. To calculate the thermal noise we assume an external periodic force and it is not immediately clear which frequencies we would have to use in the matrix generalisation of the damping term in Eq. (2.2). For the complex spring constants this question does not arise. All the information is contained in \(K_v\) and M.

Table 1 The values of masses and vertical, complex spring constants in KAGRA appearing in Eq. (3.2) taken from [35]. See also main text for more details
Full size table

We can now calculate the thermal noise in a very similar way to what we discussed before in Sect. 2.1. We only have to change everything into vector and matrix quantities. First of all, we calculate the admittance by assuming again that the system is subject to a periodic external force, i.e. \(F_{\text {ext}, iv}(t)={\tilde{F}}_{\text {th},iv}(\omega ) \exp ({{\,\mathrm{\text {i}}\,}}\omega t)\) and the corresponding displacement \(x_{iv}(t)={\tilde{x}}_{iv}(\omega ) \exp ({{\,\mathrm{\text {i}}\,}}\omega t)\) related to it by

$$\begin{aligned} D_{v}(\omega ) \, \vec {{\tilde{x}}}_{v} \equiv ( -\omega ^{2} \, M + K_{v} ) \vec {{\tilde{x}}}_{v} = \frac{\vec {{\tilde{F}}}_{\text {th},v}}{L} . \end{aligned}$$
(3.4)

The corresponding \(D_c(\omega )\) in the toy model, cf. Eq. (2.5), was a number while here it is a matrix. And as we have seen before the admittance \(Y_v\) can be directly related to \(D_v(\omega )\) via

$$\begin{aligned} Y_{v}(\omega ) \equiv \text {i} \, \omega \, D_{v}^{-1}(\omega ). \end{aligned}$$
(3.5)

Now we can again use the fluctuation-dissipation theorem [38, 39] to relate the admittance to the thermal noise spectrum which is also a matrix here

$$\begin{aligned} S_{x_{iv}x_{jv}}(\omega ) = \frac{4 k_{B} \, T \, \mathfrak {R}(Y_v(\omega ))_{ij}}{L^{2} \, \omega ^{2}}. \end{aligned}$$
(3.6)

The diagonal elements of this matrix represent the thermal noise PSD and since we are probing the TM, the third coordinate, we are interested in

$$\begin{aligned} S_{\text {th},v}(\omega ) \equiv S_{x_{3v} x_{3v}}(\omega ) = \frac{4 \, k_{B} \, T_{3} \, \mathfrak {R}(Y_v)_{33} }{L^{2} \, \omega ^{2}}, \end{aligned}$$
(3.7)

where \(T_{3}=19\) K (the three masses actually have slightly different temperatures). With the definition in Eq. (2.10), the strain amplitude for the vertical thermal noise can be readily obtained as

$$\begin{aligned} h_{\text {th},v}(\omega ) =\text {VHC} \, \sqrt{4|S_{\text {th},v}(\omega )|} . \end{aligned}$$
(3.8)

where the factor of four refers to the fact that there are four equal TMs. The VHC factor accounts for the fact that there is a non-vanishing component of the horizontal motion, which is being probed by the experiment due to the tilt of the interferometer baseline. The value of this factor is 1/200 [35].

Fig. 2
figure 2

Overview of strain amplitudes of relevant noise components in KAGRA. The green (orange) line is the vertical (horizontal) suspension thermal noise. The KAGRA quantum noise is shown as blue line and the SQL is shown for comparison as light blue, dashed line. The mirror thermal noise is the brown line. The total noise is the black line

Full size image

We show the strain of the vertical thermal suspension noise in Fig. 2 as the green line. We can clearly identify three peaks which is what we expect for a system of three coupled harmonic oscillators which exhibits three normal modes. The respective peak frequencies are 12.04, 31.43 and 1044.09 Hz. We would like to mention that compared to the figures in many KAGRA documents, for instance in [35], our peaks for the noise look much higher. That is due to the difficulty of plotting very narrow resonances. We checked, that we agree with Komori’s code in [35] after increasing their plot resolution drastically.

3.1.2 Horizontal suspension thermal noise

We now turn to the horizontal thermal noise which - although very similar - still has some complications compared to the vertical case. We can again write

$$\begin{aligned} \left( M \frac{{{\,\mathrm{\text {d}}\,}}^{2}}{{{\,\mathrm{\text {d}}\,}}t^{2}} + K_{h} \right) \vec {x}_{h}(t) = \frac{\vec {F}_{\text {ext},h}(t)}{L} , \end{aligned}$$
(3.9)

with M as before and \(K_h\) has the same structure as \(K_v\). Apart from different numerical values for \(K_{2h}\) compared to \(K_{2v}\) there are two differences. First, \(K_{1h}\) is an effective spring constant given by

$$\begin{aligned} K_{1h} = \frac{4 \, \tau _1}{l_1 - 2\sqrt{\frac{E_{1h} \, I_1}{\tau _1}}} \equiv k_{1h} (1 + {{\,\mathrm{\text {i}}\,}}\phi _{1h}) , \end{aligned}$$
(3.10)

where \(\tau _1 = (m_1 +m_2 + m_3) \, g /4\) with g the gravitational acceleration, \(E_{1h}\) and \(l_1\) are the associated tension per wire, complex Young modulus of the wire and the length of the wire connecting to IM.

Table 2 The values of the horizontal, complex spring constants in KAGRA and related material parameters appearing implicitly in Eq. (3.9) taken from [35]. See also main text for more details
Full size table

Second, the horizontal spring constant for the TM is frequency dependent, i.e. \(K_{3h} = K_{3h}(\omega )\). The analytical expression for \(K_{3h}(\omega )\) is written in terms of the frequency dependent wave number of the elastic wire, \(k_{s}\), and the flexural stiffness of the wire, \(k_{e}\), defined as

$$\begin{aligned} k_{s,e}^2(\omega ) = \frac{\mp \tau _3 + \sqrt{\tau ^{2}_3+4 \, E_{w} \, I_{cw} \, \rho _{l} \, \omega ^{2}}}{2 \, E_{w} \, I_{cw}}, \end{aligned}$$
(3.11)

where \(\tau _3 = (m_{3} \, g)/4\), \(E_w\), \(I_{cw}\), and \(\rho _{l}\) are the associated tension per wire, complex Young modulus of the wire, area moment of inertia of the wire, and linear mass density of the wire respectively. The tension per wire is simply obtained by dividing the total tension due to the weight of \(m_{3}\) by the number of wires (which is four in this case). Using these definitions, \(K_{3h}(\omega )\) can be written as [35]

$$\begin{aligned} K_{3h}(\omega ) = 4 \, E_{w} \, I_{cw} \, k_{e} \, k_{s} \, \left( k^{2}_{e}+k^{2}_{s}\right) R_{3h}(\omega ) , \end{aligned}$$
(3.12)

where the factor \(R_{3h}(\omega )\) is given by

$$\begin{aligned}&R_{3h}(\omega ) \nonumber \\&= \frac{k_{e} \, \cos (k_{s} \, l_{2}) \, \sinh (k_{e} \, l_{2}) + k_{s} \, \sin (k_{s} \, l_{2}) \, \cosh (k_{e} \, l_{2})}{2 \, k_{e} \, k_{s} \left[ 1-\cos (k_{s} \, l_{2}) \, \cosh (k_{e} \, l_{2})\right] + (k^{2}_{e} - k^{2}_{s}) \, \sin (k_{s} \, l_{2}) \, \sinh (k_{e} \, l_{2})} ,\nonumber \\ \end{aligned}$$
(3.13)

where \(l_{2}\) is the length of the TM suspension wire. The numerical values of the parameters for the horizontal equation of motion, Eq. (3.9), are collected for the convenience of the reader in Table 2.

By repeating the same steps as before for the vertical noise in Eqs. (3.4)–(3.7), we get the strain amplitude of horizontal thermal noise as

$$\begin{aligned} h_{\text {th},h}(\omega ) = \sqrt{4|S_{\text {th},h}(\omega )|} . \end{aligned}$$
(3.14)

where \(S_{\text {th},h}(\omega ) \equiv S_{x_{h3}x_{h3}}(\omega )\) analogous to Eq. (3.6). Since we now discuss the horizontal modes directly we do not need to include the VHC factor.

We show the strain of the horizontal thermal suspension noise in Fig. 2 as the orange line. One immediate difference of the horizontal compared to the vertical noise is the much larger number of peaks in the horizontal noise. This is due to the \(\omega \) dependence of \(K_{3h}\) which leads to so-called violin modes. As the name suggests they originate from vibrational excitations of the suspension wires being thermally excited, see [46]. There are a total of ten modes in the window between 5 Hz and 5 kHz so we will not list them all here explicitly. The first peak at 175.44 Hz corresponds approximately to the toy model example though.

3.1.3 Other noise components

The KAGRA quantum noise, \(S_{\text {qu}}\), is actually not correctly described by the SQL, cf. Eq. (2.12). KAGRA is a second-generation interferometer with a signal recycling cavity where the quantum noise is more complicated. Since we focus here on DM and the explicit, complicated expressions for the quantum noise do not give us any insights on that, we just show the curves for illustration in Fig. 2. For more details, see [35, 42].

Between about 75 and 88 Hz, the mirror thermal noise, \(S_{\text {mir}}\), which is the sum of thermoelastic noise [47], substrate thermal noise [6] and coating thermal noise [48], is actually dominant over the suspension thermal noise and quantum noise. However, since this noise component does not contribute significantly to the total noise around the resonance peaks, we again just show the curve of this noise in Fig. 2. Since the mirror thermal noise is also proportional to the mirror temperature like the suspension thermal noise it could be suppressed by reducing the temperature as well.

The total noise we consider is given by

$$\begin{aligned} S_{\text {tot}}(\omega )&= 4 \, \text {VHC}^{2} \,S_{\text {th},v}(\omega )+ 4 \, S_{\text {th},h}(\omega ) + S_{\text {qu}}(\omega )\nonumber \\&\quad + 2 \, S_{\text {mir}}(\omega ) , \end{aligned}$$
(3.15)

where the factors of four are due to having four TMs whereas there is only a factor of two for the mirror thermal noise as there are two different coatings used. The quantum noise already includes any such factors. The strain is then given by

$$\begin{aligned} h_{\text {tot}}(\omega ) = \sqrt{h^{2}_{\text {th},v}(\omega )+h^{2}_{\text {th},h}(\omega ) + h^2_{\text {qu}}(\omega ) + h^2_{\text {mir}}(\omega )} . \end{aligned}$$
(3.16)

Within the frequency range we focus on, all the noise components are shown in Fig. 2 for illustration. We show the strain of the quantum noise as blue line and the mirror noise as brown line in Fig. 2. For comparison we also show the SQL as dashed blue line. The actual quantum noise is smaller than the SQL in the window between 54 Hz and 120 Hz where KAGRA is most sensitive. In the region where the resonance modes of the suspension system appear the SQL is instead better than the actual quantum noise. For KAGRA this makes sense since they do not want to have any thermally excited modes in their most sensitive region. For our purposes that should be constructed differently and the quantum noise should be minimal near a resonance where the DM signal can be comparatively large.

We also show in Fig. 2 the combination of all relevant noise components as black line. For the first three peaks of the total noise, the strain amplitudes can reach between \({\mathcal {O}}(10^{-16})\) and \({\mathcal {O}}(10^{-18})\) \(\hbox {Hz}^{-1/2}\). We will use this combination in our later figures in comparison to a potential DM signal.

3.2 DM signal

We now turn to the modelling of a hypothetical DM signal, which we do in analogy to our discussions for the toy model. Again we want to assume that the DM hit occurs at \(t = 0\) and it generally transmits a recoil momentum in horizontal and vertical direction.

Let us first discuss the effect of a hit in the TM in the vertical direction first. In this case, the force can be described by

$$\begin{aligned} F_{\text {DM},3v}(t) = q_{R,v} \, \delta (t) , \end{aligned}$$
(3.17)

where \(q_{R,v}\) is the recoil momentum of DM in vertical direction. The equation of motion for this case is given by Eq. (3.3) with \(F_{\text {ext},3v}\) replaced by \(q_{R,v} \, \delta (t)\). Taking the Fourier transform of it we immediately arrive at

$$\begin{aligned} \vec {{\tilde{x}}}_{v}(\omega ) = D^{-1}_{v}(\omega ) \frac{\vec {{\tilde{F}}}_{\text {DM},v}(\omega )}{L} = D^{-1}_{v}(\omega ) \begin{pmatrix} 0 \\ 0 \\ \frac{q_{R,v}}{L} \end{pmatrix} , \end{aligned}$$
(3.18)

or in component notation

$$\begin{aligned} {\tilde{x}}_{iv}(\omega ) = \sum _{j=1}^{3} \left( D^{-1}_{v}(\omega ) \right) _{ij} \frac{{\tilde{F}}_{j,v}(\omega )}{L} . \end{aligned}$$
(3.19)

Since we are probing the third component and the force is assumed to be in the third component as well we get easily

$$\begin{aligned} |{\tilde{x}}_{\text {DM},v}(\omega )|^2 \equiv |{\tilde{x}}_{3v}(\omega )|^2 = \left| \left( D^{-1}_{v}(\omega ) \right) _{33} \frac{{\tilde{F}}_{3,v}(\omega )}{L} \right| ^2 , \end{aligned}$$
(3.20)

where \({\tilde{F}}_{3,v}(\omega ) = q_{R,v}\). For a hit in the IM the formula would be instead

$$\begin{aligned} |{\tilde{x}}_{\text {DM},v}(\omega )|^2 = \left| \left( D^{-1}_{v}(\omega ) \right) _{31} \frac{{\tilde{F}}_{1,v}(\omega )}{L} \right| ^2 , \end{aligned}$$
(3.21)

with \({\tilde{F}}_{1,v}(\omega ) = q_{R,v}\). The generalisation to a hit in the BS or observation of other components is straightforward.

The corresponding strain amplitude induced by such a DM hit taking the tilt of the interferometer baseline into account is

$$\begin{aligned} h_{\text {DM},v}(\omega ) = \text {VHC} \, \sqrt{\frac{2 \, \omega }{\pi } |{\tilde{x}}_{\text {DM},v}(\omega )|^2 } , \end{aligned}$$
(3.22)

where again \(\text {VHC} = 1/200\).

The DM induced strain in horizontal direction can be derived completely analogous to the vertical case

$$\begin{aligned} h_{\text {DM},h}(\omega ) = \, \sqrt{\frac{2 \, \omega }{\pi } |{\tilde{x}}_{\text {DM},h}(\omega )|^2 } , \end{aligned}$$
(3.23)

where, i.e.

$$\begin{aligned} |{\tilde{x}}_{\text {DM},h}(\omega )|^2 \equiv |{\tilde{x}}_{3h}(\omega )|^2 = \left| \left( D^{-1}_{h}(\omega ) \right) _{33} \frac{{\tilde{F}}_{3,h}(\omega )}{L} \right| ^2 , \end{aligned}$$
(3.24)

for a horizontal hit in a TM with \({\tilde{F}}_{3,h}(\omega ) = q_{R,h}\). Again the generalisation to other components is straightforward.

For the total DM signal we use

$$\begin{aligned} |{\tilde{x}}_{\text {DM}}(\omega )|^2 = \text {VHC}^2 |{\tilde{x}}_{\text {DM},v}(\omega )|^2 + |{\tilde{x}}_{\text {DM},h}(\omega )|^2 , \end{aligned}$$
(3.25)

where we have included the \(\hbox {VHC}^2\) factor for the vertical hits since we only observe this through the tilt in the setup.

Fig. 3
figure 3

Comparison of strain amplitudes of noise shown as black line and a DM hit in the TM in vertical (horizontal) direction shown as aqua (maroon) line. For more details, see main text

Full size image
Fig. 4
figure 4

Comparison of strain amplitudes of noise shown as black line and a DM hit in the BS in vertical (horizontal) direction shown as aqua (maroon) line. For more details, see main text

Full size image
Fig. 5
figure 5

Comparison of strain amplitudes of noise shown as black line and a DM hit in the IM in vertical (horizontal) direction shown as aqua (maroon) line. For more details, see main text

Full size image

In Figs. 3, 4 and 5 we show a comparison of DM hits in the TM, BS and IM respectively. In these figures, we show two DM cases each, assuming that our estimate for the recoil momentum, \(q_{R} \sim m_{\text {DM}} |\vec {v}_{\text {DM}}|\) with the DM mass, \(m_{\text {DM}}= 1\) \(\hbox {GeV}/\text {c}^2\) and the typical velocity, \(|\vec {v}_{\text {DM}}|=220\) km/s is either completely in vertical direction (aqua line) or horizontal direction (maroon line).

In all three cases we observe that the DM signal for a hit in vertical direction has again three peaks corresponding to three eigenfrequencies, which occur also in the vertical thermal noise. Interestingly not in all cases we see a clear resonance shape, but we also see the anti-resonance-like behaviour as discussed in Sect. 2.4, for instance, for the second peak in the TM case, in Fig. 3. For hits in horizontal direction, we also observe that all resonance frequencies get excited and especially for hits in the BS and IM we see many cancellations although most of them are not around the peaks. These differences in the spectrum could be used as a way to distinguish DM hits from background noise as we mentioned before. Another way is to look for a daily or annual modulation effect [49, 50] due to the motion of the Earth with respect to the DM halo. That leads to a modulation of the hit rate but also preferred recoil direction which could be resolved with enough statistics.

In general, we see that the DM signal is much smaller than the noise. For instance, for the hit in the TM the ratio of the DM induced strain in vertical (horizontal) direction over the noise strain is always smaller than \(10^{-10}\) (\(10^{-7}\)) over the considered frequency range. With such small figures, the detection of light particle DM in KAGRA seems rather impossible. For LIGO and other earth-bound GW detectors we expect similar results since the mirrors all have similar masses and hence the recoil energy is usually much smaller than the thermal energy. Very heavy DM or DM boosted in some way to relativistic velocities can help to overcome this suppression but the number densities for both cases is usually expected to be small making any scattering event seem unlikely.

3.3 SNR

Although just looking at the DM induced strain compared to the noise strain a detection seems rather hopeless, we discuss the SNR still in some detail to comment on some insights. We will use again basically the same formula as before

$$\begin{aligned} \varrho ^2 = \int _{f_\text {min}}^{f_\text {max}} {{\,\mathrm{\text {d}}\,}}f \frac{4 \, |{\tilde{x}}_{\text {DM}}(2 \, \pi \, f)|^{2}}{S_{\text {tot}}(2 \, \pi \, f)} . \end{aligned}$$
(3.26)

A major difference is that the noise in this case is much more complicated and also the DM signal shows more than one peak. Still we want to focus on two peaks, the second peak of the vertical noise at \(f_v = 31.4\) Hz and the first peak of the horizontal noise at \(f_h = 175.4\) Hz. The quantum noise for these two peaks is comparatively small, cf. Fig. 2. For the integration boundaries we could in theory again use the FWHM of the peaks, which is nevertheless probably smaller than the KAGRA frequency resolution. Therefore, we use more conservative boundaries

$$\begin{aligned} f_{\text {min},v} = 30.4 ~\text {Hz}\quad \text {and}\quad f_{\text {max},v} = 32.4 ~\text {Hz} \end{aligned}$$
(3.27)

for the vertical suspension noise peak and

$$\begin{aligned} f_{\text {min},h} = 170 ~\text {Hz}\quad \text {and}\quad f_{\text {max},h} = 180 ~\text {Hz} \end{aligned}$$
(3.28)

for the horizontal suspension noise peak. Within these boundaries the thermal suspension noise is still dominant over the other noise components. We then get two SNR values, \(\varrho ^2_v\) and \(\varrho ^2_h\), where the index refers to the integration boundaries, i.e.

$$\begin{aligned} \varrho _h^2 = \int _{f_\text {min},h}^{f_\text {max},h} {{\,\mathrm{\text {d}}\,}}f \frac{4 \, |{\tilde{x}}_{\text {DM}}(2 \, \pi \, f)|^{2}}{S_{\text {tot}}(2 \, \pi \, f)} . \end{aligned}$$
(3.29)

For a DM hit in the TM in vertical direction (where \(|{\tilde{x}}_{\text {DM}}|^2 = \text {VHC}^2 |{\tilde{x}}_{\text {DM},v}|^2 \)) using our standard assumptions we then find \(\varrho ^2_v = 1.89 \times 10^{-21}\) and \(\varrho ^2_h = 1.73 \times 10^{-22}\) While for a DM hit in horizontal direction (where \(|{\tilde{x}}_{\text {DM}}|^2 = |{\tilde{x}}_{\text {DM},h}|^2 \)) we find \(\varrho ^2_v = 1.47 \times 10^{-17}\) and \(\varrho ^2_h = 6.94 \times 10^{-18}\). Taking the ratio \(\varrho ^2_v/\varrho ^2_h\) we can extract some information on the direction of the recoil momentum. In the extreme cases we find \(\varrho ^2_v/\varrho ^2_h = 10.9\) for a hit in purely vertical direction while for a hit in purely horizontal direction we find \(\varrho ^2_v/\varrho ^2_h = 2.1\). These numbers nevertheless suffer from ambiguities. We cannot reconstruct the sign of the recoil momentum, cf. Eq. (3.20), and we also cannot reconstruct in which of the two KAGRA arms the DM hit occurs. In a dedicated DM experiment based on an interferometer it might be useful to slightly detune the different components of the experiment to resolve these ambiguities.

The value for the SNR we computed here for a DM hit in horizontal direction, \(\varrho ^2_h = 6.94 \times 10^{-18}\), is different from the one in the toy model for the same peak, see Sect. 2.3 where \(\varrho ^2_{\text {th}} = 4.09 \times 10^{-24}\). There are three main reasons for that. First, we do not use the same boundaries here and there. Even if we would apply the same boundaries from Eq. (3.28) to the toy model for computing the SNR see Eq. (2.29), we would find \(\varrho ^2_{\text {toy}} = 3.68 \times 10^{-14}\) which is still different from the value we have here. That is due to the fact, that here \(|{\tilde{x}}_{\text {DM}}|^2/( f \, S_{\text {tot}} ) \) is not a constant as in the toy model. We can understand this since here

$$\begin{aligned} S_{\text {tot}} \approx S_{\text {th},h/v} \sim \mathfrak {I}(D_{v/h}^{-1})_{33} , \end{aligned}$$
(3.30)

while

$$\begin{aligned} |{\tilde{x}}_{\text {DM}}|^2 \sim | (D_{v/h}^{-1})_{33} |^2 . \end{aligned}$$
(3.31)

In the case of the one-dimensional single oscillator in the toy model these two had the same structure while here this is more complicated. In fact, the thermal suspension noises \(S_{\text {th},h/v}\) do not have the shape of a single Lorentzian function anymore. Also note that \(|{\tilde{x}}_{\text {DM}}|^2\) clearly exhibits cancellations which are not described in terms of a sum of Lorentzian functions emphasizing that this approximation breaks down. The third reason is that in the toy model section we did not include the quantum noise when calculating \(\varrho ^2_{\text {th}}\) which nevertheless would not alter the value as drastically as the previous two reasons since it is subdominant within the integration boundaries.

Unsurprisingly reality is more complicated than a toy model. The suppression factor \(E_R/E_{\text {th}}\) is nevertheless still there since it is related to constant factors of \(|{\tilde{x}}_{\text {DM}}|^2\) and \(S_{\text {th},h/v}\). To enhance the SNR it therefore still seems most efficient to us to focus first on enlarging \(E_R/E_{\text {th}}\) using lighter and colder mirrors.

4 Comments on other technologies

In this section, we just briefly want to comment on space-based GW detectors and atomic interferometers, which are very different setups compared to conventional terrestrial laser interferometers and hence our previously derived results cannot be immediately translated.

4.1 Space-based GW detectors

Let us begin with space-based GW detectors where the TMs should be ideally free-falling. Our approximation as damped harmonic oscillators is then inappropriate. In fact, in LISA pathfinder (LPF) [51] and LISA [52] the position of the TMs are unstable due to various sources of noise which needs to be corrected in a controlled manner.

We can nevertheless, give some rough estimate to see, if light DM could be detected in these experiments. We follow the approach in [53] where they looked for micrometeroidal events at LPF which hit the spacecraft. In this reference, the relevant Fourier transform of a force acting on the target mass for a duration much shorter than the time resolution at \(t = 0\) is just \({\tilde{F}} = q_R\). Then it is also important, that the target sensitivity in terms of the amplitude spectral density is given in terms of the differential acceleration of two TMs as

$$\begin{aligned} \sqrt{S_{\Delta g} } \le 3 \sqrt{2} \text { fm s}^{-2}/\sqrt{\text {Hz}} \times \sqrt{1 + (f/8 \text { mHz})^4} \end{aligned}$$
(4.1)

within the frequency band of 0.1 mHz \(\le f \le 1\) Hz for LISA and

$$\begin{aligned} \sqrt{S_{\Delta g} } \le 30 \text { fm s}^{-2}/\sqrt{\text {Hz}} \times \sqrt{1 + (f/3 \text { mHz})^4} \end{aligned}$$
(4.2)

within the frequency band of 1 mHz \(\le f \le 30\) Hz for LPF, cf. [54]. LPF in the end exceeded not only the LPF target sensitivity, but remarkably even the LISA target sensitivity [55]. That gives the hope that also LISA will do much better than its target sensitivity.

These target sensitivities have to be compared to the amplitude spectral density induced by a DM hit

$$\begin{aligned} \sqrt{S_{\Delta g, \text {DM}}} = 2 \sqrt{f} \left| \frac{{\tilde{F}}}{m_T} \right| = 2 \sqrt{f} \left| \frac{q_R}{m_T} \right| . \end{aligned}$$
(4.3)

This is the analogue to Eq. (2.22) with \(|{\tilde{x}}_{\text {DM}}|\) replaced by \(|{\tilde{F}}/m_T|\). Using again as a rough estimate for the recoil momentum \(|q_R| \sim m_{\text {DM}} |\vec {v}_{\text {DM}}|\) with \(m_{\text {DM}} = 1\) \(\hbox {GeV/c}^2\), \(|\vec {v}_{\text {DM}}| = 220\) km/s and \(m_T = 1.928\) kg for LPF we find

$$\begin{aligned} \sqrt{S_{\Delta g, \text {DM}}} \sim 4.1 \times 10^{-7} \, \sqrt{\frac{f}{\text {Hz}}} \; \text { fm s}^{-2}/\sqrt{\text {Hz}} . \end{aligned}$$
(4.4)

From that estimate it is clear that the up-coming space-based GW detectors are not suited to detect conventional light DM.

We can also use the LPF results [53] to estimate the expected SNR

$$\begin{aligned} \varrho ^{2}_{\text {LPF}} = \frac{|q_R|}{P_c} \sim \frac{m_{\text {DM}} |\vec {v}_{\text {DM}}|}{P_c} \approx 10^{-14} , \end{aligned}$$
(4.5)

where \(P_c \approx 3.6 \times 10^{-8}\) N s [53]. Based on this simple estimation, one can compare the SNR obtained here with the one from the toy model (with the typical KAGRA parameters) discussed in Sect. 2.3. Interestingly, LPF is much better than our toy KAGRA setup \(\varrho ^{2}_{\text {LPF}} \approx 10^{-14} \gg \varrho ^{2}_{\text {toy}} \approx \varrho ^{2}_{\text {th}} \approx 10^{-24}\). That suggests that a light DM detector based on interferometers might be more easily realised in space than on earth.

4.2 Atomic interferometers

Recently, there have also been some proposals to use atomic interferometers for GW detection instead of laser interferometers, for instance, AGIS [13], MAGIS [14, 15], AION [16], AEDGE [17], MIGA [18], ELGAR [19], ZAIGA [20] see also [21,22,23]. Many of these proposals also mention the possibility to detect wave-like, ultralight DM with masses well below 1 eV/\(\hbox {c}^2\). The signal would then be wave-like as well with a frequency determined by DM parameters quite different from the case of scattering of individual DM particles as we discuss here.

These experiments promise remarkable sensitivities. For instance, MAGIS-100, might be able to test signals with an amplitude spectral density down to \(10^{-16} \, \text {g}/\sqrt{\text {Hz}}\) [15], cf. also [56], which would be about \(0.1 \text { fm s}^{-2}/\sqrt{\text {Hz}}\) exceeding LISA requirements. Interestingly, the target mass is very small in these cases. Atomic interferometers consist of clouds of ultracold atoms. In the case of MAGIS-100 they mention fluxes of the order of \(10^8\) strontium atoms per second or \(10^{15}\) dropped atoms in a year much less than a milligram. Common strontium isotopes have an atomic weight of about 87–88 \(\hbox {GeV/c}^2\) allowing for much larger recoil energies than in conventional GW detectors that could be observed in atomic interferometers.

On the other hand, since the total target mass is so small the number of expected DM scattering events is very small as well. That is a disadvantage compared to more conventional detectors.

5 Summary and conclusions

The motivation for this work is to describe scattering of DM particles at GW detectors. To understand the physics principles behind it, we studied first a damped harmonic oscillator with internal damping as simplified toy model. In this model, it became already clear that DM can excite mechanical resonances allowing for comparatively large strain values in some frequency windows, which could help to overcome quantum noise, for instance. The catch is that these resonances are also excited by thermal energy. In conventional GW detectors a detection of light DM becomes rather hopeless. But from our toy model, we can easily understand and quantify that there are two things that can be done for improvement and which form one of the most important results of our paper. First, the temperature could be further reduced since thermal noise is proportional to it. Active thermal noise suppression might also help in the future. Second, the oscillator mass should be reduced to increase the recoil energy from the hit. That two measures would help to overcome thermal and quantum noise.

We then demonstrate how easy our formalism can be applied to the much more complicated but realistic example of the KAGRA detector. The resonance pattern gets much more involved since there are multiple mechanical resonances that can be excited, and we also encounter partial cancellations which provide a potential way to distinguish a DM signal from thermal noise. Unfortunately, the expected SNR in KAGRA is very small for light DM on which we focussed here.

We also comment briefly on space-based GW detectors and atomic interferometers. LISA and LPF turn out to be more sensitive for our physics case, but still not sensitive enough for a realistic detection. Atomic interferometers are actually promising since the target material in this case are rather few, ultracold atoms fulfilling our criteria.

In summary, conventional GW detectors have impressive sensitivities but they are not good particle DM detectors. Nevertheless, mechanical sensors at the quantum limit like KAGRA have recently been more seriously considered as potential technology for DM detection, cf. [57]. To understand what the ultimate sensitivity of this new technologies will be, further research is needed and being carried out at that very moment. We think that at least in some mass regions such technologies will become competitive to more conventional approaches and a good modeling of the DM signal as discussed in this work will be useful to separate it from irreducible backgrounds for which we have also presented some ideas.