Abstract
X-ray and extreme ultraviolet (XUV) coherent diffractive imaging (CDI) have the advantage of producing high resolution images with current spatial resolution of tens of nanometers and temporal resolution of tens of femtoseconds. Modern developments in the production of coherent, ultra-bright, and ultra-short X-ray and XUV pulses have even enabled lensless, single-shot imaging of individual, transient, non-periodic objects. The data collected in this technique are diffraction images, which are intensity distributions of the scattered photons from the object. Superfluid helium droplets are ideal systems to study with CDI, since each droplet is unique on its own. It is also not immediately apparent what shapes the droplets would take or what structures are formed by dopant particles inside the droplet. In this chapter, we review the current state of research on helium droplets using CDI, particularly, the study of droplet shape deformation, the in-situ configurations of dopant nanostructures, and their dynamics after being excited by an intense laser pulse. Since CDI is a rather new technique for helium nanodroplet research, we also give a short introduction on this method and on the different light sources available for X-ray and XUV experiments.
You have full access to this open access chapter, Download chapter PDF
Similar content being viewed by others
7.1 Introduction
X-ray and extreme ultraviolet (XUV) radiations are high energy forms of electromagnetic radiation with photon energies ranging from tens of electron volts (eV) to tens of kilo-electron volts (keV). Absorption resonances and binding energies of many atoms fall within this range, allowing the identification of the elements in a material, their oxidation states, and even their chemical environment [1,2,3,4,5]. The short wavelengths of X-ray and XUV, from a fraction to a few tens of nanometers, are also used for the structural determination of objects with high spatial resolution and chemical specificity [1,2,3,4,5]. The XUV regime from tens of electron volts to ~250 eV is commonly used in studying electronic structures, especially chemical bonding in molecules, using photoelectron spectroscopy. The X-ray regime, on the other hand, is divided into soft (low-energy, ~250 eV to ~10 keV) and hard (high-energy, ~10 to ~50 keV) X-rays. The latter is frequently employed in X-ray diffraction crystallography since the photons in this region have wavelengths comparable to interatomic distances; while the former is often used for core-level spectroscopy of many organic compounds because the K-absorption edges of carbon (284 eV), nitrogen (410 eV), and oxygen (543 eV) lie within this region. The photon range between the carbon K-edge and the oxygen K-edge is called the “water window” because carbon predominantly absorbs the photons there, whereas oxygen (or water) remains transparent. This window is particularly advantageous for improving contrast in the X-ray microscopy of many organic compounds and cellular components in their native aqueous environment.
The generation of X-rays and X-ray imaging evolve together [6]. Immediately after Röntgen’s discovery in 1895, it was demonstrated that X-ray radiation penetrates through many materials and reveals the denser internal structure. There is a good contrast between different elements in an object because of absorption, which scales as a function of the atomic number almost to the fourth power [1, 2]. These rather unusual properties of X-rays lead to some of their earliest and dramatic applications in casting shadow images of bones and hidden objects; applications that are continuously used in X-ray radiography for making medical and dental diagnoses, and in scanning for dangerous and prohibited objects in security checkpoints. Moreover, through the principles of diffraction, X-rays are used for structure determination of crystals and quasicrystals, including biologically important molecular systems such as the ribosomes and the DNA. In fact, most structures reported in molecular structure databanks are collected from X-ray crystallography [7]. Another way of imaging structures is with the use of electrons, see the work by Zhang et al. in Chap. 8 of this volume [8].
While X-ray crystallography is nowadays a routine procedure for structure determination, its application remains limited to systems that can be crystallized. Many objects in the micro- and nanoscales, which are of interest in materials, physical, and biological sciences, especially in the so called “soft materials”, (i) do not form reproducible structures, (ii) are often non-periodic, (iii) cannot be supported, (iv) are either difficult to crystallize or cannot be crystallized at all, and (v) are often too large to be imaged as a whole. X-ray microscopy addresses some of these issues [9,10,11]. However, one key challenge in X-ray microscopy comes from the fact that materials used for X-ray optics have refractive indices remarkably close to unity and do not significantly refract X-rays. The use of a zone plate is one option to focus an X-ray beam and to produce a real space X-ray image. These plates, which are also known as Fresnel zone plates, are designed with alternating opaque and transparent concentric rings and require bright and coherent light sources, usually from third-generation synchrotron sources. The resolution, however, is limited by the size of the outer most rings of the zone plates, which is of the order of a few tens of nanometers [12, 13]. Another approach to structure determination of non-periodic objects is with lensless coherent diffractive imaging (CDI) [14,15,16,17,18]. In this technique, the object of interest is directly illuminated by spatially coherent X-rays or XUV focused to a few microns. The data collected with CDI are the intensity distributions of the scattered photons recorded on a two-dimensional detector. Since only the intensities of the scattered photons are recorded, phase information is lost, and iterative transform algorithms are required to numerically calculate the density of the object giving the diffraction image [14, 19,20,21,22,23]. The X-ray or XUV laser must be sufficiently bright, and spatially and temporally coherent [2, 24]. Additionally, the focus of the light beam must also be larger than the size of the object, as this oversamples the information needed for determining the missing phase, see Sect. 7.2.3. Necessary parameters for CDI have been reached with recent technological developments of fourth generation XUV and X-ray light sources, which are also known as Free-Electron Lasers (FEL). XUV diffractive imaging with FELs was first demonstrated at the Free-Electron Laser in Hamburg (FLASH) facility in 2006 [25], and in the X-ray regime at the Linac Coherent Light Source (LCLS) at Stanford Linear Accelerator Laboratory in 2011 [26, 27]. Since then, single-shot diffraction and especially CDI has been applied to single viruses [27], soot particles [28], xenon clusters [29, 30], and silver nanocrystals [31], among others, with a nanometer resolution. Several reviews have been published recently on CDI with X-rays, especially focusing on biological samples [15, 24, 32,33,34].
The earliest X-ray CDI measurement with superfluid helium droplets was performed at LCLS with the aim of visualizing quantized vortices in finite and isolated quantum fluids [35]. Quantum vortices are the macroscopic manifestation of superfluidity, and they have been observed and studied in bulk superfluid helium and Bose–Einstein condensates [36,37,38,39]. Up until the first experiment at LCLS, traces of quantum vortices were only inferred from the electron micrographs of cluster deposits from metal-doped helium droplets on thin carbon films [40,41,42,43,44], see also the work by Lackner in Chap. 11 of this volume [45]. In contrast, spectroscopic signatures of quantum vortices in helium droplets are lacking [46, 47]. The first results published from the LCLS experiment have uncovered fresh facets of helium droplets and have reinvigorated research questions that can also be addressed by CDI, such as:
-
1.
How do superfluid helium droplets rotate? What causes the droplet’s shape to distort? Is there a correlation between the size of a droplet and its shape? And how do droplets produced from molecular beams acquire rotation? [35, 48,49,50,51,52]
-
2.
What factors control the formation of dopant nanostructures inside the droplet? Is it possible to control their aggregation? [53,54,55,56,57]
-
3.
What are the structural changes occurring in a pure or doped droplet after it has been subjected to intense light pulse such as near-infrared (NIR) radiation? [58,59,60,61].
The CDI technique is not limited to X-ray FELs. It can also be applied to other light sources producing spatially coherent radiation including visible lasers, intense light pulses in the XUV radiation from FELs, such as FLASH in Germany and the seeded Free Electron Laser Radiation for Multidisciplinary Investigations (FERMI) in Trieste, Italy, and lab-based High Harmonic Generation (HHG) sources, which are becoming widely available in many laboratories [17]. Experiments performed in the XUV regime using either seeded FELs or HHG sources have used wide-angle scattering approach to determine the three-dimensional shape of the helium droplet [49, 50].
In this chapter, we review the current progress of research and discoveries in coherent X-ray and XUV imaging with helium droplets. Since the application of imaging is rather recent in the arsenal of techniques available for helium nanodroplet science, we begin with a short introduction in Sects. 7.2 and 7.3 on single-shot, lensless coherent diffractive imaging; on how the structure of the pure and doped droplets are determined from their corresponding diffraction image; and on the general experimental setup for imaging. In Sect. 7.4, we proceed in discussing the results on the sizes and shapes of helium droplets and what the shapes of the droplets tell us about their state of spin. In Sect. 7.5, we discuss results where numerical reconstructions show the positions of dopant clusters, which in some cases reflect the configuration and distribution of quantum vortices. We also consider the possibility of controlling the growth of dopant nanostructures by using different kinds of dopants, such as xenon, silver, acetonitrile, and iodomethane. In Sect. 7.6, we introduce experimental results on imaging doped helium droplets after excitation with an intense near infrared pulse. Finally, we present a brief outlook on further opportunities for studying helium droplets with CDI in Sect. 7.7.
7.2 Imaging
7.2.1 Lens-Based and Lensless Imaging
Images map the spatial information of the scattered light from an object into an image plane. Figure 7.1 shows sketches of two types of imaging systems with and without the use of lenses. Here, the source of illumination comes from a distant light source and is already considered a plane wave when it reaches the object. Lenses are an integral part in almost all optical imaging systems, such as our eyes, microscopes, and telescopes [62]. In lens-based imaging systems, such as in Fig. 7.1a, the lens collects the scattered light and transforms it into a distribution of intensities representing the object onto an image plane (usually a screen, a photographic plate, or a two-dimensional photosensor) located at some distance behind the lens [62, 63]. Mathematically, lenses can be seen as performing Fourier transforms of the collected scattered light to reproduce the object into the image plane. Based on Abbe’s theory of image formation, the size of the lens defines the acceptance angles in collecting all the scattered light [64]. This limitation, along with lens aberrations, reduces the resolution of the image. In addition, depending on the geometry of the imaging setup, the image usually has a different magnification as that of the original object [62].
While lenses used in optical imaging are well-understood, similar components for X-ray and XUV imaging and X-ray microscopy remain in continuous development along with advances in nanofabrication [9, 10, 65]. The penetration depth of X-rays is large and the refractive index of most materials in the X-ray regime is very close to one. XUV radiation, on the other hand, is strongly absorbed in almost any material, rendering transmission optics almost unfeasible. The design, therefore, of X-ray and XUV optics is markedly different than that used in optical imaging. One of the key developments in X-ray focusing is the Kirkpatrick-Baez (KB) mirrors, which are a pair of ellipsoidal-shaped mirrors placed orthogonal with respect to each other. The incoming radiation is focused to a line by the first mirror, while the second focuses this line to a point [2]. These mirrors take advantage of the strong reflection of X-rays at glancing incidence angles with respect to the curved surface of the KB mirrors. Another kind of optics used with X-rays is the Fresnel zone plates. The current resolution achieved by these plates is limited to a few tens of nanometers [10, 65]. Overviews of X-ray and XUV microscopy methods and applications can be found in a number of reviews [1, 2, 9,10,11, 65].
In the absence of a lens, the type of image formed depends on the distance of the camera sensor with respect to the object [1, 62, 63]. From an optical point of view, an object consists of infinitesimal volume elements, where each element acts as a point source of spherical waves. After illumination, a path length difference develops among these scattered waves as they propagate towards a particular section of the detector. The path length difference is approximately given as \(a^2 \cdot z^{ - 1}\), where \(a\) is the typical object dimension, and \(z\) is the distance between the object and the detector. If the detector is very close to the object, only a projection of the object is created on it; any visible contrast can be accounted from the different absorption properties of the materials that make up the object. This type of imaging is called contact regime and is commonly employed in X-ray radiography. As the detector is brought a bit farther, the effect of the path length difference becomes important. Fringes are observed in addition to the projection of the object on the detector. If the path difference is comparable to the wavelength of light, \(\lambda\), i.e., \(\lambda \approx a^2 \cdot z^{ - 1}\), the imaging is in the near field or Fresnel regime. When the detector is brought even farther, such that the arriving waves at the detector are approximately planar, the imaging is classified as Fraunhofer or far-field regime. In this case, the “image” on the detector no longer bears resemblance to the object. Rather, the image is a diffraction pattern corresponding to the Fourier transform of the density of the object. Positioning the detector even farther from the object does not change the diffraction pattern but only scales the size of it. The categorization of these different regimes is based on the Fresnel number, \(f\), which is given as [1, 17]:
If \(f\gg\) 1, imaging falls under the contact regime; Fresnel diffraction if \(f\approx\) 1; and Fraunhofer diffraction if \(f\ll\) 1. For a droplet with a diameter of 1000 nm, a wavelength of 0.826 nm (1.5 keV), and an object-detector distance of 565 mm, \(f=\) 2.1 × 10–3. With the same droplet diameter but for a wavelength of 72 nm (17 eV), which is within the short wavelength margin produced from an HHG source, and a detector distance of 50 mm, \(f=\) 2.8 × 10–4. Hence, for all intents and the purposes of X-ray and XUV imaging described in this chapter, the measured diffractions are classified under Fraunhofer or far-field diffraction.
In Fig. 7.1b, the diffraction image is registered within the field of view of the sensor. Because of the limited response time of the sensor, only the intensities, i.e., the squares of the scattering amplitudes, are measured, and the phase information of the scattered wave is lost. In order to recover the phase and to completely reconstruct the object from its diffraction image, numerical methods are applied that iterate between the Fourier space and the real space. These numerical methods analogously perform the same role as a lens in lens-based imaging. The resolution of lensless imaging at small scattering angles theoretically depends on the maximum collection angle subtended by the sensor, and by the wavelength of light used for imaging. Simply, the theoretical resolution is defined as [17] (Figs. 7.2 and 7.3):
where \(\lambda\) is the wavelength of light; \(\theta_{\max }\) is the field of view as defined by the distance between the object and the detector, \(z\); and the length along one side of the detector, \(N \cdot \Delta r\), where \(N\) is the number of pixels along one axis and \(\Delta r\) is the size of one pixel, see Fig. 7.4. For imaging with X-rays at 0.826 nm using a 1024 × 1024 pixels detector, where each square pixel has a size of 75 µm, and located 565 mm from the object, \(r_t\approx\) 6 nm. Similarly, the depth of field is given by [17]:
For the same conditions as above, \(r_l\) ≈ 90 nm.
7.2.2 Coherent Light Sources
A light source is considered coherent when there is a perfect correlation between the emanating complex field amplitudes, i.e., if the electric field is known at one point in space then the electric field at another point can be predicted based on their separation in space and time [2, 62, 63]. On the other hand, if a source produces light at various frequencies with no phase relationship whatsoever, then the source is incoherent. An image formed from coherent illumination is a result of the square of the linear superposition of individual exit waves from the different scattering points of the object, whereas an image formed from an incoherent illumination is due to the summation of individual intensities from the scattering points. Further comparisons between coherent and incoherent imaging are given in standard textbooks in Optics, in particular Fourier Optics [62, 63].
Real sources are only partially coherent since they are not perfectly monochromatic and do not propagate in a perfectly defined direction [1, 2]. Nevertheless, a region of coherence can be defined where the electromagnetic waves from a real light source remain in phase. Along the direction of propagation, the length of coherence, \(l_L\), delimits the region from the source until the waves become out of phase. Mathematically, \(l_L\) is defined as:
where, \(\Delta \lambda\) is the spectral bandwidth of a source. The longitudinal coherence length is also known as temporal coherence. Transverse to the direction of propagation, the coherence length or spatial coherence, \(l_T\), indicates the uniformity of the wavefront as it moves from a source and is defined as:
where, \(s_d\) is the typical spot size of a light source. Examples of spatially coherent light sources include optical lasers and FELs. However, incoherent light sources such as many synchrotrons, the sun, or arc lamps can also be made coherent through an introduction of a pinhole in between the object and the light source [2]. The setup of many X-ray imaging experiments done at synchrotrons is often based on spatial filtering using pinholes [9,10,11].
Developments in X-ray and XUV light sources usher new experimental techniques in imaging. These light sources produce coherent, intense, sub-100 fs pulses, which are characteristics conducive for single-shot CDI of nanometer-sized samples in free flight. The list of these new light sources includes: (i) X-rays from self-amplified spontaneous emission (SASE) FELs; and (ii) XUV radiation from SASE and seeded FELs, and lab-based HHG sources. All these new light sources can be used for CDI of large helium nanodroplets.
The concept of X-ray FELs builds on the technology of synchrotrons [1, 2]. Figure 7.2a shows the decade by decade development of X-ray sources from rotating anodes to FELs. Different X-ray sources are characterized by a quantity called brilliance, which is defined as the number of photons a source produces per second, the spectral bandwidth of a source at 0.1%, the focus size of the beam, and the beam divergence in milliradians. FELs deliver X-ray pulses with more than six orders of magnitude peak brilliance than synchrotron sources, such as ESRF (European Synchrotron Radiation Facility) in Grenoble, France, and Spring-8 in Hyogo Prefecture in Japan. The coherent emission of X-rays is driven by the SASE process, where electron bunches from an injector gun are first accelerated through a linear accelerator (linac) hundreds of meters in length. Once the electron bunches travel close to the speed of light, they enter a series of undulators composed of a periodic series of alternating magnetic dipolar fields. As the electrons wiggle in the undulator, they radiate electromagnetic energy. Due to the high quality of the electron bunch or more precisely its small volume and narrow velocity spread, the electrons coactively interact with this emitted radiation, accelerating some of the electrons in the bunch and decelerating some depending on their position with respect to the crest of the electric field of the emitted radiation. This process creates electron microbunches that wiggle concurrently with the radiation and results into the exponential amplification of the radiation intensity within the SASE process. The photon energy produced can be tuned by adjusting the kinetic energy of the electrons and the vertical distance between the two sheets of the undulator, see Refs. [66, 67] for reviews on the physics of X-ray Free-Electron Lasers.
a The X-ray peak brilliance of light sources has improved by 20 orders of magnitude in last sixty years, see text for the definition of brilliance. b Decade by decade improvement in the pulse durations of light sources (Adapted with permission from Ref. [33].
Due to the statistical fluctuations within the microbunches, which basically start from noise, the spectral bandwidth in the SASE process remains rather broad. This effect limits the application of the SASE pulse in studying few-femtosecond and attosecond electron dynamics in many atomic and molecular systems. Control over the spectral bandwidth and phase of FELs can be achieved by seeding the FELs with intense laser pulses or through self-seeding by introducing magnetic chicanes or dispersive elements along the trajectory of the electron bunch. The seed field arrives synchronously with the electron bunch at the beginning of the undulator, and the electric field of the seed laser dictates the microbunching process, significantly reducing the bandwidth of the FEL [68,69,70]. The FERMI FEL is one of these seeded FELs and can produce phase-coherent radiation in the XUV and soft X-ray regimes down to wavelengths as short as 4 nm [71].
FELs are large facilities. Access to these facilities is contingent upon a successful appropriation of a beamtime after an experimental proposal has been peer-reviewed. In short, experiments at FELs are limited by the allocation of available beamtimes. Alternatively, lab-based XUV sources are being developed from the nonlinear generation of high harmonics from an infrared (IR) drive laser, such as a femtosecond Ti:Sapphire laser centered at around 800 nm. Intense XUV pulses can be created via high harmonic generation (HHG) in gas using loose focusing geometries [72]. Atoms of a noble gas are ionized by the electric field of the loosely focused IR laser. The electrons are subsequently accelerated and thrown back onto the parent ion in the slowly changing IR field. This process results in recombination and emission of sub-femtosecond XUV bursts [2, 73, 74]. As the process is repeated twice for each IR cycle, the interaction produces odd harmonics of the driving laser [2, 73, 74]. In order to create high pulse energies, phase matching has to be achieved in a large volume of the focal area and requires optimizing conditions in a multiparameter space of IR intensity, gas pressure, and position relative to the focus [75]. The HHG can produce XUV pulse energies up to a few microjoules with pulse lengths as short as a few hundreds of attoseconds, see Fig. 7.2b. Short pulses open a new pathway for studying electron dynamics, such as electron density motions [76]. In terms of XUV imaging, tabletop HHG sources have been used in ptychographic reconstruction of patterned titanium on a silicon substrate [77, 78], ultrafast charge and spin dynamics in electronics [79], thermal transport in nanoscale systems [80], and wide-angle scattering of superfluid helium droplets [49]. Using HHG pulses for single-pulse, single-particle CDI, especially for dynamics studies, is very promising but still in its infancy.
7.2.3 Coherent Diffractive Imaging
Coherent diffractive imaging (CDI) is a lensless imaging technique where numerical methods are employed to reconstruct the object from its diffraction image, which represents the moduli squared of the complex scattering amplitudes [14, 15]. Details in the diffraction pattern play a crucial role in determining the location, amplitude, and spatial features of the different components in an object. For instance, speckles in a diffraction pattern denote specific spatial frequency that reflects the location or arrangement of substructures in the object. To regain the phase lost during the measuring process, iterative transform algorithms (ITA) are used to iteratively calculate Fourier transforms between the Fourier space and real space with the application of constraints in each space [15, 33, 81, 82]. These constraints are applied in order to minimize the error between the measured diffraction image from the calculated one.
Phasing algorithms usually do not converge to a unique solution due to ambiguities from unknown overall object boundary (“support”), signal noise, and missing data due to detector limitations. ITAs such as error-reduction (ER) [19] and hybrid input–output (HIO) [20, 21] were developed to bridge between the experimental data and the mathematical paradigm of oversampling theorem [21, 22]. The scattering phases can be retrieved from oversampling the recorded diffraction images, i.e., the volume of the object has to be smaller than the coherent volume of the light beam [81, 82]. Oversampling is essential in the convergence of ITAs. The phase retrieval is usually guided by self-consistency arguments, such as a good agreement between the Fourier transformation of the obtained densities and the measured diffraction amplitudes, along with the application of various physical constraints to minimize the sampled phase space and to prevent the algorithms from trapping in a local minimum that normally results into centro-symmetric image reconstructions. Trapping is often associated with the incorrect determination of the object boundary, which in some cases is unknown a priori. One pathway, called the “shrink-wrap” technique, progressively determines the object's support during reconstruction iterations [83]. The calculated object density or the output of a phasing algorithm is always represented by an average of hundreds of independent reconstruction runs in which each run consists of thousands of iterations [84,85,86]. Such a procedure is computationally expensive and incompatible with real-time data analysis [87]. The common practice of performing large numbers of reconstruction runs, where “acceptable” runs are averaged and “failed” runs are discarded, may also contribute to reconstruction ambiguity and reduce the image resolution defined by the wavelength of light and the geometry of the imaging setup, see Eq. (7.2). In Sect. 7.3.3, we discuss how helium droplets with embedded nanostructures promote the convergence of an iterative transform algorithm, since the overall object dimension, associated with the size and shape of the droplet, is easily determined from the diffraction pattern [53].
Although ITAs determine the missing phase information through iterative computation, another approach closely related to CDI is to encode phase information directly into the diffraction image through holographic imaging technique. Here, a point or an object with known dimensions placed in close proximity to the object of interest serves as a reference scatterer and interferes with the exit waves from the object [88,89,90,91]. Single-shot Fourier transform holography (FTH) has been successfully used in determining the structure of single viruses [91]. While FTH may provide a quick retrieval process, it is yet to be applied with helium droplets.
7.2.4 Small-Angle and Wide-Angle Scattering
Figure 7.3 shows a comparison between small- and wide-angle scattering regimes. Although there is no clear boundary separating them, small-angle scattering is taken to be \(\theta_{\max }<\) 5°, while wide-angle scattering is certainly reached for angles larger than 10°. \(\theta_{\max }\) is determined from the angle subtended by the edge of the detector at a certain distance from the interaction point. In Born's approximation, the scattering amplitude for a certain transferred momentum vector, \(\vec{q}\), can be calculated from the two-dimensional Fourier transform of the projected density onto the plane defined by the normal vector \(\vec{n}_p = 0.5\left( {\vec{k_{in}} + \vec{k_{out}} } \right)\). For small scattering angles, see Fig. 7.3a, the normal \(\vec{n}_p\) vector is, to a good approximation, always parallel to the axis of direction of the main light beam. In this case, the scattering amplitude for all momentum vectors can be calculated in one step as the two-dimensional Fourier transform of the projected density onto the plane defined by \(\vec{k_{\rm{in}}}\). In other words, only information on the two-dimensional projection of the object is contained in the whole diffraction image. One visible signature of small angle scattering is that the diffraction image is point symmetric since the two-dimensional Fourier transform is a point symmetric operation, see Figs. 7.3a and 7.5.
Comparison between a small and b wide-angle scattering for a truncated octahedron (a common shape for silver clusters). The \(\vec{k}_{in}\) and \(\vec{k}_{out}\) are the wave vectors of the incoming and scattered light, respectively. For a certain transferred momentum vector \(\vec{q}\), the diffracted intensity in Born's approximation can be calculated by the Fourier transform of the object's density projected on a plane perpendicular to the sum vector of \(\vec{k}_{in}\) and \(\vec{k}_{out}\)(displayed as blue rectangle). The normal vector of this projection plane is denoted as \(\vec{n}_p\). In a, the transferred momentum vector \(\vec{q}\) is always small compared to incoming and scattered wave vectors and the projection plane is therefore approximately parallel to the detector (represented as a red rectangle). In b, the length of the transferred momentum vector \(\vec{q}\) is comparable to the wave vectors and large scattering angles are reached. Correspondingly, the projection planes are tilted to the detection plane. The diffraction patterns up to the same \(\vec{q}\) vector differ in the outer features (Adapted with permission from Ref. [31], licensed under CC-BY)
One aim of X-ray and XUV imaging, however, is to determine the full three-dimensional structure of an object. In order to realize this goal, imaging techniques were developed in which multiple diffraction images are collected from different orientations of the same object (or its replica), or, similar to tomography, from different cross sections of the object [1, 18]. The application of these two techniques is feasible if the orientation of the object can be controlled, as a common practice in X-ray crystallography, or if the object itself is reproducible. Many objects of interest in the micro- and nanoscales, on the other hand, are non-reproducible, and some only exist transiently. Therefore, only single-shot diffraction images can be collected for these transient objects. Some three-dimensional information can be retrieved when two particles are inside the focal volume of the light beam. This occurrence gives rise to concentric, off-axis diffraction rings [29] or in a holographic manner, the observation of Newton Rings [92]. Additionally, it also remains possible to encode some three-dimensional structural information from a single-shot coherent diffraction image of an isolated nanoparticle by collecting scattering information at wide scattering angles. In this case, different projection planes at large angles away from the main beam axis are recorded on the plane of the detector, see Fig. 7.3b [31, 93, 94].
Wide angle scattering is usually limited to rather long wavelengths in the extreme ultraviolet (XUV) regime, since the scattering intensity decreases dramatically with scattering angle due to Porod’s law, and the scattering angle is proportional to the wavelength [1]. Diffraction images collected at wide angles are no longer necessarily point symmetric, see Figs. 7.3b, 7.8 and 7.9, and are no longer connected to the projected density by a simple two-dimensional Fourier transform. Additionally, these characteristics make data analysis more complicated as compared to those used for small angle scattering, where various phase retrieval methods are already available. In Sect. 7.3.4, we explain how the shape of an object can still be obtained from its wide-angle diffraction image through the forward fitting of a guess shape followed by an adaptive algorithm iteratively adjusting itself until the calculated diffraction pattern agrees well with that of the experimental data [31].
The choice between X-ray or XUV radiations for a particular experiment needs to be carefully adapted to the problem at hand. While scattering cross-sections are typically higher in the XUV regime than in the X-ray region and the wide-angle diffraction connected to XUV can provide three-dimensional information on the shape and orientation of the object being imaged, the non-trivial shape retrieval and the reduced spatial resolution both have to be taken into account as a clear trade-off.
7.3 Coherent Diffractive Imaging with Helium Droplets
7.3.1 Experimental Setup for X-Ray and XUV Imaging
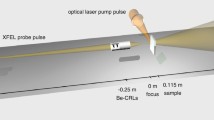
The pioneering X-ray imaging of superfluid helium droplets was performed using the soft X-ray FEL at LCLS [35]. Since then, imaging experiments have been extended in the extreme ultraviolet regime using a seeded FEL [50], a lab-based HHG laser [49], and a multi-colored seeded FEL [95]. A general overview of the experimental setup of X-ray and XUV imaging of helium droplets is given in this section. Figure 7.4 shows an experimental layout for both static and dynamic imaging of pure and doped helium droplets, and Table 7.1 gives a list of contemporary imaging experiments. Images from static imaging are collected with one single pulse of the light beam and represent the instantaneous state of the droplet. These images describe the size and shape of a droplet, and, in the case of small scattering measurements of doped droplets, the different configurations of dopant nanoclusters assembled inside a droplet. On the other hand, the data collected with dynamic imaging represent the state of the droplet after it has been excited usually by an intense near-infrared pulse. These images build a picture on how the excited state of the droplet evolves through time.
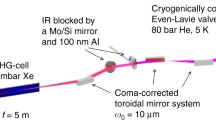
General schematic for imaging experiments. Helium droplets are produced either from a continuous or a pulsed nozzle. Depending on the experiment, the droplet can capture different types of dopants as it travels through the pickup cell. The droplet is imaged at the interaction point and the scattered photons are detected by a photon sensitive detector at some distance away from the interaction point. The droplet and the light beam are perpendicular with respect to each other. Note that the pixel size of the detector is exaggerated (Adapted with permission from Ref. [53], licensed under CC-BY 3.0)
Droplets of various sizes are generated from a nozzle cooled from ~14 to 3.5 K, spanning the gas condensation, liquid fragmentation, and jet disintegration regimes of droplet production [96], see also the work by Toennies in Chap. 1 of this volume [97]. While these helium droplets are created at nozzle temperatures above the superfluid transition, the droplets reach a temperature of ~0.4 K through cooling by evaporation at very short distances from the nozzle [96, 98,99,100,101]. This temperature is below the superfluid transition at 2.17 K. Currently, the types of nozzles used for the imaging experiments include the continuous nozzle based on the Göttingen design [101, 102], Even-Lavie valve [103, 104], and Parker valve [105,106,107]. The continuous source employs a pinhole nozzle with a nominal diameter of 5 µm, commonly used as an aperture for electron microscopes. The Even-Lavie valve is a commercially available cryogenic pulsed nozzle and is usually shipped with a trumpet-shaped nozzle having a throat diameter of 100 µm and an opening half-angle of 20°. The Parker valve is also commercially available; although, the nozzle plate can easily be replaced, for example, by a conical nozzle with a waist-diameter of 150–200 microns and an opening angle of 3–4°. The design of these conical nozzles are optimized for the generation of different types of large rare-gas clusters, which are samples used for studying the interaction between intense X-ray/XUV pulses and clusters [108]. Each nozzle is operated at different nozzle temperatures and stagnation pressures to produce droplet sizes at least on the order of ~100 nm in radius.
Helium droplets are known to capture different kinds of dopants [96, 109, 110]. These dopants may be introduced through a pick-up cell for gas and liquid samples, or through a ceramic oven for solid samples. The current list of dopants that have been used in imaging experiments includes xenon, silver, acetonitrile, and iodomethane. How these different dopant materials are assembled in the droplet can contribute to further understanding the mechanisms involved in the assembly of nanomaterials inside a superfluid droplet, see Sect. 7.5.
At the interaction point, the droplets, either pure or doped, meet the X-ray or the XUV pulse for single-shot imaging. For time-resolved dynamics imaging experiments, the pump laser arrives at the interaction point before or after the X-ray or XUV pulse. The scattered photons are collected either by a pnCCD (positive–negative charged-coupled device) sensor or a triumvirate of a microchannel plate, a phosphor screen, and a commercial camera. The pnCCD detector is a large area detector consisting of about one million pixels, where each pixel is sensitive to single photon and can detect linearly as many as a few hundred photons [111,112,113]. This detector consists of the two half plates (512 × 1024 pixels) above and below the main axis of the FEL beam. In addition, the position of the detector with respect to the interaction point may be varied, which would change the maximum half scattering angles the detector could collect, from ~4 to 50° [111, 113]. In some instruments, two pairs of detectors are used with one being much closer to the interaction region than the other [111]. This configuration allows the simultaneous recording of scattering images at wide-angles and small-angles. The operation of the pnCCD detector is, however, rather complicated and expensive, requiring its own vacuum chamber and cooling system. A more affordable detector is a microchannel plate in tandem with a phosphor screen [29, 108]. The detected photons are converted to electrons and amplified by the microchannel plate, which consists of a two-dimensional array of microchannels acting as electron multipliers. These electrons then hit the phosphor screen. In this setup, a hole is introduced in the detector assembly since the intensity of the undeflected portion of the light beam is enough to damage it [29, 108]. Furthermore, a mirror, also with a hole, is placed at ~45° with respect to the plane of the phosphor screen and redirects the diffraction image on the phosphor screen to a camera sensor located outside vacuum [29, 108]. Unlike the pnCCD detector, however, the microchannel plate triumvirate does not give a linear response of the detected photons. As a consequence, the diffraction image cannot be easily processed with iterative transform algorithms for numerical image reconstructions. Further discussion on the treatment of data with the microchannel plate detector is presented in Sect. 7.3.4.
One important experimental parameter in performing imaging experiments is the hit rate, \(HR\). Although the true hit rate is only known a posteriori of an experiment, it is possible to estimate the hit rate a priori. Two common definitions of hit rate in single-shot imaging are: (i) the number of images collected at a certain amount of time, with units in hits per hour; and (ii) the total number of images with respect to the total number of laser pulses at a given time. The latter definition is normally expressed in percentage. The hit rate indicates the probability of detecting a droplet in the focal volume of the laser pulse, \(V_{{\text{focal}}}\), which is a function of the spot size of the FEL and its Rayleigh length [101]. From the first definition:
in which the first factor gives the average number density of the helium droplets in the focal volume, \(F_D\) is the flux of helium droplets, \(v_D\) is the droplet velocity, \(d_{nozzle - IP}\) is the distance between the nozzle and the interaction point, and \(R{}_{rr}\) is the repetition rate of the light source. The second definition is similar to the definition of a duty factor and is based on the number of images collected as a function of the number of pulses from the light source:
where \(t_{acq}\) is the total time duration of measurement, and the factor 100 is for conversion to percentage.
The hit rate is affected by the overlap between the droplet beam and the laser beam, and the droplet density at the interaction point. Due to the stochastic nature of the SASE process and high harmonic generation, pulse intensities can vary from shot to shot, consequently varying the total number of detected photons from droplets of the same size. In addition, the X-ray or the XUV beam presumably has a Gaussian profile. The position of the droplet with respect to the beam axis will vary the intensity distribution in the diffraction image, i.e., with all things being the same, a droplet at the center of the Gaussian beam is expected to give a more intense diffraction image than those droplets imaged at the periphery of the light beam.
7.3.2 Diffraction Imaging of Helium Nanodroplets
The interaction between radiation and matter is important to image formation, and the optical response of matter strongly depends on the wavelength of light [1, 2, 114]. Changing the wavelength also changes the number of scattered or absorbed photons, assuming of course the intensity of light remains the same. In addition, for an object consisting of different materials, such as a doped helium droplet, variations in the refractive index or densities give contrast to imaging due to photoabsorption, which can induce structural damage and can contribute in reducing imaging resolution. Photoabsorption processes further lead to a cascade of ionization processes, including emission of photoelectrons, Auger electrons, and fluorescence [1, 2, 114,115,116]. Similarly, for helium droplets, the fraction of absorbed photons induces structural changes due to photoionization, where some of the photoionized electrons will escape and lead to charging of the droplet. The electrons that remained trapped in the Coulomb potential of a multiply-ionized droplet will further cause secondary ionization of the helium atoms that may result into the complete ionization of all the atoms in the droplet, creating a droplet nanoplasma. However, the details of these processes remain to be elucidated [117,118,119,120,121,122,123,124,125,126,127,128]. Experimentally, the disintegration of the droplet manifests itself through bursts of Hen+ ions, which can be detected with a time-of-flight mass spectrometer. Some of the dynamics induced by the photoabsorption of intense infrared radiation can be studied with CDI, see Sect. 7.6. Although, photoabsorption causes structural changes in the droplet, the pulse length of X-ray and XUV light sources, on the order of a few hundreds of femtoseconds, is considered fast enough to capture the instantaneous state of the droplet before the onset of structural changes [14, 129, 130]. Imaging with the use of ultrashort light pulses is referred to as diffraction before destruction in single particle imaging. It must be noted, however, that electronic changes arising from photoionization and plasma formation in large xenon clusters occur on a sub-femtosecond time scale and may drastically influence the diffraction response [131, 132]. An example of accounting for the number of scattered and absorbed X-ray photons for a pure helium droplet is described in Ref. [101]. The power radiated by the free and bound electrons experiencing acceleration due to an incident electromagnetic field redirects radiation in a wide range of angles [2]. Due to both scattering and absorption, the intensity of the incident radiation is attenuated in the forward direction. The number of scattered and absorbed photons from an object can then be accounted from the scattering and absorption cross-sections of the elements constituting the object and the incident photon flux.
The collective interaction of X-ray or XUV with condensed matter can be described by the refractive index, \(n\). In the X-ray regime, \(n\) differs only by a small amount from unity [2, 133]. In the XUV region, many materials, including helium, exhibit strong electronic resonances that correspond to large deviations from unity. The refractive index is commonly written as:
in which \(\delta\) and \(\beta\) account for the phase variation and absorption of propagating waves, respectively. The term \(r_e=\) 2.82 × 10–6 nm is the classical electron radius, and \(f_1^0 \left( \lambda \right)\) and \(f_2^0 \left( \lambda \right)\) are the atomic scattering factors of an element. For helium at \(\lambda =\) 0.826 nm (\(hv=\) 1.5 keV), \(f_{1,He}^0 \left( \lambda \right)=\) 2.0 and \(f_{2,He}^0 \left( \lambda \right)=\) 2.4 × 10–3 [133]. For XUV, \(\delta\) and \(\beta\) can be obtained from Ref. [134]. Equation (7.8) has both refractive and absorptive components. The real part of the refractive index describes how the phase velocity of the X-ray/XUV wavefront changes due to the oscillations of the free and bound electrons; whereas the imaginary part corresponds to the amount of light absorbed during propagation. For a pure spheroidal droplet, these effects produce a diffraction pattern consisting of concentric rings. For a doped droplet, the dopants have different refractive indices and contribute to a phase shift with respect to that of helium. In coherent diffractive imaging, the exit waves from the helium and from the dopants interfere and thus modify the concentric ring patterns produced by a pure droplet alone. Figure 7.5 shows examples of diffraction patterns obtained from a pure spheroidal droplet and from a doped droplet [35, 53]. The detector is placed 565 mm from the interaction point and the wavelength of light used for imaging is ~0.826 nm. In the diffraction from a doped droplet, concentric rings are observed close to the center of the diffraction and specular patterns far from the center. These specular patterns correspond to the structure of the dopants inside the helium droplet. The dopant structures are naturally smaller than that of the droplet. A reconstruction algorithm in solving the structures of dopant clusters inside a helium droplet is presented in Sect. 7.3.3.
Using the droplet’s diffraction pattern at small scattering angles, one can quickly estimate the droplet radius at a particular azimuthal angle, \(\vartheta\), on the plane of the detector by determining the distance between the maxima of the rings, \(\Delta N\):
For example, \(\Delta N\) for the rings in the diffraction images shown in Fig. 7.5 is about 20 pixels for both the pure and doped droplets. Substituting this number in Eq. (7.9) and with \(\Delta r=\) 75 µm give a droplet radius of about 300 nm or about 2.5 × 109 helium atoms. For the diffraction images from doped droplets, the distance between the maxima of the concentric rings gives the size of the droplet after it has been doped. If the number and identity of the dopants are known, one can also estimate the initial size of the droplet before doping [101].

© copyright <American Association for the Advancement of Science> All rights reserved.), and from b a xenon-doped droplet (adapted with permission from Ref. [53], licensed under CC-BY 3.0) at small angle scattering. Only the central section of the diffraction is shown here
Examples of diffraction images obtained from a a pure droplet (adapted with permission from Ref. [35].
Following a more rigorous analysis from a collection of diffraction images of pure and doped droplets, it is also possible to determine droplet size distribution, which is historically presented in numbers of atoms per droplet. For superfluid helium-4 droplets produced using 5 μm pinhole nozzle at a stagnation pressure of 20 bars and nozzle temperature of 5 K, which fall under the liquid fragmentation regime of droplet production, both pure and doped droplets follow an exponential size distribution with its steepness increasing as more dopants are added [57]. Droplets produced using an Even-Lavie pulsed nozzle at a stagnation pressure of 80 bars and a nozzle temperature of 5.4 K also follow an exponential size distribution with an average droplet size of 6 × 109 or a radius of 400 nm [50]. These results agree with earlier measurements that determined an exponential size distribution for droplets produced from liquid fragmentation [96, 97, 135]. Similarly, helium-3 droplets, which remain as classical viscous droplets under experimental conditions, produced using a 5 μm nozzle at a stagnation pressure of 20 bars and at nozzle temperatures less than 5 K are likewise found to follow an exponential size distribution [52].
7.3.3 Dopant Clusters Image Reconstruction
There are two main interests in the static coherent diffractive imaging with helium droplets; the overall shape of the droplet, which indicates the rotational state of the droplet, and the assembly of dopant nanostructures inside the droplet, such as the dopant aggregation along the length of a vortex. In Sect. 7.2.4, we mention that methods are available to determine the two-dimensional or three-dimensional shape of the droplet, depending on whether diffraction was recorded at small or wide scattering angles. For the second interest, iterative numerical methods have to be utilized in order to reconstruct these nanostructures from the diffraction images of doped droplets. At the moment, these numerical methods are only applied at small scattering angles, where the idea that the diffraction image is simply the Fourier transform of the object density, including the nanostructures inside the droplet, holds. Hence, this section is only concerned with data from small-angle scattering. One critical prerequisite for the convergence of iterative numerical methods to a meaningful solution is the determination of the overall extent or dimension of the object being imaged. In the jargon of iterative transform algorithms, the overall dimension of the object is called the support, which could be the full dimension of a nanocrystal, a complex biological protein, a mimivirus, or a helium droplet. In many instances, the support is unknown a priori due to varying sizes and shapes of the object being imaged. An incorrect determination of the support leads to incorrect numerical reconstructions. Many techniques have been developed that address the determination of the support, such as a technique called “shrinkwrap” algorithm [82, 83]. Additionally, support determination methods usually require ingenious integration of another set of algorithms that runs simultaneously with the iterative transform algorithms [83, 136,137,138].
The support in X-ray imaging of nanostructures in a helium droplet, on the other hand, is already defined by the dimensions of the droplet, which may also be taken as a reference scatterer aiding the convergence of an algorithm that solve for the missing phase information. Diffraction patterns from pure droplets have concentric circular or elliptical patterns ascribed to spherical or oblate pseudo-spheroidal droplet shapes, respectively, see Figs. 7.5 and 7.11 [35, 48]. The details of the droplet size and shape determination from the diffraction scattering patterns are described elsewhere [35, 48]. In addition to defining the support, the helium droplets also serve as vehicles to deliver and localize the dopant cluster structures in the laser focus. This technique of using the helium droplet as a support is referred to as droplet coherent diffractive imaging (DCDI). The primary goal of which is on the retrieval of the location and shapes of these dopant nanostructures from diffraction images of doped droplets.
The DCDI algorithm is based on the well-known error-reduction (ER) algorithm [21]. Figure 7.6 shows a flow diagram of the DCDI algorithm and the description follows from Ref. [53]. The algorithm is initiated by using the droplet density determined from the concentric ring patterns close to the center of the diffraction. After Fourier transform of this droplet density, the modulus of the scattering amplitude at each pixel is replaced by the square root of the measured intensity, \(I_{Meas}\), whereas the initial phase, \(\phi\), is retained. The intermediate scattering amplitude is called \(G^{\prime}\). The inverse Fourier transform of \(G^{\prime}\) gives an approximate solution, \(\rho^{\prime}\). However, as can be seen in Fig. 7.5, some of the intensity information are missing due to the central detector hole, the gap between the detector plates, and some arrays of damaged pixels. In this case, the algorithm sets some constraints in the real space, such that the missing pieces of information are ignored and that the approximate solution should not exceed the boundary defined by the droplet. This adjusted \(\rho^{\prime}\) then serves as a new input density, \(\rho\), for the DCDI algorithm. In comparison to other methods, which require thousands of iterations and multiple initial guess inputs, DCDI converges to a meaningful solution within less than 100 iterations, as demonstrated in Fig. 7.7. Intermediate solutions at different stages of iterations are also shown. Aside from image reconstructions, results from DCDI algorithm can also be used to determine numerical values pertaining to the number of dopants in the droplet and the initial size of the droplet [53].
Schematic of droplet coherent diffractive imaging (DCDI). The algorithm is initiated using a preset helium droplet density, \(\rho_{input}\). The series of Fourier and inverse Fourier transforms between the object- and reciprocal-space with iterative reinforcement of constraints in both spaces rapidly converge to yield the density of xenon clusters inside the droplet (Adapted with permission from Ref. [53], licensed under CC-BY 3.0)
DCDI convergence and evolution of densities and phases within a 100-iteration run. The plot shows the rapid decrease in the reconstruction error as a function of the number of iterations. The middle row shows the calculated density modulus in a linear intensity scale. The black circles represent the droplet boundary enclosing the clusters. The bottom row corresponds to complex density phases at the same iteration as the droplets above it. Initially, DCDI finds a center-symmetric cluster configuration, but as the number of iterations increases, the enantiomer having positive imaginary density becomes dominant (Adapted with permission from Ref. [53], licensed under CC-BY 3.0)
7.3.4 Forward Simulation and Machine Learning
While X-ray small-angle scattering images can be analysed using iterative transform algorithms, the analysis of wide-angle diffraction images is made more complicated by the large index of refraction, both real and imaginary parts, at longer XUV wavelengths, where photoabsorption and phase shift along the direction of light beam propagation cannot be neglected. This phase shift also depends on the scattering angle, often exceeding several tens of degrees in wide-angle scattering, and can impede in the determination of the object structure. Even though obtaining structural information from wide-angle scattering images is nontrivial, these images can still be simulated using ideas developed in tomography in which full three-dimensional structure of an object, such as bones or internal organs, is reconstructed by combining different two-dimensional X-ray image projections of this object [139].
Currently, no rigorous algorithm is known that efficiently determines the object’s structure form its wide-angle diffraction without prior information [140]. This problem has so far been approached via forward fitting methods, which simulate the diffraction image from a well-defined model shape [30, 31, 49, 50, 94, 141]. The simulated diffraction is then compared with that of the experimental, and shape parameters are refined to optimize the match between the diffraction images. Suitable pre-defined model shapes are chosen based on some known physical properties of the object being imaged, from general considerations on observed symmetries in individual diffraction patterns, or from the whole variety of observed patterns in the complete data set. In addition, the size, orientation, and other parameters of the model shape, such as eccentricity of an ellipsoid, are parametrized and used for fitting the simulation to the measured pattern. On the other end, the choice of the simulation method must (i) correctly reproduce the wide-angle features, (ii) account for (at least approximately) the optical properties of the particle, and (iii) be fast enough for a reasonable computational time in fitting many patterns. One simulation method for retrieving the object’s structure from wide-angle scattering image is called the multi-slice Fourier transfom (MSFT), which has been previously applied in Refs. [31, 49, 50, 141, 142]. MSFT was originally developed for electron diffraction [143] and has been previously applied to soft X-ray diffraction of supported particles [139]. Figure 7.8 shows a schematic of the MSFT approach. Here, the object is first divided into a stack of two-dimensional slices, whose normal vectors are oriented parallel to the incident photon beam, see Fig. 7.8b. Diffraction fields are then calculated from each slice, which corresponds to a two-dimensional distribution of refractive indices, see Fig. 7.8c. The final scattering intensity corresponds to the modulus square of the phase-corrected sum of the two-dimensional Fourier transforms from these different slices, see Fig. 7.8d. A fast implementation of the MSFT simulation code can be found in Ref. [141]. Material properties are approximately accounted by reducing the scattering amplitude as a function of propagation through the material according to Beer–Lambert’s law. Multiple scattering events due to the rescattering of light inside the sample cannot be accounted correctly within the MSFT method. These events, however, only become significant when the real part of the index of refraction is exceptionally large. For the analysis of helium nanodroplets using near resonant wavelengths, an approximation for the phase slip was also included in the MSFT simulations by considering an effective complex refractive index [50]. For the case of silver clusters imaged with non-resonant XUV wavelengths, the MSFT approach without an effective phase slip was benchmarked against full finite difference time domain (FDTD) simulations using tabulated optical constants, and a reasonable agreement between these two methods was obtained [31]. Although there are differences between the results of the MSFT and FDTD simulations, these differences are subtle.
Schematic representation of the multi-slice Fourier transform (MSFT) approach: a three-dimensional rendering of the sample; b visualization of the spatial domain slicing following the multi-slice approach; c amplitudes of the fields scattered from each slice in b; and d square of the phase-corrected sum of all the wavefield amplitudes in c, which represents the final output of the simulation (This figure is a courtesy to the authors by Alessandro Colombo)
XUV wide-angle diffraction imaging has the advantage of clearly distinguishing between shapes with similar two-dimensional projections. Therefore, experiments in the wide-angle regime substantially contribute to the discussion of rotation and shapes of helium droplets [49, 50]. As visualized in Fig. 7.9, wide-angle diffraction patterns from a pill-shaped droplet and a wheel-shaped droplet differ in a characteristic way. The scattering patterns for wheel and pill shaped droplet calculated with MSFT are displayed for different orientations to the incoming XUV pulse [144]. Since both shapes may result in an identical outline and a very similar two-dimensional projection, they are difficult to distinguish in the small-angle scattering regime. In contrast, there are noticeable deviations from the point symmetry of a diffraction image collected at wide scattering angles, especially those obtained for a tilted pill-shaped droplet. If the oblate particle’s symmetry axis is neither oriented along the optical axis nor perpendicular to it, the diffraction patterns exhibit straight streaks to only one side. At 90° tilt angle between the symmetry axis and the optical axis or when one of the particle’s symmetry axes is aligned along the optical axis, the two-dimensional projections are similar. However, the intensity distributions are clearly different and decay much faster for wheel-type than for pill-type shapes, compare Fig. 7.9a, b.

Modified from Ref. [144], licensed under CC-BY 4.0)
Scattering patterns calculated with MSFT for different rotation angles and droplet shapes: a pill-shaped, b wheel-shaped. The long axis is set to 950 nm, the short to 300 nm. The pill-shaped droplet is rotated around the y-axis, while the wheel-shaped droplet around the x-axis. In these simulations, the light beam propagates towards the image plane in a and out of the image plane in b (
So far, forward fitting has only been applicable to small data sets with rather simple model shapes. However, huge data sets up to several million scattering patterns can be acquired in single-shot diffraction imaging during a single beamtime, emphasizing the need for rigorous and rapid reconstruction methods on data collected from both wide- and small-angle scattering regimes. Developments in X-ray and XUV light sources are proceeding toward high repetition rates as well. For instance, the European XFEL can run up to 4.5 MHz [145]; within an hour, it is possible to collect ~1.6 × 1010 diffraction images [146,147,148]. This situation is rather similar to other fields of big data science, such as in particle physics, where powerful analytical methods and algorithms are needed to extract significant information [140, 146,147,148,149,150]. Machine learning and neural networks are some contemporary approaches in managing these huge data. Some tools are available in structural biology [151,152,153], whereas the adaption of neural networks to coherent diffraction imaging of individual nanoparticles is still incipient [50, 142].
Being trained on a large augmented data set of simulated scattering patterns, neural networks can be of great help in extracting structural information and can especially account for image artefacts, such as noise, center hole, and the limited size of the detector [140]. In a recent wide-angle study on helium droplet shapes [50, 142], a supervised approach was used to exclude the existence of patterns from wheel-shaped droplet images, see Fig. 7.9b, from a large data set, see Sect. 7.4.1. In general, deep neural networks consist of many hierarchically structured nonlinear functions, referred to as layers of the neural network, which enable the network to learn intricate structures in the very high dimensional input space [154]. Having many layers between input and output levels, deep neural networks are well suited for extracting structural parameters as this procedure is equivalent to retrieving a small number of parameters from high-dimensional spaces [154]. A convolutional neural network is trained (supervised training) starting with a few thousand scattering patterns classified manually into a number of different classes [142]. The manual classification is a tedious process and could take weeks to sort through thousands of diffraction images. After training, a much larger data set can subsequently be analysed by the network and the scattering patterns are classified according to the learned classes, see Fig. 7.10. To optimize the classification accuracy of a given convolutional neural network, a priori knowledge about diffraction images can be used. For example, a logarithmically scaling activation function was introduced that boosted classification accuracy by about 2–4% as it accounts for the exponentially decaying intensity observed in diffraction images [142]. The network finally provides as output the classification of the scattering patterns independent of particle/droplet size, e.g., it gives statistics on how many spherical, oblate, prolate droplets are present in a droplet beam [142]. These results provide a first step towards using deep learning techniques for a direct and fast determination of the object’s shape from a diffraction pattern. Another key goal would be a routine from the unsupervised learning [155] paradigm for online analysis during an experiment, where manual pre-classification is no longer needed to sort through a large dataset.
Schematic diagram of a convolutional neural network. First, sets of representative diffraction patterns are manually categorized. These patterns are then used as inputs to train the program. After which, the code runs through all the collected hits and sorts them into the manually classified categories. Finally, statistics from the automatically sorted files are produced, such as size and shape distributions, and possible three-dimensional reconstructions (Reused with permission from Ref. [142], licensed under CC-BY 4.0)
7.4 Imaging Pure Helium Droplets
An isolated liquid droplet in equilibrium and held together by surface tension forces will adapt a spherical shape to minimize its surface area [156,157,158,159,160]. Once the droplet starts to rotate, its shape gets deformed, and capillary waves may be created on its surface [161]. For axisymmetric droplets, the shape deformation is given by their aspect ratio, \(AR\), which is defined as the ratio between the droplet’s half major and half minor axes. A spherical droplet has an \(AR\) = 1. The droplet becomes more oblate spheroidal as the droplet spins faster, or as the value of \(AR\) increases from one [156,157,158,159,160]. Studies on the shapes and stabilities of liquid droplets have a long history, where a liquid drop serves as a model system in various length scales, from the shapes of self-gravitating astronomical and cosmological bodies, the fission of atomic nuclei, and the shapes of spinning uniformly-charged bodies [156,157,158,159,160,161,162,163,164]. The coupling between surface oscillations and rotation has also been considered in studying the stability of spinning droplets [165, 166].
Classical droplets are viscous, and their shape deformation may be described from the equilibrium shapes of rotating rigid bodies. In a rigid body rotation (RBR), its azimuthal speed, \(\upsilon_{RBR}\), is a function of its angular velocity and the distance \(r\) from the axis of rotation, while its vorticity, \(\nabla \times \vec{\upsilon }\), where \(\vec{\upsilon }\) is the velocity vector, is twice the angular velocity. In contrast, the viscosity of superfluid helium is negligible and superfluid flow is irrotational, i.e., \(\nabla \times \vec{\upsilon }=\) 0 [38, 167]. In a closed two-dimensional path of arbitrary shape in the superfluid, however, a phase defect may be present in order for the superfluid’s wavefunction to be the same at the beginning and end of the closed path [168]. This also implies that the circulation around the closed path must either be zero or a multiple of the quantum of circulation, \(\kappa = {h / {m_{He} }}=\) 9.97 × 10–8 m2 s−1, where \(h\) is the Planck’s constant, and \(m_{He}\) is the mass of the helium atom. The phase defect is known as a quantum vortex and the fluid’s azimuthal speed, \(\upsilon_{vort}\), around the vortex is given by [38, 168]:
where \(q\) is a whole number multiplying the quantum of circulation, and \(r\) is centred on the vortex core. Each of these vortices has a quantized circulation, hence the name. For superfluids at high angular momentum, it is energetically favourable to evenly distribute the angular momentum to many vortices than to a single vortex possessing all of the angular momentum [168]. The rotation of superfluid helium droplets depends on the presence of quantum vortices, in addition to surface shape oscillations [51, 169,170,171]. A collection of these vortices significantly contributes to the total angular momentum of the droplet [51, 171]. Early studies of magnetically levitated, charged, millimeter-sized superfluid helium droplets are interested in the decay of surface oscillations and the possible nucleation of quantum vortices [172,173,174,175,176]. In this section, we discuss the shapes and sizes of helium droplets in the size range of 107 up to 1012 atoms, which are currently the size range of what can be measured with CDI, and how the shape of superfluid droplets is related to the droplet stability curve, which was derived from studies of classical viscous droplets.
7.4.1 Shapes of Pure Helium Droplets
Imaging the sizes and shapes of individual nanometer-sized superfluid helium droplets has only recently become possible with CDI. As discussed in Sect. 7.4.2, the diffraction images can be used to determine the state of rotation of the droplet. Figure 7.11 shows some characteristic single-shot diffraction images of helium droplets produced from a 5 µm pinhole orifice at a stagnation pressure of 20 bars and a nozzle temperature of around 5 K [35, 48]. These images were obtained at small scattering angles, where only the two-dimensional projection of the object is recorded onto the detector plane, and only the half-major axis and an upper bound of the half-minor axis of the droplet could be obtained from the image. Moreover, small angle diffraction cannot distinguish between a prolate and an oblate spheroidal droplet since both will generally result into similar patterns in the diffraction image, see Sect. 7.3.4. For small scattering angles, a handy equation in quickly determining the radius of the droplet at a particular azimuthal angle based on the distances between the maxima of the concentric rings in the diffraction image is given in Eq. (7.9). For a long time, helium droplets were thought to be spherical and not rotating [96]. The diffraction images in Fig. 7.11 show droplets with increasing \(AR\), from about 1–2. These images revealed that the droplets are spinning tremendously fast as indicated by large shape deformations in the diffraction patterns. It was initially proposed that rotating helium droplets remain axially symmetric [35]. As will be shown later, further studies reveal that at high angular momentum the superfluid droplet may adapt a two-lobed shape [48,49,50], similar to what was observed in classical droplets [159, 160].
Diffraction images from helium droplets obtained at small scattering angles using soft X-ray FEL. The logarithmic intensity color scale reflects the number of photons per pixel and is shown on the right. Images a–c exemplify patterns corresponding to spheroidal droplets, whereas images d–f show streaks, which are features indicating high deformity of droplet shape (Modified with permission from Ref. [48].
Figure 7.12 shows diffraction images of droplets, with an average droplet radius of ~400 nm, obtained from wide scattering angles, at most 30°, in the XUV regime at 19–24 eV [50]. The figure also shows the corresponding three-dimensional models of the droplets along with calculated diffraction images. In this experiment, the droplets were produced at ~5.4 K and 80 bars with a trumpet shaped nozzle, where a large dataset with a total of 38,500 bright scattering patterns was recorded at FERMI FEL. The vast majority (92.9%) of the bright scattering images exhibit concentric rings, see Fig. 7.12a, while the remaining images show various pronounced deformations of the rings. Some collected diffraction images at wide scattering angles, see Fig. 7.12b–e, show deviation from point symmetry, which is key to determining three-dimensional structure, see Sect. 7.3.4. Based on characteristic features in the diffraction image, five shape groups were identified. The respective relative abundance for each group was estimated using a neural network for automated image reconstruction [50, 142]. These groups are: (i) spherical (concentric circles, 92.9%), (ii) spheroidal (elliptical patterns or one-sided asymmetry, 5.6%), (iii) ellipsoidal (bent patterns, 0.8%), (iv) pill-shaped (streaked patterns, 0.6%), and (v) dumbbell-shaped (streaks with side maxima or pronounced side minima, less than 0.1%).
Diffraction images from helium droplets obtained at wide scattering angles using XUV as the light source. Panels a–e show the experimental data and show implied evolution of spinning helium droplets. Panels f–j show simulated three-dimensional droplet sizes and shapes. Panels k–o show respective calculated diffraction images for the droplets in f–j. The data have been classified into five groups (I)–(V), with a transition from f spherical to g oblate and h–j prolate shapes (Reused with permission from Ref. [50], licensed under CC-BY 4.0)
In addition to using an XUV FEL, wide-angle scattering has also been demonstrated using a lab-based HHG laser [49], transfering a very powerful imaging technique from large X-ray facilities to laboratories at research institutes and universities. Moreover, HHG sources can also be very intense and have the potential in producing very short XUV pulses up to the attosecond pulse duration [73, 74]. Figure 7.13a shows a scattering image obtained using a HHG laser consisting of the 11th until the 17th odd harmonics of the 792 nm IR seed laser. Figure 7.13 also shows simulations (panels b–c), which aid in the unique identification of the droplet shape. The optical axis of the extreme ultraviolet beam is directed into the image plane, while the tilt angle between the symmetry axis of the droplet and the optical axis is ~35°. From the simulations, the diffraction image is from a pill-shaped droplet with semi-minor radii of \(b=c=370\) nm and a semi-major radius of \(a\) = 950 nm. Figure 7.13c illustrates the origin of bent streaks occurring when a tilted pill-shaped structure diffracts the light. The constructive interference is analogous to the specular reflection at the surface of a macroscopic pill. Two bundles of constructively interfering rays are explicitly sketched. Note that the different ray colours in the figure do not refer to wavelengths but are applied to facilitate distinction in the specular reflection. Despite having a blurred pattern, due to multiple HHG harmonics involved in imaging, and weaker scattering intensity as compared to images obtained using FELs, the droplet shape is still successfully retrieved from the HHG diffraction data.
Scattering pattern obtained from a HHG laser and simulations of the scattering pattern. a Measured image and b matching simulation result. The droplet shape and orientation are visualized in yellow. c Illustration of the origin of bent streaks occurring when a tilted pill-shaped structure diffracts light (Adapted with permission from Ref. [49], licensed under CC-BY)
7.4.2 Droplet Stability Curve
The shape of a droplet undergoing rigid body rotation is maintained by the balance between surface tension and centrifugal forces [158]. For classical viscous droplets, dimensionless parameters are introduced in order to facilitate comparison between different experiments and theories for droplets of different sizes and composition. The red curve in Fig. 7.14a shows the evolution of droplet shapes as given by the classical droplet stability curve, which is described in terms of reduced angular momentum, \(\Lambda\), and reduced angular velocity, \(\Omega\) [156, 158, 159]:

© copyright <American Physical Society> All rights reserved.). b Ratios of the principal semiaxis lengths, a, b, and c, and V the volume of the droplet. The dashed line is from the analytical model of Chandrasekhar [156]. The squares are from numerical models for classical droplet shapes [163]. The triangles are data obtained from wide-angle scattering imaging of helium droplets using an XUV light source (Reused with permission from Ref. [50], licensed under CC-BY 4.0)
a Stability diagram for rotating droplets in equilibrium as a function of the reduced angular velocity, \(\Omega\), and the reduced angular momentum, \(\Lambda\), see Eqs. (7.11) and (7.12). The upper branch of the solid red line corresponds to oblate axisymmetric shapes, whereas the lower branch to prolate two-lobed shapes. The bifurcation point is located at \(\Lambda =\) 1.2, \(\Omega =\) 0.56 with \(AR =\) 1.48. As for rigid bodies, they will show no distortions and would follow a straight line. The dashed red lines indicate the unstable portion of the droplet stability curve (Adapted with permission from Ref. [48].
where \(L\) and \(\omega\) are the angular momentum and angular velocity of the droplet, respectively. The surface tension of the liquid droplet is given by \(\sigma\), the density by \(\rho\), and its droplet radius by \(R_D\). Droplets with different sizes but with the same values of \(\Lambda\) and \(\Omega\) belong to the same class of droplet shapes, which evolve from being spherical to oblate axisymmetric when the value of \(\Lambda\) is increased from zero [156, 158, 159]. The curve starts to bifurcate at \(\Lambda=\) 1.2 and \(\Omega=\) 0.56. The upper branch, \(\Omega>\) 0.56, adapts a toroidal shape and is unstable to quadrupolar shape deformations, while the lower branch, 1.2 \(< \Lambda <\) 1.5, is stable and represents prolate triaxial droplets. At \(\Lambda \approx\) 1.5, the droplet starts to be highly deformed, first by forming a two-lobed droplet at \(\Lambda >\) 1.5, before undergoing fission at \(\Lambda \approx\) 2. Figure 7.14a also shows sketches of the droplet shapes at different parts of the stability curve. The solid red lines indicate the stable evolution of droplet shapes, from spherical to oblate spheroidal until it transforms into prolate triaxial. The dashed lines represent the unstable portion of the droplet stability curve.
For stable structures, \(\Lambda\) and \(\Omega\) exhibit a clear relation to the principal axes of the droplets, \(a\), \(b\), and \(c\). The droplet radii at each of the principal axes are experimentally measurable quantities and represent the distances from the droplet’s center of mass to the droplet’s surface along each respective principal axes. Following convention, \(a\) and \(c\) are taken as the largest and smallest radii, respectively. For oblate droplets, \(a = b \ne c\), while for prolate triaxial droplets, \(a \ne b \ne c\). In small-angle scattering measurements, one of the principal axes in axisymmetric droplets is assumed to be the same as that of the major half-axis. On the other hand, wide-angle scattering measurements allow the determination of all these principal axes. Figure 7.14b shows the plot of \({{b^3 } / V}\), where \(V\) is the volume of the droplet, versus the aspect ratio \({a / c}\). At \(AR=\) 1, \({{b^3 } / V} = {{R_D } / V} = {3 / {4\pi \approx }}\) 0.24. The open square symbols in Fig. 7.14b were derived from classical models of rotating drops [163].
What is surprising with the results shown in Fig. 7.14 is that the evolution of shapes for large, oblate-spheroidal, superfluid helium nanodroplets seems to follow a similar behaviour as that of spinning classical viscous liquid drops. The diagram in Fig. 7.14b is another dimensionless representation of droplets that is used in classifying the shapes of spinning droplets. The numerical model, represented as purple squares, shows how the shape of classical spinning droplets evolves from axisymmetric oblate spheroid, \({a / c} <\) 1.5, to triaxial prolate shapes, \({a / c} >\) 1.5. The red triangles represent the different shape classes of superfluid helium droplets determined from diffraction images collected at wide scattering angles [50]. Aside from the points around \({a / c} =\) 1.5, there seems to be a good agreement between the different shape classes of superfluid helium droplets with that of the classical droplets.
Quantum fluids, such as Bose–Einstein condensates and superfluid helium, are inviscid due to their negligible viscosity [38, 168]. The fluid is constrained to rotate with a quantized circulation around topological point defects, which are manifested as quantum vortices and store the most amount of the fluid’s angular momentum [38, 168]. Due to the presence of a vortex array, a meniscus is formed in a rotating superfluid cylinder that would have otherwise been absent without the vortices [177]. It can be said that in the limit of multiple vortices, superfluids behave like classical viscous liquids [168, 177]. Other elementary excitations, such as phonons, rotons, and ripplons can also store angular momentum [47, 101]. However, due to the low temperature of the droplet at 0.4 K, the contribution of these excitations is negligible [39, 47]. A large, axisymmetric nanodroplet containing a large number of vortices, which arrange in a triangular lattice, rotates similarly to a classical droplet due to the velocity flow fields produced by each vortex [51, 169, 171, 178]. On the other hand, the shape of small helium droplets, \(N_{He} <\) 20,000, containing a few number of vortices deviate from the classical behaviour, as determined from density functional theory (DFT) calculations [171, 179, 180]. Capillary waves on the surface of the droplets also contribute to the angular momentum of the droplet, however, their contribution only becomes important for prolate-shaped droplets [50, 51, 171, 181]. Finally, the rather strong agreement between the different kinds of drops with theoretical models suggest a unified theory of the dynamics of fluid masses [161]. However, a caveat must be kept in mind that the rotational behavior of superfluid helium droplets is generally contingent upon the size of the droplet and the number of vortices in it [182].
7.4.3 Non-superfluid Helium Droplets
The results shown in earlier sections have demonstrated that superfluid helium-4 droplets produced from free jet expansion conditions are spinning considerably fast, as manifested by the shape distortion of these droplets. The droplet’s shape distortion is ascribed to the presence of quantum vortices, which account for most of the angular momentum of the droplet [171]. The nucleation of these vortices, however, remains unknown and requires further experimental studies. One hypothesis speculates that the interaction of the droplets at the dense region around the proximity of the nozzle exit significantly contributes to the rotational state of superfluid helium-4 droplets, and thus nucleates the vortices in the droplet [40, 48]. To test this hypothesis, Ref. [52] produced non-superfluid helium-3 droplets using the same experimental setup as that used for the production of helium-4 droplets. The first creation of a beam of helium-3 droplets was done in late 1970’s in Karlsruhe, Germany [183, 184]. Helium-3 is chemically equivalent to helium-4, and the strength of the van der Waals bonding is virtually identical. However, the smaller mass of helium-3 means that its zero-point energy is greater than that of helium-4 [185]. Therefore, in order to achieve the same average size as that of the helium-4 droplets, lower nozzle temperature is needed. While pairs of helium-3 atoms also undergo superfluid transition at a very low temperature of ~2.7 mK [185, 186], in molecular beam apparatus, helium-3 only cools down to ~0.15 K and, thus, remains non-superfluid [98]. It is interesting to note that seven different kinds of quantum vortices are determined in bulk superfluid helium-3 [187].
Figure 7.15 shows diffraction images of non-superfluid helium-3 droplets collected at small-angle scattering and demonstrates that the shapes of helium-3 droplets mostly correspond to oblate spheroids falling within the classical droplet stability curve shown in Fig. 7.14 [52]. Furthermore, these results agree with the shapes of superfluid helium-4 droplets, which were also produced and imaged under similar experimental conditions, i.e., same 5 µm diameter pinhole nozzle was used and the droplets were produced within the liquid fragmentation regime. Both isotopes were found to have the same average reduced angular velocities, \(\Omega\), and reduced angular momenta, \(\Lambda\), quantities which describe the rotational state of a droplet. One particular importance of this experiment is that it corroborates that similar mechanisms are involved in the shape distortion of the droplets, and that the origin of the droplet’s vorticity may be due very well to the interaction of the droplets with the walls of the nozzle orifice and with each other close to the region of the nozzle exit [52]. It is also possible that quantized vortices are nucleated during the merging and coagulation of smaller droplet into bigger droplets [181, 188]. DFT calculations in a semi-classical approach for a \(N_{He3} =\) 1500 droplet also found that the shapes of spinning helium-3 droplets agree with that of classical droplets, although, the derived stability curve for helium-3 droplets has a slight deviation [189].
X-ray coherent diffractive imaging of pure 3He droplets at different rotational states. Only the central section of the diffraction is shown here (Adapted with permission from Ref. [52].
7.5 Imaging Dopant Cluster Structures in a Superfluid Helium Droplet
The unusual properties of superfluid helium droplets make them conducive media for investigating the formation and growth of out-of-equilibrium nanostructures in self-contained and isolated droplets, see also Chap. 11 in this volume [45, 55, 190]. This viability is due to the droplets’ superfluidity, their very cold ambient temperatures of ~0.4 K, and the possibility to control the size and composition of embedded dopants [96, 109]. Dopants are captured by the droplets within pickup cells positioned along the droplets’ flight path, see Fig. 7.4. Once a dopant is captured, it quickly thermalizes to the droplet temperature and is decelerated until it moves inside without friction [109]. When several dopants are successively captured, they coalesce stochastically with the influence of long-range van der Waals interaction allowing the dopants to form far-from-equilibrium nanostructures [190]. While some dopant materials may form compact clusters at one or several sites in the droplets [191], some polar molecules can arrange in long linear chains [192]. Other studies have shown a core–shell structure of a multicomponent doped droplet [193,194,195] or indicated to the formation of foam structures [196, 197]. Superfluid droplets are also used as a weakly interacting matrix for the study and control of orientation and alignment of embedded molecules [198,199,200]. Up to now, almost all of these very special structures could only be inferred from spectroscopic measurements on ensembles of many different droplet sizes. In the presence of quantum vortices, these vortices dominate structure formation processes [40,41,42,43, 53, 54, 178]. Imaging these nanostructures in situ can give us unprecedented insights into the processes underlying their formation.
7.5.1 Vortex Structures in Superfluid Helium Droplets
Probably, the most peculiar and clear manifestation of superfluidity is with the presence of quantum vortices in the droplet [39, 46, 170, 178, 201]. Traces of these vortices were first discovered from silver-doped helium droplets deposited on a carbon film for Transmission Electron Microscopy (TEM) imaging [40,41,42,43]. Silver atoms are attracted to the cores of the vortices. Some examples of these silver nanostructures are shown in Fig. 7.16. Further experiments showed that the traces of the vortex line remain observable even though room temperature induces structural changes in the deposits on the carbon film [43]. While the deposition and TEM imaging gave an idea on the traces of vortices inside the droplet, this type of ex situ imaging technique didn’t provide enough information on the native configuration of the vortices in the droplet. Gessner and Vilesov [178] wrote a recent review on imaging quantum vortices in superfluid helium droplets.

(Adapted from Ref. [40]. © copyright <American Physical Society> All rights reserved.) b Typical silver traces obtained in 1000 nm helium droplets (from Ref. [40]. © copyright <American Physical Society> All rights reserved.). The inset shows an enlarged track segment. c Structure evolution of a silver nanowire at increasing carbon film temperature at 253 and 293 K (from Ref. [43], licensed under CC-BY 3.0)
Traces of quantum vortices in superfluid helium nanodroplets. Panel a shows the schematic of the experiment. The droplet is first doped with silver atoms before being deposited on a carbon film for TEM imaging. The droplet evaporated as it collides with the carbon film
In X-ray imaging experiments, the droplet needs to be doped first in order to visualize the in situ structures and positions of quantum vortices in the droplet, since bare quantum vortices have a diameter of roughly 2 Å [38] and have no noticeable contribution to the diffraction intensity. The dopants serve as contrast agents for imaging. The DCDI algorithm described in Sect. 7.3.3 solves for the positions and morphologies of the dopant structures inside the droplet, while the size and shape of the droplets can be determined from known analytical equations of light scattering by small particles [35, 202]. Almost all of the static images of doped helium droplets have so far used xenon as the dopant, partly due to its ease of handling. In Sect. 7.5.3, diffraction images of doped droplets from different dopant materials are presented.
Figure 7.17 shows how xenon clusters are arrange symmetrically in small droplets, <200 nm in diameter. Foreign particles approaching a quantized vortex core are attracted to it due to the pressure gradient experienced by the particles [38, 203]. The arrangement of these xenon clusters reflects the positions and configurations of quantum vortices in the droplet. However, compared to the symmetric positions of vortices observed in the bulk [36], or to the positions of bare vortices calculated for a nanocylinder [204] and nanodroplet [180], the positions of the xenon-traced vortices are farther away from the center of the droplet [54, 205]. This deviation can be accounted from the conservation of angular momentum. When the vortex core is filled with a dopant, the dopant rotates with the vortex core, which contributes to the total angular momentum. As a consequence, the angular momentum of the vortex must decrease resulting into the vortex slowing down and moving farther away from the center [54, 180, 205, 206]. The obtained symmetric positions of the vortices is in agreement with that expected for vortices having the same strength and with the same value as that of the quantum of circulation, \(\kappa\). The kinematics of dopant positions is studied in Ref. [205].
Symmetric vortex structures for droplets with radius from 80 to ~100 nm. The upper row shows single-shot diffraction images of xenon-doped droplets. The bottom row shows corresponding DCDI reconstructions, where the black circle represents the shape and boundary of the droplet. The diffraction images only show the central part of the pnCCD detector (Adapted with permission from Ref. [54].
In larger droplets, >200 nm in diameter, with moderate number of dopant atoms, >106, the configurations of the vortices also appear symmetric. However, one starts to see that the shape of the xenon-traced vortex filaments is not straight but wavy, see Fig. 7.18. In this category, the shapes of the vortex cores are given by the shape of the filaments due to particle trapping of the xenon atoms along the length of the vortex core. Aside from the undulations along a vortex length, vortices far from the center of the droplet are also curved, which is expected from calculations [47, 170, 180]. In Fig. 7.18, the appearance of vortex filaments indicate that the droplets are imaged with their rotational axis almost perpendicular to the propagation direction of the X-ray beam. It is energetically favourable to have the vortices aligned parallel to the rotational axis [38, 207]. Therefore, if the droplet is spheroidal, 1 \(< AR <\) 1.5, the vortices are aligned parallel to the semi-minor axis of the droplet. Vortices along the major axis are not favourable. Similar observations of vortices aligning parallel to the axis of rotation have been noted in rotating Bose–Einstein condensates [201, 208,209,210]. On the other hand, if droplets are imaged with their rotational axis parallel to the direction of the X-ray beam propagation, then the filaments would appear as dots and would have a triangular lattice, as seen in Fig. 7.17 [54]. For example, the droplet in the first column of Fig. 7.18 is consistent with an approximately hexagonal pattern of C-shaped filaments imaged at some angle with respect to the symmetry axis [53]. The vortices in the droplets are expected to be curved as they must terminate perpendicular to the surface [47, 170, 206]. In addition, the vortices in Fig. 7.18 are still well-separated from the other vortices in the droplet.
Xenon-traced quantum vortices for larger droplets, >200 nm in diameter. The upper row shows single-shot diffraction images of xenon-doped droplets. The bottom row shows corresponding DCDI reconstructions, where the black circle represents the shape and boundary of the droplet. The diffraction images only show the central part of the pnCCD detector (Adapted with permission from Ref. [53], licensed under CC-BY 3.0)
The waviness of the dopant-traced vortex filaments is a tell-tale sign of the dynamics involved as the dopant particles are trapped by the vortex lines, see Fig. 7.18. After being captured by the droplet, the dopant would walk randomly as it thermalizes. The droplet’s surface acts as some sort of a net that prevents dopant particles from escaping. The droplet surface also bounces the dopant until it finds its most stable position [179, 206]. The process of penetration and translation of dopant particles in the droplet creates surface excitations. This process is also enough to create undulations along the vortex line as simulated using semi-classical matter wave theory [211] and DFT [206]. Distortions along a vortex line are classically known as Kelvin waves [38]. The dynamical picture is, of course, more complicated. In a superfluid helium droplet, the vortex lines are anchored perpendicular to the surface of the droplet [47, 170]. When a dopant particle, such as xenon and argon, approaches the vortex core, it is not captured right away. Instead, as demonstrated by the DFT numerical simulations, a dopant particle first orbits around the vortex core before being captured [206]. The dopant particle penetration and its orbiting motion would twist the vortex core. Upon vortex capture, the particle can cause bends and kinks along the vortex lines, which further create Kelvin waves [203, 212, 213]. The descriptions above are for a particle approaching a vortex core. Furthermore, since equilibrium positions of vortices can be determined from the reconstructed images, one can also infer the coupling between the dopant atoms and the vortices, i.e., from the images one can make a conjecture on the dynamics inside the superfluid, such as excitation of waves along the length of the vortex as the dopant approaches it. Further studies are of course needed to understand the undulations along the vortex filaments in the presence of multiple dopants and multiple vortices in a droplet [205].
7.5.2 Vortex Lattices and Angular Momentum Determination
Diffraction patterns obtained from very large droplets with droplet radius ranging from 500 to 1000 nm often contain a series of high intensity spots far from the center of the diffraction. These bright spots are known in X-ray crystallography as Bragg spots and indicate a crystal lattice structure in the object being imaged. For the xenon-doped droplets, the Bragg spots originate from the interference caused by the xenon-traced vortex lattice. Figure 7.19 gives some examples of diffraction images containing Bragg spots that either lie on a line crossing the image center, see Fig. 7.19a, or form an equilateral triangular pattern, see Fig. 7.19b. The diffraction pattern in Fig. 7.19b provides a direct measure of the vortex density, \(n_V =\) 4.5 × 1013 m−2 [35]. The angular velocity of a rotating droplet can be calculated using [38, 214]:
Diffraction images showing vortex lattice in the droplet. The red circles indicate the positions of the Bragg peaks (Reused with permission from Ref. [35].
where, \(\kappa = {h / {m_{He} }}\) is again the quantum of circulation. For the droplet considered in Fig. 7.19b, \(\omega =\) 2.2 \(\times\) 106 s−1, and for a droplet radius of \(R_D =\) 1100 nm, the total number of vortices is 170 [35].
Vortex configurations inside the droplet also give access to the rotational state of the droplet since both the structures of the vortices and the droplet shapes are imaged at the same time. From the positions of the vortices, one can estimate the angular velocity of the droplet due to the presence of quantum vortices using Eq. (7.13), while the droplet shape gives an overall account of the droplet’s angular momentum. From these pieces of information, one can determine the total angular momentum state of the droplet and how they are distributed between different global excitations in the droplet, such as shape oscillations due to capillary surfaces waves and quantum vortices [51]. Figure 7.20 shows the evolution of vortex arrangements with changing droplet shapes. In axisymmetric, oblate superfluid droplets, the quantum vortices are arranged in a triangular lattice and solely contribute to the angular momentum of the droplet [51]. On the other hand, quantum vortices and capillary waves both contribute to the angular momentum of the droplet, especially for triaxial droplets [51, 171, 182].
Diffraction patterns from xenon-doped droplets with various droplet shapes. Upper row, left to right: axisymmetric, near spherical droplet shape; triaxial pseudo ellipsoidal; and capsule shaped. The lower row shows the numerically reconstructed droplets using the DCDI algorithm. The diffraction images only show the central part of the pnCCD detector (Adapted with permission from Ref. [51].
7.5.3 Controlling Structures Formed in Helium Droplets
Droplets with quantum vortices are usually produced from the fragmentation of liquid helium close to the nozzle exit [178]. It is conjectured that vortices are nucleated due to the interaction of the droplets with each other and with the walls of the nozzle [40, 48, 52]. When dopants are introduced, the presence of these vortices dominate structure formation, and, consequently, the shapes of the dopants resemble that of a vortex core/line or a vortex lattice. One approach in reducing this type of vorticity acquisition is to produce large nanodroplets from the condensation of cold helium gas with the use of a conical nozzle. The design of conical nozzles promotes the condensation process and thus creates large clusters/droplets from the gas phase [215]. For a fixed stagnation pressure and nozzle temperature, the size of the cluster is increased by changing the effective diameter of the nozzle, \(d_{eff}\), which can be estimated using [215]:
The variables \(d_{throat}\) and \(\varphi\) correspond to the throat diameter and the opening half-angle of the nozzle, respectively. In a recent experiment at the European XFEL, helium nanodroplets were produced using a conical nozzle with \(d_{throat} =\) 150 µm, \(\varphi =\) 3°, and \(d_{eff} \approx\) 2 mm [55]. This configuration allows the generation of helium nanodroplets, >100 nm in diameter, from the gas phase. The increase in \(d_{eff}\) also leads to an increase in the mass flow from the nozzle, and similarly the gas load on vacuum pumps. In order to avoid using large pumps, pulsed valves are employed.
Almost all diffraction images from pure droplets produced using a conical nozzle [55] exhibit the same concentric ring pattern as that shown in Fig. 7.5a. This observation indicates that an overwhelming majority of the droplets is spherical in shape. In contrast, some of the droplets produced at the liquid fragmentation regime from previous experiments at LCLS in the USA [35, 48], at FERMI FEL in Italy [50], and a HHG laser [49] showed extreme shape distortions, e.g. pill shapes or dumbbell shapes [178]. Theoretical work supports the idea that the shape of these distorted droplets is controlled by the presence of quantum vortices [171, 180].
In the absence of vortices, it may be possible to control the formation of dopant nanostructures by using different kinds of dopant materials. Figure 7.21 shows diffraction images for differently doped droplets: xenon, silver, acetonitrile, and iodomethane. The intermolecular interactions of these dopants include van der Waals, metallic, and dipole–dipole. The observed diffraction patterns show distinct features that were not previously observed, see Sect. 7.5.1. The diffraction images collected from atomic clusters suggest the presence of one to two cluster cores in the droplet, while that from molecular clusters suggest a complicated network of dopant clusters [55]. These results, however, are preliminary, further studies are needed in order to fully explore and understand factors influencing dopant nanostructure formation inside superfluid helium droplet using coherent diffractive imaging. Another possible means of investigating the formation of nanostructures inside a quantum fluid is through the use of non-superfluid helium-3 droplets, where xenon clusters were found to aggregation along the equatorial plane of the droplet [56].
Examples of diffraction images from superfluid helium droplets containing different dopant materials. These images also demonstrate the possibility of CDI for superfluid helium droplet containing different dopant materials, opening opportunities for studying nanostructure formation inside the droplet (Modified with permission from Ref. [55])
7.6 Imaging Dynamical Processes in Helium Droplets
In an era of powerful lasers with intensities exceeding 1012 W cm−2, the electric field strength of these lasers can become comparable to the Coulombic-binding fields in matter [216]. Atoms and molecules no longer simply absorb single or multiple photons [114, 217]. Instead, at these high-power densities, nonlinear ionization processes may occur. Moreover, molecules may start to get aligned along the direction of the laser polarization, and structural deformations can happen in addition to Coulomb explosion. At even higher intensities, plasmas may form that could lead to X-ray emission by relaxation of high-energy electrons in the system [114, 217]. In many studies, the energy and momentum distributions of ions and electrons upon strong-field ionization are detected using time-of-flight spectrometers or with velocity map imaging. These data are used to deduce the underlying dynamics in the system. On the other hand, with the development of ultra-bright and coherent light sources, these dynamical processes may also be directly imaged on the system. In clusters, structural changes are determined from the series of diffraction images at different delays after the introduction of an intense near-infrared pulse on the system [108, 218, 219]. One particularly intriguing result is the discovery that in a xenon cluster the surface first becomes less dense while keeping the core of the cluster relatively intact. In time, the blurred surface expands while the core shrinks [108, 218, 219]. Similarly, microscopic particle-in-cell or Mic-PIC calculations predict surface softening process for a 50 nm diameter hydrogen nanoplasma [220]. This result goes against earlier ideas that the cluster uniformly expands after excitation [221, 222]. The intensity of the FEL pulses needed for imaging clusters or droplets is so very high that fast ionization and, eventually, complete cluster destruction take place. In most cases, however, scattering images are collected before these events happen.
The CDI setup for investigating the mechanisms following strong field excitation is similar to that shown schematically in Fig. 7.4. The NIR pulse excites the droplet and initiates dynamical processes, while the X-ray or XUV pulse images the state of the droplet at a particular time delay after excitation. The NIR pulse is naturally synchronized at the same focal volume as that of the imaging pulse. Additionally, time-of-flight spectrometers for ions and electrons are placed perpendicular to the direction of both the light beam and the droplet beam. The combination of CDI with electrons/ions distribution measurements can address key questions such as: (i) how samples get damaged after interacting with the intense laser pulse; (ii) to what extent do samples get damaged; and (iii) how an excited system dissipates its available energy. Since most light sources now have pulse durations of a few femtoseconds, it is also possible to image these processes at their natural timescales [108, 114, 116]. It can be said that new XUV and X-ray light sources offer many exciting opportunities in imaging processes occurring in intense-light matter interaction, including helium nanodroplets.
At low laser intensities, liquid helium is transparent from far-infrared to vacuum ultraviolet radiation because of the large ionization potential of helium at ~25 eV or ~50 nm [96, 223]. This property quickened high resolution spectroscopy of many atoms and molecules inside a superfluid helium droplet [96, 224]. Theoretical studies, however, have predicted that ionization can be induced in a pure droplet with intense NIR pulses (800 nm, ~1017 W/cm2) [120] or with a moderately intense NIR pulse (800 nm, ~1014 W/cm2) if the droplets are doped [117]. Experimental studies for these ionization processes have so far been inferred from the energy and momentum distributions of ejected electrons and ions with time-of-flight spectrometers or with velocity map imaging [122, 124].
The first dynamics CDI was performed on pure, sub-micron sized, helium droplets [59]. The authors of this experiment reported an anisotropic surface softening on the droplet, in addition to a similar anisotropic shrinking of the plasma core [59]. The process of charging and ion ejection has similarly been studied by recording X-ray images at different time delays after excitation of pure helium droplets with an NIR pulse [61]. In the case of helium nanodroplets doped with rare gas atoms, such as xenon, which has a lower ionization potential than helium, irradiation with a moderate NIR laser pulse was theoretically predicted to lead to the formation of a nanoplasma around the dopant cluster core, as shown in Fig. 7.22a [117]. The dopants provide seed electrons, which in turn will ionize the helium environment in an avalanche-like process [225, 226]. Hence, the dynamics following irradiation with the intense light field might be linked to the position of the dopants in a droplet. For example, the distribution of the He2+ ions indicates whether the dopant is located at the surface, just below the surface, or very close to the center of the droplet [122].

© copyright <American Physical Society> All rights reserved.) b Wide-angle diffraction pattern of a xenon doped droplet recorded 20 ps after NIR irradiation. (Adapted with permission from Ref. [60], licensed under CC-BY 4.0) c Small-angle diffraction pattern and corresponding reconstruction of a xenon doped droplet revealing the vortex structure. (Adapted with permission from Ref. [54]. © copyright <American Physical Society> All rights reserved.) The similarity of the diffraction patterns in b and c points at a connection between the dynamics and the dopant cluster positions
Nanoplasma dynamics in xenon doped helium nanodroplets and connection to vortex array. a Theory predicts that after irradiation with an NIR pulse a nanoplasma forms around the dopant cluster core. (Adapted with permission from Ref. [117].
In an experiment at the FERMI FEL, the light-induced dynamics in xenon doped helium nanodroplets were studied [60]. The doped droplet is first irradiated with a moderately intense NIR pulse (785 nm, ~8 × 1013 W/cm2) followed by an XUV pulse that can be delayed up to 800 ps. The diffraction images were recorded at wide scattering angles up to ~30° and exhibit different features as compared to the ones obtained from static diffraction images [60]. For example, a scattering image taken 20 ps after irradiation with the NIR pulse is shown in Fig. 7.22b. The pattern exhibits intensity maxima in a hexagonal configuration, indicating some kind of density fluctuation at multiple sites in the droplet with an intriguingly symmetric arrangement. In comparison, Fig. 7.22c shows a similar diffraction pattern from a xenon-doped droplet taken with a single X-ray pulse from LCLS and its corresponding DCDI reconstruction, which reveals a hexagonal pattern of xenon clusters [54]. Since the dopant atoms are attracted to the cores of the vortices, the hexagonal pattern is attributed to the vortex structure in the droplet, see also Sect. 7.5.1. However, the underlying processes leading to the observed diffraction patterns in Fig. 7.22b, c are completely different, as the XUV wavelength is not sensitive on the xenon filaments themselves. Changes in the diffraction pattern of xenon doped helium nanodroplets are only visible picoseconds after NIR irradiation. While data analysis is still ongoing, the similarity of the experimental patterns in Fig. 7.22b, c suggests that light-induced dynamics is connected to the position of the dopants in a superfluid helium droplet. The ignition of a nanoplasma at multiple sites and the nature of the dynamics in the droplet should be addressed in future studies.
7.7 Summary and Outlook
Recent developments of new light sources, such as X-ray and XUV Free-Electron Lasers and intense High Harmonic Generation sources, are enabling technologies that push the boundaries in studying the structure of matter to unprecedented resolution. These light sources are very intense and have pulse durations on the order of a few tens of femtoseconds down to the attosecond regime. These extraordinary characteristics are paving avenues to new experimental possibilities, such as single-shot imaging of non-periodic and transient systems, and new investigations on how matter interacts with intense light pulses on the timescale of electronic motions.
This chapter reviews developments in single-shot imaging of helium nanodroplets. In Sect. 7.2, the topic of lensless coherent diffractive imaging with the use of these new light sources is introduced. Scattering data are collected at small and wide angles. For small-angle scattering with X-rays, high spatial resolution can be achieved, although, only the two-dimensional density projection of the object is accessible. In contrast, wide-angle scattering with XUV wavelengths can provide three-dimensional information of the object but with reduced resolution. Both scattering techniques are complementary, and the choice on which technique to use depends on the goal of an experiment. In Sect. 7.3, the response of helium droplets with X-ray and XUV radiation is discussed, as well as strategies for solving the structures inside the droplet, and on how to simulate the wide-angle diffraction image of a three-dimensional droplet. In addition, since single-particle imaging can potentially collect millions of images in an hour, schemes for machine learning supported analysis that may handle huge amount of data during the experiment were also presented.
As for the experimental results presented in Sects. 7.4, 7.5 and 7.6, there are two types of studies that have been performed so far, static imaging and dynamic imaging. In the former, images of droplets are collected where the main research interests lie in determining the shapes of helium droplets and the structures of dopant clusters assembled inside them. The results from these experiments are rather surprising. For instance, the presence of multiple quantized vortices in superfluid helium-4 nanodroplets made them behave like classical droplets and generally follow the same droplet stability curve for classical droplets. In addition, two main types of droplets were identified, oblate spheroidal, which is axisymmetric, and prolate triaxial. The native configurations of xenon-traced vortices in the droplet were also seen for the first time. The arrangements of these vortices were even used in identifying factors that contribute to the angular momentum of the droplet. In dynamic imaging, the interest is on the behaviour of the helium droplets after they have been irradiated with an intense near-infrared pulse. For doped droplets, the diffraction images seem to suggest that the location of the dopants determine where the growth of nanoplasma is initiated in the droplet.
Our understanding of the many peculiar facets of helium nanodroplets has been advanced through new possibilities connected to imaging individual droplets with high spatio-temporal resolution. As is often the case with new fields of research, further questions are asked as new discoveries are made. One aspect that needs to be explored is the controlled rotation of the droplet. The experiments that have been done so far used a molecular beam apparatus with no control on the rotation of the droplet. In fact, the collection of highly deformed droplets is fortuitous. A more controlled evolution of the droplet rotation may help in exploring how its shape evolves as it spins faster and faster. This kind of experiment would also visualize the formation of a pill-shaped helium droplet and what conditions would favour its formation. Such controlled experiments would clearly define the rotational state of the droplet, along with the effect of capillary waves on the droplet shape. In addition, one might also be able to determine the nucleation of quantum vortices in the droplet. Another aspect that can be explored is with the production of helium droplets from the fragmentation of a liquid jet [227,228,229, 231]. Droplets produced this way have a narrow size distribution, and the droplet size can be controlled by changing the size of the nozzle diameter. The generation of droplets on demand, with known size and repetition, will aid in synchronizing the imaging pulse with the arrival of the droplet at the interaction point, creating the possibility of having 100% hit rate. Similarly, delivery of biological samples at the focus of a light source is continuously being developed in order to maximize the use of every single pulse [230, 232].
We also foresee a demand for further innovations in imaging the dopant nanostructures inside the droplet. For instance, X-ray imaging may be similarly extended to particle tracking methods commonly used in fluid mechanics experiments, where the trajectory of a particle can be traced in the droplet. Of course, this idea is still fraught with difficulties considering structural damages that may be incurred by the droplet and the dopant particles from photoabsorption. The possibility of X-ray particle tracking can help in visualizing how a dopant particle gets trapped by the vortex, how multiple dopants are distributed in a droplet containing many vortices, how the particle induces undulations along the vortex line, and how vortices connect and reconnect. The last two topics are related to quantum turbulence [233,234,235]. Another possible development is with three-dimensional imaging of the clusters inside the droplet. So far, only two-dimensional projections of xenon-traced vortices are reported.
One key technical challenge, which is now a limiting factor in CDI experiments and will become even more serious with the development of high repetition rate FELs, is connected to data management and processing. The strong need for fast and robust computational tools may be answered partially by the ongoing employment and adaption of machine learning techniques into the toolboxes of CDI. Finally, dynamic studies are currently receiving a strong push by the latest advances of FEL and HHG sources towards producing high intensity attosecond pulses. Thanks to its simple electronic structure, helium is an ideal model system for exploring ultrafast electron dynamics.
Single-shot coherent diffractive imaging is inaugurating new avenues of research in superfluid helium droplet science. The first experimental results were published in 2014, and many more experiments are being carried out by a growing number of research groups in pace with increasing availability of X-ray and XUV lasers around the world. At the time of this writing, there are roughly 13 experimental publications [35, 48,49,50,51,52,53,54,55,56,57, 59, 61], two reviews [101, 178], and more under way. We expect fruitful investigations and exciting discoveries using CDI technique in the years to come.
References
J. Als-Nielsen, D. McMorrow, Elements of modern X-ray physics, 2nd edn. (John Wiley & Sons, Ltd., West Sussex, United Kingdom, 2011)
D. Attwood, A.E. Sakdinawat, X-rays and extreme ultraviolet radiation: Principles and applications (Cambridge University Press, Cambridge United Kingdom, 2017)
C. Bostedt, S. Boutet, D.M. Fritz, Z.R. Huang, H.J. Lee, H.T. Lemke, A. Robert, W.F. Schlotter, J.J. Turner, G.J. Williams, Linac coherent light source: The first five years. Rev. Mod. Phys. 88(1), 015007 (2016)
J.A. van Bokhoven, C. Lamberti, X-ray absorption and X-ray emission spectroscopy: Theory and applications (Wiley, United Kingdom, 2016)
L. Young, K. Ueda, M. Gühr, P.H. Bucksbaum, M. Simon, S. Mukamel, N. Rohringer, K.C. Prince, C. Masciovecchio, M. Meyer, A. Rudenko, D. Rolles, C. Bostedt, M. Fuchs, D.A. Reis, R. Santra, H. Kapteyn, M. Murnane, H. Ibrahim, F. Légaré, M. Vrakking, M. Isinger, D. Kroon, M. Gisselbrecht, A. L’Huillier, H.J. Wörner, S.R. Leone, Roadmap of ultrafast X-ray atomic and molecular physics. J. Phys. B Atomic Mol. Opt. Phys. 51(3), 032003 (2018)
H.H. Seliger, Wilhelm Conrad Röntgen and the glimmer of light. Phys. Today 48(11), 25–31 (1995)
J.C. Cole, S. Wiggin, F. Stanzione, New insights and innovation from a million crystal structures in the Cambridge structural database. Struc. Dyn. 6(5), 054301 (2019)
J. Zhang, Y. He, L. Lei, Y. Yao, S. Bradford, W. Kong, Electron diffraction of molecules and clusters in superfluid helium droplets, in Molecules in helium nanodroplets, ed. by A. Slenczka, J.P. Toennies (Springer, Berlin, 2021)
J. Kirz, C. Jacobsen, M. Howells, Soft-X-ray microscopes and their biological applications. Q. Rev. Biophys. 28(1), 33–130 (1995)
A. Sakdinawat, D. Attwood, Nanoscale X-ray imaging. Nat. Photonics 4(12), 840–848 (2010)
R. Falcone, C. Jacobsen, J. Kirz, S. Marchesini, D. Shapiro, J. Spence, New directions in X-ray microscopy. Contemp. Phys. 52(4), 293–318 (2011)
W.L. Chao, B.D. Harteneck, J.A. Liddle, E.H. Anderson, D.T. Attwood, Soft X-ray microscopy at a spatial resolution better than 15 nm. Nature 435(7046), 1210–1213 (2005)
T. Salditt, M. Osterhoff, X-ray focusing and optics, in Nanoscale photonic imaging. ed. by T. Salditt, A. Egner, D.R. Luke (Springer International Publishing, Cham, 2020), pp. 71–124
S. Marchesini, H.N. Chapman, S.P. Hau-Riege, R.A. London, A. Szöke, H. He, M.R. Howells, H. Padmore, R. Rosen, J.C.H. Spence, U. Weierstall, Coherent X-ray diffractive imaging: Applications and limitations. Opt. Express 11(19), 2344–2353 (2003)
H.N. Chapman, K.A. Nugent, Coherent lensless X-ray imaging. Nat. Photonics 4(12), 833–839 (2010)
A. Barty, J. Küpper, H.N. Chapman, Molecular imaging using X-ray free-electron lasers. Annu. Rev. Phys. Chem. 64(1), 415–435 (2013)
W. Boutu, B. Carré, H. Merdji, Coherent diffractive imaging, in Attosecond and XUV physics: Ultrafast dynamics and spectroscopy. ed. by T. Schultz, M. Vrakking (Wiley-VCH, Singapore, 2014), pp. 557–597
R.A. Kirian, H.N. Chapman, Imaging of objects by coherent diffraction of X-ray free-electron laser pulses, in Synchrotron light sources and free-electron lasers: Accelerator physics, instrumentation and science applications. ed. by E. Jaeschke, S. Khan, J.R. Schneider, J.B. Hastings (Springer International Publishing, Cham, 2015), pp. 1–55
R.W. Gerchberg, W.O. Saxton, A practical algorithm for the determination of phase from image and diffraction plane pictures. Optik 35, 237–246 (1972)
J.R. Fienup, Reconstruction of an object from the modulus of its Fourier transform. Opt. Lett. 3(1), 27–29 (1978)
J.R. Fienup, Phase retrieval algorithms—a comparison. Appl. Opt. 21(15), 2758–2769 (1982)
S. Marchesini, Invited article: A unified evaluation of iterative projection algorithms for phase retrieval. Rev. Sci. Instrum. 78(4), 049901 (2007)
K.A. Nugent, Coherent methods in the X-ray sciences. Adv. Phys. 59(1), 1–99 (2010)
A. Aquila, A. Barty, C. Bostedt, S. Boutet, G. Carini, D. de Ponte, P. Drell, S. Doniach, K.H. Downing, T. Earnest, H. Elmlund, V. Elser, M. Guhr, J. Hajdu, J. Hastings, S.P. Hau-Riege, Z. Huang, E.E. Lattman, F.R.N.C. Maia, S. Marchesini, A. Ourmazd, C. Pellegrini, R. Santra, I. Schlichting, C. Schroer, J.C.H. Spence, I.A. Vartanyants, S. Wakatsuki, W.I. Weis, G.J. Williams, The linac coherent light source single particle imaging road map. Struct. Dyn. 2(4), 041701 (2015)
H.N. Chapman, A. Barty, M.J. Bogan, S. Boutet, M. Frank, S.P. Hau-Riege, S. Marchesini, B.W. Woods, S. Bajt, H. Benner, R.A. London, E. Plonjes, M. Kuhlmann, R. Treusch, S. Dusterer, T. Tschentscher, J.R. Schneider, E. Spiller, T. Möller, C. Bostedt, M. Hoener, D.A. Shapiro, K.O. Hodgson, D. Van der Spoel, F. Burmeister, M. Bergh, C. Caleman, G. Huldt, M.M. Seibert, F.R.N.C. Maia, R.W. Lee, A. Szöke, N. Timneanu, J. Hajdu, Femtosecond diffractive imaging with a soft-X-ray free-electron laser. Nat. Phys. 2(12), 839–843 (2006)
H.N. Chapman, P. Fromme, A. Barty, T.A. White, R.A. Kirian, A. Aquila, M.S. Hunter, J. Schulz, D.P. DePonte, U. Weierstall, R.B. Doak, F.R.N.C. Maia, A.V. Martin, I. Schlichting, L. Lomb, N. Coppola, R.L. Shoeman, S.W. Epp, R. Hartmann, D. Rolles, A. Rudenko, L. Foucar, N. Kimmel, G. Weidenspointner, P. Holl, M.N. Liang, M. Barthelmess, C. Caleman, S. Boutet, M.J. Bogan, J. Krzywinski, C. Bostedt, S. Bajt, L. Gumprecht, B. Rudek, B. Erk, C. Schmidt, A. Homke, C. Reich, D. Pietschner, L. Struder, G. Hauser, H. Gorke, J. Ullrich, S. Herrmann, G. Schaller, F. Schopper, H. Soltau, K.U. Kuhnel, M. Messerschmidt, J.D. Bozek, S.P. Hau-Riege, M. Frank, C.Y. Hampton, R.G. Sierra, D. Starodub, G.J. Williams, J. Hajdu, N. Timneanu, M.M. Seibert, J. Andreasson, A. Rocker, O. Jonsson, M. Svenda, S. Stern, K. Nass, R. Andritschke, C.D. Schroter, F. Krasniqi, M. Bott, K.E. Schmidt, X.Y. Wang, I. Grotjohann, J.M. Holton, T.R.M. Barends, R. Neutze, S. Marchesini, R. Fromme, S. Schorb, D. Rupp, M. Adolph, T. Gorkhover, I. Andersson, H. Hirsemann, G. Potdevin, H. Graafsma, B. Nilsson, J.C.H. Spence, Femtosecond X-ray protein nanocrystallography. Nature 470(7332), 73–77 (2011)
M.M. Seibert, T. Ekeberg, F.R.N.C. Maia, M. Svenda, J. Andreasson, O. Jonsson, D. Odic, B. Iwan, A. Rocker, D. Westphal, M. Hantke, D.P. DePonte, A. Barty, J. Schulz, L. Gumprecht, N. Coppola, A. Aquila, M.N. Liang, T.A. White, A. Martin, C. Caleman, S. Stern, C. Abergel, V. Seltzer, J.M. Claverie, C. Bostedt, J.D. Bozek, S. Boutet, A.A. Miahnahri, M. Messerschmidt, J. Krzywinski, G. Williams, K.O. Hodgson, M.J. Bogan, C.Y. Hampton, R.G. Sierra, D. Starodub, I. Andersson, S. Bajt, M. Barthelmess, J.C.H. Spence, P. Fromme, U. Weierstall, R. Kirian, M. Hunter, R.B. Doak, S. Marchesini, S.P. Hau-Riege, M. Frank, R.L. Shoeman, L. Lomb, S.W. Epp, R. Hartmann, D. Rolles, A. Rudenko, C. Schmidt, L. Foucar, N. Kimmel, P. Holl, B. Rudek, B. Erk, A. Homke, C. Reich, D. Pietschner, G. Weidenspointner, L. Struder, G. Hauser, H. Gorke, J. Ullrich, I. Schlichting, S. Herrmann, G. Schaller, F. Schopper, H. Soltau, K.U. Kuhnel, R. Andritschke, C.D. Schroter, F. Krasniqi, M. Bott, S. Schorb, D. Rupp, M. Adolph, T. Gorkhover, H. Hirsemann, G. Potdevin, H. Graafsma, B. Nilsson, H.N. Chapman, J. Hajdu, Single mimivirus particles intercepted and imaged with an X-ray laser. Nature 470(7332), 78–81 (2011)
N.D. Loh, C.Y. Hampton, A.V. Martin, D. Starodub, R.G. Sierra, A. Barty, A. Aquila, J. Schulz, L. Lomb, J. Steinbrener, R.L. Shoeman, S. Kassemeyer, C. Bostedt, J. Bozek, S.W. Epp, B. Erk, R. Hartmann, D. Rolles, A. Rudenko, B. Rudek, L. Foucar, N. Kimmel, G. Weidenspointner, G. Hauser, P. Holl, E. Pedersoli, M. Liang, M.S. Hunter, L. Gumprecht, N. Coppola, C. Wunderer, H. Graafsma, F.R.N.C. Maia, T. Ekeberg, M. Hantke, H. Fleckenstein, H. Hirsemann, K. Nass, T.A. White, H.J. Tobias, G.R. Farquar, W.H. Benner, S.P. Hau-Riege, C. Reich, A. Hartmann, H. Soltau, S. Marchesini, S. Bajt, M. Barthelmess, P. Bucksbaum, K.O. Hodgson, L. Strüder, J. Ullrich, M. Frank, I. Schlichting, H.N. Chapman, M.J. Bogan, Fractal morphology, imaging and mass spectrometry of single aerosol particles in flight. Nature 486(7404), 513–517 (2012)
C. Bostedt, M. Adolph, E. Eremina, M. Hoener, D. Rupp, S. Schorb, H. Thomas, A.R.B. de Castro, T. Möller, Clusters in intense FLASH pulses: Ultrafast ionization dynamics and electron emission studied with spectroscopic and scattering techniques. J. Phys. B Atomic Mol. Opt. Phys. 43(19), 194011 (2010)
D. Rupp, M. Adolph, L. Flückiger, T. Gorkhover, J.P. Müller, M. Müller, M. Sauppe, D. Wolter, S. Schorb, R. Treusch, C. Bostedt, T. Möller, Generation and structure of extremely large clusters in pulsed jets. J. Chem. Phys. 141(4), 044306 (2014)
I. Barke, H. Hartmann, D. Rupp, L. Flükiger, M. Sauppe, M. Adolph, S. Schorb, C. Bostedt, R. Treusch, C. Peltz, S. Bartling, T. Fennel, K.H. Meiwes-Broer, T. Möller, The 3D-architecture of individual free silver nanoparticles captured by X-ray scattering. Nat. Commun. 6, 6187 (2015)
I. Robinson, R. Harder, Coherent X-ray diffraction imaging of strain at the nanoscale. Nat. Mater. 8(4), 291–298 (2009)
J.W. Miao, T. Ishikawa, I.K. Robinson, M.M. Murnane, Beyond crystallography: Diffractive imaging using coherent X-ray light sources. Science 348(6234), 530–535 (2015)
H.N. Chapman, X-ray free-electron lasers for the structure and dynamics of macromolecules. Annu. Rev. Biochem. 88(1), 35–58 (2019)
L.F. Gomez, K.R. Ferguson, J.P. Cryan, C. Bacellar, R.M.P. Tanyag, C. Jones, S. Schorb, D. Anielski, A. Belkacem, C. Bernando, R. Boll, J. Bozek, S. Carron, G. Chen, T. Delmas, L. Englert, S.W. Epp, B. Erk, L. Foucar, R. Hartmann, A. Hexemer, M. Huth, J. Kwok, S.R. Leone, J.H.S. Ma, F.R.N.C. Maia, E. Malmerberg, S. Marchesini, D.M. Neumark, B. Poon, J. Prell, D. Rolles, B. Rudek, A. Rudenko, M. Seifrid, K.R. Siefermann, F.P. Sturm, M. Swiggers, J. Ullrich, F. Weise, P. Zwart, C. Bostedt, O. Gessner, A.F. Vilesov, Shapes and vorticities of superfluid helium nanodroplets. Science 345(6199), 906–909 (2014)
E.J. Yarmchuk, M.J.V. Gordon, R.E. Packard, Observation of stationary vortex arrays in rotating superfluid-helium. Phys. Rev. Lett. 43(3), 214–217 (1979)
J.R. Abo-Shaeer, C. Raman, J.M. Vogels, W. Ketterle, Observation of vortex lattices in Bose-Einstein condensates. Science 292(5516), 476–479 (2001)
R.J. Donnelly, Quantized vortices in helium II, vol. 3, ed. by A.M. Goldman, P.V.E. McKlintock, M. Springford (Cambridge University Press, Cambridge, 1991)
F. Dalfovo, S. Stringari, Helium nanodroplets and trapped Bose-Einstein condensates as prototypes of finite quantum fluids. J. Chem. Phys. 115(22), 10078–10089 (2001)
L.F. Gomez, E. Loginov, A.F. Vilesov, Traces of vortices in superfluid helium droplets. Phys. Rev. Lett. 108(15), 155302 (2012)
E. Latimer, D. Spence, C. Feng, A. Boatwright, A.M. Ellis, S.F. Yang, Preparation of ultrathin nanowires using superfluid helium droplets. Nano Lett. 14(5), 2902–2906 (2014)
D. Spence, E. Latimer, C. Feng, A. Boatwright, A.M. Ellis, S.F. Yang, Vortex-induced aggregation in superfluid helium droplets. Phys. Chem. Chem. Phys. 16(15), 6903–6906 (2014)
A. Volk, D. Knez, P. Thaler, A.W. Hauser, W. Grogger, F. Hofer, W.E. Ernst, Thermal instabilities and Rayleigh breakup of ultrathin silver nanowires grown in helium nanodroplets. Phys. Chem. Chem. Phys. 17(38), 24570–24575 (2015)
M. Schnedlitz, M. Lasserus, D. Knez, A.W. Hauser, F. Hofer, W.E. Ernst, Thermally induced breakup of metallic nanowires: Experiment and theory. Phys. Chem. Chem. Phys. 19(14), 9402–9408 (2017)
F. Lackner, Synthesis of metallic nanoparticles in helium droplets, in Molecules in helium nanodroplets, ed. by A. Slenczka, J.P. Toennies (Springer, Berlin, 2021)
J.D. Close, F. Federmann, K. Hoffmann, N. Quaas, Helium droplets: A nanoscale cryostat for high resolution spectroscopy and studies of quantized vorticity. J. Low Temp. Phys. 111(3–4), 661–676 (1998)
K.K. Lehmann, R. Schmied, Energetics and possible formation and decay mechanisms of vortices in helium nanodroplets. Phys. Rev. B Condens. Matter 68(22), 224520 (2003)
C. Bernando, R.M.P. Tanyag, C. Jones, C. Bacellar, M. Bucher, K.R. Ferguson, D. Rupp, M.P. Ziemkiewicz, L.F. Gomez, A.S. Chatterley, T. Gorkhover, M. Muller, J. Bozek, S. Carron, J. Kwok, S.L. Butler, T. Möller, C. Bostedt, O. Gessner, A.F. Vilesov, Shapes of rotating superfluid helium nano-droplets. Phys. Rev. B Condens. Matter 95(6), 064510 (2017)
D. Rupp, N. Monserud, B. Langbehn, M. Sauppe, J. Zimmermann, Y. Ovcharenko, T. Möller, F. Frassetto, L. Poletto, A. Trabattoni, F. Calegari, M. Nisoli, K. Sander, C. Peltz, M.J. Vrakking, T. Fennel, A. Rouzee, Coherent diffractive imaging of single helium nanodroplets with a high harmonic generation source. Nat. Commun. 8, 493 (2017)
B. Langbehn, K. Sander, Y. Ovcharenko, C. Peltz, A. Clark, M. Coreno, R. Cucini, M. Drabbels, P. Finetti, M. Di Fraia, L. Giannessi, C. Grazioli, D. Iablonskyi, A.C. LaForge, T. Nishiyama, V. Oliver Álvarez de Lara, P. Piseri, O. Plekan, K. Ueda, J. Zimmermann, K.C. Prince, F. Stienkemeier, C. Callegari, T. Fennel, D. Rupp, T. Möller, Three-dimensional shapes of spinning helium nanodroplets. Phys. Rev. Lett. 121(25), 255301 (2018)
S.M.O. O'Connell, R.M.P. Tanyag, D. Verma, C. Bernando, W.Q. Pang, C. Bacellar, C.A. Saladrigas, J. Mahl, B.W. Toulson, Y. Kumagai, P. Walter, F. Ancilotto, M. Barranco, M. Pi, C. Bostedt, O. Gessner, A.F. Vilesov, Angular momentum in rotating superfluid droplets. Phys. Rev. Lett. 124(21), 215301 (2020)
D. Verma, S.M.O. O'Connell, A.J. Feinberg, S. Erukala, R.M.P. Tanyag, C. Bernando, W.W. Pang, C.A. Saladrigas, B.W. Toulson, M. Borgwardt, N. Shivaram, M.F. Lin, A. Al Haddad, W. Jager, C. Bostedt, P. Walter, O. Gessner, A.F. Vilesov, Shapes of rotating normal fluid He-3 versus superfluid He-4 droplets in molecular beams. Phys. Rev. B 102(1), 014504 (2020)
R.M.P. Tanyag, C. Bernando, C.F. Jones, C. Bacellar, K.R. Ferguson, D. Anielski, R. Boll, S. Carron, J.P. Cryan, L. Englert, S.W. Epp, B. Erk, L. Foucar, L.F. Gomez, R. Hartmann, D.M. Neumark, D. Rolles, B. Rudek, A. Rudenko, K.R. Siefermann, J. Ullrich, F. Weise, C. Bostedt, O. Gessner, A.F. Vilesov, Communication: X-ray coherent diffractive imaging by immersion in nanodroplets. Struct. Dyn. 2(5), 051102 (2015)
C.F. Jones, C. Bernando, R.M.P. Tanyag, C. Bacellar, K.R. Ferguson, L.F. Gomez, D. Anielski, A. Belkacem, R. Boll, J. Bozek, S. Carron, J. Cryan, L. Englert, S.W. Epp, B. Erk, L. Foucar, R. Hartmann, D.M. Neumark, D. Rolles, A. Rudenko, K.R. Siefermann, F. Weise, B. Rudek, F.P. Sturm, J. Ullrich, C. Bostedt, O. Gessner, A.F. Vilesov, Coupled motion of Xe clusters and quantum vortices in He nanodroplets. Phys. Rev. B Condens. Matter 93(18), 180510 (2016)
R.M.P. Tanyag, D. Rupp, A. Ulmer, A. Heilrath, B. Senfftleben, B. Kruse, L. Seiffert, S.M.O. O’Connell, K. Kolatzki, B. Langbehn, A. Hoffmann, T. Baumann, R. Boll, A. Chatterley, A. de Fanis, B. Erk, S. Erukala, A.J. Feinberg, T. Fennel, P. Grychtol, R. Hartmann, S. Hauf, M. Ilchen, M. Izquierdo, B. Krebs, M. Kuster, T. Mazza, K.H. Meiwes-Broer, J. Montaño, G. Noffz, D. Rivas, D. Schlosser, F. Seel, H. Stapelfeldt, L. Strüder, J. Tiggesbäumker, H. Yousef, M. Zabel, P. Ziolkowski, A. Vilesov, M. Meyer, Y. Ovcharenko, T. Möller, Taking snapshots of nanostructures in superfluid helium droplets, in European XFEL Annual Report 2019 (2020), pp. 20–21
A.J. Feinberg, D. Verma, S.M. O’Connell-Lopez, S. Erukala, R.M.P. Tanyag, W. Pang, C.A. Saladrigas, B.W. Toulson, M. Borgwardt, N. Shivaram, M.-F. Lin, A.A. Haddad, W. Jäger, C. Bostedt, P. Walter, O. Gessner, A.F. Vilesov, Aggregation of solutes in bosonic versus fermionic quantum fluids. Sci. Adv. 7(50) (2021)
R.M.P. Tanyag, C. Bacellar, W. Pang, C. Bernando, L.F. Gomez, C.F. Jones, K.R. Ferguson, J. Kwok, D. Anielski, A. Belkacem, R. Boll, J. Bozek, S. Carron, G. Chen, T. Delmas, L. Englert, S.W. Epp, B. Erk, L. Foucar, R. Hartmann, A. Hexemer, M. Huth, S.R. Leone, J.H. Ma, S. Marchesini, D.M. Neumark, B.K. Poon, J. Prell, D. Rolles, B. Rudek, A. Rudenko, M. Seifrid, M. Swiggers, J. Ullrich, F. Weise, P. Zwart, C. Bostedt, O. Gessner, A.F. Vilesov, Sizes of pure and doped helium droplets from single shot X-ray imaging. J. Chem. Phys. 156(4), 041102 (2022)
C. Bacellar, Ultrafast dynamics in helium nanodroplets probed by XUV spectroscopy and X-ray imaging. Ph.D. thesis, University of California, Berkeley, 2017
C. Bacellar, A.S. Chatterley, F. Lackner, C.D. Pemmaraju, R.M.P. Tanyag, C. Bernando, D. Verma, S. O’Connell, M. Bucher, K.R. Ferguson, T. Gorkhover, N.C. Ryan, G. Coslovich, D. Ray, T. Osipov, D.M. Neumark, C. Bostedt, A.F. Vilesov, O. Gessner, Evaporation of an anisotropic nanoplasma. EPJ Web Conf. 205, 06006 (2019)
B. Langbehn, Imaging the shapes and dynamics of superfluid helium nanodroplets. Ph.D. thesis, Technical University of Berlin, 2021
C.A. Saladrigas, A.J. Feinberg, M.P. Ziemkiewicz, C. Bacellar, M. Bucher, C. Bernando, S. Carron, A.S. Chatterley, F.-J. Decker, K.R. Ferguson, L. Gomez, T. Gorkhover, N.A. Helvy, C.F. Jones, J.J. Kwok, A. Lutman, D. Rupp, R.M.P. Tanyag, T. Möller, D.M. Neumark, C. Bostedt, A.F. Vilesov, O. Gessner, Charging and ion ejection dynamics of large helium nanodroplets exposed to intense femtosecond soft X-ray pulses. Eur. Phys. J. Spec. Top. 230(23), 4011–4023 (2021)
E. Hecht, Optics, 5th edn. (Pearson Education Limited, Essex, UK, 2017)
J.W. Goodman, Introduction to Fourier optics (The McGraw-Hill Companies Inc., New York, New York, 1996)
B.R. Masters, Abbe’s theory of image formation in the microscope, in Superresolution optical microscopy: The quest for enhanced resolution and contrast. ed. by B.R. Masters (Springer International Publishing, Cham, 2020), pp. 65–108
A.T. Macrander, X. Huang, Synchrotron X-ray optics. Annu. Rev. Mater. Res. 47(1), 135–152 (2017)
B.W.J. McNeil, N.R. Thompson, X-ray free-electron lasers. Nat. Photonics 4(12), 814–821 (2010)
C. Pellegrini, A. Marinelli, S. Reiche, The physics of X-ray free-electron lasers. Rev. Mod. Phys. 88(1), 015006 (2016)
E. Allaria, R. Appio, L. Badano, W.A. Barletta, S. Bassanese, S.G. Biedron, A. Borga, E. Busetto, D. Castronovo, P. Cinquegrana, S. Cleva, D. Cocco, M. Cornacchia, P. Craievich, I. Cudin, G. D’Auria, M. Dal Forno, M.B. Danailov, R. De Monte, G. De Ninno, P. Delgiusto, A. Demidovich, S. Di Mitri, B. Diviacco, A. Fabris, R. Fabris, W. Fawley, M. Ferianis, E. Ferrari, S. Ferry, L. Froehlich, P. Furlan, G. Gaio, F. Gelmetti, L. Giannessi, M. Giannini, R. Gobessi, R. Ivanov, E. Karantzoulis, M. Lonza, A. Lutman, B. Mahieu, M. Milloch, S.V. Milton, M. Musardo, I. Nikolov, S. Noe, F. Parmigiani, G. Penco, M. Petronio, L. Pivetta, M. Predonzani, F. Rossi, L. Rumiz, A. Salom, C. Scafuri, C. Serpico, P. Sigalotti, S. Spampinati, C. Spezzani, M. Svandrlik, C. Svetina, S. Tazzari, M. Trovo, R. Umer, A. Vascotto, M. Veronese, R. Visintini, M. Zaccaria, D. Zangrando, M. Zangrando, Highly coherent and stable pulses from the FERMI seeded free-electron laser in the extreme ultraviolet. Nat. Photonics 6(10), 699–704 (2012)
E. Allaria, D. Castronovo, P. Cinquegrana, P. Craievich, M. Dal Forno, M.B. Danailov, G. D’Auria, A. Demidovich, G. De Ninno, S. Di Mitri, B. Diviacco, W.M. Fawley, M. Ferianis, E. Ferrari, L. Froehlich, G. Gaio, D. Gauthier, L. Giannessi, R. Ivanov, B. Mahieu, N. Mahne, I. Nikolov, F. Parmigiani, G. Penco, L. Raimondi, C. Scafuri, C. Serpico, P. Sigalotti, S. Spampinati, C. Spezzani, M. Svandrlik, C. Svetina, M. Trovo, M. Veronese, D. Zangrando, M. Zangrando, Two-stage seeded soft-X-ray free-electron laser. Nat. Photonics 7(11), 913–918 (2013)
O.Y. Gorobtsov, G. Mercurio, F. Capotondi, P. Skopintsev, S. Lazarev, I.A. Zaluzhnyy, M.B. Danailov, M. Dell’Angela, M. Manfredda, E. Pedersoli, L. Giannessi, M. Kiskinova, K.C. Prince, W. Wurth, I.A. Vartanyants, Seeded X-ray free-electron laser generating radiation with laser statistical properties. Nat. Commun. 9(1), 4498 (2018)
E. Allaria, L. Badano, S. Bassanese, F. Capotondi, D. Castronovo, P. Cinquegrana, M.B. Danailov, G. D’Auria, A. Demidovich, R. De Monte, G. De Ninno, S. Di Mitri, B. Diviacco, W.M. Fawley, M. Ferianis, E. Ferrari, G. Gaio, D. Gauthier, L. Giannessi, F. Iazzourene, G. Kurdi, N. Mahne, I. Nikolov, F. Parmigiani, G. Penco, L. Raimondi, P. Rebernik, F. Rossi, E. Roussel, C. Scafuri, C. Serpico, P. Sigalotti, C. Spezzani, M. Svandrlik, C. Svetina, M. Trovo, M. Veronese, D. Zangrando, M. Zangrando, The FERMI free-electron lasers. J. Synchrotron Radiat. 22(3), 485–491 (2015)
P. Rudawski, C.M. Heyl, F. Brizuela, J. Schwenke, A. Persson, E. Mansten, R. Rakowski, L. Rading, F. Campi, B. Kim, P. Johnsson, A. L’Huillier, A high-flux high-order harmonic source. Rev. Sci. Instrum. 84(7), 073103 (2013)
F. Krausz, M. Ivanov, Attosecond physics. Rev. Mod. Phys. 81(1), 163–234 (2009)
T. Popmintchev, M.C. Chen, P. Arpin, M.M. Murnane, H.C. Kapteyn, The attosecond nonlinear optics of bright coherent X-ray generation. Nat. Photonics 4(12), 822–832 (2010)
C.M. Heyl, C.L. Arnold, A. Couairon, A. L’Huillier, Introduction to macroscopic power scaling principles for high-order harmonic generation. J. Phys. B Atomic Mol. Opt. Phys. 50(1), 013001 (2016)
M. Nisoli, P. Decleva, F. Calegari, A. Palacios, F. Martín, Attosecond electron dynamics in molecules. Chem. Rev. 117(16), 10760–10825 (2017)
M.D. Seaberg, D.E. Adams, E.L. Townsend, D.A. Raymondson, W.F. Schlotter, Y.W. Liu, C.S. Menoni, L. Rong, C.C. Chen, J.W. Miao, H.C. Kapteyn, M.M. Murnane, Ultrahigh 22 nm resolution coherent diffractive imaging using a desktop 13 nm high harmonic source. Opt. Express 19(23), 22470–22479 (2011)
M.D. Seaberg, B. Zhang, D.F. Gardner, E.R. Shanblatt, M.M. Murnane, H.C. Kapteyn, D.E. Adams, Tabletop nanometer extreme ultraviolet imaging in an extended reflection mode using coherent fresnel ptychography. Optica 1(1), 39–44 (2014)
D. Rudolf, C. La-O-Vorakiat, M. Battiato, R. Adam, J.M. Shaw, E. Turgut, P. Maldonado, S. Mathias, P. Grychtol, H.T. Nembach, T.J. Silva, M. Aeschlimann, H.C. Kapteyn, M.M. Murnane, C.M. Schneider, P.M. Oppeneer, Ultrafast magnetization enhancement in metallic multilayers driven by superdiffusive spin current. Nat. Commun. 3(1), 1037 (2012)
K.M. Hoogeboom-Pot, J.N. Hernandez-Charpak, X. Gu, T.D. Frazer, E.H. Anderson, W. Chao, R.W. Falcone, R. Yang, M.M. Murnane, H.C. Kapteyn, D. Nardi, A new regime of nanoscale thermal transport: Collective diffusion increases dissipation efficiency. Proc. Natl. Acad. Sci. 112(16), 4846–4851 (2015)
J. Miao, D. Sayre, H.N. Chapman, Phase retrieval from the magnitude of the Fourier transforms of nonperiodic objects. J. Opt. Soc. Am. A 15(6), 1662–1669 (1998)
H.N. Chapman, A. Barty, S. Marchesini, A. Noy, S.R. Hau-Riege, C. Cui, M.R. Howells, R. Rosen, H. He, J.C.H. Spence, U. Weierstall, T. Beetz, C. Jacobsen, D. Shapiro, High-resolution ab initio three-dimensional X-ray diffraction microscopy. J. Opt. Soc. Am. A-Opt. Image Sci. Vis. 23(5), 1179–1200 (2006)
S. Marchesini, H. He, H.N. Chapman, S.P. Hau-Riege, A. Noy, M.R. Howells, U. Weierstall, J.C.H. Spence, X-ray image reconstruction from a diffraction pattern alone. Phys. Rev. B. 68(14), 140101 (2003)
M.F. Hantke, D. Hasse, F.R.N.C. Maia, T. Ekeberg, K. John, M. Svenda, N.D. Loh, A.V. Martin, N. Timneanu, D.S.D. Larsson, G. van der Schot, G.H. Carlsson, M. Ingelman, J. Andreasson, D. Westphal, M.N. Liang, F. Stellato, D.P. DePonte, R. Hartmann, N. Kimmel, R.A. Kirian, M.M. Seibert, K. Muhlig, S. Schorb, K. Ferguson, C. Bostedt, S. Carron, J.D. Bozek, D. Rolles, A. Rudenko, S. Epp, H.N. Chapman, A. Barty, J. Hajdu, I. Andersson, High-throughput imaging of heterogeneous cell organelles with an X-ray laser. Nat. Photonics 8(12), 943–949 (2014)
T. Kimura, Y. Joti, A. Shibuya, C.Y. Song, S. Kim, K. Tono, M. Yabashi, M. Tamakoshi, T. Moriya, T. Oshima, T. Ishikawa, Y. Bessho, Y. Nishino, Imaging live cell in micro-liquid enclosure by X-ray laser diffraction. Nat. Commun. 5, 3052 (2014)
G. van der Schot, M. Svenda, F.R.N.C. Maia, M. Hantke, D.P. DePonte, M.M. Seibert, A. Aquila, J. Schulz, R. Kirian, M. Liang, F. Stellato, B. Iwan, J. Andreasson, N. Timneanu, D. Westphal, N.F. Almeida, D. Odic, D. Hasse, G.H. Carlsson, D.S.D. Larsson, A. Barty, A.V. Martin, S. Schorb, C. Bostedt, J.D. Bozek, D. Rolles, A. Rudenko, S. Epp, L. Foucar, B. Rudek, R. Hartmann, N. Kimmel, P. Holl, L. Englert, N.T.D. Loh, H.N. Chapman, I. Andersson, J. Hajdu, T. Ekeberg, Imaging single cells in a beam of live cyanobacteria with an X-ray laser. Nat. Commun. 6, 5704 (2015)
H.J. Park, N.D. Loh, R.G. Sierra, C.Y. Hampton, D. Starodub, A.V. Martin, A. Barty, A. Aquila, J. Schulz, J. Steinbrener, R.L. Shoeman, L. Lomb, S. Kassemeyer, C. Bostedt, J. Bozek, S.W. Epp, B. Erk, R. Hartmann, D. Rolles, A. Rudenko, B. Rudek, L. Foucar, N. Kimmel, G. Weidenspointner, G. Hauser, P. Holl, E. Pedersoli, M.N. Liang, M.S. Hunter, L. Gumprecht, N. Coppola, C. Wunderer, H. Graafsma, F.R.N.C. Maia, T. Ekeberg, M. Hantke, H. Fleckenstein, H. Hirsemann, K. Nass, H.J. Tobias, G.R. Farquar, W.H. Benner, S. Hau-Riege, C. Reich, A. Hartmann, H. Soltau, S. Marchesini, S. Bajt, M. Barthelmess, L. Strüder, J. Ullrich, P. Bucksbaum, M. Frank, I. Schlichting, H.N. Chapman, M.J. Bogan, V. Elser, Toward unsupervised single-shot diffractive imaging of heterogeneous particles using X-ray free-electron lasers. Opt. Express 21(23), 28729–28742 (2013)
W.F. Schlotter, R. Rick, K. Chen, A. Scherz, J. Stöhr, J. Lüning, S. Eisebitt, C. Günther, W. Eberhardt, O. Hellwig, I. McNulty, Multiple reference Fourier transform holography with soft X-rays. Appl. Phys. Lett. 89(16), 163112 (2006)
S.G. Podorov, K.M. Pavlov, D.M. Paganin, A non-iterative reconstruction method for direct and unambiguous coherent diffractive imaging. Opt. Express 15(16), 9954–9962 (2007)
B. Pfau, S. Eisebitt, X-ray holography, in Synchrotron light sources and free-electron lasers: Accelerator physics, instrumentation and science applications. ed. by E.J. Jaeschke, S. Khan, J.R. Schneider, J.B. Hastings (Springer International Publishing, Cham, 2016), pp. 1093–1133
T. Gorkhover, A. Ulmer, K. Ferguson, M. Bucher, F.R.N.C. Maia, J. Bielecki, T. Ekeberg, M.F. Hantke, B.J. Daurer, C. Nettelblad, J. Andreasson, A. Barty, P. Bruza, S. Carron, D. Hasse, J. Krzywinski, D.S.D. Larsson, A. Morgan, K. Mühlig, M. Müller, K. Okamoto, A. Pietrini, D. Rupp, M. Sauppe, G. van der Schot, M. Seibert, J.A. Sellberg, M. Svenda, M. Swiggers, N. Timneanu, D. Westphal, G. Williams, A. Zani, H.N. Chapman, G. Faigel, T. Möller, J. Hajdu, C. Bostedt, Femtosecond X-ray Fourier holography imaging of free-flying nanoparticles. Nat. Photonics 12(3), 150–153 (2018)
T. Gorkhover, S. Schorb, R. Coffee, M. Adolph, L. Foucar, D. Rupp, A. Aquila, J.D. Bozek, S.W. Epp, B. Erk, L. Gumprecht, L. Holmegaard, A. Hartmann, R. Hartmann, G. Hauser, P. Holl, A. Hömke, P. Johnsson, N. Kimmel, K.-U. Kühnel, M. Messerschmidt, C. Reich, A. Rouzée, B. Rudek, C. Schmidt, J. Schulz, H. Soltau, S. Stern, G. Weidenspointner, B. White, J. Küpper, L. Strüder, I. Schlichting, J. Ullrich, D. Rolles, A. Rudenko, T. Möller, C. Bostedt, Femtosecond and nanometre visualization of structural dynamics in superheated nanoparticles. Nat. Photonics 10(2), 93–97 (2016)
K.S. Raines, S. Salha, R.L. Sandberg, H. Jiang, J.A. Rodríguez, B.P. Fahimian, H.C. Kapteyn, J. Du, J. Miao, Three-dimensional structure determination from a single view. Nature 463(7278), 214–217 (2010)
D. Rupp, M. Adolph, T. Gorkhover, S. Schorb, D. Wolter, R. Hartmann, N. Kimmel, C. Reich, T. Feigl, A.R.B. de Castro, R. Treusch, L. Strüder, T. Möller, C. Bostedt, Identification of twinned gas phase clusters by single-shot scattering with intense soft X-ray pulses. New J. Phys. 14(5), 055016 (2012)
L. Hecht, Zweifarben-Streubildaufnahme von Helium-Nanotröpfchen: Planung, Durchführung und erste Ergebnisse. Master Thesis, Technical University Berlin, 2018
J.P. Toennies, A.F. Vilesov, Superfluid helium droplets: A uniquely cold nanomatrix for molecules and molecular complexes. Angew. Chem. Int. Ed. 43(20), 2622–2648 (2004)
J.P. Toennies, Helium nanodroplets: Formation, physical properties, and superfluidity, in Molecules in helium nanodroplets, ed. by A. Slenczka, J.P. Toennies (Springer, Berlin, 2021)
D.M. Brink, S. Stringari, Density of states and evaporation rate of helium clusters. Zeitschrift Fur Physik D-Atoms Molecules and Clusters 15(3), 257–263 (1990)
K.B. Whaley, Structure and dynamics of quantum clusters. Int. Rev. Phys. Chem. 13(1), 41–84 (1994)
M. Barranco, R. Guardiola, S. Hernandez, R. Mayol, J. Navarro, M. Pi, Helium nanodroplets: An overview. J. Low Temp. Phys. 142(1–2), 1–81 (2006)
R.M.P. Tanyag, C.F. Jones, C. Bernando, S.M.O. O’Connell, D. Verma, A.F. Vilesov, Experiments with large superfluid helium nanodroplets, in Cold chemistry: Molecular scattering and reactivity near absolute zero. ed. by O. Dulieu, A. Osterwalder (The Royal Society of Chemistry, London, UK, 2018), pp. 389–443
H. Buchenau, R. Goetting, Scheidemann A., J.P. Toennies, Experimental studies of condensation in helium nozzle beams, in Conference Proceedings of the 15th International Symposium on Rarefied Gas Dynamics, ed. by V. Boffi, C. Cercignani (1986), pp. 197–207
U. Even, J. Jortner, D. Noy, N. Lavie, C. Cossart-Magos, Cooling of large molecules below 1 K and He clusters formation. J. Chem. Phys. 112(18), 8068–8071 (2000)
D. Pentlehner, R. Riechers, B. Dick, A. Slenczka, U. Even, N. Lavie, R. Brown, K. Luria, Rapidly pulsed helium droplet source. Rev. Sci. Instrum. 80(4), 043302 (2009)
M.N. Slipchenko, S. Kuma, T. Momose, A.F. Vilesov, Intense pulsed helium droplet beams. Rev. Sci. Instrum. 73(10), 3600–3605 (2002)
S. Kuma, T. Azuma, Pulsed beam of extremely large helium droplets. Cryogenics 88, 78–80 (2017)
D. Verma, A.F. Vilesov, Pulsed helium droplet beams. Chem. Phys. Lett. 694, 129–134 (2018)
C. Bostedt, T. Gorkhover, D. Rupp, T. Möller, Clusters and nanocrystals, in Synchrotron light sources and free-electron lasers: Accelerator physics, instrumentation and science applications. ed. by E.J. Jaeschke, S. Khan, J.R. Schneider, J.B. Hastings (Springer International Publishing, Cham, 2020), pp. 1525–1573
M. Lewerenz, B. Schilling, J.P. Toennies, Successive capture and coagulation of atoms and molecules to small clusters in large liquid-helium clusters. J. Chem. Phys. 102(20), 8191–8207 (1995)
J. Tiggesbäumker, F. Stienkemeier, Formation and properties of metal clusters isolated in helium droplets. Phys. Chem. Chem. Phys. 9(34), 4748–4770 (2007)
L. Strüder, S. Eppa, D. Rolles, R. Hartmann, P. Holl, G. Lutz, H. Soltau, R. Eckart, C. Reich, K. Heinzinger, C. Thamm, A. Rudenko, F. Krasniqi, K.U. Kuhnel, C. Bauer, C.D. Schroter, R. Moshammer, S. Techert, D. Miessner, M. Porro, O. Halker, N. Meidinger, N. Kimmel, R. Andritschke, F. Schopper, G. Weidenspointner, A. Ziegler, D. Pietschner, S. Herrmann, U. Pietsch, A. Walenta, W. Leitenberger, C. Bostedt, T. Möller, D. Rupp, M. Adolph, H. Graafsma, H. Hirsemann, K. Gartner, R. Richter, L. Foucar, R.L. Shoeman, I. Schlichting, J. Ullrich, Large-format, high-speed, X-ray pnCCDs combined with electron and ion imaging spectrometers in a multipurpose chamber for experiments at 4th generation light sources. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 614(3), 483–496 (2010)
H. Ryll, M. Simson, R. Hartmann, P. Holl, M. Huth, S. Ihle, Y. Kondo, P. Kotula, A. Liebel, K. Müller-Caspary, A. Rosenauer, R. Sagawa, J. Schmidt, H. Soltau, L. Strüder, A pnCCD-based, fast direct single electron imaging camera for TEM and STEM. J. Instrum. 11(04), P04006–P04006 (2016)
M. Kuster, K. Ahmed, K.-E. Ballak, C. Danilevski, M. Ekmedzic, B. Fernandes, P. Gessler, R. Hartmann, S. Hauf, P. Holl, M. Meyer, J. Montano, A. Munnich, Y. Ovcharenko, N. Rennhack, T. Ruter, D. Rupp, D. Schlosser, K. Setoodehnia, R. Schmitt, L. Struder, R.M.P. Tanyag, A. Ulmer, H. Yousef, The 1-megapixel pnCCD detector for the small quantum systems instrument at the european XFEL: System and operation aspects. J. Synchrotron Radiat. 28(2), 576–587 (2021)
S. Hau-Riege, High-intensity X-rays—interaction with matter: Processes in plasmas, clusters, molecules, and solids (Wiley-VCH Verlag, Weinheim, Germany, 2011)
U. Saalmann, C. Siedschlag, J.M. Rost, Mechanisms of cluster ionization in strong laser pulses. J. Phys. B Atomic Mol. Opt. Phys. 39(4), R39–R77 (2006)
T. Fennel, K.H. Meiwes-Broer, J. Tiggesbäumker, P.G. Reinhard, P.M. Dinh, E. Suraud, Laser-driven nonlinear cluster dynamics. Rev. Mod. Phys. 82(2), 1793–1842 (2010)
A. Mikaberidze, U. Saalmann, J.M. Rost, Laser-driven nanoplasmas in doped helium droplets: Local ignition and anisotropic growth. Phys. Rev. Lett. 102(12), 128102 (2009)
S.R. Krishnan, L. Fechner, M. Kremer, V. Sharma, B. Fischer, N. Camus, J. Jha, M. Krishnamurthy, T. Pfeifer, R. Moshammer, J. Ullrich, F. Stienkemeier, M. Mudrich, A. Mikaberidze, U. Saalmann, J.M. Rost, Dopant-induced ignition of helium nanodroplets in intense few-cycle laser pulses. Phys. Rev. Lett. 107(17), 173402 (2011)
S.R. Krishnan, C. Peltz, L. Fechner, V. Sharma, M. Kremer, B. Fischer, N. Camus, T. Pfeifer, J. Jha, M. Krishnamurthy, C.D. Schröter, J. Ullrich, F. Stienkemeier, R. Moshammer, T. Fennel, M. Mudrich, Evolution of dopant-induced helium nanoplasmas. New J. Phys. 14(7), 075016 (2012)
T.V. Liseykina, D. Bauer, Plasma-formation dynamics in intense laser-droplet interaction. Phys. Rev. Lett. 110(14), 145003 (2013)
A.C. LaForge, M. Drabbels, N.B. Brauer, M. Coreno, M. Devetta, M. Di Fraia, P. Finetti, C. Grazioli, R. Katzy, V. Lyamayev, T. Mazza, M. Mudrich, P. O’Keeffe, Y. Ovcharenko, P. Piseri, O. Plekan, K.C. Prince, R. Richter, S. Stranges, C. Callegari, T. Möller, F. Stienkemeier, Collective autoionization in multiply-excited systems: A novel ionization process observed in helium nanodroplets. Sci. Rep. 4, 3621 (2014)
M. Mudrich, F. Stienkemeier, Photoionisaton of pure and doped helium nanodroplets. Int. Rev. Phys. Chem. 33(3), 301–339 (2014)
Y. Ovcharenko, V. Lyamayev, R. Katzy, M. Devetta, A. LaForge, P. O’Keeffe, O. Plekan, P. Finetti, M. Di Fraia, M. Mudrich, M. Krikunova, P. Piseri, M. Coreno, N.B. Brauer, T. Mazza, S. Stranges, C. Grazioli, R. Richter, K.C. Prince, M. Drabbels, C. Callegari, F. Stienkemeier, T. Möller, Novel collective autoionization process observed in electron spectra of He clusters. Phys. Rev. Lett. 112(7), 073401 (2014)
M.P. Ziemkiewicz, D.M. Neumark, O. Gessner, Ultrafast electronic dynamics in helium nanodroplets. Int. Rev. Phys. Chem. 34(2), 239–267 (2015)
M. Kelbg, M. Zabel, B. Krebs, L. Kazak, K.H. Meiwes-Broer, J. Tiggesbäumker, Auger emission from the coulomb explosion of helium nanoplasmas. J. Chem. Phys. 150(20), 204302 (2019)
M. Kelbg, M. Zabel, B. Krebs, L. Kazak, K.H. Meiwes-Broer, J. Tiggesbäumker, Temporal development of a laser-induced helium nanoplasma measured through Auger emission and above-threshold ionization. Phys. Rev. Lett. 125(9), 093202 (2020)
M. Mudrich, A.C. LaForge, A. Ciavardini, P. O’Keeffe, C. Callegari, M. Coreno, A. Demidovich, M. Devetta, M.D. Fraia, M. Drabbels, P. Finetti, O. Gessner, C. Grazioli, A. Hernando, D.M. Neumark, Y. Ovcharenko, P. Piseri, O. Plekan, K.C. Prince, R. Richter, M.P. Ziemkiewicz, T. Möller, J. Eloranta, M. Pi, M. Barranco, F. Stienkemeier, Ultrafast relaxation of photoexcited superfluid He nanodroplets. Nat. Commun. 11(1), 112 (2020)
Y. Ovcharenko, A.C. LaForge, B. Langbehn, O. Plekan, R. Cucini, P. Finetti, P. O’Keeffe, D. Iablonskyi, T. Nishiyama, K. Ueda, P. Piseri, M. Di Fraia, R. Richter, M. Coreno, C. Callegari, K.C. Prince, F. Stienkemeier, T. Möller, M. Mudrich, Autoionization dynamics of helium nanodroplets resonantly excited by intense XUV laser pulses. New J. Phys. 22(8), 083043 (2020)
R. Neutze, R. Wouts, D. van der Spoel, E. Weckert, J. Hajdu, Potential for biomolecular imaging with femtosecond X-ray pulses. Nature 406(6797), 752–757 (2000)
H.N. Chapman, C. Caleman, N. Timneanu, Diffraction before destruction. Philos. Trans. R. Soc. B Biol. Sci. 369(1647), 20130313 (2014)
C. Bostedt, E. Eremina, D. Rupp, M. Adolph, H. Thomas, M. Hoener, A.R.B. de Castro, J. Tiggesbäumker, K.H. Meiwes-Broer, T. Laarmann, H. Wabnitz, E. Plönjes, R. Treusch, J.R. Schneider, T. Möller, Ultrafast X-ray scattering of xenon nanoparticles: Imaging transient states of matter. Phys. Rev. Lett. 108(9), 093401 (2012)
D. Rupp, L. Flückiger, M. Adolph, A. Colombo, T. Gorkhover, M. Harmand, M. Krikunova, J.P. Müller, T. Oelze, Y. Ovcharenko, M. Richter, M. Sauppe, S. Schorb, R. Treusch, D. Wolter, C. Bostedt, T. Möller, Imaging plasma formation in isolated nanoparticles with ultrafast resonant scattering. Struct. Dyn. 7(3), 034303 (2020)
B.L. Henke, E.M. Gullikson, J.C. Davis, X-ray interactions—photoabsorption, scattering, transmission, and reflection at E = 50–30,000 eV, Z = 1–92. At. Data Nucl. Data Tables 54(2), 181–342 (1993)
A.A. Lucas, J.P. Vigneron, S.E. Donnelly, J.C. Rife, Theoretical interpretation of the vacuum ultraviolet reflectance of liquid helium and of the absorption spectra of helium microbubbles in aluminum. Phys. Rev. B 28(5), 2485–2496 (1983)
E.L. Knuth, U. Henne, Average size and size distribution of large droplets produced in a free-jet expansion of a liquid. J. Chem. Phys. 110(5), 2664–2668 (1999)
J.R. Fienup, C.C. Wackerman, Phase-retrieval stagnation problems and solutions. J. Opt. Soc. Am. A 3(11), 1897–1907 (1986)
J.R. Fienup, Reconstruction of a complex-valued object from the modulus of its Fourier transform using a support constraint. J. Opt. Soc. Am. A 4(1), 118–123 (1987)
T.R. Crimmins, J.R. Fienup, B.J. Thelen, Improved bounds on object support from autocorrelation support and application to phase retrieval. J. Opt. Soc. Am. A 7(1), 3–13 (1990)
A. Hare, G. Morrison, Near-field soft X-ray diffraction modelled by the multislice method. J. Mod. Opt. 41(1), 31–48 (1994)
T. Stielow, R. Schmidt, C. Peltz, T. Fennel, S. Scheel, Fast reconstruction of single-shot wide-angle diffraction images through deep learning. Mach. Learn. Sci. Technol. 1(4), 045007 (2020)
A. Colombo, J. Zimmermann, B. Langbehn, T. Möller, C. Peltz, K. Sander, B. Kruse, P. Tummler, I. Barke, D. Rupp, T. Fennel, The Scatman: An approximate method for fast wide-angle scattering simulations. Preprint at https://arxiv.org/abs/2202.03411 (2022)
J. Zimmermann, B. Langbehn, R. Cucini, M. Di Fraia, P. Finetti, A.C. LaForge, T. Nishiyama, Y. Ovcharenko, P. Piseri, O. Plekan, K.C. Prince, F. Stienkemeier, K. Ueda, C. Callegari, T. Möller, D. Rupp, Deep neural networks for classifying complex features in diffraction images. Phys. Rev. E 99(6), 063309 (2019)
J.M. Cowley, A.F. Moodie, The scattering of electrons by atoms and crystals. I. A new theoretical approach. Acta Crystallogr. 10(10), 609–619 (1957)
K. Sander, Reconstruction methods for single shot diffraction imaging of free nanostructures with ultrashort XUV laser pulses. Ph.D. thesis, Universität Rostock, 2019
S. Decking, et.al, A MHz-repetition-rate hard X-ray free-electron laser driven by a superconducting linear accelerator. Nat. Photonics 14(6), 391–397 (2020)
S.A. Bobkov, A.B. Teslyuk, R.P. Kurta, O.Y. Gorobtsov, O.M. Yefanov, V.A. Ilyin, R.A. Senin, I.A. Vartanyants, Sorting algorithms for single-particle imaging experiments at X-ray free-electron lasers. J. Synchrotron Radiat. 22(6), 1345–1352 (2015)
E. Sobolev, S. Zolotarev, K. Giewekemeyer, J. Bielecki, K. Okamoto, H.K.N. Reddy, J. Andreasson, K. Ayyer, I. Barak, S. Bari, A. Barty, R. Bean, S. Bobkov, H.N. Chapman, G. Chojnowski, B.J. Daurer, K. Dörner, T. Ekeberg, L. Flückiger, O. Galzitskaya, L. Gelisio, S. Hauf, B.G. Hogue, D.A. Horke, A. Hosseinizadeh, V. Ilyin, C. Jung, C. Kim, Y. Kim, R.A. Kirian, H. Kirkwood, O. Kulyk, J. Küpper, R. Letrun, N.D. Loh, K. Lorenzen, M. Messerschmidt, K. Mühlig, A. Ourmazd, N. Raab, A.V. Rode, M. Rose, A. Round, T. Sato, R. Schubert, P. Schwander, J.A. Sellberg, M. Sikorski, A. Silenzi, C. Song, J.C.H. Spence, S. Stern, J. Sztuk-Dambietz, A. Teslyuk, N. Timneanu, M. Trebbin, C. Uetrecht, B. Weinhausen, G.J. Williams, P.L. Xavier, C. Xu, I.A. Vartanyants, V.S. Lamzin, A. Mancuso, F.R.N.C. Maia, Megahertz single-particle imaging at the european XFEL. Commun. Phys. 3(1), 97 (2020)
K. Ayyer, P.L. Xavier, J. Bielecki, Z. Shen, B.J. Daurer, A.K. Samanta, S. Awel, R. Bean, A. Barty, M. Bergemann, T. Ekeberg, A.D. Estillore, H. Fangohr, K. Giewekemeyer, M.S. Hunter, M. Karnevskiy, R.A. Kirian, H. Kirkwood, Y. Kim, J. Koliyadu, H. Lange, R. Letrun, J. Lübke, T. Michelat, A.J. Morgan, N. Roth, T. Sato, M. Sikorski, F. Schulz, J.C.H. Spence, P. Vagovic, T. Wollweber, L. Worbs, O. Yefanov, Y. Zhuang, F.R.N.C. Maia, D.A. Horke, J. Küpper, N.D. Loh, A.P. Mancuso, H.N. Chapman, 3D diffractive imaging of nanoparticle ensembles using an X-ray laser. Optica 8(1), 15–23 (2021)
G. Carleo, I. Cirac, K. Cranmer, L. Daudet, M. Schuld, N. Tishby, L. Vogt-Maranto, L. Zdeborová, Machine learning and the physical sciences. Rev. Mod. Phys. 91(4), 045002 (2019)
E.R. Cruz-Chú, A. Hosseinizadeh, G. Mashayekhi, R. Fung, A. Ourmazd, P. Schwander, Selecting XFEL single-particle snapshots by geometric machine learning. Struct. Dyn. 8(1), 014701 (2021)
T. Ekeberg, M. Svenda, C. Abergel, F.R. Maia, V. Seltzer, J.-M. Claverie, M. Hantke, O. Jönsson, C. Nettelblad, G. van der Schot, Three-dimensional reconstruction of the giant mimivirus particle with an X-ray free-electron laser. Phys. Rev. Lett. 114(9), 098102 (2015)
H. Liu, J.C. Spence, XFEL data analysis for structural biology. Quant Biol 4(3), 159–176 (2016)
B.J. Daurer, K. Okamoto, J. Bielecki, F.R. Maia, K. Mühlig, M.M. Seibert, M.F. Hantke, C. Nettelblad, W.H. Benner, M. Svenda, Experimental strategies for imaging bioparticles with femtosecond hard X-ray pulses. IUCrJ 4(3), 251–262 (2017)
Y. LeCun, Y. Bengio, G. Hinton, Deep learning. Nature 521(7553), 436–444 (2015)
C.H. Yoon, P. Schwander, C. Abergel, I. Andersson, J. Andreasson, A. Aquila, S. Bajt, M. Barthelmess, A. Barty, M.J. Bogan, Unsupervised classification of single-particle X-ray diffraction snapshots by spectral clustering. Opt. Express 19(17), 16542–16549 (2011)
S. Chandrasekhar, The stability of a rotating liquid drop. Proc. R. Soc. London Ser. A Math. Phys. Sci. 286(1404), 1–26 (1965)
S. Chandrasekhar, Ellipsoidal figures of equilibrium—an historical account. Commun. Pure Appl. Math. 20(2), 251–265 (1967)
S. Cohen, F. Plasil, W.J. Swiatecki, Equilibrium configurations of rotating charged or gravitating liquid masses with surface tension. II. Ann. Phys. 82(2), 557–596 (1974)
R.A. Brown, L.E. Scriven, The shape and stability of rotating liquid-drops. Proc. R. Soc. London Ser. A Math. Phys. Eng. Sci. 371(1746), 331–357 (1980)
R.J.A. Hill, L. Eaves, Nonaxisymmetric shapes of a magnetically levitated and spinning water droplet. Phys. Rev. Lett. 101(23), 234501, (2008)
T.G. Wang, Equilibrium shapes of rotating spheroids and drop shape oscillations. in Advances in applied mechanics, ed. by J.W. Hutchinson, T.Y. Wu (Elsevier, Amsterdam, 1988), pp. 1–62
N. Bohr, J.A. Wheeler, The mechanism of nuclear fission. Phys. Rev. 56(5), 426–450 (1939)
K.A. Baldwin, S.L. Butler, R.J.A. Hill, Artificial tektites: An experimental technique for capturing the shapes of spinning drops. Sci. Rep. 5, 7660 (2015)
L. Liao, R.J.A. Hill, Shapes and fissility of highly charged and rapidly rotating levitated liquid drops. Phys. Rev. Lett. 119(11), 114501 (2017)
F.H. Busse, Oscillations of a rotating liquid drop. J. Fluid Mech. 142, 1–8 (1984)
N. Ashgriz, M. Movassat, Oscillation of droplets and bubbles, in Handbook of atomization and sprays: Theory and applications, ed. by N. Ashgriz (Springer US, Boston, MA, 2011), pp. 125–144
R.P. Feynman, Chapter II application of quantum mechanics to liquid helium, in Progress in low temperature physics, ed. by C.J. Gorter (Elsevier, Amsterdam, 1955), pp. 17–53
C. Barenghi, N.G. Parker, A primer on quantum fluids (Springer, Switzerland, 2016)
G.M. Seidel, H.J. Maris, Morphology of superfluid drops with angular-momentum. Phys. B 194, 577–578 (1994)
G.H. Bauer, R.J. Donnelly, W.F. Vinen, Vortex configurations in a freely rotating superfluid drop. J. Low Temp. Phys. 98(1–2), 47–65 (1995)
F. Ancilotto, M. Barranco, M. Pi, Spinning superfluid He-4 nanodroplets. Phys. Rev B 97(18), 184515 (2018)
M.A. Weilert, D.L. Whitaker, H.J. Maris, G.M. Seidel, Laser levitation of superfluid helium. J. Low Temp. Phys. 98(1), 17–35 (1995)
J.J. Niemela, Electrostatic charging and levitation of helium II drops. J. Low Temp. Phys. 109(5), 709–732 (1997)
M.A. Weilert, D.L. Whitaker, H.J. Maris, G.M. Seidel, Magnetic levitation of liquid helium. J. Low Temp. Phys. 106(1–2), 101–131 (1997)
D.L. Whitaker, C. Kim, C.L. Vicente, M.A. Weilert, H.J. Maris, G.M. Seidel, Shape oscillations in levitated He II drops. J. Low Temp. Phys. 113(3–4), 491–499 (1998)
J.J. Niemela, Vortex nucleation and the levitation of charged helium II drops. J. Low Temp. Phys. 119(3), 351–356 (2000)
A.J. Leggett, Superfluidity. Rev. Mod. Phys. 71(2), S318–S323 (1999)
O. Gessner, A.F. Vilesov, Imaging quantum vortices in superfluid helium droplets. Annu. Rev. Phys. Chem. 70, 173–198 (2019)
F. Ancilotto, M. Barranco, F. Coppens, J. Eloranta, N. Halberstadt, A. Hernando, D. Mateo, M. Pi, Density functional theory of doped superfluid liquid helium and nanodroplets. Int. Rev. Phys. Chem. 36(4), 621–707 (2017)
F. Ancilotto, M. Pi, M. Barranco, Vortex arrays in nanoscopic superfluid helium droplets. Phys. Rev. B Condens. Matter 91(10), 100503 (2015)
J.M. Escartín, F. Ancilotto, M. Barranco, M. Pi, Vorticity and quantum turbulence in the merging of superfluid helium nanodroplets. Phys. Rev. B 99(14) (2019)
M. Pi, J.M. Escartín, F. Ancilotto, M. Barranco, Coexistence of vortex arrays and surface capillary waves in spinning prolate superfluid 4He nanodroplets. Phys. Rev. B 104(9) (2021)
J. Gspann, H. Vollmar, Metastable excitations of large clusters of He-3, He-4 or Ne atoms. J. Chem. Phys. 73(4), 1657–1664 (1980)
J. Gspann, H. Vollmar, Ejection of positive cluster ions from large electron-bombarded He-3 or He-4 clusters. J. Low Temp. Phys. 45(3–4), 343–355 (1981)
W.E. Keller, Helium-3 and helium-4 (Plenum Press, New York, USA, 1969)
D.D. Osheroff, R.C. Richardson, D.M. Lee, Evidence for a new phase of solid He-3. Phys. Rev. Lett. 28(14), 885–888 (1972)
O.V. Lounasmaa, E. Thuneberg, Vortices in rotating superfluid 3He. Proc. Natl. Acad. Sci. 96(14), 7760–7767 (1999)
J.M. Escartín, F. Ancilotto, M. Barranco, M. Pi, Merging of superfluid helium nanodroplets with vortices. Phys. Rev. B 105(2) (2022)
M. Pi, F. Ancilotto, M. Barranco, Rotating 3He droplets. J. Chem. Phys. 152(18), 184111 (2020)
S.G. Alves, A.F. Vilesov, S.C. Ferreira, Effects of the mean free path and relaxation in a model for the aggregation of particles in superfluid media. J. Chem. Phys. 130(24), 244506 (2009)
E. Loginov, L.F. Gomez, N. Chiang, A. Halder, N. Guggemos, V.V. Kresin, A.F. Vilesov, Photoabsorption of Ag-N(N similar to 6–6000) nanoclusters formed in helium droplets: Transition from compact to multicenter aggregation. Phys. Rev. Lett. 106(23), 233401 (2011)
K. Nauta, R.E. Miller, Nonequilibrium self-assembly of long chains of polar molecules in superfluid helium. Science 283(5409), 1895–1897 (1999)
E. Loginov, L.F. Gomez, A.F. Vilesov, Formation of core-shell silver-ethane clusters in He droplets. J. Phys. Chem. A 117(46), 11774–11782 (2013)
E. Loginov, L.F. Gomez, B.G. Sartakov, A.F. Vilesov, Formation of large Ag clusters with shells of methane, ethylene, and acetylene in He droplets. J. Phys. Chem. A 120(34), 6738–6744 (2016)
E. Loginov, L.F. Gomez, B.G. Sartakov, A.F. Vilesov, Formation of core-shell ethane-silver clusters in He droplets. J. Phys. Chem. A 121(32), 5978–5982 (2017)
A. Przystawik, S. Göde, T. Döppner, J. Tiggesbäumker, K.H. Meiwes-Broer, Light-induced collapse of metastable magnesium complexes formed in helium nanodroplets. Phys. Rev. A 78(2), 021202 (2008)
S. Göde, R. Irsig, J. Tiggesbäumker, K.H. Meiwes-Broer, Time-resolved studies on the collapse of magnesium atom foam in helium nanodroplets. New J. Phys. 15, 015026 (2013)
K. Nauta, D.T. Moore, R.E. Miller, Molecular orientation in superfluid liquid helium droplets: High resolution infrared spectroscopy as a probe of solvent-solute interactions. Faraday Discuss. 113, 261–278 (1999)
A.S. Chatterley, B. Shepperson, H. Stapelfeldt, Three-dimensional molecular alignment inside helium nanodroplets. Phys. Rev. Lett. 119(7), 073202 (2017)
J.W. Niman, B.S. Kamerin, D.J. Merthe, L. Kranabetter, V.V. Kresin, Oriented polar molecules trapped in cold helium nanodropets: Electrostatic deflection, size separation, and charge migration. Phys. Rev. Lett. 123(4), 043203 (2019)
H. Saarikoski, S.M. Reimann, A. Harju, M. Manninen, Vortices in quantum droplets: Analogies between boson and fermion systems. Rev. Mod. Phys. 82(3), 2785–2834 (2010)
H.C. van de Hulst, Light scattering by small particles (Dover Publications Inc., New York City, 1957)
S.W. van Sciver, C.F. Barenghi, Visualisation of Quantum turbulence, in Progress in low temperature physics: Quantum turbulence. ed. by M. Tsubota, W.P. Halperin (Elsevier, Amsterdam, 2009), pp. 247–303
F. Ancilotto, M. Pi, M. Barranco, Vortex arrays in a rotating superfluid He-4 nanocylinder. Phys. Rev. B Condens. Matter 90(17), 174512 (2014)
C. Bernando, A.F. Vilesov, Kinematics of the doped quantum vortices in superfluid helium droplets. J. Low Temp. Phys. 191, 242–256 (2018)
F. Coppens, F. Ancilotto, M. Barranco, N. Halberstadt, M. Pi, Capture of Xe and Ar atoms by quantized vortices in He-4 nanodroplets. Phys. Chem. Chem. Phys. 19(36), 24805–24818 (2017)
G.P. Bewley, D.P. Lathrop, K.R. Sreenivasan, Superfluid helium—visualization of quantized vortices. Nature 441(7093), 588–588 (2006)
C. Raman, J.R. Abo-Shaeer, J.M. Vogels, K. Xu, W. Ketterle, Vortex nucleation in a stirred Bose-Einstein condensate. Phys. Rev. Lett. 87(21), 210402 (2001)
P. Rosenbusch, V. Bretin, J. Dalibard, Dynamics of a single vortex line in a Bose-Einstein condensate. Phys. Rev. Lett. 89(20), 200403 (2002)
A.L. Fetter, Rotating trapped Bose-Einstein condensates. Rev. Mod. Phys. 81(2), 647–691 (2009)
I.A. Pshenichnyuk, N.G. Berloff, Inelastic scattering of xenon atoms by quantized vortices in superfluids. Phys. Rev. B 94(18), 184505 (2016)
D. Kivotides, C.F. Barenghi, Y.A. Sergeev, Interactions between particles and quantized vortices in superfluid helium. Phys. Rev. B 77(1), 014527 (2008)
D. Kivotides, Y.A. Sergeev, C.F. Barenghi, Dynamics of solid particles in a tangle of superfluid vortices at low temperatures. Phys. Fluids 20(5), 055105 (2008)
D.R. Tilley, J. Tilley, Superfluidity and superconductivity. Graduate student series in physics, ed. D.F. Brewer. (Institute of Physics Publishing, Bristol, 1990)
O.F. Hagena, W. Obert, Cluster formation in expanding supersonic jets—effect of pressure, temperature, nozzle size, and test gas. J. Chem. Phys. 56(5), 1793–1802 (1972)
B. Sheehy, L.F. DiMauro, Atomic and molecular dynamics in intense optical fields. Annu. Rev. Phys. Chem. 47(1), 463–494 (1996)
K. Yamanouchi, The next frontier. Science 295(5560), 1659 (2002)
T. Gorkhover, M. Adolph, D. Rupp, S. Schorb, S.W. Epp, B. Erk, L. Foucar, R. Hartmann, N. Kimmel, K.U. Kuhnel, D. Rolles, B. Rudek, A. Rudenko, R. Andritschke, A. Aquila, J.D. Bozek, N. Coppola, T. Erke, F. Filsinger, H. Gorke, H. Graafsma, L. Gumprecht, G. Hauser, S. Herrmann, H. Hirsemann, A. Homke, P. Holl, C. Kaiser, F. Krasniqi, J.H. Meyer, M. Matysek, M. Messerschmidt, D. Miessner, B. Nilsson, D. Pietschner, G. Potdevin, C. Reich, G. Schaller, C. Schmidt, F. Schopper, C.D. Schroter, J. Schulz, H. Soltau, G. Weidenspointner, I. Schlichting, L. Strueder, J. Ullrich, T. Möller, C. Bostedt, Nanoplasma dynamics of single large xenon clusters irradiated with superintense X-ray pulses from the linac coherent light source free-electron laser. Phys. Rev. Lett. 108(24), 245005 (2012)
T. Nishiyama, Y. Kumagai, A. Niozu, H. Fukuzawa, K. Motomura, M. Bucher, Y. Ito, T. Takanashi, K. Asa, Y. Sato, D. You, Y. Li, T. Ono, E. Kukk, C. Miron, L. Neagu, C. Callegari, M. Di Fraia, G. Rossi, D.E. Galli, T. Pincelli, A. Colombo, T. Kameshima, Y. Joti, T. Hatsui, S. Owada, T. Katayama, T. Togashi, K. Tono, M. Yabashi, K. Matsuda, C. Bostedt, K. Nagaya, K. Ueda, Ultrafast structural dynamics of nanoparticles in intense laser fields. Phys. Rev. Lett. 123(12), 123201 (2019)
C. Peltz, C. Varin, T. Brabec, T. Fennel, Time-resolved X-ray imaging of anisotropic nanoplasma expansion. Phys. Rev. Lett. 113(13), 133401 (2014)
T. Ditmire, T. Donnelly, A.M. Rubenchik, R.W. Falcone, M.D. Perry, Interaction of intense laser pulses with atomic clusters. Phys. Rev. A 53(5), 3379–3402 (1996)
T. Ditmire, J.W.G. Tisch, E. Springate, M.B. Mason, N. Hay, J.P. Marangos, M.H.R. Hutchinson, High energy ion explosion of atomic clusters: Transition from molecular to plasma behavior. Phys. Rev. Lett. 78(14), 2732–2735 (1997)
B. Tabbert, H. Günther, G. zu Putlitz, Optical investigation of impurities in superfluid 4He. J. Low Temp. Phys. 109(5), 653–707 (1997)
A. Mauracher, O. Echt, A.M. Ellis, S. Yang, D.K. Bohme, J. Postler, A. Kaiser, S. Denifl, P. Scheier, Cold physics and chemistry: Collisions, ionization and reactions inside helium nanodroplets close to zero K. Phys. Rep. Rev. Sect. Phys. Lett. 751, 1–90 (2018)
B. Schütte, M. Arbeiter, A. Mermillod-Blondin, M.J.J. Vrakking, A. Rouzee, T. Fennel, Ionization avalanching in clusters ignited by extreme-ultraviolet driven seed electrons. Phys. Rev. Lett. 116(3), 033001 (2016)
A. Heidenreich, B. Grüner, M. Rometsch, S.R. Krishnan, F. Stienkemeier, M. Mudrich, Efficiency of dopant-induced ignition of helium nanoplasmas. New J. Phys. 18(7), 073046 (2016)
C.C. Tsao, J.D. Lobo, M. Okumura, S.Y. Lo, Generation of charged droplets by field ionization of liquid helium. J. Phys. D Appl. Phys. 31(17), 2195–2204 (1998)
R.E. Grisenti, J.P. Toennies, Cryogenic microjet source for orthotropic beams of ultralarge superfluid helium droplets. Phys. Rev. Lett. 90(23), 234501 (2003)
R.M.P. Tanyag, A.J. Feinberg, S.M.O. O'Connell, A.F. Vilesov, Disintegration of diminutive liquid helium jets in vacuum. J. Chem. Phys. 152(23): 234306. 2020 (2020)
A. Echelmeier, M. Sonker, A. Ros, Microfluidic sample delivery for serial crystallography using XFELs. Anal. Bioanal. Chem. 411(25), 6535–6547 (2019)
K. Kolatzki, M.L. Schubert, A. Ulmer, T. Möller, D. Rupp, R.M.P. Tanyag, Micrometer-sized droplets from liquid helium jets at low stagnation pressures. Phys. Fluids 34(1), 012002 (2022)
F.-Z. Zhao, B. Zhang, E.-K. Yan, B. Sun, Z.-J. Wang, J.-H. He, D.-C. Yin, A guide to sample delivery systems for serial crystallography. FEBS J. 286(22), 4402–4417 (2019)
M.S. Paoletti, D.P. Lathrop, Quantum turbulence. Ann. Rev. Condens. Matter Phys. 2(2), 213–234 (2011)
W. Guo, M. La Mantia, D.P. Lathrop, S.W. Van Sciver, Visualization of two-fluid flows of superfluid helium-4. Proc. Natl. Acad. Sci. U.S.A. 111, 4653–4658 (2014)
E. Fonda, D.P. Meichle, N.T. Ouellette, S. Hormoz, D.P. Lathrop, Direct observation of Kelvin waves excited by quantized vortex reconnection. Proc. Natl. Acad. Sci. U.S.A. 111, 4707–4710 (2014)
Acknowledgements
This book chapter is made possible by the support provided by the Bundesministerium für Bildung und Forschung (BMBF) via grant No. 05K16KT3 within the BMBF Forschungsschwerpunkt Freie-Elektronen-Laser FSP-302, by the Leibniz-Gemeinschaft via grant No. SAW/2017/MBI4, by NCCR MUST of SNF, SNF grant 200021E_193642/1, and by the Deutsche Forschungsgemeinschaft (DFG) grants Mo 719/13 and Mo 719/14. The authors would also like to express their gratitude to Charles Bernando, Alessandro Colombo, Oliver Gessner, Luis F. Gomez, Curtis F. Jones, Katharina Kolatzki, Sean Marcus O’Connell-Lopez, Anatoli Ulmer, Deepak Verma, Andrey Vilesov, and Julian Zimmermann for constructive discussions and for providing us figures from their publications. In addition, we are grateful for Oliver Gessner and Andrey Vilesov for helping us in improving the content of our manuscript.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2022 The Author(s)
About this chapter
Cite this chapter
Tanyag, R.M.P., Langbehn, B., Möller, T., Rupp, D. (2022). X-Ray and XUV Imaging of Helium Nanodroplets. In: Slenczka, A., Toennies, J.P. (eds) Molecules in Superfluid Helium Nanodroplets. Topics in Applied Physics, vol 145. Springer, Cham. https://doi.org/10.1007/978-3-030-94896-2_7
Download citation
DOI: https://doi.org/10.1007/978-3-030-94896-2_7
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-94895-5
Online ISBN: 978-3-030-94896-2
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)