2.1 Introduction

Helium, being the second most abundant element in the universe, is a unique system in terms of its macroscopic and microscopic properties [1]. It is the only known substance that does not have a solid phase at the lowest temperatures under normal pressure. Helium is the only liquid that becomes superfluid in its natural state. This bulk behaviour is partially determined by microscopic properties such as an atomic polarizability, which is exceptionally small for helium. The polarizability is responsible for an extremely weak van der Waals interaction between two helium atoms, which was a reason for a long standing debates about existence of the helium dimer, until it was experimentally observed in the early 1990s [2, 3]. The helium dimer is a very distinctive quantum system, not alike commonly known covalent molecules and other van der Waals clusters. He\(_2\) has only one weakly bound state; higher vibrational and even rotational states are not supported by the He-He potential. A tiny binding energy is a reason for huge spatial extent with an average interatomic distance of 4.7 nm. Moreover, two helium atoms in the dimer can be most frequently found outside the potential well in the classically forbidden tunnelling region.

The combination of three helium atoms, the helium trimer, is extraordinary as well. Though the ground state of the trimer is spatially more compact than the single state of the helium dimer, it is still exceptionally defuse, such that almost all triangular shapes are equally probable. In addition, the helium trimer forms an Efimov state of extreme spatial extent under natural conditions.

In this chapter we discuss application of the laser-based Coulomb explosion imaging for determination of structures and binding energies of small helium clusters consisting of two and three helium atoms. We will show the images of the Efimov state and discuss how a strong laser field can modify the interaction between helium atoms and how the helium dimer reacts to such modification.

2.2 Experimental

Small helium clusters are imaged using the experimental setup that consists of two parts: cluster preparation and their detection (Fig. 2.1). As a cluster source we use the supersonic expansion of helium gas into vacuum (Sect. 2.2.1). Subsequently, the clusters of desired size are selected using mater wave diffraction on a transmission grating. For cluster detection we employ the laser-based Coulomb explosion imaging (Sect. 2.2.2). The momenta of ions after Coulomb explosion are measured by the COLTRIMS technique (Sect. 2.2.3). The initial cluster structures are deduced from the ion momenta using the reconstruction procedure based on the classical simulation of Coulomb explosion (Sect. 2.2.4).

Fig. 2.1
figure 1

The experimental setup

Full size image

2.2.1 Preparation of Small Helium Clusters

Helium clusters are produced by expanding gaseous helium into vacuum through a nozzle with a 5 \(\upmu \)m orifice. During such free jet expansion, the cluster formation, i.e. nucleation, is governed by collision processes and depends on the temperature and pressure of the gas prior to expansion [4] (see the Chap. 1 by J. Peter Toennies in this volume). Effective cluster formation with yields up to 6% was found at low nozzle temperatures below 30 K [4]. In our experiments we used temperatures in the range of 8–12 K. The nozzle temperature is stabilized within better than ±0.01 K by a continuous flow cryogenic cryostat (Model RC110 UHV, Cryo Industries of America, Inc.). The pressure dependence of the cluster yield (in s\(^{-1}\)) at a nozzle temperature of 8 K is shown in Fig. 2.2.

As seen in Fig. 2.2 it is barely possible to find expansion conditions (i.e. back pressure) where clusters of a particular size are formed. Another complication in the cluster experiments is that helium monomers dominate in the molecular beam under all expansion conditions [4]. In order to select a single cluster size from the molecular beam we make use of matter wave diffraction. The technique was pioneered in the early 90s in the group of Prof. J. P. Toennies in Göttingen and is based on a transmission grating with a period of 100 nm [3, 5]. The clusters in the beam, having the same velocity, can be sorted by mass as their diffraction at the grating depends on the de Broglie wavelength \(\lambda _{dB} = \frac{h}{mv}\) (h is the Planck’s constant, m and v are the mass and the velocity of a cluster, respectively). Clusters of different size are deflected to different angles that results in spatial separation of clusters at the detection site (Fig. 2.1).

Fig. 2.2
figure 2

The figure is adapted from [6], Copyright (2016) by American Association for the Advancement of Science

Dependence of the \(^{4}\)He cluster rates on the back pressure at a temperature of 8 K for a nozzle with a 5 \(\upmu \)m orifice. The very low rate of the He\(_{3}\) excited state (He\(_{3}^{*}\), red) is scaled by a factor of 10\(^{3}\). The background caused by ground state structures has been subtracted from the excited state rate. The rates for the He\(_{3}\) ground state and He\(_{2}\) are shown in green and blue, respectively. The statistical error bars correspond to the standard deviation.

Full size image

2.2.2 Coulomb Explosion Imaging

Coulomb explosion imaging (CEI) was introduced in 1989 [7] as a relatively direct method for determining structure of small molecules (see [8] for the recent review). The main idea is to produce multiple charges in a molecule by, for instance, ionization, and let its constituents fly apart due to the mutual Coulomb repulsion. The momenta or kinetic energy that these charged molecular fragments (e.g. atomic ions) gain during this so-called Coulomb explosion depends on the initial distances between the parts in the neutral molecule. Thus, measuring momenta of charged fragments allows determining structural information about the molecule.

In the poof-of-the-principle experiment [7] the charges in the methane cation were produced by stripping off electrons when the cation was passing at high velocity through a thin solid film. Alternatively, electrons can be removed from a molecule using single photon ionization with the subsequent multiple Auger-decay [9], collision with a charged projectile [10, 11] or strong field ionization in ultrashort laser pulses [12,13,14,15].

Coulomb explosion imaging has been widely used for obtaining structural information about van-der-Waals clusters, wave packet dynamics [16, 17], imaging of excited vibrational states [11] as well as determination of absolute configuration of chiral molecules [18, 19].

Within the classical description of the Coulomb explosion, so-called frozen nuclei reflection approximation (FNRA), the potential energy of N singly charged ions located at distances \(R_{ij}\) from each other is converted into a kinetic energy release (KER):

$$\begin{aligned} \text {KER}_{N} = \sum _{i\ne j} \frac{1}{R_{ij}}, i,j = 1,2,..,N. \end{aligned}$$
(2.1)

If the ionization process is instantaneous, distances \(R_{ij}\) correspond to the structure of the neutral cluster. Therefore, by measuring the magnitudes and directions of the momenta (and correspondingly the KER) that the ions acquire during the Coulomb explosion, information on the geometrical structure of the cluster as well as its orientation in space can be obtained. Repeated measurements allow one to reconstruct the quantum mechanical structure distribution of the neutral cluster prior to the application of the ionization laser field. Note, that relation (2.1) is only valid for pure Coulomb repulsion, which in one dimension described by the 1/R potential. This is the case for weakly bound van-der-Waals clusters, which atomic orbitals are feebly overlapped.

Although, the FNRA has been successfully applied for obtaining ground state probability distributions of variety of small atomic and molecular clusters [14, 15, 20], including helium clusters [6, 21, 22], it was found to be inaccurate in imaging excited vibrational states of the H\(_{2}^{+}\) cation [11]. The reason is two-fold: 1) the electronic and nuclear degrees of freedom are not fully decoupled in this system and 2) the local kinetic energy (kinetic energy at a given R) can be comparable to the 1/R potential energy.

In general, the following conditions should be fulfilled for accurate description of Coulomb explosion imaging by the frozen nuclei reflection approximation:

  1. 1.

    The ionization of the cluster, that transfers the neutral wave packet to the final repulsive ionic state should be faster than possible movements of the wave packet on the intermediate states.

  2. 2.

    The ionization probability should be independent of internuclear distances \(R_{ij}\).

  3. 3.

    The recoil of electrons to the residual ion during ionization should be lower than the energy gained on the repulsive potential during Coulomb explosion.

  4. 4.

    There should be only one repulsive potential along which the cluster dissociates during Coulomb explosion.

  5. 5.

    The motion of the wave packet on the repulsive energy potential should be to a large extent “classical”.

Coulomb explosion of small helium clusters in general meets all these requirements. The ionization of the cluster in a strong laser field happens sequentially via tunnelling ionization processes [23]:

$$\begin{aligned} He_N \rightarrow He_N^{+} + e^{-} \rightarrow , ..., \rightarrow He_N^{(N-1)+} + (N-1)e^{-} \rightarrow He_N^{N+} + Ne^{-}. \end{aligned}$$

Since tunnelling ionization is highly nonlinear process it mainly happens within a short time interval close to the field maximum. This interval is about 20 fs in case of 30 fs laser pulses with a peak intensity of about 10\(^{16}\) W/cm\(^2\). On this time scale the ionization process can be treated as instantaneous, since intermediate ionic potentials of He\(_2\) and He\(_3\) are rather shallow [24, 25].

In general, the ionization probability of the ionization sequence shown above depends on the internuclear distance R. The reason for this is that the R-dependence of the ionic potentials determines the vertical ionization potential of the corresponding ionization step. The ionization potential, in turn, governs the ionization probability in a highly nonlinear manner [23]. It turns out, however, that the R-dependence is extremely weak in case of high laser intensities (\(\sim \)10\(^{16}\) W/cm\(^2\)) for which the single ionization is saturated.

Upon ionization the electrons “kick” the residual ions providing them with initial momenta prior to Coulomb explosion. According to our measurements, these initial momenta follow a Gaussian distribution centered around zero with a width of about few atomic units and point along the direction of the probe field polarization. In case of the dimer the FNRA, which does not account for the electron “kick”, underestimates the probability distribution for large interatomic distances. Using simulation we estimated the corresponding correction and applied it to the FNRA data in order to get the probability distribution of the interatomic distance in the helium dimer (2.5). The recoil of electrons is also taken into account during structure reconstruction of the helium trimer (2.2.4).

2.2.3 COLTRIMS

The 3D momenta of the ions acquired during the Coulomb explosion are measured by cold target recoil ion momentum spectroscopy (COLTRIMS) [26]. In the COLTRIMS spectrometer a homogenous electric field (3–4 V/cm) guides ions onto a time and position sensitive micro-channel plate detector with hexagonal delay-line position readout [27] and an active area with a diameter of 80 mm (Fig. 2.1). The detector is typically placed at a distance of 40–50 mm away from the laser focus, which results in a 4\(\pi \) collection solid angle for atomic ions with an energy of up to 3 eV.

2.2.4 Structure Reconstruction from the Momentum Space

COLTRIMS allows to measure ion momenta after Coulomb explosion. In case of the dimer the interatomic distance can be deduced from these momenta using 2.1. In case of the trimer the structural reconstruction is not that straightforward. We devised a look-up table approach in which Coulomb explosion was simulated classically for many different trimer structures [6]. The obtained relations between structures and momenta were saved in a table. In order to reduce the dimensionality of the table we utilized two-dimensional representation proposed by Dalitz [28] for both structures and momenta (Fig. 2.3). Since the Dalitz representation encodes only the shape of a structure, we used the measured KER for deducing the absolute size of the trimer.

The Dalitz coordinates x, y for both coordinate and momentum space are defined as follows:

$$\begin{aligned} x = \frac{\varepsilon _2 - \varepsilon _3}{\sqrt{3}}, y= \varepsilon _1 - \frac{1}{3} \end{aligned}$$

where

$$\begin{aligned} \varepsilon _i^{\text {coordinate}} = \frac{|\mathbf {r_i}|^2 }{ \sum \limits _{n=1}^3 |\mathbf {r_n}|^2 } ~,~ \varepsilon _i^{\text {momentum}} = \frac{|\mathbf {p_i}|^2 }{ \sum \limits _{n=1}^3 |\mathbf {p_n}|^2 } \end{aligned}$$

with \(\mathbf {r_i}\) being a position vector of ith atom of the trimer with respect to the center-of-mass and \(\mathbf {p_i}\) being a momentum vector of ith atom after Coulomb explosion.

Fig. 2.3
figure 3

Dalitz plot. Triangles correspond to structures of a trimer (for the coordinate space). Arrows represent the momentum vectors (for the momentum space)

Full size image

The coordinate and momentum Dalitz’s spaces were binned by \(1000\times 1000\). For each bin the corresponding structure in coordinate space was numerically “exploded” several times with different randomly generated small initial momenta using Newton’s equations of motion. These initial momenta is a result of the electron recoil during ionization. The three-dimensional distribution of the initial momenta was chosen in the way to match the experimental distribution of the singly charged helium ion.

2.3 Helium Dimer

The helium dimer is bound by a potential with a well depth of about 11 K. The well depth almost equals to the zero-point energy of the dimer, which was the reason for long debates about existence of the helium dimer. It turned out that the binding energy is below 2 mK. This tiny binding energy poses a challenge to the theory requiring very high accuracy in calculation of the interatomic potential. The accuracy of ab-initio methods was mediocre until 1990s. In those early days mainly empirical analytical expressions modelling the He-He potential have been proposed. The parameters in such expressions were optimized in order to reproduce the viral coefficients and other thermophysical properties of helium. The binding energies and the expectation values of the interatomic distance for some potentials are collected in Fig. 2.4. In the 1990s the accuracy of ab-initio methods based on the Born-Oppenheimer approximation was improved, which allowed developing better model potentials. One such potential is LM2M2; it has been frequently used for theoretical treatment of small helium clusters. In the 2000s it became possible to improve ab-initio methods further by including many corrections beyond the Born-Oppenheimer approximation. The most recent potential of Szalewicz and co-workers [2, 29, 30] accounts for adiabatic, relativistic, QED corrections as well as retardation. These corrections change the binding energy of the helium dimer by 6–10%. The biggest of these corrections is retardation (about 9%).

Fig. 2.4
figure 4

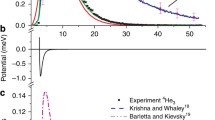
Predicted and experimental binding energies (a) and average interatomic distances (b) of the helium dimer. The following He-He potentials have been considered: HFDHE2 [31], HFIMD [32], TT [33], HFD-B(HE) [34],HFD-B2(HE) [35], LM2M2 [36], LM2M2* [37], TTY [38], HFD-B3-FCl1a [39], HFD-B3-FCl1c* [39], SAPT1* [40, 41], SAPT2* [40, 41], SAPT [40, 41], r12-MR-ACPF* [42], EQMC* [43], Jeziorska [44], Jeziorska* [44], PCKLJS* [30, 45]. Star symbol indicates inclusion of correction for retardation. The experimental values are labelled as “exp. Luo” [2], “exp. Grisenti” [46] and “exp. Zeller” [22]. Theoretical and experimental data is shown in blue and red, respectively. Panel (a) is adapted from [22], Copyright (2016) by National Academy of Sciences of the United States of America

Full size image

The tiny binding energy is responsible for a huge spatial extent of the dimer that spreads far beyond the potential well, such that about 80% of the probability distribution resides in the classically forbidden tunnelling region. Such few body systems have been termed “quantum halos”. An expectation value of the interatomic distance of the helium dimer is predicted to be about 47 Å (Fig. 2.4).

Such fragile systems as helium dimer pose challenges also for experimentalists. During preparation of the dimer the temperature of environment should be lower than the binding energy, i.e. as low as 1 mK. Moreover, since the helium dimer does not possess any bound ro-vibrational states, it cannot be detected by standard spectroscopic tools. First experimental evidence for existence of the helium dimer was provided in 1993 by mass-spectrometry [37]. There, the helium gas at room temperature was expanded into the vacuum through the nozzle with an orifice of 150 \(\upmu \)m. Subsequently, the supersonic gas expansion was collimated and ionized by electron impact ionization that allowed to detect He\(_2^+\) ions. The main criticism of this experimental concept was that He\(_2^+\) ions could originate from fragmentation of larger helium clusters. This issue was addressed by measuring dependence of the ion signal on the nozzle back pressure [37]. The pressure dependence turned out to be quadratic for the He\(_2^+\) ion yield, which contradicts the scenario of large clusters fragmentation. Subsequent experiment in 1996 [47] utilized transmission through nanoscale sieves for measuring the mean internuclear distance of the cluster corresponding to the He\(_2^+\) ion signal. The obtained value of 62±10 Å was very close to the predicted expectation value of the interatomic distance in the helium dimer at that time (55 Å).

Another and more direct evidence of the existence of the helium dimer was obtained in 1994 using matter wave diffraction [3] in the group of Prof. J. P. Toennies. In experiments the helium beam produced under supersonic expansion was deflected by a tiny transmission grating with a period of 200 nm [48]. The different clusters were deflected at different angles due to the difference in the de Broglie wavelength. Analysis of many diffraction orders of He\(_2\) with the theory that took into account dispersive interaction with the grating bars allowed to estimate a mean internuclear distance and a binding energy of 52±4 Å and 1.1+0.3/-0.2 mK, respectively.

Using CEI we measured the square of the nuclear wave function of the helium dimer [22], which is shown in Fig. 2.5. This probability distribution consists of one experimental set, where Coulomb explosion was initiated by a strong laser field (\(I_0 \approx 3\times 10^{15} ~{\text {W}}\cdot \mathrm {cm}^{-2}\), \(\lambda = 780\) nm, \(\Delta t_{\text {FWHM}} \approx ~\)30 fs). In this respect, the experimental data presented here is different from that in [22], which consists of two experimental sets: the region of short interatomic distances (\(R<14\) Å) were measured using a femtosecond laser, while the range of long interatomic distances (\(R \geqslant 14\) Å) were measured at the free-electron laser facility in Hamburg (FLASH). As predicted, the distribution spreads far beyond the classically allowed region (shown in green in Fig. 2.5). The expectation value of the interatomic distance was found to be 45 ± 2 Å, which is in line with the most recent theoretical predictions (Fig. 2.4b).

Fig. 2.5
figure 5

The measured square of the nuclear wave function of the helium dimer. The distribution is corrected for the electron recoil during ionization. a Green and pink colored areas under the distribution visualize the classically allowed and forbidden regions, respectively. The He-He interaction potential is shown in black. Note the logarithmic scale on the x-axis. b Fit of the experimental probability distribution by expression (2.2) is shown in red. Note the logarithmic scale on the y-axis. Statistical error bars are smaller than the radius of blue circles. Based partially on results reported in [22]

Full size image

Apart from being a benchmark system for theoretical methods, the helium dimer, as a quantum halo, is a perfect candidate for testing general predictions of quantum mechanics such as the exponential decay of the wave function in the tunnelling region. Indeed, as seen in Fig. 2.5b the decay of the measured squared wave function for \(R>25\) Å resembles closely the exponential one (note the logarithmic scale on the y-axis). Solving the Schrödinger equation for a particle below the barrier, one obtains the following expression for the squared wave function:

$$\begin{aligned} \Psi ^2(R) \propto e^{-\frac{2}{\hbar }\sqrt{2\mu E_{\text {bind}}}R}. \end{aligned}$$
(2.2)

Here \(E_{\text {bind}}\) is the binding energy of the helium dimer, which corresponds to the barrier height, and \(\mu =m_{\text {He}}/2\) is the reduced mass of the dimer. Fitting the experimental probability distribution in Fig. 2.5 with expression (2.2), we found the binding energy of the helium dimer to be \(1.77\pm 0.15\) mK. This experimental value is very close to the one obtained in [22] (\(1.76\pm 0.15\) mK) using interatomic distance distribution of the helium dimer measured at FLASH. Both experimental binding energies are in good agreement with the most recent theoretical calculations (Fig. 2.4a).

2.4 Helium Trimer

Presently it is known that the helium trimer, \(^4\)He\(_3\), has two vibrational states: the ground state and the excited one of the Efimov nature [49]. Though the former state was observed experimentally back in 1994 using the matter wave diffraction technique [3], the excited Efimov state remained elusive for longer time and was detected only in 2014 [6], 37 years after its theoretical prediction [50].

In the following the size and structure of both states of \(^4\)He\(_3\) as well as the single state of \(^3\)He\(^4\)He\(_2\) will be discussed.

2.4.1 \(^4\)He\(_3\): Ground State

The recent theory [51] predicts that the ground state of the helium trimer is more strongly bound (\(E_{\text {bind}}\)=131.84 mK) comparing to the helium dimer and, thus, has a more compact size with an average interatomic distance of 9.53 Å. This is in agreement within error bars with the experimentally obtained value of 11\(^{+4}_{-5}\) Å  [52]. We measured the trimer using the CEI technique, where ionization was performed by a strong 30 fs laser field [21]. The trimer structures were reconstructed from the momentum space using the procedure described in 2.2.4. The obtained interatomic distance distribution (Fig. 2.6a) as well as the distribution of corner angles in a trimer (Fig. 2.6b) resemble closely theoretical ones, calculated with quantum Monte Carlo (QMC) [21, 53] and coupled-channel [6, 54] methods. In the Monte Carlo simulation the TTY helium-helium potential [38] was used, whereas the coupled-channel method utilized the most recent PCKLJS potential [30, 45]. Average interatomic distances estimated from the distributions in Fig. 2.6a are 9.3 ± 1 Å  (experimental), 9.61 Å  (QMC) and 9.53 Å  (coupled-channel).

Fig. 2.6
figure 6

Interatomic distance and corner angle distributions of the helium trimer, \(^4\)He\(_3\). The distributions obtained in the QMC (blue) and coupled-channel (green) simulations are almost identical. Based on results reported in [6, 21]

Full size image

Though many theories agreed on the binding energy and the size of the helium trimer, for long time no consensus was achieved about its shape. The suggested typical structures were ranging from a nearly linear [55,56,57,58] to an equilateral triangle [59, 60]. Bressanini and co-workers pointed out that the question of typical structure in case of \(^4\)He\(_3\) is ill-posed. Considering the two-dimensional angle distributions they found that more or less all structures are equally probable. The fact that some structures seem to be more favoured explained solely by the choice of the visualisation approach.

The idea of the not-well-defined structure of He\(_3\) was additionally supported by the random cloud model proposed by Voigtsberger et al. [21]. In the model a trimer was constructed by picking three atoms randomly from the hypothetical three-dimensional cloud, defined by a spherically symmetric atom density. The density was considered to be constant within a sphere of a certain radius and decayed exponentially outside that sphere. The cloud was thus characterized by two parameters: a radius and a decay rate [21]. Here we have simplified the random cloud model by using only an exponential decay of the radial atom density of the cloud defined by the following function:

$$\begin{aligned} \rho (R) = e^{-aR}. \end{aligned}$$
(2.3)

Fitting the interatomic distance distribution obtained from this random cloud model to the experimental one, the decay parameter \(a=0.525\) Å\(^{-1}\) was determined. Hence, even a single parameter model is sufficient for fairly good reproduction of interatomic distance and angle distributions of the helium trimer in Fig. 2.6. In the region of interatomic distances \(R<4\) Å  the agreement is rather poor (Fig. 2.6a), since the simple model does not account for repulsion between two helium atoms at short distances.

Another way of visualising the trimer structure is to plot three atoms in the coordinate system defined by two principal axes of inertia, \(\mathbf {a}\) (corresponding to the smallest moment of inertia) and \(\mathbf {b}\) and having the center-of-mass of the cluster at the origin, as proposed by Nielsen et al. [59]. Using this representation (Fig. 2.7) one could argue that the shape of the helium trimer closely resembles the equilateral triangle. However, more or less the same two-dimensional distribution results from the random cloud model.

Fig. 2.7
figure 7

Structure of the ground state of the helium trimer, \(^4\)He\(_3\). Three helium atoms are plotted in the coordinate system defined by the principal axes of inertia with the origin in the center-of-mass. Based on results reported in [6, 21]

Full size image

2.4.2 \(^4\)He\(_3\): Excited Efimov State

In 1970 Vitaly Efimov predicted a peculiar quantum effect in a three-body system consisting of bosons [49]. Namely, at the limit of extremely weak interaction between two bosons, when a single state of a two-body system becomes unbound, infinite number of three-body bound states appear. It turned out, that an effective long range \(1/R^2\) potential that arises between three particles under such conditions is responsible for such behavior. The effect is independent of the details of the underlying two-body interactions. In this respect, the Efimov effect is an universal phenomenon, which can be found in different fields of physics such as atomic [6, 61], nuclear [62], condensed matter [63] and high energy physics [64].

Seven years after Efimov’s prediction it was suggested that the helium trimer could have an Efimov state [50]. However, not all calculations based on different realistic helium-helium potentials supported this conclusion [39]. Using most recent potential it was shown that \(^4\)He\(_3\), indeed, has two states [51]. In theory one can investigate how binding energies of both states depend on the scattering length a (relates to the depth of the two-body potential well) by artificially scaling the helium-helium potential. The corresponding so-called Efimov plot consists of three areas (Fig. 2.8). The top violet area (\(E>0\)) belongs to three particle continuum. The area to the right of the blue line (binding energy of the dimer) corresponds to the three particle region where two particles are bound forming a dimer and the third one being free. To the left of the dimer binding energy curve lies the area where trimer bound states can exist. Two bound states of the trimer, one of which is the Efimov one (labelled as “1st ES”), correspond to the native scattering length of helium \(a = 90.4\) Å. An ideal Efimov case with an infinite number of bound states would be at \(a=\infty \). The size and the binding energy of such ideal Efimov states are scaled by factors 22.7 and \(22.7^2\), respectively.

Fig. 2.8
figure 8

The figure is adapted from [6], Copyright (2016) by American Association for the Advancement of Science

Theoretical dependence of the binding energy E of two \(^4\)He\(_3\) states: the ground state (GS) and the first excited state (1st ES) on the two-body scattering length a. The vertical dashed line corresponds to the naturally occurring \(^4\)He\(_3\) with a scattering length of 90.4 Å. The area for \(E>0\) is the unbound three-particle continuum. The blue line corresponds to the binding energy of the helium dimer. To the right of this line the dimer-atom region that describes the dimer and a separate helium atom. To the left of the blue line the area where three helium atoms are bound.

Full size image

In 2005 an experimental attempt was undertaken to detect the Efimov state of the helium trimer using matter wave diffraction at a 100 nm period transmission grating [52]. In the experiment the grating was rotated by an angle of 21\(^{\circ }\), which allowed to almost halve the slit width and, consequently, increase sensitivity of the method for the trimer detection. Since the effective slit width, which determines the diffraction pattern, depends furthermore on the cluster dimension, the authors were able to estimate the average trimer size (see Sect. 2.4.1). Comparing this value to the theoretical one it was concluded that the contribution of the large Efimov state was below experimental sensitivity (6%). According to the theory of cluster formation, the concentration of the Efimov state under experimental conditions was estimated to be about 10%. The fact that the Efimov state was not detected led to doubting its existence.

One can see from Fig. 2.2 that the relative yield of the Efimov state (He\(^*_3\), in red) with respect to the ground state (He\(_3\), in green) is well below 1% under expansion conditions that are optimized for the ground state yield (\(p\approx 1.2\) bar). This might be an explanation why the Efimov state was not detected in the experiment of Brühl et al. [52].

In 2014 we successfully observed the Efimov state of the helium trimer using laser-based CEI [6]. We used two approaches to reconstruct the pair distance distribution from the measured ion momenta after Coulomb explosion. In the first approach the filter in the momentum space was applied to cut the contribution of the ground state (Fig. 2.9 in black, for details see [6]), which was dominant in the molecular beam under all expansion conditions (Fig. 2.2). In the second reconstruction approach the ground state pair distance distribution was subtructed from that of the mixture of the ground and Efimov states (Fig. 2.9 in red). Both experimental distributions match the theoretical one (Fig. 2.9 in violet) very well for large interatomic distances (\(R>100\) Å). At small distances the resemblance is poor due to the remaining contamination of the ground state.

Fig. 2.9
figure 9

The figure is adapted from [6], Copyright (2016) by American Association for the Advancement of Science

Pair distance distribution of the Efimov state of the helium trimer, \(^4\)He\(_3\). Note logarithmic scale of the y axis. Two experimental distributions (labelled as “reconstr. 1” and “reconstr. 2”) are obtained using different reconstruction approaches, see text for details. The fitted exponential decay according to expression (2.2) is shown in blue. Statistical error bars correspond to the standard deviation.

Full size image

As seen from Fig. 2.9 the Efimov state of \(^4\)He\(_3\) has a huge spatial extent, spreading beyond 300 Å. It thus also belongs to the family of quantum halos, i.e. most of its probability distribution resides well outside the potential well in the classically forbidden region. Therefore the asymptotic part of the pair distance distribution shows an exponential decay, likewise the wave function of the helium dimer. Similarly, the expression (2.2) can be used for obtaining the binding energy of the Efimov state. In this case, however, the binding energy is defined not with respect to the dissociation continuum of three atoms, but relative to the binding energy of the helium dimer [51]. From the fit (Fig. 2.9, blue) this partial binding energy \(\Delta E\) was found to be \(0.98\pm 0.20\) mK. Given the dimer binding energy of \(1.77\pm 0.15\) mK, the binding energy of the Efimov state with respect to the three-body dissociation continuum is estimated to be \(2.75\pm 0.25\) mK. This experimental value is in a good agreement with the theoretical value of 2.65 mK [6, 51].

Fig. 2.10 presents the first experimental image of the Efimov state [6]. For this representation the same coordinate system as in Fig. 2.7, namely, based on the principal axes of inertia, was used. The structure of the Efimov state looks substantially different to that of the ground state in Fig. 2.7. Whereas in the ground state all structures are equally probable (see Sect. 2.4.1), the excited Efimov state is dominated by configurations in which two atoms are close to each other with the third one being farther away.

Fig. 2.10
figure 10

The figure is adapted from [6], Copyright (2016) by American Association for the Advancement of Science

Structure of the Efimov state of the helium trimer, \(^4\)He\(_3\). Three helium atoms are plotted in the coordinate system defined by the principal axes of inertia with the origin in the center-of-mass.

Full size image

Further insights in the structure of the Efimov state can be gained by considering the distribution of the shortest interatomic distance (Fig. 2.11). This distribution resembles very closely the interatomic distance distribution of the helium dimer (Fig. 2.5), implying that the Efimov state consists of a dimer to which the third helium atom is weakly attached and located at even larger distance than two atoms in the dimer. This shape is justified by the position of the Efimov state in the Efimov plot (Fig. 2.8). Namely, it is located very close to the dimer-atom region.

Fig. 2.11
figure 11

Distributions corresponding to the shortest and two longest (labelled as “long”) interatomic pair distances of the Efimov state of \(^4\)He\(_3\). The experimental distribution of He\(_2\) (from Fig. 2.5) is shown in blue

Full size image

2.4.3 \(^3\)He\(^4\)He\(_2\)

Substitution of one \(^4\)He atom in the trimer by the lighter \(^3\)He isotop decreases the binding energy of the ground state by about 8 times due to the increase in the zero-point vibrational energy [59, 65, 66]. Only one state in such heterotrimer remains bound [59]. It is so-called Tango state [62, 67], where only one pair of atoms out of three can form the two-body bound state. The existence of the cluster was confirmed in experiments with matter wave diffraction [68].

Voigtsberger et al. [21] measured the \(^3\)He\(^4\)He\(_2\) trimer using laser-based CEI. The pair distance distributions are in fairly good agreement with the QMC theory by Dario Bressanini [21, 69]. It was found that the \(^3\)He-\(^4\)He distances are longer than \(^4\)He-\(^4\)He ones, and that size of the heterotrimer is larger than that of the \(^4\)He\(_3\) ground state as expected from the lower binding energy (Fig. 2.12a). Along with angle distributions (Fig. 2.12b) one can conclude that \(^3\)He\(^4\)He\(_2\) exists as an acute triangle having \(^3\)He atom at the corner with a smallest angle. As was however pointed out [69], the trimer is very defuse to talk about the well defined structure. The same conclusion can be drawn by considering plots in the coordinate system defined by the principal axes of inertia (Fig. 2.13).

Fig. 2.12
figure 12

Interatomic distance and corner angle distributions of the helium heterotrimer, \(^3\)He\(^4\)He\(_2\). Based on results reported in [21]

Full size image
Fig. 2.13
figure 13

Structure distribution of the helium heterotrimer, \(^3\)He\(^4\)He\(_2\). The coordinate system is defined by the principal axes of inertia with the origin in the center-of-mass

Full size image

2.5 Field-Induced Dynamics in the Helium Dimer

So far we have considered steady state structures and binding energies of small helium clusters consisting of two and three atoms. Ability of controlling interaction between helium atoms in a cluster would open up a door to series of experiments, where not only new exotic states can be created but also response dynamics of these unique quantum objects to an external disturbance can be investigated. In case of ultracold atomic gases such interaction control is achieved in the vicinity of Feshbach resonances through an application of a magnetic field [70, 71]. This is however not suitable for non-magnetic helium atoms. Nielsen and co-workers [72] suggested to use an external electric field to tune interaction between helium atoms and predicted appearance of bound states in the naturally unbound \(^3\)He\(^4\)He and \(^4\)He\(^3\)He\(_2\). In addition, it has been suggested to use intense laser fields to modify rovibrational states of weakly bound molecules [73,74,75,76] as well as to turn the helium dimer into a “covalent”-like molecule that supports many bound states [75, 77]. These phenomena are unexplored experimentally due to challenges in preparation and detection of such fragile quantum states.

Another interesting aspect of a laser field interaction with molecules is a non-adiabatic alignment of molecules in space (see the Chap. 9 by Nielsen et al. in this volume). How this interaction manifests itself in quantum halos that do not support any bound rotational states? Would one expect to see angular anisotropy? Would the spatially extended system reacts as whole to a rotational “kick”? In order to answer these questions we applied a 310 fs laser pulse (\(1.3\times 10^{14}~\mathrm{{W}} \cdot \text {cm}^{-2}\)) to the helium dimer and watched its response using CEI initiated by the delayed probe pulse (30 fs, ca. \(10^{16}~\mathrm{{W}} \cdot \text {cm}^{-2}\)) [78]. The pump laser pulse induces dipoles on helium atoms changing the native interaction potential. The overall potential becomes anisotropic: repulsive perpendicular to the laser polarization direction and about 3 times more attractive along the polarization direction than the native potential (Fig. 2.14). Note that the laser field modifies the interaction potential only in a very small region, namely, in the vicinity of the potential well (\(R<10\)  Å).

Fig. 2.14
figure 14

The figure is adapted from [78], Copyright (2021) by Springer Nature

Field-induced interatomic potential of the helium dimer. A volume averaged intensity of the laser field is \(1.3\times 10^{14}~\text {W} \cdot \mathrm {cm}^{-2}\) (\(E \approx 3.13 \times 10^8 ~\mathrm {V} \cdot \text {cm}^{-1}\)).

Full size image

The response of the helium dimer to the pump pulse is shown in Fig. 2.15 in terms of alignment parameter \(\langle \text {cos}^2\theta \rangle \). Prior to the pump pulse the angular distribution of the dimer axis in space is isotropic for all interatomic distances (\(\langle \text {cos}^2\theta \rangle = 1/3\)). Right after arrival of the pump pulse the positive alignment (\(\langle \text {cos}^2\theta \rangle > 1/3\)) emerges at short interatomic distances. Subsequently the alignment wave moves to larger interatomic distances and gets broader. This response is very different to what is known from typical alignment experiments, namely, periodic in time alignment signal, called recurrences [79]. The experimental observation is accurately reproduced by the parameter-free quantum simulation [78].

Fig. 2.15
figure 15

The figure is adapted from [78], Copyright (2021) by Springer Nature

Temporal evolution of the field-induced alignment of \(^4\)He\(_2\). a experiment, b theory. Expectation value of \(\text {cos}^2\theta \) is shown in color. \(\theta \) is an angle between the dimer axis and the direction of laser polarization.

Full size image

The field-induced dynamics of He\(_2\) can also be visualised by changes in the probability density. These changes are shown in Fig. 2.16 for two orientations of the dimer axis with respect to the polarization direction of the laser field: parallel and perpendicular. Changes in the probability density resemble the outgoing alignment wave in Fig. 2.15. Remarkably, not only magnitude, but also the phase of the density wave is resolved. According to quantum mechanics, the phase of the wave packet is only accessible through interference with another wave packet or wave function. Note that two wave packets, propagating along the laser polarization (Fig. 2.16a) and perpendicular to it (Fig. 2.16b) are out of phase.

The picosecond response of the single state He\(_2\) to an intense laser field (Figs. 2.15 and 2.16) can be understood as follows. Initially the laser field induces an isotropic effective potential in the short interatomic region of the dimer (Fig. 2.14). This potential results in transfer of some part of the ground state wave function at these distances to the unbound \(J=2\) rotational state, creating a dissociating wave packet. Subsequently, the wave packet moves along the repulsive \(J=2\) potential towards larger interatomic distances and spreads with time due to intrinsic dispersion of the matter wave. Its interference with a huge isotropic ground state wave function allows to measure the quantum phase of the wave packet. At large interatomic distances the \(J=2\) potential is very flat, implying that the dissociating wave packet moves without influence of any force. This is confirmed by the temporal evolution of the semi-classical phase of a free particle with a reduced mass of 2 amu (Fig. 2.16b, green dashed lines). Thus, the experiment shows not only how a halo state reacts to the non-adiabatic tuning of the two-body interaction, but also visualizes propagation of a freely moving quantum particle in space.

Fig. 2.16
figure 16

The figure is adapted from [78], Copyright (2021) by Springer Nature

Temporal evolution of the field-induced changes in the probability distribution of \(^4\)He\(_2\). a Dimer axis is within \(\pm 40^{\circ }\) to the laser polarization direction. b Dimer axis is within \(90 \pm 40^{\circ }\) to the laser polarization direction. The green dashed lines in panel b show the calculated constant-phase evolution of a free particle with a reduced mass of 2 amu.

Full size image

2.6 Conclusions

Coulomb explosion imaging is a powerful tool for retrieving probability distributions and binding energies of small helium clusters. Extension of the method towards larger clusters is feasible though the structure reconstruction seems to be rather challenging. A cluster consisting of four helium atoms, the helium tetramer, is particular interesting for the following reason. It has been shown [80, 81] that four-body systems with a huge two-body scattering length also show universal behaviour and have states that are connected to Efimov states in a trimer.

Combination of Coulomb explosion imaging with a control of interaction between helium atoms in a pump-probe manner, as demonstrated using the helium dimer, paving the way for studying field-induced dynamics in these peculiar quantum systems. One might envision application of such technique to the helium trimer in order to explore the birth and decay of an Efimov state in time.