Abstract
The most efficient way to calculate strong bisimilarity is by finding the relational coarsest partition of a transition system. We provide the first linear-time algorithm to calculate strong bisimulation using parallel random access machines (PRAMs). More precisely, with n states, m transitions and \(| Act |\le m\) action labels, we provide an algorithm for \(\max (n,m)\) processors that calculates strong bisimulation in time \(\mathcal {O}(n+| Act |)\) and space \(\mathcal {O}(n+m)\). The best-known PRAM algorithm has time complexity \(\mathcal {O}(n\log n)\) on a smaller number of processors making it less suitable for massive parallel devices such as GPUs. An implementation on a GPU shows that the linear time-bound is achievable on contemporary hardware.
This work is carried out in the context of the NWO AVVA project 612.001751 and the NWO TTW ChEOPS project 17249.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
The notion of bisimilarity for Kripke structures and Labelled Transition Systems (LTSs) is commonly used to define behavioural equivalence. Deciding this behavioural equivalence is important in the field of modelling and verifying concurrent and multi-component systems [4, 15]. Kanellakis and Smolka proposed a partition refinement algorithm for obtaining the bisimilarity relation for Kripke structures [11]. The proposed algorithm has a run time complexity of \(\mathcal {O}(nm)\) where n is the number of states and m is the number of transitions of the input. Later, a more sophisticated refinement algorithm running in \(\mathcal {O}(m~log~n)\) steps was proposed by Paige and Tarjan [16].
In recent years the increase in the speed of sequential chip designs has stagnated due to a multitude of factors such as energy consumption and heat generation. In contrast, parallel devices such as graphics processing units (GPUs) keep increasing rapidly in computational power. In order to profit from the acceleration of these devices, we require algorithms with massive parallelism. The article “There’s plenty of room at the Top: What will drive computer performance after Moore’s law” by Leierson et al. [13] indicates that the advance in computational performance will come from software and algorithms that can employ hardware structures with a massive number of simple, parallel processors, such as GPUs. In this paper, we propose such an algorithm to decide bisimilarity.
Deciding bisimilarity is P-complete [1], which suggests that bisimilarity is an inherently sequential problem. This fact has not withheld the community from searching for efficient parallel algorithms for deciding bisimilarity of Kripke structures. In particular, Lee and Rajasekaran [12, 17] proposed a parallel algorithm based on the Paige Tarjan algorithm that works in \(\mathcal {O}(n\ log\ n)\) time complexity using \(\frac{m}{\log n}\log \log n\) Concurrent, Read Concurrent Write (CRCW) processors, and one using only \(\frac{m}{n}log~n\) Concurrent Read Exclusive Write (CREW) processors. Jeong et al. [10] presented a linear time parallel algorithm, but it is probabilistic in the sense that it has a non-zero chance to output the wrong result. Furthermore, Wijs [22] presented a GPU implementation of an algorithm to solve the strong and branching bisimulation partition refinement problems. In a distributed setting, Blom and Orzan studied algorithms for refinement [2]. Those algorithms use message passing as a way of communication between different workers in a network and rely on a small number of processors. Therefore, they are very different in nature than our algorithm. Those algorithms were extended and optimized for branching bisimulation [3].
In this work, we improve on the best known theoretical bound for PRAM algorithms using a higher degree of parallelism. The proposed algorithm improves the run time complexity to \(\mathcal {O}(n)\) on \(\max (n,m)\) processors and is based on the sequential algorithm of Kanellakis and Smolka [11]. The larger number of processors used in this algorithm favours the increasingly parallel design of contemporary and future hardware. In addition, the algorithm is optimal w.r.t. the sequential Kanellakis-Smolka algorithm, meaning that overall, it does not perform more work than its sequential counterpart.
We first present our algorithm on Kripke structures where transitions are unlabelled. However, as labelled transition systems (LTSs) are commonly used, and labels are not straightforward to incorporate in an efficient way (cf. for instance [21]), we discuss how our algorithm can be extended to take action labels into account. This leads to an algorithm with a run time complexity of \(\mathcal {O}(n + | Act |)\), with \( Act \) the set of action labels.
Our algorithm has been designed for and can be analyzed with the CRCW PRAM model, following notations from [20]. This model is an extension of the normal RAM model, allowing multiple processors to work with shared memory. In the CRCW PRAM model, parallel algorithms can be described in a straightforward and elegant way. In reality, no device exists that completely adheres to this PRAM model, but with recent advancements, hardware gets better and better at approximating the model since the number of parallel threads keeps growing. We demonstrate this by translating the PRAM algorithm to GPU code. We straightforwardly implemented our algorithm in CUDA and experimented with an NVIDIA Titan RTX, showing that our algorithm performs mostly in line with what our PRAM algorithm predicts.
The paper is structured as follows: In Sect. 2, we recall the necessary preliminaries on the CRCW PRAM model and state the partition refinement problems this paper focuses on. In Sect. 3, we propose a parallel algorithm to compute bisimulation for Kripke structures, which is also called the Relational Coarsest Partition Problem (RCPP). In this section, we also prove the correctness of the algorithm and provide a complexity analysis. In Sect. 4, we discuss the details for an implementation with multiple action labels, thereby supporting LTSs, which forms the Bisimulation Coarsest Refinement Problem (BCRP). In Sect. 5 we discuss the results of the implementation and in Sect. 6 we draw conclusions.
2 Preliminaries
2.1 The PRAM Model
The Parallel Random Access Machine (PRAM) is a natural extension of the normal Random Access Machine (RAM), where an arbitrary number of parallel processors can access the memory. Following the definitions of [20] we use a version of PRAM that is able to Concurrently Read and Concurrently Write (CRCW PRAM). It differs from the model introduced in [6] in which the PRAM model was only allowed to concurrently read from the same memory address, but concurrent writes (to the same address) could not happen.
A CRCW PRAM consists of a sequence of numbered processors \(P_0, P_1, \dots \). These processors have all the natural instructions of a normal RAM such as addition, subtraction, and conditional branching based on the equality and less-than operators. There is an infinite amount of common memory the processors have access to. The processors have instructions to read from and write to the common memory. In addition, a processor \(P_i\) has an instruction to obtain its unique index i. A PRAM also has a function \(\mathcal {P}:{\mathbb {N}}\rightarrow {\mathbb {N}}\) which defines a bound on the number of processors given the size of the input.
All the processors have the same program and run synchronized in a single instruction, multiple data (SIMD) fashion. In other words, all processors execute the program in lock-step. Parallelism is achieved by distributing the data elements over the processors and having the processors apply the program instructions on ‘their’ data elements.
Initially, given input consisting of n data elements, the CRCW PRAM assumes that the input is stored in the first n registers of the common memory, and starts the first \(\mathcal {P}(n)\) processors \(P_0, P_1, \dots ,P_{\mathcal {P}(n)-1}\).
Whenever a concurrent write happens to the same memory cell, we assume that one arbitrary write will succeed. This is called the arbitrary CRCW PRAM.
A parallel program for a PRAM is called optimal w.r.t. a sequential algorithm if the total work done by the program does not exceed the work done by the sequential algorithm. More precisely, if T is the parallel run time and P the number of processors used, then the algorithm is optimal w.r.t. a sequential algorithm running in S steps if \(P\cdot T \in \mathcal {O}(S)\).
2.2 Strong Bisimulation
To formalise concurrent system behaviour, we use LTSs.
Definition 1 (Labeled Transition System)
A Labeled Transition System (LTS) is a three-tuple \(A=(S, Act, \rightarrow )\) where S is a finite set of states, Act a finite set of action labels, and \(\rightarrow \subseteq S\times Act \times S\) the transition relation.
Let \(A = (S, Act, {\rightarrow })\) be an LTS. Then, for any two states \(s,t\in S\) and \(a \in Act\), we write  iff \((s,a,t)\in {\rightarrow }\).
iff \((s,a,t)\in {\rightarrow }\).
Kripke structures differ from LTSs in the fact that the states are labelled as opposed to the transitions. In the current paper, for convenience, instead of using Kripke structures where appropriate, we reason about LTSs with a single action label, i.e., \(| Act | = 1\). Computing the coarsest partition of such an LTS can be done in the same way as for Kripke structures, apart from the fact that in the latter case, a different initial partition is computed that is based on the state labels (see, for instance, [8, 9]).
Definition 2 (Strong bisimulation)
On an LTS \(A = (S,Act, {\rightarrow })\) a relation \(R\subseteq S\times S\) is called a strong bisimulation relation if and only if it is symmetric and for all \(s,t\in S\) with sRt and for all \(a\in Act\) with  , we have:
, we have:

Whenever we refer to bisimulation we mean strong bisimulation. Two states \(s, t \in S\) in an LTS A are called bisimilar, denoted by  , iff there is some bisimulation relation R for A that relates s and t.
, iff there is some bisimulation relation R for A that relates s and t.
A partition \(\pi \) of a finite set of states S is a set of subsets that are pairwise disjoint and whose union is equal to S, i.e., \(\bigcup _{B\in \pi } B = S\). Every element \(B\in \pi \) of this partition \(\pi \) is called a block.
We call partition \(\pi '\) a refinement of \(\pi \) iff for every block \(B'\in \pi '\) there is a block \(B \in \pi \) such that \(B' \subseteq B\). We say a partition \(\pi \) of a finite set S induces the relation \(R_{\pi } = \{(s,t) \mid \exists B \in \pi . s \in B \wedge t \in B \}\). This is an equivalence relation of which the blocks of \(\pi \) are the equivalence classes.
Given an LTS \(A = (S, Act, {\rightarrow })\) and two states \(s,t\in S\) we say that s reaches t with action \(a\in Act\) iff  . A state s reaches a set \(U\subseteq S\) with an action a iff there is a state \(t\in U\) such that s reaches t with action a. A set of states \(V\subseteq S\) is called stable under a set of states \(U\subseteq S\) iff for all actions a either all states in V reach U with a, or no state in V reaches U with a. A partition \(\pi \) is stable under a set of states U iff each block \(B\in \pi \) is stable under U. The partition \(\pi \) is called stable iff it is stable under all its own blocks \(B\in \pi \).
. A state s reaches a set \(U\subseteq S\) with an action a iff there is a state \(t\in U\) such that s reaches t with action a. A set of states \(V\subseteq S\) is called stable under a set of states \(U\subseteq S\) iff for all actions a either all states in V reach U with a, or no state in V reaches U with a. A partition \(\pi \) is stable under a set of states U iff each block \(B\in \pi \) is stable under U. The partition \(\pi \) is called stable iff it is stable under all its own blocks \(B\in \pi \).
Fact 1
[16] Stability is inherited under refinement, i.e. given a partition \(\pi \) of S and a refinement \(\pi '\) of \(\pi \), then if \(\pi \) is stable under \(U\subseteq S\), then \(\pi '\) is also stable under U.
The main problem we focus on in this work is called the bisimulation refinement problem (BCRP). It is defined as follows:
Input: An LTS \(M = (S,Act, {\rightarrow })\).
Output: The partition \(\pi \) of S which is the coarsest partition, i.e., has the smallest number of blocks, that forms a bisimulation relation.
In a Kripke structure, the transition relation forms a single binary relation, since the transitions are unlabelled. This is also the case when an LTS has a single action label. In that case, the problem is called the Relational Coarsest Partition Problem (RCPP) [11, 12, 16]. This problem is defined as follows:
Input: A set S, a binary relation \(\rightarrow : S\times S\) and an initial partition \(\pi _0\)
Output: The partition \(\pi \) which is the coarsest refinement of \(\pi _0\) and which is a bisimulation relation.
It is known that BCRP is not significantly harder than RCPP as there are intuitive translations from LTSs to Kripke structures [5, Dfn. 4.1]. However, some non-trivial modifications can speed-up the algorithm for some cases, hence we discuss both problems separately. In Sect. 3, we discuss the basic parallel algorithm for RCPP, and in Sect. 4, we discuss the modifications required to efficiently solve the BCRP problem for LTSs with multiple action labels.
3 Relational Coarsest Partition Problem
In this section, we discuss a sequential algorithm based on the one of Kanellakis and Smolka [11] for RCPP (Sect. 3.1). This is the basic algorithm that we adapt to the parallel PRAM algorithm (Sect. 3.2). The algorithm starts with an input partition \(\pi _0\) and refines all blocks until a stable partition is reached. This stable partition will be the coarsest refinement that defines a bisimulation relation.
3.1 The Sequential Algorithm
The sequential algorithm, Algorithm 1, works as follows. Given are a set S, a transition relation \(\rightarrow \subseteq S\times S\), and an initial partition \(\pi _0\) of S. Initially, we mark the partition as not necessarily stable under all blocks by putting these blocks in a set \( Unstable \). In any iteration of the algorithm, if a block B of the current partition is not in \( Unstable \), then the current partition is stable under B. If \( Unstable \) is empty, the partition is stable under all its blocks, and the partition represents the required bisimulation.
As long as some blocks are in \( Unstable \) (line 3), a single block \(B\in \pi \) is taken from this set (line 4) and we split the current partition such that it becomes stable under B. Therefore, we refer to this block as the splitter. The set \(S' = \{s \in S \mid \exists t \in B. s\rightarrow t \}\) is the reverse image of B (line 6). This set consists of all states that can reach B, and we use \(S'\) to define our new blocks. All blocks \(B'\) that have a non-empty intersection with \(S'\), i.e., \(B' \cap S' \ne \emptyset \), and are not a subset of \(S'\), i.e., \(B'\cap S' \ne B'\) (line 7), are split in the subset of states in \(S'\) and the subset of states that are not in \(S'\) (lines 8–9). These two new blocks are added to the set of \( Unstable \) blocks (line 10). The number of states is finite, and blocks can be split only a finite number of times. Hence, blocks are only finitely often put in \( Unstable \), and so the algorithm terminates.

3.2 The PRAM Algorithm
Next, we describe a PRAM algorithm to solve RCPP that is based on the sequential algorithm given in Algorithm 1.
Block Representation. Given an LTS \(A = (S, Act, \rightarrow )\) with \(|A| = 1\) and \(|S| = n\) states, we assume that the states are labeled with unique indices \(0, \dots , n-1\). A partition \(\pi \) in the PRAM algorithm is represented by assigning a block label from a set of block labels \(L_B\) to every state. The number of blocks can never be larger than the number of states, hence, we use the indices of the states as block labels: \(L_B=S\). We exploit this in the PRAM algorithm to efficiently select a new block label whenever a new block is created. We select the block label of a new block by electing one of its states to be the leader of that block and using the index of that state as the block label. By doing so, we maintain an invariant that the leader of a block is also a member of the block.
In a partition \(\pi \), whenever a block \(B\in \pi \) is split into two blocks \(B'\) and \(B''\), the leader s of B which is part of \(B'\) becomes the leader of \(B'\), and for \(B''\), a new state \(t \in B''\) is elected to be the leader of this new block. Since the new leader is not part of any other block, the label of t is fresh with respect to the block labels that are used for the other blocks. This method of using state leaders to represent subsets was first proposed in [22, 23].
Data Structures. The common memory contains the following information:
-
1.
\(n:{\mathbb {N}}\), the number of states of the input.
-
2.
\(m:{\mathbb {N}}\), the number of transitions of the input relation.
-
3.
The input, a fixed numbered list of transitions. For every index \(0\le i<m\) of a transition, a source \(\textit{source}_i\in S\) and target \(\textit{target}_i\in S\) are given, representing the transition \(\textit{source}_i\rightarrow \textit{target}_i\).
-
4.
\(C: L_B\cup \{\bot \}\), the label of the current block that is used as a splitter; \(\bot \) indicates that no splitter has been selected.
-
5.
The following is stored in lists of size n, for each state with index i:
-
(a)
\( mark _i: {\mathbb {B}}\), a mark indicating whether state i is able to reach the splitter.
-
(b)
\( block _i:L_B\), the block of which state i is a member.
-
(a)
-
6.
The following is stored in lists of size n, for each potential block with block label i:
-
(a)
\( new\_leader _i : L_B\) the leader of the new block when a split is performed.
-
(b)
\( unstable _i : {\mathbb {B}}\) indicating whether \(\pi \) is possibly unstable w.r.t. the block.
-
(a)
As input, we assume that each state with index i has an input variable \(I_i\in L_B\) that is the initial block label. In other words, the values of the \(I_i\) variables together encode \(\pi _0\). Using this input, the initial values of the block label \(\textit{block}_i\) variables are calculated to conform to our block representation with leaders. Furthermore in the initialization, \(\textit{unstable}_i = \mathrm {false}\) for all i that are not used as block label, and \(\mathrm {true}\) otherwise.
The Algorithm. We provide our first PRAM algorithm in Algorithm 2. The PRAM is started with \(\max (n,m)\) processors. These processors are dually used for transitions and states.
The algorithm performs initialisation (lines 1–6), after which each block has selected a new leader (lines 3–4), ensuring that the leader is one of its own states, and the initial blocks are set to unstable. Subsequently, the algorithm enters a single loop that can be explained in three separate parts.
-
Splitter selection (lines 8–14), executed by n processors. Every variable \(mark_i\) is set to \(\mathrm {false}\). After this, every processor with index i will check \( unstable _i\). If block i is marked unstable the processor tries to write i in the variable C. If multiple write accesses to C happen concurrently in this iteration, then according to the arbitrary PRAM model (see Sect. 2), only one process j will succeed in writing, setting \(C:=j\) as splitter in this iteration.
-
Mark states (lines 15–17), executed by m processors. Every processor i is responsible for the transition
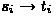 and checks if \(t_i\) (\( target _i\)) is in the current block C (line 15). If this is the case the processor writes \(\mathrm {true}\) to \(mark_{ source _i}\) where \( source _i\) is \(s_i\). This mark now indicates that \(s_i\) reaches block C.
and checks if \(t_i\) (\( target _i\)) is in the current block C (line 15). If this is the case the processor writes \(\mathrm {true}\) to \(mark_{ source _i}\) where \( source _i\) is \(s_i\). This mark now indicates that \(s_i\) reaches block C. -
Performing splits (lines 18–26), executed by n processors. Every processor i compares the mark of state i, i.e., \( mark _i\), with the mark of the leader of the block in which state i resides, i.e., \( mark _{ block _i}\) (line 20). If the marking is different, state i has to be split from \( block _i\) into a new block. At line 21, a new leader is elected among the states that form the newly created block. The index of this leader is stored in \( new\_leader _{ block _i}\). The instability of block \( block _i\) is set to \(\mathrm {true}\) (line 22). After that, all involved processors update the block index for their state (line 23) and update the stability of the new block (line 24).
The steps of the program are illustrated in Fig. 1. The notation \(B_{s_i}\) refers to a block containing all states that have state \(s_i\) as their block leader. In the figure on the left, we have two blocks \(B_{s_1}\) and \(B_{s_4}\), of which at least \(B_{s_4}\) is marked unstable. Block \(B_{s_4}\) is selected to be splitter, i.e., \(C = B_{s_4}\) at line 12 of Algorithm 2. In the figure in the middle, \( mark _i\) is set to \(\mathrm {true}\) for each state i that can reach \(B_{s_4}\) (line 16). Finally, block \(B_{s_4}\) is set to stable (line 19), all states compare their mark with the leader’s mark, and the processor working on state \(s_3\) discovers that the mark of \(s_3\) is different from the mark of \(s_1\), so \(s_3\) is elected as leader of the new block \(B_{s_3}\) at line 21 of Algorithm 2. Both \(B_{s_1}\) and \(B_{s_3}\) are set to unstable (lines 22 and 24).
The algorithm repeats execution of the while-loop until all blocks are marked stable.

3.3 Correctness
The \( block _i\) list in the common memory at the start of iteration k defines a partition \(\pi _k\) where states \(s\in S\) with equal block labels block\(_i\) form the blocks:
A run of the program produces a sequence \(\pi _0, \pi _1, \dots \) of partitions. Partition \(\pi _k\) is a refinement of every partition \(\pi _0,\pi _1,\dots , \pi _{k-1}\), since blocks are only split and never merged.
A partition \(\pi \) induces a relation of which the blocks are the equivalence classes. For an input partition \(\pi _0\) we call the relation induced by the coarsest refinement of \(\pi _0\) that is a bisimulation relation  .
.
We now prove that Algorithm 2 indeed solves RCPP. We first introduce Lemma 1 which is invariant throughout the execution and expresses that states which are related by  are never split into different blocks. This lemma implies that if a refinement forms a bisimulation relation, it is the coarsest.
are never split into different blocks. This lemma implies that if a refinement forms a bisimulation relation, it is the coarsest.
Lemma 1
Let S be the input set of states, \(\rightarrow :S\times S\) the input relation and \(\pi _0\) the input partition. Let \( \pi _1,\pi _2, \dots \) be the sequence of partitions produced by Algorithm 2, then for all initial blocks \(B\in \pi _0\), states \(s,t\in B\) and iterations \(k\in {\mathbb {N}}\):

Proof
This is proven by induction on k. In the base case, \(\pi _0\), this is true by default. Now assume for a particular \(k\in {\mathbb {N}}\) that the property holds. We know that the partition \(\pi _{k+1}\) is obtained by splitting with respect to a block \(C\in \pi _k\). For two states \(s,t\in S\) with  we know that s and t are in the same block in \(\pi _k\). In the case that both s and t do not reach C, then \(mark_s = mark_t =\mathrm {false}\). Since they were in the same block, they will be in the same block in \(\pi _{k+1}\).
we know that s and t are in the same block in \(\pi _k\). In the case that both s and t do not reach C, then \(mark_s = mark_t =\mathrm {false}\). Since they were in the same block, they will be in the same block in \(\pi _{k+1}\).
Now consider the case that at least one of the states is able to reach C. Without loss of generality say that s is able to reach C. Then there is a transition \(s\rightarrow s'\) with \(s'\in C\). By Definition 2, there exists a \(t'\in S\) such that \(t\rightarrow t'\) and  . By the induction hypothesis we know that since
. By the induction hypothesis we know that since  , \(s'\) and \(t'\) must be in the same block in \(\pi _k\), i.e., \(t'\) is in C. This witnesses that t is also able to reach C and we must have \( mark _s = mark _t = \mathrm {true}\). Since the states s and t are both marked and are in the same block in \(\pi _k\), they will remain in the same block in \(\pi _{k+1}\).
, \(s'\) and \(t'\) must be in the same block in \(\pi _k\), i.e., \(t'\) is in C. This witnesses that t is also able to reach C and we must have \( mark _s = mark _t = \mathrm {true}\). Since the states s and t are both marked and are in the same block in \(\pi _k\), they will remain in the same block in \(\pi _{k+1}\).
Lemma 2
Let S be the input set of states with \(\rightarrow :S \times S\), \(L_B= S\) the block labels, and \(\pi _n\) the partition stored in the memory after the termination of Algorithm 2. Then the relation induced by \(\pi _n\) is a bisimulation relation.
Proof
Since the program finished, we know that for all block indices \(i\in L_B\) we have \( unstable _i = \mathrm {false}\). For a block index \(i \in L_B\), \( unstable _i\) is set to \(\mathrm {false}\) if the partition \(\pi _k\), after iteration k, is stable under the block with index i and set to \(\mathrm {true}\) if it is split. So, by Fact 1, we know \(\pi _n\) is stable under every block B, hence stable. Next, we prove that a stable partition is a bisimulation relation.
We show that the relation R induced by \(\pi _n\) is a bisimulation relation. Assume states \(s,t\in S\) with sRt are in block \(B\in \pi _n\). Consider a transition \(s\rightarrow s'\) with \(s'\in S\). State \(s'\) is in some block \(B' \in \pi _n\), and since the partition is stable under block \(B'\), and s is able to reach \(B'\), by the definition of stability, we know that t is also able to reach \(B'\). Therefore, there must be a state \(t'\in B'\) such that \(t\rightarrow t'\) and \(s'Rt'\). Finally, by the fact that R is an equivalence relation we know that R is also symmetric, therefore it is a bisimulation relation.
Theorem 1
The partition resulting from executing Algorithm 2 forms the coarsest relational partition for a set of states S and a transition relation \(\rightarrow : S \times S\), solving RCPP.
Proof
By Lemma 2, the resulting partition is a bisimulation relation. Lemma 1 implies that it is the coarsest refinement which is a bisimulation.
3.4 Complexity Analysis
Every step in the body of the while-loop can be executed in constant time. So the asymptotic complexity of this algorithm is given by the number of iterations.
Theorem 2
RCPP on an input with m transitions and n states is solved by Algorithm 2 in \(\mathcal {O}(n)\) time using \(\max (n,m)\) CRCW PRAM processors.
Proof
In iteration \(k \in {\mathbb {N}}\) of the algorithm, let us call the total number of blocks \(N_k \in {\mathbb {N}}\) and the number of unstable blocks \(U_k \in {\mathbb {N}}\). Initially, \(N_0 = U_0 = |\pi _0|\). In every iteration k, a number of blocks \(l_k \in {\mathbb {N}}\) is split, resulting in \(l_k\) new blocks, so the new total number of blocks at the end of iteration k is \( N_{k+1} = N_k +l_k \).
First the current block C in iteration k which was unstable is set to stable which causes the number of unstable blocks to decrease by one. In this iteration k the \(l_k\) blocks \(B_1, \dots , B_{l_k}\) are split, resulting in \(l_k\) newly created blocks. These \(l_k\) blocks are all unstable. A number of blocks \(l_k' \le l_k\) of the blocks \(B_1, \dots B_{l_k}\), were stable and are set to unstable again. The block C which was set to stable is possibly one of these \(l_k'\) blocks which were stable and set to unstable again. The total number of unstable blocks at the end of iteration k is \(U_{k+1} = U_{k} + l_k + l_k' - 1\).
For all \(k\in {\mathbb {N}}\), in iteration k we calculate the total number of blocks \(N_k = |\pi _0|+ \sum _{i=0}^{k-1}(l_i)\) and unstable blocks \(U_k =|\pi _0| - k + \sum _{i=0}^{k-1}(l_i + l_i')\). The number of iterations is given by \(k = \sum _{i=0}^{k-1}(l_i + l_i') - U_k + |\pi _0|\). By definition, \(l_i' \le l_i\), and the total number of newly created blocks is \(\sum _{i=0}^{k-1}(l_i) = N_k - |\pi _0|\), hence \(\sum _{i=0}^{k-1}(l_i + l_i')\le 2\sum _{i=0}^{k-1}(l_i)\le 2N_k-2|\pi _0|\). The number of unstable blocks is always positive, i.e., \(U_k \ge 0\), and the total number of blocks can never be larger than the number of states, i.e., \(N_k \le n\), so the total number of iterations z is bounded by \(z \le 2N_z - |\pi _0| \le 2n - |\pi _0|\).
4 Bisimulation Coarsest Refinement Problem
In this section we extend our algorithm to the Bisimulation Coarsest Refinement Problem (BCRP), i.e., to LTSs with multiple action labels.
Solving BCRP can in principle be done by translating an LTS to a Kripke structure, for instance by using the method described in [18]. This translation introduces a new state for every transition, resulting in a Kripke structure with \(n+m\) states. If the number of transitions is significantly larger than the number of states, then the number of iterations of our algorithm increases undesirably.
4.1 The PRAM Algorithm
Instead of introducing more states, we introduce multiple marks per state, but in total we have no more than m marks. For each state s, we use a mark variable for each different outgoing action label relevant for s, i.e., for each a for which there is a transition  to some state t. Each state may have a different set of outgoing action labels and thus a different set of marks. Therefore, we first perform a preprocessing procedure in which we group together states that have the same set of outgoing action labels. This is valid, since two bisimilar states must have the same outgoing actions. That two states of the same block have the same set of action labels is then an invariant of the algorithm, since in the sequence of produced partitions, each partition is a refinement of the previous one. For the extended algorithm, we need to maintain extra information in addition to the information needed for Algorithm 2. For an input LTS
to some state t. Each state may have a different set of outgoing action labels and thus a different set of marks. Therefore, we first perform a preprocessing procedure in which we group together states that have the same set of outgoing action labels. This is valid, since two bisimilar states must have the same outgoing actions. That two states of the same block have the same set of action labels is then an invariant of the algorithm, since in the sequence of produced partitions, each partition is a refinement of the previous one. For the extended algorithm, we need to maintain extra information in addition to the information needed for Algorithm 2. For an input LTS  with n states and m transitions the extra information is:
with n states and m transitions the extra information is:
-
1.
Each action label has an index \(a \in \{0, \dots ,|Act| -1\}\).
-
2.
The following is stored in lists of size m, for each transition
 with transition index \(i \in \{0, \dots , m-1\}\):
with transition index \(i \in \{0, \dots , m-1\}\): -
(a)
\(a_i := a\)
-
(b)
\( order _i : {\mathbb {N}}\), the order of this action label, with respect to the source state s. E.g., if a state s has the list [1, 3, 6] of outgoing action labels, and transition i has label 3, then \( order _i\) is 1 (we start counting from 0).
-
(a)
-
3.
\( mark : [{\mathbb {B}}]\), a list of up to m marks, in which there is a mark for every state, action pair for which it holds that the state has at least one outgoing transition labelled with that action. This list can be interpreted as the concatenation of sublists, where each sublist contains all the marks for one state. For each state \(s \in S\) we have:
-
(a)
\( off (s) : {\mathbb {N}}\), the offset to access the beginning of the sublist of the marks of the state s in \( mark \). The positions \( mark _{ off (s)}\) up to \( mark _{ off (s+1)}\) contain the sublist of marks for state s. E.g., if state s has outgoing transitions with 3 distinct action labels, we know that \( off (s+1) \equiv off (s) + 3\), and we have 3 marks for state s. We write \( mark _{ off (s) + order _i}\) to access the mark for transition i which has source state s.
-
(a)
-
4.
\( mark\_length \): The length of the mark list. This allows us to reset all marks in constant time using \( mark\_length \) processors. This number is not larger than the number of transitions (\( mark\_length \le m\)).
-
5.
In a list of size n, we store for each state \(s \in S\) a variable \( split _s : {\mathbb {B}}\). This indicates if the state will be split off from its block.
With this extra information, we can alter Algorithm 2 to work with labels. The new version is given in Algorithm 3. The changes involve the following:
-
1.
Lines 7–9: Reset the \( mark \) list.
-
2.
Line 11: Reset the \( split \) list.
-
3.
Line 17: When marking the transitions, we do this for the correct action label, using \( order _i\). Note the indexing into \( mark \). It involves the offset for the state \( source _i\), and \( order _i\).
-
4.
Lines 19–21: We tag a state to be split when it differs for any action from the block leader.
-
5.
Line 24: If a state was tagged to be split in the previous step, it should split from its leader.
-
6.
Line 29: If any block was split, the partition may not be stable w.r.t. the splitter.

To use Algorithm 3, we need to do two preprocessing steps. First, we need to partition the states w.r.t. their set of outgoing action labels. This can be done with an altered version of Algorithm 2, which does one iteration for each action label. For the second preprocessing step, we need to gather the extra information that is needed in Algorithm 3. This is done via sorting the action labels and subsequently performing some parallel segmented (prefix) sums [19]. In total the preprocessing takes \(\mathcal {O}(|Act| + \log m)\) time. For details how this is implemented see the full version of this paper [14].
4.2 Complexity and Correctness
For Algorithm 3, we need to prove why it takes a linear number of steps to construct the final partition. This is subtle, as an iteration of the algorithm does not necessarily produce a stable block.
Theorem 3
Algorithm 3 on an input LTS with n states and m transitions will terminate in \(\mathcal {O}(n + |Act|)\) steps.
Proof
The total preprocessing takes \(\mathcal {O}(|Act| + \log m)\) steps, after which the while-loop will be executed on a partitioning \(\pi _0\) which was the result of the preprocessing on the partition \(\{S\}\). Every iteration of the while-loop is still executed in constant time. Using the structure of the proof of Theorem 2, we derive a bound on the number of iterations.
At the start of iteration \(k\in {\mathbb {N}}\) the total number of blocks and unstable blocks are \(N_k,U_k\in {\mathbb {N}}\), initially \(U_0 = N_0 = |\pi _0|\). In iteration k, a number \(l_k\) of blocks is split in two blocks, resulting in \(l_k\) new blocks, meaning that \(N_{k+1} = N_{k} + l_k\). All new \(l_k\) blocks are unstable and a number \(l_k' \le l_k\) of the old blocks that are split were stable at the start of iteration k and are now unstable. If \(l_k = l_k' = 0\) there are no blocks split and the current block C becomes stable. We indicate this with a variable \(c_k\): \(c_k=1\) if \(l_k = 0\), and \(c_k = 0\), otherwise. The total number of iterations up to iteration k in which no block is split is given by \(\sum _{i=0}^{k-1} c_i\). The number of iterations in which at least one block is split is given by \(k - \sum _{i=0}^{k-1} c_i\).
If in an iteration k at least one block is split, the total number of blocks at the end of iteration k is strictly higher than at the beginning, hence for all \(k\in {\mathbb {N}}\), \(N_k \ge k - \sum _{i=0}^{k-1}c_i\). Hence, \(N_k+\sum _{i=0}^{k-1}c_i\) is an upper bound for k.
We derive an upper bound for the number of iterations in which no blocks are split using the total number of unstable blocks. In iteration k there are \(U_k = \sum _{i=0}^{k-1}(l_i + l_i') - \sum _{i=0}^{k-1} c_i + |\pi _0|\) unstable blocks. Since the sum of newly created blocks \(\sum _{i=0}^{k-1}(l_i) = N_k-|\pi _0|\) and \(l_i' \le l_i\), the number of unstable blocks \(U_k\) is bounded by \(2N_k-\sum _{i=0}^{k-1}c_i - |\pi _0|\). Since \(U_k\ge 0\) we have the bound \(\sum _{i=0}^{k-1}c_i\le 2N_k-|\pi _0|\). This gives the bound on the total number of iterations \(z \le 3N_z-|\pi _0| \le 3n - |\pi _0|\).
With the time for preprocessing this makes the run time complexity \(\mathcal {O}(n + |Act| + \log m)\). Since the number of transitions m is bounded by \(|Act| \times n^2\), this simplifies to \(\mathcal {O}(n + |Act|)\).
5 Experimental Results
In this section we discuss the results of our implementation of Algorithm 3 from Sect. 4. Note that this implementation is not optimized for the specific hardware it runs on, since the goal of this paper is to provide a generic parallel algorithm. This implementation is purely a proof of concept, to show that our algorithm can be mapped to contemporary hardware and to understand how the algorithm scales with the size of the input.
The implementation targets GPUs since a GPU closely resembles a PRAM and supports a large amount of parallelism. The algorithm is implemented in CUDA version 11.1 with use of the Thrust library.Footnote 1 As input, we chose all benchmarks of the VLTS benchmark suiteFootnote 2 for which the implementation produced a result within 10 min. The VLTS benchmarks are LTSs that have been derived from real concurrent system models.
The experiments were run on an NVIDIA Titan RTX with 24 GB memory and 72 Streaming Multiprocessors, each supporting up to 1,024 threads in flight. Although this GPU supports 73,728 threads in flight, it is very common to launch a GPU program with one or even several orders of magnitude more threads, in particular to achieve load balancing between the Streaming Multiprocessors and to hide memory latencies. In fact, the performance of a GPU program usually relies on that many threads being launched.
The left-hand side of Table 1 shows the results of the experiments we conducted. The \(| Act |\) column corresponds to the number of different action labels. The \(| Blocks |\) column indicates the number of different blocks at the end of the algorithm, where each block contains only bisimilar states. With \(\# It \) we refer to the number of while-loop iterations that were executed (see Algorithm 3), before all blocks became stable. The number of states and transitions can be derived from the benchmark name. In the benchmark ‘\(X\_N\_M\)’, \(N*1000\) is the number states and \(M*1000\) is the number of transitions. The \(T_ pre \) give the preprocessing times in milliseconds, which includes doing the memory transfers to the GPU, sorting the transitions and partitioning. The \(T_ alg \) give the times of the core algorithm, in milliseconds. The \(T_\textit{Par-BCRP}\) is the sum of the preprocessing and the algorithm, in milliseconds. We have not included the loading times for the files and the first CUDA API call that initializes the device. We ran each benchmark 10 times and took the averages. The standard deviation of the total times varied between 0% and 3% of the average, thus 10 runs are sufficient. All the times are rounded with respect to the standard error of the mean.
We see that the bound as proven in Sect. 4.2 (\(k \le 3n\)) is indeed respected, \(\# It /n\) is at most 2.20, and most of the time below that. The number of iterations is tightly related to the number of blocks that the final partition has, the \(\# It / | Blocks |\) column varies between 1.00 and 2.53. This can be understood by the fact that each iteration either splits one or more blocks or marks a block as stable, and all blocks must be checked on stability at least once. This also means that for certain LTSs the algorithm scales better than linearly in n. The preprocessing often takes the same amount of time (about a few milliseconds). Exceptions are those cases with a large number of actions and/or transitions.
Concerning the run times, it is not true that each iteration takes the same amount of time. A GPU is not a perfect PRAM machine. There are two key differences. Firstly, we suspect that the algorithm is memory bound since it is performing a limited amount of computations. The memory accesses are irregular, i.e., random, which caches can partially compensate, but for sufficiently large n and m, the caches cannot contain all the data. This means that as the LTSs become larger, memory accesses become relatively slower. Secondly, at a certain moment, the maximum number of threads that a GPU can run in parallel is achieved, and adding more threads will mean more run time. These two effects can best be seen in the \(T_ alg /\# It \) column, which corresponds to the time per iteration. The values are around 0.02 up to 300, 000 transitions, but for a larger number of states and transitions, the amount of time per iteration increases.
5.1 Experimental Comparison
We compared our implementation (Par-BCRP) with an implementation of the algorithm by Lee and Rajasekaran (LR) [12] on GPUs, and the optimized GPU implementation by Wijs based on signature-based bisimilarity checking [2], with multi-way splitting (Wms) and with single-way splitting (Wss) [22]. Multi-way splitting indicates that a block is split in multiple blocks at once, which is achieved by computing a signature for each state in every partition refinement iteration, and splitting each block off into sets of states, each containing all the states with the same signature. The signature of a state is derived from the labels of the blocks that this state can reach in the current partition. Note that we are not including comparisons with CPU bisimulation checking tools; the fact that those tools run on completely different hardware makes a comparison problematic, and such a comparison does not serve the purpose of evaluating the feasibility of implementing Algorithm 3. Optimising our implementation to make it competitive with CPU tools is planned for future work.
The running times of the different algorithms can be found in the right-hand side of Table 1. Similarly to our previous benchmarks, the algorithms were run 10 times on the same machine using the same VLTS benchmark suite with a time-out of 10 min. In some cases, the non-deterministic behaviour of the algorithms Wms and Wss led to high variations in the runs. In cases where the standard error of the mean was more than 5% of the mean value, we have added the standard error in Table 1 in between parentheses. Furthermore, all the results are rounded with respect to the standard error of the mean. As a pre-processing step for the LR, Wms and Wss algorithms the input LTSs need to be sorted. We did not include this in the times, nor the reading of files and the first CUDA API call (which initializes the GPU).
This comparison confirms the expectation that our algorithm in all cases (except one small LTS) out-performs LR. This confirms our expectation that LR is not suitable for massive parallel devices such as GPUs.
Furthermore, the comparison demonstrates that in most cases our algorithm (Par-BCRP) outperforms Wss. In some benchmarks (Cwi_1_2, Cwi_214_684, Cwi_2165_8723 and Cwi_2416_17605) Wss is more than twice as fast, but in 16 other cases our algorithm is more than twice as fast. The last comparison shows us that our algorithm does not out-perform Wms. Wms employs multi-way splitting which is known to be very effective in practice. Furthermore, contrary to our implementation, Wms is optimized for GPUs while the focus of the current work is to improve the theoretical bounds and describe a general algorithm.
In order to understand the difference between Wms and our algorithm better, we analysed the complexity of Wms [22]. In general this algorithm is quadratic in time, and the linearity claim in [22] depends on the assumption that the fan-out of ‘practical’ transition systems is bounded, i.e., every state has no more than c outgoing transitions for c a (low) constant. We designed the transition systems \(\textit{Fan\_out}_n\) for \(n\in {\mathbb {N}}^+\) to illustrate the difference. The LTS  has n states: \(S=\{0,\dots ,n-1\}\). The transition function contains
has n states: \(S=\{0,\dots ,n-1\}\). The transition function contains  for all states \(1<i< n-1\). Additionally, from state 0 and 1 there are transitions to every state:
for all states \(1<i< n-1\). Additionally, from state 0 and 1 there are transitions to every state:  for all \(i\in S\). This LTS has n states, \(3n-3\) transitions and a maximum out degree of n transitions.
for all \(i\in S\). This LTS has n states, \(3n-3\) transitions and a maximum out degree of n transitions.
Figure 2 shows the results of calculating the bisimulation equivalence classes for  , with Wms and Par-BCRP. It is clear that the run time for Wms increases quadratically as the number of states grows linearly, already becoming untenable for a small amount of states. On the other hand, in conformance with our analysis, our algorithm scales linearly.
, with Wms and Par-BCRP. It is clear that the run time for Wms increases quadratically as the number of states grows linearly, already becoming untenable for a small amount of states. On the other hand, in conformance with our analysis, our algorithm scales linearly.
6 Conclusion
We proposed and implemented an algorithm for RCPP and BCRP. We proved that the algorithm stops in \(\mathcal {O}(n + |Act|)\) steps on \(\max (n,m)\) CRCW PRAM processors. We implemented the algorithm for BCRP in CUDA, and conducted experiments that show the potential to compute bisimulation in practice in linear time. Further advances in parallel hardware will make this more feasible.
For future work, it is interesting to investigate whether RCPP can be solved in sublinear time, that is \(\mathcal {O}(n^{\epsilon })\) for a \(\epsilon < 1\), as requested in [12]. It is also intriguing whether the practical effectiveness of the algorithm in [22] by splitting blocks simultaneously can be combined with our algorithm, while preserving the linear time upperbound. Furthermore, it remains an open question whether our algorithm can be generalised for weaker bisimulations, such as weak and branching bisimulation [7, 9]. The main challenge here is that the transitive closure of so-called internal steps needs to be taken into account.
Notes
- 1.
The source code can be found at https://github.com/sakehl/gpu-bisimulation.
- 2.
References
Balcázar, J., Gabarro, J., Santha, M.: Deciding bisimilarity is P-complete. Formal Aspects Comput. 4(1), 638–648 (1992). https://doi.org/10.1007/BF03180566
Blom, S., Orzan, S.: Distributed branching bisimulation reduction of state spaces. Electr. Notes Theoret. Comput. Sci. 89(1), 99–113 (2003). https://doi.org/10.1016/S1571-0661(05)80099-4
Blom, S., van de Pol, J.: Distributed branching bisimulation minimization by inductive signatures. In: Brim, L., van de Pol, J. (eds.) Proceedings 8th International Workshop on Parallel and Distributed Methods in verification, PDMC 2009, Eindhoven, The Netherlands, 4th November 2009, EPTCS, vol. 14, pp. 32–46 (2009). https://doi.org/10.4204/EPTCS.14.3
Bunte, O., et al.: The mCRL2 toolset for analysing concurrent systems. In: Vojnar, T., Zhang, L. (eds.) TACAS 2019. LNCS, vol. 11428, pp. 21–39. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17465-1_2
De Nicola, R., Vaandrager, F.: Action versus state based logics for transition systems. In: Guessarian, I. (ed.) LITP 1990. LNCS, vol. 469, pp. 407–419. Springer, Heidelberg (1990). https://doi.org/10.1007/3-540-53479-2_17
Fortune, S., Wyllie, J.: Parallelism in random access machines. In: Proceedings of the Tenth Annual ACM Symposium on Theory of Computing, pp. 114–118 (1978). https://doi.org/10.1145/800133.804339
van Glabbeek, R.J., Weijland, W.P.: Branching time and abstraction in bisimulation semantics. J. ACM 43(3), 555–600 (1996). https://doi.org/10.1145/233551.233556
Groote, J.F., Wijs, A.: An \(O(m\log n)\) algorithm for stuttering equivalence and branching bisimulation. In: Chechik, M., Raskin, J.-F. (eds.) TACAS 2016. LNCS, vol. 9636, pp. 607–624. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49674-9_40
Jansen, D.N., Groote, J.F., Keiren, J.J.A., Wijs, A.: An O(m log n) algorithm for branching bisimilarity on labelled transition systems. In: TACAS 2020. LNCS, vol. 12079, pp. 3–20. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-45237-7_1
Jeong, C., Kim, Y., Oh, Y., Kim, H.: A faster parallel implementation of Kanellakis-Smolka algorithm for bisimilarity checking. In: Proceedings of the International Computer Symposium. Citeseer (1998)
Kanellakis, P., Smolka, S.: CCS expressions, finite state processes, and three problems of equivalence. Inf. Comput. 86(1), 43–68 (1990). https://doi.org/10.1016/0890-5401(90)90025-D
Lee, I., Rajasekaran, S.: A parallel algorithm for relational coarsest partition problems and its implementation. In: Dill, D.L. (ed.) CAV 1994. LNCS, vol. 818, pp. 404–414. Springer, Heidelberg (1994). https://doi.org/10.1007/3-540-58179-0_71
Leiserson, C.E., et al.: There’s plenty of room at the top: what will drive computer performance after Moore’s law? Science 368(6495) (2020). https://doi.org/10.1126/science.aam9744
Martens, J., Groote, J., Haak, L.v.d., Hijma, P., Wijs, A.: A linear parallel algorithm to compute bisimulation and relational coarsest partitions. arXiv preprint arXiv:2105.11788 (2021)
Milner, R. (ed.): A Calculus of Communicating Systems. LNCS, vol. 92. Springer, Heidelberg (1980). https://doi.org/10.1007/3-540-10235-3
Paige, R., Tarjan, R.E.: Three partition refinement algorithms. SIAM J. Comput. 16(6), 973–989 (1987). https://doi.org/10.1137/0216062
Rajasekaran, S., Lee, I.: Parallel algorithms for relational coarsest partition problems. IEEE Trans. Parallel Distrib. Syst. 9(7), 687–699 (1998). https://doi.org/10.1109/71.707548
Reniers, M.A., Schoren, R., Willemse, T.: Results on embeddings between state-based and event-based systems. Comput. J. 57(1), 73–92 (2014). https://doi.org/10.1093/comjnl/bxs156
Sengupta, S., Harris, M., Garland, M., Owens, J.: Efficient parallel scan algorithms for GPUs. In: Scientific Computing with Multicore and Accelerators, chap. 19, pp. 413–442. Taylor & Francis (2011)
Stockmeyer, L., Vishkin, U.: Simulation of parallel random access machines by circuits. SIAM J. Comput. 13(2), 409–422 (1984). https://doi.org/10.1137/0213027
Valmari, A.: Simple bisimilarity minimization in \(O(m \log n)\) time. Fundam. Informaticae 105(3), 319–339 (2010). https://doi.org/10.3233/FI-2010-369
Wijs, A.: GPU accelerated strong and branching bisimilarity checking. In: Baier, C., Tinelli, C. (eds.) TACAS 2015. LNCS, vol. 9035, pp. 368–383. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46681-0_29
Wijs, A., Katoen, J.-P., Bošnački, D.: Efficient GPU algorithms for parallel decomposition of graphs into strongly connected and maximal end components. Formal Methods Syst. Des. 48(3), 274–300 (2016). https://doi.org/10.1007/s10703-016-0246-7
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2021 The Author(s)
About this paper
Cite this paper
Martens, J., Groote, J.F., van den Haak, L., Hijma, P., Wijs, A. (2021). A Linear Parallel Algorithm to Compute Bisimulation and Relational Coarsest Partitions. In: Salaün, G., Wijs, A. (eds) Formal Aspects of Component Software. FACS 2021. Lecture Notes in Computer Science(), vol 13077. Springer, Cham. https://doi.org/10.1007/978-3-030-90636-8_7
Download citation
DOI: https://doi.org/10.1007/978-3-030-90636-8_7
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-90635-1
Online ISBN: 978-3-030-90636-8
eBook Packages: Computer ScienceComputer Science (R0)





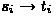 and checks if
and checks if 
 with transition index
with transition index 
 .
.