Abstract
We present the first parallel algorithms that decide strong and branching bisimilarity in linear time. More precisely, if a transition system has n states, m transitions and \(\vert Act \vert \) action labels, we introduce an algorithm that decides strong bisimilarity in \(\mathcal {O}(n+\vert Act \vert )\) time on \(\max (n,m)\) processors and an algorithm that decides branching bisimilarity in \(\mathcal {O}(n+\vert Act \vert )\) time using up to \(\max (n^2,m,\vert Act \vert n)\) processors.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The notion of bisimilarity for Kripke structures and labelled transition systems (LTSs) is commonly used to define behavioural equivalence. Deciding this equivalence is essential for modelling and verifying discrete event systems [1, 2]. Kanellakis and Smolka proposed a partition refinement algorithm for obtaining the bisimilarity relation for Kripke structures [3]. The proposed algorithm has a run time complexity of \(\mathcal {O}(nm)\) where n is the number of states and m is the number of transitions of the input. Later, a more sophisticated refinement algorithm running in \(\mathcal {O}(m~log~n)\) steps was proposed by Paige and Tarjan [4].
In recent years, the increase in the speed of sequential chip designs has stagnated due to a multitude of factors such as energy consumption and heat generation. In contrast, parallel devices, such as graphics processing units (GPUs), keep increasing rapidly in computational power. In order to profit from the acceleration of these devices, we require algorithms with massive parallelism. The article ‘There’s plenty of room at the Top: What will drive computer performance after Moore’s law’ by Leierson et al. [5] indicates that the advance in computational performance will come from software and algorithms that can employ hardware structures with a massive number of simple, parallel processors, such as GPUs. In this article, we propose two such algorithms to decide strong and branching bisimilarity.
For strong bisimilarity, we improve on the best-known theoretical time complexity for parallel bisimulation algorithms using a higher degree of parallelism. The proposed algorithm improves the run time complexity to \(\mathcal {O}(n)\) on \(\max (n,m)\) processors, and we base it on the sequential algorithm of Kanellakis and Smolka [3]. This time complexity matches the theoretical lower bound for parallel partition refinement algorithms given in [6]. The larger number of processors used in this algorithm favours the increasingly parallel design of contemporary and future hardware. In addition, the algorithm is optimal w.r.t. the sequential Kanellakis–Smolka algorithm, meaning that overall, it does not perform more work than its sequential counterpart.
We first present our algorithm on Kripke structures where transitions are unlabelled. However, as labelled transition systems (LTSs) are commonly used, and labels are not straightforward to incorporate in an efficient way (cf. for instance [7]), we discuss how to extend our algorithm to take action labels into account. This leads to an algorithm with a run time complexity of \(\mathcal {O}(n + \vert Act \vert )\) on \(\max (n,m)\) processors, with \( Act \) the set of action labels.
Our algorithm has been designed for and can be analysed with the Concurrent Read Concurrent Write (CRCW) PRAM model, following notations from [8]. This model extends the normal RAM model, allowing multiple processors to work with shared memory. In the CRCW PRAM model, parallel algorithms can be described in a straightforward and elegant way. In reality, no device exists that completely adheres to this PRAM model. Still, with recent advancements, hardware gets better and better at approximating the model since the number of parallel threads keeps growing. We demonstrate this by translating the PRAM algorithm to GPU code. We straightforwardly implemented our algorithm that decides strong bisimilarity in CUDA and experimented with an NVIDIA Titan RTX, a state-of-the-art GPU, showing that our algorithm performs mostly in line with what our PRAM algorithm predicts.
The present article is an extended version of our conference paper [9]. We have extended that work with a new algorithm that decides branching bisimilarity. Algorithms deciding branching bisimilarity typically propagate information over \(\tau \)-paths sequentially, which can take \(\mathcal {O}(n)\) time. We opt to use up to \(n^2\) processors to propagate this information in constant time. In this way, we manage to keep a linear time bound on the algorithm. As far as we know, this is the first algorithm deciding branching bisimilarity that uses extra parallelism to propagate this information. We explain this new algorithm and provide correctness proofs.
The article is structured as follows: In Sect. 2, we recall the necessary preliminaries on the CRCW PRAM model and state the partition refinement problems this article focuses on. In Sect. 3, we propose a parallel algorithm to compute strong bisimulation for Kripke structures, which is also called the relational coarsest partition problem (RCPP). In this section, we also prove the correctness of the algorithm and provide a complexity analysis. In Sect. 4, we discuss the details for an adjustment to the algorithm that deals with multiple action labels, thereby supporting LTSs, which forms the bisimulation coarsest refinement problem (BCRP). In this section, we also provide a complexness and correctness argument, and the results of experiments on a GPU implementation. In Sect. 5, we discuss the modification of the algorithm to compute branching bisimilarity (branching-BCRP). We discuss the details of the modifications, prove them correct and give the complete algorithm. In Sect. 6, we discuss related work. Lastly, in Sect. 7 we draw conclusions and discuss future work.
2 Preliminaries
2.1 The PRAM model
A parallel random access machine (PRAM) is a natural extension of the normal random access machine (RAM), where an arbitrary number of parallel processors can access the memory. Following the definitions of [8], we use a version of a PRAM that is able to concurrently read and concurrently write (CRCW PRAM). It differs from the model introduced in [10] in which the PRAM model was only allowed to concurrently read from the same memory address, but concurrent writes (to the same address) could not happen.
A CRCW PRAM consists of a sequence of numbered processors \(P_0, P_1, \dots \). These processors have all the natural instructions of a normal RAM, such as addition, subtraction and conditional branching based on the equality and less-than operators. There is an infinite amount of common memory the processors have access to. The processors have instructions to read from and write to the common memory. In addition, a processor \(P_i\) has an instruction to obtain its unique index i.
All the processors have the same program and run in a synchronised way in a single-instruction, multiple-data (SIMD) fashion. In other words, all processors execute the program in lock step. Parallelism can be achieved by distributing the data elements over the processors and having the processors apply the program instructions to ‘their’ data elements.
We assume that one arbitrary write will succeed whenever a concurrent write happens to the same memory cell. This is called the arbitrary CRCW PRAM.
A parallel program for a PRAM is called optimal w.r.t. a sequential algorithm if the total work done by the program does not exceed the work done by the sequential algorithm. More precisely, if T is the parallel run time and P the number of processors used, then the algorithm is optimal w.r.t. a sequential algorithm running in S steps if \(P\cdot T \in \mathcal {O}(S)\).
2.2 Strong bisimulation
To formalise concurrent system behaviour, we use LTSs.
Definition 2.1
(Labelled Transition System) A labelled transition system (LTS) is a three-tuple \(A=(S, Act, \rightarrow )\) where S is a finite set of states, Act a finite set of action labels and \(\rightarrow \subseteq S\times Act \times S\) the transition relation.
Let  be an LTS. Then, for any two states \(s,t\in S\) and \(a \in Act\), we write
be an LTS. Then, for any two states \(s,t\in S\) and \(a \in Act\), we write  iff
iff  .
.
Kripke structures differ from LTSs in the fact that the states are labelled as opposed to the transitions. In the current article, for convenience, instead of using Kripke structures where appropriate, we reason about LTSs with a single action label, i.e. \(\vert Act \vert = 1\). Computing the coarsest partition of such an LTS can be done in the same way as for Kripke structures, apart from the fact that in the latter case, a different initial partition is computed that is based on the state labels (see, for instance, [11]).
Definition 2.2
(Strong bisimulation) On an LTS  a relation \(R\subseteq S\times S\) is called a strong bisimulation relation if and only if it is symmetric and for all \(s,t\in S\) with sRt and for all \(a\in Act\) with
a relation \(R\subseteq S\times S\) is called a strong bisimulation relation if and only if it is symmetric and for all \(s,t\in S\) with sRt and for all \(a\in Act\) with  , we have:
, we have:

Whenever we refer to bisimulation, we mean strong bisimulation. Two states \(s, t \in S\) in an LTS A are called bisimilar, denoted by  , iff there is a bisimulation relation R for A that relates s and t.
, iff there is a bisimulation relation R for A that relates s and t.
A partition \(\pi \) of a finite set of states S is a set of subsets that are pairwise disjoint and whose union is equal to S, i.e. \(\bigcup _{B\in \pi } B = S\). Every element \(B\in \pi \) of this partition \(\pi \) is called a block.
We call partition \(\pi '\) a refinement of \(\pi \) iff for every block \(B'\in \pi '\) there is a block \(B \in \pi \) such that \(B' \subseteq B\). We say a partition \(\pi \) of a finite set S induces the relation \(R_{\pi } = \{(s,t) \mid \exists B \in \pi .~s \in B \text { and } t \in B \}\). This is an equivalence relation of which the blocks of \(\pi \) are the equivalence classes.
Given an LTS  and two states \(s,t\in S\), we say that s reaches t with action \(a\in Act\) iff
and two states \(s,t\in S\), we say that s reaches t with action \(a\in Act\) iff  .
.
A state s reaches a set \(U\subseteq S\) with an action a iff there is a state \(t\in U\) such that s reaches t with action a.
A set of states \(V\subseteq S\) is called stable under a set of states \(U\subseteq S\) iff for all actions a either all states in V reach U with a, or no state in V reaches U with a. A partition \(\pi \) is stable under a set of states U iff each block \(B\in \pi \) is stable under U. The partition \(\pi \) is called stable iff it is stable under all its own blocks \(B\in \pi \).
Fact 2.3
[4] Stability is inherited under refinement, i.e. given a partition \(\pi \) of S and a refinement \(\pi '\) of \(\pi \). If \(\pi \) is stable under \(U\subseteq S\), then \(\pi '\) is also stable under U.
2.3 Problems
The main problem we focus on in this work is called the bisimulation coarsest refinement problem (BCRP). It is defined as follows:
Input: An LTS  .
.
Output: The partition \(\pi \) of S which is the coarsest partition, i.e. has the smallest number of blocks, that forms a bisimulation relation.
In a Kripke structure, the transition relation forms a single binary relation, since the transitions are unlabelled. This is also the case when an LTS has a single action label. In that case, the problem is called the relational coarsest partition problem (RCPP) [3, 4, 12]. This problem is defined as follows:
Input: A set S, a binary relation \(\rightarrow : S\times S\) and an initial partition \(\pi _0\)
Output: The partition \(\pi \) which is the coarsest refinement of \(\pi _0\) and which forms a bisimulation relation.
It is known that BCRP is not significantly harder than RCPP as there are intuitive translations from LTSs to Kripke structures [13, Dfn. 4.1]. However, some non-trivial modifications can speed up the algorithm in some cases; hence, we discuss both problems separately.
In Sect. 3, we discuss the basic parallel algorithm for RCPP, and in Sect. 4, we discuss the modifications required to efficiently solve the BCRP problem for LTSs with multiple action labels.
3 Relational coarsest partition problem
In this section, we discuss a sequential algorithm based on the one of Kanellakis and Smolka [3] for RCPP (Sect. 3.1). This is the basic algorithm that we adapt to the parallel PRAM algorithm (Sect. 3.2). The algorithm starts with an input partition \(\pi _0\) and refines all blocks until a stable partition is reached. This stable partition will be the coarsest refinement that defines a bisimulation relation.
3.1 The sequential algorithm
The sequential algorithm, Algorithm 1, works as follows. Given are a set S, a transition relation \({\rightarrow }\subseteq S\times S\), and an initial partition \(\pi _0\) of S. Initially, we mark the partition as not necessarily stable under all blocks by putting these blocks in a set \( Waiting \). In any iteration of the algorithm, if a block B of the current partition is not in \( Waiting \), then the current partition is stable under B. If \( Waiting \) is empty, the partition is stable under all its blocks, and the partition represents the required bisimulation.
As long as some blocks are in \( Waiting \) (line 3), a single block \(B\in \pi \) is taken from this set (line 4), and we split the current partition such that it becomes stable under B. Therefore, we refer to this block as the splitter. The set \(S' = \{s \in S \mid \exists t \in B. s\rightarrow t \}\) is the reverse image of B (line 6). This set consists of all states that can reach B, and we use \(S'\) to define our new blocks. All blocks \(B'\) that have a non-empty intersection with \(S'\), i.e. \(B' \cap S' \ne \emptyset \), and are not a subset of \(S'\), i.e. \(B'\cap S' \ne B'\) (line 7), are split into the subset of states in \(S'\) and the subset of states that are not in \(S'\) (lines 9–10). These two new blocks are also added to the set of \( Waiting \) blocks (line 11–12). The number of states is finite, and blocks can be split only a finite number of times. Hence, blocks are only finitely often put in \( Waiting \), so the algorithm is guaranteed to terminate.

3.2 The PRAM algorithm
Next, we describe a PRAM algorithm to solve RCPP that is based on the sequential algorithm given in Algorithm 1.
3.2.1 Block representation
Given an LTS \(A = (S, Act, \rightarrow )\) with \(\vert Act\vert = 1\) and \(\vert S\vert = n\) states, we assume that the states are labelled with unique indices \(0, \dots , n-1\). A partition \(\pi \) in the PRAM algorithm is represented by assigning a block label from a set of block labels \(L_B\) to every state. The number of blocks can never be larger than the number of states; hence, we use the indices of the states as block labels: \(L_B=S\). We exploit this in the PRAM algorithm to efficiently select a new block label whenever a new block is created. We select the block label of a new block by electing one of its states to be the leader of that block and using the index of that state as the block label. By doing so, we maintain an invariant that the leader of a block is also a member of the block.
In a partition \(\pi \), whenever a block \(B\in \pi \) is split into two blocks \(B'\) and \(B''\), the leader s of B, which is part of \(B'\) becomes the leader of \(B'\), and for \(B''\), a new state \(t \in B''\) is elected to be the leader of this new block. Since the new leader is not part of any other block, the label of t is fresh with respect to the block labels that are used for the other blocks. This method of using state leaders to represent subsets was first proposed in [14, 15].
3.2.2 Data structures
The common memory contains the following information:
-
1.
\(n:{\mathbb {N}}\), the number of states of the input.
-
2.
\(m:{\mathbb {N}}\), the number of transitions of the input relation.
-
3.
The input, a fixed numbered list of transitions. For every index \(0\le i<m\) of a transition, a source \(\textit{source}_i\in S\) and target \(\textit{target}_i\in S\) are given, representing the transition \(\textit{source}_i\rightarrow \textit{target}_i\).
-
4.
\(C: L_B\cup \{\bot \}\), the label of the current block that is used as a splitter; \(\bot \) indicates that no splitter has been selected.
-
5.
The following is stored in lists of size n, for each state with index i:
-
(a)
\( mark _i: {\mathbb {B}}\), a mark indicating whether state i is able to reach the splitter.
-
(b)
\( block _i:L_B\), the block of which state i is a member.
-
(a)
-
6.
The following is stored in lists of size n, for each potential block with block label i:
-
(a)
\( new\_leader _i : L_B\) the leader of the new block when a split is performed.
-
(b)
\( waiting _i : {\mathbb {B}}\) indicating whether \(\pi \) might not be stable w.r.t. the block and should be checked as splitter.
-
(a)
As input, we assume that each state with index i has an input variable \(I_i\in L_B\) that is the initial block label. In other words, the values of the \(I_i\) variables together encode \(\pi _0\). Using this input, the initial values of the block label \(\textit{block}_i\) variables are calculated to conform to our block representation with leaders. Furthermore, in the initialisation, executed on n processors, \(\textit{waiting}_i = \textrm{false}\) for all i that are not used as block label, and \(\textrm{true}\) otherwise.
3.2.3 The algorithm
We provide our first PRAM algorithm in Algorithm 2. The PRAM is started with \(\max (n,m)\) processors. These processors are used for transitions, states and blocks.
The algorithm performs initialisation (lines 1–6) using n processors, where each block selects a new leader (lines 3–4). In line 3, we exploit the feature of a CRCW PRAM that only one write will succeed when multiple processors try to write to the same memory location. In line 4, the write that has succeeded is the same for each block, ensuring that the leader is one of its own states. Next, the algorithm sets the initial block to waiting. Subsequently, the algorithm enters a single loop that we explain in three separate parts.
-
Splitter selection (lines 8–14), using n processors. Every variable \(mark_i\) is set to \(\textrm{false}\). After this, every processor with index i will check \( waiting _i\).Footnote 1 If block i is marked waiting, the processor tries to write i in the variable C. If multiple write accesses to C happen concurrently in this iteration, then according to the arbitrary PRAM model (see Sect. 2), only one process j will succeed in writing, setting \(C:=j\) as the splitter in this iteration.
-
Mark states (lines 15–17), using m processors. Every processor i is responsible for the transition
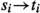 and checks if \(t_i\) (\( target _i\)) is in the current block C (line 15). If this is the case the processor writes \(\textrm{true}\) to \(mark_{ source _i}\) where \( source _i\) is \(s_i\). This mark now indicates that \(s_i\) reaches block C.
and checks if \(t_i\) (\( target _i\)) is in the current block C (line 15). If this is the case the processor writes \(\textrm{true}\) to \(mark_{ source _i}\) where \( source _i\) is \(s_i\). This mark now indicates that \(s_i\) reaches block C. -
Splitting blocks (lines 18–26), using n processors. Every processor i compares the mark of state i, i.e. \( mark _i\), with the mark of the leader of the block in which state i resides, i.e. \( mark _{ block _i}\) (line 20). If the marking is different, state i has to be split from \( block _i\) into a new block. At line 21, a new leader is elected among the states that form the newly created block. The index of this leader is stored in \( new\_leader _{ block _i}\). The block \( block _i\) is set to be \( waiting \) (line 22). After that, all involved processors update the block index for their state (line 23) and indicate that the new blocks should be checked as splitter by adding the blocks to the \( waiting \) set (line 24).
The steps of the program are illustrated in Fig. 1. The notation \(B_{s_i}\) refers to a block containing all states that have state \(s_i\) as their block leader. In the figure on the left, we have two blocks \(B_{s_1}\) and \(B_{s_4}\), of which at least \(B_{s_4}\) is marked as waiting. Block \(B_{s_4}\) is selected to be splitter, i.e. \(C = B_{s_4}\) at line 12 of Algorithm 2. In the figure in the middle, \( mark _i\) is set to \(\textrm{true}\) for each state i that can reach \(B_{s_4}\) (line 16). Finally, block \(B_{s_4}\) is removed from waiting (line 19), all states compare their mark with the leader’s mark, and the processor working on state \(s_3\) discovers that the mark of \(s_3\) is different from the mark of \(s_1\), so \(s_3\) is elected as leader of the new block \(B_{s_3}\) at line 21 of Algorithm 2. Both \(B_{s_1}\) and \(B_{s_3}\) are set to waiting (lines 22 and 24).
The algorithm repeats execution of the while-loop until no blocks are marked waiting.

3.3 Correctness
The \( block _i\) list in the common memory at the start of iteration k defines a partition \(\pi _k\) where states \(s\in S\) with equal block labels block \(_i\) form the blocks:
A run of the program produces a sequence \(\pi _0, \pi _1, \dots \) of partitions. Partition \(\pi _k\) is a refinement of every partition \(\pi _0,\pi _1,\dots , \pi _{k-1}\), since blocks are only split and never merged.
A partition \(\pi \) induces a relation in which the blocks are the equivalence classes. For an input partition \(\pi _0\) we call the relation induced by the coarsest refinement of \(\pi _0\) that is a bisimulation relation  .
.
We now prove that Algorithm 2 indeed solves RCPP. We first introduce Lemma 3.1 which is invariant throughout the execution and expresses that states which are related by  are never split into different blocks. This lemma implies that if a refinement forms a bisimulation relation, it is the coarsest.
are never split into different blocks. This lemma implies that if a refinement forms a bisimulation relation, it is the coarsest.
Lemma 3.1
Let S be the input set of states, \(\rightarrow :S\times S\) the input relation and \(\pi _0\) the input partition. Let \( \pi _1,\pi _2, \dots \) be the sequence of partitions produced by Algorithm 2, then for all initial blocks \(B\in \pi _0\), states \(s,t\in B\) and iterations \(k\in {\mathbb {N}}\):

Proof
This is proved by induction on k. In the base case, \(\pi _0\), this is true by default. Now assume for a particular \(k\in {\mathbb {N}}\) that the property holds. We know that the partition \(\pi _{k+1}\) is obtained by splitting with respect to a block \(C\in \pi _k\). For two states \(s,t\in S\) with  we know that s and t are in the same block in \(\pi _k\). In the case that both s and t do not reach C, then \(mark_s = mark_t =\textrm{false}\). Since they were in the same block, they will be in the same block in \(\pi _{k+1}\).
we know that s and t are in the same block in \(\pi _k\). In the case that both s and t do not reach C, then \(mark_s = mark_t =\textrm{false}\). Since they were in the same block, they will be in the same block in \(\pi _{k+1}\).
Now consider the case that at least one of the states is able to reach C. Without loss of generality say that s is able to reach C. Then there is a transition \(s\rightarrow s'\) with \(s'\in C\). By Definition 2.2, there exists \(t'\in S\) such that \(t\rightarrow t'\) and  . By the induction hypothesis we know that since
. By the induction hypothesis we know that since  , \(s'\) and \(t'\) must be in the same block in \(\pi _k\), i.e. \(t'\) is in C. This witnesses that t is also able to reach C and we must have \( mark _s = mark _t = \textrm{true}\). Since the states s and t are both marked and are in the same block in \(\pi _k\), they will remain in the same block in \(\pi _{k+1}\). \(\square \)
, \(s'\) and \(t'\) must be in the same block in \(\pi _k\), i.e. \(t'\) is in C. This witnesses that t is also able to reach C and we must have \( mark _s = mark _t = \textrm{true}\). Since the states s and t are both marked and are in the same block in \(\pi _k\), they will remain in the same block in \(\pi _{k+1}\). \(\square \)
Lemma 3.2
Let S be the input set of states with \(\rightarrow :S \times S\), \(L_B= S\) the block labels, and \(\pi _n\) the partition stored in the memory after the termination of Algorithm 2. Then the relation induced by \(\pi _n\) is a bisimulation relation.
Proof
Since the program finished, we know that for all block indices \(i\in L_B\) we have \( waiting _i = \textrm{false}\). For a block index \(i \in L_B\), \( waiting _i\) is set to \(\textrm{false}\) if the partition \(\pi _k\), after iteration k, is stable under the block with index i and set to \(\textrm{true}\) if it is split. So, by Fact 2.3, we know \(\pi _n\) is stable under every block B, hence stable. Next, we prove that a stable partition is a bisimulation relation.
We show that the relation R induced by \(\pi _n\) is a bisimulation relation. Assume states \(s,t\in S\) with sRt are in block \(B\in \pi _n\). Consider a transition \(s\rightarrow s'\) with \(s'\in S\). State \(s'\) is in some block \(B' \in \pi _n\), and since the partition is stable under block \(B'\), and s is able to reach \(B'\), by the definition of stability, we know that t is also able to reach \(B'\). Therefore, there must be a state \(t'\in B'\) such that \(t\rightarrow t'\) and \(s'Rt'\). Finally, by the fact that R is an equivalence relation we know that R is also symmetric; therefore, it is a bisimulation relation. \(\square \)
Theorem 3.3
The partition resulting from executing Algorithm 2 forms the coarsest relational partition for a set of states S and a transition relation \(\rightarrow : S \times S\), solving RCPP.
Proof
By Lemma 3.2, the resulting partition is a bisimulation relation. Lemma 3.1 implies that it is the coarsest refinement which is a bisimulation. \(\square \)
3.4 Complexity analysis
Every step in the body of the while-loop can be executed in constant time. So the asymptotic complexity of this algorithm is given by the number of iterations.
Theorem 3.4
RCPP on an input with m transitions and n states is solved by Algorithm 2 in \(\mathcal {O}(n)\) time using \(\max (n,m)\) CRCW PRAM processors.
Proof
In iteration \(k \in {\mathbb {N}}\) of the algorithm, let us call the total number of blocks \(N_k \in {\mathbb {N}}\) and the number of blocks marked as waiting \(U_k \in {\mathbb {N}}\). Initially, \(N_0 = U_0 = \vert \pi _0\vert \). In every iteration k, a number of blocks \(l_k \in {\mathbb {N}}\) is split, resulting in \(l_k\) new blocks, so the new total number of blocks at the end of iteration k is \(N_{k+1} = N_k +l_k \).
First the current block C in iteration k which was marked as waiting is no longer waiting which causes the number of waiting blocks to decrease by one. In this iteration k, the set of \(l_k\) blocks \(B_1, \dots , B_{l_k}\) are split, resulting in \(l_k\) newly created blocks. These \(l_k\) blocks are all marked as waiting. A number of blocks \(l_k' \le l_k\) of the blocks \(B_1, \dots B_{l_k}\) were not yet marked as waiting and are now set to waiting. The current block C is possibly one of these \(l_k'\) blocks which were not marked as waiting and are now waiting again. The total number of blocks marked as waiting at the end of iteration k is \(U_{k+1} = U_{k} + l_k + l_k' - 1\).
For all \(k\in {\mathbb {N}}\), in iteration k we calculate the total number of blocks \(N_k = \vert \pi _0\vert + \sum _{i=0}^{k-1}(l_i)\) and waiting blocks \(U_k =\vert \pi _0\vert - k + \sum _{i=0}^{k-1}(l_i + l_i')\). The number of iterations is given by \(k = \sum _{i=0}^{k-1}(l_i + l_i') - U_k + \vert \pi _0\vert \). By definition, \(l_i' \le l_i\), and the total number of newly created blocks is \(\sum _{i=0}^{k-1}(l_i) = N_k - \vert \pi _0\vert \); hence, \(\sum _{i=0}^{k-1}(l_i + l_i')\le 2\sum _{i=0}^{k-1}(l_i)\le 2N_k-2\vert \pi _0\vert \). The number of waiting blocks is always positive, i.e. \(U_k \ge 0\), and the total number of blocks can never be larger than the number of states, i.e. \(N_k \le n\), so the total number of iterations z is bounded by \(z \le 2N_z - \vert \pi _0\vert \le 2n - \vert \pi _0\vert \). \(\square \)
4 Bisimulation coarsest refinement problem
In this section, we extend our algorithm to the bisimulation coarsest refinement problem (BCRP), i.e. to LTSs with multiple action labels.
Solving BCRP can in principle be done by translating an LTS to a Kripke structure, for instance by using the method described in [16]. This translation introduces a new state for every transition, resulting in a Kripke structure with \(n+m\) states. If the number of transitions is significantly larger than the number of states, then the number of iterations of our algorithm increases undesirably.
4.1 The PRAM algorithm
Instead of introducing more states, we introduce multiple marks per state, but in total we have no more than m marks. For each state s, we use a mark variable for each different outgoing action label relevant for s, i.e. for each a for which there is a transition  to some state t. Each state may have a different set of outgoing action labels and thus a different set of marks. Therefore, we first perform a preprocessing procedure in which we group together states as blocks in the initial partition that have the same set of outgoing action labels. This is valid, since two bisimilar states must have the same outgoing actions. Since in the sequence of produced partitions each partition is a refinement of the previous one, the algorithm has the invariant that two states of the same block have the same set of action labels. For the extended algorithm, we need to maintain extra information in addition to the information needed for Algorithm 2. For an input LTS
to some state t. Each state may have a different set of outgoing action labels and thus a different set of marks. Therefore, we first perform a preprocessing procedure in which we group together states as blocks in the initial partition that have the same set of outgoing action labels. This is valid, since two bisimilar states must have the same outgoing actions. Since in the sequence of produced partitions each partition is a refinement of the previous one, the algorithm has the invariant that two states of the same block have the same set of action labels. For the extended algorithm, we need to maintain extra information in addition to the information needed for Algorithm 2. For an input LTS  with n states and m transitions, the extra information is:
with n states and m transitions, the extra information is:
-
1.
Each action label has an index \(a \in \{0, \dots ,\vert Act \vert -1\}\).
-
2.
The following is stored in lists of size m, for each transition
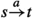 with transition index \(i \in \{0, \dots , m-1\}\):
with transition index \(i \in \{0, \dots , m-1\}\): -
(a)
\(a_i := a\), the action label of transition i,
-
(b)
\( order _i : {\mathbb {N}}\), the order of this action label, with respect to the source state s. For example, if a state s has the list [1, 3, 6] of outgoing action labels, and transition i has label 3, then \( order _i\) is 1 (we start counting from 0).
-
(a)
-
3.
\( mark : [{\mathbb {B}}]\), a list of up to m marks, in which there is a mark for every state, action pair for which it holds that the state has at least one outgoing transition labelled with that action. This list can be interpreted as the concatenation of sublists, where each sublist contains all the marks for one state. For each state \(s \in S\), we have:
-
(a)
\( off (s) : {\mathbb {N}}\), the offset to access the beginning of the sublist of the marks of the state s in \( mark \). The positions \( mark _{ off (s)}\) up to \( mark _{ off (s+1)}\) contain the sublist of marks for state s. For example, if state s has outgoing transitions with 3 distinct action labels, we know that \( off (s+1) \equiv off (s) + 3\), and we have 3 marks for state s. We write \( mark _{ off (s) + order _i}\) to access the mark for transition i which has source state s.
-
(a)
-
4.
\( mark\_length : {\mathbb {N}}\), the length of the mark list. This allows us to reset all marks in constant time using \( mark\_length \) processors. This number is not larger than the number of transitions (\( mark\_length \le m\)).
-
5.
In a list of size n, we store for each state \(s \in S\) a variable \( split _s : {\mathbb {B}}\). This indicates if the state will be split off from its block.
With this extra information, we can modify Algorithm 2 to work with labels. The new version is given in Algorithm 3. The changes involve the following:
-
1.
Lines 7–9: Reset the \( mark \) list.
-
2.
Line 11: Reset the \( split \) list.
-
3.
Line 17: When marking the transitions, we do this for the correct action label, using \( order _i\). Note the indexing into \( mark \). It involves the offset for the state \( source _i\) and \( order _i\).
-
4.
Lines 19–21: We tag a state to be split when it differs for any action from the block leader.
-
5.
Line 24: If a state was tagged to be split in the previous step, it should split from its leader.
-
6.
Line 29: If any block was split, the partition may not be stable w.r.t. the splitter.

To use Algorithm 3, two preprocessing steps are required. First, we need to partition the states w.r.t. their set of outgoing action labels. This can be done with a modified version of Algorithm 2, which performs one iteration for each action label. For the second preprocessing step, we need to gather the extra information that is needed in Algorithm 3. This is done via sorting the action labels and subsequently performing some parallel segmented (prefix) sums [17]. In total, the preprocessing takes \(\mathcal {O}(\vert Act\vert + \log m)\) time. For details how this is implemented, see Appendix A.
4.2 Complexity and correctness
The correctness of this algorithm follows directly from the arguments in Sect. 3.3.
Theorem 4.1
Given an LTS  , the partition \(\pi \) resulting from executing Algorithm 3 is the coarsest partition that induces a bisimulation relation, solving BCRP.
, the partition \(\pi \) resulting from executing Algorithm 3 is the coarsest partition that induces a bisimulation relation, solving BCRP.
Proof
The proof goes in a completely analogous way to the proof of Theorem 3.3.
We can modify the proof of Lemma 3.1, for it to still hold in the setting of labels. The \( mark \) for each action label is the same for two bisimilar states. This means bisimilar states have the same value for \( split \). Therefore, they will always be split into the same block together. Thus, bisimilar states will always be in the same block.
The proof of Lemma 3.2 still works in the setting with labels, proving that the partition \(\pi \) is stable with respects to all blocks \(B\in \pi \), and thereby that \(\pi \) induces a bisimulation relation.
Thus, these two facts imply that \(\pi \) is the coarsest partition inducing a bisimulation relation. \(\square \)
For Algorithm 3, we need to prove why it takes a linear number of steps to construct the final partition. This is subtle, as an iteration of the algorithm does not necessarily remove a block from the waiting set.
Theorem 4.2
BCRP on an input with m transitions and n states is solved by Algorithm 3 in \(\mathcal {O}(n + \vert Act\vert )\) time using \(\max (n,m)\) CRCW PRAM processors.
Proof
The total preprocessing takes \(\mathcal {O}(\vert Act\vert + \log m)\) steps, after which the while-loop will be executed on a partitioning \(\pi _0\) which was the result of the preprocessing on the partition \(\{S\}\). Every iteration of the while-loop is executed in constant time. Using the structure of the proof of Theorem 3.4, we derive a bound on the number of iterations.
At the start of iteration \(k\in {\mathbb {N}}\) the total number of blocks and waiting blocks are \(N_k,U_k\in {\mathbb {N}}\), initially \(U_0 = N_0 = \vert \pi _0\vert \). In iteration k, a number \(l_k\) of blocks is split into two blocks, resulting in \(l_k\) new blocks, meaning that \(N_{k+1} = N_{k} + l_k\). All new \(l_k\) blocks are marked as waiting and a number \(l_k' \le l_k\) of the old blocks that are split were not waiting at the start of iteration k and are now marked as waiting. If \(l_k = l_k' = 0\) there are no blocks split and the current block C is no longer marked as waiting. We indicate this with a variable \(c_k\): \(c_k=1\) if \(l_k = 0\), and \(c_k = 0\), otherwise. The total number of iterations up to iteration k in which no block is split is given by \(\sum _{i=0}^{k-1} c_i\). The number of iterations in which at least one block is split is given by \(k - \sum _{i=0}^{k-1} c_i\).
If in an iteration k at least one block is split, the total number of blocks at the end of iteration k is strictly higher than at the beginning; hence, for all \(k\in {\mathbb {N}}\), \(N_k \ge k - \sum _{i=0}^{k-1}c_i\). Hence, \(N_k+\sum _{i=0}^{k-1}c_i\) is an upper bound for k.
We derive an upper bound for the number of iterations in which no blocks are split using the total number of waiting blocks. In iteration k there are \(U_k = \sum _{i=0}^{k-1}(l_i + l_i') - \sum _{i=0}^{k-1} c_i + \vert \pi _0\vert \) waiting blocks. Since the sum of newly created blocks \(\sum _{i=0}^{k-1}(l_i) = N_k-\vert \pi _0\vert \) and \(l_i' \le l_i\), the number of blocks marked as waiting \(U_k\) is bounded by \(2N_k-\sum _{i=0}^{k-1}c_i - \vert \pi _0\vert \). Since \(U_k\ge 0\) we have the bound \(\sum _{i=0}^{k-1}c_i\le 2N_k-\vert \pi _0\vert \). This gives the bound on the total number of iterations \(z \le 3N_z-\vert \pi _0\vert \le 3n - \vert \pi _0\vert \).
With the time for preprocessing this makes the run time complexity \(\mathcal {O}(n + \vert Act\vert + \log m)\). Since the number of transitions m is bounded by \(\vert Act\vert \times n^2\), this simplifies to \(\mathcal {O}(n + \vert Act\vert )\). \(\square \)
4.3 Experimental results
In this subsection, we discuss the results of our implementation of Algorithm 3. Note that this implementation is not optimised for the specific hardware it runs on, since the goal of this article is to provide a generic parallel algorithm. This implementation is purely a proof of concept, to show that our algorithm can be mapped to contemporary hardware and to understand how the algorithm scales with the size of the input.
The implementation targets GPUs since a GPU closely resembles a PRAM and supports a large amount of parallelism. The algorithm is implemented in CUDA C++ version 11.1 with use of the Thrust library.Footnote 2 As input, we chose all benchmarks of the VLTS benchmark suiteFootnote 3 for which the implementation produces a result within 10 minutes. The VLTS benchmarks are LTSs that have been obtained from various case studies derived from real concurrent system models.
The experiments were run on an NVIDIA Titan RTX with 24 GB memory and 72 Streaming Multiprocessors, each supporting up to 1024 threads in flight. Although this GPU supports 73,728 threads in flight, it is very common to launch a GPU program with one or even several orders of magnitude more threads, in particular to achieve load balancing between the Streaming Multiprocessors and to hide memory latencies. In fact, the performance of a GPU program usually relies on that many threads being launched.
Table 1 shows the results of the experiments we conducted. The \(\vert Act \vert \) column corresponds to the number of different action labels. The \(\vert Blocks \vert \) column indicates the number of different blocks at the end of the algorithm, where each block contains only bisimilar states. With \(\# It \), we refer to the number of while-loop iterations that were executed (see Algorithm 3). The number of states and transitions can be derived from the benchmark name. In the benchmark ‘\(X\_N\_M\),’ \(N*1000\) is the number of states and \(M*1000\) is the number of transitions. The \(T_ pre \) give the preprocessing times in milliseconds, which includes the memory transfers to the GPU, sorting the transitions and initial partitioning. The \(T_ alg \) give the times of the core algorithm, in milliseconds. The \(T_\textit{BCRP}\) is the sum of the preprocessing and the algorithm, in milliseconds. We have not included the loading times for the files and the first CUDA API call that initialises the device. We ran each benchmark 10 times and took the averages. The standard deviation of the total times varied between 0% and 3% of the average; thus, 10 runs are sufficient. All the times are rounded with respect to the standard error of the mean.
We see that the bound as proved in Sect. 4.2 (\(k \le 3n\)) is indeed respected, \(\# It /n\) is at most 2.20, and in most cases below that. The number of iterations is tightly related to the number of blocks that the final partition has, the \(\# It / \vert Blocks \vert \) column varies between 1.00 and 2.53. This can be understood by the fact that each iteration either splits one or more blocks or marks a block as non-waiting, and all blocks are waiting at least once. This also means that for certain LTSs the algorithm scales better than linearly in n. The preprocessing often takes the same amount of time (about a few milliseconds). Exceptions are those cases with a large number of actions and/or transitions, for instance Vasy_25_25 or Vasy_574_13561.
Concerning the run times, it is not true that each iteration takes the same amount of time. A GPU is not a perfect PRAM machine. There are two key differences. Firstly, we suspect that the algorithm is memory bound since it is performing a limited amount of computations. The memory accesses are irregular, i.e. random, which caches can partially compensate, but for sufficiently large n and m, the caches cannot contain all the data. This means that as the LTSs become larger, memory accesses become relatively slower. Secondly, at a certain moment, the maximum number of threads that a GPU can run in parallel is achieved, and adding more threads will mean more run time. These two effects can best be seen in the \(T_ alg /\# It \) column, which corresponds to the time per iteration. The values are around 0.02 up to 300, 000 transitions, but for a larger number of states and transitions, the amount of time per iteration increases.
4.4 Experimental comparison
We compared our implementation (BCRP) with an implementation of the algorithm by Lee and Rajasekaran (LR) [12] on GPUs, and the optimised GPU implementation by Wijs based on signature-based bisimilarity checking [18], with multi-way splitting (Wms) and with single-way splitting (Wss) [14]. Multi-way splitting indicates that a block is split into multiple blocks at once, which is achieved by computing a signature for each state in every partition refinement iteration, and splitting each block off into sets of states, each containing all the states with the same signature. The signature of a state is derived from the labels of the blocks that this state can reach in the current partition. Note that we are not including comparisons with CPU bisimulation checking tools; the fact that those tools run on completely different hardware makes a comparison problematic, and such a comparison does not serve the purpose of evaluating the feasibility of implementing Algorithm 3. Optimising our implementation to make it competitive with CPU tools is planned for future work.
The running times of the different algorithms can be found in Table 2. Similarly to our previous benchmarks, the algorithms were run 10 times on the same machine using the same VLTS benchmark suite with a time-out of 10 minutes. In some cases, the nondeterministic behaviour of the algorithms Wms and Wss led to high variations in the runs. In cases where the standard error of the mean was more than 5% of the mean value, we have added the standard error in Table 2 in parentheses. Furthermore, all the results are rounded with respect to the standard error of the mean. As a preprocessing step for the LR, Wms and Wss algorithms the input LTSs need to be sorted. We did not include this in the times, nor the reading of files and the first CUDA API call (which initialises the GPU).
This comparison confirms the expectation that our algorithm in all cases (except the small LTS Cwi_1_2) outperforms LR and that LR is not suitable for massive parallel devices such as GPUs.
Furthermore, the comparison demonstrates that in most cases our algorithm (BCRP) outperforms Wss. In some benchmarks (Cwi_1_2, Cwi_214_684, Cwi_2165_8723 and Cwi_2416_17605) Wss is more than twice as fast, but in 16 other cases our algorithm is more than twice as fast. The last comparison shows that our algorithm does not outperform Wms. Wms employs multi-way splitting which is known to be very effective in practice. Furthermore, contrary to our implementation, Wms is optimised for GPUs while the focus of the current work is to improve the theoretical bounds and describe a general algorithm.
In order to understand the difference in performance between Wms and our algorithm better, we analysed the complexity of Wms [14]. In general this algorithm is quadratic in time, and the linearity claim in [14] depends on the assumption that the fan-out of ‘practical’ transition systems is bounded, i.e. every state has no more than c outgoing transitions for c a (low) constant. We designed the transition systems \(\textit{Fan}\_\textit{out}_n\) for \(n\in {\mathbb {N}}^+\) to illustrate the difference. The LTS  has n states: \(S=\{0,\dots ,n-1\}\). The transition function contains
has n states: \(S=\{0,\dots ,n-1\}\). The transition function contains  for all states \(1<i< n-1\). Additionally, from state 0 and 1 there are transitions to every state:
for all states \(1<i< n-1\). Additionally, from state 0 and 1 there are transitions to every state:  for all \(i\in S\). This LTS has n states, \(3n-3\) transitions and a maximum out degree of n transitions.
for all \(i\in S\). This LTS has n states, \(3n-3\) transitions and a maximum out degree of n transitions.
Fig. 2 shows the results of calculating the bisimulation equivalence classes for \(\textit{Fan}\_\textit{out}_n\), with Wms and BCRP. It is clear that the run time for Wms increases quadratically as the number of states grows linearly, already becoming untenable for a small number of states. On the other hand, in conformance with our analysis, our algorithm scales linearly.
5 Branching bisimilarity
When systems get more complex, abstractions are an essential tool to gain insight into the behaviour of the system. Often a special action label \(\tau \) is used to model internal behaviour in LTSs. Branching bisimilarity, as introduced by Van Glabbeek and Weijland [19] is an equivalence that takes these internal actions into account. It is defined as follows.
Definition 5.1
(Branching bisimulation [19, Definition 2.4]) Given an LTS \(A = (S, \rightarrow , Act)\) a relation \(R \subseteq S\times S\) is called a branching bisimulation relation iff it is symmetric and for all states \(s,t \in S\) such that sRt and for all actions \(a\in Act\): if  then either
then either
-
\(a = \tau \) and \(s' R t\), or
-
there is a sequence
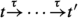 of zero or more \(\tau \)-transitions such that \(sRt'\),
of zero or more \(\tau \)-transitions such that \(sRt'\), 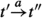 and \(s' R t''\).
and \(s' R t''\).
Branching bisimilarity is the coarsest branching bisimulation relation, and we denote this as  .
.
The problem we address in this section is taking into account branching bisimulation relations. We define the branching bisimulation refinement problem (branching-BCRP) as follows:
Input: An LTS  with a dedicated internal action \(\tau \in Act\).
with a dedicated internal action \(\tau \in Act\).
Output: The partition \(\pi \) of S, which is the coarsest partition, i.e. has the smallest number of blocks, that forms a branching bisimulation relation.
This section explains how to adapt our parallel algorithm for strong bisimilarity (BCRP) to decide branching bisimilarity (branching-BCRP) in \(O(n + \vert Act \vert )\) parallel time using \(\max (n^2,m,\vert Act \vert n)\) parallel processors.
The section is structured as follows: In Sect. 5.1, we recall some preliminaries specific to branching bisimulations and establish the notation we use throughout this section. Next, in Sect. 5.2, we explain key ingredients from the sequential algorithm by Groote and Vaandrager [20]. After that, in Sect. 5.3, we explain the key modifications in a parallel setting. Then, in Sect. 5.4, we give the details of the algorithm. Lastly, in Sect. 5.5, we prove the correctness and complexity bounds of the parallel algorithm.
5.1 Preliminaries on branching bisimulation
For the next section, we assume that in any LTS the internal \(\tau \)-action is available, so \(\tau \in Act\).
Fig. 3 shows an LTS at the top with all states in one block. We group branching bisimilar states at the bottom, where we denote the branching bisimilarity equivalence classes \(B_1\) up to \(B_7\).
Next, we define bottom states, which are states that do not have an outgoing \(\tau \)-transition to another state in the same block.
Definition 5.2
(Bottom state [20]) Let \(A=(S, Act, \rightarrow )\) be an LTS, \(\pi \) a partition of S, and \(s \in B \in \pi \) where B is a block. We call s a bottom state iff there is no \(s' \in B\) such that  .
.
In Fig. 3, at the top states \(s_5\), \(s_6\) and \(s_7\) are bottom states. In the situation at the bottom every state except \(s_3\) is a bottom state.
We call a \(\tau \)-transition silent when both the source and target state are in the same block.
Definition 5.3
(Silent \(\tau \)-transition) Let \(A=(S, Act, \rightarrow )\) be an LTS. Let \(\pi \) be a partition of S. We call a \(\tau \)-transition  silent with respect to \(\pi \) iff \(s, s' \in B \in \pi \).
silent with respect to \(\pi \) iff \(s, s' \in B \in \pi \).
So in Fig. 3 on the top side all \(\tau \)-transitions are silent and on the bottom only  is silent.
is silent.
Below we define the silent transitive closure of  transitions, denoted by \(\Rightarrow _\pi \), which relates each state s to all states that are reachable starting from s via a path of zero or more silent \(\tau \)-transitions.
transitions, denoted by \(\Rightarrow _\pi \), which relates each state s to all states that are reachable starting from s via a path of zero or more silent \(\tau \)-transitions.
Definition 5.4
(Transitive and reflexive \(\tau \)-closure) Let \(A=(S, Act, \rightarrow )\) be an LTS. Let \(\pi \) be a partition of S. We denote \(s \Rightarrow _\pi s'\) iff s can reach \(s'\) performing zero or more silent \(\tau \)-transitions  where for some \(B \in \pi \) all \(s, s', s_1, \ldots , s_n \in B\). We call \(\Rightarrow _\pi \) the transitive and reflexive \(\tau \)-closure with respect to \(\pi \).
where for some \(B \in \pi \) all \(s, s', s_1, \ldots , s_n \in B\). We call \(\Rightarrow _\pi \) the transitive and reflexive \(\tau \)-closure with respect to \(\pi \).
In Fig. 3, we indicate the transitive \(\tau \)-closure for the two different partitions. To improve readability, we do not show the reflexive part.
The following lemma expresses that not only the first state t and the last state \(t'\) on a silent \(\tau \)–path  are related but every intermediate state is related to t.
are related but every intermediate state is related to t.
Lemma 5.5
(cf. [19, Lemma 2.5]) Let  be an LTS, and let for some \(n>0\),
be an LTS, and let for some \(n>0\),  be a path of \(\tau \)-transitions in A with
be a path of \(\tau \)-transitions in A with  . Then for every
. Then for every  .
.
In order to talk about the directly reachable non-silent transitions of a state, we define the direct markings of a state.
Definition 5.6
(Direct markings) Let \(A=(S, Act, \rightarrow )\) be an LTS, and \(\pi \) a partition of S. Let \(s \in S\) and \(B \in \pi \). We define the direct markings of s to B as:

For branching bisimulations, the stability condition changes slightly. Given an LTS  and \(\pi \) a partition of S. A block B is called stable modulo branching bisimulation with respect to a block \(B'\in \pi \), iff for all actions \(a\in Act\) either for all states \(s\in B\) there is an \(s'\in B\) such that \(s\Rightarrow _\pi s'\) and \(a\in dir(s', B')\), or for all states \(s\in B\), \(a\not \in dir(s,B')\).
and \(\pi \) a partition of S. A block B is called stable modulo branching bisimulation with respect to a block \(B'\in \pi \), iff for all actions \(a\in Act\) either for all states \(s\in B\) there is an \(s'\in B\) such that \(s\Rightarrow _\pi s'\) and \(a\in dir(s', B')\), or for all states \(s\in B\), \(a\not \in dir(s,B')\).
A partition \(\pi \) is again called stable under a block \(B'\) iff each block \(B\in \pi \) is stable under \(B'\). The partition \(\pi \) is called stable iff it is stable under all its own blocks \(B\in \pi \).
5.2 The sequential algorithm
In this section, we explain the key ideas used in the sequential Groote–Vaandrager algorithm [20] to decide branching bisimilarity. In this algorithm, similar to the sequential Kanellakis–Smolka algorithm as explained in Sect. 3.1, a partition is maintained and iteratively refined based on behaviour that distinguishes states. For strong bisimulation, a block is split into the set of states that can directly reach a splitter block. However, in the Groote–Vaandrager algorithm, states are also split if they can reach the splitter by first doing a sequence of silent \(\tau \) actions. In [20], this initial silent path is called stuttering and comes from the related problem of deciding stuttering equivalence on Kripke structures [21].
Another subtle but essential difference between the two algorithms is that stability modulo branching bisimulation is not necessarily preserved under refinement, i.e. Fact 2.3 may not hold. This is also observed in [20, Lemma 5.2.3] and is addressed by always considering all blocks as potential splitters.
In summary, when solving branching-BCRP the two main modifications we need to address with respect to the parallel algorithm for BCRP.
-
1.
Modification 1: A different splitting strategy, that takes into account initial \(\tau \)-paths.
-
2.
Modification 2: After refinement of partition \(\pi \) into \(\pi '\) check that blocks that are stable w.r.t \(\pi \) are still stable for \(\pi '\).
5.3 The parallel algorithm
This section addresses the necessary modifications in the parallel setting such that we have a linear parallel algorithm to decide branching bisimilarity.
In the strong bisimilarity algorithm, we choose a block as a splitter. We check which actions can reach this splitter for each state by going over all transitions and storing a mark for each action label. We also store a marking for each action label for branching bisimulation, but we must consider the \(\tau \)-paths. Therefore, to address Modification 1, we need to propagate the markings over the \(\tau \)-paths. For example, in Fig. 3 any marking that state \(s_5\) has can potentially propagate to state \(s_1\), \(s_2\), \(s_3\) and \(s_4\).
This method of propagating information backwards over \(\tau \)-paths is also used in the sequential algorithms [11, 20]. Likewise, the parallel algorithm [14] for branching bisimilarity propagates information from the bottom states backwards over the silent \(\tau \)-paths. However, this approach is inherently sequential since, in the worst case, we propagate state information over long silent paths before we can calculate a refinement. For a better asymptotic complexity, we calculate a transitive closure in the style of [22, 23].
In our parallel algorithm, we maintain the relation \(\Rightarrow _{\pi }\) that is the transitive and reflexive closure of all silent \(\tau \)-transitions in \(\pi \). This closure changes throughout the algorithm, but we can update this information in constant parallel time. Lemma 5.9 states that if \(\pi \) refines into \(\pi '\), we only need to check the source and target of a silent \(\tau \)-path to see whether it remains silent in \(\pi '\).
For Modification 2 regarding stability, we use the fact that a block not in the waiting list can only make the partition unstable if a state has become newly bottom, as Lemma 5.8 shows.
A state that is non-bottom can become bottom only once, and this happens if a silent \(\tau \)-transition becomes non-silent. For example, in Fig. 3 the transition  is non-silent at the bottom in the picture; thus, \(s_1\) became a bottom state at some point.
is non-silent at the bottom in the picture; thus, \(s_1\) became a bottom state at some point.
Finally, we add a further modification. Throughout the algorithm, we ensure that each block has a bottom state as a leader. This is well defined since we consider LTSs with a finite number of states, and in the preprocessing phase, we remove \(\tau \)-loops, and therefore, each block has at least one bottom state. This modification makes it easier to compare states since bottom states do not get extra marks via silent \(\tau \)-steps.
5.3.1 Modification 1: splitting
We split blocks by considering all actions a state can reach via the silent transitive \(\tau \)-closure. A similar approach is used in [20] where the set of states that can reach a certain block with a specific action label after an initial inert \(\tau \)-path is considered. We initially mark all states with the actions they can take directly to the splitter block. Afterwards, we distribute all the marks via the silent transitive \(\tau \)-closure. This results in a similar set of states as in [20] but not with respect to a specific action label but with respect to all action labels. Distributing the marks naively would mean we hand out up to \(\vert Act \vert n^2\) marks since there can be \(\vert Act \vert \) markings per state and up to \(n^2\) elements in the transitive \(\tau \)-closure. Thus, we opt only to distribute one element per state if a state should split, thus distributing \(n^2\) elements maximally.
For a partition \(\pi \) of S, we consider a block \(B\in \pi \) that acts as a splitter, and we let \(B_{s_b}\) denote any block in \(\pi \) that has the bottom state \(s_b\in S\) as its leader. We define:
Informally \(\textit{PreSplit}_\pi (B_{s_b},B)\) contains all the states of \(B_{s_b}\) that have a behaviour with respect to B that \(s_b\) cannot mimic, and it also contains the bottom states that cannot mimic the behaviour of \(s_b\) with respect to B. The first means that the state can reach B with an action a which \(s_b\) cannot. The second means that s is a bottom state, and \(s_b\) can reach B with an action a, which s cannot. The set \(\textit{Split}_\pi (B_{s_b}, B)\) contains all states that have silent \(\tau \)-transitions to states that are in \(\textit{PreSplit}_\pi \). These states are also necessarily not branching bisimilar to \(s_b\).
The states that are in the set \(\textit{Split}_\pi (B_{s_b},B)\) are all the states that should split from the block \(B_{s_b}\) into a new block. Based on this function we derive a new partition \(\textit{Ref}(\pi , B)\) in which every block \(B_{s_b}\) is split into \(\textit{Split}_\pi (B_{s_b},B)\) and the states not in \(\textit{Split}_\pi (B_{s_b},B)\)
From the initial partition \(\pi _0 = \{S\}\), we iteratively refine the current partition \(\pi \) by finding a splitter for which \(\textit{Ref}(\pi , B) \ne \pi \) and continue based on the partition \(\pi '= \textit{Ref}(\pi , B)\). The correctness relies on the fact that \(\textit{Ref}(\pi , B)\) never splits states that are branching bisimilar and the fact that if the partition \(\pi \) does not induce the relation  then there still is a splitter B such that \(\textit{Ref}(\pi , B) \ne \pi \).
then there still is a splitter B such that \(\textit{Ref}(\pi , B) \ne \pi \).
In Sect. 5.5.1, we will prove that this splitting procedure is correct.
5.3.2 Modification 2: stability
The key property (Fact 2.3) does not hold for stability modulo branching bisimilarity. Counterexamples show that refinement can cause blocks to lose stability. See [20, Remark 3.4], where a counterexample is given. In the Groote–Vaandrager algorithm, the authors resolve this by reconsidering all blocks if new bottom states are added [20, Lemma 3.3]. This strategy would result in a quadratic worst-case algorithm in our parallel setting.
The following lemma expresses when a block can act as a splitter. We observe that only item 5.7 from Lemma 5.7 is not inherited under refinement.
Lemma 5.7
(cf. [20, Lemma 5.2.2]). Let  be an LTS, \(\pi \) a partition of S refined by
be an LTS, \(\pi \) a partition of S refined by  and blocks \(B, B'\in \pi \). The block \(B'\) is a splitter of B (\(\textit{Split}_\pi (B, B') \ne \emptyset \)) iff there is an \(a\in Act\) such that:
and blocks \(B, B'\in \pi \). The block \(B'\) is a splitter of B (\(\textit{Split}_\pi (B, B') \ne \emptyset \)) iff there is an \(a\in Act\) such that:
-
1.
\(a\ne \tau \) or \(B\ne B'\),
-
2.
for some \(s\in B\) and
 , and
, and -
3.
there is some bottom state \(s_b\in B\) such that for no
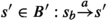 .
.
Proof sketch
The proof is similar to the one in [20, Lemma 3.2 and 5.2.2]; thus, a full proof is omitted. We provide a rough sketch since the splitting condition is different. We only need to prove that the conditions 1 to 3 hold iff \(\textit{PreSplit}_\pi (B, B') \ne \emptyset \), since \(\textit{Split}_\pi (B, B')\) is only empty when \(\textit{PreSplit}_\pi (B, B')\) is as well.
For the (\({\implies }\)) part, we make a case distinction on the two sets that define \(\textit{PreSplit}_\pi (B, B')\) and it follows that we find a state and bottom state for which the three conditions of this lemma hold. For the (\({\Longleftarrow }\)) part, we make a case distinction on whether the bottom state in condition 3 of this lemma is the block leader of B. In both cases, we can prove that there are states in \(\textit{PreSplit}_\pi (B, B')\). \(\square \)
In order to maintain our invariant that if a block is not marked as waiting the partition is stable modulo branching bisimulation under this block of states, we perform extra steps for each new bottom state to check if there is a block that now is a splitter conform Lemma 5.7. Since a bottom state never becomes a non-bottom state, this is maximally done at most once for each state.
The following lemma is a slight modification of Lemma 5.7. However, here we specify that a new bottom state must witness that the partition is not stable anymore with respect to a block. We define \(bottom(\pi )\) as all states that are bottom in the partition \(\pi \).
Lemma 5.8
Let  be an LTS. Let \(\pi \) be a partition of S and \(\pi '\) be a refinement of \(\pi \) and both are refined by
be an LTS. Let \(\pi \) be a partition of S and \(\pi '\) be a refinement of \(\pi \) and both are refined by  . Now suppose \(B' \in \pi \) and \(B' \in \pi '\) and that \(\textit{Ref}(\pi , B') = \pi \), thus \(\pi \) is stable with respect to \(B'\).
. Now suppose \(B' \in \pi \) and \(B' \in \pi '\) and that \(\textit{Ref}(\pi , B') = \pi \), thus \(\pi \) is stable with respect to \(B'\).
Now for some block \(B \in \pi '\) we find that \(B'\) is a splitter of B (\(\textit{Split}_{\pi '}(B, B')\ne \emptyset \)) iff for all actions \(a\in Act\):
-
1.
\(a\ne \tau \) or \(B\ne B'\),
-
2.
for some \(s\in B\) and
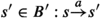 , and
, and -
3.
there is some bottom state \(s_b\in (bottom(\pi ') \setminus bottom(\pi )) \cap B\) such that for no
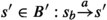 .
.
Proof
(\(\Longleftarrow \)): This follows immediately from Lemma 5.7.
(\(\implies \)): Suppose \(\textit{Split}_{\pi '}(B, B') \ne \emptyset \), then we know by Lemma 5.7 that we have for some \(s \in B\) and  , \(a \ne \tau \) or \(B \ne B'\), and there is a bottom \(s_b \in B\) such that for no
, \(a \ne \tau \) or \(B \ne B'\), and there is a bottom \(s_b \in B\) such that for no  . We now need to show that \(s_b \in bottom(\pi ') \setminus bottom(\pi )\). We assume to the contrary that \(s_b\) is not part of this set and show that this leads to a contradiction.
. We now need to show that \(s_b \in bottom(\pi ') \setminus bottom(\pi )\). We assume to the contrary that \(s_b\) is not part of this set and show that this leads to a contradiction.
If \(s_b\) \(\not \in bottom(\pi ') \setminus bottom(\pi )\), this must mean that \(s_b \in bottom(\pi )\). Since \(\pi '\) refines \(\pi \), we must have a \(C \in \pi \) such that \(B \subseteq C\). Now \(s_b \in C\) and there is a bottom state \(s \in C\) and either \(a \ne \tau \) or \(C \ne B'\). Thus, we have found an \(s_b\), and s to which Lemma 5.7 applies and we know that \(\textit{Split}_\pi (C, B') \ne \emptyset \). This means that \(\textit{Ref}(\pi , B) \ne \pi \) which is a contradiction. \(\square \)
This lemma implies that a block \(B'\), which is not in the waiting set, is a new splitter for the partition iff there is a newly created bottom state in block B that is unable to reach this block \(B'\), while there is some state in the block B that can reach this block \(B'\). A procedure to find these blocks \(B'\) for a newly created bottom state \(s_b\in B \in \pi \), can be run in parallel (see Algorithm 7). This procedure can be summarised as follows.
-
For every transition
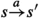 , if \(s\in B\) do:
, if \(s\in B\) do:-
Find block \(B'\) such that \(s'\in B'\).
-
If \(s = s_b\) mark that \(s_b\) reaches \(B'\) with a.
-
If \(s \ne s_b\) check if \(s_b\) was able to reach \(B'\) with a if not split by \(B'\) immediately.
-
5.4 Algorithm
Based on the modifications, we mention in Sect. 5.3 and the parallel algorithm for strong bisimilarity, we construct an algorithm that decides branching bisimulation in \(O(n + \vert Act \vert )\) time in parallel on a PRAM with \(\max (n^2,m,\vert Act \vert n)\) processors. In Algorithm 4, we give the main structure of our algorithm. The algorithm is similar to the parallel algorithm for strong bisimilarity. We add the modifications mentioned in Sect. 5.3 to subroutines, which we give in Algorithms 5, 6 and 7.
In this subsection, we first define the additional data we store in memory. Next, we discuss preprocessing. Finally, we discuss the algorithm in more detail and give an example iteration.
5.4.1 Data structure
The main memory contains the following extra data for our algorithm for branching bisimulation:
-
We indicate \(s_b: S\) as the current bottom state we are inspecting for unstability. It has value \(\bot \) if no new bottom state has been selected.
-
For every index \(0 \le i <n\) of a state \(s_i\) we added the boolean values:
-
\(\textit{bottom}_i\) indicating whether the state is a bottom state;
-
\(\textit{old}\_\textit{bottom}_i\) showing whether the state was already bottom in the previous iteration;
-
\(\textit{new}\_\textit{bottom}_i\) telling whether \(s_i\) is a new bottom state;
-
\(sure\_split_i: {\mathbb {B}}\) expressing whether state \(s_i\) can take an action that its leader cannot;
-
\(same\_marks_i: {\mathbb {B}}\) specifying whether the state \(s_i\) has the same direct markings as its leader.
-
-
An array of booleans of size m such that for index \(0 \le i < m\) of a transition i the boolean value \( silent _i : {\mathbb {B}}\) indicates whether the transition is silent.
-
We use \(t: {\mathbb {N}}\) to indicate the number of transitive \(\tau \)-transitions.
-
For every index \(0 \le i <t\) of a transitive \(\tau \)-transition (\(s \Rightarrow _{\pi } s'\)):
-
\(t\_source_i: S\) the source state (s);
-
\(t\_target_i: S\) the target state (\(s'\));
-
\(t\_silent_i: {\mathbb {B}}\) which is true iff the transitive \(\tau \)-transition is silent.
-
-
We need to adjust the \(mark_i: {\mathbb {B}}\) array to not only contain the marks for directly reachable actions, but also actions that can be reached after performing \(\tau \)-steps. This is needed since states with the same reachable actions can be in the same block and must be able to compare marks with each other. Each state always has a mark for the \(\tau \)-action, regardless of whether it has \(\tau \)-actions. For example, state \(s_3\) of Fig. 3 has markings for \(\tau \), a and b. Additionally, for each mark, we now keep track of
-
\(mark\_source_i: S\) the state to which this mark belongs;
-
\(mark\_order_i: {\mathbb {N}}\) the order of the mark. For example, state \(s_3\) of Fig. 3 has order 0, 1 and 2 for its \(\tau \), a and b marks, respectively.
-
-
In the algorithm we use \(order_i: {\mathbb {N}}\) such that a transition can set the correct mark of a state. Since \(mark_i\) is different, we need to update this array as well.
-
An array that has for each block B and action \(a\in Act\) the boolean value \( reachable _{B,a}: {\mathbb {B}}\). This is used for storing whether the current new bottom state under inspection can reach block B with a non-silent a action. We note that we can maximally have n blocks. Thus, this array has size \(n \cdot \vert Act \vert \).
5.4.2 Preprocessing
An example LTS and its derived preprocessing information. The variables \( action\_switch _i\), \( order _i'\), \( nr\_marks _{source_i}'\) are auxiliary and we explain them in Sect. 1 of Appendix

First, we calculate the transitive \(\tau \)-closure, which we can view as a pairwise shortest path computation. We can compute this using \(n^2\) processors in \(\mathcal {O}(n)\) [22, 23]. If we consider the transitive \(\tau \)-closure as transitions, we can end up with up to \(n^2\) of these transitions. Thus, we need \(n^2\) processors to go over them in \(\mathcal {O}(1)\) time. In real-life examples of LTSs, especially when only considering the silent \(\tau \)-steps, the number of these transitions is much smaller than \(n^2\).
An iteration of Algorithm 4 on example LTS from Fig. 3
As in Groote and Vaandrager [20], we first remove \(\tau \)-cycles since all states in a cycle end up in the same block of the final partition. We use the transitive \(\tau \)-closure to remove the \(\tau \)-cycles. We start a processor for each state s, and each state iterates over each other state \(s'\), and looks if both \(s \Rightarrow _{\pi } s'\) and \(s' \Rightarrow _{\pi } s\) hold. We note that \(\pi = \{ S\}\) here. We store the lowest state number, \(s_l\), for which this holds, which we use to replace all references to s with \(s_l\). All states in a cycle have one such number, namely the lowest. So this is consistent. In this way, we removed all \(\tau \)-cycles in \(\mathcal {O}(n)\) time using \(\mathcal {O}(n)\) processors.
As opposed to the original algorithm, we now need to group states on directly possible actions and actions that a state can take after performing silent \(\tau \)-steps. Therefore, we again use the base algorithm to split the sets of states into blocks based on the actions they can take and additionally let the transitive \(\tau \)-closure distribute the marks for silent \(\tau \)-paths. We describe this procedure in Appendix in Algorithm 8. Afterwards, we set all the blocks of this new partition to waiting, i.e. \(waiting_{block_i} = \textsf {true}\). Since we loop over all the actions and execute the loop body in constant time, this step takes \(\mathcal {O}(\vert Act \vert )\) time.
Initially we mark all states as non-bottom (\(bottom_i := \textsf {false}\)), all non-\(\tau \)-transitions as non-silent and all \(\tau \)- and transitive \(\tau \)-transitions as silent (\(silent_i := \textsf {true}\), \(t\_silent_i := \textsf {true}\)). In the first partition, not every (transitive) \(\tau \)-transition is actually silent anymore and we need to know which states are bottom. We use the procedure SetSilentAndBottom to determine this. To elect bottom states as leaders, we also execute ElectBottomLeaders. Both these procedures can be found in Algorithm 5. Finally, we mark all the values for \(new\_bottom_i\) to false since we actually do not have to fix stability for these bottom states because every block is already waiting.
We can now remove any transitive \(\tau \)-transitions which are not silent anymore. This step is unnecessary to guarantee correctness, but we expect it to significantly reduce the number of transitive \(\tau \)-transitions. Therefore, this would improve the run time of the algorithm. Filtering these transitions takes \(\mathcal {O}(\log t)\) time when using a parallel scan to put the elements in a consecutive array again. Note that we can write \(\mathcal {O}(\log t)\) as \(\mathcal {O}(\log n)\), since \(t \le n^2\).
Finally, we must preprocess the mark and order arrays differently. We only had a mark for each possible direct action in the original preprocessing. We now consider actions that a state can reach using silent \(\tau \)-steps. Thus, a state can have a mark for an action that it cannot take directly. Since a bottom state only takes direct actions, and we always pick a bottom state as a block leader, we let each state look at its block leader to determine the needed marks. Each state also needs a mark for a \(\tau \)-action. For more details, see Sect. 1 in Appendix. At most, this preprocessing step takes \(\mathcal {O}(\log n + \vert Act \vert )\) time on \(\max (n^2,m,\vert Act \vert n)\) processors.
Combining all the bounds on the complexity of the complete preprocessing procedure, we end up with \(\mathcal {O}(n + \vert Act \vert )\) time using \(\max (n^2,m,\vert Act \vert n)\) processors in the worst case.
5.4.3 Algorithm
In Fig. 5, an iteration of Algorithm 4 is performed on the example LTS from Fig. 3, starting at Line 13, after a splitter C has been selected.



Following Algorithm 4, the first lines up to Line 13 are to reset the variables and select a splitter. In the procedure CheckStability, the condition from Lemma 5.8 is used to determine whether there is a new bottom state that causes a split. If this procedure finds a splitter C, we use it. On the other hand, if this procedure does not yield a splitter, a splitter is selected uniformly among the blocks for which the partition is not considered stable yet (Line 9–10).
In Lines 13–15, the direct markings are set for each transition reaching the currently selected splitter C. After which the procedure DetermineSplits, given in Algorithm 6, marks states that are supposed to split. For each state \(s\in B_{s_b} \in \pi \), the variable \(\textit{split}_i\) is set (Algorithm 6 Lines 14–16) to indicate whether the state is in the \(\textit{PreSplit}_\pi (B_{s_b}, C)\). Finally the transitive \(\tau \)-closures are followed to also set the \(\textit{split}_i\) variable for states that are in the set \(\textit{Split}_\pi (B_{s_b},C)\).
In lines 17–25, the new partition \(\textit{Ref}(\pi , C)\) is calculated. This is done in the same way as in the algorithm for strong bisimulation. The partition \(\pi \) is only considered stable with respect to C if \(\textit{Ref}(\pi ,C)= \pi \), meaning not a single split happened.
The final step is updating the necessary information. The procedure SetSilentAndBottom updates all the silent \(\tau \)-paths by checking the conditions from Lemma 5.9. With all \(\tau \)-steps now correctly marked silent, we can calculate the new bottom states, and the procedure ElectBottomLeaders ensures that for each new block, the leader is a bottom state. After we found the new leaders for split blocks, we set the newly split blocks to waiting.
5.5 Complexity and correctness
First, we proof that our splitting procedure of Sect. 5.3.1 is correct. Next, showing the correctness of the algorithm can be done in a similar fashion as in the previous algorithm. By first showing the resulting partition induces a branching bisimulation relation, and secondly showing it is the coarsest partition forming a branching bisimulation relation. Lastly, we prove the complexity of the algorithm.
5.5.1 Correct splitting
To establish that we have a valid splitting procedure, we need to prove that branching bisimilar states never end up in different blocks and that if we cannot split blocks anymore, the partition induces a branching bisimulation relation. We prove these two properties in the remainder of this subsection, but we first prove two auxiliary lemmas.
Firstly, the following auxiliary lemma shows that updating the silent transitive closure \(\Rightarrow _\pi \) by only checking whether states are still in the same block is correct with the given splitting procedure.
Lemma 5.9
Let \(A= (S, \rightarrow , Act)\) be an LTS where S contains no \(\tau \)-cycles, \(\pi \) a partition of S, \(s,s' \in S\) two states, \(C\in \pi \) a splitter, and \(\pi '\) the partition given by \(\pi '=\textit{Ref}(\pi ,C)\). Then \(s\Rightarrow _{\pi '} s'\) if and only if \(s \Rightarrow _{\pi } s'\) and s and \(s'\) are in the same block \(B\in \pi '\).
Proof
Given a partition \(\pi \) of an LTS \(A=(S \rightarrow , Act)\), two states \(s,s'\in S\) and a partition \(\pi ' = \textit{Ref}(\pi ,C)\), as mentioned in the lemma. We prove both directions:
(\({\varvec{\implies }}\)) If \(s\Rightarrow _{\pi '} s'\) then since there is a silent path we know that s and \(s'\) are in the same block \(B\in \pi '\). Since \(\pi '\) is a refinement of \(\pi \) there is a block \(B'\in \pi \) such that \(B\subseteq B'\), and \(s\Rightarrow _{\pi } s'\).
(\(\varvec{\Longleftarrow }\)) Assuming \(s\Rightarrow _{\pi }s'\) and there is a block \(B'\in \pi '\) such that \(s,s'\in B'\) we show that \(s\Rightarrow _{\pi '}s'\). Since \(\pi '\) refines \(\pi \) there is a block \(B_{s_b}\in \pi \) that contains s and \(s'\) and has the state \(s_b\) as leader. There is a set of states \(s_1, \dots , s_n\in B_{s_b}\) that witnesses the silent path  . The block \(B_{s_b}\) will either remain the same in \(\pi '\) or be split into \(\textit{Split}_\pi (B_{s_b},C)\) and the remainder. If \(s,s' \in \textit{Split}_\pi (B_{s_b}, C)\) then by the transitive closure \(s_1, \dots , s_n \in \textit{Split}_\pi (B_{s_b},C)\), since every \(s_1,\dots , s_n\) reaches \(s'\) with inert \(\tau \) steps. If \(s, s'\not \in \textit{Split}_\pi (B_{s_b}, C)\) then also \(s_1, \dots , s_n\not \in \textit{Split}_\pi (B_{s_b}, C)\) since if for any \(1\le i \le n\) we have \(s_i\in \textit{Split}_\pi (B_{s_b},C)\) then since \(s\Rightarrow _{\pi }s_i\) it holds that \(s\in \textit{Split}_\pi (B_{s_b},C)\). Thus, we conclude that \(s_1,\dots , s_n \in B'\) witnessing \(s\Rightarrow _{\pi '}s'\). \(\square \)
. The block \(B_{s_b}\) will either remain the same in \(\pi '\) or be split into \(\textit{Split}_\pi (B_{s_b},C)\) and the remainder. If \(s,s' \in \textit{Split}_\pi (B_{s_b}, C)\) then by the transitive closure \(s_1, \dots , s_n \in \textit{Split}_\pi (B_{s_b},C)\), since every \(s_1,\dots , s_n\) reaches \(s'\) with inert \(\tau \) steps. If \(s, s'\not \in \textit{Split}_\pi (B_{s_b}, C)\) then also \(s_1, \dots , s_n\not \in \textit{Split}_\pi (B_{s_b}, C)\) since if for any \(1\le i \le n\) we have \(s_i\in \textit{Split}_\pi (B_{s_b},C)\) then since \(s\Rightarrow _{\pi }s_i\) it holds that \(s\in \textit{Split}_\pi (B_{s_b},C)\). Thus, we conclude that \(s_1,\dots , s_n \in B'\) witnessing \(s\Rightarrow _{\pi '}s'\). \(\square \)
Secondly, the next auxiliary lemma shows that two bisimilar states can always reach branching bisimilar states within a block via silent \(\tau \)-paths.
Lemma 5.10
Let  be an LTS. Given a partition \(\pi \) of S such that
be an LTS. Given a partition \(\pi \) of S such that  is a refinement of \(\pi \). For two states s, t in the same block \(B\in \pi \), if
is a refinement of \(\pi \). For two states s, t in the same block \(B\in \pi \), if  and \(s \Rightarrow _{\pi } s'\) then there is a state \(t'\in B\) such that \(t\Rightarrow _{\pi }t'\),
and \(s \Rightarrow _{\pi } s'\) then there is a state \(t'\in B\) such that \(t\Rightarrow _{\pi }t'\),  .
.
Proof
We prove this using induction on i.
Induction Hypothesis: If  ,
,  and \(s_0, s_1, \ldots , s_i \in B\), then there is a state \(t'\in B\) such that \(t\Rightarrow _{\pi }t'\) and
and \(s_0, s_1, \ldots , s_i \in B\), then there is a state \(t'\in B\) such that \(t\Rightarrow _{\pi }t'\) and  .
.
For \(i=0\), we have \(s_0 = s_i\); thus, we can take t as \(t'\) and the induction hypothesis holds.
Now, assume that the induction hypothesis holds for i, we prove that it holds for \(i+1\). We have  and we want to find a \(t''\) such that \(t\Rightarrow _{\pi }t''\) and
and we want to find a \(t''\) such that \(t\Rightarrow _{\pi }t''\) and  . From the induction hypothesis, we know that we have a \(t'\) such that \(t\Rightarrow _{\pi }t'\),
. From the induction hypothesis, we know that we have a \(t'\) such that \(t\Rightarrow _{\pi }t'\),  . We now have two cases.
. We now have two cases.
Case 1:  . Then also
. Then also  and if we take \(t'' = t'\) we are done.
and if we take \(t'' = t'\) we are done.
Case 2:  . We have
. We have  and
and  . The first case of the definition of
. The first case of the definition of  does not hold, so we know from the second case that there exists a sequence
does not hold, so we know from the second case that there exists a sequence  such that
such that  ,
,  and
and  . Now all states of the sequence
. Now all states of the sequence  are in B, because
are in B, because  refines \(\pi \) and by Lemma 5.5 all intermediate states are related. Because \(s_{i+1} \in B\) we know \(t'' \in B\) also holds. Thus, we have \(t \Rightarrow _{\pi } t''\) and
refines \(\pi \) and by Lemma 5.5 all intermediate states are related. Because \(s_{i+1} \in B\) we know \(t'' \in B\) also holds. Thus, we have \(t \Rightarrow _{\pi } t''\) and  which proves the induction hypothesis for \(i+1\).
which proves the induction hypothesis for \(i+1\).
Thus, by mathematical induction, the lemma holds. \(\square \)
We now prove that we never move two branching bisimilar states to different blocks.
Lemma 5.11
Let  be an LTS where S contains no \(\tau \)-cycles. Given a partition \(\pi \) which is refined by
be an LTS where S contains no \(\tau \)-cycles. Given a partition \(\pi \) which is refined by  and two states \(s,t\in S\) in a block \(B\in \pi \). Then for all \(B'\in \pi \) if
and two states \(s,t\in S\) in a block \(B\in \pi \). Then for all \(B'\in \pi \) if  either \(s,t \in \textit{Split}_\pi (B,B')\) or \(s,t \not \in \textit{Split}_\pi (B, B')\).
either \(s,t \in \textit{Split}_\pi (B,B')\) or \(s,t \not \in \textit{Split}_\pi (B, B')\).
Proof
Let \(s_b\) be the leader state of B. This allows us to write \(B_{s_b}\) for B. Consider a partition \(\pi \), and two branching bisimilar states \(s,t \in B_{s_b}\in \pi \), i.e.  as in the lemma. Assume that \(s\in \textit{Split}_\pi (B_{s_b}, B')\) for any \(B'\in \pi \), we will show that \(t\in \textit{Split}_\pi (B_{s_b}, B')\). First we distinguish on whether \(s\in \textit{PreSplit}_\pi (B_{s_b}, B')\).
as in the lemma. Assume that \(s\in \textit{Split}_\pi (B_{s_b}, B')\) for any \(B'\in \pi \), we will show that \(t\in \textit{Split}_\pi (B_{s_b}, B')\). First we distinguish on whether \(s\in \textit{PreSplit}_\pi (B_{s_b}, B')\).
In the first case, we assume that \(s\in \textit{PreSplit}_\pi (B_{s_b}, B')\), and show that this implies \(t\in \textit{Split}_\pi (B_{s_b}, B')\). Assuming \(s\in \textit{PreSplit}_\pi (B_{s_b}, B')\), we can distinguish the following two cases:
-
If it is the case that \(dir(s,B') \nsubseteq dir(s_b, B')\), this means there is an action \(a\in Act\) such that
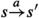 for some \(s'\in B'\) and
for some \(s'\in B'\) and 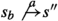 for any \(s''\in B'\). From the definition of \(\textit{dir}\), we know that it is not the case that \(a = \tau \) and
for any \(s''\in B'\). From the definition of \(\textit{dir}\), we know that it is not the case that \(a = \tau \) and 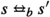 ; thus, we can ignore the first case of the definition of
; thus, we can ignore the first case of the definition of 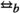 . Following the second case, since
. Following the second case, since 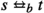 there is a sequence
there is a sequence  such that
such that  ,
, 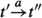 and
and 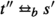 . Since
. Since 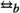 refines \(\pi \) we know that \(t'\in B_{s_b}, t''\in B'\) and, using Lemma 5.5, \(t\Rightarrow _{\pi } t'\). Therefore, with \(dir(t',B') \not \subseteq dir(s_b, B')\), \(t' \in \textit{PreSplit}_\pi (B_{s_b}, B')\) holds, and hence, \(t\in \textit{Split}_\pi (B_{s_b}, B')\).
refines \(\pi \) we know that \(t'\in B_{s_b}, t''\in B'\) and, using Lemma 5.5, \(t\Rightarrow _{\pi } t'\). Therefore, with \(dir(t',B') \not \subseteq dir(s_b, B')\), \(t' \in \textit{PreSplit}_\pi (B_{s_b}, B')\) holds, and hence, \(t\in \textit{Split}_\pi (B_{s_b}, B')\). -
For the other case where s is a bottom state and \(dir(s_b, B') \not \subseteq dir(s,B')\), notice that there is at least one bottom state \(t'\in B_{s_b}\) such that \(t\Rightarrow _{\pi }t'\). By Lemma 5.10 as
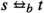 there has to be a \(s'\in B_{s_b}\) such that \(s\Rightarrow _{\pi }s'\) and
there has to be a \(s'\in B_{s_b}\) such that \(s\Rightarrow _{\pi }s'\) and 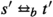 . Since s is a bottom state it has to be the case that
. Since s is a bottom state it has to be the case that  . By the definition of branching bisimilarity and the states are bottom states it has to be the case that \(dir(t',B') \subseteq dir(s, B')\). Since for every letter \(a\in Act\) and \(s''\in B_{s_b}\), if
. By the definition of branching bisimilarity and the states are bottom states it has to be the case that \(dir(t',B') \subseteq dir(s, B')\). Since for every letter \(a\in Act\) and \(s''\in B_{s_b}\), if 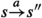 then there is a \(t''\in B'\) such that
then there is a \(t''\in B'\) such that  and
and  . Since \(dir(s_b,B')\not \subseteq dir(s,B')\) and \(dir(t',B') \subseteq dir(s,B')\) we know that also \(dir(s_b, B')\not \subseteq dir(t',B')\), and thus, \(t'\in \textit{PreSplit}_\pi (B_{s_b}, B')\), meaning \(t\in \textit{Split}_\pi (B_{s_b}, B')\).
. Since \(dir(s_b,B')\not \subseteq dir(s,B')\) and \(dir(t',B') \subseteq dir(s,B')\) we know that also \(dir(s_b, B')\not \subseteq dir(t',B')\), and thus, \(t'\in \textit{PreSplit}_\pi (B_{s_b}, B')\), meaning \(t\in \textit{Split}_\pi (B_{s_b}, B')\).
This concludes that if \(s\in \textit{PreSplit}_\pi (B_{s_b}, B')\) it is the case that \(t\in \textit{Split}_\pi (B_{s_b}, B')\).
In the second case we assume \(s\not \in \textit{PreSplit}_\pi (B_{s_b}, B')\) but s is part of the split, i.e. \(s \in \textit{Split}_\pi (B_{s_b}, B')\), and show that \(t\in \textit{Split}_\pi (B_{s_b}, B')\). In this case there is a state \(s'\in B_{s_b}\) such that \(s'\in \textit{PreSplit}_\pi (B_{s_b}, B')\) and \(s\Rightarrow _{\pi } s'\). According Lemma 5.10 there is a \(t'\in B_{s_b}\) such that  , and since \(s'\in \textit{PreSplit}_\pi (B_{s_b},B')\) by the previous argumentation we know that \(t'\in \textit{Split}_\pi (B_{s_b}, B')\) and since \(t\Rightarrow _{\pi }t'\) also \(t\in \textit{Split}_\pi (B_{s_b}, B')\).
, and since \(s'\in \textit{PreSplit}_\pi (B_{s_b},B')\) by the previous argumentation we know that \(t'\in \textit{Split}_\pi (B_{s_b}, B')\) and since \(t\Rightarrow _{\pi }t'\) also \(t\in \textit{Split}_\pi (B_{s_b}, B')\).
We are now ready to conclude that if \(s\in \textit{Split}_\pi (B_{s_b}, B')\) then also \(t\in \textit{Split}_\pi (B_{s_b}, B')\). Since s, t are chosen arbitrarily if \(t\in \textit{Split}_\pi (B_{s_b},B')\) then also \(s\in \textit{Split}_\pi (B_{s_b}, B')\). This means that either both states \(s,t\in \textit{Split}_\pi (B_{s_b},B')\), or both \(s,t\not \in \textit{Split}_\pi (B_{s_b}, B')\), proving this lemma. \(\square \)
Lastly, we show that if the current partition is not yet branching bisimilar, there is still a block that refines the partition with our splitting procedure.
Lemma 5.12
Let \(A=(S,\rightarrow , Act)\) be an LTS, and \(\pi \) a partition of S. If for all blocks \(B\in \pi \) it holds that \(\textit{Ref}(\pi , B) = \pi \) then the relation \(R_\pi \) induced by the partition \(\pi \) is a branching bisimulation.
Proof
Let \(\pi \) be a partition of S for which every \(B\in \pi \) it holds that \(\textit{Ref}(\pi ,B) =\pi \) as in the lemma. Assume two states \(s,t\in S\) are related \(s R_\pi t\), i.e. there is a block \(B_{s_b}\in \pi \), with leader \(s_b\in S\) such that \(s,t \in B_{s_b}\). For all actions \(a\in Act\) and \(s'\in B'\) such that  , if \(a=\tau \) and \(B'=B_{s_b}\) we know that \(s',t\in B_{s_b}\). Hence, \(s'\mathrel {R_\pi } t\). If this is not the case then \(a\in dir(s,B')\). We know that since \(\textit{Ref}(\pi , B') = \pi \), also \(\textit{Split}_\pi (B_{s_b}, B') = \textit{PreSplit}_\pi (B_{s_b}, B') = \emptyset \). This means that \(s\not \in \textit{PreSplit}_\pi (B_{s_b}, B')\), and hence, \(dir(s, B') \subseteq dir(s_b,B')\). Additionally, we know that there is at least one bottom state \(t'\in B_{s_b}\) such that \(t\Rightarrow _{\pi }t'\), and thus, \(t R_\pi t'\). Since \(t'\) is a bottom state and also \(t'\not \in \textit{PreSplit}_\pi (B_{s_b},B')\) we know that \(dir(t', B') \supseteq dir(s_b, B') \supseteq dir(s,B')\). This means \(a\in dir(t',B')\), so there is a state \(t''\in B'\) such that
, if \(a=\tau \) and \(B'=B_{s_b}\) we know that \(s',t\in B_{s_b}\). Hence, \(s'\mathrel {R_\pi } t\). If this is not the case then \(a\in dir(s,B')\). We know that since \(\textit{Ref}(\pi , B') = \pi \), also \(\textit{Split}_\pi (B_{s_b}, B') = \textit{PreSplit}_\pi (B_{s_b}, B') = \emptyset \). This means that \(s\not \in \textit{PreSplit}_\pi (B_{s_b}, B')\), and hence, \(dir(s, B') \subseteq dir(s_b,B')\). Additionally, we know that there is at least one bottom state \(t'\in B_{s_b}\) such that \(t\Rightarrow _{\pi }t'\), and thus, \(t R_\pi t'\). Since \(t'\) is a bottom state and also \(t'\not \in \textit{PreSplit}_\pi (B_{s_b},B')\) we know that \(dir(t', B') \supseteq dir(s_b, B') \supseteq dir(s,B')\). This means \(a\in dir(t',B')\), so there is a state \(t''\in B'\) such that  and \(s'\mathrel {R_\pi } t''\). Since \(R_\pi \) is also symmetric, it follows that \(R_\pi \) forms a branching bisimulation. \(\square \)
and \(s'\mathrel {R_\pi } t''\). Since \(R_\pi \) is also symmetric, it follows that \(R_\pi \) forms a branching bisimulation. \(\square \)
5.5.2 Correctness of algorithm
Theorem 5.13
Let  be an LTS that contains no \(\tau \)-loops. The partition \(\pi \) resulting from executing Algorithm 4 with input A forms the coarsest partition inducing a branching bisimulation, solving branching-BCRP.
be an LTS that contains no \(\tau \)-loops. The partition \(\pi \) resulting from executing Algorithm 4 with input A forms the coarsest partition inducing a branching bisimulation, solving branching-BCRP.
Proof
At the end of the iteration for all block labels \(i\in {\mathbb {N}}, i \le \vert S \vert \), \( waiting_i = \textrm{false}\). Since for all new bottom states we did the extra stability procedure in Algorithm 7 by Lemma 5.8 we know that the partition is stable modulo branching bisimulation. By Lemma 5.12 this means \(\pi \) is a branching bisimulation relation.
Finally by Lemma 5.11 it never happens that two branching bisimilar states are split. This means that \(\pi \) is the coarsest partition inducing a branching bisimulation, solving branching-BCRP. \(\square \)
5.5.3 Complexity of algorithm
Theorem 5.14
The algorithm for branching bisimulation terminates in \(O(n+ \vert Act \vert )\) parallel time on \(\max (n^2,m,\vert Act \vert n)\) processors.
Proof
As indicated in the preprocessing section, the preprocessing takes \(\mathcal {O}(n + \vert Act \vert )\) time using \(\max (n^2,m,\vert Act \vert n)\) processors in the worst case.
In every iteration of the algorithm, either there is a splitter that causes the number of blocks to increase, or a block is removed from waiting. This means that the proof of Theorem 4.2 still holds with our modifications. So there are maximally 3n iterations of the main algorithm. Except for the procedure to maintain stability, every part of the algorithm runs in constant time. So our total running time is the number of iterations in addition to the number of iterations of CheckStability that does not result in a splitter. The stability check only happens at most once for every new bottom state since a bottom state can never become non-bottom.
We use \(\max (n, m, t, mark\_length)\) processors. We observe that the size of the transitive closure t is maximally size \(n^2\) and \(mark\_length \le \vert Act \vert n\). Therefore, we need \(\max (n^2, m, \vert Act \vert n)\) processors.
Thus, the main part of the algorithm runs in \(\mathcal {O}(n)\) time using \(\max (n^2,m,\vert Act \vert n)\) processors.
Therefore, the total complexity of preprocessing and running the algorithm is \(\mathcal {O}(n + \vert Act \vert )\) using \(\max (n^2,m, \vert Act \vert n)\) processors. \(\square \)
6 Related work
Deciding bisimilarity is P-complete [24], which suggests that bisimilarity is an inherently sequential problem. This fact has not withheld the community from searching for efficient parallel algorithms for deciding the bisimilarity of Kripke structures. In particular, Lee and Rajasekaran [12, 25] proposed a parallel algorithm based on the Paige–Tarjan algorithm that works in \(\mathcal {O}(n\ log\ n)\) time complexity using \(\frac{m}{\log n}\log \log n\) Concurrent, Read Concurrent Write (CRCW) processors, and one using only \(\frac{m}{n}log~n\) Concurrent Read Exclusive Write (CREW) processors. Jeong et al. [26] presented a linear-time parallel algorithm, but it is probabilistic in the sense that it has a nonzero chance of producing an incorrect result.
Furthermore, Wijs [14] presented a GPU implementation of an algorithm to solve the strong and branching bisimulation partition refinement problems. But as shown in Sect. 4.3 it has only linear complexity in the number of states if the fan-out of an LTS is bounded and can otherwise have quadratic complexity. However, the multi-way splitting Wijs employs is effective in practice.
In a distributed setting, Blom and Orzan studied algorithms for refinement [18]. These algorithms use message passing to communicate between different workers in a network and rely on a small number of processors. Therefore, they are very different in nature from our algorithm. The algorithms of Blom and Orzan [18] were extended and optimised for branching bisimulation [27].
Parallel partition refinement algorithms are also studied in the problem of minimising deterministic finite automata (DFAs) [28]. These DFAs can be seen as the restricted LTSs where the transition relation is deterministic, and there is an initial partitioning distinguishing accepting and non-accepting states. This means our algorithm also works in the setting of DFAs. To our knowledge, this is the first linear-time parallel algorithm for DFA minimisation.
The sequential algorithm introduced in [11] requires time \(\mathcal {O}(m \log n)\) compared to the original Groote–Vaandrager algorithm that requires \(\mathcal {O}(m n)\) time [20]. The techniques in [11] are complex, using among others the principle of the smaller half [4]. These are therefore less suitable when aiming for maximal parallelism.
Recent work [6] provides a linear lower bound for the class of parallel partition refinement algorithms, matching the run time of our algorithm. The most efficient algorithms that decide bisimilarity use partition refinement; however, there is a possibility that other techniques give rise to algorithms that are faster than \(\mathcal {O}(n)\).
Examples of these different techniques can be found in [29,30,31]. In [30], a linear-time sequential algorithm is given to decide bisimilarity in the restricted setting of deterministic automata with only a single action label. In the same setting, a parallel version of this algorithm is proposed in [31] with a time complexity of \(\mathcal {O}(\log n)\). The run time complexity of these algorithms is fundamentally faster than the partition refinement algorithms. However, we do not think this approach can be generalised to a setting with multiple action labels or non-determinism.
The sequential algorithm proposed in [29] finds and merges bisimilar states in a way different from partition refinement. However, this algorithm performs in a run time complexity that is worse than that of partition refinement algorithms.
7 Conclusions and future work
In this work, we proposed linear-time PRAM algorithms to decide strong and branching bisimilarity. We implemented the strong bisimilarity algorithm in CUDA and conducted experiments that show the potential to compute bisimulation in practice in linear time on contemporary hardware. Further advances in parallel hardware will make this more feasible.
Other work suggests no significant improvement on the time complexity \(\mathcal {O}(n)\) is possible using partition refinement [6]. On the other hand, the sequential run time of \(\mathcal {O}((m+n)\log n)\) of the Paige–Tarjan algorithm suggests there might be an improvement in the number of processors needed. For future work, it would be interesting to see whether a linear algorithm deciding bisimilarity is feasible using fewer processors, for instance \(\frac{m}{n}\log (n)\).
Another future direction is to optimise these algorithms for the available highly parallel hardware, such as GPUs. Optimising these algorithms should give a better insight into whether using an abundance of processors performs well in practice or other trade-offs should be made in practice. For instance, data locality and synchronisation play an important role in GPU performance but are not taken into account in a PRAM model.
Notes
Here processor i is used to both directly go over state i and block i. Checking \( waiting _ block_{i} \) would also be correct. However, we can directly access the blocks using n processors since there are a maximum of n blocks.
The source code can be found at https://github.com/sakehl/gpu-bisimulation.
References
Bunte, O., Groote, J.F., Keiren, J.J.A., Laveaux, M., Neele, T., de Vink, E.P., Wesselink, W., Wijs, A.J., Willemse, T.A.C.: The mCRL2 toolset for analysing concurrent systems—improvements in expressivity and usability. In: Tools and Algorithms for the Construction and Analysis of Systems—25th International Conference (TACAS 2019), Proceedings, Part II, pp. 21–39 (2019). https://doi.org/10.1007/978-3-030-17465-1_2
Milner, R.: A Calculus of Communicating Systems. Lecture Notes in Computer Science, vol. 92. Springer, Cham (1980)
Kanellakis, P., Smolka, S.: CCS expressions, finite state processes, and three problems of equivalence. Information and Computation 86(1), 43–68 (1990). https://doi.org/10.1016/0890-5401(90)90025-D
Paige, R., Tarjan, R.E.: Three partition refinement algorithms. SIAM Journal on Computing 16(6), 973–989 (1987). https://doi.org/10.1137/0216062
Leiserson, C.E., Thompson, N.C., Emer, J.S., Kuszmaul, B.C., Lampson, B.W., Sanchez, D., Schardl, T.B.: There’s plenty of room at the top: What will drive computer performance after Moore’s law? Science (2020). https://doi.org/10.1126/science.aam9744
Groote, J.F., Martens, J., de Vink, E.P.: Lowerbounds for bisimulation by partition refinement. pre-print (2022). arXiv:2203.07158
Valmari, A.: Simple bisimilarity minimization in \(O(m \log n)\) time. Fundam. Informaticae 105(3), 319–339 (2010). https://doi.org/10.3233/FI-2010-369
Stockmeyer, L., Vishkin, U.: Simulation of parallel random access machines by circuits. SIAM J. Comput. 13(2), 409–422 (1984). https://doi.org/10.1137/0213027
Martens, J., Groote, J.F., Haak, L.v.d., Hijma, P., Wijs, A.: A linear parallel algorithm to compute bisimulation and relational coarsest partitions. In: International Conference on Formal Aspects of Component Software, pp. 115–133. Springer, Berlin (2021). https://doi.org/10.1007/978-3-030-90636-8_7
Fortune, S., Wyllie, J.: Parallelism in random access machines. In: Proceedings of the Tenth Annual ACM Symposium on Theory of Computing, pp. 114–118 (1978). https://doi.org/10.1145/800133.804339
Jansen, D.N., Groote, J.F., Keiren, F.J.A., Wijs, A.J.: An \(O(m \log n)\) algorithm for branching bisimilarity on labelled transition systems. In: Biere, A., Parker, D. (eds.) Tools and Algorithms for the Construction and Analysis of Systems, vol. 12079, pp. 3–20. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-45237-7_1
Lee, I., Rajasekaran, S.: A parallel algorithm for relational coarsest partition problems and its implementation. In: Dill, D.L. (ed.) Computer Aided Verification, vol. 818, pp. 404–414. Springer, Cham (1994). https://doi.org/10.1007/3-540-58179-0_71
De Nicola, R., Vaandrager, F.: Action versus state based logics for transition systems. In: LITP Spring School on Theoretical Computer Science, pp. 407–419. Springer (1990). https://doi.org/10.1007/3-540-53479-2_17
Wijs, A.J.: GPU accelerated strong and branching bisimilarity checking. In: TACAS. Lecture Notes in Computer Science, vol. 9035, pp. 368–383. Springer, Cham (2015). https://doi.org/10.1007/978-3-662-46681-0_29
Wijs, A.J., Katoen, J.-P., Bošnački, D.: Efficient GPU algorithms for parallel decomposition of graphs into strongly connected and maximal end components. Formal Methods Syst. Design 48(3), 274–300 (2016). https://doi.org/10.1007/s10703-016-0246-7
Reniers, M.A., Schoren, R., Willemse, T.A.C.: Results on embeddings between state-based and event-based systems. Comput. J. 57(1), 73–92 (2014). https://doi.org/10.1093/comjnl/bxs156
Sengupta, S., Harris, M., Garland, M., Owens, J.: Efficient Parallel Scan Algorithms for Manycore GPUs. In: Scientific Computing with Multicore and Accelerators, pp. 413–442. Taylor & Francis, Boca Raton (2011). Chap. 19. https://doi.org/10.1201/b10376
Blom, S., Orzan, S.: Distributed branching bisimulation reduction of state spaces. Electron. Notes Theor. Comput. Sci. 89(1), 99–113 (2003). https://doi.org/10.1016/S1571-0661(05)80099-4
Van Glabbeek, R.J., Weijland, W.P.: Branching time and abstraction in bisimulation semantics. JACM 43(3), 555–600 (1996). https://doi.org/10.1145/233551.233556
Groote, J.F., Vaandrager, F.: An efficient algorithm for branching bisimulation and stuttering equivalence. In: International Colloquium on Automata, Languages, and Programming, pp. 626–638. Springer, Cham (1990). https://doi.org/10.1007/BFb0032063
Browne, M.C., Clarke, E.M., Grümberg, O.: Characterizing finite Kripke structures in propositional temporal logic. Theor. Comput. Sci. 59(1), 115–131 (1988). https://doi.org/10.1016/0304-3975(88)90098-9
Bošnački, D., Odenbrett, M.R., Wijs, A., Ligtenberg, W., Hilbers, P.: Efficient reconstruction of biological networks via transitive reduction on general purpose graphics processors. BMC Bioinform. 13(1), 281 (2012). https://doi.org/10.1186/1471-2105-13-281
Han, Y., Pan, V., Reif, J.: Efficient parallel algorithms for computing all pair shortest paths in directed graphs. In: Proceedings of the Fourth Annual ACM Symposium on Parallel Algorithms and Architectures, pp. 353–362 (1992). https://doi.org/10.1145/140901.141913
Balcázar, J., Gabarro, J., Santha, M.: Deciding bisimilarity is P-complete. Formal Aspects Comput. 4(1), 638–648 (1992). https://doi.org/10.1007/BF03180566
Rajasekaran, S., Lee, I.: Parallel algorithms for relational coarsest partition problems. IEEE Trans. Parallel Distrib. Syst. 9(7), 687–699 (1998). https://doi.org/10.1109/71.707548
Jeong, C., Kim, Y., Oh, Y., Kim, H.: A faster parallel implementation of Kanellakis–Smolka algorithm for bisimilarity checking. In: Proceedings of the International Computer Symposium. Citeseer (1998)
Blom, S., van de Pol, J.: Distributed branching bisimulation minimization by inductive signatures. In: Brim, L., van de Pol, J. (eds.) Proceedings 8th International Workshop on Parallel and Distributed Methods in verifiCation, PDMC 2009, Eindhoven, The Netherlands, 4th November 2009. EPTCS, vol. 14, pp. 32–46 (2009). https://doi.org/10.4204/EPTCS.14.3
Tewari, A., Srivastava, U., Gupta, P.: A parallel DFA minimization algorithm. In: International Conference on High-Performance Computing, pp. 34–40. Springer, Berlin (2002)
Björklund, J., Cleophas, L.: Aggregation-based minimization of finite state automata. Acta Informatica 58(3), 177–194 (2021)
Paige, R., Tarjan, R.E., Bonic, R.: A linear time solution to the single function coarsest partition problem. Theor. Comput. Sci. 40, 67–84 (1985)
JáJá, J.F., Ryu, K.W.: An efficient parallel algorithm for the single function coarsest partition problem. Theor. Comput. Sci. 129(2), 293–307 (1994)
Cole, R.: Parallel merge sort. SIAM J. Comput. 17(4), 770–785 (1988)
Acknowledgements
This work is carried out in the context of the NWO AVVA project 612.001751 and the NWO TTW ChEOPS project 17249. We thank the reviewers for their careful reviews and helpful comments.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Gwen Salaun.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Preprocessing for strong bisimulation
To use the Algorithm 3, we need to do two preprocessing steps. First, we need to partition the states w.r.t. their set of outgoing action labels. This can be done with an altered version of Algorithm 2. Instead of splitting on a block, we split on an action \(a \in A\). We visit all transitions, and we mark the source if it has the same action label a. This can be done by the following PRAM pseudocode.

Each block can be split into two blocks: a block that contains states that have a as an outgoing action label and a block with states that do not have this outgoing action label. After doing this for all different action labels, we end up with a partition of blocks, in which all states of a block have the same set of outgoing action labels, and each pair of states from different blocks have different sets of outgoing action labels. Using m processors, this partition can be constructed in \(\mathcal {O}(\vert Act \vert )\) time.
For the second preprocessing step, we need to gather the extra information that is needed in Algorithm 3. Only \(a_i\) is part of the input, the other information like \( order \) and \( offset \) need to be calculated. We start our preprocessing by sorting the transitions by \(( source _i, a_i)\), which can be done in \(\mathcal {O}(\log m)\) time with m processors, for instance using a parallel merge sort [32]. In order to calculate \( order _i\) and \( nr\_marks \), we first calculate \( action\_switch _i\) for each transition i, which is done as follows:

See Fig. 6 for an example. Now, \( order _i\) can be calculated with a parallel segmented inclusive scan [17] of \( action\_switch \). A parallel segmented sum can be performed on \( action\_switch \) to calculate \( nr\_marks \), where we make sure to set \( nr\_marks _{s}\) to 0, if state s has no outgoing transitions. Finally, \( off _s\), for the mark offsets, can be constructed as a list and calculated by applying a parallel exclusive scan on \( nr\_marks \). Calculating \(action\_switch\) takes \(\mathcal {O}(1)\) time on m processors, and a parallel (segmented) sum/scan takes \(\mathcal {O}(\log m)\) time [17].
In total, the preprocessing takes \(\mathcal {O}(\vert Act \vert + \log m)\) time using m processors.
Appendix B: Preprocessing for branching bisimulation
We need marks to keep track of all actions a state can directly take or can take after performing silent \(\tau \)-transitions. After executing Algorithm 8, all states are now in blocks for which the reachable actions are the same. Each block now has a leader, which is a bottom state, and a bottom state cannot perform silent \(\tau \)-steps. Thus, the leader has only direct actions for which we need to store markings. Therefore, we can first calculate how many marks we need for visible markings and afterwards, each state updates this by looking at its leader. See Fig. 4 for an example of the preprocessing we do in this section.
First we sort the transitions again on \((source_i, a_i)\), we note that we consider \(\tau \)-actions and place them before action labels in the sorted list. Next, we need the help variable \(action\_switch_i\) which keeps track of not counting the same action label for the same source state twice. It is defined exactly by the code below:

We cannot calculate \( order \) and \( nr\_marks \) directly, so we calculate them first as a sort of approximation which we call \( order' \) and \( nr\_marks' \), which only contain the correct values for bottom states.

We calculate a \(order'\) by doing a parallel segmented inclusive scan on \(action\_switch\). We calculate \( nr\_marks' \) by performing a segmented sum on \(action\_switch\) and adding 1 to each result. We note that states with no transitions still get a mark for \(\tau \). Now each state s determines its actual \( nr\_marks \) by copying this from its leader: \( nr\_marks _s := nr\_mark' _{block_s}\). Next, we calculate \( off \) by performing an exclusive scan on the \( nr\_marks \) array and \(mark\_length\) by calculating the sum of the \( nr\_marks \) array. We can now calculate \(mark\_source\) by starting \(mark\_length\) processors and letting each processor do a binary search on \( off \). Now, we create \(mark\_order\) using a segmented exclusive scan on an array filled with ones and \(mark\_source\) as a segment indicator. Lastly, we need to update \(order_i\) again. First, by going over all transitions, we store the action label of a mark in \(mark\_action\) for transitions that start in a leader state (using \(order'\)). Next, we look if the order indexes the correct action label in the mark array for each transition. If this is not the case, we loop and increase the index where we look and see whether this is the correct action label. Here is the exact code:

This procedure is correct since a state never has fewer marks than the original \( nr\_marks' \). Thus, we always find the correct action later in the mark array. This loop has at most \(\vert Act \vert \) iterations.
Eventually, parallel sorting takes \(\mathcal {O}(\log m)\) time, a parallel sum or scan also takes \(\mathcal {O}(\log m)\) time, the binary search takes \(\mathcal {O}(\log mark\_length)\) time, and the looping takes \(\mathcal {O}(\vert Act \vert )\) time. Therefore, this preprocessing takes \(\mathcal {O}(\log m + \log mark\_length + \vert Act \vert )\) time on \(\max (n,m,t,mark\_length)\) processors. This can be simplified to \(\mathcal {O}(\log n + \vert Act \vert )\) on \(\max (n^2,m,\vert Act \vert n)\) processors, when observing that \(m \le \vert Act \vert n^2\), \(t \le n^2\) and \(mark\_length \le \vert Act \vert n\).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Martens, J., Groote, J.F., Haak, L.B.v.d. et al. Linear parallel algorithms to compute strong and branching bisimilarity. Softw Syst Model 22, 521–545 (2023). https://doi.org/10.1007/s10270-022-01060-7
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10270-022-01060-7





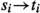 and checks if
and checks if 
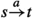 with transition index
with transition index 
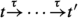 of zero or more
of zero or more  and
and 
 , and
, and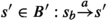 .
.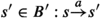 , and
, and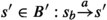 .
.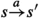 , if
, if 

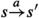 for some
for some 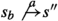 for any
for any 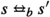 ; thus, we can ignore the first case of the definition of
; thus, we can ignore the first case of the definition of 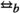 . Following the second case, since
. Following the second case, since 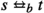 there is a sequence
there is a sequence  such that
such that  ,
, 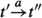 and
and 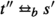 . Since
. Since 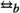 refines
refines 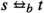 there has to be a
there has to be a 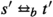 . Since s is a bottom state it has to be the case that
. Since s is a bottom state it has to be the case that  . By the definition of branching bisimilarity and the states are bottom states it has to be the case that
. By the definition of branching bisimilarity and the states are bottom states it has to be the case that 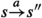 then there is a
then there is a  and
and  . Since
. Since 