1 Introduction

Recent advances in high-performance computing and an ever-increasing amount of experimental data have enabled a new class of data driven, biophysically detailed mammalian brain tissue models. Specifically, we refer to the reconstruction and simulation of neocortical microcircuitry developed previously by the Blue Brain Project (Markram et al. 2015), which has since been extended to build models of brain regions such as the Hippocampal CA1 model described in Chap. 11.

Data-driven brain tissue models complement existing experimental and theoretical approaches. They provide a unique framework for the integration of multi-modal and multi-scale data in a systematic way. Relating different datasets makes it possible to identify missing data while simultaneously providing quantitative predictions about knowledge gaps by leveraging constraints from the known data. For example, Markram et al. (2015) showed that in the absence of a complete, measured connectome it is possible to predict a large portion of the microconnectome from the morphological shapes of neurons and their placement in space. These biological models built from first principles serve as a virtual replica of brain tissue, where scientific questions can be explored in silico; in other scientific and technical contexts such models are also referred to as ‘digital twins’.

As much as this is enabled by data and computational capabilities, it is also methodological and algorithmic innovations that make the construction, validation, refinement, and use of these models possible. When models reach the complexity where individual neurons are described by tens of thousands of differential equations and the brain tissue models can comprise multiple millions of neurons, it becomes necessary to remove hand tuning and replace ad hoc decisions with repeatable workflows. Such an approach makes it possible to continuously refine models by integrating new data as it becomes available.

This chapter builds upon previous work to reconstruct and simulate prototypical neocortical microcircuitry constrained by biological first principles (Markram et al. 2015). This chapter does not intend to describe the individual steps or software tools to reconstruct and simulate such a model, which is information that is found in the original study and in the respective open-source software tools. Rather, this chapter intends to explain the relevant computational science concepts that make reconstruction and simulation possible in the first place.

In order to do this, the chapter follows the essential steps of the data-driven approach to reconstructing and simulating brain tissue as developed by the EPFL Blue Brain Project and as illustrated in Fig. 10.1.

Fig. 10.1
figure 1

Schematic illustration of the core steps to reconstruct and simulate brain tissue as previously described in Markram et al. (2015) and for which this chapter elaborates the underlying computational concepts

Full size image

2 Data Organization

Numerous studies have characterized the structural and functional properties of the mammalian brain. This has resulted in a treasure-trove of knowledge on types of neuronal (DeFelipe and Fariñas 1992; Freund and Buzsáki 1996; Klausberger and Somogyi 2008; Markram et al. 2004; Peters and Kaiserman-Abramof 1970), axonal and dendritic morphologies (Helmstaedter and Feldmeyer 2010; Larkman 1991; Lübke and Feldmeyer 2010; Spruston 2008; Thomson et al. 1996), laminar organization (DeFelipe et al. 2002; Kätzel et al. 2011; Mountcastle 1997; Rockland 2019; Rockland and Lund 1982; Woolsey and Van der Loos 1970), their gene expression profiles (Kawaguchi and Kubota 1997; Rudy et al. 2011; Toledo-Rodriguez et al. 2005; Yuste et al. 2020) and ion channel kinetics (Bekkers 2000; Hille 2001; Kole et al. 2006; Korngreen and Sakmann 2000; Lai and Jan 2006; Markram and Sakmann 1994; Ranjan et al. 2011), morphological and electrophysiological properties (Connors et al. 1982; Hestrin and Armstrong 1996; Kasper et al. 1994; Larkman 1991; Markram et al. 1997; Ramaswamy and Markram 2015; Steriade 2004; Zhu 2000), synaptic connections (Feldmeyer et al. 1999; Gupta et al. 2000; Jiang et al. 2015; Markram et al. 1997; Mason et al. 1991; Szabadics et al. 2006; Thomson and Lamy 2007), microcircuit anatomy (Avermann et al. 2012; DeFelipe et al. 2002; Lefort et al. 2009; Martin 2002; Rockland 2010), and physiology and function (Haider et al. 2006; McCormick et al. 2003; Petersen 2007; Traub 2005).

The approach described in Markram et al. (2015) aims to make sense of these multi-modal and multi-scale datasets by using a data-driven model as an integration framework. For example, Markram et al. (2015) use information on the location and morphology of cells from biocytin stains, and electrophysiology from patch-clamp recordings to derive a neuron-type nomenclature. As another example, it uses NeuN-stained tissue blocks to derive dimensions, layer delineations, absolute cell counts and a combination of DAPI, NeuN, and GABA stainings to establish the fraction of excitatory and inhibitory cells in the brain tissue. The specific computational workflows to derive the nomenclature or tissue properties have been described previously (Markram et al. 2015).

In this chapter, we elaborate on the common computational concepts in these examples: for each of them it is necessary to leverage data from different modalities and possibly different laboratories to derive an integrated synopsis. Furthermore, a certain discipline is needed to correctly interpret these diverse data, e.g., a nomenclature based on the set of input data is needed and it may have to be refined if new data become available. Lastly, in order to store the results of the synopsis, in some cases it may be useful to use a data structure that allows representation of its spatial heterogeneity.

To this end, we highlight three computational concepts that complement traditional neuroinformatics approaches to organize data for brain tissue models: (1) a Knowledge Graph-based Data Repository, (2) Dataset Releases, and (3) a Generalized voxel-based data structure.

2.1 Knowledge Graph-Based Data Repository

By now, a number of neuroinformatics initiatives have succeeded in the integration of select types of experimental data into dedicated databases (Ascoli et al. 2007; Gouwens et al. 2019; Ramaswamy et al. 2015; Tripathy et al. 2014; Wheeler et al. 2015) and have proposed standards for ontologies and file formats (Garcia et al. 2014; Gillespie et al. 2020; Teeters et al. 2015). As already alluded to, the specific challenge for reconstructing brain tissue lies in finding and integrating available data at different levels of biological organization, in our case data sets of genetic, electrophysiological, morphological, synaptic, or microcircuit nature. In part, this is a conceptual challenge in the sense that it requires overarching and at the same time fact-based ontologies that can help bridge multiple community definitions (Bug et al. 2008; Hamilton et al. 2012; Larson and Martone 2009). But surprisingly, it is also a technical challenge as none of the readily available databasing approaches such as transaction-based databases, key-value stores or no-SQL approaches combine the usefulness of schematized data with the flexibility to be able to evolve those schemas as the knowledge of the data increases. What is needed is a data repository combined with a knowledge graph, which makes it possible to efficiently and effectively relate the metadata and track its evolution; see Fig. 10.2. In practice, the integration of data into a knowledge graph as provided by Blue Brain NexusFootnote 1 involves the curation of data to standardize the file format and attach contextual metadata to the dataset.Footnote 2 The integrated data is furthermore linked to other data using common provenance standards. For instance, an electrophysiology recording will be linked to a particular protocol and to a particular experimentalist. It is furthermore linked upstream to a particular brain slice with its metadata and it may be linked downstream to a particular staining protocol and a resulting stained cell.

Fig. 10.2
figure 2

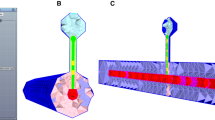
Schematic illustrating exemplar multi-modal data and their provenance. The provenance tree of morphologies reconstructions (a) is stored in the knowledge graph and connected to the multi-modal data (b), a consistent dataset is built from multiple reconstructions (c), and marked as suitable (d) once validations have been successful. The ontology follows the W3C Prov-O standard

Full size image

2.2 Dataset Releases

Managing data for their use in a model requires additional practices as compared to managing data for archival and general dissemination purposes (Bouwer et al. 2011). This stems from the fact that possibly only a subset of the data in a general data repository is being used for a model, either because the scope of the model is narrower than the data available in the repository (e.g., requiring morphologies of neurons from a certain brain region and species, while the repository has data for multiple species), or that not all selected data passes other thresholds for quality control or other reasons (e.g., incomplete reconstructions).Footnote 3 Once it has been identified which data qualifies for inclusion, it needs to be named for further downstream use and provenance purposes (see Fig. 10.2c). Selecting, verifying, and ultimately approving data for modeling are steps that actually are best understood as a staged process leading to a release for a specific purpose or use, quite similar to what is done for releasing a piece of software. This analogy does not stop at giving a certain selection of data a name or version number, but also extends to explicitly encoding the maturity of that entity. In the context of dataset releases, the maturity defines whether the data is suitable for downstream usage in a model and ultimately publication (see Fig. 10.2d).

2.3 Generalized Voxel-Based Data Structure

Brain atlases have become a central resource for brain research (Hawrylycz et al. 2014; Papp et al. 2014; Paxinos and Watson 1998). On the one hand, they give a spatial map of the brain allowing the navigation and selection of areas of interest. On the other hand, they further allow the registration of other data within the atlas, giving spatial context to the data and making localized comparisons of data possible. The automatic creation of atlases from imaging datasets furthermore lends itself to define atlases in a voxel representation, assigning to each region a set of specific voxels. While this could be seen as a technicality, a voxel-based representation becomes particularly useful if an atlas is not only used as a look-up resource but also as a generalized data structure to store additional data and information.Footnote 4 Such a data structure in principle is simply a voxel-based atlas, with the same parcellation, but provides machine interfaces to retrieve and populate additional data. This data can be other experimental modalities or data derived during the modeling process. With respect to modeling processes described below, such a generalized voxel-based data structure makes it easy to store the heterogeneity of the input parameters in the respective voxels, and to provide configuration data for model building in the form of this data structure.

3 Model Building

Biophysically detailed models of brain tissue have proven useful to link anatomy and physiology across multiple levels of detail to emergent behavior (Arkhipov et al. 2018; Billeh et al. 2020; Einevoll et al. 2013; Hay et al. 2011; Newton et al. 2019; Nolte et al. 2019; Ramaswamy et al. 2012; Reimann et al. 2013). Ideally, the values that are needed to parameterize such models are obtained directly from experimental measurements. However, even in well-characterized neurons such as layer 5 pyramidal cells (Markram et al. 1997; Ramaswamy and Markram 2015; Ramaswamy et al. 2012), parameters such as quantal synaptic conductances are difficult to measure experimentally (Ramaswamy and Markram 2015; Ramaswamy et al. 2012). It becomes obvious that such data are rather sparse when one attempts to find similar parameters for diverse cell types and their connectivity in specific brain regions, species, and developmental ages (Qi et al. 2020).

There are several approaches that attempt to overcome this challenge, ranging from more experiments (Gouwens et al. 2019; Oh et al. 2014; Ranjan et al. 2019) to rule-based regularization of parameters (Billeh et al. 2020; Ecker et al. 2020; Reimann et al. 2015). We previously described a complementary approach to reconstructing neocortical microcircuitry by leveraging sparse biological data and identifying interdependencies to predict missing data (Markram et al. 2015). It can be broken down into two main workflows, the building of biophysically detailed neuron models and the building of detailed brain tissue models comprising those neurons.

3.1 Biophysical Neuron Models

The multi-compartment Hodgkin-Huxley formalism (Hodgkin and Huxley 1952a, b; Koch and Segev 1998, 2000; Rall 1962) faithfully captures the diverse electrical behavior in neurons from somatic firing (Druckmann et al. 2007) to dendritic integration (Hay et al. 2011) and provides a platform to integrate experimental data at the level of single neurons (Gupta et al. 2000; Toledo-Rodriguez et al. 2004; Wang et al. 2002). More recent experimental data is more standardized, more specific, and recorded previously unattainable properties of the neurons—providing a more quantitative description of neuronal parameters and behavior (DeFelipe et al. 2013; Petilla Interneuron Nomenclature Group 2008; Yuste et al. 2020). Despite these advances, experimental data is not always sufficient to completely parameterize the neuron models, especially since with the current state of the experimental art certain parameters are difficult to obtain such as the actual ion channel composition of a neuron and their placement and absolute numbers.

Here, we highlight the computational strategies underlying an automated workflow for large-scale reconstruction of single neurons described previously (Druckmann et al. 2007, 2008, 2011; Hay et al. 2011). In contrast to other computer-aided approaches to constrain neuronal model parameters (Van Geit et al. 2007, 2008) and single neuron models (Huys et al. 2006; Keren et al. 2005), our approach aims at minimizing the overall number of parameters to be searched and at giving clear indications to the algorithm as to what makes a good model. This overall strategy reduces the risk that in the process of optimization biophysically non-plausible parameters get chosen (Podlaski et al. 2017). The four elements that in our hands lead to successful automation of parameter constraining for neurons are: (1) effective distance functions, (2) a multi-dimensional error term, (3) a powerful search strategy, and (4) leveraging other constraints.

3.1.1 Effective Distance Functions

A distance function allows to quantify how far apart a model is from the desired target behavior. A common choice is an L2 norm on the point-wise output of the model with the target, equally weighing each point of the output trace (Van Geit et al. 2007). In some cases, this can be overly restrictive and does not give any indication to the algorithm whether matching some parts of the trace may be more important than others (e.g., spiking behavior) (Druckmann et al. 2008). The conceptual advancement we introduced is the use of feature-basedFootnote 5 distance metrics (Druckmann et al. 2007). A feature can be anything from the time to first spike, a firing frequency, or an adaptation index, and basically describes a property of interest of an output trace; see Fig. 10.3-1. By using a feature-based distance function, we achieve two things: First, we indicate to the search algorithm the importance of particular aspects of the output trace that otherwise would be competing with all the other data points, leading more consistently to models that express this behavior. Secondly, we can express the difference of a model to the target behavior in multiples of the variation measured in the target system, which gives a very clear quantification of the quality of the model in this aspect.

Fig. 10.3
figure 3

Illustration of central concepts for reconstructing biophysical neuron models. (1) Features are extracted from electrophysiological recordings. (2) Pareto set of solutions plotted for two dimensions (two objectives) of a multi-dimensional optimization. (3) Indicator-based evolutionary algorithms help to establish dominance between solutions while maintaining diversity; in this example, the solution with the smallest (red) square will be sorted out

Full size image

3.1.2 Multi-dimensional Error Term

The distance function is used by the search algorithm to determine whether one set of parameters preferable over another. A large class of search algorithms uses a single scalar per solution to do this ranking, necessitating the combination of the distance functions arithmetically into a single value, in case multiple distance functions are used (Deb and Deb 2014). In practice, choosing the weighting can be complicated and ill defined. In order to overcome this, we decided to use a multi-dimensional error term, i.e., maintaining the different distance terms individually in a set or vector and using a multi-dimensional comparison predicate instead of a “smaller equal” scalar predicate (Deb et al. 2002a; Konak et al. 2006). Such a multi-dimensional comparison can lead to cases where two solutions are equal in all individual distance functions, but each respectively worse in one (but different ones), which are typically referred to as a “pareto set”; see Fig. 10.3-2. This property proves extremely useful in practice as it reveals to the modeler which properties in a model are non-attainable at the same time, possibly requiring different model ingredients rather than more search rounds.

3.1.3 Search Strategy

In the case of optimizing the parameters of neurons, metaheuristics that do not make any assumption on the function they are optimizing and that can find sufficiently good solutions (while not necessarily the best) are particularly useful. Genetic or evolutionary algorithms fall into this class (Deb and Deb 2014), but there are many others (e.g., swarm optimization (Kennedy and Eberhart 1995)). In our case, we wanted the search strategy to be able to be combined with the multi-objective error function. Our first results were obtained with an elitist non-dominated sorting genetic algorithm NSGA-II (Deb et al. 2002b). However, with increasing numbers of dimensions in the error term, the switch to the family of indicator-based evolutionary algorithms (IBEA) proved useful (Zitzler and Künzli 2004). IBEA algorithms manage to select better solutions in multiple objective searches while at the same time maintaining more diversity amongst the solutions; see Fig. 10.3-3. These strategies have been made readily available for neuronal optimization in the open-source software BluePyOpt.Footnote 6

3.1.4 Leveraging Other Constraints

In addition to the effectiveness of the distance function, the ability to combine multiple distance terms into one error term, and a powerful search strategy, an additional key element is the minimization of the overall search space. This can be achieved in various ways. Parameters that can be measured should be set directly, e.g. by determining passive parameters from experiments. Parameters can be regularized by fixing ion channel kinetics (Ranjan et al. 2019) or e.g., the use of functions for controlling how ion channels get distributed along the dendrites. Furthermore, the search space can be bounded by setting upper and lower limits for e.g., ion channel densities. All these measures help to focus the power of the search strategy on those parameters that are difficult to measure or which in biology may have a non-uniqueness/degeneracy to begin with (Prinz et al. 2004).

This approach to reconstructing neuron models has proven to be applicable to neurons from diverse brain regions in rodents, including hippocampus (see Chap. 11), thalamus (O’Reilly et al. 2020), striatum (Hjorth et al. 2020), cerebellum (Casali et al. 2019), and even other species (Deitcher et al. 2017).

3.2 Brain Tissue Models

A brain tissue model is a specific type of neural network that not only in its neuronal components and its topology resembles brain circuitry (Brunel 2000), but actually aims to capture other biophysical properties such as the physical extent of the very tissue or the spatial placement of the components. These brain tissue models thus are no longer only models of networks and their signal processing but actually are biophysical models of the tissue itself; see (Markram et al. 2015), on which this chapter is based, Chap. 11 for an application of this approach to the hippocampus, or other models such as (Billeh et al. 2020; Casali et al. 2019; Egger et al. 2020; Hjorth et al. 2020).

From a model use perspective, this offers the opportunity to link the network activity to spatial biophysical observables and biochemical processes that extend beyond the confines of neurons and makes it possible to interact with the model as if it was a virtual tissue rather than an abstraction thereof. From a model building perspective, this allows the use of experimental recordings that are measured spatially and not only recordings from single neurons.

Specifically, we have introduced computational workflows to reconstruct neuron densities, ratios, and composition using multi-modal datasets and methods to overcome the sparseness of the microconnectome by leveraging interdependencies among data that could be measured (Markram et al. 2015). For example, by explicitly considering space and the spatial 3D shape of neurons, it becomes possible to use neuronal processes to predict potential connections in the absence of a full connectome. Conversely, one can use volume counts of boutons, for example, as a valid target for the connections predicted by the model. Similarly, Markram et al. (2015) describe an approach to reconstruct the diversity of synaptic physiology within a microcircuit.

Here, we focus on four important concepts underlying this computational approach to predict a dense model from sparse data: (1) space as a modality, (2) apposition-based constraints, (3) density-based constraints, and (4) functional parameterization through regularization and sampling.

3.2.1 Space as a Modality

Explicitly modeling space in neural networks offers the ability to treat them as models of physical objects where model components and properties have a spatial consequence and in turn can be constrained (e.g., the number of spatially extended neurons that fit into a volume is limited). It turns out that 3D reconstructions of neurons done without space as a modality in mind often times show artifacts (e.g., wiggly branches that stem from tissue shrinkage before reconstruction, or incomplete reconstruction of axons) that may not affect the electrical models of the neurons but that lead to a mismatch when placing them in absolute space. Similarly, since neuron morphologies are not necessarily obtained from the same animal or even the same region, they may come in different absolute sizes and their height and arborizations within a certain layer of cortex may not fit if they were to be used together. Consequently, we developed computational methods that remove artifacts in neuronal morphologies,Footnote 7,Footnote 8 that can complete missing arborization of neurons so that they become statistically indistinguishable from complete reconstructions of neurons in the same class, and otherwise select, scale, and rotate morphologies so that they fulfil 3D constraints in the model (Anwar et al. 2009). To correctly guide this, it is important to not only consider the intended model’s shape and extent, but to allow for a flexible description of spatial heterogeneity throughout the volume. In practice, this means that we use the previously described generalized voxel-based data structure derived from the specific species, which allows diverse experimental data to be registered spatially in an absolute reference frame. The model parameters can then be sourced on a per position basis and it is not necessary to define average “recipes” of cell composition, for example, for an entire region.

3.2.2 Apposition-Based Constraints

An easily underestimated set of parameters for building network models is the detailed information about the structural connectivity. Not only does the number of these parameters scale quadratically with the number of neuron classes defined, but experimental data also shows that there is important distance-dependence and higher-order motifs. One proposed answer to this question is EM-based connectome reconstructions of entire microcircuits and brain regions (Kasthuri et al. 2015; Motta et al. 2019; Zeng 2018). Recent advances hold promise that initial instances of these datasets may become available in the not-too-distant future, however, the statistical power of these hard-earned instances remains challenging. Here, we describe a complementary computational view to the problem: the fact that neuron morphologies cluster into classes [across animals and despite anatomical specificity and plasticity (Reimann et al. 2017; Stepanyants and Chklovskii 2005; Stepanyants et al. 2002)] indicates that there is structure that possibly can be exploited for predicting the connectome or at least parts of it from these underlying elements. For the example of the microconnectome, i.e., the structural connectivity between neurons within the same volume such as a microcircuit, we have shown that a large percentage of known neuron- to neuron-class innervations patterns (i.e., where do synapses form within the dendritic and axonal trees) can be predicted by computing spatial proximities (putative synapse locations) of dendrites and axons from 3D morphologies placed in space and this despite the fact that they came from different animals across the same species, age, and region (Reimann et al. 2015). Not only are the putative locations mostly indistinguishable from experiments (Hill et al. 2012; Ramaswamy et al. 2012), but it is also possible due to the explicit consideration of space to exploit deeper interdependencies of parameters such as cell density, axonal length, connection probability, mean number of synapses/connection, and bouton density. By exploiting these interdependencies, we showed that it is possible to derive a prediction about which and how neurons are connected, including higher-order motifs, based on only partially known connectome properties (Reimann et al. 2015). These predictions are not limited to the structural connectome but extend to an actual functional instance thereof. Figure 10.4-1 illustrates the main steps of this process when dendritic and axonal 3D reconstructions of neurons are available. While further validation of these predictions with further experiments remains desirable, those results show that the microconnectome in cortical tissue to a large degree is an emergent property that can be computationally predicted. Such predictions will go hand in hand with EM connectome reconstructions in the future to confirm patterns for emergence or cases where more specific construction rules are in play.

Fig. 10.4
figure 4

Illustration of the different concepts to computationally reconstruct a connectome depending on the available source data (in all cases it is assumed that dendritic reconstructions are available): (1) if reconstructed axons are available, (2) if reconstructed axons are not available but they can be modeled by a simplified geometry, and (3) if only a regional targeting is available. Step 2 illustrates how putative contact locations can be derived and step 3 illustrates the pruning to functional synapses

Full size image

3.2.3 Density-Based Constraints

If axon reconstructions are not available, the apposition-based constraints cannot be readily exploited as described above. This is particularly a problem for long-range connections, such as inputs from the thalamus or intra-cortical connections or Schaffer collaterals as described in Chap. 11 on the hippocampus. In these cases, however, one can still exploit density-based constraints: if one has synapse density profiles available (Kawaguchi et al. 2006), one can sample the detailed dendrites in the target region according to the density profiles. In some cases, it may suffice to model the incoming fibers as straight lines in space and estimate their density from literature and assign synapses from the previous step to these fibers based on distance probability (see Fig. 10.4-2). In other cases, where the origins of innervation are less obvious, we have developed a computational approach (Reimann et al. 2019) that exploits a small set of complete axon reconstructions (Winnubst et al. 2019) in combination with region-to-region projection datasets (for example, the Allen Institute’s AAV tracer injections (Oh et al. 2014)); see Fig 10.4-3 for an illustration. In a first step, the algorithm derives a first-order probability for a neuron to innervate a region and a second-order probability for multiple region innervation. In a second step, the algorithm combines the strength of the connection with the layer density profiles to derive a density of synapses in 3D, while constraining the synapses to be on the target neuron’s dendritic tree. In a last step, it uses a topological 2D flatmap between a source and a target region to assign source neurons to the synapses.

3.2.4 Functional Parameterization Through Regularization and Sampling

The final step in functionalizing connectomes of brain tissue models involves prescribing parameters to individual synaptic contacts based on sparse experimental data on the synaptic types as well as the individual synaptic connections (Markram et al. 2015; Ramaswamy et al. 2015; Thomson and Lamy 2007). In the cortex, synapses have been found to display certain forms of short-term synaptic dynamics, namely facilitating, depressing, or pseudo-linear. These synapse types (s-types) are determined from the combination of their pre- and postsynaptic neurons. In the absence of the specific knowledge about how each of the possible pre/post-connections map to these types, a viable path is to use regularization, i.e., use rules that map connections to these classes such as pyramidal-to-pyramidal connections are always depressing or synaptic dynamics are preserved across layers for all connections of specific types. After assignments of a type, parameters for the synaptic dynamics of individual synapses are drawn from experimental distributions. Specifically, the absolute value of the unitary synaptic conductance is adjusted by comparing paired-recording experiments that also measure somatic postsynaptic potentials (PSP) between specific pairs of m-types, and compare the resulting in silico PSPs with the corresponding in vitro PSPs (Markram et al. 2015; Ramaswamy et al. 2015).

4 Simulation Experiment

In the previous sections, we described the reconstruction of a neuron or a piece of brain tissue in a model and the required various computational processes to parameterize them. A reconstructed model lends itself to exploring scientific questions in their own right, for example, on the model’s make-up, intrinsic structure, and prediction of missing data. In this section, we describe the simulation of a model—understood as the process of solving the mathematical equations (typically differential equations) governing the dynamics of the model’s components and their interactions in time.

As elaborated recently (Einevoll et al. 2019), the numerical integration methods, simulation schemes, and software engineering aspects required to faithfully and efficiently perform these calculations require mature simulator software. In addition to being able to instantiate various computational models for processing with the necessary simulation algorithms, these simulators provide means to set up simulated experiments, i.e., the equivalent of experimental manipulation devices such as a patch electrode and experimental recording/imaging devices, e.g., multielectrode array. In essence, the simulators provide the machinery for setting up and executing simulation experiments.

Markram et al. (2015) describe a barrage of simulation experiments on the neocortical microcircuit model. They range from simulating spontaneous activity and thalamic activation of the microcircuit to reproducing in vivo findings such as neuronal responses to single-whisker deflection or the identification of soloist and chorister neurons. These simulation experiments rely on the NEURON simulator (Hines and Carnevale 1997), which is the most widely used open-source simulator for biophysically detailed models of neurons and networks.

Here, we describe computational concepts that proved particularly useful to adopt when simulating brain tissue models, namely (1) global unique identifiers for neurons, (2) explicit model definition, (3) cell targets, and (4) strategies for efficient simulation. Some of these concepts such as the global unique identifier for neurons come out of the box with the simulator software, but they deserve to be highlighted. Other concepts such as the explicit model definition and cell targets have been necessary to adopt to effectively connect simulations into a wider set of model building and analysis workflows as described by Markram et al. (2015). The question of efficiency of the simulations, finally, is determining how many simulation experiments can be performed in practice.

4.1 Global Unique Identifier

A minimal concept that proved essential in being able to reconstruct and simulate brain tissue models had already been introduced to neurosimulators when they started to embrace parallel computing systems (Morrison et al. 2005; Migliore et al. 2006). At that point, it became necessary to assign each neuron an explicit globally unique identifier (GID). What we realized for the study in (Markram et al. 2015) is that the identification of neurons needs to be an explicit property of the model, i.e., the GIDs need to be stored with the model (and not only in the simulator) and thus can be used in any software that interacts with the model whether it is for the model building, simulation or visualization and analysis. This allows the linking of additional information to any given neuron as required by the context. See Fig. 10.5-1 for an illustration.

Fig. 10.5
figure 5

Schematic of computational concepts for simulation experiments. (1) Global Unique Identifier: Cells are uniquely identified by GIDs (a), the cells’ properties and connectome are explicitly defined (a,b). (2) Cell targets: are defined based on gids or other properties (a). Cell targets are used to easily define stimulation on a population (S) or recording the activity of another population (R) in 2b

Full size image

4.2 Explicit Model Definition

The need for uniquely identifying neurons goes beyond any single step in the workflow. In order to ensure that different tools resolve the various GIDs in the same way, it is important to externalize the model definition in a formatFootnote 9 that can be read by a variety of tools. In other contexts, such as networks of point neuron models (Potjans and Diesmann 2014), a rule-based definition of the network is commonly used, see for instance PyNN (Davison et al. 2009) or CSA (Djurfeldt 2012), which is compact and allows a fast instantiation in the respective software tool. However, it also leaves the interpretation of the rules to the respective tools and thus potentially makes it more difficult to clearly refer to a specific model component among various software interacting with the model. Thus, by storing the model explicitly in a container such as SONATA (Dai et al. 2020), a model exists independently of the software and rules used to produce it. This makes it possible to unambigously identify the same model components across tools.

4.3 Cell Targets

Especially for brain tissue models, which today contain hundreds of thousands or even multiple millions of neurons, it becomes important to efficiently be able to address specific portions of the model. In one way, this is analogous to a query operation in a database. For example, if the brain tissue model stores additional properties with the GIDs, for instance, cell type, spatial location, etc., it becomes straightforward to find cells of a certain type (e.g., layer 5 pyramidal cells) or even cell groups such as disynaptic loops between layer 5 pyramidal and Martinotti cells (Silberberg and Markram 2007) and refer to them with a simple set of GIDs, which we refer to as a cell target. Analogous to views in databases, cell targets can also be thought of as a named subset of the model (see Fig. 10.5-2a), in cases where only a mini-column should be used for simulation or for singling out specific cells during analysis or visualization. Lastly, cell targets can also be thought of as an addressing scheme that allows to uniquely identify and address any set of cells. Such an addressing scheme is most relevant to set a model up for in silico experimentation. For example, a specific instance of the aforementioned pyramidal-Martinotti loop cell target can be selected and a stimulation device attached to the first pyramidal cell as well as intracellular recording devices attached to the Martinotti cell and the two pyramidal cells, effectively recreating the experimental protocol in a simulation experiment (see Fig. 10.5-2b).

4.4 Strategies for Efficient Simulation

The time it takes to numerically solve a brain tissue model for 1 s of biological time directly governs the scientific questions that can be asked with the model. Rarely does one accept simulations to run for longer than a few weeks. In practice, a few days is the limit by which simulations have to come back with results. The primary reason is that simulations are typically part of a larger scientific workflow either requiring iteration or parameter variation and ultimately human feedback. The efficiency of simulations is thus an important prerequisite for the study of brain tissue models, where a single neuron may be governed by tens of thousands of differential equations and the network model may contain multiple millions of neurons. An in depth treatment of the required computational realization of this is beyond the scope of this chapter, however, it should be noted that several engineering and computational science techniques have to play together. It is necessary for efficient simulations to embrace modern computers and clusters of computers, and in particular their parallel nature (Cremonesi and Schürmann 2020). Simulators such as NEURON have thus been parallelized to execute millions of computations in parallel (Migliore et al. 2006), in turn necessitating to solve problems arising from this parallelization such as consistent parallel random numbers, load-balancing and efficient loading of the model and recording of output. At very large scales, it furthermore proved necessary to strip unnecessary data structures away to reduce the overall memory footprint and reduce the amount of memory that needs to be transferred to the CPU for every computation; these strategies have been incorporated in CoreNEURONFootnote 10 that transparently integrates with NEURONFootnote 11 for large scale simulations (Kumbhar et al. 2019).

5 Validation

A key concept of Markram et al. (2015) is to validate the artefacts of the reconstruction process not only at the very end but rather to apply validation tests along the process. Cell models, for example, are validated against independent data not used in the reconstruction process, serving to validate the generalization of the cell models and to be able to compose them into a network model where they lead to emergent behavior without any further tuning. At the same time, the brain tissue reconstruction is evaluated by a variety of anatomical and physiological validation tests that assess emergent properties of the model against known experimental data that was not used during reconstruction.

While validation is a standard activity in computational science, the complexity of brain tissue models necessitates a specific approach to validation that draws inspiration from the validation of complex software systems with unit testing, integration testing, and regression testing (Orso et al. 2004). Here, we describe 4 types of validation that were used by Markram et al. (2015) and which build on top of each other: (1) individual components (e.g., neuron models) are validated in a high-throughput way. Once they pass this component-level validation, (2) components are integrated into a composite system (e.g., a network model) where they are validated in the context of that system. Once the components are validated, (3) the system itself is validated first against the data/rules being used to build it and then (4) against external datasets that have not been used to build it.

5.1 High-Throughput Model Component Validation

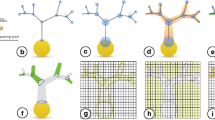
In Biophysical Neuron Models (Sect. 3.1), an approach was described that can create a variety of neuron models, namely how multi-objective optimization strategies result in a pool of models with different trade-offs. The number of models resulting from this can potentially be large, reaching thousands of models. Yet, depending on the scientific starting point, it can be desirable for even more neurons in a brain tissue model to be unique. In such cases, it is quite common to transplant electrical parameters from one neuron model into a different morphological shape, which is computationally much cheaper than constraining the electrical parameters from scratch. At this point, only a high-throughput approach can perform the validation of the models against experimental data. In case of neuron models, these validations check for soma voltage responses from step current, for example, or ramp current injections. In order to automate the validation, the same approaches used in the building of the neuron models can be used, namely to define Effective Distance Functions as previously defined. The quality of the generalization of the combinations is then quantified by comparing model and biological neurons in terms of their median z-scores for all electrical features. In difference to the model building process, in the validation step only one pass is made per neuron; this computation is embarrassingly parallel and lends itself to efficient execution on parallel systems;Footnote 12 Fig. 10.6 shows an example of such high-throughput validations for electrical neuron models.

Fig. 10.6
figure 6

An example of high-throughput validation of biophysical neuron models. (a) shows the morphology and model behavior to step current injection as generated by BluePyOpt. (b) The same model is assigned to multiple morphology reconstructions to create a diverse set of model neurons. (c) These model neurons are validated by comparing a variety of features on their electrical behavior to the equivalent features in experimental recordings. (d) Generalization of the models for various neuron types (different morpho-electrical classes)

Full size image

5.2 Sample-Based In Situ Model Component Validation

Once a model component is validated, it can be integrated into a composite model. However, here the challenge is twofold. First, one has to validate that the component is also generalizing when it is embedded into the composite system. In the case of a neuron that is embedded into a tissue model, for example, those integration effects come from the synapses the neuron will then receive and which could drive the neuron out of its dynamic range. However, validating the component inside the composite system raises a scalability issue: the composite system sometimes needs to be taken into account in the validation itself increasing the computing cost of the simulation. Since the contexts of embedding can be unique, this cost may scale with the number of instances of the component rather than just with the number of component types. This scalability issue prevents an exhaustive high-throughput validation as described above, but rather necessitates a sample-based approach. As an example, we use a validation called “Morphology Collage” that samples a certain number of neurons, displays them in a slice along with meshes visualizing the layer boundaries; see Fig. 10.7. This makes it easy for a human to inspect the placement of these neurons, for instance, to identify if certain neurites target the appropriate location or if the neurites are located in the expected layer.

Fig. 10.7
figure 7

3D Morphology collage for the hippocampus CA1 region model as an example of Sample-based in situ Model Component Validation. These collages enable the scientist quickly to validate the dendritic targeting and that the axon trees are located in the appropriate layer; see also Chap. 11 for more details

Full size image

5.3 Intrinsic Validation: Validation Against Input Parameters

Data-driven model building pipelines as described in this chapter take datasets of multiple modalities and rules as input, and integrate those by trying to fulfil various and possibly conflicting constraints originating from them. In such a constraint resolution process, it cannot a priori be taken for granted that the final model—after the constraints are resolved to the extent possible—still complies with the desired initial specification. Deviations can come from the metrics steering the constraint resolution process and from random seeds used in the process to instantiate certain parts of the model. For methods as those described in Brain Tissue Models (Sect. 3.2), where we use apposition and density-based constraints to predict the microconnectome, it is thus necessary to validate the model against its initial specification after it has been built. To that end, we have developed a validation frameworkFootnote 13 that defines the testbed and performs appropriate statistical tests built on top of an interfaceFootnote 14 to query and analyze our model and in silico experiments.

5.4 Extrinsic Validations: Validation of Emergent Properties

The previous validation steps provide the first sanity check that the resulting model has been built according to the initial specification and that the process of model building was completed as intended. They thus represent a form of verification and they are also somewhat similar to testing the performance of a machine learning model on training data. Obviously, this is only necessary, but not sufficient for a good model, which needs to be tested for its emergent properties in novel regimes and against previously unused datasets. The extrinsic validation step is thus about validating properties of the model that were not explicitly controlled for in the construction process against independent data. The properties in question range from structural properties of the model to its behavior in an in silico experiment. For example, brain tissue models that have been built using the previously mentioned methods can be validated against in vitro staining profiles of molecular markers in brain slices. These molecular markers are not a property of the model per se, but these 2D maps of molecular markers can be calculated from parameters present in the model such as the spatial composition, the neuronal type, or their association with the molecular markers. Similarly, data from paired recordings of synaptically connected pairs of neurons can be used to validate the model’s functional emergent properties that were only explicitly constrained on single neuron electrophysiology and the connectivity resulting from their morphologies. Lastly, the ultimate test is to see whether the resulting model shows an emergent behavior that is in line with experiments that were not used to constrain the model. A simple example of this is the validation of the behavior of the model in response to tonic depolarization and comparing this to slice experiments. A more complex example is the changing of a bath parameter to explore different computational regimes of the model and the comparison to respective multi-electrode array measurements of brain slices. In practice, the analysis of these types of in silico experiments is a combination of predefined tests and interactive analyses with dedicated software frameworks as described above combined with scientific visualizationFootnote 15,Footnote 16,Footnote 17 that allows the inspection of the model and its simulations in ways similar to what microscopes and imaging methods provide in a wet lab.

6 Model and Experiment Refinement

Data-driven reconstructions of brain tissue models as described in Markram et al. (2015) provide a scaffold that enables the integration of available experimental data, identifies missing experimental data, and facilitates the iterative refinement of constituent models. Validations are a crucial part of the data-driven modeling process that reduces the risk that errors could lead to major inaccuracies in the reconstruction or in simulations of its emergent behavior. Successful validations not only enable the systematic exploration of the emergent properties of the model but also establish predictions for future in vitro experiments or question existing experimental data. Failure in validation could also indicate errors in experimental data and identify future refinements. Rigorous validation of a metric at one level of detail, therefore, also prevents error amplification to the next level and triggers specific experimental or model refinements.

An example of refinement at the interface between experiment and model proved necessary at the single neuron level, more specifically, the liquid junction potential artifact. This artifact arises due to the interaction of electrolytes of different concentrations—i.e., intracellular recording and extracellular bath solutions used in whole-cell patch clamp experiments. When single-cell electrophysiology recordings are reported in literature, the values are usually not corrected for the voltage difference in the liquid junction potential, which is estimated to be around −10 to −14 mV. As a result, the true measurement of membrane potentials is often distorted and requires a systematic correction to further constrain single neurons models, especially when combined with other absolute quantities such as the reversal potentials that can be calculated directly from ion concentrations. The validation process identified this inconsistency, which led to a careful re-evaluation of the experimental data and the precise conditions to adjust for the liquid junction potential offset in the experimental data used for the final model.

An example for experimental refinement occurred at the level of microcircuit structure while integrating previously published data on neuron densities into data-driven models of neocortical tissue. The experimentally reported values vary by a factor of two (40,000–80,000 neurons/mm3) and yet failed to result in the overall number and density of synapses reported in other studies. Consequently, we performed new experiments, counting cells in stained tissue blocks, which yielded a mean cell density of 108,662 ± 2754 neurons/mm3, comparable to other independent observations in the rat barrel cortex (Meyer et al. 2010). This is a clear-cut use case of how the data-driven brain tissue reconstruction approach enables the refinement of specific data through triggering new experiments.

As a third example, we encountered the need to refine the data-driven model of neocortical tissue at the level of microcircuit function when it was simulated to study the emergent dynamics of spontaneous activity. As mentioned previously, model parameters to recreate experimentally observed properties of synaptic physiology were obtained from in vitro experiments, which are typically performed at high levels of Ca2+ in the recording bath (2 mM). Simulating microcircuit function with synaptic parameters at high Ca2+ levels resulted in highly synchronous, low-frequency oscillatory behavior of spontaneous network activity. However, in order to explore network behavior under in vivo-like conditions, we refined model parameters for synaptic physiology by using experimental data acquired at low levels of Ca2+ in the recording bath (0.9–1.1 mM), which approximates in vivo conditions. As a result, network activity transitioned from synchronous activity to highly asynchronous spontaneous network activity, consistent with experimental observations (Markram et al. 2015).

We have discussed three specific examples to outline the symbiosis of the model-experiment refinement cycle. Indeed, we will continue to integrate and acquire more experimental data to validate brain tissue models as we scale up spatially from microcircuits to brain regions. Additional datasets will help to fill in biological details that are not included in the current first draft reconstruction (e.g., data on gap junctions, cholinergic modulatory mechanisms, rules for activity-dependent plasticity, extrasynaptic glutamate, and GABA receptors, kinetics of metabotropic glutamate receptors, non-synaptic transmission, and autaptic connections).

7 Conclusions

Understanding the brain is probably one of the final frontiers of modern science. Since the brain is a complex biological system that has evolved over billions of years, it is difficult to know a priori the details that matter in the healthy or diseased brain, in turn posing challenges for computational models. We previously introduced a data-driven reconstruction and simulation approach to build biophysically detailed models of the neocortical microcircuitry (Markram et al. 2015), sometimes also referred to as a digital twin. Our approach builds models from first principles in the sense that it avoids a priori simplifications or abstractions beyond the biophysical starting point, which lends itself to capturing the brain’s cellular structure and function. By treating the modeling of the microcircuitry as building a model of a piece of tissue, it is possible to leverage constraints arising from different modalities, allowing the prediction of parameters that are experimentally not available. Our approach describes a way to progressively and incrementally improve models by systematically validating their emergent properties against data not used in the reconstruction process, and a refinement process that is executed when the model displays aberrant properties or behaviors that are inconsistent with experimental data.

Over the years, the approach has been successfully applied to larger portions of the neocortex and other brain regions. For example, Chap. 11 describes how this approach was applied to reconstruct the hippocampal CA1 region through necessary adaptations. Therefore, this chapter deconstructs the approach described previously (Markram et al. 2015) into its underlying computational concepts. This makes it possible to not only better identify the necessary computational methods to reconstruct and simulate brain tissue in computer models but also recognize the knowledge gaps in data and modeling challenges that could be surmounted.

In addition, even if the goal is not to reconstruct an entire brain region but rather only a single neuron, aspects of the section on Data Organization and Biophysical Neuron Models (Sects. 2 and 3.1) still remain relevant. Similarly, selected concepts underlying simulation and validation could be applicable to network models using simpler neuron models.

The presentation of the computational concepts in this chapter is complemented with links to available open-source software that implement the reconstruction, modeling, and validation procedures and make them easily accessible to the interested reader.Footnote 18