AIGEN: Random Generation of Symbolic Transition Systems

Abstract

AIGEN is an open source tool for the generation of transition systems in a symbolic representation. To ensure diversity, it employs a uniform random sampling over the space of all Boolean functions with a given number of variables. AIGEN relies on reduced ordered binary decision diagrams (ROBDDs) and canonical disjunctive normal form (CDNF) as canonical representations that allow us to enumerate Boolean functions, in the former case with an encoding that is inspired by data structures used to implement ROBDDs. Several parameters allow the user to restrict generation to Boolean functions or transition systems with certain properties, which are then output in AIGER format. We report on the use of AIGEN to generate random benchmark problems for the reactive synthesis competition SYNTCOMP 2019, and present a comparison of the two encodings with respect to time and memory efficiency in practice.

1 Introduction

Verification and synthesis algorithms require benchmark problems that can be used for testing and evaluation. Unfortunately, a diverse set of benchmarks is very hard to obtain. This is a problem not only for tool developers, but also for organizers of competitions [3, 4, 8, 11] that need to evaluate tools on a wide range of benchmarks, and to regularly search for new meaningful benchmarks.

If done properly, the generation of random benchmarks can be a solution to this problem by providing the best possible diversity and by generating new benchmarks whenever needed. On the other hand, random benchmarks come with a few caveats. First of all, completely random generation is usually not desired, since it could result in many benchmarks that, while drawn from a diverse set, are not interesting, e.g., they may be too easy or too difficult to solve for existing tools. Secondly, users may be interested in how their implementation handles benchmarks with specific properties, for instance those that require long chains of computations to reach a conclusion. Finally, if users know how realistic benchmarks for a certain type of verification or synthesis problem usually look like, they may want to restrict the random generation to such benchmarks, e.g., by forcing them to comply with certain conditions on their structure.

In this paper we present AIGEN, a tool for random generation of transition systems in a symbolic representation. We generated transition systems with partitioned transition relation, i.e., consisting of sets of Boolean functions. We ensure diversity at the level of individual Boolean functions by requiring a uniform random sampling over all Boolean functions with a given number of variables.

While for some application areas there exist tools that generate random Boolean functions in a specific form (e.g. randomly generated propositional formulas in CNF [9, 16]), to the best of our knowledge none of these supports uniformly random distributions. The obvious benefit of this approach is that random samplings allow to make statements about the actual space of Boolean functions, instead of statements about a specific representation of the functions, and these benefits extend to the random generation of transition systems.

To ensure uniform random sampling, we rely on an enumeration of all Boolean functions with a given number of variables, based on their truth tables. From the truth tables one can generate in a straightforward way standard canonical representations of the functions, e.g., in canonical disjunctive normal form (CDNF) or canonical conjunctive normal form. As a more memory-efficient alternative, we developed an encoding that is inspired by data structures used for implementing reduced ordered binary decision diagrams (ROBDDs).

AIGEN implements our ROBDD-based algorithm and a CDNF-based algorithm. Development of AIGEN was motivated by the evaluation of reactive synthesis tools [13], and it was used to generate benchmarks for the reactive synthesis competition (SYNTCOMP) [11, 12]. Since the existing benchmark library of SYNTCOMP consists mostly of benchmarks that were hand-crafted by tool developers, the diversity of benchmarks is limited, and their choice may be skewed towards problems or encodings that are well-suited for the existing tools. Hence, as an addition to the existing hand-crafted examples, random benchmarks are a valuable source of insight into the performance of synthesis algorithms.

Outline. We introduce BDDs and ROBDDs in Sect. 2. In Sect. 3 we present our basic idea for the random generation of symbolic transition systems, based on enumerating Boolean functions. In Sect. 4, we present a detailed description of the ROBDD-based algorithm, and in Sect. 5 the algorithm based on CDNF. Finally, in Sect. 6 we present a comparison between the ROBDD and the CDNF approaches, and we give details about our implementation and how to effectively use the tool to produce diverse benchmarks.

2 Canonical Representation of Boolean Functions

A Binary Decision Diagram (BDD) over a set of variables X is a directed acyclic graph $G=(V,E)$ with $V \subset \mathbb {N}$, exactly one root $v_r \in V$, and a labeling on nodes. Each terminal node $v \in V$ is labeled with a value $val(v) \in \{0, 1\}$. Each non-terminal node $v \in V$ is labeled with a variable $var(v) \in X$ and has exactly two outgoing edges, leading to nodes that are denoted by $high(v) \in V$ and $low(v) \in V$, respectively. Note that if $v \in V$ is a non-terminal node, then the directed acyclic graph rooted in v is also a BDD. It is called the sub-BDD of G with root v.

A BDD G(V, E) over a set of variables X is ordered if on every path from the root to a terminal node, variables in node labels occur in the same order and each variable occurs at most once. A BDD is reduced if it does not contain any of the following:

• non-terminal nodes $v \ne w \in V$ with $var(v) = var(w)$, $low(v) = low(w)$ and $high(v) = high(w)$,

• terminal nodes $v \ne w \in V$ with $val(v) = val(w)$,

• a non-terminal node $v \in V$ with $low(v) = high(v)$.

Any ordered BDD can be transformed into a reduced BDD by using the isomorphism and Shannon reductions (cp. [10]). A BDD that is reduced and ordered is called a Reduced Ordered Binary Decision Diagram (ROBDD).

Note that in an ROBDD, a triple (x, high(v), low(v)) of a node v, where $x=var(v)$, uniquely defines a sub-ROBDD. This implies that ROBDDs are a canonical representation of Boolean functions [10], i.e., for a fixed variable order there is a unique ROBDD representation for every Boolean function.

3 Enumerating Boolean Functions

Based on a canonical representation of Boolean functions, we define an enumeration, i.e., a bijective mapping from natural numbers to Boolean functions (or ROBDDs), such that any procedure that produces uniformly random natural numbers (in some range) can be used to produce uniformly random Boolean functions (in some range, see below for details).

To define our mapping, we first describe the data structure for ROBDDs that is used by various BDD packages. Then we will illustrate the data structure we use for ROBDDs and how it guarantees canonicity and uniform random distribution. In the following, we assume that $X = \{x_1,\ldots ,x_m\}$ is a set of variables with a fixed order.

Unique Table. BDD packages use the so-called unique table as a data structure for storing ROBDD nodes. The unique table of a BDD $G =(V,E)$ over a set of variables X is a hash table that establishes a bijection between nodes $v \in V$ and triples $(x,h,l) \in X \times V \times V$ that uniquely identify them, where $x=val(v)$ if v is a terminal node, and $x=var(v)$ otherwise, $h=high(v)$ and $l=low(v)$.

Virtual ROBDD Table. We will use the ideas from the unique table that is used in BDD packages to define the virtual ROBDD table that enumerates all possible ROBDDs with respect to our variable order. This table can of course not be constructed explicitly, but the idea of this table can be used to define a (bijective) mapping from natural numbers to ROBDDs. We want to generate random Boolean functions that are based on a uniform distribution. For this reason the algorithm generates randomly a natural number $bddID \le 2^{2^m}$ (since there are $2^{2^m}$ different Boolean functions of type $\mathbb {B}^m \rightarrow \mathbb {B}$), then computes a unique triple similar to the one above that corresponds to bddID, and then iteratively builds the complete ROBDD.

For the sake of illustrating how the algorithm computes the triple, assume that there exists a table, called Virtual ROBDD Table (or short: VRT), that maps natural numbers to ROBDDs, identified by a triple of variable index, and high and low children. In other words, every entry in the table maps uniquely a number $bddID \in \mathbb {N}$ (i.e. a BDD node) to a triple (level, high, low) where level is a variable index, $high = high(bddID)$, and $low = low(bddID)$. Like the unique table, none of the entries (i.e., ROBDDs) appears twice. However, in contrast to the unique table, the VRT is based on the fixed variable order, and uses the variable index in this order instead of the variable itself. Table 1 depicts a sketch of the VRT.

Table 1. VRT: Entries in the table are in ascending order over bddID. Each row is annotated with a level and a sublevel. $L_i$ denotes the $i^{th}$ level, containing all triples with variable index i. The sublevel $sl_{i_j}$ denotes the $j^{th}$ sublevel of $L_i$ which contains all triples of $L_i$ in which j is the high or the low child, and the other child $j'$ is a bddID that belongs to a level $L_{i'}$ with $i' < i$ such that $[j.j']$ has not appeared before in $L_i$. Each cell in a row annotated with $L_i$ and $sl_{i_j}$ is of the form (bddID)[high.low] where bddID is the unique identifier of the triple (i, high, low). Let $Y_1=2^{2^{i-1}}$ and $Y_2 = \underset{m=1}{\overset{j-1}{\sum }}2(2^{2^{i-1}}-m)$.

Fig. 1.

BDD generated for number 16. Equivalent to boolean function: $x_2x_1 + \bar{x_2}\bar{x_1}$. The numbers on the left of the BDD represent the level i.e. corresponding variable indices.

Note that a bddID between 1 and $2^{2^m}$ corresponds to a Boolean function with at most m input variables, and a bddID between $2^{2^{m-1}} + 1$ and $2^{2^m}$ corresponds to a function with exactly m input variables. Thus, to uniformly sample Boolean functions, we can use a random number generator that uniformly samples natural numbers in such a range.

It is important to remember that the VRT is not constructed explicitly. Instead, given a number of variables m, and based on the predefined ordering of ROBDD in the VRT ($2^{2^m}$ ROBDDs), the algorithm generates first a random number $bddID \le 2^{2^m}$, then computes the triple (level, high, low) to which bddID maps. We note: level (or i) is equal to $\lceil {log_2(log_2(bddID))}\rceil$. Let $Y_1=2^{2^{i-1}}$, then we solve the following system of equations to compute x which is equivalent to the sublevel:

$Y_1 + 2(Y_1 - 1) + \ldots + 2(Y_1 - x) < bddID$

$Y_1 + 2(Y_1 - 1) + \ldots + 2(Y_1 - (x+1)) \ge bddID$

High and low are then computed according to what is given in the table, see Sect. 4 for more details. Figure 1 shows the BDD generated for $bddID=16$ which is equivalent to: $x_2x_1 + \bar{x_2}\bar{x_1}$.

4 Random Generation of (Controllable) Transition Systems

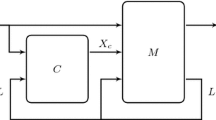
In this section we present our algorithm for generating random transition systems, represented as AIGER circuits [5]. We use a generalization of the usual notion of transition systems that allows some of the input signals to be declared as controllable. This is useful to define synthesis problems, i.e., a synthesis procedure can define how these inputs should behave depending on the state and uncontrollable inputs of the system.

A controllable transition system (or short: controllable system) TS is a 6-tuple $(L,X_u,X_c,$ $\mathbf {F}, BAD,q_0)$, where L is a set of state variables (also called latches), $X_u$ is a set of uncontrollable input variables, $X_c$ is a set of controllable input variables, $\mathbf {F} = (f_1,...,f_{|L|})$ with $f_i: \mathbb {B}^L \times \mathbb {B}^{X_u} \times \mathbb {B}^{X_c} \rightarrow \mathbb {B}$ is a vector of update functions for the latches, $BAD: \mathbb {B}^L \rightarrow \mathbb {B}$ is the set of unsafe states, and $q_0$ is the initial state where all latches are initialized to 0.

Then, the idea of our tool for random generation of transition systems can be summarized in the following way:

• The user input determines parameters of the system, such as the number of latches and controllable or uncontrollable inputs.

• For every latch, we generate a random Boolean function that determines how this latch is updated based on the current state and input of the system, represented as ROBDD as described in Sect. 3.

• Additionally, we generate a random Boolean function that determines the set of unsafe states of the system.

• The system composed of these functions is then encoded into an AIGER circuit.

4.1 Random Generation Algorithm

The procedure GenerateRandomAiger takes as input the number of latches l, uncontrollable inputs u, controllable inputs c, the bound o, optionally a list of seeds (i.e., natural numbers used to initialize a pseudorandom number generator). As output it produces a file in AIGER format.

Lines 3–6 generate for every latch a random ROBDD that represents an update function $\mathbb {B}^{l+c+u} \rightarrow \mathbb {B}$ for the latch, i.e., a function that takes all current values of inputs and latches as input, and returns a new value for the given latch. Line 4 generates a random integer with $2^{vars}$ random bits, i.e., a natural number between 1 and $2^{2^{vars}}$. All the seeds used for generating the random integers will be written in the comment section at the end of the generated file. These seeds can be fed to the algorithm in order to regenerate the same instance. Line 5 constructs the ROBDD that corresponds to the generated number. Line 6 converts the constructed ROBDD into an AIG (And-Inverter Graph) relying on the fact that a BDD can be seen as a network of multiplexers.

Lines 8–10 construct the ROBDD of the function $f_{BAD}: \mathbb {B}^o \rightarrow \mathbb {B}$ which uses $o \le l$ latch variables. The set of unsafe states BAD is then defined as $f(x_{i_1},\ldots ,x_{i_o}) \wedge \bigwedge _{j \in \{1,\ldots , l\}\setminus \{i_1,\ldots ,i_o\}} x_j$ where the indices $\{i_1,\ldots ,i_o\}$ are also picked randomly. Line 11 creates the AIGER file that corresponds to the total number of variables and to the update functions that were randomly generated. Line 12 uses the ABC [7] tool to reduce the size of the generated AIGER file.

ConstructBDD is a recursive procedure for constructing all the nodes of the ROBDD that corresponds to the unique ID bddID. It starts with the root node and recursively proceeds to the child nodes until it reaches the nodes 0 or 1. Line 14 checks if the node was already created. If not, Line 15 computes the triple (level, high, low) that uniquely represent the node and adds it to the table robddTable. Lines 18–17 construct the child nodes. Note that the robddTable is initialized with the IDs 1 and 2 which correspond respectively to nodes 0 and 1.

Given an ID, procedure GetChildren computes the triple (level, high, low). Line 20 computes the level. Lines 21–24 compute the sublevel. Note that, as depicted in Table 1, a sub-level $s_{i_j}$ has size $2(2^{2^{i-1}} -j)$, where $2^{2^{i-1}}$ is the sum of the sizes of all levels that are smaller than i. To compute the sublevel, we have to compute the single solution of the system of inequations in Lines 22, 23, to see that check the VRT table. Line 25 computes the ID of the left-most bit in the sub-level. Lines 26–27 compute the ID of the second child node, and Lines 28–30 check which node is the low edge and which node is the high edge.

5 CDNF-based Algorithm

An obvious alternative to our ROBDD approach is to make use of the canonical disjunctive or conjunctive normal forms to generate random Boolean functions. Algorithm 2 employs CDNF as it is easier to convert to And-Inverter graph. CDNF is usually constructed directly from a truth table by taking the OR of all satisfying assignments. To convert a Boolean formula $f_i=cl_1 \vee cl_2 \vee \ldots \vee cl_n$ in CDNF to AIG, we consider its equivalent $f'_i=\lnot (\lnot cl_1 \wedge \lnot cl_2 \wedge \ldots \wedge \lnot cl_n)$.

The procedure DNFGenerateRandomAiger takes as input the number of latches l, uncontrollable inputs u, controllable inputs c, the bound o, and produces a file in AIGER format as output. Lines 3–6 generate a random update function for every latch. Line 4 generates a random bit vector of size $2^{vars}$. This bit vector represents the valuation of all the minterms¹ of the truth table that represents the random function $f_i$. For instance, if the left-most bit of the bit vector is equal to 1, then $x_{c_0} = 0,\ldots ,x_{c_{|c|-1}}=0,x_{u_0} = 0,\ldots , x_{u_{|u|-1}}=0,x_{l_0} = 0,\ldots ,x_{l_{|l|-1}}=0$ is a satisfying assignment of $f_i$. Similarly, if the last element of the bit vector is equal to 1, then $x_{c_0} = 1,\ldots ,x_{c_{|c|-1}}=1,x_{u_0} = 1, \ldots ,x_{u_{|u|-1}}=1,x_{l_0} = 1,\ldots ,x_{l_{|l|-1}}=1$ is a satisfying assignment of $f_i$. Line 5 builds the random function that corresponds to the generated bit vector, and Line 6 converts it to AIG. Lines 8–10 generate the output random function, and Lines 11, 12 creates the AIGER file and call ABC to minimize it.

The procedure ConstructDNF takes as input a bit vector and the number of variables and generates the corresponding Boolean function. Line 14 initializes the DNF function to be created. For every element in the bit vector, if the ith element is equal to 1 (Line 15) then, in order to obtain the corresponding minterm, Line 17 converts the positive integer i to binary. For instance if $i=3$ and vars = 3, then the minterm $x_c \wedge \lnot x_u \wedge x_l$ is created. Line 18 creates the corresponding minterm. Line 19 negates the created clause and adds is to the DNF formula. Line 20 returns the negation of the constructed formula. As mentioned earlier, as the formula represented by the truth table is in DNF, we need to generate its equivalent that includes only AND and NOT logical gates. For instance giving a formula $f_i=cl_1 \vee cl_2 \vee \ldots \vee cl_n$ in CDNF, we construct its equivalent $f'_i=\lnot (\lnot cl_1 \wedge \lnot cl_2 \wedge \ldots \wedge \lnot cl_n)$.

Fig. 2.

Average number of AND gates.

Fig. 3.

Average running time in seconds including the time needed to minimize the generated Aiger circuit using ABC tool.

Fig. 4.

Average running times.

6 Implementation and Evaluation

AIGEN is implemented in Python, and a virtual machine with the tool ready to run is available at https://doi.org/10.5281/zenodo.4721314 [14]. The source code of AIGEN is also publicly available at https://github.com/mhdsakr/AIGEN-Tool, allowing interested users to add functionality, e.g., in order to add further parameters to generate only Boolean functions or transition systems with certain properties. It uses the mpmath [15] library together with GMPY [1] to deal with large numbers. By default, mpmath uses Python integers, however if GMPY is also installed on the operating system, mpmath will automatically detect it and use gmpy integers intead. This makes mpmath perform much faster, particularly at high precision (approximately above 100 digits). Furthermore, AIGEN uses ABC [7], and the AIGER tool set [6] to post-process AIGER circuits.

AIGEN has been used to generate thousands of random transition systems. Figures 4, 2, 3 shows average times and sizes for generating systems where, for example, 4.3.7 denotes systems with 4 controllable inputs, 3 uncontrollable inputs, and 7 latches ($o=l =7$). These times were measured on a laptop with quad-core i7-6600U CPU at 2.6 GHz and 20 GB RAM.

Figures 4 and 2 compare average running time and average number of AND-gates between the ROBDD and DNF approaches. These results are without the use of the ABC tool (i.e. the command “ABCMinimize(aigerFilePath)” was skipped). Figure 4 shows that the DNF approach was faster in all cases which was expected due to the fact that generating a random ROBDD is much more complex than generating a truth table. Figure 2 shows that the ROBDD approach is much better in all cases. Figure 3 compares average running time between the ROBDD and DNF approaches, including the time needed for the ABC tool to minimize the generated transition system. Benchmarks 8.8.4, 9.9.4, and 10.11.2 timed out for the DNF approach(we used 10 h as a time limit). Obviously the ABC tool needed a lot of time to process these benchmarks. After a thorough inspection, the reason was, in addition to the huge size of these circuits, the incredibly long chains of AND-gates for every generated Boolean function. This figure shows that the total running time of the tool was way better when used with the ROBDD approach.

The Effect of Parameters. Although the benchmarks are randomly generated, AIGEN allows the user to choose the input parameters to obtain benchmarks with certain properties that correspond to their needs, for example:

• The degree of the generated graph (i.e., the transition system) is equal to $2^{u+c}$, therefore increasing the ratio $(u+c)/l$ will make the graph more congested and consequently more complex.

• The parameter o gives the user the ability to determine the size of the set of unsafe states, i.e., the number of unsafe states cannot exceed $2^o$. Accordingly, increasing the ratio o/l will increase the probability that the error set is reachable, and decreasing this ratio will lower the probability.

• Increasing the ratio c/u will increase the probability that the benchmark is realizable, and decreasing it will serve the opposite goal. Moreover, if this ratio is close to 1 the realizability check will be harder, since the probability of realizability will be roughly equal to the probability of unrealizability.

To demonstrate the effect of these parameters, Table 2 shows the running time and results (realizable or unrealizable) of the synthesis tool SimpleBDDSolver on selected benchmarks, generated using the ROBDD-based approach, in SyntComp 2019. SimpleBDDSolver has won all previous iterations of the Syntcomp competition. A benchmark name contains the parameters that were used to generate the file, e.g., random_n_19_1_3_15_14_1_abc means that the benchmark has in total 19 variables with 1 controllable input, 3 uncontrollable inputs, 15 latches, and $o=14$. The table shows that the example benchmarks with ratio $c/u = 1/3$ or $c/u = 1/5$ were unrealizable, the benchmarks with ratio $c/u = 2$ were realizable, while benchmarks with ratio $c/u = 1/2$ were difficult to solve for the tool, which timed out while trying to solve them. Note that a benchmark with $c/u = 1/5$ can still be realizable, and one with $c/u = 2$ can be unrealizable—it is just unlikely that this is the case for a randomly generated benchmark.

Table 2. Results of SimpleBDDSolver on selected random benchmarks generated by AIGEN in SyntComp 2019 [2]

7 Conclusion

We have presented AIGEN, a tool for the generation of random transition systems in a symbolic representation, using either ROBDDs or CDNF for representing Boolean functions. Although the ROBDD based approach generates much smaller symbolic transition systems, the CDNF approach is faster when ABC minimization procedure is disabled. In contrast to the ROBDD approach, to generate a random formula in CDNF, no complex computation is needed. However, when using minimization, the huge size of these formulas becomes a problem for ABC as it has to deal and inspect all the generated AND-gates.

In future work, instead of using a fixed variable order, we will also allow to use a random order. The drawback of a fixed order is that some Boolean functions only have a large ROBDD representation, even though smaller ones exist with different orderings, and vice versa. Going further, we plan to include variable reorder techniques to find an order that leads to small ROBDDs at runtime. Finally, we also plan to investigate the use of AIGEN for finding bugs in verification and synthesis tools.