Abstract
First-Order Linear Temporal Logic (FOLTL) is particularly convenient to specify distributed systems, in particular because of the unbounded aspect of their state space. We have recently exhibited novel decidable fragments of FOLTL which pave the way for tractable verification. However, these fragments are not expressive enough for realistic specifications. In this paper, we propose three transformations to translate a typical FOLTL specification into two of its decidable fragments. All three transformations are proved sound (the associated propositions are proved in Coq) and have a high degree of automation. To put these techniques into practice, we propose a specification language relying on FOLTL, as well as a prototype which performs the verification, relying on existing model checkers. This approach allows us to successfully verify safety and liveness properties for various specifications of distributed systems from the literature.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others

1 Introduction
Verifying properties of distributed protocols is a demanding endeavor. Several approaches have been proposed, ranging from verification frameworks, like IronFleet [12] or Verdi [27] to tool-supported languages like TLA\(^{+}\) [17], Event-B [1] or Ivy [20, 21]. However, when systems of arbitrary size are considered, verifying properties usually requires some remarkable effort: inductive invariants must be sought and exhibited (possibly with tool support), and some manual proof effort may still be necessary. Worse, when liveness properties are checked, this effort becomes very substantial and tool support is still quite limited.
A natural setting for specification, in particular for safety and liveness properties of infinite-state systems, is (mono- and many-sorted) first-order linear temporal logic (FOLTL). However, it is highly undecidable [13, 14]. In recent work [23, 24], some of the present authors devised the “Geneva” fragments of FOLTL, which were shown to be decidable. More precisely, these fragments enjoy a “bounded domain property” (BDP), a form of computable finite model property over the first-order domains. Decidability is obtained by expanding first-order quantifiers over the domains (using the computed bounds) and then relying on (decidable) propositional-LTL satisfiability checking.
The Geneva fragments are rather expressive but still have limitations that thwart their use for the specification of systems. In particular, most forms of fairness assumptions, as well as frame conditions (which specify what does not change when a transition happens in a system), do not fit in the fragments. Furthermore, topological properties of systems (such as ring topologies) are hard or even impossible to specify.
In this article, we mitigate this deficiency by exhibiting three transformations that allow to map an undecidable, expressive fragment of FOLTL\(^{*}_{=}\) (FOLTL with equality and reflexive-transitive closure, to characterize topological properties) into decidable fragments (akin to the Geneva ones), thus allowing the automatic verification of safety and liveness properties of infinite-state systems. Then we apply these techniques to the verification of properties of various protocols.
Notice that none of the proposed transformations is complete. It is actually impossible to devise complete transformations, even assuming a procedure that would be fed additional user input. This is because FOLTL is not even semi-decidable.Footnote 1
In more detail, we make the following contributions (cf. Fig. 1):
-
we define an undecidable, expressive specification language, called Cervino, the semantics of which is expressed in terms of FOLTL\(^{*}_{=}\);
-
we exhibit two fragments of many-sorted FOLTL that enjoy the BDP;
-
we devise three abstraction transformations that map (the semantics of) Cervino into one of the said two fragments:
-
the first of these transformations (called TEA) is fully automatic while the other two (TTC and TFC) must be passed additional data (in the shape of peculiar formulas);
-
these three transformations, as well as other minor ones, are implemented as tactics in a prototype tool [22];
-
the associated theorems and lemmas are also formalized and proved correct, using Coq [22];
-
-
we demonstrate our approach on several case studies that are often used as benchmarks in the literature.
This article is organized as follows: in Sect. 2, we illustrate our approach using an example (a leader election protocol). Section 3 introduces definitions as well as the two fragments used in the rest of the paper. In Sect. 4, we present basic techniques, which are used in some of our transformations. Then, in Sect. 5, we formalize the automatic TEA transformation. Section 6 and 7 present, respectively, the TFC and TTC transformations. In Sect. 8, we evaluate our approach on various protocols. Finally, we compare our results with related work in Sect. 9.
2 The Cervino Language
In this section, we present the Cervino modeling language informally. Its semantics, given in terms of many-sorted \(\mathrm {FOLTL} _{=}^*\) (\(\mathrm {FOLTL}\) with equality and reflexive-transitive closure), is formally introduced in Sect. 3.3. This language is suitable for specifying infinite-state systems. It is undecidable but we enforce some syntactic constraints anyway, in order to ease the further application of transformations mapping into decidable fragments of logic.
Cervino is illustrated in Fig. 2 using the example of a leader election protocol [6] in a ring of unbounded size. Nodes sit in a directed ring and each node has a unique ID. There is a total order on IDs. The goal of the protocol is to elect a leader (in practice, the one with the greatest ID). A node can send to its successor in the ring the IDs it knows about, the receiver keeping those that are greater than its own ID. A node is elected if it receives its own ID.
2.1 Sorts, Relations and Axioms
A Cervino specification may define sorts, (first-order) sorted relations and sorted constants. An interpretation structure for such a specification is a set of infinite traces of states. Classically, a state maps a sort to a non-empty set, a constant to an element of such a set and a relation to a set of tuples, all respecting the obvious sorting and arity constraints. The interpretation of sets and constants is rigid while that of relations is flexible.
In the example, nodes and their IDs are conflated into a single sort Node; and: an elected relation represents the set of elected nodes; a succ relation represents if two nodes are successive in the ring topology; a toSend relation represents the mailbox for each node; an lte relation defines a total ordering on nodes; an lmax constant represents the highest maximal identifier among nodes.
States can be constrained by axioms, i.e. sets of formulas. The latter belong to \(\mathrm {FOLTL} _{=}^*\), that is they can mix first-order logic (with equality) with the “always” (\(\mathbf {G}\)), “eventually” (\(\mathbf {F}\)) and “next” (written as a prime symbol and only applied to atoms), as well as a reflexive-transitive closure connective (written \(^*\)). However, we enforce a syntactic constraint on axioms: after converting them to negation normal form (NNF), an existential quantifier cannot appear in the scope of a universal quantifier or of a \(\mathbf {G}\) connective (no \(\forall \ldots \exists \ldots \), no \(\mathbf {G}\ldots \exists \ldots \)).
A binary relation r can by “tagged” (written using btw) to force r to be a functionFootnote 2 and enable a special ternary relation btw[r]. Then, btw[r](x,y,z) means that there is an acyclic path between x and z passing through y. The semantics of btw[r] is given through axioms (see Definition 14) and is related to r\(^*\) through the following equivalence: \(\mathrm{r}^*(\mathrm{x,y}) \Leftrightarrow \mathbf{btw}[\mathrm{r}](\mathbf{x,y,y})\).
2.2 Events
Events specify how the system may evolve from one state to another. Events (more precisely: event schemas) are declared with a name and a list of arguments that are the only variables that can appear free in the body of the event. The declaration of an event also features a modifies section describing which tuples of which relations may be modified by the event. Other relations or parts of relations are necessarily left unchanged. The body of an event is specified in primed FO (\(\mathrm {FO} \) augmented with primed relation symbols representing the value of these relations in the next state) with the additional constraint that no existential quantifier may appear positively in the body.
The semantics for events is standard and comparable to the one used in TLA\(^+\) or Electrum: in every state, at least one event is fired. In other words, there is a valuation for arguments of at least one event such that the body of the said event evaluates to true. More formally (and ignoring sorting constraints for the sake of readability), given event bodies \(\phi _1 , \ldots , \phi _n\) and arguments \(y_1 , \ldots , y_{m_i}\) appearing as free variables in \(\phi _i\), the semantics of event is given by the formula: \( \mathbf {G}( \bigvee \limits _{i=1}^n \exists y_1 , \ldots y_{m_i} \cdot \phi _i) \). We insist that this formula is only implicit: it cannot be input by the specifier as it is the purpose of transformations to massage it. Finally, if needed, fairness constraints must be added by the specifier .
In the example, the send event represents the fact that a node updates its successor’s mailbox by adding all IDs that are larger than the successor’s ID. This way, the largest ID is passed along the ring. Notice we use universal quantification: we could have defined dst and id as parameters of send, but the implicit existential quantification, although theoretically acceptable, can be costly performance-wise (as succ is a function, this is significant for the id argument only). We also specify that the event modifies the toSend relation for specific pairs of a node and an identifier, only if these satisfy a condition saying that the ID is in the sender’s mailbox (or corresponds to the sender’s ID) and if the node is the sender’s successor (the body of the event says what happens in that case).
2.3 Commands
A check declares a command to verify whether a property holds. To do so, a command uses a certain tactic (TEA, TFC, TTC), as well as additional parameters in the case of TFC and TTC (these are presented in Sect. 5 and 6, respectively). The purpose of this article is precisely to present these transformations. We notice that a command may also be associated with additional, specific axioms in an assuming section (in the example, this section contains a fairness property, necessary to prove the liveness property).
3 Background on \(\mathrm {FOLTL}\)
3.1 Syntax and Semantics of \(\mathrm {FOLTL}\)
The basic vocabulary of MS\(\mathrm {FOLTL}\) (that we simply call \(\mathrm {FOLTL}\) in the following) is defined out of a signature \(\varSigma = (\mathcal {S}, Const , \mathcal {R})\) where \(\mathcal {S}\) is a set of sorts, \( Const \) is the set of (sorted) constant symbols and \(\mathcal {R}= (\mathcal {R}_{\vec {s}})_{\vec {s} \in \mathcal {S}^\star }\)) is a family of sets of relation symbols, with \(\mathcal {R}_{\vec {s}}\) the set of relation symbols over tuples of sort \(\vec {s}\).
Definition 1 (Formulas)
Given a signature \(\varSigma = (\mathcal {S}, Const , \mathcal {R})\) and a set of variables \(\mathcal {V} \), \(\mathrm {FOLTL} _=\) formulas over \(\varSigma \) and \(\mathcal {V} \) are defined inductively by the following grammar:
where \(x \in \mathcal {V} _s\), \(r \in \mathcal {R}_{s_1, \ldots s_n}\) and \(t_{i} \in \mathcal {V} _{s_i} \cup Const _{s_i}\) for each i, with \(\mathcal {V} _s\) (resp. \( Const _s\)) the set of variables (resp. constants) of sort s.
\(\mathbf {X}\) and \(\mathbf {F}\) stand for the “next” and “eventually” connectives. Usually \(\mathrm {FOLTL}\) includes the \(\mathbin {\mathbf {U}}\) connectives, however it is not required in this paper. We also define “always” as \(\mathbf {G}\psi = \lnot \mathbf {F}( \lnot \psi )\). Similarly, classical propositional connectives \(\wedge \), \(\Rightarrow \) and \(\Leftrightarrow \) are defined in the natural way. Additionally:
-
We write \(\psi [x]\) for a formula \(\psi \) having x as a free variable.
-
We write \(\mathrm {FV}(\phi )\) for the set of free variables of a formula, defined in the obvious way. A formula \(\phi \) is said to be closed if \(\mathrm {FV}(\phi )=\varnothing \).
-
Classically, a formula is in negation normal form (NNF) if negations only appear in front of relation symbols.
-
If \(\mathbf{C} \) is a subset of \(\{ \mathbf {X}, \mathbf {F}, \mathbf {G}\}\) then we denote by \(\mathrm {FOLTL} _= (C)\) (resp. \(\mathrm {FOLTL} (C)\)) the set of \(\mathrm {FOLTL} _=\) formulas (resp. \(\mathrm {FOLTL} \) formulas without equality) in NNF containing only temporal operators from \(\mathbf{C} \).
-
A formula l is called literal if \(l = r(t_1, \ldots , t_n)\) or \(l = \lnot r(t_1, \ldots , t_n)\) where \(x \in \mathcal {V} \), \(r \in \mathcal {R}_{n}\) and \(t_{i} \in Const \cup \mathcal {V} \) for each i.
We now introduce the semantics of \(\mathrm {FOLTL} _=\). In the interpretation structures defined below, the interpretation of relations varies over time while that of function symbols does not.
Definition 2 (Interpretation Structure)
Given a signature \(\varSigma =(\mathcal {S}, Const , \mathcal {R})\), an (interpretation) structure \(\mathcal {M}\) (over \(\varSigma \)) is a triple \(((D_s)_{s \in \mathcal {S}}, \sigma , \rho )\) where:
-
\(D=(D_s)_{s \in \mathcal {S}}\) is a family of pairwise-disjoint nonempty sets and each \(D_s\) is the domain of the sort s.
-
\(\sigma \) maps each constant \(c \in Const _s\) to an domain element \( \sigma (c) \in D_s\).
-
\(\rho \) maps any pair \((i,r)\in \mathbb {N}\times \mathcal {R}_{s_1 \ldots s_n}\) of instant and relation to the set \(\rho (i,r)\subseteq D_{s_1} \times \ldots \times D_{s_n}\) of tuples satisfying r at instant i.
Definition 3 (Assignment)
An assignment \(\mathcal {C} \) in domains \((D_s)_{s \in \mathcal {S}}\) for variables in \(\mathcal {V} \) is a map \(\mathcal {V} \rightarrow D \). We write \(\mathcal {C} [x \mapsto d]\) the assignment defined as \(\mathcal {C} [x \mapsto d](x)=d\) and \(\mathcal {C} [x \mapsto d](y)=\mathcal {C} (y)\) if \(y \ne x\). The extension of \(\mathcal {C} \) to terms, also written \(\mathcal {C} \), is defined in the obvious way.
Definition 4 (Satisfaction)
Given a structure \(\mathcal {M}= (D, \sigma , \rho )\) and an assignment \(\mathcal {C} \), the satisfaction relation \(\vDash \) is defined by induction on formulas, for any \(i \in \mathbb {N}\), as follows:
-
\(\mathcal {M}, i, \mathcal {C} \vDash t_1 = t_2\) iff \(\mathcal {C} (t_1) = \mathcal {C} (t_2)\);
-
\(\mathcal {M}, i, \mathcal {C} \vDash r(t_1, \ldots ,t_n)\) iff \((\mathcal {C} (t_1), \ldots ,\mathcal {C} (t_n)) \in \rho _i(r)\);
-
\(\mathcal {M}, i, \mathcal {C} \vDash \lnot \phi \) iff \( \mathcal {M}, i, \mathcal {C} \nvDash \phi \);
-
\(\mathcal {M}, i, \mathcal {C} \vDash \phi _1 \vee \phi _2\) iff \(\mathcal {M}, i, \mathcal {C} \vDash \phi _1\) or \(\mathcal {M}, i, \mathcal {C} \vDash \phi _2\);
-
\(\mathcal {M}, i, \mathcal {C} \vDash \mathbf {X}\phi \) iff \( \mathcal {M}, i+1, \mathcal {C} \vDash \phi \);
-
\(\mathcal {M}, i, \mathcal {C} \vDash \mathbf {F}\phi \) iff there exists \(k \in \mathbb {N}\) s.t. \(\mathcal {M}, i+k, \mathcal {C} \vDash \phi \);
-
\(\mathcal {M}, i, \mathcal {C} \vDash \exists y : s \cdot \phi \) iff there exists \(d \in D_s\) s.t. \(\mathcal {M}, i, \mathcal {C} [y \mapsto d] \vDash \phi \);
-
\(\mathcal {M}, i, \mathcal {C} \vDash \forall x :s \cdot \phi \) iff for every \(d \in D_s\), we have \(\mathcal {M}, i, \mathcal {C} [x \mapsto d] \vDash \phi \).
Given a closed formula \(\phi \), we write \(\mathcal {M},k \vDash \phi \) if \(\mathcal {M},k,[] \vDash \phi \), where [] is the empty assignment. Then \(\mathcal {M}od(\phi )\) denotes the set of structures \(\mathcal {M}\) such that \(\mathcal {M}, 0 \vDash \phi \).
Definition 5
(Reflexive-Transitive ClosureFootnote 3). We write \(\mathrm {FOLTL} _=^*\) for the enrichment of \(\mathrm {FOLTL} _=\) with a reflexive-transitive closure connective. Then for any sort \(s \in \mathcal {S}\) and any binary relation symbol \(r \in \mathcal {R}_{s,s}\), the language of \(\mathrm {FOLTL} _=^*\) is augmented with a fresh binary relation symbol : \(r^* \in \mathcal {R}_{s,s}\), and we have:
\(\mathcal {M}, i, \mathcal {C} \vDash r^*(t_1, t_2)\) iff \(\mathcal {M}, i, \mathcal {C} \vDash t_1 = t_2\) or there exists \(n \in \mathbb {N}\) s.t. \(\mathcal {M}, i, \mathcal {C} \vDash \exists x_0, \ldots , x_n \cdot t_1 = x_0 \wedge t_2 = x_n \wedge (\bigwedge \limits _{0 \leqslant i \leqslant n-1} r(x_i, x_{i+1}) )\).
Let \(\phi , \phi '\) be two \(\mathrm {FOLTL} _=^*\) formulas. If for any structure \(\mathcal {M}\) and any assignment \(\mathcal {C} \), we have \(\mathcal {M}, 0, \mathcal {C} \vDash \phi \) iff \(\mathcal {M}, 0, \mathcal {C} \vDash \phi '\) then we say that \(\phi \) and \(\phi '\) are logically equivalent, written \(\phi \equiv \phi '\).
3.2 Bounded Domain Property
In this section we introduce the Bounded Domain Property (BDP) and present two fragments of \(\mathrm {FOLTL}\) that enjoy the BDP. These fragments play an important role in the verification procedures presented in this article.
Definition 6 (Bounded Domain Property)
A fragment \( Frag \) of \(\mathrm {FOLTL}\) enjoys the bounded domain property (BDP) if given \(\phi \in Frag \), \(\phi \) is not satisfiable, or there is a domain-finite structure \(\mathcal {M}\) s.t. \(\mathcal {M},0 \vDash \phi \) whose the domain size is computable from \(\phi \). Additionally, BDP implies decidability.
We now present the two fragments that are used in this paper. Both fragments are included in a larger fragment for which the BDP is established in [24].
Definition 7
(LTR fragment). A formula \(\phi \) of \(\mathrm {FOLTL} _= \) is said to belong to the (multisorted) Linear-Temporal Reasoning (LTR) fragment if \(\phi \) is in NNF and existential quantifiers only appear in the head of \(\phi \).
Theorem 1
([16, 24]). Any formula \(\phi \in \textsf {LTR} \) (even with equality) enjoys the BDP. The bound of verification for each sort is the sum of the numbers of existential quantifiers and constant symbols over this sort.
Definition 8
An \(\mathrm {FOLTL}\) formula \(\psi \) is in \({\mathrm {FOLTL}}( {\exists \!\! \uparrow } , {\forall \!\! \downarrow } ) \) if \(\psi = \exists y_1 : s_1 \ldots y_n : s_n \cdot \theta [y_1, \ldots , y_n]\), where \(\theta \) has the following syntax: \( \theta {:}{:}= \ell \mid \alpha \mid \theta \vee \theta \mid \theta \wedge \theta \mid \mathbf {X}\theta \mid \mathbf {G}\theta \mid \mathbf {F}\theta \), where \(\alpha \) is an FO formula in NNF without any existential quantifier and \(\ell \) is a literal.
Definition 9
\({\mathrm {FOLTL}}({\mathbf {X}},{\mathbf {F}}, {\forall \!\! \downarrow } ) \) is defined by the following grammar: \( \phi {:}{:}= \ell \mid \alpha \mid \phi \vee \phi \mid \phi \wedge \phi \mid \mathbf {X}\phi \mid \mathbf {F}\phi \mid \exists y :s \cdot \phi \), with \(\alpha \) an FO formula in NNF without any existential quantifier, \(\ell \) a literal and \(y \in \mathcal {V} \).
Definition 10
(Geneva fragment). The \(\textsf {Geneva} \) fragment of \(\mathrm {FOLTL} \) consists of formulas \(\psi \wedge \mathbf {G}(\phi )\) s.t. \(\phi \) is a closed formula of \({\mathrm {FOLTL}}({\mathbf {X}},{\mathbf {F}}, {\forall \!\! \downarrow } ) \) and \(\psi \) is a closed formula of \({\mathrm {FOLTL}}( {\exists \!\! \uparrow } , {\forall \!\! \downarrow } ) \).
Definition 11
Given a formula \(\phi \in \mathrm {FOLTL} (\mathbf {X}, \mathbf {F})\) in NNF, we define its stride \(K_\phi \) as the maximal number of nested \(\mathbf {X}\) connectives. Formally :
Theorem 2
([24]). The \(\textsf {Geneva} \) fragment enjoys the FDP. If \(\psi \wedge \mathbf {G}(\phi )\) is a satisfiable formula in this fragment, for each sort s the (exact) bound on the domain size is: \(| Const _s|+ (K_\phi +1 ) \times |\mathcal {V} _s |\).
3.3 Semantics of Cervino
In this section, we define the semantics of a Cervino machine as an \(\mathrm {FOLTL} _=^*\) formula. Notice first that, in Cervino, the next instant is referred using the prime symbol, applied to relations only: this translates to an \(\mathrm {FOLTL}\) sub-formula using the \(\mathbf {X}\) connective, after application of the semantics.
Now, a frame condition is defined as a formula that specifies that a certain relation will not change (between the instant before and after the event occuring) for tuples satisfying some constraints.
Definition 12 (Frame condition)
We define a frame condition as a formula expressing that, under some hypotheses, a certain relation does not change along a transition. Given the the tuple \((r , \vec {x} , \psi )\) where \(r \in \mathcal {R}_{\vec {s}}\) , \(\vec {x} \in \mathcal {V} ^{\mid \vec {s} \mid }\) , \(\psi \) is a Boolean formula, where variables in \(\vec {x}\) may appear free, we define the frame condition \(\textsf {unchanged}[r , \vec {x}, \psi ]\) as the formula \(\forall \vec {x} : \vec {s} \cdot \psi \Rightarrow ( r(\vec {x}) \Leftrightarrow \mathbf {X}r(\vec {x}))\).
Definition 13 (Semantics of an event)
Let ev be an event of a Cervino machine declared as follows:
 , with modif = modifies \(q_1\) at \(\{(\vec {x}_1) \cdot \psi _1\}, \ldots , q_j\) at \(\{(\vec {x}_j) \cdot \psi _j\}\), where the free variables in each \(\psi _k\) are included in \(\vec {x_k}, \vec {y}\). Its semantics is defined as
, with modif = modifies \(q_1\) at \(\{(\vec {x}_1) \cdot \psi _1\}, \ldots , q_j\) at \(\{(\vec {x}_j) \cdot \psi _j\}\), where the free variables in each \(\psi _k\) are included in \(\vec {x_k}, \vec {y}\). Its semantics is defined as
 , where
, where

where each list \(\vec {x}\) of variables have sorts corresponding to the profile of r.
For any binary relation r that enables btw[r], the ternary relation btw[r] stating that there exists an acyclic path between two elements passing through a third element is axiomatized in FO following [18].
Definition 14 (Semantics of between)
Given a binary relation symbol r, the semantics of btw[r] is given by adding axioms of transitivity, antisymmetry, partial totality, partial reflexivity, cycle maximality, transitivity of reachability, path consistency, taken from [18] in addition to the following axiom:

The property (TC) relating btw[r] and r\(^*\) can be deduced from the axioms provided that the domain of s is finite.

Then, calling \(\textsc {btw}\) the conjunction of all between axioms,
 .
.
Definition 15 (Semantics of Cervino)
Let \(\textit{Mch}\) be a Cervino machine with axioms \(\psi _1, \ldots , \psi _n \), events \(ev_1, \ldots ,ev_m\) and such that the relations enabling btw are \(r_1, \ldots , r_l\). Then its semantics is given by the following \(\mathrm {FOLTL} ^*\) formula:

where \(\phi _0= \bigwedge \limits _{i=1}^n \psi _i\), \(\phi _{tr}= \bigvee \limits _{i=1}^m [\![\textit{ev}_i]\!]\) and

The semantics of a Cervino machine is then an \(\mathrm {FOLTL} _=^*\) formula describing the set of its traces. But, since we aim at verifying systems, we are not only interested in the set of traces but also in the set of counterexamples of a property. This set is also described by an \(\mathrm {FOLTL} _=^*\) formula which is the conjunction of the semantics of the machine and the negation of the property we aim to check.
Definition 16 (Counterexamples)
If \(\textit{Mch}\) is a Cervino machine and \(\phi \) is an \(\mathrm {FOLTL} _=^*\) formula. Then we define \([\![\textit{Mch}]\!]_\phi = [\![\textit{Mch}]\!] \wedge [\![\lnot \phi ]\!]\)
4 Basic Transformations
In this section, we present basic transformations used to build the more complex TFC and TTC tactics (respectively presented in Sect. 6 and 7). These transformations are used to map (the semantics of) a system specification into a more general \(\textsf {Geneva} \) formula.
4.1 Transforming Equality
Equality is replacedFootnote 4 by a dynamic congruence relation \(\equiv _s\), for every sort s. The signature is therefore extended with these fresh \(\equiv _s\) relations.
Definition 17 (Equality transformation)
Given a fresh binary relation \(\equiv _s\) for every sort s of a formula, the transformation of equality is defined recursively:
-
\(\textit{Abs}_{=}(t_1 = t_2) = t_1 \equiv _s t_2\) if the sort of \(t_1\) (and necessarily of \(t_2\)) is s
-
\(\textit{Abs}_{=}(\ell ) = \ell \)
-
(the rest is just a recursive walk on formulas)
Furthermore, the following set \(\mathbf{Eq} _{\equiv }\) of axioms is added to the whole specification:
-
for any sort s: \(\mathbf {G}\forall x:s \cdot x \equiv _s x\)
-
for any sort s: \(\mathbf {G}\forall x:s,y:s \cdot x \equiv _s y \Rightarrow y \equiv _s x\)
-
for any sort s: \(\mathbf {G}\forall x:s,y:s,z:s \cdot x \equiv _s y \wedge y \equiv _s z \Rightarrow x \equiv _s z\)
-
for any relation r and adequate sorts \(\vec {s}\) conforming to the profile of r:\(\mathbf {G}\,\forall \vec {x}:\vec {s}, \vec {y}:\vec {s} \cdot (x_1 \equiv _{s_1} y_1 \wedge \ldots \wedge x_n \equiv _{s_n} y_n) \Rightarrow (r(\vec {x}) \Leftrightarrow r(\vec {y})) \)
Lemma 1
Given an \(\mathrm {FOLTL} _=\) formula \(\phi \), if \(\phi \) is satisfiable then \(\textit{Abs}_{=}(\phi )\) is satisfiable (and does contain \(=\) anymore).
Proof
Proof validated in Coq. It is easy to see that equality is a particular case of the equivalence relation introduced by this transformation. \(\square \)
4.2 Restricted Skolemization
The following transformation corresponds to a form of Skolemization meant to create only new constants symbols. Its main purpose is to introduce constants that can then be used by instantiation (Sect. 4.3). Existentially-quantified variables can be substituted by fresh constants, except when under a \(\mathbf {G}\) connective.
Definition 18 (Skolemization)
Skolemization is defined by the following operation (all fresh constant symbols are added to the signature):
-
\(\textit{Abs}_{\exists }(t_1 = t_2) = t_1 = t_2\) and \(\textit{Abs}_{\exists }(\ell ) = \ell \)
-
\(\textit{Abs}_{\exists }(\mathbf {G}\phi ) = \mathbf {G}\phi \)
-
\(\textit{Abs}_{\exists }(\forall x:s \cdot \phi ) = \forall x:s \cdot \phi \)
-
\(\textit{Abs}_{\exists }(\exists y:s \cdot \phi ) = \textit{Abs}_{\exists }(\phi [y \mapsto c])\) where c is a fresh constant symbol
-
(the rest is just a recursive walk on formulas)
Lemma 2
Given an \(\mathrm {FOLTL} _=\) formula \(\phi \), then \(\textit{Abs}_{\exists }(\phi )\) and \(\phi \) are equisatisfiable.
Proof
Proof validated in Coq. Corresponds to a usual Skolemization procedure. \(\square \)
4.3 Instantiation
One of the main limitations of the \(\textsf {Geneva} \) fragment is the prohibition of temporal operators under universal quantifiers. The solution we propose to this problem is to finitely instantiate such universal quantifiers. The following transformation formalizes this idea: all universal quantifiers over temporal formulas are replaced by a conjunction over the set of constants and existentially-bound variables.
Definition 19 (Forall instantiation)
Given a set \(\mathcal {I}\) of constant and variable symbols, we define the transformation of universal quantifiers as follows:
-
\(\textit{Abs}_{\forall , \mathcal {I}}(t_1 = t_2) = t_1 = t_2\) and \(\textit{Abs}_{\forall , \mathcal {I}}(\ell ) = \ell \)
-
\(\textit{Abs}_{\forall , \mathcal {I}}(\exists y:s \cdot \phi ) = \exists y:s \cdot \textit{Abs}_{\forall , \mathcal {I}\cup \{ y \}}(\phi )\)
-
if \(\phi \in \mathrm {FO} \) (\(\phi \) does not contain temporal connectives) then \(\textit{Abs}_{\forall , \mathcal {I}}(\forall x:s \cdot \phi ) = \forall x:s \cdot \phi \), otherwise \(\textit{Abs}_{\forall , \mathcal {I}}(\forall x:s \cdot \phi ) = \bigwedge \limits _{c \in \mathcal {I}_s} \textit{Abs}_{\forall , \mathcal {I}}(\phi [x \mapsto c])\) (where \(\mathcal {I}_s\) is the set of terms in \(\mathcal {I}\) of sort s)
-
(the rest is just a recursive walk on formulas)
Remark 1
There is no need to transform a universal quantifier if all temporal operators in its scope permute with it, for instance: \(\forall x \cdot \mathbf {G}P \) is equivalent to \( \mathbf {G}(\forall x \cdot P)\) and \(\forall x \cdot (\mathbf {X}P) \Rightarrow (\mathbf {X}Q) \) is equivalent to \( \mathbf {X}(\forall x \cdot P \Rightarrow Q)\).
Lemma 3
Given an \(\mathrm {FOLTL} _=\) formula \(\phi \), if \(\phi \) is satisfiable and \(\mathcal {I}\subseteq Const \) then \(\textit{Abs}_{\forall , \mathcal {I}}(\phi )\) is satisfiable.
Proof
Proof validated in Coq. This operation consists in instantiating universal operators, thus preserving satisfiability. \(\square \)
4.4 Addressing Transitive Closure and the Between Relation
Since we target fragments of \(\mathrm {FOLTL}\) (without transitive closure), we define the transformation \(\textit{Abs}_{*}()\), which leaves a formula unchanged except it uninterprets the operator \(^*\), i.e., \(\textit{Abs}_{*}(\phi )\) returns \(\phi \) where every occurrence of \({r}^*\) is considered as a new relation symbol, unrelated with r.
Besides, the between relation axioms does not fit into \(\textsf {Geneva} \) or LTR, so we define their abstract semantics as follows.
Definition 20 (Transformation of between axioms)
Given a binary relation symbol r, we define
 where \(\textsc {btw}\) is the conjunction of the axioms from Definition 14, except that
where \(\textsc {btw}\) is the conjunction of the axioms from Definition 14, except that
-
the axiom S is replaced by the axiom (AS) (in order to prevent existential quantifier in the scope of a universal one)
-
and the property (TC) relating r\(^*\) and btw[r] is now considered as an axiom (since r\(^*\) has no semantics in the targeted \(\mathrm {FOLTL}\) fragments)


4.5 Geneva Transformation
The basic transformations introduced above are mainly used together, in a specific order.
Definition 21
(Geneva Transformation). We define:
Theorem 3
Given \(\psi \in {\mathrm {FOLTL}}_{\vec {y}_1}(\forall ) \) and \(\phi \in {\mathrm {FOLTL}}_{\vec {y}_1 \cup \vec {y}_2}({\mathbf {X}},{\mathbf {F}}, \forall ) \) then \(\textit{Abs}_{Gen}(\exists \vec {y}_1 : \vec {s_1} \cdot (\psi \wedge \mathbf {G}(\exists \vec {y}_2 : \vec {s_2} \cdot \phi )))\) belongs to the \(\textsf {Geneva} \) fragment.
Proof
Recall the conditions to belong to Geneva: (1) no \(\mathbf {G}\) operator in the scope of an existential quantifier that is itself under an \(\mathbf {G}\) connective; (2) no existential quantifier in the scope of a universal quantifier; (3) no equality; (4) no temporal quantifier in the scope of universal quantifiers; and (5) no transitive closure. Given \(\psi , \phi \) satisfying the given hypotheses, let us write \(\alpha = \exists \vec {y}_1 : \vec {s_1} \cdot (\psi \wedge \mathbf {G}(\exists \vec {y}_2 : \vec {s_2} \cdot \phi ))\). Then, in \(\alpha \), existential quantifiers appear either at the head of the formula or under an \(\mathbf {G}\) operator over the \(\phi \) formula. Since \(\phi \) contains no other temporal connectives than \(\mathbf {X}\) and \(\mathbf {F}\), condition (1) is met. Condition (2) is met as all existential quantifiers appear before universal quantifiers. \(\textit{Abs}_{=}(.)\) ensures that equality is not used in the final formula, thus ensuring condition (3). \(\textit{Abs}_{\forall , Const }(.)\) instantiates all universal quantifiers that contain temporal connectives in their scope (we assume that if such operator could have been swapped with an universal quantifier, it has been done beforehand), which ensures condition (4). Finally \(\textit{Abs}_{*}(.)\) erases the reflexive transitive closure, ensuring condition (5). Since it is obvious that none of the transformations can introduce formulas breaking any of the conditions, we conclude that \(\textit{Abs}_{Gen}(\alpha )\) belongs to Geneva. \(\square \)
5 TEA: Transforming Existential Quantifiers
We now present the fully-automatic TEA transformation. It starts with the observation that the formula specifying events (see Definition 13) is of the shape \(\mathbf {G}\exists \vec {x} \cdot \bigvee _{\!i} \textit{ev}_i(\vec {x})\), that is, in every state, at least an event is fired. The gist of the TEA transformation is then twofold: (1) we replace these existential quantifiers by universal ones; (2) for every such existential quantifier, we add a fresh relation \(\mathbb {E}\), which holds only for the constant semantically associated to this quantifier.
The whole resulting abstract specification lies in the LTR fragment, which enjoys the BDP (Theorem 1). The formula specifying events is however more general than the original one, because it allows more transitions to happen. The abstract system may thus violate a property holding on the original specification. But it is now decidable to check whether the property holds in the abstract system and, if so, this entails that it also holds in the original system.
Before presenting the transformation, notice that, in the following, we consider event formulas, that is primed \(\mathrm {FO} _{=}\) formulas of the shape \(\phi = \exists y_1 : s_{y_1}, \ldots , y_n : s_{y_n} \cdot \forall x_1 : s_{x_1},\ldots , x_m : s_{x_m} \cdot \psi \), where \(\psi \) is in NNF and does not contain any first-order quantifiers. These formulas naturally arise when putting the semantics of events in prenex normal form. We also suppose we have a supply of fresh relation symbols, written \(\mathbb {E}_i\) (one for every \(y_i\), \(1\leqslant i\leqslant n\)).
To devise the transformation and prove its soundness, we first introduce a formula specifying that the \(\mathbb {E}\) relations are functional. This schema appears in the final abstract specification.
Definition 22
(Functional \(\mathbb {E}\) relations). Given an event formula \(\phi = \exists y_1 : s_{y_1}, \ldots , y_n : s_{y_n} \cdot \forall x_1 : s_{x_1},\ldots , x_m : s_{x_m} \cdot \psi \), we define the functional formula based on \(\phi \) as:  where \(\mathbb {E}_1, \ldots , \mathbb {E}_n\) are fresh unary relation symbols.
where \(\mathbb {E}_1, \ldots , \mathbb {E}_n\) are fresh unary relation symbols.
As we introduce these \(\mathbb {E}\) relations, we also define an enrichment of the event formula accounting for the extended signature. This new formula appears as a link between the two lemmas entailing soundness.
Definition 23 (Enriched event formula)
Given an event formula \(\phi = \exists y_1 : s_{y_1}, \ldots , y_n : s_{y_n} \cdot \forall x_1 : s_{x_1},\ldots , x_m : s_{x_m} \cdot \psi \), we define the enriched event formula based on \(\phi \) as:

where \(\mathbb {E}_1, \ldots , \mathbb {E}_n\) are fresh unary relation symbols.
We now present the essential part of the transformation, transforming an event formula \(\phi \) into a purely universal one  , more general than \(\overline{ \phi }\). In other words,
, more general than \(\overline{ \phi }\). In other words,  allows more transitions than \(\phi \) if we ignore the specification of \(\mathbb {E}_1 , \ldots \mathbb {E}_n\). To do that, for any variable y whose corresponding fresh relation is \(\mathbb {E}\), we proceed with the following steps. First: equality between y and another variable is replaced with the relation \(\mathbb {E}\) applied to the latter; and any other literal \(\ell \) containing y is replaced by \(\mathbb {E}(y) \Rightarrow \ell \). Once these transformation are done, it is possible to replace existential quantification over y by a universal quantification.
allows more transitions than \(\phi \) if we ignore the specification of \(\mathbb {E}_1 , \ldots \mathbb {E}_n\). To do that, for any variable y whose corresponding fresh relation is \(\mathbb {E}\), we proceed with the following steps. First: equality between y and another variable is replaced with the relation \(\mathbb {E}\) applied to the latter; and any other literal \(\ell \) containing y is replaced by \(\mathbb {E}(y) \Rightarrow \ell \). Once these transformation are done, it is possible to replace existential quantification over y by a universal quantification.
Definition 24 (Transformation)
Given an event formula \(\phi \) of shape \( \exists y_1 : s_{y_1}, \ldots , y_n : s_{y_n} \cdot \forall x_1 : s_{x_1},\ldots , x_m : s_{x_m} \cdot \psi \), we define the (TEA) transformation function on \(\phi \) as:

where \(\vec {y}= \{ y_1, \ldots , y_n \}\) and where \(\mathbb {E}_1,\ldots ,\mathbb {E}_n\) are fresh relation symbols (one for every \(y \in \vec {y}\)); with  defined recursively as follows:
defined recursively as follows:
-

-

-
 where \(d \not \in \vec {y}\) (d is either a constant or a variable in \(\vec {x}\))
where \(d \not \in \vec {y}\) (d is either a constant or a variable in \(\vec {x}\)) -
 where \(d \not \in \vec {y}\) (d is either a constant or a variable in \(\vec {x}\))
where \(d \not \in \vec {y}\) (d is either a constant or a variable in \(\vec {x}\)) -
 where \(\ell \) is a (possibly primed) literal and \(\{ y_{a_1} , \ldots y_{a_i} \} = \mathrm {FV}(\ell ) \cap \vec {y}\)
where \(\ell \) is a (possibly primed) literal and \(\{ y_{a_1} , \ldots y_{a_i} \} = \mathrm {FV}(\ell ) \cap \vec {y}\) -
(the rest is just a recursive walk on formulas)
Example 1
Consider the following event formula, stating that there is an event making R true in the next state for a variable y (other variables remain unchanged w.r.t. R): \( \phi = \exists y : A \cdot R'(y) \wedge (\forall x : A \cdot x \ne y \Rightarrow (R(x) \Leftrightarrow R'(x))) \) that is, in prenex form: \( \exists y : A \cdot \forall x : A \cdot R'(y) \wedge ( x = y \vee (\lnot R(x) \wedge \lnot R'(x)) \vee (R(x) \wedge R'(x))) \). Then there is only one fresh \(\mathbb {E}\) relation, and  is:
is:

Now, the following lemma states that every model of the enriched event formula is also a model for the transformed event formula.
Lemma 4
Given an event formula \(\phi = \exists y_1 : s_{y_1}, \ldots , y_n : s_{y_n} \cdot \forall x_1 : s_{x_1},\ldots , x_m : s_{x_m} \cdot \psi \), we have  .
.
Proof
Proof validated in Coq.
Lemma 5 applies to a formula representing a whole specification: if such a specification is satisfiable, then a certain transformed version of it is satisfiable too.
Lemma 5
Let \(\theta \) be an \(\mathrm {FOLTL} _=\) formula, and \(\phi \) be an event formula on the same signature. Then if \(\theta \wedge \mathbf {G}\phi \) is satisfiable,  is also satisfiable.
is also satisfiable.
Proof
Proof validated in Coq.
Definition 25 (Abstract semantics)
Given a Cervino machine \(\textit{Mch}\) such that the relations enabling btw are \({r}_1, \ldots , {r}_l\), we define
 , where \(\phi _0\) and \(\phi _{tr}\) are defined as in Definition 15 and
, where \(\phi _0\) and \(\phi _{tr}\) are defined as in Definition 15 and
 . Also, given an \(\mathrm {FOLTL} _=\) formula \(\phi \), we define
. Also, given an \(\mathrm {FOLTL} _=\) formula \(\phi \), we define  .
.
Theorem 4 (Soundness)
If \([\![\textit{Mch}]\!]_\phi \) is satisfiable, then  is also satisfiable.
is also satisfiable.
Proof
This is a direct application of Lemma 5.
Theorem 5
Given a Cervino machine \(\textit{Mch}\) such that \(\phi _0\) and \(\phi _{tr}\) are defined as in Definition 15, if \(\phi _0, \phi \in \textsf {LTR} \) then  .
.
Proof
Directly follows from the definition of  .
.
6 TFC: Transforming Frame Conditions
The TEA transformation has the advantage of being fully automatic but it can be inconclusive in a number of cases. For instance, the verification of a distributed system involving strong interactions between its components, which induces events with two or more parameters, is likely to be inconclusive using TEA. This is because the universal quantifiers that are introduced by TEA are abstracting these interactions (which are naturally expressed with existential quantifiers) in a too drastic way.
In this section, we present another transformation, called TFC, which overcomes these limitations but requires some intervention from the specifier.
Instead of targeting the LTR fragment, we now target the Geneva one, which allows for existential quantifiers in the scope of \(\mathbf {G}\), but forbids temporal formulas in the scope of a universal quantifier. As a consequence, frame conditions, which are typically of shape \(\forall x:s \cdot \varphi _{cond} \Rightarrow (r(x) \Leftrightarrow \mathbf {X}r(x))\), are not expressible in Geneva. In order to fit into it, such universal quantifiers are instantiated over constants (see \(\textit{Abs}_{\forall , Const }(\cdot )\) defined in Sect. 4.3). But then a large part of the information included in the frame conditions is lost. Therefore, we associate some particular kind of invariant properties, called stability axioms, with each event, as a finer transformation of frame conditions. Intuitively, a stability axiom is a pure FO formula that is preserved by an event. Since it is expressed in pure FO, the preservation of a stability axiom is then expressible in Geneva.
Definition 26 (Stability Axiom)
Given a set of frame conditions \(\mathcal {C} \), an \(\mathrm {FO} \) formula \(\phi \) is a stability axiom for \(\mathcal {C} \) if \(\mathcal {C} \vDash \phi \Rightarrow \mathbf {X}\phi \).
\(\mathrm {St}_{\mathcal {C}}\) denotes the set of stability axioms for \(\mathcal {C} \).
The specification of stability axioms is a creative step, but it can be eased with the help of a syntactic condition, which is sufficient to be a stability axiom. The idea is that a formula of the following shape is necessarily a stability axiom: \(\varphi _\text {hyp} \Rightarrow \varphi \), were \(\varphi _\text {hyp}\) corresponds to the guard of a frame condition that leaves a relation r unchanged, and \(\varphi \) only refers to the relation r.
Example 2
In order to illustrate the use of stability axioms, let us consider the leader election distributed system, introduced in Sect. 2. Since TEA does not succeed in proving the safety property, we can try TFC with the following stability axiom for event send:

This axiom expresses that if a node x different from the successor of src has an ID y in its mailbox, then the node with the greatest ID is located between x and y (recall that a node and its ID are conflated). This means that outside the scope of the event, an ID cannot jump over the node with the greatest identifier.
Exhibiting this stability axiom requires some work. It would also be possible to proceed using an inductive invariant but, since the property to check is not inductive, doing so would also require some effort.
Example 3
In order to illustrate the difference between stability axioms and inductive invariants, we take a toy token protocol as an example. For the sake of simplicity, we consider a property to check that is already inductive. The protocol features one token passing from nodes to nodes with only one send event send(x,y), with body:
 , where
, where
 .
.
The (inductive) property to check is that there is always at most one node holding the token. To prove this property without relying on its inductiveness, we can use the following stability axiom:
 . Contrary to the inductive invariant, the stability axiom has free variables matching the parameters of the event (which are implicitly quantified existentially). Also the preservation of the stability axiom follows from the frame condition as \(\mathrm{frame} \vDash \mathrm{stab} \Rightarrow \mathbf {X}\mathrm{stab}\), while the preservation of the inductive invariant follows from the whole transition.
. Contrary to the inductive invariant, the stability axiom has free variables matching the parameters of the event (which are implicitly quantified existentially). Also the preservation of the stability axiom follows from the frame condition as \(\mathrm{frame} \vDash \mathrm{stab} \Rightarrow \mathbf {X}\mathrm{stab}\), while the preservation of the inductive invariant follows from the whole transition.
Remark 2
Notice that this property is also true for the nodes that are in the scope of the event, i.e., src and its successor. So in this case, the stability axiom is very close to an invariant property. But this is not the case in general. A distinguishing aspect is that TFC with this stability axiom succeeds in proving the safety property, whereas it would not be possible to deduce it from the “invariant” version of this stability axiom.
The TFC transformation is performed in two phases:
-
1.
Stability axioms, which are provided by the specifier, are added to the body of each event. At this step, the semantics of Cervino is strengthened by the transformation. The obtained formula is not in the Geneva fragment, in particular because of the frame conditions.
-
2.
The Geneva transformation, which is presented in Sect. 4, is applied. In particular, the frame conditions are abstracted by equality transformation and instantiation, but the stability axioms are left unchanged.
Definition 27 (Event enrichment with a stability axiom)
Let ev be an event of a Cervino machine declared as:
 and \(\mathcal {C} \) be the frame condition of ev,
and \(\mathcal {C} \) be the frame condition of ev,
 . Given a stability axiom \(\mathcal {I}\) for \(\mathcal {C} \), we define the enrichment
. Given a stability axiom \(\mathcal {I}\) for \(\mathcal {C} \), we define the enrichment
 of ev with \(\mathcal {I}\) as:
of ev with \(\mathcal {I}\) as:  .
.
Definition 28 (Cervino machine enrichment with stability axioms)
Let \(\textit{Mch}\) be a Cervino machine with axioms \(\psi _1, \ldots , \psi _n \), events \(ev_1, \ldots , ev_m\) declared as
 for each \(i\in 1..m\) and such that the relations enabling
for each \(i\in 1..m\) and such that the relations enabling
 are \(r_1, \ldots , r_l\). Let \(\mathsf {sta}\) be a function mapping each event to a stability axiom for the according frame condition. Using the same notation as Definition 27, we define the stability axiom enrichment
are \(r_1, \ldots , r_l\). Let \(\mathsf {sta}\) be a function mapping each event to a stability axiom for the according frame condition. Using the same notation as Definition 27, we define the stability axiom enrichment  of \(\textit{Mch}\) as
of \(\textit{Mch}\) as

where \(\phi _0= \bigwedge \limits _{i=1}^n \psi _i\),  and
and
 .
.
Definition 29 (Abstract semantics)
Given a Cervino machine \(\textit{Mch}\) and a function \(\mathsf {sta} \), mapping each event to a stability axiom, we define the stability axiom semantics as 
Theorem 6 (Soundness)
If \([\![\textit{Mch}]\!]_\phi \) is satisfiable then  is satisfiable.
is satisfiable.
Proof
Follows from Lemmas 1, 2 and 3.
Theorem 7
If \( \lnot \phi \in \textsf {LTR} \) then  .
.
Proof
Follows from Theorem 3.
7 TTC: Transforming Reflexive-Transitive Closure
We now present a simple, effective transformation technique to approximate reflexive-transitive closure (which is present in Cervino and its \(\mathrm {FOLTL} _=^*\) semantics). This technique has shown to be useful to prove some liveness properties.
As is well known, transitive closure cannot be fully specified in pure \(\mathrm {FO} \). On the other hand, it can be specified in pure \(\mathrm {FOLTL} \), but the axiomatization we are aware of does not fit in the fragments considered here. However, it is possible to define an interesting approximation that does fit in the Geneva fragment.
Informally, the crux of our technique relies on the following observation: any property propagating along a binary relation will eventually propagate to the reflexive-transitive closure thereof. This is proved (see Theorem 8 below) by following the definitions of the transitive closure and of the eventually connective.
Definition 30 (Propagation schema)
Given binary relations \(\mathbf{r} \) and \(\mathbf{t} \) on a sort s, given a formula P with \(k+1\) free variables (\(k \geqslant 0\)), the first of which (of sort s) is distinguished in the following. Given k variables \(\vec {x}\) of appropriate typing, we define the propagation and closure schemas as follows:
Theorem 8 (Propagation)
Given a binary relations \(\mathbf{r} \) on a sort s, the following property over its reflexive-transitive \(\mathbf{r} ^\star \) closure is valid: \( \mathbf{Closure} [\mathbf{r} , \mathbf{r} ^\star , P, \vec {x}]\).
Proof
Proof validated in Coq.
The proof sketch is the following : we consider the set of element to which the property eventually propagates. Then we use the hypothesis that the property propagates along a binary relation r to show that this set is closed under the relation r. Then as the transitive closure from some element is the smallest set closed under the relation r, we know that the property propagates to any element in the transitive closure.
We prove that under the \(\mathbf{Propagates} [\mathbf{r} , P, \vec {x}]\) hypothesis, for any u, the set of v’s satisfying \(\mathbf {G}\left( P[u, \vec {x}] \Rightarrow \mathbf {F}P[v, \vec {x}]\right) \) is included in the set of v’s that are reachable from u along \(\mathbf{r} \). Let \(\mathcal {M}\) be a structure and \(\mathcal {C} \) an assignment s.t. \(\mathcal {M}, \mathcal {C} \vDash \mathbf{Propagates} [\mathbf{r} , P, \vec {x}]\). We assume that there is an instant i such that \(P[u, \vec {x}]\) holds (otherwise the satisfaction of the axiom is trivial). Then \(\mathcal {M}, i, \mathcal {C} \vDash \mathbf {F}P[u, \vec {x}]\). Also, given v s.t. \(\mathcal {M}, i, \mathcal {C} \vDash \mathbf {F}P[v, \vec {x}]\), there exists \(k \geqslant i\) s.t. \(\mathcal {M}, k, \mathcal {C} \vDash P[v, \vec {x}]\). For any \(v'\) s.t. \(\mathcal {M}, 0, \mathcal {C} \vDash \mathbf{r} (v,v')\) \(\mathbf{Propagates} [\mathbf{r} , P, \vec {x}]\) implies \(\mathcal {M}, k, \mathcal {C} \vDash \mathbf {F}P[v', \vec {x}]\). Thus \(\mathcal {M}, i, \mathcal {C} \vDash P[v', \vec {x}]\). Then \(\mathcal {M}, 0, \mathcal {C} \vDash \mathbf{r} ^\star (u,v)\) implies \(\mathcal {M}, i, \mathcal {C} \vDash \mathbf {F}P[v, \vec {x}]\). Hence \(\mathbf{Closure} [\mathbf{r} , \mathbf{r} ^\star , P, \vec {x}]\) is valid. \(\square \)
Given this theorem, the technique we propose consists in replacing the reflexive-transitive closure of a relation (which fits in Cervino and \(\mathrm {FOLTL} _=^*\)) by an uninterpreted relation satisfying the closure schema shown above, for some property P that depends on the sort of the considered binary relation as well as, possibly, other arguments. Remark that finding such a property P requires creativity: the specifier must come up with a relevant propagating property.
Example 4
In the case of the leader election example, we use TTC to check that a leader will be elected at some point. The property we use is propagation along succ of having a given ID in one’s mailbox (\(\mathbf{Propagates} [ succ , toSend , id ]\)).
Definition 31 (Abstract semantics)
Let \(\textit{Mch}\) be a Cervino machine, such that \(r_{j_1}, \ldots , r_{j_l}\) are binary relations enabling btw, and \(r_{k_1}, \ldots , r_{k_m}\) are binary relations whose reflexive-transitive closure is used in \(\textit{Mch}\). Now, given formulas \(P_1 , \ldots , P_\ell \), where for every \(1\leqslant i\leqslant m\), \(\mathrm {FV}(P_i) = \{ x, x_1, \ldots , x_{n_i} \}\) (with x the distinguished free variable), we define the transitive closure transformation as:

where \(\phi _0\) and \(\phi _{tr}\) are defined as in Definition 15 and
 .
.
We also define  (notice that, due to the application of the Geneva transformation, the \(r_i^*\) relations become uninterpreted).
(notice that, due to the application of the Geneva transformation, the \(r_i^*\) relations become uninterpreted).
Theorem 9 (Soundness)
If \([\![\textit{Mch}]\!]_\phi \) is satisfiable then  is satisfiable.
is satisfiable.
Proof
Follows directly from Theorem 8 and Lemmas 1, 2 and 3.
Theorem 10
If \( \lnot \phi \in \textsf {LTR} \) then  .
.
Proof
Follows from Theorem 3.
8 Evaluation
To evaluate the relevance of our three tactics, we applied them to several models of distributed protocols. Our research questions were (1) to check that our methods were applicable to real models; (2) to check whether our approach was efficient enough; and (3) to assess the effort for the specifier to come up with parameters for TFC and TTC. Our strategy was always first to apply the TEA tactic. If TEA failed, then in the case of safety properties, we devised stability axioms in order to apply TFC. Otherwise, for liveness properties and for systems relying on transitive closure, we relied on TTC.
The Cervino prototype takes a Cervino specification as input and generates Electrum models which are then fed to the Electrum Analyzer [4], which itself calls a complete procedure in nuXmv [5]. On a general note, efficiency can be compromised in the case of the TTC and TFC tactics due to larger inferred bounds than for TEA. Furthermore, the size of LTL formulas generated by Electrum for nuXmv grows quickly as the tool merely unfolds quantifiers into conjunction and disjunctions, depending on the bounds. For this reason, we leveraged some properties of the Geneva fragment to end up with smaller models: (1) the size of each domain is an exact bound rather than just an upper one; (2) all constants are distinct; (3) existential quantifiers can be unfolded on a limited part of the domain. This is the case because the proof of the BDP for the Geneva fragment [24] shows that, if there is a model of a Geneva formula, there is a model satisfying these properties. The specifications we evaluated are of moderate complexity but are not just toy models:
-
TLB shootdown The TLB Shootdown algorithm [3] is part of the Mach operating system. Processors keep a cache of page tables in a Translation Look-aside Buffer (TLB). The safety property we prove is that whenever the protocol ensures that the page table is updated, the corresponding update will be flushed by either the initiator or the responder.
-
Dining philosophers This classic protocol features an unbounded number of philosophers sharing forks. We prove a mutual exclusion property, that is that a fork cannot be simultaneously held by two different philosophers.
-
Lock server We present a simple lock server protocol studied in Verdi [27] and Ivy [21]. The protocol features a single server and an unbounded number of clients willing to hold a lock. The safety property we verify is that two different clients cannot simultaneously hold the lock.
-
Gset and 2Pset Conflict-free Replicated Data Types (CRDTs) are a family of concurrent protocols where a data structure is replicated in a network and where the replicas can be independently and concurrently updated. We model the Grow-only Set (G-Set) [26] and the 2-Phase Set [26] CRDTs. In both cases, we prove that any update is eventually delivered to all replicas.
-
Leader election The leader election protocol, presented in Sect. 2, is inspired by [6]. We notice however that a node sends all the contents of its mailbox at once, which is a strong simplification.
-
Token ring Token Ring is a classic protocol where a token is passed through nodes with mailboxes in a ring. We prove a safety and a liveness property. In the first case, we use the TFC tactic with 2 stability axioms, one for each event, which basically state that if there is no token apart from the one transferred, then no token can appear on unmodified nodes during the event. The TTC parameter says that the property of holding the token is the one that should propagate, under strong fairness.
-
FIFO This protocol is a simple mutual exclusion protocol based on a FIFO strategy. We prove a liveness property using TTC, stating that for any integer i, being in the i-th position of the list is a propagating property.
Our conclusion to these case studies is the following (Fig. 3). First the TEA tactic is only efficient for models involving few interactions, which can be attributed to the loss of precision when using universal quantifiers. Regarding TFC, the effort required to find stability axioms seems to be similar to finding an inductive invariant. For TTC, all propagating properties were very simple. Finally, we noticed that, for more complex systems, TTC and TFC can lead to problems that are too large for the model-checker to answer in time (e.g. 1 h.)
9 Related Work
The usual way to check a safety property is to exhibit an inductive invariant for the system. The TEA tactic is completely automatic and can handle safety properties but remains quite limited. In our experiments, the TFC tactic showed to be as flexible as an invariant to prove safety properties. Finding stability axioms or an inductive invariant appear similar in difficulty. However, once found, checking an inductive invariant is quicker in computation time than checking the abstract system obtained with stability axioms. On the other hand, stability axioms allow to check complex temporal properties.
Regarding liveness properties, important approaches are based on exhibiting a variant or using the Liveness-to-Safety reduction method proposed in [19]. For the simple examples done with TEA, such methods would allow to prove the properties with little efforts, if done right, but are not fully automatic contrary to the TEA tactic. In both case the computation time is really low.
With the TTC approach, we do not need to exhibit any sort of invariant and the propagating property to exhibit has always been straightforward. To our knowledge there is no easiest method to prove some of the examples we presented. For example, the liveness property of the leader election protocol requires to exhibit a variant and an invariant and both are harder to exhibit than the propagating property. The Liveness-to-Safety reduction method also applies here, but it requires to find an invariant on the system obtained by reduction, as well as finding an axiomatization of the reflexive-transitive closure preserving the Liveness property (while this axiomatization is embedded in TTC tactic). However, despite being more immediate in our examples, the TTC tactic is less flexible than these two alternatives since it applies for liveness properties based on the reflexive-transitive closure.
Our approach can also be compared with the specification of parameterized systems. Cubicle [7,8,9,10] is an SMT-based model-checker for the verification of safety properties on parameterized systems. Cubicle is efficient for challenging systems but, contrary to our techniques, it enforces strict syntactic constraints on guards and on the checked property. Others techniques based on labelled proof systems have also been proposed [2]. In [15], the safety of the TLB Shootdown algorithm is proved using such a technique. The user must exhibit the correct invariant for the proof system to conclude; while the TEA tactic is automatic. Also, some methods, such as invisible invariants [25], rely on finding automatically a candidate for being an inductive invariant and then checking if this is the case without needing any input from the user. Such an approach is automatic and efficient but only applies to Bounded-Data Parameterized Systems while our methods applies to a wider context. While most work on parameterized systems focuses on safety properties, [11] addresses liveness properties, but remains essentially theoretical. We remark that the techniques mainly used for parameterized systems are mostly orthogonal to those presented in this paper, and a combination of both could be fruitful.
10 Conclusion
We devised three original, sound (but incomplete) transformations, that allow to check that a state machine specification, expressed in a rather expressive fragment of \(\mathrm {FOLTL} _=^*\), enjoys a temporal property, expressed in the same setting, whatever the bounds on domains (associated with sorts) are. The transformations were proved correct in Coq. We evaluated our approach on several case studies and found that the transformations were effective and, for the semi-automatic ones, demanded an effort comparable to other approaches. A drawback is that the computed bounds can sometimes grow too much for model-checking to be feasible with the back-end tools we used. Notice that our approach is orthogonal to the main other approaches (for instance, inference of invariants) and could certainly be combined with some of them. Once a universally quantified inductive invariant Inv is found, such a combination would be possible by adding an axiom of the form \(\mathbf {G}\) Inv to our abtract specification. This refines the abstraction while fitting in both LTR and Geneva. This is left for future work.
Notes
- 1.
Indeed, having such a transformation would give a procedure for semi-decidability by testing all possible inputs on this transformation.
- 2.
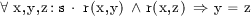 .
. - 3.
It is possible to fully axiomatize the transitive closure in pure \(\mathrm {FOLTL}\), however since it does not fit into the scope of this paper such an axiomatization is not presented here and we simply extends \(\mathrm {FOLTL}\) with the classical definition of transitive closure.
- 4.
In practice, we ensure that the semantics of the modifies section, which uses equality, is also affected by this transformation.
References
Abrial, J.R.: Modeling in Event-B: System and Software Engineering, 1st edn. Cambridge University Press, Cambridge (2010). https://doi.org/10.1017/cbo9781139195881
Arons, T., Pnueli, A., Ruah, S., Xu, Y., Zuck, L.: Parameterized verification with automatically computed inductive assertions? In: Berry, G., Comon, H., Finkel, A. (eds.) CAV 2001. LNCS, vol. 2102, pp. 221–234. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44585-4_19
Black, D.L., Rashid, R.F., Golub, D.B., Hill, C.R.: Translation lookaside buffer consistency: a software approach. ACM SIGARCH Comput. Archit. News 17(2), 113–122 (1989). https://doi.org/10.1145/68182.68193
Brunel, J., Chemouil, D., Cunha, A., Macedo, N.: The electrum analyzer: model checking relational first-order temporal specifications. In: 33rd ACM/IEEE International Conference on Automated Software Engineering (ASE 2018). Proceedings of the 33rd ACM/IEEE International Conference on Automated Software Engineering, ACM Press, Montpellier, France, September 2018. https://doi.org/10.1145/3238147.3240475
Cavada, R., et al.: The nuXmv symbolic model checker. In: Biere, A., Bloem, R. (eds.) CAV 2014. LNCS, vol. 8559, pp. 334–342. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-08867-9_22
Chang, E., Roberts, R.: An improved algorithm for decentralized extrema-finding in circular configurations of processes. Commun. ACM 22(5), 281–283 (1979). https://doi.org/10.1145/359104.359108
Conchon, S., Declerck, D., Zaïdi, F.: Cubicle-\(\cal{W}\) : Parameterized model checking on weak memory. In: International Joint Conference on Automated Reasoning, pp. 152–160. Springer (2018). https://doi.org/10.1007/978-3-319-94205-6_11
Conchon, S., Declerck, D., Zaïdi, F.: Parameterized model checking on the TSO weak memory model. J. Autom. Reason. 64(7), 1307–1330 (2020). https://doi.org/10.1007/s10817-020-09565-w
Conchon, S., Goel, A., Krstić, S., Mebsout, A., Zaïdi, F.: Cubicle: a parallel SMT-based model checker for parameterized systems. In: Madhusudan, P., Seshia, S.A. (eds.) CAV 2012. LNCS, vol. 7358, pp. 718–724. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-31424-7_55
Conchon, S., Mebsout, A., Zaïdi, F.: Certificates for parameterized model checking. In: Bjørner, N., de Boer, F. (eds.) FM 2015. LNCS, vol. 9109, pp. 126–142. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-19249-9_9
Farzan, A., Kincaid, Z., Podelski, A.: Proving liveness of parameterized programs. In: 2016 31st Annual ACM/IEEE Symposium on Logic in Computer Science (LICS), pp. 1–12 (2016). https://doi.org/10.1145/2933575.2935310
Hawblitzel, C., et al.: Ironfleet: proving practical distributed systems correct. In: Proceedings of the 25th Symposium on Operating Systems Principles, pp. 1–17 (2015). https://doi.org/10.1145/2815400.2815428
Hodkinson, I., Wolter, F., Zakharyaschev, M.: Decidable fragments of first-order temporal logics. Ann. Pure Appl. Logic 106(1–3), 85–134 (2000). https://doi.org/10.1016/s0168-0072(00)00018-x
Hodkinson, I., Wolter, F., Zakharyaschev, M.: Monodic fragments of first-order temporal logics: 2000–2001 A.D. In: Nieuwenhuis, R., Voronkov, A. (eds.) LPAR 2001. LNCS (LNAI), vol. 2250, pp. 1–23. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-45653-8_1
Hoenicke, J., Majumdar, R., Podelski, A.: Thread modularity at many levels: a pearl in compositional verification. ACM SIGPLAN Not. 52(1), 473–485 (2017). https://doi.org/10.1145/3009837.3009893
Kuperberg, D., Brunel, J., Chemouil, D.: On finite domains in first-order linear temporal logic. In: Artho, C., Legay, A., Peled, D. (eds.) ATVA 2016. LNCS, vol. 9938, pp. 211–226. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-46520-3_14
Lamport, L.: Specifying Systems: The TLA+ Language and Tools for Hardware and Software Engineers. Addison-Wesley Professional (2002)
Padon, O.: Deductive Verification of Distributed Protocols in First-Order Logic. Ph.D. thesis, Ph.D. Dissertation. Tel Aviv University (2018)
Padon, O., Hoenicke, J., Losa, G., Podelski, A., Sagiv, M., Shoham, S.: Reducing liveness to safety in first-order logic. In: Proceedings of the ACM Conference on Principles of Programming Languages (POPL) 2, 26 (2017). https://doi.org/10.1145/3158114
Padon, O., Losa, G., Sagiv, M., Shoham, S.: Paxos made epr: decidable reasoning about distributed protocols. Proc. ACM on Program. Lang. 1(OOPSLA), 108 (2017). https://doi.org/10.1145/3140568D
Padon, O., McMillan, K.L., Panda, A., Sagiv, M., Shoham, S.: Ivy: safety verification by interactive generalization. ACM SIGPLAN Not. 51(6), 614–630 (2016). https://doi.org/10.1145/2980983.2908118
Peyras, Q., Bodeveix, J.P., Brunel, J., Chemouil, D.: Cervino prototype, Coq formalization and Benchmarks (CAV 2021 artifact) (Apr 2021). https://doi.org/10.5281/zenodo.4725675
Peyras, Q., Brunel, J., Chemouil, D.: A bounded domain property for an expressive fragment of first-order linear temporal logic. In: Gamper, J., Pinchinat, S., Sciavicco, G. (eds.) 26th International Symposium on Temporal Representation and Reasoning, TIME 2019, October 16–19, 2019, Málaga, Spain. LIPIcs, vol. 147, pp. 15:1–15:16. Schloss Dagstuhl - Leibniz-Zentrum für Informatik (2019). https://doi.org/10.4230/LIPIcs.TIME.2019.15
Peyras, Q., Brunel, J., Chemouil, D.: A decidable and expressive fragment of many-sorted first-order linear temporal logic. Information and Computation p. 104641 (2020). https://doi.org/10.1016/j.ic.2020.104641
Pnueli, A., Ruah, S., Zuck, L.: Automatic deductive verification with invisible invariants. In: Margaria, T., Yi, W. (eds.) TACAS 2001. LNCS, vol. 2031, pp. 82–97. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-45319-9_7
Shapiro, M., Preguiça, N., Baquero, C., Zawirski, M.: A comprehensive study of convergent and commutative replicated data types. Ph.D. thesis, Inria-Centre Paris-Rocquencourt; INRIA (2011)
Wilcox, J.R., Woos, D., Panchekha, P., Tatlock, Z., Wang, X., Ernst, M.D., Anderson, T.: Verdi: a framework for implementing and formally verifying distributed systems. In: Proceedings of the 36th ACM SIGPLAN Conference on Programming Language Design and Implementation, pp. 357–368 (2015). https://doi.org/10.1145/2737924.2737958
Acknowledgements
We thank the article and artifact anonymous reviewers for their remarks that helped improve this work, as well as Nuno Macedo for his technical assistance.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2021 The Author(s)
About this paper
Cite this paper
Peyras, Q., Bodeveix, JP., Brunel, J., Chemouil, D. (2021). Sound Verification Procedures for Temporal Properties of Infinite-State Systems. In: Silva, A., Leino, K.R.M. (eds) Computer Aided Verification. CAV 2021. Lecture Notes in Computer Science(), vol 12760. Springer, Cham. https://doi.org/10.1007/978-3-030-81688-9_16
Download citation
DOI: https://doi.org/10.1007/978-3-030-81688-9_16
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-81687-2
Online ISBN: 978-3-030-81688-9
eBook Packages: Computer ScienceComputer Science (R0)









 where
where  where
where  where
where 
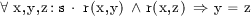 .
.