Playback Robot Programming with Loop Increments

Abstract

Playback robot programming is fast and easy to use for non-experts, because the robot only needs to be manually guided. However, it is only capable of replaying the trajectory exactly as it was taught. We present the concept of loop increments for playback programmed robots to allow the user to teach tasks like palletizing or stacking without having to explicitly guide the robot through each trajectory. Only the base trajectory for one repetition needs to be program med. After each loop iteration, the user-defined increment is added to the incremental configurations, e.g. to the pick or place configurations. To achieve this, two methods of defining the loop increments are shown. Afterwards, linear, Gaussian, and cosine blending functions in combination with the point and interval method are introduced for weighting the increments and as a foundation for the adaption algorithm. The evaluation showed, that the cosine blending function with the interval method best fits the needs of our programming system.

1 Introduction

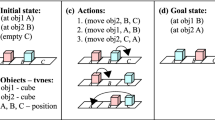
Programming robots using the playback programming approach is rather easy to understand and fast to use for the user. However, when it comes to repetitive tasks where after each iteration small changes to the trajectory are needed, the playback programming approach reaches its limits. This is the case with tasks such as stacking and palletizing. Every iteration of the task needs to be programmed explicitly when using the classic playback programming approach. In a previous work, we already presented an approach that allows the user to define sensor-based loops within a playback-programmed robot program, so that repetitive tasks that always play back exactly same trajectory can be programmed. The novel was, that the number of repetitions of the loop is defined by sensor input, e.g. camera images [1]. In this paper, we present an extension to the concept of loops for playback-programmed robot programs called loop increments. With these loop increments, we allow the user to program repetitive tasks with small changes to the trajectory after each iteration without the need to program all trajectories explicitly. Only the base trajectory, i.e. the trajectory of the first iteration of the loop, needs to be programmed and then the increments need to be defined. An example depalletizing and stacking task is shown in Fig. 1. This is a major extension to the playback programming approach, because until now, playback-programmed robot only replayed trajectory exactly as it was programmed and no adaption of the programs was possible during execution.

Fig. 1

a Example task consisting of depalletizing (left robot) and stacking (right robot) that can be programmed with loop increments by demonstrating only one pick and place trajectory. b Timeline representation in our programming system of the above task

In the rest of the paper, we show how increments are defined within the existing programming system. Afterwards, the adapting of the trajectory with the help of blending functions during playback of the robot program is presented. Finally, we compare the different blending functions and evaluate, which blending function best fits our programming system.

2 Related Work

The playback programming approach for industrial robots is one of the oldest programming paradigms. It was described for the first time in [2]. It consists of two phases, the programming phase where the user manually guides the robot through the desired trajectory, and the playback phase where the robot exactly reproduces the taught trajectory. Because no knowledge of textual programming in general and no robot programming skills in particular are needed, it is suitable for non-experts that have only knowledge about the task that should be fulfilled, but not about programming itself. There are several application areas that use this kind of programming technique. A lot of applications are in the field of surface treatment, e.g. spray painting [3], deburring [4], welding [5], gluing [6], contour following [7], or fiber spraying [8]. There are also applications in pick-and-place scenarios, e.g. workpiece assembly [9], moving workpieces from one machine to another [1], or placing of workpieces [10]. When it comes to pick-and-place tasks, there is the problem of palletizing or stacking objects. Until now, this was only solvable with the playback programming approach by guiding each trajectory explicitly by hand, even though a stacking or palletizing task has a lot of similar trajectories that only need a slight adjustment of the trajectory. This is because of the paradigm, that a playback programmed task is played back exactly the same as it was taught by the user.

This problem should be solved with the concept of loop increments for playback programmed trajectories that we present in this work. We have given a robot trajectory, a start and end configuration of a loop within this trajectory, and certain incremental configurations within this loop. After each loop iteration, the corresponding loop increment of the incremental configuration shall be applied to it, so that afterwards these incremental configurations are shifted and tilted according to the applied increment. The wanted algorithm should now adapt the original trajectory to a new, similar trajectory that runs through the incremented configurations.

To achieve this, we need to take a look at existing algorithms to adapt trajectories. There are various approaches in the field of programming by demonstration. Most of them are using multiple demonstrations of trajectories to learn a generalized behavior and derive a new trajectory out of the learned behavior [11,12,13]. Some other approaches utilize only one demonstration of the trajectory (one-shot), but still try to generalize behavior and try to derive a new trajectory during execution [14, 15].

These algorithms are not suitable for adapting playback programmed trajectories, because they are mostly used to learn and generalize from one ore multiple demonstrations to completely different trajectories. In our case, we want to get a trajectory that is still similar to the original one, but runs through the incremented configurations. The proportional editing function of Blender Blender [16] does something similar, only on three dimensional meshes. Since a trajectory in our case is similar to a mesh, we have oriented ourselves on Blender when designing and implementing the adaption algorithm.

3 Loop Increments for Playback Robot Programs

In this work, we present the concept of loop increments for the playback programming approach. These increments should work as follows: First of all, the base trajectory needs to be programmed by hand guiding the robot through the desired trajectory. Afterwards the user defines the repetitive part of the trajectory as a loop, such as described in [1]. Our novel approach extends the programming of a loop, so that the repetitive trajectories may now be adapted after each loop iteration by a predefined loop increment at runtime.

Within the loop, the user defines certain configurations as incremental configuration that are changed during each iteration of the loop. For each nesting level of loops around these incremental configurations, the user needs to define an additional increment. E.g., if there are two loops around a incremental configuration, two different increments need to be defined for this position - one for the inner loop and one for the outer loop. These increments are the transformations that is applied to the incremental configuration after each loop iteration. If the user wants to stack objects, the increment would be a trajectory in negative z direction of the tool center point coordinate system. Both, translation and rotation, can be defined within an increment by the user. The definition of increments within our programming system is described in Sect. 3.1.

When executing the trajectory, an algorithm is needed that adapts the original playback-programmed trajectory in a way, so that the incremented configurations are reached during playback. To achieve this, a adapting method with suitable blending functions is needed. This algorithm and the different blending functions are described in Sect. 3.2.

3.1 Definition of Increments Within the Programming System

Before we can define the increments, we first need to introduce variables that we are going to use during calculation of the increment and the adapted trajectory. For each incremental configuration, we need the initial pose $P_0$ and the pose after once applying the increment $P_1$. From these two poses the incremental transformation D can be calculated. $P_0$, $P_1$, and D are all homogeneous $4\times 4$ transformations matrices with $P_1 = P_0 \cdot D$. With the help of this equation, D can be calculated as $D = P_0^{-1}\cdot P_1$. Therefore, only $P_0$ and $P_1$ need to be given to define D. With these definitions, we are now able to show how loop increments can be defined in our playback robot programming system.

Fig. 2

a A photo of a non-expert teaching an increment by manually guiding the robot with a screenshot of the feedback for the user. b The user interface for the expert to define the transformation

Since our programming system is designed to be easy and fast to use by both, non-experts and experts in the field of robot programming Riedl and Henrich ([1]), we allow two ways of defining loop increments. The first step for both ways is to define the incremental configurations within an existing trajectory. This is done by selecting the position within a loop in the timeline representation of the robot program and by activating the loop increment feature of our programming system. With this step, the incremental position $P_0$ that should be adapted after each loop iteration is selected.

The non-expert way of defining the increment is to manually guide the robot to $P_1$. To allow the user to do this, the robot is automatically moved to the initial pose $P_0$. Then it is set to manual guiding mode and the user moves it to $P_1$. During guiding, the user gets feedback from the programming system in the form that the current transformation D is shown as Cartesian translation and Euler angles in the user interface (Fig. 2a). Once the user is satisfied with the increment, it has to be confirmed and the definition process is over. It is still possible for the user to use the expert menu to adapt D manually afterwards.

If the user has expert knowledge about the process and wants to define D exactly, the user interface offers the possibility to enter the transformation D as Cartesian translation and Euler angle rotation. So the user may insert the transformation in x, y, and z direction and the rotation around the x-, y-, and z-axes (Fig. 2b). It should be noted that the non-expert way defines D implicitly by defining $P_1$ while the expert way defines D directly within the user interface.

After showing the different methods of defining increments within our programming system, the following subsection shows how the original trajectory is adapted after each loop iteration.

3.2 Trajectory Blending During Playback

The last section described two ways of defining the increments. Now, we will explain how the actual adapting of the original trajectory after each loop iteration works. To achieve this, we first define a trajectory T as a sequence of $n \in \mathbb {N}$ joint configurations $q_t$ with $0 \le t \le n$ and $q_t \in \mathbb {R}^d$ for robots with $d \in \mathbb {N}$ axes. Additionally, since a trajectory also includes temporal information, we define that the duration between two joint configurations $q_t$ and $q_{t+1}$ is isochronous for all adjacent joint configurations in T and the duration is always a fixed number of milliseconds.

We now introduce two methods, to determine to which configurations the increment is applied to $100 \%$. The first method only applies the increment to the defined incremental configuration to $100 \%$ (point method), whereas the second method applies the increment to $100 \%$ to all configurations around the incremental configuration as long as the robot stands still (interval method). Both methods weight the increment according to the proximity to the next and previous incremental configuration using sigmoid functions. The further away from the incremental configuration the current configuration is, the lower is the impact of the increment to the blending function. The following part showing how the adapted trajectory is calculated works for both, the point method, and the interval method.

Before we are able to adapt each position of T according to the increments D, we first need to define a blending function that calculates the weighting of D for each configuration within the trajectory. This blending functions need to return a value between 0 and 1 that defines to which extent the corresponding increment needs to be added to the current configuration. A blending function is defined as ${f_{\text {blend}}: i, j, x \rightarrow w}$ with $i, j, x \in \{0, \dots , n\}$ and $w \in [0; 1]$ while i is the index of the incremental configuration, j is the index of the last configuration that should be affected by the increment, x is the index of the current configuration that should be adapted, and w is the weighting of the increment at configuration i for the configuration x. All blending functions need to fulfill two constraints, the first one is ${f_{\text {blend}}(i, j, i) = 1}$ and the second one ${f_{\text {blend}}(i, j, j) = 0}$. We compare three different blending functions: linear, Gaussian, and Cosine in combination with the point and the interval method. In Sect. 4 we show, which blending function fits best.

To define the linear blending function, we use ${f(x) = m\cdot x + t}$ as base formula. With the two constraints that should be fulfilled, we get Eq. 1 for the linear blending function.

$$\begin{aligned} f_{\text {blend, linear}}(i, j, x) = \frac{1}{i-j}\left( x-j\right) \end{aligned}$$

(1)

For the Gaussian blending function we use ${f(x) = a\cdot \exp \left( {-\frac{\left( x-b\right) ^2}{2c^2}}\right) }$ as base formula. For the first constraint we get $a = 1$ and $b = i$. This type of formula is not capable of fulfilling the second constraint, because ${\forall x \in \mathbb {R}: f(x) > 0}$. So we soften this constraint to ${f(i,j,j) \approx 0}$. To fulfill this constraint, we need to find a suitable c that results in a small enough but not too small exponent. If the exponent becomes too small, f(x) will have a too big gradient and the blending function will be too steep. A steeper blending function generates a worse adapted trajectory (See Sect. 4). For our purposes, $c = \frac{i-j}{d}$ with $d=3.5$ is the best trade-off between the second constraint and a gradient that is not too big. A bigger d results in f(i, j, j) getting closer to 0, but is also steeper. A smaller d results in f(i, j, j) being not so steep but also further away from 0. Example values for f(i, j, j) with different d are: $d=3 \rightarrow f(i,j,j) \approx 0.0111$, $d=3.5 \rightarrow f(i,j,j) \approx 0.0021$, and $d=4 \rightarrow f(i,j,j) \approx 0.0003$. Equation 2 shows the Gaussian blending function that we use in our programming system.

$$\begin{aligned} f_{\text {blend, gaussian}}(i, j, x) = \exp \left( {-\frac{\left( x-i\right) ^2}{2\cdot \left( \frac{i-j}{3.5}\right) ^2}}\right) \end{aligned}$$

(2)

The last blending function we use is a cosine blending function. To define it, we use the base formula $f(x) = a \cdot \cos \left( b+c\cdot x\right) +d$. In addition to the two constraints it should range between 0 and 1. To fulfill this, we need to set $a=0.5$ and $d=0.5$. For the other two constraints ${\cos \left( b+ci\right) =1 \rightarrow b+ci=0}$ and ${\cos \left( b+cj\right) = 0}$ ${\rightarrow b+cj=\pi }$ need to be fulfilled. This results in $b=-\frac{\pi }{j-i}\cdot i$ and $c=\frac{\pi }{j-i}$. The simplified cosine blending function is shown in Eq. 3.

$$\begin{aligned} f_{\text {blend, cosine}}(i, j, x) = 0.5\cdot \cos \left( \frac{\pi }{j-i}\cdot \left( x-i\right) \right) +0.5 \end{aligned}$$

(3)

With the defined blending functions, we are now able to adapt the configurations. After each loop iteration, each joint configuration $q_t \in T$ needs to be recalculated. In general, each joint configuration is affected by two increments, increment $D_l$ belonging to the incremental configuration $q_l$ left of $q_t$ and increment $D_r$ belonging to the incremental configuration $q_r$ right of $q_t$. With one of the three Eqs. 1, 2, or 3, the weightings for each increment are calculated as $w_l = f_{\text {blend, }b}(l, r, c)$ and $w_r = f_{\text {blend, }b}(r, l, c)$ with $\text {b} \in \{\text {linear}, \text {gaussian}, \text {cosine}\}$. In the next step, all $D_x$ with $x \in \{l, r\}$ are divided into their Cartesian translations $t_x$ and Euler angles $r_x$. Then the translatory ($t_{\text {shift, }x}$) and rotatory ($r_{\text {shift, }x}$) shifts are calculated as $t_{\text {shift, }x} = w_x \cdot t_x$ and $r_{\text {shift, }x} = w_x \cdot r_x$. Now all translatory and rotatory shifts are converted back into $4\times 4$ homogeneous transformation matrices $D_{\text {shift}, x}$. With the help of the robot specific forward kinematics $f_{\text {forward}}: \mathbb {R}^d \rightarrow \mathbb {R}^{4\times 4}$ that transforms joint configurations into position and orientation of the tool-center-point in homogeneous Cartesian coordinates and the robot specific inverse kinematics $f_{\text {inverse}}: \mathbb {R}^{4\times 4} \rightarrow \mathbb {R}^d$ that transforms the tool-center-point into joint configurations, we are able to calculate the adapted joint configuration $q'_c$ with the weighted increments $D_{\text {shift}, l}$ and $D_{\text {shift}, r}$:

$$\begin{aligned} q'_c = f_{\text {inverse}}\left( f_{\text {forward}}\left( q_t\right) \cdot D_{\text {shift}, l} \cdot D_{\text {shift}, r}\right) \end{aligned}$$

(4)

Equation 4 is used to calculate the adapted configuration within a loop after each loop iteration. The resulting trajectory is then played back, so that the repetitive task with slightly different configurations is executed. Section 4 will compare and evaluate the three blending functions shown in Eqs. 1 to 3 with both, the point and interval method.

4 Comparison and Evaluation of Blending Functions

After describing how the trajectories are adapted with the help of the loop increments and the blending functions, we will evaluate this method in this section. In Subsection 4.1, we are going to compare the three different blending functions in combination with both, the point method and the interval method. Afterwards, in Subsection 4.1, we show which of the six combinations of blending function and weighting method is the best for the playback programming approach.

4.1 Comparison

Figure 3 shows the six different combinations of the three blending functions and both, the point method and the interval method for an example trajectory with 343 configurations. This is the trajectory that was taught by manual guiding to fulfill the example depalletizing and stacking task of Fig. 1. Within the graphs, the loop start, the loop end, and the two positions where increments are added to the configurations are depicted. Furthermore, the intervals where the robot is stopped and therefore where the interval method interferes are marked, so that the difference between the point method in Fig. 3a and interval method in Fig. 3b can be seen.

Fig. 3

Comparison of the different blending functions for the trajectory from the task in Fig. 1. Chart a shows the result for the blending functions the point method, chart b with the interval method. The red graphs show the cosine, the green graphs the Gaussian and the blue graphs the linear blending functions

If we compare the different blending functions, we can see that both, the linear and the cosine blending function are point symmetrical within an interval between two increments. However, the Gaussian blending function has a shorter interval where it weights the increment with a high weight and a wider interval where the increments are weighted with a low weight compared to linear and cosine. Furthermore, the Gaussian blending function has the disadvantage that it is not continuous at the last configuration that shall be affected by the increment. This is because the Gaussian blending function never reaches the value 0 as already stated in the derivation of Eq. 2. Additionally, if we compare the linear and cosine blending function, we see that the linear function is not smooth at the loop start, loop end and the increments, whereas the cosine blending function is smooth over the whole trajectory. Therefore the cosine blending function is to be preferred over the other two blending functions, regardless of whether the point method or the interval method is chosen. To determine, which of the two weighting methods is better, we are going to evaluate an example trajectory in the next section.

4.2 Evaluation

To determine if the point method or the interval method is better, we evaluate the six combinations of blending function and weighting methods. Figure 4 shows the three dimensional trajectory for the example task shown in Fig. 1.

When using the point method, it is recognizable that regardless of the chosen blending function, the trajectory makes a dip shortly before the green position. If these trajectories are played back, this dip would result in a collision of the robot with the stacked objects and therefore a failure to fulfill the task. This dip is explainable with the graphs of Fig. 3, because we have a interval at increment two where the robot does not move, but the point method already results in the blending function to decrease the weight of the increment. This results in the green position being dragged in z-direction downwards, because the increment is not applied fully to the position anymore.

Fig. 4

Simulation of the blending functions for the task in Fig. 1. In each screenshot the original trajectory is drawn in light blue and the adapted trajectory in black with the increment in x-direction for the depalletizing position (red cube in the figure) and the increment in z-direction for the stacking position (green cube in the figure). Subfigures (a), (b), and (c) show the adapted trajectories for the point method. Subfigures (d), (e), and (f) show the adapted trajectories for the interval method. The cosine blending function is shown in (a) and (d), the Gaussian blending function in (b) and (a), and the linear blending function in (c) and (f)

To avoid this kind of error, we can use the interval method that starts using the blending function to apply the blending function only when the robot is moving. The result of this method for the three dimensional trajectory is depicted in (d), (e), and (f) of Fig. 4. It can be seen that the trajectories do not have the dip anymore and therefore all result in a successful execution of the task.

Because of the outcomes of the comparison of the different blending function and the evaluation of the point method and the interval method, we chose the cosine blending function with the interval method as our preferred trajectory adapted algorithm. It showed the best results in our simulation and is the best with regard to mathematical aspects such as continuity and smoothness. The implementation in our playback programming system showed promising results and different tasks increment tasks were programmed and executed successfully.

5 Conclusion

In this paper we presented an approach to adapt playback programmed trajectories after each loop iteration during runtime, so that tasks like stacking and palletizing can be programmed with our playback programming system. To achieve this, we first showed two ways of defining loop increments, both for non-experts and experts. Afterwards we showed an algorithm that iterates through all joint configurations after each loop iteration and applies the corresponding loop increments with a weighting factor to each configuration, so that the adapted trajectory reaches the next position on the pallet or stacks the next item on top of the previous one. In the evaluation, we compared different blending functions and two weighting methods and showed that the cosine blending function with the interval method is the best for the playback programming approach. This is a next step into the direction of making the playback programming approach more versatile and powerful, because up to now, trajectories could only be played back exactly as they were taught by the user.

Future work may include finding and evaluating other blending functions to further improve the trajectory adaption or using this concept for applications in the field of surface treatment.