Keywords

1 Introduction and Motivation

Proton exchange membrane fuel cells (PEM FC) can be characterized as a highly volatile market. One of the main challenges for a broad application of fuel cells in mobility is the available infrastructure. Initial fields of application will be developed when the necessary hydrogen infrastructure can be built up, which will be followed by a more widespread use. Consequently, the demand for fuel cells and production capacities will only gradually increase.

Manufacturing systems with fixed cycle time are most efficient at the designated production quantity. A demand higher than the capacity leads to opportunity costs for missed profit. A production volume lower than the planed yield results in low utilization rates and tied capital. In contrast, an agile manufacturing system is characterized by a piece number scalability, ensuring less tied capital and the avoidance of opportunity costs by scaling it up. By the complementary and substitutive use of similar systems the agility costs can be reduced, thus ensuring scalability by piece. For the application scenario of fuel cell production this means that a system must be able to cover a wide range of production steps with no loss of quality. The clocking process for fuel cell stack assembly is the individual part stacking, which shall be further investigated within this paper. The herein presented system is able to stack different fuel cell components with different designs. It is therefore necessary to determine the product and production interaction, with the focus of this paper being on single membrane handling and optimization of the parameter setting for this application. This includes the gripper design as well as the parameter settings.

2 Fuel Cell Stack Assembly

2.1 State of the Art

The base material for hydrogen fuel cells are proton exchange membranes (PEM), which are coated with catalysts to form a catalyst coated membrane (CCM). The CCM allows proton conductivity and gas tightness. To distribute the reactant gases to the membrane and drag electrons from the membrane a so-called gas diffusion layer (GDL) is at both sides of the CCM. To further improve the system durability the GDL is coated with a micro-porous layer on the sides facing towards the membrane. So-called bipolar plates (BPP) ensure the gas supply. The design to assemble the components as well as the sealing concept varies between manufacturers. CCM, GDL and a gasket can be assembled to a so-called membrane electrode assembly (MEA), for example by heat pressing. The seal can be applied onto the bipolar plate (seal-on BPP) or on the GDL (seal-on GDL) [1]. Figure 1 shows the important steps in fuel cell stack production with a seal-on GDL approach as also described in Stahl [1], Porstmann et al. [2].

Fig. 1
figure 1

Assembly of fuel cell stacks

Full size image

The overall sealing concept has a huge impact on the production system, as the number of parts varies and the components can be more fragile or limp during handling. The above described single cell is then stacked with up to 400 individual cells. The assembly of fuel cell stacks has only come into focus in recent years and thus is yet not discussed in literature deeply. In Bobka et al. [3, 4] a fuel cell stacking system is presented which features various cameras mounted overhead for position measurement before and after handling. For the assembly itself preassembled MEA’s have been used, the investigations are focused on an improvement of stacking accuracy. The gripper has been mentioned as a major source of inaccuracy but has not been investigated further. Another system is presented in Williams et al. [5], Laskowski and Derby [6]. Robots are used for the assembly and guidance pins are used for the alignment of the individual components. However, this system is limited in stack size, as the guidance pins are rather short and a stacking accuracy of only 0.51 mm was stated. In this concept preassembled MEA’s have been used. There have been several research projects investigating fuel cell stack assembly with seal-on GDL such as MontaBS [7, 8]. and Fit-4-AMandA [2], however there is only little information on the assembly system itself and its core components. Numerous patents, such as Dreier [9], Munthe [10], HoKyun and Yoon [11] suggest that more attention is being paid to fuel cell stack assembly in an industrial environment. However, no information is available on the implementation of the registered property right. All the assembly systems mentioned above feature vacuum or low pressure grippers for handling the components in pick and place operations. Especially the gripping of the individual CCM and the porous GDL, that are not preassembled, have not been investigated yet, although being relevant for a seal-on GDL approach as mentioned in Porstmann et al. [2].

2.2 Concept for a Scalable and Flexible Production System

A comprehensive overview of requirements for an agile manufacturing system is given in Ramsauer and Rabitsch [12] and can be characterized by three key elements: proactive preparation, fast reaction time and optimized efficiency. On the machine level this requires an understanding of the material-production interaction to cover future material developments. With pre-developed production modules for a successive expansion a wide range of steps in the process chain can be covered. In Porstmann et al. [2] this is resolved by a high degree of specialisation, so that each task is assigned to a single handling system. The approach presented in Bobka et al. [4] is capable of doing several operations, but can only grasp pre-assembled MEA. A rough concept for an agile manufacturing system that is also capable of assembling MEA’s is shown in Fig. 2.

Fig. 2
figure 2

Concept for a scalable production system with identical production machines

Full size image

Thus, there are two important optimization goals for agile systems:

  1. (a)

    In the very first phase the system must be able to fulfil all handlings tasks.

  2. (b)

    The system must easily be adapted to new products, which requires preliminary investigations and model building, which are conducted in this paper.

2.3 Materials in Fuel Cells

Table 1 shows the typical properties of materials for fuel cell components. Components like the bipolar plates or the GDL show a great variation in their properties due to the lack of standards. Furthermore, the components behave very different when being handled. The bipolar plate is gas tight and rigid, whereas GDL and CCM are limp and prone to being damaged during handling. Not only does this usually require a different set of grippers for each component, it also makes it inevitable to adapt it to the desired specifications.

Table 1 Material properties relevant for stacking
Full size table

2.4 Constraints

For the assembly all the components need to be handled. Especially the membrane poses a great challenge for grippers, as it is not only very thin, but also has low mechanical properties. Common base materials are Nafion® NR211 and Nafion® NC700. Their respective properties are given in Table 2 [16, 17], the poisson value for Nafion® based materials is 0.4 [18]

Table 2 Fuel cell membrane properties [16, 17]
Full size table

Whilst gripping the pressure difference causes a bending of the membrane. The bending of a thin membrane can be described by Eq. (1) [13] with the materials young’s modulus E and the poisson value ν as well as the radius R of the suction openings of the gripper, the differential pressure \(\Delta p\) and the material thickness d.

$${w}_{0}=\frac{3}{16}*\frac{{\mathrm{R}}^{4}}{{\mathrm{d}}^{3}} *\frac{1-{\nu }^{2}}{E}*\Delta p$$
(1)

Fuel cell membranes subjected to mechanical stress show no distinct transition between elastic and plastic behaviour. In general, plastic deformation should be avoided. As the membranes tend to become thinner for higher efficiency fuel cells this can be challenging for defect-free handling. Therefore, FEM-simulations were carried out with the membrane being subjected to a pressure difference at a circular opening, as it can be found in vacuum or low-pressure grippers. The membrane was modelled in Abaqus as a shell encastrated at the outer circumference with five integration points along the thickness and Simpson integration rule as well as Abaqus’ standard static solver applied. The element size was set to 0.01 mm. The model as well as maximum Mises stress under variation of pressure difference and suction opening are shown in Fig. 3.

Fig. 3
figure 3

Equivalent stress for different substrate materials, gripper diameters and differential pressure

Full size image

Whilst NR211 membranes are uncritical for the investigated parameter setting, NC700 is prone to being damaged due to handling. In Kundu et al. [20] yield strength between 1.55 MPa and 2.5 MPa were obtained for Nafion based materials. Based on the FEM results a diameter of less than 0.5 mm is recommended for safe handling of membranes.

2.5 Investigation of Position Accuracy

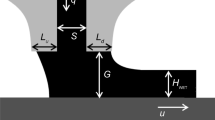
For the assessment of an achievable repeatability, a test stand was designed. It features a z-axis, a pressure control and differential pressure measurement system and a camera mounted below the transparent table. The gripper is slightly bigger than the CCM, the openings have a diameter of 0.5 mm, Fig. 4 shows the corresponding experimental setup. The level settings were based on the upper and lower limits in preliminary investigations and are shown in Table 3, the differential air pressure results from the characteristics of the vacuum generator and set supply air pressure.

Fig. 4
figure 4

Experimental setup for the design of experiment

Full size image
Table 3 Parameters for the design of experiments
Full size table

The central composite design has 16 different parameter settings for the full-factorial inner part (24-plan; - and + settings) and an additional nine parameter settings for centre and star points (+ + , 0 and - -). Each parameters setting has been carried out four times resulting in a total of 100 runs and position deviation measurements.

Figure 5 shows the analysis of means (ANOM) for the parameter settings in Table 3 with the average standard deviation represented in grey. To obtain an overall position deviation the mean value of x- and y-deviation on a single corner have been measured.

Fig. 5
figure 5

Analysis of means for the complete central composite design of experiments

Full size image

An analysis of variance (ANOVA) has been carried out with the results being shown in Table 4. After determination of the F-value the lift-off and drop-down distance are significant. The ANOVA shows, that a large fraction of the variation cannot be explained by the factor settings, thus leading to a relatively high error.

Table 4 ANOVA results for the design of experiments
Full size table

For the inner part of the central composite design first order interactions were investigated as well, showing no significant interactions. Hence the error cannot be explained by factor interactions alone. One of the reasons for a high variation might be the membrane rolling alongside its edges. The rolling is temperature and humidity induced. This curling leads to an unpredictable position after gripping. This also explains why a higher accuracy can be achieved for a higher pick-up distance: If the distance is bigger than the curling induced curvature, the CCM could be shifted before gripping. CCM flatness and curling have not been measured during experiments. Generally it is recommended to lay the CCM flat, as a higher drop-drown distance reduces accuracy.

2.6 Analysis of the Assembly Procedure and Tolerances

The assembly of fuel cell stacks involves several pick and place operations. The tolerance field for the final placement of the component itself is quite narrow, depending on the stack design from ± 0.1 mm to ± 0.4 mm [1]. Positioning itself cannot be carried out by a fixed stop as the components are too limp. For this reason optical position measurements have to be carried out. The total tolerance of the machine can be calculated as a combination between the handling device and the measurement device. The pixel density limits the accuracy of the camera, furthermore the handling device has a limited repeat accuracy. If the camera and gripper are not mounted to the same component and share a common origin these inaccuracies add up (camera position A, B and D in Fig. 6 with the camera coordinate system in blue, the gripper coordinate system in black and the world coordinate system in red).

Fig. 6
figure 6

Camera positioning in fuel cell stack assembly

Full size image

Based on the results of Fig. 5 it is assumed that the gripper inaccuracy is ± 0.025 mm for gripping and placement. In contrast to the test setup there will also be an additional repeat inaccuracy of ± 0.02 mm by the robot itself, resulting in ± 0.045 mm for gripping and placement. The camera accuracy is set to ± 0.005 mm in all cases. The measuring station is assumed to have the same repeat accuracy as the robot. Concept D only allows for quality assurance, a perfect alignment of the component prior to gripping is assumed. The estimated inaccuracies are shown in Table 5 with concept C promising to have the lowest inaccuracy, which therefore will be pursued further in future.

Table 5 Tolerances in fuel cell pick and place-assembly
Full size table

3 Summary and Outlook

A flat surface gripper has been used to grasp and release a CCM for fuel cell production. Through FEM the critical suction hole opening size has been investigated and optimized for given materials. A direct link between material properties and gripper design was made. This proactive preparation allows for fast reaction times if the CCM is changed to another material, therefore contributing to an agile manufacturing system, with the planned base unit shown in Fig. 7. The multi component gripper allows for high utilization rates in low volume production and can be easily extended by the integration of identical systems for higher volume production as outlined in Fig. 2.

Fig. 7
figure 7

Target system for scalable fuel cell manufacturing

Full size image

Through the investigation of the parameter setting an optimization trend for higher pick and place accuracies was derived. Especially the distance between gripper and component during grasping and releasing plays a crucial role. It is concluded, that higher accuracies are achieved with slight distance during grasping and no distance during release. According to the results it still can be very challenging to reduce the inaccuracy below 0.1 mm. Possible countermeasures include an externally actuated position frame with integrated position detection, thus eliminating errors due to membrane curling prior to grasping. Cause-effect relationships need to be further investigated, for example air turbulences or electrostatic effects can be taken into account. With reference to the idea of an agile manufacturing system similarly designed investigations for GDL and bipolar plate will be carried out.