Failure Mechanisms of Alloys with a Bimodal Graine Size Distribution

Abstract

A multi-scale computational approach was used for the investigation of a high strain rate deformation and fracture of magnesium and titanium alloys with a bimodal distribution of grain sizes under dynamic loading. The processes of inelastic deformation and damage of titanium alloys were investigated at the mesoscale level by the numerical simulation method. It was shown that localization of plastic deformation under tension at high strain rates depends on grain size distribution. The critical fracture stress of alloys depends on relative volumes of coarse grains in representative volume. Microcracks nucleation at quasi-static and dynamic loading is associated with strain localization in ultra-fine grained partial volumes. Microcracks arise in the vicinity of coarse and ultrafine grains boundaries. It is revealed that the occurrence of a bimodal grain size distributions causes increased ductility, but decreased tensile strength of UFG alloys. The increase in fine precipitation concentration results not only strengthening but also an increase in ductility of UFG alloys with bimodal grain size distribution.

1 Introduction

Hexagonal close-packed (HCP) metals, such as Ti, Mg, Zn and Zr, are of interest for engineering and medical applications due to their unique combination of high ductility and strength. In recent years, intensive efforts have been focused on investigations of the physical and mechanical properties of alloys, whose grain structure is formed by surface rolling, severe plastic deformation, selective laser melting, or selective laser sintering, and friction stir processing [1,2,3,4,5].

Recently Long et al. showed a bimodal microstructure formation in the ultrafine-grained Ti–6Al–4V alloy produced by means of the spark plasma sintering of a mixture of ball-milled and unmilled powders [6]. The additive manufacturing technology of HCP metals opens new possibilities for obtaining parts from alloys combining high strength, ductility, and fracture toughness.

Usually, the formation of nano-sized and ultra-fine grained structures in metal alloys leads to increased strength and decreased ductility. The low ductility of ultrafine (UFG) alloys limits their applications as advanced engineering materials. In recent years it was found that the alloys with a bimodal grain size distribution may exhibit increased yield strength without reducing ductility [7, 8]. Guo showed the ductility of fine-grained (FG) Zr with an average grain size of 2–3 μm was 17% higher than that of coarse-grained alloy [2]. Pozdnyakov [9], Malygin [10], Ulacia [11] showed that the bimodal grain distribution can be formed in light alloys by means of severe plastic deformation and follow-up heat treatment. It was revealed that hexagonal close-packed (HCP) alloys with a bimodal grain size distribution exhibit a number of anomalies in mechanical behavior [12, 13]. Therefore, the optimization of strength and ductility requires a profound knowledge of volume fraction and distribution of ultra-fine grains and coarse grain in multi-modal alloys. Research of the influence of the grain structure on the strength and ductility of the alloys under cyclic loadings, dynamic loadings, quasistatic loadings are carried out using experimental methods and by computer simulation [14,15,16,17].

Berbenni proposed a theoretical micromechanical model taking into account the grain size distribution and representing the accommodation of grain deformation in HCP metals (Zirconium-$\alpha$) [7]. Raeisinia proposed a model to examine the effect of unimodal and bimodal grain size distributions on the uniaxial tensile behavior of a number of polycrystals [12]. The model demonstrated that bimodal grain size distributions have enhanced macro mechanical properties as compared with their unimodal counterparts. The authors of this article proposed a multiscale model of UFG metals with bimodal grain size to predict the localization of plastic flow in UFG light alloys under dynamic loads with respect to the ratio of volume concentrations of small and large grains. Results of calculations have shown increased dynamic ductility of UFG titanium and magnesium alloys, when the specific volume of coarse grains is greater than 30%.

Zhu proposed a micromechanics-based model to investigate the mechanical behavior of polycrystalline dual-phase metals with a bimodal grain size distribution, and fracture by means of nano/microcracks generation during plastic deformation. Results have shown that the volume fraction of coarse grains controls the strength and ductility of metals [18,19,20,21]. Clayton developed a continuum model of crystal plasticity for the interpretation of experimental data on shock wave propagation and spall fracture in polycrystalline aggregates [22]. The model accounted for complex features of the mechanical response of alloys: plastic anisotropy, large volumetric strain, heat conduction, thermos-elastic heating, rate- and temperature-dependent flow stress. Magee proposed a multiscale modeling technique to simulate the microstructural deformation of an alloy with bimodal grain size distribution. The simulation has shown that intergranular cracks nucleate at the coarse grains/ultra-fined grains interfaces [23]. Although much research is carried out on the mechanical properties of alloys with a bimodal grain size distribution, a number of issues remains poorly understood. The effect of the bimodal grain structure of alloys on the ultimate strain to failure at high strain rates is poorly studied [24]. The laws of localization of plastic deformation and the laws of damage accumulation in HCP alloys with a bimodal grain size distribution under dynamic impacts are not well studied. These problems are of great practical importance and are associated with the transition to new technologies for digital design and production of technical and medical products.

In this paper, we develop a multilevel approach to study the mechanical behavior of HCP alloys in a wide range of strain rates.

2 Computational Model

Titanium, zirconium, and magnesium alloys with a hexagonal closed-packed (HCP) structure have a significant low crystal symmetry compared to the face-centered cubic (FCC) and body-centered cubic (BCC) crystal structures of engineering alloys. The mechanical behavior of HCP alloys under quasistatic and dynamic loading at temperatures $T/T_{m}$ less than 0.5 is determined by dislocation mechanisms and twinning [25,26,27,28,29]. Authors used modifications of the constitutive equations developed in the framework of the micro-dynamical approach and taking into account the thermally activated dislocation mechanisms [15,16,17, 30,31,32].

The grain sizes and the grain-boundary phase structure affect the glide of dislocations and the formation of dislocation substructures during the plastic flow [27].

Mechanical response of polycrystalline alloys can be described by parameters of states averaging over the model representative volume element (RVE). Therefore, it is required for model volume to represent not only a given grain size distribution but also realistic values of the physical properties of the system.

We use the approach of a finite mixture model for the estimation of average sizes in multimodal grain size distribution [7, 17, 33].

The multimodal grain size distribution described by probability density function $g(d_{g} )$. Distribution $g(d_{g} )$ is a mixture of $k$ component distributions $g_{1}$, $g_{2}$, $g_{3}$ of ultra-fined grains (UFG), fine grains (FG), coarse grains (CG), respectively:

$$ g(d_{g} ) = \sum\limits_{k = 1}^{m} {\lambda_{k} g_{k} (d_{g} )} , $$

(1)

where $\lambda_{k}$ are the mixing weights, $\lambda_{k} > 0$, $\sum\nolimits_{k = 1}^{3} {\lambda_{k} = 1}$, $k = 1,2,3$.

This method allows us to determine the multimodal grain size distribution function and the range of grain size groups (UFG, FG, CG). In this paper, we present simulation results for unimodal and bimodal (UFG and CG) grain distribution. We used experimental data of grain size distribution of alloys after severe plastic deformation to calibrate the computational model.

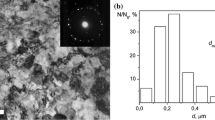
The RVE can be created using the experimental data on grain structures obtained by the analysis of Electron Backscatter Diffraction (EBSD) based on scanning electron microscopy (SEM) [34,35,36]. This analysis gives quantitative information about sizes and shapes of grains, Euler angles, angles of misorientation at the grain/subgrain boundaries with angular resolution ~0.5°. The shape coefficient was determined by the relation of minimal grain size to maximal size $\left( {\xi_{k} = d_{g}^{\hbox{min} } /d_{g}^{\hbox{max} } } \right)_{k}$, where $k$ is the number of grain size group.

The analysis of grain structure distributions has shown that there are several types of grains structure characterized by unimodal (near log-normal) distribution, and bimodal grain size distribution, multimodal grain size distribution [2, 7, 8, 35].

The specific volume of ultrafine grains (with grain size $100\,{\text{nm}} < d_{g} < 1\,\upmu{\text{m}}$), microstructural grains $\left( {1 < d_{g} < 10\,\upmu{\text{m}}} \right)$, and coarse grains $\left( {10\,\upmu{\text{m}} < d_{g} < d_{g} \hbox{max} } \right)$ was estimated using the probability density function $g\left( {d_{g} } \right)$ of grain size distribution:

$$ C_{UFG} = \int\limits_{{d_{g}^{\hbox{min} } }}^{{1\,\upmu{\text{m}}}} {g_{1} (x)d} x,\quad C_{FG} = \int\limits_{{1\upmu{\text{m}}}}^{{10\upmu{\text{m}}}} {g_{2} (x)d} x,\;\;C_{CG} = \int\limits_{{10\,\upmu{\text{m}}}}^{{d_{g}^{\hbox{max} } }} {g_{3} (x)d} x, $$

(2)

where $C_{UFG}$, $C_{FG}$, $C_{CG}$ are specific volumes of UFG, FG, and CG, $g_{1}$, $g_{2}$, $g_{3}$ are the probability density functions of UFG, FG, and CG systems, respectively.

The relative volume of coarse and ultra-fine grains in model RVE was determined in accordance with the probability density function of the grain size distribution.

Figure 1 shows a 3D RVE model of a titanium alloy with a bimodal grain size distribution. An RVE with dimensions of 14 × 8 × 1 (μm)³ was used.

Fig. 1

Scheme of boundary conditions

Computational domains were meshed with eight-node linear bricks and reduced integration together with hourglass control.

The kinematic boundary conditions correspond to macroscopic tension. The scheme of boundary conditions is shown in Fig. 1.

$$ \begin{aligned} & u_{x} (x_{k} ,t) = 0,\quad x_{k} \in S_{1} \\ & u_{x} (x_{k} ,t) = v_{x} ,\quad x_{k} \in S_{2} \\ & \sigma_{22} = 0,\quad x_{k} \in S_{3} ,\;\;x_{k} \in S_{4} \\ & u_{z} = 0,\quad x_{k} \in S_{5} ,\;\;x_{k} \in S_{6} \\ & u_{k}^{A} - u_{k}^{B} = 0,\quad \sigma_{n}^{A} = - \sigma_{n}^{B} ,\;\;k = 1,2,3,\;\;x_{k} \in S_{7} \\ \end{aligned} $$

(3)

where $u_{k}^{A}$, $u_{k}^{B}$ are the projections of the displacement rate onto the external normal to the boundary $S_{7}$ of the grain and the grain boundary phase at the boundary points, respectively, $\sigma_{n}^{A} , \, \sigma_{n}^{B} \,$ are the components of the surface forces along the external normal $\vec{n}$ to the boundary $S_{7}$, respectively, $x_{k}$ is the Cartesian coordinate.

Mechanical behavior at the mesoscale level is described within the approach of the damaged elastic-plastic medium. The system of equations includes:

Conservation equations (4);

Kinematic relations (5);

Constitutive relations (8);

Equation of State (9);

Relaxation equation for the deviatoric stress tensor (10).

$$ \frac{d\rho }{dt} = \rho \frac{{\partial u_{i} }}{{\partial x_{i} }},\quad \frac{{\partial \sigma_{ij} }}{{\partial x_{j} }} = \rho \frac{{du_{i} }}{dt},\;\;\rho \frac{dE}{dt} = \sigma_{ij} \dot{\varepsilon }_{ij} , $$

(4)

where $\rho$ is the mass density, $u_{i}$ is the components of the particle velocity vector, $x_{i}$ is the Cartesian coordinates, $i = 1,2,3$, $E$ is the specific internal energy, $\sigma_{ij}$ are the components of the effective stress tensor of the damaged medium, $\dot{\varepsilon }_{ij}$ are the components of strain rate tensor.

Kinematics of the medium was described by the local strain rate tensor:

$$ \dot{\varepsilon }_{ij} = (1/2)[\partial u_{i} /\partial x_{j} + \partial u_{j} /\partial x_{i} )],\quad \dot{\omega }_{ij} = (1/2)[\partial u_{i} /\partial x_{j} \, - \partial u_{j} /\partial x_{i} )], $$

(5)

where $\dot{\varepsilon }_{ij} ,\dot{\omega }_{ij}$ are the components of strain rate tensor and the bending-torsion tensor, $u_{i}$ is the component of particles velocity vector.

The components of strain rate tensor are expressed by the sum of elastic and inelastic terms:

$$ \dot{\varepsilon }_{ij}^{{}} = \dot{\varepsilon }_{ij}^{e} + \dot{\varepsilon }_{ij}^{p} ,\quad \dot{\varepsilon }_{ij}^{p} = \dot{e}_{ij}^{p} + \delta_{ij} \dot{\varepsilon }_{kk}^{p} /3, $$

(6)

where $\dot{\varepsilon }_{ij}^{e}$ are the components of the elastic strain rate tensor, $\dot{\varepsilon }_{ij}^{p}$ are the components of the inelastic strain rate tensor.

The bulk inelastic strain rate is described by relation:

$$ \dot{\varepsilon }_{kk}^{p} = \dot{f}_{growth} /(1 - f), $$

(7)

where $f$ is the damage parameter, the substantial time derivative is denoted via dot notation.

The bulk inelastic strain rate $\varepsilon_{kk}^{p}$ is equal to zero only when the material is undamaged.

$$ \sigma_{ij} = \sigma_{ij}^{(m)} \varphi (f),\quad \sigma_{ij}^{(m)} = - p^{(m)} \delta_{ij} + S_{ij}^{(m)} , $$

(8)

$$ \begin{aligned} p^{(m)} & = p_{{_{x} }}^{(m)} (\rho ) +\Gamma (\rho )\rho E_{T} ,\quad E_{T} = C_{p} T, \\ p_{x}^{(m)} & = \frac{3}{2}B_{0} \cdot \left( {(\rho_{0} /\rho )^{ - 7/3} - (\rho_{0} /\rho )^{ - 5/3} } \right)\left[ {1 - \frac{3}{4}(4 - B_{1} ) \cdot ((\rho_{0} /\rho )^{ - 2/3} - 1)} \right] \\ \end{aligned} $$

(9)

$$ DS_{ij}^{(m)} /Dt = 2\mu (\dot{\varepsilon }_{ij}^{e} - \delta_{ij} \dot{\varepsilon }_{kk}^{e} /3),\quad \dot{e}_{ij}^{p} = \lambda \partial\Phi /\partial \sigma_{ij} , $$

(10)

the function $\varphi (f)$ establishes a relation between the effective stresses of the damaged medium and the stresses in the condensed phase, $\Gamma$ is the Grüneisen coefficient, $\rho_{0}$ is the initial mass density of the condensed phase of the alloy, $\gamma_{R} , \, \rho_{R} , \, n, \, B_{0} , \, B_{1}$ are the material’s constants, $C_{p}$ is the specific heat capacity, $D\left( \cdot \right)/Dt$ is the Jaumann derivative, $\mu$ is the shear modulus, $\dot{f}_{growth}$ is the void growth rate, $f$ is the void volume fraction in the damaged medium, $\dot{\lambda }$ is the plastic multiplier derived from the consistency condition $\dot{\Phi } = 0$, and $\Phi$ is the plastic potential. The plastic potential was described using the Gurson–Tvergaard model (GTN) [32, 37,38,39].

The Grüneisen coefficient $\Gamma$ was equal to 1.42 and 1.09 for Mg–3Al–1Zn and Ti–5Al–2.5Sn, respectively.

The function $\varphi (f)$ takes the form of $(1 - f\,)$ for pressure and is implicitly defined for the deviatoric stress tensor [40].

The temperature rise associated with energy dissipation during plastic flow can be evaluated by relation [25, 32]:

$$ T = T_{0} + \int\limits_{0}^{{\varepsilon_{eq}^{p} }} {(\beta /\rho C_{p} )\sigma_{eq} d\varepsilon_{eq}^{p} } , $$

(11)

where $T_{0}$ is the initial temperature and $\beta \sim 0.9$ is the parameter representing a fraction of plastic work converted into heat.

The specific heat capacity for Ti–5Al–2.5Sn titanium was calculated by the phenomenological relations within the temperature range 293–1115 K [32]:

$$ C_{p} = 248.389 + 1.53067T - 0.00245T^{2} \,({\text{J}}/{\text{kg K}})\;\;{\text{for}}\;\;0 < T < T_{\alpha \beta } = 1320\,{\text{K}}, $$

(12)

The temperature dependence of the shear modulus for alpha titanium alloy was described by the equation:

$$ \mu (T) = 48.66 - 0.03223T\,({\text{GPa}}),\quad (273K < T < 1200\,{\text{K}}). $$

(13)

The flow stress was described by equation:

$$ \begin{aligned} \sigma _{s} & = \sigma _{{s0}} \exp \left\{ {C_{1} \sqrt {(1 - T/T_{m} )} } \right\} + C_{2} \sqrt {1 - \exp \{ - k_{0} \varepsilon _{{eq}}^{p} \} } \\ & \quad \exp \{ - C_{3} T\} \exp \left\{ {C_{4} T\ln (\dot{\varepsilon }_{{eq}} /\dot{\varepsilon }_{{eq0}} )} \right\}, \\ \end{aligned} $$

(14)

where $\dot{\varepsilon }_{eq}^{{}} \, = [(2/3)\dot{\varepsilon }_{ij} \dot{\varepsilon }_{ij} \,]^{1/2}$, $\dot{\varepsilon }_{eq0}^{{}} = \gamma_{1} \exp \{ - T/\gamma_{2} \} + \gamma_{3}$, $\varepsilon_{eq}^{p} = \int\nolimits_{0}^{t} {\dot{\varepsilon }_{eq}^{p} dt}$ is the equivalent plastic strain $\gamma_{1} = 2 1 1 5. 0 8 6 1 5\,{\text{s}}^{ - 1}$, $\gamma_{2} = 3 8. 2 6 5 8 9\,{\text{K}}$, $\gamma_{3} = 9. 8 2 3 8 8\times 1 0^{ - 5} \,{\text{s}}^{ - 1}$ and $T_{m}$ is the melting temperature, ${\dot{\varepsilon }}_{eq0}^{{}} = 1.0\,s^{ - 1}$.

$$ \sigma_{s} = \sigma_{s0} + C_{5} (\varepsilon_{eq}^{p} )^{{n_{1} }} + k_{hp} d_{g}^{ - 1/2} - C_{2} \exp \left\{ { - C_{3} T + C_{4} T\ln (\dot{\varepsilon }_{eq}^{{}} /\dot{\varepsilon }_{eq0}^{{}} )} \right\}, $$

(15)

where $\,\sigma_{s0} ,C_{5} ,n_{1} ,k_{hp} ,C_{2} ,C_{3} ,C_{4}$ are the material parameters, $d_{g}$ is the average grain size.

The impact of grain size distribution on the stress of hcp alloys with average grain sizes in single-mode and bimodal microstructures was taken into account in Eq. (15) by analogy with the Hall-Petch relation.

Material parameters of Ti–5Al–2.5Sn and Mg–3Al–1Zn are shown in Tables 1 and 2, respectively.

Table 1 Material parameters of Eq. (14)

Table 2 Material parameters of Eq. (15)

The influence of damage on the flow stress was taken into account using the Gurson–Tvergaard model [32, 36, 38]:

$$ (\sigma_{eq}^{2} /\sigma_{s}^{2} ) + 2q_{1} f^{*} \cosh ( - q_{2} p/2\sigma_{s} ) - 1 - q_{3} (f^{*} )^{2} = 0, $$

(16)

where $\sigma_{s}$ is the yield stress and $q_{1}$, $q_{2}$ and $q_{3}$ are the model parameters, $\sigma_{eq} \, = \,\sqrt {\frac{3}{2}\sigma_{ij} \sigma_{ij} - \frac{1}{2}\sigma_{kk} \sigma_{kk} } \,$.

$$ \begin{aligned} \dot{f} & = \dot{f}_{nucl} + \dot{f}_{growth} , \\ \dot{f}_{nucl} & = \varepsilon^{p}_{{^{eq} }} (f_{N} /s_{N} )\exp \left\{ { - 0.5[(\varepsilon^{p}_{{^{eq} }} - \varepsilon_{N} )/s_{N} ]^{2} } \right\}, \\ \dot{f}_{growth} & = (1 - f)\dot{\varepsilon }_{kk}^{p} , \\ \end{aligned} $$

(17)

where $\varepsilon_{N}$ and $S_{N}$ are the average nucleation strain and the standard deviation, respectively. The amount of nucleating voids is controlled by the parameter $f_{N}$

$$ \begin{aligned} f^{*} & = f\;\;{\text{for}}\;\;f \le f_{c} ; \\ f^{*} & = f_{c} + (\bar{f}_{F} - f_{c} )/(f_{F} - f_{c} )\;\;{\text{for}}\;\;f > f_{c} , \\ \end{aligned} $$

(18)

where $\bar{f}_{F} \,\, = \,(q_{1} + \,\sqrt {q_{1}^{2} - q_{3} } )/q_{3}$.

The final stage in ductile fracture comprises the voids coalescence [38]. This causes softening of the material and accelerated growth rate of the void fraction $f^{*}$.

The model parameters for Ti–5Al–2.5Sn and Mg–3Al–1Zn were determined using numerical simulation. These parameters are given in Table 3.

Table 3 Dimensionless parameters for the Gurson–Tvergaard–Needleman (GTN) model for alpha titanium and magnesium alloys

We use the ductile fracture criteria for alloys at the room and elevated temperatures owing to relatively low melting temperature [31, 38, 41].

Finite elements are removed from the grid model and free boundary conditions are introduced at the formed boundary, when the local fracture criterion is met.

Specific features of mechanical properties of nanostructured materials are connected to distinctions of matter properties in a crystalline phase of grains and in the boundary of grains. A decrease in the mass density of nanostructured materials is caused by increased defect’s density and relative volume of grain boundary phase.

3 Results and Discussion

Figure 2 shows the fields of equivalent plastic strain under tension at $v_{x} = 2.3\;{\text{m/s}}$. Damages were localized near the grain boundary of coarse grains.

Fig. 2

Effective plastic strain field at time, a 0.332 μs, b 0.3895 μs, c 0.398 μs in Ti–5Al–2.5Sn alloy with bimodal grain structure

Damage nucleation in alloys with a bimodal grain size distribution occurs in shear bands and zones of their intersection.

These results agree with experimental observations of strain localization and fracture of titanium alloys by Sharkeev [42], authors of this work [32, 43], Valoppi [44] and Zheng [45]. It is significant that increases in fine precipitates concentration in alloys caused the increase in resistance to plastic flow within both coarse and ultrafine grains.

Thus, the fracture of alloys with bimodal grain structures is caused by the damage nucleation at the boundary of coarse grains with an ultrafine-grained structure and further growth of damage in mesoscopic bands of localized plastic deformation.

Thus, the process of fracture of alloys with bimodal grain structures is associated with the formation of mesoscopic bands of localized plastic deformation.

The segregation of impurity atoms in the grain-boundary phase affects the formation of plastic shear bands [14, 46].

The mechanical properties of the grain boundary phase were varied to take into account the effect of segregation of impurity atoms on the yield stress in the simulation.

Figure 2b shows the field of equivalent strains, indicating that the formation of cracks in large grains can be accompanied by a change in the orientation of the shear localization bands at the mesoscopic level. This occurs as a result of a change in the orientation of the plane of maximum shear stresses during the evolution of a triaxial stress state near cracks. A macroscopic crack obtained by modeling the tension of flat samples has the same configuration as the cracks observed in experimental studies by Verleysen [24] and authors of this work [31, 32].

The averaged strain along the axis of tension of the computational domain at the moment of crack crossed the representative volume was interpreted as the ultimate strain to fracture of the alloy.

Figure 3 shows the dependence of strain to fracture of titanium and magnesium alloys on the logarithm of strain rates. Experimental data reported by Ulacia for coarse-grained Mg–3Al–1Zn alloy are marked by filled square symbols [11]. The experimental data for the Ti–5Al–2.5Sn alloy are shown by filled triangular symbols [32, 47].

Fig. 3

The strain to fracture versus logarithm of strain rates for magnesium and titanium alloys with a unimodal (curve 2, 3) and a bimodal grain sizes distribution (curve 1, the concentration of coarse grains is 70%)

Strains to fracture behave nonmonotonically and nonlinearly with increasing strain rate in the range from 0.001 to 1000 1/s as shown in Fig. 3 (Curves 1 and 3). In coarse-grained HCP alloys, this is related to more intense twinning under dynamic loading.

Curve 2 is obtained by the approximation of calculated values of the strains to fracture under tension of a magnesium alloy with a bimodal grain structure with a specific volume of large grains of 70%. With an increase in the concentration of micron and submicron grains in the alloy, the strain to failure under tension decreases nonlinearly. The simulation results agree with the available experimental data [11, 45,46,47,48,49,50].

The strain to fracture of alloy with bimodal grain size distribution versus specific volume of coarse grains under quasi-static tension can be described by the relation:

$$ \varepsilon_{f}^{n} = 0.01\exp (C_{cg} /0.363), $$

(19)

where $\varepsilon_{f}^{n}$ is the strain to fracture under quasi-static tension, $C_{cg}$ is the specific volume of coarse grains.

Equation (19) describes the ductility of alloys with a bimodal grains distribution versus the specific volume of coarse grains. The increase in ductility of HCP alloys under quasi-static tension occurs when a specific volume of coarse grains is greater than 30%.

4 Conclusions

The multiscale approach was used in the computer simulation of fracture of magnesium and titanium alloys at high strain rates. Structured RVEs were proposed to predict the mechanical properties of alloys taking into account the grain size distribution and the segregation impurity atoms in the grain-boundary.

The results of computer simulation showed that damage nucleation in alloys with a bimodal grain size distribution occurs in the shear bands and their intersection zones. Damage arises at the boundary between coarse- and ultrafine-grained structures. Further damage growth occurs in the mesoscopic bands of localized plastic deformation.

Thus the computer simulation can be used to estimate the influence of grains size distribution on the dynamic strength and ductility of HCP alloys.

Localization of plastic flow in HCP alloys with bimodal grain size distribution under tension at high strain rates depends on the ratio between volume concentrations of fine and coarse grains. As a result, the strain to fracture of hcp alloys with bimodal grain size distribution varies nonlinearly with tensile strain rate in the range from 0.001 to 1000 1/s.

The dynamic ductility of HCP alloys with bimodal grain size distribution is increased when a specific volume of coarse grains is greater than 30%.