Simple algebras and involutions

Abstract

In this chapter, we examine further connections between quaternion algebras, simple algebras, and involutions.

In this chapter, we examine further connections between quaternion algebras, simple algebras, and involutions.

1 $\triangleright$ The Brauer group and involutions

An involution on an F-algebra B induces an isomorphism , for example such an isomorphism is furnished by the standard involution on a quaternion algebra B. More generally, if $B_1,B_2$ are quaternion algebras, then the tensor product $B_1 \otimes _F B_2$ has an involution provided by the standard involution on each factor giving an isomorphism to $(B_1 \otimes _F B_2)^{op } \simeq B_1^{op } \otimes _F B_2^{op }$—but this involution is no longer a standard involution (Exercise 8.1). The algebra $B_1 \otimes _F B_2$ is a central simple algebra over F called a biquaternion algebra. In some circumstances, we may have

$$\begin{aligned} B_1 \otimes _F B_2 \simeq {{\,\mathrm{M}\,}}_2(B_3) \end{aligned}$$

(8.1.1)

where $B_3$ is again a quaternion algebra, and in other circumstances, we may not; following Albert, we begin this chapter by studying (8.1.1) and biquaternion algebras in detail.

To this end, we look at the set of isomorphism classes of central simple algebras over F, which is closed under tensor product; if we think that the matrix ring is something that is ‘no more complicated than its base ring’, it is natural to introduce an equivalence relation on central simple algebras that identifies a division ring with the matrix ring (of any rank) over this division ring. More precisely, if $A,A'$ are central simple algebras over F we say $A,A'$ are Brauer equivalent if there exist $n,n' \ge 1$ such that ${{\,\mathrm{M}\,}}_{n}(A) \simeq {{\,\mathrm{M}\,}}_{n'}(A')$. In this way, (8.1.1) reads $B_1 \otimes _F B_2 \sim B_3$. The set of Brauer equivalence classes [A] has the structure of a group under tensor product, known as the Brauer group ${{\,\mathrm{Br}\,}}(F)$ of F, with identity element [F] and inverse $[A]^{-1} = [A^{op }]$. The class $[B] \in {{\,\mathrm{Br}\,}}(F)$ of a quaternion algebra B is a 2-torsion element, and therefore so is a biquaternion algebra. In fact, by a striking theorem of Merkurjev, when ${{\,\mathrm{char}\,}}F \ne 2$, all 2-torsion elements in ${{\,\mathrm{Br}\,}}(F)$ are represented by a tensor product of quaternion algebras (see section 8.3).

Finally, our interest in involutions in Chapter 3 began with an observation of Hamilton: the product of a nonzero element with its involute in $\mathbb H$ is a positive real number (its norm, or square length). We then proved that the existence of such an involution characterizes quaternion algebras in an essential way. However, one may want to relax this setup and instead consider when the product of a nonzero element with its involute merely has positive trace. Such involutions are called positive involutions and they arise naturally in algebraic geometry: the Rosati involution is a positive involution on the endomorphism algebra of an abelian variety, and it is a consequence that this algebra (over $\mathbb Q$) is semisimple, and unsurprisingly quaternion algebras once again feature prominently (see sections 8.4–8.5).

2 Biquaternion algebras

Let F be a field. All tensor products in this section will be taken over F.

8.2.1

Let $B_1,B_2$ be quaternion algebras over F. The tensor product $B_1 \otimes B_2$ is a central simple algebra over F of dimension $4^2=16$ called abiquaternion algebra. A biquaternion algebra may be written as a tensor product of two quaternion algebras in different ways, so the pair is not intrinsic to the biquaternion algebra.

By the Wedderburn–Artin theorem (Main Theorem 7.3.10), we have exactly one of the three following possibilities for this algebra:

• $\bullet$ $B_1 \otimes B_2$ is a division algebra;

• $\bullet$ $B_1 \otimes B_2 \simeq {{\,\mathrm{M}\,}}_2(B_3)$ where $B_3$ is a quaternion division algebra over F; or

• $\bullet$ $B_1 \otimes B_2 \simeq {{\,\mathrm{M}\,}}_4(F)$.

We could combine the latter two and just say that $B_1 \otimes B_2 \simeq {{\,\mathrm{M}\,}}_2(B_3)$ where $B_3$ is a quaternion algebra over F, since ${{\,\mathrm{M}\,}}_2({{\,\mathrm{M}\,}}_2(F)) \simeq {{\,\mathrm{M}\,}}_4(F)$ as F-algebras.

Example 8.2.2

By Exercise 8.2, when ${{\,\mathrm{char}\,}}F \ne 2$ we have

$$\begin{aligned} \displaystyle {\biggl (\frac{a,b_1}{F}\biggr )} \otimes \displaystyle {\biggl (\frac{a,b_2}{F}\biggr )} \simeq {{\,\mathrm{M}\,}}_2(B_3) \end{aligned}$$

where $B_3=\displaystyle {\biggl (\frac{a,b_1b_2}{F}\biggr )}$. In particular, $\displaystyle {\biggl (\frac{a,b}{F}\biggr )} \otimes \displaystyle {\biggl (\frac{a,b}{F}\biggr )} \simeq {{\,\mathrm{M}\,}}_4(F)$, since $\displaystyle {\biggl (\frac{a,b^2}{F}\biggr )} \simeq {{\,\mathrm{M}\,}}_2(F)$.

Example 8.2.2 is no accident, as the following proposition indicates.

Proposition 8.2.3

(Albert). The following are equivalent:

• (i) There exists a quadratic field extension $K \supset F$ that can be embedded as an F-algebra in both $B_1$ and $B_2$;

• (ii) $B_1$ and $B_2$ have a common quadratic splitting field; and

• (iii) $B_1 \otimes B_2$ is not a division algebra.

Proof. The equivalence (i) $\Leftrightarrow$ (ii) follows from Lemma 5.4.7.

For the implication (i) $\Rightarrow$ (iii), for $i=1,2$ let $\alpha _i \in B_i$ generate K so $\alpha _i^2=t\alpha _i-n$ with $t,n \in F$. Let

$$\begin{aligned} \beta :=\alpha _1 \otimes 1 - 1 \otimes \alpha _2. \end{aligned}$$

Then

$$\begin{aligned} \begin{aligned} \beta (\alpha _1 \otimes 1 + 1 \otimes \alpha _2 - t)&= \alpha _1^2 \otimes 1 - 1 \otimes \alpha _2^2 - t\beta \\&= (t\alpha _1-n) \otimes 1 - 1 \otimes (t\alpha _2 - n) - t\beta = 0. \end{aligned} \end{aligned}$$

(8.2.4)

Therefore $\beta$ is a zerodivisor and $B_1 \otimes B_2$ is not a division algebra.

To finish, we prove (iii) $\Rightarrow$ (i). We have an embedding

$$\begin{aligned} B_1&\hookrightarrow B_1 \otimes B_2 \\ \alpha&\mapsto \alpha \otimes 1 \end{aligned}$$

and similarly $B_2$; the images of $B_1$ and $B_2$ in $B_1 \otimes B_2$ commute. Write $B_2=({K,b_2} \mid {F})$. Consider $(B_1)_K=B_1 \otimes K \subset B_1 \otimes B_2$; then $(B_1)_K$ is a quaternion algebra over K (with $\dim _F (B_1)_K=8$). If $(B_1)_K$ is not a division algebra, then K splits $B_1$ and $K \hookrightarrow B_1$ and we are done. So suppose that $(B_1)_K$ is a division algebra. Then

$$\begin{aligned} B_1 \otimes B_2 = (B_1)_K + (B_1)_K j \end{aligned}$$

is free of rank 2 as a left $(B_1)_K$-module.

Since $B_1 \otimes B_2 \simeq {{\,\mathrm{M}\,}}_2(B_3)$ is not a division algebra, there exists $\epsilon \in B_1 \otimes B_2$ nonzero such that $\epsilon ^2=0$. Without loss of generality, we can write $\epsilon =\alpha _1 \otimes z + j$ where $\alpha _1 \in B_1$ and $z \in K$. Then

$$\begin{aligned} 0=\epsilon ^2=\alpha _1^2\otimes z^2 + (\alpha _1 \otimes z)j + (\alpha _1 \otimes \overline{z})j+b_2. \end{aligned}$$

(8.2.5)

From the basis 1, j over $(B_1)_K$, if $\overline{z}=t-z$ with $t \in F$, we conclude that

$$\begin{aligned} \alpha _1 \otimes z + \alpha _1 \otimes (t-z) = \alpha _1 \otimes t = 0. \end{aligned}$$

Therefore $t=0$, and $z^2=c$ for some $c \in F^\times$. Then from (8.2.5) $c\alpha _1^2+b_2=0$ so $\alpha _1^2=-b_2/c$ and $B_1$ contains the quadratic field $F(\sqrt{-b_2c})$. But so does $B_2$, as $(zj)^2=-b_2c$ as well.

(For an alternate proof, see Jacobson [Jacn2009, Theorem 2.10.3].)

Remark 8.2.6. In view of Proposition 8.2.3, we say that two quaternion algebras $B_1,B_2$ over F are linked if they contain a common quadratic field extension $K \supseteq F$. For further discussion of biquaternion algebras and linkage in characteristic 2 (where one must treat separable and inseparable extensions differently), see Knus [Knu93], Lam [Lam2002], or Sah [Sah72]. Garibaldi–Saltman [GS2010] study the subfields of quaternion algebra over fields with ${{\,\mathrm{char}\,}}F \ne 2$.

From now on, we suppose that ${{\,\mathrm{char}\,}}F \ne 2$. (For the case ${{\,\mathrm{char}\,}}F = 2$, see Chapman–Dolphin–Laghbribi [CDL2015, §6].)

8.2.7

Motivated by Proposition 8.2.3, we consider the quadratic extensions represented by $B_1$ and $B_2$ encoded in the language of quadratic forms (recalling Lemma 5.5.4). Let

$$\begin{aligned} V=\{\alpha _1 \otimes 1 - 1 \otimes \alpha _2 \in B_1 \otimes B_2 : {{\,\mathrm{trd}\,}}(\alpha _1)={{\,\mathrm{trd}\,}}(\alpha _2)\}. \end{aligned}$$

Then $\dim _F V=6$, and we may identify $V=B_1^0 \otimes 1 - 1 \otimes B_2^0$. The reduced norm on each factor separately defines a quadratic form on V by taking the difference: explicitly, if $B_1=({a_1,b_1} \mid {F})$ and $B_2=({a_2,b_2} \mid {F})$, then taking the standard bases for $B_1,B_2$

$$\begin{aligned} Q(B_1,B_2)&\simeq \langle -a_1,-b_1,a_1b_1 \rangle \boxplus -\langle -a_2,-b_2,a_2b_2 \rangle \\&\simeq \langle -a_1,-b_1,a_1b_1,a_2,b_2,-a_2b_2 \rangle . \end{aligned}$$

The quadratic form $Q(B_1,B_2):V \rightarrow F$ is called the Albert form of the biquaternion algebra $B_1 \otimes B_2$.

We then add onto Proposition 8.2.3 as follows.

Proposition 8.2.8

(Albert). Let $B_1 \otimes B_2$ be a biquaternion algebra over F (with ${{\,\mathrm{char}\,}}F \ne 2$) with Albert form $Q(B_1,B_2)$. Then the following are equivalent:

• (i) $B_1,B_2$ have a common quadratic splitting field;

• (iv) $Q(B_1,B_2)$ is isotropic.

Proof. The implication (ii) $\Rightarrow$ (iv) follows by construction 8.2.7. To prove (iv) $\Rightarrow$ (ii), without loss of generality, we may suppose $B_1,B_2$ are division algebras; then an isotropic vector of Q corresponds to elements $\alpha _1 \in B_1$ and $\alpha _2 \in B_2$ such that $\alpha _1^2=\alpha _2^2=c \in F^\times$. Therefore $K=F(\sqrt{c})$ is a common quadratic splitting field.

Remark 8.2.9. Albert’s book [Alb39] on algebras still reads well today. The proof of Proposition 8.2.3 is due to him [Alb72]. (“I discovered this theorem some time ago. There appears to be some continuing interest in it, and I am therefore publishing it now.”) Albert used Proposition 8.2.8 to show that

$$\begin{aligned} B_1=\displaystyle {\biggl (\frac{-1,-1}{F}\biggr )} \quad \text {and} \quad B_2=\displaystyle {\biggl (\frac{x,y}{F}\biggr )} \end{aligned}$$

over $F=\mathbb R (x,y)$ have tensor product $B_1 \otimes _F B_2$ a division algebra by verifying that the Albert form $Q(B_1,B_2)$ is anisotropic over F. See Lam [Lam2005, Example VI.1] for more details. For the fields of interest in this book (local fields and global fields), a biquaternion algebra will never be a division algebra—the proof of this fact rests on classification results for quaternion algebras over these fields, which we will take up in earnest in Part II.

3 Brauer group

Motivated to study the situation where $B_1 \otimes B_2 \simeq {{\,\mathrm{M}\,}}_2(B_3)$ among quaternion algebras $B_1,B_2,B_3$ more generally, we now turn to the Brauer group.

Let ${{\,\mathrm{CSA}\,}}(F)$ be the set of isomorphism classes of central simple F-algebras. The operation of tensor product on ${{\,\mathrm{CSA}\,}}(F)$ defines a commutative binary operation with identity F, but inverses are lacking (for dimension reasons). So we define an equivalence relation $\sim$ on ${{\,\mathrm{CSA}\,}}(F)$ by

(8.3.1)

and we say then that $A,A'$ are Brauer equivalent. In particular, $A \sim {{\,\mathrm{M}\,}}_n(A)$ for all $A \in {{\,\mathrm{CSA}\,}}(F)$ as needed above.

Lemma 8.3.2

The set of equivalence classes of central simple F-algebras under the equivalence relation $\sim$ has the structure of an abelian group under tensor product, with identity [F] and inverse $[A]^{-1}=[A^{op }]$.

Proof. By Exercise 8.5, the operation is well-defined: if $A,A' \in {{\,\mathrm{CSA}\,}}(F)$ and $A' \sim A'' \in {{\,\mathrm{CSA}\,}}(F)$ then $A \otimes A' \sim A \otimes A''$. To conclude, we need to show that inverses exist. This is furnished by Lemma 7.5.4: if $\dim _F A = n$ and $A^{op }$ is the opposite algebra of A (3.2.2) then the map

$$\begin{aligned} A \otimes _{F} A^{op }&\rightarrow {{\,\mathrm{End}\,}}_F(A) \simeq {{\,\mathrm{M}\,}}_{n}(F) \\ \alpha \otimes \beta&\mapsto (\mu \mapsto \alpha \mu \beta ) \end{aligned}$$

is an isomorphism of F-algebras, so $[A]^{-1}=[A^{op }]$ provides an inverse to [A]. $\square$

So we make the following definition.

Definition 8.3.3

The Brauer group of F is the set ${{\,\mathrm{Br}\,}}(F)$ of Brauer equivalence classes of central simple F-algebras (8.3.1) under the group operation of tensor product.

8.3.4

Let B be a quaternion algebra over F. We have $B \simeq {{\,\mathrm{M}\,}}_2(F)$ if and only if $[B]=[F]$ is the identity. Otherwise, B is a division algebra. Then the standard involution gives an F-algebra isomorphism , and hence in ${{\,\mathrm{Br}\,}}(F)$ we have $[B]^{-1}=[B]$ and so [B] is an element of order 2. Since ${{\,\mathrm{Br}\,}}(F)$ is abelian, it follows that biquaternion algebras, or more generally tensor products $B_1 \otimes \dots \otimes B_t$ of quaternion algebras $B_i$, are also elements of order at most 2 in ${{\,\mathrm{Br}\,}}(F)$.

Theorem 8.3.5

(Merkurjev). Let ${{\,\mathrm{char}\,}}F \ne 2$. Then ${{\,\mathrm{Br}\,}}(F)[2]$ is generated by quaternion algebras over F, i.e., every (finite-dimensional) central division F-algebra with involution is Brauer equivalent to a tensor product of quaternion algebras.

Remark 8.3.6. More generally, Merkurjev [Mer82] proved in 1981 that a division algebra with an involution is Brauer equivalent to a tensor product of quaternion algebras; more precisely, if D is a division F-algebra with (not necessarily standard) involution, then there exists $n \in \mathbb Z _{\ge 1}$ such that ${{\,\mathrm{M}\,}}_n(D)$ is isomorphic to a tensor product of quaternion algebras. His theorem, more properly, says that the natural map $K_2(F) \rightarrow {{\,\mathrm{Br}\,}}(F)[2]$ is an isomorphism. (Some care is required in this area: for example, Amitsur–Rowen–Tignol [ART79] exhibit a division algebra D of degree 8 with involution that is not a tensor product of quaternion algebras, but ${{\,\mathrm{M}\,}}_2(D)$ is a tensor product of quaternion algebras.) For an elementary proof of Merkurjev’s theorem, see Wadsworth [Wad86].

Remark 8.3.7. Just as quaternion algebras are in correspondence with conics (Corollary 5.5.2), with a quaternion algebra split if and only if the corresponding conic has a rational point (Theorem 5.5.3), similarly the Brauer group of a field has a geometric interpretation (see e.g. Serre [Ser79, §X.6]): central simple algebras correspond to Brauer–Severi varieties—for each degree $n \ge 1$, both are parametrized by the Galois cohomology set $H^1({{\,\mathrm{Gal}\,}}(F{}^{sep }\,|\,F),{{\,\mathrm{PGL}\,}}_n)$.

4 Positive involutions

We now turn to study algebras with involution more general than a standard involution. Throughout this section, let $F \subseteq \mathbb R$ be a subfield of $\mathbb R$ and B a finite-dimensional F-algebra. We define the trace map ${{\,\mathrm{Tr}\,}}:B \rightarrow \mathbb R$ by the trace of left multiplication.

Definition 8.4.1

An involution ${}^*:B \rightarrow B$ ispositive if ${{\,\mathrm{Tr}\,}}(\alpha ^*\alpha )>0$ for all $\alpha \in B \smallsetminus \{0\}$.

Since the map $(\alpha ,\beta ) \mapsto {{\,\mathrm{Tr}\,}}(\alpha ^*\beta )$ is bilinear, an involution ${}^*$ on B is positive if and only if ${{\,\mathrm{Tr}\,}}(\alpha ^*\alpha )>0$ for $\alpha$ in a basis for B and so is positive if and only if its extension to $B \otimes _F \mathbb R$ is positive.

Example 8.4.2

The standard involutions on $\mathbb R$, $\mathbb C$, and $\mathbb H$, defined by $\alpha \mapsto {{\,\mathrm{trd}\,}}(\alpha )-\alpha$, are positive involutions. The standard involution on $\mathbb R \times \mathbb R$ is not positive since for $\alpha =(x_1,x_2) \in \mathbb R \times \mathbb R$ we have ${{\,\mathrm{Tr}\,}}(\alpha \overline{\alpha })=2x_1x_2$. The standard involution on ${{\,\mathrm{M}\,}}_2(\mathbb R )$ is also not positive, since for $\alpha \in {{\,\mathrm{M}\,}}_2(\mathbb R )$ we have ${{\,\mathrm{Tr}\,}}(\alpha \overline{\alpha })=4\det (\alpha )$.

8.4.3

Let D be one of $\mathbb R$, $\mathbb C$, or $\mathbb H$. Let $B={{\,\mathrm{M}\,}}_n(D)$. The standard involution $\overline{\phantom {x}}$ on D extends to an involution on B, acting on coordinates. Theconjugate transpose (or, perhaps better the standard involution transpose) map

$$\begin{aligned} {}^*:B&\rightarrow B \\ \alpha&\mapsto \alpha ^*=\overline{\alpha }^{\textsf {t} }\end{aligned}$$

also defines an involution on B, where ${}^{\textsf {t} }$ is the transpose map. If $\alpha =(a_{ij})_{i,j=1,\dots ,n}$ then

$$\begin{aligned} {{\,\mathrm{Tr}\,}}(\alpha ^*\alpha )=n(\dim _\mathbb{R } D)\sum _{i,j=1}^n \overline{a_{ij}}a_{ij}>0; \end{aligned}$$

(8.4.4)

thus ${}^*$ is positive, and the norm $\alpha \mapsto {{\,\mathrm{Tr}\,}}(\alpha ^*\alpha )$ is (an integer multiple of) the Frobenius norm on B.

We will soon see that every positive involution can be derived from the conjugate transpose as in 8.4.3. First, we reduce to the case where B is a semisimple algebra.

Lemma 8.4.5

Suppose that B admits a positive involution ${}^*$. Then B is semisimple.

Proof. We give two proofs. First, we appeal to Theorem 7.9.4: since the trace pairing is positive definite, it is nondegenerate and immediately B is semisimple.

For a second (more general) proof, let $J={{\,\mathrm{rad}\,}}B$ be the Jacobson radical of B. By Lemma 7.4.2, B is semisimple if and only if ${{\,\mathrm{rad}\,}}B=\{0\}$, and by Lemma 7.4.8, $J={{\,\mathrm{rad}\,}}B$ is nilpotent. Suppose for purposes of contradiction that $J \ne \{0\}$. Then there exists $n >0$ such that $J^n \ne \{0\}$ but $J^{n+1}=\{0\}$. Let $\epsilon \in J$ be such that $\epsilon ^n \ne 0$ but $\epsilon ^{n+1} =0$. The involution gives an isomorphism $B \rightarrow B^{\text {op}}$ taking maximal left ideals to maximal right ideals and therefore by Corollary 7.4.6 we conclude $J^*=J$. Thus $\epsilon ^n \epsilon ^*=0$ so ${{\,\mathrm{Tr}\,}}(\epsilon ^n (\epsilon ^*)^n)={{\,\mathrm{Tr}\,}}(\epsilon ^n (\epsilon ^n)^*)=0$, contradicting that ${}^*$ is positive. $\square$

8.4.6

Suppose B is semisimple with a positive involution ${}^*$, and let $B_i$ be a simple factor of B. Then ${}^*$ preserves $B_i$: for if $B_i^* = B_j \ne B_i$, then $B_j$ is a simple factor and $B_iB_j=0$ so ${{\,\mathrm{Tr}\,}}(B_i B_i^*)={{\,\mathrm{Tr}\,}}(B_i B_j)=\{0\}$, a contradiction.

Putting Lemma 8.4.5 with 8.4.6, we see it is enough to classify positive involutions on simple $\mathbb R$-algebras. By the theorem of Frobenius (Corollary 3.5.8), a simple algebra over $\mathbb R$ is isomorphic to ${{\,\mathrm{M}\,}}_n(D)$ with $D=\mathbb R ,\mathbb C ,\mathbb H$, so 8.4.3 applies.

Proposition 8.4.7

Let $B \simeq {{\,\mathrm{M}\,}}_n(D)$ be a simple $\mathbb R$-algebra and let ${}^*$ be the conjugate transpose involution on B. Let ${}^\dagger :B \rightarrow B$ be another positive involution on B. Then there exists an element $\mu \in B^\times$ with $\mu ^*=\mu$ such that

$$\begin{aligned} \alpha ^{\dagger }=\mu ^{-1} \alpha ^* \mu \end{aligned}$$

for all $\alpha \in B$.

Proof. First suppose B is central over $\mathbb R$. Then the involutions ${}^\dagger$ and ${}^*$ give two $\mathbb R$-algebra maps $B \rightarrow B^{op }$. By the Skolem–Noether theorem (Main Theorem 7.7.1), there exists $\mu \in B^\times$ such that $\alpha ^{\dagger }=\mu ^{-1}\alpha ^*\mu$. Since

$$\begin{aligned} \alpha =(\alpha ^{\dagger })^\dagger = (\mu ^{-1} \alpha ^* \mu )^{\dagger }=\mu ^{-1}(\mu ^{-1} \alpha ^* \mu )^* \mu = (\mu ^{-1} \mu ^*) \alpha (\mu ^{-1}\mu ^*)^{-1} \end{aligned}$$

(8.4.8)

for all $\alpha \in B$, we have $\mu ^{-1}\mu ^* \in Z(B)=\mathbb R$, so $\mu ^*=c\mu$ for some $c \in \mathbb R$. But $(\mu ^{*})^*=\mu =(c\mu ^*)^*=c^2\mu$, thus $c=\pm 1$. But if $c=-1$, then $\mu$ is skew-symmetric so its top-left entry is $\mu _{11}=0$; but then for the matrix unit $e_{11}$ we have

$$\begin{aligned} {{\,\mathrm{Tr}\,}}(e_{11}e_{11}^{\dagger }) = {{\,\mathrm{Tr}\,}}(e_{11} \mu ^{-1} e_{11}^* \mu ) = {{\,\mathrm{Tr}\,}}(\mu ^{-1} e_{11} \mu e_{11}) = {{\,\mathrm{Tr}\,}}(\mu ^{-1} \mu _{11})=0, \end{aligned}$$

(8.4.9)

a contradiction.

A similar argument holds if B has center $Z(B)=\mathbb C$. The restriction of an involution to Z(B) is either the identity or complex conjugation; the latter holds for the conjugate transpose involution, as well as for ${}^\dagger$: if $z \in Z(B)$ then ${{\,\mathrm{Tr}\,}}(zz^{\dagger })=n^2(zz^{\dagger })>0$, and we must have $z^{\dagger }=\overline{z}$. So the map $\alpha \mapsto (\alpha ^*)^\dagger$ is a $\mathbb C$-linear automorphism, and again there exists $\mu \in B^\times$ such that $\alpha ^{\dagger }=\mu ^{-1}\alpha ^*\mu$. By the same argument, we have $\mu ^*=z\mu$ with $z \in \mathbb C$, but now $\mu =(\mu ^*)^*=\overline{z}z\mu$ so $|z \,|=1$. Let $w^2=w/\overline{w}=z$; then $(w\mu )^*=\overline{w}\mu ^*=\overline{w}z\mu =w\mu$. Replacing $\mu$ by $w\mu$, we may take $z=1$. $\square$

Corollary 8.4.10

The only positive involution on a real division algebra is the standard involution.

Proof. Apply Proposition 8.4.7 with $n=1$, noting that $\mu ^*=\overline{\mu }=\mu$ implies $\mu \in \mathbb R$. $\square$

8.4.11

Let $\mu \in B^\times$ with $\mu ^*=\mu$. Then $\mu$ is self-adjoint with respect to the pairing $(\alpha ,\beta ) \mapsto {{\,\mathrm{Tr}\,}}(\alpha ^*\beta )$:

$$\begin{aligned} (\mu \alpha ,\beta )={{\,\mathrm{Tr}\,}}((\mu \alpha )^*\beta )={{\,\mathrm{Tr}\,}}(\alpha ^*\mu ^*\beta )={{\,\mathrm{Tr}\,}}(\alpha ^*\mu \beta )=(\alpha ,\mu \beta ). \end{aligned}$$

It follows from the spectral theorem that the $\mathbb R$-linear endomorphism of B given by left-multiplication by $\mu$ on B as an $\mathbb R$-algebra is diagonalizable (with real eigenvalues) via a symmetric matrix. We say $\mu$ ispositive definite (for ${}^*$) if all eigenvalues of $\mu$ are positive. The map $\alpha \mapsto {{\,\mathrm{Tr}\,}}(\alpha ^*\mu \alpha )$ defines a quadratic form on B, and $\mu$ is positive definite if and only this quadratic form is positive definite.

Lemma 8.4.12

Let $\mu ^*=\mu$. Then the involution $\alpha ^{\dagger }=\mu ^{-1}\alpha ^*\mu$ is positive if and only if either $\mu$ or $-\mu$ is positive definite.

Proof. Diagonalize the quadratic form $\alpha \mapsto {{\,\mathrm{Tr}\,}}(\alpha ^*\mu \alpha )$ to get $\langle a_1,\dots ,a_m \rangle$ in a normalized basis $e_1,\dots ,e_m$, and suppose without loss of generality that $a_i = \pm 1$. If all $a_i=-1$, then we can replace $\mu$ with $-\mu$ without changing the involution to suppose they are all $+1$.

Suppose $\mu$ is not positive, and without loss of generality $a_1<0$ and $a_2>0$, then ${{\,\mathrm{Tr}\,}}((e_1+e_2)^*\mu (e_1+e_2))=-1+1=0$, a contradiction. Conversely, if $\mu$ is positive definite, then all eigenvalues are $+1$. Let $\nu =\sqrt{\mu }$ be such that $\nu ^*=\nu$, and then

$$\begin{aligned} \begin{aligned} {{\,\mathrm{Tr}\,}}(\alpha ^*\mu ^{-1}\alpha \mu )&= {{\,\mathrm{Tr}\,}}(\alpha ^*\nu ^{-2}\alpha \nu ^2)={{\,\mathrm{Tr}\,}}((\nu \alpha ^*\nu ^{-1})(\nu ^{-1}\alpha \nu )) \\&={{\,\mathrm{Tr}\,}}((\nu ^{-1}\alpha \nu )^*(\nu ^{-1}\alpha \nu ))>0 \end{aligned} \end{aligned}$$

(8.4.13)

for all $\alpha \in B$, so ${}^\dagger$ is positive. $\square$

Example 8.4.14

If $n=1$, and $B=D$, then the condition $\mu ^*=\mu$ implies $\mu \in \mathbb R$, and the condition $\mu$ positive implies $\mu >0$; rescaling does not affect the involution, so we can take $\mu =1$ and there is a unique positive involution on D given by ${}^*$.

Example 8.4.15

Let $B={{\,\mathrm{M}\,}}_2(\mathbb R )$. Then $\mu =\begin{pmatrix} 2a &{} b \\ b &{} 2c \end{pmatrix}$ is positive definite if and only if $a>0$ and $b^2-4ac<0$. Combining Proposition 8.4.7 with Lemma 8.4.12, we see that all positive involutions ${}^\dagger$ on B are given by $\alpha ^\dagger = \mu ^{-1}\alpha ^* \mu$ where $\mu$ is positive definite.

We can instead relate positive involutions to the standard involution $\overline{\alpha }$ instead of the transpose; to this end, it is enough to find $\jmath \in B^\times ={{\,\mathrm{GL}\,}}_2(\mathbb R )$ such that $\overline{\alpha } = \jmath ^{-1} \alpha ^* \jmath$, and the element $\jmath =\begin{pmatrix} 0 &{} 1 \\ -1 &{} 0 \end{pmatrix}$ does the trick, because

$$\begin{aligned} \begin{pmatrix} 0 &{} 1 \\ -1 &{} 0 \end{pmatrix} \begin{pmatrix} a &{} c \\ b &{} d \end{pmatrix} \begin{pmatrix} 0 &{} -1 \\ 1 &{} 0 \end{pmatrix} = \begin{pmatrix} d &{} -b \\ -c &{} a \end{pmatrix}. \end{aligned}$$

(8.4.16)

From the product $\begin{pmatrix} 0 &{} 1 \\ -1 &{} 0 \end{pmatrix} \begin{pmatrix} 2a &{} b \\ b &{} 2c \end{pmatrix} = \begin{pmatrix} b &{} 2c \\ -2a &{} -b \end{pmatrix}$, we conclude that all positive involutions are given by $\alpha ^\dagger = \mu ^{-1} \overline{\alpha } \mu$ where $\mu ^2 \in \mathbb R _{<0}$.

Remark 8.4.17. Beyond the application to endomorphism algebras, Weil [Weil60] has given a more general point of view on positive involutions, connecting them to the classical groups. For more on involutions on finite-dimensional algebras over real closed fields, see work of Munn [Mun2004].

5 $*\,$Endomorphism algebras of abelian varieties

We conclude this chapter with an advanced (optional) application: we characterize endomorphism algebras of (simple) abelian varieties in terms of algebras with involutions. We borrow from the future the notions from section 43.4. Briefly, a complex torus of dimension g is a complex manifold of the form $A= V/\Lambda$ for $g \ge 0$, where $\Lambda \subset V \simeq \mathbb C ^g$ is a lattice (discrete subgroup) and $\Lambda \simeq \mathbb Z ^{2g}$. A complex abelian variety is a certain kind of complex torus. A complex abelian variety A is simple if A has no abelian subvariety other than $\{0\}$ and A.

An endomorphism of A is a $\mathbb C$-linear map $\alpha :V \rightarrow V$ such that $\alpha (\Lambda ) \subseteq \Lambda$. Let ${{\,\mathrm{End}\,}}(A)$ be the ring ($\mathbb Z$-algebra) of endomorphisms of A.

Proposition 8.5.1

$B={{\,\mathrm{End}\,}}(A) \otimes \mathbb Q$ is a finite-dimensional algebra over $\mathbb Q$ that admits a positive involution ${}^{\dagger } :B \rightarrow B$.

Proof. The algebra B acts faithfully on $\Lambda \otimes \mathbb Q \simeq \mathbb Q ^{2g}$, so is isomorphic to a subalgebra of ${{\,\mathrm{M}\,}}_{2g}(\mathbb Q )$ hence is finite-dimensional over $\mathbb Q$. For positivity, see Proposition 43.4.24 (for the case when A is principally polarized). $\square$

Remark 8.5.2. The involution ${}^{\dagger } :B \rightarrow B$ is called theRosati involution (and depends on a choice ofpolarization , where is the dual abelian variety).

Now Lemma 8.4.5 and Proposition 8.5.1 imply that B is semisimple as a $\mathbb Q$-algebra, with

$$\begin{aligned} B \simeq \prod _{i=1}^r {{\,\mathrm{M}\,}}_{n_i}(D_i) \end{aligned}$$

where each $D_i \subseteq B$ is a division algebra. It follows that A is isogenous to a product

$$\begin{aligned} A_1^{n_1} \times \dots \times A_r^{n_r} \end{aligned}$$

where $n_1,\dots ,n_r>0$ and $A_1,\dots ,A_r$ are simple pairwise nonisogenous abelian subvarieties of A such that $D_i={{\,\mathrm{End}\,}}(A_i) \otimes _\mathbb{Z } \mathbb Q$.

We therefore reduce to the case where A is simple, and $D :={{\,\mathrm{End}\,}}(A) \otimes \mathbb Q$ is a division algebra. Let $K :=Z(D)$ be the center of D and let

$$\begin{aligned} K_0 :=K^{\langle \dagger \rangle }=\{a \in K : a^{\dagger }=a\} \end{aligned}$$

be the subfield of K where ${}^\dagger$ acts by the identity.

Lemma 8.5.3

$K_0$ is a totally real number field, i.e., every embedding $K_0 \hookrightarrow \mathbb C$ factors through $\mathbb R$, and if $\dagger$ acts nontrivially on K, then K is a CM field, i.e., K is a totally imaginary extension of $K_0$.

Proof. The positive involution ${}^\dagger$ restricts to complex conjugation on Z(D) by Proposition 8.4.7, so for all embeddings $K_0 \hookrightarrow \mathbb C$, the image lies in $\mathbb R$. For the same reason, we cannot have ${}^\dagger$ acting nontrivially on K and have an embedding $K \hookrightarrow \mathbb R$. $\square$

The following theorem of Albert classifies the possibilities for D.

Theorem 8.5.4

(Albert). Let D be a (finite-dimensional) division algebra over $\mathbb Q$ with positive involution ${}^\dagger$ and center $K=Z(D)$, let $K_0 :=K^{\langle \dagger \rangle }$ and $n :=[K_0:\mathbb Q ]$. Then $K_0$ is a totally real number field, and one of the four following possibilities holds:

• (I) $D=K=K_0$ and ${}^\dagger$ is the identity;

• (II) $K=K_0$ and D is a quaternion algebra over $K_0$ such that

  $$\begin{aligned} D \otimes _\mathbb{Q } \mathbb R \simeq {{\,\mathrm{M}\,}}_2(\mathbb R )^n, \end{aligned}$$

  and there exists $\mu \in D^\times$ such that $\mu ^2=d \in K_0^\times$ is totally negative and $\alpha ^\dagger =\mu ^{-1} \overline{\alpha } \mu$ for all $\alpha \in D$;

• (III) $K=K_0$ and D is a quaternion algebra over $K_0$ such that

  $$\begin{aligned} D \otimes _\mathbb{Q } \mathbb R \simeq \mathbb H ^n, \end{aligned}$$

  and ${}^\dagger$ is the standard involution; or

• (IV) $K \supsetneq K_0$ and

  $$\begin{aligned} D \otimes _\mathbb{Q } \mathbb R \simeq {{\,\mathrm{M}\,}}_d(\mathbb C )^n \end{aligned}$$

  for some $d \ge 1$, and ${}^\dagger$ extends to the conjugate transpose ${}^*$ on each factor ${{\,\mathrm{M}\,}}_d(\mathbb C )$.

Proof. We have assembled many of the tools needed to prove this theorem, and hopefully motivated its statement sufficiently well—but unfortunately, a proof remains just out of reach: we require some results about quaternion algebras over number fields not yet in our grasp. For a proof, see Mumford [Mum70, Application I, §21] or Birkenhake–Lange [BL2004, §§5.3–5.5].

To connect a few dots as well as we can right now, we give a sketch in the case where $K=K_0$ for the reader who is willing to flip ahead to Chapter 14. In this case, D is a central division algebra over $K=K_0$ and has a $K_0$-linear involution giving an isomorphism of $K_0$-algebras. Looking in the Brauer group ${{\,\mathrm{Br}\,}}(K_0)$, we conclude that $[D]=[D^{op }]=[D]^{-1}$, so $[D] \in {{\,\mathrm{Br}\,}}(K_0)$ has order at most 2. By class field theory (see Remark 14.6.10), we conclude that either $D=K_0$ or D is a (division) quaternion algebra over $K_0$. If $D=K_0$, we are in case (I), so suppose D is a quaternion algebra over $K_0$. We have $D \otimes _\mathbb{Q } \mathbb R \simeq \prod _{v \mid \infty } D_v$ a direct product of n quaternion algebras $D_v$ over $\mathbb R$ indexed by the real places v of $K_0$. We have $D_v \simeq {{\,\mathrm{M}\,}}_2(\mathbb R )$ or $D_v \simeq \mathbb H$, and our positive involution induces a corresponding positive involution on each $D_v$. If there exists v such that $D_v \simeq \mathbb H$, then by Corollary 8.4.10, the positive involution on $D_v$ is the standard involution, so it is so on D, and then all components must have $D_v \simeq \mathbb H$ as the standard involution is not positive on ${{\,\mathrm{M}\,}}_2(\mathbb R )$—and we are in case (II). Otherwise, we are in case (III), with Proposition 8.4.7 and Example 8.4.15 characterizing the positive involution. $\square$

Exercises

Let F be a field.

1.:

Let $B_1,B_2$ be quaternion algebras over F, with standard involution written $\overline{\phantom {x}}$ in both cases. Let $A :=B_1 \otimes B_2$.

(a):

Show that the map $\sigma :A \rightarrow A$ defined by $\alpha _1 \otimes \alpha _2 \mapsto \overline{\alpha _1} \otimes \overline{\alpha _2}$ for $\alpha _1 \in B_1$ and $\alpha _2 \in B_2$ extends to an involution on A, but it is not a standard involution. [Hint: consider sums.]

(b):

Suppose that ${{\,\mathrm{char}\,}}F \ne 2$. Diagonalize $A = A^+ \oplus A^-$ into $+1$ and $-1$ eigenspaces for $\sigma$. Show that

$$\begin{aligned} A^+ = F \oplus (B_1^- \otimes B_2^-) \quad \text {and}\quad A^-=(B_1^- \otimes F) \oplus (F \otimes B_2^-). \end{aligned}$$

$\triangleright$ 2.:

Suppose ${{\,\mathrm{char}\,}}F \ne 2$ and let $B_1 :=\displaystyle {\biggl (\frac{a,b_1}{F}\biggr )}$ and $B_2 :=\displaystyle {\biggl (\frac{a,b_2}{F}\biggr )}$ be quaternion algebras over F.

(a):

Let $B_3$ be the F-span of 1, $i_3 :=i_1 \otimes 1$, $j_3 :=j_1 \otimes j_2$, and $k_3 :=i_3j_3 = i_1j_1 \otimes j_2$ inside $B_1 \otimes B_2$. Show that $B_3 \simeq \displaystyle {\biggl (\frac{a,b_1b_2}{F}\biggr )}$ as F-algebras.

(b):

Similarly, let $B_4$ be the F-span of 1, $i_4 :=1 \otimes j_2$, $j_4 :=(i_1 \otimes k_2)/a$, and $k_4 :=i_4j_4$. Show that $B_4 \simeq \displaystyle {\biggl (\frac{b_2,-b_2}{F}\biggr )} \simeq {{\,\mathrm{M}\,}}_2(F)$.

(c):

Show that

$$\begin{aligned} B_1 \otimes B_2 \simeq B_3 \otimes B_4 \simeq {{\,\mathrm{M}\,}}_2(B_3). \end{aligned}$$

[Hint: Show that $B_3$ and $B_4$ are commuting subalgebras, or consider the map $B_3 \otimes B_4 \rightarrow B_1 \otimes B_2$ given by multiplication.]

(d):

Restore symmetry and repeat (a)–(c) to find algebras $B_3' \simeq B_3$ and $B_4' \simeq \displaystyle {\biggl (\frac{b_1,-b_1}{F}\biggr )}$ with $B_1 \otimes B_2 \simeq B_3' \otimes B_4' \simeq {{\,\mathrm{M}\,}}_2(B_3')$.

3.:

Suppose ${{\,\mathrm{char}\,}}F \ne 2$. Show that $B_1 \otimes B_2 \simeq {{\,\mathrm{M}\,}}_4(F)$ if and only if the Albert form $Q(B_1,B_2)$ is totally hyperbolic.

4.:

Let G be a finite group. Show that the map induced by $g \mapsto g^{-1}$ for $g \in G$ defines an positive involution on $\mathbb R [G]$. Then show that this map composed with coordinatewise complex conjugation defines a positive involution on $\mathbb C [G]$ (as an $\mathbb R$-algebra).

$\triangleright$ 5.:

Show that if $\sim$ is the equivalence relation (8.3.1) on ${{\,\mathrm{CSA}\,}}(F)$, then $\sim$ is compatible with tensor product, i.e., if $A,A' \in {{\,\mathrm{CSA}\,}}(F)$ and $A' \sim A'' \in {{\,\mathrm{CSA}\,}}(F)$ then $A \otimes A' \sim A \otimes A''$.

6.:

Show that every class in the Brauer group ${{\,\mathrm{Br}\,}}(F)$ contains a unique division F-algebra, up to isomorphism.

7.:

Show that ${{\,\mathrm{Br}\,}}F=\{1\}$ if F is separably closed, and that ${{\,\mathrm{Br}\,}}(\mathbb R ) \simeq \mathbb Z /2\mathbb Z$ and ${{\,\mathrm{Br}\,}}(\mathbb F _q)=\{1\}$.

8.:

Let $B \in {{\,\mathrm{CSA}\,}}(F)$ and suppose that B has an involution (not necessarily standard). Show that [B] has order at most 2 in ${{\,\mathrm{Br}\,}}F$.

9.:

Let $K \supseteq F$ be a field extension. Show that the map $A \mapsto A \otimes _F K$ induces a group homomorphism ${{\,\mathrm{Br}\,}}F \rightarrow {{\,\mathrm{Br}\,}}K$. Conclude that the set of isomorphism classes of central division F-algebras D such that $D \otimes _F K \simeq {{\,\mathrm{M}\,}}_n(K)$ for some $n \ge 1$ forms a subgroup of ${{\,\mathrm{Br}\,}}F$, called therelative Brauer group ${{\,\mathrm{Br}\,}}(K \mid F)$.

10.:

In this exercise, we give an example of a central simple algebra of infinite dimension, called the Weyl algebra.

Suppose ${{\,\mathrm{char}\,}}F = 0$, let F[x] be the polynomial ring over F in the variable x. Inside the enormous algebra ${{\,\mathrm{End}\,}}_F F[x]$ is the operator $f(x) \mapsto xf(x)$, denoted also x, and the differentiation operator $\delta :F[x] \rightarrow F[x]$. These two operators are related by the product rule:

$$\begin{aligned} \delta (xf(x)) - x\delta (f(x)) = f(x). \end{aligned}$$

Accordingly, the subalgebra of ${{\,\mathrm{End}\,}}_F F[x]$ generated by $\delta ,x$ is isomorphic to an algebra given in terms of generators and relations:

$$\begin{aligned} W :=F\langle \delta ,x \rangle /\langle \delta x - x\delta - 1 \rangle , \end{aligned}$$

the quotient of the “noncommutative polynomial ring” in two variables $F\langle \delta ,x \rangle$ by the two-sided ideal generated by $\delta x - x \delta - 1$.

(a):

Show that every element of W can be written in the form $\sum _{i=0}^n f_i(x) \delta ^i$ where $f_i(x) \in F[x]$ for all i, i.e., W has F-basis elements $x^i \delta ^j$ for $i,j \ge 0$.

(b):

Show that $Z(W)=F$.

(c):

Let I be a two-sided of W. Show that if there exists nonzero $f(x) \in F[x] \cap I$, then $I=W$. Similarly, show that if $\delta ^n \in I$ for some $n \ge 0$, then $I=W$.

(d):

Show that W is simple. [Hint: argue by induction.]

11.:

Let B be a finite-dimensional $\mathbb R$-algebra with positive involution ${}^*:B \rightarrow B$. Let

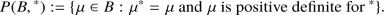
(a):

Show that $B^\times$ acts on $P(B,{}^*)$ by $\beta \cdot \mu :=\beta ^* \mu \beta$.

(b):

Show that $P(B,{}^*)$ is a convex open subset of $\{\alpha \in B : \alpha ^*=\alpha \}$, an $\mathbb R$-vector subspace of B.

(c):

Let $\psi :B \rightarrow B$ be an $\mathbb R$-algebra automorphism or anti-automorphism. Show that $\alpha ^{\dagger } :=\psi ^{-1}(\psi (\alpha )^*)$ defines a positive involution for $\alpha \in B$, and that $\psi$ maps $P(B,{}^{\dagger })$ bijectively to $P(B,{}^{\psi })$.