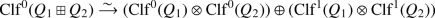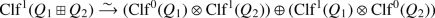Abstract
Continuing our treatment of quadratic forms, in this chapter we connect quaternion algebras to ternary quadratic forms.
You have full access to this open access chapter, Download chapter PDF
Continuing our treatment of quadratic forms, in this chapter we connect quaternion algebras to ternary quadratic forms.
1 \(\triangleright \) Reduced norm as quadratic form
Let F be a field with \({{\,\mathrm{char}\,}}F \ne 2\) and let \(B=({a,b} \mid {F})\) be a quaternion algebra over F. We saw in the previous chapter (4.1.1) that the reduced norm defines a quadratic form. But always have scalar norms \({{\,\mathrm{nrd}\,}}(t)=t^2\) for \(t \in F\), so the form carries the same information when restricted to the space of pure quaternions
with basis \(i,j,ij\). This quadratic form restricted to \(B^0\) is
with discriminant \((-a)(-b)(ab) = (ab)^2\), so the trivial class in \(F^{\times }/F^{\times 2}\).
We might now try to classify quaternion algebras over F up to isomorphism in terms of this quadratic form. Recall as in the previous chapters that for morphisms between quadratic forms, one allows either isometries, an invertible change of basis preserving the quadratic form, or similarities, which allow a rescaling of the quadratic form by a nonzero element of F. Our main result is as follows (Corollary 5.2.6).
Theorem 5.1.1
The map \(B \mapsto {{\,\mathrm{nrd}\,}}|_{B^0}\) induces a bijection:

The map \(B \mapsto {{\,\mathrm{nrd}\,}}|_{B^0}\) in Theorem 5.1.1 has inverse defined by the even Clifford algebra (see section 5.3). The similarity class of a nondegenerate ternary quadratic form cuts out a well-defined plane conic \(C \subseteq \mathbb P ^2\) over F, so one also has a bijection between isomorphism classes of quaternion algebras over F and isomorphism classes of conics over F. Finally, keeping track of an orientation allows one to fully upgrade this bijection to an equivalence of categories (Theorem 5.6.8).
The classification of quaternion algebras over F is now rephrased in terms of quadratic forms, and a more detailed description depends on the field F. In this vein, the most basic question we can ask about a quaternion algebra B is if it is isomorphic to the matrix ring \(B \simeq {{\,\mathrm{M}\,}}_2(F)\): if so, we say that B is split over F. For example, every quaternion algebra over \(\mathbb C \) (or an algebraically closed field) is split, and a quaternion algebra \(({a,b} \mid \mathbb{R })\) is split if and only if \(a>0\) or \(b>0\).
Ultimately, we will identify six equivalent ways (Main Theorem 5.4.4) to check if a quaternion algebra B is split; in light of Theorem 5.1.1, we isolate the following.
Proposition 5.1.2
B is split if and only if the quadratic form \({{\,\mathrm{nrd}\,}}|_{B^0}\) represents 0 nontrivially.
In later chapters, we will return to this classification problem, gradually increasing the “arithmetic complexity” of the field F.
2 Isomorphism classes of quaternion algebras
In Section 2.4, we found that the unit Hamiltonians act by conjugation on the pure quaternions \(\mathbb H ^0 \simeq \mathbb R ^3\) as rotations, preserving the standard inner product. In this section, we return to this theme for a general quaternion algebra, and we characterize isomorphism classes of quaternion algebras in terms of isometry classes of ternary quadratic forms.
Throughout this chapter, let F be a field with \({{\,\mathrm{char}\,}}F \ne 2\), and let \(B=({a,b} \mid {F})\) be a quaternion algebra over F.
Definition 5.2.1
\(\alpha \in B\) isscalar if \(\alpha \in F\) and pure if \({{\,\mathrm{trd}\,}}(\alpha )=0\).
5.2.2
Recalling (3.3.5), we have the F-vector space of pure (trace 0) elements of B given by \(B^0 =\{1\}^\perp \). The standard involution restricted to \(B^0\) is given by \(\overline{\alpha }=-\alpha \) for \(\alpha \in B^0\), so equivalently \(B^0\) is the \(-1\)-eigenspace for \(\overline{\phantom {x}}\). We have \(B^0= Fi \oplus Fj \oplus Fij\) and in this basis
so that \({{\,\mathrm{disc}\,}}({{\,\mathrm{nrd}\,}}|_{B^0})=(ab)^2 = 1 \in F^{\times }/F^{\times 2}\) (cf. Example 4.3.8).
Proposition 5.2.4
Let \(B,B'\) be quaternion algebras over F. Then the following are equivalent:
-
(i)
\(B \simeq B'\) are isomorphic as F-algebras;
-
(ii)
\(B \simeq (B')^{op }\) are isomorphic as F-algebras;
-
(iii)
\(B \simeq B'\) are isometric as quadratic spaces; and
-
(iv)
\(B^0 \simeq (B')^0\) are isometric as quadratic spaces.
If  is an isometry, then f extends uniquely to either an isomorphism
is an isometry, then f extends uniquely to either an isomorphism  or an isomorphism
or an isomorphism  of F-algebras.
of F-algebras.
Proof. We follow Lam [Lam2005, Theorem III.2.5]. The equivalence (i) \(\Leftrightarrow \) (ii) follows from postcomposing with the standard involution  .
.
The implication (i) \(\Rightarrow \) (iii) follows from the fact that the standard involution on an algebra is unique and the reduced norm is determined by this standard involution, so the reduced norm on B is identified with the reduced norm on \(B'\).
The implication (iii) \(\Rightarrow \) (iv) follows from Witt cancellation (Theorem 4.2.22); and (iv) \(\Rightarrow \) (iii) is immediate, since \(B = \langle 1 \rangle \boxplus B^0\) and \(B' = \langle 1 \rangle \boxplus (B')^0\) so the isometry extends by mapping \(1 \mapsto 1\). (Or use Witt extension, Theorem 4.2.22(b).)
So finally we prove (iv) \(\Rightarrow \) (i). Let \(f:B^0 \rightarrow (B')^0\) be an isometry of quadratic spaces. Suppose \(B \simeq ({a,b} \mid {F})\). Since f is an isometry, \({{\,\mathrm{nrd}\,}}(f(i))={{\,\mathrm{nrd}\,}}(i)=-a\) and
so \(f(i)^2=a\). Similarly \(f(j)^2=b\). Finally, \(ji=-ij\) since \(i,j\) are orthogonal (as in the proof of Main Theorem 4.4.1), but then f(i), f(j) are orthogonal as well and so \(f(j)f(i)=-f(i)f(j)\).
Similarly, we know that \(ij\) is orthogonal to \(i,j\), thus \(f(ij)\) is orthogonal to both f(i) and f(j) and so \(f(ij)=uf(i)f(j)\) for some \(u \in F^\times \); taking reduced norms gives \({{\,\mathrm{nrd}\,}}(ij)=u^2{{\,\mathrm{nrd}\,}}(i){{\,\mathrm{nrd}\,}}(j)\) so \(u^2=1\) thus \(u=\pm 1\). If \(u=1\), then \(f(ij)=f(i)f(j)\), and f extends via \(f(1)=1\) to an F-algebra isomorphism  . Otherwise, \(u=-1\) and \(f(ij)=-f(i)f(j)=f(j)f(i)\), in which case f extends to an F-algebra anti-isomorphism, or equivalently an F-algebra isomorphism
. Otherwise, \(u=-1\) and \(f(ij)=-f(i)f(j)=f(j)f(i)\), in which case f extends to an F-algebra anti-isomorphism, or equivalently an F-algebra isomorphism  ; but then postcomposing with the standard involution we obtain an F-algebra isomorphism
; but then postcomposing with the standard involution we obtain an F-algebra isomorphism  . \(\square \)
. \(\square \)
MainTheorem 5.2.5
Let F be a field with \({{\,\mathrm{char}\,}}F \ne 2\). Then the functor \(B \mapsto {{\,\mathrm{nrd}\,}}|_{B^0}\) yields an equivalence of categories between

and

Proof. The association \(B \mapsto {{\,\mathrm{nrd}\,}}|_{B^0}\) gives a functor from quaternion algebras to nondegenerate ternary quadratic forms with discriminant 1, by 5.2.2; the map sends isomorphisms and anti-isomorphisms to isometries and vice versa by Proposition 5.2.4. Therefore the functor is fully faithful. To conclude, we show that the functor is essentially surjective. Let V be a nondegenerate ternary quadratic space with discriminant \(1 \in F^{\times }/F^{\times 2}\). Choose a normalized basis for V, so that \(Q \simeq \langle -a,-b,c \rangle \) with \(a,b,c \in F^{\times }\). By hypothesis, we have \({{\,\mathrm{disc}\,}}(Q)=abc \in F^{\times 2}\), so applying the isometry rescaling the third basis vector we may suppose \(c=ab\). We then associate to V the isomorphism class of the quaternion algebra \(({a,b} \mid {F})\). The result follows. \(\square \)
Corollary 5.2.6
The map \(B \mapsto {{\,\mathrm{nrd}\,}}|_{B^0}\) yields a bijection

that is functorial with respect to F.
By the expression functorial with respect to F, we mean that this bijection respects (is compatible with) field extensions: explicitly, if \(F \hookrightarrow K\) is an inclusion of fields, and B is a quaternion algebra with associated ternary quadratic form \(Q :B^0 \rightarrow F\), then the quaternion algebra \(B_K=B \otimes _F K\) has associated ternary quadratic form \(Q_K :B_K^0 = B^0 \otimes _F K \rightarrow K\).
Proof of Corollary 5.2.6. Functoriality boils down to the fact that
for \(F \hookrightarrow K\) an inclusion of fields. The first bijection is an immediate consequence of Main Theorem 5.2.5. We do not need anti-isomorphisms once we restrict to classes, since if there is an anti-isomorphism  then composing with the standard involution gives a straight up isomorphism.
then composing with the standard involution gives a straight up isomorphism.
Next, we examine the natural map from isometry classes to similarity classes and show it is surjective. Every nondegenerate ternary quadratic form (or any quadratic form in odd dimension) is similar to a unique isometry class of quadratic forms with trivial discriminant: if \(Q= \langle a,b,c \rangle \) with \(a,b,c \in F^\times \), then \({{\,\mathrm{disc}\,}}(\langle a,b,c \rangle )=abc\) and
and \({{\,\mathrm{disc}\,}}(\langle bc, ac, ab \rangle ) = (abc)^2 = 1 \in F^\times /F^{\times 2}\). Therefore the map is surjective.
To conclude, we show this map is injective. Suppose that \(Q,Q'\) are forms of discriminant 1, so \(\det T, \det T' \in F^{\times 2}\). Suppose there is a similarity \(Q \sim Q'\), so \(Q'(f(x))=uQ(x)\) for some \(f:V \rightarrow V'\) and \(u \in F^\times \); we show in fact that \(Q \simeq Q'\) are isometric. By Exercise 4.10, we have \(\det T' = u^3 \det T\), and \(u=c^2 \in F^{\times 2}\). Therefore
and  is the sought after isometry. \(\square \)
is the sought after isometry. \(\square \)
Remark 5.2.7. We will refine Main Theorem 5.2.5 in section 5.6 by restricting the isometries to those that preserve orientation.
3 Clifford algebras
In this section, we define a functorial inverse to \(B \mapsto {{\,\mathrm{nrd}\,}}|_{B^0}=Q\) in Main Theorem 5.2.5: this is the even Clifford algebra of Q. The Clifford algebra is useful in many contexts, so we define it more generally. Loosely speaking, the Clifford algebra of a quadratic form Q is the algebra generated by V subject to the condition \(x^2=Q(x)\) for all \(x \in V\), so the multiplication on the Clifford algebra is induced by the quadratic form.
Let \(Q:V \rightarrow F\) be a quadratic form with \(\dim _F V=n<\infty \); in this section, we pause our assumption and allow F of arbitrary characteristic.
Proposition 5.3.1
There exists an F-algebra \({{\,\mathrm{Clf}\,}}Q\) with the following properties:
-
(i)
There is an F-linear map \(\iota :V \rightarrow {{\,\mathrm{Clf}\,}}Q\) such that \(\iota (x)^2=Q(x)\) for all \(x \in V\); and
-
(ii)
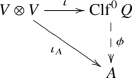
\({{\,\mathrm{Clf}\,}}Q\) has the following universal property: if A is an F-algebra and \(\iota _A:V \rightarrow A\) is a map such that \(\iota _A(x)^2=Q(x)\) for all \(x \in V\), then there exists a unique F-algebra homomorphism \(\phi :{{\,\mathrm{Clf}\,}}Q \rightarrow A\) such that the diagram
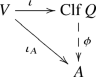
commutes.
The pair \(({{\,\mathrm{Clf}\,}}Q,\iota )\) is unique up to unique isomorphism.
The algebra \({{\,\mathrm{Clf}\,}}Q\) in Proposition 5.3.1 is called the Clifford algebra of Q.
Proof. Let
where
so that
Then \({{\,\mathrm{Ten}\,}}V\) has a multiplication given by tensor product: for \(x \in V^{\otimes d}\) and \(y \in V^{\otimes e}\) we define
(concatenate, and possibly distribute, tensors). In this manner, \({{\,\mathrm{Ten}\,}}V\) has the structure of an F-algebra, and we call \({{\,\mathrm{Ten}\,}}V\) the tensor algebra of V.
Let
be the two-sided ideal generated the elements \(x\otimes x - Q(x)\) for all \(x \in V\). Let
The algebra \({{\,\mathrm{Clf}\,}}Q\) by construction satisfies (i). And if \(\iota _A:V \rightarrow A\) is as in (ii), then the map \(\iota (x) \mapsto \iota _A(x)\) for \(x \in V\) extends to a unique F-algebra map \({{\,\mathrm{Ten}\,}}V \rightarrow A\); since further \(\iota _A(x)^2=Q(x)\) for all \(x \in V\), this algebra map factors through \(\phi :{{\,\mathrm{Clf}\,}}Q \rightarrow A\). By abstract nonsense (taking \(A={{\,\mathrm{Clf}\,}}Q\)), we see that any other algebra having the same property as \({{\,\mathrm{Clf}\,}}(Q)\) is uniquely isomorphic to it, i.e., \({{\,\mathrm{Clf}\,}}Q\) is unique up to unique isomorphism. \(\square \)
Example 5.3.5
If \(Q:F \rightarrow F\) is the quadratic form \(Q(x)=ax^2\) with \(a \in F\), then \({{\,\mathrm{Clf}\,}}(F) \simeq F[x]/(x^2-a)\) (Exercise 5.6).
Example 5.3.6
In the extreme case where \(Q=0\) identically,  is canonically identified with the exterior algebra on V.
is canonically identified with the exterior algebra on V.
5.3.7
Let \(x,y \in V\). Then in \({{\,\mathrm{Clf}\,}}Q\), we have
In particular, x, y are orthogonal if and only if \(x\otimes y=-y\otimes x\).
5.3.9
Let \(e_1,\dots ,e_n\) be an F-basis for V. Then finite tensors on these elements are an F-basis for \({{\,\mathrm{Ten}\,}}V\). In \({{\,\mathrm{Clf}\,}}Q\), by 5.3.7 we have \(e_i \otimes e_i = Q(e_i)\) and \(e_j \otimes e_i = T(e_i,e_j) - e_i \otimes e_j\), so an F-spanning set for \({{\,\mathrm{Clf}\,}}Q\) is given by \(e_{i_1} \otimes \dots \otimes e_{i_d}\) with \(1 \le i_1< i_2< \dots < i_d \le n\) (including 1 arising from the empty tensor product), and so
It is customary to abbreviate \(e_{i_1} \otimes \dots \otimes e_{i_d}=e_{i_1}\cdots e_{i_d}\).
Example 5.3.11
If \(Q \simeq \langle a_1,\dots ,a_n \rangle \) is diagonal in the basis \(e_i\), then
Example 5.3.12
Suppose \({{\,\mathrm{char}\,}}F \ne 2\) and let \(Q:F^2 \rightarrow F\) be the quadratic form \(Q(x)=\langle a,b \rangle \). Then by a direct calculation using 5.3.9, we find
with multiplication \(e_1^2=a\) and \(e_2^2=b\) and \(e_2e_1=-e_1e_2\), i.e., with \(i :=e_1\) and \(j :=e_2\) we have identified \({{\,\mathrm{Clf}\,}}Q \simeq \displaystyle {\biggl (\frac{a,b}{F}\biggr )}\) when \(a,b \ne 0\).
Example 5.3.12 generalizes as follows.
Lemma 5.3.14
The map \(\iota :V \rightarrow {{\,\mathrm{Clf}\,}}Q\) is injective, and \(\dim _F {{\,\mathrm{Clf}\,}}(Q)=2^n\).
Proof. By Lemma 4.3.1, we may choose a basis \(e_1,\dots ,e_n\) for V in which \(Q \simeq \langle a_1, \cdots , a_n \rangle \) is diagonal. Let A be the F-vector space with basis the symbols \(z_{i_1}\cdots z_{i_d}\) for \(1 \le i_1< i_2< \dots < i_d \le n\). In the same way as what was considered for the relations (2.2.2), we verify directly that there is a unique, associative multiplication on A such that \(z_i^2=a_i\) and \(z_jz_i = -z_iz_j\). (Alternatively, this can be viewed as a graded tensor product; see Exercise 5.21.) The map \(\iota _A :V \rightarrow A\) by \(e_i \mapsto z_i\) has \(\iota _A(x)^2 = \iota _A(\sum _i x_i e_i)^2 = a_1x_1^2+\cdots +a_nx_n^2 = Q(x)\), so by the universal property of \({{\,\mathrm{Clf}\,}}(Q)\), there exists a unique F-algebra homomorphism \(\phi :{{\,\mathrm{Clf}\,}}(Q) \rightarrow A\) such that \(\phi \iota = \iota _A\). Since the elements \(z_{i_1}\cdots z_{i_d}\) are F-linearly independent in A, so too are their preimages \(e_{i_1}\cdots e_{i_d}\) in \({{\,\mathrm{Clf}\,}}Q\), so the spanning set given in 5.3.9 is in fact a basis and \(\phi \) is an isomorphism. \(\square \)
As it will cause no confusion, we may identify V with its image \(\iota (V) \hookrightarrow {{\,\mathrm{Clf}\,}}Q\).
5.3.15
The reversal map, given by
on pure tensors (and extended F-linearly) is well-defined, as it maps the ideal I(Q) to itself, and so it defines an involution on \({{\,\mathrm{Clf}\,}}Q\) that we call the reversal involution.
Lemma 5.3.17
The association \(Q \mapsto {{\,\mathrm{Clf}\,}}Q\) induces a faithful functor from the category of
to the category of
Proof. Let \(Q':V' \rightarrow F\) be another quadratic form and let \(f:V \rightarrow V'\) be an isometry. Then f induces an F-algebra map \({{\,\mathrm{Ten}\,}}V \rightarrow {{\,\mathrm{Ten}\,}}(V')\) and
so f also induces an F-algebra map \({{\,\mathrm{Clf}\,}}Q \rightarrow {{\,\mathrm{Clf}\,}}(Q')\). Repeating with the inverse map, and applying the universal property, we see that these maps are inverse, so define isomorphisms. The functor is faithful because  , so if
, so if  acts as the identity on \({{\,\mathrm{Clf}\,}}Q\) then it acts as the identity on V, so f itself is the identity. (This can be rephrased in terms of the universal property: see Exercise 5.13.) \(\square \)
acts as the identity on \({{\,\mathrm{Clf}\,}}Q\) then it acts as the identity on V, so f itself is the identity. (This can be rephrased in terms of the universal property: see Exercise 5.13.) \(\square \)
5.3.18
The tensor algebra \({{\,\mathrm{Ten}\,}}V\) has a natural \(\mathbb Z _{\ge 0}\) grading by degree, and by construction (5.3.4), the quotient \({{\,\mathrm{Clf}\,}}Q={{\,\mathrm{Ten}\,}}V/I(Q)\) retains a \(\mathbb Z /2\mathbb Z \)-grading
where \({{\,\mathrm{Clf}\,}}^0 Q \subseteq {{\,\mathrm{Clf}\,}}Q\) is the F-subalgebra of terms of even degree and \({{\,\mathrm{Clf}\,}}^1 Q\) the \({{\,\mathrm{Clf}\,}}^0 Q\)-bimodule of terms with odd degree. The reversal involution 5.3.15 preserves \({{\,\mathrm{Clf}\,}}^0 Q\) and so descends to an involution on \({{\,\mathrm{Clf}\,}}^0 Q\).
We call \({{\,\mathrm{Clf}\,}}^0 Q\) the even Clifford algebra and \({{\,\mathrm{Clf}\,}}^1 Q\) the odd Clifford bimodule of Q. The former admits the following direct construction: let
and let \(I^0(Q) :=I(Q) \cap {{\,\mathrm{Ten}\,}}^0 V\); then \({{\,\mathrm{Clf}\,}}^0 Q \simeq {{\,\mathrm{Ten}\,}}^0 V/I^0(Q)\).
5.3.19
Referring to 5.3.9, the elements \(e_1e_2,\dots ,e_{n-1}e_n\) generate \({{\,\mathrm{Clf}\,}}^0 Q\) as an F-algebra, and \({{\,\mathrm{Clf}\,}}^0 Q\) has basis \(e_{i_1}\cdots e_{i_d}\) where d is even (including the empty product 1), so \(\dim _F {{\,\mathrm{Clf}\,}}^0(Q)=2^{n-1}\).
Example 5.3.20
Continuing Example 5.3.12, we see that the reversal involution fixes i, j and acts as the standard involution on \({{\,\mathrm{Clf}\,}}^0 Q\). So the algebra \({{\,\mathrm{Clf}\,}}Q\) is not just a quaternion algebra, but one retaining a \(\mathbb Z /2\mathbb Z \)-grading.
Lemma 5.3.21
The association \(Q \mapsto {{\,\mathrm{Clf}\,}}^0 Q\) defines a functor from the category of
to the category of
Proof. Let \(Q':V' \rightarrow F\) be another quadratic form and let (f, u) be a similarity, with \(f:V \rightarrow V'\) and \(u \in F^\times \), so that \(uQ(x)=Q'(f(x))\) for all \(x \in V\). We modify the proof in Lemma 5.3.17: we define a map
Then under this map, we have
so \(I^0(Q)\) maps to \(I^0(Q')\), and the induced map \({{\,\mathrm{Clf}\,}}^0 Q \rightarrow {{\,\mathrm{Clf}\,}}^0(Q')\) is an F-algebra isomorphism. \(\square \)
5.3.22
Note that unlike the Clifford functor, the even Clifford functor need not be faithful: for example, the map \(-1 :F^2 \rightarrow F^2\) has \(e_1e_2 \mapsto (-e_1)(-e_2)=e_1e_2\) so acts by the identity on \({{\,\mathrm{Clf}\,}}^0 Q\).
We now come to the important immediate application.
5.3.23
Suppose that \({{\,\mathrm{char}\,}}F \ne 2\) and let \(Q(x)=\langle a,b,c \rangle \) be a nondegenerate ternary quadratic form. Then the even Clifford algebra \({{\,\mathrm{Clf}\,}}^0 Q\) is given by
where \(i=e_1e_2\), \(j=e_2e_3\), subject to the multiplication
So
Letting \(k=e_3e_1\), we obtain symmetrically with the other two pairs of generators j, k or k, i that
The reversal involution is the standard involution on \({{\,\mathrm{Clf}\,}}^0 Q\). Letting \(B={{\,\mathrm{Clf}\,}}^0 Q\),
So if \({{\,\mathrm{disc}\,}}Q(x)=abc \in F^{\times 2}\), then \({{\,\mathrm{nrd}\,}}|_{B^0}\) is isometric to Q. In a similar way, if \(B=\displaystyle {\biggl (\frac{a,b}{F}\biggr )}\), then in Main Theorem 5.2.5 we associate \(Q={{\,\mathrm{nrd}\,}}_{B^0}=\langle -a,-b,ab \rangle \), and
This gives another tidy proof of the bijection in Corollary 5.2.6.
Remark 5.3.25. The even Clifford map does not furnish an equivalence of categories for the same reason as in 5.3.22; one way to deal with this issue is to restrict the isometries to those that preserve orientation: we carry this out in section 5.6.
4 Splitting
The moral of Main Theorem 5.2.5 is that the problem of classifying quaternion algebras depends on the theory of ternary quadratic forms over that field (and vice versa). We now pursue the first consequence of this moral, and we characterize the matrix ring among quaternion algebras. Suppose that \({{\,\mathrm{char}\,}}F \ne 2\), but still \(Q :V \rightarrow F\) a quadratic form with \(\dim _F V < \infty \).
Definition 5.4.1
The hyperbolic plane is the quadratic form \({H :F^2 \rightarrow F}\) defined by \(H(x,y)=xy\). A quadratic form is a hyperbolic plane if it is isometric to H.
A hyperbolic plane H is universal, its associated bilinear form has Gram matrix \(\begin{pmatrix} 0 &{} 1 \\ 1 &{} 0 \end{pmatrix}\) in the standard basis, and H has normalized form \(H \simeq \langle 1,-1 \rangle \).
Lemma 5.4.2
Suppose Q is nondegenerate. Then Q is isotropic if and only if there exists an isometry \({Q \simeq H \boxplus Q'}\) with \(Q'\) nondegenerate and H a hyperbolic plane.
Proof. For the implication (\(\Leftarrow \)), we have an isotropic vector from either one of the two basis vectors. For the implication (\(\Rightarrow \)), let \(x \in V\) be isotropic, so \(x \ne 0\) and satisfy \(Q(x)=0\). Since Q is nondegenerate, there exists \(y \in V\) such that \(T(x,y) \ne 0\); rescaling y, we may assume \(T(x,y)=1\). If \(T(y,y)=2Q(y,y) \ne 0\), replacing \(y \leftarrow y-2x/T(y,y)\) gives \(T(y,y)=0\). Thus Q restricted to \(Fx+Fy\) is isometric to H, and in particular is nondegenerate. Therefore letting \(V' :=(Fx+Fy)^\perp \) and \(Q' :=Q|_{V'}\), we have \(V \simeq (Fx+Fy) \boxplus V'\) and \(Q \simeq H \boxplus Q'\). \(\square \)
Lemma 5.4.3
Suppose Q is nondegenerate and let \(a \in F^\times \). Then the following are equivalent:
-
(i)
Q represents a;
-
(ii)
\(Q \simeq \langle a \rangle \boxplus Q'\) for some nondegenerate form \(Q'\); and
-
(iii)
\(\langle -a \rangle \boxplus Q\) is isotropic.
Proof. For (i) \(\Rightarrow \) (ii), we take \(Q'=Q|_{W}\) and \(W=\{v\}^\perp \subset V\) where \(Q(v)=a\). For (ii) \(\Rightarrow \) (iii), we note that \(\langle -a \rangle \boxplus Q \simeq \langle a,-a \rangle \boxplus Q'\) is isotropic. For (iii) \(\Rightarrow \) (i), suppose \((\langle -a \rangle \boxplus Q)(v)=0\), so \(Q(v)=ax^2\) for some \(x \in F\). If \(x=0\), then Q is isotropic and by Lemma 5.4.2 represents a; if \(x \ne 0\), then by homogeneity \(Q(v/x)=a\) and again Q represents a. \(\square \)
We now come to a main result.
MainTheorem 5.4.4
Let \(B=\displaystyle {\biggl (\frac{a,b}{F}\biggr )}\) be a quaternion algebra over F (with \({{\,\mathrm{char}\,}}F \ne ~2\)). Then the following are equivalent:
- (i):
-
\(B \simeq \displaystyle {\biggl (\frac{1,1}{F}\biggr )} \simeq {{\,\mathrm{M}\,}}_2(F)\);
- (ii):
-
B is not a division ring;
- (iii):
-
The quadratic form \({{\,\mathrm{nrd}\,}}\simeq \langle 1,-a,-b,ab \rangle \) is isotropic;
- (iv):
-
The quadratic form \({{\,\mathrm{nrd}\,}}|_{B^0} \simeq \langle -a,-b,ab \rangle \) is isotropic;
- (v):
-
The binary form \(\langle a,b \rangle \) represents 1;
- (vi):
-
\(b\in {{\,\mathrm{Nm}\,}}_{K|F}(K^\times )\) where \(K=F[i]\); and
- (vi\({}^\prime \)):
-
\(b \in {{\,\mathrm{Nm}\,}}_{K|F}(K^\times )\) where \(K=F(\sqrt{a})\).
Condition (vi) holds if and only if there exist \(x,y \in F\) such that \(x^2-ay^2=b\); if K is not a field then \(K \simeq F \times F\) and \({{\,\mathrm{Nm}\,}}_{K|F}(K^\times )=F^\times \). In condition (vi\({}^\prime \)), we take \(F(\sqrt{a})\) to be a splitting field for \(x^2-a\) over F, so equal to F if \(a \in F^\times \). (Depending on the circumstances, one of these formulations may be more natural than the other.)
Proof. We follow Lam [Lam2005, Theorem 2.7]. The isomorphism \(({1,1} \mid {F}) \simeq {{\,\mathrm{M}\,}}_2(F)\) in (i) follows from Example 2.2.4. The implication (i) \(\Rightarrow \) (ii) is clear. The equivalence (ii) \(\Leftrightarrow \) (iii) follows from the fact that \(\alpha \in B^\times \) if and only if \({{\,\mathrm{nrd}\,}}(\alpha ) \in F^\times \) (Exercise 3.5).
We now prove (iii) \(\Rightarrow \) (iv). Let \(0 \ne \alpha \in B\) be such that \({{\,\mathrm{nrd}\,}}(\alpha )=0\). If \({{\,\mathrm{trd}\,}}(\alpha )=0\), then we are done. Otherwise, \({{\,\mathrm{trd}\,}}(\alpha ) \ne 0\). Let \(\beta \) be orthogonal to \(1,\alpha \), so that \({{\,\mathrm{trd}\,}}(\alpha \beta )=0\). We cannot have both \(\alpha \beta =0\) and \(\overline{\alpha }\beta =({{\,\mathrm{trd}\,}}(\alpha )-\alpha )\beta =0\), so we may suppose \(\alpha \beta \ne 0\). But then \({{\,\mathrm{nrd}\,}}(\alpha \beta )={{\,\mathrm{nrd}\,}}(\alpha ){{\,\mathrm{nrd}\,}}(\beta )=0\) as desired.
To complete the equivalence of the first four we prove (iv) \(\Rightarrow \) (i). Let \(\beta \in B^0\) satisfy \({{\,\mathrm{nrd}\,}}(\beta )=0\). Since \({{\,\mathrm{nrd}\,}}|_{B^0}\) is nondegenerate, there exists \(0 \ne \alpha \in B^0\) such that \({{\,\mathrm{trd}\,}}(\alpha \overline{\beta }) \ne 0\). Therefore, the restriction of \({{\,\mathrm{nrd}\,}}\) to \(F \alpha \oplus F \beta \) is nondegenerate and isotropic. By Lemma 5.4.2, we conclude there exists a basis for \(B^0\) such that \({{\,\mathrm{nrd}\,}}|_{B^0} \simeq \langle 1, -1 \rangle \boxplus \langle c \rangle = \langle 1, -1, c \rangle \); but \({{\,\mathrm{disc}\,}}({{\,\mathrm{nrd}\,}}|_{B^0}) = -c \in F^{\times 2}\) by 5.2.2; rescaling, we may suppose \(c=-1\). But then by Proposition 5.2.4 we have \(B \simeq ({1,1} \mid {F})\).
Now we show (iv) \(\Rightarrow \) (v). For \(\alpha \in B^0\),
as in 5.2.2. Suppose \({{\,\mathrm{nrd}\,}}(\alpha )=0\). If \(z=0\), then the binary form \(\langle a,b \rangle \) is isotropic so is a hyperbolic plane by Lemma 5.4.2 and thus represents 1. If \(z \ne 0\) then
Next we prove (v) \(\Rightarrow \) (vi). If \(a \in F^{\times 2}\) then \(K \simeq F \times F\) and \({{\,\mathrm{Nm}\,}}_{K|F}(K^\times )=F^\times \ni b\). If \(a \not \in F^{\times 2}\), then given \(ax^2+by^2=1\) we must have \(y \ne 0\) so
In the equivalence (vi) \(\Leftrightarrow \) (vi\({}^\prime \)), the two statements are identical if \(a \not \in F^{\times 2}\) and both automatically satisfied if \(a \in F^{\times 2}\).
To conclude, we prove (vi) \(\Rightarrow \) (iii). If \(b = x^2-ay^2 \in {{\,\mathrm{Nm}\,}}_{K|F}(K^\times )\), then \(\alpha =x+yi+j \ne 0\) has \({{\,\mathrm{nrd}\,}}(\alpha )=x^2-ay^2-b=0\). \(\square \)
We give a name to the equivalent conditions in Main Theorem 5.4.4.
Definition 5.4.5
A quaternion algebra B over F is split if \(B \simeq {{\,\mathrm{M}\,}}_2(F)\). A field K containing F is a splitting field for B if \(B \otimes _F K\) is split.
Example 5.4.6
The fundamental example of a splitting field for a quaternion algebra is that \(\mathbb C \) splits the real Hamiltonians \(\mathbb H \): we have \(\mathbb H \otimes _\mathbb R \mathbb C \simeq {{\,\mathrm{M}\,}}_2(\mathbb C )\) as in (2.4.1).
Lemma 5.4.7
Let \(K \supset F\) be a quadratic extension of fields. Then K is a splitting field for B if and only if there is an injective F-algebra homomorphism \(K \hookrightarrow B\).
Proof. First, suppose \(\iota :K \hookrightarrow B\). We may suppose that \(K=F(\sqrt{d})\) with \(d \in F^\times \). Let \(\mu = \iota (\sqrt{d})\), so \(\mu ^2=d\). Then \(1 \otimes \sqrt{d} - \mu \otimes 1\) is a zerodivisor in \(B \otimes _F K\):
By Main Theorem 5.4.4, we conclude that \(B \otimes _F K \simeq {{\,\mathrm{M}\,}}_2(K)\).
Next we prove the converse. If \(B \simeq {{\,\mathrm{M}\,}}_2(F)\) already, then any quadratic field K embeds in B (take a matrix in rational normal form) and \(B \otimes _F K \simeq {{\,\mathrm{M}\,}}_2(K)\) for any K. So by Main Theorem 5.4.4, we may suppose B is a division ring. Let \(K=F(\sqrt{d})\). We have \(B \otimes _F K \simeq {{\,\mathrm{M}\,}}_2(K)\) if and only if \(\langle -a,-b,ab \rangle \) is isotropic over K, which is to say there exist \(x,y,z,u,v,w \in F\) such that
Let \(\alpha =xi+yj+zij\) and \(\beta =ui+vj+wij\). Then \({{\,\mathrm{trd}\,}}(\alpha )={{\,\mathrm{trd}\,}}(\beta )=0\). Expansion of (5.4.8) (Exercise 5.14) shows that \(\alpha \) is orthogonal to \(\beta \), so \({{\,\mathrm{trd}\,}}(\alpha \beta )=0\), and that \({{\,\mathrm{nrd}\,}}(\alpha )+d{{\,\mathrm{nrd}\,}}(\beta )=0\). Since B is a division ring, if \({{\,\mathrm{nrd}\,}}(\beta )=c=0\) then \(\beta =0\) so \({{\,\mathrm{nrd}\,}}(\alpha )=0\) as well and \(\alpha =0\), a contradiction. So \({{\,\mathrm{nrd}\,}}(\beta ) \ne 0\), and the element \(\gamma =\alpha \beta ^{-1}=c^{-1}\alpha \beta \in B\) has \({{\,\mathrm{nrd}\,}}(\gamma )=-d\) and \({{\,\mathrm{trd}\,}}(\gamma )=c^{-1}{{\,\mathrm{trd}\,}}(\alpha \beta )=0\) so \(\gamma ^2=d\) as desired. \(\square \)
Example 5.4.9
If \(B=\displaystyle {\biggl (\frac{a,b}{F}\biggr )}\), then either \(a \in F^{\times 2}\) and \(B \simeq \displaystyle {\biggl (\frac{1,b}{F}\biggr )} \simeq {{\,\mathrm{M}\,}}_2(F)\) is split, or \(a \not \in F^{\times 2}\) and \(K=F(\sqrt{a})\) splits B.
Example 5.4.10
Let p be an odd prime and let a be a quadratic nonresidue modulo p. We claim that \(\displaystyle {\biggl (\frac{a,p}{\mathbb{Q }}\biggr )}\) is a division quaternion algebra over \(\mathbb Q \). By Main Theorem 5.4.4, it suffices to show that the quadratic form \(\langle 1,-a,-p,ap \rangle \) is anisotropic. So suppose that \(t^2-ax^2=p(y^2-az^2)\) with \(t,x,y,z \in \mathbb Q \) not all zero. The equation is homogeneous, so we can multiply through by a common denominator and suppose that \(t,x,y,z \in \mathbb Z \) with \(\gcd (t,x,y,z)=1\). Reducing modulo p we find \(t^2 \equiv ax^2 \pmod {p}\); since a is a quadratic nonresidue, we must have \(t \equiv x \equiv 0 ~(\text{ mod } ~{p})\). Plugging back in and cancelling a factor of p we find \(y^2 \equiv az^2 \equiv 0 ~(\text{ mod } ~{p})\), and again \(y \equiv z \equiv 0 ~(\text{ mod } ~{p})\), a contradiction.
5 Conics, embeddings
Following Main Theorem 5.2.5, we are led to consider the zero locus of the quadratic form \({{\,\mathrm{nrd}\,}}|_{B^0}\) up to scaling; this gives a geometric way to view the preceding results.
Definition 5.5.1
A conic \(C \subset \mathbb P ^2\) over F is a nonsingular projective plane curve of degree 2. An isomorphism of conics \(C,C'\) over F is an element \(f \in {{\,\mathrm{PGL}\,}}_3(F)={{\,\mathrm{Aut}\,}}(\mathbb P ^2)(F)\) that induces an isomorphism of curves  .
.
If we identify
with (the points of) the projective plane over F, then the vanishing locus \(C=V(Q)\) of \(Q={{\,\mathrm{nrd}\,}}|_{B^0}\) defines a conic over F: if we take the basis \(i,j,ij\) for \(B^0\), then the conic C is defined by the vanishing of the equation
Here, nondegeneracy of the quadratic form is equivalent to the nonsingularity of the associated plane curve (Exercise 4.13).
The following corollary is then simply a rephrasing of Main Theorem 5.2.5.
Corollary 5.5.2
The map \(B \mapsto C=V({{\,\mathrm{nrd}\,}}|_{B^0})\) yields a bijection

that is functorial with respect to F.
Main Theorem 5.4.4 also extends to this context.
Theorem 5.5.3
The following are equivalent:
-
(i)
\(B \simeq {{\,\mathrm{M}\,}}_2(F)\);
-
(vii)
The conic C associated to B has an F-rational point.
By Lemma 5.4.7, a quadratic field K over F embeds in B if and only if the ternary quadratic form \({{\,\mathrm{nrd}\,}}|_{B^0}\) represents 0 over K. We can also rephrase this in terms of the values represented by \({{\,\mathrm{nrd}\,}}|_{B^0}\).
Lemma 5.5.4
Let K be a quadratic extension of F of discriminant d. Then \(K \hookrightarrow B\) if and only if \({{\,\mathrm{nrd}\,}}|_{B^0}\) represents \(-d\) over F.
Proof. Write \(K=F(\sqrt{d})\). Then \(K \hookrightarrow B\) if and only if there exists \(\alpha \in B\) such that \(\alpha ^2=d\) if and only if there exists \(\alpha \in B\) with \({{\,\mathrm{trd}\,}}(\alpha )=0\) and \({{\,\mathrm{nrd}\,}}(\alpha )=-d\), as claimed. \(\square \)
Remark 5.5.5. Two conics over F are isomorphic (as plane curves) if and only if their function fields are isomorphic (Exercise 5.23).
6 Orientations
To conclude, we show that the notion of orientation underlying the definition of special isometries (as in Example 4.5.5) extends more generally to isometries between two different quadratic spaces by keeping track of one bit of extra information, refining Main Theorem 5.2.5. We follow Knus–Murkurjev–Rost–Tignol [KMRT98, Theorem 15.2]. We retain our hypothesis that \({{\,\mathrm{char}\,}}F \ne 2\).
Let \(Q:V \rightarrow F\) be a quadratic space with \(\dim _F V=n\) odd.
Lemma 5.6.1
Suppose Q has signed discriminant \({{\,\mathrm{sgndisc}\,}}Q=d \in F^\times /F^{\times 2}\). Let \(A :={{\,\mathrm{Clf}\,}}Q\) be the Clifford algebra of Q, and let \(K=Z(A)\) be the center of A. Then \(K \simeq F[x]/(x^2-d)\).
The signed discriminant gives a simpler statement; one could equally well work with the usual discriminant and keep track of the sign.
Proof. We do the case \(n=3\). We may suppose \(V \simeq F^3\) with standard basis \(e_1,e_2,e_3\) and that \(Q \simeq \langle a,b,c \rangle \) is diagonal, with \({{\,\mathrm{sgndisc}\,}}(Q)=-abc=d\). We have the relation \(e_ie_j=-e_je_i\) for \(i \ne j\); for all \(i=1,2,3\), conjugation by \(e_i\) acts by \(-1\) on \(e_j\) and \(e_ie_j\) for \(j \ne i\). This implies \(Z(A) \subseteq F + Fe_1e_2e_3\). Let \(\delta :=e_1e_2e_3=e_2e_3e_1=e_3e_1e_2\); then \(\delta e_i = e_i \delta \) for \(i=1,2,3\), so \(Z(A)=F[\delta ]\). We compute
Therefore \(K \simeq F[x]/(x^2-d)\).
The general case is requested in Exercise 5.19: with a basis \(e_1,\dots ,e_n\) for V, the center is generated over F by \(\delta =e_1\cdots e_n\). \(\square \)
From now on, suppose \({{\,\mathrm{sgndisc}\,}}(Q)=d=1\).
Definition 5.6.3
An orientation of Q is a choice of \(\zeta \in Z({{\,\mathrm{Clf}\,}}Q) \smallsetminus F\) with \(\zeta ^2=1\).
5.6.4
Q has exactly two choices of orientation \(\zeta \), differing by sign, by Lemma 5.6.1: under an isomorphism \(Z({{\,\mathrm{Clf}\,}}Q) \simeq F \times F\), the two orientations are \((-1,1)\) and \((1,-1)\). More intrinsically, given an orientation \(\zeta \), we have a projection \(K \rightarrow K/(\zeta -1) \simeq F\), and conversely given a projection \(\pi :K \rightarrow F\), there is a unique orientation \(\zeta \) with \(\pi (\zeta )=1\) (the other maps to \(-1\), by F-linearity).
Definition 5.6.5
Let \(\zeta ,\zeta '\) be orientations on \(Q,Q'\). An isometry \(f:V \rightarrow V'\) is oriented (with respect to \(\zeta ,\zeta '\)) if in the induced map \( f:Z({{\,\mathrm{Clf}\,}}Q) \rightarrow Z({{\,\mathrm{Clf}\,}}Q')\) we have \(f(\zeta )=\zeta '\).
5.6.6
An oriented isometry is the same as a special isometry (Definition 4.5.1) when \(V \simeq F^n\) (n still odd), as follows. Let \(A={{\,\mathrm{Clf}\,}}Q\). Let \(e_1,\dots ,e_n\) be a basis for V adapted as in the proof of Lemma 5.6.1 and \(\delta =e_1\dots e_n\). Then Z(A) is generated by \(\delta \) and \(\delta ^2=1\). If \(f \in {{\,\mathrm{O}\,}}(Q)(F)\), then \(f(\delta )=(\det f)\delta \), so \(\zeta = \pm \delta \) is preserved if and only if \(\det (f)=1\), and this is independent of the choice of orientation.
So we define the oriented or special orthogonal group of a quadratic space by choosing an orientation and letting
the resulting group is independent of the choice, and we recover the same group as in Definition 4.5.1.
5.6.7
Let \(B=\displaystyle {\biggl (\frac{a,b}{F}\biggr )}\) be a quaternion algebra over F. In previous sections, we took \({{\,\mathrm{nrd}\,}}|_{B^0}:B^0 \rightarrow F\), a nondegenerate ternary quadratic space of discriminant 1. Since we are working with the signed discriminant, we take instead \(-{{\,\mathrm{nrd}\,}}|_{B^0}:B^0 \rightarrow F\) with \({{\,\mathrm{sgndisc}\,}}(-{{\,\mathrm{nrd}\,}}|_{B^0})=1\); this map has a nice description as the squaring map, since \(\alpha ^2=-{{\,\mathrm{nrd}\,}}(\alpha )\) for \(\alpha \in B^0\).
We claim that \(B^0\) has a canonical orientation. We have an inclusion \(\iota :B^0 \hookrightarrow B\) with \(\iota (x)^2=-{{\,\mathrm{nrd}\,}}(x)\) for all \(x \in B^0\). By the universal property of Clifford algebras, we get an F-algebra homomorphism \(\phi :{{\,\mathrm{Clf}\,}}(B^0) \rightarrow B\). We see that \(\phi \) is surjective so it induces an F-algebra map \(\pi :Z({{\,\mathrm{Clf}\,}}(B^0)) \rightarrow Z(B)=F\) (Exercise 2.8). This defines a unique orientation \(\zeta _B=\zeta \) with \(\zeta -1 \in \ker \pi \), by 5.6.4.
Explicitly, let i, j, k be the standard basis for B with \(k=ij\). Then \({{\,\mathrm{nrd}\,}}(k)=ab\), and i, j, k is a basis for \(B^0\). Let \(\zeta =ijk^{-1} = -ijk/(ab) \in Z({{\,\mathrm{Clf}\,}}(B^0))\). Then \(\delta ^2=-ab(-ab)/(ab)^2=1\) as in (5.6.2). Multiplying out in B, we get \(\phi (\zeta )=1 \in B\), so \(\zeta \) is the same orientation as in the previous paragraph.
The following theorem then refines Main Theorem 5.2.5.
Theorem 5.6.8
Let F be a field with \({{\,\mathrm{char}\,}}F \ne 2\). Then the functors

yield an equivalence of categories between
Oriented ternary quadratic forms over F with signed discriminant \(1 \in F^{\times }/F^{\times 2}\),
under oriented isometries.
and
Quaternion algebras over F, under F-algebra isomorphisms.
Proof. Let B be a quaternion algebra. As in 5.6.7, the inclusion \(\iota :B^0 \hookrightarrow B\) gives an F-algebra homomorphism \({{\,\mathrm{Clf}\,}}(-{{\,\mathrm{nrd}\,}}|_{B^0}) \rightarrow B\) which restricts to a canonical F-algebra homomorphism \({{\,\mathrm{Clf}\,}}^0(-{{\,\mathrm{nrd}\,}}|_{B^0}) \rightarrow B\). In fact, in coordinates, this map is the isomorphism (5.3.24): choosing the standard basis i, j, k for \(B=({a,b} \mid {F})\), and letting \(e_1=i,e_2=j,e_3=k\), we have
with the standard generators \(i_0 :=e_1e_2=ij\) and \(j_0 :=e_2e_3=jk\). We define the isomorphism
Therefore, the canonical isomorphism  yields a natural isomorphism between these composed functors and the identity functor, giving an equivalence of categories.
yields a natural isomorphism between these composed functors and the identity functor, giving an equivalence of categories.
Conversely, let \((Q,\zeta )\) be an oriented ternary quadratic space, let \(B={{\,\mathrm{Clf}\,}}^0 Q\), and consider \((-{{\,\mathrm{nrd}\,}}|_{B^0},\zeta _B)\). We define a natural oriented isometry between these two spaces. We have a natural inclusion \(V \hookrightarrow {{\,\mathrm{Clf}\,}}Q\), and we define the linear map
since \(v,\zeta \in {{\,\mathrm{Clf}\,}}^1 Q\), we have \(v\zeta \in {{\,\mathrm{Clf}\,}}^0 Q=B\). We now show that \(m_\zeta \) induces an oriented isometry \(m_\zeta :V \rightarrow B^0\). To do so, we let \(V\simeq F^3\) by choosing an orthogonal basis \(e_1,e_2,e_3\) in which \(Q \simeq \langle a,b,c \rangle \) and \(-abc=1\). We identify \(B \simeq ({-ab,-bc} \mid {F})\) as in 5.3.23, with \(i=e_1e_2\) and \(j=e_2e_3\), and we let \(k=ij=-be_3e_1\) so \(k^2=b^2(-ac)=b\). Then \(\zeta =\epsilon e_1e_2e_3\) with \(\epsilon =\pm 1\), and
so in particular \(m_\zeta (V) \subseteq B^0\). The map is an isometry, because
since \(\zeta ^2=1\) and \(\zeta \) is central. Finally, the map is oriented:
This natural oriented isometry gives a natural transformation between these composed functors and the identity functor, and the statement follows. \(\square \)
Remark 5.6.11. Theorem 5.6.8 can be seen as a manifestation of the isomorphism of Dynkin diagrams \(A_1 \simeq B_1\) (consisting of a single node \(\bullet \)), corresponding to the isomorphism of Lie algebras \(\textsf {sl}_2 \simeq \textsf {so}_3\). This is just one of the (finitely many) exceptional isomorphisms—the others are just as beautiful, with deep implications, and the reader is encouraged to read the bible by Knus–Merkurjev–Rost–Tignol [KMRT98, §15].
We record the following important consequence.
Corollary 5.6.12
We have \({{\,\mathrm{Aut}\,}}(B) \simeq B^\times /F^\times \).
Proof. We take stabilizers of objects on both sides of the equivalence of categories in Theorem 5.6.8; we find \({{\,\mathrm{Aut}\,}}(B) \simeq {{\,\mathrm{SO}\,}}(Q)(F)\) if B corresponds to Q. But by Proposition 4.5.10, there is an isomorphism \(B^\times /F^\times \simeq {{\,\mathrm{SO}\,}}(Q)(F)\), and the result follows. \(\square \)
Remark 5.6.13. We will return to Corollary 5.6.12 in the Skolem–Noether theorem in section 7.7, generalizing to the context of embeddings into a simple algebra.
To conclude, we extend the notion of oriented isometry to similarities.
5.6.14
Let \(\zeta ,\zeta '\) be orientations on quadratic spaces \(V,V'\) and suppose \(\dim \,V=\dim \,V'=n=2m\) is even. Then a similarity (f, u) from V to \(V'\) induces an F-linear map  , and we say (f, u) is oriented if the map
, and we say (f, u) is oriented if the map  preserves orientations. We define
preserves orientations. We define
and recover the same group as in 4.5.4. If n is odd, we declare that every similarity is oriented and let \({{\,\mathrm{GSO}\,}}(Q)(F) :={{\,\mathrm{GO}\,}}(Q)(F)\).
Exercises
Throughout, let F be a field with \({{\,\mathrm{char}\,}}F \ne 2\).
-
1.
Let \(B,B'\) be quaternion algebras over F. Show that if the quadratic forms \({{\,\mathrm{nrd}\,}}_B\) and \({{\,\mathrm{nrd}\,}}_{B'}\) are similar, then they are isometric.
-
2.
Consider the hyperbolic quaternions \(H_{Mac }\) of Macfarlane (1.2.1).
-
(a)
Show that \(H_{Mac }\) is the Clifford algebra of \(\langle 1,1,1 \rangle \) over \(\mathbb R \).
-
(a)
Show that \(H_{Mac }\) is isomorphic as an algebra over \(\mathbb C =\mathbb R (\sqrt{-1})\) to the even Clifford algebra of the ternary quadratic form \(-\sqrt{-1}\langle 1,1,1 \rangle \).
-
(a)
-
3.
Prove the implication (vi) \(\Rightarrow \) (v) of Main Theorem 5.4.4 directly.
-
4.
Use Main Theorem 5.4.4(vi) to give another proof that there is no division quaternion algebra B over a finite field \(F=\mathbb F _q\) (with q odd).
-
5.
-
(a)
Show that the quadratic form \(Q(x,y,z)=x^2+y^2+z^2\) is isotropic over \(\mathbb F _p\) for all odd primes p. Conclude that \(({-1,-1} \mid \mathbb{F _p}) \simeq {{\,\mathrm{M}\,}}_2(\mathbb F _p)\). [Hint: count squares and nonsquares.]
-
(b)
More generally, show that every ternary quadratic form over a finite field \(\mathbb F _q\) (with q odd) is isotropic. [Hint: Reduce to the case of finding a solution to \(y^2=f(x)\) where f is a polynomial of degree 2.] Use Main Theorem 5.4.4(iv) to give yet another proof that there is no division quaternion algebra B over \(\mathbb F _q\).
-
(c)
Show that over a finite field \(\mathbb F _q\) with q odd, there is a unique anisotropic binary quadratic form up to isometry.
-
(a)
-
6.
Show that if \(Q:F \rightarrow F\) is the quadratic form \(Q(x)=ax^2\) with \(a \in F\), then \({{\,\mathrm{Clf}\,}}(F) \simeq F[x]/(x^2-a)\).
-
7.
Show that \((-1,26)_\mathbb{Q }=1\), i.e., \(\displaystyle {\biggl (\frac{-1,26}{\mathbb{Q }}\biggr )} \simeq {{\,\mathrm{M}\,}}_2(\mathbb Q )\).
-
8.
Let p be prime. Show that \(\displaystyle {\biggl (\frac{-1,p}{\mathbb{Q }}\biggr )} \simeq {{\,\mathrm{M}\,}}_2(\mathbb Q )\) if and only if \(p=2\) or \(p \equiv 1 \pmod {4}\).
-
9.
Show that
$$\displaystyle {\biggl (\frac{-2,-3}{\mathbb{Q }}\biggr )} \simeq \displaystyle {\biggl (\frac{-1,-1}{\mathbb{Q }}\biggr )} \text { but that }\displaystyle {\biggl (\frac{-2,-5}{\mathbb{Q }}\biggr )} \not \simeq \displaystyle {\biggl (\frac{-1,-1}{\mathbb{Q }}\biggr )}.$$ -
10.
Let \(B=({a,b} \mid {F})\) be a quaternion algebra over F. Give a constructive (algorithmic) proof of the implication (iv) \(\Rightarrow \) (i) in Main Theorem 5.4.4, as follows.
Let \(\epsilon = xi+yj+zij \in B\) satisfy \({{\,\mathrm{nrd}\,}}(\epsilon )=-ax^2-by^2+abz^2=-\epsilon ^2=0\).
-
(a)
Show that there exists \(k \in \{i,j,ij\}\) such that \({{\,\mathrm{trd}\,}}(\epsilon k)=s \ne 0\).
-
(b)
Let \(t :={{\,\mathrm{trd}\,}}(k)\) and \(n :={{\,\mathrm{nrd}\,}}(k)\), and let \(\epsilon ' :=s^{-1} \epsilon \). Let
$$\begin{aligned} i'&:=\epsilon ' k - (k+t)\epsilon ' \\ j'&:=k + (-tk+n+1)\epsilon '. \end{aligned}$$Show that \(i',j'\) generate B as an F-algebra, and that \((i')^2=(j')^2=1\) and \(j'i'=-i'j'\). Conclude that \(B \simeq {{\,\mathrm{M}\,}}_2(F)\).
-
(c)
Show that \(I :=F\epsilon ' + Fk\epsilon '\) is a left ideal of B with \(\dim _F I=2\), and interpret (b) as arising from the left multiplication map \(B \rightarrow {{\,\mathrm{End}\,}}_F(I) \simeq {{\,\mathrm{M}\,}}_2(F)\).
-
(a)
-
11.
Let B be a quaternion algebra over F. Let Q be the reduced norm on B, and for clarity write \(e_0=1\), \(e_1=i\), \(e_2=j\), \(e_3=k\) as a basis for the domain of Q.
-
(a)
Let \(C^0={{\,\mathrm{Clf}\,}}^0 Q\) be the even Clifford algebra of the reduced norm Q. Show that \(Z(C^0) \simeq F \times F\). [Hint: \(Z(C^0)\) is generated by \(e_0e_1e_2e_3\).]
-
(b)
Show that \(C^0 \simeq B \times B^{op } (\simeq B \times B)\) as F-algebras.
-
(c)
Prove that if \(B'\) is a quaternion algebra over F then \(B \simeq B'\) are isomorphic as F-algebras if and only if the reduced norms \(Q \sim Q'\) are similar as quadratic spaces.
-
(a)
-
12.
Let \(Q:V \rightarrow F\) be a nondegenerate quadratic form. Show that the reversal map \(\overline{\phantom {x}}:{{\,\mathrm{Clf}\,}}^0 Q \rightarrow {{\,\mathrm{Clf}\,}}^0 Q\) on the Clifford algebra has the property that \(x\overline{x} \in F\) for all pure tensors \(x=e_1e_2\cdots e_d\), but defines a standard involution on \({{\,\mathrm{Clf}\,}}Q\) if and only if \(V = \{0 \}\) and on \({{\,\mathrm{Clf}\,}}^0 Q\) if and only if \(\dim _F V \le 3\).
-
13.
Give another proof of Lemma 5.3.17 using the universal property of the Clifford algebra.
- \(\triangleright \) 14.:
-
Expand (5.4.8) and prove as a consequence that if \(\alpha =xi+yj+zij\) and \(\beta =ui+vj+wij\), then \({{\,\mathrm{trd}\,}}(\alpha \beta )=0\) (so \(\alpha \) is orthogonal to \(\beta \)) and moreover \({{\,\mathrm{nrd}\,}}(\alpha )+d{{\,\mathrm{nrd}\,}}(\beta )=0\).
-
15.
Show that the Hilbert symbol is Galois equivariant, in the following sense: for all field automorphisms \(\sigma \in {{\,\mathrm{Aut}\,}}(F)\) and all \(a,b \in F^\times \), we have \((\sigma (a),\sigma (b))_F = (a,b)_F\).
-
16.
Let \(a,b,b' \in F^\times \). Show that there exists an F-linear isomorphism
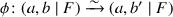 with \(\phi (i)=i'\) if and only if \(b/b' \in {{\,\mathrm{Nm}\,}}_{K|F}(K^\times )\) where \(K=F(\sqrt{a})\). [More generally, see Corollary 7.7.6.]
with \(\phi (i)=i'\) if and only if \(b/b' \in {{\,\mathrm{Nm}\,}}_{K|F}(K^\times )\) where \(K=F(\sqrt{a})\). [More generally, see Corollary 7.7.6.] -
17.
Let \(a \in \mathbb Q ^\times \smallsetminus \mathbb Q ^{\times 2}\). Show that there are infinitely many distinct isomorphism classes of conics \(x^2-ay^2=bz^2\) for \(b \in \mathbb Q ^\times \).
-
18.
Let \(K=F(a,b)\) with a, b algebraically independent, transcendental elements. Show that the generic quaternion algebra \(\displaystyle {\biggl (\frac{a,b}{K}\biggr )}\) is a division algebra. [Hint: show the associated ternary quadratic form is anisotropic.]
- \(\triangleright \) 19:
-
Prove Lemma 5.6.1 for general odd n as follows.
- (a):
-
For a subset \(I=\{i_1,\dots ,i_r\} \subseteq \{1,\dots ,n\}\), let \(e_I=e_{i_1}\cdots e_{i_r}\) with \(i_1<\dots <i_r\). Then for subsets \(I,J \subseteq \{1,\dots ,n\}\), show that
$$\begin{aligned} e_I e_J=e_J e_I (-1)^{\#I \cdot \#J - \#(I \cap J)}. \end{aligned}$$ - (b):
-
Show that \(Z({{\,\mathrm{Clf}\,}}Q)=F[\delta ] \simeq F[x]/(x^2-d)\) where \(\delta =e_1e_2\dots e_n\) and \(d={{\,\mathrm{sgndisc}\,}}(Q)\). [Hint: Argue on bases and choose \(\#J = 2\) with \(I \cap J = 1\).]
-
20.
Let \(Q:V \rightarrow F\) be a quadratic form. Show that the even Clifford algebra \({{\,\mathrm{Clf}\,}}^0 Q\) with its map \(\iota :V \otimes V \rightarrow {{\,\mathrm{Clf}\,}}^0 Q\) has the following universal property: if A is an F-algebra and \(\iota _A:V \otimes V \rightarrow A\) is an F-linear map such that
-
(i)
\(\iota _A(x \otimes x)=Q(x)\) for all \(x \in V\), and
-
(ii)
\(\iota _A(x \otimes y)\iota _A(y \otimes z)=Q(y)\iota _A(x \otimes z)\) for all \(x,y,z \in V\),
then there exists a unique F-algebra homomorphism \(\phi :{{\,\mathrm{Clf}\,}}^0 Q \rightarrow A\) such that the diagram
commutes. Conclude that the pair \(({{\,\mathrm{Clf}\,}}^0 Q,\iota )\) is unique up to unique isomorphism.
-
(i)
-
21.
In this exercise, we consider graded tensor products, giving an alternate verification of Lemma 5.3.14.
Let \(A=A_0 \oplus A_1\) and \(B=B_0\oplus B_1\) be finite-dimensional F-algebras equipped with a \(\mathbb Z /2\mathbb Z \)-grading. We define the graded tensor product \(A \widehat{\otimes } B\) to be the usual tensor product as an F-vector space but with multiplication law defined on simple tensors by
$$\begin{aligned} (a \otimes b)\cdot (a' \otimes b') = (-1)^{(\deg a')(\deg b)}(aa' \otimes bb'). \end{aligned}$$-
(a)
Show that \(A \widehat{\otimes } B\) is an F-algebra of dimension \((\dim _F A)(\dim _F B)\).
-
(b)
Let \(Q_1 :V_1 \rightarrow F\) and \(Q_2 :V_2 \rightarrow F\), and let \(Q :=Q_1 \boxplus Q_2\) be the orthogonal direct sum on the quadratic space \(V :=V_1 \boxplus V_2\). Show there is a canonical isomorphism of Clifford algebras
$$\begin{aligned} {{\,\mathrm{Clf}\,}}(Q) \cong {{\,\mathrm{Clf}\,}}(Q_1) \widehat{\otimes } {{\,\mathrm{Clf}\,}}(Q_2). \end{aligned}$$ -
(c)
Observe that (b) gives another proof of Lemma 5.3.14.
-
(a)
-
22.
For \(i=1,2\), let \(Q_i:V_i \rightarrow F\) be quadratic forms over F.
-
(a)
Prove that there exists a canonical R-algebra isomorphism
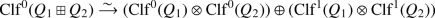
where \({{\,\mathrm{Clf}\,}}^1(Q_1) \otimes {{\,\mathrm{Clf}\,}}^1(Q_2)\) has multiplication induced from the full Clifford algebras \({{\,\mathrm{Clf}\,}}(Q_1)\) and \({{\,\mathrm{Clf}\,}}(Q_2)\).
-
(b)
Prove that there is a \({{\,\mathrm{Clf}\,}}^0(Q_1 \boxplus Q_2)\)-bimodule isomorphism
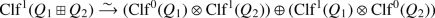
with bimodule structure induced by multiplication in the full Clifford algebra.
-
(a)
-
23.
In this exercise, we assume background in algebraic curves. Show that two conics over F are isomorphic (as projective plane curves) if and only if their function fields are isomorphic. [Hint: conics are anticanonically embedded—the restriction of \(\mathscr {O}_\mathbb{P ^2}(-1)\) to the conic is a canonical sheaf—so an isomorphism of function fields induces an linear isomorphism of conics.]
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
This chapter is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, duplication, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, a link is provided to the Creative Commons license and any changes made are indicated.The images or other third party material in this chapter are included in the work's Creative Commons license, unless indicated otherwise in the credit line; if such material is not included in the work's Creative Commons license and the respective action is not permitted by statutory regulation, users will need to obtain permission from the license holder to duplicate, adapt or reproduce the material.
Copyright information
© 2021 The Author(s)
About this chapter
Cite this chapter
Voight, J. (2021). Ternary quadratic forms and quaternion algebras. In: Quaternion Algebras. Graduate Texts in Mathematics, vol 288. Springer, Cham. https://doi.org/10.1007/978-3-030-56694-4_5
Download citation
DOI: https://doi.org/10.1007/978-3-030-56694-4_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-56692-0
Online ISBN: 978-3-030-56694-4
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)



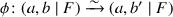 with
with