Abstract
In the previous chapter, we showed that Brandt matrices for an order in a definite quaternion algebra B contain a wealth of arithmetic. In the special case where \({{\,\mathrm{disc}\,}}B=p\) is prime, there is a further beautiful connection between Brandt matrices and the theory of supersingular elliptic curves, arising from the following important result: there is an equivalence of categories between supersingular elliptic curves over \(\overline{\mathbb{F }}_p\) and right ideals in a (fixed) maximal order \(\mathcal {O}\subset B\). We pursue this important connection in this chapter for the reader who has a bit more background in algebraic curves.
You have full access to this open access chapter, Download chapter PDF
In the previous chapter, we showed that Brandt matrices for an order in a definite quaternion algebra B contain a wealth of arithmetic. In the special case where \({{\,\mathrm{disc}\,}}B=p\) is prime, there is a further beautiful connection between Brandt matrices and the theory of supersingular elliptic curves, arising from the following important result: there is an equivalence of categories between supersingular elliptic curves over \(\overline{\mathbb{F }}_p\) and right ideals in a (fixed) maximal order \(\mathcal {O}\subset B\). We pursue this important connection in this chapter for the reader who has a bit more background in algebraic curves.
1 Supersingular elliptic curves
In this section, we briefly review what we will need from the theory of elliptic curves; see Silverman [Sil2009] for further general reference. Let F be a field with algebraic closure \(F{}^{al }\).
Definition 42.1.1
An elliptic curve is a smooth projective curve (variety of dimension 1) of genus 1 equipped with a rational point. Every elliptic curve E is isomorphic over F to the projective curve associated to the affine equation
with \(a_i \in F\).
Definition 42.1.2
An isogeny \(\phi :E \rightarrow E'\) is a nonconstant morphism of pointed curves; such a map is automatically surjective and a group homomorphism, with the marked point as origin.
Let \({{\,\mathrm{Hom}\,}}(E,E')\) be the collection of isogenies from E to \(E'\) defined over F; if we need to allow isogenies defined over a larger field, we will similarly extend the field of definition of our elliptic curves. Then \({{\,\mathrm{Hom}\,}}(E,E')\) is a torsion-free \(\mathbb Z \)-module of rank at most four. Let \({{\,\mathrm{End}\,}}(E) :={{\,\mathrm{Hom}\,}}(E,E)\) be the endomorphism ring of E and let \({{\,\mathrm{End}\,}}(E)_\mathbb{Q } :={{\,\mathrm{End}\,}}(E) \otimes _\mathbb{Z } \mathbb Q \) be the endomorphism algebra.
42.1.3
For each nonzero isogeny \(\phi :E \rightarrow E'\), there exists a dual isogeny
 such that
such that  and
and  are equal to multiplication by the degree \(\deg \phi \in \mathbb Z _{>0}\) on E and \(E'\), respectively. In particular, the dual
are equal to multiplication by the degree \(\deg \phi \in \mathbb Z _{>0}\) on E and \(E'\), respectively. In particular, the dual  is a standard involution on \({{\,\mathrm{End}\,}}(E)\) that is positive (see 8.4.1); the \(\mathbb Q \)-algebra \({{\,\mathrm{End}\,}}(E)_\mathbb{Q } :={{\,\mathrm{End}\,}}(E) \otimes _\mathbb{Z } \mathbb Q \) is therefore a division ring. In particular, we have the equality
is a standard involution on \({{\,\mathrm{End}\,}}(E)\) that is positive (see 8.4.1); the \(\mathbb Q \)-algebra \({{\,\mathrm{End}\,}}(E)_\mathbb{Q } :={{\,\mathrm{End}\,}}(E) \otimes _\mathbb{Z } \mathbb Q \) is therefore a division ring. In particular, we have the equality

in \({{\,\mathrm{End}\,}}(E)_\mathbb Q \) for all nonzero \(\phi \in {{\,\mathrm{End}\,}}(E)\).
From now on, let E be an elliptic curve over F.
Lemma 42.1.5
The endomorphism algebra \({{\,\mathrm{End}\,}}(E)_\mathbb{Q }\) of E is either \(\mathbb Q \), an imaginary quadratic field K, or a definite quaternion algebra over \(\mathbb Q \).
Proof. We apply Theorem 3.5.1 to conclude that \({{\,\mathrm{End}\,}}(E)_\mathbb{Q }\) is either \(\mathbb Q \), a quadratic field, or a division quaternion algebra. Then by Example 8.4.2, the involution is positive if and only if \({{\,\mathrm{End}\,}}(E)_\mathbb{R }\) is \(\mathbb R \), \(\mathbb C \), or \(\mathbb H \), so in the second case we must have an imaginary quadratic field and in the third case we must have a definite quaternion algebra. \(\square \)
42.1.6
Among the possibilities in Lemma 42.1.5, if \({{\,\mathrm{End}\,}}(E_{F{}^{al }})_\mathbb{Q }\) is a quaternion algebra, then we say E is supersingular.
See Silverman [Sil2009, §V.3] for a treatment of supersingular elliptic curves.
Proposition 42.1.7
If E is supersingular, then \({{\,\mathrm{char}\,}}F = p > 0\). Moreover, the following are equivalent:
-
(i)
E is supersingular;
-
(ii)
\(E[p](F{}^{al }) = \{0\}\); and
-
(iii)
the map \([p]:E \rightarrow E\) is purely inseparable and \(j(E) \in \mathbb F _{p^2}\);
If F is a finite field, then these are further equivalent to
-
(iv)
 , where \(\phi :E \rightarrow E\) is the Frobenius endomorphism.
, where \(\phi :E \rightarrow E\) is the Frobenius endomorphism.
Proof. See Silverman [Sil2009, V.3.1]. \(\square \)
42.1.8
One can often reduce questions about supersingular elliptic curves to ones where the base field F is \(\mathbb F _{p^2}\) as follows: by Proposition 42.1.7(iii), if E is supersingular then E is isomorphic over \(F{}^{al }\) to a curve E defined over \(\mathbb F _{p^2}\).
The following fundamental result is due to Deuring [Deu41]; we give a proof due to Lenstra [Len96, §3].
Theorem 42.1.9
Let E be an elliptic curve over F and suppose that \({{\,\mathrm{rk}\,}}_\mathbb{Z } {{\,\mathrm{End}\,}}(E) = 4\). Then \(B={{\,\mathrm{End}\,}}(E)_\mathbb Q \) is a quaternion algebra over \(\mathbb Q \) ramified at \(p={{\,\mathrm{char}\,}}F\) and \(\infty \), and \({{\,\mathrm{End}\,}}(E)\) is a maximal order in B.
In particular, if over F we have \(\dim {{\,\mathrm{End}\,}}(E)=4\), then automatically E has all of its endomorphisms defined over F.
Proof. Let \(\mathcal {O}={{\,\mathrm{End}\,}}E \subseteq B={{\,\mathrm{End}\,}}(E)_\mathbb Q \). Let \(n>0\) be prime to p. Then there is an isomorphism [Sil2009, Corollary III.6.4(b)]
as abelian groups, and the endomorphism ring of this abelian group is \({{\,\mathrm{End}\,}}E[n] \simeq {{\,\mathrm{M}\,}}_2(\mathbb Z /n\mathbb Z )\).
We claim that the structure map \(\mathcal {O}/n\mathcal {O}\rightarrow {{\,\mathrm{End}\,}}E[n]\) is injective, which is to say, E[n] is a faithful module over \(\mathcal {O}/n\mathcal {O}\). Indeed, suppose \(\phi \in \mathcal {O}\) annihilates E[n]; then since multiplication by n is separable, by the homomorphism theorem for elliptic curves [Sil2009, Corollary III.4.11] there exists \(\psi \in \mathcal {O}\) such that \(\phi =n\psi \), so \(\phi \equiv 0 \in \mathcal {O}/n\mathcal {O}\), proving injectivity. But further, since \(\# \mathcal {O}/n\mathcal {O}= \# {{\,\mathrm{End}\,}}E[n]=n^4\), the structure map is an isomorphism.
Since \(\mathcal {O}\) is a free \(\mathbb Z \)-module, we have
The structure isomorphisms in the previous paragraph are compatible with respect to powers of \(\ell \), so with the previous line they provide an isomorphism

of \(\mathbb Z _\ell \)-algebras, and in particular \(\mathcal {O}_\ell \) is maximal and \(B_\ell \simeq {{\,\mathrm{M}\,}}_2(\mathbb Q _\ell )\) so B is split at \(\ell \).
Since B is definite, it follows from the classification theorem (Main Theorem 14.1.3, equivalent to quadratic reciprocity) that \({{\,\mathrm{Ram}\,}}(B)=\{p,\infty \}\), so \(B_p\) is a division algebra over \(\mathbb Q _p\).
To conclude, we show that \(\mathcal {O}_p\) is maximal. For \(\phi \in \mathcal {O}\) an isogeny, let \(\deg _i \phi \) be the inseparable degree of \(\phi \), which is a power of p. We put \(\deg _i 0 = \infty \). Then \(\deg _i \phi \) is divisible by \(q=p^r\) if and only if \(\phi \) factors via the qth power Frobenius morphism \(E \rightarrow E^{(q)}\). The map
for \(a \in \mathbb Q \) and \(\phi \in {{\,\mathrm{End}\,}}(E)\) is well-defined (since \(\deg _i [p] = \deg [p] = p^2\)). Factoring an isogeny into its separable and inseparable parts shows that
so (42.1.10) is precisely the valuation (13.3.1) on \(B={{\,\mathrm{End}\,}}(E)_\mathbb Q \) extending the p-adic valuation on \(\mathbb Q \). (See also Exercise 42.2.)
To conclude, we show that \(\mathcal {O}_{(p)}\) is the valuation ring (13.3.3) of B and is therefore maximal (Proposition 13.3.4). If \(\alpha \in \mathcal {O}_{(p)} = \mathcal {O}\otimes _\mathbb{Z } \mathbb Z _{(p)}\) then \(\deg \alpha \in \mathbb Z _{(p)}\) so \(\alpha \) is in the valuation ring. Conversely, let \(\alpha \in B\) be a rational isogeny with \(v(\alpha ) \ge 0\), and write \(\alpha =a \phi \) where \(\phi \) is an (actual) isogeny not divisible by any integer. Then\(v(\alpha )={{\,\mathrm{ord}\,}}_p(a) + v(\phi ) \ge 0\) and \(0 \le v(\phi ) \le 1/2\), since the multiplication by p is purely inseparable; so \({{\,\mathrm{ord}\,}}_p(a) \ge -1/2\) and therefore \(a \in \mathbb Z _{(p)}\), and hence \(\alpha \in \mathcal {O}_{(p)}\).
Finally, since an order is maximal if and only if it is locally maximal, \(\mathcal {O}\) itself is a maximal order in the quaternion algebra B. \(\square \)
In light of 42.1.8, we now let \(F=\mathbb F {}^{al }_p\) be an algebraic closure of \(\mathbb F _p\). Let \(E,E'\) be elliptic curves over F. If E is isogenous to \(E'\), then E is supersingular if and only if \(E'\) is supersingular (see Exercise 42.1). The converse is also true, as follows.
Lemma 42.1.11
Let \(E,E'\) be supersingular elliptic curves over F. Then \({{\,\mathrm{Hom}\,}}(E,E')\) is a \(\mathbb Z \)-module of rank 4 that is invertible as a right \({{\,\mathrm{End}\,}}(E)\)-module under precomposition and a left \({{\,\mathrm{End}\,}}(E')\)-module under postcomposition.
In particular, if \(E,E'\) are supersingular elliptic curves over \(\mathbb F {}^{al }_p\), then there exists a separable isogeny \(E \rightarrow E'\).
Proof. We may suppose E is defined over a finite field \(\mathbb F _q\) such that E has all of its endomorphisms defined over \(\mathbb F _q\). Let \(\pi \in \mathcal {O}={{\,\mathrm{End}\,}}(E)\) be the q-power Frobenius endomorphism. Then \(B=\mathcal {O}\otimes _\mathbb Z \mathbb Q \) is a quaternion algebra over \(\mathbb Q \). Since \({{\,\mathrm{End}\,}}(E)\) is defined over \(\mathbb F _q\), the endomorphism \(\pi \) commutes with every isogeny \(\alpha \in \mathcal {O}\), and so \(\pi \) lies in the center of \(\mathcal {O}\); since \(Z(B)=\mathbb Q \), we have \(\pi \in \mathbb Z =Z(\mathcal {O})\). But \(\deg \pi = \pi \overline{\pi }=\pi ^2=q\) so \(\pi =\pm \sqrt{q} \in \mathbb Z \). Therefore \(\#E(\mathbb F _q)=q+1 \mp 2\sqrt{q}\). Therefore \(\#E(\mathbb F _{q^2})=q^2+1 - 2q = (q-1)^2\).
Continuing to enlarge \(\mathbb F _q\), we may repeat the above argument with \(E'\) to conclude that \(\#E(\mathbb F _q)=\#E'(\mathbb F _q)\). It then follows that \(E,E'\) are isogenous over \(\mathbb F _q\) [Sil2009, Exercise III.5.4(b)], but we will show this and more. Let \(\ell \ne p\) be prime and let \(T_\ell (E) = \varprojlim _n E[\ell ^n] \simeq \mathbb Z _\ell ^2\) is the \(\ell \)-adic Tate module of E. By the Isogeny Theorem [Sil2009, Theorem III.7.7(a)], for every prime \(\ell \ne p\), the natural map
is an isomorphism, where \({{\,\mathrm{Hom}\,}}_\mathbb{F _q}(E,E')\) denotes the group of isogenies \(E \rightarrow E'\) defined over \(\mathbb F _q\) and \({{\,\mathrm{Hom}\,}}_\mathbb{F _q}(T_\ell (E),T_\ell (E'))\) denotes the group of \(\mathbb Z _\ell \)-linear maps that commute with the action of the q-power Frobenius Galois automorphism. In the first paragraph, we showed that this Frobenius action is scalar so commuting is automatic, and
and \({{\,\mathrm{Hom}\,}}_\mathbb{F _q}(E,E')={{\,\mathrm{Hom}\,}}(E,E')\) has \({{\,\mathrm{rk}\,}}_\mathbb Z {{\,\mathrm{Hom}\,}}(E,E')=4\).
Finally, we can precompose by endomorphisms of \(\mathcal {O}\) so \({{\,\mathrm{Hom}\,}}(E,E')\) is a torsion-free \(\mathbb Z \)-module with a right action by \(\mathcal {O}\). Let \(\psi \in {{\,\mathrm{Hom}\,}}(E,E')\) be nonzero and let  be the dual isogeny. Then
be the dual isogeny. Then  is an integral right \(\mathcal {O}\)-ideal; since \(\mathcal {O}\) is a maximal order by Theorem 42.1.9, the right \(\mathcal {O}\)-ideal I is necessarily invertible (see 23.1.1), and the same then holds for \({{\,\mathrm{Hom}\,}}(E,E')\) as a right \(\mathcal {O}\)-module. The same is true as a left \({{\,\mathrm{End}\,}}(E')\)-module, and these two actions commute. \(\square \)
is an integral right \(\mathcal {O}\)-ideal; since \(\mathcal {O}\) is a maximal order by Theorem 42.1.9, the right \(\mathcal {O}\)-ideal I is necessarily invertible (see 23.1.1), and the same then holds for \({{\,\mathrm{Hom}\,}}(E,E')\) as a right \(\mathcal {O}\)-module. The same is true as a left \({{\,\mathrm{End}\,}}(E')\)-module, and these two actions commute. \(\square \)
2 Supersingular isogenies
We now investigate the quaternionic endomorphism rings of supersingular elliptic curves in more detail; we use Waterhouse [Wate69, §3] as our main reference. Let E be a supersingular elliptic curve over \(F :=\mathbb F {}^{al }_p\), let \(\mathcal {O}:={{\,\mathrm{End}\,}}(E)\), and let \(B :=\mathcal {O}\otimes \mathbb Q \). By Theorem 42.1.9, we have \({{\,\mathrm{Ram}\,}}(B)=\{p,\infty \}\), and \(\mathcal {O}\subseteq B\) is a maximal order. Thus \({{\,\mathrm{disc}\,}}B=p={{\,\mathrm{discrd}\,}}\mathcal {O}\) (recalling section 15.1).
We temporarily and briefly need the language of group schemes, at the level of Waterhouse [Wate69]. The reader who is unfamiliar with this language is advised to skip to 42.2.4 and restrict consideration to left ideals I with \({{\,\mathrm{nrd}\,}}(I)\) coprime to p (or equivalently, separable isogenies).
42.2.1
Let \(I \subseteq \mathcal {O}\) be a nonzero integral left \(\mathcal {O}\)-ideal. Since \(\mathcal {O}\) is maximal, necessarily I is locally principal (in particular, invertible) by Proposition 16.1.2.
We define \(E[I] \subseteq E\) to be the scheme-theoretic intersection
where \(E[\alpha ] = \ker \alpha \) as a group scheme over F.
Accordingly, there exists an isogeny \(\phi _I : E \rightarrow E_I\) where \(E_I=E/E[I]\).
42.2.3
We will not need much about the theory of group schemes except that we can measure the degree of an isogeny via the rank of its kernel. Let \(H \le E(F)\) be a finite F-subgroup scheme, for example, \(H:=\ker \phi \) for \(\phi :E \rightarrow E'\) an isogeny. Then \(H={{\,\mathrm{Spec}\,}}A_H\) is affine and \(A_H\) is a finite F-algebra; we define the rank of H by \({{\,\mathrm{rk}\,}}H :=\dim _F A_H\). In all cases, we have \({{\,\mathrm{rk}\,}}\ker \phi = \deg \phi \), even when \(\phi \) is inseparable.
This general, scheme-theoretic construction can usually be given plainly, as follows.
42.2.4
If there is a nonzero \(\alpha \in I\) giving a separable isogeny \(\alpha :E \rightarrow E\), then
We then have the more familiar separable isogeny \(\phi _I : E \rightarrow E/E[I]\) with \(\ker (\phi _I) = E[I]\) [Sil2009, Proposition III.4.12], and \({{\,\mathrm{rk}\,}}\ker \phi _I = \# \ker \phi _I(F) = \deg \phi _I\).
What remains are inseparable isogenies. Since \({{\,\mathrm{Ram}\,}}B=\{p,\infty \}\) and \(\mathcal {O}\) is maximal, by Theorem 18.1.3 (more generally, see 23.3.19), there is a unique two-sided \(\mathcal {O}\)-ideal \(P \subseteq \mathcal {O}\) of reduced norm p. Then the map \(E \rightarrow E_P \simeq E^{(p)}\) is the p-Frobenius map, and \({{\,\mathrm{rk}\,}}\ker \phi _P = p = \deg \phi \) even though \((\ker \phi )(F) = \{0\}\). The equality \(P^2=p\mathcal {O}\) corresponds to the fact that \(E[P^2]=E[p]\), and this lies behind the fact that \(j(E) \in \mathbb F _{p^2}\) as in Proposition 42.1.7.
Accordingly, a left \(\mathcal {O}\)-ideal I can be written uniquely as \(I=P^r I'\) with \({{\,\mathrm{nrd}\,}}(I')\) coprime to p, and this corresponds to a factorization
with \(E_{I} \simeq E_{P^r}/E_{P^r}[I']\), the isogeny \(E \rightarrow E_{P^r}\) purely inseparable and the isogeny \(E_{P^r} \rightarrow E_{I}\) separable. (This corresponds to the factorization of the extension of function fields into first a separable extension, then a purely inseparable extension [Sil2009, Corollary II.2.12].)
Lemma 42.2.7
The pullback map
is an isomorphism of left \(\mathcal {O}\)-modules.
Proof. The image of \({{\,\mathrm{Hom}\,}}(E_I,E)\) under precomposition by \(\phi _I\) lands in \({{\,\mathrm{End}\,}}(E)=\mathcal {O}\) and factors through \(\phi _I\) so lands in I by definition. The map \(\phi _I^*\) is an injective homomorphism of abelian groups. It compatible with the left \(\mathcal {O}\)-action, given by postcomposition on \({{\,\mathrm{Hom}\,}}(E_I,E)\) and left multiplication on I.
To conclude, we show it is also surjective. Let \(\alpha \in I\); then \(\alpha (E[I]) = \{0\}\) by construction. If \(\alpha \) is separable, then \(\alpha \) factors through \(\phi _I : E \rightarrow E_I\) [Sil2009, Corollary III.4.11]. In general, we factor \(\phi _I\) as in (42.2.6), and then combine the separable case in the previous sentence with the \(p^r\)-Frobenius map. \(\square \)
Finally, we can identify the right module structure as follows.
Lemma 42.2.9
The ring homomorphism

is injective and \(\iota ({{\,\mathrm{End}\,}}(E_I))=\mathcal {O}{}_{\textsf {\tiny {R}} }(I)\).
Proof. The equality in (42.2.10) is justified in (42.1.4). The content of the lemma follows from the identification in the previous Lemma 42.2.7, by transporting structure: for \(\beta \in {{\,\mathrm{End}\,}}(E_I)\) acting by precomposition, we fill in the diagram

to find that
and so \(\iota \) defines the induced action on I by right multiplication, giving an inclusion \(\iota ({{\,\mathrm{End}\,}}(E_I)) \subseteq \mathcal {O}{}_{\textsf {\tiny {R}} }(I)\). But \({{\,\mathrm{End}\,}}(E_I)\) is a maximal order and \(\mathcal {O}{}_{\textsf {\tiny {R}} }(I)\) is an order, so equality holds. \(\square \)
Next, we show that the isomorphism class of \(E_I\) depends only on the left ideal class of I.
Lemma 42.2.13
If \(J=I\beta \subseteq \mathcal {O}\) with \(\beta \in B^\times \), then \(E_I \simeq E_{J}\).
Proof. First, suppose \(\beta \in \mathcal {O}\). Then
We claim that \(\beta E[I\beta ] = E[I]\). The containment \((\subseteq )\) is immediate. For the containment \((\supseteq )\), let \(Q \in E[I]\). Since \(\beta \) is surjective (it is nonconstant), there exists \(P \in E(F)\) such that \(\beta (P)=Q\). Thus for all \(\alpha \in I\), we have \((\alpha \beta )(P)=\alpha (Q)=0\) so \(P \in E[I\beta ]\). By the claim, we conclude that \(\phi _{I\beta } = \phi _I \beta \) and \(E_{I\beta } \simeq E_I\).
In general, there exists nonzero \(m \in \mathbb Z \) such that \(m\beta \in \mathcal {O}\). By the previous paragraph, we have isomorphisms \(E_I \simeq E_{I(m\beta )}=E_{(I\beta )m} \simeq E_{I\beta }\). \(\square \)
So far, we have shown how to pass from classes of left \(\mathcal {O}\)-ideals to (isogenous) supersingular elliptic curves via kernels. We can also go in the other direction.
42.2.14
Given a finite subgroup scheme \(H \le E(F)\), we define
then I(H) is a left \(\mathcal {O}\)-ideal, nonzero because \(\# H \in I(H)\).
If \(H_1 \le H_2 \le E(F)\) are two such subgroups, then \(I(H_1) \supseteq I(H_2)\).
Lemma 42.2.15
If \(H_1 \subseteq H_2\) and \(I(H_1)=I(H_2)\), then \(H_1=H_2\).
Proof. Let \(\phi _1 :E \rightarrow E/H_1\). Factoring, without loss of generality we may assume that \(\phi _1\) is either separable or purely inseparable. Suppose first that \(\phi _1\) is separable, and let \(n=\#H_2(F)\). By the proof of Theorem 42.1.9, the structure map \(\mathcal {O}/n\mathcal {O}\rightarrow {{\,\mathrm{End}\,}}E[n]\) is faithful. So if \(H_2>H_1\), then there exists \(\alpha \in \mathcal {O}\) such that \(\alpha (H_1) = \{0\}\) but \(\alpha (H_2) \ne \{0\}\), so \(I(H_2) \ne I(H_1)\). Second, suppose that \(\phi _1\) is purely inseparable: then \(H_1 = \ker \phi _p^{r_1}\) is the kernel of the \(r_1\)-power Frobenius for some \(r_1>0\), and \(I(H_1)=P^{r_1}\) as in 42.2.4. Then \(p^{r_1} \in I(H_1)=I(H_2)\), so \(E \rightarrow E/H_2\) is also purely inseparable, and \(H_2=\ker \phi _p^{r_2}\) and \(I(H_2)=P^{r_2}\). We conclude \(r_1=r_2\), and then \(H_1=H_2\). \(\square \)
Proposition 42.2.16
The following statements hold.
-
(a)
\(\deg \phi _I = {{\,\mathrm{nrd}\,}}(I)\).
-
(b)
\(I(E[I]) = I\).
Proposition 42.2.16 justifies the use of overloaded notation. Our proof follows Waterhouse [Wate69, Theorem 3.15].
Proof. We begin with (a). We first prove it in an illustrative special case. Suppose \(I=\mathcal {O}\beta \) is a principal left \(\mathcal {O}\)-ideal. Then \(E[I]=E[\beta ]\) where \(\phi _I= \beta :E \rightarrow E\), and
is the constant term of the (reduced) characteristic polynomial of \(\beta \).
We now return to the general case. We first show that \(\deg (I) \mid \deg \phi _I\). Let \(\mathcal {O}' :=\mathcal {O}{}_{\textsf {\tiny {R}} }(I) = \mathcal {O}{}_{\textsf {\tiny {L}} }(I^{-1})\). By Exercise 17.5, there exists \(\alpha \in B^\times \) such that \(I'=I^{-1}\alpha \subseteq \mathcal {O}'\) is in the same right \(\mathcal {O}'\)-ideal class as \(I^{-1}\) and with \({{\,\mathrm{nrd}\,}}(I')\) coprime to \(\deg \phi _I\). Thus \(II'=\mathcal {O}\alpha \subseteq \mathcal {O}\) is a compatible product and \(\alpha \in \mathcal {O}\). By the previous paragraph, we have
The map \(\phi _{II'}\) factors through \(\phi _I\), so \(\deg \phi _I \mid \deg \phi _{II'}\). Since \({{\,\mathrm{nrd}\,}}(I')\) is coprime to \(\deg \phi _I\) we have \(\deg \phi _I \mid {{\,\mathrm{nrd}\,}}(I)\).
Repeating this argument, we have \(\deg \phi _{I'} \mid {{\,\mathrm{nrd}\,}}(I')\) as well. We combine these to conclude (a). We have
But
Putting together (42.2.17)–(42.2.18), we see that equality holds, so \(\deg \phi _I={{\,\mathrm{nrd}\,}}(I)\).
Now we prove (b). Let \(J=I(E[I])\). Then \(I \subseteq J\) since \(IE[I]=\{0\}\); thus \(E[I] \supseteq E[J]\). At the same time, we have
so equality holds and \(E[I]=E[J]\). Thus \(\deg \phi _I=\deg \phi _J\). By (a), we have
Since \(I \subseteq J\), we have \(\mathcal {O}\subseteq JI^{-1}\). From Proposition 16.4.3 and (42.2.20), we have \({{\,\mathrm{nrd}\,}}(JI^{-1})=[\mathcal {O}:JI^{-1}]=1\) so \(\mathcal {O}=JI^{-1}\) and therefore \(I=J\). \(\square \)
Corollary 42.2.21
For every isogeny \(\phi :E \rightarrow E'\), there exists a left \(\mathcal {O}\)-ideal I and an isomorphism \(\rho :E_I \rightarrow E'\) such that \(\phi = \rho \phi _I\). Moreover, for every maximal order \(\mathcal {O}' \subseteq B\), there exists \(E'\) such that \(\mathcal {O}' \simeq {{\,\mathrm{End}\,}}(E')\).
Proof. Let H be the scheme-theoretic kernel of \(\phi \). Then \(H \subseteq E[I(H)]\), so \(\phi _{I(H)}\) factors through \(\phi \) with \(\phi _{I(H)}=\rho \phi \) for some isogeny \(\rho :E_{I(H)} \rightarrow E'\). But \(I(H) = I(E[I(H)])\) by Proposition 42.2.16, so \(H=E[I(H)]\) by Lemma 42.2.15. Thus \(\deg \phi _{I(H)}=\deg \phi \), and so \(\deg \rho =1\) and \(\rho \) is an isomorphism, with \(\phi =\rho ^{-1}\phi _{I(H)}\). The second statement follows similarly using a connecting ideal between orders (see section 17.4). \(\square \)
We may now compare endomorphisms analogously to Lemma 42.2.7.
Lemma 42.2.22
Let \(I,I' \subseteq \mathcal {O}\) be nonzero integral left \(\mathcal {O}\)-ideals. Then the natural map
is bijective, giving a further bijection
Proof. By Lemma 42.2.7, we have \({{\,\mathrm{Hom}\,}}(E_I,E)\phi _I = I\). By Proposition 42.2.16, we have \(m=\deg \phi _I={{\,\mathrm{nrd}\,}}(I)\). The left ideal \(I \subseteq \mathcal {O}\) is invertible thus \(m={{\,\mathrm{nrd}\,}}(I) \in I\overline{I}\), hence there exist finitely many \(\alpha _i,\beta _i \in {{\,\mathrm{Hom}\,}}(E_I,E)\) such that

therefore

For \(\psi \in {{\,\mathrm{Hom}\,}}(E_{I'},E)\), postcomposing with (42.2.25) gives

so the natural injective map is bijective. This gives
and thereby the bijective map (42.2.23). \(\square \)
3 Equivalence of categories
We now show that the association from supersingular elliptic curves to right ideals is an equivalence of categories. We recall that F is an algebraically closed field with \(p={{\,\mathrm{char}\,}}F\) prime.
42.3.1
Let \(E_0\) be a supersingular elliptic curve over \(F :=\mathbb F {}^{al }_p\); it will serve the role as a base object. Let \(\mathcal {O}_0 :={{\,\mathrm{End}\,}}(E_0)\) and \(B_0 :=\mathcal {O}_0 \otimes \mathbb Q \).
Theorem 42.3.2
The association \(E \mapsto {{\,\mathrm{Hom}\,}}(E,E_0)\) is functorial and defines and equivalence between the category of
supersingular elliptic curves over F, under isogenies
and
invertible left \(\mathcal {O}_0\)-modules, under nonzero left \(\mathcal {O}_0\)-module homomorphisms.
Remark 42.3.3. Written this way, the functor \({{\,\mathrm{Hom}\,}}(-,E_0)\) is contravariant. One can equally well take \({{\,\mathrm{Hom}\,}}(E_0,-)\) to get a covariant functor with right \(\mathcal {O}_0\)-modules; using the standard involution, these are seen to contain the same content.
Proof. To begin, we need to show \({{\,\mathrm{Hom}\,}}(-,E_0)\) is a functor. The association \(E \mapsto {{\,\mathrm{Hom}\,}}(E,E_0)\) makes sense on objects by Lemma 42.1.11. On morphisms, to an isogeny \(\phi :E \rightarrow E'\) we associate
The map \(\phi ^*\) is a homomorphism of left \(\mathcal {O}_0\)-modules, since it is compatible with postcomposition with \(\mathcal {O}_0={{\,\mathrm{End}\,}}(E)\), so \({{\,\mathrm{Hom}\,}}(-,E_0)\) is functorial.
Next, we claim that \({{\,\mathrm{Hom}\,}}(-,E_0)\) is essentially surjective. Let I be an invertible left \(\mathcal {O}_0\)-module. Tensoring with \(\mathbb Q \) we get an injection \(I_0 \hookrightarrow I_0 \otimes \mathbb Q \simeq B_0\), so up to isomorphism of left \(\mathcal {O}_0\)-modules, we may suppose \(I \subseteq B_0\). Scaling by an integer, we may suppose \(I \subseteq \mathcal {O}_0\) is a left \(\mathcal {O}_0\)-ideal. Let \(E_I = E/E[I]\). By Lemma 42.2.7, we have \({{\,\mathrm{Hom}\,}}(E_I,E_0) \simeq I\) as left \(\mathcal {O}_0\)-modules, as desired.
Finally, we show that \({{\,\mathrm{Hom}\,}}(-,E_0)\) is fully faithful, i.e., the map
(the former as isogenies, the latter as homomorphisms of left \(\mathcal {O}_0\)-modules) is bijective. This bijectivity is made plain by an application of Corollary 42.2.21: there is a left \(\mathcal {O}_0\)-ideal I such that \(E \simeq E_{0,I}\); applying this isomorphism, we may suppose without loss of generality that \(E=E_{0,I}\). Then by Lemma 42.2.7, we have \(I = {{\,\mathrm{Hom}\,}}(E_{0,I},E_0) \phi _{0,I}\). Repeat with \(E'\) and \(I'\). Then after these identifications, we are reduced to the setting of Lemma 42.2.22 (with the location of the prime swapped): the map
is indeed bijective. \(\square \)
Remark 42.3.6. See also Kohel [Koh96, Theorem 45], where the categories are enriched with a Frobenius morphism.
Corollary 42.3.7
(Deuring correspondence). There is a bijection between isomorphism classes of supersingular elliptic curves over F and the left class set \({{\,\mathrm{Cls}\,}}\!{}_{\textsf {\tiny {L}} }\mathcal {O}_0\). Under this bijection, if \(E \leftrightarrow [I]\), then \({{\,\mathrm{End}\,}}(E) \simeq \mathcal {O}{}_{\textsf {\tiny {R}} }(I)\) and \({{\,\mathrm{Aut}\,}}(E) \simeq \mathcal {O}{}_{\textsf {\tiny {R}} }(I)^\times \).
Proof. Take isomorphism classes on both sides of the equivalence in Theorem 42.3.2, and compare endomorphism groups and automorphism groups. (We had to work with left \(\mathcal {O}_0\)-modules in the equivalence of categories, but each isomorphism class of objects is represented by a left \(\mathcal {O}_0\)-ideal \(I \subseteq B\).) \(\square \)
42.3.8
From the Eichler mass formula and Corollary 42.3.7 (swapping left for right, as in Remark 42.3.3), we conclude that
where the sum on the left is over isomorphism classes of supersingular elliptic curves over \(F=\mathbb F {}^{al }_p\).
Similarly, from the Eichler class number formula (Theorem 30.1.5), the number of isomorphism classes of supersingular elliptic curves over F is equal to
Remark 42.3.10. We can generalize this setup slightly as follows. Let \(M \in \mathbb Z _{>0}\) be coprime to p, and let \(C_0 \le E_0(F)\) be a cyclic subgroup of order M. Then \({{\,\mathrm{End}\,}}(E_0,C_0) \simeq \mathcal {O}_0(M)\) is an Eichler order of level M and reduced discriminant pM in \(B_0\). In a similar way as above, one can show that \({{\,\mathrm{Hom}\,}}(-,(E_0,C_0))\) defines an equivalence of categories between the category of supersingular elliptic curves equipped with a cyclic M-isogeny (under isogenies identifying the cyclic subgroups), to the category of left invertible \(\mathcal {O}_0(M)\)-modules (under homomorphisms). The mass formula now reads
One can also consider instead the category of cyclic M-isogenies \(\phi :E \rightarrow E'\).
Example 42.3.11
Consider \(p=11\). The algebra \(B=\displaystyle {\biggl (\frac{-1,-11}{\mathbb {Q}}\biggr )}\) has discriminant 11 and the maximal order \(\mathcal {O}=\mathbb Z \langle i, (1+j)/2 \rangle \). We have \(\# {{\,\mathrm{Cls}\,}}\mathcal {O}= 2\), with the nontrivial class represented by the ideal I generated by 2 and \(1+i(1+j)/2\).
We have \(\mathcal {O}^\times = \langle i \rangle \) of order 4 and \(\mathcal {O}{}_{\textsf {\tiny {L}} }(I)= \langle 1/2 - i(1+j)/4 \rangle \) of order 6, and indeed \(1/4+1/6 = 10/24 = 5/12\). The two supersingular curves modulo 11 are the ones with j-invariants 0 and \(1728 \equiv 1 \pmod {11}\), and \({{\,\mathrm{End}\,}}(E) \simeq \mathcal {O}\) if \(j(E)=1728\) whereas for \({{\,\mathrm{End}\,}}(E') \simeq \mathcal {O}'\) we have \({{\,\mathrm{Hom}\,}}(E,E') \simeq I\), in other words, \(E' \simeq E/E[I]\).
Example 42.3.12
We return to Example 41.1.2. The order \(\mathcal {O}=\mathcal {O}_1\) is the endomorphism ring of the elliptic curve \(E_1:y^2=x^3-x\) with \(j(E_1)=1728 \equiv 3 ~(\text{ mod } ~{23})\), and similarly \(E_2 :y^2=x(x-1)(x+2)\) with \(j(E_2)=19\) and \(E_3 :y^2=x^3+1\) with \(j(E_3)=0\). We have \(2w_i=\#{{\,\mathrm{Aut}\,}}(E_i)\) is the order of the automorphism group of \(E_i\). And the p-Brandt graph is the graph of p-isogenies among the three supersingular elliptic curves over \(\overline{\mathbb{F }}_{23}\).
42.3.13
Finally, and most importantly, in the above correspondence the entries of the Brandt matrix T(n) have meaning as counting isogenies. For n coprime to p, the entry \(T(n)_{ij}\) is equal to the number of subgroups \(H \le E_i(F)\) such that \(E_i/H \simeq E_j\). This statement is just a translation of Lemma 42.2.22. Gross [Gro87] gives a beautiful and essentially self-contained presentation of the results of the previous chapter in the special case that \({{\,\mathrm{disc}\,}}B=p\).
Remark 42.3.14. The approach via supersingular elliptic curves connects back in another way: Serre [Ser96] gives an alternative approach to modular forms modulo p in a letter to Tate: one evaluates classical modular forms at supersingular elliptic curves and then relates these to quaternionic modular forms modulo p.
4 Supersingular endomorphism rings
In this section, we give a second categorical perspective, giving a base-object free refinement of Corollary 42.3.7 following Ribet [Rib1989, p. 360–361] (who credits Mestre–Oesterlé). To get there, we need to deal with a small subtlety involving the field of definition (fixed by keeping track of extra data). Recall that \(F=\mathbb F {}^{al }_p\).
Lemma 42.4.1
Let \(\mathcal {O}\) be a maximal order. Then there exist one or two supersingular elliptic curves E up to isomorphism over F such that \({{\,\mathrm{End}\,}}(E) \simeq \mathcal {O}\). There exist two such elliptic curves if and only if \(j(E) \in \mathbb F _{p^2} \smallsetminus \mathbb F _p\) if and only if the unique two-sided ideal of \(\mathcal {O}\) of reduced norm p is not principal.
Proof. In Corollary 42.2.21, we proved that there is always at least one supersingular elliptic curve E with \({{\,\mathrm{End}\,}}(E) \simeq \mathcal {O}\) using a connecting ideal. We now elaborate on this point, refining our count.
By Corollary 42.3.7, the isomorphism classes of supersingular elliptic curves are in bijection with the left class set \({{\,\mathrm{Cls}\,}}\!{}_{\textsf {\tiny {L}} }\, \mathcal {O}_0\); their endomorphism rings are then given by \({{\,\mathrm{End}\,}}(E) \simeq \mathcal {O}{}_{\textsf {\tiny {R}} }(I)\) for \([I] \in {{\,\mathrm{Cls}\,}}\!{}_{\textsf {\tiny {L}} }\,\mathcal {O}_0\). By Lemma 17.4.13 (interchanging left for right), the map
is a surjective map of sets. The connecting ideals are precisely the fibers of this map, and by the bijection of Corollary 42.3.7, there is a bijection between the set of supersingular elliptic curves E with \({{\,\mathrm{End}\,}}(E) \simeq \mathcal {O}\) and the fiber of this map over the isomorphism class of \(\mathcal {O}\).
We now count these fibers. We recall Theorem 18.1.3 with \(D=p\) and the text that follows (interchanging left for right): the fibers are given by the quotient group \({{\,\mathrm{PIdl}\,}}\mathcal {O}\backslash \!{{\,\mathrm{Idl}\,}}\mathcal {O}\) of the two-sided invertible fractional two-sided \(\mathcal {O}\)-ideals by the subgroup of principal such ideals. There is a surjection \({{\,\mathrm{Pic}\,}}(\mathcal {O}) \rightarrow {{\,\mathrm{PIdl}\,}}\mathcal {O}\backslash \!{{\,\mathrm{Idl}\,}}\mathcal {O}\) and \({{\,\mathrm{Pic}\,}}(\mathcal {O}) \simeq \mathbb Z /2\mathbb Z \) is generated by the unique maximal two-sided ideal P of reduced norm P. The class of P in the quotient is trivial if and only if \(P=\mathcal {O}\pi \) is principal.
To conclude we recall 42.2.4: the Frobenius map is the map \(E \rightarrow E_P \simeq E^{(p)}\). So P is principal if and only if \(E^{(p)} \simeq E\) if and only if \(j(E)=j(E^{(p)})=j(E)^p\) if and only if \(j(E) \in \mathbb F _p\). \(\square \)
We dig into this issue a bit further.
42.4.3
Let E be a supersingular elliptic curve over \(\mathbb F {}^{al }_p\). Let \(\omega \) be a nonzero invariant differential on E. Then there is a ring homomorphism
(see Silverman [Sil2009, Corollary III.5.6]) independent of the choice of \(\omega \).
In light of 42.4.3, we make the following definitions. Let B be a quaternion algebra over \(\mathbb Q \) of discriminant \({{\,\mathrm{disc}\,}}B=p\); such an algebra B is unique up to isomorphism. Let \(\mathcal {O}\subseteq B\) be a maximal order in B; then \({{\,\mathrm{discrd}\,}}\mathcal {O}=p\).
Definition 42.4.5
An orientation of \(\mathcal {O}\) is a ring homomorphism \(\mathcal {O}\rightarrow \mathbb F {}^{al }_p\).
42.4.6
We claim that there are two possible orientations of \(\mathcal {O}\). In fact, \(P=[\mathcal {O},\mathcal {O}]\) is the commutator ideal (cf. Exercise 13.7) and an orientation factors through the commutator. Since \({{\,\mathrm{nrd}\,}}(P)=p\), localizing we have \(\mathcal {O}/P \simeq \mathcal {O}_p/P_p \simeq \mathbb F _{p^2}\) by Theorem 13.3.11(c). The claim follows as there are two possible inclusions \(\mathbb F _{p^2} \hookrightarrow \mathbb F {}^{al }_p\).
The notion of isomorphism of oriented maximal orders is evident.
Definition 42.4.7
An isomorphism of oriented maximal orders from \((\mathcal {O},\zeta )\) to \((\mathcal {O}',\zeta ')\) is an isomorphism of orders \(\phi :\mathcal {O}\rightarrow \mathcal {O}'\) such that \(\zeta ' \phi = \zeta \).
We define the set of reduced isomorphisms to be \({{\,\mathrm{Isom}\,}}(E,E')/\{\pm 1\}\).
Proposition 42.4.8
The association \(E \mapsto ({{\,\mathrm{End}\,}}(E) \subseteq {{\,\mathrm{End}\,}}(E)_\mathbb Q ,a)\) is functorial and induces an equivalence from the category of
supersingular elliptic curves over \(\mathbb F {}^{al }_p\), under reduced isomorphisms
to the category of
oriented maximal orders \((\mathcal {O}\subseteq B, \zeta )\)
in a quaternion algebra B of discriminant p,
under isomorphisms.
In the latter category, we do not choose the representative of the isomorphism class of quaternion algebra of discriminant p; it is tagging along only to provide a quaternionic wrapper for the order.
Proof. The association has the right target by Theorem 42.1.9 for the order and 42.4.3 for the orientation. This association is (covariantly) functorial with respect to isomorphisms. Indeed, if  is an isomorphism of elliptic curves, then we have an induced isomorphism
is an isomorphism of elliptic curves, then we have an induced isomorphism
that is compatible with composition. The isomorphism (42.4.9) is also compatible with orientations, as follows. Let \(\omega '\) be a nonzero invariant differential on \(E'\); then \(\psi ^* \omega '\) is so on E. Thus for all \(\phi \in {{\,\mathrm{End}\,}}(E)\), we have
so \(a'_{\psi \phi \psi ^{-1}}=a_\phi \), which is the desired compatibility.
The functor is essentially surjective, which is to say that every oriented maximal order arises up to isomorphism: that every maximal order arises is a consequence of Corollary 42.2.21, and that the orientation may be so chosen corresponds to applying the Frobenius morphism, by 42.2.4 and 42.4.6.
Finally, we show the map is fully faithful, which is to say the map of finite sets
from (42.4.9) is bijective. Any two reduced isomorphisms on the left differ by an automorphism of E, and the same on the right, so it suffies to show that the map
is bijective. Let \(\mathcal {O}={{\,\mathrm{End}\,}}(E)\), so \({{\,\mathrm{Aut}\,}}(E) \simeq \mathcal {O}^\times \). Then \({{\,\mathrm{Aut}\,}}(\mathcal {O}) \simeq N_{B^\times }(\mathcal {O})/\mathbb Q ^\times \), and
where the Atkin–Lehner group \({{\,\mathrm{AL}\,}}(\mathcal {O})\) is nontrivial (and isomorphic to \(\mathbb Z /2\mathbb Z \)) if and only if \(P=\pi \mathcal {O}\) is principal; but conjugation by \(\pi \) acts nontrivially on \(\mathcal {O}/P\) and fails to commute with \(\zeta \) so does not act by an automorphism of \(({{\,\mathrm{End}\,}}(E),\zeta )\); thus
(We did not need to choose a base object in order to define this equivalence!) \(\square \)
Corollary 42.4.12
There is a bijection between isomorphism classes of supersingular elliptic curves over F and oriented maximal orders in a quaternion algebra B of discriminant p.
Proof. Again we take isomorphism classes of objects in Proposition 42.4.8. \(\square \)
Exercises
-
1.
Let \(E,E'\) be elliptic curves over F and suppose \(E,E'\) are isogenous (necessarily by a nonzero isogeny). Show that E is supersingular if and only if \(E'\) is supersingular. [Hint: show \(\dim _\mathbb Q {{\,\mathrm{End}\,}}(E_{F{}^{al }})_\mathbb Q = \dim _\mathbb Q {{\,\mathrm{End}\,}}(E'_{F{}^{al }})_\mathbb Q \); or show that \(\deg _i([p])=\deg _i([p]')\) where \([p],[p]'\) are multiplication by p on \(E,E'\).]
-
2.
Let E be an elliptic curve over F with \({{\,\mathrm{char}\,}}F = p\). Show that for all \(\phi ,\psi \in {{\,\mathrm{End}\,}}(E)\), we have
$$\begin{aligned} \deg _i(\phi \psi )&=\deg _i(\phi )\deg _i(\psi ) \\ \deg _i(\phi +\psi )&\ge \min \{\deg _i \phi ,\deg _i \psi \}. \end{aligned}$$Conclude that \(|\phi |=1/\deg _i(\phi )\) defines a nonarchimedean absolute value on \({{\,\mathrm{End}\,}}(E)_{(p)}\).
-
3.
In this exercise, we give an alternate “hands on” proof of Lemma 42.2.9.
Let E be a supersingular elliptic curve over \(F=\mathbb F {}^{al }_p\), let \(\mathcal {O}={{\,\mathrm{End}\,}}(E)\) and let \(B=\mathcal {O}\otimes \mathbb Q \). Let \(I \subseteq \mathcal {O}\) be a nonzero integral left \(\mathcal {O}\)-ideal, and let \(\phi _I :E \rightarrow E_I\) where \(E_I=E/E[I]\). Consider the pullback isomorphism \(\phi _I^* :{{\,\mathrm{Hom}\,}}(E_I,E) \rightarrow I\) by \(\psi \mapsto \psi \phi _I\) in (42.2.8).
-
(a)
Show that \(\phi ^*\) induces an isomorphism of \(\mathcal {O}\)-module endomorphism rings
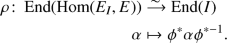
-
(b)
Show that \({{\,\mathrm{End}\,}}(I) = \mathcal {O}{}_{\textsf {\tiny {R}} }(I)^{op }\).
-
(c)
Show that \({{\,\mathrm{End}\,}}({{\,\mathrm{Hom}\,}}(E_I,E)) = {{\,\mathrm{End}\,}}(E_I)^{op }\). [Hint: \({{\,\mathrm{End}\,}}(E_I)\) is a maximal order, so the natural inclusion is an equality.]
-
(d)
Conclude that \(\rho ^{op }\) induces an isomorphism
 .
. -
(e)
Show that \(\rho ^{op }\) is the map \(\iota \) in (42.2.10).
-
(a)
-
4.
Let B be a quaternion algebra over \(\mathbb Q \) with \({{\,\mathrm{disc}\,}}B = p\) prime. Recall the definition of the Brandt matrix (e.g. (41.1.1), and more generally 41.2.2).
Let \(I_i\) for \(i=1,\dots ,h\) be the representatives of the left class set \({{\,\mathrm{Cls}\,}}\!{}_{\textsf {\tiny {L}} }\, \mathcal {O}\), with \(h=\#{{\,\mathrm{Cls}\,}}\!{}_{\textsf {\tiny {L}} }\,\mathcal {O}\). Let \(E_i\) be the supersingular elliptic curves over \(\mathbb F {}^{al }_p\) corresponding to \(I_i\) in Corollary 42.3.7.
-
(a)
For every \(m \ge 1\), show that \(T(m)_{ij}\) is equal to the number of subgroup schemes C of order m in \(E_j\) such that \(E_j/C \simeq E_i\).
-
(b)
Show that T(p) is a permutation matrix of order dividing 2 and that \(T(p^r)=T(p)^r\) for all \(r \ge 1\).
-
(c)
Show that \(E_i\) is conjugate by an element of \({{\,\mathrm{Aut}\,}}(\mathbb F {}^{al }_p)\) to \(E_j\) if and only if \(i=j\) or \(T(p)_{ij}=1\). Conclude that the number of elliptic curves \(E_i\) defined over \(\mathbb F _p\) is equal to \({{\,\mathrm{tr}\,}}T(p)\).
-
(a)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
This chapter is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, duplication, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, a link is provided to the Creative Commons license and any changes made are indicated.The images or other third party material in this chapter are included in the work's Creative Commons license, unless indicated otherwise in the credit line; if such material is not included in the work's Creative Commons license and the respective action is not permitted by statutory regulation, users will need to obtain permission from the license holder to duplicate, adapt or reproduce the material.
Copyright information
© 2021 The Author(s)
About this chapter
Cite this chapter
Voight, J. (2021). Supersingular elliptic curves. In: Quaternion Algebras. Graduate Texts in Mathematics, vol 288. Springer, Cham. https://doi.org/10.1007/978-3-030-56694-4_42
Download citation
DOI: https://doi.org/10.1007/978-3-030-56694-4_42
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-56692-0
Online ISBN: 978-3-030-56694-4
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


 , where
, where 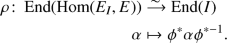
 .
.