Abstract
In this chapter, we now apply our topological and geometric interpretation of discrete groups in our case of interest: quaternion unit groups.
You have full access to this open access chapter, Download chapter PDF
In this chapter, we now apply our topological and geometric interpretation of discrete groups in our case of interest: quaternion unit groups.
1 \(\triangleright \) Rational quaternion groups
The classical modular group \({{\,\mathrm{PSL}\,}}_2(\mathbb Z )\) (chapter 35) was obtained as follows: we
-
started with the matrix algebra \({{\,\mathrm{M}\,}}_2(\mathbb Q )\),
-
looked inside for integral elements to find the order \({{\,\mathrm{M}\,}}_2(\mathbb Z )\),
-
took its unit group \({{\,\mathrm{GL}\,}}_2(\mathbb Z )\), and finally
-
restricted attention to the Fuchsian group \({{\,\mathrm{PSL}\,}}_2(\mathbb Z )\) to get a faithful action onthe upper half-plane by orientation-preserving isometries.
The wonderful thing that gives life to this part of our monograph is this: the same thing works if we replace \({{\,\mathrm{M}\,}}_2(\mathbb Q )\) with a quaternion algebra B over a global field! In this section, we derive key aspects of this program for quaternion algebras over \(\mathbb Q \) in a self-contained way, before embarking on a more general study in the remainder of the chapter.
In section 32.1, we already dealt with the case when the quaternion algebra was definite, finding a finite unit group; so here we take  indefinite. Without loss of generality (for convenience of presentation), we may further suppose \(a,b>0\) and both \(a,b \in \mathbb Z \). To be indefinite means that
indefinite. Without loss of generality (for convenience of presentation), we may further suppose \(a,b>0\) and both \(a,b \in \mathbb Z \). To be indefinite means that  ; we obtain such an embedding via a conjugate of the left-regular representation (2.3.2)
; we obtain such an embedding via a conjugate of the left-regular representation (2.3.2)
This embedding is not unique, but another embedding would correspond to post-composition by an \(\mathbb R \)-algebra automorphism of \({{\,\mathrm{M}\,}}_2(\mathbb R )\), which by the Skolem–Noether theorem (Corollary 7.1.4) is given by conjugation by an element of \({{\,\mathrm{GL}\,}}_2(\mathbb R )\), and so we can live with a choice and this ambiguity.
Let
then \(\mathcal O \subset B\) is an order, and \(\iota _\infty (\mathcal O ) \subseteq {{\,\mathrm{M}\,}}_2(\mathbb Z )\) consists of the subset of matrices in (38.1.1) with \(t,x,y,z \in \mathbb Z \). Following the script above, we define
and let
Lemma 38.1.2
The group \(\Gamma ^1(\mathcal O ) \le {{\,\mathrm{PSL}\,}}_2(\mathbb R )\) is a Fuchsian group.
Recall that a Fuchsian group (Definition 34.7.3) is a discrete subgroup of \({{\,\mathrm{PSL}\,}}_2(\mathbb R )\); by Theorem 34.2.1, a Fuchsian group acts properly on the upper half-plane \(\mathbf{\textsf {H} }^2\) by orientation-preserving isometries.
Proof Because \(\Gamma ^1(\mathcal O )\) is a group, it suffices to find an open neighborhood of 1 containing no other element of \(\Gamma ^1(\mathcal O )\). We take
If \(\gamma =(g_{ij})_{i,j} \in U \cap \Gamma ^1(\mathcal O )\), then
and since \(t,y \in \mathbb Z \) we have \(t=1\) and \(y=0\). Then
and since \(a,b,x,z \in \mathbb Z \) with \(a,b \ne 0\), we conclude \(x=z=0\), and \(\gamma = \pm 1\).\(\square \)
If \(B \simeq {{\,\mathrm{M}\,}}_2(\mathbb Q )\), then \(\Gamma ^1(\mathcal O )={{\,\mathrm{PSL}\,}}_2(\mathbb Z )\) and we investigated this case already in detail. So suppose from now on that \(B \not \simeq {{\,\mathrm{M}\,}}_2(\mathbb Q )\), or equivalently that B is a division algebra over \(\mathbb Q \).
Proposition 38.1.3
The quotient \(\Gamma ^1(\mathcal O ) \backslash \mathbf{\textsf {H} }^2\) is compact.
This proposition is analogous to the finiteness of the class set (as in section 17.5), and the proof is again inspired by the geometry of numbers. We give a proof in Main Theorem 38.4.3.
The compactness result above implies nice properties for \(\Gamma ^1(\mathcal O )\), read off from a fundamental domain (as presented in section 37.1). Let \(z_0 \in \mathbf{\textsf {H} }^2\) have trivial stabilizer \({{\,\mathrm{Stab}\,}}_{\Gamma ^1(\mathcal O )} z_0=\{1\}\). Then the Dirichlet domain
is a closed, locally finite fundamental domain for \(\Gamma ^1(\mathcal O )\) with geodesic sides by Theorem 37.1.12.
Corollary 38.1.4
 is a compact, finite-sided hyperbolic polygon, and the group \(\Gamma ^1(\mathcal O )\) is finitely presented.
is a compact, finite-sided hyperbolic polygon, and the group \(\Gamma ^1(\mathcal O )\) is finitely presented.
Proof We write \(\Gamma =\Gamma ^1(\mathcal O )\). Since \(\Gamma \backslash \mathbf{\textsf {H} }^2\) is compact by Proposition 38.1.3, the distance \(\rho (\Gamma z_0,\Gamma z)\) for \(\Gamma z \in X(\Gamma )\) is bounded. Thus by construction, the Dirichlet domain is contained in a bounded set and is therefore compact. Since  is locally finite, we conclude that \(\gamma \cap \ne \emptyset \) for only finitely many \(\gamma \in \Gamma \). But the set of such elements are the side pairing elements and they generate \(\Gamma \) (Theorem 37.3.1), so
is locally finite, we conclude that \(\gamma \cap \ne \emptyset \) for only finitely many \(\gamma \in \Gamma \). But the set of such elements are the side pairing elements and they generate \(\Gamma \) (Theorem 37.3.1), so  has finitely many sides and \(\Gamma \) is finitely generated. Thus
has finitely many sides and \(\Gamma \) is finitely generated. Thus  has finitely many vertices, the set of vertex cycle relations is finite, and these generate the relations (Proposition 37.3.14). Thus \(\Gamma \) is finitely presented.\(\square \)
has finitely many vertices, the set of vertex cycle relations is finite, and these generate the relations (Proposition 37.3.14). Thus \(\Gamma \) is finitely presented.\(\square \)
Two subgroups \(H_1,H_2 \le G\) are commensurable if \(H_1 \cap H_2\) has finite index in both \(H_1,H_2\).
38.1.5
If \(\Gamma \le {{\,\mathrm{PSL}\,}}_2(\mathbb R )\) is commensurable with \(\Gamma ^1(\mathcal O )\), we say that \(\Gamma \) is an arithmetic Fuchsian group with defining quaternion algebra B. This definition is independent of the choice of order \(\mathcal O \): another suborder or superorder has finite index, so the corresponding unit groups will also have finite index.
For every Fuchsian group \(\Gamma \le {{\,\mathrm{PSL}\,}}_2(\mathbb R )\) commensurable with \(\Gamma ^1(\mathcal O )\), the conclusions of Proposition 38.1.3 and Corollary 38.1.4 remain true: for a containment \(\Gamma ' \le \Gamma \) of finite index, the corresponding map  is finite-to-one, and the desired properties pass from one quotient to the other.
is finite-to-one, and the desired properties pass from one quotient to the other.
In this way, we have completed our task: starting with an indefinite quaternion algebra B over \(\mathbb Q \), we constructed a Fuchsian group \(\Gamma ^1(\mathcal O )\) generalizing \({{\,\mathrm{PSL}\,}}_2(\mathbb Z )\) acting on the upper half-plane. We pursue a more general construction in this chapter (considering an indefinite quaternion over a number field) and its geometry and arithmetic properties in the remainder of this book.
2 Isometries from quaternionic groups
In the remainder of this chapter, we investigate discrete groups obtained from unit groups of quaternion algebra over number fields. Throughout, let F be a number field with r real places and c complex places, so that \([F:\mathbb Q ]=r+2c=n\). Let B be a quaternion algebra over F.
38.2.1
Suppose that B is split at t real places and ramified at the remaining \(r-t\) real places, so that
Let
denote the map (38.2.2) composed with the projection onto the matrix ring factors. Then as long as \(t+c>0\), we have
We have \(t=c=0\) if and only if F is totally real and B is totally definite; in this case, the geometry disappears, and we are reduced to considering finite unit groups (see section 32.3). There is still more to say for this case, and we will return to it in chapter 41 in the context of modular forms. But in this part of the text we are following geometric threads, so
this is another way of saying that B is indefinite or equivalently satisfies the Eichler condition (Definition 28.5.1).
38.2.6
We now restrict to a subgroup acting faithfully via orientation-preserving isometries. Recall that
is the group of totally positive elements of F. Let
be the group of units of B of totally positive reduced norm. Then \(F^\times \subset B_{>0}^\times \) because \({{\,\mathrm{nrd}\,}}(a)=a^2 \in F_{>0}^\times \) for all \(a \in F^\times \). Let
be the quotient by the center; then \(\iota \) induces an inclusion
(we have \({{\,\mathrm{PSL}\,}}_2(\mathbb C ) \simeq {{\,\mathrm{PGL}\,}}_2(\mathbb C )\) and \({{\,\mathrm{PGL}\,}}_2^+(\mathbb R ) \simeq {{\,\mathrm{PSL}\,}}_2(\mathbb R )\), rescaling by the determinant). Therefore, the group \({{\,\mathrm{P\!}\,}}\iota (B_{>0}^\times )\) acts on calH]\(\mathcal H \)product of hyperbolic planes and spaces
on the left faithfully by linear fractional transformations as orientation-preserving isometries (Theorems 33.3.14 and 36.2.14), that is to say
Remark 38.2.11. One can equally well consider \({{\,\mathrm{P\!}\,}}\iota (B^\times ) \subseteq {{\,\mathrm{Isom}\,}}(\mathcal H )\). Indeed,
is the subgroup of isometries that preserve each factor and preserving orientation. The full group \({{\,\mathrm{Isom}\,}}(\mathcal H )\) includes more: permuting factors of the same kind is an isometry, and with these we have an isomorphism of groups
where \(S_m\) denotes the symmetric group. Since \({{\,\mathrm{PSL}\,}}_2(\mathbb R ) \simeq {{\,\mathrm{Isom}\,}}^+(\mathbf{\textsf {H} }^2) \le {{\,\mathrm{Isom}\,}}(\mathbf{\textsf {H} }^2)\) has index 2 and the same for \(\mathbf{\textsf {H} }^3\), we conclude that
The orientation-preserving subgroup \({{\,\mathrm{Isom}\,}}^+(\mathcal H ) \le {{\,\mathrm{Isom}\,}}(\mathcal H )\) has index 2, containing for example elements which reverse orientation in two components and preserve orientation in the others; if the orientation is reversed in two components \(\mathbf{\textsf {H} }^2\), then the resulting isometry is orientation-preserving but not holomorphic in these components.
3 Discreteness
We now seek discrete subgroups, as follows.
38.3.1
Let \(R=\mathbb Z _F\) be the ring of integers of F and let \(\mathcal O \subset B\) be an R-order. Let
be the subgroup of units of reduced norm 1, and let
Then by (38.2.10), we have \(\Gamma ^1(\mathcal O ) < {{\,\mathrm{Isom}\,}}^+(\mathcal H )\).
Definition 38.3.4
A subgroup \(\Gamma \le {{\,\mathrm{Isom}\,}}^+(\mathcal H )\) is arithmetic if \(\Gamma \) is commensurable with \(\Gamma ^1(\mathcal O )\) for a quaternion algebra B and an order \(\mathcal O \subseteq B\) (with respect to some embedding \(\iota \)).
If \(\Gamma \) is commensurable with \(\Gamma ^1(\mathcal O )\) for an order \(\mathcal O \) then it is commensurable with \(\Gamma ^1(\mathcal O ')\) for every other order \(\mathcal O '\), since every two orders have finite R-index, thus finite index—so we could equally well compare to one fixed (e.g. maximal) order. The class of arithmetic groups contains in particular the quaternionic unit groups with which we started, but contains other groups of interest (including subgroups and discrete supergroups with finite index).
Remark 38.3.5. There is a more general definition of arithmetic group which reduces to this one; see section 38.5.
Right away, we show that arithmetic groups are discrete. To do so, we will need two short lemmas.
Lemma 38.3.6
Let K, X be Hausdorff topological spaces, and suppose K is compact. Let \(\pi :K \times X \rightarrow X\) be the projection, and let \(Y \subseteq K \times X\) be discrete and closed. Then \(\pi (Y) \subseteq X\) is discrete.
Proof First, Y has no limit points: a limit point of Y would belong to Y, but then Y is discrete so every point is isolated point. For the same reason, every subset of Y is also (discrete and) closed: a limit point of the subset would be a limit point of Y.
Now let \(x \in \pi (Y)\) and let \(Y_x = Y \smallsetminus \pi ^{-1}(x)\). Then \(Y_x \subseteq K \times X\) is closed. The set \((K \times X) \smallsetminus Y_x\) is open and contains \(K \times \{x\}\), so by the tube lemma, it contains an open set \(K \times U\). Then \(U \ni x\) is the desired neighborhood.\(\square \)
Lemma 38.3.7
Let G be a Hausdorff topological group and let \(H \le G\) be a discrete subgroup. Then H is closed.
Proof Since H is discrete, there is a neighborhood \(U \ni 1\) such that \(U \cap H = \{1\}\). Further, there exists a neighborhood \(V \subseteq U\) such that \(V^{-1}V \subseteq U\) (multiplication and inversion are continuous, see Exercise 12.4).
We show \(G \smallsetminus H\) is open. For \(x \in G\), we have \(xV \ni x\) an open neighborhood, and if \(h,h' \in xV \cap H\) then \(x^{-1}h,x^{-1}h' \in V\) and so \((x^{-1}h)^{-1}(x^{-1}h')=h^{-1} h' \in V^{-1}V \subseteq U\). Therefore \(h^{-1}h'=1\) by the hypothesis on U, so \(h=h'\). Thus xV contains at most one element of H. Since G is Hausdorff, when \(x \not \in H\) we can shrink V if necessary to get \(xV \cap H = \emptyset \), as desired.\(\square \)
Proposition 38.3.8
Let \(\Gamma \le {{\,\mathrm{Isom}\,}}^+(\mathcal H )\) be an arithmetic subgroup. Then \(\Gamma \) is discrete.
Proof It is enough to prove the proposition for \(\Gamma =\Gamma ^1(\mathcal O )\), as discreteness is preserved between commensurable groups (having finite index in their intersection).
The image \(O \hookrightarrow B_\mathbb R \) as in (38.2.2) is discrete by 17.7.6: we argued using coordinates and noted that \(R=\mathbb Z _F \hookrightarrow F_\mathbb{R }\) is discrete. Therefore the image
is discrete (by restriction). Further, since \(\mathbb H ^1\) is compact, by Lemmas 38.3.6 and 38.3.7, the image of \(\mathcal O ^1 \hookrightarrow {{\,\mathrm{SL}\,}}_2(\mathbb R )^t \times {{\,\mathrm{SL}\,}}_2(\mathbb C )^c\) under the projection is discrete. (Any further projection turns out not to be discrete; see Exercise 38.2.)\(\square \)
38.3.10
The group \(\Gamma ^1(\mathcal O )\) is a Fuchsian group if and only if \(t=1\) and \(c=0\), i.e. F is totally real and B is ramified at all but one real place; \(\Gamma ^1(\mathcal O )\) is a Kleinian group if and only if \(t=0\) and \(c=1\), i.e. F has exactly one complex place and B is ramified at all real places.
Just as for Fuchsian and Kleinian groups, discrete groups admit several equivalent characterizations as follows. (For the notion of a good orbifold, see Definition .)
Proposition 38.3.11
Let \(\Gamma \le {{\,\mathrm{Isom}\,}}^+(\mathcal H )\) be a subgroup. Then the following are equivalent:
-
(i)
\(\Gamma \) is discrete (with the subspace topology);
-
(ii)
For all \(z \in \mathcal H \), we have \(\#{{\,\mathrm{Stab}\,}}_\Gamma (z)<\infty \) and there exists an open neigborhood \(U \ni z\) such that \(\gamma U \cap U \ne \emptyset \) implies \(\gamma \in {{\,\mathrm{Stab}\,}}_\Gamma (z)\);
-
(iii)
For all compact subsets \(K \subseteq \mathcal H \), we have \(K \cap \gamma K \ne \emptyset \) for only finitely many \(\gamma \in \Gamma \); and
-
(iv)
For all \(z \in \mathcal H \), the orbit \(\Gamma z \subseteq \mathcal H \) is discrete and \(\#{{\,\mathrm{Stab}\,}}_\Gamma (z)<\infty \).
Moreover, if these equivalent conditions hold, then the quotient \(\Gamma \backslash \mathcal H \) has the structure of a good Riemann orbifold of dimension \(m=2t+3c\), and the quotient map
is a local isometry at all points \(z \in \mathcal H \) with \({{\,\mathrm{Stab}\,}}_\Gamma (z)=\{1\}\).
Proof We proved this statement in Propositions 34.7.2 and 36.4.1 when \(t=0\) or \(c=0\); the general case follows similarly.\(\square \)
4 Compactness and finite generation
We now consider further properties of arithmetic groups. Refreshing our notation, let \(\Gamma \le {{\,\mathrm{Isom}\,}}^+(\mathcal H )\) be an arithmetic group arising from a quaternion algebra B.
38.4.1
The arithmetic discrete groups arising from the case \(B={{\,\mathrm{M}\,}}_2(F)\) of the matrix ring are of particular interest: they include the case \(F=\mathbb Q \) giving rise to the classical modular group \(\Gamma ={{\,\mathrm{PSL}\,}}_2(\mathbb Z )\) studied in chapter 35 as well as the case \(F=\mathbb Q (i)\) giving rise to the Picard group \(\Gamma ={{\,\mathrm{PSL}\,}}_2(\mathbb Z [i])\) examined in section 36.6 and more generally the Bianchi groups. Let \(B={{\,\mathrm{M}\,}}_2(F)\). Then necessarily \(r=t\) (the matrix ring is already split!), so \(\mathcal H = (\mathbf{\textsf {H} }^2)^r \times (\mathbf{\textsf {H} }^3)^c\), and the embedding \(\iota \) in (38.2.3) has the simple description
where we embed matrices componentwise, indexed by the archimedean places of F.
Much is written about the compactification of \(Y(\Gamma )\), and unfortunately it would take us too far afield to fully treat this important topic: the groups so obtained behave differently in several respects than the case where B is a division algebra.
We suppose throughout this section that B is a division algebra.
Let \(X(\Gamma ) :=\Gamma \backslash \mathcal H \) be the quotient, a good Riemann orbifold.
MainTheorem 38.4.3
(Hey). The orbifold \(X(\Gamma )\) is compact.
Proof We follow Zassenhaus [Zas72, §1]; see also Kleinert [Klt2000, Theorem 1.1].
First, the group \(\Gamma \) is commensurable with \(\iota (\mathcal O ^1)\) for an R-order \(\mathcal O \); by comparison under maps of finite index, we may suppose \(\Gamma =\Gamma ^1(\mathcal O )\).
Second, we claim that it suffices to show that \(\mathcal O ^1 \backslash B_\mathbb R ^1\) is compact. Indeed, recall (38.3.9) that
From the symmetric space models (34.6.3) and (36.3.14), we have homeomorphisms
so the fibers of the continuous projection map
are given by
and therefore compact, and the claim follows.
Now from (38.2.2), we have
choosing an \(\mathbb R \)-basis for \(B_\mathbb R \), we have \(B_\mathbb R \simeq \mathbb R ^{4n}\) and under the standard metric, this gives \(\mathcal O \simeq \mathbb Z ^{4n}\) the (non-canonical) structure of a Euclidean lattice. Let \(X \subseteq B_\mathbb R \) be a compact, convex, symmetric subset with volume \({{\,\mathrm{vol}\,}}(X)>2^{4n} {{\,\mathrm{covol}\,}}(\mathcal O )\). (The precise value of this covolume will not figure in the argument, and anyway would depend on the choice of Euclidean structure; all such structures induce the same topology.) Therefore, by Minkowski’s convex body theorem (Theorem 17.5.5), there exists nonzero \(\alpha \in \mathcal O \cap X\). Moreover, for all \(g=(g_v)_v \in B_\mathbb R ^1\) we have
since \(\prod _v \det (g_v)= 1\), and gX is again compact, convex, and symmetric, so similarly there exists nonzero \(\alpha _g \in \mathcal O \cap g X\).
We will show that the quotient space \(\mathcal O ^1 \backslash B_\mathbb R ^1\) is sequentially compact. To this end, let \(g_n\) be a sequence from \(B_\mathbb R ^1\). By the previous paragraph, there exist \(\alpha _n \in \mathcal O \) such that \(\alpha _n = g_n x_n\) with \(x_n \in X\) nonzero. Since X is compact, we can restrict to a subsequence such that \(x_n \rightarrow x \in X\) converges.
The reduced norm \({{\,\mathrm{nrd}\,}}:B \rightarrow F\) extends by scaling to a continuous function \({{\,\mathrm{nrd}\,}}:B_\mathbb R \rightarrow F_\mathbb R \). Since \(X \subseteq B_\mathbb R \) is bounded so too is \({{\,\mathrm{nrd}\,}}(X) \subseteq F_\mathbb R \) bounded. But
and the values \({{\,\mathrm{nrd}\,}}(\alpha _n) \in {{\,\mathrm{nrd}\,}}(\mathcal O ) \subseteq \mathbb Z _F\) lie in a discrete subset, so there are only finitely many possibilities for \({{\,\mathrm{nrd}\,}}(\alpha _n)\). Moreover, the left ideals \(I_n=\mathcal O \alpha _n\) have
bounded, so there are only finitely many possibilities for \(I_n\) by Lemma 17.7.26. Thus, by the pigeonhole principle and restricting to a subsequence, we may suppose \(I_n=\mathcal O \alpha _n = \mathcal O \alpha _1\) and \({{\,\mathrm{nrd}\,}}(\alpha _n)={{\,\mathrm{nrd}\,}}(\alpha _1)\) for all n. Therefore \(\alpha _n = \gamma _n \alpha _1\) with \(\gamma _n \in \mathcal O ^1\) for all n.
To conclude, we note that since B is a division algebra,
so
converges. Therefore
converges as well. Therefore the quotient \(\mathcal O ^1 \backslash B_\mathbb R ^1\) is sequentially compact, and therefore compact.\(\square \)
Remark 38.4.5. Main Theorem 38.4.3 was proven by Hey [Hey29, Hilfssatz 4] in her 1929 Ph.D. thesis (see also Remark 29.10.24) in the case where B is a division algebra over \(\mathbb Q \). In particular, there is no need to suppose that B is central, so it contains the Dirichlet unit theorem as a consequence: see Exercise 38.6.
After treating the decomposition of the adelic coset space, we will also see Hey’s theorem as an essentially direct consequence of Fujisaki’s lemma (Main Theorem 27.6.14): see Theorem 38.7.21.
Theorem 38.4.6
The group \(\Gamma \) is finitely generated.
Proof Let \(x_0 \in X(\Gamma )\) satisfy \({{\,\mathrm{Stab}\,}}_{\Gamma }(x_0)=\{1\}\). Then by Theorem 37.4.18, the Dirichlet domain \(=(\Gamma ;x_0)\) is a locally finite fundamental set for \(\Gamma \). By Main Theorem 38.4.3, \(X(\Gamma )\) is compact, so too is  . Then since
. Then since  is locally finite, we conclude that \(\gamma \cap \ne \emptyset \) for only finitely many \(\gamma \in \Gamma \). But then by Theorem 37.4.2, the group \(\Gamma \) is generated by such elements and \(\Gamma \) is finitely generated.\(\square \)
is locally finite, we conclude that \(\gamma \cap \ne \emptyset \) for only finitely many \(\gamma \in \Gamma \). But then by Theorem 37.4.2, the group \(\Gamma \) is generated by such elements and \(\Gamma \) is finitely generated.\(\square \)
Remark 38.4.7. In fact, \(\Gamma \) is finitely presented, and an argument similar to Proposition 37.3.14 shows that orbits of nonempty subsets
with \(\gamma \ne \gamma '\) provide a finite generating set of relations (generalizing the vertex cycle relations): see e.g. Raghunathan [Rag72, Theorem 6.15].
5 \(*\) Arithmetic groups, more generally
In this section, we briefly discuss more general definitions of arithmetic group and show that they reduce to the “working” one given above (Definition 38.3.4). As above, let F be a number field.
38.5.1
Let \(\mathsf{G }\le {{\,\mathrm{GL}\,}}_{n,F}\) be a linear algebraic group, a subgroup variety of \({{\,\mathrm{GL}\,}}_{n,F}\) defined by polynomial equations in the entries and the inverse of the determinant, with coefficients in F. Equivalently, \(\mathsf{G }\) is an affine variety over F equipped with identity, multiplication, and inversion morphisms giving it the structure of a group variety.)
We say a subgroup
is arithmetic (as a subgroup of \(\mathsf{G }(F_\infty )\)) if it is commensurable with \(\mathsf{G }(\mathbb Z _F)\). This notion of arithmetic group was developed significantly by Borel [Bor62, Bor69].
38.5.2
Let B be a quaternion algebra over F. Then there is an embedding \(\rho :B \hookrightarrow {{\,\mathrm{M}\,}}_4(F)\) as in Exercise 2.11 by the regular representation. Thus \(B^\times \le {{\,\mathrm{GL}\,}}_4(F)\) and the image is described by explicit polynomial equations (Exercise 38.5). Therefore there exists a linear algebraic group \(\mathsf{G }\le {{\,\mathrm{GL}\,}}_{4,F}\) such that \(\mathsf{G }(F) \simeq B^\times \).
Similar statements hold for \(B^1 \le {{\,\mathrm{SL}\,}}_4(F)\).
Lemma 38.5.3
A group \(\Gamma \) commensurable with \(\Gamma ^1(\mathcal O )\) for a quaternion algebra B and order \(\mathcal O \subseteq B\) is arithmetic in the sense of 38.5.1.
Proof Applying 38.5.2, we have \(\rho :B \hookrightarrow {{\,\mathrm{M}\,}}_4(F)\) realizing \(B^1 \simeq \mathsf{G }(F) \le {{\,\mathrm{GL}\,}}_4(F)\) as a linear algebraic group by appropriate polynomial equations. Under this embedding, \(\mathcal O :=\rho (B) \cap {{\,\mathrm{M}\,}}_4(\mathbb Z _F)\) is a \(\mathbb Z _F\)-order, and thus \(\mathcal O ^1 \simeq \mathsf{G }(\mathbb Z _F)\) and \(\prod _v \mathsf{G }(F_v) \simeq \prod _v B_v^1\), as required in the definition.\(\square \)
In view of Definition 38.3.4, we consider now the converse: when does the more general definition give rise to discrete subgroups of two-by-two matrices?
38.5.4
Let \(\mathsf{G }\) be a linear algebraic group over F, and suppose that \(\mathsf{G }_{\overline{F}} \simeq {{\,\mathrm{GL}\,}}_{2,\overline{F}}\), so there is a chance to obtain discrete groups of symmetries like the ones considered above. (For a complete treatment, we should consider \({{\,\mathrm{SL}\,}}_{2}\) as well as the group \({{\,\mathrm{PGL}\,}}_{2}\), but the arguments are similar.) We say then that \(\mathsf{G }\) is an F- form of the algebraic group \({{\,\mathrm{GL}\,}}_2\).
Lemma 38.5.5
Let \(\mathsf{G }\) be an F-form of \({{\,\mathrm{GL}\,}}_2\). Then there exists a quaternion algebra B over F, unique up to F-algebra isomorphism, such that \(\mathsf{G }(F) \simeq B^\times \).
Proof This is a basic result in non-abelian Galois cohomology, and it would take us too far afield to prove it here: see e.g. Milne [Milne2017, Theorem 20.3.5] and more generally Serre [Ser79, Chapter X].\(\square \)
Lemma 38.5.5 explains that more general notions of arithmetic groups do not create anything new beyond our quaternionic definition.
Remark 38.5.6. In this context, there is a criterion for compactness, generalizing Main Theorem 38.4.3 (conjectured by Godement): A discrete subgroup of \(\mathsf{G }(\mathbb R )\) is cocompact if and only if the reductive part of the connected component of \(\mathsf{G }\) is anisotropic over F. If \(\mathsf{G }\) is semisimple, then cocompactness is equivalent to asking that every element of \(\mathsf{G }(F)\) is semisimple. This criterion was proven by Borel–Harish-Chandra [BHC62] and Mostow–Tamagawa [MT62]; Godement [God62] (with Weil) extended the method of Mostow–Tamagawa and simplified the proof by working directly on adele groups. See also Platonov–Rapinchuk [PR94, §4.5].
6 \(*\) Modular curves, seen idelically
We have already seen how idelic methods can be both a conceptual and a computational simplification. The quaternion groups defined above naturally also fit into this perspective, and we describe this in the final two sections. As motivation, we begin in this section by reconsidering the classical modular curves from an idelic point of view.
38.6.1
Recall that the adeles of \(\mathbb Q \) decompose as
into finite and infinite parts. Let \(B={{\,\mathrm{M}\,}}_2(\mathbb Q )\). Then
The order \(\mathcal O ={{\,\mathrm{M}\,}}_2(\mathbb Z )\) is maximal in B, and we have the adelic order \(\widehat{\mathcal{O }}={{\,\mathrm{M}\,}}_2(\widehat{\mathbb{Z }}) \subset {{\,\mathrm{M}\,}}_2(\widehat{\mathbb{Q }})\). (We have seen that \(B={{\,\mathrm{M}\,}}_2(\mathbb Q ) \le {B}= {{\,\mathrm{M}\,}}_2(\mathbb{Q })\) sits discretely and the quotient \(B \backslash {B}\) is compact; like the adelic quotient \(F \backslash {F}\) itself, this is not very interesting.)
Similarly, we have
It was a key consequence of strong approximation—but easy to establish in this case (Lemma 28.2.4)—that
is trivial: every nonzero right (invertible) fractional \({{\,\mathrm{M}\,}}_2(\mathbb Z )\)-ideal is principal, or equivalently, every \(\widehat{\mathbb{Z }}\)-lattice in \(\widehat{\mathbb{Q }}^2\) has a basis in \(\mathbb Q ^2\).
As lovely as this is, this description leaves out the real place, and by putting it back we restore archimedean structure.
38.6.4
The projection map
yields a continuous projection
by (38.6.3). Therefore, every element of \({{\,\mathrm{GL}\,}}_2(\mathbb{Q })\) is represented in the double coset by an element of the form \((1,\alpha _\infty )\) with \(\alpha _\infty \in {{\,\mathrm{GL}\,}}_2(\mathbb R )\); and the element \(\alpha _\infty \) is well-defined up the action of the group of pairs \((\gamma ,\widehat{\mu }) \in {{\,\mathrm{GL}\,}}_2(\mathbb Q ) \times {{\,\mathrm{GL}\,}}_2(\widehat{\mathbb{Z }})\) satisfying
so \(\gamma =\widehat{\mu }^{-1} \in {{\,\mathrm{GL}\,}}_2(\mathbb Q ) \cap {{\,\mathrm{GL}\,}}_2(\widehat{\mathbb{Z }})={{\,\mathrm{GL}\,}}_2(\mathbb Z )\), acting on the left. In other words, we have a bijection
38.6.6
At this point, we are no stranger to the quotient \({{\,\mathrm{GL}\,}}_2(\mathbb Z ) \backslash {{\,\mathrm{GL}\,}}_2(\mathbb R )\)! We have studied in detail the related quotient \({{\,\mathrm{SL}\,}}_2(\mathbb Z ) \backslash {{\,\mathrm{SL}\,}}_2(\mathbb R )\): by the symmetric space description, we have an isometry
We similarly obtain a bijection
(any matrix of negative determinant interchanges the upper and lower half-planes, so we maintain a bijection). Then we can take the quotient on the left by \({{\,\mathrm{GL}\,}}_2(\mathbb Z )\) to get an identification
from (38.6.7), and we find again the classical modular curve we considered in section 35.1. (In section 40.1, we will see another version of this in that the space Y(1) parametrizes complex lattices \(\Lambda \subseteq \mathbb C \) up to scaling by \(\mathbb C ^\times \).)
Putting (38.6.9) and (38.6.5) together, we have
in the last line, we introduce the notation \(K_\infty :=\mathbb R ^\times {{\,\mathrm{SO}\,}}(2)\) and \({K}:=\widehat{\mathcal{O }}^\times \times K_\infty \) to help in grasping this double coset. Chasing down all of the maps, the bijection is obtained by sending an element \(z \in \mathbf{\textsf {H} }^2{}^{\pm }\) to the class of \((1,\alpha ) \in {{\,\mathrm{GL}\,}}_2(\widehat{\mathbb{Q }}) \times {{\,\mathrm{GL}\,}}_2(\mathbb R )\) where \(z = \alpha i\). Note there is a nice symmetry in the expression on the right-hand side of (38.6.10).
Remark 38.6.11. In this way, we just wrapped the classical quotient in ideles. This double cosetification (a beautiful monster of a word) provides a uniform way to describe the orbifold quotients obtained from quaternionic arithmetic groups more generally: in particular, class number issues are made more transparent in the language of double cosets. On the other hand, geometric structures are not always visible in this language, which is why we have treated both approaches in this text.
7 \(*\) Double cosets
In this section, we give a description of quaternionic orbifolds in terms of idelic double cosets. We retain the notation from 38.2.1, 38.2.6, and 38.3.1. In particular, F is a number field with r real places and c complex places, B is a quaternion algebra over F that is split at t real places with \(t+c>0\), we have an embedding
We have defined
where we may also write
by the symmetric space decomposition. We similarly define
where similarly
In this chapter we have been working with groups \(\Gamma \le {{\,\mathrm{Isom}\,}}^+(\mathcal H )\) commensurable with \(\Gamma ^1(\mathcal O )={{\,\mathrm{P\!}\,}}\iota (\mathcal O ^1)\). To work idelically, we restrict our attention to such groups that can be defined idelically: these are the congruence subgroups.
Definition 38.7.2
Let \({\mathfrak {M}} \) be a nonzero ideal. Let
The principal congruence subgroup of level \({\mathfrak {M}} \subseteq R\) is the group
obtained from the units of norm 1 in \(\mathcal O (\mathfrak {M})\).
A group \(\Gamma \) commensurable with \(\Gamma ^1(\mathcal O )\) is congruence if it contains \(\Gamma (\mathfrak {M})\) for some \({\mathfrak {M}}\).
A congruence subgroup is defined by (finitely many) congruence conditions. Let \(\widehat{\Gamma }\) be the closure of \(\Gamma \) with respect to the topology on \(\widehat{B}^\times \), where observe that a fundamental system of open neighborhoods of 1 is given by the images of the principal congruence subgroups.
Lemma 38.7.3
Suppose that \(\Gamma \) is commensurable with \(\Gamma ^1(\mathcal O )\). Then \(\widehat{\Gamma }\cap B^\times = \Gamma \) if and only if \(\Gamma \) is congruence.
Proof The group \(\widehat{\Gamma }\) is a closed subgroup of \(\widehat{B}^\times \) commensurable with the compact open subgroup \(\widehat{\Gamma (1)}\) and so \(\widehat{\Gamma }\) is also compact open. By definition of the topology on \(\widehat{B}^\times \), the closure of \(\overline{\Gamma } :=\widehat{\Gamma }\cap B^\times \) is the smallest congruence group containing \(\Gamma \), and \(\overline{\Gamma }\) contains \(\Gamma \) with finite index. So \(\Gamma \) is congruence if and only if \(\Gamma =\overline{\Gamma }\).\(\square \)
From now on, suppose that \(\Gamma \) is a congruence subgroup.
Remark 38.7.4. In general, we may work with the congruence closure \(\widehat{\Gamma }\cap B^\times \ge \Gamma \) of an arithmetic group \(\Gamma \).
38.7.5
In view of (38.6.10) and (38.7.1), we let \(K_\infty :=\prod _{v \mid \infty } K_v\) where
The groups \(K_v\) are the extension of a maximal compact subgroup by the center. We then let \({K}= \widehat{\Gamma }\times K_\infty \) and consider the double coset space
where \(B^\times \) acts on \({B}^\times \) by left multiplication (under the diagonal embedding) and \({K}\) acts on \({B}^\times = \widehat{B}^\times \times B_\infty ^\times \) by right multiplication.
The expression (38.7.7) is tidy, and generalizes well, but we also want to know what it looks like. Plugging back in (38.7.1), we have \(B_\infty ^\times /K_\infty = \mathcal H ^{\pm }\), so
where \(B^\times \) acts on \(\mathcal H ^{\pm }\) via \(\iota \) and on \(\widehat{B}^\times /\widehat{\Gamma }\) by left multiplication. Since there can hopefully no confusion about this action, removing parentheses we will write
Definition 38.7.9
We call \(Y{}_{Sh }(\Gamma )\) the quaternionic Shimura orbifold of level \(\Gamma \).
Definition 38.7.9 explains the subscript \({}_{{}_{Sh }}\). We immediately proceed to justify the name orbifold; moreover, we will see that the space is possibly disconnected, and we write it as a union of connected components.
38.7.10
By weak approximation, there exist elements \(\alpha \in B^\times \) with \({{\,\mathrm{nrd}\,}}(\alpha )\) having all possible real signs at the split real places of B. Therefore
38.7.12
There is a natural (continuous) projection map
Recall that \(t+c>0\), and B is indefinite. Therefore, strong approximation (as in Corollary 28.6.8) implies that there is a bijection
Therefore \({{\,\mathrm{Cl}\,}}^+_{G(\Gamma )} R\) is a (narrow) class group of F associated to the group \(\Gamma \); as such, it is a finite abelian group that surjects onto the strict class group \({{\,\mathrm{Cl}\,}}^+ R\).
38.7.15
By 38.7.12, the space \(Y{}_{Sh }(\Gamma )\) is the disjoint union of finitely many connected components indexed by the group \({{\,\mathrm{Cl}\,}}^+_{G(\Gamma )} R\). We identify these connected components explicitly as follows.
Let the ideals \(\mathfrak {b}\subseteq R\) form a set of representatives for \({{\,\mathrm{Cl}\,}}^+_{G(\Gamma )} R\), and let \(\widehat{\mathfrak {b}}= \mathfrak {b}\otimes _\mathbb{Z } \widehat{\mathbb{Z }}\) be their adelification; then for each \(\mathfrak {b}\), there exists \(\widehat{b} \in \widehat{R}\) generating \(\widehat{\mathfrak {b}}\), so
For simplicity, choose \(\mathfrak {b}=R\) and \(\widehat{b}=\widehat{1}\) for the representatives of the trivial class.
By surjectivity of the map (38.7.14), for each \(\widehat{b}\) there exists \(\widehat{\beta }\in \widehat{B}^\times \) such that \({{\,\mathrm{nrd}\,}}(\widehat{\beta })=\widehat{b}\). Therefore
For each \(\mathfrak {b}\), let
Then we have a natural bijection
Letting
we see that each \(Y(\Gamma _\mathfrak {b})\) is a connected orbifold of dimension \(2t+3c\). We abbreviate \(Y(\Gamma )=Y(\Gamma _{(1)})\) for the trivial class. Putting these together, we have
as a disjoint union of connected orbifolds.
Remark 38.7.20. When \(c=0\), i.e., F is totally real, then \(Y{}_{Sh }(\Gamma )\) can be canonically given the structure of an algebraic variety defined over a number field, by work of Shimura [Shi67] and Deligne [Del71]; in this case we upgrade \(Y{}_{Sh }(\Gamma )\) to a quaternionic Shimura variety. The theory of Shimura varieties is both broad and deep—see Milne [Milne-SV] and the references therein. We will begin the study quaternionic Shimura varieties of dimension 1 in Chapter 43, touching upon the theory of canonical models in section 43.8.
The above description has hopefully provided a more transparent way to understand arithmetic orbifolds. For example, we can prove an idelic version of Hey’s theorem (Main Theorem 38.4.3) as follows.
Theorem 38.7.21
Suppose that B is a division algebra. Then \(Y{}_{Sh }(\Gamma )\) is compact.
Proof We appeal to Fujisaki’s lemma (Main Theorem 27.6.14): the quotient \(B^\times \backslash {B}^{(1)}\) is cocompact, under the important hypothesis that B is a division algebra. Let \(K_\infty \) be as in 38.7.6, and consider the inclusion followed by the projection
These maps are continuous, and the composition is surjective as \(\mathbb R ^\times \le K_\infty \) (embedded diagonally) and \(\mathbb R ^\times {B}^{(1)} = {B}^\times \). So the target is compact, proving the statement.\(\square \)
Exercises
In these exercises, we maintain the notation in this chapter: let F be a number field with r real places and c complex places, degree \(n=[F:\mathbb Q ]\), and ring of integers R, and let \(\mathcal O \) be an R-order in a quaternion algebra B over F.
-
1.
Let \(\alpha \in \mathbb R \smallsetminus \mathbb Q \). Show that \(\mathbb Z [\alpha ]\) is not discrete in \(\mathbb R \). (Taking e.g. \(\alpha =\sqrt{d}\), this gives a reason to worry about discreteness of number fields when we project.)
-
2.
Embed \(\mathcal O ^1\) diagonally in \({{\,\mathrm{SL}\,}}_2(\mathbb R )^{r-t} \times {{\,\mathrm{SL}\,}}_2(\mathbb C )^c\). Show that a (further) projection to a proper factor is not discrete.
-
3.
Let
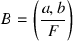 , and let v be a split real place of B. Show that \(\mathcal O ^1 \hookrightarrow B_v^1 \simeq {{\,\mathrm{SL}\,}}_2(\mathbb R )\) if and only if F is totally real and for all nonidentity real places \(v'\), we have \(v'(a)<0\) and \(v(b)<0\).
, and let v be a split real place of B. Show that \(\mathcal O ^1 \hookrightarrow B_v^1 \simeq {{\,\mathrm{SL}\,}}_2(\mathbb R )\) if and only if F is totally real and for all nonidentity real places \(v'\), we have \(v'(a)<0\) and \(v(b)<0\). -
4.
In this exercise, we give a direct argument for the discreteness of an arithmetic Fuchsian group. Suppose F is totally real, let v be a split place of B, consider \(F \hookrightarrow v(F) \subseteq \mathbb R \) as a subfield of \(\mathbb R \), and suppose that B is ramified at all other (nonidentity) real places. Prove that \(\mathcal O ^1 \subseteq {{\,\mathrm{SL}\,}}_2(\mathbb R )\) is discrete.
-
5.
Consider the regular representation \(\rho :B \hookrightarrow {{\,\mathrm{M}\,}}_4(F)\) (Exercise 2.11). Describe the image explicitly in terms of polynomial equations in matrix entries. Conclude that \(B^\times \) and \(B^1\) are also described by polynomial equations.
-
(a)
Suppose not: then there exists a sequence \(\alpha _n = t_n + x_n i + y_n j + z_n ij \rightarrow 1\) with \(t_n,x_n,y_n,z_n \in F\) with bounded denominators. Multiplying through, suppose that all coordinates are integral. Show for n sufficiently large that all of the coordinates are integral and bounded.
-
(b)
Show that for all nonidentity v, the coordinates of \(v(\alpha _n)\) are also bounded using compactness.
-
(c)
Finally, prove that there are only a finite number of elements in R that are bounded in each coordinate (all conjugates are bounded). [Hint: look at the coefficients of a minimal polynomial, and derive a contradiction.]
-
(a)
-
6.
Let F be a number field and \(R=\mathbb Z _F\) its ring of integers. In this exercise, we give a proof of Dirichlet’s unit theorem using the same method as in the proof of Main Theorem 38.4.3.
-
(a)
Show that \([R^\times : R^1] \le 2\).
-
(b)
Show (following the proof of Main Theorem 38.4.3) that \(R^1 \backslash F_\mathbb R ^1\) is compact.
-
(c)
Under the usual logarithmic embedding \(\log :F_\mathbb R ^1 \rightarrow (\prod _v \mathbb R )^0\), conclude that \(\log R^1 \backslash \log F_\mathbb R ^1\) is compact, and therefore \(\log R^1\) has rank \(r+c-1\) as an abelian group (written additively).
-
(d)
Conclude that \(R^\times \) has rank \(r+c-1\) as an abelian group (written multiplicatively).
-
(a)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
This chapter is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, duplication, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, a link is provided to the Creative Commons license and any changes made are indicated.The images or other third party material in this chapter are included in the work's Creative Commons license, unless indicated otherwise in the credit line; if such material is not included in the work's Creative Commons license and the respective action is not permitted by statutory regulation, users will need to obtain permission from the license holder to duplicate, adapt or reproduce the material.
Copyright information
© 2021 The Author(s)
About this chapter
Cite this chapter
Voight, J. (2021). Quaternionic arithmetic groups. In: Quaternion Algebras. Graduate Texts in Mathematics, vol 288. Springer, Cham. https://doi.org/10.1007/978-3-030-56694-4_38
Download citation
DOI: https://doi.org/10.1007/978-3-030-56694-4_38
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-56692-0
Online ISBN: 978-3-030-56694-4
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


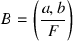 , and let v be a split real place of B. Show that
, and let v be a split real place of B. Show that