Abstract
We have seen in sections 35.1 and 36.6 that understanding a nice fundamental set for the action of a discrete group \(\Gamma \) is not only useful to visualize the action of the group by selecting representatives of the orbits, but it is also instrumental for many other purposes, including understanding the structure of the group itself. In this chapter, we pursue a general construction of nice fundamental domains for the action of a discrete group of isometries.
You have full access to this open access chapter, Download chapter PDF
We have seen in sections 35.1 and 36.6 that understanding a nice fundamental set for the action of a discrete group \(\Gamma \) is not only useful to visualize the action of the group by selecting representatives of the orbits, but it is also instrumental for many other purposes, including understanding the structure of the group itself. In this chapter, we pursue a general construction of nice fundamental domains for the action of a discrete group of isometries.
1 \(\triangleright \) Dirichlet domains for Fuchsian groups
In this introductory section, we preview the results in this chapter specialized to the case of Fuchsian groups. Let \(\Gamma \subset {{\,\mathrm{PSL}\,}}_2(\mathbb R )\) be a Fuchsian group; then \(\Gamma \) is discrete, acting properly by isometries on the hyperbolic plane \({\mathbf {\mathsf{{{H}}}}} ^2\), with metric \(\rho (\cdot ,\cdot )\) and hyperbolic area \(\mu \).
A natural way to produce fundamental sets that provide appealing tessellations of \({\mathbf {\mathsf{{{H}}}}} ^2\) is to select in each orbit the points closest to a fixed point \(z_0 \in {\mathbf {\mathsf{{{H}}}}} ^2\), as follows.
Definition 37.1.1
TheDirichlet domain for \(\Gamma \) centered at \(z_0 \in {\mathbf {\mathsf{{{H}}}}} ^2\) is

As the group \(\Gamma \) willst vary, we suppress the dependence on \(\Gamma \) and often write simply  .
.
37.1.2
The set  is an intersection
is an intersection

where
In particular, since each \(H(\gamma ;z_0)\) is closed, we conclude from (37.1.3) that  is closed.
is closed.
The sets \(H(\gamma ;z_0)\) can be further described as follows. If \(z_0=\gamma ^{-1}z_0\), then \(H(\gamma ;z_0)={\mathbf {\mathsf{{{H}}}}} ^2\). So suppose \(z_0 \ne \gamma ^{-1} z_0\). Then by Exercise 33.8, \(H(\gamma ;z_0)\) is a (half!) half-plane consisting of the set of points as close to \(z_0\) as \(\gamma ^{-1} z_0\), and \(H(\gamma ;z_0)\) is convex: if two points lie in the half-plane then so does the geodesic segment between them. The boundary
is the geodesic perpendicular bisector of the geodesic segment from \(z_0\) to \(\gamma ^{-1}z_0\), as in Figure 37.1.5.
From the description in 37.1.2, the sketch of a Dirichlet domain looks like Figure 37.1.6.
The fundamental sets we have seen are in fact examples of Dirichlet domains.
Example 37.1.7
We claim that the Dirichlet domain for \(\Gamma ={{\,\mathrm{PSL}\,}}_2(\mathbb Z )\) centered at \(z_0=2i\) is in fact the fundamental set for \(\Gamma \) introduced in section 35.1, i.e.,

Recall the generators \(S,T \in \Gamma \) with \(Sz=-1/z\) and \(Tz=z+1\). By (33.5.3)
Let \(z \in {\mathbf {\mathsf{{{H}}}}} ^2\). Visibly
or put another way
Similarly, \(H(T^{-1};2i)=\{z \in {\mathbf {\mathsf{{{H}}}}} ^2: {{\,\mathrm{Re}\,}}z \le 1/2\}\). Equivalently, the geodesic perpendicular bisector between 2i and \(2i \pm 1\) are the lines \({{\,\mathrm{Re}\,}}z=\pm 1/2\).
In the same manner, we find that
so
and \(H(S;2i)=\{z \in {\mathbf {\mathsf{{{H}}}}} ^2: |z| \ge 1\}\). To see this geometrically, the geodesic between 2i and \(S(2i)=(1/2)i\) is along the imaginary axis with midpoint at i, and so the perpendicular bisector L(S; 2i) is the unit semicircle.
The containment \((\subseteq )\) in (37.1.8) then follows directly from (37.1.9)–(37.1.10). Conversely, we show the containment \((\supseteq )\) for the interior—since  is closed, this implies the full containment. Let \(z \in {\mathbf {\mathsf{{{H}}}}} ^2\) have \(|{{\,\mathrm{Re}\,}}z \,|<1/2\) and \(|z|>1\), and suppose that
is closed, this implies the full containment. Let \(z \in {\mathbf {\mathsf{{{H}}}}} ^2\) have \(|{{\,\mathrm{Re}\,}}z \,|<1/2\) and \(|z|>1\), and suppose that  ; then there exists \(\gamma \in {{\,\mathrm{PSL}\,}}_2(\mathbb Z )\) such that \(z'=\gamma z\) has \(\rho (z',2i) < \rho (z,2i)\), without loss of generality (replacing \(z'\) by \(Sz'\) or \(Tz'\)) we may suppose \(|{{\,\mathrm{Re}\,}}z' \,| \le 1/2\) and \(|z'| \ge 1\); but then by Lemma 35.1.10, we conclude that \(z'=z\), a contradiction.
; then there exists \(\gamma \in {{\,\mathrm{PSL}\,}}_2(\mathbb Z )\) such that \(z'=\gamma z\) has \(\rho (z',2i) < \rho (z,2i)\), without loss of generality (replacing \(z'\) by \(Sz'\) or \(Tz'\)) we may suppose \(|{{\,\mathrm{Re}\,}}z' \,| \le 1/2\) and \(|z'| \ge 1\); but then by Lemma 35.1.10, we conclude that \(z'=z\), a contradiction.
(Note that the same argument works with \(z_0=ti\) for all \(t \in \mathbb R _{>1}\).)
With this example in hand, we see that Dirichlet domains have quite nice structure. To make this more precise, we upgrade our notion of fundamental set (Definition 34.1.14) as follows.
Definition 37.1.11
A fundamental set  for \(\Gamma \) islocally finite if for each compact set \(K \subset {\mathbf {\mathsf{{{H}}}}} ^2\), we have
for \(\Gamma \) islocally finite if for each compact set \(K \subset {\mathbf {\mathsf{{{H}}}}} ^2\), we have  for only finitely many \(\gamma \in \Gamma \).
for only finitely many \(\gamma \in \Gamma \).
Afundamental domain for \(\Gamma \ \circlearrowright \ {\mathbf {\mathsf{{{H}}}}} ^2\) is a fundamental set  such that
such that  .
.
The first main result of this section is as follows (Theorem 37.5.3).
Theorem 37.1.12
Let \(z_0 \in {\mathbf {\mathsf{{{H}}}}} ^2\) satisfy \({{\,\mathrm{Stab}\,}}_{\Gamma }(z_0)=\{1\}\). Then the Dirichlet domain  is a connected, convex, locally finite fundamental domain for \(\Gamma \) with geodesic boundary.
is a connected, convex, locally finite fundamental domain for \(\Gamma \) with geodesic boundary.
By geodesic boundary we mean that the boundary  is a finite or countable union of geodesic segments. As for the hypothesis: for a compact set \(K \subset {\mathbf {\mathsf{{{H}}}}} ^2\), there are only finitely many points \(z \in K\) such that \({{\,\mathrm{Stab}\,}}_{\Gamma }(z) \ne \{1\}\), indeed there are only finitely many \(\gamma \in \Gamma \) such that \(\gamma K \cap K \ne \emptyset \) (as \(\Gamma \) is discrete), and every such \(\gamma \ne 1\) has at most one fixed point in \({\mathbf {\mathsf{{{H}}}}} ^2\) (Lemma 33.4.6).
is a finite or countable union of geodesic segments. As for the hypothesis: for a compact set \(K \subset {\mathbf {\mathsf{{{H}}}}} ^2\), there are only finitely many points \(z \in K\) such that \({{\,\mathrm{Stab}\,}}_{\Gamma }(z) \ne \{1\}\), indeed there are only finitely many \(\gamma \in \Gamma \) such that \(\gamma K \cap K \ne \emptyset \) (as \(\Gamma \) is discrete), and every such \(\gamma \ne 1\) has at most one fixed point in \({\mathbf {\mathsf{{{H}}}}} ^2\) (Lemma 33.4.6).
2 \(\triangleright \) Ford domains
In this section, we reinterpret Dirichlet domains in the unit disc \({{{\mathbf {\mathsf{{D}}}}}}^2\), as it is more convenient to compute and visualize distances this model. Let \(z_0 \in {\mathbf {\mathsf{{{H}}}}} ^2\). We apply the map (33.7.3)
with \(z_0 \mapsto \phi (z_0)=w_0=0\). Then by (33.7.6),
is an increasing function of |w|.
Example 37.2.2
The Dirichlet domain from Example 37.1.7 looks like Figure 37.2.3, drawn in \({{{\mathbf {\mathsf{{D}}}}}}^2\) (with \(z_0=2i\)).
Let \(\Gamma \le {{\,\mathrm{PSL}\,}}_2(\mathbb R )\) be a Fuchsian group, and (recalling 33.7.8) to ease notation, we identify \(\Gamma \) with \(\Gamma ^{\phi }\). We analogously define a Dirichlet domain  for a Fuchsian group \(\Gamma \) centered at \(w_0 \in {{{\mathbf {\mathsf{{D}}}}}}^2\) and
for a Fuchsian group \(\Gamma \) centered at \(w_0 \in {{{\mathbf {\mathsf{{D}}}}}}^2\) and

if \(\phi (z_0)=w_0\). In particular, the statement of Theorem 37.1.12 applies equally well to  .
.
For simplicity (and without loss of generality), we only consider the case where \(w_0=0\), and then from (37.2.1)

Let
with \(c,d \in \mathbb C \) satisfying \(|d|^2-|c|^2=1\).
37.2.5
We now pursue a tidy description of the set (37.2.4). From (37.2.1), we have \(\rho (w,0) \le \rho (gw,0)\) if and only if
expanding out (37.2.6) and with a bit of patience (Exercise 37.5), we see that this is equivalent to simply
But we can derive this more conceptually, as follows. The hyperbolic metric (Definition 33.7.1) on \({{{\mathbf {\mathsf{{D}}}}}}^2\) is invariant, so
so, by the chain rule,
Therefore
The equivalence (37.2.7) also gives \(\rho (w,0)=\rho (gw,0)\) if and only if  , i.e., g acts as a Euclidean isometry at the point w (preserving the length of tangent vectors in the Euclidean metric). So we are led to make the following definition.
, i.e., g acts as a Euclidean isometry at the point w (preserving the length of tangent vectors in the Euclidean metric). So we are led to make the following definition.
Definition 37.2.8
Theisometric circle of g is
We have \(c=0\) if and only if \(g(0)=0\) if and only if \(g \in {{\,\mathrm{Stab}\,}}_{{{\,\mathrm{PSU}\,}}(1,1)}(0)\), and in this case, \(g w = (\overline{d}/d)w\) with \(|\overline{d}/d|=1\) is rotation about the origin. Otherwise, \(c \ne 0\), and then I(g) is a circle with radius 1/|c| and center \(-d/c \in \mathbb C \).
37.2.9
Summarizing, for all \(g \in {{\,\mathrm{PSU}\,}}(1,1)\), we have
In particular,

This characterization is due to Ford [For72, Theorem 7, §20].
This description of a Dirichlet domain as the intersection of the exteriors of isometric circles is due to Ford, and so we call a Dirichlet domain in \({{{\mathbf {\mathsf{{D}}}}}}^2\) centered at 0 aFord domain, as in Figure 37.2.10.
Remark 37.2.11. In the identification \({\mathbf {\mathsf{{{H}}}}} ^2\rightarrow {{{\mathbf {\mathsf{{D}}}}}}^2\), the preimage of isometric circles corresponds to the corresponding perpendicular bisector; this is the simplification provided by working in \({{{\mathbf {\mathsf{{D}}}}}}^2\) (the map \(\phi \) is a hyperbolic isometry, whereas isometric circles are defined by a Euclidean condition).
3 \(\triangleright \) Generators and relations
Continuing with our third and final survey section focused on Fuchsian groups, we consider applications to the structure of a Fuchsian group \(\Gamma \). For more, see Beardon [Bea95, §9.3] and Katok [Kat92, §3.5].
Let  be a Dirichlet domain centered at \(z_0 \in {\mathbf {\mathsf{{{H}}}}} ^2\). A consequence of the local finiteness of a Dirichlet domain is the following theorem (Theorem 37.4.2).
be a Dirichlet domain centered at \(z_0 \in {\mathbf {\mathsf{{{H}}}}} ^2\). A consequence of the local finiteness of a Dirichlet domain is the following theorem (Theorem 37.4.2).
Theorem 37.3.1
\(\Gamma \) is generated by the set

So by Theorem 37.3.1, to find generators, we must look for “overlaps” in the tessellation provided by  . If
. If  with \(\gamma \in \Gamma \ \smallsetminus \ \{1\}\), then there exists
with \(\gamma \in \Gamma \ \smallsetminus \ \{1\}\), then there exists  such that \(z=\gamma z'\), and hence
such that \(z=\gamma z'\), and hence
(twice applying the defining property of  ), so equality holds and (viz. 37.1.2)
), so equality holds and (viz. 37.1.2)  . Since the boundary of
. Since the boundary of  is geodesic, to understand generators we should organize the matching provided along the geodesic boundary of
is geodesic, to understand generators we should organize the matching provided along the geodesic boundary of  .
.
We will continue to pass between \({\mathbf {\mathsf{{{H}}}}} ^2\) and \({{{\mathbf {\mathsf{{D}}}}}}^2\), as convenient.
37.3.3
Aside is a geodesic segment of positive length of the form  with \(\gamma \in \Gamma \ \smallsetminus \ \{1\}\). If two sides intersect in \({{{\mathbf {\mathsf{{D}}}}}}^2\), the point of intersection is called avertex of
with \(\gamma \in \Gamma \ \smallsetminus \ \{1\}\). If two sides intersect in \({{{\mathbf {\mathsf{{D}}}}}}^2\), the point of intersection is called avertex of  ; equivalently, a vertex is a single point of the form
; equivalently, a vertex is a single point of the form  with \(\gamma ,\gamma ' \in \Gamma \).
with \(\gamma ,\gamma ' \in \Gamma \).
However, we make the following convention (to simplify the arguments below): if  is a maximal geodesic subset of
is a maximal geodesic subset of  and \(\gamma ^2=1\), or equivalently if \(\gamma L = L\), then \(\gamma \) fixes the midpoint of L, and we consider L to be the union of two sides that meet at the vertex equal to the midpoint. The representation of a side as
and \(\gamma ^2=1\), or equivalently if \(\gamma L = L\), then \(\gamma \) fixes the midpoint of L, and we consider L to be the union of two sides that meet at the vertex equal to the midpoint. The representation of a side as  is unique when \(\gamma ^2 \ne 1\).
is unique when \(\gamma ^2 \ne 1\).
Because  is locally finite, there are only finitely many vertices in a compact neighborhood (Exercise 37.7).
is locally finite, there are only finitely many vertices in a compact neighborhood (Exercise 37.7).
Anideal vertex is a point of the closure of  in \({{{\mathbf {\mathsf{{D}}}}}}^{2*}\) that is the intersection of the closure of two sides in \({{{\mathbf {\mathsf{{D}}}}}}^{2*}\), as in Figure 37.3.4.
in \({{{\mathbf {\mathsf{{D}}}}}}^{2*}\) that is the intersection of the closure of two sides in \({{{\mathbf {\mathsf{{D}}}}}}^{2*}\), as in Figure 37.3.4.
37.3.5
Let S denote the set of sides of  . We define a labeled equivalence relation on S by
. We define a labeled equivalence relation on S by
We say that P is aside pairing if P induces a partition of S into pairs, and we denote by G(P) the projection of P to \(\Gamma \). Since \((\gamma ,L,L^*) \in P\) implies \((\gamma ^{-1},L^*,L) \in P\), we conclude that G(P) is closed under inverses.
Lemma 37.3.7
A Dirichlet domain  has a side pairing P.
has a side pairing P.
Proof. Let L be a side with  for a unique \(\gamma \). Recalling the convention in 37.3.3, if \(\gamma ^2 \ne 1\), then equality holds, and
for a unique \(\gamma \). Recalling the convention in 37.3.3, if \(\gamma ^2 \ne 1\), then equality holds, and

so by uniqueness, the equivalence class of L contains only \(L,L^*\). If \(\gamma ^2=1\), then L meets \(\gamma L=L^*\) at the fixed point of \(\gamma \), and again the equivalence class of L contains on \(L,L^*\). In either case, we conclude that P (37.3.6) is a side pairing. \(\square \)
37.3.8
We now provide a standard picture of  in a neighborhood of a point
in a neighborhood of a point  .
.
Because  is locally finite, there is an an open neighborhood of w and finitely many distinct \(\delta _0,\delta _1, \dots , \delta _n \in \Gamma \) with \(\delta _0=1\) such that
is locally finite, there is an an open neighborhood of w and finitely many distinct \(\delta _0,\delta _1, \dots , \delta _n \in \Gamma \) with \(\delta _0=1\) such that  and
and  for all i. Shrinking U if necessary, we may suppose that U contains no vertices of
for all i. Shrinking U if necessary, we may suppose that U contains no vertices of  except possibly for w and intersects no sides of
except possibly for w and intersects no sides of  except those that contain w. Therefore, we have a picture as in Figure 37.3.9.
except those that contain w. Therefore, we have a picture as in Figure 37.3.9.
When \(n=1\), then either w can be either a vertex (fixed point of \(\delta _1\)) or not.
37.3.10
Let \(v=v_1\) be a vertex of  . The standard picture in a neighborhood of v can be reinterpreted as in Figure 37.3.11.
. The standard picture in a neighborhood of v can be reinterpreted as in Figure 37.3.11.
Let \(L_1\) be the side containing \(v_1\) traveling clockwise from the interior. Then by the side pairing (Lemma 37.3.7), there is a paired side \(L_1^*\) with \(L_1^*=\gamma _1 L_1\) and \(\gamma _1 \in G(P)\). (In fact, then  and
and  .) Let \(v_2=\gamma _1 v_1\). Then \(v_2\) is a vertex of
.) Let \(v_2=\gamma _1 v_1\). Then \(v_2\) is a vertex of  , and so is contained in a second side \(L_2\). Continuing in this way, with \(v_{i+1}=\gamma _i v_i\), by local finiteness we find after finitely many steps a final side \(L_m^*\) with next vertex \(v_m=v_1\).
, and so is contained in a second side \(L_2\). Continuing in this way, with \(v_{i+1}=\gamma _i v_i\), by local finiteness we find after finitely many steps a final side \(L_m^*\) with next vertex \(v_m=v_1\).
In terms of the standard picture (Figure 37.3.9), we see that \(\delta _1=\gamma _1^{-1}\) and by induction \(\delta _i=(\gamma _i \cdots \gamma _1)^{-1}\), since \((\gamma _i \cdots \gamma _1)(v_1)=v_{i+1}\). Thus \(\gamma _{i+1}=\delta _{i+1}^{-1}\delta _i\) for \(i=0,\dots ,m-1\). Let \(\delta =\delta _m\). Then \(\delta (v)=v\), and \(\delta \) acts by counterclockwise hyperbolic rotation with fixed point v—and m is the smallest nonzero index with this property. It follows that for all \(0 \le j \le n\), writing \(j=qm+i\) with \(q \ge 0\) and \(0 \le i<m\) we have \(\delta _{j}=\delta _m^q\delta _i\), and in particular that \(m \mid (n+1)\). Similarly,  .
.
Let \(e=(n+1)/m\). Then \(\delta ^e=1\), and we call this relation thevertex cycle relation for v. If \(v'=\gamma v\), then the vertex cycle relation for \(v'\) is the conjugate relation \((\gamma ^{-1} \delta \gamma )^e=\gamma ^{-1} \delta ^e \gamma = 1\). Let R(P) be the set of (conjugacy classes of) cycle relations arising from \(\Gamma \)-orbits of vertices in  .
.
Example 37.3.12
We compute the set R(P) of cycle relations for \(\Gamma ={{\,\mathrm{PSL}\,}}_2(\mathbb Z )\). The two \(\Gamma \)-orbits of vertices for  are represented by i and \(\rho \). The vertex i is a fixed point of \(\delta _1=S\), and we obtain the vertex cycle relation \(S^2=1\), and \(S=S^{-1}\).
are represented by i and \(\rho \). The vertex i is a fixed point of \(\delta _1=S\), and we obtain the vertex cycle relation \(S^2=1\), and \(S=S^{-1}\).
At the vertex \(\rho \), we have a picture as in Figure 37.3.13.
We find that \(\delta _1=T^{-1}\) and \(\delta =\delta _2=T^{-1}S\), and \(e=6/2=3\) so \(\delta ^3=(T^{-1}S)^3=1\). Taking inverses (so \(\delta ^{-1}\) acting instead clockwise), we find the relation \((ST)^3=1\).
Proposition 37.3.14
The set G(P) generates \(\Gamma \) with R(P) a set of defining relations. In other words, the free group on G(P) modulo the normal subgroup generated by the relations R(P) is isomorphic to \(\Gamma \) via the natural evaluation map.
Proof. Let \(\Gamma ^* \le \Gamma \) be the subgroup generated by G(P). By Theorem 37.3.1, we need to show that if  then \(\gamma \in \Gamma ^*\). So let
then \(\gamma \in \Gamma ^*\). So let  with \(\gamma \in \Gamma -\{1\}\). We refer to the standard picture (see 37.3.8); we have \(\gamma =\delta _j\) for some j. For all \(i=0,1,\dots ,n\), the intersection
with \(\gamma \in \Gamma -\{1\}\). We refer to the standard picture (see 37.3.8); we have \(\gamma =\delta _j\) for some j. For all \(i=0,1,\dots ,n\), the intersection  is a side of
is a side of  , so
, so  is a side of
is a side of  , and thus \(\delta _{i+1}^{-1}\delta _i \in G(P)\) is a side pairing element. Since \(\delta _0=1\), by induction we find that \(\delta _i \in \Gamma ^*\) for all i, so \(\gamma = \delta _j \in \Gamma ^*\) as claimed.
, and thus \(\delta _{i+1}^{-1}\delta _i \in G(P)\) is a side pairing element. Since \(\delta _0=1\), by induction we find that \(\delta _i \in \Gamma ^*\) for all i, so \(\gamma = \delta _j \in \Gamma ^*\) as claimed.
We now turn to relations, and we give an algorithmic method for rewriting a relation in terms of the cycle relations. Let \(\gamma _1 \gamma _2 \cdots \gamma _k = 1\) be a relation with each \(\gamma _i \in G(P)\), and let \(z_i=(\gamma _1 \cdots \gamma _i) z_0\) for \(i=1,\dots ,k\). Exactly because \(\gamma _1 \in G(P)\), we have that  and
and  share a side, and since
share a side, and since  is connected, we can draw a path \(z_0 \rightarrow z_1\) through the corresponding side. Continuing in this way, we end up with a path \(z_0 \rightarrow z_k=z_0\), hence a closed loop, as in Figure 37.3.15.
is connected, we can draw a path \(z_0 \rightarrow z_1\) through the corresponding side. Continuing in this way, we end up with a path \(z_0 \rightarrow z_k=z_0\), hence a closed loop, as in Figure 37.3.15.
Let V be the intersection of the \(\Gamma \) orbit of the vertices of  with the interior of the loop; by local finiteness, this intersection is a finite set, and we proceed by induction on its cardinality. The proof boils down to the fact that this loop retracts onto the loops around vertices obtained from cycle relations, as \({\mathbf {\mathsf{{{H}}}}} ^2\) is simply connected.
with the interior of the loop; by local finiteness, this intersection is a finite set, and we proceed by induction on its cardinality. The proof boils down to the fact that this loop retracts onto the loops around vertices obtained from cycle relations, as \({\mathbf {\mathsf{{{H}}}}} ^2\) is simply connected.
If the path from \(z_0 \rightarrow z_1\) crosses the same side as the path \(z_{k-1} \rightarrow z_k=z_0\), then \(z_1=z_{k-1}\) and so \(\gamma _k^{-1}=\gamma _1\), since \({{\,\mathrm{Stab}\,}}_{\Gamma }(z_0)=\{1\}\) (see Figure 37.3.16).
Conjugating the relation by \(\gamma _1\) and repeating if necessary, we may suppose that \(\gamma _k^{-1} \ne \gamma _1\), so \(z_{k-1} \ne z_1\); the set V is conjugated so it remains the same size. In particular, if V is empty, then this shows that the original relation is conjugate to the trivial relation.
Otherwise, the path \(z_0 \rightarrow z_1\) crosses a side and there is a unique vertex v on this side that is interior to the loop (working counterclockwise): see Figure 37.3.17.
The cycle relation \(\delta ^e=1\) at v traces a loop around v, and without loss of generality we may suppose \(\delta ^e=\alpha \gamma _1\) with \(\alpha \) a word in G(P). Therefore, substituting this relation into the starting relation, we obtain a relation \(\gamma _2 \cdots \gamma _k (\delta ^e \alpha )\) with one fewer interior vertex; the result then follows by induction. \(\square \)
In section 37.5, we consider a partial converse to Proposition 37.3.14, due to Poincaré: given a convex hyperbolic polygon with a side pairing that satisfies certain conditions, there exists a Fuchsian group \(\Gamma \) with the given polygon as a fundamental domain.
4 Dirichlet domains
We now consider the construction of Dirichlet fundamental domains in a general context. Let \((X,\rho )\) be a complete, locally compact geodesic space. In particular, X is connected, and by the theorem of Hopf–Rinow (see Theorem 33.2.9), closed balls in X are compact.
Let \(\Gamma \) be a discrete group of isometries acting properly on X. Right from the get go, we prove our first important result: we exhibit generators for a group based on a fundamental set with a basic finiteness property.
Definition 37.4.1
Let \(A \subseteq X\). We say A islocally finite for \(\Gamma \) if for each compact set \(K \subset X\), we have \(\gamma K \cap A \ne \emptyset \) for only finitely many \(\gamma \in \Gamma \).
The value of a locally finite fundamental set is explained by the following theorem.
Theorem 37.4.2
Let  be a locally finite fundamental set for \(\Gamma \). Then \(\Gamma \) is generated by the set
be a locally finite fundamental set for \(\Gamma \). Then \(\Gamma \) is generated by the set

Proof. Let \(\Gamma ^* \le \Gamma \) be the subgroup of \(\Gamma \) generated by the elements (37.4.3). We want to show \(\Gamma ^*=\Gamma \).
For all \(x \in X\), by Theorem 37.4.18, there exists \(\gamma \in \Gamma \) such that  . If there is another \(\gamma ' \in \Gamma \) with
. If there is another \(\gamma ' \in \Gamma \) with  , then
, then

so \(\gamma '\gamma ^{-1} \in \Gamma ^*\) and in particular \(\Gamma ^* \gamma = \Gamma ^* \gamma '\). In this way, we define a map
for all \(\gamma \in \Gamma \) such that  .
.
We now show that f is locally constant. Let \(x \in X\). Since  is locally finite, for every compact neighborhood \(K \ni x\) we can write
is locally finite, for every compact neighborhood \(K \ni x\) we can write  with a finite union, and by shrinking K we may suppose that
with a finite union, and by shrinking K we may suppose that  for all i. In particular, \(f(x)=\Gamma ^* \gamma _i^{-1}\) for any i. But then if \(y \in K\), then
for all i. In particular, \(f(x)=\Gamma ^* \gamma _i^{-1}\) for any i. But then if \(y \in K\), then  for some i, so \(f(y)=\Gamma ^* \gamma _i^{-1} = f(x)\). Thus f is locally constant.
for some i, so \(f(y)=\Gamma ^* \gamma _i^{-1} = f(x)\). Thus f is locally constant.
But X is connected so every locally constant function is in fact constant and therefore f takes only the value \(\Gamma ^*\). Let \(\gamma \in \Gamma \) and let  . Then
. Then
so \(\gamma \in \Gamma ^*\), and the proof is complete. \(\square \)
We now seek a locally finite fundamental set with other nice properties: we will choose in each \(\Gamma \)-orbit the closest points to a fixed point \(x_0 \in X\). So we first must understand the basic local properties of intersections of these half-spaces (as in 37.1.2).
37.4.5
For \(x_1,x_2 \in X\), define the closedLeibniz half-space
If \(x_1=x_2\), then \(H(x_1,x_2)=X\). If \(x_1 \ne x_2\), then \(H(x_1,x_2)\) consists of the set of points as close to \(x_1\) as \(x_2\), so
and
is called thehyperplane bisector (orequidistant hyperplane orseparator) between \(x_1\) and \(x_2\).
Remark 37.4.8. In this generality, unfortunately hyperplane bisectors are not necessarily geodesic (Exercise 37.10).
Definition 37.4.9
A set \(A \subseteq X\) isstar-shaped with respect to \(x_0 \in A\) if for all \(x \in A\), the geodesic between x and \(x_0\) belongs to A.
A set \(A \subseteq X\) that is star-shaped is path connected, so connected.
Lemma 37.4.10
A Leibniz half-plane \(H(x_1,x_2)\) is star-shaped with respect to \(x_1\).
Proof. Let \(x \in H(x_1,x_2)\) and let y be a point along the unique geodesic from x to \(x_1\). Then
If \(y \not \in H(x_1,x_2)\), then \(\rho (x_2,y)<\rho (x_1,y)\), and so
contradicting that \(x \in H(x_1,x_2)\). So \(y \in H(x_1,x_2)\) as desired. \(\square \)
Now let \(x_0 \in X\).
Definition 37.4.11
TheDirichlet domain for \(\Gamma \) centered at \(x_0 \in X\) is

We often abbreviate  .
.
37.4.12
Since \(\rho (\gamma x,x_0)=\rho (x,\gamma ^{-1}x_0)\),

each half-space is closed and star-shaped with respect to \(x_0\), so the same is true of  . In particular,
. In particular,  is connected.
is connected.
A Dirichlet domain satisfies a basic finiteness property, as follows.
Lemma 37.4.13
If \(A \subset X\) is a bounded set, then \(A \subseteq H(\gamma ;x_0)\) for all but finitely many \(\gamma \in \Gamma \).
In particular, for all \(x \in X\) we have \(x \in H(\gamma ;x_0)\) for all but finitely many \(\gamma \in \Gamma \).
Proof. Since A is bounded,
By Theorem 34.5.1, the orbit \(\Gamma x_0\) is discrete and \(\#{{\,\mathrm{Stab}\,}}_\Gamma (x_0)<\infty \); since closed balls are compact by assumption, there are only finitely many \(\gamma \in \Gamma \) such that
and for all remaining \(\gamma \in \Gamma \) and all \(x \in A\),
so \(x \in H(\gamma ;x_0)\), as in Figure 37.4.14.
This concludes the proof.
\(\square \)
37.4.15
Arguing in a similar way as in Lemma 37.4.13, one can show (Exercise 37.8): if K is a compact set, then \(K \cap L(\gamma ;x_0) \ne \emptyset \) for only finitely many \(\gamma \in \Gamma \).
Lemma 37.4.16
We have

It follows from Lemma 37.4.16 that  if and only if there exists \(\gamma \in \Gamma \ \smallsetminus \ {{\,\mathrm{Stab}\,}}_{\Gamma }(x_0)\) such that \(\rho (x,x_0)=\rho (\gamma x,x_0)\).
if and only if there exists \(\gamma \in \Gamma \ \smallsetminus \ {{\,\mathrm{Stab}\,}}_{\Gamma }(x_0)\) such that \(\rho (x,x_0)=\rho (\gamma x,x_0)\).
Proof. Let  , and let \(U \ni x\) be a bounded open neighborhood of x. By Lemma 37.4.13, we have \(U \subseteq H(\gamma ;x_0)\) for all but finitely many \(\gamma \in \Gamma \), so
, and let \(U \ni x\) be a bounded open neighborhood of x. By Lemma 37.4.13, we have \(U \subseteq H(\gamma ;x_0)\) for all but finitely many \(\gamma \in \Gamma \), so

the intersection over finitely many \(\gamma _i \in \Gamma \) with \(\gamma _i \not \in {{\,\mathrm{Stab}\,}}_{\Gamma }(x_0)\) (see Figure 37.4.17).
Thus

The lemma then follows from (37.4.7).\(\square \)
The first main result of this chapter is the following theorem.
Theorem 37.4.18
Let \(x_0 \in X\), and suppose \({{\,\mathrm{Stab}\,}}_{\Gamma }(x_0)=\{1\}\). Then  is a locally finite fundamental set for \(\Gamma \) that is star-shaped with respect to \(x_0\) and whose boundary consists of hyperplane bisectors.
is a locally finite fundamental set for \(\Gamma \) that is star-shaped with respect to \(x_0\) and whose boundary consists of hyperplane bisectors.
Specifically, in a bounded set A, by Lemma 37.4.13

for finitely many \(\gamma _i \in \Gamma \ \smallsetminus \ \{1\}\).
Proof. Abbreviate  . We saw that
. We saw that  is (closed and) star-shaped with respect to \(x_0\) in 37.4.12.
is (closed and) star-shaped with respect to \(x_0\) in 37.4.12.
Now we show that  . Let \(x \in X\). The orbit \(\Gamma x\) is discrete, so the distance
. Let \(x \in X\). The orbit \(\Gamma x\) is discrete, so the distance
is minimized at some point  with \(\gamma \in \Gamma \). Thus
with \(\gamma \in \Gamma \). Thus  contains at least one point from every \(\Gamma \)-orbit, and consequently .
contains at least one point from every \(\Gamma \)-orbit, and consequently .
We now refer to Lemma 37.4.16. Since X is complete, this lemma implies that  . And
. And  for all \(\gamma \in \Gamma \ \smallsetminus \ \{1\}\), because if
for all \(\gamma \in \Gamma \ \smallsetminus \ \{1\}\), because if  with \(\gamma \ne 1\) then
with \(\gamma \ne 1\) then
a contradiction.
Finally, we show that X is locally finite. It suffices to check this for a closed disc \(K \subseteq X\) with center \(x_0\) and radius \(r\in \mathbb R _{\ge 0}\). Suppose that \(\gamma K\) meets  with \(\gamma \in \Gamma \); then by definition there is
with \(\gamma \in \Gamma \); then by definition there is  such that \(\rho (x_0,\gamma ^{-1}x) \le r\). Then
such that \(\rho (x_0,\gamma ^{-1}x) \le r\). Then
Since  , we have \(\rho (x,x_0) \le \rho (\gamma ^{-1}x,x_0) \le r\), so
, we have \(\rho (x,x_0) \le \rho (\gamma ^{-1}x,x_0) \le r\), so
This setup can be seen in Figure 37.4.21.
For the same reason as in Lemma 37.4.13, this can only happen for finitely many \(\gamma \in \Gamma \). \(\square \)
Remark 37.4.22. Dirichlet domains are sometimes also called Voronoi domains.
5 Hyperbolic Dirichlet domains
We now specialize to the case \(X=\mathcal H \) where \(\mathcal H ={\mathbf {\mathsf{{{H}}}}} ^2\) or \(\mathcal H ={{{\mathbf {\mathsf{{H}}}}}}^3\) with volume \(\mu \); then \(\Gamma \) is a Fuchsian or Kleinian group, respectively.
Definition 37.5.1
Afundamental domain for \(\Gamma \ \circlearrowright \ X\) is a connected fundamental set  such that
such that  .
.
(A domain in topology is sometimes taken to be an open connected set; one also sees closed domains, and our fundamental domains are taken to be of this kind.)
We now turn to Dirichlet domains in this context.
37.5.2
In Theorem 37.4.18, the hypothesis that \({{\,\mathrm{Stab}\,}}_{\Gamma }(z_0)=\{1\}\) is a very mild hypothesis. If K is a compact set, then since  is locally finite, the set of points \(z \in K\) with \({{\,\mathrm{Stab}\,}}_{\Gamma }(z) \ne \{1\}\) is a finite set of points when \(\mathcal H ={\mathbf {\mathsf{{{H}}}}} ^2\) and a finite set of points together with finitely many geodesic axes when \(\mathcal H ={{{\mathbf {\mathsf{{H}}}}}}^3\).
is locally finite, the set of points \(z \in K\) with \({{\,\mathrm{Stab}\,}}_{\Gamma }(z) \ne \{1\}\) is a finite set of points when \(\mathcal H ={\mathbf {\mathsf{{{H}}}}} ^2\) and a finite set of points together with finitely many geodesic axes when \(\mathcal H ={{{\mathbf {\mathsf{{H}}}}}}^3\).
In spite of 37.5.2, we prove a slightly stronger and more useful version of Theorem 37.4.18, as follows. If \(\Gamma _0={{\,\mathrm{Stab}\,}}_{\Gamma }(z_0)\) is nontrivial, we modify the Dirichlet domain by intersecting with a fundamental set for \(\Gamma _0\); the simplest way to do this is just to choose another point which is not fixed by an element of \(\Gamma _0\) and intersect.
Theorem 37.5.3
Let \(z_0 \in \mathcal H \), let \(\Gamma _0={{\,\mathrm{Stab}\,}}_{\Gamma }(z_0)\), and let \(u_0 \in \mathcal H \) be such that \({{\,\mathrm{Stab}\,}}_{\Gamma _0}(u_0)=\{1\}\). Then

is a connected, convex, locally finite fundamental domain for \(\Gamma \) with geodesic boundary in \(\mathcal H \).
Proof. Abbreviate

First, we show that  : we have
: we have  , and by Theorem 37.4.18,
, and by Theorem 37.4.18,  is a fundamental set for \(\Gamma _0\) so there exists \(\gamma _0 \in \Gamma _0\) such that
is a fundamental set for \(\Gamma _0\) so there exists \(\gamma _0 \in \Gamma _0\) such that  .
.
Now we show that  is a fundamental set for \(\Gamma \). First we show
is a fundamental set for \(\Gamma \). First we show  . Let \(z \in \mathcal H \), and let \(\gamma \in \Gamma \) be such that \(\rho (\gamma z,z_0)\) is minimal as in (37.4.19). Let \(\gamma _0 \in \Gamma _0\) such that
. Let \(z \in \mathcal H \), and let \(\gamma \in \Gamma \) be such that \(\rho (\gamma z,z_0)\) is minimal as in (37.4.19). Let \(\gamma _0 \in \Gamma _0\) such that  . Then
. Then
so  . And
. And  for all \(\gamma \in \Gamma \ \smallsetminus \ \{1\}\), because if
for all \(\gamma \in \Gamma \ \smallsetminus \ \{1\}\), because if  with \(\gamma \ne 1\), then either \(\gamma \not \in \Gamma _0\) in which case we obtain a contradiction as in (37.4.20), or \(\gamma \in \Gamma _0-\{1\}\) and then we arrive at a contradiction from the fact that
with \(\gamma \ne 1\), then either \(\gamma \not \in \Gamma _0\) in which case we obtain a contradiction as in (37.4.20), or \(\gamma \in \Gamma _0-\{1\}\) and then we arrive at a contradiction from the fact that  is a fundamental set.
is a fundamental set.
We conclude by proving the remaining topological properties of  . We know that
. We know that  is locally finite, since it is the intersection of two locally finite sets. We saw in 37.1.2 that the Leibniz half-spaces in \({\mathbf {\mathsf{{{H}}}}} ^2\) are convex with geodesic boundary, and the same is true in \({{{\mathbf {\mathsf{{H}}}}}}^3\) by Exercise 36.9. It follows that
is locally finite, since it is the intersection of two locally finite sets. We saw in 37.1.2 that the Leibniz half-spaces in \({\mathbf {\mathsf{{{H}}}}} ^2\) are convex with geodesic boundary, and the same is true in \({{{\mathbf {\mathsf{{H}}}}}}^3\) by Exercise 36.9. It follows that  is convex, as the intersection of convex sets. Thus
is convex, as the intersection of convex sets. Thus

is geodesic and measure zero, since \(L(z_0,\gamma ^{-1}z_0)\) intersects a compact set for only finitely many \(\gamma \) by 37.4.15. \(\square \)
6 Poincaré’s polyhedron theorem
Continuing with the notation from the previous section, we now turn to a partial converse for Theorem 37.5.3 for \(\mathcal H \); we need one additional condition. Let  be a convex (finite-sided) hyperbolic polyhedron equipped with a side pairing P.
be a convex (finite-sided) hyperbolic polyhedron equipped with a side pairing P.
37.6.1
First suppose  . For a vertex v of
. For a vertex v of  , let
, let  be the interior angle of
be the interior angle of  at v. We say that
at v. We say that  satisfies the cycle condition if for all vertices v of
satisfies the cycle condition if for all vertices v of  there exists \(e \in \mathbb Z _{>0}\) such that
there exists \(e \in \mathbb Z _{>0}\) such that

Put another way,  satisfies the cycle condition if the sum of the interior angles for a \(\Gamma \)-orbit of vertices as in the standard picture is an integer submultiple of \(2\pi \).
satisfies the cycle condition if the sum of the interior angles for a \(\Gamma \)-orbit of vertices as in the standard picture is an integer submultiple of \(2\pi \).
Now suppose  . Now we work with edges: for an edge \(\ell \) of
. Now we work with edges: for an edge \(\ell \) of  , let
, let  be the interior angle of
be the interior angle of  at \(\ell \). We say that
at \(\ell \). We say that  satisfies the cycle condition if for all edges \(\ell \) of
satisfies the cycle condition if for all edges \(\ell \) of  there exists \(e \in \mathbb Z _{>0}\) such that
there exists \(e \in \mathbb Z _{>0}\) such that

Lemma 37.6.2
Let  be a Dirichlet domain. Then
be a Dirichlet domain. Then  satisfies the cycle condition.
satisfies the cycle condition.
Proof. We explain the case where  ; the case of \({{{\mathbf {\mathsf{{H}}}}}}^3\) is similar. Let v be a vertex of
; the case of \({{{\mathbf {\mathsf{{H}}}}}}^3\) is similar. Let v be a vertex of  . Referring to the standard picture 37.3.8,
. Referring to the standard picture 37.3.8,

In 37.3.10, we proved that \(\delta _m\) acts by hyperbolic rotation around v and has order \(e=(n+1)/m\), and

with  . Combining these two equations, we see that the cycle condition is satisfied. \(\square \)
. Combining these two equations, we see that the cycle condition is satisfied. \(\square \)
37.6.3
There is another condition at certain points at infinity that a fundamental domain must satisfy. We say a point \(z \in {{\,\mathrm{bd}\,}}\mathcal H \) is ainfinite vertex if z lies in the intersection of two faces and is tangent to both. We define a sequence of tangency vertices analogous to the cycle transformations to get aninfinite vertex sequence and ainfinite vertex transformation. We say that the side/face pairing is complete if the tangency vertex transformation is parabolic.
Theorem 37.6.4
(Poincaré polygon theorem). Let  be a convex finite-sided hyperbolic polygon/polyhedron with a side/face-pairing P. Suppose that
be a convex finite-sided hyperbolic polygon/polyhedron with a side/face-pairing P. Suppose that  satisfies the cycle condition and P is complete.
satisfies the cycle condition and P is complete.
Then the group \(\Gamma :=\langle G(P) \rangle \) generated by side/face-pairing elements is a Fuchsian/Kleinian group,  is a fundamental domain for \(\Gamma \), and R(P) forms a complete set of relations for G(P).
is a fundamental domain for \(\Gamma \), and R(P) forms a complete set of relations for G(P).
Proof. Unfortunately, it is beyond the scope of this book to give a complete proof of Theorem 37.6.4. See Epstein–Petronio [EP94, Theorem 4.14] or Ratcliffe [Rat2006, §11.2, §13.5]; our statement is a special case of the theorem by Maskit [Mas71], but see Remark 37.6.5. \(\square \)
Remark 37.6.5. The proof of Poincaré’s theorem [Poi1882, Poi1883] has a bit of a notorious history. From the very beginning, to quote Epstein–Petronio [EP94, §9, p. 164]:
It is clear that Poincaré understood very well what was going on. However, the papers are not easy to read. In particular, the reader of the three-dimensional case is referred to the treatment of the two-dimensional case for proofs; this is fully acceptable for a trail-blazing paper, but not satisfactory in the long term.
There are a number of reasonable published versions of Poincaré’s Theorem in dimension two. Of these, we would single out the version by de Rham [dR71] as being particularly careful and easy to read. Most published versions of Poincaré’s Theorem applying to all dimensions are unsatisfactory for one reason or another.
This sentiment is echoed by Maskit [Mas71], who presents a proof for polygons with an extension to polyhedron, with the opening remark:
There are several published proofs of [Poincaré’s classical] theorem, but there is some question as to their validity; Siegel [Sie65, p. 115] has commented on this and given an apparently valid proof under fairly restrictive conditions. None of the published proofs are as general as they might be, and they all have a convexity condition that is never really used.
This note is an attempt to clarify the situation. The problem and the solution presented below arose during the course of several informal conversations. Present at one or more of these conversations were L. V. Ahlfors, L. Bers, W. Magnus, J. E. McMillan, and B. Maskit.
Epstein and Petronio [EP94, §9, p. 165] then have this to say:
Maskit’s paper contains a nice discussion of completeness, though again it is not a constructive approach. He limits his discussion to hyperbolic space in dimensions two and three. We are not confident that the arguments in the paper are complete. For example, there seems to be an assumption that the quotient of a metric space, such that the inverse image of a point is finite, is metric. This is false, as is shown by identifying x with \(-x\) in \([-1,1]\), provided \(0 \le x < 1\).
Maskit published a book [Mas88] containing an expanded version of the proof for polyhedra, to which Epstein and Petronio [EP94, §9, p. 164] review:
The treatment in [Mas88] is difficult to understand. For example in H.9 on page 75, it is claimed that a metric is defined in a certain way, and this fact is said to be “easy to see”, but it seems to us an essential and non-trivial point, which is not so easy to see, particularly when the group generated by the face-pairings is not discrete. ...The Proposition in IV.1.6 on page 79 of this book is incorrect—a counter-example is given in Example 9.1—because there are no infinite cycles or infinite edges according to the definitions in the book.
7 Signature of a Fuchsian group
As an application of Theorem 37.5.3, we relate area and signature for good orbifolds obtained from Fuchsian groups.
37.7.1
We first recall 34.8.13: a good compact, oriented 2-orbifold X is classified up to homeomorphism by its signature \((g;e_1,\dots ,e_k)\), where g is the genus of the underlying topological surface and the \(e_1,\dots ,e_k\) are the orders of the (necessarily cyclic) nontrivial stabilizer groups. This extends to good orbifolds Y with finitely many points removed: we define the signature \((g;e_1,\dots ,e_k;\delta )\) where \(\delta \ge 0\) is the number of punctures.
Now let \(\Gamma \le {{\,\mathrm{PSL}\,}}_2(\mathbb R )\) be a Fuchsian group such that the quotient \(Y(\Gamma )=\Gamma \backslash {\mathbf {\mathsf{{{H}}}}} ^2\) has finite hyperbolic area \(\mu (Y(\Gamma ))\).
Theorem 37.7.2
(Siegel). Suppose that \(\mu (\Gamma \backslash {\mathbf {\mathsf{{{H}}}}} ^2)\) has finite hyperbolic area. Then every Dirichlet domain  has finitely many sides.
has finitely many sides.
Proof. The proof estimates the contribution to the volume from infinite vertices: for Fuchsian groups, see Siegel [Sie45, p. 716–718], or the expositions of this argument by Gel’fand–Graev–Pyatetskii-Shapiro [GG90, Chapter 1, §1.5] and Katok [Kat92, Theorem 4.1.1]. \(\square \)
37.7.3
By Theorem 37.5.3 and Siegel’s theorem (Theorem 37.7.2), a Dirichlet domain  for \(\Gamma \) is connected, convex, hyperbolic polygon. In particular, there are \(m \in \mathbb Z _{\ge 0}\) vertex cycles, which by 37.3.10 correspond to cyclic stabilizer groups of orders \(e_1,\dots ,e_m \in \mathbb Z _{\ge 1}\) listed so that \(e_1,\dots ,e_k \ge 2\), and finitely many \(\delta \in \mathbb Z _{\ge 0}\) infinite vertex cycles, corresponding to \(\delta \) stabilizer groups that are infinite cyclic.
for \(\Gamma \) is connected, convex, hyperbolic polygon. In particular, there are \(m \in \mathbb Z _{\ge 0}\) vertex cycles, which by 37.3.10 correspond to cyclic stabilizer groups of orders \(e_1,\dots ,e_m \in \mathbb Z _{\ge 1}\) listed so that \(e_1,\dots ,e_k \ge 2\), and finitely many \(\delta \in \mathbb Z _{\ge 0}\) infinite vertex cycles, corresponding to \(\delta \) stabilizer groups that are infinite cyclic.
Proposition 37.7.4
We have
Proof. Let  be a Dirichlet domain for \(\Gamma \) with 2n sides and n finite or infinite vertices. The hyperbolic area of
be a Dirichlet domain for \(\Gamma \) with 2n sides and n finite or infinite vertices. The hyperbolic area of  is given by the Gauss–Bonnet formula 33.6.9: summing vertex cycles using the cycle condition (Lemma 37.6.2), we have
is given by the Gauss–Bonnet formula 33.6.9: summing vertex cycles using the cycle condition (Lemma 37.6.2), we have

The quotient \(\Gamma \backslash {\mathbf {\mathsf{{{H}}}}} ^2\) is a (punctured) oriented topological surface of genus g, with \(k+\delta \) vertices, n edges, and 1 face. By Euler’s formula, we have
so
Therefore

as claimed.\(\square \)
8 The (6, 4, 2)-triangle group
We pause to refresh the quaternionic thread and consider a particularly nice example, showing how quaternion algebras arise naturally in the context of Fuchsian groups.
Consider a hyperbolic triangle T with angles \(\pi /2,\pi /6,\pi /6\) and vertices placed as in Figure 37.8.1.
By symmetry, we may define the side-pairing P as shown in Figure 37.8.1. This polygon satisfies the cycle condition, so by the Poincaré polygon theorem (Theorem 37.6.4), there exists a Fuchsian group \(\Delta \subset {{\,\mathrm{PSL}\,}}_2(\mathbb R )\) generated by the two side pairing elements in P and with fundamental domain T. In this section, we construct this group explicitly and observe some interesting arithmetic consequences.
37.8.2
We seek the position of the vertex \(z \in {\mathbf {\mathsf{{{H}}}}} ^2\) corresponding to \(w \in {{{\mathbf {\mathsf{{D}}}}}}^2\). Zooming in, we obtain the picture as in Figure 37.8.3.
The edge containing w and its complex conjugate is defined by an isometric circle \(|cw+d|=1\) with \(d^2-c^2=1\) and by symmetry \(c,d \in \mathbb R _{>0}\). With the angles as labeled, we find that \(w=(-d+e^{\pi i/12})/c\), and since \(\arg (w)=3\pi /4\) we compute that
so \(c^2=2\cos (\pi /12)\sin (\pi /12)=\sin (\pi /6)=1/2\) thus \(c=1/\sqrt{2}\) and \(d=\sqrt{3/2}\), so this isometric circle is defined by \(|w+\sqrt{3}|^2=2\), and \(w=(-1+i)/(1+\sqrt{3})\). By coincidence, we find that \(z=z_2=(-1+i)/(1+\sqrt{3})=w\) as well. The intersection of this circle with the imaginary axis is the point \(z_3=(\sqrt{3}-1)i/\sqrt{2}\).
The unique element mapping the sides meeting at i is obtained by pulling back rotation by \(-\pi /4\) in the unit disc model; it is given by the matrix
with
and \(\delta _4^4=1 \in {{\,\mathrm{PSL}\,}}_2(\mathbb R )\). From a similar computation, we find that the other side pairing element acting by hyperbolic rotation around \(z_3\) is
and \(\delta _2^2=1 \in {{\,\mathrm{PSL}\,}}_2(\mathbb R )\). We have \((\delta _2\delta _4)(z_4)=\delta _2(z_2)=z_4\), so the element
fixes the vertex \(z_4\), with \(\delta _6(z_1)=(1+\sqrt{-3})/2\) and \(\delta _6^6=1 \in {{\,\mathrm{PSL}\,}}_2(\mathbb R )\). These actions are summarized in Figure 37.8.8.
So recording these cycle relations,
37.8.9
From this setup, we can identify a quaternion algebra obtained from (appropriately scaled) generators of \(\Delta \). We have the characteristic polynomials
To obtain rational traces, and to simplify the presentation a bit further we consider the \(\mathbb Z \)-subalgebra \(B \subseteq {{\,\mathrm{M}\,}}_2(\mathbb R )\) generated by
we have
so as in (22.1.2) with \((a,b,c,u,v,w)=(-3,-2,-1,2,3,0)\), we obtain an order \(\mathcal {O}=\mathbb Z + \mathbb Z i + \mathbb Z j + \mathbb Z k\) of reduced discriminant \(-24+12+18=6\) and with associated ternary quadratic form
37.8.11
We now try to simplify the presentation (37.8.10) as much as possible. This kind of activity is more aesthetics than mathematics, but for this example there is a preferred way of writing the algebra and order (regrettably, not in a good basis) as follows. We write \(i'= i-1\) and \(j'= i(j-3/2 i) = -3i+k+3\) so that now \((i')^2=-1\) and \((j')^2=3\) and \(j'i'=-i'j'\); the remaining basis element of the order in terms of these generators can be taken to be \(k'=(1+i'+j'+i'j')/2=3-i-j+k\).
37.8.12
Throwing away primes from the previous paragraph, we have the algebra \(B :={\displaystyle {\biggl ({\frac{-1,3}{\mathbb{Q }}}\biggr )}}\) of discriminant \({{\,\mathrm{disc}\,}}B=6\) and order
with \(k^2-k-1=0\). (By 23.1.1, since \({{\,\mathrm{discrd}\,}}(\mathcal {O})={{\,\mathrm{disc}\,}}B = 6\), we conclude that \(\mathcal {O}\) is a maximal order in B.)
This algebra came with the embedding
Following the transformations back, we recover the triangle group as a subgroup of \(B^\times /F^\times \) after rescaling to be
and we confirm
so the images of these elements in \(B^\times /F^\times \) generate the group \(\Delta \).
In fact, the elements \(\delta _2,\delta _4,\delta _6 \in N_{B^\times }(\mathcal {O})\) normalize the order \(\mathcal {O}\):
9 Unit group for discriminant 6
In this section, we continue the example from the previous section, specifically the order \(\mathcal {O}\) in 37.8.12. Let
By organized enumeration, we will see that \(\Gamma \) is a Fuchsian group and compute a fundamental domain for the action of \(\Gamma \). We return to this example in section 38.1 as a basic example of the general theory of arithmetic groups arising from quaternion algebras.
37.9.1
Moving to the unit disc via the map \(z \mapsto \phi (z)=w=(z-i)/(z+i)\),
To avoid cumbersome notation, we identify g with \(g^{\phi }\).
The isometric circle of such an element g is a
circle of radius \(\displaystyle {\frac{1}{\sqrt{3(y^2+z^2)}}}\) centered at \(\displaystyle {\frac{-(t+ix)}{\sqrt{3}(y+iz)}}\)
when \(y^2+z^2 \ne 0\); when \(y^2+z^2=0\), the center \(w=0 \in {{{\mathbf {\mathsf{{D}}}}}}^2\) is stabilized, with stabilizer \({{\,\mathrm{Stab}\,}}_{\Gamma }(0)=\langle S \rangle \) where \(S=\begin{pmatrix} i &{} 0 \\ 0 &{} -i \end{pmatrix}\) acts by rotation by \(\pi \). We have

To make a fundamental domain, we need to intersect  with a fundamental domain for \(\langle S \rangle \), and we take the left half-plane. Then
with a fundamental domain for \(\langle S \rangle \), and we take the left half-plane. Then

is a fundamental domain for \(\Gamma \).
37.9.2
We list elements \(g=t+xi+(y+zi)j\) with \(\det g=t^2+x^2-3(y^2+z^2)=1\) and \(t,x,y,z \in \frac{1}{2} \mathbb Z \) whose doubles are all of the same parity. We enumerate them in increasing order of the (square) inverse radius \(y^2+z^2\) (ignoring the factor 3). The case \(y^2+z^2=0\) gives us the stabilizer. By parity, we cannot have \(y^2+z^2=1/4\). If \(y^2+z^2=1/2\) then we find \(y,z = \pm 1/2\) and \(t^2+x^2=5/2\). Sifting out all of the possibilities, we find
All of these elements have the radius of I(g) equal to \(\sqrt{2/3}=0.82\ldots \), and the centers are \(\pm 1.15 \pm 0.57\sqrt{-1}\) and \(\pm 0.57 \pm 1.15\sqrt{-1}\). The corresponding external domain is given in Figure 37.9.3.
37.9.4
If we continue in this way, listing elements according to decreasing radius, we find that all remaining elements have too small a radius to cut away anything extra from the external domain. The corresponding external domain looks like Figure 37.9.5.
It follows that the  is cut out by the left half with side pairing as in Figure 37.9.6.
is cut out by the left half with side pairing as in Figure 37.9.6.
Pulling back to the upper half-plane, we obtain the domain in Figure 37.9.7.
The corresponding tessellation of the upper half-plane looks like the one in Figure 37.9.8.
In addition to this side pairing, we check the cycle relations on the four orbits of vertices: the fixed points \(v_1,v_3,v_5\) and the orbit \(v_2,v_4,v_6\). In conclusion,
and letting \(\gamma _4=\gamma _3\gamma _2\gamma _1=-2i+j\), we can rewrite this more symmetrically as
The order of the stabilizers tell us the angles at each vertex, and so by the Gauss–Bonnet formula (Theorem 33.6.8) we compute that the area is

37.9.10
Finally, the quotient \(X(\Gamma )=\Gamma \backslash {\mathbf {\mathsf{{{H}}}}} ^2\) has the structure of a good complex 1-orbifold (see 34.8.14), a Riemann surface but with finitely many orbifold points. Since the fundamental domain  is compact, via the continuous surjective projection map
is compact, via the continuous surjective projection map  we see that \(X(\Gamma )\) is compact, and
we see that \(X(\Gamma )\) is compact, and  . This orbifold ‘folds’ up to a surface with topological genus 0, so the signature 34.8.13 of \(X(\Gamma )\) is (0; 2, 2, 3, 3): see Figure 37.9.11.
. This orbifold ‘folds’ up to a surface with topological genus 0, so the signature 34.8.13 of \(X(\Gamma )\) is (0; 2, 2, 3, 3): see Figure 37.9.11.
We have seen that the norm 1 group contains the (2, 4, 6)-triangle group \(\Delta \), so we have a map \(X(\Gamma )\rightarrow X(\Delta ) = \Delta \backslash {\mathbf {\mathsf{{{H}}}}} ^2\); by Gauss–Bonnet, we have
we see
as is visible from Figure 37.9.12 for \(\Gamma {\mathop {\le }\limits ^{4}} \Delta \).
Remark 37.9.13. The discriminant 6 quaternion algebra has been a favorite to study, and the fundamental domain described above is also given by e.g. Alsina–Bayer [AB2004, §5.5.2] and Kohel–Verrill [KV2003, §5.1]. We return to this example in section 43.2 in the context of abelian surfaces with quaternionic multiplication.
10 Exercises
-
1.
Let \(\Gamma ={{\,\mathrm{PSL}\,}}_2(\mathbb Z )\). Describe the Dirichlet domain
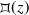 for an arbitrary \(z \in {\mathbf {\mathsf{{{H}}}}} ^2\) with \({{\,\mathrm{Im}\,}}z > 1\).
for an arbitrary \(z \in {\mathbf {\mathsf{{{H}}}}} ^2\) with \({{\,\mathrm{Im}\,}}z > 1\). -
2.
Let \(\Gamma ={{\,\mathrm{PSL}\,}}_2(\mathbb Z [i])\) (cf. section 36.6). Show that
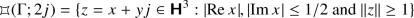
and that
$$ {{\,\mathrm{Stab}\,}}_{\Gamma }(2j)=\left\langle \begin{pmatrix} i &{} 0 \\ 0 &{} -i \end{pmatrix} \right\rangle \simeq \mathbb Z /2\mathbb Z $$so
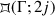 is a union of two copies of a fundamental set for \(\Gamma \).
is a union of two copies of a fundamental set for \(\Gamma \). -
3.
Let \(\Gamma \) be the cyclic Fuchsian group generated by the isometry \(z \mapsto 4z\), represented by \(\begin{pmatrix} 2 &{} 0 \\ 0 &{} 1/2 \end{pmatrix} \in {{\,\mathrm{PSL}\,}}_2(\mathbb R )\). Give an explicit description of the Dirichlet domain
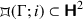 and its image
and its image 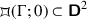 with \(i \mapsto 0\).
with \(i \mapsto 0\). -
4.
Let \(g=\begin{pmatrix} a &{} b \\ c &{} d \end{pmatrix} \in {{\,\mathrm{PSL}\,}}_2(\mathbb R )\) satisfy \(gi \ne i\). Let H be the perpendicular bisector between i and gi.
-
(a)
Show that \(\Vert g\Vert ^2 > 2\).
-
(b)
Under the map \({\mathbf {\mathsf{{{H}}}}} ^2\rightarrow {{{\mathbf {\mathsf{{D}}}}}}^2\) taking \(i \mapsto 0\), show that the perpendicular bisector between i and gi is the isometric circle \(I(g^{-1})\) inside \({{{\mathbf {\mathsf{{D}}}}}}^2\).
-
(c)
Show that H is the half-circle of square radius \(\displaystyle {\frac{\Vert g\Vert ^2-2}{(c^2+d^2-1)^2}}\) centered at \(\displaystyle {\frac{ac+bd}{c^2+d^2-1}} \in \mathbb R \), where \(\Vert g\Vert ^2=a^2+b^2+c^2+d^2\). [Hint: as a check along the way, H is described by the equation \(|(d-ic)z+i(a+ib) \,|=|z+i \,|\).]
-
(a)
-
5.
Let
$$\begin{aligned} g=\begin{pmatrix} \overline{d} &{} \overline{c} \\ c &{} d \end{pmatrix} \in {{\,\mathrm{PSU}\,}}(1,1) \ \circlearrowright \ {{{\mathbf {\mathsf{{D}}}}}}^2\end{aligned}$$with \(c,d \in \mathbb C \) satisfying \(|d|^2-|c|^2=1\). Show directly that \(|gw|=|w|\) for \(w \in {{{\mathbf {\mathsf{{D}}}}}}^2\) if and only if
$$\begin{aligned} |cw+d \,|=1 \end{aligned}$$by expanding out and simplifying.
-
6.
Show that for all \(g \in {{\,\mathrm{PSU}\,}}(1,1)\), we have \(g I(g) = I(g^{-1})\), where I(g) is the isometric circle of g. (Equivalently, show that if \(g \in {{\,\mathrm{PSL}\,}}_2(\mathbb R )\) that \(g L(g;z_0) = L(g^{-1};z_0)\) for all \(z_0 \in {\mathbf {\mathsf{{{H}}}}} ^2\).)
- \(\triangleright \) 7.:
-
Let
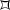 be a Dirichlet domain for a Fuchsian group \(\Gamma \). Show that in every compact set, there are only finitely many sides and finitely many vertices of
be a Dirichlet domain for a Fuchsian group \(\Gamma \). Show that in every compact set, there are only finitely many sides and finitely many vertices of 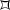 .
.
-
8.
Let \(\Gamma \) be a discrete group of isometries acting properly on a locally compact, complete metric space X, and let \(x_0 \in X\). Recall the definition of \(H(\gamma ;x_0)\) (37.4.6) for \(\gamma \in \Gamma \) and \(L(\gamma ;z_0)={{\,\mathrm{bd}\,}}H(\gamma ;z_0)\). Show that if K is a compact set, then \(K \cap L(\gamma ;x_0) \ne \emptyset \) for only finitely many \(\gamma \in \Gamma \).
-
9.
Extend Theorem 37.4.18 as follows. Let \((X,\rho )\) be a complete, locally compact geodesic space, let \(\Gamma \) be a discrete group of isometries acting properly on X. Let \(x_0 \in X\), let \(\Gamma _0={{\,\mathrm{Stab}\,}}_{\Gamma }(x_0)\), and let \(u_0 \in X\) be such that \({{\,\mathrm{Stab}\,}}_{\Gamma _0}(u_0)=\{1\}\). Show that \(\Gamma _0\) is a discrete group of isometries acting properly on X, and
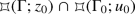
is a locally finite fundamental set for \(\Gamma \) that is star-shaped with respect to \(x_0\) and whose boundary consists of hyperplane bisectors.
-
10.
Consider the egg of revolution, a surface of revolution obtained from convex curves with positive curvature as in Figure 37.9.14.
An egg of revolution has the structure of a geodesic space with the induced metric from \(\mathbb R ^3\). Show that the separator between the top and bottom, a circle of revolution, is not geodesic. [In fact, Clairaut’s relation shows that the geodesic joining two points in the same circle of revolution above crest in the x-axis never lies in this circle of revolution.]
-
11.
In this exercise, we consider a Fuchsian group constructed from a regular quadrilateral.
-
(a)
Show that for every \(e \ge 2\), there exists a regular (equilateral and equiangular) quadrilateral
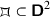 , unique up to isometry, with interior angle \(\pi /(2e)\).
, unique up to isometry, with interior angle \(\pi /(2e)\).Conclude from Poincaré’s theorem that there is a Fuchsian group, unique up to conjugation in \({{\,\mathrm{PSL}\,}}_2(\mathbb R )\), with fundamental domain
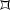 and side pairing as in Figure 37.9.15.
and side pairing as in Figure 37.9.15. -
(b)
Give a presentation for this group for all \(e \ge 2\), and find explicit matrix generators for the special case when \(e=2\).
-
(a)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
This chapter is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, duplication, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, a link is provided to the Creative Commons license and any changes made are indicated.The images or other third party material in this chapter are included in the work's Creative Commons license, unless indicated otherwise in the credit line; if such material is not included in the work's Creative Commons license and the respective action is not permitted by statutory regulation, users will need to obtain permission from the license holder to duplicate, adapt or reproduce the material.
Copyright information
© 2021 The Author(s)
About this chapter
Cite this chapter
Voight, J. (2021). Fundamental domains. In: Quaternion Algebras. Graduate Texts in Mathematics, vol 288. Springer, Cham. https://doi.org/10.1007/978-3-030-56694-4_37
Download citation
DOI: https://doi.org/10.1007/978-3-030-56694-4_37
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-56692-0
Online ISBN: 978-3-030-56694-4
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)
















 is locally finite and star-shaped
is locally finite and star-shaped












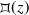 for an arbitrary
for an arbitrary 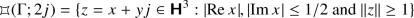
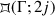 is a union of two copies of a fundamental set for
is a union of two copies of a fundamental set for 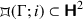 and its image
and its image 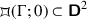 with
with 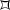 be a Dirichlet domain for a Fuchsian group
be a Dirichlet domain for a Fuchsian group 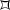 .
.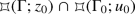
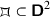 , unique up to isometry, with interior angle
, unique up to isometry, with interior angle 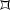 and side pairing as in Figure
and side pairing as in Figure 
