Abstract
In this chapter, we extend the notions introduced for the hyperbolic plane to hyperbolic space in three dimensions; we follow essentially the same outline, and so our exposition is similarly brief.
You have full access to this open access chapter, Download chapter PDF
In this chapter, we extend the notions introduced for the hyperbolic plane to hyperbolic space in three dimensions; we follow essentially the same outline, and so our exposition is similarly brief.
1 Hyperbolic space
A general, encyclopedic reference for hyperbolic geometry is the book by Ratcliffe [Rat2006]. For further reference, see also Elstrodt–Grunewald–Mennicke [EGM98, Chapter 1], Iversen [Ive92, Chapter VIII], and Marden [Mard2007].
Definition 36.1.1
The upper half-space is the set
Hyperbolic space is the set \({\mathbf {\mathsf{{H}}}}^3\) equipped with the metric induced by the hyperbolic length element
36.1.2
The space \({\mathbf {\mathsf{{H}}}}^3\) is the unique three-dimensional (connected and) simply connected Riemannian manifold with constant sectional curvature \(-1\). The volume element corresponding to the hyperbolic length element is accordingly
36.1.3
A vertical half-plane in hyperbolic space is a set of points with y arbitrary and the coordinate x confined to a line in \(\mathbb C \). The hyperbolic length element restricted to every vertical half-plane is (equivalent to) the hyperbolic length element on the hyperbolic plane. Therefore, \({\mathbf {\mathsf{{H}}}}^3\) contains many isometrically embedded copies of \({\mathbf {\mathsf{{H}}}}^2\).
36.1.4
The sphere at infinity is the set
(analogous to the circle at infinity for \({\mathbf {\mathsf{{H}}}}^2\)), with the image of \(\mathbb C \) corresponding to the locus of points with \(t=0\). We then define the completed upper half-space to be
The topology on \({\mathbf {\mathsf{{H}}}}^{3*}\) is defined by taking a fundamental system of neighborhoods of the point at \(\infty \) to be sets of the form
for \(M>0\), and the open balls tangent to \(z \in \mathbb C \) together with z.
36.1.5
The metric space \({\mathbf {\mathsf{{H}}}}^3\) is complete, and the topology on \({\mathbf {\mathsf{{H}}}}^3\) is the same as the topology induced by the Euclidean metric.
The geodesics in \({\mathbf {\mathsf{{H}}}}^3\) are the Euclidean hemicircles orthogonal to \(\mathbb C \) and vertical half-lines: every two points lie in a vertical hyperbolic plane (see 36.1.3), so this statement can be deduced from the case of the hyperbolic plane. (Alternatively, by applying an element of \({{\,\mathrm{PSL}\,}}_2(\mathbb C )\) it is enough to show that the vertical axis \(Z=\{(0,y):y>0\}\) is a geodesic, and arguing as in (33.5.4) we obtain the result.) Accordingly, \({\mathbf {\mathsf{{H}}}}^3\) is a uniquely geodesic space.
36.1.6
Just as in distinct points determine a geodesic, so do three distinct points determine a geodesic plane, the union of all geodesics through the third point and a point on the geodesic between the other two (the choice taken arbitrarily). In a geodesic plane, the geodesic between two points in the plane is contained in the plane. By the preceding paragraph, the geodesic planes in \({\mathbf {\mathsf{{H}}}}^3\) are the Euclidean hemispheres orthogonal to \(\mathbb C \) and the vertical half-planes, as in Figure 36.1.7.
2 Isometries
Analogous to the case of \({\mathbf {\mathsf{{H}}}}^2\), with orientation-preserving isometries given by \({{\,\mathrm{PSL}\,}}_2(\mathbb R )\) acting by linear fractional transformations, in this section we identify the isometries of hyperbolic space \({\mathbf {\mathsf{{H}}}}^3\) as coming similarly from \({{\,\mathrm{PSL}\,}}_2(\mathbb C )\).
36.2.1
The group \({{\,\mathrm{PSL}\,}}_2(\mathbb C )\) acts on the sphere at infinity \(\mathbb P ^1(\mathbb C )\) by linear fractional transformations. We extend this action to \({\mathbf {\mathsf{{H}}}}^3\) (with almost the same definition!) as follows. We identify
where we recall that \(jx=\overline{x}j\) for \(x \in \mathbb C =\mathbb R + \mathbb R i \subseteq \mathbb H \). We then define the action map
for \(g=\begin{pmatrix} a &{} b \\ c &{} d \end{pmatrix} \in {{\,\mathrm{SL}\,}}_2(\mathbb C )\). If \(z=x+yj\), then in coordinates (Exercise 36.3)
where
Therefore the image of this map lies in \({\mathbf {\mathsf{{H}}}}^3\). (Compare this formula with the action of \({{\,\mathrm{SL}\,}}_2(\mathbb R )\) in (33.3.8).)
Lemma 36.2.4
The map (36.2.2) defines a group action of \({{\,\mathrm{SL}\,}}_2(\mathbb C )\) on  .
.
Proof We define the quaternionic projective line to be the set
under the equivalence relation \((\alpha ,\beta )\sim (\alpha \gamma ,\beta \gamma )\) for \(\gamma \in \mathbb H ^\times \), and we denote by \((\alpha :\beta ) \in \mathbb P ^1(\mathbb H )\) the equivalence class of \((\alpha ,\beta )\). We verify that the group \({{\,\mathrm{SL}\,}}_2(\mathbb C )\) acts on \(\mathbb P ^1(\mathbb H )\) by
the left action of \({{\,\mathrm{SL}\,}}_2(\mathbb C )\) commutes with the right action of \(\mathbb H ^\times \). The restriction of this action to \({\mathbf {\mathsf{{H}}}}^3\hookrightarrow \mathbb P ^1(\mathbb H )\) by \(z \mapsto (z:1)\) is
as above. \(\square \)
We now show that \({{\,\mathrm{PSL}\,}}_2(\mathbb C )\) acts on \({\mathbf {\mathsf{{H}}}}^3\) by isometries. This can be verified directly by the formula, with some effort; we prefer to verify this on a convenient set of generators, and so we are first led already to the following decomposition of \({{\,\mathrm{SL}\,}}_2(\mathbb C )\) (cf. Proposition 33.4.2).
36.2.5
Let
We have \(K={{\,\mathrm{Stab}\,}}_{{{\,\mathrm{SL}\,}}_2(\mathbb C )}(j)\): from (36.2.3), we see that \(gj=(aj+b)(cj+d)^{-1}\) if and only if \(|c \,|^2+|d \,|^2=1\) and \(a\overline{c}+b\overline{d}=0\); plugging the first equation into the second, and using \(ad-bc=1\) gives \(a=\overline{d}\) and then \(b=-\overline{c}\).
Letting \(z=x+yj\), the other elements act as:
Lemma 36.2.7
(Iwasawa decomposition). The multiplication map gives a homeomorphism
Proof We apply the same method as in the proof of Proposition 33.4.2. For surjectivity, we let \(z=g(j)=x+yj\), let \(n_g=\begin{pmatrix} 1 &{} -x \\ 0 &{} 1 \end{pmatrix} \in N\) so that \((n_gg)(j)=yj\); then let \(a_g=\begin{pmatrix} 1/\sqrt{y} &{} 0 \\ 0 &{} \sqrt{y} \end{pmatrix} \in A\), so \((a_gn_gg)(j)=j\) and \(a_gn_g g \in {{\,\mathrm{Stab}\,}}_{{{\,\mathrm{SL}\,}}_2(\mathbb C )}(j)=K\). \(\square \)
Lemma 36.2.8
The group \({{\,\mathrm{SL}\,}}_2(\mathbb C )\) is generated by the subgroups A, N, and the element \(\begin{pmatrix} 0 &{} -1 \\ 1 &{} 0 \end{pmatrix}\), which acts on  by
by
where \(\Vert z \Vert ^2 = {{\,\mathrm{nrd}\,}}(z)=|x \,|^2+y^2\) for \(z=x+yj\).
Proof The proof is identical to the one in Lemma 33.4.4. \(\square \)
Remark 36.2.10. In fact, the generators \(\begin{pmatrix} a &{} 0 \\ 0 &{} 1/a \end{pmatrix}\) are redundant, but we will not use this fact here.
We are now ready to investigate the consequences of this decomposition for the geometry of hyperbolic space.
Theorem 36.2.11
The map (36.2.2) defines a faithful, transitive action of \({{\,\mathrm{PSL}\,}}_2(\mathbb C )\) on  by isometries.
by isometries.
Proof We use the generators in Lemma 36.2.8. The fact that the action is faithful follows directly. For transitivity, we show that \({\mathbf {\mathsf{{H}}}}^3\) is the orbit of j. If \(z=x+yj \in {\mathbf {\mathsf{{H}}}}^3\) then we first apply a translation \(\begin{pmatrix} 1 &{} -x \\ 0 &{} 1 \end{pmatrix}\) to reduce to the case \(z=yj\) and then reduce to the case of the hyperbolic plane.
Next, we show that \({{\,\mathrm{PSL}\,}}_2(\mathbb C ) \hookrightarrow {{\,\mathrm{Isom}\,}}^+({\mathbf {\mathsf{{H}}}}^3)\). Verification that \(\mathrm d {g(s)}=\mathrm d {s}\) for g a generator in one of the first two cases of Lemma 36.2.8 is immediate, from the definition of the metric; the third case can be checked directly (Exercise 36.4). Orientation is preserved in each case. \(\square \)
36.2.12
The group \({{\,\mathrm{PSL}\,}}_2(\mathbb C )\) acts transitively on geodesics and consequently on pairs of points at a fixed distance: by the transitive action of \({{\,\mathrm{PSL}\,}}_2(\mathbb C )\) on \({\mathbf {\mathsf{{H}}}}^3\), every point can be mapped to j; and applying an element of \({{\,\mathrm{Stab}\,}}_{{{\,\mathrm{SL}\,}}_2(\mathbb C )}{j}={{\,\mathrm{SU}\,}}(2)\), every other point u can be brought to tj with \(t \ge 1\), with \(\log t=\rho (j,u)\) by the distance in the hyperbolic plane. It follows that
by verifying (36.2.13) in the special case where \(z=j\) and \(z'=yj\) with \(y>0\), and then using the preceding transitive action and the fact that the right-hand side of (36.2.13) is invariant under the action of \({{\,\mathrm{SL}\,}}_2(\mathbb C )\), verified again using the generators in Lemma 36.2.8.
Theorem 36.2.14
We have

and

where the nontrivial element of \(\mathbb Z /2\mathbb Z \) acts by complex conjugation on \({{\,\mathrm{PSL}\,}}_2(\mathbb C )\) and \((z,t) \mapsto (\overline{z},t)\) on \({\mathbf {\mathsf{{H}}}}^3\).
Proof We argue as in Theorem 33.5.5. Let \(\phi \in {{\,\mathrm{Isom}\,}}({\mathbf {\mathsf{{H}}}}^3)\), and let
Then Z is a geodesic (see 36.1.5), so \(\phi (Z)\) is also a geodesic. By transitivity, there exists an isometry \(g \in {{\,\mathrm{PSL}\,}}_2(\mathbb C )\) that maps \(\phi (j)\) back to j, and we may suppose without loss of generality that \(\phi (j)=j\), and arguing as in the case of \({\mathbf {\mathsf{{H}}}}^2\) we may suppose in fact that \(\phi \) fixes each point of Z. Let \(\mathcal H =\mathbb R + \mathbb R j \subseteq {\mathbf {\mathsf{{H}}}}^3\). Then \(\mathcal H \) is a geodesic half-plane containing Z, so \(\phi (\mathcal H )\) is as well and must be a vertical half-plane. The isometric rotation \(\begin{pmatrix} e^{i\theta } &{} 0 \\ 0 &{} e^{-i\theta } \end{pmatrix}\) fixes Z, and applying such a rotation we may suppose further that \(\phi \) fixes \(\mathcal H \).
Now let \(z=x+yj\) and \(\phi (z)=z'=x'+y'j\). Let \(r+sj \in \mathcal H \). Then
so from (36.2.13)
letting \(s \rightarrow \infty \) we find that \(y=y'\) and \(|x-r \,|=|x'-r \,|\) for all \(r \in \mathbb R \), thus \({{\,\mathrm{Re}\,}}x={{\,\mathrm{Re}\,}}x'\) and \({{\,\mathrm{Im}\,}}x=\pm {{\,\mathrm{Im}\,}}x'\). By continuity, the sign is determined uniquely by g, and we conclude that either \(g(z)=z\) or \(g(z)=\overline{x}+yj\), as claimed. \(\square \)
36.2.17
The isometry group \({{\,\mathrm{PSL}\,}}_2(\mathbb C )\) also admits a ‘purely geometric’ definition via the Poincaré extension, as follows.
An element \(g \in {{\,\mathrm{SL}\,}}_2(\mathbb C )\) as a Möbius transformation, induces a biholomorphic map of the Riemann sphere \(\mathbb P ^1(\mathbb C )=\mathbb C \cup \{\infty \}\). This map can be represented as a composition of an even number (at most four) inversions in circles in \(\mathbb P ^1(\mathbb C )\), or circles and lines in \(\mathbb C \) (Exercise 36.2). We have identified \(\mathbb P ^1(\mathbb C )={{\,\mathrm{bd}\,}}{\mathbf {\mathsf{{H}}}}^3\) as the boundary, and for each circle in \(\mathbb P ^1(\mathbb C )\) there is a unique hemisphere in \({\mathbf {\mathsf{{H}}}}^3\) which intersects \({{\,\mathrm{bd}\,}}{\mathbf {\mathsf{{H}}}}^3\) in this circle; if this circle is a line, then we take a vertical half-plane. We then lift the action of \(g \in {{\,\mathrm{PSL}\,}}_2(\mathbb C )\) one inversion at a time with respect to the corresponding hemisphere or half-plane. It turns out that the action of this product does not depend on the choice of the circles.
To verify that \({{\,\mathrm{PSL}\,}}_2(\mathbb C )\) acts by isometries, we need to know that inversion in a hemisphere or vertical half-plane is an isometry of \({\mathbf {\mathsf{{H}}}}^3\); after observing that the first two types of generators in Lemma 36.2.8 (stretching and translating) are isometries, one reduces to the case of checking that inversion in the unit hemisphere, defined by
is an isometry; and this boils down to the same calculation as requested in Exercise 36.4.
36.2.18
We have a similar classification of isometries of \({\mathbf {\mathsf{{H}}}}^3\) as in the case of \({\mathbf {\mathsf{{H}}}}^2\) as follows. Let \(g \in {{\,\mathrm{PSL}\,}}_2(\mathbb C )\).
-
(i)
If \(\pm {{\,\mathrm{Tr}\,}}(g) \in (-2,2)\), then g is elliptic: it has two distinct fixed points in \({{\,\mathrm{bd}\,}}{\mathbf {\mathsf{{H}}}}^3\) and fixes every point in the geodesic between them, called its axis, acting by (hyperbolic) rotation around its axis.
-
(ii)
If \(\pm {{\,\mathrm{Tr}\,}}(g) \in \mathbb R \smallsetminus [-2,2]\), then g is hyperbolic; if \(\pm {{\,\mathrm{Tr}\,}}(g) \in \mathbb C \setminus \mathbb R \), then g is loxodromic. (Some authors combine these two cases.) In these cases, g has two fixed points in \({{\,\mathrm{bd}\,}}{\mathbf {\mathsf{{H}}}}^3\) and the line through these two points is stabilized, and g has no fixed point in \({\mathbf {\mathsf{{H}}}}^3\).
-
(iii)
Finally and otherwise, if \(\pm {{\,\mathrm{Tr}\,}}(g) = \pm 2\), then g is parabolic: it has a unique fixed point in \({{\,\mathrm{bd}\,}}{\mathbf {\mathsf{{H}}}}^3\) and no fixed point in \({\mathbf {\mathsf{{H}}}}^3\).
3 Unit ball, Lorentz, and symmetric space models
Definition 36.3.1
The hyperbolic unit ball is the (open) unit disc
equipped with the hyperbolic metric
and volume
The sphere at infinity is the boundary
36.3.5
The maps

define a conformal equivalence between \({\mathbf {\mathsf{{H}}}}^3\) and \({\mathbf {\mathsf{{D}}}}^3\) with \(j \mapsto \phi (j)=0\). The hyperbolic metric on \({\mathbf {\mathsf{{D}}}}^2\) is the pushforward of (induced from) the hyperbolic metric on \({\mathbf {\mathsf{{H}}}}^3\) via the identification (36.3.5). We find that
In the unit ball model, the geodesics are intersections of \({\mathbf {\mathsf{{D}}}}^3\) of Euclidean circles and straight lines orthogonal to the sphere at infinity, and similarly geodesic planes are intersections of \({\mathbf {\mathsf{{D}}}}^3\) with Euclidean spheres and Euclidean planes orthogonal to the sphere at infinity.
36.3.7
The isometries of \({\mathbf {\mathsf{{D}}}}^3\) are obtained by pushforward from \({\mathbf {\mathsf{{H}}}}^3\). Explicitly, we first identify
We then define the involution
and the group
We find that
with \(\phi \) as in 36.3.5. The group \({{\,\mathrm{SU}\,}}_2(\mathbb H ,{}^*)\) acts on \({\mathbf {\mathsf{{D}}}}^3\) by
36.3.11
Finally, there is the Lorentz model
with
and orientation-preserving isometries given by the subgroup \({{\,\mathrm{SO}\,}}^+(3,1) \le {{\,\mathrm{SO}\,}}(3,1)\) of elements mapping \({\mathbf {\mathsf{{L}}}}^3\) to itself. The relationship between the Lorentz model and the upper half-space model relies on the exceptional isomorphism of Lie algebras \(\mathfrak s \mathfrak o _{3,1} \simeq \mathfrak s \mathfrak l _{2,\mathbb C }\) and the double cover \({{\,\mathrm{SL}\,}}_2(\mathbb C ) \rightarrow {{\,\mathrm{SO}\,}}^+(3,1)\).
To conclude, we find the symmetric space model of \({\mathbf {\mathsf{{H}}}}^3\), analogous to section 34.6.
36.3.13
The group \(G :={{\,\mathrm{SL}\,}}_2(\mathbb C )\) has the structure of a metric space induced from the usual structure on \({{\,\mathrm{M}\,}}_2(\mathbb C ) \simeq \mathbb C ^4\). Since G acts transitively on \({\mathbf {\mathsf{{H}}}}^3\), and the stabilizer of j is \(K={{\,\mathrm{SU}\,}}(2)\),
from the Iwasawa decomposition (Lemma 36.2.7), there is a homeomorphism
From the identity
for \(g \in {{\,\mathrm{SL}\,}}_2(\mathbb C )\), proven in the same way as (34.6.5), the map (36.3.14) is a homeomorphism, and even an isometry under the explicit reparametrization (36.3.15) of the metric.
Remark 36.3.16. Similar statements about the unit tangent bundle hold for \({{\,\mathrm{PSL}\,}}_2(\mathbb C )\) in place of \({{\,\mathrm{PSL}\,}}_2(\mathbb R )\), as in 33.8.2.
Remark 36.3.17. More generally, one defines hyperbolic upper half-space
The space \({\mathbf {\mathsf{{H}}}}^n\) is a uniquely geodesic space and a model for hyperbolic n -space. The geodesics in \({\mathbf {\mathsf{{H}}}}^n\) are orthocircles, and via a conformal map. The upper half-space maps isometrically to the (open) unit ball model
and the hyperboloid model
with
These models (and more) are introduced and compared in Cannon–Floyd–Kenyon–Parry [CFKP97], and treated in detail in the works by Benedetti–Petronio [BP92] and Ratcliffe [Rat2006].
Hyperbolic n-space \({\mathbf {\mathsf{{H}}}}^n\) also admits a symmetric space description, as follows. The group of isometries of \({\mathbf {\mathsf{{H}}}}^n\) is \({{\,\mathrm{SO}\,}}(n,1)\), and the subgroup of orientation-preserving isometries is \({{\,\mathrm{SO}\,}}^+(n,1)\), the component of \({{\,\mathrm{SO}\,}}(n,1)\) containing the identity matrix. The stabilizer of every point in \({\mathbf {\mathsf{{H}}}}^n\) is conjugate to \({{\,\mathrm{SO}\,}}(n)\) (rotation around the origin in the unit ball model, with the fixed point at the origin), and it follows that
4 Bianchi groups and Kleinian groups
Theorem 36.4.1
Let \(G :={{\,\mathrm{PSL}\,}}_2(\mathbb C )\) and let \(\Gamma \le G\) be a subgroup. Then the following are equivalent:
-
(i)
\(\Gamma \) is discrete (with the subspace topology);
-
(ii)
For all
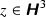 , we have \(\#{{\,\mathrm{Stab}\,}}_\Gamma (z)<\infty \) and there exists an open neighborhood \(U \ni z\) such that \(\gamma U \cap U \ne \emptyset \) implies \(\gamma \in {{\,\mathrm{Stab}\,}}_\Gamma (z)\);
, we have \(\#{{\,\mathrm{Stab}\,}}_\Gamma (z)<\infty \) and there exists an open neighborhood \(U \ni z\) such that \(\gamma U \cap U \ne \emptyset \) implies \(\gamma \in {{\,\mathrm{Stab}\,}}_\Gamma (z)\); -
(iii)
For all compact subsets
 , we have \(K \cap \gamma K \ne \emptyset \) for only finitely many \(\gamma \in \Gamma \); and
, we have \(K \cap \gamma K \ne \emptyset \) for only finitely many \(\gamma \in \Gamma \); and -
(iv)
For all
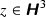 , the orbit
, the orbit 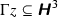 is discrete and \(\#{{\,\mathrm{Stab}\,}}_\Gamma (z)<\infty \).
is discrete and \(\#{{\,\mathrm{Stab}\,}}_\Gamma (z)<\infty \).
Moreover, if these equivalent conditions hold, then the quotient \(\Gamma \backslash {\mathbf {\mathsf{{H}}}}^3\) is Hausdorff, and the quotient map \(\pi :{\mathbf {\mathsf{{H}}}}^3\rightarrow \Gamma \backslash {\mathbf {\mathsf{{H}}}}^3\) is a local isometry at all points \(z \in {\mathbf {\mathsf{{H}}}}^3\) with \({{\,\mathrm{Stab}\,}}_\Gamma (z)=\{1\}\).
Proof Combine Theorem 34.5.1 and the appropriately modified proof of Proposition 34.7.2. The stabilizer of a point is finite because the stabilizer of \(w=0\) in \({{\,\mathrm{SU}\,}}_2(\mathbb H ,{}^*)\) is \({{\,\mathrm{SU}\,}}(2)\), so its stabilizer in \(\Gamma \) is a discrete subgroup of the compact group \({{\,\mathrm{SU}\,}}(2)\) thus is necessarily finite (not necessarily cyclic). In particular, a subgroup \(\Gamma \le {{\,\mathrm{PSL}\,}}_2(\mathbb C )\) is discrete if and only if the action of \(\Gamma \) on \({\mathbf {\mathsf{{H}}}}^3\) is wandering, hence proper. \(\square \)
Definition 36.4.2
A Kleinian group is a discrete subgroup of \({{\,\mathrm{PSL}\,}}_2(\mathbb C )\).
Let \(F \subseteq \mathbb C \) be an imaginary quadratic field with ring of integers \(R=\mathbb Z _F\). Since \(R \subseteq \mathbb C \) is discrete, and \({{\,\mathrm{PSL}\,}}_2(R) \subseteq {{\,\mathrm{PSL}\,}}_2(\mathbb C )\) is discrete.
Definition 36.4.3
The Bianchi group over F is the Kleinian group \({{\,\mathrm{PSL}\,}}_2(R) \subseteq {{\,\mathrm{PSL}\,}}_2(\mathbb C )\).
Remark 36.4.4. The Bianchi groups are so named after work of Bianchi [Bia1892]; he studied them as discrete groups acting on hyperbolic space and found generators in certain cases. For more, see the book by Fine [Fin89].
5 Hyperbolic volume
In this section, we consider volumes of hyperbolic polyhedra, following Milnor’s chapter in Thurston [Thu97, Chapter 7], published also in Milnor [Milno82, Appendix]; see also the full treatment by Ratcliffe [Rat2006, §10.4].
Definition 36.5.1
The Lobachevsky function is defined to be
The Lobachevsky function is also called Clausen’s integral or more conventionally the log sine integral.
36.5.3
The first derivative of the Lobachevsky function is \(\mathcal L '(\theta )=-\log \,|2\sin \theta \,|\) by the fundamental theorem of calculus, so \(\mathcal L \) attains its maximum value at \(\mathcal L (\pi /6)=0.50747\dots \) and minimum at \(\mathcal L (5\pi /6)=-\mathcal L (\pi /6)\). The second derivative is \(\mathcal L ''(\theta )=-\cot \theta \). A graph of this function is sketched in Figure 36.5.4.
Lemma 36.5.5
\(\mathcal L (\theta )\) is odd, periodic with period \(\pi \), and satisfies the identity
for all \(n\in \mathbb Z \).
Proof Since \(\mathcal L '(\theta )=-\log \,|2\sin \theta \,|\) is an even function and \(\mathcal L (0)=0\), we conclude \(\mathcal L (\theta )\) is an odd function, i.e., \(\mathcal L (-\theta )=-\mathcal L (\theta )\) for all \(\theta \in \mathbb R \).
Let \(n \in \mathbb Z \). From
substituting \(z=e^{-2it}\) for \(t \in \mathbb R \) and using \(|e^{2i\theta }-1 \,|=|1-e^{2i\theta } \,|=|2 \sin \theta \,|\) for all \(\theta \in \mathbb R \) gives
for all \(t \in \mathbb R \). Integrating and changing variables \(x=nt\) gives
which yields
for all \(\theta \in \mathbb R \). Plugging in \(\theta =\pi /n\) into (36.5.8) yields by telescoping
so \(\mathcal L (\pi )=0\).
Now since \(\mathcal L '(\theta )\) is periodic with period \(\pi \) and \(\mathcal L (0)=\mathcal L (\pi )=0\), we conclude that \(\mathcal L (\theta +\pi )=\mathcal L (\theta )\) is also periodic with period \(\pi \). Finally,
so \(\sum _{j=0}^{n-1} \mathcal L (j\pi /n)=0\), and the result follows from (36.5.8). \(\square \)
Corollary 36.5.9
We have
Corollary 36.5.9 is called the duplication formula for \(\mathcal L \).
Proof Take \(n=2\) in Lemma 36.5.5. \(\square \)
With the relevant function having been defined, we now return to our geometric application.
Definition 36.5.10
An ideal tetrahedron is a tetrahedron whose vertices lie on the sphere at infinity and whose edges are (infinite) geodesics.
36.5.11
An ideal tetrahedron is determined by the three dihedral angles \(\alpha ,\beta ,\gamma \) along the edges meeting at any vertex; the sum of these angles is \(2\pi \), as the shadow triangle made in \(\mathbb C \) has angles that sum to \(2\pi \). For an illustration, see Figure 36.5.12.
Proposition 36.5.13
The volume of an ideal tetrahedron with dihedral angles \(\alpha ,\beta ,\gamma \) is \(\mathcal L (\alpha )+\mathcal L (\beta )+\mathcal L (\gamma )\).
Proof We follow Milnor [Milno82, Appendix, Lemma 2]; see also Thurston(–Milnor) [Thu97, Theorem 7.2.1] and Ratcliffe [Rat2006, Theorem 10.4.10]. We may suppose without loss of generality that one vertex is at \(\infty \) and the finite face lies on the unit sphere. Projecting onto the unit disc in the x-plane, we obtain a triangle inscribed in the unit circle with angles \(\alpha ,\beta ,\gamma \) with \(\alpha +\beta +\gamma =2\pi \). We make the simplifying assumption that all three angles are acute (the argument for the case of an obtuse angle is similar). We take the barycentric subdivision of the triangle and add up 6 volumes. We integrate the volume element \(\mathrm d {x_1}\mathrm d {x_2}\mathrm d {y}/y^3\) over the region \(T(\alpha )\) defined by the inequalities
Integrating with respect to y we have
We substitute \(x_1=\cos \theta \), so \(\mathrm d {x_1}=-\sin \theta \mathrm d {\theta }\) and \(\pi /2 \ge \theta \ge \alpha \); by partial fractions, we have
So with \(a=\sqrt{1-x_1^2}=\sin \theta \), integrating with respect to \(x_2\) gives
Finally, we use the duplication formula (Corollary 36.5.9), which reads
substituting gives the volume \(\mathcal L (\alpha )/2\), and summing over the other 5 triangles gives the result. \(\square \)
We define now a standard tetrahedron for use in computing volumes. Let \(T_{\alpha ,\gamma }\) be the tetrahedron with one vertex at \(\infty \) and the other vertices A, B, C on the unit hemisphere projecting to \(A',B',C'\) in \(\mathbb C \) with \(A'=0\) to make a Euclidean triangle with angle \(\pi /2\) at \(B'\) and \(\alpha \) at \(A'\). The dihedral angle along the ray from A to \(\infty \) is \(\alpha \). Suppose that the dihedral angle along BC is \(\gamma \). The acute angles determine the isometry class of \(T_{\alpha ,\gamma }\), and we call \(T_{\alpha ,\gamma }\) the standard tetrahedron with angles \(\alpha ,\gamma \). For an illustration, see Figure 36.5.18.
Corollary 36.5.16
We have
Proof One proof realizes the standard tetrahedron as a signed combination of ideal tetrahedra, and uses Proposition 36.5.13. A second proof just repeats the integral (36.5.15) to get
which rearranges to give the result. \(\square \)
36.5.19
By Exercise 36.11, we have the Fourier expansion
The series (36.5.20) converges rather slowly, but twice integrating the Laurent series expansion for \(\cot \theta \) as in Exercise 36.12 gives
where
so \(|B_2 \,|=1/6\), \(|B_4 \,|=1/30\), etc. are the Bernoulli numbers.
6 Picard modular group
In this section, analogous to the case of the classical modular group \({{\,\mathrm{PSL}\,}}_2(\mathbb Z )\) we consider the special case of a full Bianchi group with \(K=\mathbb Q (i)\).
Definition 36.6.1
The group \({{\,\mathrm{PSL}\,}}_2(\mathbb Z [i])\) is called the (full) Picard modular group.
Throughout this section, we write \(\Gamma ={{\,\mathrm{PSL}\,}}_2(\mathbb Z [i])\). In order to understand the structure of the group \(\Gamma \), we follow the same script as in section 35.1, and first we seek a fundamental set.
Proposition 36.6.2
Let

Then  is a fundamental set for \(\Gamma \, \circlearrowright \, {\mathbf {\mathsf{{H}}}}^3\), and \({{\,\mathrm{PSL}\,}}_2(\mathbb Z [i])\) is generated by the elements
is a fundamental set for \(\Gamma \, \circlearrowright \, {\mathbf {\mathsf{{H}}}}^3\), and \({{\,\mathrm{PSL}\,}}_2(\mathbb Z [i])\) is generated by the elements
The set  in Proposition 36.6.2 is displayed in Figure 36.6.5.
in Proposition 36.6.2 is displayed in Figure 36.6.5.
Proof First, we show that for all \(z \in {\mathbf {\mathsf{{H}}}}^3\), there exists a word \(\gamma \) in the matrices (36.6.4) such that  via an explicit reduction algorithm. Let \(z=x+yj \in {\mathbf {\mathsf{{H}}}}^3\). Recalling the action (36.2.6), the element \(\begin{pmatrix} 1 &{} b \\ 0 &{} 1 \end{pmatrix}\) for \(b \in \mathbb Z [i]\) act by translation \(z \mapsto z+b\), so repeatedly applying matrices from the first two among (36.6.4), we may suppose that \(|{{\,\mathrm{Re}\,}}x \,|, |{{\,\mathrm{Im}\,}}x \,| \le 1/2\). Then applying the element \(\begin{pmatrix} i &{} 0 \\ 0 &{} -i \end{pmatrix}\), which acts by \(z \mapsto (iz)(-i)^{-1} = i^2(x-yj)=-x+yj\), we may suppose \({{\,\mathrm{Im}\,}}x \ge 0\). Now if
via an explicit reduction algorithm. Let \(z=x+yj \in {\mathbf {\mathsf{{H}}}}^3\). Recalling the action (36.2.6), the element \(\begin{pmatrix} 1 &{} b \\ 0 &{} 1 \end{pmatrix}\) for \(b \in \mathbb Z [i]\) act by translation \(z \mapsto z+b\), so repeatedly applying matrices from the first two among (36.6.4), we may suppose that \(|{{\,\mathrm{Re}\,}}x \,|, |{{\,\mathrm{Im}\,}}x \,| \le 1/2\). Then applying the element \(\begin{pmatrix} i &{} 0 \\ 0 &{} -i \end{pmatrix}\), which acts by \(z \mapsto (iz)(-i)^{-1} = i^2(x-yj)=-x+yj\), we may suppose \({{\,\mathrm{Im}\,}}x \ge 0\). Now if  , which is to say \(\Vert z \Vert ^2 \ge 1\), we are done. Otherwise, \(\Vert z \Vert ^2 < 1\), and we apply the matrix \(\gamma = \begin{pmatrix} 0 &{} -1 \\ 1 &{} 0 \end{pmatrix}\), which by (36.2.9) acts by
, which is to say \(\Vert z \Vert ^2 \ge 1\), we are done. Otherwise, \(\Vert z \Vert ^2 < 1\), and we apply the matrix \(\gamma = \begin{pmatrix} 0 &{} -1 \\ 1 &{} 0 \end{pmatrix}\), which by (36.2.9) acts by
and \(y'=y/\Vert z\Vert ^2 > y\), and we repeat. Since \(\Gamma z\) is discrete, this terminates after finitely many steps: the set
is discrete and compact, hence finite.
Next, if  and
and  with \(z'=\gamma z\) for \(\gamma \in \Gamma \), then \(\gamma =1\) and \(z=z'\); this can be proven directly as in Lemma 35.1.10 (the details are requested in Exercise 36.7). It follows that the matrices (36.6.4) generate \({{\,\mathrm{PSL}\,}}_2(\mathbb Z [i])\) as in Lemma 35.1.12, taking instead
with \(z'=\gamma z\) for \(\gamma \in \Gamma \), then \(\gamma =1\) and \(z=z'\); this can be proven directly as in Lemma 35.1.10 (the details are requested in Exercise 36.7). It follows that the matrices (36.6.4) generate \({{\,\mathrm{PSL}\,}}_2(\mathbb Z [i])\) as in Lemma 35.1.12, taking instead  . \(\square \)
. \(\square \)
A slightly more convenient set of generators, together with the gluing relations they provide on the fundamental set, is given in Figure 36.6.7.
Remark 36.6.6. By a deeper investigation into the structure of the fundamental set  , in chapter 37 we will find a presentation for \(\Gamma \) as
, in chapter 37 we will find a presentation for \(\Gamma \) as
36.6.8
We compute the volume of this fundamental domain using formulas from the previous section. First, we use symmetry to triangulate (tetrahedralize)  , as in Figure 36.6.9.
, as in Figure 36.6.9.
Let
Applying the symmetries of \(\Gamma \), we see that  . We have \(T=T_{\alpha ,\gamma }\) a standard tetrahedron, with \(\alpha =\pi /4\) and dihedral angle \(\gamma =\pi /3\).
. We have \(T=T_{\alpha ,\gamma }\) a standard tetrahedron, with \(\alpha =\pi /4\) and dihedral angle \(\gamma =\pi /3\).
Now by the hard-earned volume formula (Corollary 36.5.16) we have
By Lemma 36.5.5 with \(n=3\), we have
since
substituting (36.6.12) into (36.6.11) gives
and

36.6.14
We conclude with a beautiful consequence of this volume calculation, giving a preview of the volume formula we will prove later. By the Fourier expansion (36.5.20), we have
where
is the nontrivial Dirichlet character modulo 4. We can analytically continue the sum (36.6.15) to \(\mathbb C \) via the L-series
for \(s \in \mathbb C \) with \({{\,\mathrm{Re}\,}}s>1\) whose general study was the heart of Part III of this text. Here, we can just observe that \(L(2,\chi )=2\mathcal L (\pi /4)=0.915965\ldots \), so

More generally, the volume of the quotient by a Bianchi group is connected to an L-value attached to the associated imaginary field; we will pursue this topic further in chapter 39.
Exercises
- 1.:
-
For \(z \in {\mathbf {\mathsf{{H}}}}^3\) and \(g=\begin{pmatrix} a &{} b \\ c &{} d \end{pmatrix} \in {{\,\mathrm{PSL}\,}}_2(\mathbb C )\), show that
$$\begin{aligned} (az+b)(cz+d)^{-1} = (zc+d)^{-1}(za+b). \end{aligned}$$ - \(\triangleright \) 2.:
-
Inversion in the circle of radius r in \(\mathbb C \) centered at the origin is defined by the map
$$\begin{aligned} z \mapsto r^2\left( \frac{z}{|z \,|^2}\right) = \frac{r^2}{\overline{z}}, \end{aligned}$$as in Figure 36.6.16.
Sending \(0 \mapsto \infty \) and \(\infty \mapsto 0\) under this map, we obtain an anti-holomorphic map \(\mathbb P ^1(\mathbb C ) \rightarrow \mathbb P ^1(\mathbb C )\). Inversion in a line in \(\mathbb C \) is reflection in the line.
Verify that every element of \({{\,\mathrm{PSL}\,}}_2(\mathbb C )\) can be written as a composition of at most four inversions in circles and lines in \(\mathbb C \) (or equivalently, by stereographic projection, circles in \(\mathbb P ^1(\mathbb C )\)).
- \(\triangleright \) 3.:
-
Verify (36.2.3) for the action of \({{\,\mathrm{SL}\,}}_2(\mathbb C )\) on \({\mathbf {\mathsf{{H}}}}^3\subseteq \mathbb H \).
- \(\triangleright \) 4.:
-
Let \(g=\begin{pmatrix} 0 &{} -1 \\ 1 &{} 0 \end{pmatrix} \in {{\,\mathrm{SL}\,}}_2(\mathbb C )\). Show that g acts on \({\mathbf {\mathsf{{H}}}}^3\) by
$$\begin{aligned} gz = \frac{1}{\Vert z \Vert ^2}(-\overline{x}+yj) \end{aligned}$$where \(\Vert z \Vert ^2 = |x|^2+y^2\), and that g is a hyperbolic isometry.
- 5.:
-
Let \(\Gamma \le {{\,\mathrm{PSL}\,}}_2(\mathbb C )\) be a subgroup (with the subspace topology). Show that \(\Gamma \) has a wandering action on \({\mathbf {\mathsf{{H}}}}^3\) if and only if \(\Gamma \) is discrete (cf. Proposition 34.7.2).
- 6.:
-
Show that the reduction algorithm in Proposition 36.6.2 recovers the Euclidean algorithm for \(\mathbb Z [i]\) in a manner analogous to Exercise 35.4 for \(\mathbb Z \).
- \(\triangleright \) 7.:
-
Consider the fundamental set
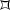 for \(\Gamma ={{\,\mathrm{PSL}\,}}_2(\mathbb Z [i])\) (36.6.3). Show that if
for \(\Gamma ={{\,\mathrm{PSL}\,}}_2(\mathbb Z [i])\) (36.6.3). Show that if 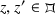 and
and 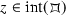 with \(z'=\gamma z\) for \(\gamma \in \Gamma \), then \(\gamma =1\) and \(z=z'\) (cf. Lemma 35.1.10).
with \(z'=\gamma z\) for \(\gamma \in \Gamma \), then \(\gamma =1\) and \(z=z'\) (cf. Lemma 35.1.10). - 8.:
-
Let \(\omega =e^{2\pi i/3} \in \mathbb C \). The field \(\mathbb Q (\omega )=\mathbb Q (\sqrt{-3})\) is Euclidean under the norm, just like \(\mathbb Q (i)\). Give a description of a fundamental domain for the group \({{\,\mathrm{PSL}\,}}_2(\mathbb Z [\omega ])\) analogous to Proposition 36.6.2. [The fields \(\mathbb Q (\sqrt{d})\) with \(d<0\) are Euclidean if and only if \(d=-3,-4,-7,-8,-11\), so similar—but increasingly difficult—arguments can be given in each of these cases. See Fine [Fin89, §4.3] for presentations.]
- \(\triangleright \) 9.:
-
We consider hyperplane bisectors in \({\mathbf {\mathsf{{H}}}}^3\) (cf. Exercise 33.8). Let \(z_1,z_2 \in {\mathbf {\mathsf{{H}}}}^3\) be distinct. Let
$$\begin{aligned} H(z_1,z_2)=\{z \in {\mathbf {\mathsf{{H}}}}^3: \rho (z,z_1) \le \rho (z,z_2)\} \end{aligned}$$be the locus of points as close to \(z_1\) as to \(z_2\), and let
$$\begin{aligned} L(z_1,z_2)={{\,\mathrm{bd}\,}}H(z_1,z_2). \end{aligned}$$Show that \(H(z_1,z_2)\) is a convex half-space (for every two points in the half-space, the geodesic between them is contained in the half-space), and that
$$\begin{aligned} L(z_1,z_2)=\{z \in {\mathbf {\mathsf{{H}}}}^3: \rho (z,z_1) = \rho (z,z_2)\} \end{aligned}$$is geodesic and equal to the perpendicular bisector of the geodesic segment from \(z_1\) to \(z_2\).
- 10.:
-
Prove the duplication formula for the Lobachevsky function \(\mathcal L (\theta )\) using the double angle formula, given that \(\mathcal L (\pi /2)=0\).
- \(\triangleright \) 11.:
-
In this exercise, we prove the Fourier expansion
$$\begin{aligned} \mathcal L (\theta )=\frac{1}{2}\sum _{n=1}^{\infty } \frac{\sin (2n\theta )}{n^2}. \end{aligned}$$(36.6.17)- (a):
-
Define the dilogarithm function by
$$\begin{aligned} {{\,\mathrm{Li}\,}}_2(z) = \sum _{n=1}^{\infty } \frac{z^n}{n^2}; \end{aligned}$$show that this series converges for \(|z \,|<1\) and that
$$\begin{aligned} {{\,\mathrm{Li}\,}}_2(z) = -\int _0^z \frac{\log (1-w)}{w}\mathrm d {w}. \end{aligned}$$ - (b):
-
Prove that
$$\begin{aligned} 2i \mathcal L (\theta )={{\,\mathrm{Li}\,}}_2(e^{2i\theta })-\frac{\pi ^2}{6}+\pi \theta -\theta ^2. \end{aligned}$$(36.6.18)[Hint: Differentiate both sides for \(0<\theta <\pi \), using the limiting value as \(\theta \rightarrow 0\) to compute the limiting value \({{\,\mathrm{Li}\,}}_2(1)=\pi ^2/6\).]
- (c):
- \(\triangleright \) 12.:
-
As in 36.5.19, we define the \(B_k \in \mathbb Q \) for \(k \ge 0\) by
$$\begin{aligned} \frac{x}{e^x-1}=\sum _{k=0}^{\infty } B_k \frac{x^k}{k!}=1-\frac{x}{2}+\frac{1}{6}\frac{x^2}{2!}-\frac{1}{30}\frac{x^4}{4!}+\ldots . \end{aligned}$$(36.6.19)- (a):
-
Plug in \(x=2iz\) into (36.6.19) to get
$$\begin{aligned} z \cot z = 1+\sum _{k=2}^{\infty } B_k \frac{(2iz)^k}{k!}. \end{aligned}$$ - (b):
-
Integrate twice in (a) to prove
$$\begin{aligned} \mathcal L (\theta )=\theta \left( 1-\log |2\theta \,|+\sum _{n=1}^{\infty } \frac{|B_{2n} \,|}{4n} \frac{(2\theta )^{2n+1}}{(2n+1)!}\right) . \end{aligned}$$
[See also Exercise 40.3.]
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
This chapter is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, duplication, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, a link is provided to the Creative Commons license and any changes made are indicated.The images or other third party material in this chapter are included in the work's Creative Commons license, unless indicated otherwise in the credit line; if such material is not included in the work's Creative Commons license and the respective action is not permitted by statutory regulation, users will need to obtain permission from the license holder to duplicate, adapt or reproduce the material.
Copyright information
© 2021 The Author(s)
About this chapter
Cite this chapter
Voight, J. (2021). Hyperbolic space. In: Quaternion Algebras. Graduate Texts in Mathematics, vol 288. Springer, Cham. https://doi.org/10.1007/978-3-030-56694-4_36
Download citation
DOI: https://doi.org/10.1007/978-3-030-56694-4_36
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-56692-0
Online ISBN: 978-3-030-56694-4
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)



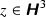 , we have
, we have  , we have
, we have 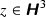 , the orbit
, the orbit 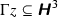 is discrete and
is discrete and 



 for the Picard group
for the Picard group 



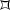 for
for 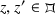 and
and 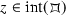 with
with