Abstract
In this chapter, we introduce the classical modular group \({{\,\mathrm{PSL}\,}}_2(\mathbb Z ) \le {{\,\mathrm{PSL}\,}}_2(\mathbb R )\), a discrete group acting on the upper half-plane that has received extensive study because of the role it plays throughout mathematics. We examine the group in detail via a fundamental domain and conclude with some applications to number theory. This chapter will serve as motivation and example for the generalizations sought later in this part of the text.
You have full access to this open access chapter, Download chapter PDF
In this chapter, we introduce the classical modular group \({{\,\mathrm{PSL}\,}}_2(\mathbb Z ) \le {{\,\mathrm{PSL}\,}}_2(\mathbb R )\), a discrete group acting on the upper half-plane that has received extensive study because of the role it plays throughout mathematics. We examine the group in detail via a fundamental domain and conclude with some applications to number theory. This chapter will serve as motivation and example for the generalizations sought later in this part of the text.
There are very many references for the classical modular group, including Apostol [Apo90, Chapter 2], Diamond–Shurman [DS2005, Chapter 2], and Serre [Ser73, Chapter VII].
1 \(\triangleright \) The fundamental set
Definition 35.1.1
The classical modular group is the subgroup of \({{\,\mathrm{PSL}\,}}_2(\mathbb R )\) defined by
The group \({{\,\mathrm{PSL}\,}}_2(\mathbb Z )\) acts faithfully on the upper half-plane \({\mathbf {\mathsf{{H}}}}^2\) by linear fractional transformations; equipping \({\mathbf {\mathsf{{H}}}}^2\) with the hyperbolic metric, this action is by orientation-preserving isometries.
Since \(\mathbb Z \subseteq \mathbb R \) is discrete, so too is \({{\,\mathrm{SL}\,}}_2(\mathbb Z ) \subseteq {{\,\mathrm{M}\,}}_2(\mathbb Z ) \subseteq {{\,\mathrm{M}\,}}_2(\mathbb R )\) discrete and therefore \({{\,\mathrm{PSL}\,}}_2(\mathbb Z ) \le {{\,\mathrm{PSL}\,}}_2(\mathbb R )\) is a Fuchsian group (Definition 34.7.3).
35.1.2
Our first order of business is to try to understand the structure of the classical modular group in terms of this action. Let
Then \(Sz=-1/z\) for \(z \in {\mathbf {\mathsf{{H}}}}^2\), so S maps the unit circle \(\{z \in \mathbb C : |z \,|=1\}\) to itself, fixing the point \(z=i\); and \(Tz=z+1\) for \(z \in {\mathbf {\mathsf{{H}}}}^2\) acts by translation. We compute that \(S^2=1\) (in \({{\,\mathrm{PSL}\,}}_2(\mathbb Z )\)) and
so \((ST)^3=1\).
35.1.3
In a moment, we will see that \({{\,\mathrm{PSL}\,}}_2(\mathbb Z )\) is generated by S and T, with a minimal set of relations given by \(S^2=(ST)^3=1\). To do so, we examine a fundamental set (cf. Definition 34.1.14) for the action of \({{\,\mathrm{PSL}\,}}_2(\mathbb Z )\) on \({\mathbf {\mathsf{{H}}}}^2\), as follows. Let
The set  is a hyperbolic triangle with vertices at \(\omega =(-1+\sqrt{-3})/2\) and \(-\omega ^2=(1+\sqrt{-3})/2\) and \(\infty \). The translates of
is a hyperbolic triangle with vertices at \(\omega =(-1+\sqrt{-3})/2\) and \(-\omega ^2=(1+\sqrt{-3})/2\) and \(\infty \). The translates of  by words in S, T tessellate the plane as in Figure 35.1.4.
by words in S, T tessellate the plane as in Figure 35.1.4.
By the Gauss–Bonnet formula 33.6.8 (or Exercise 35.1),

The elements S, T act on the edges of this triangle as in Figure 35.1.6.
In the unit disc, the triangle  is as in Figure 35.1.7.
is as in Figure 35.1.7.
The following three lemmas describe the relationship of the set  to \(\Gamma \).
to \(\Gamma \).
Lemma 35.1.8
For all  , there exists a word \(\gamma \in \langle S,T \rangle \) such that
, there exists a word \(\gamma \in \langle S,T \rangle \) such that  .
.
Proof. In fact, we can determine such a word algorithmically. First, we translate z so that \(|{{\,\mathrm{Re}\,}}z \,| \le 1/2\). If \(|z \,| \ge 1\), we are done; otherwise, if \(|z \,|<1\), then
We then repeat this process, obtaining a sequence of elements \(z=z_1,z_2,\ldots \) with \({{\,\mathrm{Im}\,}}z_1< {{\,\mathrm{Im}\,}}z_2 < \ldots \) . We claim that this process terminates after finitely many steps. Indeed, by (33.3.9)
and the number of \(c,d \in \mathbb Z \) such that \(|cz+d \,|<1\) is finite: the set \(\mathbb Z + \mathbb Z z \subseteq \mathbb C \) is a lattice, so there are only finitely many elements of bounded norm. (Alternatively, the orbit \(\Gamma z\) is discrete by Theorem 34.5.1—or the direct argument given in Proposition 34.7.2—therefore, its intersection with the compact set
is finite.) Upon termination, we have found a word \(\gamma \) in S, T such that  . \(\square \)
. \(\square \)
The procedure exhibited in the proof of Lemma 35.1.8 is called a reduction algorithm.
Lemma 35.1.10
Let  , and suppose
, and suppose  lies in the interior of
lies in the interior of  . If \(z'=\gamma z\) with \(\gamma \in \Gamma \), then \(\gamma =1\) and \(z=z'\).
. If \(z'=\gamma z\) with \(\gamma \in \Gamma \), then \(\gamma =1\) and \(z=z'\).
Proof. Let \(z'=\gamma z\) with \(\gamma =\begin{pmatrix} a &{} b \\ c &{} d \end{pmatrix} \in \Gamma \). We have \({{\,\mathrm{Im}\,}}z'=({{\,\mathrm{Im}\,}}z)/|cz+d \,|^2\). First suppose that \({{\,\mathrm{Im}\,}}z' \ge {{\,\mathrm{Im}\,}}z\); then
Since \({{\,\mathrm{Im}\,}}z > {{\,\mathrm{Im}\,}}\omega = \sqrt{3}/2\), from (35.1.11) we conclude that \(c^2 \le 4/3\) so \(|c \,| \le 1\). If \(c=0\) then \(ad-bc=ad=1\) so \(a=d=\pm 1\), and then \(z'=\gamma z = z \pm b\), which immediately implies \(b=0\) so \(\gamma =1\) as claimed. If instead \(|c \,|=1\), then the conditions
together imply \(d=0\); but then \(|cz+d \,|=|z \,| \le 1\), and since  we have \(|z \,| > 1\), a contradiction.
we have \(|z \,| > 1\), a contradiction.
If instead \({{\,\mathrm{Im}\,}}z' < {{\,\mathrm{Im}\,}}z\), we interchange the roles of \(z,z'\) and have strict inequality in (35.1.11); by the same argument and the weaker inequality \(|{{\,\mathrm{Re}\,}}z \,| \le 1/2\), we then obtain \(|z \,| < 1\), a contradiction. \(\square \)
Lemma 35.1.12
The elements S, T generate \(\Gamma ={{\,\mathrm{PSL}\,}}_2(\mathbb Z )\).
Proof. Let  . Let \(\gamma \in \Gamma \), and let \(z'=\gamma z\). By Lemma 35.1.8, there exists \(\gamma '\) a word in S, T such that
. Let \(\gamma \in \Gamma \), and let \(z'=\gamma z\). By Lemma 35.1.8, there exists \(\gamma '\) a word in S, T such that  . By Lemma 35.1.10, we have \(\gamma 'z'=(\gamma ' \gamma )z = z\), so \(\gamma '\gamma = 1\) and \(\gamma = \gamma ' \in \langle S, T \rangle \). \(\square \)
. By Lemma 35.1.10, we have \(\gamma 'z'=(\gamma ' \gamma )z = z\), so \(\gamma '\gamma = 1\) and \(\gamma = \gamma ' \in \langle S, T \rangle \). \(\square \)
Although we have worked in \({{\,\mathrm{PSL}\,}}_2(\mathbb Z )\) throughout, it follows from Lemma 35.1.12 that the matrices S, T also generate \({{\,\mathrm{SL}\,}}_2(\mathbb Z )\), since \(S^2=-1\). See Exercise 35.3 for another proof of Lemma 35.1.12.
Corollary 35.1.13
The set  is a fundamental set for
is a fundamental set for  .
.
Proof. The statement follows from Lemmas 35.1.8 and 35.1.10 (recalling the definition of fundamental set, Definition 34.1.14). \(\square \)
35.1.14
If  has \({{\,\mathrm{Stab}\,}}_\Gamma (z) \ne \{1\}\), then we claim that one of the following holds:
has \({{\,\mathrm{Stab}\,}}_\Gamma (z) \ne \{1\}\), then we claim that one of the following holds:
-
(i)
\(z=i\), and \({{\,\mathrm{Stab}\,}}_\Gamma (i)=\langle S \rangle \simeq \mathbb Z /2\mathbb Z \);
-
(ii)
\(z=\omega \), and \({{\,\mathrm{Stab}\,}}_\Gamma (\omega )=\langle ST \rangle \simeq \mathbb Z /3\mathbb Z \); or
-
(iii)
\(z=-\omega ^2\), and \({{\,\mathrm{Stab}\,}}_\Gamma (-\omega ^2)=\langle TS \rangle = T {{\,\mathrm{Stab}\,}}_\Gamma (\omega ) T^{-1}\).
Indeed, let \(\gamma z = z\) with \(\gamma =\begin{pmatrix} a &{} b \\ c &{} d \end{pmatrix}\) and \(\gamma \ne 1\). Then \(cz^2+(d-a)z-b=0\), so \(c \ne 0\) and
Thus \(D=-4\) or \(D=-3\). In either case, since  we have \({{\,\mathrm{Im}\,}}z \ge \sqrt{3}/2\), we must have \(c=\pm 1\), and replacing \(\gamma \leftarrow -\gamma \) we may take \(c=1\). If \(D=-4\), then \({{\,\mathrm{Tr}\,}}(\gamma )=a+d=0\) so \(z=a + i\), and \(a=0=d\) and \(c=1=-b\), i.e., \(z=i\) and we are in case (i). If the discriminant is \(-3\), then a similar argument gives \(z=((a \pm 1)+\sqrt{-3})/2\) so \(a=0\), and we are in cases (ii) or (iii).
we have \({{\,\mathrm{Im}\,}}z \ge \sqrt{3}/2\), we must have \(c=\pm 1\), and replacing \(\gamma \leftarrow -\gamma \) we may take \(c=1\). If \(D=-4\), then \({{\,\mathrm{Tr}\,}}(\gamma )=a+d=0\) so \(z=a + i\), and \(a=0=d\) and \(c=1=-b\), i.e., \(z=i\) and we are in case (i). If the discriminant is \(-3\), then a similar argument gives \(z=((a \pm 1)+\sqrt{-3})/2\) so \(a=0\), and we are in cases (ii) or (iii).
Therefore, if \(\gamma \in {{\,\mathrm{PSL}\,}}_2(\mathbb Z )\) has finite order, then \(\gamma \) fixes a point, thus a conjugate of \(\gamma \) would fix a point in  , and therefore by the above \(\gamma \) is conjugate in \({{\,\mathrm{PSL}\,}}_2(\mathbb Z )\) to either S or ST.
, and therefore by the above \(\gamma \) is conjugate in \({{\,\mathrm{PSL}\,}}_2(\mathbb Z )\) to either S or ST.
Let \(Y = \Gamma \backslash {\mathbf {\mathsf{{H}}}}^2\). Gluing together the fundamental set, we obtain a homeomorphism
The orbit of the limit point \(\infty \) under \(\Gamma \) is \(\mathbb P ^1(\mathbb Q ) \subseteq {{\,\mathrm{bd}\,}}{\mathbf {\mathsf{{H}}}}^2\); letting \({\mathbf {\mathsf{{H}}}}^{2*}={\mathbf {\mathsf{{H}}}}^2\cup \mathbb P ^1(\mathbb Q )\), there is a homeomorphism
as in Figure 35.1.15.
Away from the orbits \(\Gamma i, \Gamma \omega \) with nontrivial stabilizer, the complex structure on \({\mathbf {\mathsf{{H}}}}^2\) descends and gives the quotient \(Y \smallsetminus \{\Gamma i, \Gamma \omega \}\) the structure of a Riemann surface. By studying the moduli of lattices, later we will give an explicit holomorphic identification \(j:Y \rightarrow \mathbb C \).
35.1.16
By 34.8.11, the quotient Y has the structure of a good complex 1-orbifold, when we keep track of the two nontrivial stabilizers.
Alternatively, we can also give X the structure of a compact Riemann surface as follows. Let  . If \(z_0=\infty \), we take the chart \(z \mapsto e^{2\pi iz}\). Otherwise, let \(e=\#{{\,\mathrm{Stab}\,}}_{\Gamma }(z_0)<\infty \), let \(w=(z-z_0)/(z-\overline{z_0})\) be the local coordinate as in (33.7.3), and take the chart \(z \mapsto w^e\) at \(z_0\).
. If \(z_0=\infty \), we take the chart \(z \mapsto e^{2\pi iz}\). Otherwise, let \(e=\#{{\,\mathrm{Stab}\,}}_{\Gamma }(z_0)<\infty \), let \(w=(z-z_0)/(z-\overline{z_0})\) be the local coordinate as in (33.7.3), and take the chart \(z \mapsto w^e\) at \(z_0\).
Lemma 35.1.17
Every relation among S, T is obtained from \(S^2=(ST)^3=1\) after conjugation by \(\Gamma \), so that \(\Gamma \) has the presentation
Thus \(\Gamma ={{\,\mathrm{PSL}\,}}_2(\mathbb Z )\) is the free product of \(\mathbb Z /2\mathbb Z \) and \(\mathbb Z /3\mathbb Z \).
Proof. Consider a relation \(\delta _1 \cdots \delta _r = 1\) where \(\delta _i \in \{S,T,T^{-1}\}\) (recall \(S=S^{-1}\)). We may suppose that \(\delta _i \ne \delta _{i+1}^{-1}\) for \(i=1,\dots ,r-1\) or else we can cancel adjacent terms. Define \(\gamma _i :=\delta _1 \cdots \delta _i\) for \(i=1,\dots ,r\), so that \(\gamma _r=1\) and \(\gamma _{i+1}=\gamma _i \delta _{i+1}\) for all \(i=1,\dots ,r-1\). Let \(z_0 = 2i\) and let
We claim that \(z_{i+1}\) and \(z_i\) are in adjacent \(\Gamma \)-translates of  : indeed,
: indeed,

is a side of both. Draw the geodesic (shortest path, across the corresponding side) between \(z_{i+1}\) and \(z_i\) for each i. Because \(\delta _i \ne \delta _{i+1}^{-1}\), there is no backtracking; taken together, they define a loop in the upper half-plane, since \(z_r=\gamma _r z_0=z_0\).
We first conjugate the relation by T or \(T^{-1}\) so \(\delta _1=S\). If \(\delta _r=S\) as well, then we conjugate by S and begin again. So without loss of generality \(\delta _r=T,T^{-1}\); we explain the case \(\delta _r=T\), the case \(\delta _r=T^{-1}\) is similar. Then our relation looks like \(S\delta _{2}\cdots \delta _{r-1} T = 1\), and so \(\gamma _r=1=\gamma _{r-1}\delta _r=\gamma _{r-1}T\) implies \(z_{r-1}=\gamma _{r-1}z_0=T^{-1}z_0=2i-1\).
If \(z_i=\gamma _i z_0 = z_0\) for some \(0< i < r\), then \(\gamma _i=\delta _1 \cdots \delta _i=1\) and similarly \(\delta _{i+1}\cdots \delta _r=1\), so we may argue separately with each such relation and so may suppose that \(z_i \ne z_0\) for all \(i=1,\dots ,r-1\). It follows that the loop intersects  only in the path from \(z_0\) to \(z_1\) and from \(z_{r-1}\) to \(z_0\), because any other intersection would necessarily have source or target \(z_0\).
only in the path from \(z_0\) to \(z_1\) and from \(z_{r-1}\) to \(z_0\), because any other intersection would necessarily have source or target \(z_0\).
We observe that \(\omega \) is in the interior of the loop, since by continuity any path from i to \(2i-1/2\) in \({\mathbf {\mathsf{{H}}}}^2\) that does not intersect  must go from right to left through a highest value \(-1/2+it\) with \(0<t \le \sqrt{3}/2\).
must go from right to left through a highest value \(-1/2+it\) with \(0<t \le \sqrt{3}/2\).
The proof proceeds by induction on the number of points in the intersection of the interior of the loop with the set of vertices \(\Gamma \omega \). We have shown in the previous paragraph that if there are no such points, then the relation is trivial. In the general case with relation \(S\delta _2\cdots \delta _{r-1} T=1\), expanding \((ST)^3=1\) we get \(T=(ST^{-1})^2S\) and substituting we obtain another relation \(S\delta _{2} \cdots \delta _{r-1}(ST^{-1})^2 S =1\), as in Figure 35.1.19.
Reading this relation as above, we see that the loop encloses one fewer point in \(\Gamma \omega \) (it starts and ends with a backtracking step), and so the same is true for the conjugate relation \(\delta _2 \cdots \delta _{r-1}(ST^{-1})^2=1\). Cancelling any new adjacent terms and conjugating the relation does not change the number of enclosed interior vertices, so the result holds by induction.
(Alternatively, for a proof in the style of Lemma 35.1.10, see Exercise 35.5.) \(\square \)
Remark 35.1.20. Alperin [Alp93] uses the action on the irrational numbers to show directly that \({{\,\mathrm{PSL}\,}}_2(\mathbb Z )\) is the free product of \(\mathbb Z /2\mathbb Z \) and \(\mathbb Z /3\mathbb Z \) (but note the typo \(\beta (z)=1-1/z\) on the first page).
2 Binary quadratic forms
We pause to give an application to quadratic forms and class groups, after Gauss. An integral binary quadratic form, abbreviated in this section to simply form, is an expression
We define the discriminant of a form Q to be
A form Q is primitive if \(\gcd (a,b,c)=1\), and Q is positive definite if \(Q(x,y)>0\) for all nonzero \((x,y) \in \mathbb R ^2\); after completing the square, we see that a form is positive definite if and only if \(a>0\) and \({{\,\mathrm{disc}\,}}(Q)<0\).
For \(d<0\), let
be the set of primitive, positive definite forms of discriminant d. The group \(\Gamma \) acts on \(\mathcal Q _d\) the right by change of variable: for \(\gamma \in \Gamma \), we define \((Q^\gamma )(x,y) = Q(\gamma (x,y)^{\textsf {t} })\), so that if \(\gamma =\begin{pmatrix} r &{} s \\ t &{} u \end{pmatrix}\) then
We verify that \({{\,\mathrm{disc}\,}}(Q^\gamma )={{\,\mathrm{disc}\,}}(Q)=d\) for \(\gamma \in \Gamma \). We say that \(Q,Q'\) are (\(\Gamma \)-)equivalent if \(Q'=Q^\gamma \) for some \(\gamma \in \Gamma = {{\,\mathrm{SL}\,}}_2(\mathbb Z )\).
We claim that the number of equivalence classes \(h(d) :=\#\mathcal Q _d/\Gamma \) is finite. Indeed, to every \(Q \in \mathcal Q _d\), we associate the unique root
of \(Q(z,1)=0\). Then \(z_{Q^\gamma }=\gamma ^{-1}(z)\) for \(\gamma \in \Gamma \). Therefore, by the reduction theory of the previous section, we can replace Q up to equivalence by a form such that  . If we further insist that \({{\,\mathrm{Re}\,}}z<1/2\) and \({{\,\mathrm{Re}\,}}z<0\) if \(|z \,|=1\), then this representative isunique, as in Figure 35.2.1.
. If we further insist that \({{\,\mathrm{Re}\,}}z<1/2\) and \({{\,\mathrm{Re}\,}}z<0\) if \(|z \,|=1\), then this representative isunique, as in Figure 35.2.1.
Thus
so \(-a<b \le a\), or equivalently,
and
so \(a \le c\) and \(b \ge 0\) if equality holds. In sum, every positive definite form Q is equivalent to a (\({{\,\mathrm{SL}\,}}_2(\mathbb Z )\)-)reduced form satisfying
We now show that there are only finitely many reduced forms with given discriminant \(d<0\), i.e., that \(h(d)<\infty \). The inequalities \(|b \,| \le a \le c\) imply that
so \(a \le \sqrt{|d|/3}\) and \(|b|\le a\), so there are only finitely many possibilities for a, b; and then \(c=(b^2-d)/(4a)\) is determined. This gives an efficient method to compute the set \(\mathcal Q _d/\Gamma \) efficiently.
Let \(S=\mathbb Z \oplus \mathbb Z [(d+\sqrt{d})/2] \subset K=\mathbb Q (\sqrt{d})\) be the quadratic ring of discriminant \(d<0\). Let \({{\,\mathrm{Pic}\,}}(S)\) be the group of invertible fractional ideals of S modulo principal ideals. Then there is a bijection
(Exercise 35.9). In the same stroke, we have proven the finiteness of the class number \({\#{{\,\mathrm{Pic}\,}}(S)<\infty }\).
3 Moduli of lattices
In this section, we realize \({{\,\mathrm{PSL}\,}}_2(\mathbb Z ) \backslash {\mathbf {\mathsf{{H}}}}^2\) as a moduli space of complex lattices.
ambda]\(\Lambda \)lattice
35.3.1
A (complex) lattice \(\Lambda \subset \mathbb C \) is a subgroup \(\Lambda =\mathbb Z z_1 + \mathbb Z z_2\) with \(z_1,z_2\) linearly independent over \(\mathbb R \); the elements \(z_1,z_2\) are a basis for \(\Lambda \).
Two lattices \(\Lambda ,\Lambda '\) are homothetic if there exists \(u \in \mathbb C ^\times \) such that \(\Lambda '=u \Lambda \), and we write \(\Lambda \sim \Lambda '\). Let \(\Lambda =\mathbb Z z_1 + \mathbb Z z_2\) be a lattice. Then without loss of generality (interchanging \(z_1,z_2\)), we may suppose \({{\,\mathrm{Im}\,}}(z_2/z_1)>0\), and then we call \(z_1,z_2\) an oriented basis. Then there is a homothety
where \(\tau =z_2/z_1 \in {\mathbf {\mathsf{{H}}}}^2\).
Lemma 35.3.2
Let \(\Lambda =\mathbb Z +\mathbb Z \tau \) and \(\Lambda = \mathbb Z +\mathbb Z \tau '\) be lattices with  . Then \(\Lambda \sim \Lambda '\) if and only if \(\Gamma \tau = \Gamma \tau '\).
. Then \(\Lambda \sim \Lambda '\) if and only if \(\Gamma \tau = \Gamma \tau '\).
Proof. Since \(\tau ,\tau ' \in {\mathbf {\mathsf{{H}}}}^2\), the bases \(1,\tau \) and \(1,\tau '\) are oriented. We have \(\Lambda =\mathbb Z + \mathbb Z \tau \sim \mathbb Z + \mathbb Z \tau '=\Lambda '\) if and only if there exists an invertible change of basis matrix \(g = \begin{pmatrix} a &{} b \\ c &{} d \end{pmatrix} \in {{\,\mathrm{GL}\,}}_2(\mathbb Z )\) and \(u \in \mathbb C ^\times \) such that
so \(u(a\tau +b)=\tau '\) and \(u(c\tau +d)=1\). Eliminating u gives equivalently
Therefore \(g \in {{\,\mathrm{SL}\,}}_2(\mathbb Z )\), and since g is well-defined as an element of \(\Gamma ={{\,\mathrm{PSL}\,}}_2(\mathbb Z )\), the result follows. \(\square \)
35.3.3
By Lemma 35.3.2, there is a bijection
that is to say, \(Y=\Gamma \backslash {\mathbf {\mathsf{{H}}}}^2\) parametrizes complex lattices up to homothety.
To a lattice \(\Lambda \), we associate the complex torus \(\mathbb C /\Lambda \) (of rank 1); two such tori \(\mathbb C /\Lambda \) and \(\mathbb C /\Lambda '\) are isomorphic as Riemann surfaces if and only if \(\Lambda \sim \Lambda '\). Therefore, the space Y also parametrizes complex tori.
We return to this interpretation in section 40.1.
4 Congruence subgroups
The finite-index subgroups of \({{\,\mathrm{PSL}\,}}_2(\mathbb Z )\) play a central role, and of particular importance are those subgroups defined by congruence conditions on the entries.
ammaN]\(\Gamma (N)\)full congruence subgroup of level N
Definition 35.4.1
Let \(N \in \mathbb Z _{\ge 1}\). The full congruence subgroup \(\Gamma (N) \trianglelefteq {{\,\mathrm{PSL}\,}}_2(\mathbb Z )\) of level N is
To avoid confusion, from now on we will now write \(\Gamma (1)={{\,\mathrm{PSL}\,}}_2(\mathbb Z )\).
35.4.2
By strong approximation for \({{\,\mathrm{SL}\,}}_2(\mathbb Z )\) (Theorem 28.2.6), the map \({{\,\mathrm{SL}\,}}_2(\mathbb Z ) \rightarrow {{\,\mathrm{SL}\,}}_2(\mathbb Z /N\mathbb Z )\) is surjective for all \(N \ge 1\), so there is an exact sequence
Definition 35.4.3
A subgroup \(\Gamma \le \Gamma (1)\) is a congruence subgroup if \(\Gamma \ge \Gamma (N)\) for some \(N \ge 1\); if so, the minimal such N is called the level of \(\Gamma \).
Remark 35.4.4. Noncongruence subgroups (finite-index subgroups not containing \(\Gamma (N)\) for any \(N \ge 1\)) also play a role in the structure of the group \({{\,\mathrm{SL}\,}}_2(\mathbb Z )\): see the recent survey by Li–Long [LL2012] and the references therein.
35.4.5
In addition to the congruence groups \(\Gamma (N)\) themselves, we will make use of two other important congruence subgroups for \(N \ge 1\): amma0N]\(\Gamma _0(N)\), \(\Gamma _1(N)\)standard congruence subgroups of level N
Visibly, \(\Gamma (N) \le \Gamma _1(N) \le \Gamma _0(N)\). We accordingly write
where \({\mathbf {\mathsf{{H}}}}^{2*}:={\mathbf {\mathsf{{H}}}}^2\cup \mathbb P ^1(\mathbb Q )\), and similarly \(Y_1(N)\) and Y(N).
In the remainder of this section, we consider as an extended example the case \(N=2\). We can equally well write
From 35.4.2,
the nonabelian group of order 6, so in particular \([\Gamma (1):\Gamma (2)]=6\).
We can uncover the structure of the group \(\Gamma (2)\) in a manner similar to what we did for \(\Gamma (1)\) in section 35.1—the details are requested in Exercise 35.10. The group \(\Gamma (2)\) is generated by
which act on \({\mathbf {\mathsf{{H}}}}^2\) by \(z \mapsto z+2\) and \(z \mapsto z/(2z+1)\), respectively, and a fundamental set  is given in Figure 35.4.10.
is given in Figure 35.4.10.
(In fact, later we will see from more general structural results that \(\Gamma (2)\) is freely generated by these two elements, so it is isomorphic to the free group on two generators.)
The action \(\Gamma (2)\, \circlearrowright \, {\mathbf {\mathsf{{H}}}}^2\) is free: by 35.1.14, if \(\gamma z = z\) with \(z \in {\mathbf {\mathsf{{H}}}}^2\) and \(\gamma \in \Gamma (2) \le \Gamma (1)\), then \(\gamma \) is conjugate in \(\Gamma (1)\) to either S, ST; but \(\Gamma (2) \trianglelefteq \Gamma (1)\) is normal, so without loss of generality either \(S=\begin{pmatrix} 0 &{} -1 \\ 1 &{} 0 \end{pmatrix}\) or \(ST=\begin{pmatrix} 0 &{} -1 \\ 1 &{} 1 \end{pmatrix}\) belongs to \(\Gamma (2)\), a contradiction.
Let \(Y(2) :=\Gamma (2) \backslash {\mathbf {\mathsf{{H}}}}^2\). Then gluing together the fundamental set, there is a homeomorphism
The limit points of  in \({{\,\mathrm{bd}\,}}{\mathbf {\mathsf{{H}}}}^2\) are the points \(-1,0,1,\infty \) and the points \(-1,1\) are identified in the quotient (by translation). The orbit of these points under \(\Gamma (2)\) is \(\mathbb P ^1(\mathbb Q ) \subseteq {{\,\mathrm{bd}\,}}{\mathbf {\mathsf{{H}}}}^2\), so letting \({\mathbf {\mathsf{{H}}}}^{2*}={\mathbf {\mathsf{{H}}}}^2\cup \mathbb P ^1(\mathbb Q )\), there is a homeomorphism
in \({{\,\mathrm{bd}\,}}{\mathbf {\mathsf{{H}}}}^2\) are the points \(-1,0,1,\infty \) and the points \(-1,1\) are identified in the quotient (by translation). The orbit of these points under \(\Gamma (2)\) is \(\mathbb P ^1(\mathbb Q ) \subseteq {{\,\mathrm{bd}\,}}{\mathbf {\mathsf{{H}}}}^2\), so letting \({\mathbf {\mathsf{{H}}}}^{2*}={\mathbf {\mathsf{{H}}}}^2\cup \mathbb P ^1(\mathbb Q )\), there is a homeomorphism
We have a natural holomorphic projection map
via (35.4.9), the group \({{\,\mathrm{GL}\,}}_2(\mathbb F _2)\) acts on X(2) by automorphisms:
where \(\gamma \in \Gamma (1)\) is a lift, so the map (35.4.12) is obtained as the quotient by \({{\,\mathrm{GL}\,}}_2(\mathbb F _2)\).
Finally, the congruence conditions (35.4.6) imply that \(\Gamma _0(2)=\Gamma _1(2)\) has index 2 in \(\Gamma (2)\), with the quotient generated by T, and we obtain a fundamental set by identifying the two ideal triangles in  above.
above.
Exercises
-
1.
Prove that \(Y(1)={{\,\mathrm{SL}\,}}_2(\mathbb Z ) \backslash {\mathbf {\mathsf{{H}}}}^2\) has \({{\,\mathrm{area}\,}}(Y(1))=\pi /3\) by direct integration (verifying the Gauss–Bonnet formula).
-
2.
Show that \({{\,\mathrm{PSL}\,}}_2(\mathbb Z )\) is generated by T and \(U=\begin{pmatrix} 1 &{} 0 \\ 1 &{} 1 \end{pmatrix}\). [So \({{\,\mathrm{PSL}\,}}_2(\mathbb Z )\) is generated by two parabolic elements (of infinite order), just as it is generated by elements of order two and three.]
-
3.
Prove Lemma 35.1.12 using Lemma 28.3.3 (elementary matrices).
-
4.
In this exercise, we link the fact that \({{\,\mathrm{PSL}\,}}_2(\mathbb Z )\) is generated by S, T to a kind of continued fraction via the Euclidean algorithm. [So the reduction algorithm is a way to visualize the Euclidean algorithm.] Let \(a,b \in \mathbb Z _{\ge 1}\) with \(a \ge b\).
-
(a)
Show that there exist unique \(q,r \in \mathbb Z \) such that \(a=qb-r\) and \(q \ge 2\) and \(0 \le r < b\). From (a), define inductively \(r_0=a\), \(r_1=b\), and \(r_{i-1}=q_ir_i-r_{i+1}\) with \(0 \le r_{i+1} < r_i\); we then have \(r_1>r_2>\dots> r_t>r_{t+1}=0\) for some \(t>0\).
-
b)
Show that \(\gcd (a,b)=r_t\), and if \(\gcd (a,b)=1\) then
$$\begin{aligned} \frac{a}{b}=q_1 - \frac{1}{q_2-\displaystyle {\frac{1}{\cdots -\displaystyle {\frac{1}{q_t}}}}}. \end{aligned}$$Such a continued fraction is called a negative-regular or Hirzebruch–Jung continued fraction . [The Hirzebruch–Jung continued fraction plays a role in the resolution of singularities [Jun08, Hir53].]
-
c)
Show (by induction) that
$$\begin{aligned} \begin{pmatrix} 0 &{} 1 \\ -1 &{} q_t \end{pmatrix} \cdots \begin{pmatrix} 0 &{} 1 \\ -1 &{} q_1 \end{pmatrix} \begin{pmatrix} a \\ b \end{pmatrix} = \begin{pmatrix} r_t \\ 0 \end{pmatrix}. \end{aligned}$$For all \(q \in \mathbb Z \), write
$$\begin{aligned} \begin{pmatrix} 0 &{} 1 \\ -1 &{} q \end{pmatrix} \in \langle S,T \rangle \subseteq {{\,\mathrm{PSL}\,}}_2(\mathbb Z ) \end{aligned}$$as a word in S, T, and interpret the action of this matrix in terms of the reduction algorithm to the fundamental set
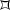 for \({{\,\mathrm{PSL}\,}}_2(\mathbb Z )\).
for \({{\,\mathrm{PSL}\,}}_2(\mathbb Z )\). -
d)
Let \(A=\begin{pmatrix} a &{} b \\ c &{} d \end{pmatrix} \in {{\,\mathrm{SL}\,}}_2(\mathbb Z )\). Show that \(\gcd (a,c)=1\) and conclude from (c) that there exists \(W \in \langle S,T \rangle \) such that
$$\begin{aligned} WA=\begin{pmatrix} 1 &{} b' \\ 0 &{} 1 \end{pmatrix} \end{aligned}$$with \(b' \in \mathbb Z \). Conclude that \(\langle S,T \rangle ={{\,\mathrm{PSL}\,}}_2(\mathbb Z )\). (So how, in the end, does this procedure to write A in terms of S and T relate to the one given by the reduction algorithm in Lemma 35.1.8?)
-
(a)
-
5.
In this exercise, we give a “matrix proof” that a complete set of relations satisfied by S, T in \({{\,\mathrm{PSL}\,}}_2(\mathbb Z )\) are \(S^2=(ST)^3=1\).
-
(a)
Show that it suffices to show that no word \(S(ST)^{e_1} S (ST)^{e_2} \dots S (ST)^{e_n}\) with \(e_i=1,2\) is equal to 1.
-
(b)
Observe that \(S(ST)=T\) and \(S(ST)^2\) have at least one off-diagonal entry nonzero and can be represented with a matrix whose entries all have the same sign.
-
(c)
Show that if \(A=\begin{pmatrix} a &{} b \\ c &{} d \end{pmatrix}\) has at least one off-diagonal entry nonzero and all entries of the same sign, then these properties hold also for both S(ST)A and \(S(ST)^2A\). Conclude that (a) holds.
[This argument is given by Fine [Fin89, Theorem 3.2.1].]
-
(a)
-
6.
Show that the commutator subgroup \(\Gamma ' \trianglelefteq \Gamma ={{\,\mathrm{PSL}\,}}_2(\mathbb Z )\) (the subgroup generated by commutators \(\gamma \delta \gamma ^{-1}\delta ^{-1}\) for \(\gamma ,\delta \in \Gamma \)) has index 6 and \(\Gamma /\Gamma ' \simeq \mathbb Z /6\mathbb Z \).
-
7.
Compute the class number h(d) and the set of reduced (positive definite) binary quadratic forms of discriminant \(d=-71\).
-
8.
Let \(\mathcal Q _d\) be the set of primitive, positive definite binary quadratic forms of discriminant \(d<0\) and let \(\mathcal Q =\bigcup _d \mathcal Q _d\).
-
(a)
Show that the group \({{\,\mathrm{GL}\,}}_2(\mathbb Z )\) acts naturally on \(\mathcal Q \) by change of variables, with \({{\,\mathrm{PGL}\,}}_2(\mathbb Z )\) acting faithfully.
-
(b)
Consider the action of \({{\,\mathrm{PGL}\,}}_2(\mathbb Z )\) on \({\mathbf {\mathsf{{H}}}}^2\). Show that every \(Q \in \mathcal Q _d\) is equivalent to a \({{\,\mathrm{GL}\,}}_2(\mathbb Z )\) -reduced form \(ax^2+bxy+cy^2\) satisfying
$$\begin{aligned} 0 \le b \le a \le c. \end{aligned}$$[Hint: Find a nice fundamental set
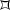 for \({{\,\mathrm{PGL}\,}}_2(\mathbb Z )\).]
for \({{\,\mathrm{PGL}\,}}_2(\mathbb Z )\).] -
(c)
By transport, 35.1.14 computes the stabilizer of \({{\,\mathrm{PSL}\,}}_2(\mathbb Z )\) on \(Q \in \mathcal Q _d\). Compute \({{\,\mathrm{Stab}\,}}_{{{\,\mathrm{PGL}\,}}_2(\mathbb Z )}(Q)\) for \(Q \in \mathcal Q _d\).
-
(a)
-
\(\triangleright \) 9. Let
$$\begin{aligned} S=\mathbb Z \oplus \mathbb Z [(d+\sqrt{d})/2] \subset K=\mathbb Q (\sqrt{d}) \end{aligned}$$be the quadratic ring of discriminant \(d<0\). Let \({{\,\mathrm{Pic}\,}}(S)\) be the group of invertible fractional ideals of S modulo principal ideals. Show that the map
$$\begin{aligned} \mathcal Q _d/\Gamma&\rightarrow {{\,\mathrm{Pic}\,}}(S) \\ [ax^2+bxy+cy^2]&\mapsto [\mathfrak a ]=\left[ \left( a,\frac{-b+\sqrt{d}}{2}\right) \right] \end{aligned}$$is a bijection, where \(\mathcal Q _d/\Gamma \) is the set of (\({{\,\mathrm{SL}\,}}_2(\mathbb Z )\)-)equivalence classes of (primitive, positive definite) binary quadratic forms of discriminant d.
-
\(\triangleright \) 10. Show that the elements
$$\begin{aligned} \begin{pmatrix} 1 &{} 2 \\ 0 &{} 1 \end{pmatrix}, \begin{pmatrix} 1 &{} 0 \\ 2 &{} 1 \end{pmatrix} \end{aligned}$$generate \(\Gamma (2)\) using the fundamental set
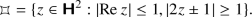
[Hint: adapt the method used in section 35.1.]
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
This chapter is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, duplication, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, a link is provided to the Creative Commons license and any changes made are indicated.The images or other third party material in this chapter are included in the work's Creative Commons license, unless indicated otherwise in the credit line; if such material is not included in the work's Creative Commons license and the respective action is not permitted by statutory regulation, users will need to obtain permission from the license holder to duplicate, adapt or reproduce the material.
Copyright information
© 2021 The Author(s)
About this chapter
Cite this chapter
Voight, J. (2021). Classical modular group. In: Quaternion Algebras. Graduate Texts in Mathematics, vol 288. Springer, Cham. https://doi.org/10.1007/978-3-030-56694-4_35
Download citation
DOI: https://doi.org/10.1007/978-3-030-56694-4_35
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-56692-0
Online ISBN: 978-3-030-56694-4
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)






 in
in 





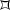 for
for 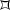 for
for