Abstract
Our ongoing goal in this part of the text is to understand quotient spaces that locally look like (products of) hyperbolic spaces. In order to get off the ground, here we put the previous two chapters in a more general context, seeking to understand nice group actions on topological spaces and indicating how these fit in with more general notions in topology. Pathologies exist! Our goal in this chapter is to provide basic context (for further references see 34.5.4) before turning to the central case of interest: a discrete group acting properly on a locally compact, Hausdorff topological space.
You have full access to this open access chapter, Download chapter PDF
Our ongoing goal in this part of the text is to understand quotient spaces that locally look like (products of) hyperbolic spaces. In order to get off the ground, here we put the previous two chapters in a more general context, seeking to understand nice group actions on topological spaces and indicating how these fit in with more general notions in topology. Pathologies exist! Our goal in this chapter is to provide basic context (for further references see 34.5.4) before turning to the central case of interest: a discrete group acting properly on a locally compact, Hausdorff topological space.
1 Topological group actions
Group actions will figure prominently in what follows, so we set a bit of notation. There are many references for topological groups, including Arhangel’skii–Tkachenko [AT2008, Chapter 1] and McCarty [McC2011, Chapter V].
Let G be a group and let X be a set. Recall that a left action of G on X is a map
satisfying \(1x=x\) and \((gg')x=g(g'x)\) for all \(x \in X\) and all \(g,g' \in G\). A right action is instead a map \(X \times G \rightarrow X\) by \((x,g) \mapsto xg\) satisfying \(x1=x\) and \(x(g'g)=(xg')g\) for all \(x \in X\) and \(g,g' \in g\). We will need to consider actions both on the left and the right; if not specified, a left action is assumed.
We will also sometimes write \(G \circlearrowright X\) for an action of G on X.
Example 34.1.2
A group G acts on itself by left multiplication, the (left) regular group action of G. If \(H \le G\) is a subgroup, then H also acts on G by left multiplication. For example, if V is an \(\mathbb R \)-vector space with \(\dim _\mathbb R V=n\), and \(\Lambda \subseteq V\) is a (full) \(\mathbb Z \)-lattice in V, then \(\Lambda \simeq \mathbb Z ^n\) is a group and \(\Lambda \) acts on V by translation.
Another important and related example is the left action of G on the set of right cosets \(X=G/H\) again by multiplication, namely
Let G act on X. The G- orbit of \(x \in X\) is \(Gx=\{gx : g \in G \}\). The set of G-orbits forms the quotient set \(G \backslash X = \{Gx : x \in X\}\), with a natural surjective quotient map \(\pi :X \rightarrow G \backslash X\).
Remark 34.1.3. We write \(G \backslash X\) for the quotient, as G acts on the left; for a right action, we write X/G, etc.
Example 34.1.4
A group G acts transitively on a nonempty set X if and only if \(G \backslash X\) is a single point; in this case, we call X homogeneous under G. In particular, if \(H \le G\), then the action of G on G/H is transitive.
If \(H \le G\), then the quotient set \(H \backslash G\) is the set of left cosets of H in G. For example, if \(\Lambda =\mathbb Z ^n \le \mathbb R ^n=V\), then \(\Lambda \backslash V \simeq (\mathbb R /\mathbb Z )^n\).
For \(x \in X\), we define the stabilizer of x by \({{\,\mathrm{Stab}\,}}_G(x) = \{g \in G : gx=x\}\).
Definition 34.1.5
The action of G on X is free (and we say G acts freely on X) if \({{\,\mathrm{Stab}\,}}_G(x)=\{1\}\) for all \(x \in X\), i.e., \(gx=x\) implies \(g=1\) for all \(x \in X\).
Definition 34.1.6
Let \(X',X\) be sets with an action of G. A map \(f:X' \rightarrow X\) is G -equivariant if \(f(gx')=g(f(x'))\) for all \(x' \in X'\) and \(g \in G\), i.e., the following diagram commutes:

If \(f:X' \rightarrow X\) is G-equivariant, then f induces a map
well-defined by the G-equivariance of f, and the following diagram commutes:

Now topology enters. Let G be a topological group (Definition 12.2.1), a group with a topology in which the multiplication and inversion maps are continuous. Let X be a topological space, and let G act on X. We want to consider only those actions in which the topology on G and on X are compatible.
Definition 34.1.8
The action of G on X is continuous if the map \(G \times X \rightarrow X\) is continuous.
Example 34.1.9
The left regular action of a group on itself is continuous—indeed, combined with continuity of inversion (and existence of the identity), this is the very definition of a topological group.
Lemma 34.1.10
Suppose G has the discrete topology. Then an action of G on X is continuous if and only if for all \(g \in G\) the left-multiplication map
is continuous; and when this holds, each \(\lambda _g\) is a homeomorphism.
Proof. Exercise 34.2. \(\square \)
From now on, suppose G acts continuously on X; more generally, whenever G is a topological group acting on a topological space X, we will implicitly suppose that the action is continuous.
34.1.11
The quotient \(G \backslash X\) is equipped with the quotient topology, so that the quotient map \(\pi :X \rightarrow G \backslash X\) is continuous: a subset \(V \subseteq G \backslash X\) is open if and only if \(\pi ^{-1}(V) \subseteq X\) is open.
The projection \(\pi \) is an open map, which is to say if \(U \subseteq X\) is open then \(\pi (U)=GU \subseteq G \backslash X\) is open: if U is open then \(\pi ^{-1}(\pi (U))=\bigcup _{g \in G} gU\) is open, so \(\pi (U)\) is open by definition of the topology.
34.1.12
If G acts continuously on X, then the topologies on G and X are related by this action. In particular, for all \(x \in X\), the natural map
is continuous (it is the restriction of the action map to \(G \times \{x\}\)). Let \(K={{\,\mathrm{Stab}\,}}_G(x)\). Then this map factors naturally as

where we give G/K the quotient topology; then (34.1.13) then a bijective continuous map, a topological upgrade of the orbit–stabilizer theorem. The map (34.1.13) need not always be a homeomorphism (Exercise 34.5), but we will see below that it becomes a homeomorphism under further nice hypotheses (Exercise 34.6, Proposition 34.4.11).
In order to work concretely with the quotient \(G \backslash X\), it is convenient to choose representatives of each orbit as follows. We write \({{\,\mathrm{cl}\,}}\) for topological closure and \({{\,\mathrm{int}\,}}\) for topological interior.
Definition 34.1.14
A fundamental set for \(G \circlearrowright X\) is a subset  such that:
such that:
-
(i)
 ;
; -
(ii)
 ; and
; and -
(iii)
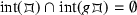 for all \(1 \ne g \in G\).
for all \(1 \ne g \in G\).
The condition (i) ensures our basic intuition about tilings (and avoids fundamental sets that contain an extraneous number of isolated points); condition (ii) says that  tiles X; and condition (iii) shows that the tiles only overlap along the boundary, and there is no redundancy in the interior. If there is a fundamental set for \(G \circlearrowright X\), then the action is faithful.
tiles X; and condition (iii) shows that the tiles only overlap along the boundary, and there is no redundancy in the interior. If there is a fundamental set for \(G \circlearrowright X\), then the action is faithful.
34.1.15
Let  be a fundamental set for \(G \circlearrowright X\). Then G induces an equivalence relation on
be a fundamental set for \(G \circlearrowright X\). Then G induces an equivalence relation on  , and
, and  is a bijection.
is a bijection.
Remark 34.1.16. In chapter 37, we place further restrictions on a fundamental set to ensure that they retain good properties, calling such a set a fundamental domain (Definition 37.1.11).
2 \(\triangleright \) Summary of results
We pause to provide a quick summary of the results in this chapter for the special case of discrete subgroups of \({{\,\mathrm{PSL}\,}}_2(\mathbb R )\) (proven in Theorem 34.5.1 and Proposition 34.7.2). The reader who is willing to accept the theorem below, and will stick to this case, can profitably skip the rest of this chapter.
The group \({{\,\mathrm{PSL}\,}}_2(\mathbb R )\) has a natural topology from the metric on \({{\,\mathrm{SL}\,}}_2(\mathbb R ) \subseteq {{\,\mathrm{M}\,}}_2(\mathbb R )\) (see 34.6.1): intuitively, two matrices in \({{\,\mathrm{PSL}\,}}_2(\mathbb R )\) are close if after a choice of sign all of their entries are close.
Theorem 34.2.1
Let \(\Gamma \le {{\,\mathrm{PSL}\,}}_2(\mathbb R )\) be a subgroup and equip \(\Gamma \) with the subspace topology. Then the following are equivalent:
-
(i)
\(\Gamma \) is discrete;
-
(ii)
For all
 , we have
, we have 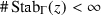 and there exists an open neigborhood \(U \ni z\) such that \(\gamma U \cap U \ne \emptyset \) implies \(\gamma \in {{\,\mathrm{Stab}\,}}_\Gamma (z)\);
and there exists an open neigborhood \(U \ni z\) such that \(\gamma U \cap U \ne \emptyset \) implies \(\gamma \in {{\,\mathrm{Stab}\,}}_\Gamma (z)\); -
(iii)
For all compact subsets \(K \subseteq {{\mathbf {\mathsf{{{{H}}}}}}}^2\), we have \(K \cap \gamma K \ne \emptyset \) for only finitely many \(\gamma \in \Gamma \); and
-
(iv)
For all
 , the orbit \(\Gamma z \subseteq {{\mathbf {\mathsf{{{{H}}}}}}}^2\) is discrete and \(\#{{\,\mathrm{Stab}\,}}_\Gamma (z)<\infty \).
, the orbit \(\Gamma z \subseteq {{\mathbf {\mathsf{{{{H}}}}}}}^2\) is discrete and \(\#{{\,\mathrm{Stab}\,}}_\Gamma (z)<\infty \).
Moreover, if these equivalent conditions hold, then the quotient \(\Gamma \backslash {{\mathbf {\mathsf{{{{H}}}}}}}^2\) is Hausdorff, and the quotient map \(\pi :{{\mathbf {\mathsf{{{{H}}}}}}}^2\rightarrow \Gamma \backslash {{\mathbf {\mathsf{{{{H}}}}}}}^2\) is a local isometry at all points \(z \in {{\mathbf {\mathsf{{{{H}}}}}}}^2\) with \({{\,\mathrm{Stab}\,}}_\Gamma (z)=\{1\}\).
A discrete subgroup \(\Gamma \le {{\,\mathrm{PSL}\,}}_2(\mathbb R )\) is called a Fuchsian group.
3 Covering space and wandering actions
Throughout the remainder of this chapter, let X be a Hausdorff topological space with a (continuous) action of a Hausdorff topological group G.
Definition 34.3.1
We say the action of G on X is a covering space action if for all \(x \in X\), there exists an open neighborhood \(U \ni x\) such that \(gU \cap U = \emptyset \) for all \(g \in G\) with \(g \ne 1\).
34.3.2
If \(G \circlearrowright X\) is a covering space action, then the quotient map \(\pi :X \rightarrow G \backslash X\) is a local homeomorphism, i.e., for every \(x \in X\), there exists an open neighborhood \(U \ni x\) such that \(\pi |_U :U \rightarrow \pi (U) \subseteq G \backslash X\) is a homeomorphism. A local homeomorphism need not conversely be a covering space map.
If G acts by a covering space action, then G acts freely on X. This is too strong a hypothesis on the group actions we will consider in the rest of this book, so we need to look for something weaker. So we consider the following.
Definition 34.3.3
We say that the action of G is wandering if for all \(x \in X\), there exists an open neighborhood \(U \ni x\) such that \(gU \cap U \ne \emptyset \) for only finitely many \(g \in G\).
Example 34.3.4
If G is a finite group, then every action of G is wandering.
34.3.5
If the action of G is wandering, then for all \(x \in X\), the orbit \(Gx \subseteq X\) is closed and discrete.
Wandering actions generalize covering space actions, and can be equivalently characterized, as follows.
Lemma 34.3.6
The following are equivalent:
-
(i)
The action of G is wandering; and
-
(ii)
For all \(x \in X\) we have \(\#{{\,\mathrm{Stab}\,}}_G(x)<\infty \), and there exists an open neighborhood \(U \ni x\) such that \(gU \cap U \ne \emptyset \) implies \(g \in {{\,\mathrm{Stab}\,}}_G(x)\).
If G acts freely, then these are further equivalent to:
-
(iii)
The action of G is by a covering space action.
Proof. The implication (ii) \(\Rightarrow \) (i) is immediate; we prove the converse. Let U be a neighborhood of \(x \in X\) such that \(gU \cap U \ne \emptyset \) for only finitely many \(g \in G\). We have \(\#{{\,\mathrm{Stab}\,}}_G(x)<\infty \) since \(g \in {{\,\mathrm{Stab}\,}}_G(x)\) implies \(x \in gU \cap U\). Let
Since X is Hausdorff, for all i there exist open neighborhoods \(V_i,W_i \subseteq X\) of \(x,g_ix\), respectively, such that \(V_i \cap W_i =\emptyset \). Replacing \(V_i\) with \(V_i \cap U\) (still with \(x \in V_i\) and \(V_i \cap W_i=\emptyset \)), we may suppose that \(V_i \subseteq U\). Since G acts continuously, there exists an open neighborhood \(W_i' \subseteq X\) of x such that \(g_iW_i' \subseteq W_i\). Let \(U_i :=V_i \cap W_i'\). Since \(V_i \subseteq U\) we have \(U_i \subseteq U\) for all i. Further, \(x \in U_i\) and
We claim that \(U'=\bigcap _i U_i\) has the desired property in (ii). Suppose that \(gU' \cap U' \ne \emptyset \) for some \(g \in G\). Since \(U_i \subseteq U\) for all i we have \(U' \subseteq U\), so \(gU \cap U \ne \emptyset \); then by (34.3.7), either \(gx = x\) or \(g=g_i\) for some i. We cannot have \(g=g_i\), since this would imply \(g_iU' \cap U' \subseteq g_i U_i \cap U_i = \emptyset \), contradicting (34.3.8). So \(gx=x\), and \(g \in {{\,\mathrm{Stab}\,}}_G(x)\) as claimed.
Finally, if G acts freely, then \({{\,\mathrm{Stab}\,}}_G(x)\) is trivial for all x, whence the equivalence (ii) \(\Leftrightarrow \) (iii). \(\square \)
34.3.9
Suppose the action of G is wandering. We recall Lemma 34.3.6(ii). At a point x with open neighborhood \(U \ni x\) and finite stabilizer \({{\,\mathrm{Stab}\,}}_G(x)\), we can replace U by \(\bigcap _{g \in {{\,\mathrm{Stab}\,}}_G(x)} gU\) so that \(U \ni x\) is an open neighborhood on which \({{\,\mathrm{Stab}\,}}_G(x)\) acts (see Exercise 34.12). Then the projection map factors as
and the latter map \({{\,\mathrm{Stab}\,}}_G(x) \backslash U \rightarrow G \backslash X\) is a homeomorphism onto its image; we say \(\pi \) is a local homeomorphism modulo stabilizers. If the action of G is free, then we recover 34.3.2.
Remark 34.3.10. If G has the discrete topology and the condition in Lemma 34.3.6(ii) holds, then some authors call the action of G properly discontinuous. This is probably because G is then as broken (“discontinuous”) as possible: G has the discrete topology, and we should be able to find neighborhoods that pull apart the action of G. (Klein [Kle79, p. 321] uses the term discontinuous because “points that are ‘equivalent’ with respect to [the group] are separated”.) This nomenclature is strange because we still want the action to be continuous, just by a discrete group. Adding to the potential confusion is the issue that different authors give different definitions of “properly discontinuous” depending on their purposes; most of these can be seen to be equivalent under the right hypotheses on the space, but not all. We avoid this term.
It turns out that a wandering action is too weak a property in this level of generality for us to work with. However, it is close, and we will shortly see that it suffices with additional hypotheses on the space X.
Remark 34.3.11. Let X be a topological space, and let G be a set of continuous maps \(X \rightarrow X\). Then there is a natural map \(G \hookrightarrow X^X\) defined by \(g \mapsto (gx)_x\). We give \(X^X\) the compact-open topology and G the subspace topology, so a subbasis of the topology on G is given by
for \(K \subseteq X\) compact and \(U \subseteq X\) open.
If X is Hausdorff and locally compact, then the compact-open topology on G is the weakest topology (smallest, fewest open sets) for which the map \(G \times X \rightarrow X\) is continuous (also called an admissible topology on G) [McC2011, §VII, pp. 171–172]. Under the hypotheses of Exercise 34.4, this implies that the topology of pointwise convergence and the compact-open topology coincide.
4 Hausdorff quotients and proper group actions
In this section we define proper group actions; to motivate this definition, we first ask for conditions that imply that a quotient space is Hausdorff. Throughout this section and the next, let X be a Hausdorff topological space and let G be a Hausdorff topological group acting continuously on X.
Lemma 34.4.1
The following are equivalent:
-
(i)
The quotient \(G \backslash X\) is Hausdorff;
-
(ii)
If \(Gx \ne Gy \in G \backslash X\), then there exist open neighborhoods \(U \ni x\) and \(V \ni y\) such that \(gU \cap V = \emptyset \) for all \(g \in G\); and
-
(iii)
The image of the action map
$$\begin{aligned} \begin{aligned} G \times X&\rightarrow X \times X \\ (g,x)&\mapsto (x,gx) \end{aligned} \end{aligned}$$(34.4.2)is closed.
Proof. The implication (i) \(\Leftrightarrow \) (ii) follows directly from properties of the quotient map: the preimage of open neighborhoods separating Gx and Gy under the continuous projection map have the desired properties, and conversely the pushforward of the given neighborhoods under the open projection map separate Gx and Gy.
To conclude, we prove (i) \(\Leftrightarrow \) (iii). We use the criterion that a topological space is Hausdorff if and only if the diagonal map has closed image. The continuous surjective map \(\pi :X \rightarrow G \backslash X\) is open, so the same is true for
Therefore the diagonal \(G \backslash X \hookrightarrow (G \backslash X) \times (G \backslash X)\) is closed if and only if its preimage is closed in \(X \times X\). But this preimage consists exactly of the orbit relation
and this is precisely the image of the action map (34.4.2). \(\square \)
The conditions Lemma 34.4.1(i)–(ii) can sometimes be hard to verify, so it is convenient to have a condition that implies Lemma 34.4.1(iii); this definition will seek to generalize the situation when G is compact. First, we make a definition.
Definition 34.4.3
Let \(f:X \rightarrow Y\) be a continuous map.
-
(a)
We say \(f:X \rightarrow Y\) is quasi-proper if \(f^{-1}(K)\) is compact for all compact \(K \subseteq Y\).
-
(b)
We say f is proper if f is quasi-proper and closed (the image of every closed subset is closed).
Example 34.4.4
If X is compact, then every continuous map \(f:X \rightarrow Y\) is proper because f is closed and if \(K \subseteq Y\) is compact, then K is closed, so \(f^{-1}(K) \subset X\) is closed hence compact, since X is compact.
Lemma 34.4.5
Suppose that Y is locally compact and Hausdorff, and let \(f:X \rightarrow Y\) be continuous and quasi-proper. Then X is locally compact, and f is proper.
Proof. For the first statement, cover Y with open relatively compact sets \(U_i \subseteq K_i\); then \(V_i=f^{-1}(U_i)\) is an open cover of X by relatively compact sets.
Next, we claim that f is in fact already proper; that is to say, we show that f is closed. Let \(W \subseteq X\) be a closed set and consider a sequence \(\{y_n\}_n\) from f(W) with \(y_n \rightarrow y\). Let K be a compact neighborhood of y containing \(\{y_n\}\); taking a subsequence, we may suppose all \(y_n \in K\). Let \(x_n \in f^{-1}(y_n) \cap W\) be primages. Since f is quasi-proper, we have \(f^{-1}(K)\) is compact. Suppose for a moment that \(f^{-1}(K)\) is sequentially compact (for example, if X is second countable or metrizable). Then again taking a subsequence, we may suppose that \(x_n \rightarrow x\) with \(x \in W\) since W is closed. By continuity, \(f(x_n) \rightarrow f(x)=y\), so f(W) is closed. To avoid the extra hypothesis that \(f^{-1}(K)\) is sequentially compact, replace the sequence \(\{y_n\}\) with a net; the argument proceeds identically. \(\square \)
Remark 34.4.6. There is an alternate characterization of proper maps as follows: a continuous map \(f:X \rightarrow Y\) is proper if and only if the map \(f \times {{\,\mathrm{id}\,}}:X \times Z \rightarrow Y \times Z\) is closed for every topological space Z. See 34.5.4 for more discussion.
Partly motivated by Lemma 34.4.1(iv), we make the following definition.
Definition 34.4.7
The action of G on X is proper (G acts properly on X) if the action map
is proper.
Proposition 34.4.9
If G is compact, then every (continuous) action of G on (a Hausdorff space) X is proper.
Proof. Let \(K \subseteq X \times X\) be compact; then K is closed (because X is Hausdorff). Let \(K_1\) be the projection of K onto the first factor. Then \(K_1\) is compact, and \(\lambda ^{-1}(K)\) is a closed subset of the compact set \(G \times K_1\), so it is compact. This shows that the action map is quasi-proper. Finally, the action map is closed. We factor the map as
the first map is the graph of a continuous map to a Hausdorff space and is closed (Exercise 34.9); the second (projection) map is closed, as G is compact (by a standard application of the tube lemma). Therefore the composition of these maps is closed. \(\square \)
Example 34.4.10
If G is a finite discrete group, then G acts properly by Proposition 34.4.9.
Proper actions have many of the properties we need.
Proposition 34.4.11
Let G act properly on X. Then the following are true.
-
(a)
\(G \backslash X\) is Hausdorff.
-
(b)
The orbit \(Gx \subseteq X\) is closed for all \(x \in X\).
-
(c)
The natural map
$$\begin{aligned} \iota _x:G/{{\,\mathrm{Stab}\,}}_G(x)&\rightarrow Gx \\ g&\mapsto gx \in X \end{aligned}$$is a homeomorphism.
-
(d)
The group \({{\,\mathrm{Stab}\,}}_G(x)\) is compact for all \(x \in X\).
Proof. For part (a), by Lemma 34.4.1, it is enough to note that by definition the image of the action map \(\lambda \) in (34.4.8) is closed. Part (b) follows in the same way, as
This also implies part (c) (cf. 34.1.12): the map \(\iota _x\) is bijective and continuous, and it is also closed (whence a homeomorphism) since \(\iota _x\) is a factor of the closed map \(G \rightarrow Gx\).
Finally, for part (d), let \(\lambda :G \times X \rightarrow X \times X\) be the action map and let \(x \in X\). Then by definition that \(\lambda ^{-1}(x,x)={{\,\mathrm{Stab}\,}}_G(x) \times \{x\} \simeq {{\,\mathrm{Stab}\,}}_G(x)\), so by definition \({{\,\mathrm{Stab}\,}}_G(x)\) is compact. \(\square \)
5 Proper actions on a locally compact space
When X is locally compact, our central case of interest, there are several equivalent characterizations of a proper discrete action \(G\, \circlearrowright \, X\). For more about proper group actions and covering spaces, see Lee [Lee2011, Chapter 12].
Recall our running assumption that X and G are Hausdorff.
Theorem 34.5.1
Suppose that X is locally compact and let G act (continuously) on X. Then the following are equivalent:
-
(i)
G is discrete and acts properly on X;
-
(ii)
For all compact subsets \(K \subseteq X\), we have \(K \cap g K \ne \emptyset \) for only finitely many \(g \in G\);
-
(iii)
For all compact subsets \(K,L \subseteq X\), we have \(K \cap g L \ne \emptyset \) for only finitely many \(g \in G\); and
-
(iv)
For all \(x,y \in X\), there exist open neighborhoods \(U \ni x\) and \(V \ni y\) such that \(U \cap gV \ne \emptyset \) for only finitely many \(g \in G\).
Moreover, if X is a locally compact metric space and G acts by isometries, then these are further equivalent to:
-
(v)
The action of G on X is wandering; and
-
(vi)
For all \(x \in X\), the orbit \(Gx \subseteq X\) is discrete and \(\#{{\,\mathrm{Stab}\,}}_G(x)<\infty \).
Proof. First, we show (i) \(\Rightarrow \) (ii). Let \(\lambda :G \times X \rightarrow X \times X\) be the action map. Let \(K \subseteq X\) be compact. Then
is compact by definition. The projection of \(\lambda ^{-1}(K \times K)\) onto G is compact, and since G is discrete, this projection is finite and includes all \(g \in G\) such that \(K \cap gK \ne \emptyset \).
Next we show (ii) \(\Leftrightarrow \) (iii): The implication (ii) \(\Leftarrow \) (iii) is immediate, and conversely we apply (ii) to the compact set \(K \cup L\) to conclude
for only finitely many \(g \in G\).
Next we show (ii) \(\Rightarrow \) (iv). For all \(x \in X\), since X is locally compact there is a compact neighborhood \(K \supseteq U \ni x\), with U open and K compact. If \(U \cap gU \ne \emptyset \) then \(K \cap gK \ne \emptyset \) and this happens for only finitely many \(g \in G\).
Finally, we show (iv) \(\Rightarrow \) (i). We first show that the action map is quasi-proper, and conclude that it is proper by Lemma 34.4.5. Let \(K \subseteq X \times X\) be compact. By (iv), for all \((x,y) \in K\), there exist open neighborhoods \(U \ni x\) and \(V \ni y\) such that the set
is finite. The set \(U \times V \ni (x,y)\) is an open neighborhood of \((x,y) \in K\), and so the collection of these neighborhoods ranging over \((x,y) \in K\) is an open cover of K, so finitely many \(U_i \times V_i \ni (x_i,y_i)\) suffice, and with corresponding sets \(\#W_i<\infty \). Let \(W=\bigcup _i W_i \subseteq G\). Let \(K_1 \subseteq X\) be the projection of K onto the first coordinate. We claim that \(\lambda ^{-1}(K) \subseteq W \times K_1\). Indeed, if \(\lambda (g,x)=(x,gx) \in K\) then \(x \in K_1\) and \((x,gx) \in U_i \times V_i\) for some i, so \(gx \in gU_i \cap V_i\) and \(g \in W_i\), and thus \((g,x) \in W \times K_1\). Since \(\#W<\infty \) and \(K_1\) is compact, \(W \times K_1\) is compact; and then since K is compact, K is closed so \(\lambda ^{-1}(K) \subseteq W \times K_1\) is also closed, hence compact.
To conclude that G is discrete, we argue as follows. For all \(x \in X\), the orbit \(Gx \subseteq X\) is discrete: taking \(U=V\) and a neighborhood \(U \ni x\) with \(U \cap gU \ne \emptyset \) for only finitely many \(g \in G\), we see that \(U \cap Gx\) is finite so Gx is discrete (as X is Hausdorff). By Proposition 34.4.11(d), the map
is a homeomorphism for all \(x \in X\). Therefore, \({{\,\mathrm{Stab}\,}}_G(x)\) (the preimage of x) is an open, finite (Hausdorff) neighborhood of 1; but then \({{\,\mathrm{Stab}\,}}_G(x)\) is discrete, and transporting we conclude that the topological group G has an open cover by discrete sets, and thus G is discrete. This completes the equivalence (i)–(iv).
The implication (iv) \(\Rightarrow \) (v) holds in all cases: taking \(x=y\), the neighborhood \(U \cap V\) is as required in the definition of a wandering action. The implication (v) \(\Rightarrow \) (vi) also holds in all cases from 34.3.5 and Lemma 34.3.6.
To conclude, we show (vi) \(\Rightarrow \) (ii) under the extra hypothesis that X is a metric space with G acting by isometries. Assume for purposes of contradiction that there exist infinitely many \(g_n \in G\) such that \(K \cap g_n K \ne \emptyset \), and accordingly let \(x_n \in K\) with \(g_n x_n \in K\). The points \(x_n\) accumulate in K, so we may suppose \(x_n \rightarrow x \in K\); by taking a further subsequence, we may suppose also that \(g_n x_n \rightarrow y \in K\). We then claim that the set \(\{g_nx\}_n\) accumulates near y. Since \(\#{{\,\mathrm{Stab}\,}}_G(x)<\infty \), we may suppose without loss of generality that the points \(g_n x\) are all distinct. Then, given \(\epsilon >0\),
for n sufficiently large, so \(g_n x \rightarrow y\). Let \(h_n=g_{n+1}^{-1}g_n \in G\). By the Cauchy criterion,
for n sufficiently large. Since \(h_n x \ne x\) for all n, this contradicts that the orbit Gx is discrete, having no limit points. \(\square \)
Remark 34.5.2. The hypothesis “X is a metric space with G acting by isometries” providing the equivalent condition Theorem 34.5.1(v) is necessary: see Exercise 34.11.
34.5.3
From Lemma 34.3.6 and the implication Theorem 34.5.1(v) \(\Rightarrow \) (i), we see that proper actions generalize covering space actions when X is locally compact metric space and G acts by isometries. In fact, a more general statement is true: if G is a discrete group with a covering space action on X such that \(G \backslash X\) is Hausdorff, then G acts properly on X. The (slightly involved) proof in general is requested in Exercise 34.16.
Remark 34.5.4. Bourbaki discusses proper maps [Bou60, Chapter I, §10] and more generally groups acting properly on topological spaces [Bou60, Chapter III, §§1,4]; the definition of proper is equivalent to ours as follows. Let \(f:X \rightarrow Y\) be continuous, and say f is Bourbaki proper to mean that \(f \times {{\,\mathrm{id}\,}}:X \times Z \rightarrow Y \times Z\) is closed for every topological space Z. If f is Bourbaki proper, then f is proper [Bou60, Chapter I, §10, Proposition 6]. In the other direction, if f is proper then f is closed and \(f^{-1}(y)\) is compact for all \(y \in Y\), and this implies that f is Bourbaki proper [Bou60, Chapter I, §10, Theorem 1].
6 Symmetric space model
In this section, before proceeding with our treatment of discrete group actions in our case of interest, we pause to give a very important way to think about hyperbolic space in terms of symmetric spaces. The magical formulas in hyperbolic geometry beg for a more conceptual explanation: what is their provenance? Although it is important for geometric intuition to begin with a concrete model of hyperbolic space and ask about its isometries directly, from this point of view it is more natural to instead start with the desired group and have it act on itself in a natural way.
34.6.1
Let \(G={{\,\mathrm{SL}\,}}_2(\mathbb R )\). As a matrix group, G comes with a natural metric. The space \({{\,\mathrm{M}\,}}_2(\mathbb R ) \simeq \mathbb R ^4\) has the usual structure of a metric space, with
We give \({{\,\mathrm{SL}\,}}_2(\mathbb R ) \subset {{\,\mathrm{M}\,}}_2(\mathbb R )\) the subspace metric and \({{\,\mathrm{PSL}\,}}_2(\mathbb R )\) the quotient metric. Intuitively, in this metric \(g,h \in {{\,\mathrm{PSL}\,}}_2(\mathbb R )\) are close if there exist matrices representing g, h (corresponding to a choice of sign) with all four entries of the matrix close in \(\mathbb R \).
34.6.2
Recall from 34.1.12 that if G acts (continuously and) transitively on X, then for all \(x \in X\), the natural map \(g \mapsto gx\) gives a continuous bijection

Let \(X={\mathbf {\mathsf{{H}}}}^2\) be the hyperbolic plane and let \(G={{\,\mathrm{SL}\,}}_2(\mathbb R )\). Then G acts transitively on X. The stabilizer of \(x=i\) is the subgroup \(K={{\,\mathrm{Stab}\,}}_G(x)={{\,\mathrm{SO}\,}}(2) \le {{\,\mathrm{SL}\,}}_2(\mathbb R )\), so there is a continuous bijection

From the Iwasawa decomposition (Proposition 33.4.2), it follows that
In fact, the map (34.6.3) is a homeomorphism. To prove this, we observe the following beautiful equation: for \(g \in {{\,\mathrm{SL}\,}}_2(\mathbb R )\),
This formula follows directly from the formula (33.5.3) for distance; the calculation is requested in Exercise 34.17. It follows that the map \(G \rightarrow X\) is open, and thus (34.6.3) is a homeomorphism. In fact, by (34.6.5), if we reparametrize the metric on either \({{\,\mathrm{SL}\,}}_2(\mathbb R )/{{\,\mathrm{SO}\,}}(2)\) or \({\mathbf {\mathsf{{H}}}}^2\) by the appropriate factor involving the hyperbolic cosine, the map (34.6.3) becomes an isometry.
We conclude this section with a view to a more general setting where the above situation applies.
34.6.6
Let G be a connected, Hausdorff, locally compact topological group. We recall (section 29.3) that G has a Haar measure, a Borel measure \(\mu \) that is left-translation invariant (so \(\mu (gA)=\mu (A)\) for all Borel sets \(A \subseteq G\) and \(g \in G\)). The Haar measure is unique up to scaling, with the Haar measure on \(G=\mathbb R ^n\) the usual Lebesgue measure.
G has a maximal compact subgroup \(K \le G\), unique up to conjugation in G, and the quotient \(X=G/K\) is homeomorphic to Euclidean space—in particular, X is contractible.
A lattice \(\Gamma \le G\) is a discrete subgroup such that \(\mu (\Gamma \backslash G)<\infty \). A lattice \(\Gamma \) acts properly on X by left multiplication.
Remark 34.6.7. More generally, a (globally) symmetric space is a space of the form G/K where G is a Lie group and \(K \le G\) a maximal compact subgroup. Alternatively, it can be defined as a space where every point has a neighborhood where there is an isometry of order 2 fixing the point. For more reading on the theory of symmetric spaces, and the connection to differential geometry and Lie groups, see the book by Helgason [Hel2001].
7 Fuchsian groups
We now specialize to our case of interest and consider the group \({{\,\mathrm{PSL}\,}}_2(\mathbb R )\) acting by isometries on the geodesic space \({\mathbf {\mathsf{{H}}}}^2\). A gentle introduction to the geometry of discrete groups is provided by Beardon [Bea95], with a particular emphasis on Fuchsian groups and their fundamental domains—in the notes at the end of each chapter are further bibliographic pointers. See also Jones–Singerman [JS87].
Lemma 34.7.1
Let \(\Gamma \le {{\,\mathrm{SL}\,}}_2(\mathbb R )\). Then the following are equivalent:
-
(i)
\(\Gamma \) is discrete;
-
(ii)
If \(\gamma _n \in \Gamma \) and \(\gamma _n \rightarrow 1\), then \(\gamma _n=1\) for almost all n; and
-
(iii)
For all \(M \in \mathbb R _{>0}\), the set \(\{\gamma \in \Gamma : \Vert \gamma \Vert \le M\}\) is finite.
Proof. The equivalence (i) \(\Leftrightarrow \) (ii) is requested in Exercise 34.15. The implication (i) \(\Leftrightarrow \) (iii) follows from the fact that the ball of radius M in \({{\,\mathrm{SL}\,}}_2(\mathbb R )\) is a compact subset of \({{\,\mathrm{M}\,}}_2(\mathbb R )\), and a subset of a compact set is finite if and only if it is discrete. Slightly more elaborately, a sequence of matrices with bounded norm has a subsequence where the entries all converge; since the determinant is continuous, the limit exists in \({{\,\mathrm{SL}\,}}_2(\mathbb R )\) so \(\Gamma \) is not discrete. \(\square \)
In particular, we find from Lemma 34.7.1 that a discrete subgroup of \({{\,\mathrm{SL}\,}}_2(\mathbb R )\) is countable.
Proposition 34.7.2
Let \(\Gamma \le {{\,\mathrm{PSL}\,}}_2(\mathbb R )\) be a subgroup (with the subspace topology). Then \(\Gamma \) has a wandering action on \({{\mathbf {\mathsf{{{{H}}}}}}}^2\) if and only \(\Gamma \) is discrete.
Proof. The implication \(\Rightarrow \) is a consequence of Theorem 34.5.1(v) \(\Rightarrow \) (i). Conversely, suppose that \(\Gamma \) is discrete; we show that Theorem 34.5.1(vi) holds: that for all \(x \in X\), the orbit \(Gx \subseteq X\) is discrete and \(\#{{\,\mathrm{Stab}\,}}_G(x)<\infty \).
First we show that the stabilizer of a point is finite. We may work in the unit disc \({\mathbf {\mathsf{{D}}}}^2\) and take the point to be \(w=0 \in {\mathbf {\mathsf{{D}}}}^2\), as in 33.7.8. The stabilizer of \(w=0\) in \({{\,\mathrm{SU}\,}}(1,1)\) is \({{\,\mathrm{SO}\,}}(2) \simeq \mathbb R /(2\pi )\mathbb Z \), so its stabilizer in \(\Gamma \) is a discrete subgroup of the compact group \({{\,\mathrm{SO}\,}}(2)\) and is necessarily finite (indeed, cyclic).
Next we show that orbits of \(\Gamma \) on \({\mathbf {\mathsf{{H}}}}^2\) are discrete. We apply the identity (34.6.5). This identity with Lemma 34.7.1 shows that the orbit \(\Gamma i\) is discrete. But for all \(z \in {\mathbf {\mathsf{{H}}}}^2\), there exists \(\phi \in {{\,\mathrm{PSL}\,}}_2(\mathbb R )\) such that \(\phi (i)=z\), and conjugation by \(\phi \) induces an isomorphism  of topological groups. Since
of topological groups. Since
applying the above argument to \(\phi ^{-1}\Gamma \phi \) shows that the orbit \(\Gamma z\) is discrete. This concludes the proof.
Alternatively, here is a self-contained proof that avoids the slightly more involved topological machinery. We again work in the unit disc \({\mathbf {\mathsf{{D}}}}^2\). First we prove \((\Leftarrow )\). Since \(\Gamma \) is discrete, there is an \(\epsilon \)-neighborhood \(U \ni 1\) with \(U \subseteq {{\,\mathrm{PSU}\,}}(1,1)\) such that \(U \cap \Gamma = \{1\}\); therefore, if
then \(|b \,|>\epsilon \) or (without loss of generality) \(|a-1 \,|>\epsilon \). We claim that in either case
and thus the orbit is discrete. Indeed, if \(|b \,|>\epsilon \), then since \(|a \,|<1\) anyway immediately \(|b/a \,|>\epsilon \); if \(|a-1 \,|>\epsilon \) then \(|a \,|<1-\epsilon \) so \(|a \,|^2<1-\epsilon ^2\) and \(1/|a \,|^2>1+\epsilon ^2\), giving
For \((\Rightarrow )\), suppose that \(\Gamma \) is not discrete; then there is a sequence \(\gamma _n \in \Gamma \setminus \{1\}\) of elements such that \(\gamma _n \rightarrow 1\). Therefore, for all \(z \in {\mathbf {\mathsf{{H}}}}^2\), we have \(\gamma _n z \rightarrow z\) and \(\gamma _n z = z\) for only finitely many n, so every neighborhood of z contains infinitely many distinct points \(\gamma _n z\). \(\square \)
With this characterization, we make the following important definition.
Definition 34.7.3
A Fuchsian group is a discrete subgroup of \({{\,\mathrm{PSL}\,}}_2(\mathbb R )\).
A Fuchsian group \(\Gamma \) acts by orientation-preserving isometries on \({\mathbf {\mathsf{{H}}}}^2\); this action is proper and wandering by Theorem 34.5.1.
34.7.4
A Fuchsian group \(\Gamma \le {{\,\mathrm{PSL}\,}}_2(\mathbb R )\) is elementary if there is a nonempty \(\Gamma \)-invariant set in \({\mathbf {\mathsf{{H}}}}^2\cup {{\,\mathrm{bd}\,}}{\mathbf {\mathsf{{H}}}}^2\) that contains at most two points. Equivalently, an elementary group is a cyclic subgroup or a (possibly) dihedral group—in particular, an elementary group is virtually abelian (has a finite index, abelian subgroup). The elementary groups are easy to analyze, but their inclusion into theorems about more general Fuchsian groups can cause problems; and so in general we are only interested in non-elementary groups.
Non-elementary Fuchsian groups \(\Gamma \) are categorized by the set of limit points \(L(\Gamma ) \subseteq {{\,\mathrm{bd}\,}}{\mathbf {\mathsf{{H}}}}^2\) of \(\Gamma z\) with \(z \in {\mathbf {\mathsf{{H}}}}^2\). If \(L(\Gamma )={{\,\mathrm{bd}\,}}{\mathbf {\mathsf{{H}}}}^2\), then \(\Gamma \) is said to be a Fuchsian group of the first kind; otherwise \(\Gamma \) is of the second kind, and \(L(\Gamma )\) is a nowhere-dense perfect subset of \({{\,\mathrm{bd}\,}}{\mathbf {\mathsf{{H}}}}^2\), topologically a Cantor set. We will see later that if \(\Gamma \) has quotient with finite hyperbolic area, then \(\Gamma \) is finitely generated of the first kind.
8 Riemann uniformization and orbifolds
Our understanding of group actions has an important consequence for the classification of Riemann surfaces, and we pause (again) to provide this application.
First, we have the important structural result.
Theorem 34.8.1
(Riemann uniformization theorem). Every (connected and) simply connected Riemann surface H is isomorphic to either the Riemann sphere \(\mathbb P ^1(\mathbb C )\), the complex plane \(\mathbb C \), or the hyperbolic plane \({{\mathbf {\mathsf{{{{H}}}}}}}^2\).
A consequence of Riemann uniformization is as follows.
34.8.2
The universal cover \(\widetilde{X}\) of a compact Riemann surface X is simply connected, so by the theory of covering spaces, X is a quotient \(X\simeq \Gamma \backslash \widetilde{X}\) where \(\Gamma \) is the fundamental group of X, a subgroup of isometries of \(\widetilde{X}\) acting by a covering space action.
When \(\widetilde{X}=\mathbb P ^1(\mathbb C )\), the only possible group \(\Gamma \) (acting freely) is trivial. When \(\widetilde{X}=\mathbb C \), by classification one sees that the only Riemann surfaces of the form \(X=\mathbb C /\Gamma \) are the plane \(X=\mathbb C \), the punctured plane \(\mathbb C ^\times \simeq \mathbb C /\langle u \rangle \) with \(u \in \mathbb C ^\times \), and complex tori \(\mathbb C /\Lambda \) where \(\Lambda \subset \mathbb C \) is a lattice with \(\Lambda \simeq \mathbb Z ^2\). We will embark on a classification of these tori up to isomorphism by their j-invariants in section 40.1.
All other Riemann surfaces are hyperbolic with \(\widetilde{X}={\mathbf {\mathsf{{H}}}}^2\), and so are of the form \(X=\Gamma \backslash {\mathbf {\mathsf{{H}}}}^2\) with \(\Gamma \le {{\,\mathrm{PSL}\,}}_2(\mathbb R )\) a torsion-free Fuchsian group.
Remark 34.8.3. Klein and Poincaré conjectured the uniformization theorem for algebraic curves over \(\mathbb C \), with rigorous proofs were given by Poincaré: see Gray [Gray94].
Finally, before departing our topological treatment, we consider quotients of manifolds by the (continuous) action of a group. As we have seen, it is quite restrictive to suppose that this group action is free: we will still want to take quotients by such groups. Accordingly, we need to model not spaces that are locally modelled by \(\mathbb R ^n\) but those that are locally modelled by the quotient of \(\mathbb R ^n\) by a finite group.
Definition 34.8.4
An n -orbifold X is a (second-countable) Hausdorff topological space that is locally homeomorphic to a quotient \(G \backslash \mathbb R ^n\) with G a finite group acting (continuously). An atlas for an orbifold X is the data
-
(i)
An open cover \(\{U_i\}_{i \in I}\) of charts \(U_i\) closed under finite intersection; and
-
(ii)
For each \(i \in I\), an open subset \(V_i \subseteq \mathbb R ^n\) equipped with the (continuous) action of a finite group \(G_i \circlearrowright V_i\), and a homeomorphism

satisfying the atlas axiom: for all \(U_i \subseteq U_j\), there exists an injective group homomorphism \(f_{ij}:G_i \hookrightarrow G_j\) and a \(G_i\)-equivariant map \(\psi _{ij}:V_i \hookrightarrow V_j\) satisfying \(\phi _j \circ \psi _{ij} = \phi _i\) (see Figure 34.8.5).
Orbifolds were introduced by Thurston [Thu97, Chapter 13], who adds a wealth of motivation and examples; see also the surveys by Scott [Sco83, §2] and Gordon [Gor2012] as well as the chapter by Ratcliffe [Rat2006, Chapter 13].
34.8.6
We can further ask that the transition maps \(f_{ij}\) in an atlas be smooth to get a smooth orbifold, preserve a \(G_i\)-Riemannian metric to get a Riemann orbifold, etc.; replacing \(\mathbb R ^n\) by \(\mathbb C ^n\) and smooth by holomorphic, we similarly define a n complex n -orbifold, locally modelled on the quotient \(G \backslash \mathbb C ^n\) with G a finite group acting holomorphically.
Definition 34.8.7
Let X be an n-orbifold.
-
(a)
A point \(z \in X\) such that there exists a chart \(U_i \ni z\) with group \(G_i \ne \{1\}\) fixing z is called an orbifold point of X, with stabilizer group (or isotropy group) \(G_i\); the set of orbifold points of X is called the orbifold set of X.
-
(b)
If \(z \in U_i\) is an isolated orbifold point and its stabilizer group is cyclic, we call z a cone point.
34.8.8
The prototypical example of an orbifold is the quotient of \(\mathbb C \) by a finite group of rotations. Such a group is necessarily cyclic (as a finite subgroup of \(\mathbb C ^\times \)) of some order \(m \ge 2\); the quotient is a cone, a fundamental set for the action being a segment with angle \(2\pi /m\), and the fixed point is a cone point of order m. The cone is homeomorphic to \(\mathbb R ^2\) but it is not isometric: away from the cone point, this space is locally isometric to \(\mathbb R ^2\), but at the cone point the angle is less than \(2\pi \), so shortest paths that do not start or end at the cone point never go through the cone point.
34.8.9
Let X be a manifold and let G be a finite group acting (continuously) on X such that action of G is wandering (Definition 34.3.3). We define an orbifold [X/G] as follows: by Lemma 34.3.6 and 34.3.9, we can refine an atlas of X to one consisting of open neighborhoods \(U_i\) on which \(G \circlearrowright U_i\) acts, and we make this into an orbifold atlas by taking \(G_i=G\) for each i; the atlas axiom is tautologically satisfied.
When X is smooth, complex, Riemann, etc., we ask that G act diffeomorphically, holomorphically, etc., to obtain an orbifold with the same properties.
A full, suitable definition of the category of orbifolds—in particular, morphisms between them—is more subtle than it may seem. In this text, we will be primarily interested in an accessible and well-behaved class of orbifolds obtained as the quotient of a manifold.
Definition 34.8.10
An orbifold is good if is of the form [X/G], i.e., it arises as the quotient of a manifold by a finite group.
34.8.11
The quotient [X/G] of a Riemannian manifold X by a discrete group G of isometries acting properly is a good Riemann orbifold.
Example 34.8.12
A complex 1-orbifold is good if and only if it has a branched cover by a Riemann surface. By Exercise 34.18, the only complex 1-orbifolds that are not good are the teardrop, a sphere with one cone point, and the football, a sphere with two cone points of different orders.
34.8.13
Good (topological) compact, oriented 2-orbifolds admit a classification (extending the usual classification of surfaces by genus) up to homeomorphism by their signature \((g;e_1,\dots ,e_k)\), where g is the genus of the underlying topological surface and the \(e_1,\dots ,e_k\) are the orders of the (necessarily cyclic) nontrivial stabilizer groups.
34.8.14
Putting these two pieces together, now let \(\Gamma \le {{\,\mathrm{PSL}\,}}_2(\mathbb R )\) be a Fuchsian group. Then the discrete group \(\Gamma \circlearrowright {\mathbf {\mathsf{{H}}}}^2\) acts properly. Then \(\Gamma \backslash {\mathbf {\mathsf{{H}}}}^2\) has the structure of a good complex 1-orbifold, by the main theorem (Theorem 34.2.1(ii)).
Remark 34.8.15. From certain topological points of view, especially with an eye towards generalizations, an orbifold is best understood as a topological groupoid (a point of view first noticed by Haefliger [Hae84, §4]): the objects of the category are elements of the disjoint union of the charts \(U_i\), and a morphism from \(u_i \in U_i\) to \(u_j \in U_j\) is the germ of a local homeomorphism that commutes with the projections. For more on the categorical perspective of orbifolds as groupoids, see Moerdijk [Moe2002] and Moerdijk–Pronk [MP1997].
Exercises
Unless otherwise specified, let \(G \circlearrowright X\) be an action of a group G on a set X.
-
1.
Show that the quotient map \(\pi :X \rightarrow G \backslash X\) is defined by a universal property: if \(f:X \rightarrow Z\) is a G-equivariant map where Z has a trivial G-action, then f factors uniquely through \(\pi \), i.e., there exists a unique map \(h:G \backslash X \rightarrow Z\) making the diagram

commute.
- \(\triangleright \) 2.:
-
Prove Lemma 34.1.10, in the following form. Let G be a topological group acting on a topological space X.
- (a):
-
Show that if the action is continuous, then for all \(g \in G\) the map \(X \rightarrow X\) by \(x \mapsto gx\) is continuous (therefore, a homeomorphism).
- (b):
-
Show the converse of (a) if G is discrete.
-
3.
Let G be a topological group acting continuously on a topological space X. Show that the orbits of G are closed (\(Gx \subseteq X\) is closed for all \(x \in X\)) if and only if \(G \backslash X\) is \(T _1\) (see Exercise 12.2).
-
4.
Let X be a metric space. Then \({{\,\mathrm{Isom}\,}}(X)\) has naturally the topology of pointwise convergence, as follows. There is an embedding
$$\begin{aligned} {{\,\mathrm{Isom}\,}}(X)&\hookrightarrow X^X=\prod _{x \in X} X \\ g&\mapsto (g(x))_{x \in X}. \end{aligned}$$The product \(X^X\) has the product topology, and so \({{\,\mathrm{Isom}\,}}(X)\) (and every space of maps from X to X) has an induced subspace topology. A basis of open sets for \({{\,\mathrm{Isom}\,}}(X)\) in this topology consists of finite intersections of open balls
$$\begin{aligned} V(g;x,\epsilon )=\{h \in {{\,\mathrm{Isom}\,}}(X) : \rho (g(x),h(x)) < \epsilon \}. \end{aligned}$$Equip the group \(G={{\,\mathrm{Isom}\,}}(X)\) with the topology of pointwise convergence.
-
(a)
Show that G is a topological group.
-
(b)
Show that G acts continuously on X.
-
(a)
-
5.
Let \(G=\mathbb Z \) be given the discrete topology, and let \(G \circlearrowright X=\mathbb R /\mathbb Z \) act by \({x \mapsto x+na \in \mathbb R /\mathbb Z }\) for \(n \in \mathbb Z \) for \(a \in \mathbb R - \mathbb Q \). Show that this action is free and continuous, and show that for all \(x \in X\) the map (34.1.13)
$$\begin{aligned} G/{{\,\mathrm{Stab}\,}}_G(x) = G&\rightarrow Gx \\ g&\mapsto gx \end{aligned}$$is (continuous and bijective but) not a homeomorphism, giving \(Gx \subseteq X\) the subspace topology.
- \(\triangleright \) 6.:
-
Let G act (continuously and) transitively on X. Suppose that G, X are (Hausdorff and) locally compact, and suppose further that G has a countable base of open sets. Let \(x \in X\) and let \(K={{\,\mathrm{Stab}\,}}_G(x)\). Show that the natural map \(G/K \rightarrow X\) is a homeomorphism.
-
7.
Let \(G \circlearrowright X\) be a free and wandering action, and let U be an open set such that \(gU \cap U=\emptyset \) for all \(g \ne 1\). Show that the map \(G \times U \rightarrow \pi ^{-1}(\pi (U))\) is a homeomorphism and the restriction \(\pi :G \times U \rightarrow \pi (U) \simeq U\) is a (split) covering map.
-
8.
Let X be (Hausdorff and) locally compact, let \(x \in X\), and let \(U \ni x\) be an open neighborhood. Show that there exists an open neighborhood \(V \ni x\) such that \(K={{\,\mathrm{cl}\,}}(V) \subseteq U\) is compact.
- \(\triangleright \) 9.:
-
Let X, Y be (Hausdorff) topological spaces, let \(f:X \rightarrow Y\) be a continuous map, and let
$$\begin{aligned} {{\,\mathrm{gr}\,}}(f):X&\rightarrow X \times Y \\ x&\mapsto (x,f(x)) \end{aligned}$$be the graph of f. Show that f is a closed map.
-
10.
One way to weaken the running hypothesis that X is Hausdorff in this chapter is to instead assume only that X is locally Hausdorff: every \(x \in X\) has an open neighborhood \(U \ni x\) such that U is Hausdorff.
Show that a weakened version of Lemma 34.3.6(i) \(\Rightarrow \) (ii) is not true with only the hypothesis that X is locally Hausdorff: that is, exhibit a locally Hausdorff topological space X with a (continuous) wandering action of a group G such that \(\pi :X \rightarrow G \backslash X\) is not a local homeomorphism, and so Lemma 34.3.6(ii) does not hold. [Hint: Let X be the bug-eyed line and \(G \simeq \mathbb Z /2\mathbb Z \) acting by \(x \mapsto -x\) on \(\mathbb R ^\times \) and swapping points in the doubled origin.]
-
11.
Let \(G=\mathbb Z \) and let \(G \hookrightarrow X=\mathbb R ^2 \smallsetminus \{(0,0)\}\) act by \(n\cdot (x,y) = (2^n x, y/2^n)\). In other words, G is the group of continuous maps \(X \rightarrow X\) generated by \((x,y) \mapsto (2x,y/2)\).
-
(a)
Show that the action of G on X is free and wandering.
-
(b)
Show that the quotient \(G \backslash X\) is not Hausdorff.
-
(c)
Let \(K=\{(t,1-t) : t \in [0,1]\}\). Then K is compact. Show that \({K \cap g K \ne \emptyset }\) for infinitely many \(g \in G\). [So Theorem 34.5.1(v) holds but (ii) does not, and in particular that the action of G is not proper. Can you see this directly from the definition of proper?]
-
(a)
-
12.
Let X be a Hausdorff topological space with a continuous action of a Hausdorff topological group G. Suppose that the action of G is wandering. Show that for all \(x \in X\), there is an open neighborhood \(U \ni x\) such that the finite group \({{\,\mathrm{Stab}\,}}_G(x)\) acts on U (i.e., \(gU \subseteq U\) for all \(g \in {{\,\mathrm{Stab}\,}}_G(x)\)).
-
13.
Show that a subgroup \(\Gamma \le \mathbb R ^n\) is discrete if and only if \(\Gamma =\mathbb Z v_1 + \dots + \mathbb Z v_m\) with \(v_1,\dots ,v_m \in \Gamma \) linearly independent over \(\mathbb R \). As a consequence, show that \(\Gamma \le \mathbb R ^n\) is a lattice if and only if \(\Gamma \) is discrete with \(m=n\).
-
14.
Exhibit an injective group homomorphism \({{\,\mathrm{SO}\,}}(n) \hookrightarrow {{\,\mathrm{SO}\,}}(n+1)\) and a homeomorphism
$$\begin{aligned} {\mathbf {\mathsf{{S}}}}^n \simeq {{\,\mathrm{SO}\,}}(n+1)/{{\,\mathrm{SO}\,}}(n), \end{aligned}$$where \({{\mathbf {\mathsf{{S}}}}^n=\{x \in \mathbb R ^{n+1} : \Vert x \Vert ^2=1\}}\) is the n-dimensional sphere, analogous to (34.6.3).
- \(\triangleright \) 15.:
-
Let G be a topological group with a countable system of fundamental open neighborhoods of \(1 \in G\) (for example, this holds if G is metrizable). Show that G is discrete if and only if whenever \(\{g_n\}_n\) is a sequence from G with \(g_n \rightarrow 1\), then \(g_n=1\) for all but finitely many n.
-
16.
Let G be a discrete group with a (continuous) covering space action on a Hausdorff space X such that \(G \backslash X\) is Hausdorff. Show that G acts quasi-properly on X.
- \(\triangleright \) 17.:
-
Show that for \(g \in {{\,\mathrm{SL}\,}}_2(\mathbb R )\),
$$\begin{aligned} \Vert g\Vert ^2 = 2\cosh \rho (i,gi) \end{aligned}$$
-
18.
-
(a)
Show that a compact, complex 1-orbifold is good if and only if it has a branched cover by a compact Riemann surface.
-
(b)
Use the Riemann–Hurwitz theorem to show that the only compact, complex 1-orbifolds that are not good are the teardrop (a sphere with one cone point) and the football (a sphere with two cone points of different orders).
-
(c)
Show that every finitely generated discrete group of isometries of a simply connected Riemann surface with compact quotient has a torsion free subgroup of finite index. [Hint: find a torsion free subgroup of finite index by avoiding the finitely many conjugacy classes of torsion in \(\Gamma \).] Use this to give another proof of (b).
-
(a)
-
19.
Show that the stabilizer group of an orbifold point is well-defined up to group isomorphism, independent of the chart.
-
20.
The group \({{\,\mathrm{SL}\,}}_2(\mathbb R )\) acts on \(\mathbb P ^1(\mathbb R )=\mathbb R \cup \{\infty \}\) by linear fractional transformations. Show that \(G={{\,\mathrm{SL}\,}}_2(\mathbb Z ) \le {{\,\mathrm{SL}\,}}_2(\mathbb R )\) is discrete, but G does not act properly on \(\mathbb P ^1(\mathbb R )\). [So discrete groups can act on locally compact spaces without necessarily acting properly.]
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
This chapter is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, duplication, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, a link is provided to the Creative Commons license and any changes made are indicated.The images or other third party material in this chapter are included in the work's Creative Commons license, unless indicated otherwise in the credit line; if such material is not included in the work's Creative Commons license and the respective action is not permitted by statutory regulation, users will need to obtain permission from the license holder to duplicate, adapt or reproduce the material.
Copyright information
© 2021 The Author(s)
About this chapter
Cite this chapter
Voight, J. (2021). Discrete group actions. In: Quaternion Algebras. Graduate Texts in Mathematics, vol 288. Springer, Cham. https://doi.org/10.1007/978-3-030-56694-4_34
Download citation
DOI: https://doi.org/10.1007/978-3-030-56694-4_34
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-56692-0
Online ISBN: 978-3-030-56694-4
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


 ;
; ; and
; and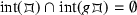 for all
for all  , we have
, we have 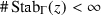 and there exists an open neigborhood
and there exists an open neigborhood  , the orbit
, the orbit 

