Abstract
We have seen that the group of unit Hamiltonians \(\mathbb H ^1\) acts by rotations of Euclidean space and therefore by isometries of the unit sphere, and that in spherical geometry the discrete subgroups are beautifully realized as classical finite groups: cyclic, dihedral, and the symmetry groups of the Platonic solids.
You have full access to this open access chapter, Download chapter PDF
In this chapter, we give background on the geometry of the hyperbolic plane.
1 \(\triangleright \) The beginnings of hyperbolic geometry
We have seen that the group of unit Hamiltonians \(\mathbb H ^1\) acts by rotations of Euclidean space and therefore by isometries of the unit sphere, and that in spherical geometry the discrete subgroups are beautifully realized as classical finite groups: cyclic, dihedral, and the symmetry groups of the Platonic solids.
Replacing \(\mathbb H \) with \({{\,\mathrm{M}\,}}_2(\mathbb R )\), the group \({{\,\mathrm{SL}\,}}_2(\mathbb R )\) of determinant 1 matrices possesses a much richer supply of discrete subgroups. In fact, \({{\,\mathrm{PSL}\,}}_2(\mathbb R )\) can be naturally identified with a circle bundle over the hyperbolic plane, and so the structure of quaternionic unit groups is naturally phrased in the language of hyperbolic geometry. Indeed, it was work on automorphic functions and differential equations invariant under discrete subgroups of \({{\,\mathrm{PSL}\,}}_2(\mathbb R )\) that provided additional early original motivation to study hyperbolic space: their study provides an incredibly rich interplay between number theory, algebra, geometry, and topology, with quaternionic applications. This interplay is the subject of the final parts of the text.
In this chapter, we provide a rapid introduction to the hyperbolic plane. Hyperbolic geometry has its roots preceding the quaternions, in efforts during the early 1800s to understand Euclid’s axioms for geometry. Since the time of Euclid, there had been attempts to prove the quite puzzling parallel postulate (given a line and a point not on the line, there is a unique line through the point parallel to the given line) from the other four simpler, self-evident axioms for geometry. In hyperbolic geometry, the parallel postulate fails to hold—there are always infinitely many distinct lines through a point that do not intersect a given line—and so it is a non-Euclidean geometry.
The underpinnings of what became hyperbolic geometry can be found in work by Euler and Gauss in their study of curved surfaces (the differential geometry of surfaces). It was then Lobachevsky and Bolyai who suggested that curved surfaces of constant negative curvature could be used in non-Euclidean geometry, and finally Riemann who generalized this to what are now called Riemannian manifolds. Klein coined the term “hyperbolic” for this geometry because its formulae can be obtained from spherical geometry by replacing trigonometric functions by their hyperbolic counterparts. See [Sco83, §1] for a nice overview of the 2-dimensional geometries.
Hyperbolic geometry, and in particular the hyperbolic plane, remains an important prototype for understanding negatively-curved spaces in general. Milnor [Milno82] gives a comprehensive early history of hyperbolic geometry; see also the survey by Cannon–Floyd–Kenyon–Parry [CFKP97], which includes an exposition of five models for hyperbolic geometry. (It is also possible to work out hyperbolic geometry in a manner akin to what Euclid did for his geometry without a particular model, following Lobachevsky [LP2010].)
For further references on hyperbolic plane geometry, see Jones–Singerman [JS87, Chapter 5], Anderson [And2005], Ford [For72], Katok [Kat92, Chapter 1], Iversen [Ive92, Chapter III], and Beardon [Bea95, Chapter 7]. There are a wealth of geometric results and formulas from Euclidean geometry that one can try to reformulate in the world of hyperbolic plane geometry, and the interested reader is encouraged to pursue these further.
2 Geodesic spaces
In geometry, we need notions of length, distance, and the straightness of a path. These notions are defined for a certain kind of metric space, as follows.
Let X be a metric space with distance \(\rho \). An isometry  is a bijective map that preserves distance, i.e., \(\rho (x,y)=\rho (g(x),g(y))\) for all \(x,y \in X\). (Any distance-preserving map is automatically injective and so becomes an isometry onto its image.) The set of isometries \({{\,\mathrm{Isom}\,}}(X)\) forms a group under composition.
is a bijective map that preserves distance, i.e., \(\rho (x,y)=\rho (g(x),g(y))\) for all \(x,y \in X\). (Any distance-preserving map is automatically injective and so becomes an isometry onto its image.) The set of isometries \({{\,\mathrm{Isom}\,}}(X)\) forms a group under composition.
33.2.1
A path from x to y, denoted \(\upsilon :x \rightarrow y\), is a continuous map \(\upsilon :[0,1] \rightarrow X\) where \(\upsilon (0)=x\) and \(\upsilon (1)=y\). (More generally, we can take the domain to be any compact real interval.) The length \(\ell (\upsilon )\) of a path \(\upsilon \) is the supremum of sums of distances between successive points over all finite subdivisions of the path (the path is rectifiable if this supremum is finite). Conversely, if X is a set with a notion of (nonnegative) length of path, then one recovers a candidate (intrinsic) metric as
a metric when this infimum exists (i.e., there exists a path of finite length \(x \rightarrow y\)) for all \(x,y \in X\). If the distance on X is of the form (33.2.2), we call X a length metric space or a path metric space, and by construction \(\ell (g \upsilon )=\ell (\upsilon )\) for all paths \(\upsilon \) and \(g \in {{\,\mathrm{Isom}\,}}(X)\).
Example 33.2.3
The space \(X=\mathbb R ^n\) with the ordinary Euclidean metric is a path metric space; it is sometimes denoted \({\mathbf {\mathsf{{E}}}}^n\) as Euclidean space (to emphasize the role of the metric).
33.2.4
If X is a path metric space and \(\upsilon \) achieves the infimum in (33.2.2), then we say \(\upsilon \) is a geodesic segment in X. A geodesic is a continuous map \((-\infty ,\infty ) \rightarrow X\) such that the restriction to every compact interval defines a geodesic segment. If X is a path metric space such that every two points in X are joined by a geodesic segment, we say X is a geodesic space, and if this geodesic is unique we call X a uniquely geodesic space.
33.2.5
If X is a geodesic space, then an isometry of X maps geodesic segments to geodesic segments, and hence geodesics to geodesics: i.e., if \(g \in {{\,\mathrm{Isom}\,}}(X)\) and \(\upsilon :x \rightarrow y\) is a geodesic segment, then \(g\upsilon :gx\rightarrow gy\) is a geodesic segment. After all, g maps the set of paths \(x\rightarrow y\) bijectively to the set of paths \(gx \rightarrow gy\), preserving distance.
33.2.6
In the context of differential geometry (our primary concern), these notions can be made concrete with coordinates. Suppose \(U \subseteq \mathbb R ^n\) is an open subset. Then a convenient way to specify the length of a path in U is with a length element in real-valued coordinates. To illustrate, the ordinary metric on \(\mathbb R ^n\) is given by the length element
so if \(\upsilon :[0,1] \rightarrow U\) is a piecewise continuously differentiable function written as \(\upsilon (t)=(x_1(t),\dots ,x_n(t))\), then
as usual.
More generally, if \(\lambda :U \rightarrow \mathbb R _{>0}\) is a positive continuous function, then the length element \(\lambda (x)\,\mathrm{d }{s}\) defines a metric (33.2.2) on U, as follows. The associated length (33.2.7) is symmetric, nonnegative, and satisfies the triangle inequality. To show that \(\rho (x,y)>0\) when \(x \ne y\), by continuity \(\lambda \) is bounded below by some \(\eta >0\) on a suitably small \(\epsilon \) ball neighborhood of x not containing y, so every path \(\upsilon :x \rightarrow y\) has \(\ell (\upsilon ) \ge \epsilon \eta \) and \(\rho (x,y) >0\).
In this context, we also have a notion of orientation, and we may restrict to isometries that preserve this orientation. We return to this in section 33.8, rephrasing this in terms of Riemannian geometry.
Remark 33.2.8. The more general study of geometry based on the notion of length in a topological space (the very beginnings of which are presented here) is the area of metric geometry. Metric geometry has seen significant recent applications in group theory and dynamical systems, as well as many other areas of mathematics. For further reading, see the texts by Burago–Burago–Ivanov [BBI2001] and Papadopoulous [Pap2014].
In particular, geodesic spaces are quite common in mathematics, including complete Riemannian manifolds; Busemann devotes an entire book to the geometry of geodesics [Bus55]. Uniquely geodesic spaces are less common; examples include simply connected Riemannian manifolds without conjugate points, \(\mathrm {CAT}(0)\) spaces, and Busemann convex spaces.
The following theorem nearly characterizes geodesic spaces.
Theorem 33.2.9
(Hopf–Rinow). Let X be a complete and locally compact length metric space. Then X is a geodesic space and every bounded closed set in X is compact.
Proof. See e.g. Bridson–Haefliger [BH99, Proposition 3.7]). \(\square \)
3 Upper half-plane
We now present the first model of two-dimensional hyperbolic space (see Figure 33.3.2).
Definition 33.3.1
The upper half-plane is the set
Definition 33.3.3
The hyperbolic length element on \({\mathbf {\mathsf{{H}}}}^2\) is defined by
As described in 33.2.6, the hyperbolic length element induces a metric on \({\mathbf {\mathsf{{H}}}}^2\), and this provides it with the structure of a path metric space.
Definition 33.3.5
The set \({\mathbf {\mathsf{{H}}}}^2\) equipped with the hyperbolic metric is (a model for) the hyperbolic plane.
Remark 33.3.6. The space \({\mathbf {\mathsf{{H}}}}^2\) can be intrinsically characterized as the unique two-dimensional (connected and) simply connected Riemannian manifold with constant sectional curvature \(-1\).
The hyperbolic metric and the Euclidean metric on \({\mathbf {\mathsf{{H}}}}^2\) are equivalent, inducing the same topology (Exercise 33.1). However, lengths and geodesics are different under these two metrics, as we will soon see.
33.3.7
The group \({{\,\mathrm{GL}\,}}_2(\mathbb R )\) acts on \(\mathbb C \) via linear fractional transformations:
since
we have
and so if \({{\,\mathrm{Im}\,}}z>0\), then \({{\,\mathrm{Im}\,}}gz>0\) if and only if \(\det g>0\). Therefore, the subgroup
preserves the upper half-plane \({\mathbf {\mathsf{{H}}}}^2\). Moreover, because the action of \({{\,\mathrm{GL}\,}}_2^+(\mathbb R )\) is holomorphic, it is orientation-preserving.
The kernel of this action, those matrices acting by the identity as linear fractional transformations, are the scalar matrices, since \((az+b)/(cz+d)=z\) identically if and only if \(c=b=0\) and \(a=d\). Taking the quotient we get a faithful action of \({{\,\mathrm{PGL}\,}}_2^+(\mathbb R )={{\,\mathrm{GL}\,}}_2^+(\mathbb R )/\mathbb R ^\times \) on \({\mathbf {\mathsf{{H}}}}^2\). There is a canonical isomorphism

with the same action on the upper half-plane.
33.3.10
The determinant \(\det :{{\,\mathrm{PGL}\,}}_2(\mathbb R ) \rightarrow \mathbb R ^\times /\mathbb R ^{\times 2} \simeq \{\pm 1\}\) has the inverse image of \(+1\) equal to \({{\,\mathrm{PGL}\,}}_2^+(\mathbb R )\) both open and closed in \({{\,\mathrm{PGL}\,}}_2(\mathbb R )\); therefore, any g with \(\det (g)<0\) together with \({{\,\mathrm{PGL}\,}}_2^+(\mathbb R )\) generates \({{\,\mathrm{PGL}\,}}_2(\mathbb R )\): for example, we may take
In view of (33.3.9), we extend the action of \({{\,\mathrm{PGL}\,}}_2(\mathbb R )\) on \({\mathbf {\mathsf{{H}}}}^2\) by defining for \(g \in {{\,\mathrm{PGL}\,}}_2(\mathbb R )\) and \(z \in {\mathbf {\mathsf{{H}}}}^2\)
The elements \(g \in {{\,\mathrm{PGL}\,}}_2(\mathbb R )\) with \(\det g<0\) act anti-holomorphically and so are orientation-reversing. The matrix g in (33.3.11) then acts by \(g(z)=-\overline{z}\).
This action also arises naturally from another point of view. Let
be the lower half-plane, let \({\mathbf {\mathsf{{H}}}}^2{}^{+} = {\mathbf {\mathsf{{H}}}}^2\), and let
Then \({{\,\mathrm{PGL}\,}}_2(\mathbb R )\) acts on \({\mathbf {\mathsf{{H}}}}^2{}^{\pm }\) (it preserves \(\mathbb R \) hence also its complement in \(\mathbb C \)). Complex conjugation \(z \mapsto \overline{z}\) interchanges \({\mathbf {\mathsf{{H}}}}^2{}^+\) and \({\mathbf {\mathsf{{H}}}}^2{}^-\), and there is a canonical identification

from which we obtain the action (33.3.12) of \({{\,\mathrm{PGL}\,}}_2(\mathbb R )\) on \({\mathbf {\mathsf{{H}}}}^2\).
Remark 33.3.13. The fact that \({{\,\mathrm{PSL}\,}}_2(\mathbb R )\) has elements \(g \in {{\,\mathrm{PSL}\,}}_2(\mathbb R )\) that are matrices up to sign means that whenever we do a computation with a choice of matrix, implicitly we are also checking that the computation goes through with the other choice of sign. Most of the time, this is harmless—but in certain situations this sign plays an important role!
Let \({{\,\mathrm{Isom}\,}}^+({\mathbf {\mathsf{{H}}}}^2) \le {{\,\mathrm{Isom}\,}}({\mathbf {\mathsf{{H}}}}^2)\) be the subgroup of isometries of \({\mathbf {\mathsf{{H}}}}^2\) that preserve orientation.
Theorem 33.3.14
The group \({{\,\mathrm{PSL}\,}}_2(\mathbb R )\) acts on  via orientation-preserving isometries, i.e.,
via orientation-preserving isometries, i.e.,  .
.
Proof. Because the metric is defined by a length element \(\mathrm{d }{s}\), we want to show that \(\mathrm{d }{(gs)}=\mathrm{d }{s}\) for all \(g \in {{\,\mathrm{PSL}\,}}_2(\mathbb R )\), i.e.,
for all \(g \in {{\,\mathrm{PSL}\,}}_2(\mathbb R )\). Since \(|\mathrm{d }{(gz)} \,|=|\mathrm{d }{g}(z)/\mathrm{d }{z} \,||\mathrm{d }{z} \,|\), it is equivalent to show that
for all \(g \in {{\,\mathrm{PSL}\,}}_2(\mathbb R )\).
Let \(g \in {{\,\mathrm{PSL}\,}}_2(\mathbb R )\) act by
with \(ad-bc=1\). Then
by (33.3.9),
so taking the ratio, the two factors \(|cz+d \,|^2\) exactly cancel, establishing (33.3.15).
Finally, the action is holomorphic so (by the Cauchy–Riemann equations) it lands in the orientation-preserving subgroup. \(\square \)
33.3.17
The action of \({{\,\mathrm{PSL}\,}}_2(\mathbb R )\) extends to the boundary as follows. We define the circle at infinity to be the boundary
(The name comes from viewing \({\mathbf {\mathsf{{H}}}}^2\) in stereographic projection as a half-sphere with circular boundary.) The group \({{\,\mathrm{PSL}\,}}_2(\mathbb R )\) still acts on \({{\,\mathrm{bd}\,}}{\mathbf {\mathsf{{H}}}}^2\) by linear fractional transformations. We define the completed upper half-plane to be
The topology on \({\mathbf {\mathsf{{H}}}}^{2*}\) is the same as the Euclidean topology on \({\mathbf {\mathsf{{H}}}}^2\), and we take a fundamental system of neighborhoods of the point \(\infty \) to be sets of the form
for \(M>0\) and a system of neighborhoods of the point \(z_0\) to be
i.e. open disks tangent to the real axis at \(z_0\), together with \(z_0\).
Remark 33.3.18. Although the hyperbolic plane cannot be embedded in \(\mathbb R ^3\), it can be locally embedded. One way to visualize plane hyperbolic geometry (locally) is by the pseudosphere, the surface of revolution generated by a tractrix: it is a surface with constant negative curvature and so locally models the hyperbolic plane (Figure 33.3.19).
Remark 33.3.20. We will compactify quotients of \({\mathbf {\mathsf{{H}}}}^2\) in other ways below. In that context, we will add only a subset of the boundary of \({\mathbf {\mathsf{{H}}}}^{2*}\); this overloading should cause no confusion.
4 Classification of isometries
On our way to classifying isometries, we pause to identify three natural subgroups of \({{\,\mathrm{SL}\,}}_2(\mathbb R )\):
We have \(K={{\,\mathrm{Stab}\,}}_{{{\,\mathrm{SL}\,}}_2(\mathbb R )}(i)\) since \(\displaystyle {\frac{ai+b}{ci+d}}=i\) if and only if \(d=a\) and \(c=-b\), and then the determinant condition implies \(a^2+b^2=1\). An element \(\begin{pmatrix} a &{} 0 \\ 0 &{} 1/a \end{pmatrix}\) acts by \(z \mapsto a^2 z\), fixing the origin and stretching along lines through the origin. An element \(\begin{pmatrix} 1 &{} n \\ 0 &{} 1 \end{pmatrix}\) acts by the translation \(z \mapsto z+b\).
Proposition 33.4.2
(Iwasawa decomposition). The multiplication map gives a homeomorphism

In particular, for all \(g \in {{\,\mathrm{SL}\,}}_2(\mathbb R )\), we can write uniquely \(g=n_ga_gk_g\) with \(n_g \in N\), \(a_g \in A\), and \(k_g \in K\) in a way continuously varying in g.
Proof. The multiplication map \(N \times A \times K \rightarrow {{\,\mathrm{SL}\,}}_2(\mathbb R )\) is continuous and open, so we need to show it is bijective. It is injective, because checking directly we see that
This map is surjective as follows. Let \(g \in {{\,\mathrm{SL}\,}}_2(\mathbb R )\), and let \(z=g(i)\). Let \(n_g=\begin{pmatrix} 1 &{} -{{\,\mathrm{Re}\,}}z \\ 0 &{} 1 \end{pmatrix} \in N\), so that \((n_g g)(i) = yi\). Let \(a_g=\begin{pmatrix} 1/\sqrt{y} &{} 0 \\ 0 &{} \sqrt{y} \end{pmatrix} \in A\); then \((a_gn_g g)(i)=i\), so \(a_gn_g g \in {{\,\mathrm{Stab}\,}}_{{{\,\mathrm{SL}\,}}_2(\mathbb R )}(i)=K\), and peeling back we get \(g \in NAK\), proving surjectivity. \(\square \)
Remark 33.4.3. We have \(AN=NA\), and we showed in the proof of Proposition 33.4.2 that NA acts transitively on \({\mathbf {\mathsf{{H}}}}^2\) (by \(z \mapsto a^2z+b\)). In section 34.6, we reinterpret this as providing a direct link between \({\mathbf {\mathsf{{H}}}}^2\) and \({{\,\mathrm{SL}\,}}_2(\mathbb R )\).
Lemma 33.4.4
The group \({{\,\mathrm{SL}\,}}_2(\mathbb R )\) is generated by the subgroups A, N, and the element \(\begin{pmatrix} 0 &{} -1 \\ 1 &{} 0 \end{pmatrix}\), which acts on  by \(z \mapsto -1/z\).
by \(z \mapsto -1/z\).
Proof. Let \(\begin{pmatrix} a &{} b \\ c &{} d \end{pmatrix} \in {{\,\mathrm{SL}\,}}_2(\mathbb R )\). The lemma follows by performing row reduction on the matrix using the given generators. We find that if \(c \ne 0\), then
and if \(c=0\) then
\(\square \)
The subgroups N, A, K can be characterized by their traces; with a view to working on \({{\,\mathrm{PSL}\,}}_2(\mathbb R )\), we consider the absolute traces:
Definition 33.4.5
An element \(g \in {{\,\mathrm{PSL}\,}}_2(\mathbb R )\) with \(g \ne \pm 1\) is calledelliptic,hyperbolic, orparabolic according to whether \(|{{\,\mathrm{Tr}\,}}(g) \,|<2\), \(|{{\,\mathrm{Tr}\,}}(g) \,|>2\), or \(|{{\,\mathrm{Tr}\,}}(g) \,|=2\).
Every nonidentity element \(g \in {{\,\mathrm{PSL}\,}}_2(\mathbb R )\) belongs to one of these three types (even though g need not belong to one of the subgroups N, A, K individually).
Lemma 33.4.6
An element \(g \in {{\,\mathrm{PSL}\,}}_2(\mathbb R )\) is

Proof. Let \(g=\begin{pmatrix} a &{} b \\ c &{} d \end{pmatrix}\) have \(\det (g)=ad-bc=1\). We look to solve the equation
or equivalently \(cz^2+(d-a)z-b=0\). The discriminant is \((d-a)^2+4bc = (a+d)^2-4={{\,\mathrm{Tr}\,}}(g)^2-4\). Therefore g is elliptic if and only if this discriminant is negative if and only if there is a unique root in \({\mathbf {\mathsf{{H}}}}^2\); g is parabolic if and only if this discriminant is zero if and only if there is a unique root in \({{\,\mathrm{bd}\,}}{\mathbf {\mathsf{{H}}}}^2\); and g is hyperbolic if and only if this discriminant is positive if and only if there are two roots in \({{\,\mathrm{bd}\,}}{\mathbf {\mathsf{{H}}}}^2\). \(\square \)
33.4.7
Let \(g \in {{\,\mathrm{PSL}\,}}_2(\mathbb R )\). If g is elliptic, then g acts by hyperbolic rotation in a neighborhood around its fixed point, as in Figure 33.4.8; every such element is conjugate to an element of K, fixing i. (Indeed, in the unit disc model with its fixed point as the center, an elliptic element acts literally by rotation in the disc; see section 33.7.)
A hyperbolic element can be thought of as a translation along the geodesic between the two fixed points on \({{\,\mathrm{bd}\,}}{\mathbf {\mathsf{{H}}}}^2\), as in Figure 33.4.9.
Moving these fixed points to \(0,\infty \), every such element is conjugate to an element of A, acting by \(z \mapsto a^2 z\) with \(a \ne 1\), as in Figure 33.4.10.
Finally, a parabolic element should be thought of as a limit of the other two types, where correspondingly the fixed point tends to the boundary or the two fixed points move together; every such element is conjugate to an element of N, acting by translation \(z \mapsto z+n\) for some \(n \in \mathbb R \).
Lemma 33.4.11
For all  , there exists \(g \in {{\,\mathrm{PSL}\,}}_2(\mathbb R )\) such that \(gz,gz' \in \mathbb R _{>0}i\) are pure imaginary.
, there exists \(g \in {{\,\mathrm{PSL}\,}}_2(\mathbb R )\) such that \(gz,gz' \in \mathbb R _{>0}i\) are pure imaginary.
Proof. The proof follows directly by using translations and scaling (33.4.1), requested in Exercise 33.5. \(\square \)
5 Geodesics
In this section, we prove two important theorems: we describe geodesics, giving a formula for the distance, and we classify isometries.
Theorem 33.5.1
The hyperbolic plane  is a uniquely geodesic space. The unique geodesic passing through two distinct points
is a uniquely geodesic space. The unique geodesic passing through two distinct points  is a semicircle orthogonal to \(\mathbb R \) or a vertical line, and
is a semicircle orthogonal to \(\mathbb R \) or a vertical line, and
Proof. We first prove the imaginary axis is a geodesic with \(z,z' \in \mathbb R _{>0}i\). Let \(\upsilon (t)=x(t)+iy(t):z \rightarrow z'\) be a path; then
with equality if and only if \(x(t)=0\) identically and \(\mathrm{d }{y}/\mathrm{d }{t} \ge 0\) for all \(t \in [0,1]\). This is achieved for the path
so \(\rho (z,z')=\log \,|z'/z \,|\), and the imaginary axis is the unique geodesic.
For arbitrary points \(z,z' \in {\mathbf {\mathsf{{H}}}}^2\), we apply Lemma 33.4.11. The statement on geodesics follows from the fact that the image of \(\mathbb R _{>0}i\) under an element of \({{\,\mathrm{PSL}\,}}_2(\mathbb R )\) is either a semicircle orthogonal to \(\mathbb R \) or a vertical line (Exercise 33.6).
The formula (33.5.2) for the case \(z,z' \in \mathbb R _{>0}i\) follows from (33.5.4) and plugging in along the imaginary axis; the general case then follows from the invariance of both \(\rho (z,z')\) and
under \(g \in {{\,\mathrm{PSL}\,}}_2(\mathbb R )\), checked on the generators in Lemma 33.4.4 (Exercise 33.10). Finally, the formula (33.5.3) follows directly from formulas for hyperbolic cosine, requested in Exercise 33.11. \(\square \)
Theorem 33.5.5
We have

and

Proof. Let \(Z=\{ti : t>0\}\) be the positive part of the imaginary axis. By Theorem 33.5.1, Z is the unique geodesic through any two points of Z.
Let \(\phi \in {{\,\mathrm{Isom}\,}}({\mathbf {\mathsf{{H}}}}^2)\). Then \(\phi (Z)\) is a geodesic (33.2.5), so by Exercise 33.7, there exists \(g \in {{\,\mathrm{PSL}\,}}_2(\mathbb R )\) such that \(g\phi \) fixes Z pointwise. Replacing \(\phi \) by \(g\phi \), we may suppose \(\phi \) fixes Z pointwise.
Let \(z=x+iy \in {\mathbf {\mathsf{{H}}}}^2\) and \(z'=x'+iy' = \phi (z)\). For all \(t>0\),
Plugging this into the formula (33.5.3) for the distance, we obtain
Dividing both sides by \(t^2\) and taking the limit as \(t \rightarrow \infty \), we find that \(y=y'\), and consequently that \(x^2=x'^2\) and \(x=\pm x'\). The choice of sign ± varies continuously over the connected set \({\mathbf {\mathsf{{H}}}}^2\) and so must be constant. Therefore \(\phi (z)=z\) or \(\phi (z)=-\overline{z}\) for all \(z \in {\mathbf {\mathsf{{H}}}}^2\). The latter generates \({{\,\mathrm{PGL}\,}}_2(\mathbb R )\) over \({{\,\mathrm{PSL}\,}}_2(\mathbb R )\) (33.3.10), and both statements in the theorem follow. \(\square \)
6 Hyperbolic area and the Gauss–Bonnet formula
In this section, we consider hyperbolic area. We measure hyperbolic area by considering a small Euclidean rectangle whose sides are parallel to the axes at the point (x, y); the hyperbolic length of the sides are \(\mathrm{d }{x}/y\) and \(\mathrm{d }{y}/y\), and we obtain the hyperbolic area form from the product.
Definition 33.6.1
We define the hyperbolic area form by
For a subset \(S \subseteq {\mathbf {\mathsf{{H}}}}^2\), we define the hyperbolic area of S by
when this integral is defined.
Proposition 33.6.2
The hyperbolic area is invariant under  .
.
Proof. We verify that the hyperbolic area form is invariant. We first check this for the orientation-reversing isometry
visibly \(\mathrm{d }{(gA)} = \mathrm{d }{A}\) in this case.
It suffices then to consider \(g \in {{\,\mathrm{PSL}\,}}_2(\mathbb R )\). Let \(z=x+iy\) and let
with \(ad-bc=1\). By (33.3.9), \(\displaystyle {v=\frac{y}{|cz+d \,|^2}}\). We compute that
Now g is holomorphic; so by the Cauchy–Riemann equations, its Jacobian is given by
therefore
\(\square \)
A major role will be played in what follows by hyperbolic polygons, defined formally as follows.
33.6.4
Let \(z,z' \in {\mathbf {\mathsf{{H}}}}^{2*}\) be distinct. Then there is a unique geodesic in \({\mathbf {\mathsf{{H}}}}^2\) whose closure in \({\mathbf {\mathsf{{H}}}}^{2*}\) passes through \(z,z'\), and the segment from z to \(z'\) is denoted \([z,z']\).
Definition 33.6.5
A hyperbolic polygon is a connected, closed subset of \({\mathbf {\mathsf{{H}}}}^{2*}\) whose boundary consists of finitely many geodesic sides of the form \([z,z']\) with \(z,z'\) vertices . A hyperbolic triangle is a hyperbolic polygon with three sides.
Definition 33.6.6
A subset \(A \subseteq {\mathbf {\mathsf{{H}}}}^2\) is convex if the geodesic segment between any two points in A lies inside A.
An example of a (convex) hyperbolic polygon is given in Figure 33.6.7.
A hyperbolic triangle is visibly convex; for more on convexity, see Exercises 33.8–33.9. The following key formula expresses the hyperbolic area of a triangle in terms of its angles.
Theorem 33.6.8
(Gauss–Bonnet formula). Let T be a hyperbolic triangle with angles \(\alpha ,\beta ,\gamma \). Then
Proof. See e.g. Katok [Kat92, Theorem 1.4.2]. \(\square \)
33.6.9
Let P be a convex hyperbolic polygon with n sides. By convexity, each side meets at each vertex a unique side, so P has n vertices with angles \(\theta _1,\dots ,\theta _n\). Triangulating P and applying the Gauss–Bonnet formula, we conclude that
Remark 33.6.10. Theorem 33.6.8 is called the Gauss–Bonnet formula because it is closely related to the more general formula relating curvature to Euler characteristic. The simplest formula of this kind is
for a compact Riemann surface X. The expression (33.6.11) is quite remarkable: it says that the total curvature of X is determined by its topology; if you flatten out a surface in one place, the curvature is forced to rise somewhere else. If instead one has a surface X with geodesic boundary, then the formula (33.6.11) becomes
where \(\theta _i\) are the angles at the vertices. For a triangle X with constant curvature \(-1\) and angles \(\alpha ,\beta ,\gamma \), we have \(\int _X K\,\mathrm{d }{A}=-\mu (X)\) and \(\chi (X)=V-E+F=1\) (as for any polygon), so we find
and we recover Theorem 33.6.8.
7 Unit disc and Lorentz models
In this section, we consider two other models for the hyperbolic plane.
First, we consider the unit disc model.
Definition 33.7.1
The hyperbolic unit disc is the (open) unit disc
equipped with the hyperbolic metric
The hyperbolic unit disc \({\mathbf {\mathsf{{D}}}}^2\) is also called thePoincaré model of planar hyperbolic geometry. Thecircle at infinity is the boundary
33.7.2
For all \(z_0 \in {\mathbf {\mathsf{{H}}}}^2\), the maps

define a conformal equivalence between \({\mathbf {\mathsf{{H}}}}^2\) and \({\mathbf {\mathsf{{D}}}}^2\) with \(z_0 \mapsto \phi (z_0)=0\). A particularly nice choice is \(z_0=i\), giving
The hyperbolic metric on \({\mathbf {\mathsf{{D}}}}^2\) is the pushforward of (induced from) the hyperbolic metric on \({\mathbf {\mathsf{{H}}}}^2\) via the identification (33.7.4) (Exercise 33.12). Ordinarily, one would decorate the pushforward metric, but because we will frequently move between the upper half-plane and unit disc as each has its advantage, we find it notationally simpler to avoid this extra decoration. The distance on \({\mathbf {\mathsf{{D}}}}^2\) is
so that
The map \(\phi \) (33.7.3) maps the geodesics in \({\mathbf {\mathsf{{H}}}}^2\) to geodesics in \({\mathbf {\mathsf{{D}}}}^2\), and as a Möbius transformation, maps circles and lines to circles and lines, preserves angles, and maps the real axis to the unit circle; therefore the geodesics in \({\mathbf {\mathsf{{D}}}}^2\) are diameters through the origin and semicircles orthogonal to the unit circle, as in Figure 33.7.7.
Accordingly, triangles from the upper half-plane map to triangles in the unit disc.
33.7.8
Via the map \(\phi \), the group \({{\,\mathrm{PSL}\,}}_2(\mathbb R )\) acts on \({\mathbf {\mathsf{{D}}}}^2\) as
Explicitly, an isometry of \({\mathbf {\mathsf{{D}}}}^2\) is a map of the form
for \(a \in \mathbb C \) with \(|a|<1\) and \(\theta \in \mathbb R \). (A direct substitution can be used to give an alternate verification that these transformations are isometries of \({\mathbf {\mathsf{{D}}}}^2\) with the hyperbolic metric.)
The orientation reversing isometry \(g(z)=-\overline{z}\) on \({\mathbf {\mathsf{{H}}}}^2\) acts by \(g(w)=\overline{w}\) on \({\mathbf {\mathsf{{D}}}}^2\) with the choice \(p=i\) (Exercise 33.13).
The induced area on \({\mathbf {\mathsf{{D}}}}^2\) is given by
for \(w=x+yi\).
Second, we present the Lorentz model.
Definition 33.7.9
The Lorentz metric on \(\mathbb R ^3\) is the indefinite metric
33.7.10
The indefinite Lorentz metric is associated to the quadratic form
in the natural way. Lengths in this metric can be positive or nonpositive. However, on the hyperboloid
the metric becomes positive definite: a nonzero tangent vector to the hyperboloid has positive length (Exercise 33.16). The hyperboloid can be thought of as the sphere of radius i about the origin with respect to q; taking an imaginary radius shows that hyperbolic geometry is dual in some sense to spherical geometry, where \({\mathbf {\mathsf{{S}}}}^2 \subseteq \mathbb R ^3\) has real radius 1.
Definition 33.7.11
The Lorentz hyperboloid is the set
equipped with the Lorentz metric.
The Lorentz hyperboloid is the upper sheet of the (two-sheeted) hyperboloid; it is also called the hyperboloid model or the Lorentz model of planar hyperbolic geometry, and it can be visualized as in Figure 33.7.13. (The choice of signs has to do with the physics of spacetime.)
The map
is bijective and identifies the metrics on \({\mathbf {\mathsf{{L}}}}^2\) and \({\mathbf {\mathsf{{D}}}}^2\) (Exercise 33.15). Moreover, the map (33.7.12) maps geodesics in \({\mathbf {\mathsf{{D}}}}^2\) to intersections of the hyperboloid with planes through the origin.
By pullback, \({{\,\mathrm{Isom}\,}}^+({\mathbf {\mathsf{{L}}}}^2) \simeq {{\,\mathrm{PSL}\,}}_2(\mathbb R )\). However, other isometries are also apparent: a linear change of variables that preserves the quadratic form q also preserves the Lorentz metric. Let
Then
so if \(g \in {{\,\mathrm{O}\,}}(2,1)\) then immediately \(\mathrm{d }{gs}^2 = \mathrm{d }{s}^2\).
Next, if \(g \in {{\,\mathrm{O}\,}}(2,1)\), then \(g^tmg=m\) implies \(\det (g)=\pm 1\). The elements of \({{\,\mathrm{O}\,}}(2,1)\) that map the hyperboloid to itself comprise the subgroup
let \({{\,\mathrm{SO}\,}}^+(2,1) \le {{\,\mathrm{SO}\,}}(2,1)\) be the further subgroup that maps the upper sheet of the hyperboloid to itself, the connected component of the identity.
Remark 33.7.14. We have proven that there is an isomorphism of Lie groups
it corresponds to the isomorphism of Lie algebras \(\mathfrak {so}_{2,1} \simeq \mathfrak {sl}_2\).
8 Riemannian geometry
The hyperbolic metric (33.3.4) is induced from a Riemannian metric as follows.
33.8.1
A Riemannian metric \(\mathrm{d }{s^2}\) on an open set \(U \subseteq \mathbb R ^n\) is a function that assigns to each point \(x \in U\) a (symmetric, positive definite) inner product on the tangent space \({{\,\mathrm{T}\,}}_x(U)\) at \(x \in U\), varying differentiably. Such an inner product defines the length of a tangent vector \(\Vert \phantom {x}\Vert \), the angle between two tangent vectors, and the length element \(\mathrm{d }{s}=\sqrt{\mathrm{d }{s^2}}\). In coordinates, we write
for standard coordinates \(x_i\) on \(\mathbb R ^n\), and the matrix \((\eta _{ij})\) is symmetric, positive definite, and differentiable. The metric determines a volume formula as
A Riemannian metric gives \(U \subseteq \mathbb R ^n\) the structure of a path metric space, as explained in 33.2.6: if \(\upsilon :[0,1] \rightarrow U\) is continuously differentiable, then we define its length to be
If \(\phi :\mathbb R ^k \rightarrow \mathbb R ^n\) is continuously differentiable, the pullback metric \(\phi ^*(\mathrm{d }{s^2})\) is defined by
where \(v,w \in {{\,\mathrm{T}\,}}_z(U)\) and \(\mathrm {D}\) is the derivative map.
The language of 33.8.1 gives another way to interpret the hyperbolic metric on \({\mathbf {\mathsf{{H}}}}^2\). This point of view extends to provide a description of the full isometry group \({{\,\mathrm{PSL}\,}}_2(\mathbb R )\) as the unit tangent bundle of \({\mathbf {\mathsf{{H}}}}^2\), as follows.
33.8.2
The tangent space to \({\mathbf {\mathsf{{H}}}}^2\) at a point \(z \in {\mathbf {\mathsf{{H}}}}^2\) is \({{\,\mathrm{T}\,}}_z\!{\mathbf {\mathsf{{H}}}}^2\simeq \mathbb C \) and the tangent bundle
is trivial (parallelizable), with \({{\,\mathrm{T}\,}}({\mathbf {\mathsf{{H}}}}^2) \simeq {\mathbf {\mathsf{{H}}}}^2\times \mathbb C \). The Riemannian metric on \({\mathbf {\mathsf{{H}}}}^2\) is then defined by the metric on \({{\,\mathrm{T}\,}}_z\!{\mathbf {\mathsf{{H}}}}^2\) given by
for \(v,w \in {{\,\mathrm{T}\,}}_z({\mathbf {\mathsf{{H}}}}^2)\), a rescaling of the usual inner product on \(\mathbb C \) over \(\mathbb R \). In particular, \(\Vert v\Vert =|v \,|/({{\,\mathrm{Im}\,}}z)\) for \(v \in {{\,\mathrm{T}\,}}_z({\mathbf {\mathsf{{H}}}}^2)\). The angle between two geodesics at an intersection point \({z \in {{\,\mathrm{T}\,}}_z\!{\mathbf {\mathsf{{H}}}}^2}\) is then defined to be the angle between their tangent vectors in \({{\,\mathrm{T}\,}}_z\!{\mathbf {\mathsf{{H}}}}^2\); this notion of an angle coincides with the Euclidean angle measure.
The action of \({{\,\mathrm{PSL}\,}}_2(\mathbb R )\) on \({\mathbf {\mathsf{{H}}}}^2\) extends to an action on \({{\,\mathrm{T}\,}}({\mathbf {\mathsf{{H}}}}^2)\) in the expected way:
Since isometries of \({\mathbf {\mathsf{{H}}}}^2\) are differentiable, they act on the tangent bundle by differentials preserving the norm and angle, and therefore \({{\,\mathrm{Isom}\,}}({\mathbf {\mathsf{{H}}}}^2)\) acts conformally or anti-conformally on \({\mathbf {\mathsf{{H}}}}^2\).
If we restrict to the unit tangent bundle
then we obtain a bijection

(Exercise 33.17).
Remark 33.8.3. The natural generalization of Euclid’s geometry is performed on a Riemannian manifold X that is homogeneous, i.e., the isometry group \({{\,\mathrm{Isom}\,}}(X)\) acts transitively on X, as well as isotropic, i.e., \({{\,\mathrm{Isom}\,}}(X)\) acts transitively on frames (a basis of orthonormal tangent vectors) at a point. In this way, homogeneous says that every point “looks the same”, and isotropic says that the geometry “looks the same in every direction” at a point. Taken together, these natural conditions are quite strong, and there are only three essentially distinct simply connected homogeneous and isotropic geometries in any dimension, corresponding to constant sectional curvatures zero, positive, or negative: these are Euclidean, spherical, and hyperbolic geometry, respectively. Put this way, the hyperbolic plane is the unique complete, simply connected Riemann surface with constant sectional curvature \(-1\). For more on geometries in this sense, we encourage the reader to consult Thurston [Thu97].
To conclude this section, we briefly review a few facts from the theory of Riemannian manifolds.
33.8.4
A (topological) n-manifold is a (second-countable) Hausdorff topological space X locally homeomorphic to \(\mathbb R ^n\), i.e., for every \(x \in X\), there exists an open neighborhood \(U \ni x\) and a continuous map \(\phi :U \hookrightarrow \mathbb R ^n\) that is a homeomorphism onto an open subset; the map \(\phi :U \rightarrow \phi (U) \subseteq \mathbb R ^n\) is called a chart (at \(x \in X\)), and an open cover of charts is called an atlas .
Two charts \(\phi _1 :U_1 \rightarrow \mathbb R ^n\) and \(\phi _2 :U_2 \rightarrow \mathbb R ^n\) are (C\(^\infty \)-) smoothly compatible if the transition map
(see Figure 33.8.5) is \(C^\infty \)-smooth (i.e., has continuous partial derivatives of all orders). An atlas on a manifold is smooth on a manifold if all charts are smoothly compatible. A smooth manifold is a manifold equipped with a smooth atlas.
A morphism of smooth manifolds is a continuous map \(f:Y \rightarrow X\) such that for the atlases \(\{(\phi _i,U_i)\}_i\) of X and \(\{(\psi _j,V_j)\}_j\) of Y, each map
is smooth. An isomorphism (diffeomorphism) of smooth manifolds is a bijective morphism  such that f and \(f^{-1}\) are (\(C^\infty \)-)smooth.
such that f and \(f^{-1}\) are (\(C^\infty \)-)smooth.
By the same definition as 33.8.1, we define a Riemannian metric on a smooth n-manifold.
One could similarly define \(C^k\)-smooth manifolds for any \(1 \le k \le \infty \).
33.8.6
We similarly define a complex n -manifold, and morphisms between them, by replacing \(\mathbb R \) by \(\mathbb C \) and smooth by holomorphic in the definition of a smooth manifold. A Riemann surface is a complex 1-manifold. For further reference, see e.g. Donaldson [Don2011] or Miranda [Mir95].
A complex 1-manifold (Riemann surface) defines a smooth, orientable Riemannian 2-manifold by choosing the standard Euclidean metric on the complex plane; conversely, a conformal structure on a smooth, oriented Riemannian 2-manifold determines a complex 1-manifold. In other words, the category of Riemann surfaces is equivalent to the category of smooth, orientable Riemannian 2-manifolds with conformal transition maps and with conformal morphisms.
Example 33.8.7
The field \(\mathbb C \) of complex numbers is the “original” Riemann surface, and every open subset of \(\mathbb C \) is a Riemann surface.
The simplest nonplanar example of a Riemann surface is the Riemann sphere \(\mathbb P ^1(\mathbb C ) = \mathbb C \cup \{\infty \}\). The atlas on \(\mathbb P ^1(\mathbb C )\) is given by the open sets
\(U_1=\mathbb P ^1(\mathbb C ) \smallsetminus \{\infty \}=\mathbb C \) and \(U_2=\mathbb P ^1(\mathbb C ) \smallsetminus \{0\}\)
and charts \(\phi _1:U_1 \rightarrow \mathbb C \) by \(\phi _1(z)=z\) and \(\phi _2:U_2 \rightarrow \mathbb C \) by \(\phi _2(z)=1/z\); the map \(\phi _2\phi _1^{-1}(z)=1/z\) is analytic on \(\phi _1(U_1 \cap U_2)=\mathbb C \smallsetminus \{0\}\). Topologically, the Riemann sphere is the one-point compactification of \(\mathbb C \), and becomes a sphere by stereographic projection.
Example 33.8.8
The inverse function theorem implies that if X is a smooth projective algebraic variety over \(\mathbb C \), then \(X(\mathbb C )\) has the canonical structure of a compact, complex manifold.
Exercises
-
1.
Show that the hyperbolic metric has the same topology as the Euclidean metric in two ways.
-
(a)
Show directly that open balls nest: for all \(z \in {\mathbf {\mathsf{{H}}}}^2\) and all \(\epsilon >0\), there exist \(\eta _1,\eta _2>0\) such that
$$\begin{aligned} \rho (z,w)<\eta _1 \Rightarrow |z-w|<\epsilon \Rightarrow \rho (z,w)<\eta _2 \end{aligned}$$for all \(w \in {\mathbf {\mathsf{{H}}}}^2\).
-
(b)
Show that the collection of Euclidean balls coincides with the collection of hyperbolic balls. [Hint: applying an isometry, reduce to the case of balls around i and check this directly; it is perhaps even clearer moving to the unit disc model.]
-
(a)
-
2.
Check that in \(\mathbb R ^n\), the metric specified in (33.2.7)
$$\begin{aligned} \ell (\upsilon )=\int _{\upsilon } \sqrt{x'_1(t)^2 +\cdots + x_n'(t)^2}\,\mathrm{d }{t} \end{aligned}$$has lines as geodesics.
-
3.
From differential geometry, the curvature of a Riemann surface with metric
$$\begin{aligned} ds=\sqrt{f(x,y)\,\mathrm{d }{x}^2 + g(x,y)\,\mathrm{d }{y}^2} \end{aligned}$$is given by the formula
$$ -\frac{1}{\sqrt{fg}} \left( \frac{\partial }{\partial x}\left( \frac{1}{\sqrt{f}}\frac{\partial \sqrt{g}}{\partial x}\right) +\frac{\partial }{\partial y}\left( \frac{1}{\sqrt{g}}\frac{\partial \sqrt{f}}{\partial y}\right) \right) $$for suitably nice functions f, g. Using this formula, verify that the curvature of \({\mathbf {\mathsf{{H}}}}^2\) and \({\mathbf {\mathsf{{D}}}}^2\) is \(-1\).
-
4.
Consider \(\mathbb C \) with the standard metric. Let
$$\begin{aligned} {{\,\mathrm{Isom}\,}}^h(\mathbb C ) = \{g \in {{\,\mathrm{Isom}\,}}(\mathbb C ) : g \text { is holomorphic}\} \le {{\,\mathrm{Isom}\,}}(\mathbb C ). \end{aligned}$$Exhibit an isomorphism of groups
$$\begin{aligned} {{\,\mathrm{Isom}\,}}^h(\mathbb C ) \simeq \left\{ \begin{pmatrix} a &{} b \\ 0 &{} 1 \end{pmatrix} \in {{\,\mathrm{GL}\,}}_2(\mathbb C ) : |a \,|=1 \right\} \end{aligned}$$and an isometry of \(\mathbb C \) that is not holomorphic. [Hint: An invertible holomorphic map \(\mathbb C \rightarrow \mathbb C \) is of the form \(z \mapsto az+b\).]
- \(\triangleright \) 5.:
-
Show that for every \(z,z' \in {\mathbf {\mathsf{{H}}}}^2\), there exists \(g \in {{\,\mathrm{PSL}\,}}_2(\mathbb R )\) such that \({{\,\mathrm{Re}\,}}gz = {{\,\mathrm{Re}\,}}gz' = 0\). [Hint: Work in \({\mathbf {\mathsf{{D}}}}^2\).]
- \(\triangleright \) 6.:
-
Show that the image of \(\mathbb R _{>0}i\) under an element of \({{\,\mathrm{PSL}\,}}_2(\mathbb R )\) is either a semicircle orthogonal to \(\mathbb R \) or a vertical line. [Hint: Look at the endpoints.]
- \(\triangleright \) 7.:
-
We consider the action of \({{\,\mathrm{PSL}\,}}_2(\mathbb R )\) on geodesics in \({\mathbf {\mathsf{{H}}}}^2\).
- (a):
-
Show that \({{\,\mathrm{PSL}\,}}_2(\mathbb R )\) acts transitively on the set of geodesics in \({\mathbf {\mathsf{{H}}}}^2\).
- (b):
-
Show that given \(z,z' \in {\mathbf {\mathsf{{H}}}}^2\), there exists \(g \in {{\,\mathrm{PSL}\,}}_2(\mathbb R )\) such that \(gz=z'\) and such that g that maps the geodesic through z and \(z'\) to itself.
- (c):
-
Show that every isometry of \({\mathbf {\mathsf{{H}}}}^2\) that maps a geodesic to itself and fixes two points on this geodesic is the identity.
- \(\triangleright \) 8.:
-
Let \(z_1,z_2 \in {\mathbf {\mathsf{{H}}}}^2\) be distinct. Let
$$\begin{aligned} H(z_1,z_2)=\{z \in {\mathbf {\mathsf{{H}}}}^2: \rho (z,z_1) \le \rho (z,z_2)\} \end{aligned}$$be the locus of points as close to \(z_1\) as to \(z_2\), and let \(L(z_1,z_2)={{\,\mathrm{bd}\,}}H(z_1,z_2)\).
Show that \(H(z_1,z_2)\) is a convex (Definition 33.6.6) half-plane, and that
$$\begin{aligned} L(z_1,z_2)=\{z \in {\mathbf {\mathsf{{H}}}}^2: \rho (z,z_1) = \rho (z,z_2)\} \end{aligned}$$is geodesic and equal to the perpendicular bisector of the geodesic segment from \(z_1\) to \(z_2\).
-
9.
Show that a hyperbolic polygon is convex if and only if it is the intersection of finitely many half-planes \(H(z_1,z_2)\) as in Exercise 33.8.
- \(\triangleright \) 10.:
-
Show that the expression
$$\begin{aligned} \frac{|z-\overline{z'} \,|+|z-z' \,|}{|z-\overline{z'} \,|-|z-z' \,|} \end{aligned}$$with \(z,z' \in {\mathbf {\mathsf{{H}}}}^2\) is invariant under \(g \in {{\,\mathrm{PSL}\,}}_2(\mathbb R )\). [Hint: check this on a convenient set of generators.]
- \(\triangleright \) 11.:
-
Show that
$$\begin{aligned} \cosh \log \frac{|z-\overline{z'} \,|+|z-z' \,|}{|z-\overline{z'} \,|-|z-z' \,|} = 1+\frac{|z-z' \,|^2}{2{{\,\mathrm{Im}\,}}(z){{\,\mathrm{Im}\,}}(z')} \end{aligned}$$for all \(z,z' \in {\mathbf {\mathsf{{H}}}}^2\).
- \(\triangleright \) 12.:
-
Verify that the hyperbolic metric on \({\mathbf {\mathsf{{D}}}}^2\) is induced from the hyperbolic metric on \({\mathbf {\mathsf{{H}}}}^2\) from the identification (33.7.4), as follows.
- (a):
-
Show that
$$\begin{aligned} \frac{2|\phi '(z) \,|}{1-|\phi (z) \,|^2} = \frac{1}{{{\,\mathrm{Im}\,}}z}. \end{aligned}$$ - (b):
-
Let \(w=\phi (z)\), and using part (a) conclude that
$$\begin{aligned} \frac{2\,|\mathrm{d }{w} \,|}{1-|w \,|^2} = \frac{|\mathrm{d }{z} \,|}{{{\,\mathrm{Im}\,}}z}. \end{aligned}$$
-
13.
Show that the orientation-reversing isometry \(g(z)=-\overline{z}\) induces the map
$$\begin{aligned} (\phi g \phi ^{-1})(w) = \overline{w} \end{aligned}$$on \({\mathbf {\mathsf{{D}}}}^2\) via the conformal transformation \(\phi :{\mathbf {\mathsf{{H}}}}^2\rightarrow {\mathbf {\mathsf{{D}}}}^2\) in (33.7.4).
-
14.
Show that the Iwasawa decomposition (Proposition 33.4.2) can be given explicitly as
$$ \begin{pmatrix} a &{} b \\ c &{} d \end{pmatrix} = \begin{pmatrix} 1 &{} (ac+bd)/r^2 \\ 0 &{} 1 \end{pmatrix} \begin{pmatrix} 1/r &{} 0 \\ 0 &{} r \end{pmatrix} \begin{pmatrix} s &{} -t \\ t &{} s \end{pmatrix} \in NAK={{\,\mathrm{SL}\,}}_2(\mathbb R ) $$where \(r=\sqrt{c^2+d^2}\), \(s=d/r\), \(t=c/r\).
-
15.
Show that the map
$$\begin{aligned} {\mathbf {\mathsf{{L}}}}^2&\rightarrow {\mathbf {\mathsf{{D}}}}^2\\ (t,x,y)&\mapsto \frac{x+iy}{t+1} \end{aligned}$$identifies the metrics on \({\mathbf {\mathsf{{L}}}}^2\) and \({\mathbf {\mathsf{{D}}}}^2\), via pullback.
- \(\triangleright \) 16.:
-
Show that the Lorentz metric restricted to the hyperboloid is an honest (Riemannian) metric. [Hint: Show that a tangent vector v at a point p satisfies \(b(p,v)=0\), where b is the bilinear form associated to q; then show that the orthogonal complement to p has signature \(+2\).]
- \(\triangleright \) 17.:
-
Show that there is a bijection
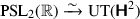 defined by the action of g on a fixed base point in \({{\,\mathrm{UT}\,}}({\mathbf {\mathsf{{H}}}}^2)\). [Hint: Observe that elliptic elements rotate the tangent vector.]
defined by the action of g on a fixed base point in \({{\,\mathrm{UT}\,}}({\mathbf {\mathsf{{H}}}}^2)\). [Hint: Observe that elliptic elements rotate the tangent vector.]
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
This chapter is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, duplication, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, a link is provided to the Creative Commons license and any changes made are indicated.The images or other third party material in this chapter are included in the work's Creative Commons license, unless indicated otherwise in the credit line; if such material is not included in the work's Creative Commons license and the respective action is not permitted by statutory regulation, users will need to obtain permission from the license holder to duplicate, adapt or reproduce the material.
Copyright information
© 2021 The Author(s)
About this chapter
Cite this chapter
Voight, J. (2021). Hyperbolic plane. In: Quaternion Algebras. Graduate Texts in Mathematics, vol 288. Springer, Cham. https://doi.org/10.1007/978-3-030-56694-4_33
Download citation
DOI: https://doi.org/10.1007/978-3-030-56694-4_33
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-56692-0
Online ISBN: 978-3-030-56694-4
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)











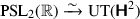 defined by the action of g on a fixed base point in
defined by the action of g on a fixed base point in