Abstract
Having moved from algebra and arithmetic to analysis, and in particular the study of class numbers, in this part we consider geometric aspects of quaternion algebras, and the unit group of a quaternion order acting by isometries on a homogeneous space.
You have full access to this open access chapter, Download chapter PDF
Having moved from algebra and arithmetic to analysis, and in particular the study of class numbers, in this part we consider geometric aspects of quaternion algebras, and the unit group of a quaternion order acting by isometries on a homogeneous space.
1 \(\triangleright \) Quaternion unit groups
By way of analogy, we consider what happens for quadratic orders. In this case, just as with class groups, the behavior of unit groups is quite different depending on whether the asociated quadratic field K is real or imaginary.
In the imaginary case, the unit group is finite, as the norm equation \({{\,\mathrm{Nm}\,}}_{K|\mathbb Q }(\gamma )=1\) has only finitely many solutions for integral \(\gamma \): these are elements of a 2-dimensional lattice in \(\mathbb C \) that lie on the unit circle. Such an element is a root of unity that satisfies a quadratic equation over \(\mathbb Q \), and so only two imaginary quadratic orders having units other than \(\pm 1\) are the Gaussian order \(\mathbb Z [i]\) of discriminant \(-4\) and the Eisenstein order \(\mathbb Z [\rho ]\) with \(\rho :=(-1+\sqrt{-3})/2\) of discriminant \(-3\): see Figure 32.1.1.
Orders \(\mathcal {O}\) in a definite quaternion algebra B over \(\mathbb Q \) behave like orders in an imaginary quadratic field. The unit group of such an order is finite, as the solutions to \({{\,\mathrm{nrd}\,}}(\alpha )=1\) with \(\alpha \in \mathcal {O}\) are elements of a 4-dimensional lattice in \(\mathbb R ^4\) again with bounded size. In section 11.5, after a close investigation of the case of Hurwitz units, we classified the possibilities, embedding \(\mathcal {O}^\times /\{\pm 1\} \hookrightarrow \mathbb H ^1/\{\pm 1\} \simeq {{\,\mathrm{SO}\,}}(3)\) as a finite rotation group: the groups \(\mathcal {O}^\times \) that arise over \(\mathbb Q \) are either cyclic of order 2, 4, 6, quaternion \(Q_8\) of order 8, binary dihedral \(2D_{6}\) of order 12, or the binary tetrahedral group 2T of order 24. In this chapter, we take up this task in the context of a general definite quaternion order, and realize all finite rotation groups using quaternions.
Now we turn to real quadratic fields and correspondingly indefinite quaternion algebras. For the real quadratic order \(\mathbb Z [\sqrt{d}]\) with \(d>0\), the units are solutions to the Pell equation \({{\,\mathrm{Nm}\,}}_{K|\mathbb Q }(x-y\sqrt{d})=x^2-dy^2=\pm 1\) with \(x,y \in \mathbb Z \). All solutions up to sign are given by powers of a fundamental solution which can be computed explicitly using continued fractions; consequently, \(\mathbb Z [\sqrt{d}]^\times = \langle -1, u \rangle \simeq \mathbb Z /2\mathbb Z \times \mathbb Z \) where \(u=x+y\sqrt{d}\) is the fundamental unit. The fundamental unit often (but not always) has large height (in the sense that \(x,y \in \mathbb Z \) are large in absolute value), being of exponential size in the discriminant, by theorems of Schur and Siegel. The unit group of the ring of integers of \(\mathbb Q (\sqrt{d})\) for \(d \equiv 1 \pmod {4}\) is treated in a similar way, by considering the norm equation \(x^2-xy+cy^2=\pm 1\) where \(c=(1-d)/4\).
For quaternions, we are led to consider units in the standard order

in an indefinite quaternion algebra, with \(a,b \in \mathbb Z \) and say \(a>0\). The norm condition \({{\,\mathrm{nrd}\,}}(\gamma )=\pm 1\) for \(\gamma =t+xi+yj+zij\) then reads
with \(t,x,y,z \in \mathbb Z \). Amusingly, this “quaternion Pell equation” includes the Pell equation for \(\mathbb Z [\sqrt{a}]\) by setting \(y=z=0\), and in fact by considering embeddings of quadratic orders (the subject of Chapter 30), we see that this equation combines all Pell equations satisfying certain congruence conditions. Combining these Pell equations, we see that the group of solutions is an infinite, noncommutative group. (The case of an order different from the standard one will give a different norm equation, but the same conclusions.) See Jahangiri [Jah2010] for a Diophantine interpretation of the structure of the unit group of a quaternion order as a quaternionic Pell equation.
We will seek to understand the group \(\mathcal {O}^\times \) by its action on a suitable space, and in this way we are led to consider groups acting discretely on symmetric spaces; we will discover that the group \(\mathcal {O}^\times \) is finitely presented and in particular finitely generated, so we still can think of a set of fundamental solutions (given by generators) whose products generate all solutions to (32.1.2). For example, we may take \(\mathcal {O}={{\,\mathrm{M}\,}}_2(\mathbb Z ) \subseteq {{\,\mathrm{M}\,}}_2(\mathbb Q )\), where \(\mathcal {O}^\times ={{\,\mathrm{GL}\,}}_2(\mathbb Z )\), generated by the elementary matrices \(\begin{pmatrix} 1 &{} 1 \\ 0 &{} 1 \end{pmatrix}, \begin{pmatrix} 0 &{} 1 \\ 1 &{} 0 \end{pmatrix}\). Accordingly, our investigation is detailed but fruitful, involving the theory of Fuchsian and Kleinian groups.
In this chapter, we begin by discussing the general structure of these groups.
2 Structure of units
Throughout this chapter, we use the following notation, recalling our notation for global fields from section 14.4. Let F be a global field, let \({{{\texttt {\textit{S}}}}}\subseteq {{\,\mathrm{Pl}\,}}(F)\) be an eligible set of places of F, and let \(R=R_{{{{\texttt {\textit{S}}}}}}\) be the global ring associated to \({{{\texttt {\textit{S}}}}}\), the ring of \({{{\texttt {\textit{S}}}}}\)-integers of F. (As always, the reader may keep the case \(F=\mathbb Q \), \({{{\texttt {\textit{S}}}}}=\{\infty \}\), and \(R=\mathbb Z \) in mind.) Further, let B be a quaternion algebra over F, and let \(\mathcal {O}\subset B\) be an R-order.
We are interested in the structure of the group \(\mathcal {O}^\times \). Since \(Z(B^\times )=F^\times \), we have \(R^\times \le Z(\mathcal {O}^\times )\) central. We understand the structure of \(R^\times \) by Dirichlet’s unit theorem, as follows.
32.2.1
From Dirichlet’s unit theorem (and its extension to \({{{\texttt {\textit{S}}}}}\)-units and the function field case), the group \(R^\times \) of units is a finitely generated abelian group of rank \(\#{{{\texttt {\textit{S}}}}}- 1\), so that
where w is the number of roots of unity in F. (The proof is briefly recalled in 32.3.1.)
The group \(\mathcal {O}^\times \) is (in general) noncommutative, so we should not expect a description like 32.2.1. But to get started, we consider the quotient \(\mathcal {O}^\times /R^\times \), and the reduced norm map which gets us back into \(R^\times \).
32.2.3
We recall the theorem on norms (see section 14.7): as before, let
be the set of real ramified places in B (recalling that complex places cannot be ramified), and
the set of elements that are positive at the places \(v \in \Omega \). If F is a function field, then \(\Omega =\emptyset \), and \(R_{>_{\Omega } 0}^{\times }=R^\times \). The Hasse–Schilling norm theorem (Main Theorem 14.7.4) says that \({{\,\mathrm{nrd}\,}}(B^\times ) = F_{>_{\Omega } 0}^{\times }\). Letting
we conclude that \({{\,\mathrm{nrd}\,}}(\mathcal {O}^\times ) \le R_{>_{\Omega } 0}^{\times }\). (Strictly speaking, we only needed the containment \({{\,\mathrm{nrd}\,}}(B^\times ) \le F_{>_{\Omega } 0}^{\times }\) which follows directly from local considerations; but we pursue finer questions below.)
32.2.7
In light of 32.2.3, the reduced norm gives an exact sequence
where
is the subgroup of units of reduced norm 1.
Since \({{\,\mathrm{nrd}\,}}(R^\times )=R^{\times 2}\) by the squaring map, we have \(\mathcal {O}^1 \cap R^\times = \{\pm 1\}\), so (32.2.8) yields
Since the group \(R^\times \) is finitely generated, the group \(R_{>_{\Omega } 0}^{\times }/R^{\times 2}\) is a finite, elementary abelian 2-group. (In general, the reduced norm (the last) map in (32.2.10) need not be surjective.)
32.2.11
In general, the exact sequence (32.2.10) does not split, so the group \(\mathcal {O}^\times /R^\times \) will be a nontrivial extension of \(\mathcal {O}^1/\{\pm 1\}\) by an elementary abelian 2-group.
Example 32.2.12
If \(B={{\,\mathrm{M}\,}}_2(F)\) and \(\mathcal {O}={{\,\mathrm{M}\,}}_2(R)\), then \(\mathcal {O}^\times ={{\,\mathrm{GL}\,}}_2(R)\) and \(\mathcal {O}^\times /R^\times = {{\,\mathrm{GL}\,}}_2(R)/R^\times =:{{\,\mathrm{PGL}\,}}_2(R)\). The reduced norm is the determinant, which is surjective, and so the exact sequence (32.2.10) can be extended to
32.2.13
In light of Example 32.2.12, it is natural to write \({{\,\mathrm{P\!}\,}}\mathcal {O}^\times :=\mathcal {O}^\times /R^\times \) and \({{\,\mathrm{P\!}\,}}\mathcal {O}^1 :=\mathcal {O}^1/\{\pm 1\}\).
Remark 32.2.14. Some authors write \({{\,\mathrm{GL}\,}}_1(\mathcal {O})=\mathcal {O}^\times \) and \({{\,\mathrm{SL}\,}}_1(\mathcal {O}) = \mathcal {O}^1\), and this notation suggests generalizations. In such situations, it is natural to write \({{\,\mathrm{PGL}\,}}_1(\mathcal {O})=\mathcal {O}^\times /R^\times \) and \({{\,\mathrm{PSL}\,}}_1(\mathcal {O})=\mathcal {O}^1/\{\pm 1\}\).
32.2.15
Suppose F is a number field. Then the group \(R_{>_{\Omega } 0}^{\times }/R^{\times 2}\) is canonically isomorphic to a quotient of class groups, as follows. Let \(\mathbb Z _F\) be the ring of integers of F, and let \({{\,\mathrm{Cl}\,}}_\Omega \mathbb Z _F\) denotes the class group of F given by the quotient of the group of fractional ideals by the subgroup of principal ideals with a generator positive at all places in \(\Omega \). Then \(R_{>_{\Omega } 0}^{\times }/R^{\times 2}\) is isomorphic to the quotient of \({{\,\mathrm{Cl}\,}}_\Omega \mathbb Z _F\) by \({{\,\mathrm{Cl}\,}}\mathbb Z _F\) and the group generated by the finite primes in \({{{\texttt {\textit{S}}}}}\).
3 Units in definite quaternion orders
In this section, we show that for a definite quaternion order \(\mathcal {O}\), the scalar units \(R^\times \) are of finite index in \(\mathcal {O}^\times \)—i.e., the group \({{\,\mathrm{P\!}\,}}\mathcal {O}^\times = \mathcal {O}^\times /R^\times \) is a finite group.
32.3.1
To build intuition, suppose F is a number field with r real places and c complex places. Recall the proof of Dirichlet’s unit theorem: we define a map
The kernel of this map is the group of roots of unity (the torsion subgroup of \(R^\times \)). The image lies inside the trace zero hyperplane \(\sum _{v \in {{{\texttt {\textit{S}}}}}} x_v = 0\) by the product formula (14.4.6), and it is discrete and cocompact inside this hyperplane, so it is isomorphic to \(\mathbb Z ^{{{{\texttt {\textit{S}}}}}-1}\). In particular, \(R^\times \) is finite if and only if \(\#{{{\texttt {\textit{S}}}}}=1\); since \({{{\texttt {\textit{S}}}}}\) always contains the set of archimedean places of size \(r+c\), we see that \(R^\times \) is finite if and only if \((r,c)=(1,0),(0,1)\), so \(F=\mathbb Q \) or F is an imaginary quadratic field.
Remark 32.3.3. Informally, one might say that \(R^\times \) is finite only when the completions at the places in \({{{\texttt {\textit{S}}}}}\) provide “no room” for the unit group to become infinite. This is analogous to the informal case for strong approximation in 28.5.4: if there is a place \(v \in {{{\texttt {\textit{S}}}}}\) where \(B_v^1\) is not compact, then there is enough room for \(B^1\) to “spread out” and become dense.
32.3.4
Recall (Definition 28.5.1) that B is \({{{\texttt {\textit{S}}}}}\)-definite if \({{{\texttt {\textit{S}}}}}\subseteq {{\,\mathrm{Ram}\,}}(B)\), i.e., every place in \({{{\texttt {\textit{S}}}}}\) is ramified in B. In particular, if F is a number field, then since a complex place is split and \({{{\texttt {\textit{S}}}}}\) contains the archimedean places, if B is \({{{\texttt {\textit{S}}}}}\)-definite then F is totally real; in this case, when \({{{\texttt {\textit{S}}}}}\) is exactly the set of archimedean places, we simply say that B is definite.
32.3.5
Consider the setup in analogy with Dirichlet’s unit theorem 32.3.1. We consider the embedding of B into the completions at all places in \({{{\texttt {\textit{S}}}}}\):
By Exercise 27.14, R is discrete in  and \(\mathcal {O}\) is discrete in
and \(\mathcal {O}\) is discrete in  (the point being that in the number field case, \({{{\texttt {\textit{S}}}}}\) contains all archimedean places). Consequently, the injections
(the point being that in the number field case, \({{{\texttt {\textit{S}}}}}\) contains all archimedean places). Consequently, the injections
have discrete image.
Depending on whether the place v is nonarchimedean (split or ramified) or archimedean (split real, ramified real, or complex), we have a different target component \(B_v^\times /F_v^\times \) or \(B_v^1\). The major task of Part IV is to describe these possibilities in detail and look at the associated symmetric spaces.
We begin with the simplest case, where the unit groups involved are finite.
Proposition 32.3.7
The group \(\mathcal {O}^\times /R^\times \) is finite if and only if \(\mathcal {O}^1\) is finite if and only if B is \({{{\texttt {\textit{S}}}}}\)-definite.
Proof. By the exact sequence (32.2.10), the group \(\mathcal {O}^\times /R^\times \) is finite if and only if the group \(\mathcal {O}^1\) is finite.
First, suppose that B is \({{{\texttt {\textit{S}}}}}\)-definite. Then by definition, for each \(v \in {{{\texttt {\textit{S}}}}}\), the completion \(B_v\) is a division algebra over \(F_v\). But each \(B_v^1\) is compact, from the topological discussion in section 13.5. Therefore in (32.3.6), the group \(\mathcal {O}^1\) is a closed, discrete subgroup of a compact group—hence finite.
Now suppose B is not \({{{\texttt {\textit{S}}}}}\)-definite. Then there is a place \(v_0 \in {{{\texttt {\textit{S}}}}}\) that is unramified; we will correspondingly find an element of infinite order (like solutions to the quaternion Pell equation coming from the original Pell’s equation (32.1.2)). We have \(B_{v_0} \simeq {{\,\mathrm{M}\,}}_2(F_{v_0})\), so there exists \(\alpha \in B\) be such that the reduced characteristic polynomial splits in \(F_{v_0}\); we may suppose without loss of generality that \(K=F[\alpha ]\) is a field. Let S be the integral closure of R in K (not to be confused with the set \({{{\texttt {\textit{S}}}}}\)). Then by the Dirichlet \({{{\texttt {\textit{S}}}}}\)-unit theorem (32.2.1), the rank of \(S^\times /R^\times \) is at least 1: the set of places \(w \in {{\,\mathrm{Pl}\,}}(K)\) such that w lies above \(v \in {{{\texttt {\textit{S}}}}}\) contains at least one element from each v and two above \(v_0\), because it is split. So there is an element \(\gamma \in S^\times /R^\times \) of infinite order. As R-lattices, the order \(S \cap \mathcal {O}\) has finite R-index and hence finite index in S, so \(S^\times /(S \cap \mathcal {O})^\times \) is a finite group, and therefore a sufficiently high power of \(\gamma \) lies in \((S \cap \mathcal {O})^\times \subseteq \mathcal {O}^\times \), and \(\mathcal {O}^\times \) is infinite. \(\square \)
Example 32.3.8
Let  and let \(\mathcal {O}\) be the \(\mathbb Z \)-order generated by i, j, so that \({{{\texttt {\textit{S}}}}}=\{\infty \}\). Then B is \({{{\texttt {\textit{S}}}}}\)-definite, and \(\mathcal {O}^\times = \langle i,j \rangle \simeq Q_8\) is the quaternion group of order 8.
and let \(\mathcal {O}\) be the \(\mathbb Z \)-order generated by i, j, so that \({{{\texttt {\textit{S}}}}}=\{\infty \}\). Then B is \({{{\texttt {\textit{S}}}}}\)-definite, and \(\mathcal {O}^\times = \langle i,j \rangle \simeq Q_8\) is the quaternion group of order 8.
Now consider \({{{\texttt {\textit{S}}}}}=\{2,\infty \}\); then B is still \({{{\texttt {\textit{S}}}}}\)-definite. We find
(Exercise 32.2).
Finally, if we take \({{{\texttt {\textit{S}}}}}=\{5,\infty \}\), then B is no longer \({{{\texttt {\textit{S}}}}}\)-definite; and \(\mathcal {O}[1/5]^\times \) contains the element \(2+i\) of norm \(5 \in \mathbb Z [1/5]^\times \) and infinite order.
32.3.10
Suppose B is \({{{\texttt {\textit{S}}}}}\)-definite. Then by Proposition 32.3.7, the group \(\mathcal {O}^\times /R^\times \) is finite. Since we have an embedding
it follows that a \(\mathcal {O}^\times /R^\times \) is a finite subgroup of \({{\,\mathrm{P\!}\,}}B^\times \), so a classification of finite subgroups of \({{\,\mathrm{P\!}\,}}B^\times \) gives a list of possible definite unit groups; we make this our task in the remainder of this chapter.
4 Finite subgroups of quaternion unit groups
We now embark on a classification of finite subgroups of \({{\,\mathrm{P\!}\,}}B^\times = B^\times /F^\times \) and \({{\,\mathrm{P\!}\,}}B^1 = B^1/\{\pm 1\}\); this is akin to first getting acquainted with the roots of unity in a number field. Suppose throughout the rest of this chapter that F is a number field; we allow B to be definite or indefinite.
We begin in this section with the classification of the possible groups up to isomorphism that goes back at least to Klein [Kle56, Chapter II]: the original book dates back to 1884 and is undoubtedly one of the most influential books of 19th century mathematics. See also the descriptions by Coxeter [Coxtr40] and Lamotke [Lamo86, Chapters I–II] for a presentation of the regular solids, finite rotation groups, as well as finite subgroups of \({{\,\mathrm{SL}\,}}_2(\mathbb C )\).
Proposition 32.4.1
Let \(\Gamma < {{\,\mathrm{P\!}\,}}B^\times \) be a finite group. Then \(\Gamma \) is cyclic, dihedral, or an exceptional group \(A_4,S_4,A_5\).
We met these groups already in Proposition 11.5.2, and the proof is an extension of this result.
Proof. Let v be an archimedean place of F. Then the natural map \(B^\times \rightarrow B_v^\times /F_v^\times \) has kernel \(F_v^\times \cap B^\times = F^\times \), so the group homomorphism \(B^\times /F^\times \hookrightarrow B_v^\times /F_v^\times \) is injective.
First suppose that v is a ramified (real) place, so \(B_v \simeq \mathbb H \) and
By Corollary 2.4.21, we have \(\mathbb H ^1/\{\pm 1\} \simeq {{\,\mathrm{SO}\,}}(3)\) so \(\Gamma \) is a finite rotation group: these are classified in Proposition 11.5.2.
In general, we seek to conjugate the group \(\Gamma \) in order to reduce to the case above. We may prove the lemma after making a base extension of F, so we may suppose that v is complex, with \(B_v \simeq {{\,\mathrm{M}\,}}_2(\mathbb C )\). Then \(B_v^\times /F_v^\times \simeq {{\,\mathrm{PGL}\,}}_2(\mathbb C )\), and via the injection \(B^\times /F^\times \hookrightarrow {{\,\mathrm{PGL}\,}}_2(\mathbb C )\) we obtain a finite subgroup \(\Gamma \subseteq {{\,\mathrm{PGL}\,}}_2(\mathbb C )\). The natural map \({{\,\mathrm{SL}\,}}_2(\mathbb C ) \rightarrow {{\,\mathrm{PGL}\,}}_2(\mathbb C )\) is surjective, as we may rescale every invertible matrix by a square root of its determinant to have determinant 1, and its kernel is \(\{\pm 1\}\), giving an isomorphism \({{\,\mathrm{PSL}\,}}_2(\mathbb C ) \simeq {{\,\mathrm{PGL}\,}}_2(\mathbb C )\). We then lift \(\Gamma \) under the projection \({{\,\mathrm{SL}\,}}_2(\mathbb C ) \rightarrow {{\,\mathrm{PSL}\,}}_2(\mathbb C )\) to a finite group (containing \(-1\)). We have
as in 2.4.2. If \(\langle \ ,\ \!\rangle \) denotes the canonical (Hermitian) inner product on \(\mathbb C ^2\) defined by \(\langle z,w\rangle =z^* w\) (as column vectors), then \({{\,\mathrm{SU}\,}}(2)\) is precisely the group of matrices of determinant 1 preserving \(\langle \ ,\ \!\rangle \), i.e.,
since \(\langle Az, Aw \rangle = z^* (A^* A) w = z^* w\) if and only if \(A^*A=1\). We now define a \(\Gamma \)-invariant Hermitian inner product on \(\mathbb C ^2\) by averaging: for \(z,w \in \mathbb C ^2\), we define
Choose an orthonormal basis for \(\langle \ ,\ \!\rangle _\Gamma \) and let \(T \in {{\,\mathrm{SL}\,}}_2(\mathbb C )\) be the change of basis matrix relative to the standard basis. Then \(\langle z,w\rangle _\Gamma = \langle Tz,Tw \rangle \) and therefore \(T\Gamma T^{-1} \subset {{\,\mathrm{SU}\,}}(2)\). The result now follows from (32.4.2) and the previous case. \(\square \)
5 Cyclic subgroups
In the next few sections, we discuss each of the possibilities in Proposition 32.4.1 in turn, following Chinburg–Friedman [CF2000]. We begin with cyclic subgroups.
There are always many subgroups of \({{\,\mathrm{P\!}\,}}B^\times \) of order 2: every nonscalar element \(\alpha \in B^\times \) with trace zero has \(\alpha ^2 \in F^\times \).
Proposition 32.5.1
Let \(m>2\) and let \(\zeta _m \in F{}^{al }\) be a primitive mth root of unity. Then \({{\,\mathrm{P\!}\,}}B^\times \) contains a cyclic subgroup of order m if and only if \(\zeta _m+\zeta _m^{-1} \in F\) and \(F(\zeta _m)\) splits B. Such a cyclic subgroup is unique up to conjugation in \({{\,\mathrm{P\!}\,}}B^\times \).
Proof. First we prove \((\Leftarrow )\). Suppose \(\zeta _m+\zeta _m^{-1} \in F\) and \(F(\zeta _m)\) splits B. If in fact \(\zeta _m \in F\), then F splits B, i.e. \(B \simeq {{\,\mathrm{M}\,}}_2(F)\); then \(\gamma :=\begin{pmatrix} 1 &{} 0 \\ 0 &{} \zeta _m \end{pmatrix}\) has order m in \({{\,\mathrm{P\!}\,}}B^\times \simeq {{\,\mathrm{PGL}\,}}_2(F)\). Otherwise, since \(\zeta _m+\zeta _m^{-1} \in F\), we have \([F(\zeta _m):F]=2\), with \(\zeta _m\) a root of the polynomial \(T^2-(\zeta _m+\zeta _m^{-1})T + 1\). By Lemma 5.4.7, this implies there is an embedding \(F(\zeta _m) \hookrightarrow B\); let \(\zeta \) be the image of \(\zeta _m\) under this embedding. If \(\zeta \) has order d in \({{\,\mathrm{P\!}\,}}B^\times \), then \(\mathbb Q (\zeta _m+\zeta _m^{-1},\zeta _m^d) \subseteq F\); since \(\zeta _m \not \in F\), we must have \(d=m\) if m is odd or \(d=m/2\) if m is even. Let \(\gamma =1+\zeta \). Then \(\gamma ^2\zeta ^{-1} = 2+ \zeta +\zeta ^{-1} \in F^\times \), so \(\gamma \) has order m in \({{\,\mathrm{P\!}\,}}B^\times \).
Now we prove \((\Rightarrow )\). Suppose that \(\gamma \in B^\times \) has image in \({{\,\mathrm{P\!}\,}}B^\times \) of order \(m>2\), so that \(\gamma ^m = a \in F^\times \). We do calculations in the commutative F-algebra \(K :=F[\gamma ]\). Let \(\varsigma :=\overline{\gamma }\gamma ^{-1} \in K^\times \). Then
so \(\varsigma ^m=1\). If \(\varsigma ^d=1\) for \(d \mid m\) then \(\overline{\gamma }^d=\varsigma ^d \gamma ^d = \gamma ^d\) so \(\gamma ^d \in F^\times \) and thus \(d=m\); thus \(\varsigma \) has order m in \(B^\times \). Applying the standard involution again gives
thus \(\overline{\varsigma }=\varsigma ^{-1}\), so \(\varsigma \not \in F\) and \({{\,\mathrm{trd}\,}}(\varsigma )=\varsigma +\varsigma ^{-1} \in F\). Taking an appropriate power to match up the root of unity, we conclude \(\zeta _m+\zeta _m^{-1} \in F\). Finally, either K is a quadratic field in B, in which case K splits B by Lemma 5.4.7, or K is not a field and \(B \simeq {{\,\mathrm{M}\,}}_2(F)\), in which case F already splits B.
We conclude with uniqueness. Continuing from the previous paragraph, we have shown that \(\gamma +\overline{\gamma }=(1+\varsigma )\gamma \in F^\times \), so \(\gamma \) and \(1+\varsigma \) generate the same cyclic subgroup of \({{\,\mathrm{P\!}\,}}B^\times \), where \(\varsigma ^m=1\). If \(K=F(\varsigma )\) is a field, then all embeddings \(F(\zeta _m) \hookrightarrow B\) are conjugate in \(B^\times \) by the Skolem–Noether theorem (Corollary 7.1.5), and consequently every two cyclic subgroups of order m are conjugate. Otherwise, the reduced characteristic polynomial of \(\varsigma \) factors, so \(B \simeq {{\,\mathrm{M}\,}}_2(F)\), and its roots (the eigenvalues of \(\varsigma \)) belong to F. If the eigenvalues are repeated, then up to conjugation in \({{\,\mathrm{GL}\,}}_2(F)\), \(\varsigma \) is a scalar multiple of \(\begin{pmatrix} 1 &{} b \\ 0 &{} 1\end{pmatrix}\) with \(b \in F\), and therefore has infinite order, impossible. Thus the roots are distinct, and \(\varsigma \) is conjugate to a multiple of \(\begin{pmatrix} 1 &{} 0 \\ 0 &{} \lambda \end{pmatrix}\) and so \(\lambda \) is a primitive mth root of unity and the cyclic subgroup is unique up to conjugation. \(\square \)
32.5.4
The splitting condition in Proposition 32.5.1 can alternatively be phrased in local-to-global terms (Proposition 14.6.7): \(K=F(\zeta _m)\) splits B if and only if every place \(v \in {{\,\mathrm{Ram}\,}}B\) is not split in K. Since the field \(F(\zeta _m)\) is totally complex, every archimedean place splits, and so when \(K \ne F\) we have \(K \hookrightarrow B\) if and only if no prime \(\mathfrak p \in {{\,\mathrm{Ram}\,}}B\) splits in K.
32.5.5
The proof of Proposition 32.5.1 describes the cyclic subgroup explicitly, up to conjugation (still with \(m>2\)):
-
(i)
If \(\zeta _m \in F\), then \(B \simeq {{\,\mathrm{M}\,}}_2(F)\) and every cyclic subgroup of \({{\,\mathrm{PGL}\,}}_2(F)\) of order m is conjugate to the subgroup generated by \(\gamma _m=\begin{pmatrix} 1 &{} 0 \\ 0 &{} \zeta _m \end{pmatrix}\);
-
(ii)
Otherwise, \(K=F(\zeta _m)\) is a quadratic extension of F with \(K \hookrightarrow B\), and every subgroup of \({{\,\mathrm{P\!}\,}}B^\times \) of order m is conjugate to the subgroup generated by the image of \(\gamma _m=1+\zeta _m\).
The F-algebra \(K_m=F[\gamma _m]\) is separable and uniquely determined up to isomorphism.
In contrast to Proposition 32.5.1, there are a great many cyclic subgroups of order \(m=2\) in \({{\,\mathrm{P\!}\,}}B^\times \), described as follows.
32.5.6
If \(\gamma \in {{\,\mathrm{P\!}\,}}B^\times \) has order \(m=2\), then \(\gamma ^2=a \in F^\times \) and \(\gamma \not \in F^\times \). Therefore, either \(a \not \in F^{\times 2}\), equivalently \(K=F[\gamma ] \simeq F(\sqrt{a})\) is a field, and the embedding \(K \hookrightarrow B\) is unique up to conjugation in \(B^\times \) by the Skolem–Noether theorem; or \(a \in F^{\times 2}\), in which case after rescaling \(\gamma ^2=1\) so \(B \simeq {{\,\mathrm{M}\,}}_2(F)\) and \(\gamma \) is conjugate to \(\begin{pmatrix} 1 &{} 0 \\ 0 &{} -1 \end{pmatrix}\).
The following corollary shows that we can often reduce to the case of an even order subgroup.
Corollary 32.5.7
Let \(m \ge 1\) be odd. Then \({{\,\mathrm{P\!}\,}}B^\times \) contains a cyclic subgroup of order m if and only if \({{\,\mathrm{P\!}\,}}B^\times \) contains a cyclic subgroup of order 2m.
Proof. If \(m=1\), then we are all set by 32.5.6. If \(m \ge 3\), then Proposition 32.5.1 applies, and we see that the hypotheses hold for m if and only if they hold for 2m, since \(\zeta _{2m}=-\zeta _m\). \(\square \)
Corollary 32.5.8
\({{\,\mathrm{P\!}\,}}B^\times \) contains a cyclic subgroup of order 2m if and only if \({{\,\mathrm{P\!}\,}}B^1\) contains a cyclic subgroup of order m.
Proof. The corollary follows from 32.5.5: the subgroup of \({{\,\mathrm{P\!}\,}}B^\times \) of order 2m generated by \(\gamma _{2m}\) yields the subgroup of \({{\,\mathrm{P\!}\,}}B^1\) of order m generated by \(\zeta _{2m}\), and vice versa. \(\square \)
6 \(*\) Dihedral subgroups
We now turn to the dihedral case, where we show that every cyclic subgroup extends (in general, in many ways) to a dihedral subgroup, continuing to follow Chinburg–Friedman [CF2000, Lemma 2.3].
Lemma 32.6.1
Let \(m \ge 2\). Then the following statements hold.
-
(a)
Every cyclic subgroup of \({{\,\mathrm{P\!}\,}}B^\times \) of order m is contained in a dihedral subgroup of order 2m; in particular, \({{\,\mathrm{P\!}\,}}B^\times \) contains a dihedral subgroup of order 2m if and only if it contains a cyclic subgroup of order m.
-
(b)
Let \(\gamma \in B^\times \) have order m in \({{\,\mathrm{P\!}\,}}B^\times \), and let \(K=F[\gamma ]\). For \(j \in B^\times \), we have \(\langle \gamma , j \rangle \subseteq {{\,\mathrm{P\!}\,}}B^\times \) dihedral if and only if \(j^2=b \in F\) and
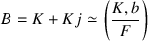 .
.
Proof. First (a). The implication \((\Rightarrow )\) is immediate, so we prove \((\Leftarrow )\). Let \(m \ge 2\) and suppose that \({{\,\mathrm{P\!}\,}}B^\times \) contains a cyclic subgroup of order m, generated by the image of \(\gamma \in B^\times \), and let \(K=F[\gamma ]\). Let \(j \in B\) be orthogonal to K under \({{\,\mathrm{nrd}\,}}\). Then \(j^2=b \in F^\times \), and \(j \alpha = \overline{\alpha } j = \alpha ^{-1} j \in {{\,\mathrm{P\!}\,}}B^\times \) for all \(\alpha \in K\), so the subgroup \(\langle \gamma , j \rangle \) is dihedral of order 2m in \({{\,\mathrm{P\!}\,}}B^\times \), and  , as in Exercise 6.2.
, as in Exercise 6.2.
Now (b). We just showed \((\Rightarrow )\) in the previous part, so we show \((\Leftarrow )\). Let \(\Gamma \subseteq {{\,\mathrm{P\!}\,}}B^\times \) be a dihedral subgroup of order 2m, where \(\Gamma = \langle \gamma , j \rangle \) has \(\gamma \in B^\times \) generating a cyclic subgroup of order m in \({{\,\mathrm{P\!}\,}}B^\times \) and \(j \in B^\times \) satisfies
Let \(K=F[\gamma ]\). We claim that  .
.
First we show \(j^{-1} \gamma j = \overline{\gamma }\). This follows from a direct argument using reduced norm and trace (see Exercise 32.4), but we have also the following argument. Since \(K=F[\gamma ]\) is semisimple (see 32.5.5) and conjugation by j acts as an F-algebra automorphism of \(K=F[\gamma ]\), it is either the identity or the standard involution, and thus \(j^{-1}\gamma j = \gamma ,\overline{\gamma }\). But we cannot have \(j^{-1}\gamma j = \gamma \), because then \(K[j] \subseteq B\) would be a commutative subalgebra of dimension \(\ge 3\), a contradiction.
Now by (4.2.16), expanding the trace gives
Since \(1,\gamma \) are linearly independent we conclude \({{\,\mathrm{trd}\,}}(j)={{\,\mathrm{trd}\,}}(j\overline{\gamma })=0\), i.e., j is orthogonal to K under \({{\,\mathrm{nrd}\,}}\), so \(j^2=b \in F^\times \) and  . \(\square \)
. \(\square \)
The dihedral subgroups of order 2m for \(m>2\) are classified as follows.
Lemma 32.6.3
Let \(m>2\). Then the set of dihedral subgroups of order 2m up to conjugation in \({{\,\mathrm{P\!}\,}}B^\times \) are in bijection with the group
where \(K_m\) is as in 32.5.5 and \(\delta =2+\zeta _m+\zeta _m^{-1}\).
Proof. Let \(\Gamma = \langle \gamma , j \rangle \) and \(\Gamma '=\langle \gamma , j' \rangle \) be two dihedral subgroups as in Lemma 32.6.1(b) with \(j^2=b\) and \((j')^2=b'\). Then \(j' \in K^\perp = K j\) so \(j'=\beta j\) with \(\beta \in K^\times \), and \({{\,\mathrm{nrd}\,}}(j')=b'={{\,\mathrm{nrd}\,}}(\beta )b\), so \(bb' \in {{\,\mathrm{Nm}\,}}_{K|F}(K^\times )\) (as in Exercise 6.4). Then we claim that \(\Gamma ,\Gamma '\) are conjugate in \({{\,\mathrm{P\!}\,}}B^\times \) if and only if
If \(\Gamma '=\alpha ^{-1} \Gamma \alpha \) with \(\alpha \in B^\times \), then conjugation by \(\alpha \) normalizes the unique cyclic subgroup on both sides, so \(\gamma ^r j' = \alpha ^{-1} j \alpha \) for some r, and therefore
as desired. Conversely, if \(bb' \in F^{\times 2} \langle \delta \rangle \) then so too for \({{\,\mathrm{nrd}\,}}(\beta )=b'b^{-1}\); rescaling \(\beta \) by \(F^\times \) and replacing \(\beta \) by \(\gamma \beta \) if necessary, we may suppose \({{\,\mathrm{nrd}\,}}(\beta )={{\,\mathrm{Nm}\,}}_{K|F}(\beta )=1\) (without changing \(\Gamma '\)); by Hilbert’s theorem 90, there exists \(\alpha \in K^\times \) such that \(\beta =\overline{\alpha }\alpha ^{-1}\), and conjugation by \(\alpha \) again normalizes the cyclic subgroup and satisfies
as desired. \(\square \)
Remark 32.6.5. One can rephrase Lemma 32.6.3 in terms of a global equivalence relation, further encompassing the case \(m=2\): see Chinburg–Friedman [CF2000, Lemma 2.4].
Corollary 32.6.6
The group \({{\,\mathrm{P\!}\,}}B^1\) contains a dihedral group of order \(2m>4\) if and only if  .
.
Proof. We first prove \((\Rightarrow )\). If \({{\,\mathrm{P\!}\,}}B^1\) contains a dihedral group \(\Gamma =\langle \gamma , j \rangle \) of order 2m then it contains a cyclic subgroup of order m so by Corollary 32.5.8 the group \({{\,\mathrm{P\!}\,}}B^\times \) contains a cyclic subgroup of order 2m, which we may take to be generated by \(\gamma _{2m}\) as in 32.5.5 with \(K_{2m}=F[\gamma _{2m}]=F[\gamma ]\); by hypothesis we have \(j^2=-{{\,\mathrm{nrd}\,}}(j)=-1\), and so  as in the classification in Lemma 32.6.1.
as in the classification in Lemma 32.6.1.
Next we prove the converse implication \((\Leftarrow )\). We refer to 32.5.5. In case (i) where \(\zeta _{2m} \in F\), we have \({{\,\mathrm{nrd}\,}}(\zeta _{2m}^{-1} \gamma _{m})=\zeta _{2m}^2 \zeta _m = 1\) so we may take \(\Gamma = \langle \zeta _{2m}^{-1} \gamma _m, j \rangle \); in case (ii), where \(\zeta _{2m} \not \in F\), we take \(\Gamma = \langle \zeta _{2m}, j \rangle \). \(\square \)
7 \(*\) Exceptional subgroups
Finally we treat exceptional groups (cf. Gehring–Maclachlan–Martin–Reid [GMMR97, p. 3635]). We found quaternionic realizations of the exceptional groups in section 11.5 when  (and \(\sqrt{5} \in F\) for \(A_5\)).
(and \(\sqrt{5} \in F\) for \(A_5\)).
Proposition 32.7.1
The following statements hold.
-
(a)
\({{\,\mathrm{P\!}\,}}B^\times \) contains a subgroup isomorphic to \(A_4\) if and only if \({{\,\mathrm{P\!}\,}}B^1\) contains a subgroup isomorphic to \(A_4\) if and only if
 .
. -
(b)
\({{\,\mathrm{P\!}\,}}B^\times \) contains a subgroup isomorphic to \(S_4\) if and only if it contains a subgroup isomorphic to \(A_4\); and \({{\,\mathrm{P\!}\,}}B^1\) contains a subgroup isomorphic to \(S_4\) if and only if
 and \(\sqrt{2} \in F\).
and \(\sqrt{2} \in F\). -
(c)
\({{\,\mathrm{P\!}\,}}B^\times \) contains a subgroup isomorphic to \(A_5\) if and only if \({{\,\mathrm{P\!}\,}}B^1\) contains a subgroup isomorphic to \(A_5\) if and only if
 and \(\sqrt{5} \in F\).
and \(\sqrt{5} \in F\).
Any two such exceptional subgroups of \({{\,\mathrm{P\!}\,}}B^\times \) (or \({{\,\mathrm{P\!}\,}}B^1\)) are conjugate by an element of \(B^\times \) if and only if they are isomorphic as groups.
Proof. First we prove (a); let \(\Gamma \subseteq {{\,\mathrm{P\!}\,}}B^\times \) be a subgroup with \(\Gamma \simeq A_4\). The reduced norm gives a homomorphism \(\Gamma \rightarrow {{\,\mathrm{nrd}\,}}(\Gamma ) \subseteq F^\times /F^{\times 2}\), but \(A_4\) has no nontrivial homomorphic image of exponent 2, so \({{\,\mathrm{nrd}\,}}(\Gamma ) \subseteq F^{\times 2}\). Therefore, there is a unique lift of \(\Gamma \) to \(B^1/\{\pm 1\}\), and the map \(B^1/\{\pm 1\} \rightarrow B^\times /F^\times \) is an isomorphism from this lift to H. This shows the first implication; its converse follows from the injection \({{\,\mathrm{P\!}\,}}B^1 \hookrightarrow {{\,\mathrm{P\!}\,}}B^\times \). For the second implication, let \(i,j \in B^1\) generate the \(V_4\)-subgroup (the normal subgroup of index 3 isomorphic to the Klein 4 group) of \(A_4\) in \({{\,\mathrm{P\!}\,}}B^1\). Then \(i,j \not \in F^\times \), and \(i^2=-{{\,\mathrm{nrd}\,}}(i)=-1=j^2\); and similarly \((ij)^2=-1\) implies \(ji=-ij\). By Lemma 2.2.5, we conclude  . The converse follows from the Hurwitz unit group 11.2.4.
. The converse follows from the Hurwitz unit group 11.2.4.
For part (b), the implication \((\Rightarrow )\) is immediate; the implication \((\Leftarrow )\) follows by taking the Hurwitz units and adjoining the element \(1+i\), as in 11.5.4 but working modulo scalars. For the second statement, an element of order 4 in \(B^1/\{\pm 1\}\) lifts to an element of order 8 in \(B^1\) and therefore has reduced trace \(\pm \sqrt{2} \in F\); the converse follows again from the explicit construction in 11.5.4.
For part (c), we argue similarly. Since \(A_5\) is generated by its subgroups isomorphic to \(A_4\), we may apply (a) to get a lift, and by the reduced trace we get \(\sqrt{5} \in F\).
The uniqueness statement is requested in Exercise 32.5. \(\square \)
Exercises
Unless otherwise indicated, let F be a number field with ring of integers R, let B be a quaternion algebra over F and let \(\mathcal {O}\subseteq B\) be an R-order.
-
1.
Let F be a totally real field, let \(K \supseteq F\) be a totally imaginary quadratic extension of F, so \(K=F(\sqrt{d})\) with d totally negative. Let S be the ring of integers of K. Consider the group homomorphism
$$\begin{aligned} \phi :S^\times&\rightarrow S^\times \\ u&\mapsto u/\overline{u} \end{aligned}$$where \(\overline{\phantom {x}}\) is the nontrivial F-involution of K.
-
(a)
Show that if \(u \in \mu (S)R^\times \) then \(u \in \ker \phi \).
-
(b)
Show that \(\phi (u)\) is a root of unity for all \(u \in S^\times \). [Hint: It is an algebraic integer of absolute value 1 under all complex embeddings.]
-
(c)
Let \(\mu (S)\) be the subgroup of roots of unity of \(S^\times \), and let \(\psi :S^\times \rightarrow \mu (S)/\mu (S)^2\) be the map induced by \(\phi \). Show that if \(u \in \ker \psi \), so \(\phi (u)=\zeta ^2\) with \(\zeta \in \mu (S)\), then \(\zeta ^{-1} u \in R^\times \). Conclude that \(\ker \psi = \mu (S)R^\times \).
-
(d)
Show that \([S^\times :\mu (S)R^\times ] \le [S^\times :S^1R^\times ] \le 2\).
[The index \([S^\times :\mu (S)R^\times ]\) is known as the Hasse unit index.]
-
(a)
-
2.
Let
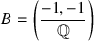 and let \(\mathcal {O}\) be the \(\mathbb Z \)-order generated by i, j. Prove that \(\mathcal {O}[1/2]^\times \simeq \langle 2, i, j, 1+i \rangle \) and describe \(\mathcal {O}[1/2]^\times /\mathbb Z [1/2]^\times \) as an extension of \(Q_8\) by \(\mathbb Z /2\mathbb Z \).
and let \(\mathcal {O}\) be the \(\mathbb Z \)-order generated by i, j. Prove that \(\mathcal {O}[1/2]^\times \simeq \langle 2, i, j, 1+i \rangle \) and describe \(\mathcal {O}[1/2]^\times /\mathbb Z [1/2]^\times \) as an extension of \(Q_8\) by \(\mathbb Z /2\mathbb Z \). -
3.
Show that
$$\begin{aligned}{}[\mathcal {O}^\times : \mathcal {O}^1 R^\times ] = [{{\,\mathrm{nrd}\,}}(\mathcal {O}^\times ) : R^{\times 2}] = \frac{[R_{\Omega }^{\times } : R^{\times 2}]}{[R_{\Omega }^{\times } : {{\,\mathrm{nrd}\,}}(\mathcal {O}^\times )]} \end{aligned}$$where \(R_{>_{\Omega } 0}^{\times }\) is the subgroup of units positive at ramified infinite places of B, defined in (32.2.6).
-
4.
Let B be a quaternion algebra over a field F with \({{\,\mathrm{char}\,}}F \ne 2\), and let \(\gamma ,j \in B^\times \) be such that \(j^{-1}\gamma j = \gamma ^{-1}\). Show by looking at the reduced norm and trace that \(j^{-1}\gamma j = \overline{\gamma }\) (cf. Lemma 32.6.1).
- \(\triangleright \) 5.:
-
Prove the uniqueness statement in Proposition 32.7.1: Show that every two isomorphic exceptional subgroups of \({{\,\mathrm{P\!}\,}}B^\times \) are conjugate by an element of \(B^\times \), and the same for \(B^1\).
-
6.
Let \(\Gamma \le \mathcal {O}^1\) be a maximal finite subgroup. Combining results from sections 11.2 and 11.5 and this chapter, prove the following.
-
(a)
\(\Gamma \) is isomorphic to one of the following groups:
-
cyclic of order 2m with \(m \ge 1\),
-
binary dihedral (dicyclic) \(2D_{2m}\) of order 4m with \(m \ge 1\),
-
binary tetrahedral 2T of order 24,
-
binary octahedral 2O of order 48, or
-
binary icosahedral 2I of order 120.
In the latter three cases, we call \(\Gamma \)exceptional.
-
-
(b)
If \(\Gamma \simeq 2O\) then \(F \supseteq \mathbb Q (\sqrt{2})\) and if \(\Gamma \simeq 2I\) then \(F \supseteq \mathbb Q (\sqrt{5})\).
-
(c)
If \(\Gamma \) is exceptional, then
 .
.
-
(a)
-
7.
Continuing with the previous exercise, suppose that B is totally definite, so F is totally real. Prove the following statements.
-
(a)
If \(\mathcal {O}^1\) does not contain an element of order 4, then \(\mathcal {O}^1\) is cyclic.
-
(b)
If \(\mathcal {O}^1\) is quaternion \(Q_8 \simeq 2D_4\) or exceptional, then \(R[\sqrt{-1}] \hookrightarrow \mathcal {O}\) and \({{\,\mathrm{discrd}\,}}(\mathcal {O})\) is only divisible by primes dividing 2.
-
(c)
If \(\mathcal {O}^1 \simeq 2D_{2m}\) with \(m \ge 3\), then \(R[\sqrt{-1}],R[\zeta _{2m}] \hookrightarrow \mathcal {O}\) and \({{\,\mathrm{discrd}\,}}(\mathcal {O})\) is only divisible by primes dividing \(\lambda _{2m}^2-4\), where \(\lambda _{2m} :=\zeta _{2m}+\zeta _{2m}^{-1}\).
-
(a)
-
8.
Continuing further with the previous exercise, we compare \(\mathcal {O}^\times \) and \(\mathcal {O}^1\).
-
(a)
Show that \([\mathcal {O}^\times : \mathcal {O}^1] = 1,2,4\). [Hint: Use Exercise 32.1.]
-
(b)
Show that if \(\mathcal {O}^1 \simeq 2O,2I\), then \(\mathcal {O}^\times = \mathcal {O}^1\).
-
(c)
Show that if \(\mathcal {O}^1 \simeq 2T\), then \([\mathcal {O}^\times : \mathcal {O}^1] \le 2\), and equality holds if and only if there exists \(\gamma \in (1+i)F^\times \cap \mathcal {O}^\times \) such that \({{\,\mathrm{nrd}\,}}(\gamma ) \not \in F^{\times 2}\).
[For a complete account covering all cases, see Vignéras-Guého [VG74].]
-
(a)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
This chapter is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, duplication, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, a link is provided to the Creative Commons license and any changes made are indicated.The images or other third party material in this chapter are included in the work's Creative Commons license, unless indicated otherwise in the credit line; if such material is not included in the work's Creative Commons license and the respective action is not permitted by statutory regulation, users will need to obtain permission from the license holder to duplicate, adapt or reproduce the material.
Copyright information
© 2021 The Author(s)
About this chapter
Cite this chapter
Voight, J. (2021). Unit groups. In: Quaternion Algebras. Graduate Texts in Mathematics, vol 288. Springer, Cham. https://doi.org/10.1007/978-3-030-56694-4_32
Download citation
DOI: https://doi.org/10.1007/978-3-030-56694-4_32
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-56692-0
Online ISBN: 978-3-030-56694-4
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)



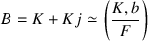 .
. .
. and
and  and
and 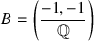 and let
and let  .
.