Selectivity

Abstract

In the previous chapter, we saw that (conjugacy classes of) embeddings of a quadratic order into a quaternion algebra are naturally distributed over the genus of a quaternion order; in applications, we want to compare the number of embeddings over orders in a genus. Such a comparison can be thought of as a strong integral refinement of the local-global principle for embeddings of quadratic fields (Proposition 14.6.7), which belongs to the more general framework of the Albert–Brauer–Hasse–Noether theorem.

In the previous chapter, we saw that (conjugacy classes of) embeddings of a quadratic order into a quaternion algebra are naturally distributed over the genus of a quaternion order; in applications, we want to compare the number of embeddings over orders in a genus. Such a comparison can be thought of as a strong integral refinement of the local-global principle for embeddings of quadratic fields (Proposition 14.6.7), which belongs to the more general framework of the Albert–Brauer–Hasse–Noether theorem.

This chapter is quite technical, and it may be skipped on a first reading. To reward the reader who persists, we conclude this chapter with the construction of isospectral, nonisometric hyperbolic Riemannian manifolds, following Vignéras.

1 Selective orders

To get a preview of what selectivity is all about, right off the bat we give an example of the failure for a quadratic order to embed equitably in the genus of an order.

Example 31.1.1

Let $F :=\mathbb Q (\sqrt{-5})$ and $R :=\mathbb Z _F=\mathbb Z [\sqrt{-5}]$. Then ${{\,\mathrm{Cl}\,}}R \simeq \mathbb Z /2\mathbb Z$, and the nontrivial class is represented by the ideal $\mathfrak p =\langle 2,1+\sqrt{-5}\rangle \subseteq \mathbb Z _F$ with $\mathfrak p ^2=2\mathbb Z _F$. By class field theory, the Hilbert class field $K \supseteq F$ is a quadratic extension, and the genus theory of Gauss gives $K=F(\sqrt{-1})=F(\sqrt{5})$. The maximal order of K is $\mathbb Z _K = \mathbb Z _F[w]$ where

$$\begin{aligned} w = \sqrt{-1}\left( \frac{1+\sqrt{5}}{2}\right) = \frac{\sqrt{-1}+\sqrt{-5}}{2} \end{aligned}$$

satisfies $w^2 - \sqrt{-5}w - 1 = 0$, a polynomial of discriminant $-5+4=-1$.

We take $B={{\,\mathrm{M}}}_2(F)$ and the maximal order $\mathcal {O}={{\,\mathrm{M}}}_2(\mathbb Z _F)$. By 17.3.7, there is a bijection ${{\,\mathrm{Cl}\,}}R \xrightarrow {\smash {{\sim }}}{{\,\mathrm{Cls}\,}}\!{}_{\textsf {\tiny {R}} }\,\mathcal {O}$, with the nontrivial right ideal class represented by

$$\begin{aligned} I=\begin{pmatrix} \mathfrak p &{} 0 \\ 0 &{} R \end{pmatrix}{{\,\mathrm{M}}}_2(R) = \begin{pmatrix} \mathfrak p &{} \mathfrak p \\ R &{} R \end{pmatrix}; \end{aligned}$$

its left order is

$$\begin{aligned} \mathcal {O}' = \mathcal {O}{}_{\textsf {\tiny {L}} }(I) = \begin{pmatrix} R &{} \mathfrak p \\ \mathfrak p ^{-1} &{} R \end{pmatrix}. \end{aligned}$$

These two orders are not isomorphic and up to isomorphism represent the two types of maximal R-orders in ${{\,\mathrm{M}}}_2(F)$.

We claim that there is an embedding $\mathbb Z _K \hookrightarrow \mathcal {O}$ but no embedding $\mathbb Z _K \hookrightarrow \mathcal {O}'$. The first part of the claim is easy: taking the rational canonical form, we take the embedding

$$\begin{aligned} w \mapsto \alpha = \begin{pmatrix} 0 &{} 1 \\ 1 &{} \sqrt{-5} \end{pmatrix}. \end{aligned}$$

(31.1.2)

The proof that $\mathbb Z _K \not \hookrightarrow \mathcal {O}'$ is more difficult. (The embedding (31.1.2) does not extend to $\mathcal {O}'$ because of the off-diagonal coefficients; and we cannot conjugate this embedding in an obvious way because the ideal $\mathfrak p$ is not principal.) Such an embedding would be specified by a matrix

$$\begin{aligned} \alpha ' = \begin{pmatrix} a &{} b \\ c &{} -a+\sqrt{-5} \end{pmatrix} \in \begin{pmatrix} R &{} \mathfrak p \\ \mathfrak p ^{-1} &{} R \end{pmatrix} \end{aligned}$$

with

$$\begin{aligned} -\det (\alpha ') = a^2-\sqrt{-5}a+bc = 1; \end{aligned}$$

(31.1.3)

so the content in the second claim is that there is no solution to the quadratic equation (31.1.3).

Indeed, suppose there is a solution. Let $f(x)=x^2-\sqrt{-5}x-1 \in \mathbb Z _F[x]$, so that $f(a)+bc=0$. We may factor $b\mathbb Z _F = \mathfrak p \mathfrak b$ with $\mathfrak b \subseteq \mathbb Z _F$ and $[\mathfrak b ] \in {{\,\mathrm{Cl}\,}}\mathbb Z _F$ nontrivial; by parity, there exists a prime $\mathfrak q \mid \mathfrak b$ with $[\mathfrak q ]$ nontrivial. Factoring $c\mathbb Z _F=\mathfrak p ^{-1}\mathfrak c$ with $\mathfrak c \subseteq \mathbb Z _F$, we have $bc\mathbb Z _F = \mathfrak b \mathfrak c \subseteq \mathfrak q$, so $f(a)=-bc \equiv 0 ~(\text{ mod } ~\mathfrak{q })$. But f(x) has trivial discriminant, and modulo a prime $\mathfrak q \subseteq \mathbb Z _F$ it either splits (into distinct linear factors) or remains irreducible. And by the Artin map, f(x) splits modulo $\mathfrak q$ if and only if $\mathfrak q$ splits in K if and only if the class $[\mathfrak q ] \in {{\,\mathrm{Cl}\,}}\mathbb Z _F$ is trivial. Putting these two pieces together, we have $f(a) \equiv 0 ~(\text{ mod } ~\mathfrak{q })$ and f(x) is irreducible modulo $\mathfrak q$. This is a contradiction, and there can be no solution.

With this cautionary but illustrative example in hand, we state our main theorem. We return to the idelic notation of section 30.4. We will consider embeddings in the context of strong approximation (see Chapter 28).

The following notation will be in use throughout this chapter.

31.1.4

Let $R=R_{({{{\texttt {\textit{T}}}}})}$ be a global ring with eligible set ${{{\texttt {\textit{T}}}}}$ and let $F={{\,\mathrm{Frac}\,}}R$ be its field of fractions. Let B be a quaternion algebra over F and suppose that B is ${{{\texttt {\textit{T}}}}}$-indefinite. Let $\mathcal {O}\subseteq B$ be an R-order.

Let $K \supseteq F$ be a separable quadratic F-algebra and let $S \subseteq K$ be an R-order. Suppose that ${{\,\mathrm{Emb}\,}}(\widehat{S};\widehat{\mathcal {O}}) \ne \emptyset$, which is to say, for all primes $\mathfrak p \subseteq R$, the $R_\mathfrak p$-algebra $S_\mathfrak p$ embeds optimally into $\mathcal {O}_\mathfrak p$.

Our struggle will be to understand when the local optimal embeddings glue together to give a global optimal embedding. As a start, we know by Corollary 30.4.18 that there exists some order $\mathcal {O}' \in {{\,\mathrm{Gen}\,}}\mathcal {O}$ in the genus of $\mathcal {O}$ (i.e., locally isomorphic to $\mathcal {O}$) such that ${{\,\mathrm{Emb}\,}}(S,\mathcal {O}') \ne \emptyset$.

Definition 31.1.5

We say that ${{\,\mathrm{Gen}\,}}\mathcal {O}$ is genial for S if ${{\,\mathrm{Emb}\,}}(S,\mathcal {O}') \ne \emptyset$ for all $\mathcal {O}' \in {{\,\mathrm{Gen}\,}}\mathcal {O}$. If ${{\,\mathrm{Gen}\,}}\mathcal {O}$ is not genial, i.e., there exists $\mathcal {O}' \in {{\,\mathrm{Gen}\,}}\mathcal {O}$ such that

$$ {{\,\mathrm{Emb}\,}}(S,\mathcal {O}')=\emptyset , $$

then we say that ${{\,\mathrm{Gen}\,}}\mathcal {O}$ is optimally selective for S.

By definition, ${{\,\mathrm{Gen}\,}}\mathcal {O}$ is genial for S if and only if S embeds optimally in every order $\mathcal {O}'$ that is locally isomorphic to $\mathcal {O}$.

31.1.6

We define the following condition, called the optimal selectivity condition:

• (OS) K is a subfield of the class field $H_{GN(\mathcal {O})}$ of F obtained from ${{\,\mathrm{Cl}}}_{GN(\mathcal {O})} R$.

In particular, if K is not a field, then (OS) does not hold. We now state our main theorem, with notation and hypotheses in 31.1.4.

MainTheorem 31.1.7

(Optimal selectivity). Suppose that $\mathcal {O}$ is an Eichler order. Then the following statements hold.

• (a) ${{\,\mathrm{Gen}\,}}\mathcal {O}$ is optimally selective for S if and only if the optimal selectivity condition (OS) holds.

• (b) If ${{\,\mathrm{Gen}\,}}\mathcal {O}$ is optimally selective for S, then ${{\,\mathrm{Emb}\,}}(S,\mathcal {O}') \ne \emptyset$ for precisely half of the types $[\mathcal {O}'] \in {{\,\mathrm{Typ}\,}}\mathcal {O}$.

• (c) In all cases,

  $$\begin{aligned} m(S,\mathcal {O}';\mathcal {O}'^\times )=m(S,\mathcal {O};\mathcal {O}^\times ) \end{aligned}$$

  for all $\mathcal {O}' \in {{\,\mathrm{Gen}\,}}\mathcal {O}$ whenever both sides are nonzero.

Since the optimal selectivity condition (OS) only depends on K, if ${{\,\mathrm{Gen}\,}}\mathcal {O}$ is optimally selective for S then it is optimally selective for all R-orders in K.

Remark 31.1.8. It was first noted by Chevalley [Chev36] in the more general situation of matrix algebras that it was possible for a commutative order to embed into some, but not all, maximal orders. An approach to selectivity is sketched by Vignéras [Vig80a, Théorème III.5.15], but there are some glitches [CF99, Remark 3.4]. Maclachlan [Macl2008, Theorem 1.4] gives a proof of Main Theorem 31.1.7(a)–(b) for hereditary orders (Eichler orders of squarefree level). For a more detailed literature survey and further comments, see 31.7.7.

31.1.9

When ${{\,\mathrm{Gen}\,}}\mathcal {O}$ is optimally selective for S, then we can refine Main Theorem 31.1.7(b) detecting the half of types of orders for which there is an optimal embedding of S.

From our hypothesis ${{\,\mathrm{Emb}\,}}(\widehat{S},\widehat{\mathcal {O}}) \ne \emptyset$, we know that S embeds into some order in the genus of $\mathcal {O}$; we might as well take this to be $\mathcal {O}$ itself, so we suppose that ${{\,\mathrm{Emb}\,}}(S,\mathcal {O}) \ne \emptyset$. Let $\mathcal {O}' \in {{\,\mathrm{Gen}\,}}\mathcal {O}$. Then $\mathcal {O}'$ is connected to $\mathcal {O}$, so $\mathcal {O}'=\mathcal {O}{}_{\textsf {\tiny {L}} }(I)$ for an invertible right $\mathcal {O}$-ideal $I \subseteq \mathcal {O}$. Let

$$\begin{aligned} \mathfrak a =[\mathcal {O}:\mathcal {O}\cap \mathcal {O}'] = [\mathcal {O}':\mathcal {O}\cap \mathcal {O}']. \end{aligned}$$

Then ${{\,\mathrm{Emb}\,}}(S,\mathcal {O}') \ne \emptyset$ if and only if ${{\,\mathrm{Frob}}}_\mathfrak{a }$ is trivial in ${{\,\mathrm{Gal}\,}}(K\,|\,F)$.

For example, if $\mathfrak a =\mathfrak p$ is prime, then ${{\,\mathrm{Frob}}}_\mathfrak p$ is trivial in ${{\,\mathrm{Gal}\,}}(K\,|\,F)$ if and only if $\mathfrak p$ is not inert in K. For maximal orders, we can equivalently formulate the index in terms of distance on the Bruhat–Tits tree (see section 23.5 and Exercise 23.9).

The core application of the optimal selectivity theorem is the following corollary.

Corollary 31.1.10

Suppose that ${{\,\mathrm{Gen}\,}}\mathcal {O}$ is genial for S. Then

$$ m(S,\mathcal {O};\mathcal {O}^\times ) = \frac{h(S)}{\#{{\,\mathrm{Cls}\,}}\mathcal {O}} m(\widehat{S},\widehat{\mathcal {O}};\widehat{\mathcal {O}}^\times ). $$

Proof We combine Main Theorem 31.1.7 and Theorem 30.4.7. $\square$

We conclude this introduction with a second application, a generalization of Corollary 28.6.4. Let $\Omega$ be the set of real, ramified places of B, and let $R_{>_{\Omega } 0}^\times :=R^\times \cap F_{>_{\Omega } 0}^\times$ be the subgroup of $R^\times$ of elements that are positive at all $v \in \Omega$.

Corollary 31.1.11

Let $\mathcal {O}\subseteq B$ be an Eichler R-order. Then

$$\begin{aligned} {{\,\mathrm{nrd}\,}}(\mathcal {O}^\times ) = R_{>_{\Omega } 0}^{\times }. \end{aligned}$$

Proof Let $u \in R_{>_{\Omega } 0}^{\times }$. We repeat the argument of Corollary 28.6.4: we find $\gamma ' \in \mathcal {O}'$ with ${{\,\mathrm{nrd}\,}}(\gamma ')=u$ and $\mathcal {O}' \in {{\,\mathrm{Gen}\,}}\mathcal {O}$. We may suppose further that ${{\,\mathrm{Gen}\,}}\mathcal {O}$ is not selective for $R[\gamma ']$ by shrinking the open set to ensure that $K={{\,\mathrm{Frac}\,}}R[\gamma '] \not \subseteq H_{GN(\mathcal {O})}$. Let $S=K \cap \mathcal {O}'$. Then $S \subseteq \mathcal {O}'$ is optimally embedded; and by Main Theorem 31.1.7(c), there exists an optimal embedding $\phi :S \hookrightarrow \mathcal {O}$, hence $\phi (\gamma ')=\gamma \in \mathcal {O}$ has ${{\,\mathrm{nrd}\,}}(\gamma )=u$ as desired. $\square$

2 Selectivity conditions

In this brief section, we make the somewhat opaque optimal selectivity condition (OS) explicit for Eichler orders.

Proposition 31.2.1

Let $\mathcal {O}$ be an Eichler order of level $\mathfrak M$. Then Condition (OS) holds if and only if all of the following four conditions hold:

• (a) The extension $K \supseteq F$ and the quaternion algebra B are ramified at the same (possibly empty) set of archimedean places of F;

• (b) K and B are unramified at all nonarchimedean places $v \in {{\,\mathrm{Pl}\,}}F$;

• (c) Every nonarchimedean place $v \in {{{\texttt {\textit{T}}}}}$ splits in K; and

• (d) If $\mathfrak p \subset R$ is a nonzero prime and ${{\,\mathrm{ord}}}_\mathfrak p (\mathfrak M )$ is odd, then $\mathfrak p$ splits in K.

Proof We determine the class field $H_{GN(\mathcal {O})}$ obtained from the group $GN(\mathcal {O})=F_{>_{\Omega } 0}^\times {{\,\mathrm{nrd}\,}}(N_{\widehat{B}^\times }(\widehat{\mathcal {O}}))$.

Recall we have $G(\mathcal {O}) = F_{>_{\Omega } 0}^\times {{\,\mathrm{nrd}\,}}(\widehat{\mathcal {O}}^\times ) = F_{>_{\Omega } 0}^\times \widehat{R}^\times$, since $\mathcal {O}$ is an Eichler order and therefore locally norm-maximal, so $H_{G(\mathcal {O})}$ is the maximal abelian extension of F unramified away from the real places in ${{\,\mathrm{Ram}\,}}(B)$ and such that the remaining places $v \in {{{\texttt {\textit{T}}}}}$ split completely.

The normalizer ${{\,\mathrm{nrd}\,}}(N_{\widehat{B}^\times }(\widehat{\mathcal {O}}))$ is the restricted direct product of local normalizers, computed in (23.2.8) for $\mathfrak p \mid \mathfrak D$ and Corollary 23.3.14 for $\mathfrak p \not \mid \mathfrak D$: for the latter,

$$ {{\,\mathrm{nrd}\,}}(N_{B_\mathfrak p ^\times }(\mathcal {O}_\mathfrak p )) = {\left\{ \begin{array}{ll} F_\mathfrak p ^{\times 2} R_\mathfrak p ^\times , &{} \text { if }{{\,\mathrm{ord}}}_\mathfrak p (\mathfrak M )\text { is even;} \\ F_\mathfrak p ^\times , &{} \text { if }{{\,\mathrm{ord}}}_\mathfrak p (\mathfrak M )\text { is odd.} \end{array}\right. } $$

Therefore, the quotient ${{\mathrm{Cl}}}_{G(\mathcal {O})} R \rightarrow {{\mathrm{Cl}}}_{GN(\mathcal {O})} R$ factors through the quotient by squares ${{\mathrm{Cl}}}_{G(\mathcal {O})} R/({{\mathrm{Cl}}}_{G(\mathcal {O})} R)^2$ and then the further quotient by the primes $\mathfrak p \mid \mathfrak D ={{\,\mathrm{disc}\,}}B$ and $\mathfrak p \mid \mathfrak M$ with ${{\mathrm{ord}}}_\mathfrak p (\mathfrak M )$ odd.

We now conclude the proof. If K is not a field then all of the desired conclusions hold; so suppose K is a field. Since $K \hookrightarrow B$, if $v \in {{\,\mathrm{Pl}\,}}F$ ramifies in B then v also ramifies in B. A containment $K \subseteq H_{GN(\mathcal {O})}$ is permitted at archimedean places if and only if the archimedean ramification in $K \supseteq F$ is no bigger than this. In a similar way, the conditions in the previous paragraph establish (c)–(d), and K is unramified at all nonarchimedean places v. To conclude (b), if $\mathfrak p \mid \mathfrak D$ then $\mathfrak p$ splits in $H_{GN(\mathcal {O})}$ and therefore in K; but we are assuming that $K \hookrightarrow B$ so $K_\mathfrak p \hookrightarrow B_\mathfrak p$, a contradiction since $B_\mathfrak p$ is a division algebra, and there can be no such $\mathfrak p$. $\square$

3 $*$ Selectivity setup

We now embark on a proof of the selectivity theorem (Main Theorem 31.1.7); this goal will occupy us for the remainder of this chapter. In this section, we begin to isolate the problem: there is a group that is at worst $\mathbb Z /2\mathbb Z$ and is usually trivial, and we pin it down using strong approximation, the reduced norm, and class field theory. Our basic reference is Vignéras [Vig80a, Théorème III.5.15], and the surrounding text.

Our notation is as in 31.1.4.

31.3.1

To establish the main theorem in the case where $K \simeq F \times F$ is straightforward. We leave this case as an exercise (Exercise 31.1).

We suppose throughout the rest of this chapter that K is a field.

Let $\mathcal {O}^1 \le \Gamma \le N_{B^\times }(\mathcal {O})$ (as in 30.3.10). Recall that there is a bijection (30.3.13)

$$\begin{aligned} {{\,\mathrm{Emb}\,}}(S,\mathcal {O};\Gamma ) \leftrightarrow K^\times \backslash E / \Gamma \end{aligned}$$

where

$$\begin{aligned} E = \{\beta \in B^\times : K^\beta \cap \mathcal {O}= S^\beta \} \end{aligned}$$

and we abbreviate conjugation $K^\beta = \beta ^{-1} K \beta$ for conciseness. Conjugating if necessary, we may suppose that $1 \in E$, i.e., we start with an order and an optimal embedding $K \cap \mathcal {O}= S$.

We employ idelic notation as in section 30.4. The inclusion $B^\times \hookrightarrow \widehat{B}^\times$ gives an inclusion

$$\begin{aligned} E/\Gamma \hookrightarrow \widehat{E}/\widehat{\Gamma }\end{aligned}$$

(31.3.2)

with

$$\begin{aligned} \widehat{E}:=\bigl \{\widehat{\beta }\in \widehat{B}^\times : \widehat{K}^{\widehat{\beta }} \cap \widehat{\mathcal {O}}= \widehat{S}^{\widehat{\beta }} \bigr \}. \end{aligned}$$

The hypothesis of strong approximation allows us to identify precisely the image of the map (31.3.2) via the reduced norm in the following way.

31.3.3

As in Theorem 28.5.5 (a motivating application of strong approximation), the reduced norm induces a bijection

$$\begin{aligned} B^\times \backslash \widehat{B}^\times / \widehat{\Gamma }\xrightarrow {\smash {{\sim }}}F_{>_{\Omega } 0}^\times \backslash \widehat{F}^\times / {{\,\mathrm{nrd}\,}}(\widehat{\Gamma }) = {{\,\mathrm{Cl}}}_{G(\Gamma )} R \end{aligned}$$

(31.3.4)

where $G(\Gamma ) :=F_{>_{\Omega } 0}^\times {{\,\mathrm{nrd}\,}}(\widehat{\Gamma })$.

Lemma 31.3.5

We have

$$\begin{aligned} E/\Gamma = \{ \widehat{\beta }\widehat{\Gamma }\in \widehat{E}/\widehat{\Gamma }: {{\,\mathrm{nrd}\,}}(\widehat{\beta }) \in G(\Gamma )\} \subseteq \widehat{E}/\widehat{\Gamma }. \end{aligned}$$

That is to say, if $\widehat{\beta }\in \widehat{E}$, then there exists $\beta \in E$ such that $\widehat{\beta }\widehat{\Gamma }= \beta \widehat{\Gamma }$ if and only if ${{\,\mathrm{nrd}\,}}(\widehat{\beta }) \in G(\Gamma )$.

Proof We find a $\beta \in B^\times$ (without the condition that $\beta \in E$) immediately from the bijection (31.3.4). But $\beta =\widehat{\beta }\widehat{\gamma }\in \widehat{\beta }\widehat{\Gamma }$ and $\widehat{\Gamma }\le N_{\widehat{B}^\times }(\widehat{\mathcal {O}})$ gives

$$\begin{aligned} \widehat{K}^\beta \cap \widehat{\mathcal {O}}^{\widehat{\gamma }} = \widehat{K}^\beta \cap \widehat{\mathcal {O}}= \widehat{S}^\beta \end{aligned}$$

and intersecting with B we find $\beta \in E$. $\square$

Lemma 31.3.5 points the way more generally, at least to detect if there is an embedding in the first place in an order. First, we need to give representatives of the type set.

31.3.6

Recalling 28.5.7, there is a bijection

$$\begin{aligned} {{\,\mathrm{Typ}\,}}\mathcal {O}\leftrightarrow B^\times \backslash \widehat{B}^\times / N_{\widehat{B}^\times }(\widehat{\mathcal {O}}); \end{aligned}$$

explicitly, every isomorphism class of order in ${{\,\mathrm{Typ}\,}}\mathcal {O}$ is of the form

$$\begin{aligned} \mathcal {O}' = \widehat{\nu }\widehat{\mathcal {O}}\widehat{\nu }^{-1} \cap B = \widehat{\mathcal {O}}^{\widehat{\nu }^{-1}} \cap B \end{aligned}$$

(yes, the choice of inverse is deliberate), with the class of $\widehat{\nu }\in \widehat{B}^\times$ in $B^\times \backslash \widehat{B}^\times / N_{\widehat{B}^\times }(\widehat{\mathcal {O}})$ uniquely defined.

In the presence of strong approximation (Corollary 28.5.10), we have a further bijection

$$\begin{aligned} {{\,\mathrm{Typ}\,}}\mathcal {O}\leftrightarrow {{\,\mathrm{Cl}}}_{GN(\mathcal {O})} R \end{aligned}$$

where

$$\begin{aligned} GN(\mathcal {O})=G(N_{B^\times }(\mathcal {O}))=F_{>_{\Omega } 0}^\times {{\,\mathrm{nrd}\,}}(N_{\widehat{B}^\times }(\widehat{\mathcal {O}})). \end{aligned}$$

Now we look back at embeddings and reduced norms.

31.3.7

Let

$$\begin{aligned} {{\,\mathrm{nrd}\,}}(\widehat{E}) = \{{{\,\mathrm{nrd}\,}}(\widehat{\beta }) : \widehat{\beta }\in \widehat{E}\} \subseteq \widehat{F}^\times . \end{aligned}$$

(31.3.8)

The set $\widehat{E}$ does not obviously have a group structure, so ${{\,\mathrm{nrd}\,}}(\widehat{E})=\{{{\,\mathrm{nrd}\,}}(\widehat{\beta }) : \widehat{\beta }\in \widehat{E}\}$ is a subset. But $\widehat{E}$ is stable under $\widehat{K}^\times$, so ${{\,\mathrm{nrd}\,}}(\widehat{E})$ is a union of cosets of ${{\,\mathrm{nrd}\,}}(\widehat{K}^\times )$.

The set ${{\,\mathrm{nrd}\,}}(\widehat{E})$ is quite large, because it contains reduced norms from $\widehat{K}^\times \subseteq \widehat{E}$ and $N_{\widehat{B}^\times }(\widehat{\mathcal {O}}) \subseteq \widehat{E}$.

31.3.9

By the main theorem of class field theory (Theorem 27.5.10), the Artin map gives a bijection

$$\begin{aligned} \underline{F}^\times /F^\times {{\,\mathrm{Nm}}}_{K|F}(\underline{K}^\times ) \xrightarrow {\smash {{\sim }}}{{\,\mathrm{Gal}\,}}(K\,|\,F) \simeq \mathbb Z /2\mathbb Z . \end{aligned}$$

(31.3.10)

Let ${{{\texttt {\textit{S}}}}}\subseteq {{{\texttt {\textit{T}}}}}$ be the set of archimedean places of F. Recall the isomorphism (27.5.8)

$$\begin{aligned} \underline{F}^\times /F^\times F_{\infty ,>0}^\times \xrightarrow {\smash {{\sim }}}\underline{F}_{\not {S}}^\times /F_{>0}^\times . \end{aligned}$$

We have

$$\begin{aligned} F_{\infty ,>0}^\times \le {{\,\mathrm{Nm}}}_{K|F}(K_\infty ^\times ) \le {{\,\mathrm{Nm}}}_{K|F}(\underline{K}^\times ) \end{aligned}$$

(the latter embedded at the infinite place with the other components 1), and by the same argument as in Lemma 27.5.6, the image of $F^\times {{\,\mathrm{Nm}}}_{K|F}(\underline{K}^\times )$ under the isomorphism (27.5.8) is $F_{>_{\Sigma } 0}^\times {{\,\mathrm{Nm}}}_{K|F}(K_{\not {S}}^\times )$ where $\Sigma \subseteq {{\,\mathrm{Pl}\,}}(F)$ is the set of places ramified in K (going from real to complex in the extension $F \subseteq K$) and

$$\begin{aligned} F_{>_{\Sigma } 0}^\times :=\{a \in F^\times : v(a)>0 \text { for all real }v \in \Sigma \}. \end{aligned}$$

Therefore we have an isomorphism

$$\begin{aligned} \underline{F}^\times /F^\times {{\,\mathrm{Nm}}}_{K|F}(\underline{K}^\times ) \xrightarrow {\smash {{\sim }}}\underline{F}_{\not {S}}^\times /F_{>_{\Sigma } 0}^\times {{\,\mathrm{Nm}}}_{K|F}(K_{\not {S}}^\times ). \end{aligned}$$

(31.3.11)

We then further project from the target of (31.3.11) to to obtain the map

$$\begin{aligned} \underline{F}^\times /F^\times {{\,\mathrm{Nm}}}_{K|F}(\underline{K}^\times ) \rightarrow \widehat{F}^\times /F_{>_{\Sigma } 0}^\times {{\,\mathrm{Nm}}}_{K|F}(\widehat{K}^\times ). \end{aligned}$$

(31.3.12)

Lemma 31.3.13

We have

$$\begin{aligned} F_{>_{\Sigma } 0}^\times {{\,\mathrm{Nm}}}_{K|F}(\widehat{K}^\times ) \le \widehat{F}^\times \end{aligned}$$

with total index at most 2, and index equal to 2 if and only if every nonarchimedean place $v \in {{{\texttt {\textit{T}}}}}$ is split in K.

Proof In the projection (31.3.12), we start with a group of order 2; in order to keep it this size, the projection away from the nonarchimedean places in ${{{\texttt {\textit{T}}}}}$ must be an isomorphism, which holds if and only if for all nonarchimedean places $v \in {{{\texttt {\textit{T}}}}}$ we must have v split in K. $\square$

We conclude this setup section with an overview.

31.3.14

Selectivity arises from an examination of layers in the following selectivity sandwich:

$$\begin{aligned} F_{>_{\Sigma } 0}^\times {{\,\mathrm{nrd}\,}}(\widehat{K}^\times ) \overset{(OS) }{\le } F_{>_{\Omega } 0}^\times {{\,\mathrm{nrd}\,}}(\widehat{K}^\times ) {{\,\mathrm{nrd}\,}}(N_{\widehat{B}^\times }(\widehat{\mathcal {O}})) \overset{m}{\le } F_{>_{\Omega } 0}^\times {{\,\mathrm{nrd}\,}}(\widehat{E}) \overset{s}{\le } \widehat{F}^\times \end{aligned}$$

(31.3.15)

In terms of the sandwich bread, the left-most group $F_{>_{\Sigma } 0}^\times {{\,\mathrm{nrd}\,}}(\widehat{K}^\times )$ has index at most 2 in the right-most group $\widehat{F}^\times$ by Lemma 31.3.13. The set $F_{>_{\Omega } 0}^\times {{\,\mathrm{nrd}\,}}(\widehat{E})$ is stable under multiplication by $F_{>_{\Sigma } 0}^\times {{\,\mathrm{nrd}\,}}(\widehat{K}^\times )$ so is a union of its cosets in $\widehat{F}^\times$; therefore, it is actually a subgroup.

Much ado about a (possible) group of order two!

Again by Lemma 31.3.13, the sandwich collapses if there is a nonarchimedean place $v \in {{{\texttt {\textit{T}}}}}$ that is inert in $K \supseteq F$, so there is only work to do when every $v \in {{{\texttt {\textit{T}}}}}$ is split. Under this assumption, we will show in Lemma 31.4.1 that the first inequality labelled (OS) is an equality if and only if the optimal selectivity condition (OS) holds. In Propositions 31.5.1 and 31.5.7, we will show that the middle inequality labelled m is always an equality and that such an equality implies equality of embedding numbers (when they are nonzero). Last but not least, in Proposition 31.4.4 we will show that the final inequality labelled s is an equality if and only if there is no selectivity obstruction, i.e., ${{\,\mathrm{Emb}\,}}(S,\mathcal {O}') \ne \emptyset$ for all $\mathcal {O}' \in {{\,\mathrm{Gen}\,}}\mathcal {O}$.

4 $*$ Outer selectivity inequalities

In this section, we consider the outer ends of the selectivity sandwich 31.3.14.

The left-most inequality is interpreted in the language of class field theory as follows.

Lemma 31.4.1

We have

$$\begin{aligned} F_{>_{\Sigma } 0}^\times {{\,\mathrm{nrd}\,}}(\widehat{K}^\times ) \le F_{>_{\Omega } 0}^\times {{\,\mathrm{nrd}\,}}(\widehat{K}^\times ) {{\,\mathrm{nrd}\,}}(N_{\widehat{B}^\times }(\widehat{\mathcal {O}})) \end{aligned}$$

(31.4.2)

with index at most 2, and equality holds if and only if either the optimal selectivity condition (OS) holds or there exists a nonarchimedean place $v \in {{{\texttt {\textit{T}}}}}$ inert or ramified in K.

Proof Recall that $GN(\mathcal {O})=F_{>_{\Omega } 0}^\times {{\,\mathrm{nrd}\,}}(N_{\widehat{B}^\times }(\widehat{\mathcal {O}}))$. In the side sandwich

$$\begin{aligned} F_{>_{\Sigma } 0}^\times {{\,\mathrm{nrd}\,}}(\widehat{K}^\times ) \le F_{>_{\Omega } 0}^\times {{\,\mathrm{nrd}\,}}(\widehat{K}^\times ) {{\,\mathrm{nrd}\,}}(N_{\widehat{B}^\times }(\widehat{\mathcal {O}})) \le \widehat{F}^\times \end{aligned}$$

(31.4.3)

we again have total index at most 2. By class field theory and the Galois correspondence relative to the corresponding tower of class groups, we have

$$\begin{aligned} F_{>_{\Sigma } 0}^\times {{\,\mathrm{nrd}\,}}(\widehat{K}^\times ) = F_{>_{\Omega } 0}^\times {{\,\mathrm{nrd}\,}}(\widehat{K}^\times ) {{\,\mathrm{nrd}\,}}(N_{\widehat{B}^\times }(\widehat{\mathcal {O}})) < \widehat{F}^\times \end{aligned}$$

(so first equality, then strict inequality in (31.4.3)) if and only if $K \subseteq H_{GN(\mathcal {O})}$ if and only if (OS) holds. The result then follows by Lemma 31.3.13. $\square$

We next consider the right-most inequality, and we show that it contains the obstruction to selectivity.

Proposition 31.4.4

Let $[\mathcal {O}'] \in {{\,\mathrm{Typ}\,}}\mathcal {O}$ be represented by the class $B^\times \widehat{\nu }N_{\widehat{B}^\times }(\widehat{\mathcal {O}})$. Then ${{\,\mathrm{Emb}\,}}(S,\mathcal {O}') \ne \emptyset$ if and only if ${{\,\mathrm{nrd}\,}}(\widehat{\nu }) \in F_{>_{\Omega } 0}^\times {{\,\mathrm{nrd}\,}}(\widehat{E})$.

Proof Define

$$\begin{aligned} E' = \{ \beta ' \in B^\times : K^{\beta '} \cap \mathcal {O}' = S^{\beta '} \} \end{aligned}$$

so that ${{\,\mathrm{Emb}}}_R(S,\mathcal {O}') \xrightarrow {\smash {{\sim }}}K^\times \backslash E'$, and similarly $\widehat{E}'$.

Suppose ${{\,\mathrm{Emb}\,}}(S,\mathcal {O}') \ne \emptyset$, represented by $\beta ' \in E'$. Then

$$\begin{aligned} \widehat{K}^{\beta '} \cap \widehat{\mathcal {O}}' = \widehat{K}^{\beta '} \cap \widehat{\mathcal {O}}^{\widehat{\nu }^{-1}} = \widehat{S}^{\beta '} \end{aligned}$$

so $\beta '\widehat{\nu }=\widehat{\beta }\in \widehat{E}$. Therefore

$$\begin{aligned} {{\,\mathrm{nrd}\,}}(\widehat{\nu })={{\,\mathrm{nrd}\,}}(\beta '^{-1}){{\,\mathrm{nrd}\,}}(\widehat{\beta }) \in F_{>_{\Omega } 0}^\times {{\,\mathrm{nrd}\,}}(\widehat{E}). \end{aligned}$$

Conversely, suppose that ${{\,\mathrm{nrd}\,}}(\widehat{\nu }) \in F_{>_{\Omega } 0}^\times {{\,\mathrm{nrd}\,}}(\widehat{E})$; then there exists $a \in F_{>_{\Omega } 0}^\times$ and $\widehat{\beta }\in \widehat{E}$ such that ${{\,\mathrm{nrd}\,}}(\widehat{\nu })= a {{\,\mathrm{nrd}\,}}(\widehat{\beta })$. Since $\widehat{\beta }\in \widehat{E}$, we have

$$\begin{aligned} \widehat{K}^{\widehat{\beta }} \cap \widehat{\mathcal {O}}= \widehat{S}^{\widehat{\beta }} \end{aligned}$$

thus if $\widehat{\beta }' = \widehat{\beta }\widehat{\nu }^{-1}$ we get

$$\begin{aligned} \widehat{K}^{\widehat{\beta }'} \cap \widehat{\mathcal {O}}^{\widehat{\nu }^{-1}} = \widehat{K}^{\widehat{\beta }'} \cap \widehat{\mathcal {O}}' = \widehat{S}^{\widehat{\beta }'} \end{aligned}$$

(31.4.5)

and $\widehat{\beta }' \in \widehat{E}'$. We have

$$\begin{aligned} {{\,\mathrm{nrd}\,}}(\widehat{\beta }')={{\,\mathrm{nrd}\,}}(\widehat{\beta }\widehat{\nu }^{-1})=a^{-1} \in F_{>_{\Omega } 0}^\times \end{aligned}$$

So by Lemma 31.3.5, there exists $\beta ' \in E'$ mapping to $\widehat{\beta }'$, and ${{\,\mathrm{Emb}\,}}(S,\mathcal {O}') \ne \emptyset$ as claimed. $\square$

The following corollary indicates the significance of the preceding proposition.

Corollary 31.4.6

If $F_{>_{\Omega } 0}^\times {{\,\mathrm{nrd}\,}}(\widehat{E}) = \widehat{F}^\times$, then ${{\,\mathrm{Emb}\,}}(S,\mathcal {O}') \ne \emptyset$ for all orders $\mathcal {O}' \in {{\,\mathrm{Gen}\,}}\mathcal {O}$ in the genus of $\mathcal {O}$. Otherwise, $F_{>_{\Omega } 0}^\times {{\,\mathrm{nrd}\,}}(\widehat{E}) < \widehat{F}^\times$ has index 2 and ${{\,\mathrm{Emb}\,}}(S,\mathcal {O}') \ne \emptyset$ for precisely half of the types of orders in ${{\,\mathrm{Typ}\,}}\mathcal {O}$: we have ${{\,\mathrm{Emb}\,}}(S,\mathcal {O}') \ne \emptyset$ for

$$\begin{aligned} \mathcal {O}'=\widehat{\nu }\mathcal {O}\widehat{\nu }^{-1} \cap B \end{aligned}$$

if and only if ${{\,\mathrm{nrd}\,}}(\widehat{\nu }) \in F_{>_{\Omega } 0}^\times {{\,\mathrm{nrd}\,}}(\widehat{K}^\times )$.

In particular, in the latter case we have $\#{{\,\mathrm{Typ}\,}}\mathcal {O}$ even.

Proof We apply Proposition 31.4.4, with indexing of the type set as in 31.3.6. $\square$

5 $*$ Middle selectivity equality

In this section, we pursue the middle inequality in the selectivity sandwich 31.3.14.

First, we show that equality in this middle equality implies equality of embedding numbers, whenever they are nonzero.

Proposition 31.5.1

We have

$$\begin{aligned} F_{>_{\Omega } 0}^\times {{\,\mathrm{nrd}\,}}(\widehat{K}^\times ){{\,\mathrm{nrd}\,}}(N_{\widehat{B}^\times }(\widehat{\mathcal {O}})) \le F_{>_{\Omega } 0}^\times {{\,\mathrm{nrd}\,}}(\widehat{E}) \end{aligned}$$

(31.5.2)

with index at most 2. If equality holds in (31.5.2), then whenever $\mathcal {O}' \in {{\,\mathrm{Gen}\,}}\mathcal {O}$ and ${{\,\mathrm{Emb}\,}}(S,\mathcal {O}')$ is nonempty, we have

$$\begin{aligned} m(S,\mathcal {O};\mathcal {O}^\times ) = m(S,\mathcal {O}';\mathcal {O}'^\times ). \end{aligned}$$

Proof The statement about index follows from the layering of the sandwich (31.3.15). For the second statement, suppose that ${{\,\mathrm{Emb}\,}}(S,\mathcal {O}')$ is nonempty; then by Proposition 31.4.4, we have $\mathcal {O}'=\widehat{\mathcal {O}}^{\widehat{\nu }^{-1}} \cap B$ with ${{\,\mathrm{nrd}\,}}(\widehat{\nu }) \in F_{>_{\Omega } 0}^\times {{\,\mathrm{nrd}\,}}(\widehat{E})$. If equality holds in (31.5.2), then there exists $a \in F_{>_{\Omega } 0}^\times$, $\widehat{\alpha }\in \widehat{K}^\times$, and $\widehat{\eta }\in N_{\widehat{B}^\times }(\widehat{\mathcal {O}})$ such that

$$\begin{aligned} {{\,\mathrm{nrd}\,}}(\widehat{\nu }) = a{{\,\mathrm{nrd}\,}}(\widehat{\alpha }){{\,\mathrm{nrd}\,}}(\widehat{\eta }). \end{aligned}$$

(31.5.3)

We restore notation from Proposition 31.4.4, and modify the argument in the converse. We define the map

$$\begin{aligned} \begin{aligned} E&\rightarrow \widehat{E}' \\ \beta&\mapsto \widehat{\beta }' = \widehat{\alpha }\beta \widehat{\eta }\widehat{\nu }^{-1} \end{aligned} \end{aligned}$$

(31.5.4)

We argue as in (31.4.5). From $\beta \in E$, we have $\widehat{K}^\beta \cap \widehat{\mathcal {O}}= \widehat{S}^\beta$. We have $\widehat{\alpha }\in \widehat{K}^\times$, so $\widehat{K}^{\widehat{\alpha }}=\widehat{K}$. And $\widehat{\eta }\in N_{\widehat{B}^\times }(\widehat{\mathcal {O}})$, so $\widehat{\mathcal {O}}^{\widehat{\eta }} = \widehat{\mathcal {O}}$. Therefore

$$\begin{aligned} \widehat{K}^{\widehat{\beta }'} \cap \widehat{\mathcal {O}}^{\widehat{\nu }^{-1}} = \widehat{K}^{\widehat{\beta }'} \cap \widehat{\mathcal {O}}' = \widehat{S}^{\widehat{\beta }'} \end{aligned}$$

(31.5.5)

and indeed $\widehat{\beta }' \in \widehat{E}'$. Finally, by (31.5.3)

$$\begin{aligned} {{\,\mathrm{nrd}\,}}(\widehat{\beta }') = {{\,\mathrm{nrd}\,}}(\widehat{\alpha }\beta \widehat{\eta }\widehat{\nu }^{-1}) = a^{-1}{{\,\mathrm{nrd}\,}}(\beta ) \in F_{>_{\Omega } 0}^\times . \end{aligned}$$

By Lemma 31.3.5, there exists $\beta ' \in E'$ such that $\beta ' \widehat{\mathcal {O}}'^\times = \widehat{\beta }' \widehat{\mathcal {O}}'^\times$, well-defined up to $\mathcal {O}^\times$. Therefore, (31.5.4) descends to a map $E \rightarrow E'/\mathcal {O}'^\times$, and it further descends to a map

$$\begin{aligned} \begin{aligned} E/\mathcal {O}^\times&\rightarrow E'/\mathcal {O}'^\times \\ \beta \mathcal {O}^\times&\mapsto \beta ' \mathcal {O}'^\times \end{aligned} \end{aligned}$$

(31.5.6)

because

$$\begin{aligned} \widehat{\alpha }\beta \mu \widehat{\eta }\widehat{\nu }^{-1} \widehat{\mathcal {O}}' = \widehat{\alpha }\beta \mu \widehat{\eta }\widehat{\mathcal {O}}\widehat{\nu }^{-1} = \widehat{\alpha }\beta \mu \widehat{\mathcal {O}}\widehat{\eta }\widehat{\nu }^{-1} = \widehat{\alpha }\beta \widehat{\mathcal {O}}\widehat{\eta }\widehat{\nu }^{-1} = \widehat{\alpha }\beta \widehat{\eta }\widehat{\nu }^{-1} \widehat{\mathcal {O}}'. \end{aligned}$$

This map works as well interchanging the roles of $\mathcal {O}$ and $\mathcal {O}'$, and after a little chase, we verify that the map (31.5.6) is bijective. Taking orbits under $K^\times$ on the left, we conclude the proof. $\square$

In fact, equality holds in the middle for Eichler orders.

Proposition 31.5.7

If $\mathcal {O}$ is an Eichler order, then the inequality (31.5.2) is an equality.

Proof We will prove that

$$\begin{aligned} {{\,\mathrm{nrd}\,}}(\widehat{K}^\times ){{\,\mathrm{nrd}\,}}(N_{\widehat{B}^\times }(\widehat{\mathcal {O}})) = {{\,\mathrm{nrd}\,}}(\widehat{E}); \end{aligned}$$

(31.5.8)

the inclusion ($\le$) was direct, so we prove $(\ge )$. The desired equality is now idelic, so we reduce to checking in the completion at a prime $\mathfrak p$. If $B_\mathfrak p$ is a division algebra, then $\mathcal {O}_\mathfrak p$ is maximal, and $m(S_\mathfrak p ,\mathcal {O}_\mathfrak p ;N_{B_\mathfrak p ^\times }(\mathcal {O}_\mathfrak p ))=1$ by Proposition 30.5.3(b) we have the stronger equality $E_\mathfrak p =N_{B_\mathfrak p ^\times }(\mathcal {O}_\mathfrak p )=B_\mathfrak p ^\times$.

Otherwise, $B_\mathfrak p \simeq {{\,\mathrm{M}}}_2(F_\mathfrak p )$ is split. Without loss of generality, we may suppose that $\mathcal {O}_\mathfrak p$ is a standard Eichler order. Further, by Lemma 30.6.3, after conjugating by a normalizing element if necessary, we may suppose that the reference optimal embedding $S_\mathfrak p \hookrightarrow \mathcal {O}_\mathfrak p$ is normalized. But then this embedding extends to an optimal embedding $S_\mathfrak p \hookrightarrow {{\,\mathrm{M}}}_2(R_\mathfrak p )$: the upper-right entry is 1.

Now let $\beta _\mathfrak p \in E_\mathfrak p$ be arbitrary, with associated embedding $\phi _\mathfrak p ^{\beta _\mathfrak p } :S_\mathfrak p \hookrightarrow \mathcal {O}_\mathfrak p$. We repeat the argument in the previous paragraph: by Lemma 30.6.3, replacing $\beta _\mathfrak p$ by $\beta _\mathfrak p \nu _\mathfrak p$ if necessary with $\nu _\mathfrak p \in N_{B_\mathfrak p ^\times }(\mathcal {O}_\mathfrak p )$, we may suppose that $\phi _\mathfrak p ^{\beta _\mathfrak p }$ is normalized, and therefore extends to an optimal embedding into ${{\,\mathrm{M}}}_2(R_\mathfrak p )$. But by Proposition 30.5.3(a), we have $m(S_\mathfrak p ,{{\,\mathrm{M}}}_2(R_\mathfrak p );{{\,\mathrm{GL}}}_2(R_\mathfrak p ))=1$—all optimal embeddings into ${{\,\mathrm{M}}}_2(R_\mathfrak p )$ are conjugate under ${{\,\mathrm{GL}}}_2(R_\mathfrak p )$—so there exists $\mu _\mathfrak p \in {{\,\mathrm{GL}}}_2(R_\mathfrak p )$ such that $\phi _\mathfrak p ^{\beta _\mathfrak p }=\phi _\mathfrak p ^{\mu _\mathfrak p }$. Therefore $\beta _\mathfrak p \in \mu _\mathfrak p K_\mathfrak p ^\times$ so

$$\begin{aligned} {{\,\mathrm{nrd}\,}}(\beta _\mathfrak p ) \in {{\,\mathrm{nrd}\,}}(K_\mathfrak p ^\times )R_\mathfrak p ^\times \le {{\,\mathrm{nrd}\,}}(K_\mathfrak p ^\times ){{\,\mathrm{nrd}\,}}(\mathcal {O}_\mathfrak p ^\times ) \le {{\,\mathrm{nrd}\,}}(K_\mathfrak p ^\times ){{\,\mathrm{nrd}\,}}(N_{B_\mathfrak p ^\times }(\mathcal {O}_\mathfrak p )) \end{aligned}$$

(31.5.9)

as claimed. $\square$

6 $*$ Optimal selectivity conclusion

We now officially complete the proof of the selectivity theorem for Eichler orders.

Proof of Main Theorem 31.1.7

By 31.3.1, we may suppose K is a field. We refer to the selectivity sandwich (31.3.15), using Proposition 31.5.7 to simplify the middle equality:

$$ F_{>_{\Sigma } 0}^\times {{\,\mathrm{nrd}\,}}(\widehat{K}^\times ) \overset{(OS) }{\le } F_{>_{\Omega } 0}^\times {{\,\mathrm{nrd}\,}}(\widehat{K}^\times ) {{\,\mathrm{nrd}\,}}(N_{\widehat{B}^\times }(\widehat{\mathcal {O}})) \overset{m}{=} F_{>_{\Omega } 0}^\times {{\,\mathrm{nrd}\,}}(\widehat{E}) \overset{s}{\le } \widehat{F}^\times , $$

with total index at most 2.

By Proposition 31.4.4, we have that ${{\,\mathrm{Gen}\,}}\mathcal {O}$ is optimally selective for S if and only if the right-most inequality (labelled s) is strict. Such an inequality is strict if and only if the total index is 2 and the left-most inequality is an equality. By Lemma 31.4.1, this happens if and only if the condition (OS) holds. This proves (a).

Statement (b) is a restatement of Corollary 31.4.6, and statement (c) follows from the second statement in Proposition 31.5.1. $\square$

It has been a long and pretty technical road, so as refreshment we work through an example (cf. Maclachlan [Macl2008, §4, Example 1]).

Example 31.6.1

Let F be the totally real cubic field $\mathbb Q (b)$ where $b^3-4b-1=0$; then F has discriminant 229 and ring of integers $R=\mathbb Z _F=\mathbb Z [b]$. The usual class group ${{\,\mathrm{Cl}\,}}R$ is trivial, but the narrow class group is ${{\,\mathrm{Cl}\,}}^+ R \simeq \mathbb Z /2\mathbb Z$, represented by the ideal $\mathfrak p =(b+1)\mathbb Z _F$ of norm 2—the ideal $\mathfrak p$ is principal, but there is no generator that is totally positive. The narrow class field $K=H^+ \supseteq F$ is quadratic, with $H^+=F(\sqrt{b})$.

Let $B=\displaystyle {\biggl (\frac{-1,b}{F}\biggr )}$. Then b is positive at precisely one real place and negative at the other two, and $b \in \mathbb Z _F^\times$. Computing the Hilbert symbol at the even primes, we conclude that ${{\,\mathrm{Ram}\,}}(B)$ is equal to two real places. In particular, B is indefinite. The class group ${{\,\mathrm{Cl}}}_{G(\mathcal {O})} R$ with modulus equal to these two real places is equal to ${{\,\mathrm{Cl}\,}}^+ R$, as we see by the real signs of b.

Next, we compute representatives of the type set of maximal orders for B. By strong approximation (Corollary 28.5.10), we have ${{\,\mathrm{Typ}\,}}\mathcal {O}$ in bijection with ${{\,\mathrm{Cl}}}_{GN(\mathcal {O})} R$, so we need to compute the idelic normalizer: but B is unramified at all nonarchimedean places, and

$$\begin{aligned} N_{\widehat{B}^\times }(\widehat{\mathcal {O}}) = N_{{{\mathrm{GL}}}_2(\widehat{F})}({{\,\mathrm{M}}}_2(\widehat{R})) = \widehat{F}^\times \widehat{\mathcal {O}}^\times . \end{aligned}$$

Thus ${{\,\mathrm{nrd}\,}}(N_{\widehat{B}^\times }(\widehat{\mathcal {O}}))=\widehat{F}^{\times 2}\widehat{R}^\times$, and

$$\begin{aligned} GN(\mathcal {O}) = F_{>_{\Omega } 0}^\times \widehat{F}^{\times 2}\widehat{R}^\times = F_{>_{\Omega } 0}^\times \widehat{R}^\times = G(\mathcal {O}). \end{aligned}$$

In other words, the quotient map ${{\,\mathrm{Cl}}}_{G(\mathcal {O})} R \rightarrow {{\,\mathrm{Cl}}}_{GN(\mathcal {O})} R$ is an isomorphism, still a group of order 2. We conclude that $\#{{\,\mathrm{Typ}\,}}\mathcal {O}=2$.

We compute a maximal order

$$\begin{aligned} \mathcal {O}=\mathcal {O}_1 = \mathbb Z _F \oplus \mathbb Z _F i \oplus \mathbb Z _F\frac{b^2i+j}{2} \oplus \mathbb Z _F\frac{b^2+ij}{2}. \end{aligned}$$

We conjugate this order by an ideal of reduced norm $\mathfrak p$ to get the second representative

$$\begin{aligned} \mathcal {O}_2 = \mathbb Z _F \oplus \mathbb Z _F i \oplus \mathbb Z _F\frac{(b^2+b+1)+(b+1)i+j}{2} \oplus \mathbb Z _F\frac{(b+1)+(b^2+b+1)i+ij}{2}. \end{aligned}$$

Therefore these orders represent the two types of maximal orders, and ${{\,\mathrm{Typ}\,}}\mathcal {O}= \{[\mathcal {O}_1],[\mathcal {O}_2]\}$.

With all of these elements in place, we can observe selectivity (Main Theorem 31.1.7). We saw that both K and B are ramified at no nonarchimedean places and exactly the same set of real places. In particular, the field $K \hookrightarrow B$ embeds by the local-global principle. Let $S=\mathbb Z _K=\mathbb Z _F[w]$ be the maximal order in K. Then $w^2-bw+1=0$. Then ${{\,\mathrm{Emb}\,}}(\widehat{S};\widehat{\mathcal {O}}) \ne \emptyset$ (Proposition 30.5.3(a)).

The optimal selective condition (OS) holds because we took it so, $K=H^+$. It follows that S embeds in exactly one of $\mathcal {O}_1$ or $\mathcal {O}_2$. We find that

$$\begin{aligned} \alpha =\frac{b^2+ij}{2b} \in \mathcal {O}_1 \end{aligned}$$

satisfies $\alpha ^2-b\alpha +1=0$ as desired; so S embeds in $\mathcal {O}_1$ (and not $\mathcal {O}_2$).

Remark 31.6.2. Without the hypothesis of strong approximation, it is very difficult to tease apart the contributions from different orders in the genus: indeed, the generating series for representation numbers for a definite quaternion order give coefficients of modular forms, discussed in Chapter 41.

7 $*$ Selectivity, without optimality

To conclude this chapter, we compare the above with a weaker condition than optimal selectivity, and close with connections to the literature. We continue notation and hypotheses from 31.1.4.

Definition 31.7.1

We say that ${{\,\mathrm{Gen}\,}}\mathcal {O}$ is selective for S if there exists $\mathcal {O}' \in {{\,\mathrm{Gen}\,}}\mathcal {O}$ such that there is no embedding $S \hookrightarrow \mathcal {O}'$ of R-algebras.

The difference between Definition 31.1.5 and Definition 31.7.1 is that in the latter, we do not insist that the embedding is optimal. It may happen that ${{\,\mathrm{Gen}\,}}\mathcal {O}$ is selective for S, but ${{\,\mathrm{Gen}\,}}\mathcal {O}$ is not optimally selective for S: such a situation arises exactly when there is an order $\mathcal {O}' \in {{\,\mathrm{Gen}\,}}\mathcal {O}$ such that S embeds in $\mathcal {O}'$ but does not optimally embed in $\mathcal {O}'$.

Example 31.7.2

We return to Example 31.1.1. We saw that ${{\,\mathrm{Gen}\,}}\mathcal {O}$ is optimally selective for the maximal order $\mathbb Z _K$. By Main Theorem 31.1.7, ${{\,\mathrm{Gen}\,}}\mathcal {O}$ is also optimally selective for $S=\mathbb Z _F[\sqrt{-1}] \subseteq \mathbb Z _K$.

We claim that ${{\,\mathrm{Gen}\,}}\mathcal {O}$ is not selective for S. For $\mathcal {O}={{\,\mathrm{M}}}_2(\mathbb Z _K)$, we take the normalized embedding

$$\begin{aligned} w \mapsto \alpha = \begin{pmatrix} 0 &{} 1 \\ -1 &{} 0 \end{pmatrix}. \end{aligned}$$

The surprise is that we can also find an embedding $S \hookrightarrow \mathcal {O}'=\begin{pmatrix} R &{} \mathfrak p \\ \mathfrak p ^{-1} &{} R \end{pmatrix}$, just not an optimal one: we take

$$\begin{aligned} w \mapsto \alpha '=\begin{pmatrix} -\sqrt{-5} &{} 2 \\ 2 &{} \sqrt{-5} \end{pmatrix}. \end{aligned}$$

(31.7.3)

(The argument given in Example 31.1.1 no longer applies, because the polynomial $x^2-1$ has nontrivial discriminant, giving just enough room for the prime $\mathfrak p$ to sneak in.)

For sanity (to show there is no contradiction with the main theorem of optimal selectivity), we confirm that the embedding (31.7.3) does not define an optimal embedding into $\mathcal {O}'$. We have $2\mathbb Z _F=\mathfrak p ^2$, so

$$\begin{aligned} \alpha '+1 = \begin{pmatrix} 1-\sqrt{-5} &{} 2 \\ 2 &{} 1+\sqrt{-5} \end{pmatrix} \in \mathfrak p \mathcal {O}' \end{aligned}$$

so the order $R+\mathfrak p ^{-1}(\alpha '+1) \supseteq R+R\alpha ' \simeq S$ embeds in $\mathcal {O}'$.

31.7.4

If ${{\,\mathrm{Gen}\,}}\mathcal {O}$ is optimally selective for S but not selective for S, then $S \subseteq \mathcal {O}$ is optimal but there is an order $\mathcal {O}'$ such that $\phi ':S \hookrightarrow \mathcal {O}'$ is an embedding but not an optimal embedding. Let $S'=\phi '(K) \cap \mathcal {O}' \supsetneq S$. So there exists a prime $\mathfrak p \mid [S':S]_R$, and in particular, S is not maximal at $\mathfrak p$. In particular, if S is integrally closed, then ${{\,\mathrm{Gen}\,}}\mathcal {O}$ is selective for S if and only if ${{\,\mathrm{Gen}\,}}\mathcal {O}$ is optimally selective for S.

Theorem 31.7.5

(Chinburg–Friedman, Chan–Xu, Guo–Qin). Let $\mathcal {O}$ be an Eichler order of level $\mathfrak M$ and suppose that ${{\,\mathrm{Gen}\,}}\mathcal {O}$ is optimally selective for S. Then ${{\,\mathrm{Gen}\,}}\mathcal {O}$ is selective for S if and only if the following condition holds:

• (S) If $\mathfrak p \mid {{\,\mathrm{disc}}}_R S$ and ${{\,\mathrm{ord}}}_\mathfrak p (\mathfrak M ) \ne {{\,\mathrm{ord}}}_\mathfrak p ({{\,\mathrm{disc}}}_R S)$, then $\mathfrak p$ splits in $K \supseteq F$.

Proof Our very setup (section 31.3) is designed to count optimal embeddings, so to avoid lengthening this chapter, we refer the reader to Chinburg–Friedman [CF99, Theorem 3.3] for the case of maximal orders, and Chan–Xu [CX2004, Theorem 4.7] and Guo–Qin [GQ2004, Theorem 2.5] (independently) for Eichler orders. $\square$

Remark 31.7.6. The condition Proposition 31.2.1(d) (one part of (OS) for Eichler orders) is not visible in the selectivity theorem for Eichler orders, but is implied by it: by (b), the extension $K \supseteq F$ is unramified so $\mathfrak p$ is unramified in K, thus ${{\,\mathrm{ord}}}_\mathfrak p ({{\,\mathrm{disc}}}_R(S))$ is even and necessarily not equal to ${{\,\mathrm{ord}}}_\mathfrak p (\mathfrak M )$ if the latter is odd.

31.7.7

Chinburg–Friedman [CF99, Theorem 3.3] prove Theorem 31.7.5 for maximal orders, and they applied this theorem to embeddings in maximal arithmetic groups [CF99, Theorem 4.4]. Chinburg–Friedman proved their results in the language of the Bruhat–Tits tree of maximal orders. This selectivity theorem was then generalized to Eichler orders by Chan–Xu [CX2004, Theorem 4.7] and Guo–Qin [GQ2004, Theorem 2.5] (independently). Interestingly, while Guo–Qin follow Chinburg–Friedman in their proof, Chan–Xu instead use results on exceptional spinor genera and their results are phrased and proven in the language of indefinite integral quadratic forms. (These results are given for number fields, but the proofs adapt to global fields as pursued here.)

Some selectivity theorems beyond those for Eichler orders are also known. Arenas-Carmona [A-C2013, Theorem 1.2] considers more general intersections of maximal orders. Linowitz [Lin2012, Theorems 1.3–1.4] gives a selectivity theorem for (optimal) embeddings into arbitrary orders, subject to some additional technical (coprimality) hypotheses. More generally, selectivity theorem have been pursued in the more context of central simple algebras: see e.g. Linowitz–Shemanske [LS2012] and Arenas-Carmona [A-C2012].

However, these selectivity results do not prove Main Theorem 31.1.7 on the nose, either because they deal with selectivity instead of optimal selectivity or do not prove the more powerful statement that the embedding numbers are in fact equal. On the latter point, a general setup to establish equality of embedding numbers can be found in work of Linowitz–Voight [LV2015, §2].

8 $*$ Isospectral, nonisometric manifolds

We conclude with an application to geometry. We need to borrow from the future, so the reader is invited to read this section lightly, using it as present and future motivation; and then to return to this section after a more careful reading of Chapter 38.

In 1966, Kac [Kac66] famously asked: “Can one hear the shape of a drum?” Put another way, if you know the frequencies at which a drum vibrates, can you determine its shape? This beautiful question has led to an almost countless number of articles: see Giraud–Thas [GT2010] for a survey.

To restate the question in a mathematical framework, let M be a connected, compact Riemannian manifold. Associated to M is the Laplace operator, defined by $\Delta (f) :=-{{\,\mathrm{div}\,}}({{\,\mathrm{grad}\,}}(f))$ for $f \in L^2(M)$ a square-integrable function on M. The eigenvalues of $\Delta$ on the space $L^2(M)$ form an infinite, discrete sequence of nonnegative real numbers $0=\lambda _0 < \lambda _1 \le \lambda _2 \le \dots$, called the spectrum of M. By the study of the wave equation, the spectrum of M can essentially be thought of as the frequencies produced by a drum “in the shape of M”. Two Riemannian manifolds are said to be Laplace isospectral if they have the same spectra. We are led to ask: if two Riemannian manifolds are Laplace isospectral, are they isometric?

A general algebraic method for constructing Laplace isospectral manifolds is due to Sunada [Sun85] (see the surveys by Gordon [Gor2000, Gor2009]), arising from almost conjugate subgroups of a finite group of isometries acting on a manifold—providing a negative answer to Kac’s question by Gordon–Webb–Wolpert [GWW92]. But preceding Sunada, in 1980 Vignéras [Vig80b] constructed such examples—indeed, one of the applications in her book on quaternion algebras [Vig80a] was to explain this construction!

Theorem 31.8.1

(Vignéras). For every $m \ge 2$, there exist Laplace isospectral and nonisometric manifolds of dimension m.

We sketch a proof of this theorem in this section, with attention to the particular detail of selectivity. In 1994, Maclachlan–Rosenberger [MacRos94] claimed to have produced a pair of Laplace isospectral, nonisometric hyperbolic 2-orbifolds of genus 0, but then Buser–Flach–Semmler [BFS2008] later showed that these examples were too good to be true! The subtle issue they found: the phenomenon of selectivity.

Our construction is quaternionic, of course. We consider the situation of sections 38.2–38.3, specifically the setup in 38.2.1 and 38.3.1. Let F be a number field with r real places and c complex places, so that $[F:\mathbb Q ]=r+2c=n$. Let B be a quaternion algebra over F and suppose that B is split at t real places. We have an embedding (38.2.2) $\iota :B \hookrightarrow {{\,\mathrm{M}}}_2(\mathbb R )^t \times {{\,\mathrm{M}}}_2(\mathbb C )^c$. Letting $\mathcal H :=({{\mathbf {\mathsf{{H}}}}}^2)^t \times ({{\mathbf {\mathsf{{H}}}}}^3)^c$ as in (38.2.9) and

$$\begin{aligned} {{\,\mathrm{P\!}\,}}B_{>0}^\times :=B_{>0}^\times /F^\times , \end{aligned}$$

we see that $\iota ({{\,\mathrm{P\!}\,}}B_{>0}^\times ) \le {{\,\mathrm{Isom}\,}}^+(\mathcal H )$ acts on $\mathcal H$ by linear fractional transformations as orientation-preserving isometries.

Let $R=\mathbb Z _F$ be the ring of integers of F and let $\mathcal {O}\subset B$ be an R-order. Then the group $\Gamma ^1(\mathcal {O}) :=\iota (\mathcal {O}^1/\{\pm 1\}) \le {{\,\mathrm{P\!}\,}}B_{>0}^\times$ is a discrete subgroup acting properly on $\mathcal H$ by isometries. Suppose now that B is a division algebra, and further that the only elements of $\mathcal {O}^1$ of finite order are $\pm 1$. (We will soon see that this assumption can be satisfied; in some sense, it is quite typical.) Let $X^1(\mathcal {O}) :=\Gamma ^1(\mathcal {O}) \backslash \mathcal H$ be the quotient, a Riemannian manifold of dimension $m :=2t+3c$.

The condition of Laplace isospectrality is implied by the following arithmetic condition in terms of conjugacy classes of embeddings.

Theorem 31.8.2

Let $\mathcal {O}' \in {{\,\mathrm{Gen}\,}}\mathcal {O}$. Suppose that for every quadratic field $K \supseteq F$ and every quadratic R-order $S \subseteq K$, we have the equality of embedding numbers

$$\begin{aligned} m(S,\mathcal {O};\mathcal {O}^1)=m(S,\mathcal {O}';\mathcal {O}'^1). \end{aligned}$$

(31.8.3)

Then $X^1(\mathcal {O})$ and $X^1(\mathcal {O}')$ are Laplace isospectral.

Proof See Vignéras [Vig80b, Théorème 6]. The statement there is in terms of all embeddings, not just optimal embeddings—but the total count of conjugacy classes of embeddings of an quadratic order is a sum of the corresponding count of optimal embeddings of superorders (as in 31.7), so it is sufficient to have a genial order.

The key ingredient in the proof is the Selberg trace formula, which allows us to show that the spectra of the Laplace operators agree by the stronger condition of representation equivalence: for a more general point of view on this deduction, see Deturck–Gordon [DG89]. $\square$

The rub is in the equality (31.8.3). The restriction of the equivalence classes to units of reduced norm 1 is harmless: by Lemma 30.3.14, we have $m(S,\mathcal {O};\mathcal {O}^1)=m(S,\mathcal {O};\mathcal {O}^\times )[{{\,\mathrm{nrd}\,}}(\mathcal {O}^\times ):{{\,\mathrm{nrd}\,}}(S^\times )]$, and as a consequence of strong approximation we have $[{{\,\mathrm{nrd}\,}}(\mathcal {O}^\times ):{{\,\mathrm{nrd}\,}}(S^\times )]=[{{\,\mathrm{nrd}\,}}(\widehat{\mathcal {O}}^\times :{{\,\mathrm{nrd}\,}}(\widehat{S}^\times )]$. Thus if $\mathcal {O}' \in {{\,\mathrm{Typ}\,}}\mathcal {O}$, then (31.8.3) holds if and only if $m(S,\mathcal {O};\mathcal {O}^\times )=m(S,\mathcal {O}';\mathcal {O}'^\times )$.

Finally, selectivity enters! We suppose that $\mathcal {O}$ is an Eichler order. By Main Theorem 31.1.7(c), we have the desired equality when ${{\,\mathrm{Gen}\,}}\mathcal {O}$ is genial (i.e., not optimally selective)—and by part (b), this equality may fail for some S.

Corollary 31.8.4

Suppose that ${{\,\mathrm{Gen}\,}}\mathcal {O}$ is genial and $\mathcal {O}' \in {{\,\mathrm{Gen}\,}}\mathcal {O}$ has $\mathcal {O}' \not \simeq \mathcal {O}$. Suppose further that $\sigma ({{\,\mathrm{Ram}\,}}(B)) \ne {{\,\mathrm{Ram}\,}}(B)$ for all $\sigma \in {{\,\mathrm{Aut}\,}}(F)$. Then $X^1(\mathcal {O})$ and $X^1(\mathcal {O}')$ are Laplace isospectral, nonisometric Riemannian manifolds of dimension m.

Proof Isospectrality follows from Theorem 31.8.2 with Main Theorem 31.1.7. To show that $X,X'$ are not isometric, since $\mathcal {O}' \not \simeq \mathcal {O}$ we know that ${{\,\mathrm{P\!}\,}}\mathcal {O}'$ is not conjugate to ${{\,\mathrm{P\!}\,}}\mathcal {O}$ in $B^\times$, but we need this for the groups $\Gamma ^1(\mathcal {O}'),\Gamma ^1(\mathcal {O})$ in ${{\,\mathrm{Isom}\,}}^+(\mathcal H )$, which is slightly larger (see Remark 38.2.11). We leave the details to Exercise 31.3 (or see Linowitz–Voight [LV2015, Proposition 2.24]). $\square$

The remainder of the proof of Theorem 31.8.1 involves finding suitable data $F,B,\mathcal {O}$. We exhibit a pair for $m=2$ following Linowitz–Voight [LV2015, Example 5.2], giving a pair of compact hyperbolic 2-manifolds of genus 6 which are isospectral but not isometric.

Example 31.8.5

Let $F=\mathbb Q (w)$ where w is a root of the polynomial $x^4{-}5x^2-2x{+}1{=}0$. Then F is a totally real quartic field with discriminant $d_F=5744=2^4 359$, Galois group $S_4$, class number $\#{{\,\mathrm{Cl}\,}}R=1$ and narrow class number $\#{{\,\mathrm{Cl}\,}}^+ R=2$. Let B be the quaternion algebra over F which is ramified at the prime ideal $\mathfrak p _{13}$ of norm 13 generated by $b :=w^3-w^2-4w$ and three of the four real places, with split place $w \mapsto -0.751024\ldots$: then $B=\displaystyle {\biggl (\frac{a,b}{F}\biggr )}$ where $a = w^3 - w^2 - 3w - 1$ is a root of $x^4+8x^3+12x^2-1$.

A maximal order $\mathcal {O}\subset B$ is given by

$$\begin{aligned} \mathcal {O}= R \oplus R i \oplus \frac{(w^3+1)+w^2i + j}{2}R \oplus \frac{(w+1)+(w^3+1)i+ij}{2}R; \end{aligned}$$

$\mathcal {O}$ has type number 2, so there exists two isomorphism classes of maximal orders $\mathcal {O}_1=\mathcal {O}$ and $\mathcal {O}_2$.

We claim that $\mathcal {O}_1$ and $\mathcal {O}_2$ have no elements of finite order other than $\pm 1$. Indeed, if we had such an element of order q then $F(\zeta _{2q})$ is a cyclotomic quadratic extension of F, whence $\mathbb Q (\zeta _{2q})^+ \subseteq F$; but F is primitive, so the only cyclotomic quadratic extensions of F are $K=F(\sqrt{-1})$ and $K=F(\sqrt{-3})$. But as $\mathfrak p_{13}$ splits completely in $F(\sqrt{-1})$ and $F(\sqrt{-3})$, neither field embeds into B. We conclude that the groups $\Gamma _i$ are torsion free.

Since B is ramified at a finite place, the genus of $\mathcal {O}$ is genial by Proposition 31.2.1, and since ${{\,\mathrm{Aut}\,}}(F)$ is trivial, the hypothesis of Corollary 31.8.4 are satisfied: $X_1^1,X_2^1$ are Laplace isospectral, but not isometric.

Finally, by Theorem 39.1.13, we have ${{\,\mathrm{area}\,}}(X_i)=20\pi$, so $g(X_i)=6$ for $i=1,2$. Fundamental domains for these are given in Figure 31.8.6.

Figure 31.8.6:

Fundamental domain for the genus 6 manifolds $X(\Gamma _1^1)$,$X(\Gamma _2^1)$

We obtain a second example by choosing the split real place $w \mapsto -1.9202\ldots$, and since F is not Galois, as in the case of the 2-orbifold pairs 2 and 3, these are pairwise nonisometric.

For an example with $m=3$, see Exercise 31.4.

Exercises

$\triangleright$ 1.:

Prove Main Theorem 31.1.7 in the case $K \simeq F \times F$: to be precise, show that an R-order $S \subseteq F \times F$ embeds equally in all Eichler R-orders. [Hint: we must have $B \simeq {{\,\mathrm{M}}}_2(F)$, so reduce to the case where S is embedded in the diagonal and then conjugate.]

• 2. The following exercise gives insight into the proof of Theorem 31.7.5 on selectivity. Let R be local, and let $\mathcal {O}$ be an Eichler order of level $\mathfrak p ^e$.

  Let $\phi :S \hookrightarrow \mathcal {O}$ be an optimal embedding that is normalized and associated to $x \in R$, so represented by

  $$\begin{aligned} \alpha =\begin{pmatrix} x &{} 1 \\ -f_\gamma (x) &{} t-x \end{pmatrix} \end{aligned}$$

  as in Definition 30.6.8.

  • (a) Compute $\nu ^{-1}\alpha \nu$ for the matrix

    $$\begin{aligned} \nu = \begin{pmatrix} a &{} b \\ c &{} d \end{pmatrix}. \end{aligned}$$

  • (b) Show that the off-diagonal entries are equal to

    $$\begin{aligned}&(ad-bc)^{-1}{{\,\mathrm{Nm}}}_{K|F}(b\gamma -(bx+d)), \\&(ad-bc)^{-1}{{\,\mathrm{Nm}}}_{K|F}(a\gamma -(ax+c)) \end{aligned}$$

    so belong to $(\det \nu )^{-1}{{\,\mathrm{Nm}}}_{K|F}(K^\times )$.

  • (c) Suppose $\alpha '=\nu ^{-1}\alpha \nu$ gives a normalized, optimal embedding. Show that if $\mathfrak p$ is inert in $K \supseteq F$, then $\det \nu$ has even valuation.

$\triangleright$ 3.:

With notation as in section 31.8, let $\Gamma ,\Gamma ' \le B^\times /F^\times$ and $\iota :B_{>0}^\times /F^\times \hookrightarrow {{\,\mathrm{Isom}\,}}^+(\mathcal H )$. Then $X(\Gamma ),X(\Gamma ')$ are isometric if and only if there exists a permutation $\sigma$ of the factors of $G :={{\,\mathrm{Isom}\,}}^+(\mathcal H )$ and $\nu \in \iota (B^\times )$ such that $\sigma (\Gamma )=\nu \Gamma ' \nu ^{-1}$ and a $\mathbb Q$-algebra automorphism $\tau :B \rightarrow B$ such that the diagram

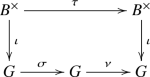
commutes, where $\nu$ acts on G by conjugation. [Hint: use the Skolem–Noether theorem.]

• 4. In this exercise, we exhibit Laplace isospectral, nonisometric hyperbolic 3-manifolds, following Linowitz–Voight [LV2015, Example 6.3]. Let $F=\mathbb Q (w)$ be the quintic field with discriminant $-43535$ and defining polynomial $x^5-x^4+3x^3-3x+1$. Let $B :=\displaystyle {\biggl (\frac{3w^3-2,-13}{F}\biggr )}$.

  • (a) Show that B is ramified at the three real places of F and the prime ideal $\mathfrak p =(w^4-w^3+3w^2-w-2)$ of norm 13.

  • (b) Let $\mathcal {O}$ be a maximal order in B. Show that the type number of $\mathcal {O}$ is equal to 2.

  • (c) Let $\mathcal {O}=\mathcal {O}_1$ and $\mathcal {O}_2$ be representatives of ${{\,\mathrm{Typ}\,}}\mathcal {O}$. Show that the only elements of finite order in $\mathcal {O}_i^1$ are $\pm 1$.

  • (d) Show that ${{\,\mathrm{Gen}\,}}\mathcal {O}$ is genial.

  • (e) Let $X_i^1 :=\Gamma ^1(\mathcal {O}_i) \backslash {{\mathbf {\mathsf{{H}}}}}^3$, with notation as in section 31.8. Show that $X_1^1$ and $X_2^1$ are Laplace isospectral, nonisometric 3-manifolds.

  • (f) Show that ${{\,\mathrm{vol}\,}}(X_1^1)={{\,\mathrm{vol}\,}}(X_2^1)=51.024566\ldots$