Abstract
To conclude our analytic part, we apply idelic methods to understand embeddings of quadratic orders into quaternion orders.
You have full access to this open access chapter, Download chapter PDF
To conclude our analytic part, we apply idelic methods to understand embeddings of quadratic orders into quaternion orders.
1 \(\triangleright \) Representation numbers
A subject of classical (and continuing) interest is the number of representations of an integer by an integral quadratic form, in particular as a sum of squares. Because of the subject of this text, we consider quadratic forms in three and four variables where quaternions provide insight.
Lagrange famously proved that every positive integer is the sum of four squares. We proved Lagrange’s theorem (Theorem 11.4.3) by viewing the sum of four squares as the reduced norm on the Lipschitz order, and concluded the argument by comparison to the Hurwitz order, which is Euclidean. In Theorem 14.3.8, we proved Legendre’s three-square theorem: every integer \(n \ge 0\) not of the form \(4^a(8b+7)\) is the sum of three squares. The proof is harder for three squares than for four (see Remark 11.4.4): our proof used the Hasse–Minkowski theorem (the local-global principle for quadratic forms over \(\mathbb Q \)) and again the fact that the Hurwitz order has class number 1. (We gave a variant in Exercise 14.5, where we used the local-global principle for embeddings.)
In each of these cases, we may also ask for a count of the number of such representations. For \(k \in \mathbb Z _{\ge 1}\) and \(n \in \mathbb Z _{\ge 0}\), let
be the number of ways of writing n as the sum of k squares; equivalently, this is the number of lattice points on the sphere of radius \(\sqrt{n}\) in \(\mathbb R ^k\). The number \(r_4(n)\) is computed in terms of the factorization of n in the Hurwitz (or Lipschitz) orders, and has a simple answer: we saw in Exercise 11.3 that for an odd prime p,
and we upgraded this in Exercise 26.7 to a general formula for \(r_4(n)\) in terms of the sum of (odd) divisors of n.
We may similarly ask for a formula for \(r_3\), but it is more difficult both to state and to prove. Define
as the number of primitive representations of n as the sum of three squares. Then \(r_3^{\text {prim}}(n)=r_3(n)\) if n is squarefree, and more generally
Let \(h(d)=\#{{\,\mathrm{Pic}\,}}S_d\) be the class number of the quadratic order of discriminant \(d<0\); equivalently, h(d) is the number of reduced primitive integral positive definite binary quadratic forms of discriminant d.
Gauss [Gau86, Section 291] showed that \(r_3^{\text {prim}}(n)\) is a constant multiple of \(h(-4n)\) as follows.
Theorem 30.1.3
(Gauss). We have \(r_3(1)=6\), \(r_3(3)=8\), and for \(n \in \mathbb Z _{\ge 0}\):
(One can uniformly include the cases \(n=1,3\) by accounting for the extra roots of unity in \(\mathbb Q (\sqrt{-n})\).)
Theorem 30.1.3 is a special case of Theorem 30.4.7—see Exercise 30.4—but for historical and motivational reasons, we also give in the next section an essentially self-contained proof for the case \(n \equiv 1,2 ~(\text{ mod } ~{4})\), following Venkov [Ven22, Ven29].
The main obstacle to generalizing Gauss’s theorem (Theorem 30.1.3) is that quaternion orders need not have class number 1: a generalization with this hypothesis “following the general plan described by Venkov” is given by Shemanske [Shem86]. Another annoyance is the growing technicality of the local computations giving the explicit constants involved. Both of these issues are in some sense resolved by employing idelic methods (hence the placement of this chapter in this text) and even the proof of Gauss’s theorem itself is simplified by these methods (in the next section). The result is Theorem 30.4.7: representations are spread across the genus of an order, with the constants given by local factors (computed in this chapter for maximal orders and then Eichler orders).
30.1.4
For indefinite quaternion orders, strong approximation applies, and we are almost always able to prove that the contribution to each order in the genus is equal, with one quite subtle issue known as selectivity: in certain rare circumstances, a quadratic order embeds in precisely half of the orders in a genus. We pursue selectivity in the next chapter (Chapter 31): technical and rather extraordinary, it is a subject that demands care.
Happily, a locally norm-maximal order (such as an Eichler order) over \(\mathbb Z \) is not selective!
An important application of this theory is a refinement of the mass formula to a class number formula. Recall the Eichler mass formula (Theorem 25.3.18): if B is a definite quaternion algebra over \(\mathbb Q \) of discriminant D and \(\mathcal {O}\subset B\) is an Eichler order of level M, then
where \(w_J=\#\mathcal {O}{}_{\textsf {\tiny {L}} }(J)/\{\pm 1\}\). We can account for the necessary correction:
The latter “error term” is accounted for by (finite) cyclic subgroups spread across representative left orders \(\mathcal {O}{}_{\textsf {\tiny {L}} }(J)\)—and this is precisely the contribution computed idelically above!
Theorem 30.1.5
(Eichler class number formula). Let B be a definite quaternion algebra over \(\mathbb Q \) of discriminant D, and let \(\mathcal {O}\subset B\) be an Eichler order of level M. Let \(N=DM={{\,\mathrm{discrd}\,}}\mathcal {O}\). Then
where
and
2 Sums of three squares
In this section, we prove the theorem of Gauss showing that the number of representations of an integer as a sum of three squares is a class number. For further reading, see also Grosswald [Gro85, Chapter 4] and the references therein.
A few parts are easy to establish. The count \(r_3(1)=6\) is immediate. If \(4 \mid n\), then \(r_3^{\text {prim}}(n)=0\) since \(x^2+y^2+z^2 \equiv 0 ~(\text{ mod } ~{4})\) implies \(x \equiv y \equiv z \equiv 0 ~(\text{ mod } ~{2})\). Similarly, if \(n \equiv 7 ~(\text{ mod } ~{8})\) then \(r_3^{\text {prim}}(n)=r_3(n)=0\) by the three-square theorem.
The two remaining cases lie deeper. A proof using quaternions is due to Venkov [Ven22, Ven29]; alternate accounts are given by Hanlon [Hanlon81, Chapter 2] and Rehm [Reh76]. To accomplish the task of giving an argument that is as self-contained as possible and still previews the ideas and structure contained in this chapter, we give a proof in the case \(n \equiv 1,2 ~(\text{ mod } ~{4})\).
Proof of Theorem 30.1.3 for \(n \equiv 1,2 ~(\text{ mod } ~{4})\). Suppose \(n \equiv 1,2 ~(\text{ mod } ~{4})\). Let \(S :=\mathbb Z [\sqrt{-n}] \subset K :=\mathbb Q (\sqrt{-n})\). Then S is maximal and ramified at 2, i.e., \(S \otimes \mathbb Z _2\) is the ring of integers of the field \(K \otimes \mathbb Q _2 = \mathbb Q _2(\sqrt{-n})\).
Let \(B=({-1,-1} \mid \mathbb{Q })\) be the rational Hamiltonians and \(\mathcal {O}\subset B\) the Hurwitz order. We consider the set
then \(\#W=r_3^{\text {prim}}(n)\). By the three-square theorem, \(W \ne \emptyset \), so let \(\alpha \in W\). We embed
and for convenience identify K with its image. By the Skolem–Noether theorem (Corollary 7.1.5), every other element \(\alpha ' \in W\) is the form \(\alpha ' = \beta ^{-1}\alpha \beta \) with \(\beta \in B^\times \) (but not necessarily conversely!). Let
The set E has a right action of the normalizer \(N_{B^\times }(\mathcal {O})\) (checking that primitivity is preserved).
We relate E to the group of fractional ideals \({{\,\mathrm{Idl}\,}}S\) as follows. Let \(\mathfrak b \subseteq K\) be a fractional S-ideal. Since \(\mathcal {O}\) is (right) Euclidean, \(\mathfrak b \mathcal {O}= \beta \mathcal {O}\) for some \(\beta \in B^\times \) that is well-defined up to right multiplication by \(\mathcal {O}^\times \). The heart of the proof is the following claim: the map
is a well-defined, surjective map of sets. The most efficient (and clear) proof of this claim is idelic, and we prove it in two steps.
First, the map (30.2.3) is well-defined: that is to say, \(\beta \in E\). Write \(\mathfrak b \widehat{S}= \widehat{b} \widehat{S}\), so that \(\beta \widehat{\mathcal {O}}= \widehat{b} \widehat{\mathcal {O}}\) and \(\beta =\widehat{b} \widehat{\mu }\) with \(\widehat{\mu }\in \widehat{\mathcal {O}}^\times \). Then \(\widehat{b}\) commutes with \(\alpha \) (in \(\widehat{K}\subseteq \widehat{B}\)), so
To show that the map is surjective, we need to establish one other important point comparing the global and the idelic: we claim that there exists \(\widehat{\nu }\in N_{\widehat{B}^\times }(\widehat{\mathcal {O}})\) such that
The existence of \(\widehat{\nu }\) may be established locally. We prove this in Proposition 30.5.3: for \(p \ne 2\), it amounts to showing that two elements of \({{\,\mathrm{M}\,}}_2(\mathbb Z _p)\) with square \(-n\) are conjugate under \({{\,\mathrm{GL}\,}}_2(\mathbb Z _p)\), and for \(p=2\) it follows from the description of the valuation ring: it is here where we use the fact that S is maximal at 2, but this is only a technical issue. (The reader may accept (30.2.4) and proceed, or pause here and work this out, in Exercise 30.3.)
Given (30.2.4), we see that \(\beta \widehat{\nu }^{-1}\) centralizes \(\alpha \) in \(B^\times \) and so belongs to \(\widehat{K}^\times \), whence
Finally, since 2 is ramified in K—using \(n=1,2 ~(\text{ mod } ~{4})\) again—and the nontrivial class in \(N_{\widehat{B}^\times }(\widehat{\mathcal {O}})/\widehat{\mathcal {O}}^\times \simeq \mathbb Z /2\mathbb Z \) is represented by an element of reduced norm 2, we have
and therefore \(\beta = \widehat{\mathfrak{b }}\widehat{\mu }\) with \(\widehat{\mathfrak{b }}\in \widehat{K}^\times \) and \(\widehat{\mu }\in \widehat{\mathcal {O}}^\times \). Therefore \(\widehat{\mathfrak{b }}\widehat{\mathcal {O}}= \beta \widehat{\mathcal {O}}\) and so \(\beta \mathcal {O}= \mathfrak b \mathcal {O}\) where \(\mathfrak b = \widehat{\mathfrak{b }}\widehat{S}\).
From the claim, we conclude the theorem. We have \(\beta ^{-1} \alpha \beta = \alpha \) if and only if \(\beta \) centralizes \(\alpha \) if and only if \(\beta \in K^\times \), so the desired elements \(\beta ^{-1}\alpha \beta \) up to \(N_{B^\times }(\mathcal {O})\) are uniquely determined by the class \([\mathfrak b ] \in {{\,\mathrm{Pic}\,}}S = {{\,\mathrm{Idl}\,}}S/{{\,\mathrm{PIdl}\,}}S\). Finally, when \(n>1\) we have \(S^\times =\{\pm 1\}\) so \(\#\mathcal {O}^\times /S^\times = 12\), and the result follows.
Importantly, Venkov’s proof of Gauss’s theorem given above is explicit and constructive, given at least one representation as a sum of three squares.
The early observation made in the proof above is that the sum of three squares is the restriction of the reduced norm to the trace zero elements of the Hurwitz order. One then seeks a similar statement for quadratic forms \(Q={{\,\mathrm{nrd}\,}}|_{\mathcal {O}^0}\) obtained more generally. (This is almost the same thing as the ternary quadratic form associated to \(\mathcal {O}\) itself via the Clifford algebra construction in Chapter 22; the difference is that for the latter we take the dual of the order and scale, as in (22.1.3).)
Just as in the proof above, for a representation \(Q(x,y,z)=n\) corresponding to \(\alpha \in \mathcal {O}\) with \(\alpha ^2+n=0\), we obtain an embedding \(S=\mathbb Z [\sqrt{-n}] \hookrightarrow \mathcal {O}\) of a quadratic order into the quaternion order; conversely, to such an embedding we find a representation. It is more convenient to work with embeddings, as they possess more structure. Viewed in this way, we may equivalently restrict the reduced norm from \(\mathcal {O}\) to the order S itself, and then we are asking for the representation of a binary quadratic form by a quaternary quadratic form.
3 Optimal embeddings
We now begin in earnest. We start by considering quadratic embeddings into quaternions, both rationally and integrally. Let R be a Dedekind domain with \(F={{\,\mathrm{Frac}\,}}R\), and let B be a quaternion algebra over F.
Let K be a separable quadratic F-algebra: then either \(K \supseteq F\) is a separable quadratic field extension or \(K \simeq F \times F\). Suppose that \(K \hookrightarrow B\).
30.3.1
The set of embeddings of K in B is identified with the set \(K^\times \backslash B^\times \), by 7.7.12: if \(\phi :K \hookrightarrow B\) is another embedding, then by the Skolem–Noether theorem there exists \(\beta \in B^\times \) such that \(\phi (\alpha )=\beta ^{-1} \alpha \beta \) for all \(\alpha \in K\) with \(\beta \) well-defined up to left multiplication by \(K^\times \), the centralizer of K under conjugation by \(B^\times \).
We now turn to the integral theory. Let \(\mathcal {O}\subseteq B\) be a quaternion R-order, and let \(S \subseteq K\) be a quadratic R-order; we will be interested in embeddings \(\phi :S \hookrightarrow \mathcal {O}\). Such an embedding gives an embedding \(\phi :K \hookrightarrow B\) by extending scalars. We keep the embeddings for various suborders organized as follows.
Definition 30.3.2
An R-algebra embedding \(\phi :S \hookrightarrow \mathcal {O}\) is optimal if
Let
When no confusion can result, we drop the subscript R and write simply \({{\,\mathrm{Emb}\,}}(S,\mathcal {O})\).
30.3.4
If an embedding \(\phi :S \hookrightarrow \mathcal {O}\) is not optimal, then it is optimal for a larger order \(S' \supseteq S\). Accordingly, there is a natural decomposition
Lemma 30.3.6
An R-algebra embedding \(\phi :S \hookrightarrow \mathcal {O}\) is optimal if and only if the induced \(R_\mathfrak p \)-algebra embeddings \(S_\mathfrak p \hookrightarrow \mathcal {O}_\mathfrak p \) are optimal for all primes \(\mathfrak p \subseteq R\).
Proof Immediate from the local-global dictionary for lattices (Theorem 9.4.9).\(\square \)
Lemma 30.3.6 says that for an embedding \(\phi \), the property of being optimal is a local property.
We define
(The set E also depends on the fixed embedding \(K \hookrightarrow B\), but this ‘reference’ embedding will remain fixed throughout.) In equation 30.3.7, we see two different ways to think about embeddings: we either move S and see how it fits into \(\mathcal {O}\), or we fix K and move \(\mathcal {O}\).
Lemma 30.3.8
The map
where \(\phi _\beta (\alpha ) :=\beta ^{-1}\alpha \beta \) for \(\alpha \in S\) is a bijection.
Proof Immediate from 30.3.1.\(\square \)
We further organize our optimal embeddings up to conjugation as follows.
30.3.10
Let \(\mathcal {O}^1 \le \Gamma \le N_{B^\times }(\mathcal {O})\). Then the image of \(\Gamma \) in \(N_{B^\times }(\mathcal {O})/F^\times \) has finite index. For example, we may take \(\Gamma =\mathcal {O}^\times \). (The scalars do not play a role in the theory of embeddings: they act by the identity under conjugation.)
For \(\gamma \in \Gamma \), and an optimal embedding \(\phi \in {{\,\mathrm{Emb}\,}}(S,\mathcal {O})\), we obtain a new embedding via \(\alpha \mapsto \gamma ^{-1} \phi (\alpha ) \gamma \), i.e., \(\Gamma \) acts on the right on \({{\,\mathrm{Emb}\,}}(S,\mathcal {O})\) by conjugation, and correspondingly on the right on E by right multiplication.
Let
and
The quantity \(m(S,\mathcal {O};\Gamma )\) only depends on the type (isomorphism class) of \(\mathcal {O}\) (transporting \(\Gamma \) under the isomorphism of orders, of course).
By Lemma 30.3.8, there is a bijection
We conclude this section by a comparison: for groups \(\Gamma \) sitting between unit groups and norm 1 unit groups, we can compare embedding numbers as follows.
Lemma 30.3.14
If \(\mathcal {O}^1 \le \Gamma \le \mathcal {O}^\times \), then
Proof We have a surjective map
and the lemma amounts to looking at the fibers. From (30.3.13), we turn instead to
For \(\beta \in E\), the fiber over \(K^\times \beta \mathcal {O}^\times \) is
where \(K^\beta =\beta ^{-1} K \beta \). But by hypothesis on \(\beta \), we have \(K^{\beta \times } \cap \mathcal {O}^\times = S^{\beta \times }\), so the fiber is in bijection with
Finally, the reduced norm gives a homomorphism \(\mathcal {O}^\times \rightarrow R^\times \) with kernel \(\mathcal {O}^1\), so since \(\mathcal {O}^1 \le \Gamma \le \mathcal {O}^\times \), we have
independent of \(\beta \), giving the result.\(\square \)
Remark 30.3.17. The term optimal goes back at least to Schilling [Schi35], but the notion was studied in the context of maximal orders as well by Chevalley [Chev34], Hasse [Hass34], and Noether [Noe34]. The theory of optimal embeddings was developed thereupon by Eichler [Eic56a, §3]; many key ideas can be seen transparently in Eichler [Eic73, Chapter II, §§3–5]. For further history up to the present, see Remark 30.6.18.
4 Counting embeddings, idelically: the trace formula
In this section, we give a formula the number of conjugacy classes of embeddings, using local-global (idelic) methods. We retain notation from the previous section, but now specialize to the case where R is a global ring with \(F={{\,\mathrm{Frac}\,}}R\). We use adelic (mostly idelic) notation as in 27.6.4.
We began in the previous section with a first embedding \(K \hookrightarrow B\). As a reminder, the existence of such an embedding is determined by a local-global principle as follows.
30.4.1
By the local-global principle for embeddings (Proposition 14.6.7, and 14.6.8 for the case \(K \simeq F \times F\)), there exists an F-algebra embedding \(K \hookrightarrow B\) if and only if there exist \(F_v\)-algebra embeddings \(K_v \hookrightarrow B_v\) for all \(v \in {{\,\mathrm{Pl}\,}}F\) if and only if \(K_v\) is a field for all \(v \in {{\,\mathrm{Ram}\,}}B\).
30.4.2
The definitions in the previous section extend to each completion. Let \(\widehat{K}= K \otimes _F \widehat{F}\) and similarly \(\widehat{S}= S \otimes _R \widehat{R}\). Let
be a subgroup whose image in \(N_{\widehat{B}^\times }(\widehat{\mathcal {O}})/\widehat{F}^\times \) has finite index. For example, we can take \(\widehat{\Gamma }\) the congruence closure of \(\Gamma \).
We then analogously define
and
30.4.5
As in Lemma 30.3.8, we define
and obtain a bijection
under conjugation.
We now show that the number of global embeddings is counted by a class number times the number of local embeddings. In view of Lemma 30.3.14, we may focus on the case \(\widehat{\Gamma }=\widehat{\mathcal {O}}^\times \). As usual, we write \({{\,\mathrm{Cls}\,}}\mathcal {O}\) for the right class set of \(\mathcal {O}\).
Theorem 30.4.7
(Trace formula). Let \(h(S) :=\#{{\,\mathrm{Pic}\,}}S\). Then
See Remark 30.4.24 for an explanation of the name trace formula.
Proof We decompose the set \(K^\times \backslash \widehat{E}/ \widehat{\mathcal {O}}^\times \) in two different ways.
First, there is a natural map
which is a surjective map of pointed sets. The fiber of (30.4.9) over the identity element is
We claim that the fibers of (30.4.9) may be similarly identified. Indeed, the fiber over \(\widehat{K}^\times \widehat{\beta }\widehat{\mathcal {O}}^\times \) consists of the double cosets \(K^\times \widehat{\nu }\widehat{\beta }\widehat{\mathcal {O}}^\times \) with \(K^\times \widehat{\nu }\in K^\times \backslash \widehat{K}^\times \), and
if and only if
with \(\rho \in K^\times \) and \(\widehat{\mu }\in \widehat{\mathcal {O}}^\times \), if and only if
(since \(\widehat{\beta }\in \widehat{E}\)), if and only if \(K^\times \widehat{\nu }\subseteq K^\times \widehat{S}^\times \), as claimed. From the claim and (30.4.6), we conclude that
On the other hand, each \(\widehat{\beta }\widehat{\mathcal {O}}^\times \in \widehat{E}/\widehat{\mathcal {O}}^\times \) defines a right \(\widehat{\mathcal {O}}\)-ideal; intersecting with B and organizing these right ideals by their classes, we will now show that they give rise to optimal embeddings of the corresponding left order. For brevity, write \(\mathcal {O}_I=\mathcal {O}{}_{\textsf {\tiny {L}} }(I)\). There is a map of pointed sets
Choose representatives
so that \(I=\widehat{\alpha }_I\widehat{\mathcal {O}}\cap B\). Then
Let
Now if
then there exists a unique I such that
and therefore
for some \(\beta \in B^\times \). If \(\beta ' \in B^\times \) is another, then
so the class \(\beta \mathcal {O}_I^\times \) is well-defined.
We claim that \(\beta \in E_I\), and conversely if \(\beta \in E_I\) then \(\widehat{\beta }=\beta \widehat{\alpha }_I^{-1} \in \widehat{E}\). Indeed,
so \(K \cap \beta \mathcal {O}_I \beta ^{-1}=S\) if and only if \(\widehat{K}\cap \widehat{\beta }\widehat{\mathcal {O}}\widehat{\beta }^{-1} = \widehat{S}\). Therefore there is a bijection
Putting (30.4.12) and (30.4.16) together and counting, the theorem follows.\(\square \)
When \(\mathcal {O}\) has class number 1, we hit the embedding number on the nose.
Corollary 30.4.17
If \(\#{{\,\mathrm{Cls}\,}}\mathcal {O}=1\), then
Proof Immediate from Theorem 30.4.7.\(\square \)
We recall that the genus of \(\mathcal {O}\) (Definition 17.4.8) is the set \({{\,\mathrm{Gen}\,}}\mathcal {O}\) of R-orders \(\mathcal {O}' \subseteq B\) locally isomorphic to \(\mathcal {O}\).
Corollary 30.4.18
If \({{\,\mathrm{Emb}\,}}(S_\mathfrak p ,\mathcal {O}_\mathfrak p ) \ne \emptyset \) for all primes \(\mathfrak p \), then there exists an order \(\mathcal {O}' \in {{\,\mathrm{Gen}\,}}\mathcal {O}\) such that \({{\,\mathrm{Emb}\,}}(S,\mathcal {O}') \ne \emptyset \).
Proof By the trace formula, we have \(\prod _\mathfrak p m(S_\mathfrak p ,\mathcal {O}_\mathfrak p ;\mathcal {O}_\mathfrak p ^\times ) = m(\widehat{S},\widehat{\mathcal {O}};\widehat{\mathcal {O}}^\times ) > 0\), so since all terms in the formula are nonnegative integers, we have \(m(S,\mathcal {O}{}_{\textsf {\tiny {L}} }(I);\mathcal {O}{}_{\textsf {\tiny {L}} }(I)^\times ) > 0\) for some \([I] \in {{\,\mathrm{Cls}\,}}\mathcal {O}\), and \(\mathcal {O}{}_{\textsf {\tiny {L}} }(I) \in {{\,\mathrm{Gen}\,}}\mathcal {O}\).
Remark 30.4.19. The possible failure of local optimal embeddings to ‘glue’ to a global optimal embedding into \(\mathcal {O}\) is measured by the phenomenon of selectivity, studied in Chapter 31.
30.4.20
More generally, an isomorphism \(\phi :\mathcal {O}\xrightarrow {\smash {{\sim }}}\mathcal {O}'\) of orders induces a bijection \({{\,\mathrm{Emb}\,}}_R(S,\mathcal {O}) \leftrightarrow {{\,\mathrm{Emb}\,}}_R(S,\mathcal {O}')\), and \(\phi (\mathcal {O}^\times )=\mathcal {O}'^\times \), so we may group together the terms in (30.4.8) according to the type set \({{\,\mathrm{Typ}\,}}\mathcal {O}\). Let
be index of the subgroup principal two-sided fractional \(\mathcal {O}\)-ideals inside the invertible ones, studied in section 18.5. By Proposition 18.5.10, the equation (30.4.8) then becomes
Remark 30.4.22. The foundational formula (30.4.8) is proven by counting a set two different ways. As such, it admits a purely combinatorial proof: Brzezinski [Brz89] shows that it follows from looking at “transitive actions of groups on pairs of sets and on relations invariant with respect to these actions” [Brz89, p. 199].
We also record the following corollary (in the vein of Remark 30.4.22).
Corollary 30.4.23
Left multiplication defines a group action
that defines a free action of the group \({{\,\mathrm{Pic}\,}}S\) on the set
Proof In the proof of the trace formula, we identified \(K^\times \backslash \widehat{K}^\times / \widehat{S}^\times \simeq {{\,\mathrm{Pic}\,}}S\) and established an idelic to global bijection in (30.4.16); in (30.4.11), each fiber of the map (30.4.9) is identified with \({{\,\mathrm{Pic}\,}}S\), describing the orbits of the action. (See also Exercise 30.12, where a direct proof is requested.)\(\square \)
Remark 30.4.24. Theorem 30.4.7 is called a trace formula as it can be applied to compute the trace of certain matrices (called Brandt matrices) that encode the action of Hecke operators on a space of modular forms. We return to this important point of view in detail in Chapter 41, and apply the above formula to compute traces in section 41.5.
5 Local embedding numbers: maximal orders
In view of Theorem 30.4.7, we see that up to a class number of the base ring, optimal embeddings are counted in purely local terms. In this section and the next, we compute the relevant local embedding numbers; after that, we will return to the global setting to put the results together.
To this end, in this section and the next, we suppose R is local (as in 23.2.1): so R is a complete DVR with maximal ideal \(\mathfrak p =\pi R\) and finite residue field \(k :=R/\mathfrak p \).
30.5.1
Since we are now local, the R-order S is free and so \(S=R[\gamma ]\) for some (not unique) \(\gamma \in S\). Let \(f_\gamma (x) :=x^2-t_\gamma x+n_\gamma \) be the minimal polynomial of \(\gamma \), and let \(d_\gamma :=t_\gamma ^2-4n_\gamma \) be the discriminant of \(f_\gamma \), equal to the discriminant of S in \(R/R^{\times 2}\). An R-algebra embedding from S is then determined uniquely by the image of \(\gamma \).
We now compute (local) embedding numbers in the case of a maximal order; to do so, we introduce some notation.
30.5.2
Recalling that \(K \supseteq F\) is a separable quadratic F-algebra and \(\mathfrak p \) is the maximal ideal of R, we define a symbol recording the splitting of the prime \(\mathfrak p \) in K (mirroring the Kronecker symbol):
If \(q=\#k\) is odd, and \(K \simeq F[x]/(x^2-d)\), then
is the usual Legendre symbol.
Proposition 30.5.3
The following statements hold.
-
(a)
We have \(m(S,{{\,\mathrm{M}\,}}_2(R);{{\,\mathrm{GL}\,}}_2(R))=1\).
-
(b)
Suppose B is a division algebra and \(\mathcal {O}\subseteq B\) its valuation ring. If K is a field and \(S=R_K\) is integrally closed, then
If K is not a field or if S is not integrally closed, then \({{\,\mathrm{Emb}\,}}(S,\mathcal {O})=\emptyset \).
We recall that \(N_{{{\,\mathrm{GL}\,}}_2(F)}({{\,\mathrm{M}\,}}_2(R))=F^\times {{\,\mathrm{GL}\,}}_2(R)\), so (a) also includes the case of the normalizer.
Proof First, part (a). We have at least one embedding \(\phi :S \hookrightarrow {{\,\mathrm{End}\,}}_R(S) \simeq {{\,\mathrm{M}\,}}_2(R)\) given by the regular representation of S on itself (in a basis): in the basis \(1,\gamma \), we have
a matrix in rational canonical form. This embedding is optimal, because if \(x,y \in F\) satisfy
then \(x,y \in R\) already, so \(\phi (K) \cap {{\,\mathrm{M}\,}}_2(R)=\phi (S)\).
To finish (a), we need to show that the embedding (30.5.4) is the unique one, up to conjugation by \({{\,\mathrm{GL}\,}}_2(R)\). So let \(\psi :S \hookrightarrow {{\,\mathrm{M}\,}}_2(R)\) be another optimal embedding. Then via \(\psi \), the R-module \(M=R^2\) (column vectors) has the structure of a left S-module; the condition that \(\psi \) is optimal translates into the condition that the (left) multiplicator ring of \(R^2\) in K is precisely S, and therefore M is invertible as a left S-module by Exercise 16.13, and therefore principal, generated by \(x \in M\), so that \(M=Sx = Rx + R\gamma x\). In the R-basis \(x,\gamma x\), the left regular representation has the form (30.5.4), completing the proof.
Here is a second quick matrix proof (finding explicitly the cyclic basis). Let \(\gamma \mapsto \begin{pmatrix} a &{} b \\ c &{} d \end{pmatrix} \in {{\,\mathrm{M}\,}}_2(R)\) be an optimal embedding; then at least one of \(b,c,d-a \in R^\times \). Therefore there exist \(x_1,x_2 \in R\) such that \(q(x_1,x_2)=cx_1^2+(d-a)x_1x_2-bx_2^2 \in R^\times \). Let \(x=(x_1,x_2)^{\textsf {t} }\); then \(\gamma x=(ax_1+bx_2,cx_1+dx_2)^{\textsf {t} }\). Let \(\alpha \in {{\,\mathrm{M}\,}}_2(R)\) be the matrix with columns \(x,\gamma x\). Then \(\det \alpha = q(x_1,x_2) \in R^\times \), so in fact \(\alpha \in {{\,\mathrm{GL}\,}}_2(R)\). We then compute
as claimed. (This matrix proof will be generalized in the next section, when we work more generally with Eichler orders.)
Next, part (b). By Corollary 13.4.5, there exists an embedding \(K \hookrightarrow B\) if and only if K is a field, so suppose K is a field. By Proposition 13.3.4, the valuation ring \(\mathcal {O}\) is the unique maximal R-order in B, consisting of all integral elements, so the embedding restricts to an embedding \(S \hookrightarrow \mathcal {O}\) by uniqueness. Suppose \(S=R_K\); then an embedding \(S \hookrightarrow \mathcal {O}\) extends to \(K \hookrightarrow B\) so is conjugate 30.3.1 to every other under the action of \(B^\times \). But the valuation ring is unique, thus \(N_{B^\times }(\mathcal {O})=B^\times \). Thus \(m(S,\mathcal {O};N_{B^\times }(\mathcal {O}))=1\). Finally, we have \(N_{B^\times }(\mathcal {O})/(F^\times \mathcal {O}^\times ) \simeq \mathbb Z /2\mathbb Z \), generated by any \(j \in \mathcal {O}\) with \({{\,\mathrm{nrd}\,}}(j)=\pi \). If the extension \(K \supseteq F\) is ramified, then \(K=F(j)\) so j centralizes K, and \(m(S,\mathcal {O};N_{B^\times }(\mathcal {O}))=m(S,\mathcal {O};\mathcal {O}^\times )=1\). If instead \(K \supseteq F\) is inert, then \(B \simeq ({K,j} \mid {F})\), and conjugation by j normalizes but does not centralize K, and \(m(S,\mathcal {O};\mathcal {O}^\times )=2\).\(\square \)
In all cases, the local embedding numbers are finite.
Corollary 30.5.5
\(m(S,\mathcal {O};\Gamma )<\infty \).
Proof Recalling that the image of \(\Gamma \) in \(N_{B^\times }(\mathcal {O})/F^\times \) is a subgroup of finite index, we know that the natural surjective map
is finite-to-one; applying this argument twice we reduce to the case that \(\Gamma =\mathcal {O}^\times \).
Let \(\mathcal {O}' \supseteq \mathcal {O}\) be a maximal R-order. Then \(\mathcal {O}^\times \le \mathcal {O}'^\times \). Moreover, each \(\phi \in {{\,\mathrm{Emb}\,}}(S,\mathcal {O})\) gives (by composing with \(\mathcal {O}\hookrightarrow \mathcal {O}'\)) an embedding \(\phi :S \hookrightarrow \mathcal {O}'\) that is optimal for some superorder \(S' \supseteq S\). Thus
There are only finitely many superorders \(S'\) in the sum, since the integral closure \(R_K\) contains all \(S'\) so \([R_K:S']_R \mid [R_K:S]_R\)—or equally well, compare discriminants. Applying Proposition 30.5.3, we conclude \(m(S,\mathcal {O};\mathcal {O}^\times )<\infty \).\(\square \)
6 \(*\) Local embedding numbers: Eichler orders
At this point, the presentation of local embedding numbers begins to run off the rails: for more general classes of orders, formulas for local embedding numbers are rarely as simple as in Proposition 30.5.3. To avoid tumbling too far, we present formulas for the case where \(\mathcal {O}\) is a local Eichler (residually split) order following Hijikata [Hij74, Theorem 2.3]. See Remark 30.6.18 for further reference.
In this section, we retain the assumption that R is local and the notation in 30.5.1. Further, we suppose \(\mathcal {O}\) is an Eichler order of level \(\mathfrak p ^e\) with \(e \ge 0\).
30.6.1
Let
then
If \(e=0\), then \(\varpi \in \mathcal {O}^\times \) and \(N_{B^\times }(\mathcal {O})=F^\times \mathcal {O}^\times \); if instead \(e \ge 1\), then \(\langle \varpi \rangle \simeq \mathbb Z /2\mathbb Z \).
For \(\phi \in {{\,\mathrm{Emb}\,}}(S,\mathcal {O})\), let \(\phi ^\varpi \) be defined by
By (30.6.2), \(\phi ,\phi ' \in {{\,\mathrm{Emb}\,}}(S,\mathcal {O})\) are equivalent in \({{\,\mathrm{Emb}\,}}(S,\mathcal {O};N_{B^\times }(\mathcal {O}))\) if and only if \(\phi '\) is equivalent to either \(\phi \) or \(\phi ^\varpi \) in \({{\,\mathrm{Emb}\,}}(S,\mathcal {O};\mathcal {O}^\times )\).
Lemma 30.6.3
Let \(\phi \in {{\,\mathrm{Emb}\,}}(S,\mathcal {O})\). Then there exist \(x \in R\) and \(\nu \in N_{B^\times }(\mathcal {O})\) such that
and
Proof We may suppose that \(\mathcal {O}\) is the standard Eichler order. Let \(\phi :S \hookrightarrow \mathcal {O}\) be an embedding, with
so that \(a,b,c,d \in R\). We have \(t_\gamma ={{\,\mathrm{trd}\,}}(\gamma )=a+d\) and \(n_\gamma ={{\,\mathrm{nrd}\,}}(\gamma )=ad-bc \pi ^e\). We observe that \(\phi \) is optimal if and only if at least one of \(b,c,a-d \in R^\times \): indeed, there exists \(z \in R\) such that \((\gamma -z)/\pi \in \mathcal {O}\) if and only if all belong to \(\mathfrak p \).
Suppose now that \(\phi \) is optimal. We have three cases.
If \(b \in R^\times \), then take \(\nu =\begin{pmatrix} 1 &{} 0 \\ 0 &{} b^{-1} \end{pmatrix} \in \mathcal {O}^\times \); we compute
and
as desired.
If \(c \in R^\times \), then we take \(\nu =\varpi =\begin{pmatrix} 0 &{} 1 \\ \pi ^e &{} 0 \end{pmatrix}\); now
and we apply the previous case.
Finally, if \(a-d \in R^\times \), we may suppose \(b \in \mathfrak p \) as well as \(c \in \mathfrak p \) if \(e=0\), and then we take \(\nu =\begin{pmatrix} 1 &{} 1 \\ 0 &{} 1 \end{pmatrix}\) to find
to reduce again to the first case.\(\square \)
Definition 30.6.8
An optimal embedding \(\phi \in {{\,\mathrm{Emb}\,}}(S,\mathcal {O})\) is normalized and associated to \(x \in R\) if
(as in (30.6.4)).
The statement of Lemma 30.6.3 is that for all \(\phi \in {{\,\mathrm{Emb}\,}}(S,\mathcal {O})\), either the class of \(\phi \) or of \(\phi ^\varpi \) in \({{\,\mathrm{Emb}\,}}(S,\mathcal {O};\mathcal {O}^\times )\) is represented by a normalized embedding. To conclude our efforts, we need to check which of these are equivalent. We recall that \(d_\gamma = t_\gamma ^2-4n_\gamma \).
Lemma 30.6.9
Let \(\phi ,\phi '\) be normalized embeddings associated to \(x,x' \in R\). Then the following statements hold.
-
(a)
\(\phi ,\phi '\) are conjugate by \(\mathcal {O}^\times \) if and only if \(x \equiv x' ~(\text{ mod } ~\mathfrak{p ^e})\).
-
(b)
If \(d_\gamma \in R^\times \) or \(e=0\), then \(\phi ^\varpi \) is equivalent to \(\phi '\) in \({{\,\mathrm{Emb}\,}}(S,\mathcal {O};\mathcal {O}^\times )\) if and only if \(x' \equiv t_\gamma -x ~(\text{ mod } ~\mathfrak{p ^e})\).
-
(c)
If \(d_\gamma \not \in R^\times \) and \(e \ge 1\), then \(\phi ^\varpi \) is equivalent to \(\phi '\) in \({{\,\mathrm{Emb}\,}}(S,\mathcal {O};\mathcal {O}^\times )\) if and only if \(x' \equiv t_\gamma -x ~(\text{ mod } ~\mathfrak{p ^e})\) and \(f_\gamma (x) \not \equiv 0 ~(\text{ mod } ~\mathfrak{p ^{e+1}})\).
Proof First (a). If \(\phi ,\phi '\) are conjugate by some \(\mu \in \mathcal {O}^\times \), we reduce modulo \(\mathfrak p ^e{{\,\mathrm{M}\,}}_2(R)\) to obtain the ring of upper triangular matrices, and see that the diagonal entries of \(\phi (\gamma ),\phi '(\gamma )\) are congruent modulo \(\mathfrak p ^e\) and in particular \(x \equiv x' \pmod \mathfrak{p ^e}\). Conversely, if \(x \equiv x' ~(\text{ mod } ~\mathfrak{p ^e})\), then let \(\mu =\begin{pmatrix} 1 &{} 0 \\ x'-x &{} 1 \end{pmatrix}\); we confirm that
In preparation for (b) and (c), we note that
We now prove (b). If \(e=0\), the statement is true: \(\varpi \in \mathcal {O}^\times \) and all embeddings are conjugate. Suppose \(e \ge 1\). Since \(f_\gamma (x) \equiv 0 ~(\text{ mod } ~\mathfrak{p ^e})\) we have
so \(t_\gamma -2x \in R^\times \). For \(u \in R\), let \(\mu = \begin{pmatrix} 1 &{} u \\ 0 &{} 1 \end{pmatrix}\) and consider
Thus we may choose u so that the top-right entry of (30.6.11) is equal to 1. The result then follows from (a).
We conclude with (c), and we are given \(e \ge 1\) and \(d_\gamma \not \in R^\times \). If \(\pi ^{-e}f_\gamma (x) \in R^\times \) then from (30.6.10) and looking back at (30.6.5), already \(\phi ^\varpi \) is conjugate under \(\mathcal {O}^\times \) to the normalized embedding associated to \(t_\gamma -x\), so by (a), we then have \(\phi ^\varpi \) equivalent to \(\phi '\) if (and only if) \(x \equiv t-x ~(\text{ mod } ~\mathfrak{p ^e})\). To finish, suppose \(f_\gamma (x) \in \mathfrak p ^{e+1}\) and \(d \in \mathfrak p \). Reducing modulo \(\mathfrak p ^e {{\,\mathrm{M}\,}}_2(R)\), the ring \(\mathcal {O}/(\mathfrak p ^e {{\,\mathrm{M}\,}}_2(R))\) consists of upper-triangular matrices and its unit group is generated by diagonal matrices and units \(\mu \) as in the previous paragraph. But then by (30.6.11), the top-right entry of every \(\mathcal {O}^\times \)-conjugate of \(\phi ^\varpi (\gamma )\) belongs to \(\mathfrak p \), and so it cannot be equal to \(\phi '(\gamma )\).\(\square \)
The statements above give a way to compute the local embedding number in terms of arithmetic of R.
Proposition 30.6.12
For \(s \in \mathbb Z _{\ge 1}\), let
Then for \(e \ge 1\),
Proof By Lemma 30.6.3, the set \({{\,\mathrm{Emb}\,}}(S,\mathcal {O};\mathcal {O}^\times )\) is represented by the set of normalized embeddings and their conjugates under \(\varpi \). By Lemma 30.6.9(a), the normalized embeddings according to \(x \in M(s)\) are distinct; by (b)–(c), the remaining conjugate embeddings are new when they lift to \(M(e+1)\).\(\square \)
Example 30.6.14
Let \(R=\mathbb Z _2\) and \(S=\mathbb Z _2[\sqrt{-1}]\), so \(\gamma =\sqrt{-1}\) and \(f_\gamma (x)=x^2+1\). We have
Therefore by Proposition 30.6.12, if \(\mathcal {O}\) is an Eichler order of level \(2^e\) over \(\mathbb Z _2\), then
We record an important special case.
Lemma 30.6.16
If \(e=1\) and S is a maximal R-order in K (equivalently, S is integrally closed in K), then
Proof Referring to Proposition 30.6.12, we first compute \(\#M(1)\), the number of solutions to \(f_\gamma (x) \equiv 0 ~(\text{ mod } ~\mathfrak{p })\), so over the finite field \(k=R/\mathfrak p \): this number is 2, 1, 0 according as 
. If \(d \in R^\times \), we are done; so suppose \(d \not \in R^\times \), hence 
. Let \(x \in M(2)\). We claim that \((\gamma -x)/\pi \) is integral over R, contradicting that S is maximal. Indeed, \(\pi ^2 \mid f_\gamma (x)=x^2-t_\gamma x+n_\gamma ={{\,\mathrm{nrd}\,}}(\gamma -x)\); and 
, so 
. Thus \(M(2)=\emptyset \) and so the count remains the same.\(\square \)
To conclude, when \(q=\#k\) is odd, we can make Proposition 30.6.12 completely explicit.
Lemma 30.6.17
Suppose \(\#k=q\) is odd, that \(e \ge 1\), and let 
.
-
(a)
If \(f=0\), then
-
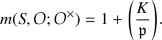
(b)
If \(e < f\), then
$$ m(S,\mathcal {O};\mathcal {O}^\times ) = {\left\{ \begin{array}{ll} 2q^{(e-1)/2}, &{} \text { if }e\text { is odd;} \\ q^{e/2-1}(q+1), &{} \text { if }e\text { is even.} \\ \end{array}\right. } $$ -
(c)
If \(e= f\), then
-
(d)
If \(e> f > 0\), then
Proof Since the residue field k has odd characteristic, we can complete the square and without loss of generality we may suppose that \({{\,\mathrm{trd}\,}}(\gamma )=0\), and
We will abbreviate \(m=m(S,\mathcal {O};\mathcal {O}^\times )\) and repeatedly refer to Proposition 30.6.12.
First suppose \(f=0\). Then \(d_\gamma \in R^\times \), so by Proposition 30.6.12, we have \(m=\#M(e)\). But by Hensel’s lemma, \(\#M(e)=0\) or 2 according as d is a square or not in R for all \(e \ge 1\).
Next suppose that \(e<f\). The solutions to the equation 
are those with 
. Thus \(\#M(e)=q^{e-\lceil e/2 \rceil } = q^{\lfloor e/2 \rfloor }\) and we see that 
, so \(m=2q^{(e-1)/2}\) if e is odd and \(m=q^{e/2}+q^{e/2-1}=q^{e/2-1}(q+1)\) if e is even.
If \(e=f\), then again \(\#M(e)=q^{\lfloor e/2 \rfloor }\). To count the second contributing set, we must solve 
. If \(e=f\) is odd then this congruence has no solution. If instead e is even then we must solve 
where \(\pi \) is a uniformizer at 
. This latter congruence has zero or two solutions according as d is a square, and given such a solution y we have the solutions \(x \equiv y \pmod {\pi ^{f/2+1}}\) to the original congruence, and hence there are 0 or \(2q^{f-(f/2+1)}=2q^{f/2-1}\) solutions, as claimed.
Finally, suppose \(e>f>0\). If f is odd, there are no solutions to 
. If f is even, there are no solutions if \(d_\gamma \) is not a square and otherwise the solutions are 
as above so they total \(2q^{f/2}+2q^{f/2-1}=2q^{f/2-1}(q+1)\).\(\square \)
On the other hand, when the residue field k has even characteristic, the computations become even more involved!
Remark 30.6.18. Eichler studied optimal embeddings [Eic38b, §2] very early on, computing the contribution of units (coming from embeddings of \(\mathbb Z [\omega ]\) and \(\mathbb Z [i]\) in a maximal order \(\mathcal {O}\)) in the mass formula. He then [Eic56a, §3] studied more generally optimal embeddings of quadratic orders into his Eichler orders of squarefree level. Hijikata [Hij74, §2] studied optimal embeddings in the context of computing traces of Hecke operators on \(\Gamma _0(N)\) (general N), with embedding numbers given for certain orders. See also Eichler’s treatment [Eic73, §3] in the context of the basis problem for modular forms, as well as Pizer’s presentation [Piz76a, §3]. (See Remark 41.5.13 for further detail.) Brzezinski [Brz91, Corollary 1.16] (a typo has it appear as Corollary 1.6) gives a general formula for Eichler orders (which is to say, a generalization of Lemma 30.6.17 to include q even)—the proof method is different than the method of Hijikata above, and the answer is organized a bit differently than Lemma 30.6.17.
But these papers are just the beginning, and there is a cornucopia of further results. Many of these are obtained in pursuit of progressively more general forms of the trace formula (see for example the summary of results by Hashimoto [Hash77]) for Eichler orders. Shimizu [Shz63, §§26–27] considered embedding numbers over totally real fields in computing the contribution of elliptic elements to formulas for the dimension of spaces of cusp forms and later for the trace formula [Shz65, §3]. The contributions of elliptic elements over totally real fields was also pursued by Prestel [Pre68, §5] and more generally for embeddings by Schneider [Schn75] (and quite explicitly for real quadratic fields [Schn77]) and Vignéras [Vig76a, §4].
Pizer [Piz76b, §§3–5] considered optimal embeddings for residually split orders (see 24.3.7) over \(\mathbb Q \): these were then applied to further cases of the basis problem for modular forms [Piz76c, Piz80b]. Then Hijikata–Pizer–Shemanske [HPS89b, §§1–5] developed in a uniform manner the optimal embedding theory for basic orders (they called them special, cf. Remark 24.5.7): the application to the trace formula is then contained in their monograph [HPS89a]. Brzezinski [Brz90, §3] also obtains recursive formulas for optimal embedding numbers of a local Bass (equivalently, basic) order (in characteristic not 2), using an effective description of the automorphism group of the order.
7 Global embedding numbers
We now combine the ingredients from the previous three sections to arrive at a formula for global embedding numbers.
We return to the setting of section 30.4, with R a global ring.
30.7.1
Our global ring \(R=R_{({{{\texttt {\textit{T}}}}})}\) comes from an eligible set \({{{\texttt {\textit{T}}}}}\subseteq {{\,\mathrm{Pl}\,}}F\). (This set is usually denoted \({{{\texttt {\textit{S}}}}}\), but we do not want any confusion with the quadratic R-algebra \(S \subseteq K\).)
For all but finitely many places \(v \not \in {{{\texttt {\textit{T}}}}}\), we have \(\mathcal {O}_v \simeq {{\,\mathrm{M}\,}}_2(R_v)\) maximal and \(\Gamma _v=\mathcal {O}_v^\times \). By Proposition 30.5.3(a), for such places v, we have \(\#{{\,\mathrm{Emb}\,}}_{R_v}(S_v,\mathcal {O}_v;\mathcal {O}_v^\times )=1\). Therefore the number \(m(\widehat{S},\widehat{\mathcal {O}};\widehat{\Gamma })=\#{{\,\mathrm{Emb}\,}}_{\widehat{R}}(\widehat{S},\widehat{\mathcal {O}};\widehat{\Gamma })\) of adelic embeddings is given by the (well-defined, finite) product
(well-defined and finite).
We arrive at the following first global result.
Theorem 30.7.3
Let \(\mathfrak N ={{\,\mathrm{discrd}\,}}(\mathcal {O})\). Then
Proof For all 
, we have 
, so the result follows by combining Theorem 30.4.7 with 30.7.1.\(\square \)
Working with the normalizer instead, we find the following result.
Proposition 30.7.4
Suppose that \(\mathcal {O}\) is a maximal order with \(\#{{\,\mathrm{Cls}\,}}\mathcal {O}=1\). Then
Proof As in the proof of Theorem 30.7.3, but with a further appeal to Proposition 30.5.3 to show that all local embeddings numbers are equal to 1.\(\square \)
An important illustrative special case is the following.
Example 30.7.5
Let \(\mathfrak D ={{\,\mathrm{disc}\,}}_R B\) and suppose that \(\mathcal {O}\subseteq B\) is an Eichler R-order of squarefree level \(\mathfrak M \), so \({{\,\mathrm{discrd}\,}}\mathcal {O}= \mathfrak D \mathfrak M \). Suppose further that S is a maximal R-order in K. Then Theorem 30.7.3 reads
with the local embedding numbers computed in Proposition 30.5.3(b) for 
and Lemma 30.6.16 for 
.
Suppose further that B is \({{{\texttt {\textit{T}}}}}\)-indefinite and that \(\#{{\,\mathrm{Cl}\,}}_\Omega R = 1\); then \(\#{{\,\mathrm{Cls}\,}}\mathcal {O}= \#{{\,\mathrm{Cl}\,}}_\Omega R\) by Corollary 28.5.17 (an application of strong approximation), so
Embeddings of cyclotomic orders are of particular interest.
Example 30.7.7
Consider the case \(F=\mathbb Q \) and \(R=\mathbb Z \). Let \(D={{\,\mathrm{disc}\,}}B\) and suppose that \(\mathcal {O}\) is an Eichler order of level M, so \(N=DM={{\,\mathrm{discrd}\,}}\mathcal {O}\). We recall D is squarefree and \(\gcd (D,M)=1\). Suppose B is indefinite. Then by Theorem 28.2.11 (an application of strong approximation), \(\#{{\,\mathrm{Cls}\,}}\mathcal {O}=1\).
If \(K \supseteq \mathbb Q \) is a cyclotomic quadratic extension, then either \(K=\mathbb Q (\omega )=\mathbb Q (\sqrt{-3})\) or \(K=\mathbb Q (i)=\mathbb Q (\sqrt{-4})\) with corresponding rings of integers \(\mathbb Z _K=\mathbb Z [\omega ]\) and \(\mathbb Z _K=\mathbb Z [i]\), each with \(h(\mathbb Z _K)=1\). With local embedding numbers computed in Lemma 30.6.17, Theorem 30.7.3 then gives
Similarly, using (30.6.15),
Absent further hypothesis, it is difficult to tease apart the term \(m(S,\mathcal {O};\mathcal {O}^\times )\) from the sum over left orders in Theorem 30.4.7. In the next chapter, we will show that the hypothesis that B is \({{{\texttt {\textit{T}}}}}\)-indefinite is almost enough.
8 Class number formula
In this section, we explain how the theory of optimal embeddings can be used to convert the mass formula into a class number formula, following Eichler.
Suppose throughout this section that B is \({{{\texttt {\textit{T}}}}}\)-definite. By Lemma 26.5.1, the group \(\mathcal {O}^\times /R^\times \) is finite; let \(w_\mathcal {O}=[\mathcal {O}^\times : R^\times ]\).
30.8.1
To a nontrivial cyclic subgroup of \(\mathcal {O}^\times /R^\times \), we associate the quadratic field K it generates over F; such a field is necessarily cyclotomic, with \(K \simeq F(\zeta _{2q})\) for q the order of the cyclic subgroup. (Only certain \(F(\zeta _{2q})\) arise as quadratic extensions of F, and different values of q can give rise to the same quadratic field up to isomorphism.)
Conversely, to a quadratic field \(K \supseteq F\), we obtain a (possibly trivial) cyclic subgroup \((K^\times \cap \mathcal {O}^\times )/R^\times \).
Lemma 30.8.2
Every nontrivial \(\alpha R^\times \in \mathcal {O}^\times /R^\times \) belongs to a unique maximal cyclic subgroup.
Proof Since \(\mathcal {O}^\times /R^\times \) is finite, \(\alpha \) belongs to at least one maximal cyclic subgroup; if it belonged to two, then the corresponding quadratic fields would both contain the field corresponding to \(\alpha \), hence by degrees would be equal, so by maximality the cyclic subgroups would have to be equal.\(\square \)
30.8.3
Recall that \(m(S,\mathcal {O};\mathcal {O}^\times )\) counts optimal embeddings \(\phi :S \hookrightarrow \mathcal {O}\) up to conjugation by \(\mathcal {O}^\times \). Since \(\mathcal {O}^\times /R^\times \) is finite, the set \({{\,\mathrm{Emb}\,}}(S,\mathcal {O})\) is itself finite. Precisely two embeddings give rise to the same image \(\phi (S)\), differing by the (necessarily nontrivial) standard involution. The stabilizer of \(\mathcal {O}^\times \) on \(\phi \in {{\,\mathrm{Emb}\,}}(S,\mathcal {O})\) is \(\mathcal {O}^\times \cap \phi (S) = \phi (S)^\times \simeq S^\times \). Let \(w_S=[S^\times :R^\times ]\). We have shown that
Proposition 30.8.5
We have
Proof We count off the group \(\mathcal {O}^\times /R^\times \) by maximal cyclic subgroups, keeping track of the trivial class. By Lemma 30.8.2, every nontrivial \(\alpha R^\times \in \mathcal {O}^\times /R^\times \) belongs to a unique maximal cyclic subgroup of some order \(q \ge 2\): such a subgroup is of the form \(\phi (S)^\times /R^\times \) with \(\phi (S) \subseteq \mathcal {O}\) an optimally embedded order, and has \(q-1\) nontrivial elements. Therefore
Plugging in (30.8.4), we obtain
dividing through by \(w_\mathcal {O}\) gives the result.\(\square \)
We now recall the Eichler mass formula (Main Theorem 26.1.5), giving an explicit formula for the weighted class number
where \(w_I=[\mathcal {O}{}_{\textsf {\tiny {L}} }(I)^\times :R^\times ]\).
MainTheorem 30.8.6
(Eichler class number formula). Let R be a global ring with eligible set \({{{\texttt {\textit{T}}}}}\), let B be an \({{{\texttt {\textit{T}}}}}\)-definite quaternion algebra over \(F={{\,\mathrm{Frac}\,}}R\), and let \(\mathcal {O}\subset B\) be an R-order. Then
where the inner sum is over all quadratic R-algebras \(S \supseteq R\) such that \([S^\times :R^\times ]=q \in \mathbb Z _{\ge 2}\), and \(h(S)=\#{{\,\mathrm{Pic}\,}}S\).
Proof We apply Proposition 30.8.5 to each order \(\mathcal {O}{}_{\textsf {\tiny {L}} }(I)\) for \([I] \in {{\,\mathrm{Cls}\,}}\mathcal {O}\) and sum. We obtain
the last equality by Theorem 30.4.7.\(\square \)
The expressions in the Eichler class number formula (Main Theorem 30.8.6) are arithmetically involved but can be computed effectively. In special cases, they give reasonably simple formulas, as previously advertised.
Example 30.8.7
When \(F=\mathbb Q \), Main Theorem 30.8.6 yields the formula given in Theorem 30.1.5, with the computation of local class numbers given in Example 30.7.7.
Remark 30.8.8. The formula for the class number for Eichler orders of squarefree level (i.e., hereditary orders) was given by Eichler [Eic56a, Satz 10–11]; for Eichler orders over \(\mathbb Q \) of arbitrary level (as in Example 30.8.7), it was given by Pizer [Piz76a, Theorem 16]. Main Theorem 30.8.6 is proven by Vignéras [Vig80a, Corollaire V.2.5] and Körner [Kör87, Theorem 2]. For further reference and discussion (in the context of computing local embedding numbers), see Remark 30.6.18.
30.8.9
Let \(K \supset F\) be a quadratic field extension, let \(R_K\) be the integral closure of R in K, and let \(S \subseteq K\) be an R-order of conductor \(\mathfrak f \). Then there is an exact sequence
giving rise to the formula of Dedekind
where 
is the absolute norm and 
is given (globally) as in 30.5.2:
9 Type number formula
We continue with the hypotheses of the previous section. A further application of the strategy to compute the class number is to also compute the type number. The methods are indeed quite similar: rearranging Corollary 18.5.12, we have
where \(z_{\mathcal {O}'} = [N_{B^\times }(\mathcal {O}') : F^\times \mathcal {O}'^\times ]\). But now the structure of the normalizer groups come into play, and one can give a type number formula similar to the class number formula 30.8.6 in terms of certain embedding numbers at least for Eichler orders. Unfortunately, even over \(\mathbb Q \), these formulas quickly get very complicated! To give a sense of what can be proven, in this section we provide a type number formula in a special but interesting case due originally to Deuring [Deu51], and we refer to Remark 30.9.12 for further reference.
Proposition 30.9.2
(Deuring). Let B be a definite quaternion algebra over \(\mathbb Q \) with \({{\,\mathrm{disc}\,}}B=p\) prime and let \(\mathcal {O}\subset B\) be a maximal order. Then \(\#{{\,\mathrm{Typ}\,}}\mathcal {O}=1\) for \(p=2,3\), and for \(p\ge 5\),
where \([h(-p)]=h(-p)\) when \(p \equiv 3 ~(\text{ mod } ~{4})\) and is 0 otherwise.
Proof In light of (30.9.1), we begin by considering the Picard group \({{\,\mathrm{Pic}\,}}\mathcal {O}\) (with \(R=\mathbb Z \)): by 18.4.8, we have an isomorphism \({{\,\mathrm{Pic}\,}}(\mathcal {O}) \simeq \mathbb Z /2\mathbb Z \) generated by the unique right ideal \(J \subseteq \mathcal {O}\) with \({{\,\mathrm{nrd}\,}}(J)=p\). The ideal J is automatically two-sided and contains all elements of reduced norm divisible by p (see 13.3.7); and thus J is principal if and only if there exists an element \(\alpha \in \mathcal {O}\) with \({{\,\mathrm{nrd}\,}}(\alpha )=p\) if and only if \(z_\mathcal {O}=2\).
Therefore, (30.9.1) reads
We now compute this sum in terms of embedding numbers. First, the map \(\alpha \mapsto \alpha \mathcal {O}\) gives
where \(w_\mathcal {O}= [\mathcal {O}^\times :\mathbb Z ^\times ]\).
Next, we claim that if \(\alpha \in \mathcal {O}\) has \({{\,\mathrm{nrd}\,}}(\alpha )=p\), then \({{\,\mathrm{trd}\,}}(\alpha )=0\), i.e., \(\alpha ^2+p=0\). Indeed, if \(t={{\,\mathrm{trd}\,}}(\alpha )\) then the field \(K=\mathbb Q (\alpha )\) has discriminant \(t^2-4p <0\) (since B is definite) so \(|t \,| < 2\sqrt{p}\). If \(t \ne 0\), then the polynomial \(x^2-tx+p\) splits modulo p, so p splits in K; but \(K_p \hookrightarrow B_p\) and \(B_p\) is a division algebra, so \(K_p\) is a field, a contradiction. Thus \(t=0\).
With these results in hand, we can bring in the theory of embedding numbers. We have
The group \(\mathcal {O}^\times /\{\pm 1\}\) acts by conjugation on \({{\,\mathrm{Emb}\,}}(S,\mathcal {O})\) without fixed points as in 30.8.3: since \(p \ne 2,3\), we have \(S^\times =\{\pm 1\}\). Thus
Combining (30.9.4), (30.9.5), and (30.9.6), and plugging into (30.9.3), we have
By (30.4.21) (rewriting Theorem 30.4.7), for \(S \supseteq \mathbb Z [\sqrt{-p}]\) we have
where \(h(\mathcal {O}')=[{{\,\mathrm{Idl}\,}}\mathcal {O}':{{\,\mathrm{PIdl}\,}}\mathcal {O}']\); but \(h(\mathcal {O}')=1\) whenever \(m(S,\mathcal {O}';\mathcal {O}'^\times ) \ne 0\) by the first paragraph, so we may substitute into (30.9.7) to get
The order \(\mathcal {O}\) is maximal, so the adelic embedding number is the product of local embedding numbers computed in Proposition 30.5.3: there is only a possible contribution at p, since \(p \ne 2\) the order S is maximal, and K is ramified so \(m(S_p,\mathcal {O}_p;\mathcal {O}_p^\times )=1\), thus \(m(\widehat{S},\widehat{\mathcal {O}};\widehat{\mathcal {O}}^\times )=1\).
Finally, the order \(\mathbb Z [\sqrt{-p}]\) of discriminant \(-4p\) is maximal whenever \(p \equiv 1 ~(\text{ mod } ~{4})\) and the sum becomes simply \(h(-4p)\); when \(p \equiv 3 ~(\text{ mod } ~{4})\), this order is contained in the maximal order of discriminant \(-p\), so the sum is \(h(-p)+h(-4p)\). The result is proven.\(\square \)
Remark 30.9.9. For an alternate direct proof of Proposition 30.9.2 working with elliptic curves, see Cox [Cox89, Theorem 14.18].
30.9.10
The sum of class numbers in Proposition 30.9.2 can be rewritten uniformly in terms of the ring of integers as follows:
When \(p \equiv 1 ~(\text{ mod } ~{4})\), there is nothing to do. For \(p \equiv 3 ~(\text{ mod } ~{4})\), we have
according as 2 is inert or split in \(K=\mathbb Q (\sqrt{-p})\).
Remark 30.9.11. In section 42.1–42.2, we relate quaternion algebras to supersingular elliptic curves; in this language, Proposition 30.9.2 gives rise to a formula for the number of supersingular elliptic curves defined over \(\mathbb F _p\) up to isomorphism.
Remark 30.9.12. Eichler [Eic56a, Satz 11] gave a type number formula for definite hereditary orders over a totally real field; this formula has an error which was corrected by Peters [Pet69, Satz 14, Satz 15] over fields of class number one and by Pizer [Piz73, Theorem A] in general. Pizer [Piz76a, Theorem 26] gives a formula for the type number for (general) Eichler orders over \(\mathbb Q \). Finally, Vignéras [Vig80a, Corollaire V.2.6] gives a “structural” type number formula (without explicit evaluation of the sum) for Eichler orders, and Körner [Kör87, Theorem 3] gives a general type number formula. For a generalization to totally definite orders in central simple algebras of prime index over global fields, see Brzezinski [Brz97].
Exercises
- 1.:
-
As in section 30.1, for \(k \ge 1\) let
$$\begin{aligned} r_k(n) :=\#\{(x_1,x_2,\dots ,x_k) \in \mathbb Z ^k : x_1^2+x_2^2+\dots +x_k^2=n\}. \end{aligned}$$We gave formulas for \(r_3(n),r_4(n)\). For completeness, observe that \(r_1(n)=2,0\) according as n is a square or not, and give a formula for \(r_2(n)\) in terms of the factorization of n in the ring \(\mathbb Z [i]\).
- \(\triangleright \) 2.:
-
Let B be a quaternion algebra over \(\mathbb Q \), let \(\mathcal {O}\subset B\) be an order, let K be a quadratic field with an embedding \(K \hookrightarrow B\) and suppose \(S = K \cap \mathcal {O}\) is the ring of integers of K.
- (a):
-
Let \(\mathfrak b \subset K\) be an invertible fractional S-ideal. Show that \(\mathfrak b \mathcal {O}\cap K = \mathfrak b \). [Hint: since \(1 \in \mathcal {O}\), we have \(\mathfrak b \mathcal {O}\cap K \supseteq \mathfrak b \). For the other inclusion, consider
$$\begin{aligned} (\mathfrak b \mathcal {O}\cap K)\cdot \mathfrak b ^{-1}\mathfrak b \subseteq (\mathfrak b \mathfrak b ^{-1}\mathcal {O}\cap K)\cdot \mathfrak b = \mathfrak b .{] } \end{aligned}$$ - (b):
-
Rewrite the proof in (a) idelically.
- \(\triangleright \) 3.:
-
Let \(n \equiv 1,2 ~(\text{ mod } ~{4})\).
- (a):
-
Let p be an odd prime, and let \(\alpha ,\alpha ' \in {{\,\mathrm{M}\,}}_2(\mathbb Z _p)\) satisfy \(\alpha ^2+n=0\). Show that there exists \(\mu \in {{\,\mathrm{GL}\,}}_2(\mathbb Z _p)\) such that \(\alpha '=\mu ^{-1}\alpha \mu \).
- (b):
-
Let
and \(\mathcal {O}_2\) its valuation ring. Show that if \(\alpha ,\alpha '\) satisfy the same reduced characteristic polynomial, then there exists \(\nu \in N_{B_2^\times }(\mathcal {O}_2)\) such that \(\alpha '=\nu ^{-1}\alpha \nu \). [Hint: \(N_{B_2^\times }(\mathcal {O}_2)=B_2^\times \).] - (c):
-
Put together (a) and (b) to conclude (30.2.4).
- 4.:
-
Deduce the theorem of Gauss (Theorem 30.1.3) from Theorem 30.4.7.
- 5.:
-
Let \(m,n \in \mathbb Z _{>0}\) be odd, coprime, with \(m<2\sqrt{n}\). Show that there are \(12h(m^2-4n)\) solutions to the equations
$$\begin{aligned} a^2+b^2+c^2+d^2&= n \\ a+b+c+d&= m \end{aligned}$$with \(a,b,c,d \in \mathbb Z \). [Hint: consider the unit \((1-i-j-k)/2\) of the Hurwitz order.]
- 6.:
-
Specialize Theorem 30.1.5 to the case \(D=p\) and \(N=1\), as follows. Let B be a definite quaternion algebra over \(\mathbb Q \) of discriminant \(D=p\) prime and let \(\mathcal {O}\subset B\) be a maximal order (Eichler order of level \(M=1\)). Show that
$$ \#{{\,\mathrm{Cls}\,}}\mathcal {O}= {\left\{ \begin{array}{ll} 1, &{} \text { if }p=2,3\text {;} \\ (p-1)/12, &{} \text { if }p \equiv 1 ~(\text{ mod } ~{12})\text {;} \\ (p+7)/12, &{} \text { if }p \equiv 5 ~(\text{ mod } ~{12})\text {;} \\ (p+5)/12, &{} \text { if }p \equiv 7 ~(\text{ mod } ~{12})\text {; and} \\ (p+13)/12, &{} \text { if }p \equiv 11 ~(\text{ mod } ~{12})\text {.} \end{array}\right. } $$ - 7.:
-
Let R be local and \(\mathcal {O}\) be an Eichler R-order of level
(so \(\mathcal {O}\) is hereditary, but not maximal). Let K be a quadratic F-algebra and \(S \subseteq K\) an R-order. Show that \(m(S,\mathcal {O};\mathcal {O}^\times )=\emptyset \) if and only if S is maximal and 
. - 8.:
-
Let B be an indefinite quaternion algebra over \(\mathbb Q \) of discriminant D and let \(\mathcal {O}\subseteq B\) be an Eichler order. Let \(S \subseteq K\) be a quadratic order of discriminant \(d_S = df^2\), where d is a fundamental discriminant.
- (a):
-
Suppose \(\mathcal {O}\) is maximal. Show that there exists an optimal embedding \(S \hookrightarrow \mathcal {O}\) if and only if for all \(p \mid D\), we have \(({K} \mid {p}) \ne 1\) and \(p \not \mid f\).
- (b):
-
Suppose \(\mathcal {O}\) is Eichler of level M and (for simplicity) that \(N :=DM\) is odd. Show that there exists an optimal embedding \(S \hookrightarrow \mathcal {O}\) if and only if the following conditions hold:
\(\bullet \) For all \(p \mid D\), we have \(({K} \mid {p}) \ne 1\).
\(\bullet \) For all \(p^e \parallel M\), either \(({K} \mid {p})=1\) or \(p^e \mid d_S\).
[Hint: recall that \(\#{{\,\mathrm{Typ}\,}}\mathcal {O}=1\).]
[It is possible to extend this to all N by analyzing local embeddings at \(p=2\) working over \(\mathbb Q _2\).]
- 9.:
-
Let \(F=\mathbb Q (\sqrt{d})\) be a real quadratic field of discriminant \(d>0\). Show that there exists \(q \ne 2,3\) such that \([F(\zeta _{2q}):F]=2\) if and only if \(d=5,8,12\).
- 10.:
-
Let R be a global ring with field of fractions F, let B be a quaternion algebra over F, and let \(\mathcal {O},\mathcal {O}' \subseteq B\) be maximal R-orders. Let \(K \subseteq B\) be a quadratic F-algebra in B, and suppose that \(K \cap \mathcal {O}= K \cap \mathcal {O}'\); let S be this common, optimally embedded quadratic R-order. Show that there exists an invertible fractional S-ideal \(\mathfrak a \subseteq K\) such that \(\mathcal {O}\mathfrak a = \mathfrak a \mathcal {O}'\). [Hint: the statement is local, so put the Eichler order \(\mathcal {O}\cap \mathcal {O}'\) and generator \(\gamma \in S\) in standard form; show that there exists
and 
such that 
generates the normalizer.] - 11.:
-
In this exercise, we prove a local-global principle for optimal embeddings in a self-contained manner. [For a much more precise result, read on to Chapter 31!]
Let F be a number field with ring of integers R. Let B be a quaternion algebra over F and let \(\mathcal {O}\subseteq B\) be an R-order. Let K be a quadratic F-algebra and let \(S \subseteq K\) be an R-order. Suppose that \(K \hookrightarrow B\); equivalently, by the local-global principle for embeddings (Proposition 14.6.7), every place \(v \in {{\,\mathrm{Pl}\,}}F\) does not split in K.
- (a):
-
Suppose that for all primes
of R, there exists an optimal embedding 
. Show that there exists an order \(\mathcal {O}' \in {{\,\mathrm{Gen}\,}}(\mathcal {O})\) (so \(\mathcal {O}'\) is locally isomorphic to \(\mathcal {O}\)) and an optimal embedding \(\phi :S \hookrightarrow \mathcal {O}'\). [Hint: choose a maximal order containing S and apply finitely many local corrections.] - (b):
-
Now suppose that \(\#{{\,\mathrm{Cl}\,}}_{G(\mathcal {O})} R=1\). Show that there exists an optimal embedding \(\phi :S \hookrightarrow \mathcal {O}\).
- (c):
-
Show that parts (a) and (b) follow from the trace formula (Theorem 30.4.7).
- 12.:
-
Give a direct proof of Corollary 30.4.23.
and 
(so 
.
and 
such that 
generates the normalizer.]
of R, there exists an optimal embedding 
. Show that there exists an order Author information
Authors and Affiliations
Corresponding author
Rights and permissions
This chapter is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, duplication, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, a link is provided to the Creative Commons license and any changes made are indicated.The images or other third party material in this chapter are included in the work's Creative Commons license, unless indicated otherwise in the credit line; if such material is not included in the work's Creative Commons license and the respective action is not permitted by statutory regulation, users will need to obtain permission from the license holder to duplicate, adapt or reproduce the material.
Copyright information
© 2021 The Author(s)
About this chapter
Cite this chapter
Voight, J. (2021). Optimal embeddings. In: Quaternion Algebras. Graduate Texts in Mathematics, vol 288. Springer, Cham. https://doi.org/10.1007/978-3-030-56694-4_30
Download citation
DOI: https://doi.org/10.1007/978-3-030-56694-4_30
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-56692-0
Online ISBN: 978-3-030-56694-4
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)