Abstract
We have already seen that the local-global dictionary is a powerful tool in understanding the arithmetic of quaternion algebras. In this section, we formalize this connection by consideration of adeles and ideles.
You have full access to this open access chapter, Download chapter PDF
We have already seen that the local-global dictionary is a powerful tool in understanding the arithmetic of quaternion algebras. In this section, we formalize this connection by consideration of adeles and ideles.
The basic idea: we want to consider all of the completions of a global field at once. There are at least two benefits to this approach:
- \(\bullet \):
-
We will gain notational efficiency, resulting in brief and well-behaved proofs that would be difficult or impossible to state clearly in classical language.
- \(\bullet \):
-
Each completion is a locally compact field and so amenable to harmonic analysis, and by extension to the adele ring and its group of units, we can do harmonic analysis on global objects.
The adelic framework, and its use in class field theory, is a vast topic whose complete development deserves its own book. We do our best in this chapter to develop this notation and state what is needed for the case of quaternion algebras. For further background reading, see Childress [Chi2009] and the references given at the start of section 27.4
1 \(\triangleright \) The rational adele ring
In this first section, we work purely over \(\mathbb Q \) to give a concrete flavor to the abstract definitions to come.
27.1.1
Recall in section 12.1 that for a prime p we defined \(\mathbb Z _p=\varprojlim _r \mathbb Z /p^r \mathbb Z \) as a projective limit, and each \(\mathbb Z _p\) is compact. We can package these together to make the direct product ring
equipped with the product topology: as a profinite group, it is Hausdorff, compact, and totally disconnected.
We can see \(\widehat{\mathbb{Z }}\) itself as projective limit as follows. By the Sun Zi theorem (CRT) theorem, we have an isomorphism
of topological rings, with the projective limit indexed by positive integers partially ordered under divisibility; so under this isomorphism, we may identify
The natural ring homomorphism \(\mathbb Z \rightarrow \widehat{\mathbb{Z }}\) which takes every element to its reduction modulo n is injective; the image of \(\mathbb Z \) is discrete and dense in \(\widehat{\mathbb{Z }}\) again by the CRT. One warning is due: \(\widehat{\mathbb{Z }}\) is not a domain.
27.1.4
We now make the ring \(\widehat{\mathbb{Z }}\) a bit bigger so that it contains \(\mathbb Q \) as a subring. If we were to take the ring \(\prod _p \mathbb Q _p\), a product of locally compact rings, unfortunately we would no longer have something that is locally compact (see Exercise 27.1): the product \(\prod _p \mathbb Q _p\) is much too big, allowing denominators in every component, whereas the image of \(\mathbb Q \) will only have denominators in finitely many positions. We should also keep track of archimedean information at the same time.
With these in mind we define, for each finite set \({{{\texttt {\textit{S}}}}}\) of primes, the ring
equipped with the product topology, so that \(U_{{{{\texttt {\textit{S}}}}}}\) is locally compact. For example,
To assemble these rings together, allowing more denominators and arbitrarily large sets S, we take the injective limit of \(U_{{{{\texttt {\textit{S}}}}}}\) under the natural directed system \(U_{{{{\texttt {\textit{S}}}}}} \hookrightarrow U_{{{{\texttt {\textit{S}}}}}'}\) for \({{{\texttt {\textit{S}}}}}\subseteq {{{\texttt {\textit{S}}}}}'\). The resulting object is the restricted direct product of \(\mathbb Q _p\) relative to \(\mathbb Z _p\) and is called the adele ring \(\underline{\mathbb{Q }}\) of \(\mathbb Q \):

We declare the sets \(U_{{{{\texttt {\textit{S}}}}}} \subseteq \underline{\mathbb{Q }}\) with the product topology to be open in \(\underline{\mathbb{Q }}\); and with this basis of open neighborhoods of 0 (open in \(U_{{{{\texttt {\textit{S}}}}}}\) for some \({{{\texttt {\textit{S}}}}}\)), we have given \(\underline{\mathbb{Q }}\) the structure of a topological ring. The sets \(U_{{{{\texttt {\textit{S}}}}}} \subseteq \underline{\mathbb{Q }}\) are also closed. Note that the topology on \(\underline{\mathbb{Q }}\subset \prod _v \mathbb Q _v\) is not the subspace topology.
27.1.8
For a finite set \({{{\texttt {\textit{S}}}}}\), we write

for the projection of \(\underline{\mathbb{Q }}\) onto the factors away from \({{{\texttt {\textit{S}}}}}\). We also write
We embed each of these into \(\underline{\mathbb{Q }}\) extending by zero and identify them with their images, so that  .
.
Remark 27.1.11. Our notation \(\underline{\mathbb{Q }}\) for the adele ring returns to the notation of Weil [Weil82] but is not standard; more typically, the adele ring is denoted \(\mathbb A \) (which we find markedly problematic).
Remark 27.1.12. Although  and \(\mathbb Q _{{{{\texttt {\textit{S}}}}}}\) are rings and (via projection) are naturally quotient rings of \(\underline{\mathbb{Q }}\), they are not subrings because they do not contain 1. This subtlety should cause no confusion in what follows (especially because we will be focused on the multiplicative case and working with groups, where there is no issue extending by the multiplicative identity 1).
and \(\mathbb Q _{{{{\texttt {\textit{S}}}}}}\) are rings and (via projection) are naturally quotient rings of \(\underline{\mathbb{Q }}\), they are not subrings because they do not contain 1. This subtlety should cause no confusion in what follows (especially because we will be focused on the multiplicative case and working with groups, where there is no issue extending by the multiplicative identity 1).
We have a natural continuous embedding \(\mathbb Q \hookrightarrow \mathbb Q _v\) for all \(v \in {{\,\mathrm{Pl}\,}}\mathbb Q \), and this extends to a diagonal embedding \(\mathbb Q \hookrightarrow \underline{\mathbb{Q }}\).
Lemma 27.1.13
The diagonal embedding \(\mathbb Q \hookrightarrow \underline{\mathbb{Q }}\) is a continuous injective ring homomorphism and the image is closed and discrete as a subring of \(\underline{\mathbb{Q }}\).
Proof. The embedding is continuous because it is so in each component. Because \(\underline{\mathbb{Q }}\) is a topological group under addition, to prove the remaining part it is enough to find a neighborhood \(0 \in U \subseteq \underline{\mathbb{Q }}\) such that \(U \cap \mathbb Q = \{0\}\). We take
By definition, U is open in \(\underline{\mathbb{Q }}\) as it is open in \(U_{\emptyset }\) (for a reminder, see (27.1.6)). And if \(a \in U\cap \mathbb Q \), then \(a \in \mathbb Z _p\) for all p, so \(a \in \mathbb Z \), and \(|a \,|_\infty <1\), and thus \(a=0\). \(\square \)
Lemma 27.1.14
The image of \(\mathbb Q \hookrightarrow \underline{\mathbb{Q }}\) is cocompact, i.e., \(\underline{\mathbb{Q }}/\mathbb Q \) is compact.
Proof. Let \(W :=[0,1] \times \widehat{\mathbb{Z }}\). Then W is compact. By strong approximation—for a snapshot review, flip ahead to Theorem 28.1.9 and its corollary—we have \(\underline{\mathbb{Q }}=\mathbb Q + W\). Therefore the continuous quotient map \(\underline{\mathbb{Q }}\rightarrow \underline{\mathbb{Q }}/\mathbb Q \) restricted to W is surjective, so \(\underline{\mathbb{Q }}/\mathbb Q \) equal to the image of the compact set W is compact. (W is a fundamental set for the action of \(\mathbb Q \) on \(\underline{\mathbb{Q }}\): see Exercise 27.2.) \(\square \)
27.1.15
The proof of Lemma 27.1.14 shows that the natural map \(\mathbb R \times \widehat{\mathbb{Z }}\rightarrow \underline{\mathbb{Q }}/\mathbb Q \) is surjective; its kernel is \(\mathbb Z \) diagonally embedded, so we have an isomorphism
of topological groups. The resulting topological group \({{\,\mathrm{Sol}\,}}:=(\mathbb R \times \widehat{\mathbb{Z }})/\mathbb Z \) is called a solenoid: it is compact, Hausdorff, connected, but not path-connected (Exercise 27.5), which can be visualized as in Figure 27.1.16.
Very often, we will want to tease apart the nonarchimedean and archimedean parts of the adele ring \(\underline{\mathbb{Q }}\), and will write

so that extending by zero we have \(\underline{\mathbb{Q }}= \widehat{\mathbb{Q }}\times \mathbb R \).
2 \(\triangleright \) The rational idele group
Having dealt with the additive version in adeles, now we talk about the multiplicative version, ideles.
27.2.1
We define the rational idele group to be

That is to say, \(\underline{\mathbb{Q }}^\times \) is the restricted direct product of the spaces \(\mathbb Q _p^\times \) with respect to \(\mathbb Z _p^\times \). The topology is such that for \({{{\texttt {\textit{S}}}}}\) a finite set of primes, the set
is open and closed as a subgroup of \(\underline{\mathbb{Q }}^\times \).
Remark 27.2.3. Chevalley first used the name élément idéal for elements of \(\underline{\mathbb{Q }}^\times \), but at Hasse’s suggestion he abbreviated it to idèle; the name adèle was then shorthand for an “additive idele”. Anglifying, we drop the accents on these words.
27.2.4
The topology on \(\underline{\mathbb{Q }}^\times \) is not the subspace topology \(\underline{\mathbb{Q }}^\times \subset \underline{\mathbb{Q }}\), because inversion need not be continuous. Instead, we think of \(\underline{\mathbb{Q }}^\times \) as a subset of \(\underline{\mathbb{Q }}\times \underline{\mathbb{Q }}\) via the map \(x \mapsto (x,x^{-1})\), and then \(\underline{\mathbb{Q }}^\times \) inherits the structure of a topological group.
Lemma 27.2.5
The diagonal map \(\mathbb Q ^\times \hookrightarrow \underline{\mathbb{Q }}^\times \) is an injective continuous group homomorphism, and the image of \(\mathbb Q ^\times \) is closed and discrete.
Proof. Since \(\mathbb Q \) is closed and discrete in \(\underline{\mathbb{Q }}\) and \(\underline{\mathbb{Q }}^\times \subseteq \underline{\mathbb{Q }}\times \underline{\mathbb{Q }}\) has the subspace topology, so too is \(\mathbb Q ^\times \) closed and discrete. \(\square \)
27.2.6
We now give an explicit description of the quotient \(\underline{\mathbb{Q }}^\times /\mathbb Q ^\times \): we will see it is not compact.
There is a canonical isomorphism of topological groups
by p-adic valuation. Since \(\langle p \rangle =p^\mathbb{Z } \simeq \mathbb Z \), we have a topological group isomorphism
A direct sum appears because an element of the restricted direct product is a p-adic unit for all but finitely many p. We project \(\underline{\mathbb{Q }}^\times \) onto the product of the first and last factor, getting a continuous surjective map
Looking at \(r \in \mathbb Q ^\times \subseteq \underline{\mathbb{Q }}^\times \), if we write \(r=\epsilon \prod _p p^{n(p)}\), where \(\epsilon \in \{\pm 1\}\) and \(n(p)={{\,\mathrm{ord}\,}}_p(r)\), then \(r \mapsto (\epsilon ,(n(p))_p)\) in the projection. Therefore \(\mathbb Q ^\times \) is canonically identified with \(\{\pm 1 \} \times \bigoplus _p \mathbb Z \) in \(\underline{\mathbb{Q }}^\times \). So the projection map (27.2.8) restricts to an isomorphism on the diagonally embedded \(\mathbb Q ^\times \). Therefore
By the logarithm map, there is an isomorphism \(\mathbb R _{>0} \simeq \mathbb R \), so
and we have an isomorphism of topological groups
(This is not a solenoid!)
In a similar way, we see that \(\widehat{\mathbb{Q }}^\times \!/\mathbb Q _{>0}^\times \simeq \widehat{\mathbb{Z }}^\times \), where \(\mathbb Q _{>0}^\times = \{ x \in \mathbb Q : x > 0 \}\), and so \(\widehat{\mathbb{Q }}^\times \!/\mathbb Q ^\times \) is compact.
Remark 27.2.12. In 27.2.6 we used that \(\mathbb Z \) is a UFD and \(\mathbb Z ^\times =\{\pm 1\}\); for a general number field, we face problems associated with units and the class group of the field, and the relevant exact sequences will not split!
3 \(\triangleright \) Rational quaternionic adeles and ideles
In the remainder of this chapter, we generalize the above construction to the adele ring and idele group of a global field and then a quaternion algebra over a global field. For the reader on a brisk read, in this section we briefly consider the constructions for a quaternion algebra over \(\mathbb Q \).
Let B be a quaternion algebra over \(\mathbb Q \), and let \(\mathcal {O}\subset B\) be an order.
27.3.1
The adele ring of B is

the restricted direct product of the topological rings \(B_v\) with respect to \(\mathcal {O}_v\) for places v of \(\mathbb Q \); this definition is independent of the choice of order \(\mathcal {O}\), because any two orders are equal at all but finitely many places by the local-global dictionary for lattices (Theorem 9.4.9). We embed \(B \hookrightarrow \underline{B}\) diagonally: the image is discrete, closed, and cocompact since the same is true for \(\mathbb Q \hookrightarrow \underline{\mathbb{Q }}\) (Lemmas 27.1.13–27.1.14). We write

so extending by zero we may identify \(\underline{B}= \widehat{B}\times B_\infty \). We also define
The idele group of B is \(\underline{B}^\times :=\prod ^{\prime }_v\, B_v^\times \), the restricted direct product of the topological groups \(B_v^\times \) with respect to \(\mathcal {O}_v^\times \); we similarly define

Working adelically is notationally quite convenient, as the following lemma illustrates (Lemma 27.6.8 for \(F=\mathbb Q \)).
Lemma 27.3.6
The set of invertible right fractional \(\mathcal {O}\)-ideals is in bijection with \(\widehat{B}^\times /\widehat{\mathcal {O}}^\times \) via the map \(I \mapsto \widehat{\alpha }\widehat{\mathcal {O}}^\times \), where \(I_p = \alpha _p \mathcal {O}_p\) and \(\widehat{\alpha }= (\alpha _p)_p\); this map induces a bijection
The most fundamental result in this chapter is the following (see Main Theorem 27.6.14, taking \(F=\mathbb Q \)).
Theorem 27.3.7
Let B be a division quaternion algebra over \(\mathbb Q \). Then \(B^\times \le \underline{B}^\times \) is cocompact and the set \(B^\times \backslash \widehat{B}^\times / \widehat{\mathcal {O}}^\times \) is finite.
In particular, combining Lemma 27.3.6 and Theorem 27.3.7, we conclude that the class set of \(\mathcal {O}\) is finite, something we proved earlier using the geometry of numbers for B definite in section 17.5.
4 Adeles and ideles
In pursuit of more generality, we now repeat the constructions of adeles and ideles over a global field. For further reference, see e.g. Cassels [Cas2010], Goldstein [Gol71], Knapp [Kna2016, Chapter VI], Lang [Lang94, Chapter VII], Neukirch [Neu99, Chapter VI], or Ramakrishnan–Valenza [RM99, Chapter 5].
Throughout the rest of this chapter, let F be a global field.
27.4.1
We recall notation from section 14.4 for convenience. The set of places of F is denoted \({{\,\mathrm{Pl}\,}}F\). For a place v of F, we denote by \(F_v\) the completion of F at the place v, with preferred (normalized) absolute value \(|\,|_v\) so that the product formula holds in F: see 14.4.12. If v is nonarchimedean, we let
be the valuation ring of \(F_v\), where we write v also for the discrete valuation associated to the place v. If F is a number field, we will sometimes denote an archimedean place by writing \(v \mid \infty \), and for an archimedean place we just take \(R_v=F_v\). A set \({{{\texttt {\textit{S}}}}}\subseteq {{\,\mathrm{Pl}\,}}F\) of places is eligible if it is finite, nonempty, and contains all archimedean places.
27.4.3
The adele ring of F is the restricted direct product of \(F_v\) with respect to \(R_v\):

with the restricted direct product topology. The topology is uniquely characterized (as a topological ring) by the condition that \(\underline{R} :=\prod _v R_v\) (with the product topology) is open. Accordingly, a subset \(U \subseteq \underline{F}\) is open if and only if for all \(\underline{a} \in \underline{F}\), the set \((\underline{a}+U)\cap \prod _v R_v\) is open in the product topology.
Giving F the discrete topology, we have an isomorphism of topological rings \(\underline{\mathbb{Q }}\otimes _\mathbb Q F \xrightarrow {\smash {{\sim }}}\underline{F}\): see Exercise 27.14.
27.4.5
We embed \(F \subseteq \underline{F}\) under the product of the embeddings \(F \hookrightarrow F_v\), i.e., by \(x \mapsto (x)_v\); this map is well-defined because \(|x \,|_v \le 1\) for all but finitely many places v of F. The image of F in \(\underline{F}\) has the discrete topology and is closed in \(\underline{F}\); the quotient \(\underline{F}/F\) is compact (i.e., F is cocompact in \(\underline{F}\)): for \(\underline{x} \in \underline{F}\), find \(a \in F\) such that \(x_v-a_v \in R_v\) for all v by the Sun Zi theorem (CRT).
27.4.6
Let \({{{\texttt {\textit{S}}}}}\subset {{\,\mathrm{Pl}\,}}F\) be an eligible set. We will write

and extending by zero we identify these sets with their images in \(\underline{F}\), so that  ; we call
; we call  the \({{{\texttt {\textit{S}}}}}\)-finite adele ring
of F.
the \({{{\texttt {\textit{S}}}}}\)-finite adele ring
of F.
We pass now to the multiplicative situation.
27.4.8
The idele group of F is the restricted direct product of \(F_v^\times \) with respect to \(R_v^\times \):

27.4.10
The topology on \(\underline{F}^\times \) (as a topological ring) is uniquely characterized by the condition that \(\prod _v R_v^\times \) (with the product topology) is open. Thus, \(U \subseteq \underline{F}^\times \) is open if and only if for all \(a \in \underline{F}^\times \), the set \(aU \cap \prod _v R_v^\times \) is open in the product topology.
Note that \(\underline{F}^\times \) does not have the topology induced from being a subspace of \(\underline{F}\), since inversion is not a continuous operation. In general, if A is a topological ring, \(A^\times \) becomes a topological group when \(A^\times \) is given the relative topology from
(See Exercise 27.13.)
Just as \(F \subseteq \underline{F}\) is discrete, \(F^\times \subseteq \underline{F}^\times \) is also discrete.
Definition 27.4.11
The group \(C_F :=\underline{F}^\times /F^\times \) is the idele class group of F.
The justification for calling this the idele class group is given in section 27.5.
27.4.12
As above, if \({{{\texttt {\textit{S}}}}}\subset {{\,\mathrm{Pl}\,}}F\) is an eligible set, we define the \({{{\texttt {\textit{S}}}}}\)-finite ideles

which is missing the product at the places in \({{{\texttt {\textit{S}}}}}\) (a finite product), namely
extending by 1, we identify these with their images in \(\underline{F}^\times \), so that  .
.
27.4.13
With respect to the normalized absolute values 14.4.12, we have a natural map

When F is a number field, the map (27.4.14) is surjective; when F is a function field with constant field \(\mathbb F _q\), the image is \(q^\mathbb{Z }\), the cyclic subgroup of \(\mathbb R _{>0}\) generated by q. Let

so that \(\underline{F}^{(1)}\) is the kernel of (27.4.14). Then \(F^\times \le \underline{F}^{(1)}\) by the product formula (14.4.6).
The following theorem is fundamental.
Theorem 27.4.16
The quotient \(\underline{F}^{(1)}/F^\times \) is compact, i.e., \(F^\times \) is cocompact in \(\underline{F}^{(1)}\).
Proof. We give a proof in a more general context in Main Theorem 27.6.14 below. Or see e.g. Cassels [Cas2010, §16, p. 69] for a direct proof. \(\square \)
Theorem 27.4.16 is equivalent (!) to the Dirichlet unit theorem and the finiteness of the class group in the number field case, and finite generation of the unit group of a coordinate ring of a curve and the finiteness of the group of rational divisors of degree zero in the function field case [Cas2010, §§17–18].
Via the projection map  , we have \(F^\times \) cocompact also in
, we have \(F^\times \) cocompact also in  .
.
5 Class field theory
Let \(F{}^{sep }\) be a separable closure of F. In this chapter, we summarize the idelic approach to class field theory; unfortunately, we must omit most proofs, as a full treatment would require a lengthy development—but the reader who is willing to accept the statements should be able to digest what follows and will hopefully be motivated to dig deeper! For further reading, see Tate [Tate2010], Lang [Lang94, Chapters XI-XI], Neukirch [Neu99, Chapters IV–VI], or Janusz [Jan96, Chapter V].
27.5.1
Let \(R=R_{({{{\texttt {\textit{S}}}}})}\) be a global ring (the ring of \({{{\texttt {\textit{S}}}}}\)-integers) for the eligible set \({{{\texttt {\textit{S}}}}}\subseteq {{\,\mathrm{Pl}\,}}F\). Then R is a Dedekind domain with field of fractions F. The class group of R admits an idelic description, embodying the definitions above, as follows.
To simplify notation, throughout we abbreviate \(\underline{F}_{\not {S}} = \widehat{F}\), as we take the set \({{{\texttt {\textit{S}}}}}\) to be fixed. To an invertible fractional ideal \(\mathfrak a \subseteq F\) of R, we have \(\mathfrak a _\mathfrak p =R_\mathfrak p \) for all but finitely many primes \(\mathfrak p \), so we can consider its idelic image \((\mathfrak a _\mathfrak p )_\mathfrak{p } \subseteq \widehat{F}\) under the product of completions. Since \(\mathfrak a \) is locally principal, we can write each \(\mathfrak a _\mathfrak p =a_\mathfrak p R_\mathfrak p \) with \(a_\mathfrak p \in F_\mathfrak p ^\times \), well-defined up to an element of \(R_\mathfrak p ^\times \); putting these together we obtain an element
and
We recover \(\mathfrak a = \widehat{\mathfrak{a }}\cap F\) from Lemmas 9.4.6 and 9.5.3. Therefore the group of invertible fractional ideals of R is canonically isomorphic to the quotient
The principal (invertible) fractional ideals correspond to the image of \(F^\times \) in \(\widehat{F}^\times \). Therefore there is a canonical isomorphism
27.5.4
Suppose F is a number field. If \({{{\texttt {\textit{S}}}}}\) consists of the set of archimedean places, then \(R=\mathbb Z _F\) is the ring of integers, and \({{\,\mathrm{Cl}\,}}R\) is the usual class group. For larger sets \({{{\texttt {\textit{S}}}}}\), we have a natural quotient map \({{\,\mathrm{Cl}\,}}\mathbb Z _F \rightarrow {{\,\mathrm{Cl}\,}}R\) obtained by the quotient by the classes of primes \(\mathfrak p \) corresponding to nonarchimedean places in \({{{\texttt {\textit{S}}}}}\).
More generally, one may restrict (27.5.3) to the subgroup of principal fractional ideals which have a totally positive generator; we then obtain the narrow (or strict) \({{{\texttt {\textit{S}}}}}\)-class group
In idelic class field theory, it is often convenient to move between quotients of the finite ideles and quotients of the full idele group as follows.
Lemma 27.5.6
Let \(F_\infty :=\prod _{v \mid \infty } F_v\) and let
Then the map
induces isomorphisms of topological groups
Proof. Composing with the projection to \(\underline{F}^\times /F^\times F_{\infty ,>0}^\times \), we see that the kernel is \(F_{>0}^\times \) and that the induced map is surjective; similarly for the quotient by \(F^\times F_\infty ^\times \). The few details are requested in Exercise 27.9. \(\square \)
Using Lemma 27.5.6, we have
27.5.9
Class field theory relates class groups to abelian extensions. For example, let
Then \(H \le C_F\) is an open subgroup of finite index, and the projection map
is an isomorphism, which together with (27.5.3) gives an isomorphism to \({{\,\mathrm{Cl}\,}}R\). So we are led to consider the finite-index open subgroups of \(C_F\).
The main theorem of idelic class field theory for finite extensions is as follows.
Theorem 27.5.10
There is a bijection
together with functorial isomorphisms \(C_F/H \xrightarrow {\smash {{\sim }}}{{\,\mathrm{Gal}\,}}(K\,|\,F)\).
The map \(C_F/H \xrightarrow {\smash {{\sim }}}{{\,\mathrm{Gal}\,}}(K\,|\,F)\) is called the Artin isomorphism for H, K.
Proof. See e.g. Tate [Tate2010, §5]. \(\square \)
27.5.12
Rewriting the main theorem (Theorem 27.5.10) slightly, we see that if \(H \le \widehat{F}^\times \) is an open finite-index subgroup containing \(F_{>0}^\times \), then there is a finite abelian extension \(K \supseteq F\) with the Artin isomorphism
27.5.13
Combining the surjections \(C_F \rightarrow {{\,\mathrm{Gal}\,}}(K\,|\,F)\), we obtain a continuous homomorphism
called the global Artin homomorphism, where \(F{}^{ab }\subseteq F{}^{sep }\) is the maximal abelian extension of F in \(F{}^{sep }\).
If F is a number field, then \(\theta \) is surjective; let \(D_F\) be the connected component of 1 in \(C_F\). Then \(D_F\) is a closed subgroup with
(see Exercise 27.10). We therefore have an isomorphism \(C_F/D_F \simeq {{\,\mathrm{Gal}\,}}(F{}^{ab }\,|\,F)\).
If F is a function field with finite constant field k, then \(\theta \) is injective, and \(\theta (C_F)\) is the dense subgroup of automorphisms \(\sigma \in {{\,\mathrm{Gal}\,}}(F{}^{ab }\,|\,F)\) whose restriction to \({{\,\mathrm{Gal}\,}}(k{}^{al }\,|\,k) \simeq \widehat{\mathbb{Z }}\) lies in \(\mathbb Z \), i.e., acts by an integer power of the Frobenius. See Tate [Tate2010, §5.4–5.7].
We conclude with a nice application to the classification of quaternion algebras.
Proposition 27.5.15
Let \(\Sigma \subseteq {{\,\mathrm{Pl}\,}}F\) be a finite subset of noncomplex places of F of even cardinality. Then there exists a quaternion algebra B over F with \({{\,\mathrm{Ram}\,}}B = \Sigma \).
Proof. Let \(K \supseteq F\) be a separable quadratic extension that is inert (an unramified field extension) at every \(v \in \Sigma \): such an extension exists by Exercise 14.21. By the main theorem of class field theory, we have \([C_F:F^\times {{\,\mathrm{Nm}\,}}_{K/F} C_K]=[K:F]=2\), where \(C_F=\underline{F}^\times /F^\times \) and similarly \(C_K\) are idele class groups. Therefore
as well.
For each \(v \in \Sigma \), let \(\pi _v\) be a uniformizer for \(R_v\) and if v is real let \(\pi _v=-1\). Since \(K_v \supseteq F_v\) is an unramified field extension, we have \(\pi _v \not \in {{\,\mathrm{Nm}\,}}_{K_v/F_v}(K_v^\times )\). For \(v \in \Sigma \), let \(\underline{\pi _v}=(1,\dots ,1,\pi _v,\dots ) \in \underline{F}^\times \). Then \(\underline{\pi _v} \not \in {{\,\mathrm{Nm}\,}}_{K/F}(\underline{K}^\times )\).
We claim that \(\underline{\pi _v} \not \in F^\times {{\,\mathrm{Nm}\,}}_{K/F}(\underline{K}^\times )\). Otherwise, there would exist \(a \in F^\times \) such that \(a\underline{\pi _v} \in {{\,\mathrm{Nm}\,}}_{K/F}(\underline{K}^\times )\), so \(a \in {{\,\mathrm{Nm}\,}}_{K_{w'}/F_{v'}}(K_{w'}^\times )\) for all \(w' \mid v'\) with \(v' \ne v\), and \(a \not \in {{\,\mathrm{Nm}\,}}_{K_v/F_v}(K_v^\times )\); but then a is a local norm at all but one real place, so by the Hasse norm theorem (Theorem 26.8.23), \(a \in {{\,\mathrm{Nm}\,}}_{K/F}(K^\times )\) is a global norm, but this contradicts that a is not a local norm at v.
Now let \(\underline{p}=\prod _{v \in \Sigma } \underline{\pi _v}\). Since \(\#\Sigma \) is even, by the previous paragraph and (27.5.16) we get
Consider the quaternion algebra \(\displaystyle {\biggl (\frac{K,b}{F}\biggr )}\). For all places \(v \in \Sigma \), we have \(K_v\) a field and \(b=\pi _v u_v^{-1} \not \in {{\,\mathrm{Nm}\,}}_{K_v/F_v}(K_v^\times )\), so \(v \in {{\,\mathrm{Ram}\,}}B\). At every other place \(v' \not \in \Sigma \), we have either that \(K_v\) is not a field or \(b=u_v^{-1} \in {{\,\mathrm{Nm}\,}}_{K_v/F_v}(K_v^\times )\), and in either case \(v' \not \in {{\,\mathrm{Ram}\,}}B\). \(\square \)
6 Noncommutative adeles
We retain notation from the previous section, in particular the abbreviations \(R=R_{({{{\texttt {\textit{S}}}}})}\) and \(\underline{F}_{\not {S}} = \widehat{F}\). Let B be a finite-dimensional simple algebra over the global field F. In this section, we extend idelic notions to B; the main case of interest is where B is a quaternion algebra over F. We recall the topology on \(B_v\) for places v, discussed in section 13.5. Let \(\mathcal {O}\subseteq B\) be an R-order.
27.6.1
The adele ring of B is the restricted direct product of the topological rings \(B_v\) with respect to \(\mathcal {O}_v\):

The topology on \(\underline{B}\) (as a topological ring) is uniquely characterized by the property that the subring \(\prod _v \mathcal {O}_v\) is open with the product topology.
By the local-global dictionary for lattices (Theorem 9.4.9), the definition of \(\underline{B}\) is independent of the choice of order \(\mathcal {O}\) and eligible set \({{{\texttt {\textit{S}}}}}\) (and base ring \(R=R_{({{{\texttt {\textit{S}}}}})}\)).
27.6.2
Just as in 27.4.5, we embed \(B \hookrightarrow \underline{B}\) diagonally. A basis for B as an F-vector space shows that \(\underline{B}\) is a free \(\underline{F}\)-module of finite rank. Then, since the image \(F \hookrightarrow \underline{F}\) is discrete, closed, and cocompact, arguing in each coordinate (with respect to the chosen basis), we conclude that \(B \hookrightarrow \underline{B}\) is discrete, closed, and cocompact. (Details are requested in Exercise 27.11.)
We now turn to the multiplicative structure, the main object of our concern.
27.6.3
The idele group of B is the restricted direct product of the topological groups \(B_v^\times \) with respect to \(\mathcal {O}_v^\times \):

equivalently, \(\underline{B}^\times \) is the unit group of \(\underline{B}\) with the topology as in 27.4.10. The topology on \(\underline{B}^\times \) as a topological group is characterized by the condition that the subgroup \(\prod _v \mathcal {O}_v^\times \) is open with the product topology. Again, \(\underline{B}^\times \) is independent of the choice of \(\mathcal {O}\) and eligible set \({{{\texttt {\textit{S}}}}}\) because any two such constructions differ at only finitely many places.
27.6.4
The \({{{\texttt {\textit{S}}}}}\)-finite adele ring is

extending by zero, we may identify  with its image in \(\underline{B}\). The \({{{\texttt {\textit{S}}}}}\)-finite adele ring has a compact open subring
with its image in \(\underline{B}\). The \({{{\texttt {\textit{S}}}}}\)-finite adele ring has a compact open subring

We similarly define the \({{{\texttt {\textit{S}}}}}\)-finite idele group with its compact open subgroup

When no confusion can result (\({{{\texttt {\textit{S}}}}}\) is clear from context), we will drop the superscript and replace with hats, writing simply  and
and  , etc.
, etc.
Just as in 27.5.1, the ideles provide a convenient way of encoding fractional ideals, as follows.
Lemma 27.6.8
The set of locally principal, right fractional \(\mathcal {O}\)-ideals is in bijection with \(\widehat{B}^\times \!/\widehat{\mathcal {O}}^\times \) via the map \(I \mapsto \widehat{\alpha }\widehat{\mathcal {O}}^\times \), where \(I_\mathfrak p =\alpha _\mathfrak p \mathcal {O}_\mathfrak p \) and \(\widehat{\alpha }= (\alpha _\mathfrak p )_\mathfrak p \); this map induces a bijection
Proof. Let I be a locally principal right fractional \(\mathcal {O}\)-ideal, so \(I_\mathfrak p =\alpha _\mathfrak p \mathcal {O}_\mathfrak p \) for all primes \(\mathfrak p \) of R, with \(\alpha _\mathfrak p \) well-defined up to right multiplication by an element of \(\mathcal {O}_\mathfrak p ^\times \), so to I we associate \((\alpha _\mathfrak p \mathcal {O}_\mathfrak p ^\times )_\mathfrak p = \widehat{\alpha }\widehat{\mathcal {O}}^\times \in \widehat{B}^\times \!/\widehat{\mathcal {O}}^\times \). Conversely, given \(\widehat{\alpha }\in \widehat{B}^\times \!/\widehat{\mathcal {O}}^\times \) we recover \(I = \widehat{\alpha }\widehat{\mathcal {O}}\cap B\) from Lemmas 9.4.6 and 9.5.3.
The equivalence relation defining the (right) class set is given by left multiplication by \(B^\times \), so the second statement follows. \(\square \)
Remark 27.6.10. We recall by Main Theorem 16.6.1 that for B a quaternion algebra, an R-lattice \(I \subset B\) is locally principal if and only if it is invertible.
27.6.11
In analogy with 27.4.13, we have a natural multiplicative map

and we define

By the product formula (14.4.6), we have \(B^\times \le \underline{B}^{(1)}\).
By comparison, we have also the groups
satisfying \(B^1 \le \underline{B}^1 \le \underline{B}^{(1)}\).
The following theorem is fundamental (see Fujisaki [Fuj58, Theorem 8.3], Weil [Weil82, Lemma 3.1.1]).
Main Theorem 27.6.14
(Fujisaki’s lemma). Let B be a finite-dimensional division algebra over a global field F. Then the following statements hold.
-
(a)
\(B^\times \le \underline{B}^{(1)}\) is cocompact.
-
(b)
For any eligible set \({{{\texttt {\textit{S}}}}}\), the subgroup
 is cocompact and the set \(B^\times \backslash \widehat{B}^\times \!/\widehat{\mathcal {O}}^\times \) is finite.
is cocompact and the set \(B^\times \backslash \widehat{B}^\times \!/\widehat{\mathcal {O}}^\times \) is finite.
Proof. The natural place to prove this result is after some more serious analysis has been done—but it is too important to wait for this. The small amount of input needed, which can be seen as an (ineffective) idelic version of the Minkowski convex body theorem (Theorem 17.5.5), is as follows. There exists a compact subset \(\underline{E}\) such that for all \(\underline{\beta }\in \underline{B}^{(1)}\),
For the proof of (27.6.15), see Exercise 29.11: in a nutshell, there is a measure \(\underline{\mu }\) on \(\underline{B}\) in which \(\underline{\mu }(B \backslash \underline{B}) < \infty \), and a compact \(\underline{E}\) with \(\underline{\mu }(\underline{E})\) satisfies 27.6.15, as \(\underline{\mu }(\underline{\beta }\underline{E})=\underline{\mu }(\underline{E})\).
We first quickly prove part (b), assuming part (a). We have \(\widehat{\mathcal {O}}^\times \) open in \(\widehat{B}^\times \), so the open cover \(\{B^\times \widehat{\alpha }\widehat{\mathcal {O}}^\times \}_{\widehat{\alpha }\in \widehat{B}^\times }\) can be reduced to a finite cover, whence the double coset space is finite.
We now turn to prove (a), which we do in steps.
Step 1: Setup. From the set \(\underline{E}\) granted above, we define
Since \(\underline{E}\) is compact, we conclude that \(\underline{X} \subseteq \underline{B}\) is compact (subtraction is continuous). We will also use the set of products \(\underline{X}\underline{X}\), which is again compact in \(\underline{B}\).
Step 2: Measuring differences. We claim that for all \(\underline{\beta }\in \underline{B}^{(1)}\), we have \(\underline{\beta }\underline{X} \cap B^\times \ne \emptyset \). Indeed, let \(\underline{\beta }\in \underline{B}^{(1)}\). By (27.6.15), there exist distinct \(\underline{\eta },\underline{\eta }' \in \underline{E}\) (depending on \(\underline{\beta }\)) such that
Because \(\underline{\eta } \ne \underline{\eta }'\) and B is a division algebra (here is where we use this hypothesis), we have \(\underline{\beta }(\underline{\eta }-\underline{\eta }') \in B^\times \), as claimed.
A similar statement holds on the right, multiplying by \(\underline{\beta }^{-1}\).
Step 3: Cocompactness. We claim that there exists a compact set \(\underline{K} \subseteq \underline{B}^\times \times \underline{B}^\times \) such that for all \(\underline{\beta }\in \underline{B}^{(1)}\), there exist \(\beta \in B^\times \) and \(\underline{\nu } \in \underline{B}^{(1)}\) such that \(\underline{\beta }= \beta \underline{\nu }\) and \((\underline{\nu },\underline{\nu }^{-1}) \in \underline{K}\).
To prove this claim, first define \(T :=B^\times \cap \underline{X} \underline{X}\). Since T is the intersection of a discrete set and a compact set, we conclude that T is finite. Let \(T^{-1} :=\{\gamma ^{-1} : \gamma \in T\}\) and let
To check the claim, let \(\underline{\beta }\in \underline{B}^{(1)}\). By Step 2, \(\underline{\beta }\underline{X} \cap B^\times \ne \emptyset \) and (similarly) \(\underline{X}\underline{\beta }^{-1} \cap B^\times \ne \emptyset \). Therefore there exist \(\underline{\nu },\underline{\nu }' \in \underline{X}\) and \(\beta ,\beta ' \in B^\times \) such that
Therefore
Then \(\underline{\nu }^{-1} \in T^{-1}\underline{X}\), and \(T^{-1}\underline{X}\) is compact. We have shown that \(\underline{\beta }= \beta \underline{\nu }^{-1}\) with \(\beta \in B^\times \) and \((\underline{\nu }^{-1},\underline{\nu }) \in \underline{K} = T^{-1}\underline{X} \times \underline{X}\), and this proves the claim.
Step 4: Conclusion. By the definition of the topology on \(\underline{B}^\times \), the set
is compact; then, by the claim in Step 3, this set surjects onto \(B^\times \backslash \underline{B}^{(1)}\). We conclude that \(B^\times \backslash \underline{B}^{(1)}\) is compact, completing the proof of part (a). \(\square \)
Corollary 27.6.20
If B is a division algebra or \(B \simeq {{\,\mathrm{M}\,}}_n(F)\), and \(\mathcal {O}\subseteq B\) is an R-order, then the class set \({{\,\mathrm{Cls}\,}}\!{}_{\textsf {\tiny {R}} }\,\mathcal {O}\) is finite.
Proof. If B is a division algebra, we combine Lemma 27.6.8 and Main Theorem 27.6.14. Otherwise, \(B \simeq {{\,\mathrm{M}\,}}_n(F)\). If \(\mathcal {O}\) is maximal then \(\mathcal {O}\simeq {{\,\mathrm{M}\,}}_n(R)\) and the result follows from 17.3.7; and then the result for a general order \(\mathcal {O}\) follows from Exercise 17.3(b). \(\square \)
Remark 27.6.21. Corollary 27.6.20 covers all quaternion algebras B. This finiteness statement generalizes to the theorem of Jordan–Zassenhaus: see Remark 17.7.27.
27.6.22
The idelic point of view (Lemma 27.6.8) also makes it clear why the class number is independent of the order within its genus (Lemma 17.4.11): the idelic description only depends on the local orders, up to isomorphism.
We have two other objects that admit a nice idelic description.
27.6.23
The genus of an order and its type set (see section 17.4) can be similarly described. Let \(\mathcal {O}\) be an R-order, and let \(\mathcal {O}' \in {{\,\mathrm{Gen}\,}}\mathcal {O}\) be an order in the genus of \(\mathcal {O}\). Then \(\mathcal {O}'\) is locally isomorphic to \(\mathcal {O}\), so there exists \(\widehat{\nu }\in \widehat{B}^\times \) such that \(\widehat{\nu }\widehat{\mathcal {O}}\widehat{\nu }^{-1} = \widehat{\mathcal {O}}'\), well defined up to right multiplication by an element of the normalizer \(N_{\widehat{B}^\times }(\widehat{\mathcal {O}})\). We recover \(\mathcal {O}' = \widehat{\mathcal {O}}' \cap B\), so this gives a bijection
Two such orders are isomorphic if and only if there exists \(\beta \in B^\times \) such that \(\beta \mathcal {O}\beta ^{-1} = \mathcal {O}'\), so we have a bijection
Corollary 27.6.25
The type set \({{\,\mathrm{Typ}\,}}\mathcal {O}\) is finite.
Proof. In view of (27.6.24), the double coset \(B^\times \backslash \widehat{B}^\times \!/N_{\widehat{B}^\times }(\widehat{\mathcal {O}})\) is a further quotient of the set \(B^\times \backslash \widehat{B}^\times \!/\widehat{\mathcal {O}}^\times \) which is finite by Main Theorem 27.6.14. \(\square \)
27.6.26
Referring to section 18.5 locally, we see that the group of locally principal two-sided \(\mathcal {O}\)-ideals \({{\,\mathrm{Idl}\,}}(\mathcal {O})\) is in bijection with
where
is the normalizer of \(\widehat{\mathcal {O}}\) in \(\widehat{B}^\times \). Furthermore, the group of isomorphism classes of locally principal two-sided \(\mathcal {O}\)-ideals is therefore in bijection with
7 Reduced norms
To conclude, we consider reduced norms; we specialize and suppose that B is a quaternion algebra.
27.7.1
Since \({{{\texttt {\textit{S}}}}}\) contains all archimedean places, by the local norm calculation (Lemma 13.4.9), we have \({{\,\mathrm{nrd}\,}}(\widehat{B}^\times )=\widehat{F}^\times \). By the Hasse–Schilling theorem on norms (Main Theorem 14.7.4), we have \({{\,\mathrm{nrd}\,}}(B^\times )=F_{>_{\Omega } 0}^\times \), where \(\Omega \subseteq {{\,\mathrm{Ram}\,}}B\) is the set of real ramified places and \(F_{>_{\Omega } 0}^\times \) is the set of elements positive at all \(v \in \Omega \) (recalling 14.7.2). Therefore, the reduced norm (in each component) yields a surjective map
We will now see that the group \(F_{>_{\Omega } 0}^\times \backslash \widehat{F}^\times \!/{{\,\mathrm{nrd}\,}}(\widehat{\mathcal {O}}^\times )\) in (27.7.2) is a certain class group of R.
Lemma 27.7.3
The subgroup \({{\,\mathrm{nrd}\,}}(\widehat{\mathcal {O}}^\times )F_{>_{\Omega } 0}^\times \le \widehat{F}^\times \) is a finite-index open subgroup containing \(F_{>0}^\times \), the group of totally positive elements of \(F^\times \). If moreover \(\mathcal {O}\) is maximal, then \({{\,\mathrm{nrd}\,}}(\widehat{\mathcal {O}}^\times )=\widehat{R}^\times \).
Proof. In Lemma 13.4.9, we saw that if \(\mathcal {O}_\mathfrak p \) is maximal, then \({{\,\mathrm{nrd}\,}}(\mathcal {O}_\mathfrak p ^\times )=R_\mathfrak p ^\times \); for the finitely many remaining \(\mathfrak p \subseteq R\), the \(R_\mathfrak p \)-order \(\mathcal {O}_\mathfrak p \) is of finite index in a maximal superorder, so \({{\,\mathrm{nrd}\,}}(\mathcal {O}_\mathfrak p ^\times )\) is a finite index open subgroup of \(R_\mathfrak p ^\times \). Putting these together, we conclude \({{\,\mathrm{nrd}\,}}(\widehat{\mathcal {O}}^\times )\) is a finite index open subgroup of \(\widehat{R}^\times \).
But \(\widehat{F}^\times \!/\widehat{R}^\times F_{>_{\Omega } 0}^\times \simeq {{\,\mathrm{Cl}\,}}_\Omega R\) is a finite group and therefore
Finally, we have \(F_{>_{\Omega } 0}^\times \ge F_{>0}^\times \), as the latter possibly requires further positivity. \(\square \)
27.7.4
Let
From Lemma 27.7.3, \(G(\mathcal {O})\) is a finite-index open subgroup containing \(F_{>0}^\times \). By class field theory 27.5.12, there exists a class field K for \(G(\mathcal {O})\), i.e., there exists a finite abelian extension \(K \supseteq F\) and an Artin isomorphism
The group \({{\,\mathrm{Cl}\,}}_{G(\mathcal {O})} R\) only depends on the genus of \(\mathcal {O}\): if \(\mathcal {O}' \in {{\,\mathrm{Gen}\,}}\mathcal {O}\) then \(\mathcal {O}'\) is locally isomorphic to \(\mathcal {O}\), so there exists \(\widehat{\nu }\in \widehat{B}^\times \) such that \(\widehat{\mathcal {O}}'=\widehat{\nu }^{-1}\widehat{\mathcal {O}}\widehat{\nu }\) so \({{\,\mathrm{nrd}\,}}(\widehat{\mathcal {O}}'^\times )={{\,\mathrm{nrd}\,}}(\widehat{\mathcal {O}}^\times )\).
Example 27.7.7
Suppose F is a number field and \({{{\texttt {\textit{S}}}}}\) is the set of archimedean places of F, so that \(R=\mathbb Z _F\) is the ring of integers in F. Suppose further that \(\mathcal {O}\) is maximal. Then \(G(\mathcal {O})=F_{>_{\Omega } 0}^\times \widehat{R}^\times \). Recalling 17.8.2, let \(\Omega \) be the set of ramified (necessarily real) archimedean places of B, and let \({{\,\mathrm{Cl}\,}}_{\Omega } \mathbb Z _F :=F_{>_{\Omega } 0}^\times \backslash \widehat{F}^\times / \widehat{R}^\times \), equivalently, \({{\,\mathrm{Cl}\,}}_{\Omega } \mathbb Z _F\) is the group of fractional ideals of \(\mathbb Z _F\) modulo the subgroup of principal fractional ideals generated by elements in \(F_{>_{\Omega } 0}^\times \). Then \({{\,\mathrm{Cl}\,}}_{G(\mathcal {O})} \mathbb Z _F={{\,\mathrm{Cl}\,}}_{\Omega } \mathbb Z _F\) by definition, so we have a surjective map
The two extreme cases: if B is unramified at all real places, then \(\Omega =\emptyset \), and \({{\,\mathrm{Cl}\,}}_\Omega \mathbb Z _F = {{\,\mathrm{Cl}\,}}\mathbb Z _F\) is the class group; if B is ramified at all real places, then \({{\,\mathrm{Cl}\,}}_\Omega \mathbb Z _F = {{\,\mathrm{Cl}\,}}^+ \mathbb Z _F\) is the narrow class group.
Remark 27.7.8. It is a fundamental result of Eichler (Theorem 17.8.3) that whenever there exists \(v \in {{{\texttt {\textit{S}}}}}\) such that B is unramified at v, then the reduced norm map (27.7.2) is injective, and hence bijective, giving a bijection between the class set of \(\mathcal {O}\) and a certain class group of R. This topic is the main result in the next chapter.
Exercises
Unless otherwise specified, let F be a global field and let B be a quaternion algebra over F.
-
1.
If we take the direct product instead of the restricted direct product in the definition of the adele ring, we lose local compactness. More precisely, let \(\{X_i\}_{i \in I}\) be a collection of nonempty topological spaces. Show that \(X=\prod _{i \in I} X_i\) is locally compact if and only if each \(X_i\) is locally compact and all but finitely many \(X_i\) are compact.
-
2.
Review the language of group actions and fundamental sets (section 34.1).
-
a)
Equip \(\mathbb Q \) with the discrete topology. We have a group action \(\mathbb Q \,\circlearrowright \, \underline{\mathbb{Q }}\) (by addition). Show that \(\widehat{\mathbb{Z }}\times [0,1] \subseteq \widehat{\mathbb{Q }}\times \mathbb R \) is a fundamental set for this action. [Hint: Review the arguments in Lemmas 27.1.13–27.1.14.]
-
b)
Similarly, show that \(\mathbb Q ^\times \circlearrowright \underline{\mathbb{Q }}^\times \) and that \(\widehat{\mathbb{Z }}^\times \times \mathbb R _{>0} \subseteq \widehat{\mathbb{Q }}\times \mathbb R \) is a fundamental set for this action.
-
a)
-
3.
For a prime p, let \(\widehat{p}=(p,1,\dots ,1,p,1,\dots ) \in \underline{\mathbb{Q }}\) be the adele which is equal to p in the pth and \(\infty \)th component and 1 elsewhere.
-
a)
Show that the sequence \(\widehat{p}\), ranging over primes p, does not converge in \(\underline{\mathbb{Q }}^\times \); conclude that \(\underline{\mathbb{Q }}^\times \) is not compact.
-
b)
However, show that the sequence \(\widehat{p}\) has a subsequence converging to the identity in the quotient \(\underline{\mathbb{Q }}^\times /\mathbb Q ^\times \).
-
a)
-
4.
Recall that \(\widehat{\mathbb{Z }}= \varprojlim _{n} \mathbb Z /n\mathbb Z \simeq \prod _p \mathbb Z _p\).
-
(a)
Prove that each \(\widehat{\alpha }\in \widehat{\mathbb{Z }}\) has a unique representation as \(\widehat{\alpha }= \sum _{n=1}^{\infty } c_n n!\) where \(c_n \in \mathbb Z \) and \(0 \le c_n \le n\).
-
(b)
Prove that \(\widehat{\mathbb{Z }}^\times \simeq \widehat{\mathbb{Z }}\times \prod _{n=1}^{\infty } \mathbb Z /n\mathbb Z \) as profinite groups. [Hint: Consider the product of the p-adic logarithm maps and use the fact that for every prime power \(p^e\) there are infinitely many primes q such that \(p^e \parallel (q-1)\).]
-
(c)
Prove for every \(n \in \mathbb Z _{>0}\) that the natural map \(\mathbb Z /n\mathbb Z \rightarrow \widehat{\mathbb{Z }}/n\widehat{\mathbb{Z }}\) is an isomorphism.
-
(d)
Prove that there is a bijection from \(\mathbb Z _{\ge 0}\) to the set of open subgroups of \(\widehat{\mathbb{Z }}\) mapping \(n \mapsto n\widehat{\mathbb{Z }}\).
-
(a)
-
5.
We recall from 27.1.15 the solenoid \({{\,\mathrm{Sol}\,}}=(\mathbb R \times \widehat{\mathbb{Z }})/\mathbb Z \) (with \(\mathbb Z \) embedded diagonally, and given the quotient topology).
-
(a)
Prove that \({{\,\mathrm{Sol}\,}}\) is a compact, Hausdorff, and connected topological group.
-
(b)
Prove that \({{\,\mathrm{Sol}\,}}\simeq \underline{\mathbb{Q }}/\mathbb Q \) as topological groups.
-
(c)
Prove that \({{\,\mathrm{Sol}\,}}\simeq \varprojlim _n \mathbb R /\frac{1}{n}\mathbb Z \) with respect to the directed system \(n \in \mathbb Z _{\ge 1}\) under divisibility.
-
(d)
Show that the group of path components of \({{\,\mathrm{Sol}\,}}\) is isomorphic to \(\widehat{\mathbb{Z }}/\mathbb Z \), and conclude that \({{\,\mathrm{Sol}\,}}\) is not path connected. [Hint: the neutral path component is the image of \(\{0\} \times \mathbb R \subseteq \widehat{\mathbb{Q }}\times \mathbb R \).]
-
(a)
-
6.
Recall that by definition, a set \(U \subseteq \underline{F}\) is open if and only if
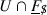 is open in
is open in  for all eligible \({{{\texttt {\textit{S}}}}}\subseteq {{\,\mathrm{Pl}\,}}F\). Show that \(U \subseteq \underline{F}\) is open if and only if for all \(\underline{a} \in \underline{F}\) that \((\underline{a}+U) \cap \prod _v R_v\) is open in \(\prod _v R_v\).
for all eligible \({{{\texttt {\textit{S}}}}}\subseteq {{\,\mathrm{Pl}\,}}F\). Show that \(U \subseteq \underline{F}\) is open if and only if for all \(\underline{a} \in \underline{F}\) that \((\underline{a}+U) \cap \prod _v R_v\) is open in \(\prod _v R_v\). -
7.
Show that the topology on \(\underline{F}^\times \) agrees with the subspace topology induced on \(\underline{F}^\times \hookrightarrow \underline{F}\times \underline{F}\) by \(x \mapsto (x,x^{-1})\).
-
8.
Show that if \({{{\texttt {\textit{S}}}}}\) is eligible and \(\mathcal {O}\subseteq B\) is an \(R_{({{{\texttt {\textit{S}}}}})}\)-order, then
$$\begin{aligned} \underline{B}= \left\{ (x_v)_v \in \textstyle {\prod _v} B_v : x_v \in \mathcal {O}_v \text { for all but finitely many }v\right\} \end{aligned}$$and
$$\begin{aligned} \underline{B}^\times = \left\{ (x_v)_v \in \textstyle {\prod _v} B_v^\times : x_v \in \mathcal {O}_v^\times \text { for all but finitely many }v\right\} \end{aligned}$$and therefore that this definition is independent of the choice of \(\mathcal {O}\) (and \({{{\texttt {\textit{S}}}}}\)).
- \(\triangleright \) 9.:
-
Prove Lemma 27.5.6.
- 10.:
-
Returning to 27.5.13, let \(D_F \le C_F\) be the connected component of 1 in the idele class group of F. Show that \(D_F\) is a closed subgroup with
$$\begin{aligned} D_F \simeq \mathbb R \times (\mathbb R /\mathbb Z )^{c} \times {{\,\mathrm{Sol}\,}}^{r+c-1} \end{aligned}$$where r is the number of real places of F and c the number of complex places. Interpret this isomorphism explicitly for F a quadratic field for both F real and imaginary: what ‘explains’ the factors that appear?
- \(\triangleright \) 11.:
-
Let B be a finite-dimensional F-algebra.
- (a):
-
Show that B is discrete and closed in \(\underline{B}\). [Hint: F is discrete in \(\underline{F}\) by the product formula.]
- (b):
-
Show that B is cocompact in \(\underline{B}\) (under the diagonal embedding), i.e., that \(\underline{B}/B\) is compact.
- 12.:
-
Give a fundamental system of neighborhoods of 0 in \(\widehat{B}\) and of 1 in \(\widehat{B}^\times \).
- \(\triangleright \) 13.:
-
Let A be a topological ring.
- (a):
-
Suppose that \(A^\times \subseteq A\) has the induced topology. Give an example to show that the map \(x \mapsto x^{-1}\) on \(A^\times \) is not necessarily continuous.
- (b):
-
Now embed
$$\begin{aligned} A^\times&\hookrightarrow A \times A \\ x&\mapsto (x,x^{-1}) \end{aligned}$$and give \(A^\times \) the subspace topology. Show that \(A^\times \) in this topology is a topological group.
- \(\triangleright \) 14.:
-
Let \({{{\texttt {\textit{S}}}}}\subset {{\,\mathrm{Pl}\,}}F\) be an eligible set.
- (a):
-
Show that \(R_{({{{\texttt {\textit{S}}}}})}\) is discrete in \(F_{{{{\texttt {\textit{S}}}}}}=\prod _{v \in {{{\texttt {\textit{S}}}}}} F_v\). [Hint: it is enough to show this for a neighborhood of 0, and then use the fact that the norm must be an integer.]
- (b):
-
Prove that if \(\mathcal {O}\) is an \(R_{({{{\texttt {\textit{S}}}}})}\)-order in B, then \(\mathcal {O}\) is discrete in \(B_{{{{\texttt {\textit{S}}}}}} = \prod _{v \in {{{\texttt {\textit{S}}}}}} B_v\).
- 15.:
-
Let F be a global field and let K be a finite separable extension of F.
- (a):
-
Show that \(\underline{K}\simeq \underline{F}\otimes _F K\). [Hint: Use the fact that \(F_v \otimes _F K \simeq \prod _w K_w\) where w runs over the places above v.]
- (b):
-
Show that
$$\begin{aligned} \underline{K}&= \left\{ (x_w)_w \in \textstyle {\prod _w} K_w : |{{\,\mathrm{Nm}\,}}_{K_w/F_v} x_v \,|_v \le 1 \text { for almost all }v\right\} \end{aligned}$$but that the inclusion
$$\begin{aligned} \underline{B}= B \otimes _F \underline{F}\subset \left\{ (x_v)_v \in \textstyle {\prod _v} B_v : |{{\,\mathrm{nrd}\,}}(x_v) \,|_v \le 1 \text { for almost all }v\right\} \end{aligned}$$is strict, so the corresponding statement is false for B.
- 16.:
-
Let \(R=R_{({{{\texttt {\textit{S}}}}})}\) be a global ring and \(\mathcal {O}\) be an R-order in B. Show that the set of R-orders which are connected to \(\mathcal {O}\) is in bijection with \(\widehat{B}^{\times }/N_{\widehat{B}^\times }(\widehat{\mathcal {O}})\), where \(N_{\widehat{B}^\times }(\widehat{\mathcal {O}})\) is the normalizer of \(\widehat{\mathcal {O}}\) in \(\widehat{B}^\times \).
- 17.:
-
Extend Lemma 27.7.3 as follows: if \(\mathcal {O}\) is an Eichler order, then \({{\,\mathrm{nrd}\,}}(\widehat{\mathcal {O}}^\times )=\widehat{R}^\times \).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
This chapter is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, duplication, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, a link is provided to the Creative Commons license and any changes made are indicated.The images or other third party material in this chapter are included in the work's Creative Commons license, unless indicated otherwise in the credit line; if such material is not included in the work's Creative Commons license and the respective action is not permitted by statutory regulation, users will need to obtain permission from the license holder to duplicate, adapt or reproduce the material.
Copyright information
© 2021 The Author(s)
About this chapter
Cite this chapter
Voight, J. (2021). Adelic framework. In: Quaternion Algebras. Graduate Texts in Mathematics, vol 288. Springer, Cham. https://doi.org/10.1007/978-3-030-56694-4_27
Download citation
DOI: https://doi.org/10.1007/978-3-030-56694-4_27
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-56692-0
Online ISBN: 978-3-030-56694-4
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)



 is cocompact and the set
is cocompact and the set 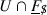 is open in
is open in  for all eligible
for all eligible