Abstract
In this chapter, we continue our tour of quaternion orders with some more advanced species.
You have full access to this open access chapter, Download chapter PDF
In this chapter, we continue our tour of quaternion orders with some more advanced species.
1 \(\triangleright \) Advanced quaternion orders
Let B be a quaternion algebra over \(\mathbb Q \) of discriminant \(D={{\,\mathrm{disc}\,}}B\) and let \(\mathcal {O}\subset B\) be an order with reduced discriminant \(N={{\,\mathrm{discrd}\,}}(\mathcal {O})\). Then \(N=DM\) with \(M \in \mathbb Z _{\ge 1}\).
24.1.1
(Gorenstein and Bass orders). Although Eichler orders may lose the property that all of its ideals are invertible, we may still insist on the invertibility of its dual. Recall (Definition 15.6.15) that the codifferent of an order is the lattice \({{\,\mathrm{codiff}\,}}(\mathcal {O})=\mathcal {O}^\sharp \) obtained as the dual of the trace pairing over R. We say \(\mathcal {O}\) is Gorenstein if \({{\,\mathrm{codiff}\,}}(\mathcal {O})\) is invertible, or equivalently (Corollary 16.8.7) every sated left or right fractional \(\mathcal {O}\)-ideal (lattice \(I \subseteq B\) with left or right order equal to \(\mathcal {O}\)) is invertible. Hereditary orders are Gorenstein, since for a hereditary order every left or right fractional \(\mathcal {O}\)-ideal (not necessarily sated) is invertible.
Being Gorenstein is a local property because invertibility is so. An Eichler order is Gorenstein, but there are Gorenstein orders that are not Eichler. An order is Gorenstein if and only if its associated ternary quadratic form is primitive, i.e. the greatest common divisor of its coefficients is 1, or equivalently its values generate \(\mathbb Z \).
We say \(\mathcal {O}\) is Bass if every superorder \(\mathcal {O}' \supseteq \mathcal {O}\) (including \(\mathcal {O}'=\mathcal {O}\)) is Gorenstein. A Bass order is Gorenstein, but not always conversely. The fact that every superorder is Gorenstein reflects into good structural properties of a Bass order. Most importantly, a \(\mathbb Z _p\)-order \(\mathcal {O}\) is Bass if and only if it contains either \(\mathbb Z _p \times \mathbb Z _p\) or the ring of integers in a quadratic extension \(K \supseteq \mathbb Q _p\) (these order are sometimes called primitive; we call them basic ). This embedded subalgebra makes it possible to calculate explicitly with the order, with important applications to the arithmetic of modular forms, a topic we pursue in the final part of this book.
In summary, there is a chain of proper implications
for orders \(\mathcal {O}\subseteq B\), and each of these implications is strict (\(\not \Leftarrow \) in general).
Given an order \(\mathcal {O}\), we construct its radical idealizer as
We have \(\mathcal {O}\subseteq \mathcal {O}^\natural \), and equality holds if and only if \(\mathcal {O}\) is hereditary. Iterating, we obtain a canonically attached sequence of superorders:
where \(\mathcal {O}_s\) is hereditary. A more refined classification of orders involves dissecting the chain (24.1.3) explicitly.
There is one final way of classifying orders that extends nicely to the noncommutative context, due to Brzezinski. By way of analogy, we recall that orders in a quadratic field are characterized by conductor. Let \(K=\mathbb Q (\sqrt{d_K})\), let \(\mathbb Z _K\) be the ring of integers of K, and let \(d_K \in \mathbb Z \) be the discriminant of \(\mathbb Z _K\). An order S in K is of the form \(S=\mathbb Z + f\mathbb Z _K\), where \(f \in \mathbb Z _{\ge 1}\) is the conductor of S (in its maximal order), and the discriminant of S is \(d=f^2 d_K\). Even in classical considerations, these orders arise naturally when considering binary quadratic forms of nonfundamental discriminant.
Proposition 24.1.4
Let B be a quaternion algebra over \(\mathbb Q \) and let \(\mathcal {O}\subseteq B\) be an order. Then there exists a unique integer \(f(\mathcal {O}) \ge 1\) and Gorenstein order \({{\,\mathrm{Gor}\,}}(\mathcal {O})\) such that
Two orders \(\mathcal {O},\mathcal {O}'\) are isomorphic if and only if \(f(\mathcal {O})=f(\mathcal {O}')\) and \({{\,\mathrm{Gor}\,}}(\mathcal {O}) \simeq {{\,\mathrm{Gor}\,}}(\mathcal {O}')\).
The order \({{\,\mathrm{Gor}\,}}(\mathcal {O})\) is called the Gorenstein saturation of \(\mathcal {O}\), and we call \(f(\mathcal {O})\) the Gorenstein conductor of the order (also sometimes called the Brandt invariant): an order is Gorenstein if and only if \(f(\mathcal {O})=1\), so this gives a ready supply of orders that are not Gorenstein. In particular, to classify all orders, via the operation of Gorenstein saturation, it is enough to classify the Gorenstein orders.
Remark 24.1.5
The first attempt to tame the zoo of quaternion orders was Eichler [Eic36, Satz 12], who classified what he called primitive (our basic) orders. Later this was generalized by Brzezinski [Brz83a, §5], who also clarified certain aspects [Brz90, §1]. A nice summary of facts about quaternion orders is given by Lemurell [Lem2011].
2 Gorenstein orders
In this section we define the well-behaved Gorenstein orders. See Remark 24.2.24 for more context on the class of Gorenstein rings.
Recall the definition of the codifferent (Definition 15.6.15):
We have \({{\,\mathrm{codiff}\,}}(\mathcal {O})\) a two-sided sated \(\mathcal {O}\)-ideal with \(\mathcal {O}\subseteq {{\,\mathrm{codiff}\,}}(\mathcal {O})\) (Lemma 15.6.16), and \({{\,\mathrm{disc}\,}}(\mathcal {O})=[{{\,\mathrm{codiff}\,}}(\mathcal {O}):\mathcal {O}]_R\). We already saw in section 16.8 the importance of the following class of orders.
Definition 24.2.1
\(\mathcal {O}\) is Gorenstein if \({{\,\mathrm{codiff}\,}}(\mathcal {O})\) is invertible.
24.2.2
The property of being a Gorenstein order is local (\(\mathcal {O}\) is Gorenstein if and only if \(\mathcal {O}_\mathfrak p \) is Gorenstein for all primes \(\mathfrak p \)), since invertibility is a local property.
Proposition 24.2.3
The following are equivalent:
-
(i)
\(\mathcal {O}\) is Gorenstein;
-
(ii)
\({{\,\mathrm{codiff}\,}}(\mathcal {O})\) is projective as a \(\mathcal {O}\)-bimodule;
-
(iii)
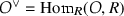 is projective as an \(\mathcal {O}\)-bimodule; and
is projective as an \(\mathcal {O}\)-bimodule; and -
(iv)
All sated left or right fractional \(\mathcal {O}\)-ideals are invertible as \(\mathcal {O}\)-ideals.
Proof. For the equivalence (i) \(\Leftrightarrow \) (ii), because \({{\,\mathrm{codiff}\,}}(\mathcal {O})\) is sated it follows from Theorem 20.3.3 that \(\mathcal {O}\) is Gorenstein if and only if \({{\,\mathrm{codiff}\,}}(\mathcal {O})\) is projective as an \(\mathcal {O}\)-bimodule. For (ii) \(\Leftrightarrow \) (iii), by Proposition 15.6.7, we have an isomorphism \({{\,\mathrm{codiff}\,}}(\mathcal {O}) \simeq {{\,\mathrm{Hom}\,}}_R(\mathcal {O},R)\) of \(\mathcal {O}\)-bimodules over R. Finally, (i) \(\Leftrightarrow \) (iv) follows from Corollary 16.8.7. \(\square \)
24.2.4
We call in for relief as well Main Theorem 20.3.9: the equivalent sided notions (on the left and right) in Proposition 24.2.3 are also all equivalent. In particular, a suitably defined notion of left Gorenstein or right Gorenstein would also be equivalent.
The Gorenstein condition can be detected on the level of norms as follows.
Lemma 24.2.5
We have
and \(\mathcal {O}\) is Gorenstein if and only if equality holds.
Proof. We refer to Proposition 16.4.3, and 16.4.5: we have
with equality if and only if \(\mathcal {O}^\sharp \) is locally principal. But by Lemma 15.6.17, we have \([\mathcal {O}^\sharp :\mathcal {O}]_R={{\,\mathrm{disc}\,}}(\mathcal {O})={{\,\mathrm{discrd}\,}}(\mathcal {O})^2\), and combining these gives the result. \(\square \)
Our next main result connects the Gorenstein condition to a property of the corresponding ternary quadratic module. Let \(Q:M \rightarrow L\) be a ternary quadratic module. We follow Gross–Lucianovic [GrLu2009, Propositions 6.1–6.2], and consider the odd Clifford bimodule.
Proposition 24.2.6
Left multiplication gives a pairing

that induces an isomorphism

of left \({{\,\mathrm{Clf}\,}}^0(Q)\)-modules.
We have a similar argument on the right.
Remark 24.2.8
If R is a Dedekind domain, then choosing a pseudobasis for M we may write \(M=\mathfrak a e_1 + \mathfrak b e_2 + \mathfrak c e_3\) for fractional ideals \(\mathfrak a ,\mathfrak b ,\mathfrak c \), and without loss of generality may take \(L=\mathfrak l \) a fractional ideal. Then \(\smash {\,{\textstyle {\bigwedge }}}^3 M = \mathfrak a \mathfrak b \mathfrak c (e_1 \wedge e_2 \wedge e_3) \simeq \mathfrak a \mathfrak b \mathfrak c \) is just the Steinitz class of M, and  as in (22.5.10). Restricting to this case is still quite illustrative.
as in (22.5.10). Restricting to this case is still quite illustrative.
Proof. By construction of the Clifford algebra, we have as R-modules that

so  . Multiplication in \({{\,\mathrm{Clf}\,}}(Q)\) induces a pairing that induces a homomorphism of \({{\,\mathrm{Clf}\,}}^0(Q)\)-bimodules by associativity of multiplication in \({{\,\mathrm{Clf}\,}}(Q)\). To conclude that the pairing induces an isomorphism, we can argue locally and suppose that \(M \simeq R^3\) with basis \(e_1,e_2,e_3\) and \(L \simeq R\) is the quadratic form
. Multiplication in \({{\,\mathrm{Clf}\,}}(Q)\) induces a pairing that induces a homomorphism of \({{\,\mathrm{Clf}\,}}^0(Q)\)-bimodules by associativity of multiplication in \({{\,\mathrm{Clf}\,}}(Q)\). To conclude that the pairing induces an isomorphism, we can argue locally and suppose that \(M \simeq R^3\) with basis \(e_1,e_2,e_3\) and \(L \simeq R\) is the quadratic form
Then \(1,e_2e_3,e_3e_1,e_1e_2\) is an R-basis for \({{\,\mathrm{Clf}\,}}^0(Q)\) and
with \({{\,\mathrm{Clf}\,}}^1(Q)/M \simeq R e_1e_2e_3\).
We then compute the dual basis of \({{\,\mathrm{Clf}\,}}^1(Q)\) to that of \({{\,\mathrm{Clf}\,}}^0(Q)\) as
for example,
so
The other products can be computed in a similarly direct fashion. \(\square \)
Recall (Definition 9.7.14) that \(Q:M \rightarrow L\) is primitive if Q(M) generates L as an R-module.
Theorem 24.2.10
\(\mathcal {O}\) is Gorenstein if and only if its associated ternary quadratic module \(Q=\psi _\mathcal {O}\) is primitive.
Proof. The statement is local, so we may suppose that R is a local domain with maximal ideal \(\mathfrak p \), and that \(M \simeq R^3\) and \(L \simeq R\), so  . Let \(J={{\,\mathrm{Clf}\,}}^1(Q)\) be the odd Clifford bimodule, thought of as a left \(\mathcal {O}\)-module. By Proposition 24.2.6 (specifically, (24.2.7)), we have \({{\,\mathrm{Clf}\,}}^1(Q) \simeq {{\,\mathrm{Hom}\,}}_R(\mathcal {O},R)\) as left \(\mathcal {O}\)-modules. By Proposition 24.2.3 and 24.2.4 (or repeating the argument on the right), we want to show that J is principal.
. Let \(J={{\,\mathrm{Clf}\,}}^1(Q)\) be the odd Clifford bimodule, thought of as a left \(\mathcal {O}\)-module. By Proposition 24.2.6 (specifically, (24.2.7)), we have \({{\,\mathrm{Clf}\,}}^1(Q) \simeq {{\,\mathrm{Hom}\,}}_R(\mathcal {O},R)\) as left \(\mathcal {O}\)-modules. By Proposition 24.2.3 and 24.2.4 (or repeating the argument on the right), we want to show that J is principal.
Suppose that Q is primitive. Let \(\alpha =xe_1+ye_2+ze_3\). We then compute that
and the determinant of the matrix in the middle is precisely \(Q(x,y,z)^2\). So \(Q(\alpha ) \in R^\times \) if and only if \(\alpha \mathcal {O}= J\).
Conversely, suppose that Q is not primitive. Then \(Q \equiv 0 ~(\text{ mod } ~\mathfrak{p })\). If \(\alpha =xe_1+ye_2+ze_3+te_1e_2e_3\) with \(x,y,z,t \in R\), then
and symmetrically with the other products, so \(\alpha \mathcal {O}\) has rank \(\le 2\) over \(R/\mathfrak p \), and it follows that \(\alpha \mathcal {O}\ne J\) for all \(\alpha \). \(\square \)
Corollary 24.2.11
Let R be a Dedekind domain. Then the associations

are mutually inverse discriminant-preserving bijections that are also functorial with respect to R.
Proof. We restrict the bijection in Main Theorem 22.5.7 and apply Theorem 24.2.10. \(\square \)
Remark 24.2.13
In view of Corollary 24.2.11, the issues in the correspondence with ternary quadratic forms for non-Gorenstein orders amounted to the failure to account for the codomain of the quadratic module: non-Gorenstein orders are obtained from quadratic modules \(Q:M \rightarrow L\) where \(Q(M) \subsetneq L\).
24.2.14
From 23.4.12 and Theorem 24.2.10, we conclude that every Eichler order is Gorenstein; a direct proof is given in Exercise 24.1.
Therefore, non-Gorenstein orders abound: indeed, any order corresponding to an imprimitive form will do. More generally, we construct a canonically associated Gorenstein order containing a given order as follows.
Proposition 24.2.15
There exists a unique ideal \(\mathfrak f (\mathcal {O}) \subseteq R\) and unique Gorenstein order \({{\,\mathrm{Gor}\,}}(\mathcal {O}) \subseteq B\) such that
In fact, we have
Before we begin the proof, we make a definition and then consider the key ingredient of the proof: how rescaling the module affects the even Clifford algebra.
Definition 24.2.17
In (24.2.16), we call \(\mathfrak f (\mathcal {O}) \subseteq R\) the conductor and \({{\,\mathrm{Gor}\,}}(\mathcal {O})\) the Gorenstein saturation of \(\mathcal {O}\).
Remark 24.2.18
Brzezinski [Brz83a] writes \(\mathfrak b (\mathcal {O})\) instead of \(\mathfrak f (\mathcal {O})\) and calls it the Brandt invariant. Other authors call \({{\,\mathrm{Gor}\,}}(\mathcal {O})\) the Gorenstein closure of \(\mathcal {O}\), but this terminology may be confusing: \({{\,\mathrm{Gor}\,}}(\mathcal {O})\) is not necessarily the smallest Gorenstein order containing \(\mathcal {O}\) (see Exercise 24.11).
24.2.19
Suppose that the ternary qudratic module \(Q:M \rightarrow L\) corresponds to a quaternion R-order \(\mathcal {O}\). For a nonzero ideal \(\mathfrak a \subseteq R\), we define \(Q(\mathfrak a ):M \rightarrow \mathfrak a ^{-1} L\) to be just Q but with values taken in \(\mathfrak a ^{-1} \supseteq L\). We claim that for all R-ideals \(\mathfrak a \), we have under the correspondence
The fact that \({{\,\mathrm{Clf}\,}}^0(Q[\mathfrak a ])=R + \mathfrak a \mathcal {O}\) is visible from the construction of the even Clifford algebra (22.2.3); it is also visible from the description (22.3.25) in Example 22.3.24. In the other direction, we have
and now we twist by \(\mathfrak a \) to get
Proof of Proposition 24.2.15. We argue using ternary quadratic modules: our proof amounts to replacing a potentially imprimitive form with a primitive form, following Theorem 24.2.10.
Let \(Q=\psi _\mathcal {O}:M \rightarrow L\) be the ternary quadratic module associated to \(\mathcal {O}\), well-defined up to twisted similarity. We may take \(L=\mathfrak l \subseteq L \otimes _R F \simeq F\) and we do so for concreteness; accordingly, suppose \(\mathfrak l \) is a fractional ideal of R. Then \(Q(M)=\mathfrak n \subseteq \mathfrak l \) is a finitely generated nonzero R-submodule; since R is a Dedekind domain, \(\mathfrak n \) is invertible. Let
Let \({{\,\mathrm{Gor}\,}}(Q)=Q(\mathfrak f ):M \rightarrow \mathfrak n \) be the primitive ternary quadratic module obtained by restricting the codomain. Then \({{\,\mathrm{Clf}\,}}^0({{\,\mathrm{Gor}\,}}(Q))\) is a Gorenstein order by Theorem 24.2.10, and
by (24.2.20), so we let \({{\,\mathrm{Gor}\,}}(\mathcal {O}) :={{\,\mathrm{Clf}\,}}^0({{\,\mathrm{Gor}\,}}(Q))\). Uniqueness follows directly from (24.2.20): if \(\mathcal {O}=R + \mathfrak a \mathcal {O}'\) and \(\mathcal {O}'\) is Gorenstein, then \(Q(\mathfrak a ^{-1}):M \rightarrow \mathfrak a \mathfrak l \) is primitive and \(Q(M)=\mathfrak n = \mathfrak a \mathfrak l \), thus \(\mathfrak a =\mathfrak f (\mathcal {O})\) and \(\mathcal {O}'={{\,\mathrm{Clf}\,}}^0(Q(\mathfrak a ))={{\,\mathrm{Gor}\,}}(\mathcal {O})\).
To prove the remaining statements, we recall Corollary 22.4.15 to get
in all cases, and the primitivity of
as in (24.2.21) is equivalent to
i.e. \(\mathfrak f ={{\,\mathrm{discrd}\,}}(\mathcal {O}){{\,\mathrm{nrd}\,}}((\mathcal {O}^\sharp )^0)\). Finally, \({{\,\mathrm{nrd}\,}}(\mathcal {O}^\sharp )={{\,\mathrm{nrd}\,}}((\mathcal {O}^\sharp )^0)\) is proven in Exercise 22.10. \(\square \)
Lemma 24.2.22
Let \(\mathcal {O}' \subseteq B\) be an R-order. Then \(\mathcal {O}\simeq \mathcal {O}'\) as R-orders if and only if \({{\,\mathrm{Gor}\,}}(\mathcal {O}) \simeq {{\,\mathrm{Gor}\,}}(\mathcal {O}')\) and \(\mathfrak f (\mathcal {O})=\mathfrak f (\mathcal {O}')\).
Proof. Immediate from the uniqueness claim in Proposition 24.2.15. \(\square \)
The translation of the Gorenstein property in terms of primitivity of the ternary quadratic form makes it quite accessible. For example, we have the following result that shows that the Gorenstein condition is stable under base change.
Proposition 24.2.23
Let \(K \supseteq F\) be a finite extension and let S be the integral closure of R in K. Then \(\mathcal {O}\) is a Gorenstein R-order if and only if \(\mathcal {O}\otimes _R S\) is a Gorenstein S-order.
Proof. Let \(Q:M \rightarrow L\) be the ternary quadratic module corresponding to \(\mathcal {O}\); denoting extension of scalars by subscripts, we have \(Q_S:M_S \rightarrow L_S\) corresponding to \(\mathcal {O}_S\). We want to show that Q is primitive if and only if \(Q_S\) is primitive, which is to say \(Q(M)=L\) if and only if \(Q_S(M)=Q(M)_S=L_S\), and this statement is true as it holds for fractional R-ideals (Exercise 23.2). \(\square \)
Remark 24.2.24
Gorenstein rings were introduced by Gorenstein [Gor52] in the context of plane curves (the results of his Ph.D. thesis); Bass [Bas62, Footnote 2] writes: “After writing this paper I discovered from Professor Serre that these rings have been encountered by Grothendieck, the latter having christened them ‘Gorenstein rings.’ They are described in his setting by the fact that a certain module of differentials is locally free of rank one.” Bass [Bas63] gives a survey of (commutative) Gorenstein rings, noting their ubiquity; see also the later survey by Huneke [Hun99]. Gorenstein rings are truly abundant: they include coordinate rings of affine plane curves and curves with only double points as singularities, complete intersections, and integral group rings of finite groups.
The above-mentioned paper of Bass [Bas63] also gave rise to the class of eponymous orders in which every superorder is Gorenstein; over a complete DVR, these orders were completely classified (and related to hereditary and Gorenstein orders) by Drozd–Kirichenko–Roiter [DKR67]. Gorenstein orders in the context of quaternion algebras, were studied by Brzezinski [Brz82]. (Brzezinski [Brz87] also considers more general orders in which every lattice is locally principal: but for quaternion algebras, these are again the Gorenstein orders.)
3 Eichler symbol
Just as local quadratic extensions are classified as being either ramified, inert, or split, it is helpful to have a similar classification for quaternion orders.
We first work locally, and we suppose until further notice that R is local (as in 23.2.1).
24.3.1
The k-algebra \(\mathcal {O}/{{\,\mathrm{rad}\,}}\mathcal {O}\) is semisimple and has a standard involution (since \({{\,\mathrm{rad}\,}}\mathcal {O}\) is preserved by it), so by Example 7.4.9 this standard involution is nondegenerate; by classification (Main Theorem 4.4.1 and Theorem 6.4.1) we have one of three posibilities: \(\mathcal {O}/{{\,\mathrm{rad}\,}}\mathcal {O}\) is either k, a separable quadratic k-algebra, or a quaternion algebra over k.
We give symbols to each of the possibilities in 24.3.1 as follows.
Definition 24.3.2
Let \(J :={{\,\mathrm{rad}\,}}\mathcal {O}\). We define the Eichler symbol

For formatting reasons, we will also write  . The similarity of the Eichler symbol to other quadratic-like symbols is intentional: because of the arguments to the symbol, it should not be confused with the others. If the reader finds this overloading of symbols unpleasant, they may wish to use the symbol \(\varepsilon _\mathfrak p (\mathcal {O})\) instead.
. The similarity of the Eichler symbol to other quadratic-like symbols is intentional: because of the arguments to the symbol, it should not be confused with the others. If the reader finds this overloading of symbols unpleasant, they may wish to use the symbol \(\varepsilon _\mathfrak p (\mathcal {O})\) instead.
24.3.3
Recall the definition of the discriminant quadratic form
that computes the discriminant of \(F[\alpha ] = F[x]/(x^2-{{\,\mathrm{trd}\,}}(x)x+{{\,\mathrm{nrd}\,}}(x))\) in the basis \(1,\alpha \). The form factors through a map \(\Delta :B/F \rightarrow F\).
Suppose that \(\#k<\infty \). For \(a \in R\), let  denote the generalized Kronecker symbol, defined to be \(0,1,-1\) according as if \(F[x]/(x^2-a)\) is ramified, split (isomorphic to \(F \times F\)), or inert. If \({{\,\mathrm{char}\,}}k \ne 2\), then
denote the generalized Kronecker symbol, defined to be \(0,1,-1\) according as if \(F[x]/(x^2-a)\) is ramified, split (isomorphic to \(F \times F\)), or inert. If \({{\,\mathrm{char}\,}}k \ne 2\), then  is the Legendre symbol. We then have the following characterization (Exercise 24.4):
is the Legendre symbol. We then have the following characterization (Exercise 24.4):
-
(a)
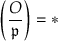 if and only if
if and only if 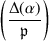 takes on all of the values \(-1,0,1\) for \(\alpha \in \mathcal {O}\).
takes on all of the values \(-1,0,1\) for \(\alpha \in \mathcal {O}\). -
(b)
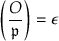 if and only if
if and only if 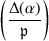 takes the values \(\{0,\epsilon \}\) for \(\alpha \in \mathcal {O}\).
takes the values \(\{0,\epsilon \}\) for \(\alpha \in \mathcal {O}\).
We now consider each of possible values of the Eichler symbol in turn.
24.3.5
We have  if and only if \({{\,\mathrm{rad}\,}}\mathcal {O}=\mathfrak p \mathcal {O}\), by dimension considerations. If further \(\# k<\infty \), then
if and only if \({{\,\mathrm{rad}\,}}\mathcal {O}=\mathfrak p \mathcal {O}\), by dimension considerations. If further \(\# k<\infty \), then  if and only if \(\mathcal {O}\simeq {{\,\mathrm{M}\,}}_2(R)\), since then the only quaternion algebra over k is \({{\,\mathrm{M}\,}}_2(k)\), and we can lift matrix units using Hensel’s lemma.
if and only if \(\mathcal {O}\simeq {{\,\mathrm{M}\,}}_2(R)\), since then the only quaternion algebra over k is \({{\,\mathrm{M}\,}}_2(k)\), and we can lift matrix units using Hensel’s lemma.
Lemma 24.3.6
The order \(\mathcal {O}\) is Eichler if and only if \(\mathcal {O}\) is maximal or residually split.
Proof. If \(\mathcal {O}\) is Eichler, then either \(\mathcal {O}\) is maximal or \(\mathcal {O}/{{\,\mathrm{rad}\,}}\mathcal {O}\simeq k \times k\) by (23.4.17). Conversely, a maximal order is an Eichler order by definition, so suppose \(\mathcal {O}\) is residually split, i.e., \(\mathcal {O}/{{\,\mathrm{rad}\,}}\mathcal {O}\simeq k \times k\). Then (as in Lemma 20.6.8), the nontrivial orthogonal idempotents of \(k \times k\) lift to orthogonal idempotents \(e_1,e_2 \in \mathcal {O}\). Since \(e_1e_2=0\), immediately \(B \simeq {{\,\mathrm{M}\,}}_2(F)\). Conjugating in B, we may suppose \(e_1=e_{11}\) and therefore \(e_2=e_{22}\), and then the result follows from Proposition 23.4.3.
For fun, here is a second proof. We have a decomposition \(\mathcal {O}=I_1 \oplus I_2 = \mathcal {O}e_1 \oplus \mathcal {O}e_2\). Thus \(\mathcal {O}=\mathcal {O}{}_{\textsf {\tiny {L}} }(I_1) \cap \mathcal {O}{}_{\textsf {\tiny {L}} }(I_2)\). Tensoring up to F, we get \(B=(I_1)_F \oplus (I_2)_F\), so by dimensions we have \((I_1)_F \simeq (I_2)_F \simeq F^2\) the simple B-module, and each \(I_i\) is isomorphic to an R-lattice \(M_i \subseteq F^2\). Thus \(\mathcal {O}{}_{\textsf {\tiny {L}} }(I_i) \simeq {{\,\mathrm{End}\,}}_F(M_i) \simeq {{\,\mathrm{M}\,}}_2(R)\), and each \(\mathcal {O}{}_{\textsf {\tiny {L}} }(I_i)\) is maximal, so \(\mathcal {O}\) is the intersection of two maximal orders. \(\square \)
24.3.7
Residually inert orders in a division quaternion algebra B over \(\mathbb Q _p\) were studied by Pizer [Piz76b], and he described them as follows. Let \(K=\mathbb Q _{p^2}\) be the unramified extension of \(\mathbb Q _p\). Then \(K \hookrightarrow B\). Consider the left regular representation \(B \rightarrow {{\,\mathrm{M}\,}}_2(K)\); it has image
The valuation ring of B consists of those with \(z,w \in \mathbb Z _{p^2}\) where \(\mathbb Z _{p^2}\) is the valuation ring of K. Pizer then considers those orders with \(z \in \mathbb Z _{p^2}\) and \(p^r \mid w\). He [Piz80a, Remark 1.5, Proposition 1.6] connected the residually inert and residually split orders by noting the striking resemblance between (24.3.8) and the standard Eichler order, remarking:
Thus \(\mathcal {O}_p'\) and \(\mathcal {O}_p\) [the Eichler order and the Pizer order] are both essentially subrings of \(\begin{pmatrix} R &{} R \\ p^{2r+1} &{} R \end{pmatrix}\) fixed by certain (different!) Galois actions induced by the Galois group of \(L/\mathbb Q _p\) and thus they can be viewed as twisted versions of each other. Hence \(\mathcal {O}\) and \(\mathcal {O}'\) are locally isomorphic at all primes \(q\ne p\) while at p they are almost isomorphic. Thus it should not be too surprising that there are close connections between [them].
Pizer works explicitly and algorithmically [Piz80a] with residually inert orders, with applications to computing modular forms of certain nonsquarefree level.
24.3.9
We can also interpret the Eichler symbol in terms of the reduction of the associated ternary quadratic form Q.
We have \(({\mathcal {O}} \mid \mathfrak{p })=*\) if and only if  is nondegenerate, defining a smooth conic over k.
is nondegenerate, defining a smooth conic over k.
If \(({\mathcal {O}} \mid \mathfrak{p })=1\), then by Lemma 24.3.6, \(\mathcal {O}\) is Eichler, and  is degenerate of rank 2 by 23.4.12, cutting out two intersecting lines over k; and conversely.
is degenerate of rank 2 by 23.4.12, cutting out two intersecting lines over k; and conversely.
Suppose \(({\mathcal {O}} \mid \mathfrak{p })=-1\). Let \(i \in \mathcal {O}\) generate the quadratic field \(\ell =\mathcal {O}/{{\,\mathrm{rad}\,}}\mathcal {O}\) over k, let \(K=F(i)\) and let S be the integral closure of R in K. Then K is unramified over F, and \(\mathfrak p S\) is the maximal ideal of S. Now the S-order \(\mathcal {O}_S :=\mathcal {O}\otimes _R S\) has \(\mathcal {O}_S/{{\,\mathrm{rad}\,}}\mathcal {O}_S \simeq \ell \times \ell \), and \(({\mathcal {O}_S} \mid \mathfrak{p S})=1\). Therefore  over \(\ell \) is degenerate of rank 2, so the same is true over k, and since we are not in the previous case, it is defined by an irreducible quadratic polynomial (the norm form from \(\ell \) to k). Therefore
over \(\ell \) is degenerate of rank 2, so the same is true over k, and since we are not in the previous case, it is defined by an irreducible quadratic polynomial (the norm form from \(\ell \) to k). Therefore  cuts out two lines defined over \(\ell \) and conjugate under \({{\,\mathrm{Gal}\,}}(\ell \,|\,k)\). In particular, a residually inert order is Gorenstein.
cuts out two lines defined over \(\ell \) and conjugate under \({{\,\mathrm{Gal}\,}}(\ell \,|\,k)\). In particular, a residually inert order is Gorenstein.
The only possibilities that remain are that  is identically zero or has rank 1 (defined by the square of a linear factor), and correspondingly cuts out the whole projective plane or a double line. These are the cases \(({\mathcal {O}} \mid \mathfrak{p })=0\).
is identically zero or has rank 1 (defined by the square of a linear factor), and correspondingly cuts out the whole projective plane or a double line. These are the cases \(({\mathcal {O}} \mid \mathfrak{p })=0\).
24.3.10
It follows from 24.3.9 that the ternary quadratic form associated to a residually inert order is similar to
just as in (23.2.7); we have e odd if and only if B is a division algebra and e even if and only if B is split.
The residually ramified orders do not admit such a simple classification; we will pursue them further in the coming sections.
Remark 24.3.11
Let R be a DVR, let \(\mathcal {O}\) be a Gorenstein R-order, and let Q be a ternary quadratic form over R representing the similarity class associated to \(\mathcal {O}\). Then Q is primitive and so defines an integral model \(\mathcal C \) of a conic \(C \subseteq \mathbb P ^2\) over \(F={{\,\mathrm{Frac}\,}}R\). By discriminants, this conic has good reduction if and only if \(\mathcal {O}\) is maximal. Moreover, we saw by direct calculation that this conic has the simplest kind of bad reduction—regular, with just one node over k—if and only if \(\mathcal {O}\) is hereditary. This is no coincidence: in fact, \(\mathcal C \) is normal if and only if \(\mathcal C \) is Bass. See Brzezinski [Brz80] for more on the relationship between integral models of conics and quaternion orders and the follow-up work [Brz85] where the increasing sequence of Bass orders ending in an hereditary order corresponds to a sequence of elementary blowup transformations.
Another motivation to study the Eichler symbol is that it controls the structure of unit groups, as follows.
Lemma 24.3.12
Let \(\#k=q\). Then \(1+\mathfrak p \mathcal {O}\subseteq \mathcal {O}^\times \), and
Proof. Since \(J \subseteq \mathfrak p \mathcal {O}\), if \(\mu \in 1+\mathfrak p \mathcal {O}\) then \(\mu -1\) is topologically nilpotent, hence \(\mu \in \mathcal {O}^\times \).
Now the indices. If \(({\mathcal {O}} \mid \mathfrak{p })=*\), then we are computing the cardinality \(\#{{\,\mathrm{GL}\,}}_2(k)=(q^2-1)(q^2-q)\). If \(({\mathcal {O}} \mid \mathfrak{p })=1\), then \(\mathcal {O}/J \simeq k \times k\) and \(\dim _k J/\mathfrak p \mathcal {O}=2\), so the index is \((q-1)^2q^2\). Similarly if \(({\mathcal {O}} \mid \mathfrak{p })=-1\), we get \((q^2-1)q^2\). If \(({\mathcal {O}} \mid \mathfrak{p })=0\), then \(\mathcal {O}/J \simeq k\) and so the index is \((q-1)q^3\). \(\square \)
We conclude with a global definition, and so we restore R to a Dedekind domain.
Definition 24.3.13
For a nonzero prime \(\mathfrak p \subseteq R\), we define the Eichler symbol at \(\mathfrak p \) to be

i.e., the Eichler symbol of the completion at \(\mathfrak p \).
We say \(\mathcal {O}\) is locally residually inert if  for all primes \(\mathfrak p \).
for all primes \(\mathfrak p \).
The analogously defined locally residually split orders already have a name: they are the Eichler orders that are not maximal.
4 Chains of orders
We have a few more classes of orders to consider, but before we continue our tour we pause to consider an aspect of the more general classification: we seek to put every order in a chain of superorders, ending in a maximal order.
Suppose throughout this section that R is local.
Definition 24.4.1
The radical idealizer of \(\mathcal {O}\) is
24.4.2
By Exercise 20.2, we have \(\mathcal {O}{}_{\textsf {\tiny {L}} }({{\,\mathrm{rad}\,}}\mathcal {O})=\mathcal {O}{}_{\textsf {\tiny {R}} }({{\,\mathrm{rad}\,}}\mathcal {O}) = \mathcal {O}^\natural \), so the symmetric definition can be replaced by either order in the intersection.
24.4.3
We recall our motivation to study extremal orders 21.2.1: \(\mathcal {O}^\natural \) radically covers \(\mathcal {O}\), and by Proposition 21.2.3 we have \(\mathcal {O}^\natural =\mathcal {O}\) if and only if \(\mathcal {O}\) is extremal. By Theorem 21.5.1, \(\mathcal {O}\) is extremal if and only if \(\mathcal {O}\) is hereditary. Iterating, we have a canonically associated chain of orders
terminating in an order \(\mathcal {O}_r\) that is hereditary. (By 23.3.1 and Proposition 23.4.3(iv), either \(\mathcal {O}_r\) is maximal or \(\mathcal {O}_r\) is contained in exactly two possible maximal orders.) We call \(\mathcal {O}_r\) the hereditary closure of \(\mathcal {O}\).
24.4.5
Suppose \(({\mathcal {O}} \mid \mathfrak{p })=1\), i.e., \(\mathcal {O}\) is an Eichler order (Lemma 24.3.6). Suppose \(\mathcal {O}\) has level \(\mathfrak p ^e\). Then \(\mathcal {O}^\natural \) is an Eichler order of level \(\mathfrak p ^{e-2}\) from (23.4.18)—it had to be Eichler of some level by Corollary 23.4.10. So the chain (24.4.4) is of length \(\lfloor e/2 \rfloor \) with quotients \(\dim _k(\mathcal {O}_i/\mathcal {O}_{i+1})=2\). On the Bruhat–Tits tree, the Eichler order corresponds to a path of length e by 23.5.16, and \(\mathcal {O}^\natural \) is the path of length \(e-2\) obtained by plucking away the vertices on the ends. (If desired, one can refine this chain by squeezing in an extra Eichler order in between each step.)
24.4.6
If \(\mathcal {O}=R+\mathfrak p \mathcal {O}'\) for an order \(\mathcal {O}'\), then \(\mathcal {O}^\natural = \mathcal {O}'\), by Exercise 24.5.
In general, write \(\mathcal {O}=R+\mathfrak p ^f{{\,\mathrm{Gor}\,}}(\mathcal {O})\) where \(\mathfrak p ^f=\mathfrak f (\mathcal {O})\) is the Gorenstein conductor of \(\mathcal {O}\) and \({{\,\mathrm{Gor}\,}}(\mathcal {O})\) is the Gorenstein saturation as in Proposition 24.2.15. Then the chain of radical idealizers begins
For each i, we have \(\dim _k(\mathcal {O}_i/\mathcal {O}_{i+1})=3\).
We next consider the chain of superorders over a (local) residually inert order.
Proposition 24.4.7
Let \(\mathcal {O}\) be a residually inert R-order. Then the following statements hold.
-
(a)
\({{\,\mathrm{rad}\,}}\mathcal {O}= {{\,\mathrm{rad}\,}}\mathcal {O}^\natural \cap \mathcal {O}= \mathfrak p \mathcal {O}^\natural \).
-
(b)
Suppose \(\mathcal {O}\) is not maximal. Then \(\mathcal {O}^\natural \) is the unique minimal superorder of \(\mathcal {O}\). Moreover, \(\mathcal {O}^\natural \) is residually inert and we have \([\mathcal {O}^\natural :\mathcal {O}]_R=\mathfrak p ^2\).
Proof. We begin with the first part of (a), and we show \({{\,\mathrm{rad}\,}}\mathcal {O}^\natural \cap \mathcal {O}= {{\,\mathrm{rad}\,}}\mathcal {O}\). As in 21.2.1, \(\mathcal {O}^\natural \) is a radical cover so \({{\,\mathrm{rad}\,}}\mathcal {O}\subseteq {{\,\mathrm{rad}\,}}\mathcal {O}^\natural \cap \mathcal {O}\). But arguing as in the proof of Lemma 21.2.4, we know that \({{\,\mathrm{rad}\,}}\mathcal {O}^\natural \) is topologically nilpotent as a \(\mathcal {O}'\)-ideal and \(\mathfrak p ^r \mathcal {O}' \subseteq \mathfrak p \mathcal {O}\) for large r, so \({{\,\mathrm{rad}\,}}\mathcal {O}^\natural \cap \mathcal {O}\) is topologically nilpotent as a \(\mathcal {O}\)-ideal, and \({{\,\mathrm{rad}\,}}\mathcal {O}^\natural \cap \mathcal {O}\subseteq {{\,\mathrm{rad}\,}}\mathcal {O}\).
We therefore have a map
since \(\mathcal {O}/{{\,\mathrm{rad}\,}}\mathcal {O}\) is a quadratic field, we must have \(({\mathcal {O}^\natural } \mid \mathfrak{p })=*,-1\), i.e., \(\mathcal {O}^\natural \) is either maximal or residually inert—and in the latter case, (24.4.8) is an isomorphism.
Let \(i \in \mathcal {O}\) generate \(\ell =\mathcal {O}/{{\,\mathrm{rad}\,}}\mathcal {O}\) as a quadratic extension of k. Let \(K=F(i)\), and let S be the integral closure of R in K. Then K is (separable and) unramified over F. We claim that \(\mathcal {O}_S = \mathcal {O}\otimes _R S\) is residually split. Indeed, we have an isomorphism of k-algebras

and since \(\ell \) is separable over k, an identification (Exercise 7.19)
giving \(({{\,\mathrm{rad}\,}}\mathcal {O})_S={{\,\mathrm{rad}\,}}(\mathcal {O}_S)\) and
But \(\mathcal {O}/{{\,\mathrm{rad}\,}}\mathcal {O}=\ell \otimes _k \ell \simeq \ell \times \ell \). This shows \(({\mathcal {O}_S} \mid \mathfrak{p S}) = 1\).
To conclude, the statements that \({{\,\mathrm{rad}\,}}\mathcal {O}^\natural \cap \mathcal {O}= \mathfrak p \mathcal {O}^\natural \) in (a) and that \([\mathcal {O}^\natural :\mathcal {O}]_R=\mathfrak p ^2\) in (b) hold for \(\mathcal {O}_S\) by (23.4.18), so they hold for \(\mathcal {O}\). Minimality follows from Proposition 24.4.12. \(\square \)
24.4.9
As a consequence of Proposition 24.4.7, if \(\mathcal {O}\) is a residually inert R-order with \({{\,\mathrm{discrd}\,}}(\mathcal {O})=\mathfrak p ^e\), then the radical idealizer chain
has length \(r=\lfloor e/2 \rfloor \), with \(\mathcal {O}_r\) maximal, and \(\dim _k (\mathcal {O}_i/\mathcal {O}_{i+1})=2\) for all i; accordingly, the case e even occurs exactly when \(B \simeq {{\,\mathrm{M}\,}}_2(F)\) and e odd occurs exactly when B is a division algebra.
We conclude the section showing that under certain hypotheses, the radical idealizer is a minimal (proper) superorder. The results are due to Drozd–Kirichenko–Roiter [DKR67, Propositions 1.3, 10.3]; we follow Curtis–Reiner [CR81, Exercises 37.5, 37.7].
Definition 24.4.10
Let \(I' \subseteq I\) be left fractional \(\mathcal {O}\)-ideals in B. We say \(I'\) is (left) hypercharacteristic in I if for every left \(\mathcal {O}\)-module homomorphism \(\phi :I' \rightarrow I\) we have \(\phi (I') \subseteq I'\).
Lemma 24.4.11
The map \(\mathcal {O}' \mapsto I'=(\mathcal {O}')^\sharp \) gives an inclusion-reversing bijection from the set of R-superorders \(\mathcal {O}' \supseteq \mathcal {O}\) to the set of right hypercharacteristic R-sublattices \(I' \subseteq \mathcal {O}^\sharp \).
Proof. Inclusing-reversing follows from Lemma 15.6.2(a). By the proof of Lemma 17.3.3, we have a natural identification \({{\,\mathrm{Hom}\,}}_{\mathcal {O}}(I',I) \simeq (I:I'){}_{\textsf {\tiny {R}} }\) given by right multiplication.
We first show that if \(\mathcal {O}' \supseteq \mathcal {O}\), then \((\mathcal {O}')^\sharp \subseteq \mathcal {O}\) is right hypercharacteristic; so we verify \((\mathcal {O}^\sharp :(\mathcal {O}')^\sharp ){}_{\textsf {\tiny {R}} }\subseteq (\mathcal {O}')^\sharp \). If \((\mathcal {O}')^\sharp \alpha \subseteq \mathcal {O}^\sharp \), then
so \(\alpha \mathcal {O}\subseteq \mathcal {O}'\), thus \(\alpha =\alpha \cdot 1 \in \mathcal {O}'=\mathcal {O}{}_{\textsf {\tiny {R}} }((\mathcal {O}')^\sharp )\). Conversely, given \(I' \subseteq \mathcal {O}^\sharp \) hypercharacteristic, we have \(\alpha \in (I')^\sharp \) if and only if \({{\,\mathrm{trd}\,}}(I'\alpha ) \subseteq R\) if and only if \(\alpha \in (I':\mathcal {O}){}_{\textsf {\tiny {R}} }=(I':I')=\mathcal {O}{}_{\textsf {\tiny {R}} }(I')\), so \((I')^\sharp =\mathcal {O}{}_{\textsf {\tiny {R}} }(I')\) is an R-order. \(\square \)
Proposition 24.4.12
Let R be local and let \(\mathcal {O}\) be a Gorenstein R-order that is not maximal and such that \(\mathcal {O}\) is indecomposable as a left \(\mathcal {O}\)-module. Then there is a unique minimal R-superorder \(\mathcal {O}' \supsetneq \mathcal {O}\) and \(\mathcal {O}'=\mathcal {O}^\natural \).
Proof. Since \(\mathcal {O}\) is projective indecomposable as a \(\mathcal {O}\)-module, and \(\mathcal {O}\) is Gorenstein so \(\mathcal {O}^\sharp \) is projective, we must have \(\mathcal {O}^\sharp =\mathcal {O}\alpha \) for some \(\alpha \in B^\times \). Let \(J={{\,\mathrm{rad}\,}}\mathcal {O}\). By Corollary 20.6.9, \(J\mathcal {O}^\sharp \) is the unique \(\mathcal {O}\)-submodule of \(\mathcal {O}^\sharp \). If \(J\mathcal {O}^\sharp \beta = \mathcal {O}^\sharp \) for some \(\beta \in B^\times \), then \(J=\mathcal {O}\alpha \beta \alpha ^{-1}\), so \(\mathcal {O}{}_{\textsf {\tiny {L}} }(J)=\mathcal {O}\) and \(\mathcal {O}\) is extremal; but an extremal order that is indecomposable is already maximal, a contradiction. Therefore, if \(J\mathcal {O}^\sharp \beta \subseteq \mathcal {O}^\sharp \) then the inclusion is strict, and by maximality we have \(J\mathcal {O}^\sharp \beta \subseteq J\mathcal {O}^\sharp \); that is to say, \(J\mathcal {O}^\sharp \) is hypercharacteristic in \(\mathcal {O}^\sharp \). By Lemma 24.4.11, and inclusion-reversing, we see that
is the unique minimal R-superorder, and \(\mathcal {O}'=\mathcal {O}{}_{\textsf {\tiny {R}} }(J^\sharp )=\mathcal {O}{}_{\textsf {\tiny {L}} }(J)\) by Proposition 15.6.6. \(\square \)
24.4.13
Let R be local and \(\mathcal {O}\) be a Gorenstein R-order. By Lemma 20.6.8, the condition that \(\mathcal {O}\) is indecomposable is equivalent to the condition that \(\mathcal {O}/{{\,\mathrm{rad}\,}}\mathcal {O}\) is simple as a k-algebra, i.e.,  or equivalently, \(\mathcal {O}\) is not Eichler. We considered the Eichler case in 24.4.5, so suppose further that \(\mathcal {O}\) is not Eichler (and in particular, not maximal). Then \(\mathcal {O}^\natural \supseteq \mathcal {O}\) is the minimal R-superorder over \(\mathcal {O}\) by Proposition 24.4.12. If \(\mathcal {O}^\natural \) is not itself Gorenstein, then we may associate its Gorenstein saturation \({{\,\mathrm{Gor}\,}}(\mathcal {O}^\natural )\). In this way, we obtain a canonical chain of Gorenstein superorders of \(\mathcal {O}\).
or equivalently, \(\mathcal {O}\) is not Eichler. We considered the Eichler case in 24.4.5, so suppose further that \(\mathcal {O}\) is not Eichler (and in particular, not maximal). Then \(\mathcal {O}^\natural \supseteq \mathcal {O}\) is the minimal R-superorder over \(\mathcal {O}\) by Proposition 24.4.12. If \(\mathcal {O}^\natural \) is not itself Gorenstein, then we may associate its Gorenstein saturation \({{\,\mathrm{Gor}\,}}(\mathcal {O}^\natural )\). In this way, we obtain a canonical chain of Gorenstein superorders of \(\mathcal {O}\).
5 Bass and basic orders
Given the importance of the Gorenstein condition, we will want to give a name to the condition that every superorder is Gorenstein.
In this section, we restore our hypothesis that R is a Dedekind domain.
Definition 24.5.1
An order \(\mathcal {O}\) is Bass if every order \(\mathcal {O}' \supseteq \mathcal {O}\) is Gorenstein.
24.5.2
Since the Gorenstein condition is local by 24.2.2, the Bass condition is also local. Moreover, an Eichler (i.e., residually split) order is Bass, because Eichler orders are Gorenstein by 24.2.14, and every superorder of an Eichler order is Eichler (Corollary 23.4.10).
For the rest of this section, we investigate the local structure of Bass orders, and we suppose that R is local. We do not use the following proposition, but we state it for context.
Proposition 24.5.3
Suppose R is local. Then the following are equivalent:
-
(i)
Every \(\mathcal {O}\)-ideal is generated by two elements;
-
(ii)
\(\mathcal {O}\) is Bass; and
-
(iii)
Every \(\mathcal {O}\)-lattice is isomorphic to a direct sum of \(\mathcal {O}\)-ideals.
Proof. See Drozd–Kirichenko–Roiter [DKR67, Propositions 12.1, 12.5] or Curtis–Reiner [CR81, §37]; the implications (i) \(\Rightarrow \) (ii) \(\Rightarrow \) (iii) always hold, and the implication (iii) \(\Rightarrow \) (i) holds because B is a quaternion algebra. \(\square \)
The residually inert orders, those with Eichler symbol \(({\mathcal {O}} \mid \mathfrak{p })=-1\), give a source of Bass orders, following Brzezinski [Brz83a, §3].
Proposition 24.5.4
Let \(\mathcal {O}\) be a residually inert R-order. Then \(\mathcal {O}\) is Bass.
Proof. We begin by arguing as in the proof of Proposition 24.4.7: letting \(i \in \mathcal {O}\) generate the field extension \(\mathcal {O}/P \supseteq k\), we then make a base extension to \(K=F(i)\) where \(i \in \mathcal {O}\) generates \(\mathcal {O}/{{\,\mathrm{rad}\,}}\mathcal {O}\): then \(\mathcal {O}_S\) is residually split, i.e., \(\mathcal {O}_S\) is Eichler.
We then appeal to Proposition 24.2.23: the Gorenstein condition is stable under base change. So for every superorder \(\mathcal {O}' \supseteq \mathcal {O}\), we have a superorder \(\mathcal {O}'_S \supseteq \mathcal {O}_S\) and so \(\mathcal {O}'_S\) is Gorenstein by 24.5.2, so \(\mathcal {O}'\) is Gorenstein. Therefore \(\mathcal {O}\) is Bass. \(\square \)
24.5.5
Combining 24.5.2 with Proposition 24.5.4, we see that if \(\mathcal {O}\) is not a Bass order, then  .
.
Another rich source of Bass orders are the basic orders.
Definition 24.5.6
We say \(\mathcal {O}\) is basic if \(\mathcal {O}\) contains a maximal R-order in a maximal commutative F-subalgebra \(K \subseteq B\).
Remark 24.5.7
Local basic orders in a division quaternion algebra were studied by Hijikata–Pizer–Shemanske [HPS89b]; they gave the global orders \(\mathcal {O}\) such that \(\mathcal {O}_{(\mathfrak p )}\) is basic if \(\mathfrak p \in {{\,\mathrm{Ram}\,}}(B)\) and Eichler if \(\mathfrak p \not \in {{\,\mathrm{Ram}\,}}(B)\) the name special . The remaining types of local basic orders (residually ramified and residually inert for the matrix ring) were studied by Brzezinski [Brz90], and further worked on by Jun [Jun97]. The role of the embedded maximal quadratic R-algebra S is that one can compute embedding numbers for them (see for example the epic work of Hijikata–Pizer–Shemanske [HPS89a]), and therefore compute explicitly with the trace formula.
Other authors use the term primitive instead of basic, but this quickly gets confusing as the word primitive is used for the ternary quadratic forms and the two notions do not coincide. The following propositions show that the sound of the word basic conveys the right meaning.
Proposition 24.5.8
Suppose R is local. Then \(\mathcal {O}\) is basic if and only if \(\mathcal {O}\) is Bass.
Proof. See Chari–Smertnig–Voight [CSV2019, Theorem 1.1]. To illustrate the proof, we explain here only the case where \(2 \in R^\times \), following Brzezinski [Brz90, Proposition 1.11].
Let \(Q:M \rightarrow R\) be the ternary quadratic form associated to \(\mathcal {O}\), a representative up to twisted similarity chosen so that Q is integral. We argue explicitly with a quadratic form (22.3.5) the multiplication table of the order as a Clifford algebra in a good basis (22.3.7).
First, suppose \(\mathcal {O}\) is Bass. Then \(\mathcal {O}\) is Gorenstein, so after rescaling we may suppose \(Q \sim \langle -1,b,c \rangle \), and the multiplication table reads:
If \({{\,\mathrm{ord}\,}}_\mathfrak p (b) \le 1\) or \({{\,\mathrm{ord}\,}}_\mathfrak p (c) \le 1\), then correspondingly R[j] or R[k] are maximal (again by valuation of discriminant), so suppose \({{\,\mathrm{ord}\,}}_\mathfrak p (b),{{\,\mathrm{ord}\,}}_\mathfrak p (c) \ge 2\). Consider the R-submodule \(\mathcal {O}'\) generated by \(1,i',j,k\) with \(i'=i/\pi \). Then the integrality of the multiplication table remains intact so \(\mathcal {O}'\) is an order, with new coefficients \(a'=\pi \), \(b'=b/\pi \), \(c'=c/\pi \). The corresponding ternary quadratic form \(Q'\), by our hypotheses on valuations, is now imprimitive and \(\mathcal {O}'\) is not Gorenstein, and this contradicts the fact that \(\mathcal {O}\) is Bass.
Conversely, suppose \(\mathcal {O}\) is basic. If the maximal R-order \(S \subseteq \mathcal {O}\) is in an unramified subalgebra \(K=FS \subseteq B\), then it generates an unramified extension over the residue field and \(({\mathcal {O}} \mid \mathfrak{p }) \ne 0\), and then by 24.5.5 we know \(\mathcal {O}\) is Bass. Now at least one of the products bc, ac, ab has valuation 1 because \(\mathcal {O}\) contains a maximal R-order; without loss of generality we may take, after rescaling, \(a=-1\) and \({{\,\mathrm{ord}\,}}_\mathfrak p (b)=1 \le {{\,\mathrm{ord}\,}}_\mathfrak p (c)\) with \(S=R[k]\). Therefore Q is primitive and \(\mathcal {O}\) is Gorenstein.
We now compute that \({{\,\mathrm{rad}\,}}\mathcal {O}= \langle \pi ,i,j,k \rangle \) and so
is the minimal superorder, and it is still basic. By minimality, to show that \(\mathcal {O}\) is Bass it suffices to show that \(\mathcal {O}'=\mathcal {O}^\natural \) is Bass. In our new parameters we have \(a',b',c'=-\pi ,b/\pi ,c/\pi \), so \({{\,\mathrm{ord}\,}}_\mathfrak p (b')=0\) and \({{\,\mathrm{ord}\,}}_\mathfrak p (c')={{\,\mathrm{ord}\,}}_\mathfrak p (c)-1\). Swapping \(i',j'\) interchanges \(a',b'\), and we are back in the original situation but with \({{\,\mathrm{ord}\,}}_\mathfrak p (c)\) reduced. By induction, we can continue in this way until \({{\,\mathrm{ord}\,}}_\mathfrak p (c)=0\), when then R[j] is a maximal order in an unramified extension, and we are done. \(\square \)
Proposition 24.5.10
Suppose \(F={{\,\mathrm{Frac}\,}}(R)\) is a number field. Then for the R-order \(\mathcal {O}\), the following are equivalent:
-
(i)
\(\mathcal {O}\) is basic;
-
(ii)
\(\mathcal {O}_{(\mathfrak p )}\) is basic for all primes \(\mathfrak p \) of R; and
-
(iii)
\(\mathcal {O}\) is Bass.
In other words, for orders in a quaternion algebra over a number field, being basic is a local property and it is equivalent to being Bass.
Proof. See Chari–Smertnig–Voight [CSV2019, Theorem 1.2], building on work of Eichler [Eic36, Satz 8] for the case \(F=\mathbb Q \). \(\square \)
Remark 24.5.11
One can similarly define basic orders for a general Dedekind domain R, but the preceding results are not known in this level of generality.
24.5.12
We established several other important features along the way in Proposition 24.5.8 that we now record. Suppose R is local with \(2 \in R^\times \) and suppose that \(\mathcal {O}\) is a residually ramified Bass (i.e., basic) order. Then the quadratic form associated to \(\mathcal {O}\) is similar to \(\langle -1, b,c \rangle \) with \({{\,\mathrm{ord}\,}}_\mathfrak p (b)=1 \le {{\,\mathrm{ord}\,}}_\mathfrak p (c)\), and so the multiplication table (24.5.9) holds. The unique superorder \(\mathcal {O}^\natural \) has \([\mathcal {O}^\natural :\mathcal {O}]_R=\mathfrak p \) and associated ternary quadratic form \(\langle -1, b, -c/b \rangle \) (see Exercise 24.13).
Corollary 24.5.13
If \(\mathcal {O}^\natural \) is not hereditary, then  .
.
Proof. Since \(\mathcal {O}^\natural \) is not hereditary, we cannot have \(\mathcal {O}\) maximal, so \(({\mathcal {O}} \mid \mathfrak{p })=1,0,-1\). If  , then \(\mathcal {O}\) is Eichler, and so too are its superorders. If
, then \(\mathcal {O}\) is Eichler, and so too are its superorders. If  and \(\mathcal {O}^\natural \) is not maximal, then
and \(\mathcal {O}^\natural \) is not maximal, then  by Proposition 24.4.7(b). For the case
by Proposition 24.4.7(b). For the case  , we appeal to 24.5.12. \(\square \)
, we appeal to 24.5.12. \(\square \)
We can repackage what we have done for basic orders to give another description in terms of its hereditary closure.
Proposition 24.5.14
Let \(\mathcal {O}\) be a basic, nonhereditary R-order with \({{\,\mathrm{discrd}\,}}(\mathcal {O})=\mathfrak p ^n\). Suppose \(2 \in R^\times \), and let \(S \subseteq \mathcal {O}\) be a maximal R-order in the F-algebra K. Let J be the Jacobson radical of the hereditary closure of \(\mathcal {O}\). Then the following statements hold.
-
(a)
Suppose \(\mathcal {O}\) is residually inert. Then \(\mathcal {O}=S + J^m\) where \(m=n/2,n-1\) according as B is ramified or split.
-
(b)
Suppose \(\mathcal {O}\) is residually ramified. Then \(\mathcal {O}=S + J^m\) where \(m=n-1\).
Proof. The statement follows by induction using the explicit descriptions of these orders in 24.3.7, 24.5.12, and 24.5.12. See Brzezinski [Brz90, Proposition 1.12]. \(\square \)
6 Tree of odd Bass orders
To conclude this chapter, we draw a picture of the containments of Bass orders.
Suppose R is local with finite residue field k and \(2 \in R^\times \). We put together the radical idealizer chains in the residually split 24.4.5, residually inert 24.4.9, and residually ramified 24.5.12 cases. The resulting tree of Bass orders is shown in Figure 24.6.1.
Each vertex of this graph represents an isomorphism class of Bass order; there is an edge between two vertices if and only if there is a minimal containment between them. In each case, such a containment is given by the radical idealizer except when the order is residually split (in which case it hops by two, skipping the minimal superorder).
For the trees when 2 is a uniformizer in R, and many other explicit calculations, see Lemurell [Lem2011, §5], as well as Pacetti–Sirolli [PS2014, §5].
Exercises
Unless otherwise specified, let R be a Dedekind domain with \(F={{\,\mathrm{Frac}\,}}R\) and let \(\mathcal {O}\subseteq B\) be an R-order in a quaternion algebra B.
- 1.:
-
Show that every Eichler order \(\mathcal {O}\) is Gorenstein by showing \(\mathcal {O}^\sharp \) is locally principal by direct computation.
- 2.:
-
Show that \({{\,\mathrm{codiff}\,}}(\mathcal {O})\) is right invertible if and only if
$$\begin{aligned} {{\,\mathrm{codiff}\,}}(\mathcal {O}) ({{\,\mathrm{codiff}\,}}(\mathcal {O})^2)^\sharp = \mathcal {O}\end{aligned}$$and \({{\,\mathrm{codiff}\,}}(\mathcal {O})\) is left invertible if and only if
$$\begin{aligned} ({{\,\mathrm{codiff}\,}}(\mathcal {O})^2)^\sharp {{\,\mathrm{codiff}\,}}(\mathcal {O}) = \mathcal {O}. \end{aligned}$$[Hint: show that \(({{\,\mathrm{codiff}\,}}(\mathcal {O})^{-1})^\sharp = {{\,\mathrm{codiff}\,}}(\mathcal {O})^2\).]
- \(\triangleright \) 3.:
-
Suppose R is local. Show that if \(\mathcal {O}\) is an R-order and B is a division algebra, then
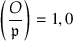 .
. - \(\triangleright \) 4.:
-
Suppose R is local with finite residue field. Recall the discriminant quadratic form and the generalized Kronecker symbol 24.3.3.
- (a):
-
Show that
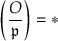 if and only if
if and only if 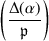 takes on all of the values \(-1,0,1\) for \(\alpha \in \mathcal {O}\).
takes on all of the values \(-1,0,1\) for \(\alpha \in \mathcal {O}\). - (b):
-
For \(\epsilon =-1,0,1\), show that
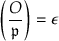 if and only if
if and only if 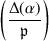 takes the values \(\{0,\epsilon \}\) for \(\alpha \in \mathcal {O}\).
takes the values \(\{0,\epsilon \}\) for \(\alpha \in \mathcal {O}\).
- \(\triangleright \) 5.:
-
Let R be local and suppose \(\mathcal {O}=R + \mathfrak p \mathcal {O}'\) for an order \(\mathcal {O}'\). Show that \({{\,\mathrm{rad}\,}}\mathcal {O}= \mathfrak p \mathcal {O}'\) and \(\mathcal {O}^\natural =\mathcal {O}'\). [Hint: Argue as in 23.4.15.]
- 6.:
-
Let \(Q:M \rightarrow L\) be a ternary quadratic module, and let \(\mathfrak a \) be a fractional ideal. Write \(\mathfrak a Q = Q \otimes \mathfrak a :M \otimes \mathfrak a \rightarrow L \otimes \mathfrak a ^2\) for the twist. Show that there is a bijection \({{\,\mathrm{Cl}\,}}Q \leftrightarrow {{\,\mathrm{Cl}\,}}\mathfrak a Q\), and conclude that there is a bijection \({{\,\mathrm{Typ}\,}}\mathcal {O}\leftrightarrow {{\,\mathrm{Typ}\,}}{{\,\mathrm{Gor}\,}}(\mathcal {O})\), where \({{\,\mathrm{Gor}\,}}(\mathcal {O})\) is the Gorenstein saturation.
- 7.:
-
- (a):
-
Show that if \({{\,\mathrm{discrd}\,}}(\mathcal {O})\) is cubefree (i.e., there is no prime \(\mathfrak p \) of R such that \(\mathfrak p ^3 \mid {{\,\mathrm{discrd}\,}}(\mathcal {O})\)) then \(\mathcal {O}\) is a Bass order.
- (b):
-
Show that there is a (local) Gorenstein order \(\mathcal {O}\) with
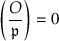 that is not Bass with \({{\,\mathrm{discrd}\,}}(\mathcal {O})=\mathfrak p ^4\).
that is not Bass with \({{\,\mathrm{discrd}\,}}(\mathcal {O})=\mathfrak p ^4\).
- 8.:
-
Suppose that \(\mathcal {O}\) is Gorenstein with
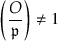 . Let \(\mathcal {O}'\) be the hereditary closure of \(\mathcal {O}\). Show that \(N_{B^\times }(\mathcal {O}) \le N_{B^\times }(\mathcal {O}')\), and further that equality holds when \(\mathcal {O}\) is residually inert.
. Let \(\mathcal {O}'\) be the hereditary closure of \(\mathcal {O}\). Show that \(N_{B^\times }(\mathcal {O}) \le N_{B^\times }(\mathcal {O}')\), and further that equality holds when \(\mathcal {O}\) is residually inert. - 9.:
-
Let R be local and let \(\mathcal {O}\) be a residually ramified quaternion R-order that is Gorenstein but not a Bass order. Let \(\mathcal {O}^\natural \) be the unique minimal order containing \(\mathcal {O}\). Show that \(\mathfrak f (\mathcal {O}^\natural )=\mathfrak p \). [See Brzezinski [Brz83a, Lemma 4.4].]
- 10.:
-
Let R be local with \(2 \in R^\times \), and let \(Q=\langle -1,b,c \rangle :R^3 \rightarrow R\) with \(0={{\,\mathrm{ord}\,}}_\mathfrak p (b)<{{\,\mathrm{ord}\,}}_\mathfrak p (c)\). Let \(\mathcal {O}={{\,\mathrm{Clf}\,}}^0(Q)\) be its even Clifford algebra. Show that
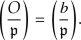
- 11.:
-
Let R be local, let \(\mathcal {O}={{\,\mathrm{M}\,}}_2(R)\), let \(\mathcal {O}_1\) be the standard Eichler order of level \(\mathfrak p ^e\) and let \(\mathcal {O}_2=R + \mathfrak p ^e \mathcal {O}\). Show that \(\mathcal {O}_2 \subsetneq \mathcal {O}_1 \subsetneq \mathcal {O}\), that \({{\,\mathrm{Gor}\,}}(\mathcal {O}_2)=\mathcal {O}\), but \({{\,\mathrm{Gor}\,}}(\mathcal {O}_1)=\mathcal {O}_1\); conclude that the Gorenstein saturation is not (necessarily) the smallest Gorenstein superorder.
- 12.:
-
Let R be local and let \(\mathcal {O}\) be the standard Eichler order of level \(\mathfrak p ^e\) with \(e \ge 2\). Show that \(\mathcal {O}\) contains no integrally closed quadratic R-order that is a domain (even though \(\mathcal {O}\) contains \(R \times R\)).
- \(\triangleright \) 13.:
-
Let R be local with \(2 \in R^\times \).
- (a):
-
Show (using the proof of Proposition 24.5.8) that \(\mathcal {O}\) is a local Bass order with
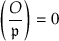 if and only if its corresponding ternary quadratic form is similar to \(\langle -1,b,c \rangle \) with \({{\,\mathrm{ord}\,}}_\mathfrak p (b)=1 \le {{\,\mathrm{ord}\,}}_\mathfrak p (c)\).
if and only if its corresponding ternary quadratic form is similar to \(\langle -1,b,c \rangle \) with \({{\,\mathrm{ord}\,}}_\mathfrak p (b)=1 \le {{\,\mathrm{ord}\,}}_\mathfrak p (c)\). - (b):
-
In case (a), show that the minimal overorder \(\mathcal {O}'\) corresponds to the (similarity class of) ternary quadratic form \(\langle -1, b, -c/b \rangle \).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
This chapter is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, duplication, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, a link is provided to the Creative Commons license and any changes made are indicated.The images or other third party material in this chapter are included in the work's Creative Commons license, unless indicated otherwise in the credit line; if such material is not included in the work's Creative Commons license and the respective action is not permitted by statutory regulation, users will need to obtain permission from the license holder to duplicate, adapt or reproduce the material.
Copyright information
© 2021 The Author(s)
About this chapter
Cite this chapter
Voight, J. (2021). Quaternion orders: second meeting. In: Quaternion Algebras. Graduate Texts in Mathematics, vol 288. Springer, Cham. https://doi.org/10.1007/978-3-030-56694-4_24
Download citation
DOI: https://doi.org/10.1007/978-3-030-56694-4_24
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-56692-0
Online ISBN: 978-3-030-56694-4
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


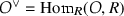 is projective as an
is projective as an 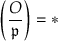 if and only if
if and only if 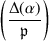 takes on all of the values
takes on all of the values 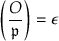 if and only if
if and only if 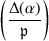 takes the values
takes the values 
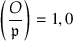 .
.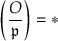 if and only if
if and only if 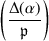 takes on all of the values
takes on all of the values 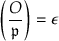 if and only if
if and only if 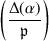 takes the values
takes the values 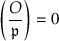 that is not Bass with
that is not Bass with 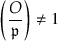 . Let
. Let 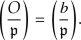
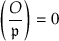 if and only if its corresponding ternary quadratic form is similar to
if and only if its corresponding ternary quadratic form is similar to