Abstract
To motivate the classification of quaternion algebras over \(\mathbb Q \), we consider by analogy a classification of quadratic fields. We restrict to the following class of quadratic fields for the best analogy.
You have full access to this open access chapter, Download chapter PDF
In this chapter, we discuss quaternion algebras over global fields and characterize them up to isomorphism.
1 \(\triangleright \) Ramification
To motivate the classification of quaternion algebras over \(\mathbb Q \), we consider by analogy a classification of quadratic fields. We restrict to the following class of quadratic fields for the best analogy.
Definition 14.1.1
A quadratic field \(F=\mathbb Q (\sqrt{d})\) of discriminant \(d \in \mathbb Z \) is mildly ramified if \(8 \not \mid d\).
A quadratic field F is mildly ramified if and only if \(F=\mathbb Q (\sqrt{m})\) where \(m \ne 1\) is odd and squarefree; then \(d=m\) or \(d=4m\) according as \(m=1,3 \pmod {4}\).
Let \(F=\mathbb Q (\sqrt{d})\) be a mildly ramified quadratic field of discriminant \(d \in \mathbb Z \) and let R be its ring of integers. A prime p ramifies in F, i.e. \(pR=\mathfrak p ^2\) for a prime ideal \(\mathfrak p \subset R\), if and only if \(p \mid d\).
But a discriminant d can be either positive or negative; to put this bit of data on the same footing, we define the set of places of \(\mathbb Q \) to be the primes together with the symbol \(\infty \), and we make the convention that \(\infty \) ramifies in F if \(d<0\) and is unramified if \(d>0\). Let \(F=\mathbb Q (\sqrt{d})\) be a mildly ramified quadratic field, and let \({{\,\mathrm{Ram}\,}}(F)\) be the set of places that ramify in F. The set \({{\,\mathrm{Ram}\,}}(F)\) determines F up to isomorphism, since the discriminant of F is the product of the odd primes in \({{\,\mathrm{Ram}\,}}(F)\), multiplied by 4 if \(2 \in {{\,\mathrm{Ram}\,}}(F)\) and by \(-1\) if \(\infty \in {{\,\mathrm{Ram}\,}}(F)\). (For bookkeeping reasons, in this context it would probably therefore be better to consider 4 and \(-1\) as primes, but we will resist the inducement here.) However, not every finite set of places \(\Sigma \) occurs: the product d corresponding to \(\Sigma \) is a discriminant if and only if \(d \equiv 0,1 \pmod {4}\). We call this a parity condition on the set of ramifying places of a mildly ramified quadratic field:
with the convention that \(\infty \) is congruent to \(-1 \pmod {4}\).
Note that if \(\Sigma \) is a finite subset of places of \(\mathbb Q \) and \(2 \not \in \Sigma \), then precisely one of either \(\Sigma \) or \(\Sigma \cup \{\infty \}\) satisfies the parity condition; accordingly, if we define \(m(\Sigma )\) to be the product of all odd primes in \(\Sigma \) multiplied by \(-1\) if \(\infty \in \Sigma \), then we can recover \(\Sigma \) from \(m(\Sigma )\).
We have proven the following result.
Lemma 14.1.2
The maps \(F \mapsto {{\,\mathrm{Ram}\,}}(F)\) and \(\Sigma \mapsto m(\Sigma )\) furnishes a bijection

This classification procedure using sets of ramifying primes and discriminants works as well for quaternion algebras over \(\mathbb Q \). Let B be a quaternion algebra over \(\mathbb Q \). When is a prime p ramified in B? In Chapter 12, we saw that the completion \(B_p=B \otimes _\mathbb Q \mathbb Q _p\) is either a division ring or the matrix ring \({{\,\mathrm{M}\,}}_2(\mathbb Q _p)\). Further, when \(B_p\) is a division ring, the valuation ring \(\mathcal {O}_p \subset B_p\) is the unique maximal order, and the unique maximal ideal \(P_p \subset \mathcal {O}_p\) satisfies \(p\mathcal {O}_p=P_p^2\). By analogy with the quadratic case, we say that a place v is ramified in B if the completion \(B_v\) is a division ring, and otherwise v is unramified (or split ).
Let  . Without loss of generality, we may suppose \(a,b \in \mathbb Z \). There are only finitely many places where B is ramified: by the calculation of the Hilbert symbol (12.4.12), if p is prime and \(p \not \mid 2ab\), then \((a,b)_\mathbb{Q _p}=1\) and p is split in B. Therefore \(\#{{\,\mathrm{Ram}\,}}B <\infty \).
. Without loss of generality, we may suppose \(a,b \in \mathbb Z \). There are only finitely many places where B is ramified: by the calculation of the Hilbert symbol (12.4.12), if p is prime and \(p \not \mid 2ab\), then \((a,b)_\mathbb{Q _p}=1\) and p is split in B. Therefore \(\#{{\,\mathrm{Ram}\,}}B <\infty \).
We say that B is definite
if \(\infty \in {{\,\mathrm{Ram}\,}}B\) and B is indefinite
otherwise. By definition, B is definite if and only if  if and only if \(a,b<0\) (Exercise 2.4).
if and only if \(a,b<0\) (Exercise 2.4).
Let \({{\,\mathrm{Ram}\,}}B\) be the set of ramified places of B. Not every finite subset \(\Sigma \) of places can occur as \({{\,\mathrm{Ram}\,}}B\) for a quaternion algebra B. It turns out that the parity condition here is that we must have \(\#\Sigma \) even. So again, if \(\Sigma \) is a finite set of primes, then precisely one of either \(\Sigma \) or \(\Sigma \cup \{\infty \}\) can occur as \({{\,\mathrm{Ram}\,}}B\). We define the discriminant of B to be the product \({{\,\mathrm{disc}\,}}B\) of primes that ramify in B, so \({{\,\mathrm{disc}\,}}B\) is a squarefree positive integer. This notion of discriminant is admittedly strange; we relate it to perhaps more familiar notions in Chapter 15.
The main result of this chapter, specialized to the case \(F=\mathbb Q \), is the following.
Main Theorem 14.1.3
The maps \(B \mapsto {{\,\mathrm{Ram}\,}}B\) and \(\Sigma \mapsto \prod _{p \in \Sigma } p\) furnish bijections

The composition of these maps is \(B \mapsto \prod _{p \in {{\,\mathrm{Ram}\,}}B} p = {{\,\mathrm{disc}\,}}B\).
As previewed at the end of section 12.1, Main Theorem 14.1.3 is a local-global principle and provides a convenient way to test when quaternion algebras over \(\mathbb Q \) are isomorphic: instead of working hard over \(\mathbb Q \), we can just test for isomorphism over the local fields \(\mathbb Q _p\) and \(\mathbb R \).
We will spend the next two sections giving a self-contained proof of Main Theorem 14.1.3 following Serre [Ser73, Chapters III–IV], assuming two statements from basic number theory (quadratic reciprocity and the existence of primes in arithmetic progression), finishing the proof in section 14.3. Although the proofs presented do not seem to generalize beyond \(F=\mathbb Q \), the argument is simple enough and its structure is good motivation for the more involved treatment in the Chapter ahead. (It is also comforting to see a complete proof in the simplest case.)
2 \(\triangleright \) Hilbert reciprocity over the rationals
To begin, we look into the parity condition: it has a simple reformulation in terms of the Hilbert symbol (section 12.4). For a place v of \(\mathbb Q \), let \(\mathbb Q _v\) denote the completion of \(\mathbb Q \) at the absolute value associated to v: if \(v=p\) is prime, then \(\mathbb Q _v=\mathbb Q _p\) is the field of p-adic numbers; if \(v=\infty \), then \(\mathbb Q _v=\mathbb R \). For \(a,b \in \mathbb Q ^\times \), we abbreviate \((a,b)_\mathbb{Q _v}=(a,b)_v\).
Proposition 14.2.1
(Hilbert reciprocity). For all \(a,b \in \mathbb Q ^\times \), we have
where the product taken over all places v of \(\mathbb Q \).
When p is odd and divides neither numerator nor denominator of a or b, we have \((a,b)_p=1\), so the product (14.2.2) is well-defined. The following corollary is an equivalent statement.
Corollary 14.2.3
Let B be a quaternion algebra over \(\mathbb Q \). Then the set \({{\,\mathrm{Ram}\,}}B\) is finite of even cardinality.
The law of Hilbert reciprocity, as it turns out, is a core premise in number theory: it is equivalent to the law of quadratic reciprocity

for odd primes p, q together with the supplement

for odd primes p.
We now give a proof of Hilbert reciprocity (Proposition 14.2.1), assuming the law of quadratic reciprocity and its supplement.
Proof of Proposition 14.2.1
Since each local Hilbert symbol is bilinear, it suffices to prove the statement when \(a,b \in \mathbb Z \) are equal to either \(-1\) or a prime number. The Hilbert symbol is also symmetric, so we may interchange a, b.
If \(a=b=-1\), then  is the rational Hamiltonians, and \((-1,-1)_{\infty }=(-1,-1)_2=-1\) and \((-1,-1)_v=1\) if \(v \ne 2,\infty \), by the computation of the even Hilbert symbol (12.4.13). Similarly, the cases with \(a=-1,2\) follow from the supplement (14.2.5), and are requested in Exercise 14.1.
is the rational Hamiltonians, and \((-1,-1)_{\infty }=(-1,-1)_2=-1\) and \((-1,-1)_v=1\) if \(v \ne 2,\infty \), by the computation of the even Hilbert symbol (12.4.13). Similarly, the cases with \(a=-1,2\) follow from the supplement (14.2.5), and are requested in Exercise 14.1.
So we may suppose \(a=p\) and \(b=q\) are primes. If \(p=q\) then  and we reduce to the previous case, so we may suppose \(p \ne q\). Since \(p,q>0\), we have \((p,q)_\infty =1\). We have \((p,q)_{\ell }=1\) for all primes \(\ell \not \mid 2pq\), and
and we reduce to the previous case, so we may suppose \(p \ne q\). Since \(p,q>0\), we have \((p,q)_\infty =1\). We have \((p,q)_{\ell }=1\) for all primes \(\ell \not \mid 2pq\), and

by 12.4.12. Finally,
i.e., \((p,q)_2=(-1)^{(p-1)(q-1)/4}\), again by the computation of the even Hilbert symbol (12.4.13). Thus the product becomes

by quadratic reciprocity. \(\square \)
Hilbert reciprocity has several aesthetic advantages over the law of quadratic reciprocity. For one, it is simpler to write down! Also, Hilbert believed that his reciprocity law is a kind of analogue of Cauchy’s integral theorem, expressing an integral as a sum of residues (Remark 14.6.4). The fact that a normalized product over all places is trivial also arises quite naturally: if we define for \(x \in \mathbb Q ^\times \) and a prime p the normalized absolute value
and \(|x \,|_\infty \) the usual archimedean absolute value, then
by unique factorization in \(\mathbb Z \); this is called the product formula for \(\mathbb Q \), for obvious reasons.
From the tight relationship between quaternion algebras and ternary quadratic forms, we obtain the following corollary.
Corollary 14.2.6
Let Q be a nondegenerate ternary quadratic form over \(\mathbb Q \). Then the set of places v such that \(Q_v\) is anisotropic is finite and of even cardinality.
In particular, by Corollary 14.2.6, if \(Q_v\) is isotropic for all but one place v of \(\mathbb Q \), then \(Q_v\) is in fact isotropic for all places v.
Proof. In the bijection implied by Main Theorem 5.2.5, the quadratic form Q corresponds to a quaternion algebra  , and by Main Theorem 5.4.4, Q is isotropic if and only if B is split if and only if \((a,b)_\mathbb{Q }=1\). By functoriality, the same is true over each completion \(\mathbb Q _v\) for v a place of \(\mathbb Q \), and therefore the set of places v where \(Q_v\) is isotropic is precisely the set of ramified places in B. The result then follows by Hilbert reciprocity. \(\square \)
, and by Main Theorem 5.4.4, Q is isotropic if and only if B is split if and only if \((a,b)_\mathbb{Q }=1\). By functoriality, the same is true over each completion \(\mathbb Q _v\) for v a place of \(\mathbb Q \), and therefore the set of places v where \(Q_v\) is isotropic is precisely the set of ramified places in B. The result then follows by Hilbert reciprocity. \(\square \)
To conclude this section, we show that every allowable product of Hilbert symbols is obtained.
Proposition 14.2.7
Let \(\Sigma \) be a finite set of places of \(\mathbb Q \) of even cardinality. Then there exists a quaternion algebra B over \(\mathbb Q \) with \({{\,\mathrm{Ram}\,}}B=\Sigma \).
Remark 14.2.8. Albert [Alb34, Theorem 2, Theorem 3] already sought to simplify the presentation of a quaternion algebra by a series of transformations, the content of which is contained in Proposition 14.2.7; this was further investigated by Latimer [Lat35].
Just as with Hilbert reciprocity, Proposition 14.2.7 touches on a deep statement in number theory concerning primes, due to Dirichlet.
Theorem 14.2.9
(Infinitude of primes in arithmetic progression). Given \(a,n \in \mathbb Z \) coprime, there are infinitely many primes \(p \equiv a ~(\text{ mod } ~{n})\).
Proof. See e.g. Serre [Ser73, Chapter VI] or Apostol [Apo76, Chapter 7]. We will prove this theorem in Exercise 26.11 as a consequence of the analytic class number formula. \(\square \)
Remark 14.2.10. Theorem 14.2.9 seems to require analysis. (For algebraic proofs in special cases, see e.g., Neukirch [Neu99, Exercise I.10.1] and Lenstra–Stevenhagen [LS91].) Ram Murty [Mur88] showed that a “Euclidean proof” of the infinitude of primes \(p \equiv a \pmod {n}\) is possible if and only if \(a^2 \equiv 1 \pmod {n}\), and Paul Pollack [Pol2010] has shown that Schnizel’s Hypothesis H gives a heuristic for this. This crucial role played by analytic methods motivates part III of this monograph.
We now prove Proposition 14.2.7 assuming Theorem 14.2.9.
Proof. Let \(D :=\prod _{p \in \Sigma } p\) be the product of the primes in \(\Sigma \), and let \(u :=-1\) if \(\infty \in \Sigma \) and \(u :=1\) otherwise. Let \(D^\diamondsuit :=uD\). We consider quaternion algebras of the form

with \(q^\diamondsuit =uq\) (and q prime) chosen to satisfy certain congruence conditions ensuring that \({{\,\mathrm{Ram}\,}}B=\Sigma \). To this end, we seek a prime q such that

and
There exists a prime satisfying the conditions (14.2.11)–(14.2.12) by Theorem 14.2.9, since the condition to be a quadratic nonresidue is a congruence condition on \(q^\diamondsuit \) and hence on q modulo p.
We now verify that B has \({{\,\mathrm{Ram}\,}}B=\Sigma \). We have \((q^\diamondsuit ,D^\diamondsuit )_\infty =u\) by choice of signs and \((q^\diamondsuit ,D^\diamondsuit )_p=1\) for all \(p \not \mid 2dq\). We compute that

by (14.2.11). For \(p=2\), we find that \((q^\diamondsuit ,D^\diamondsuit )_2=-1\) or \((q^\diamondsuit ,D^\diamondsuit )_2=1\) according as \(2 \mid D\) or not by the computation of the even Hilbert symbol (12.4.13). This shows that
The final symbol \((q^\diamondsuit ,D^\diamondsuit )_q\) is determined by Hilbert reciprocity (Proposition 14.2.1): since \(\#\Sigma \) is already even, we must have \((q^\diamondsuit ,D^\diamondsuit )_q=1\). Therefore the quaternion algebra  has \(\Sigma ={{\,\mathrm{Ram}\,}}B\). \(\square \)
has \(\Sigma ={{\,\mathrm{Ram}\,}}B\). \(\square \)
Example 14.2.13
Let \(B=({a,b} \mid \mathbb{Q })\) be a quaternion algebra of prime discriminant \(D=p\) over \(\mathbb Q \). Then:
-
(i)
For \(D=p=2\), we take \(a=b=-1\);
-
(ii)
For \(D=p \equiv 3 ~(\text{ mod } ~{4})\), we take \(b=-p\) and \(a=-1\);
-
(iii)
For \(D=p \equiv 1 ~(\text{ mod } ~{4})\), we take \(b=-p\) and \(a=-q\) where \(q \equiv 3 ~(\text{ mod } ~{4})\) is prime and
 .
.
In case (iii), by qudaratic reciprocity  so indeed B is not ramified at p. In the proof of Theorem 14.2.9 above, we would have required the more restrictive condition \(q \equiv 3 ~(\text{ mod } ~{8})\), but we can look again at the table of even Hilbert symbols (12.4.16): since \(b=-p=-1,3 ~(\text{ mod } ~{8})\), we may take \(a=-q=1,-3 ~(\text{ mod } ~{8})\) freely, so \(q \equiv 3 ~(\text{ mod } ~{4})\).
so indeed B is not ramified at p. In the proof of Theorem 14.2.9 above, we would have required the more restrictive condition \(q \equiv 3 ~(\text{ mod } ~{8})\), but we can look again at the table of even Hilbert symbols (12.4.16): since \(b=-p=-1,3 ~(\text{ mod } ~{8})\), we may take \(a=-q=1,-3 ~(\text{ mod } ~{8})\) freely, so \(q \equiv 3 ~(\text{ mod } ~{4})\).
Similarly, for discriminant D the product of two (distinct) primes:
-
(i)
For \(D=2p\) with \(p \equiv 3 ~(\text{ mod } ~{4})\), we take \(a=-1\) and \(b=p\);
-
(ii)
For \(D=2p\) with \(p \equiv 5 ~(\text{ mod } ~{8})\), we take \(a=2\) and \(b=p\);
-
(iii)
For \(D=pq\) with \(p \equiv q \equiv 3 ~(\text{ mod } ~{4})\), we take \(a=-1\) and \(b=pq\);
-
(iv)
For \(D=pq\) with \(p \equiv 1 ~(\text{ mod } ~{4})\) or \(q \equiv 1 ~(\text{ mod } ~{4})\) and
 , we take \(a=p\) and \(b=q\).
, we take \(a=p\) and \(b=q\).
For other explicit presentations of quaternion algebras over \(\mathbb Q \) with specified discriminant, see Alsina–Bayer [AB2004, §1.1.2]. See Example 15.5.7 for some explicit maximal orders.
3 \(\triangleright \) Hasse–Minkowski theorem over the rationals
To complete the proof of Main Theorem 14.1.3, we now show that the map \(B \mapsto {{\,\mathrm{Ram}\,}}B\) is injective on isomorphism classes.
Proposition 14.3.1
Let \(B,B'\) be quaternion algebras over \(\mathbb Q \). Then the following are equivalent:
-
(i)
\(B \simeq B'\);
-
(ii)
\({{\,\mathrm{Ram}\,}}B={{\,\mathrm{Ram}\,}}B'\);
-
(iii)
\(B_v \simeq B_v'\) for all places \(v \in {{\,\mathrm{Pl}\,}}(\mathbb Q )\); and
-
(iv)
\(B_v \simeq B_v'\) for all but one place v.
The statement of Proposition 14.3.1 is a local-global principle: the global isomorphism class is determined by the local isomorphism classes.
Corollary 14.3.2
Let B be a quaternion algebra over \(\mathbb Q \). Then \(B \simeq {{\,\mathrm{M}\,}}_2(\mathbb Q )\) if and only if \(B_p \simeq {{\,\mathrm{M}\,}}_2(\mathbb Q _p)\) for all primes p.
Proof. Apply Proposition 14.3.1 (i) \(\Leftrightarrow \) (iv) with \(B'={{\,\mathrm{M}\,}}_2(\mathbb Q )\) checking all but the archimedean place. \(\square \)
By the equivalence between quaternion algebras and quadratic forms (see Chapter 5, specifically section 5.2), the statement of Proposition 14.3.1 is equivalent to the statement that a ternary quadratic form over \(\mathbb Q \) is isotropic if and only if it is isotropic over all (but one) completions. In fact, the more general statement is true—and again we come in contact with a deep result in number theory.
Theorem 14.3.3
(Hasse–Minkowski). Let Q be a quadratic form over \(\mathbb Q \). Then Q is isotropic if and only if \(Q_v\) is isotropic for all places v of \(\mathbb Q \).
We will prove the Hasse–Minkowski theorem by induction on the number of variables. Of particular interest is the case of (nondegenerate) ternary quadratic forms, for which we have the following theorem of Legendre.
Theorem 14.3.4
(Legendre). Let \(a,b,c \in \mathbb Z \) be nonzero, squarefree integers that are relatively prime in pairs. Then the quadratic form
has a nontrivial solution \(x,y,z \in \mathbb Q \) if and only if a, b, c do not all have the same sign and
\(-ab\), \(-bc\), \(-ac\) are quadratic residues modulo \(|c \,|\), \(|a \,|\), \(|b \,|\), respectively.
Proof. First, the conditions for solvability are necessary. The condition on signs is necessary for a solution in \(\mathbb R \). If \(ax^2+by^2+cz^2=0\) with \(x,y,z \in \mathbb Q \) not all zero, then scaling we may suppose \(x,y,z \in \mathbb Z \) satisfy \(\gcd (x,y,z)=1\); if \(p \mid c\) then \(p \not \mid y\) (else \(p \mid x\) and \(p \mid z\), contradiction), so \((x/y)^2 \equiv (-b/a) \pmod {|c \,|}\) and \(-ba\) is a quadratic residue modulo \(|c \,|\); the other conditions hold by symmetry.
So suppose the conditions hold. Multiplying through and rescaling by squares (Exercise 14.8), we may suppose a, b are squarefree (but not necessarily coprime) and \(c=-1\), and we seek a nontrivial solution to \(ax^2+by^2=z^2\). If \(a \in \mathbb Q ^{\times 2}\), then we are done. Otherwise, we need to solve
for \(x,y,z \in \mathbb Q \) and \(y \ne 0\), i.e., we need to show that b is a norm from \(F=\mathbb Q (\sqrt{a})\). By hypothesis, a, b are not both negative and
We may also suppose \(|a \,| \le |b \,|\).
We use complete induction on \(m=|a \,|+|b \,|\). If \(m=2\), then we must consider the equation \(\pm x^2 \pm y^2=z^2\) with the case both negative signs excluded, each of which has solutions. Now suppose that \(m>2\) so \(|b \,| \ge 2\), and let \(p \mid b\) be prime divisor. By hypothesis, there exist integers \(t,b'\) such that \(t^2=a+bb'\); taking a small residue, we may suppose \(|t \,| < |b \,|/2\). Thus
so \(bb'\) is a norm from F. Thus b is a norm if and only if \(b'\) is a norm. But
because \(|b \,| \ge 2\).
Now write \(b'=b''u^2\) with \(b'',u \in \mathbb Z \) and \(b''\) squarefree. Then \(|b'' \,| \le |b' \,|<|b \,|\) and \(b''\) is a norm if and only if \(b'\) is a norm. With these manipulations, we propagate the hypothesis that \(|a \,|\) is a square modulo \(|b'' \,|\) and \(|b'' \,|\) is a square modulo \(|a \,|\). Therefore, the induction hypothesis applies to the equation \(ax^2+b''y^2=z^2\), and the proof is complete. \(\square \)
Corollary 14.3.6
Let Q be a nondegenerate ternary quadratic form over \(\mathbb Q \). Then Q is isotropic if and only if \(Q_v\) is isotropic for all places v of \(\mathbb Q \) (but one).
Proof. If Q is isotropic, then \(Q_v\) is isotropic for all v. For the converse, suppose that \(Q_v\) is isotropic for all places v of \(\mathbb Q \). As in the proof of Legendre’s Theorem 14.3.4, we may suppose \(Q(x,y,z)=ax^2+by^2-z^2\). The fact that Q is isotropic over \(\mathbb R \) implies that a, b are not both negative. Now let \(p \mid a\) be odd. The condition that \(Q_p\) is isotropic is equivalent to \((a,b)_p=(b/p)=1\); putting these together, we conclude that b is a quadratic residue modulo \(|a \,|\). The same holds for a, b interchanged, so (14.3.5) holds and the result follows. \(\square \)
We are now in a position to complete the proof of the Hasse–Minkowski theorem.
Proof of Theorem 14.3.3
We follow Serre [Ser73, Theorem 8, §IV.3.2]. We may suppose that Q is nondegenerate in \(n \ge 1\) variables. If \(n=1\), the statement is vacuous. If \(n=2\), the after scaling we may suppose \(Q(x,y)=x^2-ay^2\) with \(a \in \mathbb Q ^\times \); since \(Q_p\) is isotropic for all primes p, we have \(a \in \mathbb Q _p^{\times 2}\) so in particular \(v_p(a)\) is even for all primes p; since Q is isotropic at \(\infty \), we have \(a>0\); thus by unique factorization \(a \in \mathbb Q ^{\times 2}\), and the result follows. If \(n=3\), the statement is proven in Corollary 14.3.6.
Now suppose \(n \ge 4\). Write \(Q=\langle a,b \rangle \boxplus -Q'\) where \(Q'=\langle c_1,\dots ,c_{n-2} \rangle \) and \(a,b,c_i \in \mathbb Z \). Let \(d=2ab(c_1\cdots c_{n-2}) \ne 0\). For each prime \(p \mid d\), since Q is isotropic, there exists \(t_p \in \mathbb Q _p^\times \) represented by both \(\langle a,b \rangle \) and \(Q'\) in \(\mathbb Q _p\). (This requires a small argument, see Exercise 6.14.) Similarly, there exists \(t_\infty \in \mathbb R ^\times \) represented by these forms in \(\mathbb R \).
By another application of the infinitude of primes in arithmetic progression (Exercise 14.10), there exists \(t \in \mathbb Q ^\times \) such that:
-
(i)
\(t \in t_p\mathbb Q _p^{\times 2}\) for all primes \(p \mid d\),
-
(ii)
t and \(t_\infty \) have the same sign, and
-
(iii)
\(p \not \mid t\) for all primes \(p \not \mid d\) except possibly for one prime \(q \not \mid d\).
Now the quadratic form \(\langle a,b,-t \rangle \) is isotropic for all \(p \mid d\) and at \(\infty \) by construction and at all primes \(p \not \mid d\) except \(p=q\) since \(p \not \mid abt\). Therefore, by case \(n=3\) (using the “all but one” in Corollary 14.3.6), the form \(\langle a,b,-t\rangle \) is isotropic.
On the other side, if \(n=4\), then the form \(\langle t \rangle \boxplus Q'\) is isotropic by the same argument. If \(n \ge 5\), then we apply the induction hypothesis to \(Q'\): the hypothesis holds, since \(Q'\) is isotropic at \(\infty \) and all \(p \mid d\) by construction, and for all \(p \not \mid d\) the completion \(Q'_p\) is a nondegenerate form in \(\ge 3\) variables over \(\mathbb Z _p\) so is isotropic by the results of section 12.3, using Hensel’s lemma to lift a solution modulo the odd prime p.
Putting these two pieces together, we find that Q is isotropic over \(\mathbb Q \). \(\square \)
We conclude with the following consequence.
Corollary 14.3.7
Let \(Q,Q'\) be quadratic forms over \(\mathbb Q \) in the same number of variables. Then \(Q \simeq Q'\) if and only if \(Q_v \simeq Q_v'\) for all places v.
Proof. The implication (\(\Rightarrow \)) is immediate. We prove (\(\Leftarrow \)) by induction on the number of variables, the case of \(n=0\) variables being clear. By splitting the radical (4.3.9), we may suppose that \(Q,Q'\) are nondegenerate. Let \(a \in \mathbb Q ^\times \) be represented by Q. Since \(Q_v \simeq Q_v'\) the quadratic form \(\langle -a \rangle \boxplus Q'\) is isotropic at v for all v, so \(Q'\) represents a (Lemma 5.4.3). In both cases, we can write \(Q \simeq \langle -a \rangle \boxplus Q_1\) and \(Q' \simeq \langle -a \rangle \boxplus Q_1'\) for quadratic forms \(Q_1,Q_1'\) in one fewer number of variables. Finally, by Witt cancellation (Theorem 4.2.22), from \(Q_v \simeq Q_v'\) we have \((Q_1)_v \simeq (Q_1')_v\) for all v, so by induction \(Q_1 \simeq Q_1'\), and thus \(Q \simeq Q'\). \(\square \)
We now officially complete our proofs.
Proof of Proposition 14.3.1
The implications (i) \(\Rightarrow \) (ii) and (iii) \(\Rightarrow \) (iv) are immediate. For the implication (ii) \(\Rightarrow \) (iii): either \(v \in {{\,\mathrm{Ram}\,}}B\), in which case \(B_v \simeq B_v'\) is the unique division algebra over \(\mathbb Q _v\) (Theorem 12.1.5), or \(v \not \in {{\,\mathrm{Ram}\,}}B\), in which case \(B_v \simeq {{\,\mathrm{M}\,}}_2(\mathbb Q _v) \simeq B_v'\) by definition. For the implication (iv) \(\Rightarrow \) (i), recalling Theorem 5.1.1, by Corollary 14.3.6 applied to the ternary quadratic form associated to B, we conclude that this form is isotropic, which by Proposition 5.1.2 implies that \(B \simeq {{\,\mathrm{M}\,}}_2(\mathbb Q )\). \(\square \)
Proof of Main Theorem 14.1.3
The map \(B \mapsto {{\,\mathrm{Ram}\,}}B\) has the desired codomain, by Hilbert reciprocity (Proposition 14.2.1); it is surjective by Proposition 14.2.7; and it is injective by Corollaries 14.3.6 and 14.3.7. The second bijection (with squarefree integers) is immediate. \(\square \)
To summarize these past few sections, the classification of quaternion algebras over \(\mathbb Q \) embodies some deep statements in number theory: quadratic reciprocity (and its reformulation in Hilbert reciprocity), the Hasse–Minkowski theorem (the local-global principle for quadratic forms), and the proofs use the theorem of the infinitude of primes in arithmetic progression! It is a small blessing that we can make these essentially elementary arguments over \(\mathbb Q \). In the more general case, we must dig more deeply.
For fun, we conclude this section with a consequence in number theory: Legendre’s three-square theorem (cf. Lagrange’s four-square theorem, Theorem 11.4.3, and Remark 11.4.4).
Theorem 14.3.8
(Legendre–Gauss). An integer \(n \ge 0\) can be written as the sum of three squares \(n=x^2+y^2+z^2\) if and only if n is not of the form \(n=4^a(8b+7)\) with \(a,b \in \mathbb Z \).
Proof. Looking modulo 8, we see that the provided condition is necessary (Exercise 14.3(a)). Conversely, suppose \(n>0\) is not of the form \(n=4^a(8b+7)\), or equivalently that \(-n \not \in \mathbb Q _2^{\times 2}\) (Exercise 14.4). We may suppose \(a=0,1\).
Let \(B=({-1,-1} \mid \mathbb{Q })\) be the rational Hamiltonians. We have \({{\,\mathrm{Ram}\,}}B=\{2,\infty \}\), which is to say the associated ternary quadratic form \(x^2+y^2+z^2\) is isotropic over \(\mathbb Q _p\) for all odd primes p. Consider the quadratic form \(Q(x,y,z,w)=x^2+y^2+z^2-nw^2\). Then Q is isotropic over \(\mathbb R \) since \(n>0\), and isotropic over all \(\mathbb Q _p\) with p odd taking \(w=0\). The form is also isotropic over \(\mathbb Q _2\) (Exercise 14.3), lifting a solution modulo 8 via Hensel’s lemma. By the Hasse–Minkowski theorem (Theorem 14.3.3), Q is isotropic over \(\mathbb Q \), so there exist \(x,y,z,w \in \mathbb Q \) not all zero such that \(x^2+y^2+z^2=nw^2\). We must have \(w \ne 0\) by positivity, and dividing through we get \(x,y,z \in \mathbb Q \) not all zero such that \(x^2+y^2+z^2=n\). Let \(\alpha =xi+yj+zij \in B\). Then \(\alpha ^2+n=0\) and \(\alpha \in B\) is integral.
Let \(\mathcal {O}' \subset B\) be a maximal order containing \(\alpha \), and let \(\mathcal {O}\) be the Hurwitz order. By Proposition 11.3.7, \(\mathcal {O}'\) is conjugate to \(\mathcal {O}\); after conjugating, we may suppose \(\alpha \in \mathcal {O}\). But \({{\,\mathrm{trd}\,}}(\alpha )=0\), so necessarily \(\alpha \in \mathbb Z \langle i,j\rangle \) and \(x,y,z \in \mathbb Z \) with \({{\,\mathrm{nrd}\,}}(\alpha )=x^2+y^2+z^2=n\) as desired. \(\square \)
See also Exercise 14.5 for a variant of the proof of the three-square theorem staying in the language of quaternions.
4 Global fields
In this chapter and in many that remain, we focus on a certain class of fields of arithmetic interest: a global field is either a finite extension of \(\mathbb Q \) (a number field) or of \(\mathbb F _p(t)\) (a function field) for a prime p. Global fields are strongly governed by their completions with respect to nontrivial absolute values, which are local fields. Throughout this text, we will return to this theme that global behavior is governed by local behavior.
For the rest of this chapter, let F be a global field. We quickly introduce in this section some basic notions from algebraic number theory: for further reference, see e.g. Neukirch [Neu99, Chapters I–II], Cassels [Cas2010, Chapter II], or Janusz [Jan96, Chapter II].
Remark 14.4.1. When F is a function field, we will often insist that F is equipped with an inclusion \(F_0 \hookrightarrow F\) where \(F_0 \simeq \mathbb F _p(t)\) has pure transcendence degree 1 over \(\mathbb F _p\). (For the geometrically inclined, this corresponds to a morphism \(X \rightarrow \mathbb P ^1\) of the associated curves.) Often this inclusion will not play a role, but it will be important to treat certain aspects uniformly with the number field case where there is only one inclusion \(\mathbb Q \hookrightarrow F\).
14.4.2
The set of places of F is the set \({{\,\mathrm{Pl}\,}}F\) of equivalence classes of embeddings \(\iota _v :F \rightarrow F_v\) where \(F_v\) is a local field and \(\iota _v(F)\) is dense in \(F_v\); two embeddings \(\iota _v :F \rightarrow F_v\) and \(\iota _v':F \rightarrow F_v'\) are said to be equivalent if there is an isomorphism of topological fields \(\phi :F_v \rightarrow F_v'\) such that \(\iota _v' = \phi \circ \iota _v\).
14.4.3
Every valuation \(v :F \rightarrow \mathbb R \cup \{\infty \}\), up to scaling, defines a place \(\iota _v :F \rightarrow F_v\) where v is the completion of F with respect to the absolute value induced by v; we call such a place nonarchimedean , and using this identification we will write v for both the place of F and the corresponding valuation. For a nonarchimedean place v corresponding to a local field \(F_v\), we denote by \(R_v\) its valuation ring, \(\mathfrak p _v\) its maximal ideal, and \(k_v\) its residue field. If F is a function field, then all places of F are nonarchimedean. If F is a number field, a place \(F \hookrightarrow \mathbb R \) is called a real place and a place \(F \hookrightarrow \mathbb C \) (equivalent to its complex conjugate) is called a complex place . A real or complex place is archimedean .
14.4.4
Let \(K \supseteq F\) be a finite, separable extension of fields, and let \(v \in {{\,\mathrm{Pl}\,}}F\). We say that a place w of K is above v if \(w|_F=v\), and we write \(w \mid v\). The set of places w above v are obtained as follows: since K is separable, we have an isomorphism
where each \(K_i \supseteq F_v\) is a finite extension of local fields. Indeed, writing \(K = F[x]/(f(x))\) with \(f(x) \in F[x]\) the minimal polynomial of a primitive element, we have
where \(f(x)=f_1(x)\cdots f_r(x) \in F_v[x]\) is the factorization of f(x) into irreducibles in \(F_v[x]\), distinct because f is separable. Thus each \(K_i\) is a local field by the classification in Theorem 12.2.15, and the composition
defines a place \(w_i\) of K above v. Conversely, every place w above v is equivalent to \(w_i\) for some i [Jan96, Chapter II, Theorem 5.1; Cas78, §9; Neu99, Chapter II, Proposition (8.3)].
We say that a nonarchimedean place v ramifies in K if there exists a place \(w \mid v\) such that \(K_w \supseteq F_v\) is ramified (see 13.2.3). Only finitely many places of F ramify in K.
A global field F has a set of preferred embeddings \(\iota _v :F \hookrightarrow F_v\) corresponding to each place \(v \in {{\,\mathrm{Pl}\,}}F\)—equivalently, a preferred choice of absolute values \(|\,|_v\) for each place \(v \in {{\,\mathrm{Pl}\,}}F\)—such that the product formula holds: for all \(x \in F^\times \),
where \(m_v=2\) if v is complex and \(m_v=1\) otherwise. Admittedly, the extra exponents 2 for the complex places are annoying (see Remark 12.2.3)! Often what is done is to define normalized absolute values \(\Vert x \Vert _v :=|x \,|_v^{m_v}\) for \(v \in {{\,\mathrm{Pl}\,}}F\), so then (14.4.6) becomes
Preferred absolute values are defined as follows.
14.4.8
The set of places \({{\,\mathrm{Pl}\,}}(\mathbb Q )\) of \(\mathbb Q \) consists of the archimedean real place, induced by the embedding \(\mathbb Q \hookrightarrow \mathbb R \) and the usual absolute value \(|x \,|_\infty \), and the set of nonarchimedean places indexed by the primes p given by the embeddings \(\mathbb Q \hookrightarrow \mathbb Q _p\), with the preferred absolute value
The statement of the product formula for \(x \in \mathbb Q \) is
rearranging, (14.4.9) is equivalent to \(\prod _p p^{v_p(x)} = |x \,|\), and this follows from unique factorization in \(\mathbb Z \).
14.4.10
The set of places of \(\mathbb F _p(t)\) is indexed by monic irreducible polynomials \(f(t) \in \mathbb F _p[t]\) with preferred absolute value
and 1/t, the place at infinity, with preferred absolute value
where if \(x = f/g\) is the ratio of relatively prime polynomials \(f,g \in \mathbb F _p[t]\), then \(\deg x :=\max (\deg f, \deg g)\).
Then the statement of the product formula for \(x(t) \in \mathbb F _p(t)\) is
rearranging as over \(\mathbb Q \), but now also taking the logarithm in base p, (14.4.9) is equivalent to \(\sum _f (\deg f){{\,\mathrm{ord}\,}}_f(x) = \deg x\) which follows from unique factorization in \(\mathbb F _p[t]\).
14.4.12
More generally, let \(K \supseteq F\) be a finite, separable extension of global fields. Let v be a place of F with a preferred absolute value and let w be a place of K above v. Then the preferred absolute value for w is the unique one extending v, namely
for \(x \in K\). These absolute values fit together, with
for all \(x \in K\), a consequence of (14.4.5) [Jan96, Chapter II, Theorem 5.2; Cas78, §11, Theorem, p. 59; Neu99, Chapter II, Corollary (8.4)].
In particular, if F satisfies the product formula (14.4.6) with respect to preferred absolute values, then so does K, since
Remark 14.4.15. The definitions for the preferred absolute values are pretty dry—sorry! But we will see later that they are natural from the perspective of Haar measure: see section 29.3 and ultimately (29.6.3).
We will also make use of the following notation in many places in the text. Let F be a global field.
Definition 14.4.16
A set \({{{{\texttt {\textit{S}}}}}\subseteq {{\,\mathrm{Pl}\,}}F}\) is eligible if \({{{{\texttt {\textit{S}}}}}}\) is finite, nonempty, and contains all archimedean places of F.
Definition 14.4.17
Let \({{{{\texttt {\textit{S}}}}}}\) be an eligible set of places. The ring of \({{\texttt {\textit{S}}}}\)-integers in F is the set
A global ring is a ring of \({{{{\texttt {\textit{S}}}}}}\)-integers in a global field for an associated eligible set \({{{{\texttt {\textit{S}}}}}}\).
The expression (14.4.18) makes sense, since if \({v \not \in {{{\texttt {\textit{S}}}}}}\) then by hypothesis v is nonarchimedean. When no confusion can result, we will abbreviate \({R=R_{({{{\texttt {\textit{S}}}}})}}\) for a global ring R.
Example 14.4.19
If F is a number field and \({{{{\texttt {\textit{S}}}}}}\) consists only of the archimedean places in F then \({R_{({{{\texttt {\textit{S}}}}})}}\) is the ring of integers in F, the integral closure of \(\mathbb Z \) in F, also denoted \({R_{({{{\texttt {\textit{S}}}}})}=\mathbb Z _F}\). If F is a function field, corresponding to a curve X, then \({R_{({{{\texttt {\textit{S}}}}})}}\) is the ring of all rational functions with no poles outside \({{{{\texttt {\textit{S}}}}}}\). (So in all cases, it is helpful to think of the ring \({R_{({{{\texttt {\textit{S}}}}})}}\) as consisting of those elements of F with “no poles outside \({{{{\texttt {\textit{S}}}}}}\)”.)
5 Ramification and discriminant
Let \({R=R_{({{{\texttt {\textit{S}}}}})}}\) be a global ring, with \({{{{\texttt {\textit{S}}}}}\subset {{\,\mathrm{Pl}\,}}F}\) eligible. Let B be a quaternion algebra over F.
Definition 14.5.1
Let \(v \in {{\,\mathrm{Pl}\,}}F\). We say that B is ramified at v if \(B_v=B \otimes _F F_v\) is a division ring; otherwise we say that B is split (or unramified ) at v.
Let \({{\,\mathrm{Ram}\,}}B\) denote the set of ramified places of B.
If \(v \in {{\,\mathrm{Pl}\,}}F\) is a nonarchimedean place, corresponding to a prime \(\mathfrak p \) of R, we will also say that B is ramified at \(\mathfrak p \) when B is ramified at v.
Remark 14.5.2. We use the term ramified for the following reason: if \(B_\mathfrak p \) is a division ring with valuation ring \(\mathcal {O}_\mathfrak p \), then \(\mathfrak p \mathcal {O}_\mathfrak p = P^2\) for a two-sided maximal ideal P: see Theorem 13.3.11. (Eichler [Eic55-56, §1, Theorem 4] called them characteristic primes.)
Lemma 14.5.3
The set \({{\,\mathrm{Ram}\,}}B\) of ramified places of B is finite.
Proof. Write \(B=({K,b} \mid {F})\). Since F has only finitely many archimedean places, we may suppose v is nonarchimedean. The extension \(K \supseteq F\) is ramified at only finitely many places, so we may suppose that \(K \supseteq F\) is unramified at v. Finally, \(v(b)=0\) for all but finitely many v, so we may suppose \(v(b)=0\). But then under these hypotheses, \(B_v=({K_v,b} \mid {F_v})\) is split, by Corollary 13.4.1. \(\square \)
Motivated by the fact that the discriminant of a quadratic field extension is divisible by ramifying primes, we make the following definition.
Definition 14.5.4
The R-discriminant of B is the R-ideal
obtained as the product of all primes \(\mathfrak p \) of \({R=R_{({{{\texttt {\textit{S}}}}})}}\) ramified in B.
Remark 14.5.5. When F is a number field and \({{{{\texttt {\textit{S}}}}}}\) consists of archimedean places only, so that \(R=\mathbb Z _F\) is the ring of integers of F, we abbreviate \({{\,\mathrm{disc}\,}}_R(B)={{\,\mathrm{disc}\,}}B\). The discriminant \({{\,\mathrm{disc}\,}}_R(B)\) discards information about primes in \({{{{\texttt {\textit{S}}}}}}\): only \({{\,\mathrm{Ram}\,}}B\) records information about B that is independent of \({{{{\texttt {\textit{S}}}}}}\).
Remark 14.5.6. One could make the same definitions when R is more generally a Dedekind domain. However, unless the residue fields of R are finite, this is not as useful a notion: see Exercise 14.14. (In some sense, this is because the Brauer group of \(F={{\,\mathrm{Frac}\,}}R\) is not as simply described as when F is a global field, viz. Remark 14.6.10.)
As usual, the archimedean places play a special role for number fields, so we make the following definition.
Definition 14.5.7
Let F be a number field. We say that B is totally definite if all archimedean places of F are ramified in B; otherwise, we say B is indefinite .
14.5.8
If v is a complex place, then v is necessarily split, since the only quaternion algebra over \(\mathbb C \) is \({{\,\mathrm{M}\,}}_2(\mathbb C )\); therefore, if B is a totally definite quaternion algebra over a number field F, then F is totally real.
6 Quaternion algebras over global fields
We now generalize Main Theorem 14.1.3 to the global field F, deducing results characterizing isomorphism classes of quaternion algebras. The main result is as follows.
MainTheorem 14.6.1
Let F be a global field. Then the map \(B \mapsto {{\,\mathrm{Ram}\,}}B\) gives a bijection

In other words, if B is a quaternion algebra over a global field, then the set of places of F where B is ramified is finite and of even cardinality, this set uniquely determines B up to isomorphism, and every such set occurs.
Proof. We give a proof in section 26.8, which itself relies on an analytic result (Theorem 26.8.19) proven in Chapter 29.
Alternatively, this statement can also be viewed a direct consequence of a (hard-earned) fundamental exact sequence in class field theory: see Remark 14.6.10. \(\square \)
Recall the definition of the Hilbert symbol (as in section 12.4), computed explicitly for v an odd nonarchimedean place (12.4.9): for a place v of F, we abbreviate \((a,b)_{F_v}=(a,b)_v\). We also recall Lemma 14.5.3 that \((a,b)_v=1\) for all but finitely many places v.
Corollary 14.6.2
(Hilbert reciprocity). Let F be a global field with \({{\,\mathrm{char}\,}}F \ne 2\) and let \(a,b \in F^\times \). Then
Proof. Immediate from Main Theorem 14.6.1: Hilbert reciprocity is equivalent to the statement that \(\#{{\,\mathrm{Ram}\,}}B\) is even. \(\square \)
Remark 14.6.4. Stating the reciprocity law in the form (14.6.3) is natural from the point of view of the product formula (14.4.6). And Hilbert reciprocity can be rightly seen as a law of quadratic reciprocity for number fields (as we saw in section 14.2 for \(F=\mathbb Q \)). (For more, see Exercise 14.16.)
Hilbert saw his reciprocity law (Corollary 14.6.2) as an analogue of Cauchy’s integral theorem [Hil32, p. 367–368]; for more on this analogy, see Vostokov [Vos2009].
Corollary 14.6.5
(Local-global principle for quaternion algebras). Let \(B,B'\) be quaternion algebras over F. Then the following are equivalent:
-
(i)
\(B \simeq B'\);
-
(ii)
\({{\,\mathrm{Ram}\,}}B={{\,\mathrm{Ram}\,}}(B')\);
-
(iii)
\(B_v \simeq B'_v\) for all places \(v \in {{\,\mathrm{Pl}\,}}F\); and
-
(iv)
\(B_v \simeq B'_v\) for all but one place \(v \in {{\,\mathrm{Pl}\,}}F\).
In particular, \(B \simeq {{\,\mathrm{M}\,}}_2(F)\) if and only if \({{\,\mathrm{Ram}\,}}B=\emptyset \).
Proof. For the equivalence (i) \(\Leftrightarrow \) (ii) \(\Leftrightarrow \) (iii), combine Main Theorem 14.6.1 and the fact that for a noncomplex place v there is a unique division algebra over \(F_v\). The equivalence (iii) \(\Leftrightarrow \) (iv) follows from the parity constraint, since if v is a place and \({{\,\mathrm{Ram}\,}}B \smallsetminus \{v\}=\Sigma \), then \(v \in {{\,\mathrm{Ram}\,}}B\) or not according as \(\#\Sigma \) is odd or even. \(\square \)
Remark 14.6.6. Corollary 14.6.5 is a special case of the Albert–Brauer–Hasse–Noether theorem [AH32, BHN31]: a central simple algebra A over F such that \(A_v \simeq {{\,\mathrm{M}\,}}_n(F_v)\) for all \(v \in {{\,\mathrm{Pl}\,}}F\) has \(A \simeq {{\,\mathrm{M}\,}}_n(F)\). See Remark 14.6.10 for further discussion.
The statement of Corollary 14.6.5 is the local-global principle for quaternion algebras: the isomorphism class of a quaternion algebra over a global field is determined by its isomorphism classes over the collection of local fields obtained as completions of the global field. In a similar way, we have a local-global principle for quadratic embeddings as follows.
Proposition 14.6.7
(Local-global principle for splitting/embeddings). Let \(K \supseteq F\) be a finite separable extension of global fields. Then the following are equivalent:
-
(i)
K splits B, i.e., \(B \otimes _F K \simeq {{\,\mathrm{M}\,}}_2(K)\); and
-
(ii)
For all places \(w \in {{\,\mathrm{Pl}\,}}K\), the field \(K_w\) splits B.
If \(\dim _F K=2\), then these are further equivalent to:
-
(iii)
There is an embedding \(K \hookrightarrow B\) of F-algebras;
-
(iv)
For all places \(v \in {{\,\mathrm{Pl}\,}}F\), there is an embedding \(K_v \hookrightarrow B_v\) of \(F_v\)-algebras; and
-
(v)
Every \(v \in {{\,\mathrm{Ram}\,}}B\) does not split in K, i.e., \(K_v\) is a field for all \(v \in {{\,\mathrm{Ram}\,}}B\).
Proof. The equivalence (i) \(\Leftrightarrow \) (ii) is a consequence of Corollary 14.6.5: they are both equivalent to \({{\,\mathrm{Ram}\,}}B_K = \emptyset \), since K splits B if and only if \(B \otimes _F K \simeq {{\,\mathrm{M}\,}}_2(K)\) if and only if \({{\,\mathrm{Ram}\,}}(B \otimes _F K)=\emptyset \) if and only if for all places w of K we have \(B \otimes _F K_w \simeq {{\,\mathrm{M}\,}}_2(K_w)\).
The equivalence (i) \(\Leftrightarrow \) (iii) was given by Lemmas 5.4.7 and 6.4.12.
The implication (iii) \(\Rightarrow \) (iv) is clear. For the implication (iv) \(\Rightarrow \) (v), if \(v \in {{\,\mathrm{Ram}\,}}B\), then \(B_v\) is a division algebra; so if \(K_v\) is not a field, then we cannot have \(K_v \hookrightarrow B_v\). Finally, for (v) \(\Rightarrow \) (ii), let \(w \in {{\,\mathrm{Pl}\,}}K\) with \(w \mid v \in {{\,\mathrm{Pl}\,}}F\). If \(v \not \in {{\,\mathrm{Ram}\,}}B\) then already \(F_v\) splits B; otherwise, \(v \in {{\,\mathrm{Ram}\,}}B\) and \(K_v=K_w\) is a field with \([K_w:F_v]=2\), so by Proposition 13.4.4, \(K_w\) splits B. \(\square \)
14.6.8
The equivalences (iii) \(\Leftrightarrow \) (iv) \(\Leftrightarrow \) (v) in Proposition 14.6.7 hold also for the separable F-algebra \(K= F \times F\): for there is an embedding \(F \times F \hookrightarrow B\) if and only if \(B \simeq {{\,\mathrm{M}\,}}_2(F)\).
We also record the statement of the Hasse–Minkowski theorem over global fields, generalizing Theorem 14.3.3.
Theorem 14.6.9
(Hasse–Minkowski). Let F be a global field and let Q be a quadratic form over F. Then Q is isotropic over F if and only if \(Q_v\) is isotropic over \(F_v\) for all places v of F.
Proof. The same comments as in the proof of Main Theorem 14.6.1 apply: we give a proof in section 26.8. But see also O’Meara [O’Me73, §§65–66] for a standalone class field theory proof for the case when F is a number field. \(\square \)
This local-global principle for isotropy of quadratic forms is also called the Hasse principle. For a historical overview of the Hasse principle, and more generally Hasse’s contributions in the arithmetic theory of algebras, see Fenster–Schwärmer [FS2007].
Remark 14.6.10. The fact that quaternion algebras are classified by their ramification set (Main Theorem 14.6.1) over a global field F is a consequence of the following theorem from class field theory: there is an exact sequence
where the first map is the natural diagonal inclusion \([A] \mapsto ([A \otimes _v F_v])_v\) and the second map is the sum of the local invariant maps \({{\,\mathrm{inv}\,}}_v :{{\,\mathrm{Br}\,}}(k_v) \rightarrow \mathbb Q /\mathbb Z \) from Remark 13.4.3. The class of a quaternion algebra B in a Brauer group over a field is 2-torsion by 8.3.4, and the local invariant \({{\,\mathrm{inv}\,}}_v B_v\) is equal to 0, 1/2 according as \(B_v\) is split or ramified, and in this way we recover the main classification theorem. (In this sense, the discriminant of a quaternion algebra captures the Brauer class of a quaternion algebra at the finite places, and the ramification set captures it fully.) The exact sequence (14.6.11) is sometimes called the fundamental exact sequence of global class field theory: see Milne [Milne-CFT, §VIII.4] or Neukirch–Schmidt–Wingberg [NSW2008, Theorem 8.1.17].
7 Theorems on norms
In the previous sections, we have seen how both local-global principles allow a nice, clean understanding of quaternion algebras—and at the same time, the norm groups play an important role in this characterization. These themes will continue through the book, so we develop them here in an important first case by describing the group \({{\,\mathrm{nrd}\,}}(B^\times ) \le F^\times \).
We retain our hypotheses that F is a global field and B a quaternion F-algebra.
14.7.1
First, we recall the calculation of the local norm groups (Lemma 13.4.9): for \(v \in {{\,\mathrm{Pl}\,}}F\), we have
Under \(B \hookrightarrow B_v\), we have \({{\,\mathrm{nrd}\,}}(B^\times ) \le {{\,\mathrm{nrd}\,}}(B_v^\times )\) for all places \(v \in {{\,\mathrm{Pl}\,}}F\), and this ‘places’ a condition on the reduced norm at precisely the real ramified places.
14.7.2
Let \(\Omega \subseteq {{\,\mathrm{Ram}\,}}B\) be the set of ramified (necessarily real) archimedean places in B. (If F is a function field, then \(\Omega =\emptyset \).) Let
be the group of elements that are positive for the embeddings \(v \in \Omega \). For \(\Omega \) the set of all real places, we write simply \(F_{>0}^\times \) and call such elements totally positive.
By 14.7.1, we have \({{\,\mathrm{nrd}\,}}(B^\times ) \le F_{>_{\Omega } 0}^\times \). In fact, equality holds.
MainTheorem 14.7.4
(Hasse–Schilling). We have \({{\,\mathrm{nrd}\,}}(B^\times ) = F_{>_{\Omega } 0}^\times \).
To prove this theorem, we will use two lemmas.
Lemma 14.7.5
Let v be a noncomplex place of F. Let \(n_v \in F_v^\times \), and if v is real suppose \(n_v>0\). Then there exists \(t_v \in F_v\) such that \(x^2-t_v x + n_v\) is separable and irreducible over \(F_v\). Moreover, if \(n_v \in R_v\) then we may take \(t_v \in R_v\).
Proof. We suppose that \({{\,\mathrm{char}\,}}F_v \ne 2\) and leave the other case as an exercise (Exercise 14.22). If \(n_v \not \in F_v^{\times 2}\), then we can take \(t_v=0\); this includes the case where v is a real place. So suppose \(n_v \in F_v^{\times 2}\). Let \(K_w=F_v(\sqrt{d_v}) \supseteq F_v\) be a separable quadratic extension, and in particular \(d_v \not \in F_v^{\times 2}\). The quadratic form \(\langle 1, -4n_v \rangle \simeq \langle 1, -1 \rangle \) over \(F_v\) is a hyperbolic plane (Definition 5.4.1) so universal; let \(x_v,y_v \in F_v\) be such that \(x_v^2-4n_vy_v^2 = d_v\). We cannot have \(y_v=0\), else \(x_v^2=d_v \in F_v^{\times 2}\). Let \(t_v=x_v/y_v\). Then \(x^2-t_v x + n_v\) has discriminant \(d_v\) and so is separable and irreducible.
For the second statement, multiplying by a square we may suppose without loss of generality that \(d_v \in R\), so the equality \(t_v^2=d_v+4n_v\) implies \(v(t_v) \ge 0\) and \(t_v \in R\). \(\square \)
Next, we want to show that we can approximate a polynomial over a completion \(F_v\) by a polynomial over the global field F sufficiently well—the reader is invited to ignore this on a first reading and accept this intuitively as a consequence of the fact that F is dense in \(F_v\).
Lemma 14.7.6
Let \(v \in {{\,\mathrm{Pl}\,}}F\), let \(f_v(x)=x^2-t_v x + n_v \in F_v[x]\) be a separable polynomial, and let \(\epsilon >0\). Then there exists \(t,n \in F\) such that \(|t-t_v \,|,|n-n_v \,|<\epsilon \) and such that \(f(x)=x^2-tx + n\) has
In particular, f(x) is separable, and if \(f_v(x)\) is irreducible then so is f(x).
Further, if already \(n_v \in F\) then we may take \(n=n_v\), and similarly with t.
Proof. If \(F_v\) is nonarchimedean, the lemma follows from Corollary 13.2.9 and the fact that F is dense in \(F_v\). The case where \(F_v\) is archimedean is straightforward: see Exercise 14.23. \(\square \)
The same argument can be applied to several local fields at once, as follows.
Corollary 14.7.8
Let \(\Sigma \subseteq {{\,\mathrm{Pl}\,}}F\) be a finite set of noncomplex places. For each \(v \in \Sigma \), let \(f_v(x)=x^2-t_v x + n_v \in F_v[x]\) be a separable polynomial, and let \(\epsilon >0\). Then there exists \(t,n \in F\) such that for \(f(x)=x^2-tx+n\) and for all \(v \in \Sigma \) we have \(|t-t_v \,|,|n-n_v \,|<\epsilon \) and \(F_v[x]/(f(x)) \simeq F_v[x]/(f_v(x))\). In particular, f(x) is separable, and if \(f_v(x)\) is irreducible for some v then so is f(x).
Further, if all \(n_v=m \in F\) for \(v \in \Sigma \), then we may take \(n=m\), and similarly with t.
Proof. We repeat the argument of Lemma 14.7.6, using weak approximation (i.e., F is dense in \(\prod _v F_v\); look ahead to Lemma 28.7.1 and the adjacent discussion) for all \(v \in \Sigma \) to find t, n. \(\square \)
We now conclude with a proof of the theorem on norms.
Proof of Main Theorem 14.7.4
Let \(n \in F_{>_{\Omega } 0}^\times \). We will construct a separable quadratic extension \(K \supseteq F\) with \(K \hookrightarrow B\) such that \(n \in {{\,\mathrm{Nm}\,}}_{K|F}(K^\times )\). To this end, by Proposition 14.6.7, it is enough to find \(K \supseteq F\) such that \(K_v\) is a field for all \(v \in {{\,\mathrm{Ram}\,}}B\).
By Lemma 14.7.5, for all \(v \in {{\,\mathrm{Ram}\,}}B\), there exists \(t_v \in F_v\) such that the polynomial \(x^2-t_v x+n \in F_v[x]\) is separable and irreducible over \(F_v\); here if \(v \in \Omega \) is real we use that \(v(n)>0\). By Corollary 14.7.8, there exists \(t \in F\) such that \(x^2-t x + n\) irreducible over each \(F_v\). Let K be the extension of F obtained by adjoining a root of this polynomial. Then \(K_v\) is a field for each ramified v, and \(n \in {{\,\mathrm{Nm}\,}}_{K|F}(K^\times )\) as desired. \(\square \)
Exercises
- \(\triangleright \) 1.:
-
Complete the proof of Hilbert reciprocity (Proposition 14.2.1) in the remaining cases \((a,b)=(-1,2),(2,2),(-1,p),(2,p)\). In particular, show that
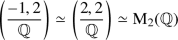
and

for \(a=-1,2\) and all primes p (cf. 12.4.13).
-
2.
Derive the law of quadratic reciprocity (14.2.4) and the supplement (14.2.5) from the statement of Hilbert reciprocity (Proposition 14.2.1).
- \(\triangleright \) 3.:
-
Let \(n \in \mathbb Z _{>0}\).
- (a):
-
Suppose n is of the form \(n=4^a(8b+7)\) with \(a,b \in \mathbb Z \). Show that there is no solution to \(x^2+y^2+z^2=n\) with \(x,y,z \in \mathbb Z \). [Hint: Look modulo 8.]
- (b):
-
Suppose n is not of the form \(n=4^a(8b+7)\) with \(a,b \in \mathbb Z \). Show that there is a solution to \(x^2+y^2+z^2=n\) with \(x,y,z \in \mathbb Z _2\). [Hint: lift a solution modulo 8 using Hensel’s lemma.]
- \(\triangleright \) 4.:
-
Let \(n \in \mathbb Z \) be nonzero. Show that n is a square in \(\mathbb Q _2\) if and only if n is of the form \(n=4^a(8b+1)\) with \(a,b \in \mathbb Z \).
-
5.
Let \(n>0\) have \(-n \not \in \mathbb Q _2^{\times 2}\). Let \(B=({-1,-1} \mid \mathbb{Q })\) and let \(K=\mathbb Q (\sqrt{-n})\). Show that K splits B. [Hint: Use the local-global principle for embeddings (Proposition 14.6.7).] Conclude that there exists \(\alpha \in B\) such that \(\alpha ^2=-n\), and conclude as in Theorem 14.3.8 that n is the sum of three squares.
-
6.
Let F be a number field. Show that every totally positive element of F is a sum of four squares of elements of F.
-
7.
Show that the law of Hilbert reciprocity (Proposition 14.2.1) implies the law of quadratic reciprocity; with the argument given in section 14.1, this completes the equivalence of these two laws.
-
8.
In the proof of Legendre’s theorem (Theorem 14.3.4), we reduced to the case \(a,b>0\) and \(c=-1\). Show that this reduction is valid.
-
9.
In this exercise, we generalize the proof of Proposition 14.2.7 to give a more general construction of quaternion quaternion algebras. Let D be a squarefree positive integer and let \(u=-1\) if D has an odd number of prime divisors, otherwise \(u :=1\).
-
(a)
For \(b \in \mathbb Z \) squarefree, show that \(K :=\mathbb Q (\sqrt{b})\) embeds in a quaternion algebra of discriminant D if and only if:
-
\(b<0\) if B is definite;
-
\(b \not \equiv 1 \pmod {8}\) if \(2 \mid D\); and
-
for all odd primes \(p \mid D\), we have
 .
.
-
-
(b)
Suppose b satisfies the conditions in (a) but with the further requirement that \(D \mid b\), i.e., in the third condition we require
 . Let q be an odd prime such that \(q^\diamondsuit :=uq\) has:
. Let q be an odd prime such that \(q^\diamondsuit :=uq\) has:-
 for all odd \(p \mid D\);
for all odd \(p \mid D\); -
 for all odd \(p \mid (b/D)\); and
for all odd \(p \mid (b/D)\); and -
\(q^\diamondsuit \equiv 1,5 \pmod {8}\) according as \(2 \not \mid D\) or \(2 \mid D\).
Note there exist infinitely many such primes q by the infinitude of primes in arithmetic progression. Then show that
 has \({{\,\mathrm{disc}\,}}B=D\) and \({{\,\mathrm{Ram}\,}}B=\Sigma \).
has \({{\,\mathrm{disc}\,}}B=D\) and \({{\,\mathrm{Ram}\,}}B=\Sigma \). -
-
(a)
- \(\triangleright \) 10.:
-
Let \({{{{\texttt {\textit{S}}}}}\subseteq {{\,\mathrm{Pl}\,}}(\mathbb Q )}\) be eligible. For each \({v \in {{{\texttt {\textit{S}}}}}}\), let \(t_v \in \mathbb Q _v^\times \) be given. Show that there exists \(t \in \mathbb Q ^\times \) such that \(t \in t_v \mathbb Q _v^{\times 2}\) for all \({v \in {{{\texttt {\textit{S}}}}}}\) and \(v_p(t)=0\) for all \({p \not \in {{{\texttt {\textit{S}}}}}\smallsetminus \{\infty \}}\) except (possibly) for one prime \(p=q\).
-
11.
Let \(F=\mathbb Q (\sqrt{d})\) be a real quadratic field. Find \(a,b \in \mathbb Q ^\times \) (depending on d) such that \(({a,b} \mid {F})\) is a division ring unramified at all finite places.
-
12.
Let \(F :=\mathbb Q (\alpha )\) where \(\alpha :=2\cos (2\pi /7)=\zeta _7+1/\zeta _7\) with \(\zeta _7=\exp (2\pi i/7)\). Let \(B :=({-1,-1} \mid {F})\). Compute \({{\,\mathrm{Ram}\,}}(B)\) and find a maximal order in B.
-
13.
Let F be a global field with \({{\,\mathrm{char}\,}}F \ne 2\) and let B be a quaternion algebra over F. Let \(L \supseteq F\) be a finite extension. An extension \(K \supseteq F\) is linearly disjoint with L over F if the multiplication map \(K \otimes _F L \xrightarrow {\smash {{\sim }}}KL\) is an isomorphism of F-algebras.
Show that there exists a splitting field \(K \supseteq F\) for B such that K is linearly disjoint with L over F.
-
14.
Show that the notion of discriminant of a quaternion algebra as the product of ramified primes is not such a great notion when R is an arbitrary Dedekind domain, as follows.
Let \(R=\mathbb Q [t]\); then R is a Dedekind domain. Let \(F={{\,\mathrm{Frac}\,}}R=\mathbb Q (t)\). Let \(B_0=({a,b} \mid \mathbb{Q })\) be a division quaternion algebra ove \(\mathbb Q \) and let \(B=B_0 \otimes _\mathbb Q F = ({a,b} \mid \mathbb{Q (t)})\). Show that there are infinitely primes at which B is “ramified”: for every prime \(\mathfrak p =(t-c)R\), show that the algebra \(B_\mathfrak p \) is a division quaternion algebra over \(F_\mathfrak p \simeq \mathbb Q ((t))\). [Hint: See Exercise 13.6.]
-
15.
Using Hilbert reciprocity, one can convert the computation of an even Hilbert symbol to the computation of several odd Hilbert symbols, as follows.
Let F be a number field, let \(\mathfrak p \mid (2)\), and let \(a,b \in F^\times \). Show that there exist (computable) \(a',b' \in F^\times \) such that the following hold:
-
(i)
\((a,b)_\mathfrak p =(a',b')_\mathfrak p \); and
-
(ii)
\({{\,\mathrm{ord}\,}}_\mathfrak q (a')={{\,\mathrm{ord}\,}}_\mathfrak q (b')=0\) for all \(\mathfrak q \mid (2)\) with \(\mathfrak q \ne \mathfrak p \).
Conclude that
$$\begin{aligned} (a,b)_\mathfrak p = \prod _{\begin{array}{c} v \in {{\,\mathrm{Pl}\,}}F \\ v \text { odd} \end{array}} (a',b')_v. \end{aligned}$$ -
(i)
-
16.
Let F be a number field with ring of integers \(\mathbb Z _F\). We say an ideal \(\mathfrak b \subseteq \mathbb Z _F\) is odd if \({{\,\mathrm{Nm}\,}}(\mathfrak b )\) is odd, and \(b \in \mathbb Z _F\) is odd if (b) is odd. For \(a \in \mathbb Z _F\) and \(\mathfrak b \subseteq \mathbb Z _F\) odd, let
 be the generalized Jacobi symbol, extending the generalized Legendre symbol by multiplicativity, and write
be the generalized Jacobi symbol, extending the generalized Legendre symbol by multiplicativity, and write  for \(a,b \in \mathbb Z _F \smallsetminus \{0\}\) with b odd.
for \(a,b \in \mathbb Z _F \smallsetminus \{0\}\) with b odd.-
(a)
Let \(a,b \in \mathbb Z _F\) satisfy \(a\mathbb Z _F+b\mathbb Z _F=\mathbb Z _F\), with b odd, and suppose \(a=a_0a_1\) with \(a_1\) odd. Then

-
(b)
Suppose that F has a computable Euclidean function N and let \(a,b \in \mathbb Z _F \smallsetminus \{0\}\) with b odd. Describe an algorithm using (a) to compute the Legendre symbol
 .
.
-
(a)
-
17.
In this exercise, we give a constructive proof of the surjectivity of the map \(B \mapsto {{\,\mathrm{Ram}\,}}B\) in Main Theorem 14.6.1 in the spirit of the proof of Proposition 14.2.7 (assuming two analytic results).
Let F be a number field, and let \(\Sigma \subseteq {{\,\mathrm{Pl}\,}}F\) be a finite set of noncomplex places of F of even cardinality. Let \(R=\mathbb Z _F\) be the ring of integers of F.
-
(a)
Let \(\mathfrak D :=\prod _\mathfrak{p \in \Sigma } \mathfrak p \) be the product of the primes corresponding to nonarchimedean places in \({{{{\texttt {\textit{S}}}}}}\). Using weak approximation (see Lemma 28.7.1), show there exists \(a \in \mathfrak D \) such that:
-
\(v(a)<0\) for all real places \(v \in \Sigma \) and \(v(a)>0\) for all real places \(v \not \in \Sigma \), if there are any; and
-
\(aR = \mathfrak D \mathfrak b \) with \(\mathfrak D +\mathfrak b =R\) and \(2R+\mathfrak b = R\).
In the special case where R has narrow class number 1 (that is, every ideal \(\mathfrak a \subseteq R\) is principal \(\mathfrak a =(a)\) and generated by an element \(a \in R\) such that \(v(a)>0\) for every real places v), show that we may take \((a)=\mathfrak D \) and \(\mathfrak b =R\).
-
-
(b)
Show that there exists \(t \in R\) coprime to 8aR such that the following hold:
-
For all primes \(\mathfrak p \mid \mathfrak D \) with \(\mathfrak p \not \mid 2R\), we have
 ;
; -
For all primes \(\mathfrak p \mid \mathfrak D \) with \(\mathfrak p \mid 2R\), the extension \(F_\mathfrak p (\sqrt{t})\) is the quadratic unramified extension of \(F_\mathfrak p \), so
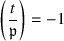 in the sense of the generalized Kronecker symbol;
in the sense of the generalized Kronecker symbol; -
For all primes \(\mathfrak q \mid \mathfrak b \) we have
 ; and
; and -
For all prime powers \(\mathfrak r ^e \parallel 8R\) with \(\mathfrak r \not \mid D\), we have \(t \equiv 1 \pmod \mathfrak{r ^e}\).
Show that t is well-defined as an element of \((R/8aR)^\times \), i.e., if \(t' \equiv t \pmod {8a}\) then \(t'\) also satisfies these conditions.
-
-
(c)
Using the infinitude of primes in arithmetic progression over number fields (Theorem 26.8.26), show there exists \(q \in R\) a prime element (i.e., qR is a prime ideal) such that \(q \equiv t \pmod {8a}\) with t as in (b) and further satisfying \(v(q)<0\) for all real places \(v \in \Sigma \).
-
(d)
Show that
 has \({{\,\mathrm{Ram}\,}}B = \Sigma \).
has \({{\,\mathrm{Ram}\,}}B = \Sigma \).
-
(a)
-
18.
Let F be a global field. Show that two quaternion algebras \(B,B'\) over F are isomorphic if and only if they have the same quadratic subfields (for a quadratic extension \(K \supset F\), we have \(K \hookrightarrow B\) if and only if \(K \hookrightarrow B'\)).
[See work of Garibaldi–Saltman [GS2010] for a discussion of the fields F with \({{\,\mathrm{char}\,}}F \ne 2\) and the property that two division quaternion algebras over F with the same subfields are necessarily isomorphic. (Roughly speaking, they are the fields for which nonzero 2-torsion elements of the Brauer group can be detected using ramification.)]
-
19.
In this exercise, we consider how ramification sets change under base extension. Let F be a global field and let \(K \supseteq F\) be a finite separable extension.
-
(a)
Let B be a quaternion algebra over F with ramification set \({{\,\mathrm{Ram}\,}}B\) and consider \(B_K = B \otimes _F K\). Show that
$$\begin{aligned} {{\,\mathrm{Ram}\,}}(B_K)=\{w \in {{\,\mathrm{Pl}\,}}(K) : w\text { lies over }v \in {{\,\mathrm{Ram}\,}}B\text { and }2 \not \mid [K_w:F_v]\}. \end{aligned}$$ -
(b)
Suppose B is a division algebra and [K : F] is odd. Show that \(B_K\) is a division algebra.
-
(c)
As a converse to (a), suppose that \(\Sigma _K \subseteq {{\,\mathrm{Pl}\,}}(K)\) is a finite subset of noncomplex places of K of even cardinality with the property that if \(w \in \Sigma _K\) lies over \(v \in {{\,\mathrm{Pl}\,}}F\), then \([K_w:F_v]\) is odd and moreover
$$\begin{aligned} \{w \in {{\,\mathrm{Pl}\,}}F : w\text { lies over }v\text { and }[K_w:F_v]\text { is odd}\} \subseteq \Sigma _K. \end{aligned}$$Show that there exists a quaternion algebra B over F with the property that \({{\,\mathrm{Ram}\,}}(B_K)=\Sigma _K\). (We say that the quaternion algebra associated to the set \(\Sigma _K\) descends to F.)
-
(d)
As a special case, what do (a) and (c) say when \([K:F]=2\)?
-
(e)
Restate (a) and (b) in terms of the kernel of the map \({{\,\mathrm{Br}\,}}(F)[2] \rightarrow {{\,\mathrm{Br}\,}}(K)[2]\) induced by \([B] \mapsto [B_K]\) (see Remark 14.6.10).
-
(a)
-
20.
Let R be a global ring with \(F={{\,\mathrm{Frac}\,}}R\), and let \(K \supseteq F\) be a finite Galois extension with S the integral closure of R in K. Let B be a quaternion algebra over F and consider \(B_K = B \otimes _F K\). Then \({{\,\mathrm{Gal}\,}}(K\,|\,F)\) acts naturally on \(B_K\) via \(\sigma (\alpha \otimes x) = \alpha \otimes \sigma (x)\). (This action is not by K-algebra isomorphism!)
Show that there exists a maximal S-order \(\mathcal {O}\subseteq B_K\) stable under \({{\,\mathrm{Gal}\,}}(K\,|\,F)\), i.e., \(\sigma (\mathcal {O})=\mathcal {O}\) for all \(\sigma \in {{\,\mathrm{Gal}\,}}(K\,|\,F)\).
- \(\triangleright \) 21.:
-
Let F be a global field, let \(v_1,\dots ,v_r\) be places of F, and for each \(v_i\) suppose we are given the condition ramified, split, or inert. Show that there exists a separable quadratic extension \(K \supseteq F\) that \(K_{v_i}\) satisfies the given condition for each i. [Hint: follow the proof of Main Theorem 14.7.4.]
-
22.
Let F be a global field, let \(B_1,B_2,\dots ,B_r\) be quaternion algebras over F, and let \(B :=B_1 \otimes B_2 \otimes \dots \otimes B_r\). Recalling section , show (in as many ways as you can) that \(B \simeq {{\,\mathrm{M}\,}}_{2^{r-1}}(B')\) for a quaternion algebra \(B'\) over F. (Recalling , by Merkurjev’s theorem this shows the class of every element in the 2-torsion of the Brauer group \({{\,\mathrm{Br}\,}}(F)[2]\) is represented by a quaternion algebra.)
- \(\triangleright \) 23.:
-
Let \(F_v\) be a local field with \({{\,\mathrm{char}\,}}F_v=2\). Let \(n \in F_v\). Show that there exists \(t \in F_v\) such that \(x^2-tx + n\) is separable and irreducible.
- \(\triangleright \) 24.:
-
Prove Lemma 14.7.6 for v an archimedean place.
-
25.
In this advanced exercise following up on Exercise , we consider features of quaternion algebras and orders in the case of a global function field, assuming background in algebraic geometry.
Let X be a smooth, projective, geometrically integral curve over a finite field k; then X is a separated, integral Dedekind scheme. Let \(\mathscr {O}_X\) be its structure sheaf. Let F be its function field, and let B be a quaternion algebra over F. Define a sheaf of \(\mathscr {O}_X\) -orders in B, or simply an \(\mathscr {O}_X\) -order in B, to be an \(\mathscr {O}_X\)-lattice \(\mathscr {B}\) in B such that for each open set \(U \subseteq X\), the \(\mathscr {O}_X(U)\)-lattice \(\mathscr {B}(U)\) is a subring of B. We recall the local-global dictionary for \(\mathscr {O}_X\)-lattices (Exercise 9.16(c)).
In parts (a)–(c) we work out an example: let \(X=\mathbb P ^1\) with function field \(F=k(t)\) where \({{\,\mathrm{div}\,}}t = (0)-(\infty )\). Suppose that \({{\,\mathrm{char}\,}}k \ne 2\), and let \(u \in k^\times \smallsetminus k^{\times 2}\). Let B be the quaternion algebra with \({{\,\mathrm{Ram}\,}}(B)=\{(0),(\infty )\}\).
-
(a)
Show that \(B=({u,t} \mid {F})\).
-
(b)
Let \(U={{\,\mathrm{Spec}\,}}k[t] = X \smallsetminus \{\infty \}\). Show that there exists a unique \(\mathscr {O}_X\)-order \(\mathscr {B}\) in B with \(\mathscr {B}(U)=k[t] + k[t]i + k[t]j + k[t]ij\) and stalk \(\mathscr {B}_{(\infty )}\) a maximal \(\mathscr {O}_{X,(\infty )}\)-order. Describe explicitly \(\mathscr {B}_{(\infty )}\) and \(\mathscr {B}({{\,\mathrm{Spec}\,}}k[1/t])\) as orders in B.
-
(c)
With \(\mathscr {B}\) from (b), show that \(\mathscr {B}(X)=k[i]\).
Restoring generality, let \(\mathscr {B}\) be an \(\mathscr {O}_X\)-order such that \(\mathscr {B}(U)\) is a maximal \(\mathscr {O}_X(U)\)-order in B for all affine open sets U.
-
(d)
Show that \(\mathscr {B}(X)\) has a zero divisor if and only if \(\mathscr {B}(X) \simeq {{\,\mathrm{M}\,}}_2(k)\) if and only if \(B \simeq {{\,\mathrm{M}\,}}_2(F)\).
-
(e)
Show that \(\mathscr {B}(X)\) is a k-algebra with a nondegenerate standard involution.
-
(f)
Suppose that B is a division algebra. Show that either \(\mathscr {B}(X)=k\) or \(\mathscr {B}(X) \simeq k_2\) is the quadratic extension of k.
-
(g)
Still supposing that B is a division algebra, show that if \(\mathscr {B}(X)=k_2\), then every ramified place of B has odd degree. [Hint: show that \(B \simeq ({K,b} \mid {F})\) where \(K=Fk_2\) is the constant field extension of F of degree 2, and \(b \in F^{\times } \smallsetminus k^\times \). Compute the Hilbert symbol at \(v \in {{\,\mathrm{Ram}\,}}(B)\) to show v(b) is odd.]
-
(a)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
This chapter is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, duplication, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, a link is provided to the Creative Commons license and any changes made are indicated.The images or other third party material in this chapter are included in the work's Creative Commons license, unless indicated otherwise in the credit line; if such material is not included in the work's Creative Commons license and the respective action is not permitted by statutory regulation, users will need to obtain permission from the license holder to duplicate, adapt or reproduce the material.
Copyright information
© 2021 The Author(s)
About this chapter
Cite this chapter
Voight, J. (2021). Quaternion algebras over global fields. In: Quaternion Algebras. Graduate Texts in Mathematics, vol 288. Springer, Cham. https://doi.org/10.1007/978-3-030-56694-4_14
Download citation
DOI: https://doi.org/10.1007/978-3-030-56694-4_14
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-56692-0
Online ISBN: 978-3-030-56694-4
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


 .
. , we take
, we take 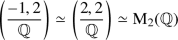

 .
. . Let q be an odd prime such that
. Let q be an odd prime such that  for all odd
for all odd  for all odd
for all odd  has
has  be the generalized Jacobi symbol, extending the generalized Legendre symbol by multiplicativity, and write
be the generalized Jacobi symbol, extending the generalized Legendre symbol by multiplicativity, and write  for
for 
 .
. ;
;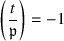 in the sense of the generalized Kronecker symbol;
in the sense of the generalized Kronecker symbol; ; and
; and has
has