1 Introduction

The study of the wall heat transfer in a combustion chamber represents one of the most relevant design criteria of a modern launcher engine. Peak temperatures up to 3500 K and heat fluxes up to 160 MW/m\(^2\) endanger the structural integrity of the engine, such that an efficient cooling system is necessary  [1]. Normally, multiple cooling systems are employed simultaneously, but in this work the film cooling technique is investigated. A coolant fluid is directly injected at the wall of the combustion chamber between the hot gas and the cold wall. The film can be injected through singular or multiple holes or slots. In this work, the film is injected through a single slot at the faceplate of the combustion chamber. This is a typical configuration for relatively short rocket engines. The analysis of the phenomena taking place in a combustion chamber is characterized by a high complexity due to the extreme physical conditions which develop in the reacting flow. Higher temperatures and pressures reached by CH\(_4\)/O\(_2\) represent a challenge for both experimental and numerical studies. The hot gas chemistry must be modeled. Close to the wall, the enthalpy loss enhances recombination processes, considerably altering the thermodynamic properties of the fluid. In the boundary layer, a stratification of the species takes place, with the lighter ones moving towards the center of the combustion chamber. Large temperature gradients at the wall must be captured either with a resolved mesh or with a proper wall function. In some works, the hot gas is represented as a single specie, averaging the physical characteristics of the single components at the inlet. Betti et al.  [2] used a so called “pseudo-injector” approach. The main hypothesis to support this method is that the authors considered all the relevant combustion processes very close to the injector, whereas afterwards the fluid is considered at chemical equilibrium. Methane was used as a cooling medium in a second test. The results showed a significant divergence from the experimental data. The “pseudo-injector” approach might be valid in the core flow where the flame is fully developed, but it fails to predict the chemical recombinations close to the wall. Stoll and Straub  [3] adopted the same approach for a nozzle set up, where mixing and recombination processes have ceased and it is more reasonable to consider the flow as a single fluid. Another possibility is to pre-tabulate the thermo-chemical properties of the fluid by means of Flamelet tables. Winter et al.  [8] have run a CH\(_4\)/O\(_2\) RANS simulation for the prediction of the wall heat fluxes, using adiabatic Flamelet tables. The results obtained are qualitatively good, but the chemical recombinations at the wall could not be captured. Perakis et al.  [9] developed a non-adiabatic Flamelet model which takes into account the negative source term of the enthalpy field at the wall of the chamber. The authors show a realistic growth of the thermal boundary layer, but did not manage to match the experimental data. In this work, Large-Eddy Simulations are performed using a non-adiabatic Flamelet approach, in order to validate the combustion model against the experimental data of a single-injector combustion chamber  [1]. A setup with and without film cooling is used, while the wall heat flux prediction is compared to the experiment. Since in rocket engine applications, wall roughness enhances the wall heat flux, a study on the effect of wall roughness on velocity and temperature profiles is also carried out. As references, the DNS of Thakkar et al.  [18] and the DNS of MacDonald et al.  [14] were adopted.

2 Governing Equations and Numerical Procedure

For this work two different CFD codes were used, CATUM  [6] and OpenFOAMFootnote 1, in order to compare the performance of the two and assess advantages and disadvantages of a pressure-based (OpenFOAM) against a density-based (CATUM) solver in combustion chamber environments.

Catum

Part of the simulations have been conducted with the in-house software package CATUM, developed at the Chair of Aerodynamik at the Technical University of Munich. The code is density-based, solving the fully compressible Navier Stokes equations in combination with an energy equation. Time integration is performed with a four-stage Runge–Kutta method. The code is finite-volume based employing block structured meshes. It computes the viscous fluxes based on a linear second-order centered scheme, whereas it computes the convective fluxes with the four-cell stencil, switching dynamically from a central difference to an upwind based scheme in regimes of high gradients using the Ducros sensor. It is based on an implicit LES subgrid model using the advection local deconvolution method by Hickel et al.  [7].

OpenFOAM

The in-house version of OpenFOAM used for the simulation is pressure-based. It solves the fully compressible Navier Stokes equations in combination with an enthalpy equation. For the present test cases, it uses an implicit Euler integrator and a second order TVD scheme of type van Leer on the scalar fields  [20]. The time step is limited by a Courant number of 0.4. The turbulence is modeled by means of IDDES  [19].

Flamelet model

To update the pressure at every iteration and making sure the chemistry is taken into account, non-adiabatic Flamelet tables had to be generated in a pre-processing step. This method has been chosen because it has been shown in the literature to be computationally cheap and to deliver good physical accuracy. The counter-flow diffusion flame approach from Peters  [4] is used. The Flamelet equations are solved in one dimension. The flamelet equations for the species mass fractions and temperature in the mixture fraction space read

$$\begin{aligned} \frac{\partial Y_k}{\partial t}=\frac{\upchi }{2} \frac{\partial ^2 Y_k}{\partial Z^2} +\frac{\dot{m}_k}{\rho },\end{aligned}$$
(1)
$$\begin{aligned} \frac{\partial T}{\partial t}=\frac{\upchi }{2} \frac{\partial ^2T}{\partial Z^2} - \frac{1}{\rho c_p} \sum ^{N}_{k=1}\dot{m}_k\,h_k. \end{aligned}$$
(2)

\(Y_k\) is the species mass fraction, Z is the mixture fraction, \(h_k\) is the species enthalpy, \(\dot{m}_k\) and \(\upchi \) are the species source terms and the scalar dissipation rates, respectively. The scalar dissipation rate is expressed through an error function

$$\begin{aligned} \upchi (Z) = \upchi _{st}\,exp(2\,({{\,\mathrm{erf}\,}}^{-1}(2Z_{st}))^2-2({{\,\mathrm{erf}\,}}^{-1}(2Z))^2), \end{aligned}$$
(3)

where \(Z_{st}\) represents the mixture fraction at stochiometric condition. The original version of FlameMasterFootnote 2 stores the thermodynamic variables as a function of the mixture fraction and the stochiometric scalar dissipation rate, \(\phi = f(Z,\upchi _{st})\). Z and \(\upchi \) are calculated at run-time and used as input for the Flamelet table. The thermodynamic state is obtained in return. Moreover the tables have then been expanded to take into account the effect of the turbulence-chemistry interaction. The flamelets are integrated with a Favre probability density function (PDF),

$$\begin{aligned} \widetilde{\phi } = \int _0^{\infty }\int _0^1\phi (Z,\upchi _{st}) \cdot \widetilde{P}(Z,\upchi _{st})\cdot dZ\,d\upchi _{st}, \end{aligned}$$
(4)

where \(\phi \) represents temperature, species mass fraction and constant-pressure specific heat respectively. In the case of the transport properties, Reynolds averages are used:

$$\begin{aligned} \bar{\phi } = \bar{\rho } \int _0^{\infty } \int _0^1 \frac{\phi (Z,\upchi _{st})}{\rho (Z,\upchi _{st})} \cdot P(Z,\upchi _{st})\cdot dZ\,d\upchi _{st}, \end{aligned}$$
(5)
$$\begin{aligned} \bar{\rho } = \frac{1}{\int _0^\infty \int _0^1 \frac{1}{\rho (Z,\upchi _{st})} \cdot P(Z,\upchi _{st})\cdot dZ\,d\upchi _{st}}. \end{aligned}$$
(6)

The PDF is decomposed assuming statistical independence of \(Z\, \text {and}\, \upchi _{st}\), which results in \(P(Z,\upchi _{st})=P(Z)\,P(\upchi _{st})\). For the scalar dissipation rate, the PDF is modeled as a Dirac function. For the mixture fraction, a \(\beta \) function is used. At the end of the integration, thermodynamic tables are built as

$$\begin{aligned} \widetilde{\phi } = f(\widetilde{Z},\widetilde{Z''^2},\widetilde{\upchi }_{st}). \end{aligned}$$
(7)

In this combustion model, the mixture variance \(\widetilde{Z''^2}\) is a measure of turbulence and is calculated from its transport equation. The Flamelet tables consider also non-adiabatic combustion, which is necessary because of the cold wall of the combustion chamber considerably lowers the enthalpy values. The method adopted is taken from the work of Ihme et al.  [5]. The new flamelets are generated by dividing the one-dimensional domain (in mixture fraction space) in two regions, one which is reacting and one which is not. In the non-reacting part the Flamelet equations become

$$\begin{aligned} \frac{\partial Y_k}{\partial t}=\frac{\upchi }{2} \frac{\partial ^2 Y_k}{\partial Z^2},\end{aligned}$$
(8)
$$\begin{aligned} \frac{\partial T}{\partial t}=\frac{\upchi }{2} \frac{\partial ^2T}{\partial Z^2}. \end{aligned}$$
(9)
Fig. 1
figure 1

Temperature profiles with different position of the permeable wall, which divides the onedimensional domain in reacting and non-reacting regions

Full size image

With the modified flamelet equations, the stored variables become

$$\begin{aligned} \widetilde{\phi } = f(\widetilde{Z},\widetilde{Z''^2},\widetilde{\upchi }_{st},\widetilde{h}). \end{aligned}$$
(10)

The flamelet tables in the end require four input parameters, which all need to be calculated by the solver. The tables could be further expanded by accounting for the influence of pressure (which would become the fifth input parameter), but this is not considered here.

Roughness Modeling

The roughness is described with the normalized sand-grain roughness \(k_s^+ = \frac{k_s u_\tau }{\nu }\), which is the standard roughness multiplied with the friction velocity and divided by the kinematic viscosity. The influence of wall roughness is accounted for in the wall-model, which solves the Turbulent Boundary Layer Equations (TBLE). Three different roughness methods have been tested. The methods proposed by Cebeci et al.  [15] and Feiereisen et al. [16] modify the turbulent viscosity of the TBLE, causing a downward shift of velocity and temperature profiles. The method proposed by Saito et al.  [17] imposes a virtual slip velocity at the boundary between the LES grid and the TBLE grid. All three methods depend on the normalized sand-grain roughness.

3 Test Case

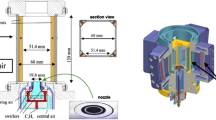
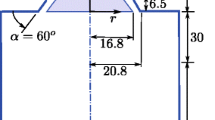
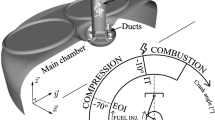
The experimental setup for a single-injector rocket combustor has been developed in the group of Prof. Haidn at the Chair of Turbomachinery at the Technical University of Munich (Fig. 2). A detailed description of the combustion chamber can be found in the work of Celano et al.  [1]. The combustion chamber is modular and is made of oxygen-free high-conductivity copper. The length of the engine is 305 mm, the diameter of the combustion chamber is 12 mm, the throat diameter in the nozzle is 7.6 mm. The contraction ratio of 2.5 is very similar to the one of real rocket engines, which guarantees realistic conditions when the sonic state is reached in the throat. Fuel and oxidizer are injected with a coaxial injector. The temperature has been measured with thermocouples 1–3 mm beneath the surface. Pressure transducers read the axial pressure profile. Since the experiment is transient, both the reading of temperature and pressure are averaged over time. Cases with and without film cooling are investigated, using gaseous methane as a cooling medium. The coolant is injected through a slot placed at the beginning of the upper wall of the combustion chamber. The simulation parameters for the test cases with film cooling are listed in Table 1. In both configurations, the CH\(_4\) mass flow rate ratio between the coolant slot and the co-axial injector is about 30 \(\%\). The same configuration is transferred to the cases without film cooling, removing the coolant injection slot.

Fig. 2
figure 2

Scheme of the experimental setup  [1]

Full size image
Table 1 Simulation setup for the investigated configurations
Full size table

3.1 Combustion Chamber Test Cases

The numerical investigation was performed using the code OpenFOAM. The configuration without film cooling was widely investigated in previous works on different meshes and combustion models [11,12,13]. The computational domain was limited to x \(=\)150 mm, i.e. approximately half of the chamber compared to the experimental case focusing on the film developing close to the injector plate. Two test cases have been computed, the 20 bar case without film cooling (T1) and the 20 bar case with film cooling (T2). The simulation was run on a coarse mesh of about 9 million volume cells, compared to the reference case at 30 million cells. The coolant temperature originally set to 270 K was reduced to 251 K in the simulation in order to match the chamber pressure at 20 bar at the faceplate. The faceplate allocates an injection slot of \(11 \times 0.25\,\mathrm{mm}^2\), from which methane is injected with a bulk velocity of 81 m/s. Both simulations were run using the hybrid LES/RANS turbulence model from Shur [19]. The combustion model is based on the non-adiabatic flamelets previously introduced, however using a single \(\upchi _{st} =\) 1 s\(^{-1}\).

3.2 Roughness Test Cases

CATUM was used to run the wall-roughness simulations. Emulating the DNS setups, a channel configuration was adopted. The meshes were composed of \(1 \cdot 10^6\) cells, with a periodic boundary condition in flow and spanwise direction. For the other two boundaries (Thakkar case  [18]), an isothermal boundary condition was imposed, using the initial temperature as wall temperature. For the MacDonald DNS  [14], two different temperatures were chosen at the two opposing walls, with a difference of 100K between them. In all cases, a constant mass flow is ensured through an artificial force in the momentum equation in flow direction.

Fig. 3
figure 3

3D mesh for case with (right) and without (left) film cooling. The contour of the instantaneous velocity field is displayed

Full size image

4 Results

4.1 Combustion Chamber Results

The 20 bar cases with and without cooling film have been simulated. Figure 4 shows the instantaneous snapshots of normalized enthalpy, mixture fraction and temperature for both configurations. The shear layers at the faceplate are still visible further downstream in the case with film cooling (cfr. temperature). As expected, the mixture fraction field shows a thicker layer of cooled CH\(_4\) on the upper wall. The position where the hot gases impinges on the wall is shifted from x \(\sim \) 10 mm to 50 mm. The enthalpy loss along the film cooling stream is also captured from the manifold.

Fig. 4
figure 4

Axial view of instantaneous LES fields (T1 and T1). Top: film. Bottom: without film

Full size image

The hot gases do not expand uniformly in the squared chamber if film cooling is applied (Fig. 5, bottom). Up to cross section x \(=\) 80 mm downstream of the faceplate, the flame becomes thinner in the vertical direction compared to the case without film cooling (top row). For cross-sections further downstream, the mixing of the coolant stream with the hot gases is completed and the flame further expands towards the upper wall.

Fig. 5
figure 5

Radial view of \(\widetilde{T}\) at cross sections x \(=\) 10, 20, 40, 80 mm. Top: without film. Bottom: film

Full size image

The comparison with the experimental data is shown in Fig. 6. The axial pressure profile (left) is taken from the configuration without film cooling. The additional CH\(_4\) slot for the film cooling increases the pressure at the faceplate, resulting in a higher pressure level. Moreover, a previous mesh study showed that with this turbulence model, coarser meshes tend to predict excessive mixing compared to more refined meshes, therefore overpredicting the pressure. The wall heat flux is represented very well in both configurations, with an excellent match for the film cooling case (on the right). This is due to the fact that the temperature boundary conditions at the chamber walls are available on a 2D surface in the case of the film cooling, while only the data in the axial direction is available for the original case. A more realistic temperature distribution at the wall allows the CFD to better approximate the calculated wall heat flux. As can seen in Fig. 6, T2 has also more wall heat flux points available in axial position.

Fig. 6
figure 6

Axial pressure and wall heat flux for reference case T1 (center) and for T2 (right)

Full size image
Fig. 7
figure 7

Convergence test for the Saito method (left), influence of Reynolds number on the models precision (right)

Full size image

4.2 Roughness Results

A convergence study has been carried out with CATUM to assess the number of TBLE points necessary to reach convergence. In Fig. 7, the convergence behaviour of the Saito method for the velocity profile is slower. The tests have been made at \(k_s^+=22.1\, \text {at} \, Re = 2.1 \cdot 10^4\). As reference, the roughness downward shift of \(u^+\) is compared with the DNS results of Thakkar et al.  [18]. Already at 20 TBLE points, the method has reached considerable precision. In Fig. 7 on the right, the relative error with respect to the velocity shift is plotted for the three methods for different values of bulk Reynolds numbers and sand-grain roughnesses. The Saito method appears to be the one performing best, especially in the transitionally rough regime (\( 4 \le k_s^+ \le 80\)).

Fig. 8
figure 8

Shift on the temperature profile for for \(k_s^+=45.1\) (left) and for \(k_s^+=90 \) (right)

Full size image

Figure 8 shows the influence of the wall roughness on the temperature profile. The reference case is the DNS of a period channel of MacDonald et al.  [14]. The tests have been made for \(k_s^+=45.1 \,\text {and}\, k_s^+=90,\, \text {at}\, Re_{\tau } = 395\). The Feiereisen model overestimates the temperature shift in both cases. On the other hand, the Cebeci method matches the DNS data of the case in the fully rough regime well, while it performs poorly for the transitionally rough regime. The Cebeci approach can not be considered as a method to choose for high values of roughness, though. Figure 7 shows the increasing divergence of the method for the velocity shift with increasing values of \(k_s^+\). For the \(k_s^+=45.1\) case, the Saito method faithfully represents the shift caused by wall roughness. For the \(k_s^+=90\) case instead, the Saito model underestimates the temperature shift. Thus the Saito model delivers the best results, both for velocity and temperature, in the transitionally rough regime. When the roughness of the wall is too large, the irregularities can not be approximated anymore as a modified boundary condition, because the geometry of the single roughness spikes have to be taken into account and the wall geometry has to be resolved.

5 Conclusions

Simulations of a CH4/O2 combustion chamber have been successfully run by means of two different CFD codes. The results deliver a good representation of the mixing phenomena, species dissociation and temperature distribution. The comparison with the experimental data on the wall heat flux available shows good agreement, in particular in case of OpenFOAM. The cooling film is completely mixed with the main flow at \(x= 150\) mm. To extend its effectiveness, additional injection slots downstream from the injector plate would be necessary, or alternatively the single slot configuration could be operated with a thicker inlet film. The first solution though would mean a more complex setup, whereas the latter provokes higher interferences on the internal hot gas with lower chamber efficiency.