1 Introduction

Efficient and pollution-reduced energy conversion are key criteria of combustion based concepts. Optimal mixing of fuel and oxidizer is therefore essential. Typically, technical applications like liquid rocket or diesel engines are operated at elevated pressure and temperature conditions. The thermodynamic properties of fuel and oxidizer can thereby even exceed their critical values. This is especially true for reservoir (injection) and ambiance conditions in rocket engines where high injection temperatures lead to injection of a supercritical, single-phase fluid. Studies showed that supercritical fuel injection entails improved mixing, and hence, burn more efficiently [3,4,5]. Nevertheless, the application of supercritical fluids involves a higher degree of complexity, as the fluid experiences non-ideal fluid behavior. Classical phase transition from liquid to vapor phase vanishes beyond the critical point and a single-phase fluid is attained. Microscopic analysis in the supercritical regime shows fluctuations and steep gradients of thermodynamic properties [10, 19, 33, 34]. Considering trans- or supercritical fluid expansion, this leads to a strong coupling of thermodynamic properties and flow phenomena. The complex behavior of fluid properties together with mutual, interacting diffusive effects remain a huge challenge for modeling and accurate description of supercritical fluids. Therefore, deep understanding of supercritical jet disintegration and subsequent mixing is of particular interest.

In this context, Baab et al. [6, 7] and Förster et al. [13] performed supercritical injection studies in order to deliver quantitative jet mixing data. Using laser-induced thermal acoustics (LITA), they measured the local speed of sound in high-pressure injection with varying temperature and ambient pressure. Two alkanes and a fluoroketone were injected into nitrogen. Precise adjustment of the initial condition allowed to cover the range of supersonic underexpanded to subsonic dense jets providing a comprehensive speed of sound database. The speed of sound is the direct measurement quantity in a LITA system. Thermometry or species determination require additional models. For the test cases of supersonic underexpanded jets, an adiabatic mixing model, including non-ideal mixing behavior, was used to derive axial concentration data.

In this work, an extended analysis of the binary jet mixing data is given. Physical analysis of the supercritical regime and binary mixing systems shows that adiabatic mixing may not be globally applicable. In fact, heat transfer and species diffusion according to Fouriers and Ficks law can already lead to significant deviations. From a numerical point of view, Ma et al. [25] found the adiabatic mixing model to be a limiting case for insufficient spatial resolution for conservative methods. Considering this, an extended analysis of the mixing data with regard to the applicability of the adiabatic mixing model is carried out. In the studies of Baab et al. [6] and Förster et al. [13], underexpanded jets followed the adiabatic mixing model quite accurately for axial distances of x/D below 110. However, in dense single-phase jets, deviations are expected in comparison to an analytical solution.

In order to simulate the experimental studies, the compressible CFD solver FLEXI  [1] was extended to handle super- and transcritical jets. Therefore, the split form discontinuous Galerkin (DG) scheme of Gassner et al. [18] was extended to multi-phase and multi-component flows. The method was combined with the double flux method of Abgrall and Karni  [2] for general tabulated equations of state (EOS) to handle spurious pressure and velocity oscillations occurring in real EOS and multi-component simulations, see Föll et al. [16]. Further needed developments were the extension of the tabulation framework of Dumbser et al. [12] to multi-component flows  [14, 15] and the implementation of a framework for cubic EOS based on the work of Bell and Jäger  [8] written in Helmholtz energy form. This work was extended to handle multi-component CFD simulations near the critical point with phase-transition. The developments and tools mentioned are used to simulate a specific experimental setup proposed in  [7]. The numerical results are interpreted in the context of Ma et al. [25].

The paper is structured as follows: In Sect. 2 phenomenological considerations on mixing jets are given. This is followed by the numerical methods and thermodynamic modeling. Numerical results of Large Eddy Simulation (LES) of n-hexane/nitrogen jet injection under supercritical conditions are presented. The paper is concluded by the comparison of numerical results with a well-defined experimental test case.

2 Phenomenological Considerations on Mixing Jets

For a given pressure, the local speed of sound in a mixture is a function of temperature and species concentration \(c_{\mathrm{mix}}\). Assuming adiabatic mixing of injectant and ambiance allows to assess the influence of each quantity respectively. For the experimental conditions, non-ideal mixing and real-gas properties have to be considered. Therefore, the thermodynamic properties used are taken from the NIST database  [24]. The mixing process can be expressed in terms of specific enthalpy. The enthalpy of a real mixture is then written as

$$\begin{aligned} h_{\mathrm{mix}}(c_{\mathrm{mix}}, T_{\mathrm{mix}}, p_{\mathrm{\infty }}) = h_{\mathrm{excess}}(c_{\mathrm{mix}}, T_{\mathrm{mix}}, p_{\mathrm{\infty }}) + h_{\mathrm{ideal}}(c_{\mathrm{mix}}, T_{\mathrm{mix}}, p_{\mathrm{\infty }}), \end{aligned}$$
(1)

where \(h_{\mathrm{ideal}}\) accounts for ideal mixing of pure components at well-known initial conditions. \(h_{\mathrm{excess}}\) contributes to non-ideal mixing of a binary system and \(T_{\mathrm{mix}}\) is the adiabatic mixing temperature. Analogous to specific enthalpy, the local speed of sound is a function of mixture composition, mixing temperature and ambient pressure. Extraction of species concentration is therefore achieved by introducing the measured speed of sound \(a_{\mathrm{meas}}\) and optimizing Eq. (1) in an iterative scheme according to

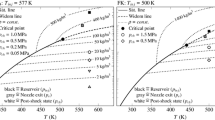
$$\begin{aligned} a_{\mathrm{mix}}(c_{\mathrm{mix}}, T_{\mathrm{mix}}, p_{\mathrm{\infty }}) \overset{!}{=} a_{\mathrm{meas}}. \end{aligned}$$
(2)

For more detailed information the reader is referred to [6]. For the means of comparability, the axial concentration data is plotted according to a similarity law proposed by Chen and Rodi [11]. It describes the axial concentration decay in momentum-controlled mixing. Scaled data that collapses onto the modified axial coordinate

$$\begin{aligned} c_{Cl} = A \left( \frac{\rho _{\mathrm{e}}}{\rho _{\mathrm{\infty }}}\right) ^{0,5} \left( \frac{x}{D}\right) ^{-1} \end{aligned}$$
(3)

follows the adiabatic mixing assumption and shows self-preservative characteristics. Here, x/D is the non-dimensional distance from the nozzle exit, scaled with the exit and ambient density respectively. A is an emperical constant that depends on the nozzle pressure ratio [17]. We chose the constant A to be 5.4, as it covers the range of our experiments best. A detailed description of the post-processing is given in Baab et al. [6].

Fig. 1
figure 1

Similarity analysis of centerline concentration of , and FK. Evaluated from database of Baab et al. [7]

Full size image

Baab et al. [6] and Förster et al. [13] showed adiabatic and self-similar characteristics within underexpanded jets for axial distances of \(x/D < 110\). Underexpansion implies high exit velocities and an eruptive discharge of the fluid. Under this consideration it is assumed that heat and mass diffusion are not the dominant effect in the mixing process and the fluid expands adiabatically into the ambiance. Keeping the latter in mind, the situation changes for the examination of fluid jets with low exit velocities. For this purpose, the speed of sound database for the subsonic high-pressure jets from Baab et al. [7] is evaluated with respect to the applicability of the adiabatic mixing assumption. The results are illustrated in Fig. 1. Here, case 1 follows the similarity law sufficiently well. Minor deviation close to the nozzle exit can be explained due to the finite measurement volume in a narrow dense jet. In contrary, the n-pentane test cases 2 and 3 show a systematic deviation from the adiabatic mixing line. For case 3 with a lower injection temperature and hence lower exit velocity, the deviation is even more pronounced. Here, it is assumed that the omission of heat fluxes lead to an overestimation of mixing temperatures. For the correlation of speed of sound to species concentration, this means that the optimization scheme from Eqs. (1) and (2) is evaluated on a higher temperature level, which consequently leads to an overprediction of concentration.

The fluoroketone cases strongly differ from the adiabatic mixing curve as well. Both cases inject with considerably lower injection velocities compared to case 1 and 2. Furthermore, fluoroketone features a significantly higher molar mass. It is not directly clear what effect causes the deviation. The high molar mass could lead to profound concentration gradients that enhance mixing. Together with the slow injection velocity, heat conduction can affect the jet for a longer time. The difference in the experimental results is subject to a combination of these diffusive effects. Yet, it cannot be assessed which physical effect is dominant and what primarily causes the deviations from the adiabatic assumption.

3 Numerical Consideration and Thermodynamic Modeling

For the analysis of the experimental results, numerical simulations that resolve the local features of the fluid flow are needed. Under super- or transcritical conditions, this is a major challenge for numerical methods and computational performance since the complex thermodynamics have to be modeled precisely. Recent findings by Ma et al. [25] showed that adiabatic and isochoric mixing are respective limits of conservative and quasi-conservative schemes that suffer from numerical approximation errors. Based on these discoveries, high resolution methods with low numerical diffusion are needed to resolve physical mixing correctly. Therefore, for our Large Eddy Simulations, we approximate the compressible Navier–Stokes equations with a discontinuous Galerkin spectral element method, which is described in detail in  [1, 14,15,16]. We apply a shock capturing on sub-cells at discontinuities or strong gradients to keep the overall high resolution, see Sonntag and Munz [35].

3.1 Thermodynamic Modeling

We use the compressible Navier–Stokes equations for real, non-reactive fluids with \(N_k\) components. The viscous stress tensor \(\underline{{\tau }}\) with the strain rate tensor \(\underline{\textit{\textbf{S}}}\) is defined for a Newtonian fluid. For multi-component simulations the heat and concentration diffusion fluxes are usually comprised of [21, 26]

$$\begin{aligned} {\textit{\textbf{q}}}={\textit{\textbf{q}}}^{\mathrm{f}}+{\textit{\textbf{q}}}^{\mathrm{c}} \qquad \text {and} \qquad \textit{\textbf{J}}_{k}=\textit{\textbf{J}}_{k}^{\mathrm{f}} + \textit{\textbf{J}}_{k}^{\mathrm{c}}, \end{aligned}$$
(4)

where \({\textit{\textbf{q}}}^\mathrm{f}\) is the specific heat flux due to conduction according to Fouriers law with thermal conductivity \(\lambda \) and temperature T, and \(\textit{\textbf{J}}_k^{\mathrm{f}}\) is the concentration diffusion flux according to the Fickian law with \(D_{k}\) being an effective species diffusion coefficient. The last two terms of Eq. (4), \({\textit{\textbf{q}}}^{\mathrm{c}}\) and \(\textit{\textbf{J}}_{k}^{\mathrm{c}}\), may be added to the equation system and represent additional cross-effects due to Onsager [29] reciprocal relations, namely the Dufour- and Soret effects. A complete description of theses effects can be obtained by, e.g. Keizer [21] and Masquelet [26], in the Irving-Kirkwood form

(5)
(6)

where \(\mathcal {R}\) denotes the universal gas constant, \(\mu _{\mathrm{m},k} \equiv \mu _{\mathrm{m},j}\) is the chemical potential for each species and \(L_{\mathrm{qq}}\), \(L_{\mathrm{qk}}\), \(L_{\mathrm{kq}}\), \(L_{\mathrm{kj}}\) are the Fourier, Dufour, Soret and Fickian diffusion contributions, respectively. The subscript \((\bullet )_{\mathrm{m}}\) indicates molar reduced quantities. Generally the chemical potential is replaced by common primitive driving forces via pressure, temperature or concentration gradients [26]. These considerations are out of scope of this paper and therefore sufficiently approximated by Fourier and Fickian diffusion parts including the most relevant parts of the Dufour effect analog to Masquelet [26]. Note that the Soret effect is neglected. The molar fraction is defined as \({\textit{\textbf{X}}}=(X_1,\dots ~,X_{N_k})^{\text {T}}\) with \(X_k = \rho _{\mathrm{m},k}/\rho _{\mathrm{m}}\).

We restrict our self to the Peng-Robinson EOS (PR-EOS) [30]. The framework for cubic EOS is based on the work of Bell and Jäger [8] and is written in Helmholtz energy form, see Kunz [22], with

(7)

where \(\mathcal {F}\) is defined as the molar Helmholtz free energy, \(\alpha ^0\) denotes the non-dimensional free Helmholtz energy in the ideal gas limit and \(\alpha ^{\mathrm{r}}\) is the non-dimensional residual free Helmholtz energy that describes the deviation from the ideal fluid behavior. The independent variables are the non-dimensional reduced volume \(\delta =\rho /\rho _{\mathrm{c}}\), the inverse reduced temperature \(\tau =T_{\mathrm{c}}/T\), and the molar fraction of the composition \({\textit{\textbf{X}}}\). The subscript \({\mathrm{c}}\) denotes the quantities at the critical point. A general extension to other equations of state is described in Föll et al. [15, 16] with fluid libraries like CoolProp v6.3 [9] and RefProp v9.1 [24].

Note that the work originally offered by Bell and Jäger [8] was extended to handle multi-component CFD simulations near the critical point. The ideal part is implemented with polynomials of Jaeschke and Schley for heat capacities [20] according to Kunz [22]. The mixture rules for the cubic EOS in this paper are defined as the one-fluid mixture model, see Michelsen and Mollerup [28]. Transport properties for the cubic EOS are approximated according to Ruiz et al. [32], who used the generalized multi-parameter correlation for high densities [30]. The effective diffusion coefficient is defined according to Blanc’s law, where the binary diffusion coefficients \(D_{jk}\) were implemented according to the Chapman-Enskog theory [30].

3.1.1 Two-Phase Thermodynamics for Multi-component Mixtures

Commonly phase equilibrium for multi-component mixtures is calculated by the methodology of the combined approach of tangent plane distance (TPD) analysis and multi-component vapor-liquid equilibrium (VLE) calculations, see e.g. Matheis and Hickel [27] and Qiu and Reitz [31]. Note that in some cases we use an alternative notation for molar fraction in the context of multi-component vapor-liquid equilibrium with \({\textit{\textbf{z}}} \equiv {\textit{\textbf{X}}}\), \({\textit{\textbf{x}}} \equiv {\textit{\textbf{X}}}^l\) and \({\textit{\textbf{y}}} \equiv {\textit{\textbf{X}}}^v\), where \({\textit{\textbf{z}}}\) is the common molar fraction, \({\textit{\textbf{x}}}\) is a liquid equilibrium molar fraction and \({\textit{\textbf{y}}}\) is a vapor equilibrium molar fraction. Note that the superscript \((\bullet )^s\) refers to saturation conditions.

The phase equilibrium calculation for multi-component mixtures is a rather difficult task and can generally be calculated analogously to the single species case by considering that equilibrium has to hold for all \(N_k\) species simultaneously

$$\begin{aligned} T^l&=T^v \equiv T^s , \end{aligned}$$
(8)
$$\begin{aligned} p^l (T^s,\rho ^l,{\textit{\textbf{X}}}^l)&=p^v (T^s,\rho ^v,{\textit{\textbf{X}}}^v) , \end{aligned}$$
(9)
$$\begin{aligned} \mu _{N_k}^l(T^s,\rho ^l,{\textit{\textbf{X}}}^l)&=\mu _{N_k}^v(T^s,\rho ^v,{\textit{\textbf{X}}}^v) \,, \quad k=1,\dots ,N_k. \end{aligned}$$
(10)

On the left and right side of Fig. 2, the phase envelopes for the binary mixture of nitrogen/n-hexane, calculated with the Peng-Robinson EOS, are visualized in a pressure-composition and density-composition phase diagram, respectively.

Fig. 2
figure 2

Binary mixture of nitrogen/n-hexane in a pressure-composition (left) and density-composition (right) diagram calculated using the PR-EOS

Full size image

The blue curves represent the liquid boundary of the hyper-plane, the red curves represent the vapor boundary of the hyper-plane. The green curves are points at constant temperature and vapor fractions. The black dot is the mixture critical point. The TPD analysis is based on the idea to directly evaluate the Gibbs free energy surface [28] by checking for a global minimum in Gibbs free energy at the present species composition. The phase-envelope and equilibrium calculations in our simulations are performed in a volume based fashion, see Kunz [22], using a Newton–Raphson method. In the macroscopic formulation, the speed of sound has to be modeled in the two-phase region. We use the Wood’s speed of sound [36].

3.1.2 Thermodynamic Mixing Process

Mixing of two or more species may occur under different thermodynamic conditions. For example, an adiabatic mixing is generally defined as a thermodynamic process where mixing is controlled solely by convective transport and is not influenced by any diffusive transport of heat or mass from the surrounding. Investigations in the context of super- and transcritical jet injections were performed by Lacaze et al., Ma and Matheis [23, 25, 27]. For a given pressure and adiabatic conditions, the specific molar enthalpy is a linear function in the molar composition space with

$$\begin{aligned} h_m(\rho ,T,{\textit{\textbf{X}}}) = \sum ^{N_k}_{k=1} X_k h_{m,k}^0(\rho ,T). \end{aligned}$$
(11)

Adiabatic mixing was observed with a fully-conservative approximation of the Navier–Stokes equations in [23, 27] with insufficient grid resolution. For a given pressure and isochoric conditions the specific molar volume is a linear function in the molar composition space with

$$\begin{aligned} \nu _m(\rho ,T,{\textit{\textbf{X}}}) = \sum ^{N_k}_{k=1} X_k \nu _{m,k}^0(\rho ,T). \end{aligned}$$
(12)

Isochoric mixing was observed with quasi-conservative approximations of the Navier–Stokes equations in [23, 27] with insufficient grid resolution. Here we use the double flux method presented by Föll et al. [14,15,16] and literature therein.

From a physical point of view, it is questionable if any of the two assumptions hold for binary jet simulations under supercritical conditions. It is important to note that the isochoric and the adiabatic mixing lines are generated by directly calculating the underlying real EOS for multi-components at a given pressure. However diffusive or non-equilibrium thermodynamic effects related to, e.g. Fourier, Fickian, Dufour or Soret contributions are not considered in plots presented in [23, 25, 27] and Fig. 4. The influence of these effects is highly non-linear and problem depending. Which mixture assumption holds for supercritical binary jet injections can generally not be stated a priori and depends on the ratio of acting (physical) parabolic effects in the equation system. Moreover, to get insight into the mixture processes with CFD simulations, the numerical diffusion must have a negligible influence.

4 Numerical Results: LES of N-Hexane/Nitrogen Jet

Baab et al. [7] experimentally investigated different binary mixtures under supercritical conditions. For the numerical investigations we have chosen the n-hexane/nitrogen case. Note that the injection and chamber conditions for this simulation are described in [7] in detail. The simulation is performed twice. The first one is a fully conservative simulation suffering from spurious pressure and velocity oscillations. The second one is a local quasi-conservative method based on the double flux method.

Fig. 3
figure 3

Mesh resolution and geometry definitions: The mesh is based on hexahedral elements with Mortar interfaces based on an unstructured mesh topology. Three different slices are visualized. Note that the overall simulation area is defined as a function of injection diameter D

Full size image

The computational setup and the mesh resolution are illustrated in Fig. 3. Note that the mesh is unstructured and contains Mortar interfaces to reduce the overall element number to \(\approx 0.4~\text {Mio}\) elements. For the multi-component mixture setup, we have chosen a polynomial degree of two with third order accuracy resulting in an overall \(\approx 10.8~\text {Mio}\) degree of freedoms (DOF). The inlet diameter of the injector was \(D=0.236~\text {mm}\). The smallest element near the injector had a size of \(\Delta x,y,z \approx D/30\).

Fig. 4
figure 4

LES results in the context of adiabatic (left) and isochoric (right) mixture process at \(p_{\infty }=5.0~\text {MPa}\): nitrogen/n-hexane in a temperature-composition diagram calculated using the PR-EOS. The gray dots (simulation results) are temporal and spacial solutions of the temperature along the jet axis, see Fig. 3

Full size image

First, we look at the results regarding the thermodynamic mixing paths. The mixing processes under adiabatic and isochoric conditions are illustrated on the left and right side of Fig. 4 for a binary mixture of nitrogen/n-hexane, respectively. The conservative simulation is compared to the adiabatic mixture lines, whereas the quasi-conservative method is compared to the isochoric mixture lines.

Fig. 5
figure 5

Speed of sound mixture lines for different thermodynamic models, Peng Robinson or NIST (RefProp), and different mixture assumptions. The markers \(\text {x}\) represents speed of sound measurement with LITA and are placed directly on the associated mixture lines to give an overview of possible molar fractions for different assumptions; Right: Quantitative speed of sound measurement data and corresponding temporal averaged simulation results. Note that these values correspond to the conservative simulation

Full size image

The VLE region is again illustrated by blue, red and green curves. The black lines are either the adiabatic mixing lines on the left side for supercritical and sub/transcritical conditions or the isochoric mixing lines on the right side for supercritical and sub/transcritical conditions. For the first temperature \(T_{\text {hex}}=627~\text {K}\), we observe that the adiabatic mixture line (on the left side) does not reach the VLE region. However, for an isochoric assumption (on the right side) the two-phase region is crossed, in contrast to the experimental evidence. The gray dots are the simulation results visualized as scattered data, which represent temporal/spatial solutions of the temperature along the jet axis, see also Fig. 3 for geometric definitions.

Fig. 6
figure 6

High pressure n-hexane/nitrogen jet: Experimental data visualized with a shadogram for n-hexane \(T_{\text {hex}}\approx 600~\text {K}\) and \(p_{\text {inj}}=5.6~\text {MPa}\) injected into nitrogen at \(T_{\text {N}_2}\approx 296~\text {K}\) and \(p_{\infty }=5.0~\text {MPa}\)

Full size image

In Baab et al. [7], LITA measurements of speed of sound were performed. Therefore, on the left side of Fig. 5 we have illustrated speed of sound mixture lines for different thermodynamic models, e.g. Peng Robinson or NIST (RefProp), and different mixture assumptions adiabatic (red) or isochoric (blue). Additionally, speed of sound measurements at different axial positions \(x/D=17,25,35,\) are included. The straight line should indicate which molar fractions may be possible under different thermodynamic models or mixture assumptions. Note that the isochoric mixing assumption is not realistic, since it would imply extremely high concentrations of nitrogen (above \(90\%\) already at \(x/D = 17\)) and almost pure nitrogen at \(x/D =25\). This result is obviously not in line with the experiments, as shown in Fig. 6, where a dense n-hexane jet is still observed at \(x/D=25\). The quantitative comparison of the speed of sound data is therefore performed only for the fully conservative method (adiabatic mixing). On the right side of Fig. 5, the quantitative speed of sound measurement data at \(x/D=17,20,25,30,35,\) and corresponding temporal averaged LES results are given. The numerical results are systematically lower than the experimental values, even though the adiabatic mixing assumption is verified both by the numerical scheme and in the experiments (see Fig. 1). A possible explanation for this may be attributed to a still insufficient grid resolution. This is also supported by the fact that the predicted nitrogen concentrations are too small for either an adiabatic or isochoric mixture. Note, that in the experiments, higher nitrogen concentrations at the specific measurement points were observed, see case 1 in Fig. 1. The standard deviation of the speed of sound measurements are given in Baab et al. [7].

5 Conclusions

In this paper, we pointed out the importance to include diffusive fluxes in the treatment of high-pressure injections. Different cases from literature [6, 7, 13] covering injection from supersonic underexpanded to subsonic dense gas jets were revised and evaluated. Herein, axial speed of sound measurements were performed, which were later converted into concentration data. It showed that underexpanded jets followed the adiabatic mixing rule accurately. Nevertheless, strong discrepancies were found for subsonic high-pressure jets. Here injection velocity and thereto related time scales need to be considered with regard to diffusion driven effects. Furthermore, deviations occurred for binary mixtures with large differences in molar mass. The data shows that the omission of diffusive fluxes can lead to substantial inaccuracies in the connection of derived fluid properties to measured speed of sound. Possible effects that lead to the deviation of the adiabatic mixing assumption were discussed, yet the particular effects cannot solely be distinguished by experimental methods.

Additionally, numerical simulations were performed for a binary jet injection with n-hexane/nitrogen under supercritical conditions and compared to the experimental results. We performed three-dimensional Large Eddy Simulations with a conservative and a stability enhanced non-conservative approximation. For the investigated fluid pair adiabatic and isochoric mixing was observed. The results are in good agreement with recent findings of Ma et al. [25], who conducted one and two-dimensional simulations. The considered experimental data tend to be more accurately predicted by the adiabatic mixing assumption. Not fully clarified is the influence of Fourier, Fickian or Dufour contributions to the jet mixing process, since the simulation was likely dominated by the numerical diffusion. The resulting speed of sound values were in a reasonable range. The underprediction compared to the experimental data indicates a still insufficient grid resolution.

For future investigations we will focus our work on the evaluation of diffusive transport. Therefore, the numerical studies on the interaction between physical and numerical diffusion, resulting from different numerical approximations, will be continued. Furthermore, the experimental setup has to be designed in such a way that the diffusive transport becomes dominant within the jet injection process. This may be achieved by decreasing the injection velocity. Binary fluid combinations, that favor strong concentration gradients, should also be taken into consideration.