1 Introduction

Unsteady aerodynamic phenomena at the base of space launch vehicles can create low-frequency loads on the engine nozzle structure, called buffeting. These loads and their “non-exhaustive definition” were determined to have contributed to the failure of at least one mission [3] and thus have been the focus of renewed research in the last years, among others in the DFG Sonderforschungsbereich Transregio 40. Due to the sudden change in diameter from the main body to the engine shroud and/or nozzle the turbulent boundary layer separates and creates a turbulent shear layer. For certain geometrical designs and flow conditions this shear layer then reattaches at the end of the nozzle structure and creates a recirculation region at the base of the vehicle. The turbulent structures are transported in this recirculation region and create a feedback loop, leading to oscillations of the reattachment position and thus partially asymmetric loads. To further investigate these loads the complex geometry of an actual space launch vehicle can be simplified to an axisymmetric backward-facing step. The most critical mechanical loads for an Ariane 5 like geometrical design occur at transonic conditions with \(M \approx 0.8\). In the past, the description and definition of these loads has been investigated in detail using scale resolving simulations as well as experimental investigations, e.g. [2, 9, 16]. It was found that vortex shedding is the main contributor to the unsteady loads and occurs with a non-dimensional frequency expressed as the Strouhal number of \(\text {Sr} = \frac{f D}{U} \approx 0.2\), where the D is the main body diameter, f is the frequency and U is the free stream velocity.

To the authors’ knowledge, all of these investigations have been conducted using either no propulsive jet exiting from the simplified nozzle structure or a jet of pressurized air. However, realistic engine plumes possess significantly different properties due to different fluids used. Two of the most important differences are the higher temperature as well as the higher velocity of the plume. In addition to the higher temperatures of the plume itself, the nozzle structure also heats up during flight. This increase in nozzle temperature in turn heats up the recirculation region located on the outside of the nozzle structure and thus might influence the recirculation region characteristics and consequently the mechanical loads the nozzle structure is subjected to.

In the present work, the effects on the recirculation region characteristics and observed fluid mechanical phenomena for a generic space launch vehicle featuring a plume originating from a Hydrogen-Oxygen combustion are investigated numerically. The model geometry corresponds to the one investigated at DLR Cologne in their wind tunnel experiment [13]. After a short introduction to the numerical methods used and the implemented improvements allowing for accurately computing multi-species flows and polar molecules at high temperatures, a Reynolds-Averaged Navier-Stokes (RANS) investigation of the combustion chamber flow of the investigated model is discussed. Additionally, the whole model including the structural thermal response is investigated to obtain realistic wall temperatures for the model at steady state conditions. Then, scale resolving simulations using Improved Delayed Detached Eddy Simulation (IDDES) are employed that use the obtained wall temperatures as boundary conditions. These simulations allow to compare the detailed aerodynamic phenomena between cases with and without a H\(_2\)O-H\(_2\) plume as well as between cases with heated and cold model walls. Finally, conclusions are drawn and an outlook to planned future investigations is given.

2 Numerical Method and Setup

The current work uses the DLR TAU code [7] that uses 2nd-order accurate schemes in space and time. For the RANS investigations in Sect. 3 a local time stepping scheme for the temporal discretization and the AUSMDV upwind scheme for spatial discretization is used. For the scale resolving simulations in Sect. 4 a dual time stepping scheme using a backward-differences formula is used for the temporal discretization that employs a 3-stage Runge–Kutta scheme to converge the inner iterations. The spatial discretization uses a central hybrid low-dissipation low-dispersion scheme [12] that has recently been extended to allow for multiple species to be considered [5].

In both cases a 2-equation \(k-\omega \) SST turbulence model [10] is used, with the IDDES version of that model [15] activated in the later section. To improve the switch from RANS to LES regions a modified filter length \(\widetilde{\Delta }_\omega \) is used [11]. The transport coefficients are computed using a novel transport model [5] that allows for an accurate description of polar molecules like water vapour which is essential to capture the combustion chamber processes of a Hydrogen-Oxygen (H\(_2\)-O\(_2\)) combustion and the heat transfer to the structure. For the coupled RANS simulations which include the combustion chamber a reaction mechanism employing 9 species [6] is used. For the scale resolving simulations air is modelled as one gas component and the plume, if present, is modelled as a second. These simulations do not include the combustion chamber and convergent nozzle part. Thus, no reactions are considered since the chemical composition is nearly frozen downstream of the throat and a possible post-combustion occurs only downstream of the recirculation region in the shear layer between plume and external flow. Precursor RANS simulations were employed to confirm no significant changes in the region of interest occur if reactions are neglected and a reduced number of species is considered [5].

Fig. 1
figure 1

Geometry and setup of the simulations

Full size image

A 2D cut through the investigated geometry is displayed in Fig. 1 where the regions only included in the simulations in Sect. 3 are denoted with “RANS” whereas those also included in the scale resolving simulations are denoted as “RANS+DES”. The coordinate system has its origin at the base of the main body in the x-direction and at the symmetry axis for the y- and z-directions. The main body has a diameter \(D=0.067\) m, the 2nd cylinder, in which the supersonic nozzle is located, has a diameter of \(D_{2nd} = 0.4 D\) and the wind tunnel exit diameter is \(D_{tunnel} \approx 5.08 D\). The nozzle length as measured from the base wall is \(L_{nozzle} \approx 1.2 D\) and the nozzle exit angle is \(5^\circ \). The Reynolds number with respect to the main body diameter is \(\text {Re}_D = 1.2 \cdot 10^6\), free stream Mach number is \(M_\infty = 0.8\), the oxidizer to fuel mass ratio in the combustion chamber is \(O/F=0.7\) with a total injected mass flux of 89.16 g/s and the resulting combustion chamber pressure is \(p_{cc} = 21.5\) bar with a nozzle throat diameter of \(D_{th} = 0.011\) m and nozzle expansion ratio of \(\epsilon =5.63\). The RANS investigations in Sect. 3 employ a 2D axisymmetric setup whereas the scale resolving investigations feature a full 360\(^\circ \) setup with inflow conditions for the external wind tunnel flow and the internal jet flow taken from precursor RANS simulations. The RANS grid used for the coupled simulations contains approx. 127000 points and with the chosen circumferential resolution of 0.94\(^\circ \) the DES grid contains approx. 33 Million points. In both grids a non-dimensional first wall normal spacing of \(\Delta y^+ < 1\) is achieved on all walls with the exception of the nozzle throat of the RANS grid where a \(\Delta y^+\) of up to 3.7 is allowed. The maximum cell aspect ratio in the RANS grid is found at the wall near the inflow boundary with a value of \(\frac{\Delta x^+}{\Delta y^+} \approx 15000\), which corresponds to a \(\Delta x^+ \approx 6000\). In the DES grid the cell aspect ratio is between 1 and 2 in the majority of the recirculation region with the exception of the shear layer (\(\frac{\Delta x^+}{\Delta y^+} < 50\)) and near walls (\(\frac{\Delta x^+}{\Delta y^+} < 200\)). The non-dimensional grid spacings in the axial and circumferential direction in the recirculation region are in the order of \(\Delta x^+ \approx \Delta z^+ \approx 70..100\).

For the determination of the temperature distribution at the surface and in the solid the RANS simulation is coupled to ANSYS Mechanical V19 [1]. A previous study [5] employed a transient coupling procedure and featured a flow domain that was restricted to the H\(_2\)/O\(_2\)-injector, the combustion chamber and the nozzle whereas at the wind tunnel side of the model (red boundary in Fig. 1) a constant heat transfer coefficient of 50 W/m\(^2\)K was applied. However, when imposing the final temperature distribution to a wind tunnel simulation large discrepancies in the heat transfer coefficient along the surface occur. Moreover, the RANS simulations covering both wind tunnel flow as well as combustion indicate flow separation at the nozzle exit which does not arise in simulations without wind tunnel flow.

Based on the assumption that measurements will be obtained at nearly steady-state operating conditions a new coupling strategy was developed aiming to determine the steady-state surface temperature distribution instead of the complete heating process of the material. In order to overcome the deficiencies of the study described above, the flow domain of the axisymmetric RANS simulation was extended to include the wind tunnel flow. Unfortunately, a steady-state simulation provokes an additional problem. If the heat fluxes obtained from the flow simulation for the initial solid temperature of 279.15 K are prescribed to the structure model, infinite solid temperatures arise due to the net heating of the structure. In order to resolve this problem, an attempt was made to prescribe the temperature in the structure solver spatially resolved along the red boundary in Fig. 1. Then, the heat fluxes obtained from the structure solver were applied to the following RANS simulation. It was found that even a small spatial variation of temperature leads to very high heat fluxes inside the structure causing large surface temperature and heat flux oscillations in subsequent coupling steps. Hence, in a second attempt the heat transfer coefficient is prescribed spatially resolved to the structure solver at the red boundary. The heat transfer coefficient is determined from the heat flux distribution from the flow solver and the local surface temperature obtained from the structure solver in the preceding structure simulation. Then, the surface temperature distribution obtained from the structure solver is prescribed as a boundary condition for the subsequent run of the flow simulation. In order to damp oscillations, the changes of heat fluxes and heat transfer coefficients were reduced employing a relaxation factor. The relaxation factor was increased from 0.01 for the initial coupling step to 0.3 for the final coupling step. Note, that each coupling step consists of preparation of boundary conditions for the structure solver, a thermal simulation of the structure followed by the generation of boundary conditions for the flow solver and a RANS simulation. In total 27 coupling steps are required to reduce the differences in surface heat flux between flow and structure solver to a few percent.

3 Results of Thermal Flow Structure Coupling

For the investigation of the influence of the surface temperature on the flow separation the combustion chamber condition RC0 described by Kirchheck and Gülhan [8] is investigated with thermally coupled axisymmetric RANS and structure simulations. Due to the low mixing ratio of \(O/F=0.7\) the average gas temperature of the exhaust gases is relatively low compared to real rocket engines. However, the condition has the advantages that the combustion is completed roughly 8 cm upstream of the nozzle throat, the expected temperatures of less than 750 K allow for a continuous, steady-state operation and experimental data can be obtained for the condition.

Selected results obtained in the final coupling step are shown in Fig. 3. The three figures on the left show from top to bottom the external heat fluxes on the two cylinders, the heat flux traces through the solid together with the temperature distribution in the solid and the surrounding gas and the heat fluxes to the combustion chamber walls and the nozzle obtained with TAU and ANSYS. The heat fluxes computed from TAU depicted by green lines with open diamonds are superpositioned by the blue lines indicating the heat fluxes from ANSYS. The figure on the right shows the heat transfer coefficient, the heat flux and the temperature distribution on the 2nd cylinder in detail. The maximum temperature of about 730 K at the external surface is obtained in the corner between base plate of the main cylinder and the 2nd cylinder. The heat transfer coefficient obtained from the simulation is between 100 W/m\(^2\)K close to the corner and 1600 W/m\(^2\)K at the nozzle exit. The static pressure in the combustion chamber obtained from the coupled solution is about 2.15 MPa and the maximum temperature in the combustion chamber is 3550 K. The maximum steady-state solid temperature is 743 K located 4.63 mm upstream of the nozzle throat. At the nozzle exit the supersonic expansion results in a pressure on the symmetry line of \(p_{exit} \approx 44\) kPa. Other important characteristic values obtained at this location are the gas temperature \(T_{exit} \approx 420\) K, Mach number \(M_{exit} \approx 3.15\) and axial velocity \(u_{exit} \approx 3.5\) km/s.

Due to the slightly lower pressure in the exit plane and the associated differences in the flow pattern of the jet the separation zone is larger than the one obtained for the case with cold jet investigated by the authors in [4].

Fig. 2
figure 2

Grid used for the scale resolving simulations. Overview over the grid (left) and readings of the grid sensor in the region of interest (right)

Full size image

4 Investigation of Aft-Body Flow Fields

An overview of the grid used for the scale resolving simulations is shown on the left of Fig. 2. Both the model and the wind tunnel walls are included in the computational domain to ensure an accurate prediction of possible interference. The grid is of hybrid nature, i.e. includes hexahedral and prismatic elements to allow for an optimized accuracy with a reduced amount of grid points. A zoomed view of the focus region is displayed in the figure as well to show the hexahedral elements and their resolution in this region. To ensure a sufficient grid resolution for the scale resolving simulations a grid sensor is used. This sensor computes the ratio between resolved and modelled turbulent kinetic energy and was shown to accurately display regions of underresolution in previous investigations of similar flows and grid topologies [14]. A sensor value of 0.8 is considered to be sufficient to capture important flow phenomena and, as shown on the right of Fig. 2, this is the case for nearly the entire region of interest in the current investigations. A small region with a ratio of about 0.7 exists in the outside of the developing shear layer where it has little influence on the developing flow structures.

Fig. 3
figure 3

Surface heat flux and temperature distribution in the solid with heat flux trace lines and the surrounding flow (left) and heat flux together with heat transfer coefficient and surface temperature along the 2nd cylinder (right)

Full size image

Three cases for the same investigated geometry and grid are considered in the following. The first features an air plume and wall temperatures that are equal to the ambient temperature of 300 K. For the second case the air plume is replaced by an H\(_2\)-H\(_2\)O plume as obtained from the combustion chamber simulations described in Sect. 3 and the nozzle internal wall temperature is adjusted accordingly. However, for this second case the outside wall temperature is still at ambient conditions of 300 K, representing e.g. the start of an experimental investigation when the structure has not absorbed sufficient heat to significantly increase its temperature yet. It also allows to investigate the difference to the third case in which the external wall temperature from the coupled RANS simulations presented in Sect. 3 is prescribed. This third case represents the steady state conditions that could be achieved in a long duration experiment.

For each case both a DES computations and an axisymmetric RANS simulation are performed. The latter feature the same settings as the DES computations (same numerical scheme, time stepping method, turbulence model, in-plane grid resolution, etc.), and only differ in whether the turbulence model is run in RANS or DES mode. Data recording for the DES computations commences after a transient start-up phase of approx. 40 convective time units (CTUs) where one CTU is defined as the ratio of main body diameter D and free stream velocity U. Subsequently, data is recorded for approx. 200 CTUs with a time step size that allows to resolve each CTU with approx. 130 time steps.

Fig. 4
figure 4

Mean flow fields of DES computation with air plume (top), hot plume and cold wall (center) and hot plume and hot wall (bottom)

Full size image

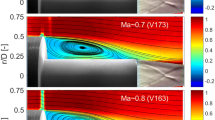
The resulting mean flow fields of the DES computations are presented in Fig. 4 in which the color contour of the axial velocity and the streamlines for the three cases are displayed. From the mean flow field the known flow behaviour with a detaching boundary layer at the diameter change and the subsequent formation of a turbulent shear layer can be observed. A strong recirculation region with a secondary corner vortex is also apparent for all three cases. It is visible that the hot plume cases feature a significantly higher exhaust velocity. This clearly affects the recirculation region. Whereas for the first case a reattachment on the nozzle structure can be observed, in the second case the recirculation region grows and reattachment occurs on the plume. Both the secondary corner vortex as well as the recirculation region length increase. Consequently, the initial shear layer angle changes as well. This seems to be a direct consequence of the higher exhaust velocities and changed plume characteristics, as no other parameters are changed. For the third case with an increased wall temperature the reattachment location is shifted even further downstream. This indicates an additional effect that is independent of the plume characteristics, but purely due to the increased temperature in the recirculation region.

The RANS solutions show qualitatively similar flow fields—and hence are not displayed here for brevity—, but differ in certain key features. For one, the reattachment region size is consistently predicted to be larger. The reattachment locations, approximated by the location of zero axial velocity at the radius of the external nozzle structure for cases with fluid reattachment, for all cases are shown in Table 1. While the relative changes between the cases qualitatively agree between RANS and DES, the actual reattachment region length differs by up to 7%. This can lead to a predicted fluid reattachment, i.e. reattachment on the plume, in RANS when the DES computation predicts a solid reattachment, i.e. reattachment on the nozzle structure, for the same case. Tthis can be observed e.g. for the configuration with an air plume for which the DES predicts a reattachment region shorter and the RANS simulation predicts it longer than \(L_{nozzle}\), respectively.

Table 1 Axial reattachment locations for different cases
Full size table

In addition to the qualitative mean flow fields the mean wall pressure distribution can be analysed for a quantitative comparison as is shown on the left of Fig. 5 where the axial distribution of the mean wall pressure coefficients is displayed. A first observation is the fact that with increasing reattachment length the pressure distribution becomes shallower, i.e. features a less distinct pressure minimum and lower pressure at the nozzle tip. The pressure in the corner of the recirculation region as well as at the nozzle tip is captured reasonably well with RANS for the first two cases, whereas for the third case the pressure at the nozzle tip deviates. However, more importantly, the inaccuracies of RANS modelling become clearly visible in the middle of the recirculation region where the RANS computations show an earlier, but less distinct pressure minimum, leading to a different shape of the distribution. For the DES investigations the wall pressure fluctuations can be assessed as well as is presented on the right side of the figure. The pressure fluctuations mirror the mean pressure distribution in that the configurations with stronger mean pressure minima and maxima also show more wall pressure fluctuations. Towards the nozzle tip all configurations show an increase in pressure fluctuations with \(c_{p,rms} \approx 0.045\) that is due to the influence of the overexpanded and slightly separated plume and the corresponding fluctuations of the nozzle separation location.

Fig. 5
figure 5

Comparison of axial mean pressure coefficient distribution (left) and rms pressure distribution (right) between different cases

Full size image
Fig. 6
figure 6

Comparison between mean temperature distributions obtained with RANS and DES (left; RANS-top, DES-bottom) and axial (on the external nozzle wall) and radial (on the base surface) mean heat flux distribution for the hot wall case (right)

Full size image

Another aspect of the investigation is the wall heat transfer. Cases with walls of ambient temperature obviously do not feature significant wall heat transfer, but for the hot wall case it might be informative to compare the results of a steady RANS solutions with the mean solutions of an unsteady DES solution. For this, both the mean temperature distribution in the recirculation region as well as the heat flux distribution are shown in Fig. 6. The temperature fields look qualitatively very similar, but in the scale resolving simulation the impact of the hot base wall propagates less far into the recirculation region. Additionally, the boundary layer temperature has a smaller footprint in the shear layer and the base corner features smaller temperatures. However, the temperature differences are in the range of 5 K to 20 K in the majority of the recirculation region, with the exception of the base corner where the temperature differs by up to 100 K. On the right of the figure the wall heat fluxes are displayed over both the axial and radial direction since a purely axial representation would neglect the distribution on the base wall. With respect to the axial distribution, for \(0.2< x/D < 1.2\) the heat flux predicted by RANS is about \(70\%\) higher than that predicted by DES, whereas in the base corner RANS predicts a \(50\%\) lower heat flux. Towards the nozzle tip both approaches lead to similar heat fluxes. At the base wall the heat fluxes between RANS and DES agree reasonably well everywhere except for the bottom and top corner where the heat flux predicted by RANS is lower. Since (in-plane) grid resolution, spatial and temporal numerical scheme and underlying turbulence model are exactly equivalent for both RANS and DES, the deviations are unlikely to originate from these aspects. Hence, the deviations between RANS and DES solutions are likely due to a combination of other model related differences. For example, the differences in the velocity fields described above will have an impact on the heat flux distributions. Additionally, the exact value of the turbulent Prandtl number \(\text {Pr}_t\), which describes the additional heat flux due to modelled turbulent fluctuations, is difficult to determine a priori since it is flow dependent. Since the amount of modelled fluctuations is significantly larger in RANS than in DES, a discrepancy in \(\text {Pr}_t\) will consequently introduce larger inaccuracies in RANS than in DES. Another possible source of inaccuracies is the limited ability of the chosen turbulence model to capture the anisotropic turbulent behaviour in the recirculation region, in particular near the walls. This is again more severe for RANS than for DES for the same reasons and could possibly be improved with a more elaborate and expensive turbulence modelling approach, e.g. using a Reynolds Stress Model (RSM).

In former investigations (e.g. [14]) the IDDES approach showed results of higher fidelity that agree well with experimental reference data regarding overall flow field, reattachment length and pressure distributions and thus are considered more accurate with respect to these quantities. This is also supported by the above argument of IDDES being less affected by turbulence modelling parameters than RANS. However, with respect to the obtained heat flux distributions a larger uncertainty exists as very little experimental heat flux reference data for the considered flow topologies is available for comparison. Hence, the superiority of IDDES over RANS in terms of heat flux distributions cannot be assumed beyond doubt.

5 Conclusions and Outlook

To investigate the impact of wall temperature on generic launch vehicle base flows the flow solver is thermally coupled to a structure solver to obtain resulting steady-state wall temperatures. The obtained wall temperatures are then used as boundary conditions for the 2-equation RANS and IDDES approaches. It is found that both modelling approaches are able to qualitatively capture the behaviour of the mean flow field when either plume characteristics or wall temperatures are changed. Both an increased plume velocity as well as an increased wall temperature lead to a further downstream reattachment of the main shear layer and thus increase the size of the recirculation region. However, differences in the exact reattachment locations as well as the mean pressure distribution on the nozzle surface between RANS and DES are observed. Similar differences are also visible in the heat flux distribution along the base and nozzle surface that could be explained by the slightly different flow fields, inaccurate values for \(\text {Pr}_t\), short-comings of the used turbulence model or, most likely, a combination of these reasons. To further determine the source of the deviations between RANS and DES results, additional RANS simulations with varied \(\text {Pr}_t\) and turbulence model will be conducted. The results of the scale resolving simulations are being further analysed, including spectral and modal analysis, to investigate the detailed changes in the flow behaviour that are associated with the change in plume characteristics and wall temperatures. Additionally, the effect of the nozzle length will be investigated by reducing the nozzle length and allowing the plume to directly interact with the recirculation region instead of being mostly separated by the nozzle structure. Furthermore, these investigations will also feature even higher wall temperatures that are in the order of magnitude expected from realistic rocket engines with radiative cooling concepts.