1 Introduction

Conventional nozzles of space launchers like the European Ariane 5 exhibit the disadvantage that the maximum area ratio of the nozzle is limited due to the risk of an asymmetric flow separation of the overexpanded jet and thereby arising side loads at sea level conditions. Since with increasing altitude and decreasing ambient pressure a larger area ratio without flow separation would be feasible which would increase the specific impulse of the nozzle, the overall performance of the nozzle is reduced by this limitation. To compensate for this constraint, Foster and Cowles  [5] proposed in 1949 an altitude adaptive nozzle with an abrupt contour inflection in the divergent part of the nozzle to obtain two expansion ratios built into one nozzle. This so-called dual-bell nozzle consists of a conventional bell nozzle, i.e., the base nozzle, and an extension nozzle. Depending on the nozzle pressure ratio (NPR), i.e., the ratio of the chamber pressure to the ambient pressure, the nozzle has two operating conditions illustrated in Fig. 1. At sea level mode (left) a controlled and symmetric separation takes place at the contour inflection minimizing the side loads. With decreasing ambient pressure the nozzle transitions into the altitude mode (right), i.e., the separation point shifts to the exit of the nozzle extension and a symmetric attached flow develops in the complete nozzle. Due to the altitude adaption a larger area ration and thus an increased expansion of the flow can be achieved at altitude mode compared to a classical rocket engine improving the overall performance. The dual-bell flow behavior, e.g., the transition behavior, the arising side loads, and the payload gain, has experimentally, e.g., by Stark et al.  [11], and numerically, e.g., by Schneider and Genin  [9], been investigated proving the functionality of the adaptive nozzle concept. More recently, Loosen et al.  [7], investigated the aerodynamic integration of the dual-bell nozzle into the launcher’s architecture and the influence of the outer flow onto the dual-bell nozzle flow for a generic planar space launcher configuration. However, the effect of a dual-bell nozzle on the wake of an axisymmetric configuration has not been investigated, yet.

Fig. 1
figure 1

Schematic of the interaction of the wake flow with a dual-bell nozzle operating at sea-level mode (a) and altitude mode (b)

Full size image

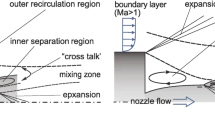
The turbulent wake flow behind the base is characterized by the separation of the incoming boundary layer at the base shoulder and its subsequent reattachment on the nozzle leading to the formation of a highly dynamic recirculation region. Many experimental and numerical investigations on a large range of different axisymmetric space launcher configurations ranging from axisymmetric backward-facing steps up to scaled real launchers have been conducted, e.g., Deprés et al.  [3], Deck and Thorigny  [2], Schrijer et al.  [10], and Statnikov et al.  [13]. Statnikov et al.  [13] performed a dynamic mode decomposition of the flow around a generic Ariane 5-like configuration to analyze the coherent structures being responsible for side forces occurring for axisymmetric configurations. Three distinct modes at \(Sr_D\approx 0.1;0.2;0.35\) which could generate those called buffet loads were detected. The low frequency mode describes a longitudinal cross-pumping motion of the separation region, the second mode is associated with a cross-flapping motion of the shear layer caused by an antisymmetric vortex shedding, and the high frequency mode represents a swinging motion of the shear layer. To manipulate this coherent motion and consequently reduce the buffet loads a large number of active and passive flow control devices have been tested, e.g. Weiss and Deck  [15] investigated the effect of jets injected at the base of a space launcher configuration onto the dynamics of the separated shear layer and the dynamic side loads.

In the present study, an axisymmetric generic space launcher equipped with a dual-bell nozzle will be investigated at transonic and supersonic flow conditions to determine the influence of the new propulsion concept onto the intricate wake-nozzle flow interaction. In addition, the impact of flow control on the spatial coherence of the wake and on the undesired buffet loads is analyzed. The flow control is realized by four in the circumferential direction equally distributed jets injecting air towards the backflow in the main recirculation region of the wake.

The paper is organized as follows. In Sect. 2, the investigated geometry, the flow parameters, the zonal RANS/LES method, and the computational grids are presented. In Sect. 3, the results of the performed simulations are discussed. First, the supersonic configuration is described. Then, the flow topology of the transonic clean configuration without flow control is presented followed by an investigation of the dynamic loads by spectral analysis and by modal analysis of the wake flow using DMD. Subsequently, the influence of the flow control device onto the wake and the buffet loads is outlined. Finally, conclusions are drawn in Sect. 4.

2 Computational Approach

In this section, the geometry and flow parameters, the zonal RANS/LES method, and the computational grids are discussed.

2.1 Geometry and Flow Conditions

The transonic \((Ma=0.8)\) and supersonic \((Ma=3)\) simulations are performed for an axisymmetric space launcher which approximates the shape of the main stage of the Ariane 5 shown in Fig. 2a. The setup is based on a reference configuration of Statnikov et al.  [13] where a classic conical nozzle was considered. The launcher model is composed of an Ariane-5 like main body with a reference thickness of D and a length of 5.6D. The nozzle fairing is modeled by a cylindrical extension with a diameter of 0.56D and a length of \(1.37\, D\) for the supersonic and a length of \(0.85\, D\) for the transonic configurations. For the inner shape of the nozzle, a dual-bell geometry with a truncated ideal contour (TIC) for the base nozzle and a constant pressure nozzle extension with a design exit Mach number at altitude mode of \(Ma_e=3.3\) is used. In the supersonic simulations, the dual-bell nozzle is operated at sea-level and altitude mode using a nozzle pressure ratio of \(NPR=4.5\) (\(NPR=97\)) for the sea-level (altitude) mode and in the transonic configurations the nozzle is operated at sea-level mode at a nozzle pressure ratio of \(NPR=10\). The freestream Reynolds number based on the launcher diameter is \(Re_D=1.2 \cdot 10^6\) for the supersonic and \(Re_D=4.3 \cdot 10^5\) for the transonic configurations. In the flow control configuration, four in circumferential direction equally distributed jets are installed at the outer nozzle fairing shown in Fig. 2b. The jets are located at \(x/D=0.283\) and inject air at an incline of \(\varphi =22.5^\circ \) towards the streamwise direction with a blowing coefficient of \(C_\mu = (m_{inj} v_{inj})/(0.5 \rho _\infty u_\infty ^2 S_{ref})\approx 0.008\). The purpose of the jets is to reduce the coherence in the wake to reduce the buffet loads. The flow control device is motivated by the investigations by Weiss and Deck  [15].

Fig. 2
figure 2

Geometry parameters of the generic axisymmetric configurations (a). Setup for the flow control configuration (b)

Full size image

2.2 Zonal RANS/LES Flow Solver

The time-resolved computations are performed using a zonal RANS/LES solver which is based on a finite-volume method. The computational domain is split into several zones, see Fig. 3. In the zones where the flow is attached, i.e., the flow around the forebody and inside the base nozzle, the RANS equations are solved. The wake flow characterized by the separated shear layer is determined by an LES.

The Navier–Stokes equations of a three-dimensional unsteady compressible fluid are discretized second-order accurate using a mixed centered/upwind advective upstream splitting method (AUSM) scheme for the Euler terms. The non-Euler terms are approximated by a second-order accurate centered scheme. For the temporal integration an explicit 5-stage Runge–Kutta method of second-order accuracy is used. The monotone integrated LES (MILES) method determines the impact of the sub-grid scales. The solution of the RANS equations is based on the same discretization method. To close the time-averaged equations the one-equation turbulence model of Fares and Schröder  [4] is used. The transition from the RANS to the LES domain is determined by the reformulated synthetic turbulence generation (RSTG) method developed by Roidl et al.  [8]. For a comprehensive description of the flow solver see Statnikov et al.  [12, 14].

Fig. 3
figure 3

Zonal grid topology; supersonic (a) and transonic (b) configuration

Full size image

2.3 Computational Mesh

In the zonal approach, the computational domain is divided into a RANS part enclosing the attached flow around the forebody and inside the base nozzle and an LES grid for the wake shown in Fig. 3. To ensure a fully developed boundary layer upstream of the backward facing step and nozzle contour inflection, the overlapping RANS/LES region extends more than three boundary-layer thicknesses in the streamwise direction as required by the RSTG approach. The characteristic grid resolution for the supersonic (transonic) configuration in the area within the transition zone in inner wall units \(l^+=u_\tau /\nu \) is \(\Delta x^+=30\, (50)\), \(\Delta r^+=1.4 \,(2)\), and \(R \Delta \varphi ^+=30\, (30)\) for the LES zone and \(\Delta x^+= 100\, (350)\), \(\Delta r^+= 1.4\, (1)\), and \(R \Delta \varphi ^+= 60\,(160)\) for the RANS domain. The resolution is chosen according to typical mesh requirements in wall-bounded flows outlined by Choi and Moin  [1]. In total, \(220\cdot 10^6\) (\(590\cdot 10^6\)) grid points are used for the supersonic (transonic) configuration.

3 Results

First, the results of the supersonic dual-bell nozzle configuration operated in sea-level and altitude mode are presented and compared to the configuration with the classical TIC nozzle. Second, the transonic configuration without flow control is shown and the origin of the buffet loads is discussed. In the end, the flow control configuration is compared to the clean configuration and the influence of the jet injection on the buffet loads is outlined.

3.1 Supersonic Configuration

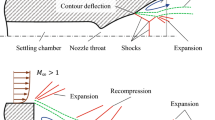
To visualize the wake topology of the supersonic configuration, the instantaneous and time averaged absolute density gradient of the zonal RANS/LES computations are given for the altitude mode (NPR \(=\) 97) in Fig. 4a and at sea-level operating conditions (NPR \(=\) 4.5) in Fig. 4b. At the mainbody’s tail, the turbulent supersonic boundary layer separates forming a supersonic shear layer. As a result of the separation, the shear layer undergoes an expansion associated with a radial deflection towards the nozzle wall, leading to the formation of a low-pressure region and a subsonic recirculation zone. Further downstream the shear layer impinges on the nozzle fairing and is redirected in streamwise direction causing a recompression shock.

Fig. 4
figure 4

Supersonic axisymmetrical configuration: Instantaneous (top) and time averaged (bottom) absolute density gradients at altitude mode (a) and sea-level mode (b)

Full size image

While the outer flow field is quite similar for the two operation conditions, the differences become obvious inside the nozzle. At altitude mode, the flow expands at the nozzle contour inflection resulting in a fully flown nozzle extension. At the nozzle lip a classic plume barrel shock and the shear layer between the outer flow and the jet is visible. Due to the constant pressure design of the nozzle extension, a further shock occurs inside the nozzle directly downstream of the expansion.

At sea-level mode, the flow separates at the inflection point resulting in a backflow region in the nozzle extension and a turbulent shear layer. At the end of the nozzle, the outer flow expands around the lip leading to a radial deflection towards the jet plume. In addition, the jet shock cells are visible in the density gradient contour.

The static pressure distribution along the nozzle wall is given for the two operating conditions in Fig. 5. Additionally, the design pressure distribution and experimental data at altitude conditions are shown. At altitude mode, the pressure rapidly drops at the contour inflection due to the expansion and is nearly constant in the second part of the nozzle as intended by the constant pressure extension design. The numerical data compares well with the experimental and design pressure distribution. At sea-level mode, the shock at the inflection point leads to a pressure increase. In the recirculation region the pressure remains at a constant value.

Fig. 5
figure 5

Streamwise pressure distribution along the inner nozzle wall for the supersonic case

Full size image
Fig. 6
figure 6

Streamwise distribution of the pressure and rms value of the pressure fluctuations along the outer nozzle surface

Full size image
Fig. 7
figure 7

Supersonic axisymmetrical configuration with TIC nozzle: Instantaneous (top) and time averaged (bottom) absolute density gradients

Full size image

To evaluate the loads onto the outer nozzle fairing, the streamwise distribution of the pressure and rms values of the pressure fluctuations are shown for the two operating modes in Fig. 6. To quantify the differences of the present cases to a conventional nozzle, the results of the supersonic axisymmetric configuration with a regular TIC nozzle are also depicted in the figure. Note that due to the different geometric requirements of the dual-bell nozzle, the diameter of the TIC nozzle is only 0.4D and the length of the nozzle only 1.2D. The flow field of this reference configuration is shown by means of the instantaneous and time averaged density gradient in Fig. 7. Except for a short range directly upstream of the nozzle lip, the distribution for the dual-bell nozzle cases do not differ. Due to the expansion at the base shoulder, a low pressure plateau exists at the base followed by a steady pressure increase caused by the gradual realignment of the supersonic shear layer along the nozzle wall. The wall pressure fluctuations feature a maximum at the impingement position of the shear layer and slowly decrease further downstream. Compared to the dual-bell nozzle configuration the TIC nozzle is underexpanded leading to an afterexpansion and consequently to a displacement in radial direction of the outer flow. As a result, the expansion at the base shoulder is weaker leading to a base pressure which is almost twice as high as in the dual-bell nozzle configurations. Due to the smaller nozzle diameter of the TIC nozzle, the shear layer realigns further downstream resulting in a delayed increase of the wall pressure and pressure fluctuations. However, the maximum values are nearly identical for the shown configurations. Caused by the expansion of the flow around the nozzle lip at sea-level conditions, the pressure drops at the end of the nozzle to almost half of the ambient pressure. As a result, the transition nozzle pressure ratio reduces to approximately \(NPR_{tr}=5\) compared to the design value of \(NPR_{tr,desg}=12.6\) neglecting the outer flow.

3.2 Transonic Configuration

Subsequently, the results of the transonic configurations are presented. First, the general characteristics of the wake flow topology of the clean configuration without flow control is shown and the dynamic behavior of the wake flow is investigated by classical statistical analysis, i.e., power spectral density and by DMD. Then, the influence of the flow control onto the wake flow dynamics and buffet loads is discussed.

Fig. 8
figure 8

Flow topology: Time-averaged streamwise velocity contours and projected streamlines (left); instantaneous distribution of the circumferential component of the vorticity (right) at the azimuthal cut \(\varphi =0^\circ \)

Full size image

3.2.1 Wake Flow Topology

Figure 8 shows the time-averaged streamwise velocity contours and streamlines and the instantaneous distribution of the spanwise vorticity component at an azimuthal cut \(\varphi =0^\circ \). At the abrupt junction between the main body and the nozzle, the incoming turbulent boundary layer separates. The shed shear layer continuously broadens due to shear layer instabilities causing the initially small turbulent structures to grow in size and intensity similar to structures observed in the planar free-shear layers by Winant and Browand  [16]. Further downstream, the structures either impinge on the surface approximately between \(0.7< x/D < 0.85\) or pass downstream without interacting with the nozzle surface. Downstream of the base, a large low pressure recirculation vortex occurs. In the dual-bell nozzle, the turbulent boundary layer separates at the contour inflection and shock cells are formed. In the nozzle extension, a backflow region forms entraining the eddies of the outer flow into the nozzle where they interact with the jet plume. Due to this interaction and the strong shear of the mean flow field between the backflow area and the jet, intensive turbulent structures are generated inside the nozzle extension. Due to the manifold of turbulent structures, a straightforward interpretation of the instantaneous flow field is quite complicated. Therefore, statistical analysis and DMD are used in the following section to identify the underlying coherent motion of the wake leading to the buffet loads.

Fig. 9
figure 9

Premultiplied normalized power spectral density of the wall pressure fluctuations \(p'/p_\infty \) at \(x/D=0.15\), \(x/D=0.4\), and \(x/D=0.8\) (a). Normalized DMD spectrum of the three-dimensional velocity and pressure field (b); eigenvalues \(\mu _n=e^{\left( \lambda _n \Delta t \right) } \) (left), normalized amplitude distribution versus frequencies \(\mathfrak {I}\left( \lambda _n\right) \) (right)

Full size image

3.2.2 Analysis of the Wake Dynamics

To evaluate the temporal periodicity of the wake dynamics and the resulting dynamic loads, the power spectral density (PSD) of the wall pressure fluctuations is discussed in the following. The premultiplied normalized PSD spectra at three streamwise positions are given in Fig. 9a. At \(x/D=0.15\) the spectrum reveals two enhanced frequencies at \(Sr_D \approx 0.04\) and \(Sr_D \approx 0.2\), where \(Sr_D\) is the Strouhal number based on the launcher’s diameter D and the freestream velocity \(u_\infty \). At the position further downstream, i.e., \(x/D=0.4\), the spectrum is dominated by a single peak at the buffet frequency, i.e., at \(Sr_D \approx 0.2\) as known from the literature for similar space launcher configurations, e.g., Deck and Thorigny  [2], Schrijer et al.  [10], and Statnikov et al.  [13]. At \(x/D=0.8\), just upstream of the end of the nozzle, the peak at \(Sr_D \approx 0.2\) is also apparent. In addition, a broadband range at higher frequencies with a maximum at \(Sr_D \approx 0.9\) resulting from the vortical structures within the separated shear layer impinging on the nozzle surface is visible. To sum up, the pressure spectrum at all three positions clearly shows a peak at the buffet frequency which is most pronounced around the center of the nozzle as known from the literature  [2].

To understand the origin of the buffet loads and to further investigate the impact of the dual-bell nozzle onto the wake flow, a dynamic mode decomposition of the wake flow is performed to extract dominant spatio-temporal modes from the time resolved three-dimensional flow field and to reduce the complex flow physics to a few degrees of freedom. The resulting DMD spectrum is shown in Fig. 9b. The selection of the important modes is based on the sparsity-promoting approach by Jovanovic et al.  [6]. The two most stable modes of interest, i.e., \(Sr_{D,1}\left( \lambda _1\right) \approx 0.04\), \(Sr_{D,2}\left( \lambda _2\right) \approx 0.2\) are identified and marked by red filled circles. The dimensionless frequencies of these modes coincide with the characteristic frequencies of the PSD spectra of the pressure fluctuations shown in Fig. 9a.

To visualize the three-dimensional shape and temporal evolution of the identified DMD modes, the spatial modes \(\phi _n\) are superimposed with the mean mode \(\phi _{0}\) and reconstructed in time. As it is known that the buffet frequency is at \(Sr_D=0.2\) only the second mode is being further investigated. The reconstructed velocity field is given for the second mode at the time instance \(t_0\) and after one half of the respective period time at \(t_0+0.5T(\lambda _n)\) in Fig. 10a. The flow is visualized by an iso-contour at a streamwise velocity of \(u/u_\infty =0.15\) and contours of streamwise velocity at the azimuthal cut \(\varphi =0^\circ \) and \(\varphi =180^\circ \).

The DMD mode describes a pronounced antisymmetric wave-like undulating motion of the shear layer. An analogous so-called cross-flapping motion was observed in the previous investigation by Statnikov et al.  [13] and associated with an antisymmetric vortex shedding. To investigate if the wave-like motion of the second mode is caused by a similar vortex shedding, the reconstructed three-dimensional fluctuating pressure field is illustrated by pressure contours in Fig. 10b at the time instance \(t_0\) and after one quarter of the time period, i.e., at \(t_0+0.25T \left( \lambda _2 \right) \). The temporal evolution of the mode exhibits the buffet phenomenon. That is, the pronounced periodic side loads are caused by large scale coherent regions with antisymmetric positive and negative pressure values propagating downstream from the base shoulder towards the nozzle lip. Since shear flows are characterized by pressure minima in the vortex center and pressure maxima at the stagnation point between two adjacent vortices, the pressure field proves that the cross-flapping motion is caused by an antisymmetric vortex shedding.

In summary, the modal decomposition of the wake flow indicates that the dynamic behavior of the wake is dominated by a cross-flapping motion of the shear layer. The detected mode is similar to the mode of the reference configuration with the conventional conical nozzle  [13] showing that in the current parameter range and operation mode the dynamics of the recirculation bubble downstream of the base shoulder is not affected by the dual-bell nozzle.

Fig. 10
figure 10

Reconstruction of the three-dimensional velocity field (a) and pressure fluctuation field (b) of the DMD mode at \(Sr_D \approx 0.2\)

Full size image

3.2.3 Flow Control

In this section, the results of the configuration with flow control are presented and the impact onto the recirculation region and the buffet loads is discussed. The objective of the flow control is to decrease the shear in the separated mixing layer and to reduce the coherence in the wake and thus the buffet loads by four in circumferential direction equally distributed jets injecting air encountering the backflow in the recirculation region.

To visualize the impact onto the mean flow field the time-averaged streamwise velocity contours at the azimuthal cut \(\varphi =0\), i.e., a plane at the center of a jet, and at \(\varphi =45^\circ \), i.e., a plane between two adjacent jets are shown in Fig. 11. At \(\varphi =0^\circ \) the flow topology is significantly altered compared to the clean configuration without flow control. The formation of a main recirculation region is suppressed and only a small recirculation region at \(x/D=0.8\) caused by the injected jet is visible. As a result, the shear in the separated mixing layer that is driving the formation of large scale structures is reduced at the first half of the separation region. At the azimuthal cut \(\varphi =45^\circ \) the recirculation region is only marginally effected. The main vortex features a focus indicating a flow deviation in the circumferential direction.

Fig. 11
figure 11

Flow topology: Time-averaged streamwise velocity contours and projected streamlines at the azimuthal cut at \(\varphi =0^\circ \) (a) and \(\varphi =45^\circ \) (b)

Full size image
Fig. 12
figure 12

Premultiplied normalized power spectral density of the wall pressure fluctuations \(p'/p_\infty \) along the outer nozzle fairing (a), and at \(x/D=0.4\) (b)

Full size image

To investigate the effect of the jets onto the pressure fluctuations and the resulting buffet loads, the premultiplied normalized power spectral density of the pressure fluctuations along the outer nozzle fairing and at \(x/D=0.4\) is depicted in Fig. 12 for the controlled and the clean case. In the clean case, the aforementioned dominant peak at a dimensionless frequency of \(Sr_D=0.2\) around the streamwise position \(x/D=0.3-0.5\) representing a footprint of the buffet phenomenon is clearly visible. In the spectral map of the controlled configuration, no dominant peak is visible, i.e., the pressure fluctuations at the buffet frequency of \(Sr_D=0.2\) are significantly reduced by the injection of the jets. The controlled configuration features slightly increased high frequency fluctuations which are, however, of minor importance for the structural stability of the nozzle.

The spatial coherence of the pressure fluctuations and the influence of the flow control onto the coherence of the wake are subsequently investigated by a two-point analysis. The complex coherence function of two pressure sensors \(p_1(x,\varphi _1,t)\) and \(p_2(x,\varphi _2,t)\) located on a circumferential circle on the outer nozzle fairing is given by

$$\begin{aligned} C\left( f,x,\Delta \varphi \right) = \dfrac{G_{12}\left( f,x,\Delta \varphi \right) }{\sqrt{G_1\left( f,x, \varphi _1 \right) \, G_2\left( f,x, \varphi _2 \right) } } = C_r + i C_i \end{aligned}$$
(1)

where \(G_{12}\) is the complex two-point cross power spectral density between \(p_1\) and \(p_2\), \(G_1\) and \(G_2\) the power spectral density of \(p_1\) and \(p_2\), and \(\Delta \varphi = \varphi _1 - \varphi _2\). If we assume a homogeneous flow field without any mean swirl, \(C_i\) is zero and \(C_r\) is symmetric in \(\Delta \varphi \), i.e., \(G_{12}(-\Delta \varphi ) = G_{12}(\Delta \varphi )\). In addition, due to the axisymmetric configuration the coherence function is periodic in the circumferential direction, i.e., \(C_r(\Delta \varphi +n 2\pi ) = C_r(\Delta \varphi )\). Due to these conditions, the real part of the coherence function can be expressed by a Fourier transform in the azimuthal direction

$$\begin{aligned} C_r(f, \Delta \varphi )=\sum _{m=0}^\infty C_{r,m}(f)\cos (m \Delta \varphi ) \quad . \end{aligned}$$
(2)

Since \(\sum _{m=0}^\infty C_{r,m}= 1\), the \(C_{r,m}\) coefficient describes the percentage of the fluctuation energy contained in each azimuthal constituent m at a specific frequency f. It is worth mentioning that \(C_{r,0}\) describes an in-phase and \(C_{r,1}\) an anti-phase relation between two pressure probes opposing in the circumferential direction. Hence, the side loads originating from the buffet phenomenon are mainly captured by the \(C_1\) coefficient.

Fig. 13
figure 13

a Spectra of the first two azimuthal pressure mode coefficients \(C_{r,0}, C_{r,1}\) at \(x/D=0.4\); b premultiplied power spectral density of the side load components

Full size image

The spectrum of the first two azimuthal coefficients \(C_{r,0}, C_{r,1}\) is given at \(x/D=0.4\), i.e., in the center of the recirculation region, for the clean and controlled case in Fig. 13a. In the clean case, the spectrum of the axisymmetric mode \(C_{r,0}\) shows a low frequency broadband content around \(Sr_D \approx 0.04\) and decreasing values with higher frequency. The antisymmetric mode \(C_{r,1}\) exhibits a distinct peak at the buffet frequency, i.e., \(Sr_D\approx 0.2\) with an amplitude of 0.65, showing that 65% of the total pressure fluctuations at the specific frequency \(Sr_D\approx 0.2\) are caused by this antisymmetric mode. The results reveal that the buffet phenomenon and the resulting loads are caused by an antisymmetric flow event as already indicated by the DMD results. In the controlled case, the peaks are considerably reduced compared to the clean case. The low frequency content of the axisymmetric mode \(C_{r,0}\) is halved and the peak at \(Sr_D\approx 0.2\) of the antisymmetric mode \(C_{r,1}\) is reduced by about \(25\%\), showing that the coherence of the wake flow can be effectively disturbed by the control device.

To analyze the influence of the flow control onto the side loads arising from the highly coherent antisymmetric pressure fluctuations, the instantaneous pressure fluctuations are integrated over the nozzle surface. The frequency-premultiplied PSD for the two cartesian components of the resulting loads is given in Fig. 13b. In the clean and in the controlled configuration one dominant peak at the buffet frequency, i.e., \(Sr_D\approx 0.2\), is clearly visible containing most of the energy of the fluctuating force. Notice that the frequency perfectly coincides with the peak detected in the pressure fluctuations and the results reported in the literature  [13]. While in both configurations a peak exists at the characteristic dimensionless frequency, the amplitude in the controlled case is strongly decreased confirming that the coherence of the pressure fluctuations, i.e., the antisymmetric mode, is reduced by the jets which leads to reduced buffet loads.

4 Conclusions

The turbulent wake of an axisymmetric space launcher equipped with a dual-bell nozzle is investigated at transonic and supersonic freestream conditions using zonal RANS/LES, classical statistical analysis, and dynamic mode decomposition. In addition, the effect of flow control onto the wake dynamics and the buffet loads is determined. In the supersonic configuration, the dual-bell nozzle is operated at sea-level and altitude mode, and the dynamic loads on the nozzle surface are compared to a configuration with a conventional TIC nozzle. It is shown that the supersonic outer flow affects the pressure at the nozzle lip and thereby the transition nozzle pressure ratio compared to the design conditions neglecting the outer flow. In the transonic simulations, the dual-bell nozzle is analyzed at sea-level mode and the dynamic behavior of the wake is investigated. The modal analysis of the wake flow based on DMD reveals that the dynamic buffet loads at \(Sr_D \approx 0.2\) are caused by an oscillating wavy motion of the shear layer that is triggered by an antisymmetric vortex shedding. The presented configuration at transonic freestream conditions exhibits a similar flow topology and wake dynamics compared to the reference configuration with a classical conical nozzle. Therefore, it is stated that for the transonic flow condition the wake downstream of the base shoulder is not affected by the dual-bell nozzle concept. Using azimuthally distributed jets to control the wake flow the pressure fluctuations at the buffet frequency and the spatial coherence of the wake, i.e., the antisymmetric mode \(C_{r,1}\), are significantly decreased, leading to a reduction of the buffet loads.