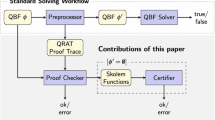
Abstract
In applications, QBF solvers are expected to not only decide whether a given formula is true or false but also return a solution in the form of a strategy. Determining whether strategies can be efficiently extracted from proof traces generated by QBF solvers is a fundamental research task. Most resolution-based proof systems are known to implicitly support polynomial-time strategy extraction through a simulation of the evaluation game associated with an input formula, but this approach introduces large constant factors and results in unwieldy circuit representations. In this work, we present an explicit polynomial-time strategy extraction algorithm for the \(\forall \hbox {-}\mathsf{Exp}\hbox {+}\mathsf{Res}\) proof system. This system is used by expansion-based solvers that implement counterexample-guided abstraction refinement (CEGAR), currently one of the most effective QBF solving paradigms. Our argument relies on a Curry-Howard style correspondence between strategies and \(\forall \hbox {-}\mathsf{Exp}\hbox {+}\mathsf{Res}\) derivations, where each strategy realizes an invariant obtained from an annotated clause derived in the proof system.
M. Schlaipfer—Supported by the Vienna Science and Technology Fund (WWTF) through the Heisenbugs project VRG11-005 and the Austrian Science Fund (FWF) through the LogiCS doctoral program W1255-N23.
F. Slivovsky—Supported by the Vienna Science and Technology Fund (WWTF) under grant number ICT19-060.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Continued improvements in the performance of satisfiability (SAT) solvers [14] are enabling a growing number of applications in areas such as electronic design automation [35]. At the same time, many of the underlying problems are hard for complexity classes beyond NP and as such cannot be expected to have succinct propositional encodings. Super-polynomial growth in encoding size imposes a limit on the problem instances that can be feasibly solved even with extremely efficient SAT solvers. Decision procedures for more succinct languages such as Quantified Boolean Formulas (QBFs) represent a potential solution to this scaling issue. QBFs extend propositional formulas with quantification over truth values and support more succinct encodings for a range of problems [32]. Recent years have seen significant advancements in QBF solver technology [20, 21, 25, 26, 29, 30, 34, 36], up to a point where reduction to QBF can be more efficient than reduction to SAT [13].
In some applications, QBF solvers are required to not only decide whether a given formula is true or false but also compute a solution in the form of a strategy. For example, if a synthesis problem is encoded as a QBF, a solver is expected to either return the synthesized program or an explanation why the specification cannot be satisfied [13]. Determining whether the proof trace of a QBF solver can be efficiently transformed into a strategy—whether the proof system supports polynomial-time strategy extraction—is a fundamental research task [2, 3, 6, 10, 27].
One of the most successful QBF solving paradigms relies on partial Shannon expansion [1, 8] of universal variables within a counterexample-guided abstraction refinement (CEGAR) loop, as implemented in RAReQS [21], and, more recently, in Ijtihad [9] and QFun [20]. The underlying proof system \(\forall \hbox {-}\mathsf{Exp}\hbox {+}\mathsf{Res}\) [22] offers exponentially shorter proofs for certain classes of formulas than Q-resolution [6], and can polynomially simulate Q-resolution on formulas with few quantifier alternations [4], which includes many practically relevant cases.Footnote 1 Polynomial-time strategy extraction follows from the fact that \(\forall \hbox {-}\mathsf{Exp}\hbox {+}\mathsf{Res}\) proofs can be used to guide the universal player in an evaluation game [6, 11], but turning this argument into circuits that compute a winning strategy is rather inefficient. An explicit construction based on this idea for Q-resolution requires the introduction of several gates for each literal in the proof and quantifier level of the input formula [27], leading to unwieldy circuits that are substantially larger than the original proof. In this work, we present a strategy extraction algorithm for \(\forall \hbox {-}\mathsf{Exp}\hbox {+}\mathsf{Res}\) that is multi-linear in the number of proof steps and universal variables. This is asymptotically optimal for a construction that follows the structure of the proof and maintains a circuit for each universal variable.
Our algorithm is inspired by [33], which for the first time has given a local soundness argument for \(\forall \hbox {-}\mathsf{Exp}\hbox {+}\mathsf{Res}\). [33] constructs partial strategies along the \(\forall \hbox {-}\mathsf{Exp}\hbox {+}\mathsf{Res}\)-proof and provides a semantic abstraction that relates the constructed strategies to the clauses in the proof. In contrast, we associate a full strategy to each node in the \(\forall \hbox {-}\mathsf{Exp}\hbox {+}\mathsf{Res}\)-proof and develop a syntactic argument that ensures the soundness of the construction. For each clause in the proof, we define a propositional invariant that corresponds to a syntactic weakening of the input formula’s negated matrix. We then show that strategies satisfying the invariants for the premises of a resolution step can be combined into a strategy that satisfies the invariant for the resolvent. The main technical challenge we had to overcome in deriving this syntactic weakening is that \(\forall \hbox {-}\mathsf{Exp}\hbox {+}\mathsf{Res}\) proofs work over an extended propositional alphabet where multiple versions of the same variable with different annotations may exist simultaneously. Our invariant translates the propositions from the extended alphabet back to formulas over the original vocabulary.
We believe that our syntactic soundness argument is more transparent than the semantic construction from [33]. The clarity of the argument is also what allows us to obtain a concise circuit representation of the resulting strategy. Further, our syntactic argument establishes a Curry-Howard correspondence between proof construction and strategy extraction. For each inference rule combining proof terms, the correspondence provides a rule combining program terms. The result is a program isomorphic to the proof. The widest-known correspondence is between natural deduction proofs and lamba-calculus programs [18]. In this paper we establish a precise correspondence between \(\forall \hbox {-}\mathsf{Exp}\hbox {+}\mathsf{Res}\)-proofs and strategies—the strategy constructed for a node in the proof DAG satisfies the invariant for the clause derived at that node. In contrast, the correspondence stays implicit in the semantic argument from [33]. We expect that our ideas of obtaining such an invariant by weakening the matrix and translating the clauses over the extended alphabet back to a formula over the original variables will have applications in studying further Curry-Howard correspondences for other resolution-based QBF proof systems.
2 Preliminaries
Quantified Boolean Formulas (QBFs). We consider quantified Boolean formulas (QBFs) with standard propositional connectives \(\wedge , \vee , \lnot , \Leftrightarrow , \oplus \), and quantifiers \(\forall , \exists \). We denote existentially quantified variables by x and y, and universally quantified variables by u. Variables range over \(\mathbb {B} = \{\mathtt {0}, \mathtt {1} \}\). A literal l is a variable x or its negation \(\lnot x\). We write \(\varvec{x}\) for a set of variables or literals. A clause is a disjunction of literals, and a propositional formula in conjunctive normal form is a conjunction of clauses. We write \(\square \) for the empty clause. Throughout the paper, QBFs are assumed to be in prenex conjunctive normal form (PCNF). A PCNF formula \(\varPhi = \varPi .\varphi \) consists of a sequence \(\varPi = Q_1 v_1 \ldots Q_nv_n\) with \(Q_i \in \{\forall , \exists \}\) for \(1 \le i \le n\), called the quantifier prefix of \(\varPhi \), and a propositional formula \(\varphi \) in conjunctive normal form, called the matrix of \(\varPhi \). We define a relation \(\prec _{\varPi }\) on variables from the quantifier prefix as \(v_i \prec _{\varPi } v_j\) whenever \(i < j\). We extend \(\prec _{\varPi }\) to a relation on literals in the obvious way and drop the quantifier prefix \(\varPi \) from the subscript when it is clear from the context. QBF Expansion Proofs. We consider a proof system for false PCNF formulas known as \(\forall \hbox {-}\mathsf{Exp}\hbox {+}\mathsf{Res}\) [22]. This system combines instantiation of universal variables with propositional resolution. Instantiation leads to existential literals \(l^{\tau }\) that are annotated with an assignment \(\tau : \varvec{u}_l \rightarrow \mathbb {B} \) of the universal variables \(\varvec{u}_l = \{ u \,| \, u \prec l\}\) that precede the variable of l in the quantifier prefix. Following Beyersdorff et al. [6], we write \(l^{[\tau ]} = l^{\{u \mapsto \tau (u) \,|\, u \prec l\}}\) to filter out assignments that are not permitted in the annotation of l. We sometimes treat an assignment \(\tau : \varvec{u} \rightarrow \mathbb {B} \) in an annotation as a set of literals and write \(l \in \tau \) if \(\tau (l) = \mathtt {1} \). We write \(C^{\tau }\) for a clause C with all its literals annotated with \([\tau ]\). The proof rules of \(\forall \hbox {-}\mathsf{Exp}\hbox {+}\mathsf{Res}\) are shown in Fig. 1. A \(\forall \hbox {-}\mathsf{Exp}\hbox {+}\mathsf{Res}\) proof of a PCNF formula \(\varPhi \) is a sequence of clauses ending with the empty clause such that each clause is derived either by universal expansion (\(\forall \)-exp) or by resolution (res) from clauses appearing earlier in the sequence.
3 Strategies
A PCNF formula can be interpreted as the specification of a game between an existential and a universal player [31]. The game proceeds by the players assigning values to their respective variables in turn, following the order of the quantifier prefix. The goal of the universal player is to falsify the matrix, the goal of the existential player is to satisfy the matrix. Strategies for either player can be conveniently represented as binary trees.
Definition 1
(Strategy). Let \(\varPhi = \varPi .\varphi \) be a PCNF formula. A (universal) strategy for \(\varPhi \) is a labeled, rooted binary tree with the following properties:
-
1.
Leaf nodes are labeled with \(\bot \), inner nodes are labeled with variables of \(\varPhi \), and edges are labeled with \(\mathtt {0} \) or \(\mathtt {1} \).
-
2.
Nodes labeled with existential variables have exactly two child nodes, and nodes labeled with universal variables have a single child node. Moreover, edges leading to distinct child nodes have distinct labels.
-
3.
The sequence of variables encountered as labels on any path from the root to a leaf follows the order \(\prec _{\varPi }\) of variables in the quantifier prefix.
A strategy P for \(\varPhi \) is complete if each path from the root of P to a leaf contains all variables of \(\varPhi \). Each path from the root to a leaf of a strategy induces a truth assignment in the obvious way. A strategy P is a (universal) winning strategy for \(\varPhi \) if every such assignment falsifies the matrix \(\varphi \).
We write \(P = \mathsf {Str}(v, P^{-}, P^{+})\) for a strategy P with root labeled by variable v and principal subtrees \(P^{-}\) and \(P^{+}\) such that the edge to the root of \(P^{-}\) is labeled with \(\mathtt {0} \) and the edge to the root of \(P^{+}\) is labeled with \(\mathtt {1} \). We use \(\emptyset \) to denote the “empty” strategy and write \(P = \mathsf {Str}(v, \emptyset , P^{+})\) and \(P = \mathsf {Str}(v, P^{-}, \emptyset )\) to denote strategies with root nodes that only have a \(\mathtt {1} \)-child and a \(\mathtt {0} \)-child, respectively.
In the next section, we will associate each clause C in a \(\forall \hbox {-}\mathsf{Exp}\hbox {+}\mathsf{Res}\) proof with a strategy P. For clauses C derived by the \(\forall \)-exp rule with assignment \(\tau \), the corresponding strategy simply sets the universal variables according to \(\tau \).
Definition 2
Let \(\varPhi = \varPi .\varphi \) be a PCNF formula and \(\tau \) an assignment of the universal variables of \(\varPhi \). We define \(\mathsf {ConstStrat}(\varPi , \tau )\) as the complete strategy for \(\varPhi \) where each assignment is consistent with \(\tau \).
Example 1
The figure to the right shows the strategy computed by \(\mathsf {ConstStrat}(\exists x_1 \forall u \exists x_2, \lnot u)\). The tree encodes the assignments \(\{\mathtt {0}/x_1, \mathtt {0}/u, \mathtt {0}/x_2\}\), \(\{\mathtt {0}/x_1, \mathtt {0}/u, \mathtt {1}/x_2\}\), \(\{\mathtt {1}/x_1, \mathtt {0}/u, \mathtt {0}/x_2\}\), \(\{\mathtt {1}/x_1, \mathtt {0}/u, \mathtt {1}/x_2\}\) falsifying u.

4 Local Soundness
We present a local soundness argument for \(\forall \hbox {-}\mathsf{Exp}\hbox {+}\mathsf{Res}\) using strategies. To this end, we will define a \(\mathsf {Combine}\) operator that joins strategies along a derivation [33]. For each derived clause C, we will show that the strategy created for this clause by the \(\mathsf {Combine}\) operator satisfies a propositional invariant obtained from C. Here, by a strategy Psatisfying a formula \(\psi \) we mean that every assignment consistent with P satisfies \(\psi \), which we will write as \(P \models \psi \).Footnote 2 In this notation, we will show that
where \(\varphi \) denotes the matrix and \(\mathsf {enc}(C)\) translates the clause C back into a formula over the original variables of the QBF as
The invariant \(\mathsf {enc}(C) \Rightarrow \lnot \varphi \) can be understood by considering the evaluation game: if the existential player responds to every universal play in an annotation by setting the literal to false, the current strategy is winning for the universal player. Ultimately, at the empty clause, \(\mathsf {enc}(\square ) = \mathtt {1} \) and the combined strategy turns into a winning strategy.
4.1 \(\mathsf {Combine}\)
We will now introduce the \(\mathsf {Combine}\) operator that merges two strategies P and Q in a top-down manner and annotates each clause in a \(\forall \hbox {-}\mathsf{Exp}\hbox {+}\mathsf{Res}\) derivation with a strategy. We write \(C~[ P ]\) for a clause C annotated with strategy P. The definition of \(\mathsf {Combine}\) as shown in Definition 4 is adapted from the definition of an operator defined by Suda and Gleiss [33]. Since we work with complete strategy trees (rather than partial strategies), the top-most variable remains equivalent between two strategies when recursing on them in lock-step, so it is sufficient to perform a case distinction on the top-most variable encountered in a strategy. Moreover, our definition of \(\mathsf {Combine}\) is tailored to \(\forall \hbox {-}\mathsf{Exp}\hbox {+}\mathsf{Res}\).
Clauses derived by \((\forall \text {-exp})\) are annotated with the strategy \(\mathsf {ConstStrat}(\varPi ,\tau )\) that plays the assignment \(\tau \). For the \((\text {res})\) rule we have the following cases:
-
The top-most variable, say u, is universal:
-
If the outgoing edge of u (\(\mathsf {lit} (u)\), see Definition 3 below) differs from the annotation \(\tau (u)\) of the pivot in at least one of P and Q, we select the strategy that differs.
-
If \(\mathsf {lit} (u)\) equals the annotation \(\tau (u)\) of the pivot in both P and Q, we recurse.
-
The top-most variable, say x, is existential:
-
If x is the pivot of the inference rule, we combine the two strategies.
-
If x is not the pivot, we recurse.
The base cases are when a universal edge differs, or we reach the pivot.
Definition 3
 We define \(\mathsf {lit} \) as the partial function mapping universal strategy nodes to the literal they represent, based on their (unique) child node.
We define \(\mathsf {lit} \) as the partial function mapping universal strategy nodes to the literal they represent, based on their (unique) child node.

Definition 4
 We define \(\mathsf {Combine}\) as a function from two strategies, P and Q, and an annotated variable \(x^{\tau }\) to a new strategy inductively on a \(\forall \hbox {-}\mathsf{Exp}\hbox {+}\mathsf{Res}\) derivation in Fig. 2. We write \(\mathsf {Combine}\) in infix notation as
We define \(\mathsf {Combine}\) as a function from two strategies, P and Q, and an annotated variable \(x^{\tau }\) to a new strategy inductively on a \(\forall \hbox {-}\mathsf{Exp}\hbox {+}\mathsf{Res}\) derivation in Fig. 2. We write \(\mathsf {Combine}\) in infix notation as  .
.
Note that in the case where both \(\mathsf {lit} (P) \ne l\) and \(\mathsf {lit} (Q) \ne l\) there is freedom of which strategy out of P and Q to select. We will use the variant selecting P.
Example 2
We introduce our running example and use it to demonstrate the combination of two strategies via \(\mathsf {Combine}\) in Fig. 3.
Theorem 1
Let C be a clause derived by \(\forall \hbox {-}\mathsf{Exp}\hbox {+}\mathsf{Res}\) and P be the corresponding strategy annotation computed by \(\mathsf {Combine}\). Then \(P \models \mathsf {enc}(C) \Rightarrow \lnot \varphi \).
Proof
By induction on the \(\forall \hbox {-}\mathsf{Exp}\hbox {+}\mathsf{Res}\) derivation. Base case. The base case corresponds to the \(\forall \text {-exp}\) rule.

We need to show that \( P \models \mathsf {enc}(C^{\tau }) \Rightarrow \lnot \varphi . \) From the definition of \(\mathsf {ConstStrat}\) we know that P satisfies all universal literals in \(\mathsf {enc}(C^{\tau })\) following the assignments determined by \(\tau \). P similarly satisfies the literals in the corresponding negated clause \(\lnot C\) in \(\lnot \varphi \), making both remaining formulas over the existential variables equivalent. The negated matrix \(\lnot \varphi \) is weaker than just \(\lnot C\), thus the implication holds.
Induction Step. For a resolution rule with strategy annotations P, Q and the combination of P and Q, i.e. 

we need to show that

Let \(\pi \) be an arbitrary complete assignment determined by strategy  . We need to show that \(\pi \models \mathsf {enc}(C_1 \vee C_2) \Rightarrow \lnot \varphi \) given the induction hypothesis. By case distinction:
. We need to show that \(\pi \models \mathsf {enc}(C_1 \vee C_2) \Rightarrow \lnot \varphi \) given the induction hypothesis. By case distinction:
-
1.
If \(\pi \not \models \mathsf {enc}(C_1 \vee C_2)\) the implication is true and we are done.
-
2.
If \(\pi \models \mathsf {enc}(C_1 \vee C_2)\) we have two cases:
-
(a)
\(\pi \not \models \bigwedge _{u \in \tau } u\) (\(\pi \) differs from the assignment determined by \(\tau \)): Let us assume, w.l.o.g., that \(\pi \) is from P, then we have the following induction hypothesis:
$$ \pi \models \mathsf {enc}(C_1) \wedge \Big (\bigwedge _{u \in \tau } u \Rightarrow x\Big ) \Rightarrow \lnot \varphi . $$Since we are in case \(\pi \models \mathsf {enc}(C_1 \vee C_2)\), by the definition of \(\mathsf {enc}\) we know that \(\pi \models \mathsf {enc}(C_1)\). Furthermore we know that \(\pi \not \models \bigwedge _{u \in \tau } u\) satisfying the left-hand side of the outer implication, thus \(\pi \) must satisfy \(\lnot \varphi \) for the IH to be valid. Since, in this case the \(\mathsf {Combine}\) operator evaluates to P and \(\pi \) is from P, \(P \models \mathsf {enc}(C_1 \vee C_2) \Rightarrow \lnot \varphi \) is valid.
-
(b)
\(\pi \models \bigwedge _{u \in \tau } u\) (\(\pi \) equals the assignment determined by \(\tau \)): Again, since we are in case \(\pi \models \mathsf {enc}(C_1 \vee C_2)\), by the definition of \(\mathsf {enc}\) we know that \(\pi \models \mathsf {enc}(C_1)\) and \(\pi \models \mathsf {enc}(C_2)\). We also know that \(\pi \models \bigwedge _{u \in \tau } u\), so when \(\pi \in P\) the IH simplifies to \(\pi \models x \Rightarrow \lnot \varphi \). Similarly the IH simplifies to \(\pi \models \lnot x \Rightarrow \lnot \varphi \) for \(\pi \in Q\). Assume \(x = \mathtt {1} \), then \(P \models \lnot \varphi \). When we assume \(x = \mathtt {0} \), then \(Q \models \lnot \varphi \). In either case, because we assume the IH to be true, we know \(\lnot \varphi \) needs to be true. \(\mathsf {Combine}\) chooses the respective paths in P and Q and combines them so that \(\mathsf {Str}(x, Q^-, P^+) \models \mathsf {enc}(C_1 \vee C_2) \Rightarrow \lnot \varphi \) is valid. \(\square \)
-
(a)
Remark on the Curry-Howard correspondence established by Theorem 1 :
-
We relate the clauses of a \(\forall \hbox {-}\mathsf{Exp}\hbox {+}\mathsf{Res}\)-proof and the extracted strategies: \(P \models \mathsf {enc}(C) \Rightarrow \lnot \varphi \) signifies that the strategy P is a witness for the validity of the QBF formula \(\varPi .\mathsf {enc}(C) \Rightarrow \lnot \varphi \).
-
We relate the rules of a \(\forall \hbox {-}\mathsf{Exp}\hbox {+}\mathsf{Res}\)-proof to strategy construction operators: For an expansion-axiom with regard to an assignment \(\tau \), the strategy is given by \(\mathsf {ConstStrat}(\varPi , \tau )\). For a resolution step, the strategy is obtained by applying the \(\mathsf {Combine}\) operator on the strategies for the parent nodes.
5 Implementing Strategies Using Circuits
The strategies we have introduced in the previous section have size exponential in the number of existential variables in the quantifier prefix. Thus, it is impractical to consider strategy extraction using such a data structure. Instead, we will now demonstrate how we can implement the \(\mathsf {Combine}\) operator on circuits. We will show how we can construct the circuit for n output variables in such a way that the size of the circuit is in the order of \(\mathcal {O}(p \cdot n)\), where p is the proof length (number of clauses). This size is asymptotically optimal when constructing circuits locally along the proof derivation for n variables, considering that each inference can potentially manipulate each circuit.
5.1 Circuit Construction
We begin by introducing a number of auxiliary circuits. In the following let L, R, and B (short for “left”, “right”, and “bottom”, according to their respective positions in the inference rule) be tuples of circuits and let \(\varvec{y}\) be the input variables. We write \(f_{u_i}\) for the circuit with output \(u_i\) for \(f \in \{L, R, B\}\).
Definition 5
 We define the circuits \(\mathsf {Equiv}^{< i}_f\) for \(f \in \{L, R\}\). These circuits decide if all \(f_{u_i}\) evaluate to \(\tau (u_i)\) up to level i, given input \(\varvec{y}\):
We define the circuits \(\mathsf {Equiv}^{< i}_f\) for \(f \in \{L, R\}\). These circuits decide if all \(f_{u_i}\) evaluate to \(\tau (u_i)\) up to level i, given input \(\varvec{y}\):
Next we define the circuits \(\mathsf {Diff}^i_L\) and \(\mathsf {Diff}^i_R\) using \(\mathsf {Equiv}\). The purpose of the \(\mathsf {Diff}\) circuits is to choose one of L and R simulating the case of \(\mathsf {Combine}\) when one of the strategies differs from \(\tau \) at a universal edge. We need to consistently select the function values from either L or R starting from some index i for all subsequent outputs \(u_j\) with \(j \ge i\).
Definition 6
 We define the circuits \(\mathsf {Diff}^i_L\) and \(\mathsf {Diff}^i_R\) symmetrically to each other. We informally describe the circuit \(\mathsf {Diff}^i_L\): \(\mathsf {Diff}^i_L\) is true, given input \(\varvec{y}\), if there has been a difference between an \(L_{u_j}\) and \(\tau (u_j)\) for \(j \le i\) and when there has been no difference between \(R_{u_k}\) and \(\tau (u_k)\) for \(k < j\). Formally:
We define the circuits \(\mathsf {Diff}^i_L\) and \(\mathsf {Diff}^i_R\) symmetrically to each other. We informally describe the circuit \(\mathsf {Diff}^i_L\): \(\mathsf {Diff}^i_L\) is true, given input \(\varvec{y}\), if there has been a difference between an \(L_{u_j}\) and \(\tau (u_j)\) for \(j \le i\) and when there has been no difference between \(R_{u_k}\) and \(\tau (u_k)\) for \(k < j\). Formally:
Proposition 1
Let \(f \in \{L, R\}\) be either the left or right circuit and let \(g \in \{L, R\} - \{f\}\) be the opposite one. Once it has been established that \(\mathsf {Diff}_f^i\) is true, we know that \(\mathsf {Diff}_g^j\) cannot turn true for \(j > i\) if it has not been true already at i. Formally,
for \(j > i\) is a tautology.
Proof
Assume that \(f = L\) and \(g = R\), with the other case symmetric. It is clear that when \(\mathsf {Diff}_L^i(\varvec{y})\) is true, \(\mathsf {Equiv}_L^{< j}(\varvec{y})\) must be false for \(j > i\). When \(\mathsf {Equiv}_L^{< j}(\varvec{y})\) is false, we know that \(\mathsf {Diff}_R^j\) will remain false, if \(\mathsf {Diff}_R^{i}\) was false. \(\square \)
Note that both \(\mathsf {Diff}_L^i\) and \(\mathsf {Diff}_R^i\) can be true at the same index i. Namely, when there is no difference up to some level \(j < i\) (\(\mathsf {Equiv}_{L}^{<j}(\varvec{y}) = \mathsf {Equiv}_{R}^{<j}(\varvec{y}) = \mathtt {1} \)) but both \(L_{u_j}(\varvec{y}) \ne \tau (u_j)\) and \(R_{u_j}(\varvec{y}) \ne \tau (u_j)\). In this case we have the same freedom as in \(\mathsf {Combine}\) when both \(\mathsf {lit} (P)\) and \(\mathsf {lit} (Q)\) differ from \(\tau \).
Definition 7
 Let R be a \(\forall \hbox {-}\mathsf{Exp}\hbox {+}\mathsf{Res}\) proof. The circuit extraction \(\mathsf {Cir}(u_i)\) for output \(u_i\) maps vertices in R to circuits as defined in Fig. 4—with the circuits \(\mathsf {Comb}_{u_i}\) defined as follows.
Let R be a \(\forall \hbox {-}\mathsf{Exp}\hbox {+}\mathsf{Res}\) proof. The circuit extraction \(\mathsf {Cir}(u_i)\) for output \(u_i\) maps vertices in R to circuits as defined in Fig. 4—with the circuits \(\mathsf {Comb}_{u_i}\) defined as follows.
Let \(\diamond \in \{\wedge , \vee \}\). For \(u_i \prec x\) we define

Let \(u_m\) be the maximum universal variable with \(u_m \prec x\). For \(x \prec u_i\), we define

Note that in the case when both \(\mathsf {Diff}^i_L\) and \(\mathsf {Diff}^i_R\) are true for i, we prefer L (like we have preferred the left strategy P in \(\mathsf {Combine}\)), due to the order of appearance in the if-then-else cascade.
Example 3
Consider again the strategies P and Q introduced in Example 2. Strategy P encodes the circuits \(L_{u_1}(x_1) = x_1\) and \(L_{u_2}(x_1, x_2) = x_1 \Leftrightarrow x_2\). Strategy Q encodes the circuits \(R_{u_1}(x_1) = \mathtt {1} \) and \(R_{u_2}(x_1, x_2) = x_1 \oplus x_2\). We will show that combining the circuits L and R results in circuits B encoded by  , i.e. \(B_{u_1}(x_1) = x_1\) and \(B_{u_2}(x_1, x_2) = x_1 \vee \lnot x_2\).
, i.e. \(B_{u_1}(x_1) = x_1\) and \(B_{u_2}(x_1, x_2) = x_1 \vee \lnot x_2\).
We will demonstrate that our circuit construction yields the same circuits: For \(B_{u_1}\) we are in the case \(u_1 \prec x_2\) and \(\mathsf {Diff}_L^{0}\) and \(\mathsf {Diff}_R^{0}\) are false by definition, \(\diamond = \wedge \) because the annotation \(u_1\) of the pivot is \(\mathtt {1} \) so Definition 7 evaluates to

For \(B_{u_2}\) we are in case \(x \prec u_2\), and \(u_1\) is the maximum \(u_i \prec x\) so we have

\(\mathsf {Diff}_L^{1}(x_1)\) evaluates to \(L_{u_1}(x_1) \oplus \tau (u_1) = x_1 \oplus \mathtt {1} = \lnot x_1\) indicating a difference in L when \(x_1 = \mathtt {0} \) leading us to choose the “if-then” branch: \(\mathtt {0} \Leftrightarrow x_2\), which is true when \(x_2 = \mathtt {0} \). \(\mathsf {Diff}_R^{1}(x_1)\) evaluates to \(R_{u_1}(x_1) \oplus \tau (u_1) = \mathtt {1} \oplus \mathtt {1} = \mathtt {0} \) indicating no difference in R. So when \(x_1 = \mathtt {1} \), we reach the “else” branch, which evaluates to \(\mathtt {1} \) for both \(x_2 = \mathtt {0} \) and \(x_2 = \mathtt {1} \). Overall, we know that only the assignment \(x_1 = \mathtt {0}, x_2 = \mathtt {1} \) makes \(B_{u_2}\) false, thus we determine that \(B_{u_2}(x_1, x_2) = x_1 \vee \lnot x_2\).
5.2 Correctness and Running Time
Lemma 1
Let P and Q be strategies and let L and R be families of circuits representing P and Q, respectively. Then the family B of circuits as specified in Definition 7 represents  .
.
Proof (Sketch)
When a function value for an output differs from the annotation in circuit L we select the circuits from L for all consecutive outputs. While this operation is implicit in \(\mathsf {Combine}\) by selecting whole sub-trees of a strategy, we need to make this operation explicit for each output in the circuit construction, by looking at all preceding outputs, which we do in the \(\mathsf {Diff}\) circuits.
If all preceding outputs equal the annotation, then we compute the new function value for the current output as a disjunction or conjunction, depending on the assignment to the output in the annotation. This operation mimics \(\mathsf {Combine}\), both in selecting the differing edge, if an edge differs, and keeping the equivalent edge, if both function values equal the annotation.
The case where we reach the pivot variable in \(\mathsf {Combine}\) and select sub-strategies from both input strategies, again needs to be made explicit in the circuit construction: We need to check that we are in this case, by inspecting whether one of the preceding outputs differs, like described above. However, we need to check only the outputs up to the level of the pivot variable. Beyond that, the selection of the sub-strategies at the pivot needs to be simulated, which we do by adding a multiplexer with the pivot being the selector input.
The case where the top-most existential variable differs from the pivot in \(\mathsf {Combine}\) and we recurse is implicit in the circuit construction: The function values depend on these variables, but we do not need to handle existential variables beyond the multiplexer construction.
The case where we recurse in \(\mathsf {Combine}\) when both universal edges adhere to the annotation is implicit in the circuit construction as well: it amounts to iterative computation of the functions according to the quantifier level. \(\square \)
Lemma 2
Given a \(\forall \hbox {-}\mathsf{Exp}\hbox {+}\mathsf{Res}\) derivation of length p from a PCNF formula \(\varPhi \) with n universal variables, the circuits as defined in Definition 7 can be computed in time \(\mathcal {O}(p \cdot n)\).
Proof
For each output \(u_i\), we need a circuit \(\mathsf {Diff}_L^{i-1}\). To compute that circuit we reuse the circuits computing \(\mathsf {Equiv}_R^{< i-1}\) and \(\mathsf {Diff}_L^{i-2}\), which we have already computed for \(u_{i-1}\), so for output \(u_i\) we only have to add the checks \(R_{u_{i-1}} \Leftrightarrow \tau (u_{i-1})\) and \(L_{u_{i-1}} \oplus \tau (u_{i-1})\) of constant size, and gates connecting these circuits, also of constant size. Thus, the number of gates of the \(\mathsf {Diff}_L\) circuits for all n outputs is in the order of \(\mathcal {O}(n)\). The same analysis applies to the \(\mathsf {Diff}_R\) circuits, adding another \(\mathcal {O}(n)\). The if-then-else cascade adds another constant, but the overall circuit complexity at a proof node remains \(\mathcal {O}(n)\). Thus, overall we have a circuit size and running time of \(\mathcal {O}(p \cdot n)\). \(\square \)
In combination with Theorem 1, the preceding lemmas imply the following.
Theorem 2
Given a \(\forall \hbox {-}\mathsf{Exp}\hbox {+}\mathsf{Res}\) derivation of length p from a PCNF formula \(\varPhi \) with n universal variables, a family of circuits implementing a universal winning strategy for \(\varPhi \) can be computed in time \(\mathcal {O}(p \cdot n)\).
Similarity to Craig Interpolation. When the circuit has a single output, note that the \(\mathsf {Diff}\) circuits are always false and we only use the “else” branches. In this case, our system resembles a symmetric Craig interpolation system, cf. [19, 24, 28].
6 Circuit Extraction for QParity
We demonstrate our strategy extraction algorithm with the QParity formulas. Each formula \(\textsc {QParity} _n\) has a single universal variable with the parity function on n variables as the unique universal winning strategy. Since Q-resolution proofs can be efficiently turned into bounded-depth circuits computing a universal winning strategy, QParity is known to be hard for Q-resolution [6]. At the same time, it has short (even tree-like) \(\forall \hbox {-}\mathsf{Exp}\hbox {+}\mathsf{Res}\) proofs, and our strategy extraction algorithm obtains a small circuit representing the n-bit parity function.
Example 4
 The formula QParity says that there exists an assignment of \(x_1, \dots , x_n\) such that \(u \ne x_1 \oplus \dots \oplus x_n\) for all assignments of u. Clearly, this formula is false, and the (unique) winning strategy for the universal player is to assign \(u = x_1 \oplus \dots \oplus x_n\). A PCNF encoding is obtained by introducing auxiliary variables satisfying \(y_i \Leftrightarrow \bigoplus _{j=1}^i x_j\) as follows:
The formula QParity says that there exists an assignment of \(x_1, \dots , x_n\) such that \(u \ne x_1 \oplus \dots \oplus x_n\) for all assignments of u. Clearly, this formula is false, and the (unique) winning strategy for the universal player is to assign \(u = x_1 \oplus \dots \oplus x_n\). A PCNF encoding is obtained by introducing auxiliary variables satisfying \(y_i \Leftrightarrow \bigoplus _{j=1}^i x_j\) as follows:
The biconditional \(u \Leftrightarrow y_n\) yields the clauses \((\lnot u \vee \lnot y_n)\) and \((u \vee y_n)\), and each formula \((y_i \Leftrightarrow (y_{i-1} \oplus x_i))\) translates to clauses \((\lnot y_{i-1} \vee x_i \vee y_i)\), \((y_{i-1} \vee \lnot x_i \vee y_i)\), \((y_{i-1} \vee x_i \vee \lnot y_i)\), and \((\lnot y_{i-1} \vee \lnot x_i \vee \lnot y_i)\). Beyersdorff et al. show how to construct short tree-like proofs for QParity in \(\forall \hbox {-}\mathsf{Exp}\hbox {+}\mathsf{Res}\) [4, Theorem 2]. We illustrate their construction for the case \(n = 2\). By expanding the universal variable u (applying the \(\forall \)-exp rule), we obtain the following initial clauses:
A resolution refutation completing the \(\forall \hbox {-}\mathsf{Exp}\hbox {+}\mathsf{Res}\) proof is shown in Fig. 5, where each clause is annotated with the circuit computed for u according to Definition 7. The empty clause is annotated \((x_1 \vee x_2) \wedge (\lnot x_1 \vee \lnot x_2) = x_1 \oplus x_2\), which is a winning strategy.
7 Related Work
Suda and Gleiss present a local soundness argument for several resolution-based QBF calculi, including a generalization of \(\forall \hbox {-}\mathsf{Exp}\hbox {+}\mathsf{Res}\) [33]. They interpret clauses derived in these systems as abstractions of partial strategies (a partial strategy does not need to be defined for all moves of the existential player), and show that resolution can be understood in terms of combining partial strategies. Soundness of a proof system is obtained by showing that partial strategies with the premises of a resolution step as their abstractions result in a partial strategy that abstracts to the resolvent. The statement that the partial strategy constructed at a particular node of a proof DAG abstracts to the clause derived at that node is proved only indirectly, through observing that there are simple partial strategies abstracting to initial clauses.
By contrast, we define a syntactic weakening of the matrix for each node in the proof DAG and show that the strategy extracted at that node satisfies the weakened matrix. Moreover, we manipulate complete strategies, which are defined for all moves of the existential player. We believe that our use of complete strategies and an explicit syntactic construction offer a considerably simpler and clearer local soundness argument for \(\forall \hbox {-}\mathsf{Exp}\hbox {+}\mathsf{Res}\).
A correspondence between Q-resolution proofs and strategies was first observed by Goultiaeva et al. [15] and later extended to long-distance Q-resolution by Egly et al. [12]. Balabanov and Jiang [2] present a linear-time strategy extraction algorithm for Q-resolution that was generalized to long-distance Q-resolution by Balabanov et al. [3]. Beyersdorff et al. [5] prove a correspondence between strategies and proofs in IRM-calc, a system that generalizes \(\forall \hbox {-}\mathsf{Exp}\hbox {+}\mathsf{Res}\). The notion that efficient extraction of winning moves from proofs leads to polynomial-time strategy extraction is folklore. Peitl et al. [27] give an explicit construction for Q-resolution with a dependency scheme. Chew and Clymo [11] provide a general argument for QBF proof systems that combine a propositional proof system with universal expansion. Surprisingly, they also identify feasible interpolation of the underlying propositional proof system (i.e, the property that interpolants can be computed from refutation proofs in polynomial time [24]) as a necessary condition for such systems to have polynomial-time strategy extraction. They further show that the QRAT proof system does not have polynomial-time strategy extraction unless P=PSPACE. By contrast, Heule et al. [16] proved that the (almost) dual proof system for true formulas does have polynomial-time strategy extraction.
Jiang et al. [23] synthesize Boolean functions with a single output using propositional Craig interpolation [19, 24, 28]. Given a Boolean relation \(\varphi : \mathbb {B} ^n \times \mathbb {B} \mapsto \mathbb {B} \), the authors of [23] derive a circuit \(f(\varvec{x})\) such that \(\forall \varvec{x}.\exists u.\varphi (\varvec{x}, u)\;\equiv \; \forall \varvec{x}.\varphi (\varvec{x}, f(\varvec{x}))\) holds. They derive a resolution refutation from \(\forall \varvec{x}.\exists u.\varphi (\varvec{x}, u)\) by negating it first and then expanding the universal quantifier to obtain an unsatisfiable CNF instance \(\lnot \varphi (\varvec{x}, \mathtt {0})\wedge \lnot \varphi (\varvec{x}, \mathtt {1})\), which is then split into two partitions \(A^{\lnot u}{\mathop {=}\limits ^{{\tiny \mathrm{def}}}}\lnot \varphi (\varvec{x}, \mathtt {0})\) and \(B^{u}{\mathop {=}\limits ^{{\tiny \mathrm{def}}}}\lnot \varphi (\varvec{x}, \mathtt {1})\). An interpolant \(I(\varvec{x})\) for these partitions satisfies \((A^{\lnot u}\rightarrow I)\) and \((B^{u}\rightarrow \lnot I)\), hence the circuit \(f(\varvec{x}){\mathop {=}\limits ^{{\tiny \mathrm{def}}}}I(\varvec{x})\) yields \(\mathtt {1} \) if \(\lnot \varphi (\varvec{x}, \mathtt {0})\) and \(\mathtt {0} \) if \(\lnot \varphi (\varvec{x}, \mathtt {1})\), satisfying the requirement above. \(I(\varvec{x})\) is obtained by annotating all clauses C in the resolution refutation by partial interpolants \(I_C\), where \(I_C{\mathop {=}\limits ^{{\tiny \mathrm{def}}}}\mathtt {0} \) if \(C\in A^{\lnot u}\), \(I_C{\mathop {=}\limits ^{{\tiny \mathrm{def}}}}\mathtt {1} \) if \(C\in B^{u}\), and \(I_c{\mathop {=}\limits ^{{\tiny \mathrm{def}}}}(x\vee I_1)\wedge (\lnot x\vee I_2)\) if C is the result of a resolution of \(C_1\) and \(C_2\) with partial interpolants \(I_1\) and \(I_2\), respectively, on the pivot literal x.
The construction of the partitions \(A^{\lnot u}\) and \(B^u\) in [23] is analogous to QBF Expansion, and propositional interpolation is a (less general) version of the circuit extraction in Fig. 4. Consequently, [23] can be seen as a special case of our framework that is limited to a single universally quantified variable. In fact, [23] proposes an iterative approach to deal with multiple outputs (universal quantifiers, respectively), requiring the repeated construction of refutations and interpolants and the substitution of outputs one at a time.
Hofferek et al. [17] extend the approach of Jiang et al. [23] to n universally quantified Boolean variables by (syntactically) expanding the quantified formula into \(2^n\) partitions and adapting the interpolation system to multiple partitions accordingly. Their approach targets the theory of uninterpreted functions with equality, which is a more expressive logic, but is limited to \(\forall \exists \forall \)-prefixes and imposes an order on the resolution steps in the propositional part of the refutation.
Beyersdorff et al. [7] present a feasible interpolation technique for the calculi LQU\(^+\) -Res and IRM-calc. Their approach is restricted to instances of the form \(\exists \varvec{p}.Q\varvec{q}.Q\varvec{r}.A(\varvec{p},\varvec{q})\wedge B(\varvec{p},\varvec{r})\) (where \(\varvec{q}\) and \(\varvec{r}\) can be quantified arbitrarily) and yields an interpolant \(I(\varvec{p})\). They show that for instances of the form \(\exists \varvec{p}.\forall u. Q\varvec{q}.Q\varvec{r}. (A(\varvec{p},\varvec{q})\vee u)\wedge (B(\varvec{p},\varvec{r})\vee \lnot u)\) the resulting interpolant \(I(\varvec{p})\) represents a strategy for instantiating u. While this approach extends Jiang et al. [23] to arbitarily quantified partitions, it is still limited to a single output u.
8 Conclusion
We presented a polynomial-time strategy extraction algorithm for \(\forall \hbox {-}\mathsf{Exp}\hbox {+}\mathsf{Res}\) with a running time that is multi-linear in the number of universal variables and resolution steps in the proof. It is based on a local soundness argument showing that each intermediate strategy constructed for a derived clause satisfies a propositional invariant obtained from that clause. This invariant translates annotated literals back to the vocabulary of the original formula and gives them a clear semantics based on the evaluation game: if the existential player responds to the universal play in the annotation by setting the literal to false, the current strategy is winning for the universal player. We believe that this idea can be extended to more general proof systems such as IRM-calc [5]. Moreover, our interpretation of annotated clauses in terms of the original variables may open up new ways of integrating search-based (QCDCL) solvers with expansion.
Notes
- 1.
Conversely, there are classes of formulas with exponentially shorter Q-resolution proofs [22], so that the systems are mutually separated.
- 2.
If the strategy P is identified with the disjunction of assignments induced by its root-to-leaf paths, the relation \(P \models \psi \) coincides with propositional entailment.
References
Ayari, A., Basin, D.: Qubos: deciding quantified boolean logic using propositional satisfiability solvers. In: Aagaard, M.D., O’Leary, J.W. (eds.) FMCAD 2002. LNCS, vol. 2517, pp. 187–201. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-36126-X_12
Balabanov, V., Jiang, J.R.: Unified QBF certification and its applications. Formal Methods Syst. Des. 41(1), 45–65 (2012)
Balabanov, V., Jiang, J.R., Janota, M., Widl, M.: Efficient extraction of QBF (counter)models from long-distance resolution proofs. In: Bonet, B., Koenig, S. (eds.) Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence (AAAI-15), pp. 3694–3701. AAAI Press (2015)
Beyersdorff, O., Chew, L., Clymo, J., Mahajan, M.: Short proofs in QBF expansion. In: Janota, M., Lynce, I. (eds.) SAT 2019. LNCS, vol. 11628, pp. 19–35. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-24258-9_2
Beyersdorff, O., Chew, L., Janota, M.: On unification of QBF resolution-based calculi. In: Csuhaj-Varjú, E., Dietzfelbinger, M., Ésik, Z. (eds.) MFCS 2014. LNCS, vol. 8635, pp. 81–93. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44465-8_8
Beyersdorff, O., Chew, L., Janota, M.: New resolution-based QBF calculi and their proof complexity. TOCT 11(4), 26:1–26:42 (2019)
Beyersdorff, O., Chew, L., Mahajan, M., Shukla, A.: Feasible interpolation for QBF resolution calculi. Logical Methods Comput. Sci. 13(2), 1–20 (2017). https://lmcs.episciences.org/3702/pdf
Biere, A.: Resolve and expand. In: Hoos, H.H., Mitchell, D.G. (eds.) SAT 2004. LNCS, vol. 3542, pp. 59–70. Springer, Heidelberg (2005). https://doi.org/10.1007/11527695_5
Bloem, R., Braud-Santoni, N., Hadzic, V., Egly, U., Lonsing, F., Seidl, M.: Expansion-based QBF solving without recursion. In: Bjørner, N., Gurfinkel, A. (eds.) 2018 Formal Methods in Computer Aided Design, FMCAD 2018, pp. 1–10. IEEE (2018)
Chew, L., Clymo, J.: The equivalences of refutational QRAT. In: Janota, M., Lynce, I. (eds.) SAT 2019. LNCS, vol. 11628, pp. 100–116. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-24258-9_7
Chew, L., Clymo, J.: How QBF expansion makes strategy extraction hard. In: International Joint Conference on Automated Reasoning, IJCAR 2020 (2020)
Egly, U., Lonsing, F., Widl, M.: Long-distance resolution: proof generation and strategy extraction in search-based QBF solving. In: McMillan, K., Middeldorp, A., Voronkov, A. (eds.) LPAR 2013. LNCS, vol. 8312, pp. 291–308. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-45221-5_21
Faymonville, P., Finkbeiner, B., Rabe, M.N., Tentrup, L.: Encodings of bounded synthesis. In: Legay, A., Margaria, T. (eds.) TACAS 2017. LNCS, vol. 10205, pp. 354–370. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-54577-5_20
Gomes, C.P., Kautz, H.A., Sabharwal, A., Selman, B.: Satisfiability solvers. In: van Harmelen, F., Lifschitz, V., Porter, B.W. (eds.) Handbook of Knowledge Representation, Foundations of Artificial Intelligence, vol. 3, pp. 89–134. Elsevier (2008)
Goultiaeva, A., Gelder, A.V., Bacchus, F.: A uniform approach for generating proofs and strategies for both true and false QBF formulas. In: Walsh, T. (ed.) IJCAI 2011, Proceedings of the 22nd International Joint Conference on Artificial Intelligence, pp. 546–553. IJCAI/AAAI (2011)
Heule, M.J.H., Seidl, M., Biere, A.: Solution validation and extraction for QBF preprocessing. J. Autom. Reason. 58(1), 97–125 (2017)
Hofferek, G., Gupta, A., Könighofer, B., Jiang, J.R., Bloem, R.: Synthesizing multiple Boolean functions using interpolation on a single proof. In: Formal Methods in Computer-Aided Design, FMCAD 2013. pp. 77–84. IEEE (2013)
Howard, W.A.: The formulas-as-types notion of construction. In: Seldin, J.P., Hindley, J.R. (eds.) To H. B. Curry: Essays on Combinatory Logic, Lambda Calculus, and Formalism, pp. 479–490. Academic Press (1980)
Huang, G.: Constructing craig interpolation formulas. In: Du, D.-Z., Li, M. (eds.) COCOON 1995. LNCS, vol. 959, pp. 181–190. Springer, Heidelberg (1995). https://doi.org/10.1007/BFb0030832
Janota, M.: Towards generalization in QBF solving via machine learning. In: McIlraith, S.A., Weinberger, K.Q. (eds.) Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, (AAAI-2018), pp. 6607–6614. AAAI Press (2018)
Janota, M., Klieber, W., Marques-Silva, J., Clarke, E.M.: Solving QBF with counterexample guided refinement. Artif. Intell. 234, 1–25 (2016)
Janota, M., Marques-Silva, J.: Expansion-based QBF solving versus Q-resolution. Theor. Comput. Sci. 577, 25–42 (2015)
Jiang, J.R., Lin, H., Hung, W.: Interpolating functions from large Boolean relations. In: Roychowdhury, J.S. (ed.) 2009 International Conference on Computer-Aided Design, ICCAD 2009, pp. 779–784. ACM (2009)
Krajícek, J.: Interpolation theorems, lower bounds for proof systems, and independence results for bounded arithmetic. J. Symb. Logic 62(2), 457–486 (1997)
Lonsing, F., Bacchus, F., Biere, A., Egly, U., Seidl, M.: Enhancing search-based QBF Solving by dynamic blocked clause elimination. In: Davis, M., Fehnker, A., McIver, A., Voronkov, A. (eds.) LPAR 2015. LNCS, vol. 9450, pp. 418–433. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48899-7_29
Peitl, T., Slivovsky, F., Szeider, S.: Dependency learning for QBF. J. Artif. Intell. Res. 65, 180–208 (2019)
Peitl, T., Slivovsky, F., Szeider, S.: Long-distance Q-resolution with dependency schemes. J. Autom. Reason. 63(1), 127–155 (2019)
Pudlák, P.: Lower bounds for resolution and cutting plane proofs and monotone computations. J. Symb. Logic 62(3), 981–998 (1997)
Rabe, M.N., Seshia, S.A.: Incremental determinization. In: Creignou, N., Le Berre, D. (eds.) SAT 2016. LNCS, vol. 9710, pp. 375–392. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-40970-2_23
Rabe, M.N., Tentrup, L.: CAQE: A certifying QBF solver. In: Kaivola, R., Wahl, T. (eds.) Formal Methods in Computer-Aided Design, FMCAD 2015, pp. 136–143. IEEE (2015)
Schaefer, T.J.: On the complexity of some two-person perfect-information games. J. Comput. Syst. Sci. 16(2), 185–225 (1978)
Shukla, A., Biere, A., Pulina, L., Seidl, M.: A survey on applications of quantified Boolean formulas. In: 31st IEEE International Conference on Tools with Artificial Intelligence, ICTAI 2019, pp. 78–84. IEEE (2019)
Suda, M., Gleiss, B.: Local soundness for QBF calculi. In: Beyersdorff, O., Wintersteiger, C.M. (eds.) SAT 2018. LNCS, vol. 10929, pp. 217–234. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-94144-8_14
Tentrup, L.: Non-prenex QBF Solving using abstraction. In: Creignou, N., Le Berre, D. (eds.) SAT 2016. LNCS, vol. 9710, pp. 393–401. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-40970-2_24
Vizel, Y., Weissenbacher, G., Malik, S.: Boolean satisfiability solvers and their applications in model checking. Proc. IEEE 103(11), 2021–2035 (2015)
Wimmer, R., Reimer, S., Marin, P., Becker, B.: HQSpre – an effective preprocessor for QBF and DQBF. In: Legay, A., Margaria, T. (eds.) TACAS 2017. LNCS, vol. 10205, pp. 373–390. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-54577-5_21
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
Schlaipfer, M., Slivovsky, F., Weissenbacher, G., Zuleger, F. (2020). Multi-linear Strategy Extraction for QBF Expansion Proofs via Local Soundness. In: Pulina, L., Seidl, M. (eds) Theory and Applications of Satisfiability Testing – SAT 2020. SAT 2020. Lecture Notes in Computer Science(), vol 12178. Springer, Cham. https://doi.org/10.1007/978-3-030-51825-7_30
Download citation
DOI: https://doi.org/10.1007/978-3-030-51825-7_30
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-51824-0
Online ISBN: 978-3-030-51825-7
eBook Packages: Computer ScienceComputer Science (R0)