A Combinator-Based Superposition Calculus for Higher-Order Logic

Abstract

We present a refutationally complete superposition calculus for a version of higher-order logic based on the combinatory calculus. We also introduce a novel method of dealing with extensionality. The calculus was implemented in the Vampire theorem prover and we test its performance against other leading higher-order provers. The results suggest that the method is competitive.

1 Introduction

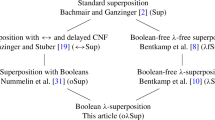
First-order superposition provers are often used to reason about problems in extensional higher-order logic (HOL) [19, 26]. Commonly, this is achieved by translating the higher-order problem to first-order logic (FOL) using combinators. Such a strategy is sub-optimal as translations generally sacrifice completeness and at times even soundness. In this paper, we provide a modification of first-order superposition that is sound and complete for a combinatory version of HOL. Moreover, it is graceful in the sense of that it coincides with standard superposition on purely first-order problems.

The work is complementary to the clausal $\lambda$-superposition calculus of Bentkamp et al. [4]. Our approach appears to offer two clear differences. Firstly, as our calculus is based on the combinatory logic and first-order unification, it is far closer to standard first-order superposition. Therefore, it should be easier to implement in state-of-the-art first-order provers. Secondly, the $>_{\mathsf {ski}}$ ordering that we propose to parameterise our calculus with can compare more terms than can be compared by the ordering presented in [4]. On the other hand, we suspect that for problems requiring complex unifiers, our approach will not be competitive with clausal $\lambda$-superposition.

Developing a complete and efficient superposition calculus for a combinatory version of HOL poses some difficulties. When working with a monomorphic logic it is impossible to select a finite set of typed combinator axioms that can guarantee completeness for a particular problem [12]. Secondly, using existing orderings, combinator axioms can superpose among themselves, leading to a huge number of consequences of the axioms. If the problem is first-order, these consequences can never interact with non-combinator clauses and are therefore useless.

We deal with both issues in the current work. To circumvent the first issue, we base our calculus on a polymorphic rather than monomorphic first-order logic. The second issue can be dealt with by an ordering that orients combinator axioms left-to-right. Consider the $\varvec{\mathsf {S}}$-combinator axiom $\varvec{\mathsf {S}}\, x \, y \, z \approx x \, z \, (y \, z)$. Assume that there exists a simplification ordering $\succ$ such that $\varvec{\mathsf {S}}\, x \, y \, z \succ x \, z \, (y \, z)$. Then, since superposition is only carried out on the larger side of literals and not at variables, there can be no inferences between the $\varvec{\mathsf {S}}$-axiom and any other combinator axiom. Indeed, in this case the axioms can be removed from the clause set altogether and replaced by an inference rule (Sect. 7).

No ground-total simplification ordering is known that is capable of orienting all axioms for a complete set of combinators.¹ The authors suspect that no such simplification ordering exists. Consider a KBO-like ordering. Since the variable x appears twice on the right-hand side of the $\varvec{\mathsf {S}}$-axiom and only once on the left-hand side, the ordering would not be able to orient it. The same is the case for any other combinator which duplicates its arguments.

In other related work [10], we have developed an ordering that enjoys most of the properties of a simplification ordering, but lacks full compatibility with contexts. In particular, the ordering is not compatible with what we call unstable contexts. We propose using such an ordering to parameterise the superposition calculus. In the standard proof of the completeness of superposition, compatibility with contexts is used to rule out the need for superposition at or beneath variables. As the ordering doesn’t enjoy full compatibility with contexts, limited superposition at and below variables needs to be carried out. This is dealt with by the addition of an extra inference rule to the standard rules of superposition, which we call SubVarSup (Sect. 3).

By turning combinator axioms into rewrite rules, the calculus represents a folding of higher-order unification into the superposition calculus itself. Whilst not as goal-directed as a dedicated higher-order unification algorithm, it is still far more goal-directed than using $\varvec{\mathsf {S}}\varvec{\mathsf {K}}$-style combinators in superposition provers along with standard orderings. Consider the conjecture $\exists z. \, \forall x y. \, z \, x \, y \approx \mathsf {f} \, y \, x$. Bentkamp et al. ran an experiment and found that the E prover [25] running on this conjecture supplemented with the $\varvec{\mathsf {S}}$- and $\varvec{\mathsf {K}}$-combinator axioms had to perform 3756 inferences in order to find a refutation [4]. Our calculus reduces this number to 427 inferences. With the addition of rewrite rules for $\varvec{\mathsf {C}}$-, $\varvec{\mathsf {B}}$- and $\varvec{\mathsf {I}}$-combinators, the required inferences reduces to 18.

We consider likely that for problems requiring ‘simple’ unifiers, folding unification into superposition will be competitive with higher-order unification whilst providing the advantages that data structures and algorithms developed for first-order superposition can be re-used unchanged. The results of the empirical evaluation of our method can be found in Sect. 8.

2 The Logic

The logic we use is polymorphic applicative first-order logic otherwise known as $\lambda$-free (clausal) higher-order logic.

Syntax. Let be a set of type variables and be a set of type constructors with fixed arities. It is assumed that a binary type constructor $\rightarrow$ is present in which is written infix. The set of types is defined:

The notation $\, \overline{t_n} \,$ is used to denote a tuple or list of types or terms depending on the context. A type declaration is of the form $\mathsf {\Pi }\, \overline{\alpha _n} \,. \, \sigma$ where $\sigma$ is a type and all type variables in $\sigma$ appear in $\, \overline{\alpha } \,$. Let $\varSigma$ be a set of typed function symbols and a set of variables with associated types. It is assumed that $\varSigma$ contains the following function symbols, known as basic combinators:

$$ \begin{array}{ll} \varvec{\mathsf {S}}: \mathsf {\Pi }\alpha \tau \gamma . \, (\alpha \rightarrow \tau \rightarrow \gamma ) \rightarrow (\alpha \rightarrow \tau ) \rightarrow \alpha \rightarrow \gamma &{} \quad \varvec{\mathsf {I}}: \mathsf {\Pi }\alpha . \, \alpha \rightarrow \alpha \\ \varvec{\mathsf {C}}: \mathsf {\Pi }\alpha \tau \gamma . \, (\alpha \rightarrow \tau \rightarrow \gamma ) \rightarrow \tau \rightarrow \alpha \rightarrow \gamma &{} \quad \varvec{\mathsf {K}}: \mathsf {\Pi }\alpha \gamma . \, \alpha \rightarrow \gamma \rightarrow \alpha \\ \varvec{\mathsf {B}}: \mathsf {\Pi }\alpha \tau \gamma . \, (\alpha \rightarrow \gamma ) \rightarrow (\tau \rightarrow \alpha ) \rightarrow \tau \rightarrow \gamma \end{array} $$

The intended semantics of the combinators is captured by the following combinator axioms:

$$ \begin{array}{ll} \varvec{\mathsf {S}}\, x \, y \, z \;\; = \;\; x \, z \, (y \, z) &{} \quad \varvec{\mathsf {I}}\, x \;\; = \;\; x \\ \varvec{\mathsf {C}}\, x \, y \, z \;\; = \;\; x \, z \, y &{} \quad \varvec{\mathsf {K}}\, x \, y \;\; = \;\; x \\ \varvec{\mathsf {B}}\, x \, y \, z \;\; = \;\; x \, (y \, z) \end{array} $$

The set of terms over $\varSigma$ and is defined below. In what follows, type subscripts are generally omitted.

The type of the term $\mathsf {f}{\langle \, \overline{\tau _n} \,\rangle }$ is $\sigma \{\, \overline{\alpha _n} \, \rightarrow \, \overline{\tau _n} \,\}$. Terms of the form $t_1 \, t_2$ are called applications. Non-application terms are called heads. A term can uniquely be decomposed into a head and n arguments. Let $t = \zeta \, \, \overline{t'_n} \,$. Then $head(t) = \zeta$ where $\zeta$ could be a variable or constant applied to possibly zero type arguments. The symbol $\varvec{\mathcal {C_{\mathsf {any}}}}$ denotes an arbitrary combinator, whilst $\varvec{\mathcal {C_\mathsf {3}}}$ denotes a member of $\{\varvec{\mathsf {S}}, \varvec{\mathsf {C}}, \varvec{\mathsf {B}}\}$. The $\varvec{\mathsf {S}}$-, $\varvec{\mathsf {C}}$- or $\varvec{\mathsf {B}}$-combinators are fully applied if they have 3 or more arguments. The $\varvec{\mathsf {K}}$-combinator is fully applied if it has 2 or more arguments and the $\varvec{\mathsf {I}}$ is fully applied if it has any arguments. The symbols $\varvec{\mathcal {C_{\mathsf {any}}}}$ and $\varvec{\mathcal {C_\mathsf {3}}}$ are only used if the symbols they represent are fully applied. Thus, in $\varvec{\mathcal {C_\mathsf {3}}}\, \, \overline{t_n} \,$, $n \ge 3$ is assumed. The symbols $x,y,z \ldots$ are reserved for variables, $\mathsf {c}, \mathsf {d}, \mathsf {f} \ldots$ for non-combinator constants and $\zeta , \xi$ range over arbitrary function symbols and variables and, by an abuse of notation, at times even terms. A head symbol that is not a combinator applied to type arguments or a variable is called first-order.

Positions over Terms: For a term t, if or $t = \mathsf {f}{\langle \, \overline{\tau } \,\rangle }$, then $pos(t) = \{\epsilon \}$ (type arguments have no position). If $t = t_1 \, t_2$ then $pos(t) = \{\epsilon \} \cup \{i.p \; \vert \; 1 \le i \le 2, \; p \in pos(t_i)\}$. Subterms at positions of the form p.1 are called prefix subterms. We define first-order subterms inductively as follows. For any term t, t is a first-order subterm of itself. If $t = \zeta \, \overline{t_n} \,$, where $\zeta$ is not a fully applied combinator, then the first-order subterms of each $t_i$ are also first-order subterms of t. The notation $s \langle u \rangle$ is to be read as u is a first-order subterm of s. Note that this definition is subtly different to that in [10] since subterms underneath a fully applied combinator are not considered to be first-order.

Stable Subterms: Let $\mathsf {LPP}(t, p)$ be a partial function that takes a term t, a position p and returns the longest proper prefix $p'$ of p such that $head(t \vert _{p'})$ is not a partially applied combinator if such a position exists. For a position $p \in pos(t)$, p is a stable position in t if p is not a prefix position and either $\mathsf {LPP}(t, p)$ is not defined or $head(t \vert _{\mathsf {LPP}(t, p)})$ is not a variable or combinator. A stable subterm is a subterm occurring at a stable position. For example, the subterm $\mathsf {a}$ is not stable in $\mathsf {f} \, (\varvec{\mathsf {S}}\, \mathsf {a} \, \mathsf {b} \, \mathsf {c})$, $\varvec{\mathsf {S}}\, (\varvec{\mathsf {S}}\, \mathsf {a}) \, \mathsf {b} \, \mathsf {c}$ (in both cases, $head(t\vert _{\mathsf {LPP}(t, p)}) = \varvec{\mathsf {S}}$) and $\mathsf {a} \, \mathsf {c}$ ($\mathsf {a}$ is in a prefix position), but is in $\mathsf {g} \, \mathsf {a} \, \mathsf {b}$ and $\mathsf {f} \, (\varvec{\mathsf {S}}\, \mathsf {a}) \, \mathsf {b}$. A subterm that is not stable is known as an unstable subterm.

The notation $t [ u ]$ denotes an arbitrary subterm u of t. The notation $t [ u_1, \ldots , u_n ]_n$, at times given as $t [ \, \overline{u} \, ]_n$ denotes that the the term t contains n non-overlapping subterms $u_1$ to $u_n$. By $u [ ]_n$, we refer to a context with n non-overlapping holes.

Weak Reduction: A term t weak-reduces to a term $t'$ in one step (denoted $t \longrightarrow _wt'$) if $t = u [ s ]_p$ and there exists a combinator axiom $l = r$ and substitution $\sigma$ such that $l\sigma = s$ and $t' = u [ r\sigma ]_p$. The term $l\sigma$ in t is called a weak redex or just redex. By $\longrightarrow _w^*$, the reflexive transitive closure of $\longrightarrow _w$ is denoted. Weak-reduction is terminating and confluent as proved in [15]. By $(t)\! \downarrow ^w$, we denote the term formed from t by contracting its leftmost redex.

Literals and Clauses: An equation $s \approx t$ is an unordered pair of terms and a literal is an equation or the negation of an equation represented $s \not \approx t$. Let $ax = l \approx r$ be a combinator axiom and $\, \overline{x_n} \,$ be a tuple of variables not appearing in ax. Then ax and $l \, \, \overline{x_n} \, \approx r \, \, \overline{x_n} \,$ for all n are known as extended combinator axioms. For example, $\varvec{\mathsf {I}}\, x_1 \, x_2 \approx x_1 \, x_2$ is an extended combinator axiom. A clause is a multiset of literals represented $L_1 \vee \cdots \vee L_n$ where each $L_i$ is a literal.

Semantics. We follow Bentkamp et al. [6] closely in specifying the semantics. An interpretation is a triple $(\mathcal {U}, \mathcal {E}, \mathcal {J})$ where $\mathcal {U}$ is a ground-type indexed family of non-empty sets called universes and $\mathcal {E}$ is a family of functions $\mathcal {E}_{\tau ,v}: \mathcal {U}_{\tau \rightarrow v} \rightarrow (\mathcal {U}_\tau \rightarrow \mathcal {U}_v)$. A type valuation $\xi$ is a substitution that maps type variables to ground types and whose domain is the set of all type variables. A type valuation $\xi$ is extended to a valuation by setting $\xi (x_\tau )$ to be a member of $\mathcal {U}_{(\tau \xi )}$. An interpretation function $\mathcal {J}$ maps a function symbol $\mathsf {f} : \mathsf {\Pi }\, \overline{\alpha _n} \,. \, \sigma$ and a tuple of ground types $\, \overline{\tau _n} \,$ to a member of $\mathcal {U}_{(\sigma \{\alpha _i \rightarrow \tau _i\})}$. An interpretation is extensional if $\mathcal {E}_{\tau , v}$ is injective for all $\tau , v$ and is standard if $\mathcal {E}_{\tau , v}$ is bijective for all $\tau , v$.

For an interpretation $\mathcal {I}= (\mathcal {U}, \mathcal {E}, \mathcal {J})$ and a valuation $\xi$, a term is denoted as follows: , and . An equation $s \approx t$ is true in an interpretation $\mathcal {I}$ with valuation function $\xi$ if and are the same object and is false otherwise. A disequation $s \not \approx t$ is true if $s \approx t$ is false. A clause is true if one of its literals is true and a clause set is true if every clause in the set is true. An interpretation $\mathcal {I}$ models a clause set N, written , if N is true in $\mathcal {I}$ for all valuation functions $\xi$.

As Bentkamp et al. point out in [4] there is a subtlety relating to higher-order models and choice. If, as is the case here, attention is not restricted to models that satisfy the axiom of choice, naive skolemisation is unsound. One solution would be to implement skolemisation with mandatory arguments as explained in [21]. However, the introduction of mandatory arguments considerably complicates both the calculus and the implementation. Therefore, we resort to the same ‘trick’ as Bentkamp et al., namely, claiming completeness for our calculus with respect to models as described above. This holds since we assume problems to be clausified. Soundness is claimed for the implementation with respect to models that satisfy the axiom of choice and completeness can be claimed if the axiom of choice is added to the clause set.

3 The Calculus

The calculus is modeled after Bentkamp et al.’s intensional non-purifying calculus [6]. The extensionality axiom can be added if extensionality is required. The main difference between our calculus and that of [6] is that superposition inferences are not allowed beneath fully applied combinators and an extra inference rule is added to deal with superposition beneath variables. We name the calculus clausal combinatory-superposition.

Term Ordering. We also demand that clausal combinatory-superposition is parameterised by a partial ordering $\succ$ that is well-founded, total on ground terms, stable under substitutions and has the subterm property and which orients all instances of combinator axioms left-to-right. It is an open problem whether a simplification ordering enjoying this last property exists, but it appears unlikely. However, for completeness, compatibility with stable contexts suffices. The $>_{\mathsf {ski}}$ ordering introduced in [10] orients all instances of combinator axioms left-to-right and is compatible with stable contexts. It is not compatible with arbitrary contexts. For terms $t_1$ and $t_2$ such that $t_1 >_{\mathsf {ski}}t_2$, it is not necessarily the case that $t_1 \, u >_{\mathsf {ski}}t_2 \, u$ or that $\varvec{\mathsf {S}}\, t_1 \, a \, b >_{\mathsf {ski}}\varvec{\mathsf {S}}\, t_2 \, a \, b$. We show that by not superposing underneath fully applied combinators and carrying out some restricted superposition beneath variables, this lack of compatibility with arbitrary contexts can be circumvented and does not lead to a loss of completeness. In a number of places in the completeness proof, we assume the following conditions on the ordering (satisfied by the $>_{\mathsf {ski}}$ ordering). It may be possible to relax the conditions at the expense of an increased number of inferences.

• P1 For terms $t, t'$ such that $t \longrightarrow _wt'$, then $t \succ t'$

• P2 For terms $t, t'$ such that $t \succ t'$ and $head(t')$ is first-order, $u [ t ] \succ u [ t' ]$

The ordering $\succ$ is extended to literals and clauses using the multiset extension as explained in [22].

Inference Rules. Clausal combinatory-superposition is further parameterised by a selection function that maps a clause to a subset of its negative literals. Due to the requirements of the completeness proof, if a term $t = x \, \, \overline{s_{n > 0}} \,$ is a maximal term in a clause C, then a literal containing x as a first-order subterm may not be selected. A literal L is $\sigma$-eligible in a clause C if it is selected or there are no selected literals in C and $L\sigma$ is maximal in $C\sigma$. If $\sigma$ is the identity substitution it is left implicit. In the latter case, it is strictly eligible if it is strictly maximal. A variable x has a bad occurrence in a clause C if it occurs in C at an unstable position. Occurrences of x in C at stable positions are good.

Positive and negative superposition:

with the following side conditions:

Definition 1

Let $l = \varvec{\mathcal {C_{\mathsf {any}}}}\, \overline{x_n} \,$ and $l \approx r$ be an extended combinator axiom. A term $v \, \, \overline{u_m} \,$ is compatible with $l \approx r$ if $\varvec{\mathcal {C_{\mathsf {any}}}}= \varvec{\mathsf {I}}$ and $m = n$ or if $\varvec{\mathcal {C_{\mathsf {any}}}}= \varvec{\mathsf {K}}$ and $m \ge n-1$ or if $\varvec{\mathcal {C_{\mathsf {any}}}}\in \{\varvec{\mathsf {B}}, \varvec{\mathsf {C}}, \varvec{\mathsf {S}}\}$ and $m \ge n - 2$.

Variable Condition: . If $u = x \, \, \overline{s_n} \,$ and D is an extended combinator axiom, then D and u must be compatible.

Because the term ordering $\succ$ is not compatible with unstable contexts, there are instances when superposition beneath variables must be carried out. The SubVarSup rule deals with this.

with the following side conditions in addition to conditions 4 – 8 of Sup:

The EqRes and EqFact inferences:

For both inferences $\sigma = mgu(u,u')$. For EqRes, $u \not \approx u'$ is $\sigma$-eligible in the premise. For EqFact, $u'\sigma \not \preceq v'\sigma$, $u\sigma \not \preceq v\sigma$, and $u \approx v$ is $\sigma$-eligible in the premise.

In essence, the ArgCong inference allows superposition to take place at prefix positions by ‘growing’ equalities to the necessary size.

The literal $s \approx s'$ must be $\sigma$-eligible in C. Let s and $s'$ be of type $\alpha _1 \rightarrow \cdots \rightarrow \alpha _m \rightarrow \beta$. If $\beta$ is not a type variable, then $\sigma$ is the identity substitution and the inference has m conclusions. Otherwise, if $\beta$ is a type variable, the inference has an infinite number of conclusions. In conclusions where $n > m$, $\sigma$ is the substitution that maps $\beta$ to type $\tau _1 \rightarrow \cdots \rightarrow \tau _{n-m} \rightarrow \beta '$ where $\beta '$ and each $\tau _i$ are fresh type variables. In each conclusion, the $x_i$s are variables fresh for C. Note that an ArgCong inference on a combinator axiom results in an extended combinator axiom.

3.1 Extensionality

Clausal combinatory-superposition can be either intensional or extensional. If a conjecture is proved by the intensional version of the calculus, it means that the conjecture holds in all models of the axioms. On the other hand, if a conjecture is proved by the extensional version, it means that the conjecture holds in all extensional models (as defined above). Practically, some domains naturally lend themselves to intensional reasoning whilst other to extensional. For example, when reasoning about programs, we may expect to treat different programs as different entities even if they always produce the same output when provided the same input. For the calculus to be extensional, we provide two possibilities. The first is to add a polymorphic extensionality axiom. Let $\mathsf {diff}$ be a polymorphic symbol of type $\mathsf {\Pi }\tau _1, \tau _2. \,(\tau _1 \rightarrow \tau _2) \rightarrow (\tau _1 \rightarrow \tau _2) \rightarrow \tau _1$. Then the extensionality axiom can be given as:

$$\begin{aligned} x \, (\mathsf {diff}{\langle \tau _1, \tau _2\rangle } \; x \; y) \;\; \not \approx \;\; y \, (\mathsf {diff}{\langle \tau _1, \tau _2\rangle } \; x \; y) \;\; \vee \;\; x \approx y \end{aligned}$$

However, adding the extensionality axiom to a clause set can be explosive and is not graceful. By any common ordering, the negative literal will be the larger literal and therefore the literal involved in inferences. As it is not of functional type it can unify with terms of atomic type including first-order terms.

In order to circumvent this issue, we developed another method of dealing with extensionality. Unification is replaced by unification with abstraction. During the unification procedure, no attempt is made to unify pairs consisting of terms of functional or variable type. Instead, if the remaining unification pairs can be solved successfully, such pairs are added to the resulting clause as negative constraint literals. This process works in conjunction with the negative extensionality rule presented below.

where $s \not \approx s'$ is $\sigma$-eligible in the premise, $\, \overline{\alpha } \,$ and $\, \overline{x} \,$ are the free type and term variable of the literal $s \not \approx s'$ and $\sigma$ is the most general type unifier that ensures the well-typedness of the conclusion.

We motivate this second approach to extensionality with an example. Consider the clause set:

$$\begin{aligned} \mathsf {g} \, x \approx \mathsf {f} \, x \qquad \mathsf {h \, g \not \approx h \, f} \end{aligned}$$

equality resolution with abstraction on the second clause produces the clause $\mathsf {g \not \approx f}$. A NegExt inference on this clause results in $\mathsf {g \, sk \not \approx f \, sk}$ which can superpose with $\mathsf {g} \, x \approx \mathsf {f} \, x$ to produce $\perp$.

The unification with abstraction procedure used here is very similar to that introduced in [24]. Pseudocode for the algorithm can be found in Algorithm 1. The inference rules other than ArgCong and SubVarSup must be modified to utilise unification with abstraction rather than standard unification. We show the updated superposition rule. The remaining rules can be modified along similar lines.

where D is the possibly empty set of negative literals returned by unification. Sup-wA shares all the side conditions of Sup given above. This method of dealing with extensionality is not complete as shown in Appendix A of [9].

4 Examples

We provide some examples of how the calculus works. Some of the examples utilised come from Bentkamp et al.’s paper [4] in order to allow a comparison of the two methods. In all examples, it is assumed that the clause set has been enriched with the combinator axioms.

Example 1

Consider the unsatisfiable clause:

$$\begin{aligned} x \, \mathsf {a} \, \mathsf {b} \not \approx x \, \mathsf {b} \, \mathsf {a} \end{aligned}$$

Superposing onto the left-hand side with the extended $\varvec{\mathsf {K}}$ axiom $\varvec{\mathsf {K}}\, x_1 \, x_2 \, x_3 \approx x_1 \, x_3$ results in the clause $x_1 \, \mathsf {b} \not \approx x_1 \, \mathsf {a}$. Superposing onto the left-hand side of this clause, this time with the standard $\varvec{\mathsf {K}}$ axiom adds the clause $x \not \approx x$ from which $\perp$ is derived by an EqRes inference.

Example 2

Consider the unsatisfiable clause set where $\mathsf {f} \, \mathsf {a} \succ \mathsf {c}$:

$$\begin{aligned} \mathsf {f} \, \mathsf {a} \approx \mathsf {c} \quad \quad \quad \mathsf {h} \, (y \, \mathsf {b})(y \, \mathsf {a}) \not \approx \mathsf {h} \, (\mathsf {g} (\mathsf {f} \, \mathsf {b}) )(\mathsf {g} \, \mathsf {c}) \end{aligned}$$

A Sup inference between the $\varvec{\mathsf {B}}$ axiom $\varvec{\mathsf {B}}\, x_1 \, x_2 \, x_3 \approx x_1 \, (x_2 \, x_3)$ and the subterm $y \, \mathsf {b}$ of the second clause adds the clause $\mathsf {h}(x_1 (x_2 \,\mathsf {b}))(x_1 (x_2 \,\mathsf {a})) \not \approx \mathsf {h}(\mathsf {g} (\mathsf {f} \, \mathsf {b}) )(\mathsf {g} \, \mathsf {c})$ to the set. By superposing onto the subterm $x_2 \, \mathsf {a}$ of this clause with the equation $\mathsf {f} \, \mathsf {a} \approx \mathsf {c}$, we derive the clause $\mathsf {h}(x_1 (\mathsf {f} \,\mathsf {b}))(x_1 \, \mathsf {c}) \not \approx \mathsf {h}(\mathsf {g} (\mathsf {f} \, \mathsf {b}) )(\mathsf {g} \, \mathsf {c})$ from which $\perp$ can be derived by an EqRes inference.

Example 3

Consider the unsatisfiable clause set where $\mathsf {f} \, \mathsf {a} \succ \mathsf {c}$. This example is the combinatory equivalent of Bentkamp et al.’s Example 6.

$$\begin{aligned} \mathsf {f} \, \mathsf {a} \approx \mathsf {c} \quad \quad \quad \mathsf {h} \, (y \, (\varvec{\mathsf {B}}\, \mathsf {g}\, \mathsf {f}) \, \mathsf {a}) \, y \not \approx \mathsf {h} \, (\mathsf {g} \, \mathsf {c}) \, \varvec{\mathsf {I}}\end{aligned}$$

A Sup inference between the extended $\varvec{\mathsf {I}}$ axiom $\varvec{\mathsf {I}}\, x_1 \, x_2 \approx x_1 \, x_2$ and the subterm $y \, (\varvec{\mathsf {B}}\, \mathsf {g}\, \mathsf {f}) \, \mathsf {a}$ of the second clause adds the clause $\mathsf {h} \, (\varvec{\mathsf {B}}\, \mathsf {g}\, \mathsf {f} \, \mathsf {a}) \, \varvec{\mathsf {I}}\not \approx \mathsf {h} \, (\mathsf {g} \, \mathsf {c}) \, \varvec{\mathsf {I}}$ to the set. Superposing onto the subterm $\varvec{\mathsf {B}}\, \mathsf {g}\, \mathsf {f} \, \mathsf {a}$ of this clause with the $\varvec{\mathsf {B}}$ axiom results in the clause $\mathsf {h} \, ( \mathsf {g}\, (\mathsf {f} \, \mathsf {a})) \, \varvec{\mathsf {I}}\not \approx \mathsf {h} \, (\mathsf {g} \, \mathsf {c}) \, \varvec{\mathsf {I}}$. Superposition onto the subterm $\mathsf {f} \, \mathsf {a}$ with the first clause of the original set gives $\mathsf {h} \, ( \mathsf {g}\, \mathsf {c})) \, \varvec{\mathsf {I}}\not \approx \mathsf {h} \, (\mathsf {g} \, \mathsf {c}) \, \varvec{\mathsf {I}}$ from which $\perp$ can be derived via EqRes.

Note that in Examples 2 and 3, no use is made of SubVarSup even though the analogous FluidSup rule in required in Bentkamp et al.’s calculus. We have been unable to develop an example that requires the SubVarSup rule even though it is required for the completeness result in Sect. 6.

5 Redundancy Criterion

In Sect. 6, we prove that the calculus is refutationally complete. The proof follows that of Bachmair and Ganzinger’s original proof of the completeness of superposition [2], but is presented in the style of Bentkamp et al. [6] and Waldmann [31]. As is normal with such proofs, it utilises the concept of redundancy to reduce the number of clauses that must be considered in the induction step during the model construction process.

We define a weaker logic by an encoding $\varvec{\lfloor } \, \varvec{\rfloor }$ of ground terms into non-applicative first-order terms with $\varvec{\lceil } \, \varvec{\rceil }$ as its inverse. The encoding works by indexing each symbol with its type arguments and argument number. For example, $\varvec{\lfloor } \mathsf {f}\varvec{\rfloor } = \mathsf {f_0}$, $\varvec{\lfloor } \mathsf {f} {\langle \, \overline{\tau } \,\rangle } \mathsf {a}\varvec{\rfloor } = \mathsf {f}^{\, \overline{\tau } \,}_1(\mathsf {a_0})$. Terms with fully applied combinators as their head symbols are translated to constants such that syntactically identical terms are translated to the same constant. For example, $\varvec{\lfloor } \varvec{\mathsf {S}}\, t_1 \, t_2 \, t_3\varvec{\rfloor } = \mathsf {s_0}$. The weaker logic is known as the floor logic whilst the original logic is called the ceiling logic. The encoding can be extended to literals and clauses in the obvious manner as detailed in [5]. The function $\varvec{\lceil } \varvec{\rceil }$ is used to compare floor terms. More precisely, for floor logic terms t and $t'$, $t \succ t'$ if $\varvec{\lceil } t\varvec{\rceil } \succ \varvec{\lceil } t'\varvec{\rceil }$. It is straightforward to show that the order $\succ$ on floor terms is compatible with all contexts, well-founded, total on ground terms and has the subterm property.

The encoding serves a dual purpose. Firstly, as redundancy is defined with respect to the floor logic, it prevents the conclusion of all ArgCong from being redundant. Secondly, subterms in the floor logic correspond to first-order subterms in the ceiling logic. This is of critical importance in the completeness proof.

An inference is the ground instance of an inference I if it is equal to I after the application of some grounding substitution $\theta$ to the premise(s) and conclusion of I and the result is still an inference.

A ground ceiling clause C is redundant with respect to a set of ground ceiling clauses N if $\varvec{\lfloor } C\varvec{\rfloor }$ is entailed by clauses in $\varvec{\lfloor } N\varvec{\rfloor }$ smaller than itself and the floor of ground instances of extended combinator axioms in $\varvec{\lfloor } N\varvec{\rfloor }$. An arbitrary ceiling clause C is redundant to a set of ceiling clauses N if all its ground instances are redundant with respect to , the set of all ground instances of clauses in N. Red(N) is the set of all clauses redundant with respect to N.

For ground inferences other than ArgCong, an inference with right premise C and conclusion E is redundant with respect to a set of clauses N if $\varvec{\lfloor } E\varvec{\rfloor }$ is entailed by clauses in smaller than $\varvec{\lfloor } C\varvec{\rfloor }$. A non-ground inference is redundant if all its ground instances are redundant.

An ArgCong inference from a combinator axiom is redundant with respect to a set of clauses N if its conclusion is in N. For any other ArgCong inference, it is redundant with respect N if its premise is redundant with respect to N, or its conclusion is in N or redundant with respect to N. A set N is saturated up to redundancy if every inference with premises in N is redundant with respect to N.

6 Refutational Completeness

The proof of refutational completeness of clausal combinatory-superposition is based on the completeness proof the $\lambda$-free HOL calculi presented in [6]. We first summarise their proof and then indicate the major places where our proof differs. A detailed version of the proof can be found in our technical report [9].

Let N be a set of clauses saturated to redundancy by one of the $\lambda$-free HOL calculi and not containing $\perp$. Then, Bentkmap et al. show that N must have a model. This is done in stages, first building a model and then lifting this to a model of and N. Most of the heavy work is in showing $R_\infty$ to be a model of . In the standard first-order proof, superposition is ruled out at or beneath variables. Consider a clause C containing a variable x. Since the orderings that parameterise standard first-order superposition are compatible with contexts, we are guaranteed for terms t and $t'$ such that $t \succ t'$ and grounding substitution $\theta$ that $C\theta [x \rightarrow t] \succ C\theta [x \rightarrow t']$. Then, the induction hypotheses is used to show that $C\theta [x \rightarrow t']$ is true in the candidate interpretation rendering superposition into x unnecessary. A similar argument works for superposition below variables.

This argument does not work for the $\lambda$-free calculi since in their case the ordering is not compatible with arguments. Consider the clause $C = \mathsf {f} \, x \approx \mathsf {g} \, x \vee x \, u \approx v$. For terms t and $t'$ such that $t \succ t'$, it cannot be guaranteed that $C\theta [x \rightarrow t] \succ C\theta [x \rightarrow t']$ since $t' \, u \succ t \, u$ is possible. Therefore, some superposition has to take place at variables. Even in those cases where it can be ruled out, the proof is more complex than the standard first-order proof. Superposition underneath variables can be ruled out entirely.

Returning to our calculus, we face a number of additional difficulties. Since the ordering that we use is not compatible with arguments, but also not compatible with stronger concept of unstable subterms, we cannot rule out superposition beneath a variable. Consider, for example, the clause $C = \mathsf {f} \, x \approx \mathsf {g} \, x \vee y \, x \, u \approx v$ and the grounding substitution $\theta = \{y \rightarrow \varvec{\mathsf {S}}\, \mathsf {a}, x \rightarrow \varvec{\mathsf {K}}\, t\}$. Let $\theta '$ be the same as $\theta$, but with x mapped to $\varvec{\mathsf {K}}\, t'$. Even if $t \succ t'$, we do not necessarily have $C\theta \succ C\theta '$ since t occurs at an unstable position. Thus, some superposition below variables must be carried out.

This introduces a new difficulty, namely, showing that superposition below a variable is the ground instance of a SubVarSup rule. In some cases it may not be. Consider the clause $C = x \, u \approx v$ and the grounding substitution $\theta = \{x \rightarrow \mathsf {f} \, t \, \mathsf {a} \}$. A superposition inference from $C\theta$ with conclusion $C'$ that replaces t with $t'$ is not the ground instance of a SubVarSup from C. The only conclusion of a SubVarSup from C is $z \, t' \, u \approx v$. There is no instantiation of the z variable that can make the term $z \, t'$ equal to $\mathsf {f} \, t' \, \mathsf {a}$. However, mapping z to $\varvec{\mathsf {C}}\, \mathsf {f \, a}$ results in a term that is equal to $\mathsf {f} \, t' \, \mathsf {a}$ modulo the combinator axioms. Let $C'' = z \, t' \, u \approx v\{z \rightarrow \varvec{\mathsf {C}}\, \mathsf {f \, a}\}$. Since it is the set N that is saturated up to redundancy, we have that all ground instances of the SubVarSup inference are redundant with respect . For this to imply that $C'$ is redundant with respect to requires $C''$ be rewritable to $C'$ using equations true in $R_{\varvec{\lfloor } C\theta \varvec{\rfloor }}$ (the partial interpretation built from clauses smaller than $C\theta$). This requires that all ground instances of combinator and extended combinator axioms be true in $R_{\varvec{\lfloor } C\theta \varvec{\rfloor }}$ for all clauses C.

This leads to probably the most novel aspect of our proof. We build our candidate interpretations differently to the standard proof by first adding rules derived from combinator axioms. Let $R_{ECA}$ be the set of rewrite rules formed by turning the floor of all ground instances of combinator axioms into left right rewrite rules. Then for all clauses , $R_C$ is defined to be $R_{ECA}\cup (\bigcup _{D \prec C}E_D)$. In the detailed proof, we show that $R_C$ and $R_\infty$ are still terminating and confluent.

In lifting $R_\infty$ to be a model of , we face a further difficulty. This is related to showing that for ceiling terms t, $t'$, u and $u'$, if and , then . The difficulty arises because t, $t'$ or both may be of the form $\varvec{\mathcal {C_\mathsf {3}}}\, t_1 \, t_2$. In such a case rewrites that can be carried out from subterms of $\varvec{\lfloor } t\varvec{\rfloor }$ cannot be carried out from $\varvec{\lfloor } t \, u\varvec{\rfloor }$ because $t \, u$ has a fully applied combinator as its head and therefore is translated to a constant in the floor logic. The fact that the ground instances of all combinator axioms are true in $R_\infty$ comes to the rescue. With these difficulties circumvented, we can prove refutational completeness.

Theorem 1

For a set of clauses N saturated to redundancy by the above calculus, N has a model iff it does not contain $\perp$. Moreover, if N contains the extensionality axiom, the model is extensional.

7 Removing Combinator Axioms

Next, we show that it is possible to replace the combinator axioms with a dedicated inference rule. We name the inference Narrow. Unlike the other inference rules, it works at prefix positions. We define nearly first-order positions inductively. For any term t, either $t = \zeta \, \overline{t_n} \,$ where $\zeta$ is not a fully applied combinator or $t = \varvec{\mathcal {C_{\mathsf {any}}}}\, \overline{t_n} \,$. In the first case, the nearly first-order subterms of t are $\zeta \, \overline{t_i} \,$ for $0 \le i \le n$ and all the nearly first-order subterms of the $t_i$. In the second case, the nearly first-order subterms are $\varvec{\mathcal {C_{\mathsf {any}}}}\, \overline{t_i} \,$ for $0 \le i \le n$. The notation $s \langle \! [ u ] \! \rangle$ is to be read as u is a nearly first-order subterm of s. The Narrow inference:

with the following side conditions:

We show that any inference that can be carried out using an extended combinator axiom can be simulated with Narrow proving completeness. It is obvious that an EqRes or EqFact inference cannot have an extended combinator axiom as its premise. By the SubVarSup side conditions, an extended combinator axiom cannot be either of its premises. Thus we only need to show that Sup inferences with extended combinator axioms can be simulated. Note that an extended axiom can only be the left premise of a Sup inference. Consider the following inference:

Let $l = \varvec{\mathsf {S}}\, \, \overline{x_{n > 3}} \,$. By the variable condition, we have that $u = \zeta \, \overline{t_{m}} \,$ where $n \ge m \ge n-2$. If $u = y \, \overline{t_{n-2}} \,$, then $\sigma = \{y \rightarrow \varvec{\mathsf {S}}\, x_1 \, x_2, x_3 \rightarrow t_1, \ldots , x_n \rightarrow t_{n-2} \}$. In this case $r\sigma = (x_1 \, x_3 \, (x_2 \, x_3) \, x_4 \ldots x_n)\sigma = x_1 \, t_1 \, (x_2 \, t_1) \, t_2 \ldots t_{n-2}$ and the conclusion of the inference is $(C' \vee [\lnot ]s \langle x_1 \, t_1 \, (x_2 \, t_1) \, t_2 \ldots t_{n-2} \rangle \approx s')\{y \rightarrow \varvec{\mathsf {S}}\, x_1 \, x_2\}$. Now consider the following Narrow inference from C at the nearly first-order subterm $y \, t_1$:

As can be seen, the conclusion of the Sup inference is equivalent to that of the Narrow inference up to variable naming. The same can be shown to be the case where $u = y \, \, \overline{t_{n-1}} \,$ or $u = y \, \, \overline{t_{n}} \,$ or $u = \varvec{\mathsf {S}}\, \, \overline{t_{n}} \,$. Likewise, the same can be shown to hold when the $l \approx r$ is an extended $\varvec{\mathsf {B}}, \varvec{\mathsf {C}}, \varvec{\mathsf {K}}$ or $\varvec{\mathsf {I}}$ axiom.

8 Implementation and Evaluation

Clausal combinatory-superposition has been implemented in the Vampire theorem prover [11, 17]. The prover was first extended to support polymorphism. This turned out to be simpler than expected with types being turned into terms and type equality checking changing to a unifiability (or matching) check. Applicative terms are supported by the use of a polymorphic function $\mathsf {app}$ of type $\mathsf {\Pi }{\alpha , \beta }. \, (\alpha \rightarrow \beta ) \rightarrow \alpha \rightarrow \beta$.

As the Sup, EqRes and EqFact inferences are identical to their first-order counterparts, these required no updating. The Narrow, SubVarSup and ArgCong inferences had to be added to the implementation. Further, though the NegExt inference is not required for completeness, empirical results suggest that it is so useful, that it is permanently on in the implementation.

The ArgCong inference implemented in Vampire does not match the rule given in the calculus. The rule provided can have an infinite number of conclusions. In Vampire, we have implemented a version of ArgCong that appends a single fresh variable to each side of the selected literal rather than a tuple and therefore only has a single conclusion. This version matches what was originally in the calculus. Shortly before the submission of this paper, it was discovered that this leads to a subtle issue in the completeness proof and the inference was changed to its current version. We expect to be able to revert to the previous version and fix the proof. As matters stand, Vampire contains a potential source of incompleteness.

A greater challenge was posed by the implementation of the $>_{\mathsf {ski}}$ ordering in the prover. The ordering is based on the length of the longest weak-reduction from a term. In order to increase the efficiency of calculating this quantity, we implemented caching and lazy evaluation. For example, when inserting a term of the form $\mathsf {f} \, t_1 \, t_2$ into the term-sharing data structure, a check is made to see if the maximum reduction lengths of $t_1$ and $t_2$ have already been calculated. If they have, then the maximum reduction length of the term being inserted is set to the sum of the maximum reduction lengths of $t_1$ and $t_2$. If not, it is left unassigned and only calculated at the time it is required.

During the experimentation phase, it was realised that many redundant clauses were being produced due to narrowing. For example, consider the clause $x \, \mathsf {a \, b} \approx \mathsf {d} \vee \mathsf {f} \, x \approx \mathsf {a}$. Narrowing the first literal with $\varvec{\mathsf {C}}$-axiom results in $x' \, \mathsf {b \, a} \approx \mathsf {d} \vee \mathsf {f} \, (\varvec{\mathsf {C}}\, x') \approx \mathsf {a}$. A second narrow with the same axiom results in $x'' \, \mathsf {a \, b} \approx \mathsf {d} \vee \mathsf {f} \, (\varvec{\mathsf {C}}\, (\varvec{\mathsf {C}}\, x'')) \approx \mathsf {a}$ which is extensionally equivalent to first clause and therefore redundant. However, it will not be removed by subsumption since it is only equivalent extensionally. To deal with this problem, we implemented some rewrite rules that replace combinator terms with smaller extensionally equivalent terms.² For example, any term of the form $\varvec{\mathsf {C}}\, (\varvec{\mathsf {C}}\, t)$ is rewritten to t. There is no guarantee that these rewrites remove all such redundant clauses, but in practice, they appear to help.

To implement unification with abstraction, we reused the method introduced in our previous work relating to the use of substitution trees as filters [8]. In our current context, this involves replacing all subterms of functional or variable sort with special symbols that unify with any term prior to inserting a term into the substitution tree index.

To evaluate our implementation, we ran a number of versions of our prover across two problem sets and compared their performance against that of some of the leading higher-order provers. The first problem set we tested on was the set of all 592 monomorphic, higher-order problems from the TPTP problem library [29] that do not contain first-class boolean subterms. We restricted our attention to monomorphic problems since some of the provers we used in our evaluation do not support polymorphism. The second benchmark set was produced by the Isabelle theorem prover’s Sledgehammer system. It contains 1253 benchmarks kindly made available to us by the Matryoshka team and is called SH-$\lambda$ following their naming convention. All tests were run with a CPU time limit of 300. Experiments were performed on StarExec [28] nodes equipped with four 2.40 GHz Intel Xeon CPUs. Our experimental results are publicly available³.

To compare out current implementation against, we chose the Leo-III, 1.4, Satallax 3.4, Zipperposition 1.5 and Vampire-THF 4.4 provers. These provers achieved the top four spots in the 2019 CASC system competition. Vampire THF 4.4 was developed by the authors, but uses different principles being based on combinatory unification. We compare the performance of these provers against four variants of our current implementation. First, Vampire-csup-ax which implements clausal combinatory-superposition as described above and uses the extensionality axiom. Second, Vampire-csup-abs which deals with extensionality via unification with abstraction. Third, Vampire-csup-ninj which incorporates an inference to synthesise left-inverses for injective functions in a manner similar to Leo-III [26, Section 4.2.5] and finally Vampire-csup-prag which introduces various heuristics to try and control the search space, though at the expense of completeness. For example, it implements a heuristic that restricts the number of narrow steps. It also switches off the SubVarSup rule which is never used in a proof produced by the other variants of Vampire-csup. All four versions are run on top of a first-order portfolio of strategies. These strategies control options such as the saturation algorithm used, which simplification inferences are switched on and so forth. The results of the experiments can be found summarised in Table 1. In brackets, the number of uniques between Vampire-csup versions is provided.

Table 1. Problems proved theorem or unsat

The closeness of the results on the TPTP benchmarks is striking. Out of the 592 benchmarks, 95 are known not to be theorems, leaving 497 problems that could possibly be proved. All the provers are remarkably close to this number and each other. Leo-III which is slightly ahead of the other provers, only manages this through function synthesis which is not implemented in any of the other provers.

It is disappointing that Vampire-csup performs worse than its predecessor Vampire-THF 4.4 on Sledgehammer problems. We hypothesise that this is related to the explosion in clauses created as a result of narrowing. Vampire-csup-prag is supposed to control such an explosion, but actually performs worst of all. This is likely due to the fact that it runs a number of lengthy strategies aimed particularly at solving higher-order problems requiring complex unifiers. Interestingly, the pragmatic version solved a difficulty rating 1.00 TPTP problem, namely, NUM829$^\wedge$5.p.

9 Conclusion and Related Work

The combinatory superposition calculus presented here is amongst a small group of complete proof calculi for higher-order logic. This group includes the RUE resolution calculus of Benzmüller which has been implemented in the Leo-II theorem prover [7]. The Satallax theorem prover implements a complete higher-order tableaux calculus [13]. More recently, Bentkamp et al. have developed a complete superposition calculus for clausal HOL [4]. As superposition is one of the most successful calculi in first-order theorem proving [22], their work answered a significant open question, namely, whether superposition could be extended to higher-order logic.

Our work is closely related to theirs, and in some senses, the SubVarSup rule of clausal combinatory-superposition mirrors the FluidSup rule of clausal $\lambda$-superposition. However, there are some crucial differences. Arguably, the side conditions on SubVarSup are tighter than those on FluidSup and some problems such as the one in Example 3 can be solved by clausal combinatory-superposition without the use of SubVarSup whilst requiring the use of FluidSup in clausal $\lambda$-superposition. Clausal $\lambda$-superposition is based on higher-order unification and $\lambda$-terms. Our calculus is based on (applicative) first-order terms and first-order unification and implementations can therefore reuse the well-studied data structures and algorithms of first-order theorem proving. On the downside, narrowing terms with combinator axioms is still explosive and results in redundant clauses. It is also never likely to be competitive with higher-order unification in finding complex unifiers. This is particularly the case with recent improvements in higher-order unification being reported [30].

Many other calculi for higher-order theorem proving have been developed, most of them incomplete. Amongst the early calculi to be devised are Andrew’s mating calculus [1] and Miller’s expansion tree method [20] both linked to tableaux proving. More recent additions include an ordered (incomplete) paramodulation calculus as implemented in the Leo-III prover [27] and a higher-order sequent calculus implemented in the AgsyHOL prover [18]. In previous work, the current authors have extended first-order superposition to use a combinatory unification algorithm [8]. Finally there is ongoing work to extend SMT solving to higher-order logic [3].

There have also been many attempts to prove theorems in HOL by translating to FOL. One of the pioneers in suggesting this approach was Kerber [16]. Since his early work, it has become commonplace to combine a dedicated higher-order theorem prover with a first-order prover used to discharge first-order proof obligations. This is the approach taken by many interactive provers and their associated hammers such as Sledgehammer [23] and CoqHammer [14]. It is also the approach adopted by leading automated higher-order provers Leo-III and Satallax.

In this paper we have presented a complete calculus for a polymorphic, boolean-free, intensional, combinatory formulation of higher-order logic. For the calculus to be extensional, an extensionality axiom can be added maintaining completeness, but losing gracefulness. Alternatively, unification can be turned into unification with abstraction maintaining gracefulness, but losing a completeness guarantee. Experimental results show an implementation of clausal combinatory-superposition to be competitive with leading higher-order provers.

It remains to tune the implementation and calculus. We plan to further investigate the use of heuristics in taming the explosion of clauses that result from narrowing. the heuristics may lead to incompleteness. It would also be of interest to investigate the use of heuristics or even machine learning to guide the prover in selecting specific combinator axioms to narrow a particular clause with. One of the advantages of our calculus is that it does not consider terms modulo $\beta$- or weak-reduction. Therefore, theoretically, a larger class of terms should be comparable by the non-ground order than is possible with a calculus that deals with $\beta$- or weak-equivalence classes. It remains to implement a stricter version of the $>_{\mathsf {ski}}$ ordering and evaluate its usefulness.

As a next step, we plan to add support for booleans and choice to the calculus. An appealing option for booleans is to extend the unification with abstraction approach currently used for functional extensionality. No attempt would be made to solve unification pairs consisting of boolean terms. Rather, these would be added as negated bi-implications to the result which would then be re-clausified.

Finally, we feel that our calculus complements existing higher-order calculi and presents a particularly attractive option for extending existing first-order superposition provers to dealing with HOL.