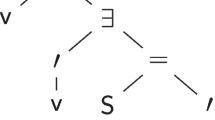Abstract
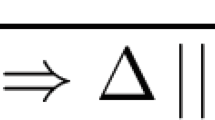
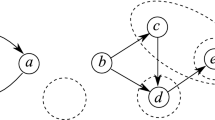
A structure which generalizes formulas by including substitution terms is used to represent proofs in classical logic. These structures, called expansion trees, can be most easily understood as describing a tautologous substitution instance of a theorem. They also provide a computationally useful representation of classical proofs as first-class values. As values they are compact and can easily be manipulated and transformed. For example, we present an explicit transformations between expansion tree proofs and cut-free sequential proofs. A theorem prover which represents proofs using expansion trees can use this transformation to present its proofs in more human-readable form. Also a very simple computation on expansion trees can transform them into Craig-style linear reasoning and into interpolants when they exist. We have chosen a sublogic of the Simple Theory of Types for our classical logic because it elegantly represents substitutions at all finite types through the use of the typed λ-calculus. Since all the proof-theoretic results we shall study depend heavily on properties of substitutions, using this logic has allowed us to strengthen and extend prior results: we are able to prove a strengthen form of the firstorder interpolation theorem as well as provide a correct description of Skolem functions and the Herbrand Universe. The latter are not straightforward generalization of their first-order definitions.
Similar content being viewed by others
References
P. B. Andrews, Resolution in type theory, Journal of Symbolic Logic 36 (1971), pp. 414–432.
P. B. Andrews, D. A. Miller, E. Longini Cohen and F. Pfenning, Automating higher-order logic, in Automated Theorem Proving: After 25 Years, AMS Contemporary Mathematics Series 29 (1984).
A. Church, A Formulation of the simple theory of types, Journal of Symbolic Logic 5 (1940), pp. 56–68.
A. Church, The Calculi of Lambda-Conversion, Princeton University Press, 1941.
W. Craig, Linear reasoning. A new form of the Herbrand-Gentzen theorem, Journal of Symbolic Logic 22 (1957), pp. 250–268.
A. P. Felty, Using Extended Tacticals to Do Proof Transformations, MSE Thesis, University of Pennsylvania, December 1986.
G. Gentzen, Investigations into logical deductions, in The Collected Papers of Gerhard Gentzen edited by M. E. Szabo, North-Holland Publishing Co., Amsterdam, 1969, pp. 68–131.
J. Herbrand, Recherches sur la théorie de la démonstration, Travaux de la Société des Sciences et des Lettres de Varsovie, Classe III Sciences Mathematiques et Physiques 33 (1930). Translated in [9].
J. Herbrand, Logical Writings, Harvard University Press, Cambridge, Mass, 1972.
G. P. Huet, A mechanization of type theory, Proceedings of the Third International Joint Conference on Artificial Intelligence 1973, pp. 139–146.
D. A. Miller, Expansion tree proofs and their conversion to natural deduction proofs, 7th International Conference on Automated Deduction edited by R. E. Shostak, Springer-Verlag, LNCS 170, pp. 375–393.
T. Pietrzykowski, A complete mechanization of second-order type theory, Journal of the Association for Computing Machinery 20 (1973), pp. 333–364.
D. Prawitz, Natural Deduction, Almqvist-Wiksell, 1965.
D. Prawitz, Hauptsatz for higher order logic, Journal of Symbolic Logic 33 (1968), pp. 452–457.
J. A. Robinson, Mechanizing higher-order logic, Machine Intelligence 4, Edinburgh University Press, 1969, pp. 151–170.
R. M. Smullyan, First-Order Logic, Springer-Verlag, New York, 1968.
Moto-o-Takahashi, A proof of cut-elimination theorem in simple type-theory Journal of the Mathematical Society of Japan 19 (1967), pp. 399–410.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Miller, D.A. A compact representation of proofs. Stud Logica 46, 347–370 (1987). https://doi.org/10.1007/BF00370646
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF00370646