Abstract
Sharing of notations and theories across an inheritance hierarchy of mathematical structures, e.g., groups and rings, is important for productivity when formalizing mathematics in proof assistants. The packed classes methodology is a generic design pattern to define and combine mathematical structures in a dependent type theory with records. When combined with mechanisms for implicit coercions and unification hints, packed classes enable automated structure inference and subtyping in hierarchies, e.g., that a ring can be used in place of a group. However, large hierarchies based on packed classes are challenging to implement and maintain. We identify two hierarchy invariants that ensure modularity of reasoning and predictability of inference with packed classes, and propose algorithms to check these invariants. We implement our algorithms as tools for the Coq proof assistant, and show that they significantly improve the development process of Mathematical Components, a library for formalized mathematics.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Mathematical structures are a key ingredient of modern formalized mathematics in proof assistants, e.g., [1, 18, 25, 41] [10, Chap. 2 and Chap. 4] [20, Sect. 3] [30, Chap. 5] [46, Sect. 4]. Since mathematical structures have an inheritance/subtyping hierarchy such that “a ring is a group and a group is a monoid”, it is usual practice in mathematics to reuse notations and theories of superclasses implicitly to reason about a subclass. Similarly, the sharing of notations and theories across the hierarchy is important for productivity when formalizing mathematics.
The packed classes methodology [16, 17] is a generic design pattern to define and combine mathematical structures in a dependent type theory with records. Hierarchies using packed classes support multiple inheritance, and maximal sharing notations and theories. When combined with mechanisms for implicit coercions [32, 33] and for extending unification procedure, such as the canonical structures [26, 33] of the Coq proof assistant [42], and the unification hints [4] of the Lean theorem prover [6, 27] and the Matita interactive theorem prover [5], packed classes enable subtyping and automated inference of structures in hierarchies. Compared to approaches based on type classes [22, 40], packed classes are more robust, and their inference approach is efficient and predictable [1]. The success of the packed classes methodology in formalized mathematics can be seen in the Mathematical Components library [45] (hereafter MathComp), the Coquelicot library [8], and especially the formal proof of the Odd Order Theorem [20]. It has also been successfully applied for program verification tasks, e.g., a hierarchy of monadic effects [2] and a hierarchy of partial commutative monoids [28] for Fine-grained Concurrent Separation Logic [39].
In spite of its success, the packed classes methodology is hard to master for library designers and requires a substantial amount of work to maintain as libraries evolve. For instance, the strict application of packed classes requires defining quadratically many implicit coercions and unification hints in the number of structures. To give some figures, the MathComp library 1.10.0 uses this methodology ubiquitously to define the 51 mathematical structures depicted in Fig. 1, and declares 554 implicit coercions and 746 unification hints to implement their inheritance. Moreover, defining new intermediate structures between existing ones requires fixing their subclasses and their inheritance accordingly; thus, it can be a challenging task.
In this paper, we indentify two hierarchy invariants concerning implicit coercions and unification hints in packed classes, and propose algorithms to check these invariants. We implement our algorithms as tools for the Coq system, evaluate our tools on a large-scale development, the MathComp library 1.7.0, and then successfully detect and fix several inheritance bugs with the help of our tools. The invariant concerning implicit coercions ensures the modularity of reasoning with packed classes and is also useful in other approaches, such as type classes and telescopes [26, Sect. 2.3], in a dependent type theory. This invariant was proposed before as a coherence of inheritance graphs [7]. The invariant concerning unification hints, that we call well-formedness, ensures the predictability of structure inference. Our tool not only checks well-formedness, but also generates an exhaustive set of assertions for structure inference, and these assertions can be tested inside Coq. We state the predictability of inference as a metatheorem on a simplified model of hierarchies, that we formally prove in Coq.
The paper is organized as follows: Sect. 2 reviews the packed classes methodology using a running example. Section 3 studies the implicit coercion mechanism of Coq, and then presents the new coherence checking algorithm and its implementation. Section 4 reviews the use of canonical structures for structure inference in packed classes, and introduces the notion of well-formedness. Section 5 defines a simplified model of hierarchies and structure inference, and shows the metatheorem that states the predictability of structure inference. Section 6 presents the well-formedness checking algorithm and its implementation. Section 7 evaluates our checking tools on the MathComp library 1.7.0. Section 8 discusses related work and concludes the paper. Our running example for Sect. 2, Sect. 4, and Sect. 6, the formalization for Sect. 5, and the evaluation script for Sect. 7 are available at [37].
2 Packed Classes
This section reviews the packed classes methodology [16, 17] through an example, but elides canonical structures. Our example is a minimal hierarchy with multiple inheritance, consisting of the following four algebraic structures (Fig. 2):
-
Additive monoids \((A, +, 0)\): Monoids have an associative binary operation \(+\) on the set A and an identity element \(0 \in A\).
-
Semirings \((A, +, 0, \times , 1)\): Semirings have the monoid axioms, commutativity of addition, multiplication, and an element \(1 \in A\). Multiplication \(\times \) is an associative binary operation on A that is left and right distributive over addition. 0 and 1 are absorbing and identity elements with respect to multiplication, respectively.
-
Additive groups \((A, +, 0, -)\): Groups have the monoid axioms and a unary operation − on A. \(- x\) is the additive inverse of x for any \(x \in A\).
-
Rings \((A, +, 0, -, \times , 1)\): Rings have all the semiring and group axioms, but no additional axioms.
Hierarchy diagram for monoids, semirings, groups, and rings, where an arrow from \(\texttt {X.type}\) to \(\texttt {Y.type}\) means that
 directly inherits from
directly inherits from
 . The monoid structure is the superclass of all other structures. Semirings and groups directly inherit from monoids. Rings directly inherit from semirings and groups, and indirectly inherit from monoids.
. The monoid structure is the superclass of all other structures. Semirings and groups directly inherit from monoids. Rings directly inherit from semirings and groups, and indirectly inherit from monoids.
We start by defining the base class, namely, the
 structure.
structure.

The above definitions are enclosed by the
 module, which forces users to write qualified names such as
module, which forces users to write qualified names such as
 . Thus, we can reuse the same name of record types (
. Thus, we can reuse the same name of record types (
 ,
,
 , and
, and
 ), their constructors (
), their constructors (
 ,
,
 , and
, and
 ), and constants (e.g.,
), and constants (e.g.,
 and
and
 ) for other structures to indicate their roles. Structures are written as records that have three different roles: mixins, classes, and structures. The mixin record (line 3) gathers operators and axioms newly introduced by the
) for other structures to indicate their roles. Structures are written as records that have three different roles: mixins, classes, and structures. The mixin record (line 3) gathers operators and axioms newly introduced by the
 structure. Since monoids do not inherit any other structure in Fig. 2, those are all the monoid operators, namely 0 and \(+\), and their axioms. The class record (line 11) assembles all the mixins of the superclasses of the
structure. Since monoids do not inherit any other structure in Fig. 2, those are all the monoid operators, namely 0 and \(+\), and their axioms. The class record (line 11) assembles all the mixins of the superclasses of the
 structure (including itself), which is the singleton record consisting of the monoid mixin. The structure record (line 13) is the actual interface of the structure that bundles a carrier of type
structure (including itself), which is the singleton record consisting of the monoid mixin. The structure record (line 13) is the actual interface of the structure that bundles a carrier of type
 and its class instance.
and its class instance.
 and
and
 are synonyms in Coq, but we reserve the latter for actual interfaces of structures. In a hierarchy of algebraic structures, a carrier set
are synonyms in Coq, but we reserve the latter for actual interfaces of structures. In a hierarchy of algebraic structures, a carrier set
 has type
has type
 ; hence, for each structure, the first field of the
; hence, for each structure, the first field of the
 record should have type
record should have type
 , and the
, and the
 record should be parameterized by that carrier. In general, it can be other types, e.g.,
record should be parameterized by that carrier. In general, it can be other types, e.g.,
 in the hierarchy of functors and monads [2], but should be fixed in each hierarchy of structures.
in the hierarchy of functors and monads [2], but should be fixed in each hierarchy of structures.
Mixin and monoid records are internal definitions of mathematical structures; in contrast, the structure record is a part of the interface of the monoid structure when reasoning about monoids. For this reason, we lift the projections for
 to definitions and lemmas for
to definitions and lemmas for
 as follows.
as follows.

The curly brackets enclosing
 mark it as an implicit argument; in contrast,
mark it as an implicit argument; in contrast,
 is the explicit application symbol that deactivates the hiding of implicit arguments.
is the explicit application symbol that deactivates the hiding of implicit arguments.
Since a monoid instance
 can be seen as a type equipped with monoid axioms, it is natural to declare
can be seen as a type equipped with monoid axioms, it is natural to declare
 as an implicit coercion. The types of
as an implicit coercion. The types of
 can be written and shown as
can be written and shown as
 rather than
rather than
 thanks to this implicit coercion.
thanks to this implicit coercion.

Next, we define the
 structure. Since semirings inherit from monoids and the semiring axioms interact with the monoid operators, e.g., distributivity of multiplication over addition, the semiring mixin should take
structure. Since semirings inherit from monoids and the semiring axioms interact with the monoid operators, e.g., distributivity of multiplication over addition, the semiring mixin should take
 rather than
rather than
 as its argument.
as its argument.

The
 class packs the
class packs the
 mixin together with the
mixin together with the
 class to assemble the mixin records of monoids and semirings. We may also assemble all the required mixins as record fields directly rather than nesting class records, yielding what is called the flat variant of packed classes [14, Sect. 4]. Since the semiring mixin requires
class to assemble the mixin records of monoids and semirings. We may also assemble all the required mixins as record fields directly rather than nesting class records, yielding what is called the flat variant of packed classes [14, Sect. 4]. Since the semiring mixin requires
 as its type argument, we have to bundle the monoid class with the carrier to provide that
as its type argument, we have to bundle the monoid class with the carrier to provide that
 instance, as follows.
instance, as follows.

The inheritance from monoids to semirings can then be expressed as a canonical way to construct a monoid from a semiring as below.

Following the above method, we declare
 as an implicit coercion, and then lift
as an implicit coercion, and then lift
 ,
,
 , and the semiring axioms from projections for the mixin to definitions for
, and the semiring axioms from projections for the mixin to definitions for
 .
.

In the statement of the
 axiom (line 6 just above), we need to explicitly write
axiom (line 6 just above), we need to explicitly write
 to get the canonical
to get the canonical
 instance for
instance for
 . We omit this subtyping function
. We omit this subtyping function
 by declaring it as an implicit coercion. In general, for a structure
by declaring it as an implicit coercion. In general, for a structure
 inheriting from other structures, we define implicit coercions from
inheriting from other structures, we define implicit coercions from
 to all its superclasses.
to all its superclasses.

The
 structure is monoids extended with an additive inverse. Following the above method, it can be defined as follows.
structure is monoids extended with an additive inverse. Following the above method, it can be defined as follows.

The
 structure can be seen both as groups extended by the semiring axioms and as semirings extended by the group axioms. Here, we define it in the first way, but one may also define it in the second way. Since rings have no other axioms than the group and semiring axioms, no additional
structure can be seen both as groups extended by the semiring axioms and as semirings extended by the group axioms. Here, we define it in the first way, but one may also define it in the second way. Since rings have no other axioms than the group and semiring axioms, no additional
 record is needed.Footnote 1
record is needed.Footnote 1

The ring structure inherits from monoids, groups, and semirings. Here, we define implicit coercions from the ring structure to those superclasses.

3 Coherence of Implicit Coercions
This section describes the implicit coercion mechanism of Coq and the coherence property [7] of inheritance graphs that ensures modularity of reasoning with packed classes, and presents the coherence checking mechanism we implemented in Coq. More details on implicit coercions can be found in the Coq reference manual [44], and its typing algorithm is described in [32]. First, we define classes and implicit coercions.
Definition 3.1
(Classes [32, Sect. 3.1] [44]). A class with n parameters is a defined name C with a type \(\forall (x_1 : T_1) \dots (x_n : T_n), sort \) where \( sort \) is
 ,
,
 ,
,
 , or
, or
 . Thus, a class with parameters is considered a single class and not a family of classes. An object of class C is any term of type \(C \, t_1 \dots t_n\).
. Thus, a class with parameters is considered a single class and not a family of classes. An object of class C is any term of type \(C \, t_1 \dots t_n\).
Definition 3.2
(Implicit coercions). A name f can be declared as an implicit coercion from a source class C to a target class D with k parameters if the type of f has the form \(\forall x_1 \dots x_k \, (y : C \, t_1 \dots t_n), D \, u_1 \dots u_m\). We then write \(f : C \rightarrowtail D\).Footnote 2
An implicit coercion \(f : C \rightarrowtail D\) can be seen as a subtyping \(C \le D\) and applied to fill type mismatches to a term of class C placed in a context that expects to have a term of class D. Implicit coercions form an inheritance graph with classes as nodes and coercions as edges, whose path \([f_1; \dots ; f_n]\) where \(f_i : C_i \rightarrowtail C_{i + 1}\) can also be seen as a subtyping \(C_1 \le C_{n + 1}\); thus, we write \([f_1; \dots ; f_n] : C_1 \rightarrowtail C_{n + 1}\) to indicate \([f_1; \dots ; f_n]\) is an inheritance path from \(C_1\) to \(C_{n + 1}\). The Coq system pre-computes those inheritance paths for any pair of source and target classes, and updates to keep them closed under transitivity when a new implicit coercion is declared [32, Sect. 3.3] [44, Sect. 8.2.5 “Inheritance Graph”]. The coherence of inheritance graphs is defined as follows.
Definition 3.3
(Definitional equality [43] [15, Sect. 3.1]). Two terms \(t_1\) and \(t_2\) are said to be definitionally equal, or convertible, if they are equivalent under \(\beta \delta \iota \zeta \)-reduction and \(\eta \)-expansion. This equality is denoted by the infix symbol \(\equiv \).
Definition 3.4
(Coherence [7, Sect. 3.2] [32, Sect. 7]). An inheritance graph is coherent if and only if the following two conditions hold.
-
1.
For any circular inheritance path \(p : C \rightarrowtail C\), \(p \, x \equiv x\), where x is a fresh variable of class C.
-
2.
For any two inheritance paths \(p, q : C \rightarrowtail D\), \(p \, x \equiv q \, x\), where x is a fresh variable of class C.
Before our work, if multiple inheritance paths existed between the same source and target class, only the oldest one was kept as a valid one in the inheritance graph in Coq, and all the others were reported as ambiguous paths and ignored. We improved this mechanism to report only paths that break the coherence conditions and also to minimize the number of reported ambiguous paths [34, 35]. The second condition ensures the modularity of reasoning with packed classes. For example, proving
 requires using both
requires using both
 and
and
 implicitly. If those
implicitly. If those
 instances are not definitionally equal, it will prevent us from proving the lemma by reporting type mismatch between
instances are not definitionally equal, it will prevent us from proving the lemma by reporting type mismatch between
 and
and
 .
.
Convertibility checking for inheritance paths consisting of implicit coercions as in Definition 3.2 requires constructing a composition of functions for a given inheritance path. One can reduce any unification problem to this well-typed term construction problem, that in the higher-order case is undecidable [19]. However, the inheritance paths that make the convertibility checking undecidable can never be applied as implicit coercions in type inference, because they do not respect the uniform inheritance condition.
Definition 3.5
(Uniform inheritance condition [44] [32, Sect. 3.2]). An implicit coercion f between classes \(C \rightarrowtail D\) with n and m parameters, respectively, is uniform if and only if the type of f has the form
Remark 3.1
Names that can be declared as implicit coercions are defined as constants that respect the uniform inheritance condition in [32, Sect. 3.2]. However, the actual implementation in the modern Coq system accepts almost any function as in Definition 3.2 as a coercion.
Saïbi claimed that the uniform inheritance condition “ensures that any coercion can be applied to any object of its source class” [32, Sect. 3.2], but the actual condition ensures additional properties. The number and ordering of parameters of a uniform implicit coercion are the same as those of its source class; thus, convertibility checking of uniform implicit coercions \(f, g : C \rightarrowtail D\) does not require any special treatment such as permuting parameters of f and g. Moreover, function composition preserves this uniformity, that is, the following lemma holds.
Lemma 3.1
For any uniform implicit coercions \(f : C \rightarrowtail D\) and \(g : D \rightarrowtail E\), the function composition of the inheritance path \([f; g] : C \rightarrowtail E\) is uniform.
Proof
Let us assume that C, D, and E are classes with n, m, and k parameters respectively, and f and g have the following types:
Then, the function composition of f and g can be defined and typed as follows:

The terms \(u_1, \dots , u_m\) contain the free variables \(x_1, \dots , x_{n + 1}\) and we omitted substitutions for them by using the same names for the binders in the above definition. Nevertheless, \((g \circ f) : C \rightarrowtail E\) respects the uniform inheritance condition. \(\square \)
In the above definition of the function composition \(g \circ f\) of implicit coercions, the types of \(x_1, \dots , x_n, x_{n + 1}\) and the parameters of g can be automatically inferred in Coq; thus, it can be abbreviated as follows:

For implicit coercions \(f_1 : C_1 \rightarrowtail C_2, f_2 : C_2 \rightarrowtail C_3, \dots , f_n : C_n \rightarrowtail C_{n + 1}\) that have \(m_1, m_2, \dots , m_n\) parameters respectively, the function composition of the inheritance path \([f_1; f_2; \dots ; f_n]\) can be written as follows by repeatedly applying Lemma 3.1 and the above abbreviation.

If \(f_1, \dots , f_n\) are all uniform, the numbers of their parameters \(m_1, \dots , m_n\) are equal to the numbers of parameters of \(C_1, \dots , C_n\). Consequently, the type inference algorithm always produces the typed closed term of most general function composition of \(f_1, \dots , f_n\) from the above term. If not all of \(f_1, \dots , f_n\) are uniform, type inference may fail or produce an open term, but if this produces a typed closed term, it is the most general function composition of \(f_1, \dots , f_n\).
Our coherence checking mechanism constructs the function composition of \(p : C \rightarrowtail C\) and compares it with the identity function of class C to check the first condition, and also constructs the function compositions of \(p, q : C \rightarrowtail D\) and performs the conversion test for them to check the second condition.
4 Automated Structure Inference
This section reviews how the automated structure inference mechanism [26] works on our example and in general. The first example is \(0 + 1\), whose desugared form is
 , where holes
, where holes
 stand for implicit pieces of information to be inferred. The left- and right-hand sides of the top application can be type-checked without any use of canonical structures, as follows:
stand for implicit pieces of information to be inferred. The left- and right-hand sides of the top application can be type-checked without any use of canonical structures, as follows:

where \(?_{\texttt {M}}\) and \(?_{\texttt {SR}}\) represent unification variables. Type-checking the application requires solving a unification problem
 , which is not trivial and which Coq does not know how to solve without hints. By declaring
, which is not trivial and which Coq does not know how to solve without hints. By declaring
 as a canonical instance, Coq can become aware of that instantiating \(?_{\texttt {M}}\) with
as a canonical instance, Coq can become aware of that instantiating \(?_{\texttt {M}}\) with
 is the canonical solution to this unification problem.
is the canonical solution to this unification problem.

The
 command takes a definition with a body of the form \(\lambda x_1 \, \dots \, x_n,\) \(\{|p_1 := (f_1 \dots ); \dots ; p_m := (f_m \dots )|\}\), and then synthesizes unification hints between the projections \(p_1, \dots , p_m\) and the head symbols \(f_1, \dots , f_m\), respectively, except for unnamed projections. Since
command takes a definition with a body of the form \(\lambda x_1 \, \dots \, x_n,\) \(\{|p_1 := (f_1 \dots ); \dots ; p_m := (f_m \dots )|\}\), and then synthesizes unification hints between the projections \(p_1, \dots , p_m\) and the head symbols \(f_1, \dots , f_m\), respectively, except for unnamed projections. Since
 has the following body, the above
has the following body, the above
 declaration synthesizes the unification hint between
declaration synthesizes the unification hint between
 and
and
 that we need:
that we need:

In general, for any structures
 and
and
 such that
such that
 inherits from
inherits from
 with an implicit coercion
with an implicit coercion
 ,
,
 should be declared as a canonical instance to allow Coq to solve unification problems of the form
should be declared as a canonical instance to allow Coq to solve unification problems of the form
 by instantiating \(?_{\texttt {A}}\) with
by instantiating \(?_{\texttt {A}}\) with
 .
.
The second example is \(- 1\), whose desugared form is
 . The left- and right-hand sides of the top application can be type-checked as follows:
. The left- and right-hand sides of the top application can be type-checked as follows:

In order to type check the application, Coq has to unify
 with
with
 , which, again, is not trivial. Moreover, groups and semirings do not inherit from each other; therefore, this case is not an instance of the above criteria to define canonical instances. Nevertheless, this unification problem means that
, which, again, is not trivial. Moreover, groups and semirings do not inherit from each other; therefore, this case is not an instance of the above criteria to define canonical instances. Nevertheless, this unification problem means that
 and
and
 are the same, and they are equipped with both group and semiring axioms, that is, the ring structure. Thus, its canonical solution should be introducing a fresh unification variable
are the same, and they are equipped with both group and semiring axioms, that is, the ring structure. Thus, its canonical solution should be introducing a fresh unification variable
 and instantiating \(?_{\texttt {G}}\) and \(?_{\texttt {SR}}\) with
and instantiating \(?_{\texttt {G}}\) and \(?_{\texttt {SR}}\) with
 and
and
 , respectively. Right after defining
, respectively. Right after defining
 , this unification hint can be defined as follows.
, this unification hint can be defined as follows.

This definition is definitionally equal to
 , but has a different head symbol,
, but has a different head symbol,
 instead of
instead of
 , in its first field
, in its first field
 . Thus, the unification hint we need between
. Thus, the unification hint we need between
 and
and
 can be synthesized by the following declarations.
can be synthesized by the following declarations.

This unification hint can also be defined conversely as follows. Whichever of those is acceptable, but at least one of them should be declared.

For any structures A and B that have common (non-strict) subclasses \(\mathcal {C}\), we say that \(C \in \mathcal {C}\) is a join of A and B if C does not inherit from any other structures in \(\mathcal {C}\). For example, if we add the structure of commutative rings to the hierarchy of Sect. 2, the commutative ring structure is a common subclass of the group and semiring structures, but is not a join of them because the commutative ring structure inherits from the ring structure which is another common subclass of them. In general, the join of any two structures must be unique, and we should declare a canonical instance to infer the join C as the canonical solution of unification problems of the form
 . For any structures A and B such that B inherits from A, B is the join of A and B; thus, the first criteria to define canonical instances is just an instance of the second criteria.
. For any structures A and B such that B inherits from A, B is the join of A and B; thus, the first criteria to define canonical instances is just an instance of the second criteria.
A hierachy that disambiguates the join of
 and
and
 in Fig. 3 by redefining
in Fig. 3 by redefining
 and
and
 to inherit from a new structure
to inherit from a new structure
 that inherits from
that inherits from
 and
and
 .
.
Figure 3 shows a minimal hierarchy that has ambiguous joins. If we declare that
 (resp.
(resp.
 ) is the canonical join of
) is the canonical join of
 and
and
 in this hierarchy, it will also be accidentally inferred for a user who wants to reason about
in this hierarchy, it will also be accidentally inferred for a user who wants to reason about
 (resp.
(resp.
 ). Since
). Since
 and
and
 do not inherit from each other, inferred
do not inherit from each other, inferred
 (resp.
(resp.
 ) can never be instantiated with
) can never be instantiated with
 (resp.
(resp.
 ); therefore, we have to disambiguate it as in Fig. 4, so that the join of
); therefore, we have to disambiguate it as in Fig. 4, so that the join of
 and
and
 can be specialized to both
can be specialized to both
 and
and
 afterwards.
afterwards.
5 A Simplified Formal Model of Hierarchies
In this section, we define a simplified formal model of hierarchies and show a metatheorem that ensures the predictability of structure inference. First, we define the model of hierarchies and inheritance relations.
Definition 5.1
(Hierarchy and inheritance relations). A hierarchy \(\mathcal {H}\) is a finite set of structures partially ordered by a non-strict inheritance relation \(\leadsto ^*\); that is, \(\leadsto ^*\) is reflexive, antisymmetric, and transitive. We denote the corresponding strict (irreflexive) inheritance relation by \(\leadsto ^+\). \(A \leadsto ^* B\) and \(A \leadsto ^+ B\) respectively mean that B non-strictly and strictly inherits from A.
Definition 5.2
(Common subclasses). The (non-strict) common subclasses of \(A, B \in \mathcal {H}\) are \(\mathcal {C} := \{C \in \mathcal {H} \mid A \leadsto ^* C \wedge B \leadsto ^* C\}\). The minimal common subclasses of A and B is \(\mathrm {mcs}(A, B) := \mathcal {C} \setminus \{C \in \mathcal {H} \mid \exists C' \in \mathcal {C}, C' \leadsto ^+ C\}\).
Definition 5.3
(Well-formed hierarchy). A hierarchy \(\mathcal {H}\) is said to be well-formed if the minimal common subclasses of any two structures are unique; that is, \(|\mathrm {mcs}(A, B)| \le 1\) for any \(A, B \in \mathcal {H}\).
Definition 5.4
(Extended hierarchy). An extended hierarchy \(\bar{\mathcal {H}} := \mathcal {H} \mathbin {\dot{\cup }} \{\top \}\) is a hierarchy \(\mathcal {H}\) extended with \(\top \) which means a structure that strictly inherits from all the structures in \(\mathcal {H}\); thus, the inheritance relation is extended as follows:

Definition 5.5
(Join). The join is a binary operator on an extended well-formed hierarchy \(\bar{\mathcal {H}}\), defined as follows:

We encoded the above definitions on hierarchies in Coq by using the structure of partially ordered finite types
 of the mathcomp-finmap library [12] and proved the following theorem.
of the mathcomp-finmap library [12] and proved the following theorem.
Theorem 5.1
The join operator on an extended well-formed hierarchy is associative, commutative, and idempotent; that is, an extended well-formed hierarchy is a join-semilattice.
If the unification algorithm of Coq respects our model of hierarchies and joins during structure inference, Theorem 5.1 implies that permuting, duplicating, and contracting unification problems do not change the result of inference; thus, it states the predictability of structure inference at a very abstract level.
6 Validating Well-Formedness of Hierarchies
This section presents a well-formedness checking algorithm that can also generate the exhaustive set of assertions for joins. We implemented this checking mechanism as a tool hierarchy.ml written in OCaml, which is available as a MathComp developer utility [45, /etc/utils/hierarchy.ml]. Our checking tool outputs the assertions as a Coq proof script which can detect missing and misimplemented unification hints for joins.
Since a hierarchy must be a finite set of structures (Definition 5.1), Definitions 5.2, 5.5, and 5.3 give us computable (yet inefficient) descriptions of joins and the well-formedness; in other words, for a given hierarchy \(\mathcal {H}\) and any two structures
 , one may enumerate their minimal common subclasses. Algorithm 1 is the checking algorithm we present, that takes in input an inheritance relation in the form of an indexed family of strict subclasses \(\texttt {subof}(A) := \{B \in \mathcal {H} \mid A \leadsto ^+ B\}\). The join function in this algorithm takes two structures as arguments, checks the uniqueness of their join, and then returns the join if it uniquely exists. In this function, the enumeration of minimal common subclasses is done by constructing the set of common subclasses \(\mathcal {C}\), and filtering out \(\texttt {subof}(C)\) from \(\mathcal {C}\) for every \(C \in \mathcal {C}\). In this filtering process, which is written as a foreach statement, we can skip elements already filtered out and do not need to care about ordering of picking up elements, thanks to transitivity.
, one may enumerate their minimal common subclasses. Algorithm 1 is the checking algorithm we present, that takes in input an inheritance relation in the form of an indexed family of strict subclasses \(\texttt {subof}(A) := \{B \in \mathcal {H} \mid A \leadsto ^+ B\}\). The join function in this algorithm takes two structures as arguments, checks the uniqueness of their join, and then returns the join if it uniquely exists. In this function, the enumeration of minimal common subclasses is done by constructing the set of common subclasses \(\mathcal {C}\), and filtering out \(\texttt {subof}(C)\) from \(\mathcal {C}\) for every \(C \in \mathcal {C}\). In this filtering process, which is written as a foreach statement, we can skip elements already filtered out and do not need to care about ordering of picking up elements, thanks to transitivity.
The hierarchy.ml utility extracts the inheritance relation from a Coq library by interacting with coqtop, and then executes Algorithm 1 to check the well-formedness and to generate assertions. The assertions generated from our running example are shown below.

An assertion
 asserts that the join of
asserts that the join of
 and
and
 is
is
 , and
, and
 is implemented as a tactic that fails if the assertion is false. For instance, if we do not declare
is implemented as a tactic that fails if the assertion is false. For instance, if we do not declare
 as a canonical instance, the assertion of line 9 fails and reports the following error.
as a canonical instance, the assertion of line 9 fails and reports the following error.


One may declare incorrect canonical instances that overwrite an existing join. For example, the join of groups and monoids must be groups; however, defining the following canonical instance in the
 section overwrites this join.
section overwrites this join.

By declaring
 as a canonical instance, the join of
as a canonical instance, the join of
 and
and
 is still
is still
 , but the join of
, but the join of
 and
and
 becomes
becomes
 , because of asymmetry of the unification mechanism. The assertion of line 1 fails and reports the following error.
, because of asymmetry of the unification mechanism. The assertion of line 1 fails and reports the following error.

7 Evaluation
This section reports the results of applying our tools to the MathComp library 1.7.0 and on recent development efforts to extend the hierarchy in MathComp using our tools. MathComp 1.7.0 provides the structures depicted in Fig. 1, except
 and
and
 , and lacked a few of the edges; thus, its hierarchy is quite large. Our coherence checking mechanism found 11 inconvertible multiple inheritance paths in the ssralg library. Fortunately, those paths concern proof terms and are intended to be irrelevant; hence, we can ensure no implicit coercion breaks the modularity of reasoning. Our well-formedness checking tool discovered 7 ambiguous joins, 8 missing unification hints, and one overwritten join due to an incorrect declaration of a canonical instance. These inheritance bugs were found and fixed with the help of our tools; thus, similar issues cannot be found in the later versions of MathComp.
, and lacked a few of the edges; thus, its hierarchy is quite large. Our coherence checking mechanism found 11 inconvertible multiple inheritance paths in the ssralg library. Fortunately, those paths concern proof terms and are intended to be irrelevant; hence, we can ensure no implicit coercion breaks the modularity of reasoning. Our well-formedness checking tool discovered 7 ambiguous joins, 8 missing unification hints, and one overwritten join due to an incorrect declaration of a canonical instance. These inheritance bugs were found and fixed with the help of our tools; thus, similar issues cannot be found in the later versions of MathComp.
The first issue was that inheritance from the
 structures (
structures (
 and its subclasses with the prefix
and its subclasses with the prefix
 ) to the
) to the
 structures (
structures (
 and its subclasses) was not implemented, and consequently it introduced 7 ambiguous joins. For instance,
and its subclasses) was not implemented, and consequently it introduced 7 ambiguous joins. For instance,
 did not inherit from
did not inherit from
 as it should; consequently, they became ambiguous joins of
as it should; consequently, they became ambiguous joins of
 and
and
 . 6 out of 8 missing unification hints should infer
. 6 out of 8 missing unification hints should infer
 or
or
 structures. The other 2 unification hints are in numeric field (
structures. The other 2 unification hints are in numeric field (
 and
and
 ) structures. Fixing the issue of missing inheritance from
) structures. Fixing the issue of missing inheritance from
 to
to
 was a difficult task without tool support. The missing inheritance itself was a known issue from before our tooling work, but the sub-hierarchy consisting of the
was a difficult task without tool support. The missing inheritance itself was a known issue from before our tooling work, but the sub-hierarchy consisting of the
 ,
,
 , and
, and
 structures in Fig. 1 is quite dense; as a result, it prevents the library developers from enumerating joins correctly without automation [38].
structures in Fig. 1 is quite dense; as a result, it prevents the library developers from enumerating joins correctly without automation [38].
The second issue was that the following canonical
 instance for
instance for
 overwrote the join of
overwrote the join of
 and
and
 , which should be
, which should be
 .
.

In this declaration,
 is a packager [26, Sect. 7] that takes a type
is a packager [26, Sect. 7] that takes a type
 and a
and a
 mixin of
mixin of
 as its arguments and construct a
as its arguments and construct a
 instance from the given mixin and the canonical
instance from the given mixin and the canonical
 instance for
instance for
 . However, if one omits its first argument
. However, if one omits its first argument
 with a placeholder as in the above, the packager may behave unpredictably as a unification hint. In the above case, the placeholder was instantiated with
with a placeholder as in the above, the packager may behave unpredictably as a unification hint. In the above case, the placeholder was instantiated with
 by type inference; as a result, it incorrectly overwrote the join of
by type inference; as a result, it incorrectly overwrote the join of
 and
and
 .
.
Our tools can also help finding inheritance bugs when extending the hierarchy of MathComp, improve the development process by reducing the reviewing and maintenance burden, and allow developers and contributors to focus better on mathematical contents and other design issues. For instance, Hivert [24] added new structures of commutative algebras and redefined the field extension and splitting field structures to inherit from them. In this extension process, he fixed some inheritance issues with help from us and our tools; at the same time, we made sure there is no inheritance bug without reviewing the whole boilerplate code of structures. We ported the order sub-library of the mathcomp-finmap library [12] to MathComp, redefined numeric domain structures [10, Chap. 4] [11, Sect. 3.1] to inherit from ordered types, and factored out the notion of norms and absolute values as normed Abelian groups [1, Sect. 4.2] with the help of our tools [13, 36]. This modification resulted in approximately 10,000 lines of changes; thus, reducing the reviewing burden was an even more critical issue. This work is motivated by an improvement of the MathComp Analysis library [3] [30, Part II], which extends the hierarchy of MathComp with some algebraic and topological structures [1, Sect. 4] [30, Chap. 5] and is another application of our tools.
8 Conclusion and Related Work
This paper has provided a thorough analysis of the packed classes methodology, introduced two invariants that ensure the modularity of reasoning and the predictability of structure inference, and presented systematic ways to check those invariants. We implemented our invariant checking mechanisms as a part of the Coq system and a tool bundled with MathComp. With the help of these tools, many inheritance bugs in MathComp have been found and fixed. The MathComp development process has also been improved significantly.
Coq had no coherence checking mechanism before our work. Saïbi [32, Sect. 7] claimed that the coherence property “is too restrictive in practice” and “it is better to replace conversion by Leibniz equality to compare path coercions because Leibniz equality is a bigger relation than conversion”. However, most proof assistants based on dependent type theories including Coq still rely heavily on conversion, particularly in their type checking/inference mechanisms. Coherence should not be relaxed with Leibniz equality; otherwise, the type mismatch problems described in Sect. 3 will occur. With our coherence checking mechanism, users can still declare inconvertible multiple inheritance at their own risk and responsibility, because ambiguous paths messages are implemented as warnings rather than errors. The Lean system has an implicit coercion mechanism based on type class resolution, that allows users to define and use non-uniform implicit coercions; thus, coherence checking can be more difficult. Actually, Lean has no coherence checking mechanism; thus, users get more flexibility with this approach but need to be careful about being coherent.
There are three kinds of approaches to defining mathematical structures in dependent type theories: unbundled, semi-bundled, and bundled approaches [46, Sect. 4.1.1]. The unbundled approach uses an interface that is parameterized by carriers and operators, and gathers axioms as its fields, e.g., [41]; in contrast, the semi-bundled approach bundles operators together with axioms as in
 records, but still places carriers as parameters, e.g., [46]. The bundled approach uses an interface that bundles carriers together with operators and axioms, e.g., packed classes and telescopes [26, Sect. 2.3] [9, 18, 29]. The above difference between definitions of interfaces, in particular, whether carriers are bundled or not, leads to the use of different instance resolution and inference mechanisms: type classes [22, 40] for the unbundled and semi-bundled approaches, and canonical structures or other unification hint mechanisms for the bundled approach. Researchers have observed unpredictable behaviors [23] and efficiency issues [46, Sect. 4.3] [41, Sect. 11] in inference with type classes; in contrast, structure inference with packed classes is predictable, and Theorem 5.1 states this predictability more formally, except for concrete instance resolution. The resolution of canonical structures is carried out by consulting a table of unification hints indexed by pairs of two head symbols and optionally with its recursive application and backtracking [21, Sect. 2.3]. The packed classes methodology is designed to use this recursive resolution not for structure inference [17, Sect. 2.3] but only for parametric instances [26, Sect. 4] such as lists and products, and not to use backtracking. Thus, there is no efficiency issue in structure inference, except that nested class records and chains of their projections exponentially slow down the conversion which flat variant of packed classes [14, Sect. 4] can mitigate. In the unbundled and semi-bundled approaches, a carrier may be associated with multiple classes; thus, inference of join and our work on structure inference (Sect. 4, 5, and 6) are problems specific to the bundled approach. A detailed comparison of type classes and packed classes has also been provided in [1]. There are a few mechanisms to extend the unification engines of proof assistants other than canonical structures that can implement structure inference for packed classes: unification hints [4] and coercions pullback [31]. For any of those cases, our invariants are fundamental properties to implement packed classes and structure inference, but the invariant checking we propose has not been made yet at all.
records, but still places carriers as parameters, e.g., [46]. The bundled approach uses an interface that bundles carriers together with operators and axioms, e.g., packed classes and telescopes [26, Sect. 2.3] [9, 18, 29]. The above difference between definitions of interfaces, in particular, whether carriers are bundled or not, leads to the use of different instance resolution and inference mechanisms: type classes [22, 40] for the unbundled and semi-bundled approaches, and canonical structures or other unification hint mechanisms for the bundled approach. Researchers have observed unpredictable behaviors [23] and efficiency issues [46, Sect. 4.3] [41, Sect. 11] in inference with type classes; in contrast, structure inference with packed classes is predictable, and Theorem 5.1 states this predictability more formally, except for concrete instance resolution. The resolution of canonical structures is carried out by consulting a table of unification hints indexed by pairs of two head symbols and optionally with its recursive application and backtracking [21, Sect. 2.3]. The packed classes methodology is designed to use this recursive resolution not for structure inference [17, Sect. 2.3] but only for parametric instances [26, Sect. 4] such as lists and products, and not to use backtracking. Thus, there is no efficiency issue in structure inference, except that nested class records and chains of their projections exponentially slow down the conversion which flat variant of packed classes [14, Sect. 4] can mitigate. In the unbundled and semi-bundled approaches, a carrier may be associated with multiple classes; thus, inference of join and our work on structure inference (Sect. 4, 5, and 6) are problems specific to the bundled approach. A detailed comparison of type classes and packed classes has also been provided in [1]. There are a few mechanisms to extend the unification engines of proof assistants other than canonical structures that can implement structure inference for packed classes: unification hints [4] and coercions pullback [31]. For any of those cases, our invariants are fundamental properties to implement packed classes and structure inference, but the invariant checking we propose has not been made yet at all.
Packed classes require the systematic use of records, implicit coercions, and canonical structures. This leads us to automated generation of structures from their higher-level descriptions [14], which is work in progress.
Notes
- 1.
One may also define a new structure that inherits from multiple existing classes and has an extra mixin, e.g., by defining commutative rings instead of rings in this example, and left algebras as
 in MathComp.
in MathComp. - 2.
In fact, the target classes can also be functions (
 ) and sorts (
) and sorts (
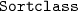 ); that is to say, a function returning functions, types, or propositions can be declared as an implicit coercion. In this paper, we omit these cases to simplify the presentation, but our discussion can be generalized to these cases.
); that is to say, a function returning functions, types, or propositions can be declared as an implicit coercion. In this paper, we omit these cases to simplify the presentation, but our discussion can be generalized to these cases.
References
Affeldt, R., Cohen, C., Kerjean, M., Mahboubi, A., Rouhling, D., Sakaguchi, K.: Competing inheritance paths in dependent type theory: a case study in functional analysis. In: Peltier, N., Sofronie-Stokkermans, V. (eds.) IJCAR 2020. LNCS, vol. 12167, pp. 3–20. Springer, Cham (2020)
Affeldt, R., Nowak, D., Saikawa, T.: A hierarchy of monadic effects for program verification using equational reasoning. In: Hutton, G. (ed.) MPC 2019. LNCS, vol. 11825, pp. 226–254. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-33636-3_9
Analysis Team: Mathematical components compliant analysis library (2017). https://github.com/math-comp/analysis
Asperti, A., Ricciotti, W., Sacerdoti Coen, C., Tassi, E.: Hints in unification. In: Berghofer, S., Nipkow, T., Urban, C., Wenzel, M. (eds.) TPHOLs 2009. LNCS, vol. 5674, pp. 84–98. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03359-9_8
Asperti, A., Ricciotti, W., Sacerdoti Coen, C., Tassi, E.: The matita interactive theorem prover. In: Bjørner, N., Sofronie-Stokkermans, V. (eds.) CADE 2011. LNCS (LNAI), vol. 6803, pp. 64–69. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22438-6_7
Avigad, J., de Moura, L., Kong, S.: Theorem Proving in Lean (2019). https://leanprover.github.io/theorem_proving_in_lean/
Barthe, G.: Implicit coercions in type systems. In: Berardi, S., Coppo, M. (eds.) TYPES 1995. LNCS, vol. 1158, pp. 1–15. Springer, Heidelberg (1996). https://doi.org/10.1007/3-540-61780-9_58
Boldo, S., Lelay, C., Melquiond, G.: Coquelicot: a user-friendly library of real analysis for coq. Math. Comput. Sci. 9(1), 41–62 (2014). https://doi.org/10.1007/s11786-014-0181-1
de Bruijn, N.G.: Telescopic mappings in typed lambda calculus. Inf. Comput. 91(2), 189–204 (1991). https://doi.org/10.1016/0890-5401(91)90066-B
Cohen, C.: Formalized algebraic numbers: construction and first-order theory. (Formalisation des nombres algébriques : construction et théorie du premier ordre). Ph.D. thesis, Ecole Polytechnique X (2012). https://pastel.archives-ouvertes.fr/pastel-00780446
Cohen, C., Mahboubi, A.: Formal proofs in real algebraic geometry: from ordered fields to quantifier elimination. Logical Methods Comput. Sci. 8(1) (2012). https://doi.org/10.2168/LMCS-8(1:2)2012
Cohen, C., Sakaguchi, K.: A finset and finmap library (2019). https://github.com/math-comp/finmap
Cohen, C., Sakaguchi, K., Affeldt, R.: Dispatching order and norm, and anticipating normed modules (2019). https://github.com/math-comp/math-comp/pull/270
Cohen, C., Sakaguchi, K., Tassi, E.: Hierarchy Builder: algebraic hierarchies made easy in Coq with Elpi (system description) (2020). Accepted in the Proceedings of FSCD 2020 https://hal.inria.fr/hal-02478907
Coquand, T., Huet, G.: The calculus of constructions. Inf. Comput. 76(2), 95–120 (1988). https://doi.org/10.1016/0890-5401(88)90005-3
Garillot, F.: Generic proof tools and finite group theory. (Outils génériques de preuve et théorie des groupes finis). Ph.D. thesis, École Polytechnique, Palaiseau, France (2011). https://tel.archives-ouvertes.fr/pastel-00649586
Garillot, F., Gonthier, G., Mahboubi, A., Rideau, L.: Packaging mathematical structures. In: Berghofer, S., Nipkow, T., Urban, C., Wenzel, M. (eds.) TPHOLs 2009. LNCS, vol. 5674, pp. 327–342. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03359-9_23
Geuvers, H., Pollack, R., Wiedijk, F., Zwanenburg, J.: A constructive algebraic hierarchy in Coq. J. Symb. Comput. 34(4), 271–286 (2002). https://doi.org/10.1006/jsco.2002.0552
Goldfarb, W.D.: The undecidability of the second-order unification problem. Theor. Comput. Sci. 13(2), 225–230 (1981). https://doi.org/10.1016/0304-3975(81)90040-2
Gonthier, G., et al.: A machine-checked proof of the odd order theorem. In: Blazy, S., Paulin-Mohring, C., Pichardie, D. (eds.) ITP 2013. LNCS, vol. 7998, pp. 163–179. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-39634-2_14
Gonthier, G., Ziliani, B., Nanevski, A., Dreyer, D.: How to make ad hoc proof automation less ad hoc. J. Funct. Program. 23(4), 357–401 (2013). https://doi.org/10.1017/S0956796813000051
Haftmann, F., Wenzel, M.: Constructive type classes in isabelle. In: Altenkirch, T., McBride, C. (eds.) TYPES 2006. LNCS, vol. 4502, pp. 160–174. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-74464-1_11
Hales, T.: A review of the Lean theorem prover, September 2018. https://jiggerwit.wordpress.com/2018/09/18/a-review-of-the-lean-theorem-prover/, Blog entry of 18 September 2018
Hivert, F.: Commutative algebras (2019). https://github.com/math-comp/math-comp/pull/406
Hölzl, J., Immler, F., Huffman, B.: Type classes and filters for mathematical analysis in Isabelle/HOL. In: Blazy, S., Paulin-Mohring, C., Pichardie, D. (eds.) ITP 2013. LNCS, vol. 7998, pp. 279–294. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-39634-2_21
Mahboubi, A., Tassi, E.: Canonical structures for the working coq user. In: Blazy, S., Paulin-Mohring, C., Pichardie, D. (eds.) ITP 2013. LNCS, vol. 7998, pp. 19–34. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-39634-2_5
de Moura, L., Kong, S., Avigad, J., van Doorn, F., von Raumer, J.: The lean theorem prover (system description). In: Felty, A.P., Middeldorp, A. (eds.) CADE 2015. LNCS (LNAI), vol. 9195, pp. 378–388. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-21401-6_26
Nanevski, A., Ley-Wild, R., Sergey, I., Delbianco, G., Trunov, A.: The PCM library (2019). https://github.com/imdea-software/fcsl-pcm
Pollack, R.: Dependently typed records in type theory. Formal Aspects Comput. 13(3), 386–402 (2002). https://doi.org/10.1007/s001650200018
Rouhling, D.: Formalisation tools for classical analysis - a case study in control theory. (Outils pour la Formalisation en Analyse Classique - Une Étude de Cas en Théorie du Contrôle). Ph.D. thesis, Université Côte d’Azur (2019). https://hal.inria.fr/tel-02333396
Sacerdoti Coen, C., Tassi, E.: Working with mathematical structures in type theory. In: Miculan, M., Scagnetto, I., Honsell, F. (eds.) TYPES 2007. LNCS, vol. 4941, pp. 157–172. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-68103-8_11
Saïbi, A.: Typing algorithm in type theory with inheritance. In: POPL 1997, pp. 292–301. ACM (1997). https://doi.org/10.1145/263699.263742
Saïbi, A.: Outils Génériques de Modélisation et de Démonstration pour la Formalisation des Mathématiques en Théorie des Types. Application à la Théorie des Catégories. (Formalization of Mathematics in Type Theory. Generic tools of Modelisation and Demonstration. Application to Category Theory). Ph.D. thesis, Pierre and Marie Curie University, Paris, France (1999). https://tel.archives-ouvertes.fr/tel-00523810
Sakaguchi, K.: Coherence checking for coercions (2019). https://github.com/coq/coq/pull/11258
Sakaguchi, K.: Relax the ambiguous path condition of coercion (2019). https://github.com/coq/coq/pull/9743
Sakaguchi, K.: Non-distributive lattice structures (2020). https://github.com/math-comp/math-comp/pull/453
Sakaguchi, K.: Supplementary materials of this manuscript (2020). http://logic.cs.tsukuba.ac.jp/~sakaguchi/src/vms-ijcar2020.tar.gz
Sakaguchi, K., Cohen, C.: Fix inheritances from countalg to finalg (2019). https://github.com/math-comp/math-comp/pull/291
Sergey, I., Nanevski, A., Banerjee, A.: Mechanized verification of fine-grained concurrent programs. In: PLDI 2015, pp. 77–87. ACM (2015). https://doi.org/10.1145/2737924.2737964
Sozeau, M., Oury, N.: First-class type classes. In: Mohamed, O.A., Muñoz, C., Tahar, S. (eds.) TPHOLs 2008. LNCS, vol. 5170, pp. 278–293. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-71067-7_23
Spitters, B., van der Weegen, E.: Type classes for mathematics in type theory. Math. Struct. Comput. Sci. 21(4), 795–825 (2011). https://doi.org/10.1017/S0960129511000119
The Coq Development Team: The Coq Proof Assistant Reference Manual (2020). https://coq.inria.fr/distrib/V8.11.0/refman/. The PDF version with numbered sections is available at https://zenodo.org/record/3744225
The Coq Development Team: Sect. 4.4.3 “Conversion rules”. In: [42] (2020). https://coq.inria.fr/distrib/V8.11.0/refman/language/cic#conversion-rules
The Coq Development Team: Sect. 8.2 “Implicit Coercions”. In: [42] (2020). https://coq.inria.fr/distrib/V8.11.0/refman/addendum/implicit-coercions
The Mathematical Components project: The mathematical components repository (2019). https://github.com/math-comp/math-comp
The mathlib Community: The Lean mathematical library. In: CPP 2020, pp. 367–381. ACM (2020). https://doi.org/10.1145/3372885.3373824
Acknowledgements
We appreciate the support from the STAMP (formerly MARELLE) project-team, INRIA Sophia Antipolis. In particular, we would like to thank Cyril Cohen and Enrico Tassi for their help in understanding packed classes and implementing our checking tools. We are grateful to Reynald Affeldt, Yoichi Hirai, Yukiyoshi Kameyama, Enrico Tassi, and the anonymous reviewers for helpful comments on early drafts. We are deeply grateful to Karl Palmskog for his careful proofreading and comments. We would like to thank the organizers and participants of The Coq Workshop 2019 where we presented preliminary work of this paper. In particular, an insightful question from Damien Pous was the starting point of our formal model of hierarchies presented in Sect. 5. This work was supported by JSPS Research Fellowships for Young Scientists and JSPS KAKENHI Grant Number 17J01683.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
Sakaguchi, K. (2020). Validating Mathematical Structures. In: Peltier, N., Sofronie-Stokkermans, V. (eds) Automated Reasoning. IJCAR 2020. Lecture Notes in Computer Science(), vol 12167. Springer, Cham. https://doi.org/10.1007/978-3-030-51054-1_8
Download citation
DOI: https://doi.org/10.1007/978-3-030-51054-1_8
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-51053-4
Online ISBN: 978-3-030-51054-1
eBook Packages: Computer ScienceComputer Science (R0)








 and
and
 directly inherit from the structures
directly inherit from the structures
 and
and
 ; thus,
; thus,
 and
and
 have two joins.
have two joins.
 in
in  ) and sorts (
) and sorts (
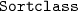 ); that is to say, a function returning functions, types, or propositions can be declared as an implicit coercion. In this paper, we omit these cases to simplify the presentation, but our discussion can be generalized to these cases.
); that is to say, a function returning functions, types, or propositions can be declared as an implicit coercion. In this paper, we omit these cases to simplify the presentation, but our discussion can be generalized to these cases.