Cyclic Deformation and Fatigue Behavior of Metastable Austenitic Steels and Steel-Matrix-Composites

Abstract

The present contribution highlights the cyclic deformation behavior of metastable austenitic steels focusing on the effects of different (i) chemical compositions, (ii) manufacturing methods and (iii) strengthening methods in terms of a particle reinforcement and a quenching and partitioning treatment. The investigations are based on total strain controlled fatigue tests and the observed mechanical properties are discussed in context with the microstructural processes in the material, in particular the fatigue-induced α′-martensite formation. Overall, a major relevance is ascribed to the stacking fault energy and the grain size of the material. The fatigue behavior of the steels with different chemical compositions and the steels processed via casting, additive manufacturing , reversion annealing and hot pressing , respectively, is dominated by these two factors. In contrast, the most important factor in case of the reinforced steel-matrix-composites are the Mg-PSZ particles. The advantage of increasing stress amplitudes with increasing particle fraction is purchased with particle-related damage mechanisms like debonding and particle rupture causing a shorter fatigue life . The quenching and partitioning steel on the other hand benefits from higher α′-martensite fractions after partitioning increasing both, the strength and the fatigue life of the material.

13.1 Introduction

Metastability of austenitic steels means the tendency of the material for a martensitic phase transformation to reach a state of lower energy. More precisely, the face centered cubic (fcc) austenite exhibits the ability to transform to the body centered cubic (bcc) α′-martensite under mechanical loading [1,2,3] or due to a temperature decrease below the material-specific martensite start temperature M_s. Under loading the diffusionless phase transformation is the reason for the so-called TRIP (TRansformation Induced Plasticity) effect, i.e. an increase in strength and ductility in comparison to a stable austenitic steel without a phase transformation, e.g. [4, 5]. Thus, these steels are also known as TRIP steels. However, in contrast to the stress-assisted phase transformation occurring during pure elastic loading, the deformation-induced α′-martensite formation requires plasticity to generate potential nucleation sites in terms of intersecting deformation bands and stacking faults, respectively [1].

Besides the austenite stability, an essential factor for activation of particular deformation mechanisms is the stacking fault energy (SFE). Of course, dislocation movement is always present in case of plastic deformation, but the dislocation glide characteristic, i.e. wavy or planar glide, strongly depends on the SFE and the presence of short range order [6]. At low SFE dislocations split up in Shockley partial dislocations forming a stacking fault promoting planar glide and the formation of α′-martensite. With increasing SFE the dominance of α′-martensite formation decreases and a transition to ε-martensite formation (cf. Sect. 13.3.2, [7]) and later on twinning sets in [5, 8, 9]. The latter leads to the TWIP (TWinning Induced Plasticity) effect which in comparison to the TRIP effect is characterized by a reduced increase in strength but an even higher increase in ductility [5]. Finally, at high SFE neither deformation-induced twinning nor a phase transformation occur but wavy dislocation glide is favored. Overall, the SFE has a quite strong influence on the mechanical properties and is itself determined by the temperature and the chemical composition of the material [5, 8,9,10,11].

Like in case of other materials, many structural components out of metastable austenitic steels are subjected to cyclic loads during their application. As fatigue cracks initiate and propagate far below characteristic quasi-static values like the yield strength or ultimate tensile strength, the knowledge of the respective fatigue properties is of utmost importance. Accordingly, the present chapter aims to describe the fundamental principles of the cyclic deformation and fatigue behavior of metastable austenitic steels and steel-matrix composites and to highlight the correlation to the observed deformation mechanisms.

At first, the influence of the chemical composition and, thus, of the SFE on the cyclic deformation behavior and in particular on the fatigue life is presented in Sect. 13.3 [12, 13]. Subsequently in Sect. 13.4, the influence of the manufacturing method of austenitic steels is discussed including additively manufactured [14, 15], cast [12] and ultrafine-grained material states [16].

However, like for other materials there are efforts to further improve the mechanical properties of austenitic steels of course. Two approaches, namely particle reinforcement and quenching and partitioning (Q&P) processing are presented in context with their individual benefits and drawbacks.

For aluminum for instance, particle reinforcement is a common and well known way for increasing the strength. In case of the present high alloy austenitic steels (cf. Sect. 13.3) particles of MgO partially-stabilized zirconia (Mg-PSZ) are used for reinforcement [17]. The MgO addition stabilizes the tetragonal phase of ZrO₂ to room temperature and, thereby, enables a stress-assisted phase transformation to the monoclinic phase during loading. This phase transformation is accompanied by a volume expansion of the Mg-PSZ producing compressive stresses in the vicinity. The influence of the particle reinforcement on the fatigue behavior is presented in Sect. 13.5 [13, 18, 19].

Quenching and partitioning (Q&P) processing [20, 21] has been another intensely investigated topic for many researchers over the last years. Their mutual aim is to design steels which meet the criteria for the 3rd generation of Advanced High Strength Steels (AHSS), i.e. a significant enhancement of the strength compared to common metastable austenitic steels (2nd generation of AHSS) but still at a reasonable ductility better than martensitic steels. So far, most publications focus on developing and investigating the process and the achieved monotonic properties, however, the fatigue behavior is hardly considered. Hence, Sect. 13.6 presents one of the first investigations on the cyclic deformation behavior of an ultra-high strength steel processed via a modified Q&P route including the fatigue life and the microstructure after cyclic deformation [22].

13.2 Methodology

This chapter introduces the experimental details and methodical issues necessary for understanding and interpretation of the results discussed afterwards. Therefore, the chemical composition and manufacturing methods of the different test materials are presented. In addition, the details of fatigue testing as well as the analytical methods used for characterization of the cyclic deformation behavior are pointed out.

13.2.1 Materials

The investigated materials are high alloy austenitic TRIP and TWIP steels and their particle-reinforced counterparts. An overview of the chemical compositions and particle size distributions is given in Table 13.1 for the steels and in Table 13.2 for the Mg-PSZ reinforcement particles. It should be noted, that the last steel of Table 13.1 (Cr14NC11.15) is austenitic at room temperature (RT) after solution annealing, but exhibited a relatively high α′-martensite fraction before cyclic deformation due to a novel quenching and partitioning (Q&P) treatment, cf. Sect. 13.2.2.

Table 13.1 Chemical compositions of the investigated steel alloys in wt.% and their designations in this chapter. In addition, the last column indicates the average grain sizes in μm

Table 13.2 Chemical composition of the delivered Mg-PSZ powder in wt.% and its designation in this book (5 and 10, respectively, indicate the volume fraction). In addition, the d₁₀, d₅₀ and d₉₀ values of the particle size distribution in μm and the phase fractions in vol.% are given

The steel powders were gas atomized by TLS (Bitterfeld, Germany) and the Mg-PSZ powder (Table 13.2) was mechanically milled and delivered by Saint-Gobain (USA). However, the steel powders used for hot pressing (HP) and electron beam melting (EBM ) differed significantly regarding the particle size distribution. Whereas the HP powders exhibited d₅₀ values in the range 26–28 μm and a d₉₀ of 44 μm, the equivalent values were 73 μm and 119 μm, respectively, for the EBM powder.

13.2.2 Manufacturing Methods

Hot pressing (HP) is a powder metallurgical processing route under vacuum atmosphere. The powder was hot pressed by Fraunhofer IKTS (Dresden, Germany) at 1250 °C for 30 min at a pressure of approximately 30 MPa applied via a piston. The heating and cooling rates were set to 10 and 5 K/min, respectively. The HP discs exhibited a diameter of 150 mm at a height of 15–20 mm.

Casting was carried out either by ACTech (Freiberg, Germany) using the sandcasting technique in case of the Cast 15-6-6 steel or by the Institute of Iron and Steel Technology (TU Bergakademie Freiberg, Germany) using die-casting for the Cast Cr14NC11.15 material. The latter was melted in a vacuum induction furnace and cast into a water-cooled copper mold placed in the furnace chamber. After casting, all steels were solution annealed for 30 min at 1050 °C (Cast 15-6-6) and at 1150 °C (Cast Cr14NC11.15), respectively.

Electron beam melting (EBM ) is a powder-bed based additive manufacturing technology. The component is built in layers under a controlled atmosphere, i.e. a low helium pressure, enabling the electron beam to melt the powder. For the fatigue tests, cylindrical rods with a diameter of 14 mm and a height of 130 mm were built upright, i.e. parallel to the building direction. An Arcam A2X (Mölndal, Sweden) EBM machine was operated at a helium pressure of 2 × 10⁻³ mbar with beam parameters set to: acceleration voltage 60 kV, beam current 7.5 mA, scan speed 4.500 mm/s and hatch distance 50 μm. A meander-shape scan strategy in combination with a rotation of the scan direction of 90° after each layer was used. The layer thickness was 50 μm.

Reversion annealing is a heat treatment step within a more comprehensive thermo-mechanically controlled processing (TMCP ) [23,24,25,26,27,28,29,30] which is the most common way for metastable austenitic steels to produce an ultrafine-grained (UFG ) microstructure. The TMCP always includes a cold deformation step to induce a high amount of α′-martensite in the microstructure.

At first, the present material UFG 17-7-6 was forged at 1200 °C reducing the diameter from an initial 50 mm to 27 mm (Fig. 13.1). Afterwards, the metastable austenite was deformed at RT by rotary swaging further reducing the diameter to 8.3 mm in 11 passes and, thereby, inducing a high α′-martensite fraction of about 75 vol.%. The final step was an annealing treatment at 700 °C for 5 min to provoke the reversion of this α′-martensite back to austenite, called reversion annealing in literature. As reported by Weidner et al. [31] for a steel of similar chemical composition, the reversion path is based on a shear process without diffusion which is typical for interstitial free steels [32,33,34,35]. Thus, this TMCP route led to an UFG microstructure with an average grain size of 0.7 μm (cf. Sect. 13.4.1).

Fig. 13.1

Schematic representation of the thermo-mechanically controlled processing to achieve an UFG microstructure. After [16]

Quenching and partitioning (Q&P) is a thermal processing technology aiming for mechanical properties meeting the demands for the third generation of advanced high-strength steels (AHSS) [36,37,38,39,40], i.e. a very high strength comparable to martensitic steels but at a higher ductility. The key factor for these properties is the microstructure after Q&P consisting of tempered α′-martensite and interstitially-enriched austenite. However, usual Q&P processing includes austenization followed by quenching to a temperature well above RT due to the relatively high martensite start (M_s) temperature of the steels. In addition, a subsequent partitioning treatment is necessary before cooling down to RT. In contrast, the present steel Cr14NC11.15 exhibits a M_s temperature slightly below RT simplifying this temperature-time control. This novel Q&P process designed by Wendler et al. [21] requires a subzero cooling in a second step (Fig. 13.2) to induce athermal α′-martensite whose target fraction can be adjusted by variation of the cooling temperature T_c. Finally, a partitioning treatment has to be performed to provoke a diffusion of interstitials C and N from the supersaturated α′-martensite to the retained austenite. For the present steel two different cooling temperatures of −120 °C and −20 °C have been used in combination with a partitioning at 450 °C for 3 min (Fig. 13.2).

Fig. 13.2

Schematic representation of the Q&P process to achieve an ultra-high strength austenitic-martensitic microstructure. After [22]

13.2.3 Fatigue Testing

All fatigue tests presented in this work are total strain controlled tests performed either on a Landmark 250 or a Landmark 100, both servo-hydraulic testing systems by MTS (Eden Prairie, USA). Constant strain amplitude tests under symmetrical push-pull conditions (strain ratio R_ε = − 1) were conducted in the range of 0.25% ≤ ∆ε_t/2 ≤ 2% following a triangular strain function with a constant strain rate of 4 × 10⁻³ s⁻¹.

Furthermore, a Feritscope^® (Fischerscope^® MMS^® PC, Sindelfingen, Germany) has been attached to the specimens to record the evolution of α′-martensite in situ during cyclic deformation. As this device is calibrated for measuring the δ-ferrite phase fraction denoted in Fe-%, its readings have to be multiplied by a correction factor of 1.7 to obtain the actual α′-martensite fraction [41]. However, this linear correlation is only valid up to 55 Fe-%, which is exceeded in some of the presented tests. Hence, all α′-martensite evolutions presented in this chapter are the pure Feritscope^® readings in Fe-% without any correction factor.

The fatigue specimens exhibited a gauge length of 14 mm at a diameter of 5 mm (UFG 17-7-6) and 6 mm (all other materials), respectively. They were ground and polished mechanically before testing.

13.2.4 Analytical Methods

Scanning electron microscopy (SEM) was used to characterize the microstructure of the different materials before and after cyclic deformation. Therefore, imaging methods like backscattered electron (BSE) imaging, electron channeling contrast imaging (ECCI) and SEM in transmission mode (t-SEM) as well as the analytical method electron backscattered diffraction (EBSD) are employed. The EBSD (EDAX, New Jersey, USA) scans are used for calculation of the average grain size $\bar{d}$ according to the following relationship

$$ \bar{d} = \frac{{\mathop \sum \nolimits_{i = 1}^{N} A_{i} \cdot d_{i} }}{{\mathop \sum \nolimits_{i = 1}^{N} A_{i} }} $$

(13.1)

where A_i and d_i are the area and diameter of the i^th grain, respectively. All SEM investigations were performed on a field emission gun Mira 3 FE-SEM by Tescan (Brno, Czech Republic) operated at an acceleration voltage between 20 and 30 kV.

Transmission electron microscopy (TEM) was applied for the UFG 17-7-6 material which was thinned by electrolytic etching. The investigations were carried out on a field emission gun JEOL JEM-2200FS operated at 200 kV.

X-ray micro-computed tomography (μ-CT) was used for defect characterization in the additive manufactured EBM 16-6-6 material and the HP 16-6-6 for reference purposes. The analyzed volumes were 45.6 mm³ (EBM ) and 48.2 mm³ (HP), respectively. The Nikon system was operated at 160 kV with a micro-focus of 3 μm using a tungsten filament for X-ray emission (further details of setup are given in [42]). The data was analyzed by the software VGSTUDIO MAX 3.1 using the algorithm “VGEasyPore”.

13.3 Influence of Chemical Composition on the Fatigue Behavior

This chapter investigates the influence of different concentrations of Ni on the fatigue behavior and deformation mechanisms of three hot pressed high alloy austenitic steels¹ (HP 16-6-4, HP 16-6-6, HP 16-6-9, cf. Table 13.1). Ni is an austenite stabilizer and increases the stacking fault energy (SFE) of a material and, thereby, strongly influences the characteristics of plastic deformation.

13.3.1 Cyclic Deformation Behavior

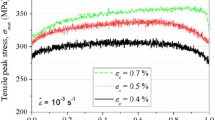
The cyclic deformation curves of Fig. 13.3 indicate a distinct difference between the variants with low and medium Ni content compared to the HP 16-6-9 with 9 wt.% Ni. The latter exhibits a pronounced primary hardening whose intensity decreases with decreasing strain amplitude and finally merges to continuous cyclic softening at ∆ε_t/2 = 0.2%. This behavior is typical for high alloy austenitic steels and related to an increase in dislocation density and interactions between the dislocations [43, 44]. For the highest strain amplitude ∆ε_t/2 = 2% cyclic hardening goes on until failure whereas it is replaced by cyclic softening for the other strain amplitudes probably caused by rearrangement of dislocations. However, in case of the high strain amplitudes ∆ε_t/2 ≥ 0.8% secondary hardening, mainly attributed to the formation of fatigue-induced twinning (Sect. 13.3.2), sets in after a certain number of cycles. The twin boundaries lead to a reduction of the mean free path of dislocations [45] often called dynamic Hall-Petch effect in literature, e.g. [46], leading to an increase of the stress amplitudes.

Fig. 13.3

Cyclic deformation curves for different strain amplitudes of the materials HP 16-6-4 (a), HP 16-6-6 (b) and HP 16-6-9 (c). After [13, 18, 19]

In the beginning of cyclic deformation the qualitative courses of the cyclic deformation curves of the other two HP steels (Fig. 13.3a, b) are similar to the described behavior, although the primary hardening slightly decreases with decreasing Ni content. A substantial difference occurs once the secondary hardening sets in. Its magnitude significantly increases with decreasing Ni content and, in addition, the secondary hardening is triggered at a lower number of cycles. Besides the chemical composition, the intensity and onset is of course affected by the applied strain amplitude, i.e. a shorter incubation period and increasing magnitude with increasing strain amplitude. Especially in case of the HP 16-6-4 the cyclic hardening merges to a saturation-like stage at low and medium strain amplitudes continuing until fracture. However, including the α′-martensite evolution (Fig. 13.4) in the investigation of cyclic deformation behavior shows obviously, that the secondary hardening correlates quite well with the cyclic deformation behavior. In fact, the α′-martensite formation causes the cyclic hardening as it is well-known for metastable austenitic steels, e.g. [9, 44, 47,48,49]. In the present alloys, this hardening effect is not solely due to the higher hardness of the martensitic phase, but a strong impact is attributed to (i) the lower grain size of the α′-martensite compared to the austenite and (ii) a reduced mean free path for dislocations as the α′-martensite nuclei preferentially form within deformation bands [4, 50].

Fig. 13.4

α′-martensite evolution during cyclic deformation at different strain amplitudes for the materials HP 16-6-4 (a) and HP 16-6-6 (b). After [13, 19]

Based on the finding that the cyclic hardening is due to the martensitic phase transformation, the reasons for the differences between the materials as well as for the different onset times and intensities can be discussed. Figure 13.5 shows the threshold value of the cumulated plastic strain λ_p,th which has to be exceeded to trigger the α′-martensite formation [9, 48, 49] plotted against the applied total strain amplitudes. This threshold value stems from the premiss that the deformation-induced α′-martensite formation is triggered by a double shear mechanism of at least two intersecting stacking faults on different slip planes [1, 51]. Thus, the threshold value decreases with increasing strain amplitude (Fig. 13.5) as a consequence of an increase in lattice defects and a higher density of deformation bands, i.e. more sites for α′-martensite nucleation [43, 49, 52]. Consequently, decreasing strain amplitudes lead to increasing incubation periods for the martensitic phase transformation (Fig. 13.4) and the accompanied secondary hardening (Fig. 13.3a, b). Furthermore, the lower threshold values of the HP 16-6-4 steel compared to HP 16-6-6 are due to its lower austenite stability.

Fig. 13.5

Threshold values of the cumulated plastic strain λ_p,th plotted against the applied strain amplitudes. After [13]

The cyclic hardening causes a decrease in the plastic strain amplitude ∆ε_pl/2, i.e. the plasticity within a cycle decreases. As a consequence of this, the driving force for further α′-martensite formation decreases as well which leads to the described stage of saturation-like behavior, especially in case of medium and small amplitudes. An additional contribution to this behavior is attributed to internal stresses due to the formation of α′-martensite inhibiting a further phase transformation.

Figure 13.6 illustrates the connection between stress amplitude and mean stress arising during cyclic deformation. As discussed above, the martensitic phase transformation provokes an increase of the stress amplitude which, in addition, goes along with a decreasing mean stress whose magnitude as well increases with increasing strain amplitude. This behavior was also observed by other authors [47, 53, 54] and is attributed to the volume expansion accompanying the α′-martensite formation. Prior to the described behavior, a stage of increasing mean stress is observed which is more pronounced with decreasing strain amplitude, i.e. with a less pronounced α′-martensite formation. This increase of the mean stress is probably due to highly faulted areas, i.e. regions with a high density of stacking faults called ε-martensite in literature. This ε-martensite causes a volume contraction and, thereby, an increasing mean stress in total strain controlled fatigue tests. However, this effect is overcompensated once the α′-martensite formation and its volume expansion sets in resulting in the described decreasing mean stresses.

Fig. 13.6

Stress amplitudes and mean stresses of selected strain amplitudes versus number of cycles for the HP 16-6-4 (a) and HP 16-6-6 (b). After [13]

13.3.2 Microstructure After Cyclic Deformation

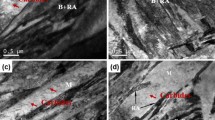
The formation of stacking faults, ε-martensite and α′-martensite is verified by SEM investigations and exemplarily shown in Fig. 13.7 for the HP 16-6-4 steel cyclically deformed at ∆ε_t/2 = 0.25%. A high amount of deformation bands is formed inside the grains (Fig. 13.7a, b) and their stacking fault density increases with ongoing plastic deformation. However, after cyclic deformation these bands are often indexed as ε-martensite by EBSD (Fig. 13.7d, yellow coloured) due to the high density of stacking faults changing the stacking sequence of the {1 1 1} planes from ABCABC of the fcc crystal lattice to the hexagonal ABAB [7]. In accordance with other authors, e.g. [55], these highly faulted deformation bands are a preferred nucleation site for α′-martensite as revealed by Fig. 13.7b (white arrows) and d indicating a martensitic phase transformation in the order γ → ε → α′.

Fig. 13.7

Microstructure of the steel HP 16-6-4 after cyclic deformation at ∆ε_t/2 = 0.25%. BSE (a, b) and ECCI (c) images as well as EBSD phase map (d, blue—α′-martensite, yellow—ε-martensite, grey—band contrast). After [13, 19]

Some individual stacking faults are also present in between the deformation bands as shown in Fig. 13.7c (white arrows). Furthermore, this micrograph reveals the quite planar glide character of the material due to its low SFE.

The increased SFE of the HP 16-6-9 on the other hand causes a change in the deformation mechanisms, which in addition are depending on the applied strain amplitude. At small strain amplitudes only few grains contain deformation bands which are usually oriented approximately 45° in relation to the loading axis (Fig. 13.8a, b). As already known for the steel HP 16-6-4 the deformation bands consist of stacking faults. In the vicinity of the crack tip a higher deformation band density (Fig. 13.8c) is observed due to the higher local plasticity. Figure 13.8d even reveals Σ3-twin boundaries which are marked in yellow indicating deformation bands of sufficient thickness with respect to the resolution of the EBSD scan thus being fatigue-induced twins.

Fig. 13.8

BSE (a) and ECCI (b, c, e) images and EBSD orientation (d) and phase (f) maps of the steel HP 16-6-9 cyclically deformed at ∆ε_t/2 = 0.4% (a–d) and ∆ε_t/2 = 0.8% (e, f), respectively. Loading axis is horizontally. After [13, 18, 19]

At a higher strain amplitude of ∆ε_t/2 = 0.8% the density of deformation bands increases. In between the bands dislocation cells are formed (Fig. 13.8e) indicating the beginning transition to a wavy glide character [56]. Nevertheless, a rare formation of α′-martensite via the intermediate ε-martensite is observed as well (Fig. 13.8f) at this high strain amplitude. However, the secondary hardening in the cyclic deformation curve (Fig. 13.3c) is rather due to fatigue-induced twinning as the α′-martensite fraction remains low and the twins are strong obstacles for dislocation movement reducing the mean free path for dislocations on a second slip system [18, 46, 57].

13.3.3 Fatigue Life

The fatigue life estimation for the HP materials according to Basquin-Manson-Coffin is shown in Fig. 13.9a. Obviously, the most metastable steel HP 16-6-4 exhibits a superior lifetime at small strain amplitudes compared to HP 16-6-9 and vice versa. Accordingly, the α′-martensite formation seems to be detrimental at high strain amplitudes due to the decreased ductility of the material which is a determining factor in this lifetime regime [58]. On the other hand, at small strain amplitudes the α′-martensite formation leads to a significant decrease in the plastic strain amplitude and, thereby, to an increase in the fatigue life . This strain amplitude-dependent impact of the martensitic phase transformation on the fatigue life causes a crossover of the lifetime curves for the different austenite stabilities at a total strain amplitude of approximately ∆ε_t/2 = 0.5% (Fig. 13.9a).

Fig. 13.9

Total strain based fatigue life curves (a), and SSP_pl parameter for lifetime estimation with one power law and corresponding scatter band of factor 3 (b). After [13, 19]

For the lifetime description of all HP variants with just one power law, Glage [13] proposed the plastic stress-strain product SSP_pl:

$$ {\text{SSP}}_{\text{pl}} = \sqrt {\frac{\Delta \sigma }{2}\frac{{\Delta \varepsilon_{\text{pl}} }}{2}E} $$

(13.2)

As already discussed, the α′-martensite formation provokes an increase of the stress amplitude ∆σ/2 which is accompanied by a decrease in the plastic strain amplitude ∆ε_pl/2. The SSP_pl considers both parameters resulting in much smaller differences between the material variants (Fig. 13.9b). Despite the fact that variant specific lifetime curves would still exhibit slightly different slopes, it is possible to provide a surprisingly good lifetime description for all materials with just one power law (Fig. 13.9b). In fact, almost all test data is located within a scatter band of factor 3.

13.4 Influence of the Manufacturing Method on the Fatigue Behavior

This section compares the fatigue properties of the same steel grade (base composition 16-6-6, cf. Table 13.1) manufactured via different processing routes: (i) Casting, (ii) additive manufacturing by EBM and (iii) reversion annealing to achieve an UFG microstructure.² In addition, the results will be compared to the HP counterpart which was introduced in Sect. 13.3. The manufacturing methods are described in more detail in Sect. 13.2.2.

13.4.1 Microstructure of the Undeformed State

The microstructures of the different material states before cyclic deformation are shown in Fig. 13.10. The biggest difference is observed regarding the average grain size . The cast material by far exhibits the biggest grain size of 774 μm whereas the smallest one is observed for the UFG state with 0.7 μm. In between these two materials, the EBM and HP states fit in with average grain sizes of 38 μm and 10 μm, respectively. However, for an additive manufactured material the microstructure of the EBM 16-6-6 (Fig. 13.10b) is relatively isotropic which is attributed to multiple phase transformations caused by the process-inherent cyclic heat treatment [14, 15]. Nevertheless, the grains are characterized by a slightly elongated shape oriented along the build direction as indicated by an average aspect ratio of 0.34 and a grain shape orientation of 91°, cf. Fig. 13.10b.

Fig. 13.10

EBSD orientation maps of the microstructures before cyclic deformation of the cast (a), EBM (b, build direction vertical), UFG (c) and HP (d) state, respectively. (d) After [14]

Besides anisotropy, another issue regarding additive manufactured materials are process-induced defects like lack of fusion which have a detrimental effect on the mechanical properties, in particular the fatigue lifetime. The present EBM 16-6-6 exhibited a relative density of 99.4% compared to over 99.99% for the HP 16-6-6 according to μCT-scans. As depicted in Fig. 13.11, the EBM material contains a high number of small pores with a sphericity of more than 0.5, i.e. with a relatively round and spherical shape. The pore density decreases significantly for higher equivalent pore diameters d_P. Accordingly, less than 20 pores with a d_P > 200 μm were detected. However, the sphericity decreases with increasing d_P and the two biggest pores with a d_P of almost 1600 μm exhibit a sphericity below 0.2. In contrast, the few defects in the HP state all exhibit a d_P < 100 μm and sphericities above 0.5.

Fig. 13.11

μCT results of the EBM and HP 16-606 materials. a 3D-volume defect distribution (LA: loading axis) and b pore density and sphericity plotted against the equivalent pore diameter. The diameter of the scanned gauge length was 3 mm. After [14]

13.4.2 Cyclic Deformation Behavior and α′-Martensite Formation

The stress amplitudes at the beginning of cyclic deformation strongly depend on the material state and, in particular, on the grain size (Fig. 13.12). The cast 15-6-6 with the biggest grain size exhibits the lowest initial stress amplitudes of 200–300 MPa. With decreasing grain size the stress amplitudes of the first cycles increase to about 290–400 MPa for the EBM state and are once again slightly higher in case of the HP reference material (Fig. 13.3b). By far the highest initial stress amplitudes are observed for the UFG state with about 600–1000 MPa. These differences are supposed to stem from a reduced mean free path for dislocation movement as the number of obstacles in terms of grain boundaries increases with decreasing grain size of the austenite. In this context it has to be noted, that the materials discussed here all exhibit a mostly planar glide character. Wavy glide materials on the other hand exhibit other dislocation arrangements like bundles or cells whose size is significantly smaller compared to conventional grain sizes , i.e. the grain boundaries have a minor influence on the dislocation movement. Accordingly, in wavy glide a grain size dependence regarding the cyclic stress is only observed for UFG and NC materials [59].

Fig. 13.12

Cyclic deformation curves of the cast (a), EBM (b) and UFG (c) states. After [12] (a), [14] (b) and [16] (c)

A further difference is observed for the cyclic hardening behavior of the material states. Whereas the cast and the EBM materials exhibit similar behavior compared to the HP state discussed in Sect. 13.3.1, i.e. a strong cyclic hardening especially at high strain amplitudes caused by α′-martensite formation (Fig. 13.13), the cyclic hardening is less pronounced for the UFG material (Fig. 13.12c). Although the α′-martensite fraction after cyclic deformation at high strain amplitudes is the highest for the UFG state, the induced cyclic hardening is the least pronounced. This is attributed to the origins of α′-martensite induced hardening, namely (i) the higher strength of α′-martensite compared to austenite, (ii) the smaller grain size of α′-martensite and (iii) the reduced mean free path for dislocation movement in the austenite due to the formation of α′-martensite nuclei in the deformation bands [4, 50]. As the average austenitic grain size of 0.7 μm in the UFG material is already quite small, the α′-martensite formation does not lead to a distinct grain refinement. Furthermore, no deformation bands are formed and the influence of the α′-martensite formation on the mean free path is negligible as will be seen in Sect. 13.4.3. However, as only the first out of three hardening mechanisms is relevant in the UFG state, the least pronounced increase of the cyclic stress compared to the other material states where all three mechanisms are active is consistent.

Fig. 13.13

α′-martensite evolution during cyclic deformation at different strain amplitudes for the material states cast (a), EBM (b) and UFG (c). After [12] (a), [14] (b) and [16] (c)

Moreover, a difference in the incubation period for the onset of α′-martensite formation is observed. Figure 13.14 shows the cumulated plastic strain threshold λ_p,th which has to be exceeded to trigger the phase transformation plotted against the applied strain amplitude. As expected, the threshold value decreases with increasing strain amplitude (cf. Sect. 13.3.1 for more detailed discussion on this). The only exception is the EBM state cyclically deformed at ∆ε_t/2 = 1.2%. As obvious in Fig. 13.13b, the signal of the Feritscope^® is quite unusual for the respective specimen probably due to a misalignment or other experimental issues during the test. However, due to this irregularity, this specimen is excluded from the following discussion on the incubation period.

Fig. 13.14

Cumulated plastic strain threshold λ_p,th which has to be exceeded to trigger the fatigue-induced α′-martensite formation plotted against the applied total strain amplitude for the different material states

The EBM and cast states exhibit similar threshold values λ_p,th (Fig. 13.14) which are reduced in comparison to the already known HP material. This difference most probably stems from differences in the chemical composition. The values given in Table 13.1 are valid for the powders of the EBM and HP states, respectively. However, the bulk EBM material contains 0.5 wt.% less Mn than the HP state due to evaporation during EBM processing [15, 60]. The cast material as well exhibits a lower Mn content and a slightly lower Ni content than the HP state. This reduced content of austenite stabilizers leads to a decrease in austenite stability [61, 62] and a shift of the cumulated plastic strain threshold λ_p,th to lower values.

The UFG state on the other hand exhibits a slightly higher Mn and Ni content than the HP material but an even lower threshold λ_p,th than the EBM and cast states. Hence, in this case another factor has to be more dominant than the higher austenite stability due to the chemical composition. This is supposed to be the significantly higher stress amplitude at the onset of α′-martensite formation. These high cyclic stresses lead to the formation of small α′-martensite nuclei at an earlier stage of deformation compared to the other material states.

13.4.3 Microstructure After Cyclic Deformation

The microstructural features developing during cyclic deformation are similar in case of the cast, EBM processed and HP states. Figures 13.15a, b exemplarily show a grain of the EBM state cyclically deformed at ∆ε_t/2 = 0.3%. Deformation bands containing a high density of stacking faults have developed inside the grain. The stacking fault density increases with ongoing plastic deformation and as already discussed in Sect. 13.3.2 at a high density the deformation bands get indexed as ε-martensite by EBSD indicating a highly faulted microstructure (Fig. 13.15b). Furthermore, α′-martensite nuclei form inside the deformation bands acting as dislocation barriers for the stacking faults. Thus, the martensitic phase transformation occurs via the intermediate ε-martensite, i.e. γ → ε → α′. At higher strain amplitudes several glide systems are activated and intersecting deformation bands provide a preferred nucleation site for α′-martensite [1, 2, 63]. In general, the α′-martensite formation is triggered by a double shear mechanism of at least two intersecting stacking faults on different slip planes.

Fig. 13.15

a, b BSE image and corresponding EBSD phase map of the EBM state cyclically deformed at ∆ε_t/2 = 0.3% (loading axis is vertical; red—austenite, yellow—ε-martensite, blue—α′-martensite). c, d t-SEM micrographs and e TEM bright field image of the UFG state cyclically deformed at ∆ε_t/2 = 0.8%. f, g SAED patterns of the areas marked by I and II in (e). After [14] (a, b) and [16] (c–g)

However, this characteristic deformation band structure is not observed in the UFG material. Instead, individual stacking faults often reach through the entire grain (Fig. 13.15c, d). At this grain size , the stacking faults are supposed not to nucleate within the grains but at the grain boundaries, i.e. single partial dislocations are emitted from grain boundaries and propagate into the grain interior until they reach the grain boundary on the opposite side or some other obstacle. However, the stacking fault density in the grains is supposed to increase in this manner until ε-martensite is indexed by EBSD as well, cf. [16]. Due to the high stresses quite small α′-martensite nuclei form inside these highly faulted grains (Fig. 13.15d, marked by I and II) and grow until the whole grain is martensitic. SAED patterns verify this assumption. The area marked by I in Fig. 13.15e is already transformed to α′-martensite as indicated by its bcc SAED pattern (Fig. 13.15f). It exhibits a Nishiyama-Wassermann orientation in relation to the adjacent fcc area marked by II (Fig. 13.15e, g). Hence, the α′martensite nucleated inside this grain, i.e. even at this small size the grains do not transform entirely at once.

13.4.4 Fatigue Life

Figure 13.16 shows the fatigue life curves of the discussed material states. In addition, a curve labeled EBM 16-6-6 ann. is plotted which represents a solution annealed (1050 °C, 30 min) state of the EBM material (see [14] for further details). However, the shortest fatigue life with the highest scatter is observed for the cast material. The quite big grain size with just a few grains per cross section may contributes to this inferior behavior. Further factors are supposed to be the inhomogeneous microstructure in terms of segregations and the porosity originating from the casting process.

Fig. 13.16

Total strain based fatigue life curves of the different material states. Data from [12] (cast), [14] (EBM ), [16] (UFG ) and [13] (HP)

In contrast, the highest fatigue life is observed for the UFG material. In the high cycle fatigue (HCF) regime where the strength is an important lifetime determining factor this is a quite usual behavior and often reported in literature, e.g. [59, 64, 65]. In the low cycle fatigue (LCF) regime on the other hand, the increased strength does not lead to a significant reduction of the plastic strain amplitude and the ductility of the material becomes an essential factor for fatigue life . Hence, coarse grained (CG) materials usually exhibit an enhanced lifetime in the LCF regime due to their higher ductility [59, 64, 65]. In contrast, the present UFG state exhibits the highest lifetime even in the LCF regime. This behavior is supposed to be related to the different phases, more precisely a more homogenous strain partitioning between the austenitic and martensitic phase in comparison to the other material states. As already discussed above, the grain size of the austenite and α′-martensite is similar in the UFG state (<1 μm). Thus, the difference in strength is due to the different hardness values of the individual phases. As Weidner et al. [50] revealed by nano indentation experiments on the present steel alloy this difference is just about 25% in favor of a higher hardness of the α′-martensite. In the CG materials the smaller grain size of the α′-martensite increases the resistance against plastic deformation significantly due to the Hall-Petch effect. Thus, in CG materials the austenite has to carry a disproportionally high share of the strain in relation to its phase fraction. With increasing α′-martensite fraction, i.e. with increasing strain amplitude, this mismatch increases as well. In the UFG state with similar grain size and, thus, similar resistance against plastic deformation, the α′-martensite has to bear its fair share of the applied strain. Hence, the more homogenous strain distribution overcompensates the decreased ductility in comparison to the CG materials and leads to a higher fatigue life in the LCF regime [16].

The fatigue life of the EBM as-built and annealed states lies in between the cast and HP material. In this context, the relatively high porosity of the material after EBM processing (cf. Sect. 13.4.1) has to be taken into account. Figure 13.17 shows the fracture surface of an annealed EBM specimen (∆ε_t/2 = 0.8%) with severe lack of fusion defects. Some of these defects reach dimensions of up to 500 μm and are located directly underneath the surface. Despite this quite detrimental condition, the cyclic deformation curve does not seem to be affected by these defects. Even the fatigue life almost matches the calculated fatigue life curve (Fig. 13.16, marked by an arrow). Moreover, the scatter of the EBM states is surprisingly low and the fatigue performance quite good when keeping in mind the severe defects. Of course the detrimental effect of the defects regarding the lifetime increases with decreasing strain amplitude because the crack initiation phase becomes more dominant [58]. Hence, the fatigue life decreases in comparison to the HP state but it is still quite reasonable. This damage tolerant behavior is supposed to stem from the high ductility of the material combined with its outstanding hardening capability. The process-inherent defects act as notches and the highest stresses occur at the roots of the notches. Thus, the deformation in the vicinity of the defects is quite pronounced at the beginning of cyclic deformation. Consequently, these areas exhibit the highest cyclic hardening and, thus, transfer the deformation to other areas of the material. Of course, this “shielding effect” gets the more effective the higher the hardening capability of the material is, which in the present alloy is quite high as revealed by the cyclic deformation curves (Fig. 13.12b). Another beneficial factor is of course the high ductility of the material which reduces the stress concentrations at the defects as also observed for an additive manufactured 316 L austenitic steel by other authors [66].

Fig. 13.17

Both sides of the fracture surface (a, b) of the EBM 16-6-6 ann. specimen cyclically deformed at ∆ε_t/2 = 0.8%. (I-VI) Magnified views of selected defects marked by I-VI in (a). After [14]

13.5 Influence of Particle Reinforcement

This section presents the influence of a particle reinforcement on the fatigue properties and cyclic deformation behavior of metastable austenitic steels.³ Therefore, composites based on the HP 16-6-6 and HP 16-6-9 (cf. Sect. 13.3.1) with 5 and 10 vol.% zirconia, respectively, were processed via HP (cf. Sect. 13.2.2). The zirconia was partially stabilized by MgO (Mg-PSZ) enabling a tetragonal phase fraction of about 32% (cf. Table 13.2).

13.5.1 Cyclic Deformation Behavior of Particle Reinforced Steel-Matrix-Composites

The cyclic deformation curves in Fig. 13.18 reveal the reinforcing effect of the Mg-PSZ particles. Especially at medium and high strain amplitudes the initial stress amplitudes increase with increasing Mg-PSZ fraction. The qualitative courses of the composites based on the HP 16-6-6 steel (Fig. 13.18a–c) are similar to the cyclic deformation curves of the particle-free steel exhibiting an initial cyclic hardening followed by cyclic softening at medium and low strain amplitudes. The subsequent cyclic hardening due to the fatigue-induced α′-martensite formation is observed as well but is considerably less pronounced and decreases significantly with increasing Mg-PSZ fraction. This diverging cyclic hardening gets even more obvious with increasing strain amplitudes.

Fig. 13.18

Cyclic deformation curves of the composites reinforced with 5% Mg-PSZ (a, d) and 10% Mg-PSZ (b, e) based on the HP 16-6-6 (a, b) and HP 16-6-9 steels (d, e), respectively. (c, f) Comparison of the composite materials with the unreinforced HP 16-6-6 (c) and HP 16-6-9 (f). After [13] (c) and [18, 19] (d–f)

For the variants based on the HP 16-6-9 steel (Fig. 13.18d–f) the secondary hardening due to deformation-induced twinning (cf. Sect. 13.3.1) is even suppressed entirely in case of the composites. A primary hardening similar to the particle-free steel but at higher stress levels is observed followed by cyclic softening until failure. Even the highest strain amplitude of ∆ε_t/2 = 1.2% does not exhibit a secondary hardening regime.

The inhibition of the cyclic hardening due to fatigue-induced α′-martensite formation and twinning, respectively, is attributed to the occurring damage inside the composite materials in terms of rupture and debonding of particles as well as coalescence of cracks. These particle-related damage mechanisms seem to be more dominant than the still active hardening mechanisms in the steel matrices and lead to the observed macroscopic cyclic softening [13, 18, 19]. Thus, the damage evolution will be discussed in more detail in the next section.

13.5.2 Damage Evolution

The damage evolution is investigated by means of the damage parameters D_T (under tension) and D_C (under compression) which are based on the changes of the specimens’ stiffness and are calculated according to Hartmann et al. [67] as follows

$$ D_{T} \left( N \right) = \frac{{E_{T,0} - E_{T} \left( N \right)}}{{E_{0} }} $$

(13.3)

$$ D_{C} \left( N \right) = \frac{{E_{C,0} - E_{C} \left( N \right)}}{{E_{0} }} $$

(13.4)

where E_T,0 and E_C,0 are the stress dependent stiffnesses of the undamaged material and E₀ is the stiffness at zero stress. A fatigue test accompanied by a Long Distance Microscope (Institute of Physics of Materials, Brno, Czech Republic) revealed the validity of D_T as an indicator for damage by comparing the latter with the evolution of the surface crack length [13]. However, among the present materials the HP 16-6-9 steel and its composites have the best ability for investigations on the damage parameter evolution as the calculations are not influenced by a phase transformation [13].

Both damage parameters generally increase with increasing number of cycles as shown in Fig. 13.19. For small strain amplitudes ∆ε_t/2 ≤ 0.3% the evolution is similar for tension (D_T) and compression (D_C) in both material states. Of course, at the end of lifetime, D_T strongly increases due to the formation of a macrocrack which significantly decreases the specimen stiffness under tensile stress. However, up to that point no considerable damage seems to take place at small strain amplitudes and the increase of the damage parameters is mainly attributed to a stiffness reduction in consequence of the plastic deformation. For higher strain amplitudes the magnitude of D_T and D_C start to differ and further diverge with increasing strain amplitude. In case of the particle-free steel, crack initiation and subsequent crack growth lead to a decrease in specimen stiffness. In the composite with 10 vol.% Mg-PSZ particle rupture, particle debonding and crack coalescence additionally contribute to the stiffness reduction under tension causing a stronger increase of D_T (Fig. 13.19b). These particle-related damage mechanisms seem to be rare and negligible at small strain amplitudes but the impact on D_T increases markedly with higher loads. The reduction of the load-bearing cross section is of course less obvious in compression as the cracks and debonded interfaces are mostly closed and, thus, are contributing to the load transfer which explains the diverging evolution of D_T and D_C [13, 67].

Fig. 13.19

Evolution of the damage parameters D_C and D_T for the particle-free HP 16-6-9 steel (a) and its counterpart reinforced with 10 vol.% Mg-PSZ (b). After [13]

13.5.3 Cyclically Deformed Microstructure

This section presents the microstructure of the composite HP 16-6-9+10Z with focus to the Mg-PSZ particles. For description of the deformation mechanisms of the steel matrix the reader is referred to Sect. 13.3.2. The BSE image in Fig. 13.20a gives an overview on the typical damage mechanisms related to the particle reinforcement , i.e. particle rupture, debonding and crack coalescence. Which of the former two mechanisms occurs depends on the particle shape and in particular its size. Particle rupture is mainly observed for large particles which often break perpendicular to the loading axis. Debonding is found for all particle sizes and is the dominant mechanism for small particles which break rarely. Similar size effects have been observed for particle reinforced aluminum matrix composites [68].

Fig. 13.20

a BSE image of HP 16-6-9+10Z showing the particle-related damage mechanisms after cyclic deformation at ∆ε_t/2 = 0.3%. b, c BSE image and EBSD phase map of the same Mg-PSZ particle in a HP 16-6-9+10Z specimen cyclically deformed at ∆ε_t/2 = 0.8% (red—m-ZrO₂, yellow—c/t-ZrO₂; grey—band contrast). Loading axis was horizontal. After [18]

Figure 13.20b shows a BSE image of a Mg-PSZ particle embedded in the austenitic matrix after cyclic deformation at a high strain amplitude. Deformation is clearly visible inside the particle and the corresponding EBSD image (Fig. 13.20c) reveals the monoclinic phase for the band-like structures. The remaining particle is most probably in the tetragonal condition of ZrO₂. Hence, it is assumed that a stress-assisted phase transformation from the tetragonal to the monoclinic condition has occurred during cyclic deformation. In contrast, the monoclinic fringe at the interface to the austenitic matrix most probably stems from a depletion of stabilizing elements (mainly Mg) due to diffusion to interface phases and/or into the austenite during HP [69].

13.5.4 Fatigue Life

The influence of the particle reinforcement on the fatigue life is shown in Fig. 13.21 for the HP 16-6-6 and HP 16-6-9. The fatigue life decreases with increasing volume fraction of Mg-PSZ particles for both variants. Nevertheless, there are differences in the lifetime in dependence of the applied strain amplitude. For the HP 16-6-9 (Fig. 13.21b) the lifetime reduction due to the particles decreases with decreasing strain amplitude and the lifetime curves converge at high fatigue lifetimes. This is in accordance with the damage behavior discussed in the previous section. As the particle-related damage decreases with decreasing strain amplitude its detrimental influence on the lifetime decreases as well leading to the convergence.

Fig. 13.21

Total strain based fatigue life curves of the composites materials based on the HP 16-6-6 (a) and the HP 16-6-9 (b) in comparison to its unreinforced counterparts. After [13] (a) and [18, 19] (b)

One would expect similar results for the HP 16-6-6 as the particle-related damage should influence the fatigue life in a similar manner. However, a convergence of the fatigue life curves is not observed (Fig. 13.21a). The lifetime reduction due to the particle reinforcement stays constant or even tends to increase with decreasing strain amplitude. This is not attributed to a change in the particle-related damage but to a less pronounced α′-martensite formation in the composites compared to the unreinforced steel, cf. [13, 17, 19]. As discussed in Sect. 13.3.3, the α′-martensite formation is beneficial for the fatigue life in the HCF regime. Thus, the decreased particle-related damage at small strain amplitudes is more or less compensated by a detrimental reduction of the α′-martensite formation. Overall, the fatigue life decreases with increasing particle volume fraction for all strain amplitudes applied.

13.6 Fatigue Properties of a Q&P Ultra-High Strength Steel

This section presents the fatigue properties of an ultra-high strength austenitic steel alloy which was designed to exceed the strength of the steels discussed in the previous sections at simultaneously reasonable ductility [21]. As this steel is fully austenitic at room temperature, the usual quenching and partitioning (Q&P) process has been modified (cf. Sect. 13.2.2), provoking the formation of α′-martensite during a cooling step. Two material states which differ in the α′-martensite fraction due to different cooling temperatures (T_c,1 = −120 °C, T_c,2 = −20 °C) have been cyclically deformed. Moreover, Q&P and, thus, the fatigue tests were performed in the cast condition of this stainless steel.⁴

13.6.1 Microstructure After Q&P

Magnetic measurements reveal different α′-martensite fractions after Q&P of 45 vol.% for the material state cooled down to T_c = −120 °C and of 22 vol.% for T_c = −20 °C, respectively. The different phase fractions are also evident in the light optical micrography images of etched specimens in Fig. 13.22. The α′-martensite appears darker and especially for T_c = −20 °C (Fig. 13.22b) the dendritic structure of the cast material is still apparent. The dendrite cores solidify first and contain less alloying elements compared to the interdendritic regions. Thus, the martensite start temperature M_s of the former is higher triggering a preferred formation of α′-martensite during the cooling stage.

Fig. 13.22

Micrographs taken by light optical micrography of the etched microstructures of the −120 °C (a) and −20 °C (b) state after Q&P. After [22]

A micrograph at higher magnification is shown in Fig. 13.23a in terms of a BSE image. The corresponding EBSD phase map (Fig. 13.23b) reveals large blocky austenitic areas of about 20 μm in size which are most probably interdentritic regions with higher austenite stability. In addition, fine so-called interlath austenite is observed in areas which are mostly martensitic. Besides mechanical properties, this is important in context with the partitioning treatment and the provoked diffusion of C and N from the supersaturated α′-martensite into austenite. Due to a limited diffusion length of the interstitial elements C and N the stabilizing effect will most likely be more pronounced in the interlath austenite [21]. Furthermore, the α′-martensite fraction after the cooling stage is supposed to have an influence on the extent of diffusion and, thus, stabilization, i.e. with increasing α′-martensite fraction the austenite stabilization should increase as well.

Fig. 13.23

BSE image (a) and corresponding EBSD phase map with superimposed band contrast (b, red—austenite, yellow—ε-martensite, blue—α′-martensite) of the −120 °C state after Q&P. After [22]

13.6.2 Cyclic Deformation Behavior

The cyclic deformation curves of the −120 °C state (partitioned condition) are given in Fig. 13.24a. The stress amplitudes are quite high and even exceed 1400 MPa for ∆ε_t/2 = 1.2%. Moreover, the cyclic stress markedly increases with increasing strain amplitude indicating a high amount of obstacles for dislocation glide most probably due to the high amount of α′-martensite. In addition, carbides inside the α′-martensite formed during partitioning may contribute to the high cyclic stress. However, at high strain amplitudes the material exhibits a continuous cyclic hardening until failure. After several cycles the hardening gets more pronounced which is attributed to a fatigue-induced formation of α′-martensite, cf. Sect. 13.3.1. In contrast, the course of the cyclic deformation curves for the small strain amplitudes ∆ε_t/2 ≤ 0.3% seem to be relatively constant, i.e. without any cyclic softening or hardening. However, this is just a scaling issue due to the wide range of the ordinate. For this reason, a cyclic hardening parameter H_cyc is introduced calculated according to

Fig. 13.24

Cyclic deformation curves of the −120 °C (a) and −20 °C (b) states, cyclic hardening parameter H_cyc for a strain amplitude of ∆ε_t/2 = 0.3% (c) and α′-martensite fraction after cyclic deformation (d), respectively, of the Q&P ultra-high strength steel. After [22]

$$ H_{\text{cyc}} = \frac{{(\Delta \sigma /2)_{{N_{i} }} }}{{(\Delta \sigma /2)_{N = 1} }} $$

(13.5)

where ∆σ/2 _Ni and ∆σ/2_N = 1 are the stress amplitudes of the current and first cycle, respectively. Figure 13.24c shows the course of H_cyc for the strain amplitude of ∆ε_t/2 = 0.3%. A similar behavior to the high alloy austenitic steels discussed in the previous sections is observed. At beginning of cyclic deformation a short stage of cyclic hardening is observed followed by cyclic softening. After an incubation period secondary hardening sets in and continues until failure, cf. Sect. 13.3.1. Thus, similar mechanisms in terms of dislocation interaction and martensitic phase transformation are supposed to be active in the Q&P steel as well.

Qualitatively, the −20 °C material state exhibits similar cyclic deformation curves (Fig. 13.24b) but the stress amplitudes at the beginning of cyclic deformation are considerably lower and the cyclic hardening is more pronounced. The reduced initial stress amplitudes are due to the lower initial α′-martensite fraction. In contrast, due to a lower austenite stability the fatigue-induced α′-martensite formation is more pronounced compared to the −120 °C state and this difference significantly increases with increasing strain amplitude. Whereas at medium and small strain amplitudes the overall α′-martensite fraction after failure (Fig. 13.24d) remains lower in case of the −20 °C state, at ∆ε_t/2 ≥ 0.8% its phase transformation during cyclic deformation even overcompensates the lower initial fraction leading to higher overall values. This is reflected in the cyclic deformation curves as well. Just in the case of the high strain amplitudes the −20 °C state exceeds its counterpart in terms of the maximum stress amplitude. Hence, the cyclic stresses correlate quite well with the α′-martensite fraction and seem to be relatively independent on the type of α′-martensite, i.e. thermally-induced or fatigue-induced. However, for the strain amplitude ∆ε_t/2 = 1.2% the crossover of stress amplitudes already occurs in an early stage of cyclic deformation (13 cycles) as the fatigue-induced phase transformation is quite strong.

13.6.3 Fatigue Life

As discussed in Sect. 13.3.3 different austenite stabilities cause a crossover of the fatigue life curves in case of high alloy austenitic steels (Fig. 13.9a). As the austenite stability of the present Q&P steels differs as well, a similar behavior could be expected. In contrast, the −120 °C state exhibits a superior fatigue life at all applied strain amplitudes (Fig. 13.25). The lifetime advantage even increases with decreasing strain amplitude. Well known for the high alloy steels, α′-martensite is assumed to have a beneficial effect on the fatigue life in the HCF regime due to the higher strength of the material, but a detrimental effect in the LCF regime due to the decrease in ductility. Thus, at high strain amplitudes the pronounced fatigue-induced phase transformation in the −20 °C state which overcompensates its lower initial α′-martensite fraction (cf. Sect. 13.6.2) leads to the inferior fatigue life . At small strain amplitudes on the other hand, the fatigue-induced phase transformation is less pronounced and the overall α′-martensite fraction as well as the cyclic stresses of the −20 °C state never reach the level of its counterpart. In this fatigue regime a higher strength markedly reduces the plastic strain amplitude and, thus, reduces the damage and enhances the lifetime. Accordingly, once again the −120 °C state exhibits a higher fatigue life .

Fig. 13.25

Total strain based fatigue life curves of the −120 °C (blue) and −20 °C (green) states of the Q&P ultra-high strength steel. After [22]

13.6.4 Microstructure After Cyclic Deformation

The BSE, ECCI and EBSD images of Fig. 13.26 give an impression of the microstructure of the Q&P steel after cyclic deformation. As already observed for the qualitative course of the cyclic deformation curves , the micrographs reveal distinct similarities with the other high alloy austenitic steels. Figure 13.26a shows an austenitic area surrounded by α′-martensite. A lot of deformation bands on different slip systems have formed inside the austenite. Within these deformation bands α′-martensite nuclei are found (marked by white arrows in Fig. 13.26a, b) which in part are quite small. According to the EBSD phase maps in Fig. 13.26g, i the deformation bands are often indexed as ε-martensite, i.e. the density of stacking faults is quite high in these areas. Thus, analogue to the other high alloy austenitic steels presented in this work, the α′-martensite is supposed to form in the sequence γ → ε → α′.

Fig. 13.26

Microstructures of the −120 °C (a–d, g, h) and −20 °C (e, f, i) state cyclically deformed at ∆ε_t/2 = 0.3% (a, c–f, i), ∆ε_t/2 = 0.5% (b) and ∆ε_t/2 = 0.8% (g, h), respectively. a, b, e, f BSE images. c, d ECCI images. g, i EBSD phase maps (red—austenite, yellow—ε-martensite, blue—α′-martensite). h EBSD orientation map of the α′-martensite phase of (g) and corresponding bcc pole figures. Loading axis is vertical for all micrographs. After [22]

However, the plasticity is not limited to the deformation bands but also stacking faults form in between the deformation bands on different slip systems as revealed by ECCI images in Fig. 13.26c, d. Moreover, all micrographs reveal a quite planar glide character as no dislocation arrangements due to wavy glide like dislocation cells have been observed.

Even though the triggered microstructural mechanisms are similar in both Q&P states, there are some indications for their different austenite stabilities as well. The α′-martensite fraction inside the deformation bands appears higher for the −20 °C state (Fig. 13.26e, f) when comparing specimens cyclically deformed at the same strain amplitude. Hence, the martensitic phase transformation occurs more rapidly in the −20 °C state due to its lower austenite stability. These observations support the statements regarding the cyclic hardening behavior discussed in Sect. 13.6.2.

13.7 Conclusions

Several aspects of the cyclic deformation and fatigue behavior of metastable austenitic steels were discussed in the present work including the influence of a particle reinforcement and the chemical composition. Furthermore, different manufacturing methods in terms of casting, additive manufacturing , hot pressing and reversion annealing and their effect on the fatigue properties were investigated. Finally, a newly designed ultra-high strength steel produced via a modified Q&P route was presented. The main conclusions are summarized in the following.

• The SFE of an austenitic steel controls its dislocation glide character (planar or wavy) and the activation of other deformation mechanisms in terms of deformation-induced α′-martensite formation and twinning. With decreasing SFE besides dislocation movement, a fluent transition from twinning to ε-martensite and α′-martensite formation is observed.

• The SFE has a major influence on the mechanical properties and the cyclic deformation behavior as the fatigue-induced twinning and even more the fatigue-induced α′-martensite formation lead to a significant cyclic hardening .

• Besides a decreasing SFE, of course increasing strain amplitudes promote the formation of α′-martensite (Fig. 13.27a).

  Fig. 13.27

  

  α′-martensite fraction ξ (a) and fatigue life N_f (b) of high alloy austenitic steels as a function of strain amplitude ∆ε_t/2, austenite stability (AS) and stacking fault energy γ_SFE, respectively. After [13]

• The fatigue life is affected by the α′-martensite formation as well. The latter is beneficial in the HCF regime due to its strengthening effect but detrimental in the LCF regime due to the lower ductility. This opposing character leads to different slopes of the fatigue life curves and, thus, to their crossover. More precisely, the slope decreases with decreasing SFE (Fig. 13.9a), i.e. the fatigue life difference between high and small strain amplitudes increases (Fig. 13.27b), and vice versa.

• The martensitic phase transformation of all investigated steels occurs via the sequence γ → ε → α′. The intermediate ε-martensite is assumed to stem from highly faulted areas, i.e. a high stacking fault density.

• The grain size of the steel affects the cyclic deformation behavior and the martensitic phase transformation. In particular ultra-fine grained (UFG ) materials with grain sizes below 1 μm exhibit significantly higher initial stress amplitudes but a less pronounced cyclic hardening due to α′-martensite formation. Furthermore, the UFG grains are not characterized by a deformation band structure but their interior is subjected to an increase in stacking fault density as a whole.

• The remarkable hardening capability in combination with the high ductility of the high alloy steels yield an outstanding damage tolerance . A shielding effect due to the high hardening at defects and a transition of the deformation to adjacent areas is assumed to occur. Especially with regard to additive manufactured materials which suffer upon process-inherent defects like lack of fusion this damage tolerance brings advantages in terms of a less affected cyclic deformation behavior and a more than reasonable fatigue life .

• A reinforcement with Mg-PSZ particles causes a strengthening effect in terms of increasing stress amplitudes with increasing Mg-PSZ particle fraction. On the other hand, the detrimental particle-related damage in terms of debonding, particle rupture and crack coalescence increases with increasing strain amplitude. Hence, the fatigue life of the composites is reduced in the total-strain controlled experiments, especially in the LCF regime.

• The cast austenitic steel subjected to a modified Q&P processing exhibited extraordinary high stress amplitudes. Of the two material states which differ in the α′-martensite fraction after Q&P especially the state with the higher fraction achieved quite high cyclic stresses right from the beginning of cyclic deformation.