1 Introduction

Over the past decade a number of works have appeared which exploit the unique properties of Hermite-Birkhoff interpolation in space to construct arbitrary-order discretization methods for hyperbolic [1, 2, 4,5,6,7, 10, 14, 16,17,18,19] as well as Schrödinger [3] equations. The precise form of the interpolant in a single cell, which here we write in one dimension labelled t, is

$$\displaystyle \begin{aligned} u(t) \approx \ mathcal{I} u (t) \in \varPi^{2m+1}, \ \ \ \ \ t \in (t_{j-1}, t_{j}) , {} \end{aligned} $$
(1)
$$\displaystyle \begin{aligned} \frac {d^k}{dt^k} \ mathcal{I} u (t_{\ell}) = \frac {d^k u}{dt^k} (t_{\ell}); \ \ k=0, \ldots ,m, \ \ \ \ \ell=j-1,j , {} \end{aligned} $$
(2)

where Π 2m+1 denotes the polynomials of degree 2m + 1. (In higher dimensions one uses a tensor-product cell interpolant based on vertex data consisting of mixed derivatives of order through m in each Cartesian coordinate.)

In contrast, there has been little work on analogous methods for time discretization. A recent exception is the manuscript by Liu et al. [15]. They develop methods for second-order semilinear hyperbolic equations using interpolants of the form (1)–(2) combined with a reformulation of the evolution problem using exact solutions of the linear part. They demonstrate excellent long-time performance.

The outline of the paper is as follows. In Sect. 2 we list a few properties of piecewise Hermite-Birkhoff interpolation. In Sect. 3 we construct the time-stepping schemes and establish some basic results, with a few numerical experiments described in Sect. 4.

2 Basic Properties of Hermite-Birkhoff Interpolation

Hermite interpolants have a number of interesting properties which make them very attractive for the solution of differential equations; see, e.g., [2]. Here we will mainly use the simplest. Precisely, for t ∈ (t j−1, t j), the Peano representation of the local error can be easily derived by noting that \(e=u- \ mathcal {I} u\) solves the two point boundary value problem

$$\displaystyle \begin{aligned} \frac {d^{2m+2} e}{dt^{2m+2}} = \frac {d^{2m+2} u}{dt^{2m+2}} , \ \ \frac {d^k e}{dt^k}=0, \ \ t=t_{j-1},t_j, \ \ k=0, \ldots m . {} \end{aligned} $$
(3)

Thus

$$\displaystyle \begin{aligned} e(t) = \int_{t_{j-1}}^{t_j} K_j(t,s) \frac {d^{2m+2} u}{dt^{2m+2}} (s) ds , {} \end{aligned} $$
(4)

where the kernel K j is the Green’s function for (3). Simple scaling arguments combined with the transformation t = t j−1 + zh j then show that \(e=O(h_j^{2m+2})\) where h j = t j − t j−1 is the time step. A fundamental feature of piecewise Hermite interpolation is the following orthogonality property. For any functions v(t), w(t)

$$\displaystyle \begin{aligned} \int_{t_{j-1}}^{t_j} \frac {d^{m+1} \ mathcal{I}v}{dt^{m+1}} (t) \cdot \frac {d^{m+1} \left( w-\ mathcal{I}w \right)}{dt^{m+1}} (t) dt =0 , {} \end{aligned} $$
(5)

which in particular implies that interpolation reduces the H m+1 seminorm.

3 Time-Stepping Methods

We begin by considering the initial value problem for a first-order system ordinary differential equations:

$$\displaystyle \begin{aligned} \frac {du}{dt} = f(u,t) , \ \ \ \ u(t_0)=u_0 , \ \ \ \ u(t) \in \mathbb{R}^d . {} \end{aligned} $$
(6)

Given a discrete time sequence t j > t j−1, j = 1, …, N, with time steps h j = t j − t j−1 we write down the Picard integral formulation of the time evolution over a single step

$$\displaystyle \begin{aligned} u(t_j) = u(t_{j-1}) + \int_{t_{j-1}}^{t_j} f(u(s),s) ds . {} \end{aligned} $$
(7)

The construction of our time integration formula proceeds in three steps. We denote by v j the approximation to u(t j).

  1. 1.

    Given v j−1 and assuming for the moment that v j is known, use the differential equation to compute m scaled derivatives of its solution, V ℓ(t), satisfying V ℓ(t ℓ) = v ℓ, ℓ = j, j − 1. Setting

    $$\displaystyle \begin{aligned} F_{\ell}(t)=f(V_{\ell}(t),t) , \end{aligned} $$
    (8)

    these are recursively defined by the formula

    $$\displaystyle \begin{aligned} \frac {d^k V_{\ell}}{dt^k} (t_{\ell}) = \frac {d^{k-1} F_{\ell}}{dt^{k-1}} (t_{\ell}) , \ \ \ \ k=0, \ldots m. {} \end{aligned} $$
    (9)
  2. 2.

    Construct the Hermite-Birkhoff interpolant of this data; that is the polynomial P j−1∕2(t;v j−1, v j) of degree 2m + 1, satisfying

    $$\displaystyle \begin{aligned} \frac {d^k P_{j-1/2}}{dt^k} (t_{\ell}; v_{j-1},v_j) = \frac {d^k V_{\ell}}{dt^k} (t_{\ell}); \ \ \ \ell=j-1,j, \ \ \ k=0, \ldots , m. {} . \end{aligned} $$
    (10)
  3. 3.

    Approximate (7) by replacing u(t ℓ) by v ℓ and replacing the integral by a q + 1-point quadrature rule with f evaluated at the Hermite interpolant:

    $$\displaystyle \begin{aligned} v_j = v_{j-1} + h_j \sum_{k=0}^q w_k f(P_{j-1/2}(t_{j,k}; v_{j-1}, v_j)) . {} \end{aligned} $$
    (11)
  4. 4.

    Solve (11) for v j. Note that this is a system of d nonlinear equations for any m; that is, unlike standard implicit Runge–Kutta methods, the size of the nonlinear system is independent of the order.

We remark that we have not studied in detail the unique solvability of (11) in the stiff case. In our numerical experiments we used the solution at the current time step as an initial approximation for Newton iterations and simply accepted the solution to which the iterates converged.

To emphasize the ideas we write down some specific examples of methods with m = 1 and m = 2 making the simplifying assumption of autonomy; that is f = f(u). The derivation of methods of arbitrary order is straightforward and the formulas can be trivially obtained using software capable of symbolic computations. To apply them at higher order one must evaluate higher derivatives of f, which is also possible using automatic differentiation tools [11].

Example (m = 1)

Set

$$\displaystyle \begin{aligned} \tau = \frac {t-t_{j-1}}{h_j} . \end{aligned}$$

Now the interpolant P j−1∕2(t;v j−1, v j) is given by:

$$\displaystyle \begin{aligned} P_{j-1/2}(t;v_{j-1},v_j)=\sum_{k=0}^3 a_k \tau^k , {} \end{aligned} $$
(12)

where

$$\displaystyle \begin{aligned} a_0=v_{j-1}, \ \ \ a_1=h_j f(v_{j-1}), \end{aligned}$$
$$\displaystyle \begin{aligned} a_2 = 3 \left(v_j - v_{j-1} \right) - h_j \left( 2 f(v_{j-1}) + f(v_j) \right) , {} \end{aligned} $$
(13)
$$\displaystyle \begin{aligned} a_3 = -2 \left(v_j - v_{j-1} \right) + h_j \left( f(v_{j-1}) + f(v_j) \right) . \end{aligned}$$

We next introduce a quadrature rule which is exact for polynomials of degree 3. Possible choices include the 2-point Gauss-Legendre (14) rules, or the 3-point Gauss-Radau (15) or Gauss-Lobatto rules. Note that by using two different rules we obtain a possible error indicator. Here are the two different methods used below. Note that the methods are identical if f is linear.

$$\displaystyle \begin{aligned} v_j = v_{j-1} + \frac {h_j}{2} \left( f\left( P_{j-1/2}(\alpha_{-};v_{j-1},v_j) \right) + f\left( P_{j-1/2}(\alpha_{+};v_{j-1},v_j) \right) \right), {} \end{aligned} $$
(14)
$$\displaystyle \begin{aligned} \begin{array}{rcl} v_j &\displaystyle = &\displaystyle v_{j-1} + \frac {h_j}{36} \left( \beta_{+} f\left( P_{j-1/2}(\gamma_{-};v_{j-1},v_j) \right) + \beta_{-} f\left( P_{j-1/2}(\gamma_{+};v_{j-1},v_j) \right) \right. \\ &\displaystyle &\displaystyle \left. + 4 f\left( v_j \right) \right) , {} \end{array} \end{aligned} $$
(15)
$$\displaystyle \begin{aligned} \alpha_{\pm}= \left( 1 \pm \frac {1}{\sqrt{3}} \right), \ \ \gamma_{\pm}= \frac {4 \pm \sqrt{6}}{10}, \ \ \ \beta_{\pm} = 16 \pm \sqrt{6}. \end{aligned} $$
(16)

A time step is executed by solving the nonlinear system, (14) or (15), for v j.

Example (m = 2)

Now we also need the second time derivative of u,

$$\displaystyle \begin{aligned} \frac {d^2 u}{dt^2} = \frac {d}{dt} f(u) = J(u) f(u) , \end{aligned} $$
(17)

where J(u) is the Jacobian derivative. The Hermite interpolant can now be written:

$$\displaystyle \begin{aligned} P_{j-1/2}(t;v_{j-1},v_j)=\sum_{k=0}^5 a_k \tau^k , {} \end{aligned} $$
(18)

where

$$\displaystyle \begin{aligned} a_0=v_{j-1}, \ \ \ a_1=h_j f(v_{j-1}), \ \ \ a_2 = \frac {h_j^2}{2} J(v_{j-1})f(v_{j-1}) , {} \end{aligned} $$
(19)
$$\displaystyle \begin{aligned} a_3 {=} 10 \left(v_j {-} v_{j{-}1} \right) {-}h_j \left( 6f(v_{j{-}1}) {+} 4f(v_j) \right) {+} \frac {h_j^2}{2} \left( {-}3 J(v_{j{-}1}) f(v_{j{-}1}) {+} J(v_j) f(v_j) \right) , \end{aligned}$$
$$\displaystyle \begin{aligned} a_4 {=} {-}15 \left(v_j {-} v_{j{-}1} \right) {+}h_j \left( 8f(v_{j{-}1}) {+} 7f(v_j) \right) {+} \frac {h_j^2}{2} \left( 3 J(v_{j{-}1}) f(v_{j{-}1}) {-} J(v_j) f(v_j) \right) , \end{aligned}$$
$$\displaystyle \begin{aligned} a_5 = 6 \left(v_j {-} v_{j{-}1} \right) {-}3h_j \left( f(v_{j{-}1}) {+} f(v_j) \right) {+} \frac {h_j^2}{2} \left( {-}J(v_{j{-}1}) f(v_{j{-}1}) {+} J(v_j) f(v_j) \right) . \end{aligned}$$

Again we can now use, for example, the 3-point Gauss-Legendre or 4-point Gauss-Radau quadrature rules to produce the equation we must solve for v j.

3.1 Stability and Consistency

The consistency of the method is a straightforward consequence of its construction, and its linear stability properties can also be established.

Theorem 1

Assume that the quadrature rule has positive weights and is exact for polynomials of degree 2m + 1. Then the implicit Hermite method is A-stable and accurate of order 2m + 2.

Proof

Assume that f is smooth and that u(t) ∈ C 2m+2(0, T). Using (4), standard estimates for quadrature errors, and the Picard formula (7) we find for the truncation error

$$\displaystyle \begin{aligned} \tau_j = \frac {u(t_j)-u(t_{j-1})}{h_j} - \sum_k w_k f(P_{j-1/2}(t_{j,k};u(t_{j-1}),u(t_j))) , \end{aligned} $$
(20)
(21)

Now consider the Dahlquist test problem, f(u) = λu. In this case all quadrature rules which are exact for the Hermite interpolant produce the same method. As interpolation is linear, we have that the coefficients of the interpolant are linear combinations \(h_j^k \lambda ^k v_{j-1}\) and \(h_j^k \lambda ^k v_j\), k = 0, …m. The Picard integral then increases the powers of h j λ by one so that the implicit system (11) can be rearranged to:

$$\displaystyle \begin{aligned} Q_{+} (h_j \lambda) v_j = Q_{-} (h_j \lambda) v_{j-1} \ \Rightarrow \ v_j = \frac {Q_{-}(h_j \lambda)}{Q_{+} (h_j \lambda)} v_{j-1}, \end{aligned} $$
(22)

where Q ±(h j λ) are polynomials of degree m + 1. Consistency implies

$$\displaystyle \begin{aligned} e^{h_j \lambda} = \frac {Q_{-}(h_j \lambda)}{Q_{+} (h_j \lambda)} + O\left( (h_j \lambda)^{2m+3} \right) . \end{aligned} $$
(23)

The only rational function of the given degree with this accuracy is the diagonal Padé approximant. We thus conclude that our methods are A-stable [12].◇

4 Numerical Experiments

Our first experiments treat standard problems from the ode literature and are restricted to the fourth and sixth order methods described above with either Gauss-Legendre or Gauss-Radau quadrature. Our practical implementations employ the classical Aitken algorithm adapted to Hermite interpolation to directly evaluate P j−1∕2(t j,k, v j−1, v j) and solve (11) using Newton’s method with the Jacobian of the implicit system approximated by finite differences. For adaptive computations we

  1. 1.

    Compute v j using the Gauss-Radau-based formulas,

  2. 2.

    Compute a residual, ρ j, by substituting v j into the Gauss-Legendre-based formulas.

We then adjust the time step by the simple rule

$$\displaystyle \begin{aligned} h_{j+1} = \left( \frac{\mathrm{tol}}{\rho_j} \right)^{1/(2m+3)} h_j , \end{aligned} $$
(24)

while also imposing a minimum time step.

Our final experiment examines the use of the method for evolving spectral discretizations of initial-boundary value problems for the Schrödinger equation.

4.1 Arentsorf Orbit

We first consider the problem of computing a periodic solutions of the restricted three-body problem which we reformulate as a first-order system of four variables:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \frac {d^2 y_1}{dt^2} &\displaystyle = &\displaystyle y_1 + 2 \frac {dy_2}{dt} - (1-\mu) \frac {y_1+ \mu}{\left( (y_1+ \mu)^2 + y_2^2 \right)^{3/2}} - \mu \frac {y_1-(1-\mu)}{\left( (y_1-(1- \mu))^2 + y_2^2 \right)^{3/2}} , \\ \frac {d^2 y_2}{dt^2} &\displaystyle = &\displaystyle y_2 - 2 \frac {dy_1}{dt} - (1-\mu) \frac {y_2}{\left( (y_1+ \mu)^2 + y_2^2 \right)^{3/2}} - \mu \frac {y_2}{\left( (y_1-(1- \mu))^2 + y_2^2 \right)^{3/2}} , \end{array} \end{aligned} $$
$$\displaystyle \begin{aligned} \mu=0.012277471, \ \ \ y_1(0)=.994, \ \ \frac {dy_1}{dt}(0)=y_2(0)=0, \end{aligned}$$
$$\displaystyle \begin{aligned} \frac {dy_2}{dt}(0)=-2.01585106379082\ldots , \ T=17.06521656015796\ldots . \end{aligned}$$

(For graphs of the solution see [13, Ch. II].)

We note that this problem is not considered to be stiff. The main difficulty is a need for very small time steps when the orbits approach the singularities of f. However, we use it to verify convergence at the design order when (woefully inefficient) uniform time steps are employed and to test the utility of our naive time step adaptivity algorithm.

Results for fixed (small) time steps are displayed in Table 1. We observe that convergence is at design order and that the results for the two quadrature formulas are comparable, though the fourth order Radau method is somewhat more accurate than Gauss-Legendre with roles reversed at sixth order. The sixth order methods are more accurate with larger time steps. The error is simply \(\sqrt {(y_1(T)-y_1(0))^2+(y_2(T)-y_2(0))^2}\).

Table 1 Convergence with fixed time steps for the Arentsorf orbit problem
Full size table

Results for adaptive computations with m = 2 are shown in Table 2. Obviously, the adaptive methods lead to a very significant reduction in the number of time steps; an accuracy of 10−7 is achieved with 264 steps of the adaptive method while 35,000 uniform steps are required. Due to the sensitivity of the problem, the global error is much larger than the error tolerance, but is reduced in proportion to it.

Table 2 Time steps and error as a function of tolerance for adaptive solutions of the Arentsorf problem with m = 2
Full size table

4.2 Van der Pol Oscillator

Our second example is the van der Pol oscillator problem, which again we rewrite as a first order system:

$$\displaystyle \begin{aligned} \frac {d^2 y}{dt^2} = \epsilon^{-1} \left( (1-y^2) \frac {dy}{dt} - y \right) , \end{aligned} $$
(25)
$$\displaystyle \begin{aligned} \epsilon=10^{-6} , \ \ y(0)=2, \ \frac {dy}{dt}(0)=0. \end{aligned}$$

We solve up to T = 11 using the adaptive method with m = 2. We plot the solution and the time step histories for a tolerance of 10−10 in Fig. 1. Note that very small steps are needed to resolve the fast transitions, while the problem is quite stiff in the regions where y is nearly constant. Plots for the other tolerances tested, 10−6 and 10−10, are similar though the number of time steps required varies.

Fig. 1
figure 1

Solution and time step history for the van der Pol oscillator with tolerance 10−8

Full size image

4.3 Schrödinger Equation

Lastly, we apply the to evolve a Fourier pseudospectral discretization of the nonlinear Schrödinger equation. Precisely we consider the real problem

$$\displaystyle \begin{aligned} \frac {\partial v}{\partial t} = - \frac {\partial^2 w}{\partial x^2} - \left( v^2+w^2 \right) w, \ \ \ \ \frac {\partial w}{\partial t} = \frac {\partial^2 v}{\partial x^2} + \left( v^2+w^2 \right) v, {} \end{aligned} $$
(26)

for x ∈ (−8, 8), t ∈ (0, 3) with periodic boundary conditions \(\frac {\partial v}{\partial x}=\frac {\partial w}{\partial x}=0\) at x = ±1. We approximate the periodization of the exact solitary wave solution

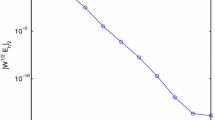
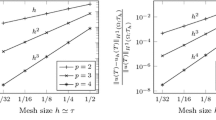
$$\displaystyle \begin{aligned} \begin{array}{rcl} v(x,t) &\displaystyle = &\displaystyle \sqrt{50} \cos{(rx-st)} \cdot \mathrm{sech}{(5(x-ct))} , \\ w(x,t) &\displaystyle = &\displaystyle \sqrt{50} \sin{(rx-st)} \cdot \mathrm{sech}{(5(x-ct))} , {} \end{array} \end{aligned} $$
(27)

with c = 2π, r = π , s = π 2 − 25. We note that the amplitude of the solitary wave is reduced by about 17 digits at a distance of 8 from its peak so that the interaction with periodic copies is negligible over the simulation time. We use 512 Fourier modes in the computation of the derivatives and experiments show that this is sufficient to represent the solitary wave to machine precision. The implicit system was solved using Newton iterations each time step. In Fig. 2 we present results for m = 3 (8th order) with varying time step and for m varying from 1 to 5 (order 4 through 12) with h = 10−2. In both cases we observe rapid convergence. We also tabulate the errors at the final time and calculate the convergence rates when m = 3 in Table 3. The results are clearly consistent with the design order.

Table 3 Relative errors for the Fourier pseudospectral discretization of the NLS (26) with solitary wave solution (27)
Full size table
Fig. 2
figure 2

Left: Relative errors for NLS with various time steps and m = 3. Right: Relative errors for NLS with h = .01 and varying m

Full size image

5 Conclusions and Future Work

In conclusion, we have demonstrated that Hermite-Birkhoff interpolation can be used to develop singly-implicit A-stable timestepping methods of arbitrary order. A number of possible generalizations and improvements to the method are possible. These include

  1. 1.

    Stability analysis for variable coefficient or nonlinear problems using the projection properties (5);

  2. 2.

    Improved time step/order adaptivity;

  3. 3.

    Preconditioning of the implicit system for applications to partial differential equations such as spectral/pseudospectral discretizations of equations of Schrödinger type (e.g. integration preconditioners [8, 9]);

  4. 4.

    Development of IMEX schemes combining Hermite and Taylor polynomials.