On the Convergence Rate of Hermite-Fejér Interpolation

Abstract

By the Peano kernel theorem, this paper establishes the convergence rates for Hermite-Fejér interpolation with the observed function values and its first derivatives at Gauss-Jacobi pointsystems. These error bounds share that for a function analytic in the Bernstein ellipse $\mathcal {E}_{\rho }$, the error decays exponentially; while for a functions of finite regularity, the error decays depending on the regularity.

1 Introduction

For an arbitrarily given system of points

$$\displaystyle \begin{aligned} \{x_1^{(n)},x_2^{(n)},\ldots,x_n^{(n)}\}_{n=1}^{\infty}, \end{aligned} $$

(1)

Faber [3] in 1914 showed that there exists a continuous function f(x) in [−1, 1] for which the Lagrange interpolation sequence L _n[f] (n = 1, 2, …) is not uniformly convergent to f in [−1, 1], where $\omega _n(x)=(x-x_1^{(n)})(x-x_2^{(n)})\cdots (x-x_n^{(n)})$

$$\displaystyle \begin{aligned} L_n[f](x) =\sum_{k=1}^nf(x_k^{(n)})\ell_k^{(n)}(x),\, \ell_k^{(n)}(x)=\frac{\omega_n(x)}{\omega^{\prime}_n(x_k^{(n)})(x-x_k^{(n)})}. \end{aligned} $$

(2)

Whereas, based on the Chebyshev pointsystem

$$\displaystyle \begin{aligned} x_k^{(n)}=\cos\left(\frac{2k-1}{2n}\pi\right),\quad k=1,2,\ldots,n,\quad n=1,2,\ldots, \end{aligned} $$

(3)

Fejér [4] in 1916 proved that if f ∈ C[−1, 1], then there is a unique polynomial H _2n−1(f, x) of degree at most 2n − 1 such that lim_n→∞∥H _2n−1(f) − f∥_∞ = 0, where H _2n−1(f, x) is determined by

$$\displaystyle \begin{aligned} H_{2n-1}(f,x_k^{(n)})=f(x_k^{(n)}),\quad H_{2n-1}^{\prime}(f,x_k^{(n)})=0,\quad k = 1, 2,\ldots, n. \end{aligned} $$

(4)

This polynomial is known as the Hermite-Fejér interpolation polynomial.

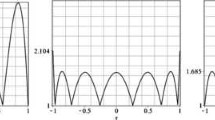
It is of particular notice that the above Hermite-Fejér interpolation polynomial converges much slower compared with the corresponding Lagrange interpolation polynomial at the Chebyshev pointsystem (3) (see Fig. 1).

Fig. 1

∥H _2n−1(f, x) − f(x)∥_∞, ∥L _n(f, x) − f(x)∥_∞ and $\|H^*_{2n-1}(f,x)-f(x)\|{ }_{\infty }$at x = −1: 0.001: 1 by using Chebyshev pointsystem (3) for $f(x)=\sin (x)$, $f(x)= \frac {1}{1+25x^2}$ and f(x) = |x|³, respectively

To get fast convergence, the following Hermite-Fejér interpolation of f(x) at nodes (1) is considered [6, 7]:

$$\displaystyle \begin{aligned} \quad \,\, H^*_{2n-1}(f,x) =\sum_{k=1}^nf(x_k^{(n)})h_k^{(n)}(x)+\sum_{k=1}^nf'(x_k^{(n)})b_k^{(n)}(x), \end{aligned} $$

(5)

where $h_k^{(n)}(x)=v_k^{(n)}(x)\left (\ell _k^{(n)}(x)\right )^2$, $b_k^{(n)}(x)=(x-x_k^{(n)})\left (\ell _k^{(n)}(x)\right )^2$ and $v_k^{(n)}(x)=1-(x-x_k^{(n)})\frac {\omega _n^{\prime \prime }(x_k^{(n)})}{\omega _n^{\prime }(x_k^{(n)})}.$

Fejér [5] and Grünwald [7] also showed that the convergence of the Hermite-Fejér interpolation of f(x) also depends on the choice of the nodes. The pointsystem (1) is called normal if for all n

$$\displaystyle \begin{aligned} v_k^{(n)}(x)\ge 0,\quad k=1,2,\ldots,n,\quad x\in [-1,1], \end{aligned} $$

(6)

while the pointsystem (1) is called strongly normal if for all n

$$\displaystyle \begin{aligned} v_k^{(n)}(x)\ge c>0,\quad k=1,2,\ldots,n,\quad x\in [-1,1] \end{aligned} $$

(7)

for some positive constant c.

Fejér [5] (also see Szegö [12, pp 339]) showed that for the zeros of Jacobi polynomial $P_n^{(\alpha ,\beta )}(x)$ of degree n (α > −1, β > −1)

$$\displaystyle \begin{aligned} {v_k^{(n)}(x)\ge \min\{-\alpha,-\beta\}\mbox{\quad for }{-1<\alpha\le 0}, {-1<\beta\le 0}, {k=1,2,\ldots,n}\mbox{ and }{x\in [-1,1]}}. \end{aligned} $$

For (strongly) normal pointsystems, Grünwald [7] showed that for every f ∈ C ¹(−1, 1), $\lim _{n\rightarrow \infty }\|H^*_{2n-1}(f)-f\|{ }_{\infty }=0$ if $\{x_k^{(n)}\}$ is strongly normal satisfying (7) and $\{f'(x_k^{(n)})\}$ satisfies

$$\displaystyle \begin{aligned} |f'(x_k^{(n)})|<n^{c-\delta} \mbox{\quad for some given positive number }{\delta},\quad k=1,2,\ldots,\quad \! n=1,2,\ldots, \end{aligned} $$

while $\lim _{n\rightarrow \infty }\|H^*_{2n-1}(f)-f\|{ }_{\infty }=0$ in [−1 + 𝜖, 1 − 𝜖] for each fixed 0 < 𝜖 < 1 if $\{x_k^{(n)}\}$ is normal and $\{f'(x_k^{(n)})\}$ is uniformly bounded for n = 1, 2, ….¹

Moreover, Szabados [11] showed the convergence of the Hermite-Fejér interpolation (5) at the Chebyshev pointsystem (3) satisfies

$$\displaystyle \begin{aligned} \|f-H^*_{2n-1}(f)\|{}_{\infty}=O(1)\|f-p^*\|{}_{C^{1}[-1,1]} \end{aligned} $$

(8)

where p ^∗ is the best approximation polynomial of f with degree at most 2n − 1 and $\|f-p^*\|{ }_{C^{1}[-1,1]}=\max _{0\le j\le 1}\|f^{(j)}-{p^*}^{(j)}\|{ }_{\infty }$.

Hermite-Fejér interpolation has plenty of use in computer geometry aided geometric design with boundary conditions including derivative information. The convergence rate under the infinity norm has been extensively studied in [5,6,7, 11, 14]. The efficient algorithm on the fast implementation of Hermite-Fejér interpolation at zeros of Jacobi polynomial can be found in [17].

In this paper, the following convergence rates of Hermite-Fejér interpolation $H^*_{2n-1}(f,x)$ at Gauss-Jacobi pointsystems are considered.

• If f is analytic in $\mathcal {E}_{\rho }$ with |f(z)|≤ M, then

  $$\displaystyle \begin{aligned} \|f(x)-H^*_{2n-1}(f,x)\|{}_{\infty}=\left\{\begin{array}{ll} {\displaystyle O\left(\frac{4\tau_nM[2n\rho^2+(1-2n)\rho]}{(\rho-1)^2\rho^{2n}}\right)},& \gamma\le 0,\\ {\displaystyle O\left(\frac{n^{2+2\gamma}[2n\rho^2+(1-2n)\rho]}{(\rho-1)^2\rho^{2n}}\right)},&\gamma> 0\end{array},\right. \, \gamma=\max\{\alpha,\beta\} \end{aligned} $$

  (9)

  where

  $$\displaystyle \begin{aligned} \tau_n=\left\{\begin{array}{ll} O(n^{-1.5-\min\{\alpha,\beta\}}\log n),& \mbox{if }{-1<\min\{\alpha,\beta\}\le\gamma\le -\frac{1}{2}}\\ O(n^{2\gamma-\min\{\alpha,\beta\}-\frac{1}{2}}),& \mbox{if }{-1<\min\{\alpha,\beta\}\le -\frac{1}{2}<\gamma\le 0}\\ O(n^{2\gamma}),& \mbox{if }{-\frac{1}{2}<\min\{\alpha,\beta\}\le \gamma}\end{array}.\right. \end{aligned} $$

  (10)

• If f(x) has an absolutely continuous (r − 1)st derivative f ^(r−1) on [−1, 1] for an integer r ≥ 3, and a rth derivative f ^(r) of bounded variation V _r = Var(f ^(r)) < ∞, then

  $$\displaystyle \begin{aligned} \|f(x)-H^*_{2n-1}(f,x)\|{}_{\infty}=\left\{\begin{array}{ll} {\displaystyle O\left(n^{-r}\log n\right)}, &\gamma\leq -\frac{1}{2}, \\ {\displaystyle O\left(n^{2\gamma-r+1}\right)},&\gamma>-\frac{1}{2},\end{array}\right. \end{aligned} $$

  (11)

  while if f(x) is differentiable and f′(x) is bounded on [−1, 1], then

  $$\displaystyle \begin{aligned} \begin{array}{lll} \|f(x)-H^*_{2n-1}(f,x)\|{}_{\infty} &=&\left\{\begin{array}{ll} {\displaystyle O\left(n^{-1}\log n\right)}, &\gamma\leq -\frac{1}{2}, \\ {\displaystyle O\left(n^{2\gamma}\right)},&\gamma>-\frac{1}{2}.\end{array}\right.\end{array} \end{aligned}$$

Comparing these results with

which is sharp and attainable (see Fig. 2), we see that $H^*_{2n-1}(f,x)$ converges much faster than H _2n−1(f, x) for analytic functions or functions of higher regularities (see Fig. 1). Particularly, H _2n−1(f, x) diverges at Gauss-Jacobi pointsystems with γ ≥ 0, whereas, $H^*_{2n-1}(f,x)$ converges for functions analytic in the Bernstein ellipse or of finite limited regularity.

Fig. 2

∥H _2n−1(f, x) − f(x)∥_∞ at x = −1: 0.001: 1 by using Gauss-Jacobi pointsystem for f(x) = |x| with different α and β, respectively

For simplicity, in the following we abbreviate $x_k^{(n)}$ as x _k, $\ell _k^{(n)}(x)$ as ℓ _k(x), $h_k^{(n)}(x)$ as h _k(x), and $b_k^{(n)}(x)$ as b _k(x). A ∼ B denotes there exist two positive constants c ₁ and c ₂ such that c ₁ ≤|A|∕|B|≤ c ₂.

2 Main Results

Suppose f(x) satisfies a Dini-Lipschitz condition on [−1, 1], then it has the following absolutely and uniformly convergent Chebyshev series expansion

$$\displaystyle \begin{aligned} f(x)=\sum_{j=0}^{\infty}{'}c_jT_j(x),\quad c_j=\frac{2}{\pi}\int_{-1}^{1}\frac{f(x)T_j(x)}{\sqrt{1-x^2}}dx,\quad j=0,1,\ldots. \end{aligned} $$

(12)

where the prime denotes summation whose first term is halved, $T_j(x)=\cos {}(j\cos ^{-1}x)$ denotes the Chebyshev polynomial of degree j.

Lemma 1

• (i) (Bernstein [ 2 ]) If f is analytic with |f(z)|≤ M in the region bounded by the ellipse $\mathcal {E}_{\rho }$ with foci ± 1 and major and minor semiaxis lengths summing to ρ > 1, then for each j ≥ 0,

  $$\displaystyle \begin{aligned} |c_j|\le {\displaystyle\frac{2M}{\rho^j}}. \end{aligned} $$

  (13)

• (ii) (Trefethen [ 13 ]) For an integer r ≥ 1, if f(x) has an absolutely continuous (r − 1)st derivative f ^(r−1) on [−1, 1] and a rth derivative f ^(r) of bounded variation V _r = Var(f ^(r)) < ∞, then for each j ≥ r + 1,

  $$\displaystyle \begin{aligned} |c_j|\le{\displaystyle\frac{2V_r}{\pi j(j-1)\cdots(j-r)}}. \end{aligned} $$

  (14)

Suppose − 1 < x _n < x _n−1 < ⋯ < x ₁ < 1 in decreasing order are the roots of $P_n^{(\alpha ,\beta )}(x)$ (α, β > −1), and $\{w_j\}_{j=1}^n$ are the corresponding weights in the Gauss-Jacobi quadrature.

Lemma 2

For j = 1, 2, …, n, it follows

$$\displaystyle \begin{aligned} \quad (x-x_j)\ell_j(x)=\sigma_n(-1)^j\frac{\sqrt{(1-x_j^2)w_j}}{2^{(\alpha+\beta+1)/2}}\sqrt{\frac{n!\Gamma(n+\alpha+\beta+1)} {\Gamma(n+\alpha+1)\Gamma(n+\beta+1)}}P_n^{(\alpha,\beta)}(x), \end{aligned} $$

(15)

where σ _n = +1 for even n and σ _n = −1 for odd n.

Proof

Let $z_n=\int _{-1}^1(1-x)^{\alpha }(1+x)^{\beta }[P_n^{(\alpha ,\beta )}(x)]^2dx$ and K _n the leading coefficient of $P_n^{(\alpha ,\beta )}(x)$. From Abramowitz and Stegun [1], we have

$$\displaystyle \begin{aligned} z_n=\frac{2^{\alpha+\beta+1}}{2n+\alpha+\beta+1}\cdot\frac{\Gamma(n+\alpha+1)\Gamma(n+\beta+1)}{n!\Gamma(n+\alpha+\beta+1)}, \quad K_n=\frac{1}{2^{n}}\frac{\Gamma(2n+\alpha+\beta+1)}{n!\Gamma(n+\alpha+\beta+1)}. \end{aligned}$$

Furthermore, by Szegö [12, (15.3.1)] (also see Wang et al. [15]), we obtain

$$\displaystyle \begin{aligned} \begin{array}{lll} (x-x_j)\ell_j(x)={\displaystyle\frac{1}{\omega_n^{\prime}(x_j)}\omega _n(x)} &=&{\displaystyle\sigma_n(-1)^j\sqrt{\frac{K_n^22n(1-x_j^2)w_j}{2n(2n+\alpha+\beta+1)z_n}}\omega_n(x)}\\ &=&{\displaystyle\sigma_n(-1)^j\sqrt{\frac{(1-x_j^2)w_j}{z_n(2n+\alpha+\beta+1)}}P_n^{(\alpha,\beta)}(x)},\end{array} \end{aligned}$$

which implies the desired result (15). □

Lemma 3

For j = 1, 2, …, n, it follows

$$\displaystyle \begin{aligned} (1-x_j^2)w_j=O\left(n^{-1}\right). \end{aligned} $$

(16)

Proof

From $w_j=O\left ( \frac {2^{\alpha +\beta +1}\pi }{n}\left (\sin \frac {\theta _j}{2}\right )^{2\alpha +1}\left (\cos \frac {\theta _j}{2}\right )^{2\beta +1}\right )$ Szegö [12, (15.3.10)], we see for $x_j=\cos \theta _j$ that $(1-x_j^2)w_j=O\left (\frac {2^{\alpha +\beta +3}\pi }{n}\left (\sin \frac {\theta _j}{2}\right )^{2\alpha +3}\left (\cos \frac {\theta _j}{2}\right )^{2\beta +3}\right )$, which derives the desired result. □

Lemma 4 ([10, 16])

For t ∈ [−1, 1], let x _m be the root of the Jacobi polynomial $P_n^{(\alpha ,\beta )}$ which is closest to t. Then for k = 1, 2, …, n, we have

$$\displaystyle \begin{aligned} \ell_k(t)=\left\{\begin{array}{ll}O\left(|k-m|{}^{-1}+|k-m|{}^{\gamma-\frac{1}{2}}\right),&k\neq m\\ O(1)&k=m\end{array}\right.,\quad \gamma=\max\{\alpha,\beta\}. \end{aligned} $$

(17)

Lemma 5 (Szegö [12, Theorem 8.1.2])

Let α, β be real but not necessarily greater than − 1 and $x_{k}=\cos \theta _{k}$ . Then for each fixed k, it follows

$$\displaystyle \begin{aligned} \lim_{n\rightarrow \infty}n\theta_{k}=j_k, \end{aligned} $$

(18)

where j _k is the kth positive zero of Bessel function J _α.

Lemma 6

For k = 1, 2, …, n, it follows

$$\displaystyle \begin{aligned} v_k(x)=1-(x-x_k)\frac{\omega_n^{\prime\prime}(x_k)}{\omega_n^{\prime}(x_k)}=O(n^2). \end{aligned} $$

(19)

Proof

Note that $P_n^{(\alpha ,\beta )}(x)$ satisfies the second order linear homogeneous Sturm-Liouville differential equation [12, (4.2.1)]

$$\displaystyle \begin{aligned} (1-x^2)y''+(\beta-\alpha-(\alpha+\beta+2)x)y'+n(n+\alpha+\beta+1)y=0. \end{aligned}$$

By $\omega _n(x)=\frac {P_n^{(\alpha ,\beta )}(x)}{K_n}$, we get

(20)

In addition, by Lemma 5 with $x_j=\cos \theta _j$, we see that $\theta _1\sim \frac {1}{n}$. Similarly, by $P_n^{(\alpha ,\beta )}(-x)=(-1)^nP_n^{(\beta ,\alpha )}(x)$ we have $\theta _n\sim \frac {1}{n}$. These together yield

$$\displaystyle \begin{aligned} \frac{1}{1-x_1^2}=O(n^{2}),\quad \frac{1}{1-x_n^2}=O(n^{2}),\quad \frac{1}{1-x_j^2}\le \max\left(\frac{1}{1-x_1^2},\frac{1}{1-x_n^2}\right)=O(n^{2}) \end{aligned}$$

and then by (20) it deduces the desired result. □

Theorem 1

Suppose $\{x_j\}_{j=1}^n$ are the roots of $P_n^{(\alpha ,\beta )}(x)$ with α, β > −1, then the Hermite-Fejér interpolation (5) for f analytic in $\mathcal {E}_{\rho }$ with |f(z)|≤ M at $\{x_j\}_{j=1}^n$ has the convergence rate (9).

Proof

Since the Chebyshev series expansion of f(x) is uniformly convergent under the assumptions, and the error of Hermite-Fejér interpolation (5) on Chebyshev polynomials satisfies $|E(T_{j},x)|=|T_j(x)-H^*_{2n-1}(T_{j},x)|=0$ for j = 0, 1, …, 2n − 1, then it yields

$$\displaystyle \begin{aligned} |E(f,x)|=|f(x)-H^*_{2n-1}(f,x)|=|\sum_{j=0}^{\infty}c_jE(T_{ j},x)|\le \sum_{j=2n}^{\infty}|c_j||E(T_{j},x)|. \end{aligned} $$

(21)

Furthermore, $|E(T_{j},x)|=|T_j(x)-\sum _{i=1}^nT_j(x_i)h_i(x)-\sum _{i=1}^nT_j^{\prime }(x_i)b_i(x)|$. In the following, we will focus on estimates of |E(T _j, x)| for j ≥ 2n.

In the case γ ≤ 0: Notice that the pointsystem is normal which implies h _i(x) ≥ 0 for all i = 1, 2, …, n and for all x ∈ [−1, 1],

$$\displaystyle \begin{aligned} 1\equiv\sum_{i=1}^nh_i(x)=\sum_{i=1}^nv_i(x)\ell^2_i(x). \end{aligned}$$

Then we have

$$\displaystyle \begin{aligned} |\sum_{i=1}^nT_j(x_i)h_i(x)|\le \sum_{i=1}^nh_i(x)=1,\quad j=0,1,\ldots. \end{aligned} $$

(22)

Additionally, by Lemma 2, it obtains for j = 2n, 2n + 1, … that

$$\displaystyle \begin{aligned} \begin{array}{lll} &&|\sum_{i=1}^nT_j^{\prime}(x_i)b_i(x)|\\&=& j|\sum_{i=1}^nU_{j-1}(x_i)(x-x_i)\ell_i^2(x)|\\ &=&\frac{j}{2^{(\alpha+\beta+1)/2}}\sqrt{\frac{n!\Gamma(n+\alpha+\beta+1)} {\Gamma(n+\alpha+1)\Gamma(n+\beta+1)}}|P_n^{(\alpha,\beta)}(x)\sum_{i=1}^nU_{j-1}(x_i)\sqrt{(1-x_i^2)w_i}\ell_i(x)|\\ &=&\frac{j}{2^{(\alpha+\beta+1)/2}}\sqrt{\frac{n!\Gamma(n+\alpha+\beta+1)} {\Gamma(n+\alpha+1)\Gamma(n+\beta+1)}}|P_n^{(\alpha,\beta)}(x)\sum_{i=1}^n\sin{}((j-1)\arccos(x_i))\sqrt{w_i}\ell_i(x)|\\ &=&jO\left(|P_n^{(\alpha,\beta)}(x)|\sqrt{\|\{w_i\}_{i=1}^n\|{}_{\infty}}\Lambda_n\right)\end{array} \end{aligned}$$

(U _j−1 is the second kind of Chebyshev polynomial of degree j − 1) since $\sqrt {\frac {n!\Gamma (n+\alpha +\beta +1)} {\Gamma (n+\alpha +1)\Gamma (n+\beta +1)}}$ is uniformly bounded in n forα, β > −1 due to

$$\displaystyle \begin{aligned} \begin{array}{rcl} \frac{(n+1)!\Gamma(n+\alpha+\beta+2)} {\Gamma(n+\alpha+2)\Gamma(n+\beta+2)}&\displaystyle =&\displaystyle \left(1-\frac{\alpha\beta}{(n+1)^2+(\alpha+\beta)(n+1)+\alpha\beta}\right)\\ &\displaystyle &\displaystyle \times\frac{n!\Gamma(n+\alpha+\beta+1)} {\Gamma(n+\alpha+1)\Gamma(n+\beta+1)}, \end{array} \end{aligned} $$

which implies $\frac {n!\Gamma (n+\alpha +\beta +1)} {\Gamma (n+\alpha +1)\Gamma (n+\beta +1)}$ is uniformly bounded in n and then $\sqrt {\frac {n!\Gamma (n+\alpha +\beta +1)} {\Gamma (n+\alpha +1)\Gamma (n+\beta +1)}}$ is uniformly bounded. Here $\Lambda _n=\max _{x\in [-1,1]}\sum _{i=1}^n|\ell _i(x)|$ is the Lebesgue constant. Then from

$$\displaystyle \begin{aligned} P_n^{(\alpha,\beta)}(x)&=\left\{\begin{array}{ll} O(n^{-\frac{1}{2}}),&\mbox{if }{\max\{\alpha,\beta\}\le -\frac{1}{2}}\\ O(n^{\max\{\alpha,\beta\}}),&\mbox{if }{\max\{\alpha,\beta\}> -\frac{1}{2}} \end{array}\right.,\\ w_i&=\left\{\begin{array}{ll} O(n^{-2-2\min\{\alpha,\beta\}}),&\mbox{if }{\min\{\alpha,\beta\}\le -\frac{1}{2}}\\ O(n^{-1}),&\mbox{if }{\min\{\alpha,\beta\}> -\frac{1}{2}} \end{array}\right. \end{aligned} $$

(see Szegö [12, pp 168, 354]) and

we have

$$\displaystyle \begin{aligned} |\sum_{i=1}^nT_j^{\prime}(x_i)b_i(x)|=j\tau_n. \end{aligned} $$

(23)

Then by (22) and (23), we find |E(T _j, x)|≤ 2 + jτ _n < 2jτ _n for j ≥ 2n, and consequently

$$\displaystyle \begin{aligned} |E(f,x)|=|f(x)-H^*_{2n-1}(f,x)|\le \sum_{j=2n}^{\infty}|c_j||E(T_{ j},x)|=2\tau_n\sum_{j=2n}^{\infty}j|c_j|, \end{aligned}$$

which, directly following [18], leads to the desired result.

In the case γ > 0: From $|E(T_{j},x)|=|T_j(x)-\sum _{i=1}^nT_j(x_i)h_i(x)-\sum _{i=1}^nT_j^{\prime }(x_i)b_i(x)|$, by Lemmas 3 and 6 we obtain

$$\displaystyle \begin{aligned} \sum_{i=1}^n|v_i(x)|\ell^2_i(x)=O\left(n^2\int_1^nt^{2\gamma-1}dt\right)=O(n^{2+2\gamma}), \end{aligned}$$

and

$$\displaystyle \begin{aligned} T_j(x)-\sum_{i=1}^nT_j(x_i)h_i(x)=T_j(x)-\sum_{i=1}^nT_j(x_i)v_i(x)\ell^2_i(x)=O\left(n^{2+2\gamma}\right). \end{aligned}$$

These together with

$$\displaystyle \begin{aligned} \begin{array}{lll} &&|\sum_{i=1}^nT_j^{\prime}(x_i)b_i(x)|\\ &=&\frac{j}{2^{(\alpha+\beta+1)/2}}\sqrt{\frac{n!\Gamma(n+\alpha+\beta+1)} {\Gamma(n+\alpha+1)\Gamma(n+\beta+1)}}|P_n^{(\alpha,\beta)}(x)\sum_{i=1}^n\sin{}((j-1)\arccos(x_i))\sqrt{w_i}\ell_i(x)|\\ &=&j\tau_n\end{array} \end{aligned}$$

and then $|E(T_{j},x)|=O\left (j^{2+2\gamma }\right )$ for j ≥ 2n, similar to the above proof in the case of γ ≤ 0, implies the desired result. □

From the definition of τ _n, we see that when $\alpha =\beta =-\frac {1}{2}$ the convergence order on n is the lowest. In addition, if f is of limited regularity, we have

Lemma 7 (Vértesi [14])

Suppose $\{x_j\}_{j=1}^n$ are the roots of $P_n^{(\alpha ,\beta )}(x)$ , for every continuous function f(x) we have

$$\displaystyle \begin{aligned} |H_{2n-1}(f,x)-f(x)| = O(1)\sum_{j=1}^n\left[w\left(f;\frac{j\sqrt{1-x^2}}{n}\right)+w\left(f;\frac{j^2|x|}{n^2}\right)\right]j^{2{\bar\gamma} -1}, \end{aligned} $$

(24)

where w(f;t) = w(t) is the modulus of continuity of f(x), and ${\bar \gamma }=\max \left (\alpha , \beta , -\frac {1}{2}\right )$.

Theorem 2

Suppose $\{x_j\}_{j=1}^n$ are the roots of $P_n^{(\alpha ,\beta )}(x)$ (α, β > −1), and f(x) has an absolutely continuous (r − 1)st derivative f ^(r−1) on [−1, 1] for some r ≥ 3, and a rth derivative f ^(r) of bounded variation V _r < ∞, then the Hermite-Fejér interpolation (5) at $\{x_j\}_{j=1}^n$ has the convergence rate (11).

Proof

Consider the special functional L(g) = E _n(g, x), where E _n(g, x) is defined for ∀g ∈ C ¹([−1, 1]) by

$$\displaystyle \begin{aligned} E_n(g,x) = g(x) - \sum_{j=1}^ng(x_j)v_j(x)\ell^2_j(x) - \sum_{j=1}^ng'(x_j)(x-x_j)\ell^2_j(x). \end{aligned} $$

(25)

By the Peano kernel theorem for n ≥ r (see Peano [9] or Kowalewski [8]), E _n(f, x) can be represented as

$$\displaystyle \begin{aligned} E_n(f,x) = \int_{-1}^1f^{(r)}(t)K_{r}(t)dt \end{aligned} $$

(26)

with $K_{r}(t) = \frac {1}{(r-1)!}L\left ((x-t)^{r-1}_{+}\right )$ for r = 3, 4, ⋯, that is

$$\displaystyle \begin{aligned} \begin{array}{rcl} K_{r}(t) &\displaystyle =&\displaystyle \frac{1}{(r-1)!}(x-t)^{r-1}_{+} - \frac{1}{(r-1)!}\sum_{j=1}^n(x_j-t)^{r-1}_{+}v_j(x)\ell^2_j(x)\\ &\displaystyle &\displaystyle - \frac{1}{(r-1)!}\sum_{j=1}^n(x_j-t)^{r-2}_{+}(x-x_j)\ell^2_j(x), \end{array} \end{aligned} $$

where

$$\displaystyle \begin{aligned} ( x-t)^{k-1}_{+} =\left\{ \begin{array}{ll} (x-t)^{k-1}, & {{x\geq t};} \\ 0, & {{x<t}.} \end{array} \right. (k\geq 2),\quad \quad \quad (x-t)^{0}_{+} =\left\{ \begin{array}{ll} 1, & {{x\geq t};} \\ 0, & {{x<t}.} \end{array} \right. (k=1). \end{aligned} $$

Moreover, noting that

$$\displaystyle \begin{aligned} \frac{1}{(k-2)!}(x-u)^{k-2}_{+} = \int_u^1\frac{1}{(k-3)!}(x-t)^{k-3}_{+}(t)dt, \quad k=3,4,\cdots, \end{aligned}$$

we get the following identity

$$\displaystyle \begin{aligned} K_{s-1}(u) = \int_u^1K_{s-2}(t)dt, \quad s=4,5,\cdots, \end{aligned}$$

where K ₂(t) is defined by

$$\displaystyle \begin{aligned} K_2(t) =(x-t)^1_{+} - \sum_{j=1}^n(x_j-t)^1_{+}v_j(x)\ell^2_j(x) - \sum_{j=1}^n(x_j-t)^{0}_{+}(x-x_j)\ell^2_j(x). \end{aligned}$$

In addition, it can be easily verified that K _s(−1) = K _s(1) = 0 for s = 2, 3, ….

Since f ^(r) is of bounded variation, directly applying the similar skills of Theorem 2 and Lemma 4 in [16], we get

$$\displaystyle \begin{aligned} \|E_n(f,x)\|{}_{\infty} \leq V_{r}\|K_{r+1}\|{}_{\infty}, \end{aligned} $$

(27)

and

$$\displaystyle \begin{aligned} \|K_{s+1}\|{}_{\infty} \leq \frac{\pi}{2n-s}\sup_{-1\leq t\leq1}|K_{s}(t)|, \quad \text{for }s=2,3,\cdots, \end{aligned} $$

(28)

respectively. Then from (27) and (28), we can obtain that

$$\displaystyle \begin{aligned} \|E_n(f,x)\|{}_{\infty} \leq \frac{\pi^{r-1} V_r}{(2n-2)(2n-3)\cdots(2n-r))}\|K_{2}\|{}_{\infty}. \end{aligned} $$

(29)

In addition, by Lemma 7, we have

$$\displaystyle \begin{aligned} \|(x-t)^{1}_{+} - \sum_{j=1}^n(x_j-t)^{1}_{+}v_j(x)\ell^2_j(x)\|{}_\infty = \left\{ \begin{array}{ll} O\left( \frac{\log n}{n}\right), &\gamma\leq -\frac{1}{2} \\ O\left(n^{2\gamma}\right), &\gamma> -\frac{1}{2}, \end{array} \right. \end{aligned} $$

(30)

while by Lemmas 2–3, we get

$$\displaystyle \begin{aligned} |\sum_{j=1}^n (x_j-t)^{0}_{+}(x-x_j)\ell^2_j(x)|\leq\sum_{j=1}^n |(x-x_j)\ell^2_j(x)| =\left\{ \begin{array}{ll} O\left(\frac{\log n}{n}\right), &\gamma\leq -\frac{1}{2} \\ O\left(n^{2\gamma}\right), &\gamma> -\frac{1}{2}. \end{array} \right. \end{aligned} $$

(31)

Together (30) and (31), we can obtain the desired results by using

$$\displaystyle \begin{aligned} K_{2}(t) =\left\{ \begin{array}{ll} O\left(\frac{\log n}{n}\right), &\gamma\leq -\frac{1}{2} \\ O\left(n^{2\gamma}\right), &\gamma> -\frac{1}{2}. \end{array}. \right. \end{aligned}$$

Finally, We use a function of analytic $f(x)=\frac {1}{1+25x^2}$ and a function of limited regularity f(x) = |x|⁵ to show that the convergence rate of $\|f(x)-H^*_{2n-1}(f,x)\|{ }_{\infty }$ is dependent on α and β in Fig. 3.

Fig. 3

$\|H^*_{2n-1}(f,x)-f(x)\|{ }_{\infty }$ at x = −1: 0.001: 1 by using Gauss-Jacobi pointsystem for $f(x)= \frac {1}{1+25x^2}$ and f(x) = |x|⁵ with different α and β, respectively