1 Introduction

When intensive care patients are subjected to mechanical ventilation, this is part of the life support. At the same time the ventilator causes damage to the muscles that govern the normal breathing. Normally, the muscles contract when we inhale, and air is pulled into the lungs. During controlled mechanical ventilation, the ventilator instead pushes the air into the lungs that then exert a pressure on the muscles. The function of the muscle tissue can deteriorate quite rapidly, leading to Ventilator Induced Diaphragmatic Dysfunction (VIDD) [2]. Because of this, the rehabilitation process, including the weaning from the ventilator, is more difficult and takes longer.

The Individual Virtual Ventilator (INVIVE) project [5] aims to study the mechanics of respiration through numerical simulation in order to learn more about the onset of VIDD, and the factors that influence its progress in a patient. This work is the first publication from the project and is a pilot study for the numerical techniques that we plan to use.

The diaphragm is the main respiratory muscle. It has not been studied as much in the literature as other muscles, and not with detailed models. However, there are a few studies that uses continuum mechanical descriptions of the muscle tissue and simulate its behaviour using FEM [6, 10]. The main drawbacks of the FEM solvers are that they are time-consuming, and that meshing of complex geometries can be difficult. We instead propose to use a meshfree RBF-FD method [4] for the numerical simulation. Some of the potential advantages are that meshing can be replaced with scattered node generation, which in some respects is easier, and allows for a lot of flexibility; that it is easy to construct high-order accurate approximations that can reduce the computational cost; and that the method is easy to implement and modify, providing flexibility when performing experiments. The objectives of the paper are

  • to show the feasibility of using the RBF-FD method for this type of problems,

  • to work with real medical data such that the results will be relevant,

  • to investigate how the high aspect ratio of the geometry affects the simulation and if this can be mitigated by using high aspect ratio node sets.

The paper is organized as follows: In Sect. 2 we describe the linear elasticity equations in three dimensions. Section 3 briefly introduces the RBF-FD method. The process from medical images to input data for the simulation is described in Sect. 4, which is followed by Sect. 5 on Numerical experiments.

2 The Elasticity Equations

The constitutive relations that describe the real behaviour of muscle tissue are non-linear. The displacement of the diaphragm is large, and should therefore also be modeled by non-linear elasticity equations. For our final simulation tool, we aim to solve the fully non-linear equations. However, for the initial development of meshless numerical methods for the diaphragm simulations, we use linear elasticity test case.

2.1 The Linearized Equations of Motion

For the linear test problem, the following simplifying assumptions are made: The relationship between stress and strain is linear, the material is isotropic and homogeneous, and displacements are small.

We define the displacement \(u(X)=(u_1(X),\,u_2(X),\,u_3(X))^T\in \mathbb {R}^{3}\) of the tissue from the initial configuration \(X=(x,\,y,\,z)^T\in \mathbb {R}^{3}\) to a later configuration \(X^*\in \mathbb {R}^{3}\) as

$$\displaystyle \begin{aligned} u(X) = X^* - X. \end{aligned} $$
(1)

The strain-displacement relationship for small displacements, ||∇u||≪ 1, has the form

$$\displaystyle \begin{aligned} \varepsilon = \frac{1}{2} \Big[\nabla u + (\nabla u)^T\Big], \end{aligned} $$
(2)

where the strain \(\varepsilon \in \mathbb {R}^{3 \times 3}\) is a tensor. For a linear material, the constitutive relation between the strain and the stress \(\sigma \in \mathbb {R}^{3 \times 3}\) is characterized by the Lamé parameters λ, and μ, leading to

$$\displaystyle \begin{aligned} \sigma = 2\mu \varepsilon + \lambda tr(\varepsilon) I. \end{aligned} $$
(3)

In tissue mechanics, the acceleration is typically small compared with the forces, and can be neglected. The equations of motion (Newton’s second law) can then be written as

$$\displaystyle \begin{aligned} \nabla \cdot \sigma + f = 0, {} \end{aligned} $$
(4)

where \(f \in \mathbb {R}^3\) represents body forces. We assume that (4) holds for all points X ∈ Ω, where Ω is the domain of interest, which for our problem is the diaphragm. To close the problem formulation, we also need boundary conditions. The first type is displacement boundary conditions

$$\displaystyle \begin{aligned} u = g,\quad X\in\Omega_D. \end{aligned} $$
(5)

These are applied where the geometry is attached, for example where the diaphragm is attached to the ribs and the spine. Traction boundary conditions are given in terms of the stress as

$$\displaystyle \begin{aligned} \sigma \cdot n = h,\quad X\in\Omega_T. {} \end{aligned} $$
(6)

These represent forces applied to the surface of the domain of interest, such as the pressure against the diaphragm from below generated by the abdominal compliance.

2.2 The Lamé-Navier PDE Formulation

The Lamé-Navier equations gives the steady-state motion equation in terms of the displacement field [13]. This means we are solving a system of three PDEs with three unknowns. We rewrite (4) and (6) in terms of u using relations (2), (3), and the identity tr(∇u + (∇u)T) = 2(∇⋅ u) to get

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} (\lambda + \mu) \nabla (\nabla \cdot u) + \mu \nabla^2 u + f &\displaystyle =&\displaystyle 0,\quad u \in \Omega {} \end{array} \end{aligned} $$
(7)
$$\displaystyle \begin{aligned} \begin{array}{rcl} u &\displaystyle =&\displaystyle g,\quad u \in \partial\Omega_D \end{array} \end{aligned} $$
(8)
$$\displaystyle \begin{aligned} \begin{array}{rcl} \Big[\lambda (\nabla \cdot u)I + \mu (\nabla u + (\nabla u)^T)\Big] \cdot n &\displaystyle =&\displaystyle h,\quad u \in \partial\Omega_T {} \end{array} \end{aligned} $$
(9)

When we later discretize the system, it is more convenient to work with the operators and the displacement in component form. The two operators in the PDE (7) applied to u expand to

$$\displaystyle \begin{aligned} \nabla (\nabla \cdot u) = \begin{pmatrix} \nabla_{xx} & \nabla_{xy} & \nabla_{xz} \\ \nabla_{xy} & \nabla_{yy} & \nabla_{yz} \\ \nabla_{xz} & \nabla_{yz} & \nabla_{zz} \end{pmatrix} \begin{pmatrix} u_1\\u_2\\u_3 \end{pmatrix}, \quad \nabla^2 u = \begin{pmatrix} \mathcal{L} & 0 & 0 \\ 0 & \mathcal{L} & 0\\ 0 & 0 & \mathcal{L} \end{pmatrix} \begin{pmatrix} u_1\\u_2\\u_3 \end{pmatrix}, \end{aligned}$$

where \(\mathcal {L} = \nabla _{xx} + \nabla _{yy} + \nabla _{zz}\). Rewriting the two terms in the traction condition (9) in the same way yields

$$\displaystyle \begin{aligned} (\nabla \cdot u)I\cdot n &= \begin{pmatrix} n_1\nabla_{x} & n_1\nabla_{y} & n_1\nabla_{z} \\ n_2\nabla_{x} & n_2\nabla_{y} & n_2\nabla_{z} \\ n_3\nabla_{x} & n_3\nabla_{y} & n_3\nabla_{z} \end{pmatrix} \begin{pmatrix} u_1\\u_2\\u_3 \end{pmatrix},\\ (\nabla u + (\nabla u)^T)\cdot n &= \begin{pmatrix} \mathcal{T}_{1x} & n_2\nabla_x & n_3\nabla_x \\ n_1\nabla_y &\mathcal{T}_{2y} & n_3\nabla_y\\ n_1\nabla_z & n_2\nabla_z & \mathcal{T}_{3z} \end{pmatrix} \begin{pmatrix} u_1\\u_2\\u_3 \end{pmatrix}, \end{aligned} $$

where \(\mathcal {T}_{iq}=n_i\nabla _q + n_1\nabla _x+n_2\nabla _y + n_3\nabla _z \).

3 The RBF-FD Numerical Method

In the RBF-FD method [4], scattered node stencil approximations are used for representing the differential operators in the PDE and the boundary conditions. Let X 1, …, X N be a global set of node points, and let u ij ≈ u i(X j). We collect the unknown displacement values in the vectors U i = (u i1, …, u iN)T. When we want to approximate the result of a differential operator \(\mathcal {D}\) applied to u i, we first find a local neighbourhood \(X_1^{(j)},\ldots ,X_n^{(j)}\) with local unknowns \(u_{ik}^{(j)}\) to the point X j, where we want to evaluate the result. The stencil approximation then takes the form

$$\displaystyle \begin{aligned} \mathcal{D}u_i(X_j) \approx \sum_{k=1}^n w_ku_{ik}^{(j)}. \end{aligned} $$
(10)

The weights are computed for each point in the global node set by solving a linear system of size n × n, where the stencil size n ≪ N. In this work, we consider stencil approximations where RBFs augmented by a polynomial basis are used. The small linear systems then take the form

$$\displaystyle \begin{aligned} \begin{pmatrix} A & P\\ P^T & 0 \end{pmatrix} \begin{pmatrix} w\\ \gamma \end{pmatrix} = \begin{pmatrix} b\\ c \end{pmatrix}, \end{aligned} $$
(11)

where \(A(i,k)=\phi (\|X_k^{(j)}-X_i^{(j)}\|)\), where ϕ(r) is an RBF, for i, k = 1, …, N, and where \(P(i,k)=p_k(X_i^{(j)})\), for i = 1, …, N and k = 1, …, m. The polynomials p k are chosen as the lowest degree monomial basis with dimension m, and m is usually chosen such that a full basis for a certain maximum degree K is obtained. The right hand side vectors are defined by \(b(i)=\mathcal {D}\phi (X_j-X_i^{(j)})\) for i = 1, …, N, and \(c(i)=\mathcal {D}p_i(X_j)\) for i = 1, …, m. The vector γ can be seen as a Lagrange multiplier in this problem and is discarded. The stencil approximation is exact for polynomials up to degree K as can be seen from the last block row in the system, and it is also exact for the RBFs centered at the stencil nodes.

A global differentiation matrix D is assembled by inserting the weights corresponding to X j in the jth row of the matrix, and in the columns corresponding to the global indices of the nodes \(X_k^{(j)}\) in the local neighbourhood (X j is normally one of the points in the neighbourhood). Then we can compute

$$\displaystyle \begin{aligned} (\mathcal{D}u_i(X_1),\ldots,\mathcal{D}u_i(X_N))^T\approx DU_i. \end{aligned} $$
(12)

When solving the PDE problem (7)–(9), u is replaced with the discrete field variables, and the differential operators are replaced with the corresponding differentiation matrices. The PDE operator is applied for interior node points, and the boundary operators at boundary node points.

In recent work on RBF-FD methods it has been found that a combination of polyharmonic spline RBFs ϕ(r) = |r|2k+1, k > 0 with polynomials up to degree K has excellent approximation properties [1, 3]. The (asymptotic) convergence rate is guided by the polynomial degree K, and oscillations near boundaries, which are common both with pure RBF and pure polynomial approximations, are suppressed as soon as K is large enough. In this work, we use the cubic polyharmonic spline

$$\displaystyle \begin{aligned} \phi(r)=|r|{}^3. \end{aligned} $$
(13)

4 The Medical Image Input Data

The medical research questions are the motivation for the INVIVE project, and it is important that the numerical simulations can emulate what is seen in the medical image data. To start with, we use medical images to extract the real diaphragm geometry. We also use image data to find the displacement of the diaphragm at different times during the respiratory cycle. Later in the project medical image data will also be used for validation of the numerical simulations.

4.1 Medical Image Acquisition

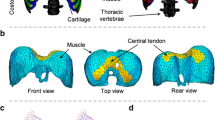
The type of medical image data that is available to us is thoracic 3-D CT images acquired using a TOSHIBA Aquilion ONE CT scan machine. The images were captured at Azienda Ospedaliera di Padova from adult patients that were subjected to the CT scan for medical reasons (the CT scans were not performed only for research). The images were made and are used in anonymous form. The computed 3-D images are associated with two specific times in the breathing cycle or, equivalently, with two different states of lung inflation. The images have a pixel size of 0.927 × 0.927 mm2 and a slice thickness of 0.3 mm. They have a resolution of 512 × 512 × 1500 that includes the thoracic and abdominal regions. Examples of image views are shown in Fig. 1.

Fig. 1
figure 1

Manual segmentation of the diaphragm. Red: diaphragm, yellow: lungs, blue: bones

Full size image

4.2 Converting Image Data to Mesh-Based Geometry Data

Automated segmentation methods are currently not able to identify the diaphragm that is barely visible in the images. Therefore, the diaphragm was manually segmented on a Wacom tablet using a method similar to the description in [14]. The segmentation time is roughly 6 h for one 3-D image. The manual segmentation method consists in following the organs that are known to surround the diaphragm such as the bottom of the lungs, the top of the liver, and the inside of the ribs. Figure 1 shows the result of the segmentation.

The labelized voxel data is then converted into a mesh with the marching cube algorithm. It contains around 1.5 ⋅ 106 vertices due to the CT scan resolution. The initial mesh is then decimated using Vorpaline [9], a fast and automatic method, where the only input is the number of final points comprising the mesh. The initial mesh and a decimated mesh are shown in Fig. 2.

Fig. 2
figure 2

Left: The initial 3D-mesh and the decimated mesh with 1000 vertices. Right: The sagittal cut and centers of gravity (green)

Full size image

Both when implementing the boundary conditions and for node generation, it is necessary to be able to identify vertices belonging to different parts of the surface of the geometry. Two relevant sections are the upper thoracic surface and the lower abdominal surface. These correspond to two different pressure regions.

To separate the surface components, we employ the following algorithm: First the whole diaphragm is separated into a left and right part. If we orient the diaphragm such that the parameter \(t\in [t_{\min },\,t_{\max }]\) describes a position from left to right, and we let V (⋅) denote the volume of a convex region, we let C(⋅) denote the convex hull of a node set, and we let Ω(t 1, t 2) be the part of the diaphragm that falls within that range of t. Then we can find the sagittal cut t sep as the position that maximizes the sum of the left and right volume

$$\displaystyle \begin{aligned} t_{\mathrm{sep}} = \underset{{t_{\min}, \leq t \leq t_{\max}}}{\arg\max} V\left(C\left(\{X_j | X_j\in\Omega(t_{\min},t)\}\right)\right)+V\left(C\left(\{X_j | X_j\in\Omega(t,t_{\max})\}\right)\right). \end{aligned}$$

The result is illustrated in the right panel of Fig. 2, where also the two centres of gravity c L and c R, for the left and right part respectively, are indicated.

For each surface vertex X j ∈ Ωi, for i = L, R, of the diaphragm, a vertex location tag is given by the dot product between the diaphragm vertex normal n j and the normalized vector v j = (X j − c i)∕∥X j − c i∥ in the direction from the center of gravity to the vertex.

$$\displaystyle \begin{aligned} \mathrm{tag}(X_j)= \begin{cases} \mathrm{thorax},& \text{if } n_j\cdot v_j\geq 0\\ \mathrm{abdomen}, & \text{otherwise} \end{cases}{} \end{aligned} $$
(14)

Finally, to avoid artifacts, only the bigger connected component of tagged locations is kept and disconnected parts the are changed to the other location.

4.3 Final Geometry Representation and Node Generation

Based on the OGr method [11, 12] and a least-squares RBF-partition of unity method [7], the mesh-based geometry is smoothed and parametrized. The details of this process are described in a forthcoming paper [8].

Scattered nodes sets of different resolutions are generated from the smoothed geometry. A level set function inside the volume is used for anisotropic node placement such that the resolution in the direction normal to the surface is higher then along the surface.

4.4 A Test Problem with Real Displacements

We are still working with the analyses of the images shown in the previous section. Therefore, we use an older data set with a bit lower resolutions for the test case and the numerical experiments. We only have the end of inhalation state segmented at this point. To define a realistic displacement function, we have identified nine different landmarks on the diaphragm. There are four insertion points of the diaphragm that we take as immobile. These are the left and right transverse processes of the two lowest thoracic vertebra T11 and T12. The five moving landmarks and their displacements are given in Table 1. We augment this information by also requiring the extremal points of the lower edge of the diaphragm to be immobile, and the thickness change from contracted to relaxed state at the two domes to be 66%. We then interpolate the displacements at the augmented landmarks by the |r|7 polyharmonic spline. The initial and displaced states are shown in Fig. 3. As the first test problem, we solve for the interior displacement given that the boundary displacement changes from the relaxed to the contracted state.

Table 1 Displacements of five landmark points
Full size table
Fig. 3
figure 3

Initial node locations (higher, red) and displaced node locations (lower, blue), using the constructed displacement function for a node set with N = 8404 nodes

Full size image

5 Numerical Experiments

A main concern when solving the linear elasticity problem for the diaphragm is the high aspect ratio of the geometry. The overall size of the diaphragm is around 30 × 20 × 15 cm, while the thickness is just a few mm. In the experiments we want to test how important the resolution in the normal direction is for the results. Our hypothesis is that it needs to be large enough to allow for a stencil with a similar number of nodes in each dimension. That is, we need at least \(\sqrt [3]{n}\) nodes in the normal direction. We compare two cases, (i) using uniform node sets with similar distances in the normal and tangential directions, and (ii) using node sets that are refined in the normal direction according to the stencil size. Convergence is tested against a reference solution computed at a higher resolution.

The left part of Fig. 4 shows the convergence of the displacements. The errors are larger for case (i), and no convergence trend is observed for the largest stencil size. The number of points in the normal direction increases gradually as N increases. For case (ii), the errors are smaller, and convergence is observed in all cases. When using polyharmonic splines in combination with polynomials, we expect the convergence rate to be of order h K+1, where h is a measure of the node spacing and K is the maximum degree of the polynomial terms [3]. However, for case (ii), we get the same rate of convergence for all K. One reason can be that the normal refinement is constant when the tangential refinement is increased. There may also be issues concerning the smoothness of the node distribution and/or the solution.

Fig. 4
figure 4

Left: Convergence of the displacement against the reference solution for uniform nodes (dashed) and nodes refined in the normal direction (solid) for n = 50, K = 3 (open square), n = 78, K = 4 (open circle), and n = 120, K = 5 (times), where n is the stencil size and K is the order of the polynomial basis augmenting the polyharmonic spline functions. Right: Convergence of the stresses against the reference solution for n = 50. The slopes p, with − p indicating the order of convergence are also shown

Full size image

In the right part of Fig. 4, we display the convergence of the functions in the stress tensor, computed for the interior nodes for case (ii). The convergence rates are similar to those of the displacement. This is also unexpected, as we would normally expect a derivative of order ℓ to converge as h K+1−ℓ [3].

In Fig. 5, we show the components of the stress tensor, computed for the interior nodes for case (ii). We can see that the magnitude of the stresses is large at the domes where we enforce compression of the muscle.

Fig. 5
figure 5

The six components of the stress tensor evaluated for the interior nodes

Full size image

6 Conclusions

We have developed a pipeline for converting CT image data into input data for numerical simulation. The main bottleneck is the manual segmentation of the diaphragm. One thing that will be investigated in future work is if a mapping from a reference geometry can be used to simplify this step.

When the thin dimension is resolved with enough node points, the RBF-FD approximations converge as the number of nodes increase. Also the stresses can be computed with similar accuracy. This shows that it is possible to use this type of discretization, but further work is needed on how to generate smooth non-uniform node sets, and also on the implementation of more advanced test problems.