1 Trefftz-DG Formulation for the Elasto-Acoustic Equation

Trefftz methods are particular finite element methods where the basis and test functions are locally solutions to the partial differential equation that governs the problem to be solved. Compared to the existing literature for solving frequency problems, space-time Trefftz methods are still not widely used. One reason could be that they require using space-time meshes [6, 12]. To our knowledge, few references on Trefftz approximations of time-dependent wave equations are available and they mainly address theoretical properties in the case of Acoustics and Electromagnetism [4, 8, 10, 11]. They provide convergence and stability studies and some numerical results are displayed by using plane wave bases in 1D +  time dimension. Numerical in 2D +  time dimensions are proposed in [4] for electromagnetism. There are also some studies devoted to the second-order formulation of the acoustic wave equation approximated in Trefftz spaces by the mean of Lagrange multipliers [1, 13]. In [3], we have proposed a Trefftz-DG formulation for elasto-acoustic. The method required the inversion of a huge sparse matrix. The goal of this paper is to show how to derive a semi-explicit scheme, requiring only the inversion of a block-diagonal matrix on each element of the mesh.

In this section, following [10] and the framework therein, we propose a formulation of the elasto-acoustic coupling reading as a first-order system. Here and further the sub-scripts F and S corresponds to the acoustic (fluid) and elastodynamic (solid) domains.

1.1 Elasto-Acoustic Equations

We introduce a space-time domain Q ≡ ( ΩF ∪ ΩS) × I, where \(\Omega _F \subset \mathbb {R}^d\) is a bounded Lipschitz domain of dimension d filled with fluid, \(\Omega _S \subset \mathbb {R}^d\) is a bounded Lipschitz elastodynamic domain of dimension d filled with solid, and I ≡ [0, T] is the time interval. All medium parameters c F ≡ c F(x) and ρ F ≡ ρ F(x), standing for the acoustic wave propagation velocity and fluid density respectively, as well as the inverted stiffness tensor \( \underline { \underline {\mathbf {C}}}^{-1}(\mathbf {x}) \equiv \underline { \underline {\mathbf {A}}}(\mathbf {x})\) and the solid density ρ S ≡ ρ S(x), are assumed to be piecewise constant and positive. We denote by ΓFS = ΩF ∩ ΩS the fluid-solid interface. The elasto-acoustic system of equations is based on the coupling of the first-order acoustic equation, written in terms of velocity v F ≡v F(x, t) and pressure p ≡ p(x, t) fields:

$$\displaystyle \begin{aligned} \left\{ \begin{aligned} & \frac{1}{c_F^2\rho_F} \dfrac{\partial p}{\partial t} + \mathrm{div} {\mathbf{v}}_F= f &\mbox{ in }Q_F, \\ & \rho_F \dfrac{\partial {\mathbf{v}}_F}{\partial t} + \mathbf{\nabla} p = 0 &\mbox{ in }Q_F,\\ & {\mathbf{v}}_F(\cdot,0)={{\mathbf{v}}_F}_0, \,\,p(\cdot,0) = p_0 &\mbox{ in }\Omega_F, \\ & {\mathbf{v}}_F\cdot {\mathbf{n}}_{\Omega_F} = {g}_F &\mbox{ in }\partial\Omega_F\backslash\Gamma _{FS} \times I , \end{aligned} \right. \end{aligned} $$
(1)

where \({\mathbf {n}}_{\Omega _F}\) is the normal vector to ∂ ΩF, the source term f ≡ f(x, t), the boundary condition g F, the velocity v F 0 and the pressure p 0 are the initial data, with the first-order elastodynamic system, written in terms of velocity v S ≡v S(x, t) and stress tensor (symmetrical and positive) \( \underline {\mathbf {\sigma }}\equiv \underline {\mathbf {\sigma }}(\mathbf {x},t)\) fields:

$$\displaystyle \begin{aligned} \left\{ \begin{aligned} & \underline{\underline{\mathbf{A}}} \dfrac{\partial \, \underline{\mathbf{\sigma}}}{\partial t} - \underline{\mathbf{\varepsilon}}({\mathbf{v}}_S)= 0 &\mbox{ in } Q_S, \\ & \rho_S \dfrac{\partial {\mathbf{v}}_S}{\partial t} - \mathbf{div} \, \underline{\mathbf{\sigma}} = 0 &\mbox{ in } Q_S ,\\ {} & {\mathbf{v}}_S(\cdot,0)={{\mathbf{v}}_S}_0, \,\,\underline{\mathbf{\sigma}}(\cdot,0) = \underline{\mathbf{\sigma}}_0 &\mbox{ in } \Omega_S,\\ & \underline{\mathbf{\sigma}}{\mathbf{n}}_{\Omega_S}= {\mathbf{g}}_S &\mbox{ in } \partial\Omega_S \backslash\Gamma _{FS}\times I, \end{aligned} \right. \end{aligned} $$
(2)

where \({\mathbf {n}}_{\Omega _S}\) is the normal vector to ∂ ΩS, the boundary condition g F, the velocity v S 0 and the stress tensor \( \underline {\mathbf {\sigma }}_0\) are the initial data. The transmission conditions between the two systems (2) and (1) represent the continuity of velocity and stress normal components ΓFS:

$$\displaystyle \begin{aligned} \left\{ \begin{aligned} & {\mathbf{v}}_F\cdot {\mathbf{n}}_{\Gamma_{FS}}={\mathbf{v}}_S\cdot{\mathbf{n}}_{\Gamma_{FS}} &\mbox{ at } \Gamma_{FS},\\ & -p{\mathbf{n}}_{\Gamma_{FS}}=\underline{\mathbf{\sigma}} {\mathbf{n}}_{\Gamma_{FS}} &\mbox{ at } \Gamma_{FS}. \end{aligned} \right. \end{aligned} $$
(3)

The velocities aligned with the interface and the tangential stress remain unconstrained.

1.2 Space-Time Trefftz-DG Formulation

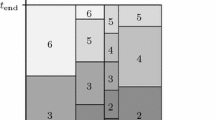
We introduce a non-overlapping space-time mesh \(\mathcal {T} _{h}\) on Q composed of space-time Lipschitz elements K F ⊂ ΩF × I and K S ⊂ ΩS × I. We denote by \(\mathcal {T}_{Fh}\) (resp. \(\mathcal {T}_{Sh}\)) the restriction of \(\mathcal {T}_{h}\) to the fluid (resp. solid) domain. Let \({\mathbf {n}}_{K_F} \equiv ({\mathbf {n}}_{K_F}^x,{n}_{K_F}^t)\) be the outward-pointing unit normal vector on ∂K F, and \({\mathbf {n}}_{K_S} \equiv ({\mathbf {n}}_{K_S}^x,{n}_{K_S}^t)\) be the outward-pointing unit normal vector on ∂K S. We assume that all medium parameters are constant in K F and K S respectively. The mesh skeleton \(\mathcal {F}_h\equiv \bigcup \limits _{K_{F,S} \in \mathcal {T} _{h}} \partial K_{F,S}\) can be decomposed into families of the internal \(\mathcal {F}_h^{Q}\) faces, the fluid-solid \(\mathcal {F}_h^{FS}\) faces, the boundary \(\mathcal {F}_h^D\) faces, the initial and final time \(\mathcal {F}_h^0\) and \(\mathcal {F}_h^T\) element faces respectively, as it shown in Fig. 1. We introduce the space \(V_h(\mathcal {T} _{h})\) as a subspace of L 2(Q) defined by \( V_h (\mathcal {T} _{h}) = \big \{ \phi \in L^2(Q), \phi _{\vert K_{F,S}} \in \mathbb {P}^{\mathrm {p}}(K_{F,S}) \big \}\). The unknowns \(({\mathbf {v}}_{Fh},\,p_h,\,{\mathbf {v}}_{Sh},\, \underline {\mathbf {\sigma }}_h)\) are supposed to be in \({\mathbf {V}}_h(\mathcal {T} _{h}) \equiv {V}_h(\mathcal {T} _{Fh})^d \times {V}_h(\mathcal {T} _{Fh})\times {V}_h(\mathcal {T} _{Sh})^d\times {V}_h(\mathcal {T} _{Sh})^{d^2}\). We consider the test functions ω F, q, ω S, \( \underline {\mathbf {\xi }}\) in \(\mathbf {T}(\mathcal {T} _{h})\) for v F, p, v S and \( \underline {\mathbf {\sigma }}\) respectively, where the Trefftz space \(\mathbf {T}(\mathcal {T} _{h})\) is defined on the mesh \(\mathcal {T} _{h}\) as follows:

$$\displaystyle \begin{aligned} \mathbf{T} (\mathcal{T} _{h})\equiv \Big\{&(\mathbf{\omega}_F,\,q,\,\mathbf{\omega}_S,\,\underline{\mathbf{\xi}}) \in {\mathbf{V}}_h(\mathcal{T} _{h}) \mbox{ s. t. } \frac{1}{c_F^2\rho_F} \dfrac{\partial q}{\partial t} + {\mathrm{div}} \mathbf{\omega}_F=0,\,\,\rho_F \dfrac{\partial \mathbf{\omega}_F}{\partial t} +\mathbf{\nabla} q = 0 \\ &\forall K_{F}\in \mathcal{T} _{Fh}, \mbox{ and } \underline{\underline{\mathbf{A}}} \dfrac{\partial \, \underline{\mathbf{\xi}}}{\partial t} - \underline{\mathbf{\varepsilon}}(\mathbf{\omega}_S)=0,\,\, \rho_S \dfrac{\partial \mathbf{\omega}_S}{\partial t} - \mathbf{div} \, \underline{\mathbf{\xi}} = 0\,\, \forall K_{S}\in \mathcal{T} _{Sh} \Big\}. \end{aligned} $$

This space is of Trefftz type since it is a subspace of the regular space \({\mathbf {V}}_h(\mathcal {T} _{h})\) composed of local solutions of the volumic governing equations (1) and (2) set in each element K F and K S respectively.

Fig. 1
figure 1

Example of 1D +  time mesh \(\mathcal {T} _{h}\) covering Q. The internal element faces \(\mathcal {F}_h^{Q}\) are represented by dotted line, the element faces of fluid-solid interface \(\mathcal {F}_h^{FS}\)—by dash-dotted line, the boundary element faces \(\mathcal {F}_h^D\)—by thick line, the initial \(\mathcal {F}_h^0\) and the final \(\mathcal {F}_h^T\) time element faces—by double and dashed line respectively

Full size image

As in the standard DG methods, the next step in order to obtain the variational formulation consists in multiplying the equations of (1) by the test functions q and ω F in \(\mathbf {T}(\mathcal {T} _{h})\), and the equations of (2) by the test functions \( \underline {\mathbf {\xi }}\) and ω S in \(\mathbf {T}(\mathcal {T} _{h})\) respectively, and, as is standard in space-time DG methods, we integrate by parts the obtained equations not only in space but also in time:

$$\displaystyle \begin{aligned} & \sum_{K_F}\int\limits_{\partial K_F} \Big[ \frac{1}{c_F^2\rho_F} \breve{p}_h q\, n_{K_F}^t + q\hat{\mathbf{v}}_{Fh}\cdot {\mathbf{n}}_{K_F}^x +\rho_F\, \breve{\mathbf{v}}_{Fh}\cdot\mathbf{\omega}_F\,n_{K_F}^t +\hat{p}_h \mathbf{\omega}_F\cdot{\mathbf{n}}_{K_F}^x \Big] d\mathrm{s}\,+ \\ &\sum_{K_S}\int\limits_{\partial K_S} \Big[ \underline{\underline{\mathbf{A}}}\,\breve{\underline{\mathbf{\sigma}}}_h:\underline{\mathbf{\xi}}\, n_{K_S}^t - \underline{\mathbf{\xi}}\hat{\mathbf{v}}_{Sh}\cdot {\mathbf{n}}_{K_S}^x + \rho_S \,\breve{\mathbf{v}}_{Sh}\cdot \mathbf{\omega}_S\,n_{K_S}^t - \hat{\underline{\mathbf{\sigma}}}_h :(\mathbf{\omega}_S \otimes {\mathbf{n}}_{K_S}^x) \Big] d\mathrm{s} = \\ &\sum_{K_F}\int\limits_{K_F} fq d\mathrm{v}. \end{aligned} $$
(4)

Thanks to the choice of test functions the left hand side of the above space-time formulation contains only surface integrals. The numerical fluxes in time \(\hat {\mathbf {v}}_{Fh}\), \(\hat {p}_{h}\), \(\hat {\mathbf {v}}_{Sh}\), \(\hat { \underline {\mathbf {\sigma }}}_h\) and in space v̆Fh, p̆h, v̆Sh, \(\breve { \underline {\mathbf {\sigma }}}_h\) are defined in the standard DG notations [2, 3, 7] as follows:

Here, α 1, α 2, β 1, β 2, δ 1, δ 2, γ 1, and γ 2 are positive penalty parameters. As in standard DG methods, a suitable choice of these penalty parameters allows one to prove stability of the overall method. It is shown in [2, 3] that they contribute to the accuracy and convergence of the numerical method. We refer to [2, 3] for more details on the definition of the numerical fluxes.

Summing the contribution (4) of all elements \(K_F, K_S \in \mathcal {T} _{h}\), and introducing the bilinear \(\mathcal {A}_{TDG}(\cdot \,;\cdot )\) and the linear ℓ TDG(⋅) forms for the left-hand side and the right-hand side expressions respectively, we obtain the Trefftz-DG formulation for the elasto-acoustic problem:

Seek \(({\mathbf {v}}_{Fh},\,p_h,\,{\mathbf {v}}_{Sh},\, \underline {\mathbf {\sigma }}_h) \in \mathbf {T}(\mathcal {T} _{h})\) such that, for all \((\mathbf {\omega }_F,\,q,\,\mathbf {\omega }_S,\, \underline {\mathbf {\xi }}) \in \mathbf {T}(\mathcal {T} _{h})\) it holds true:

$$\displaystyle \begin{aligned} \mathcal{A}_{TDG}\big(({\mathbf{v}}_{Fh},\,p_h,\,{\mathbf{v}}_{Sh},\,\underline{\mathbf{\sigma}}_h); (\mathbf{\omega}_F,\,q,\,\mathbf{\omega}_S,\,\underline{\mathbf{\xi}})\big) = \ell_{TDG}\big(\mathbf{\omega}_F,\,q,\,\mathbf{\omega}_S,\,\underline{\mathbf{\xi}}\big). \end{aligned} $$
(5)

The analysis of well-posedness of (5) is based on the coercivity and continuity estimates of the bilinear and linear forms in mesh-dependent norms [2, 3]. The proof is similar to the one given in [10] where the acoustic wave equation is addressed. In Sect. 2 we provide the algorithm of the Trefftz-DG formulation (5), and we discuss different analytical and numerical approaches for its optimization.

2 Implementation of the Algorithm

The numerical implementation of the Trefftz-DG formulation is different from the standard DG ones which address the space and time integration separately. Standard DG space integrations have the interesting feature of leading to a block-diagonal mass matrix and allow then the use of explicit time integration. The computational costs thus depend on a CFL condition which sets the value of the time step as a function of the space step. On the other hand, a naive implementation of Trefftz-DG methods require performing a space-time integration which leads to invert a sparse matrix whose size tends to be huge. It is thus not obvious that a crude implementation of the Trefftz-DG algorithm does not generate additional cost as compared to standard DG ones.

In this section we provide some important steps of implementation of Trefftz-DG formulation (5) and discuss optimization techniques. The complete algorithm with more numerical details can be found in [2, 3].

2.1 Change-Over Between the Time Slabs

To simplify the presentation, we assume here that we use the same order of approximation on each cells, so that we have \(N_{dof}^f\) degrees of freedom on fluid cells and \(N_{dof}^s\) degrees of freedom on solid cells. Once we have defined the discrete approximation space, we can solve the problem inside each element K F and K S, communicating the corresponding values at the boundaries ∂K F and ∂K S by the incoming and outgoing fluxes. Thus, the variational problem is represented by a algebraic linear system, with a sparse matrix M, of size equals to the total number of elements \(N_{el}^{f,s}\) multiplied by the number of degrees of freedom per element \(N_{dof}^{f,s}\), that is \(N^f_{el} \times N^f_{dof}+N^s_{el} \times N^s_{dof}\). When compared to the computational cost of standard DG implementation, the corresponding Trefftz-DG cost is thus increased and it is mainly due to the need of inverting the large-sized matrix. The most obvious way to reduce the size of the matrix, which is classically used in most work on space-time Trefftz method, is to consider time slabs. We restrict ourselves to the case of cartesian meshes, but this methodology can also be applied to unstructured meshed. An alternative is to use tent-pitched meshes that respect the causality, this will be the topic of a future work. In order to optimize the execution of the algorithm, we propose to divide the space-time domain Q into N t elementary time slabs \(Q_1,\, Q_2,\ldots ,\, Q_{N_t}\) and to solve the problem slab by slab, considering the final results, computed in the current time slab at time t, as initial values for the next slab at time t +  Δt (see Fig. 2). Thus the size of matrix inside each time slab is N t times smaller, compared to the initial one. Moreover, if the medium parameters are fixed in time, and the space discretization is preserved from slab to slab, the matrix can be computed and inverted once, and then re-projected onto the next time slabs, reducing thus the global numerical cost.

Fig. 2
figure 2

Example of 1D +  time mesh \(\mathcal {T} _{h}\) on Q decomposed into N t time slabs

Full size image

2.2 Polynomial Basis

One of the important advantages of Trefftz type methods is the flexibility in the choice of basis functions provided they satisfy the Trefftz property locally in each element. To perform the numerical simulations, we have extended the algorithm proposed by Maciag in [9] for computing wave polynomials, solutions of the second order transient wave equation, to the first order acoustic and elastodynamic systems of dimension one and higher. It consists in computing a polynomial basis, defined in the reference element, using Taylor expansions of generating exponential functions which are local solutions of the initial system of equations. An example of space-time wave polynomial basis for the first-order acoustic wave equation reads as follows (approximation degree p=3, dimension of the physical space d = 1):

$$\displaystyle \begin{aligned} \begin{array}{l l l l} \hat{\phi}^v_{1} = 0 & \hat{\phi}^v_{2} = 1 & \hat{\phi}^v_{3}= x & \hat{\phi}^v_{4} = c_Ft \\ \hat{\phi}^p_{1} = -c_F & \hat{\phi}^p_{2} = 0 & \hat{\phi}^p_{3}= -c_F^2t & \hat{\phi}^p_{4} = -c_Fx \\ & & & \\ {} \hat{\phi}^v_{5} = -\frac{x^2}{2}-\frac{c_F^2t^2}{2} & \hat{\phi}^v_{6} = -c_Fxt & \hat{\phi}^v_{7} = -\frac{x^3}{6}-\frac{xc_F^2t^2}{2} & \hat{\phi}^v_{8} = -\frac{c_F^3t^3}{6}-\frac{x^2c_Ft}{2} \\ \hat{\phi}^p_{5} = c_F^2xt & \hat{\phi}^p_{6} = c_F(\frac{x^2}{2}+\frac{c_F^2t^2}{2}) & \hat{\phi}^p_{7} = c_F(\frac{c_F^3t^3}{6}+\frac{x^2c_Ft}{2}) & \hat{\phi}^p_{8} = c_F(\frac{x^3}{6}+\frac{xc_F^2t^2}{2}) \\ \end{array} \end{aligned}$$

This basis contains the couples of polynomial functions (\(\hat {\phi ^v_{\cdot }},\hat {\phi ^p_{\cdot }}\)), corresponding to the velocity and pressure respectively, which are locally defined and satisfy the Trefftz property inside each element of the mesh, and of degrees less or equal to p (p = 0, 1, 2, 3) to provide an approximation of order p. By their construction, the Trefftz basis functions are not attached to the coordinates of the degrees of freedom inside the element, contrary to the Lagrange polynomials. Even if we compute only surface integrals, we can evaluate the final approximation solution in any point of the element refinement. We refer to [2] for more numerical details as well as for the acoustic and elastodynamic basis examples of higher dimensions.

2.3 Inversion of the Matrix M Inside a Time Slab

The inversion of the matrix inside the time slab can be explicitly reduced to the inversion of its block-diagonal component, which corresponds to the integration at the bottom and top of the time slab (initial and final time faces \(\mathcal {F}_h^{0}\) and \(\mathcal {F}_h^{T}\)), thanks to the Taylor expansion formulas. More precisely, let us recall the expression for the bilinear form \(\mathcal {A}_{TDG}(\cdot \,;\cdot )\) from Sect. 1.2:

$$\displaystyle \begin{aligned} \mathcal{A}_{TDG}\big( \cdot;\cdot\big)\equiv \underbrace{\int\limits_{\mathcal{F}_h^{T}} + \int\limits_{\mathcal{F}_h^{0}}}_{\mathcal{A}_{TDG}^{\Omega}} + \underbrace{\int\limits_{\mathcal{F}_h^{Q}} + \int\limits_{\mathcal{F}_h^{D}} + \int\limits_{\mathcal{F}_h^{FS}} }_{\mathcal{A}_{TDG}^{I}}. \end{aligned}$$

It consists of \(\mathcal {A}_{TDG}^{\Omega }(\cdot ;\cdot )\), that corresponds to the integration at the initial and final time element faces of the time slab, and \(\mathcal {A}_{TDG}^I(\cdot ;\cdot )\), that corresponds to the integration at the internal, boundary and fluid-solid element faces. Thus, the matrix M can be represented by the sum of two matrices ΔΩ M Ω and ΔI M I corresponding to \(\mathcal {A}_{TDG}^{\Omega }\) and \(\mathcal {A}_{TDG}^{I}\) respectively, as follows:

$$\displaystyle \begin{aligned} M = {\Delta}_\Omega M_{\Omega} + {\Delta}_I M_I. \end{aligned}$$

Here, ΔΩ ∝ ( Δx)d represents the area of the local faces in \(\mathcal {F}_h^{0}\) and \(\mathcal {F}_h^{T}\), and ΔI ∝ ( Δx)d−1 Δt represents the area of the local faces in \(\mathcal {F}_h^{Q}\), \(\mathcal {F}_h^{D}\) and \(\mathcal {F}_h^{FS}\) respectively. We refer to [2] for more details.

This decomposition is of particular interest since M Ω is block-diagonal, each block corresponding to one element. Indeed, we have:

$$\displaystyle \begin{aligned} {\Delta}_\Omega M_{\Omega} + {\Delta}_I M_I =\Big ({\Delta}_\Omega M_{\Omega} \Big ) \Big ( \mathrm{I}+ \frac{{\Delta}_I}{{\Delta}_\Omega}M_{\Omega}^{-1} M_I \Big ) =\Big ({\Delta}_\Omega M_{\Omega} \Big ) \Big ( \mathrm{I} + \kappa P \Big ) , \end{aligned}$$

Here I is the identity matrix, \(\kappa \equiv \frac {{\Delta }_I}{{\Delta }_\Omega }\propto \frac {{\Delta } t}{{\Delta } x}\), and \(P \equiv M_{\Omega }^{-1} M_I\).

If ||κP|| is sufficiently small, we can apply the Maclaurin formula in order to obtain the polynomial expansion for M −1 as follows:

$$\displaystyle \begin{aligned} M^{-1}\equiv \big ( \mathrm{I} + \kappa P \big ) ^{-1} \big ({{\Delta}_\Omega} M_{\Omega} \big )^{-1} = \big ( \sum_{n=0}^{\infty}(-1)^n \kappa ^n P^n \big ) \big ({{\Delta}_\Omega} M_{\Omega} \big )^{-1}. \end{aligned}$$

This representation reduces the inversion of the sparse matrix M to the inversion of its block-diagonal component \(M_{\Omega }^{-1}\) and the multiplication of the inverted block-diagonal M Ω by the sparse M I. It provides an explicit way for solving the initial linear system approximately. Even though it requires a CFL—type condition related to value of ||κP||, justifying the approximate solution of the system, it significantly accelerates the algorithm execution.

In Table 1 we compare the numerical accuracy (L 2-norm in time and space of numerical error as a function of cell size Δx) of the TDG method in a 2D homogeneous acoustic case for both the exact and approximate matrix inversions as a function of the mesh size and of the number n of terms in the Taylor expansion.

Table 1 Accuracy (L 2-error in space and in time) of the solution when using the approximate inversion with n = 3, 4, 5 and the exact inversion
Full size table

3 Numerical Tests

For the numerical implementation of the Trefftz-DG method we have considered a 2D medium composed of two homogeneous rectangular layers: the acoustic one and the elastodynamic one. We have set a source term at the fluid-solid interface, and two receivers in the acoustic layer and in the elastodynamic one. The numerical signals at both receivers have been validated with the analytical solutions computed with Gar6more code [5]. In Fig. 3 we show the convergence of the numerical velocity as a function of cell size for different degrees of approximation (p = 0, 1, 2, 3) computed at receivers in (a) 2D acoustic layer and (b) 2D elastodynamic layer. In each case, the convergence rate is higher than the corresponding approximation degree. We refer to [2], where we provide more examples.

Fig. 3
figure 3

Convergence of numerical velocity in function of cell size Δx. (a) 2D acoustic layer. (b) 2D elastodynamic layer

Full size image

4 Conclusion

The Trefftz-DG methodology for solving the first order elasto-acoustic system has demonstrated the important advantages, such as the use of degrees of freedom evaluated at the element faces only, the flexibility in the choice of the basis functions and the unconditional stability. However, in its initial form, it still shows some limitations due to the space-time integration that leads to the representation of the discrete system by a huge sparse matrix whose straightforward inversion is very expensive, even when using time slabs. We find ourselves in a situation of using an implicit scheme for solving the forward problem that risks to overload the iterative process of the corresponding inverse problem in order to reconstruct very large propagation domains. Fortunately, thanks to the decomposition of the matrix by separating the time variables from the space ones, we could benefit from the block-diagonal structure of the standard DG formulation ending up with an explicit scheme, that is more convenient from the numerical point of view. The performed numerical tests clearly illustrate the interest of the split version of discrete problem.