A Conservative Hybrid Method for Darcy Flow

Abstract

We present a hybrid mimetic spectral element formulation for Darcy flow. The discrete representations for (1) conservation of mass, and (2) inter-element continuity, are topological relations that lead to sparse matrix systems. These constraints are independent of the element size and shape, and thus invariant under mesh transformations. The resultant algebraic system is extremely sparse even for high degree polynomial basis. Furthermore, the system can be efficiently assembled and solved for each element separately.

1 Introduction

Hybrid formulations [1, 3, 10] are classical domain decomposition methods which reduce the problem of solving one global system to many small local systems. The local systems can then be efficiently solved independently of each other in parallel.

In this work we present a hybrid mimetic spectral element formulation to solve Darcy flow. We follow [8] which render the constraints on divergence of mass flux, the pressure gradient and the inter-element continuity metric free. The resulting system is extremely sparse and shows a reduced growth in condition number as compared to a non-hybrid system.

This document is structured as follows: In Sect. 2 we define the weak formulation for Darcy flow. The basis functions are introduced in Sect. 3. The evaluation of weighted inner product and duality pairings are discussed in Sect. 4. In Sect. 5 we discuss the formulation of discrete algebraic system. In Sect. 6 we present results for a test case taken from [7].

2 Darcy Flow Formulation

For $\Omega \in \mathbb {R}^d$, where d is the dimension of the domain, the governing equations for Darcy flow, are given by,

$$\displaystyle \begin{aligned} \left\lbrace \begin{array}{ll} \boldsymbol{u} + \mathbb{A}\ \nabla p & = 0 \\[1.1ex] \nabla \cdot \boldsymbol{u} & = f \end{array} \right. \quad \text{in}\ \Omega \quad \text{and} \quad \left\lbrace \begin{array}{lll} \partial \Omega & = \Gamma _D \cup \Gamma _N \\[1.1ex] p & = \hat{p} & \text{on}\ \Gamma _D \\[1.1ex] \boldsymbol{u}\cdot \boldsymbol{n} & = \hat{\boldsymbol{u}}_{\boldsymbol{n}} & \text{on}\ \Gamma _N \end{array} \right. \;, \end{aligned}$$

where, u is the velocity, p is the pressure, f the prescribed source term, $\mathbb {A}$ is a d × d symmetric positive definite matrix, $\hat {p}$ and $\hat {\boldsymbol {u}}_{\boldsymbol {n}}$ are the prescribed pressure and flux boundary conditions, respectively.

2.1 Notations

For$f,g \in L^2\left ( \Omega \right )$, $\left ( f,g \right )_\Omega$ denotes the usual L ²-inner product.

For vector-valued functions in L ² we define the weighted inner product by,

$$\displaystyle \begin{aligned} \left( \boldsymbol{u},\boldsymbol{v} \right)_{\mathbb{A}^{-1},\Omega} = \int _\Omega \left( \boldsymbol{u},\mathbb{A}^{-1} \boldsymbol{v} \right) d\Omega \;, \end{aligned} $$

(1)

where $\left ( \cdot \;, \cdot \right )$ denotes the pointwise inner product.

Duality pairing, denoted by $\left \langle \cdot , \cdot \right \rangle _{\Omega }$, is the outcome of a linear functional on $L^2 \left ( \Omega \right )$ acting on elements from $L^2\left ( \Omega \right )$.

Let Ω _K be a disjoint partitioning of Ω with total number of elements K, and K _i is any element in Ω_K, such that, K _i ∈ Ω_K. We define the following broken Sobolev spaces [2], $H\left ( \mathrm {div} ;\Omega _K \right ) = \prod _{i} H\left ( \mathrm {div}; K_i \right )$, and $H^{1/2} \left ( \partial \Omega _K \right ) = \prod _{i} H^{1/2}\left ( \partial K_i \right )$.

2.2 Weak Formulation

The Lagrange functional for Darcy flow is defined as,

$$\displaystyle \begin{aligned} \begin{array}{ll} \mathcal{L}\left( \boldsymbol{u}, p, \lambda;f \right) = & \frac{1}{2}\int _{\Omega _K} \boldsymbol{u}^T\mathbb{A}^{-1} \boldsymbol{u}\ \mathrm{d}\Omega _K + \int _{\Omega _K} p \left( \nabla \cdot \boldsymbol{u} - f \right) \mathrm{d}\Omega _K \\[1.1ex] &+ \int _{\partial \Omega _K \setminus \Gamma _D } \lambda \left( \boldsymbol{u} \cdot \boldsymbol{n} \right)\ \mathrm{d} \Gamma - \int _{\Gamma _D} \hat{p} \left( \boldsymbol{u} \cdot \boldsymbol{n} \right)\ \mathrm{d} \Gamma - \int _{\Gamma _N} \lambda \left( \hat{\boldsymbol{u}}_{\boldsymbol{n}} \right)\ \mathrm{d}\Gamma \end{array} \;. \end{aligned}$$

The variational problem is then given by: For given $f \in L^2\left ( \Omega _K \right )$, find u ∈ H(div; Ω_K), $p \in L^2\left ( \Omega _K \right )$, $\lambda \in H^{\frac {1}{2}}\left ( \partial \Omega _K \right )$, such that,

$$\displaystyle \begin{aligned} \left\lbrace \begin{array}{lllll} {\left( \boldsymbol{v},\boldsymbol{u} \right)_{\mathbb{A}^{-1},\Omega _K}}\,{+}\,\left\langle \nabla \cdot \boldsymbol{v}, p \right\rangle_{\Omega _K}\,{+}\,\left\langle \left( \boldsymbol{v} \cdot \boldsymbol{n} \right) , \lambda \right\rangle_{\partial \Omega_K \setminus \Gamma _D} &= \left\langle \boldsymbol{v} \cdot \boldsymbol{n}, \hat{p} \right\rangle_{\Gamma _D} & \quad \! \forall\ \boldsymbol{v} \in H(\mathrm{div} ;\Omega _K) \\[1.1ex] \left\langle q, \nabla \cdot \boldsymbol{u} \right\rangle_{\Omega _K} & = \left\langle q,f \right\rangle_{\Omega _K} & \quad \! \forall\ q \in L^2\left( \Omega _K \right) \\[1.1ex] \left\langle \mu , \left( \boldsymbol{u}\cdot \boldsymbol{n} \right) \right\rangle_{\partial \Omega_K \setminus \Gamma _D} & = \left\langle \mu, \hat{\boldsymbol{u}}_{\boldsymbol{n}} \right\rangle_{\Gamma _N} & \quad \! \forall\ \mu \in H^{\frac{1}{2}}\left( \partial \Omega _K \right) \end{array} \right. \!\!\!.\\\end{aligned} $$

(2)

3 Basis Functions

3.1 Primal and Dual Nodal Degrees of Freedom

Let ξ _j, j = 0, 1, …, N, be the N + 1 Gauss–Lobatto–Legendre (GLL) points in $I \in \left [-1,1\right ]$. The Lagrange polynomials h _i(ξ) through ξ _j, of degree N, given by,

$$\displaystyle \begin{aligned} h_i \left( \xi \right)= \frac{\left( \xi ^2 -1 \right)L^{\prime}_N\left( \xi \right)}{N\left( N+1 \right)L_N\left( \xi _i \right)\left( \xi -\xi_i \right)} \;,\end{aligned} $$

form the 1D primal nodal polynomials which satisfy, h _i(ξ _j) = δ _ij.

Let a ^h and b ^h be two polynomials expanded in terms of $h_i\left ( \xi \right )$. The L ²—inner product is then given by,

$$\displaystyle \begin{aligned} \left( a^h,b^h \right) _I = {\mathbf{a}}^T \mathbb{M}^{(0)} \mathbf{b} \;, \quad \text{where} \quad \mathbb{M}^{(0)} _{i,j} = \int _{-1}^1 {h_i} (\xi)\ {h_j} (\xi)\ \mathrm{d}\xi \;,\end{aligned} $$

and, $\mathbf {a} = \left [ \mathsf {a}_0\ \mathsf {a}_1\ \ldots \ \mathsf {a}_{N}\right ]$ and $\mathbf {b} = \left [ \mathsf {b}_0\ \mathsf {b}_1\ \ldots \ \mathsf {b}_{N}\right ]$ are the nodal degrees of freedom. We define the algebraic dual degrees of freedom, $\mathbf {\widetilde {a}}$, such that the duality pairing is simply the vector dot product between primal and dual degrees of freedom,

$$\displaystyle \begin{aligned} \left\langle a^h, b^h \right\rangle _{I} = \mathbf{\widetilde{a}}^T \mathbf{b} := {\mathbf{a}}^T \mathbb{M}^{(0)} \mathbf{b} \quad \Rightarrow \quad \mathbf{\widetilde{a}} = \mathbb{M}^{(0)} \mathbf{a} \;.\end{aligned} $$

Thus, the dual degrees of freedom are linear functionals of primal degrees of freedom.

3.2 Primal and Dual Edge Degrees of Freedom

The edge polynomials, for the N edges between N + 1 GLL points $\left ( \xi _{j-1}, \xi _j \right )$, of polynomial degree N − 1, are defined as [4],

$$\displaystyle \begin{aligned} e_j(\xi) = -\sum_{k=1}^{j-1}\frac{\text{d} h_k}{\text{d} \xi}(\xi) \;, \quad \text{such that} \quad \int _{\xi _{j-1}} ^{\xi _j} e_i (\xi) = \delta _{ij} \;. \end{aligned}$$

Let p ^h and q ^h be two polynomials expanded in edge basis functions. The inner product in L ² space is given by,

$$\displaystyle \begin{aligned} \left( p^h,q^h \right) _{I} = {\mathbf{p}}^T \mathbb{M}^{(1)} \mathbf{q} \;, \quad \text{where} \quad \mathbb{M}^{(1)} _{i,j} = \int _{-1}^1 {e_i} (\xi)\ e_j (\xi)\ \mathrm{d}\xi \;, \end{aligned}$$

and, $\mathbf {p} = \left [ \mathsf {p}_1\ \mathsf {p}_2\ \ldots \ \mathsf {p}_{N}\right ]$ and $\mathbf {q} = \left [ \mathsf {q}_1\ \mathsf {q}_2\ \ldots \ \mathsf {q}_{N}\right ]$ are the edge degrees of freedom. As before, we define the dual degrees of freedom such that,

$$\displaystyle \begin{aligned} \left\langle p^h, q^h \right\rangle _{I} = \mathbf{\widetilde{p}}^T \mathbf{q} := {\mathbf{p}}^T \mathbb{M}^{(1)} \mathbf{q} \quad \Rightarrow \quad \mathbf{\widetilde{p}} = \mathbb{M}^{(1)} \mathbf{p} \;. \end{aligned}$$

A similar construction can be used for dual degrees of freedom in higher dimensions. For construction of the dual degrees of freedom in 2D see [8] and for 3D see [9].

3.3 Differentiation of Nodal Polynomial Representation

Let $a^h\left ( \xi \right )$ be expanded in Lagrange polynomials, then

$$\displaystyle \begin{aligned} \frac{d}{d\xi}a^h\left( \xi \right) = \frac{d}{d\xi}\sum _{i=0}^N \mathsf{a}_i h_i \left( \xi \right) =\sum _{i=1}^N \left( \mathsf{a}_i - \mathsf{a}_{i-1} \right) e_i \left( \xi \right) \;. \end{aligned} $$

(3)

Therefore, taking the derivative of a polynomial involves two steps: First, take the difference of degrees of freedom; second, change of basis from nodal to edge [4].

4 Discrete Inner Product and Duality Pairing

For 2D domains, the higher dimensional primal basis are constructed using the tensor product of the 1D basis.

For the weak formulation (2) we expand the velocity u ^h in primal edge basis as,

$$\displaystyle \begin{aligned} \boldsymbol{u}^h\left( \xi, \eta \right) = \sum _{i=0}^N \sum _{j=1}^N \mathsf{u_x} _{i,j}\ h_i(\xi)\ e_j(\eta)\ \hat{\mathbf{\imath}} + \sum _{i=1}^N \sum _{j=0}^N \mathsf{u_y} _{i,j}\ e_i(\xi)\ h_j(\eta)\ \hat{\mathbf{\jmath}} \;, \end{aligned} $$

(4)

where u _{x i,j} denotes the flux, $\int \boldsymbol {u} \cdot \boldsymbol {n}$, over the vertical edges and u _{y i,j} the flux over the horizontal edges.

4.1 Weighted Inner Product

Using (1) and the expansions in (4), the weighted inner product is evaluated as,

$$\displaystyle \begin{aligned} \left( \boldsymbol{v}^h,\boldsymbol{u} ^h \right)_{\mathbb{A}^{-1}, \Omega _K} = \sum _{K}{\mathbf{v}}_{K_i}^T\ \mathbb{M}^{(1)} _{\mathbb{A}^{-1},{K_i}}\ {\mathbf{u}}_{K_i} \;, \end{aligned}$$

where, ${\mathbf {u}}_{K_i}$ are the degrees of freedom in element K _i, and

$$\displaystyle \begin{aligned} \mathbb{M}^{(1)} _{\mathbb{A}^{-1},{K_i}} = \int _{K_i} \left( \begin{array}{l} h_i({x})\ e_j({y}) \\[1.1ex] e_i({x})\ h_j({y}) \end{array} \right)^T \mathbb{A}^{-1}\left( {x},{y} \right) \left( \begin{array}{l} h_i({x})\ e_j({y}) \\[1.1ex] e_i({x})\ h_j({y}) \end{array} \right)\ \mathrm{d} {K_i} \;. \end{aligned}$$

For mapping of elements please refer to [6].

Fig. 1

Discretized domain for K = 3 × 3, N = 3. The blue dots represent the pressure boundary condition $\hat {p}$, and the blue edges represent the velocity boundary condition $\hat { \boldsymbol {u}}_{ \boldsymbol {n}}$

4.2 Divergence of Velocity

Divergence of velocity, ∇⋅u ^h, is evaluated using (3), but now for 2D,

$$\displaystyle \begin{aligned} \begin{array}{ll} \nabla \cdot \boldsymbol{u} ^h & = \frac{\partial}{\partial x} \sum _{i=0}^N \sum _{j=1}^N \mathsf{u_x} _{i,j}\ h_i(x) e_j(y) + \frac{\partial}{\partial y} \sum _{i=1}^N \sum _{j=0}^N \mathsf{u_y} _{i,j}\ e_i(x) h_j(y) \\[1.1ex] & = \sum _{i,j =1} ^N \left( \mathsf{u_x}_{i,j} - \mathsf{u_x}_{i-1,j} + \mathsf{u_y}_{i,j} - \mathsf{u_y}_{i,j-1} \right) e_i\left( x \right) e_j \left( y \right) \end{array} \;. \end{aligned} $$

(5)

For pressure we will use dual degrees of freedom. Therefore the weak constraint on divergence of velocity is a duality pairing evaluated as,

$$\displaystyle \begin{aligned} {\left\langle q^h, \nabla \cdot \boldsymbol{u}^h \right\rangle_ {\Omega_K} } = \sum _{K} \mathbf{\widetilde{q}}_{K_i}^T\ \mathbb{E}^{2,1}\ {\mathbf{u}}_{K_i} \;, \end{aligned}$$

where $\mathbb {E}^{2,1}$ represents the discrete divergence operator. It is an incidence matrix that is metric-free and topological, and remains the same for each element in Ω_K. For an extensive discussion on the incidence matrix, see for instance [6]. For an element of degree N = 3,

$$\displaystyle \begin{aligned} \mathbb{E}^{2,1} = \left[ \begin{array}{cccccccccccccccccccccccc} -1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & -1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & -1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & -1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 1 \end{array} \right] \;. \end{aligned}$$

4.3 Connectivity Matrix

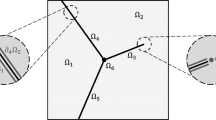
The connectivity matrix ensures continuity of the velocity across the elements. λ is the interface variable defined between the elements, shown as red dots in Fig. 1, that acts as Lagrange multiplier that imposes this continuity constraint is given by,

$$\displaystyle \begin{aligned} \left\langle \mu ^h,\boldsymbol{u}^h \cdot \boldsymbol{n} \right\rangle_{\partial \Omega _K \setminus \Gamma _D} = \sum _K \mathbf{\widetilde{\mu}}_{K_i}^T\ \mathbb{N}\ {\mathbf{u}}_{K_i} = \mathbf{\widetilde{\mu}}^T\ \mathbb{E}_{\mathbb{N}}\ \mathbf{u}\ \;,\end{aligned} $$

where $\mathbb {N}$ is the discrete trace operator. It is a sparse matrix that consists of 1, − 1 and 0 only. For construction of $\mathbb {N}$ please refer to [5]. $\mathbb {E}_{\mathbb {N}}$ is the assembled $\mathbb {N}$ for all elements. For, K = 2 × 2, N = 2, $\mathbb {E}_{\mathbb {N}}$ is shown in (6). The matrix size of $\mathbb {E}_{\mathbb {N}}$ is 8 × 64, but it has only 16 non-zero entities. It is an extremely sparse matrix that is metric free and the location of ± valued entries depend only on the connection between different elements.

(6)

5 Discrete Formulation

Using the weighted inner product and duality pairings discussed in Sect. 4, we can write the discrete form of weak formulation in (2) as,

$$\displaystyle \begin{aligned} \left[ \begin{array}{cc} \mathbb{B} & {\mathbb{E}_{\mathbb{N}}}^T \\[1.1ex] \mathbb{E}_{\mathbb{N}} & 0 \end{array} \right] \left[\begin{array}{l} \mathbf{X} \\[1.1ex] \mathbf{\lambda} \end{array} \right] = \left[ \begin{array}{l} \mathbf{F} \\[1.1ex] 0 \end{array} \right] \;, \end{aligned} $$

(7)

where, $\mathbb {B}$ is an invertible block diagonal matrix given by,

$$\displaystyle \begin{aligned} \mathbb{B} = \left[ \begin{array}{llllllllllllllllllllll} \begin{array}{lll}\mathbb{M}^{(1)} _{\mathbb{A}^{-1}, K_ 1} & {\mathbb{E}^{2,1}}^T \\[1.1ex]\mathbb{E}^{2,1} & 0\end{array} \\[1.1ex] & & \begin{array}{lll}\mathbb{M}^{(1)} _{\mathbb{A}^{-1}, K_ 2} & {\mathbb{E}^{2,1}}^T \\[1.1ex]\mathbb{E}^{2,1} & 0\end{array} \\[1.1ex] & & & & \ddots & \ddots \\[1.1ex] & & & & \ddots & \ddots \\[1.1ex] & & & & & & \begin{array}{lll}\mathbb{M}^{(1)} _{\mathbb{A}^{-1}, K_ K} & {\mathbb{E}^{2,1}}^T \\[1.1ex]\mathbb{E}^{2,1} & 0\end{array} \end{array} \right] \;, \end{aligned} $$

(8)

$\mathbb {E}_{\mathbb {N}}$ is as given in (6), $\mathbf {X} = \sum _{i} \left [ \begin {array}{c} \mathbf {u} \\[1.1ex] \mathbf {p} \end {array} \right ]_{K_i}$, and $\mathbf {F} = \sum _{i} \left [ \begin {array}{c} \hat {\mathbf {p}} \\[1.1ex] \mathbf {f} \end {array} \right ]_{K_i}$, where f are the expansion coefficients of $f^h\left ( x,y \right ) = \sum _{i,j}^N \mathsf {f}_{ij}\ e_i\left ( x \right ) e_j\left ( y \right )$.

In (8), the mass matrix $\mathbb {M}^{(1)} _{\mathbb {A}^{-1},{K_i}}$ is the only dense matrix and also the only matrix that changes with each local element, K _i. $\mathbb {E}_{\mathbb {N}}$ is a sparse incidence matrix for the global system and $\mathbb {E}^{2,1}$ is a sparse incidence matrix for the local systems that remain the same for each element.

Using the Schur complement method, the global system (7) can be reduced to solve for λ, [1],

$$\displaystyle \begin{aligned} \mathbf{\lambda} = \left( \mathbb{E}_{\mathbb{N}} \mathbb{B}^{-1}\ {\mathbb{E}_{\mathbb{N}}} ^T \right)^{-1} \cdot \left( \mathbb{E}_{\mathbb{N}} \mathbb{B}^{-1} \mathbf{F} \right) \;. \end{aligned} $$

(9)

To evaluate λ in (9) we need $\mathbb {B}^{-1}$ that can be calculated efficiently by taking inverse of each block of $\mathbb {B}$ separately. This part is trivially parallelized. Once the λ is determined the solution in each element, K _i, can be evaluated independent of each other.

The system (9) solves for interface degrees of freedom between the elements and will always be smaller than the full global system. For a comparison of the size of λ system with full system see Table 1 (for 2D), and Table 2 (for 3D). On the left of Tables 1 and 2 we see that, for constant K, increasing the order of polynomial basis the growth in size of λ system is less than the growth in size of full system. Thus, hybrid formulations are beneficial for high order methods where local degrees of freedom of an element are much higher than interface degrees of freedom.

Table 1 For 2D

Table 2 For 3D

On the right of Tables 1 and 2 we see that, for constant N, the λ system is smaller than the full system, although the growth ratio of size of λ and full systems does not change significantly.

6 Results

In this section we present the results for a test problem from [7] by solving system (7). The domain of the test problem is, $\Omega \in \left [0,1 \right ]^2$. The source term is defined as,

$$\displaystyle \begin{aligned} f_{ex} = \nabla \cdot (-\mathbb{A}\nabla p _{ex}) \;, \quad \text{where} \;, \end{aligned}$$

$$\displaystyle \begin{aligned} \begin{array}{ll} \mathbb{A} & = \frac{1}{x^2 + y^2 + \alpha} \left( \begin{array}{ll} 10^{-3}x^2 + y^2 + \alpha & \quad \left( 10^{-3}-1 \right)xy \\[1.1ex] \left( 10^{-3}-1 \right)xy & \quad x^2 + 10^{-3}y^2 + \alpha \end{array} \right) \;; \quad \quad \alpha = 0.1 \\[1.1ex] p _{ex} & = \mathrm{sin}\left( 2 \pi x \right) \mathrm{sin}\left( 2 \pi y \right) \end{array} \;, \end{aligned}$$

and Dirichlet boundary conditions are imposed along the entire boundary, Γ_D = ∂ Ω and Γ_N = ∅. We solve this problem on an orthogonal and a curved mesh, see Fig. 2.

Fig. 2

Mesh configuration: K = 3 × 3, N = 6. Left: orthogonal. Right: curved

Fig. 3

Sparsity plots K = 3 × 3, N = 6. Left: hybrid elements method. Right: continuous element method

The same problem was earlier addressed in [6], but for a method with continuous elements and primal basis functions only. For the configuration K = 3 × 3, N = 6, we compare the sparsity structure of the two approaches in Fig. 3. On the left we see the hybrid formulation, and on the right we see the continuous elements formulation [6]. The number of non zero entries are almost half in the hybrid formulation, 66, 384, as compared to the continuous element formulation, 117, 504. Here, the sparsity is due to use of algebraic dual degrees of freedom and is not because of hybridization of the scheme.

Fig. 4

Growth in condition number for hybrid elements in dark line, and continuous elements in dotted line. Left: h-refinement; Right: N-refinement. ‘c’ refers to the curved mesh

In Fig. 4, on the left we compare the growth in condition number, for the λ system (9) with full continuous element system, for N = 7 on the curved mesh, with increasing number of elements, K. We observe similar growth rates for hybrid and continuous formulation, however the condition number for continuous elements formulation is almost $\mathcal {O}\left ( 10^2 \right )$ higher. On the right we see the growth in condition number with increasing polynomial degree for K = 9 × 9 on the curved mesh. A reduced growth rate in condition number for hybrid formulation is observed. Thus hybrid formulations are beneficial for high order methods.

Fig. 5

L ²-error in divergence of velocity: Left: h-refinement; Right: N-refinement. ‘o’ refers to the orthogonal mesh and ‘c’ to the curved mesh

In Fig. 5 we show the L ²-error for ∥∇⋅u ^h − f ^h∥. On the left side as a function of element size, $h = 1 / \sqrt {K}$, and on the right side as a function of polynomial degree of the basis functions. In both cases the maximum error observed is of $\mathcal {O}\left ( 10^{-12} \right )$.

Fig. 6

Top row: error in $H \left ( \mathrm {div}; \Omega \right )$ norm for velocity; Bottom row: L ²-error in pressure. Left: h-refinement; Right: N-refinement. ‘o’ refers to the orthogonal mesh and ‘c’ to the curved mesh

In Fig. 6, on the top two figures we show the error in the $H\left ( \mathrm {div};\Omega \right )$ norm for the velocity; and at the bottom two figures we show the error in $L^2\left ( \Omega \right )$ norm for the pressure. On the left we have h-convergence plots, and on the right we have N-convergence plots. In all the figures, for the same number of elements, K, and polynomial degree, N, the error is higher for the curved mesh.

On the left we see that the error decreases with the element size. The slope of error rate of convergence is N, which is optimal for both curved and orthogonal meshes. On the right we see exponential convergence of the error with increasing polynomial degree of basis for both orthogonal and curved meshes.