Abstract
Solving hyperbolic conservation laws on general grids can be important to reduce the computational complexity and increase accuracy in many applications. However, the use of non-uniform grids can introduce challenges when using high-order methods. We propose to use a Central WENO (CWENO) scheme based on radial basis function (RBF) interpolation, which is applicable to scattered data. We develop a smoothness indicator, based on RBFs, and CWENO specific weights which depend on the mesh size of the grid to construct an arbitrarily high order RBF-CWENO method. We evaluate the method with multiple examples in one dimension.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
A broad range of physical phenomena can be described by hyperbolic conservation laws of the form
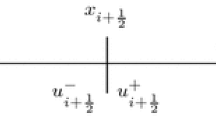
with the conserved variables \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) and the flux function \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \). The nonlinear behavior of f can lead to complex solutions, most notably shocks. It is well-known that high-order methods give good results for smooth data, but for discontinuous ones spurious oscillations are introduced. A popular class of methods to solve (1) is the finite volume method, which is based on a discretization in space … < x i−1∕2 < x i+1∕2 < … and the average values \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) of its cells C i = [x i−1∕2, x i+1∕2]. It is defined by the semi-discrete scheme
where the numerical flux term F i+1∕2 depends on the values \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) with 0 ≤ k ≤ p − 1. For more details we refer the reader to [15, 20, 22].
The class of essentially nonoscillatory (ENO) methods, introduced by Harten et al. [14], reduces spurious oscillations to a minimum. They are based on a monotone numerical flux function F(u, v) and high-order accurate reconstruction s i(x) for each cell i. The central idea is to choose the least oscillating interpolation function s i and define the numerical flux \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) with \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) being the evaluation of s i+1 and s i at the interface x i+1∕2. Based on the ENO method, Jiang and Shu [19] introduced the weighted ENO (WENO) method which considers different interpolation polynomials, based on different stencils, and combines them in a nonoscillatory manner to maximize the attainable accuracy. Further results on ENO and WENO methods can be found in [10, 11, 16].
2 CWENO
The CWENO method is based on the WENO method and was introduced by Levy et al. [23] as a third order method. Further analysis and generalization to higher orders on general grids can be found in [6, 7].
Let us consider the standard semi-discrete formulation (2) with a monotone flux function F(u, v). The goal is to construct a reconstruction P rec,i for each cell C i based on the stencil {C i−k, …, C i+k} for \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \). In the smooth regions the algorithm should choose a polynomial of degree 2k which interpolates the central stencil \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) in the mean value sense. In case of a non-smooth solution it chooses a polynomial of degree k on one stencil {C i−k+l, …, C i+l} that avoids the discontinuity. Given the reconstruction, the high-order numerical flux is F i+1∕2 = F(P rec,i+1(x i+1∕2), P rec,i(x i+1∕2)).
Specifically, let us consider P opt as the polynomial of degree 2k that interpolates all data in the 2k + 1 stencil and the polynomials P l of degree k that interpolate the data on the stencil {C i−k+l−1, …, C i+l−1} for l = 1, …, k + 1. Furthermore, the reconstruction depends on the choice of the positive real coefficients d 0, …, d k+1 ∈ [0, 1] such that \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \), d 0 ≠ 0. Then, the reconstruction polynomial of degree 2k is
with
and the nonlinear coefficients ω l that are defined as
where I[P l] indicates the smoothness of P l, \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) and t ≥ 2. A classical indicator of smoothness in the cell C for a polynomial is the Jiang–Shu indicator [19]
The choice of \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) is of importance: if it is too small, it might affect the order of convergence. On the other hand if it is too big, spurious oscillations may occur. Cravero et al. [7] show that the choice \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) for p = 1, 2 leads to the maximal order of convergence. As proposed in [7] we define the coefficients d j over the temporary weights
and we choose d 0 ∈ (0, 1) for the high-order polynomial. This gives us a possible choice for the coefficients
The main difference with respect to the classical WENO method is that for the smooth case we are not constructing P opt out of the polynomials P l, but we build it independently by resolving an additional system of equations. This method has the advantage that it is easier to generalize on general grids in high dimensions, while maintaining high-order accuracy.
3 Radial Basis Functions
An alternative to the classical polynomial interpolation is the interpolation with radial basis functions (RBF). RBFs were proposed in the seminal work by Hardy [13]. They have been successfully applied in scattered data interpolation [4, 9, 17, 24, 27] and as a basis for a generalized finite difference method (RBF-FD) [5, 12]. The advantage is its flexibility in high dimensions and the possibility to reduce the risk of ill-conditioned point constellations. Its disadvantage is the ill-conditioning of the interpolation matrix for small grid sizes [8, 21, 26].
The RBF interpolation is based on a basis \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \), obtained from a univariate continuous function \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \), composed with the Euclidean norm centered at the data points
with the shape parameter ε. Some common RBFs can be found in Table 1. Thus, for given scattered data points X = (x 1, …, x n)T with \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) and corresponding values \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) we look for
with a polynomial \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \), \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \), the interpolation condition s(x j) = f j and the additional constraints
with the coefficients \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) for all j = 1, …, n.
The same concept can be applied in the case of cell-averages. We seek functions
such that
with the averaging operator \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \). A well-known problem with RBFs is the high condition number of the interpolation matrix for small grid sizes or small shape parameters [8, 21, 26]. This problem can be resolved by using the vector-valued rational approximation method [28].
4 RBF-CWENO
Methods combining RBFs and essentially nonoscillatory methods have been proposed, e.g. RBFs with ENO [18, 25], RBFs with WENO [1,2,3]. The advantage of the CWENO method over the WENO method is its flexibility on general grids and its independence of the construction of a high-order interpolation function out of lower order ones. This facilitates the use of the whole grid in smooth regions and is important for non-polynomial interpolation functions which cannot be combined to an higher order function.
We propose the RBF-CWENO method which works as the classical CWENO method with the reconstruction function (3) and the weights (5), but as interpolation function we use RBFs instead of polynomials. Since the problem of the ill-conditioning can be solved by using the vector-valued rational approximation method [28], the main challenge for RBF methods is the choice of the smoothness indicator. For polyharmonic splines, Aboyar et al. [1] use the semi-norm of the Beppo-Levi space and Bigoni et al. [3] use a modified version of the Jiang-Shu indicator (6).
4.1 Smoothness Indicator
The smoothness indicator is the heart of the essentially nonoscillatory methods. We consider one based on the one introduced by Bigoni and Hesthaven [3]
where the first part is the sum of the derivatives of the polynomial part and the second term expresses the highest derivative of the RBF-part. The original Jiang-Shu indicator applied to (12) would include the lower derivatives of the RBF-part plus all mixed terms, but we find this to be less efficient. For simplicity the integrals can be approximated with a simple mid-point rule.
We face again the problem of ill-conditioning when recovering the coefficients a i. Numerical examples indicate that small shape parameter improve the accuracy, but they do not affect the choice of the stencil using this smoothness indicator. Thus, we use a bigger shape parameter ε R, that is smaller than the smallest distance to a singularity
which ensures the solvability of the system of equations [28].
5 Numerical Results
We now discuss the numerical results of the RBF-CWENO method and compare it with the RBF-WENO method [3] and the classical ENO method [14]. All methods are using the Lax-Friedrichs numerical flux and integration in time is done using the SSPRK-5 method [15] with time step dt = CFL ⋅ Δx∕λ max and the maximal eigenvalue λ max of ∇u F. Furthermore, we use the vector-valued rational approximation approach [28] to circumvent ill-conditioning of the interpolation matrix and a shape parameter ε = 0.1. For the nonlinear weights (5) we choose \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) with \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \).
5.1 Linear Advection Equation
Let us consider the linear advection equation
with wave speed a = 1, initial condition u 0(x) = sin(2πx) and periodic boundary conditions [22]. Note that for k = 3 we expect the order of convergence to be 7, therefore we use the reduced time step dt = CFL ⋅ Δx 7∕5∕λ max to recover the right order of convergence. The correct order of convergence of the RBF-CWENO method is shown in Table 2 and it seems to be more accurate than the RBF-WENO method.
5.2 Burger’s Equation
Considering the Burger’s equation
we analyze its robustness with respect to discontinuities. In Fig. 1 we report the results performed with CFL = 0.5 at t = 0.3. We observe no oscillations around the discontinuity at x = 0.5 and as expected an increasing accuracy for increasing number of elements.
5.3 Euler Equations
The one-dimensional Euler equations express conservation of mass, momentum and the total energy. They can be described by the density ρ, the mass flow m, the energy per unit volume E and the pressure p through
with \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) for an ideal gas with the ratio of specific heat γ = 1.4 [15]. For k = 3 we need to change the nonlinear weights (5) by using \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) with \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) to avoid oscillations.
5.3.1 Sod’s Shock Tube Problem
The Sod’s shock tube problem describes two colliding gases in [0, 1] with different densities given by the initial conditions
This results in a rarefaction wave followed by a contact and a shock discontinuity which separates the domain into four domains with constant variables. The RBF-CWENO method resolves it well, see Fig. 2. For k = 3, we observe minor oscillations, but their amplitude decreases for increasing number of elements. Furthermore, we observe the increasing accuracy for k = 3 compared to k = 2.
5.3.2 Shu–Osher Shock-Entropy Wave Interaction Problem
The Shu–Osher problem describes the interaction of a discontinuity with a low frequency wave which introduces some high frequent waves. Its initial conditions are
In Fig. 3, we observe on the left side the increasing accuracy for increasing number of elements for k = 2. On the right side we see its good approximative behaviour compared to the existing methods ENO2, ENO5 and the corresponding WENO. In particular we observe that the performance of the RBF-CWENO (k = 2) is comparable to ENO5 and superior to WENO (k = 2).
6 Conclusion
In this work, we introduce the RBF-CWENO method that relies on the CWENO method [23] and the use of radial basis functions for the interpolation. We develop a smoothness indicator that is based on RBFs but works similarly to the one for polynomials. Furthermore, we tackle the problem about the choice of the weight \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \). For \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) with \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) we get the right order of convergence, but for the 7th order method (k = 3) we choose \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) to reduce spurious oscillations for the Euler equations.
Moreover, we should point out that the choice of the linear weight d 0 can influence the result; indeed if it is too close to 1 then the reconstruction almost coincides with P opt, which can lead to spurious oscillations in case of discontinuous solutions. We present multiple numerical examples to show the robustness of the method.
We can conclude that the RBF-CWENO method works comparable to the existing RBF-WENO and ENO methods in one dimension. The advantage of RBFs is clearer when considering unstructured grids in higher dimensions where polynomial reconstruction is complex.
References
Aboiyar, T., Georgoulis, E.H., Iske, A.: High order WENO finite volume schemes using polyharmonic spline reconstruction. In: Proceedings of the International Conference on Numerical Analysis and Approximation Theory NAAT2006, Cluj-Napoca (Romania). Department of Mathematics, University of Leicester (2006)
Aboiyar, T., Georgoulis, E.H., Iske, A.: Adaptive ADER methods using kernel-based polyharmonic spline WENO reconstruction. SIAM J. Sci. Comput. 32(6), 3251–3277 (2010)
Bigoni, C., Hesthaven, J.S.: Adaptive WENO methods based on radial basis function reconstruction. J. Sci. Comput. 72(3), 986–1020 (2017)
Buhmann, M.D.: Radial Basis Functions: Theory and Implementations. Cambridge University Press, Cambridge (2003)
Chandhini, G., Sanyasiraju, Y.: Local RBF-FD solutions for steady convection–diffusion problems. Int. J. Numer. Methods Eng. 72(3), 352–378 (2007)
Cravero, I., Semplice, M.: On the accuracy of WENO and CWENO reconstructions of third order on nonuniform meshes. J. Sci. Comput. 67(3), 1219–1246 (2016)
Cravero, I., Puppo, G., Semplice, M., Visconti, G.: CWENO: uniformly accurate reconstructions for balance laws (2016). Preprint. arXiv:1607.07319
Driscoll, T.A., Fornberg, B.: Interpolation in the limit of increasingly flat radial basis functions. Comput. Math. Appl. 43(3), 413–422 (2002)
Duchon, J.: Splines Minimizing Rotation-Invariant Semi-Norms in Sobolev Spaces, pp. 85–100. Springer, Berlin (1977)
Fjordholm, U.S., Ray, D.: A sign preserving WENO reconstruction method. J. Sci. Comput. 1–22 (2016)
Fjordholm, U.S., Mishra, S., Tadmor, E.: Arbitrarily high-order accurate entropy stable essentially nonoscillatory schemes for systems of conservation laws. SIAM J. Numer. Anal. 50(2), 544–573 (2012)
Fornberg, B., Lehto, E., Powell, C.: Stable calculation of gaussian-based RBF-FD stencils. Comput. Math. Appl. 65(4), 627–637 (2013)
Hardy, R.L.: Multiquadric equations of topography and other irregular surfaces. J. Geophys. Res. 76(8), 1905–1915 (1971)
Harten, A., Engquist, B., Osher, S., Chakravarthy, S.R.: Uniformly high order accurate essentially non-oscillatory schemes, iii. J. Comput. Phys. 71(2), 231–303 (1987)
Hesthaven, J.S.: Numerical Methods for Conservation Laws: From Analysis to Algorithms. Society for Industrial and Applied Mathematics, Philadelphia (2017)
Hu, C., Shu, C.-W.: Weighted essentially non-oscillatory schemes on triangular meshes. J. Comput. Phys. 150(1), 97–127 (1999)
Iske, A.: Multiresolution Methods in Scattered Data Modelling, vol. 37. Springer, Berlin (2004)
Iske, A., Sonar, T.: On the structure of function spaces in optimal recovery of point functionals for ENO-schemes by radial basis functions. Numer. Math. 74(2), 177–201 (1996)
Jiang, G.-S., Shu, C.-W.: Efficient implementation of weighted ENO schemes. J. Comput. Phys. 126(1), 202–228 (1996)
Kröner, D.: Numerical Schemes for Conservation Laws. Wiley, Chichester (1997)
Larsson, E., Fornberg, B.: Theoretical and computational aspects of multivariate interpolation with increasingly flat radial basis functions. Comput. Math. Appl. 49(1), 103–130 (2005)
LeVeque, R.J.: Numerical Methods for Conservation Laws. Springer Science & Business Media, New York (1992)
Levy, D., Puppo, G., Russo, G.: Central WENO schemes for hyperbolic systems of conservation laws. ESAIM: Math. Model. Numer. Anal. 33(3), 547–571 (1999)
Micchelli, C.A.: Interpolation of scattered data: distance matrices and conditionally positive definite functions. Constr. Approx. 2(1), 11–22 (1986)
Mönkeberg, F., Hesthaven, J.S.: Entropy stable essentially nonoscillatory methods based on RBF reconstruction. ESAIM: Math. Model. Numer. Anal. 53, 925–958 (2019)
Schaback, R.: Multivariate interpolation by polynomials and radial basis functions. Constr. Approx. 21(3), 293–317 (2005)
Wendland, H.: Scattered Data Approximation. Cambridge University Press, Cambridge (2004)
Wright, G.B., Fornberg, B.: Stable computations with flat radial basis functions using vector-valued rational approximations. J. Comput. Phys. 331, 137–156 (2017)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2020 The Author(s)
About this paper
Cite this paper
Hesthaven, J.S., Mönkeberg, F., Zaninelli, S. (2020). RBF Based CWENO Method. In: Sherwin, S.J., Moxey, D., Peiró, J., Vincent, P.E., Schwab, C. (eds) Spectral and High Order Methods for Partial Differential Equations ICOSAHOM 2018. Lecture Notes in Computational Science and Engineering, vol 134. Springer, Cham. https://doi.org/10.1007/978-3-030-39647-3_14
Download citation
DOI: https://doi.org/10.1007/978-3-030-39647-3_14
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-39646-6
Online ISBN: 978-3-030-39647-3
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)