Cosmic Particle Accelerators

Hofmann, W.; Hinton, J. A.

doi:10.1007/978-3-030-34245-6_13

W. Hofmann³ &
J. A. Hinton³

9982 Accesses

Abstract

In the century since the measurements of Victor Hess [1]—considered as the discovery of cosmic rays—the properties of cosmic rays, as they arrive on Earth, have been studied in remarkable detail; we know their energy spectrum, extending to 10²⁰ eV, their elemental composition, their angular distribution, and we understand the basic energetic requirements of cosmic ray production in the Galaxy.

You have full access to this open access chapter, Download chapter PDF

13 Cosmic Particle Accelerators

Ultra-high energy cosmic rays

Article 08 March 2021

Physics and Astrophysics of Ultra-High Energy Cosmic Rays: Recent Results from the Pierre Auger Observatory

Article 01 April 2022

13.1 Introduction

In the century since the measurements of Victor Hess [1]—considered as the discovery of cosmic rays—the properties of cosmic rays, as they arrive on Earth, have been studied in remarkable detail; we know their energy spectrum, extending to 10²⁰ eV, their elemental composition, their angular distribution, and we understand the basic energetic requirements of cosmic ray production in the Galaxy. The energy density of cosmic rays in the Galaxy is known to be comparable to the energy density in Galactic magnetic fields and in the thermal energy of interstellar gas, hence cosmic rays play a non-negligible role in shaping the evolution of galaxies. Charged cosmic-ray particles are strongly deflected in the few μG interstellar magnetic fields—the radius of curvature of a Z = 1 particle in astronomical distance units of parsec is given by R _gyro,pc ∼ E _PeV∕B _μG (1 parsec (pc) = 3.1 × 10¹⁶ m = 3.26 light years). Therefore, except for energies in the 10²⁰ eV range, cosmic rays cannot be traced back to their sources, the cosmic particle accelerators. Much of the current effort goes into identifying and quantitatively describing cosmic accelerators, with supernova remnant shocks as the likely dominant source of Galactic cosmic rays. Properties of cosmic particle accelerators can be studied and inferred in two ways: on the one hand based on the characteristics of local cosmic rays, as they arrive—more or less isotropically—on Earth; this is subject of Sect. 13.2, with a discussion of acceleration mechanisms given in Sect. 13.3. On the other hand, cosmic rays propagating through the Galaxy and in particular cosmic particle accelerators can be imaged using neutral particles and radiation created during the acceleration process and during propagation through the interstellar medium (ISM), with synchrotron radiation in the radio and X-ray regimes, high-energy gamma rays, high-energy neutrinos, and neutrons. So far, most information is obtained from electromagnetic probes, as discussed in Sect. 13.4. The small interaction cross section makes detection of high-energy cosmic neutrino sources challenging; only recently, the first detection was reported. Neutron decay limits their range. The flux on Earth of various high-energy cosmic messengers used to explore cosmic particle accelerators is illustrated in Fig. 13.1. The following discussion will mostly concentrate on Galactic particle populations and those particle accelerators which plausibly contribute to cosmic rays observed on Earth. For further details, we refer to reviews such as [2] on cosmic rays in the Galaxy, [3, 4] on supernovae as Galactic cosmic ray sources, [5] on cosmic rays above the knee, [6, 7] on ultra-high-energy cosmic rays, and [8, 9] on very high energy gamma ray astronomy to explore cosmic particle accelerators.

13.2 Cosmic Ray Properties and Implications for Cosmic Ray Sources

Certain properties of cosmic particle accelerators can be inferred from the cosmic ray spectrum measured on Earth, from the elemental composition of cosmic rays, from any anisotropies in their arrival directions, and also from the yield of electrons and antiparticles—positrons and antiprotons–among cosmic rays. The interpretation of data, however, assumes that cosmic rays measured on Earth are reasonably representative for cosmic rays in the Galaxy, and that one is able to disentangle effects reflecting properties of cosmic ray sources from those arising from cosmic ray propagation from their sources the Earth, over kpc distances.^{Footnote 1}

13.2.1 Cosmic Ray Spectrum

At lower energies, up to at most to 10¹⁴ eV, cosmic ray properties have been studied by space-based instruments, or instruments carried by giant balloons into the upper atmosphere, equipped with magnetic spectrometers or calorimeters for momentum/energy determination, with time-of-flight systems, transition radiation detectors and/or Cherenkov detectors for velocity determination, and with ionisation measurements for determination of the charge state. Examples of such instruments, illustrating the different techniques employed, include PAMELA [10], AMS [11], TRACER [12], CALET [13] and DAMPE [14]. While direct detection in space frequently provides superior performance, in particular regarding the measurement of elemental and isotopic composition, the steeply-falling energy spectrum of cosmic rays, coupled with at most m²-scale detection areas and—in case of magnetic spectrometers—limited bending power, restricts the energy range of these detection systems. Starting at 10¹² to 10¹³ eV, ground-based instruments take over, using the Earth’s atmosphere as an absorbing medium and detecting the particle cascade created when a high-energy particle interacts in the atmosphere. Instruments detect either the shower particles reaching the ground—with an effective detection area determined by the size of the detector array, which can be as large as 3000 km² for the Pierre Auger Observatory [15]—or image the cascade by focusing onto a photosensor array the light emitted by shower particles in the atmosphere. The forward-beamed Cherenkov light illuminates areas of ∼10⁵ m² on the ground and is readily detectable for showers beyond 10¹¹ eV; the isotropically emitted air fluorescence light—imaged e.g. by the Auger fluorescence telescopes [16] and the Telescope Array instrument [17]—allows detection over multi-km distances and provides detection areas in excess of 10⁷ m², but only in the energy range above 10¹⁷ to 10¹⁸ eV. Identification of primary particles is achieved via the longitudinal and transverse development of the air shower, the radial distribution of shower particles on the ground, and the ratio of nucleons, electrons and muons among shower particles. Compared to detection in space, cosmic-ray identification power is dramatically reduced, allowing essentially to distinguish light from heavy elements, and nuclei from electrons. Examples of air-shower arrays include KASKADE [18], optimised for measurements of cosmic ray composition, the Tibet array [19], optimised for low energy threshold, and the large LHAASO array under construction in China [20].

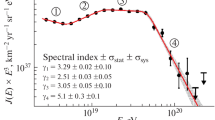
The cosmic ray energy spectrum shown in Fig. 13.2, compiled from numerous measurements using different techniques, is a mostly featureless power-law spectrum, dN∕dE ∼ E ^−Γ, ranging from GeV energies to 10²⁰ eV, covering over 30 orders of magnitude in flux, with the power-law index Γ varying at the “knee” from about 2.7 below 10¹⁵ eV to about 3 for energies from 10¹⁶ eV to 10¹⁸ eV, to flatten again at the “ankle” between 10¹⁸ eV to 10¹⁹ eV, and cutting off around 10²⁰ eV. Below about 10¹⁰ eV, the spectrum is modulated by the solar wind; at these energies particles do not penetrate into the inner Solar system. Newer measurements indicate another spectral break in the 10¹¹ eV to 10¹² eV range, with a change in proton and Helium spectral indices [21,22,23]. The power-law shape, with its lack of features and characteristic energies in the spectrum, indicates that cosmic rays are of non-thermal origin. The local energy density in cosmic rays is dominated by lower-energy particles and amounts to about 1 eV/cm³. Different mechanisms are discussed for the origin of the slight changes in spectral index: a harding of the spectrum can indicate the emergence of a new component/a new source of cosmic rays, a steepening the peak energy of accelerators, in particular if accompanied by a shift towards heavier composition, since the peak energy of accelerators will usually scale with the charge Z of the accelerated nuclei. Changes in spectral slope can, however, also indicate a change of cosmic ray propagation, i.e. of the energy-dependent diffusion coefficient. The spectral hardening observed at the ankle by 10¹⁹ eV is most easily explained as the emergence of a new component of cosmic rays, with a harder spectrum. Most models aiming at explaining the overall cosmic ray spectrum assume such a transition from Galactic sources to extragalactic sources in the 10¹⁷ to 10¹⁹ eV range (e.g. [24]). The steepening of spectra at the “knee” could be caused by a cutoff in the acceleration mechanism, characterising the upper end of the energy range of Galactic cosmic particle accelerators. A cutoff in the cosmic ray spectrum around 10²⁰ eV—the Greisen-Zatsepin-Kuzmin (GZK) cutoff [25, 26]—has been predicted as a result of pion production by ultra-high-energy protons interacting with the cosmic microwave background radiation, limiting the range of protons beyond 10²⁰ eV to about 100 Mpc or less (e.g. [27]). While early results questioned the existence of the GZK cutoff, both Auger [28, 29] and Telescope Array (TA) [17] have with much improved statistics established a cutoff in the spectrum of ultra-high-energy cosmic rays (UHECR). The energy of the cutoff is consistent with the GZK cutoff, indicating that most sources of UHECR are located at distances beyond 100 Mpc, but data are also well reproduced in terms of more nearby sources with a rigidity-dependent cutoff in the acceleration mechanism [30].

The cosmic-ray spectrum measured on Earth reflects the source spectrum (averaged over the lifetime of each source and over the population of sources), modified by factors arising from the energy-dependent propagation from sources throughout the Galaxy to Earth. Cosmic ray composition measurements discussed below have proven particularly useful in disentangling the two contributions.

13.2.2 Cosmic Ray Composition, Cosmic Ray Propagation, and Cosmic Ray Energetics

Lacking directional information, clues regarding the origin of cosmic rays (beyond those from shape of the energy spectrum) have been drawn mainly from the elemental composition (see e.g., reviews [2, 32]). In the GeV energy range, cosmic-ray chemical composition resembles the composition of solar-system material, with hydrogen and helium nuclei as dominant components (see Fig. 13.3). For some elements and isotopes, there are, however, marked differences between cosmic-ray composition and solar-system composition. This concerns e.g. boron (Z=5), which is suppressed by more than five orders of magnitude relative to carbon (Z=6) in the solar system, but is (within a factor of a few) equally represented among cosmic rays. The reason for this is that boron is not produced directly in stellar nucleosynthesis, but can easily be produced by spallation of heavier cosmic-ray nuclei interacting with interstellar gas. From the boron to carbon ratio, it is inferred that GeV cosmic rays arriving at the Earth have traversed about 10 g/cm² of interstellar medium (ISM) (e.g. [33]), with the amount of target material traversed

decreasing roughly as R ^−0.5 for higher rigidities R (defined as momentum/unit charge). Radioactive secondary nuclei, such as ¹⁰Be with its half-life of about a million years, are also detected among cosmic rays and can be used to estimate the residence time of cosmic rays in the Galaxy: the observed ¹⁰Be/⁹Be ratio implies a typical age of GeV cosmic rays reaching the Earth in the 10⁷ year range, with a trend towards lower ages at higher energy. Both the grammage traversed by cosmic rays and in particular the residence time, which is much larger than the time of about 10⁵ years required to cross the entire Galaxy on a straight path, indicate that cosmic rays are trapped inside the Galaxy and propagate diffusively away from their sources, due to frequent deflection in interstellar magnetic fields. However, the combination of the age and the grammage traversed implies that cosmic rays spend a significant fraction of their lifetime outside the Galactic disc with its typical gas density of 1 atom/cm³. This has lead to the development of “leaky box” models or diffusion models (see Fig. 13.4), where cosmic rays do not escape the Galaxy when leaving the disc with its scale height of \(\mathcal {O}\)(100 pc), but continue diffusive motion out to distances of several kpc from the disc, with the possibility of returning into the disc (for overviews see e.g. [2, 34]). Measurements of Galactic magnetic fields, via synchrotron emission or rotation measures (e.g. [35]), indeed indicate that particle-confining fields extend well beyond the height of the Galactic disc. For diffusive propagation, <r ²> = 2Dt. The diffusion coefficient D depends on the scale and degree of turbulence of Galactic magnetic fields, both poorly known. Assuming particles escape the system when reaching a halo height h above the disc, a particle will escape after a time of order T ∼ h ²∕2D. With h much larger than the disc scale height b, and a gas density in the halo which is negligible compared to the density ρ in the disc, the grammage traversed is X ∼ cTρ(b∕h) ∼ h∕D. From the residence time and the grammage, or by directly comparing element ratios with model calculations, the halo height h and the diffusion coefficient D can hence be inferred; depending on model details, halo heights of a few kpc, up to 10 kpc, and energy-dependent diffusion coefficients of D(E) of order \(10^{28}E^\alpha _{GeV}\) cm²/s are obtained, with α in the range from 0.3 to 0.6; α = 0.5 is often used as a representative value. This value of D corresponds to an rms propagation distance of cosmic rays of \(d_{pc} \sim 0.3t^{1/2}_{{\mathrm{year}}}\) at GeV energies; the diffusive approximation, however, holds only for reasonable large time and spatial scales, corresponding to many gyro radii and distances much larger than the coherence length of magnetic fields. Since the average spectrum of cosmic rays in the Galaxy is given by the source spectrum multiplied by the average residence time T(E) ∼ 1∕D(E), the average source spectrum has to be harder than the observed spectrum, Γ _source ≈ Γ _CR + 0.5. For the interpretation of cosmic rays spectra and composition, initial analytical models (e.g. [34]) have increasingly been replaced by numerical simulations such as GALPROP, allowing the inclusion of specific assumptions regarding the distribution of cosmic ray sources, of material in the Milky Way, and of energy loss and re-acceleration processes, see e.g. [2] for an overview and references. Beyond the effects of cosmic ray spallation products and radioactive decay, differences between solar system composition and cosmic ray composition are observed which seem to depend on the ionization potential or the volatility of elements (e.g. [36]), and which are attributed to the efficiency with which elements are injected into the acceleration process.

Assuming that cosmic rays more or less uniformly permeate the Galaxy, as confirmed by gamma-ray observations (see Sect. 13.4) and that they are not a temporary or local phenomenon, leaky box-models allow constraints to be placed on the energy requirements of Galactic cosmic-rays: to sustain the flux of cosmic rays in the Galaxy and its halo with a volume V of a few 10⁶⁷ cm³, a typical energy density ρ ≈ 1 eV/cm³ and a typical escape time T ≈ 10⁷ year, an energy input of ρV∕T ≈ 10⁴¹ erg/s needs to be provided by Galactic cosmic particle accelerators [37]. Only a few percent of this energy is dissipated in form of ionization and radiative or adiabatic losses; over 95% of the energy leaves the Galaxy into intergalactic space [38].

At higher energies, cosmic-ray composition is determined from ground-based measurements of the electron and muon content of air showers—heavy primaries have a higher fraction of muons—or from the depth of the shower maximum in the atmosphere, which is sensitive to the interaction cross section of the primary, which scales with mass number A roughly as the A ^2∕3, see e.g. [31]. As they are not sensitive to individual species, results are often presented in terms of the mean of \(\log (A)\) and tend to be rather sensitive to the algorithms used to model the air shower (see e.g. [18, 31]), and inconsistencies between models and data are seen [29, 39]. Nearly all measurements, however, show a change from a dominantly light (H, He) composition up to the knee, to a heavy composition above the knee (see Fig. 13.2, and also Fig. 13.11 below), and while the knee is clearly seen in showers initiated by light elements, no change in the slope of spectra of heavy primaries is evident up to 10¹⁷ eV. Well beyond the knee, at energies of few 10¹⁸ eV, studies of the height of shower maximum again suggest a light composition, with a transition to a heavy composition at a few 10¹⁹ eV [40, 41], although details remain under discussion [42]. A common interpretation is in terms of two components, a Galactic component and an extragalactic component, the latter dominating above 10¹⁷ to 10¹⁸ eV, each component with a cutoff in the acceleration mechanism at fixed particle gyro radius (i.e. rigidity), corresponding to a peak energy which scales with the nuclear charge Z. In this scenario typical Galactic accelerators are required to reach an energy in the range of a few Z × 10¹⁵ eV (e.g. [43]).

13.2.3 Cosmic Ray Anisotropy

The diffusive propagation of all but the very highest energy cosmic rays, with a gyro-radius much smaller than the scale of the Galaxy, destroys almost all directional information in cosmic rays; nevertheless, cosmic rays will on average flow away from their sources, resulting in small anisotropies.

The arrival directions of cosmic rays are indeed almost uniform on the sky, with (dipole) anisotropies at the 10⁻³ level at energies below 0.1 PeV, an indication of a minimum in anisotropy in the 0.1–1 PeV range, and an increase up to 10⁻² at higher energies (see e.g. [2, 44]). The phase of the anisotropy—i.e. the direction of maximum intensity—varies with energy. Effects which might cause anisotropies include [34]: (a) a diffusive flow of cosmic rays governed by gradients in cosmic ray density ρ, with a resulting anisotropy of order 3D∇ρ∕cρ; since the cosmic ray density likely decreases with galactocentric radius, an outward flow results at the location of the Solar System. A density gradient and hence flow might also be caused by single nearby cosmic-ray sources, in which case the magnitude and direction cannot be predicted a priori. Given that the diffusion coefficient D(E) increases with energy, density-gradient related anisotropies are expected to increase with energy. (b) Anisotropies of order (Γ + 2)(v∕c) caused by the motion of the Earth relative to the cosmic-ray rest frame (the Compton-Getting effect [45]). Cosmic-ray energies are also Doppler-shifted, for power-law spectra with index Γ the anisotropy hence depends on the spectral index, but not on the energy. Compton-Getting anisotropies could be caused by the 220 km/s motion of the Sun around the centre of the Galaxy, and/or—an order of magnitude smaller—by the orbital motion of the Earth around the sun. (c) Anisotropies arising from special magnetic field configurations near the Earth or sun, or from modulation by the solar wind. Such anisotropies should decrease with increasing rigidity (i.e. energy) of particles, but large-scale structures such as the heliotail caused by the motion of the sun relative to the local interstellar medium, possible extending beyond 1000s of AU,^{Footnote 2} could influence particles beyond multi-TeV energies. Decomposition of anisotropies into the different components is difficult also because most ground-based detectors measure the variation of rates along right ascension, for a fixed viewing direction, i.e., whereas the declination dependence is usually not measured directly. The observed energy dependence is non-trivial to explain and may include partial compensation between different contributions. In a study of a sample of simulated spiral galaxies and their cosmic-ray sources, most realisations show larger anisotropies than measured, and a uniform increase with energy [46]. The minimal anisotropy in the sub-PeV range can also be interpreted as evidence that the cosmic-ray “gas” co-rotates with the Galaxy [47]—quite plausible given that cosmic rays couple via magnetic fields to the interstellar plasma.

At TeV energies, anisotropies of a few 10⁻⁴ on smaller angular scales (few 10^∘) are observed [48, 49]. The origin of these small-scale anisotropies is not well understood; explanations e.g. assume field lines connecting a cosmic ray source and the solar system [50], but the effect may also simply reflect the local concrete realisation of the turbulent magnetic field within the cosmic ray scattering length [51].

13.2.4 Electrons and Antiparticles Among Cosmic Rays

Electrons and antiparticles among cosmic rays play a special role, since their “natural” yields are quite low and hence their fluxes are most sensitive to contributions from “exotic” sources such as annihilation of Dark Matter particles. Contrary to cosmic ray nuclei, electrons and positrons suffer significant energy losses, mostly from synchrotron radiation, with an energy loss timescale of \(\mathcal {O}(10^5\,{\mathrm{year}}/E_{{\mathrm{TeV}}})\). Combined with typical diffusion coefficients D(E), this implies that electron and positron sources need to be within a distance of \(d_{pc} \approx 500/E^{1/4}_{{\mathrm{TeV}}}\) from Earth. Unlike cosmic ray nuclei, electrons and positrons therefore act as probes of local sources. While electrons are assumed to be accelerated together with nuclei in cosmic ray sources, antiparticle yields—antiprotons and positrons—were traditionally modeled as arising exclusively from nuclear interactions during cosmic ray propagation, resulting in highly suppressed yields.

Antiproton yields have been measured up to energies of 10¹¹ eV. The antiproton to proton ratio rises with energy up to about 2 × 10⁻⁴ around 10 GeV, and then levels off, in good agreement with expectations for secondary antiprotons (e.g. [52]).

The cosmic-ray electron spectrum is illustrated in Fig. 13.5. The spectrum falls steeper than the spectrum of nuclei, with an index Γ ≈ 3, and steepens further at around 10¹² eV. The flux of cosmic-ray electrons at 10¹² eV is about 0.1% of that of cosmic ray nuclei. The spectrum can be modeled by assuming that cosmic-ray sources accelerate electrons and nuclei in a ratio of about 1:100 at a given energy; with increasing energy, and hence shorter electron range, fewer and fewer sources contribute, resulting in both a steeper spectrum and increasing uncertainty in the predicted flux due to the stochastic distribution of sources (see e.g. [57]).

Recent measurements, however, reveal deviations from this picture for the electron (plus positron) flux (see Fig. 13.5), and in particular for the positron/electron ratio (Fig. 13.6). Beyond the range of solar modulation, the electron flux is predicted to decrease slightly faster than E ⁻³; the data suggest an additional component appears in the energy range between about 100 GeV and 1 TeV, before the flux cuts off. A similar, but much more dramatic effect is seen in the electron/positron ratio, which increases beyond 10 GeV, rather than continue to drop as predicted for secondary production of positrons. This feature, first detected by PAMELA [58] and Fermi [59], and studied with high statistics using AMS-02 [56], gives rise to considerable speculation regarding its origin (e.g. [60]). Both the electron yield and the positron/electron ratio can be described by assuming an additional, charge-symmetric source of electrons and positrons, with a (propagation-modified) spectrum which rises faster than E ³ up to a few 100 GeV, and cuts off at about one TeV [60]. Dark matter annihilation of particles in the TeV mass range can account for the shape of the spectra, but would require enhanced annihilation rates compared to typical models, and annihilation modes which produce only leptons but no baryons; most conventional dark matter annihilation models predict the positron excess to be associated with an excess in antiprotons, which is not seen. An alternative explanation is provided by electrons escaping from nearby pulsars, or, more specifically, pulsar wind nebulae [61] (see also Sect. 13.4), although results regarding very low diffusion coefficients for cosmic-ray electrons disfavor this interpretation somewhat, making it difficult for electrons from known pulsars to reach the Earth [62].

13.2.5 Astronomy with Ultra High Energy Cosmic Rays

Due to the strong deflection of cosmic rays in Galactic and extragalactic magnetic fields, astronomical imaging of their sources is impossible over most of their energy range. Only at energies of several 10¹⁹ eV deflections for Z = 1 ultra high energy cosmic ray (UHECR) particles are predicted to become small enough—a few degrees—that particles can be traced back to their sources. The arrival directions of the highest-energy cosmic rays are essentially isotropic (see Fig. 13.7), but indications of correlations with astrophysical objects start to emerge. In the Auger data, the most significant over-density of UHECR lies roughly in the direction of Centaurus A, the closest AGN at 3.8 Mpc distance; the statistical significance of this fact is about 3σ after accounting for the number of trials [29]. Arrival directions also correlate with the distributions of starbust galaxies, and of gamma-ray AGN, at the 3 − 4σ level [29]. The 7-year Telescope Array data [17] exhibit at energies above 10^19.2 eV a 3.7σ post-trial enhancement around RA = 9 h 16 min, Dec = 45^∘. The interpretation of these data is not obvious. One possibility is that few sources are responsible for UHECR, emitting a mixture of light and heavy nuclei; the protons among those particles create the detected directional enhancements whereas the heavier nuclei are strongly deflected and are responsible for a uniform background, with similar spectra in both hemispheres. Verifying or disproving such a scenario requires particle-by-particle mass identification and increased statistics, both goals of next-generation UHECR experiments.

13.3 Particle Acceleration Mechanisms and Supernova Shocks as Cosmic Accelerators

A few general conditions can be imposed regarding sources of Galactic cosmic rays. To sustain the flux of cosmic rays in the Galaxy, an energy input of ≈ 10⁴¹ erg/s by Galactic cosmic ray sources is required (see Sect. 13.2), and a spectrum extending at least up to ≈ Z × 10¹⁵ eV with an average source spectral index in the range Γ ≈ 2 to 2.4. In addition, if cosmic accelerators use regular or turbulent magnetic fields to confine particles, the acceleration region has to have a size at least equal to the gyro radius of particles, R _gyro,pc ∼ E _PeV∕B _μG [7]. Figure 13.8 illustrates that there are astrophysical objects which fulfil this condition up to energies of 10²⁰ eV, but not much beyond.

In Sect. 13.3.1 below we focus on the most established mechanism, diffusive shock acceleration, and in particular the well-studied case of supernova remnants. Note however, that acceleration associated with magnetic reconnection is now increasingly discussed, in particular in the cases of objects with relativistic bulk motions such as in the jets of active galaxies.

13.3.1 Shock Acceleration in Supernova Remnants

As sources of Galactic cosmic rays, supernova explosions were suggested very early as a suitable source [64], providing both sufficient energy—10⁵¹ erg kinetic energy per explosion, or 10⁴² erg/s for a supernova rate in the Galaxy of 1/30 year—as well as a plausible acceleration mechanism—first order Fermi acceleration (see e.g. [65, 66] and further references given in [3, 4]), the appropriate spectral index Γ ≈ 2 and a peak energy around 10¹⁵ eV (see Fig. 13.8).

In a supernova explosion, stellar material of up to a few solar masses is ejected with initial speeds of up to 10⁴ km/s or β _sh = v _sh∕c ∼ 0.03, and creates a shock where the ambient interstellar medium is compressed and piled up. While the piled-up ambient material slows down the ejecta, speeds remain supersonic for time scales of order 10⁴ years (e.g. [67]). Shocks with high Mach number are characterized by a compression ratio r = (γ + 1)∕(γ − 1) = 4, governed by the adiabatic index γ = 5∕3 of the compressed monatomic gas. Charged particles which cross the shock in either direction find themselves in a medium moving with velocity ≈ v _sh relative to the medium on the other side of the shock (Fig. 13.9). Particles are scattered off anisotropies in the magnetic field and isotropised in the new medium, with an average increase in energy ΔE∕E of \(\mathcal {O}(\beta _{sh})\). In their diffusive motion, particles can cross the shock front multiple times, their energy growing as E ∼ (1 + k)ⁿ, where n is the number of crossing cycles and k = (4∕3)(1 − 1∕r)(v _sh∕c); here (1 − 1∕r)v _sh is the difference in flow speed before and after the shock and the factor 4∕3 arises from averaging over shock crossing angles. Since, viewed in the rest frame of the shock, material is inflowing (“upstream”) with speed v _sh and outflowing (“downstream”) after shock compression with speed v _sh∕r, in the long run particles tend to be carried into the downstream region, with a probability of order 4β _sh∕r not to return to the shock at each cycle (cβ _sh∕r is the downstream flow speed and hence loss rate, c∕4 the angle-averaged shock crossing speed and hence rate of initiating another cycle). Given the gain per cycle and the loss probability per cycle, the energy spectrum of accelerated particles can be calculated as dN∕dE ∼ E ^−Γ with Γ = (r + 2)∕(r − 1). The time per acceleration cycle is governed by the diffusion coefficient D. Maximum magnetic field turbulence ΔB∕B ∼ 1 implies that the mean free path of relativistic particles, between scattering off field inhomogeneities, is of order of the gyro radius. In this so-called ‘Bohm diffusion’ regime, a more detailed calculation gives D = R _gyro c∕3. The cycle time ΔT can be estimated to be 4D(1 + r)∕(v _sh c) ≈ (20∕3)(R _gyro∕v _sh) (for r = 4). With a gain per cycle of order ΔE ≈ β _sh E, the resulting acceleration rate is hence \(dE/dt \approx \Delta E/\Delta T \sim E\beta _{sh}^2/R_{gyro} \sim \beta _{sh}^2B\), of order 0.05β ² B _μG PeV/year. The maximum achievable energy is governed by the age of the system, by energy losses (in particular radiation losses of electrons), and by the scale λ of the upstream diffusion length of particles, λ ≈ R _gyro∕3β _sh (determined from the balance between the upstream medium flow speed v _sh and the diffusion speed v _Diff = D∇ρ∕ρ ≈ D∕λ), which has to be small compared to the size of the supernova remnant to give particles a chance to return to the shock. The age-limited peak energy is given by [4] as \(E_{max}(age) \approx 0.5 T_3 v_{sh,8}^2 B_{\mu G}f^{-1}\) TeV where T ₃ is the remnant age in kyr, v _sh,3 is the shock speed in units of 10³ km/s and f parametrizes diffusion effects, with f ≈ 1 for Bohm diffusion. Injection efficiency, peak energy and particle acceleration rate also depend on the angle of the average magnetic field relative to the shock front. For heavier nuclei, the acceleration rate and peak energy scale with their charge Z, reflecting the reduced gyro radius for a given energy.

The acceleration process is predicted to be highly efficient, converting as much as 50% of the kinetic energy of the ejecta into non-thermal particles. This high efficiency makes the process non-linear (e.g. [68, 69] and further references in [4]); the accelerated cosmic ray currents induce turbulent magnetic fields—determined under certain assumptions as high as 300 μG (e.g. [70])—which in turn reduce the gyro radius and the diffusion coefficient D and increase the speed of particle acceleration. A shock precursor of scale λ develops since the in-streaming gas reacts to the upstream cosmic-ray pressure, reducing the compression ratio at the subshock, see Fig. 13.9. On the other hand, since the shock now compresses a mixture of normal gas with γ = 5∕3 and relativistic cosmic ray gas with γ = 4∕3 upstream of the shock, the total compression ratio increases up to r = 7 and the spectrum of accelerated particles becomes harder, up to dN∕dE ∼ E ^−3∕2. This hardening of spectra affects mainly the highest-energy particles, with gyro radii of order λ, which probe both the shock precursor and the subshock (see Fig. 13.10).

Strictly speaking, the calculated spectral index Γ = (r + 2)∕(r − 1) applies to the particles swept downstream and confined inside the remnant. The exact mechanism of cosmic-ray escape from supernova shocks into the upstream region is not well understood; it is usually assumed that the time-integrated spectrum of particles released from the remnant reflects the spectrum of accelerated particles, but that particles of highest energy are released early, and those of low energy late in the lifecycle of the remnant [71]. The escaping cosmic rays represent a current that generates turbulent magnetic fields outside the remnant, reducing the diffusion coefficient in the upstream region, thereby enhancing the rate of particle crossing of the shock front, and speeding up the acceleration process [72].

Cosmic ray spectra measured at the Earth result from the superposition of many sources, up to distances comparable to the scale height of the halo, and are essentially stationary, despite the stochastic nature of the sources. At any given time thousands of supernovae will contribute to the cosmic rays on Earth; an individual supernova will cause a change in cosmic ray intensity over a volume of only about 100 pc in radius; beyond that the energy density of it’s cosmic rays falls below the 1 eV/cm³ level of the cosmic ray sea. The spectrum of cosmic rays on Earth is given by the source spectra multiplied by the average residence time T(E) ∼ 1∕D(E) in the Galaxy, qualitatively explaining the difference between the source spectral index Γ ≈ 2 and the observed cosmic ray spectral index Γ ≈ 2.7. The knee in the cosmic ray spectrum is then associated with the peak energy of particles in the acceleration process; heavier nuclei of charge Z can be accelerated to Z-times higher energies than protons and dominate beyond the knee. With plausible parameters, supernova remnant-based models can reproduce the observed spectrum and variation of composition across the knee, see Fig. 13.11.

Shocks, and particle acceleration in shocks, can occur in all situations where non-relativistic or relativistic outflows exist with Mach numbers greater than unity; examples include stellar winds, Galactic outflows, winds driven by pulsars, or jets emerging from the vicinity of black holes driven by matter accretion. Shocks can also arise in collisions or from the infall of matter, e.g. during structure formation in galaxies and galaxy clusters. Less well understood than supernova shocks are relativistic shocks with β _sh ≈ 1, here particles can gain significant energy in one or few shock crossings, but crossing the shock becomes increasingly difficult (e.g. [74]).

13.3.2 Pulsars as Particle Sources

An alternative mechanism for particle acceleration are neutron stars (or generally, rotating compact objects) with large magnetic fields, acting as unipolar inductors building up large electric fields and radiating Poynting flux.

A pulsar (a rotating magnetised neutron star) created in a supernova explosion radiates energy because its magnetic moment is misaligned by an angle α with respect to its rotation axis. The pulsar rotational energy \(E = I {\Omega }^2/2 \approx 2 \times 10^{52}/P_{ms}^2\) erg serves as an energy source; here I ≈ 10⁴⁵ cm²g is the pulsar moment of inertia and P _ms is the rotation period in ms, with typical pulsar birth periods of order tens of ms. Assuming energy loss through dipole radiation, energy is radiated at a rate \(\dot {E} = I {\dot {\varOmega }} {\varOmega } \approx (8 \pi /3 \mu _0 c^3) B_s^2 R^6 {\varOmega }^4 \sin ^2{\alpha } \approx 4\times 10^{43} B_{12}^2 P_{ms}^{-4} \sin ^2 \alpha \) erg/s, causing the pulsar to spin down, with \({\dot {\varOmega }} \sim {\varOmega }^3\). Here, R ≈ 10 km is the pulsar radius and B ₁₂ is the surface field in units of 10¹² G. In case other dissipation mechanisms contribute, such as outflowing winds of particles, \({\dot {\varOmega }}\) is parametrized as \({\dot {\varOmega }} = -K {\varOmega }^n\), where n is the braking index, n = 3 for dipole radiation. Measured values for n range from 2 to 3. Integrating the \({\dot {\varOmega }}({\varOmega })\) relation, one obtains \(\dot {E}(t) = \dot {E}_0/(1+t/\tau )^{-(n+1)/(n-1)}\) for the general case, or \(\dot {E}(t) = \dot {E}_0/(1+t/\tau )^{-2}\) for dipole radiation, with τ as the characteristic spin-down time. For dipole radiation, \(\tau \approx (3 \mu _0 c^3 I)/(16 \pi R^6 B_s^2 \sin ^2 \alpha ~{\varOmega }_0^2) \approx 15 P_{0,ms}^2/(B_{12}^2 \sin ^2 \alpha )\) years; in the time up to t = τ, the pulsar loses half of its rotational energy, with the energy output diminishing like 1∕t ² for t >> τ.

In the near field, the rotating pulsar magnetic field with a surface strength in the 10¹² G range creates electric fields with voltage drops of order \(10^{17} B_{12}/P_{ms}^2\) volt. Electrons and positrons are generated by pair cascades near the pulsar surface and are accelerated until currents short-circuit the fields. Inside the light cylinder, r < Ω∕c, where the magnetic field and the currents co-rotate with the neutron star, particles either near the polar cap of the pulsar or in the ‘outer gap’ close to the light cylinder create beams of radiation swept across the sky by the pulsar rotation, see [75, 76]. In the far field, magnetic fields spiral up and cause a Poynting flux of electromagnetic energy. By a mechanism, which is yet to be understood in detail (e.g. [76]), this Poynting flux drives a particle wind, effectively converting much of the radiated energy into particle kinetic energy. It is usually assumed that the particle wind is dominated by electrons and positrons, but a component of nuclei extracted from the pulsar surface cannot be excluded. In the pulsar wind, reconnection of opposite magnetic field lines can provide a mechanism for energy release and particle acceleration [77]. The particle wind, initially assumed to be spherical [78, 79] but in more recent models concentrated in the equatorial plane, ends in a standing wind termination shock where the pressure of the wind is balanced by the ambient pressure; the termination shock is visible in high-resolution X-ray images of pulsars (see e.g. [80]). In the termination shock, particle velocities are randomised, particles are accelerated and emerge in a subsonic flow, creating a large and expanding magnetised bubble filled with high-energy electrons and positrons, see e.g. [78, 79, 81]. Pulsars are hence cosmic sources of high-energy electrons and positrons, possibly of nuclei, and of a complex mix of pulsed and beamed as well as of more or less steady and isotropic radiation spanning the range from radio to gamma rays, as elaborated in Sect. 13.4.3. However, since not all supernova explosions result in pulsars and since their initial rotational energy is usually much smaller than the kinetic energy released in a supernova explosion, the contribution of pulsars to overall cosmic-ray energetics should be modest.

13.4 Probing Cosmic-Ray Sources and Propagation Using Gamma-Rays and Neutrinos

For energies below E ∼ hZeB _ISM ∼ 10¹⁸ eV to 10¹⁹ eV (see e.g. [82]) cosmic ray protons are strongly deflected when propagating in the Galaxy on scales of the Galactic halo height h in typical interstellar fields B _ISM; their arrival directions therefore carry almost no information on their source locations. Directional messengers are therefore required to study Galactic cosmic-ray sources. Strong interactions of cosmic ray protons and nuclei with target protons and nuclei in the interstellar medium (ISM) lead to pion production and hence gamma-ray, neutrino and secondary electron and positron signatures (for a detailed description, see e.g. [83]). The following discussion will focus largely on the well-explored gamma ray signatures. Protons or nuclei with power-law spectra of index Γ _p generate gamma-ray spectra with Γ _γ ≈ Γ _p, and a cutoff in proton spectra translates into a (smoother) cutoff in gamma-ray spectra about a decade in energy below the cutoff in primary spectra. For a typical ISM density, n, of 1 hydrogen atom per cm³ the energy loss timescale for relativistic protons is (f σ _pp n c)⁻¹ or a few 10⁷ years, comparable to or—in particular at high energy—longer than their residence time in the Galaxy. The fraction f of the primary energy lost in a typical collision (“inelasticity”) is ∼0.5 of which ≈ 1∕3 goes into the gamma-ray channel. Overall, about 1% of the energy injected into relativistic hadrons in the Galaxy in the end emerges in photons [38]. Inside, or in the vicinity of cosmic accelerators, particle density is strongly enhanced and the objects are visible as gamma-ray sources, assuming that sufficient amounts of target material (interstellar gas) are present. The intensity and extent of the gamma-ray or neutrino emission depends the distribution of target material, on whether accelerated particles are efficiently confined within the accelerator, and on how quickly particles diffuse away after escaping from the acceleration region (see Sect. 13.2.2) and merge into the cosmic-ray “sea”.

For cosmic electrons and positrons, ionisation, bremsstrahlung, synchrotron radiation and Inverse Compton (IC) scattering of ambient radiation fields compete as energy-loss processes [84, 85]. For the highest energy electrons, at TeV energies and above, synchrotron and IC emission dominate and synchrotron X-rays and IC gamma-rays can be used as effective tracers of electron acceleration and propagation. The targets for IC scattering are typically the cosmic microwave background radiation (CMBR), starlight, and reprocessed starlight remitted in the far infrared, with typical energy densities of order 1 eV/cm³. The typical lifetime of a high energy electron in the ISM is 5 × 10⁵(B∕5 μG + U _rad∕(eVcm⁻³))⁻¹(E∕TeV)⁻¹ years, much shorter than propagation time scales in the Galaxy. Radiative losses modify the energy spectra of very-high-energy electrons, introducing—for burst-like injection—an age-dependent cutoff in the electron spectra at the energy where the lifetime corresponds to the source age, at E _cut,TeV ≈ 3 × 10⁵∕T _year, or—for continuous injection—increasing the spectral index Γ _e by one unit, since at high energy only electrons injected within a period corresponding to the electron lifetime survive [86]. Electron spectra with power-law index Γ _e generate power-law IC and synchrotron spectra with index (Γ _e + 1)∕2, and a cutoff energy E _c in electron spectra translates into cutoffs \(E_{\gamma ,{\mathrm{TeV}}} \approx 10 E_{c,{\mathrm{TeV}}}^2 E_{ph,{\mathrm{eV}}}\) for IC gamma rays (in the Thomson regime where E _c,TeV E _ph,eV ∼< 1), where E _ph is the typical energy of the target photons, and E _X,eV ≈ 0.01E _c,TeV B _μG for X-rays. With the rapid energy loss, emission by electrons is usually concentrated relatively close to the sites of acceleration. Figure 13.12 gives an example spectral energy distribution for emission dominated by energetic electrons.

Gamma-ray detection at high energies is based on pair-production and subsequent electromagnetic cascading. The most sensitive satellite-based gamma-ray detector currently operating is the Fermi Large Area Telescope (LAT), which has ≈1 m² detection area and ≈2.5 steradian field-of-view (FoV). The LAT combines a silicon-strip tracker for directional reconstruction and a 8.6 radiation-length thick calorimeter for energy determination [90]. The angular resolution achievable is strongly energy dependent: improving from 5^∘ at 100 MeV to 0.25^∘ at 10 GeV, where photon statistics become very limited for most sources. The most sensitive ground-based approach (see e.g. [9] for a review) is the Imaging Atmospheric Cherenkov Technique (IACT), which uses the Cherenkov light produced by electromagnetic cascade electrons and positrons in the atmosphere to establish the properties of the primary gamma-ray; the gamma-ray direction is determined by imaging the cascade, the gamma-ray energy is derived from the Cherenkov light yield. The technique is in principle applicable for photon energies above ∼5 GeV, where the Cherenkov yield becomes significant. Current instruments HESS, MAGIC and VERITAS are sensitive from ∼20–50 GeV to ∼50 TeV, have ∼4^∘ field-of-view and collection areas at TeV energies of ∼10⁵ m². The directional precision achievable from the ground is limited by shower fluctuations to ≈0.01^∘∕(E∕1 TeV)^−0.6 [91], with about 0.1^∘ (and ≈15% energy resolution) achieved for current instruments [8]. Compared to Cherenkov telescopes, ground-level detection of shower particles allows large field-of-view and duty cycle, at the expense of higher energy threshold and reduced sensitivity and energy resolution [9]. The HAWC instrument, combining a high-altitude location at 4200 m asl. with the calorimetric detection of shower particle energy flow using large water Cherenkov detectors, instrumenting 60% of its 22,000 m² array area, has for the first achieved gamma-ray detection performance competitive with current IACTs [92].

At this time, over 3000 sources of GeV gamma rays have been detected using the space-based instruments Fermi [93] and AGILE, and well over 200 sources of TeV gamma rays [94] are seen with ground-based instruments, showing the abundance and indeed ubiquity of cosmic particle accelerators. Around one half of the TeV sources are of extragalactic nature, half or slightly more are associated with our Galaxy. Of the Galactic TeV gamma ray sources, a handful are SNR where shells are resolved, a similar number are clearly associated with SNR but not resolved, about two dozen are associated with pulsars and their pulsar wind nebulae, and for the remaining 15–20 sources the identification is unclear, either because of a lack of counterparts or because multiple potential counterparts exist. Despite the much larger number of GeV sources, the number of well-identified Galactic objects is similar, with pulsars, identified by their pulsed emission, as the dominant class of Galactic GeV emitters.

For hadronic sources similar fluxes are generated in gamma-rays and neutrinos (see e.g. [83]). Neutrino telescopes primarily sensitive above ∼1 TeV now exist, with the best sensitivity reached by the IceCube detector beneath the South Pole. IceCube has for the first time detected astrophysical neutrinos [95, 99], emerging at energies beyond 100 TeV, from the strong background of atmospheric neutrinos. The neutrino flux appears to be of diffuse nature (see Fig. 13.13), and no consensus exists regarding its exact origin. No localized very-high-energy cosmic neutrino source has yet been detected [97]; a detection would provide completely unambiguous identification of hadronic accelerators and allow high-density environments, from which TeV photons may not emerge, to be probed. The KM3Net collaboration [98] is building a larger detector in the Mediterranean sea with greater sensitivity and the potential for detection of neutrino sources in the inner parts of the Galaxy, and IceCube is studying options for a tenfold increase of detection volume [96].

13.4.1 Diffuse Gamma Ray Emission: Tracing Cosmic Rays in the Galaxy

The Galactic cosmic rays interact with the material, radiation fields and magnetic fields in and around the Galaxy to produce broad-band diffuse emission. This diffuse emission peaks in the gamma-ray band due to strong contributions from π ⁰ decay, inverse Compton scattering and bremsstrahlung. Diffuse emission dominates the GeV sky (see Fig. 13.14) and provides a means to test the distribution and energy spectrum of cosmic rays in the Galaxy. Probing cosmic rays in this way requires an understanding of the distribution of gas and radiation fields in the Galaxy; historically the opposite has often been the case, with the gas distribution in the Milky Way being estimated from gamma-ray observations. The main components of the Galactic diffuse emission are, however, clear: π ⁰ decay and bremsstrahlung emission from interactions with molecular material with a scale-height in the disc of ∼50 parsecs, and with a more diffuse atomic component, plus a very extensive halo generated by inverse Compton scattering on Galactic radiation fields.

The diffuse GeV γ-ray emission suggests that the ISM is permeated with cosmic ray electrons, protons and nuclei, occupying a much greater volume than the Galactic disc (consistent with the picture presented in Sect. 13.2.2). In the outer parts of the Galaxy, where it is easiest to measure, this “sea” of cosmic rays has spectral properties similar to those measured at the Earth. The emissivity (gamma-ray flux per hydrogen atom, proportional to the cosmic-ray density) is seen to be roughly constant from the location of the sun up to ∼14 kpc from the Galactic Centre [101]. This relative uniformity suggests that the radial distribution of acceleration sites in the Galaxy is flatter than that of identified SNRs or pulsars.

Diffuse Galactic gamma-ray emission has also been detected at TeV energies: from the outer parts of the Galaxy, with the wide field-of-view shower-particle detector Milagro [102] and in the Galactic Centre region with HESS [103]. The level of emission seen is well above the extrapolation of the cosmic ray “sea” emission at lower energies and suggests the existence of recently injected cosmic rays and/or unresolved cosmic ray sources. The diffuse emission seen with HESS from the ∼100 pc radius Central Molecular Zone is correlated with the distribution of target material, illuminated by cosmic rays diffusing away from the Galactic Centre and hence suggesting a π ⁰-decay origin of the emission, with the central supermassive (3 × 10⁶ M _⊙) black hole Sgr A^⋆ as likely candidate for the origin of these cosmic rays. The local density of TeV cosmic rays at the centre of the Galaxy is enhanced by an order of magnitude compared to local cosmic rays.

Diffuse emission is seen with Fermi from beyond the Milky way, in satellite galaxies such as the Large and Small Magellanic Clouds and Local Group galaxies such as Andromeda. The gamma-ray fluxes seen from these objects support the idea that the energy input into cosmic ray acceleration is proportional to the star formation rate, with this trend continuing to more distant starburst galaxies, which are undergoing phases of enhanced star-formation [104,105,106].

A completely unexpected discovery were the Fermi bubbles—kpc-size emission regions of GeV gamma rays above and below the Galactic Centre, with relatively sharp boundaries, indicating confined populations of high-energy particles well beyond the Galactic disc and near halo [107,108,109]. Similar-shaped radio features hint at the presence of (primary or secondary) electrons. The origin of the Fermi bubbles is under discussion; possibilities discussed include (a) a Gyr-old stellar wind driven by star formation in the Galactic Centre region, similar to the outflows seen in starburst galaxies such as M82 or NGC 253, carrying cosmic rays along which then interact in the thin medium above and below the disc, (b) earlier jet activity of the supermassive hole at the Galactic Centre, or (c) in-situ acceleration of electrons by plasma-wave turbulence [108, 110, 111].

13.4.2 Supernova Remnants Viewed in Gamma Rays

As described in Sect. 13.3.1, the idea that supernova remnants (SNR) accelerate the majority of the Galactic cosmic rays has been with us for half a century, until relatively recently, however, the level of experimental support for this idea was relatively modest. Radio emission from the shells of SNRs was attributed to GeV electrons, but evidence for the acceleration of very-high-energy particles, in particular protons and nuclei, was essentially absent. Observations in the X-ray band from the 1990s onwards have established the presence of synchrotron emission from > 100 TeV electrons in these objects. These observations also indicate the presence of enhanced magnetic fields [70], and for some objects “missing energy” is evident when comparing expected shock heating of the gas to measured thermal X-ray emission [70, 112]. A likely form for this missing energy is a population of cosmic-ray protons and nuclei, which may also be responsible for the amplification of magnetic fields in the SNR shell, via cosmic ray driven instabilities—the positive feedback process that leads to an increase in the efficiency and maximum energy of cosmic ray acceleration, provided that conversion of shock kinetic energy to cosmic rays occurs with a significant efficiency [113].

Detection of very-high-energy gamma rays from SNR was proposed in [114] as a test of cosmic-ray origin; the gamma-ray flux from interacting protons was predicted to be \(F({>}E)_{\,{\mathrm{cm}}^{-2}\,{\mathrm{s}}^{-1}} \approx 9 \times 10^{-11} \theta E_{{\mathrm{TeV}}}^{-1.1} E_{SNR,51} d_{kpc}^{-2} n_{{\mathrm{cm}}^{-3}}\), where θ is the efficiency of energy conversion, E _SNR the kinetic energy in the explosion in units of 10⁵¹ ergs, d the distance in kpc, and n the ambient density in hydrogen atoms per cm³. With θ assumed as 0.1 or larger and E _SNR and n typically of order unity, supernova remnants within a few kpc were predicted to be bright enough for detection with air-Cherenkov instruments.

The subsequent discovery of resolved TeV emission from the shells of SNRs with H.E.S.S.—RX J1713.7−3946, RX J0852.0−4622, RCW 86 and SN 1006—(e.g. [8]) can be seen as the direct and definitive proof that very-high-energy particles are accelerated in the shells of SNR.

Figure 13.15 shows keV X-ray and TeV gamma-ray images of the nearby Galactic SNR RX J1713.7−3946 [117], the best-studied gamma-ray remnant. However, there is still significant debate regarding the nature of the parent particle populations. The close resemblance of the X-ray and gamma-ray images, taken a factor 10⁹ apart in energy, has been taken as implying a common parent population, i.e. electrons with spectra extending to ∼100 TeV, with the observed TeV emission arising from Inverse Compton scattering rather than from proton interactions. This picture is supported by the spectral shape of the gamma-ray emission, see Fig. 13.15; in the GeV energy range, the spectral index of gamma rays is Γ ≈ 1.5, as expected from an electron population with the canonical E ⁻² energy spectrum resulting from shock acceleration, whereas proton interactions should result in a gamma-ray index Γ ≈ 2. These data do not exclude efficient proton acceleration in this SNR; in the low-density environment, protons may simply not find enough targets to create a gamma-ray flux which is competitive with the flux produced by an energetically sub-dominant, but much more efficiently-radiating population of accelerated electrons. This is illustrated in Fig. 13.16, which shows the spectrum of primary particles that reproduce the measured wide-band gamma ray spectrum: either about 6 × 10⁴⁹ ergs are required in protons above 1 TeV (assuming a target density of 1/cm³), or only about 10⁴⁷ ergs in electrons.

Other gamma-ray detected SNRs have dramatically different spectra; this may be due to a combination of the environment and evolutionary stage of the system. TeV emission is for example seen also from extremely young Galactic SNRs such as Tycho’s SNR and Cassiopeia A, although the angular resolution of TeV instruments is insufficient to resolve their shells. These objects are firmly associated with historically observed supernova and are bright X-ray and radio sources. Figure 13.15 shows the spectral energy distribution of Tycho’s SNR [116], which exhibits a spectral softening at a few hundred GeV. The maximum energy to which a particle can be accelerated inside an SNR shell is very likely time-dependent, and determined by the shock velocity and magnetic field strength. Very young SNRs with fast shocks and strong magnetic fields may accelerate extremely high energy particles (up to PeV) which can escape ahead of the shock at later times [71], leading to a decrease in the maximum or break energy with time. In addition, the presence or absence of dense target material (in the form of molecular gas) in the neighbourhood of the SNR will affect the balance between inverse Compton emission and Bremsstrahlung and π ⁰-decay emission. The nature of the environment depends strongly on the nature of the explosion. Type Ia supernova occur in evolved systems, with the explosion occurring far from the birth place of the star and typically far from molecular gas clouds. The majority of core-collapse supernova explosions occur inside massive stellar clusters, born from molecular clouds, but where powerful stellar winds have already redistributed the molecular material to produce a highly non-uniform density environment.

Emission correlated with the distribution of target material, rather than following the emission seen in radio or X-rays, would be a clear sign for a hadronic origin of gamma rays, and is seen for several Galactic SNRs (see e.g. [121]), all of which are significantly older than the ∼1000 year age of RX J1713.7−3946. W 51 is an example of this class of object: as for RX J1713.7−3946 it is thought to be the remnant of the core-collapse of a very massive (>8 M _⊙) star but its age is estimated to about 10⁴ y and it is clearly interacting with dense molecular material. The spectrum of W 51 is rather steep at TeV energies (Fig. 13.15), with the peak energy output in the GeV domain [118], in marked contrast to RX J1713.7−3946. The centroid of the GeV and TeV emission is also consistent with the point of interaction of the SNR with gas clouds rather than the centre of the remnant. Both these facts point to a hadronic origin of the gamma-ray emission, with 5 × 10⁵⁰ ergs of cosmic rays present in the SNR [118], consistent with the picture that a significant fraction of the energy of a typical SNR goes into the acceleration of cosmic ray protons and nuclei. The steep spectrum of the emission suggests that particles with TeV energies may already have escaped the SNR. Hadronic origin is also demonstrated for remnants such as W 44 and IC 443, where spectra show a clear pion-decay feature—a break in spectral index at about the pion mass [120], which is not expected in spectra from the inverse Compton process.

There is now compelling evidence that SNRs are effective accelerators of both electrons and nuclei, but due to uncertainties on the population and evolution of particle-accelerating SNRs one cannot yet confidently conclude that they are the dominant sources of the Galactic cosmic rays.

13.4.3 Pulsars and Pulsar Wind Nebulae

The newly-formed neutron stars left behind in some types of supernova explosion are generally rapidly rotating and highly magnetised. The rotational energy of such pulsars is converted into pulsed emission (primarily and gamma-ray energies) and into an ultra-relativistic outflow of electron-positron pairs, see Sect. 13.3.2. The termination shock where this wind is halted by external pressure is thought be a site of acceleration up to very high energies. After the shock the direction of particle motions become randomised and synchrotron and Inverse Compton emission is produced in a pulsar wind nebula (PWN). There is as of yet no clear physical picture of how particle acceleration operates in these systems. None the less, there is a huge body of evidence that acceleration to PeV energies occurs in these systems. The Crab Nebula, the most prominent example of a PWN, is a unique object which is bright and well-studied in every waveband of the electromagnetic spectrum, with synchrotron emission dominating from the radio up to 1 GeV and inverse Compton emission seen above, up to almost 100 TeV (see Fig. 13.12). The Crab pulsar was born in a historically observed supernova explosion in 1054 and has the most extreme rate of conversion of rotational energy (\(\dot {E} \approx 5 \times 10^{38}\) erg/s) of any Galactic pulsar. In 1989 it became the first source to be detected at TeV energies [122]. Until very recently the gamma-ray emission from the Nebula was thought to be steady in time, but recent dramatic flaring activity has been seen at GeV energies, apparently corresponding to a rapid increase in the number of synchrotron-emitting > PeV electrons (Fig. 13.12) [89, 123, 124]. It seems very difficult to explain these flares in terms of diffusive shock acceleration, as this process seems to be too slow to offset catastrophic synchrotron energy losses. A single shot acceleration mechanism such as magnetic reconnection at the termination shock is an attractive option.

The gamma-ray emission from the Crab Nebula appears almost point-like with the ∼0.1^∘ resolution of current instruments, but this situation is atypical. In the last decade, about two dozen TeV gamma-ray sources were discovered and firmly or tentatively identified as PWN, including objects such as Vela X, MSH 15–52, G 21.5−0.9, G 0.9+ 0.1, N 175B, and the nebula surrounding PSR B1706–44 (for summaries, see e.g. [8, 125,126,127]). Most of these PWN are extended TeV gamma-ray sources, with size of a fraction of a degree, often accompanied by a significantly smaller-scale X-ray nebula surrounding the pulsar. While X-ray luminosities tend to correlate quite well with the instantaneous spin-down energy loss \(\dot {E}\) of the pulsar, no clear correlation is observed between the gamma-ray luminosity and \(\dot {E}\) [126]. Gamma-ray luminosities range from a fraction of a percent of the pulsar spin-down energy loss \(\dot {E}\) to tens of percent, indicating a relatively efficient conversion of (rotational) kinetic energy into high-energy particles. A likely explanation for the difference in size between X-ray and gamma-ray PWN and for the different \(\dot {E}\)-dependence of luminosities is that in the typical μG fields derived for extended PWN, keV X-ray emitting electrons have energies of 100s of TeV and cooling times of order 1000 years, whereas TeV gamma ray emitting electrons have energies in the 10 TeV range and cooling times beyond a few 10,000 years. For pulsars with ages between a 1000 and a few 10,000 years (most of the gamma-ray PWN population), only “recently” accelerated electrons with number \({\sim }\dot {E}\) therefore contribute to the X-ray emission, whereas all electrons ever accelerated contribute to the gamma-ray emission, reflecting essentially the initial rotational energy E ₀ of the pulsar (half of which is lost during the initial few 100 years of spin-down history, see Sect. 13.3.2), rather than \(\dot {E}\). The sizes of gamma-ray PWN tend to increase with the age of the pulsar, saturating at sizes of a few tens of pc. The gamma-ray PWN are frequently displaced from the pulsar, locating the pulsar (and the associated X-ray PWN) at the edge of the gamma-ray PWN (e.g. Fig. 13.15). One explanation is that PWN are often crushed and/or displaced by the supernova reverse shock [128], another that—as discussed above—the gamma-ray PWN reflects relic electrons abundantly created in the early history of the pulsar, whereas now the pulsar may have moved away from its birth place due to a kick from the explosion. However, in the few cases where pulsar motion is known, it does not line-up well with the vector connecting the pulsar and the centroid of the VHE PWN. In a few cases, such as for the source HESS J1825−137 [129] shown in Fig. 13.15, gamma-ray PWN (as well as X-ray PWN) show energy-dependent morphology, with the nebula shrinking towards the pulsar with increasing gamma-ray energy, presumably due to radiative cooling of electrons as the propagate away from the pulsar. GeV-TeV gamma-ray emission can therefore be used to measure the time-integrated particle injection of the pulsar and to understand the propagation of relativistic particles away from their sources.

PWN represent the bulk of Galactic TeV gamma-ray sources, by far outnumbering emission traced to SNR shock-accelerated protons. At first, this seems surprising. However, contrary to supernova remnant shocks, where acceleration of very-high-energy particles stalls after a few 10³ to at most 10⁴ years, a pulsar can supply the nebula with energy for many 10⁴ years. In addition, under typical conditions, electrons and positrons are more efficient TeV gamma-ray emitters than are SNR-accelerated protons—radiative energy loss timescales are smaller by one to two orders of magnitude. Therefore, PWN dominate the Galactic population of TeV gamma-ray sources even though their energy reservoir—the rotational energy of the pulsar—is typically an order of magnitude smaller than the ≈ 10⁵¹ ergs released in a supernova explosion. In fact, it seems likely that a sizeable fraction of the currently unidentified TeV gamma-ray sources—where no counterpart is seen in other wavebands—are PWN where the pulsar is not detected (due to beaming effects or simply a lack of sensitive observations) and where radiation-cooled electrons no longer have sufficient energy to produce keV X-ray synchrotron photons.

PWN also occur inside binary systems, where the huge radiation fields and stellar wind/outflow of the companion star dramatically modify the PWN properties. PSR B1259−63 is young and powerful pulsar in an eccentric 3.4 year orbit around a ≈10 solar mass companion. Variable and point-like TeV and GeV emission is seen around the periastron passage of the neutron star when radiation densities are highest but the time-profile of the emission and the spectral energy distribution are complex and very poorly understood (e.g. [130]). Extended radio emission is seen on milliarcsecond scales supporting the idea that this system is a PWN “compactified” by the high pressure environment and rapid radiative losses. In other well-established TeV binaries systems, LS 5039, LS I +61 303 and HESS J0632+057, the nature of the compact object is not certain and the systems may be accretion-, rather than rotation-powered.

PWN naturally accelerate positrons and electrons in equal number. An increase in the proportion of cosmic ray electrons and positrons contributed by PWN (and/or the presence of a small number of dominant local/recent accelerators) may explain the increase in the fraction of positrons seen in the locally measured cosmic rays at high energies, as discussed in Sect. 13.2.4. Given a suitable pulsar age T, energy-dependent diffusion D(E) of electrons causes the detected spectrum to harden compared to the source spectrum—high energy particles reach Earth faster—and radiative energy losses during propagation over a time T cause the spectrum to cut off at a certain energy. The two effects combine to produce an excess in an E ³ weighted spectrum, the peak position and peak level being adjustable via pulsar age, distance, and energy output, and matching the detected excess contribution for plausible parameters. For example, positrons released T ≈ 10⁵ years ago exhibit a cutoff at E _cut,TeV ≈ 3 × 10⁵∕T _year ≈ 3 TeV and at TeV energies travel over a distance d ≈ (2DT)^1∕2 ≈ 500 pc (for \(D \approx 10^{28}E^{0.5}_{{\mathrm{GeV}}}\) cm²/s, see Sect. 13.2.2). Assuming that about 10% of the rotational kinetic energy of ≈ 10⁵⁰ erg of a 10 ms pulsar is released in electrons and positrons, the resulting average electron energy density in the 500 pc volume is of order 10⁻³ eV/cm³, comparable to the density of secondary electrons from nuclear interactions of cosmic rays. In an energy range where such a source dominates the flux of electrons and positrons, the positron fraction is 1/2. While many details of this scheme remain to be clarified, such an explanation of the effect in terms of conventional astrophysics would need to be ruled out first, before more exotic schemes such as Dark Matter annihilation are invoked. Local PWN, for which the signature of electron escape and subsequent propagation to the Earth may be apparent in the cosmic ray electron spectrum at very high energies, include Vela-X [131] and Geminga. A recent measurement of the cosmic-ray diffusion around from Geminga [62], however, revealed unusually small diffusion coefficients, which make it difficult for those electrons to reach Earth during the relevant time scale.

In addition to the unpulsed emission from nebulae, pulsed GeV emission from many pulsars is observed, with cutoffs at a few GeV e.g. [88], as expected since higher-energy gamma rays have difficulty escaping from the pulsar magnetosphere with its huge magnetic fields. In this context the recent detection of pulsed emission up to energies of a few 100 GeV, following a steep power law rather than the expected super-exponential cutoff [132, 133] was very surprising. Cascade processes may be responsible for transporting the pulsed signal away from the pulsar, reducing the suppression at higher energies.

13.4.4 Other Galactic Systems as Sources of High-Energy Radiation

Several additional classes of cosmic particle accelerators have recently been identified in our galaxy. These objects are generally stellar binary systems of various types, or related to the collective effects of clusters of stars. Stellar binaries containing a normal star and a black-hole are known to (episodically) host accretion-powered jets which can be relativistic. These systems are the Galactic analogs of the active galactic nuclei described in Sect. 13.4.5, and have been dubbed “micro-quasars”. Cygnus X-3 appears to be black hole with a massive stellar companion, and periodic emission has been detected using Fermi. The emission is correlated with the appearance of radio features and seems to be associated with the formation of a jet in the system. The only TeV detection of emission from a well-established black-hole binary is that of a single flare from Cygnus X-1 with the MAGIC telescope [134]. Whilst intriguing, further TeV detections will be required to confirm Cygnus X-1 as a TeV source.

The well-studied stellar binary Eta Carina contains two very massive (M > 30M _⊙) stars which both produce powerful (radiatively driven) winds. The collision of these stellar winds results in strong shocks and a situation akin to a supernova explosion, except in a much denser (in terms of both matter and radiation) and higher magnetic field environment (e.g. [135]). Gamma-ray emission is seen from this system up to ∼100 GeV [136], with two distinct components, and variability observed in the higher energy component which emerges above 20 GeV [137]. Whilst many questions remain, it now seems clear that Eta Carinae is a cosmic particle accelerator and a hadronic origin of one of the components seems plausible.

Evidence for acceleration associated with the collective effects of stellar winds is provided by the detection of very extended emission from the massive stellar cluster Westerlund 1 [138]. Degree scale emission is seen stretching well beyond the stellar cluster, which is one of the most massive in the Galaxy. However, a supernova remnant, unseen at other wavelengths due to the unusual environment, is not excluded as the origin of the TeV emission. Systems such as Westerlund 1 can be seen as the Galactic analogues of the starburst galaxies described in Sect. 13.4.1.

A single Nova (powered by a thermonuclear explosion on the surface of a degenerate white dwarf star) has been detected in high energy gamma-rays [139]. In an ∼10 day flare from the white dwarf V407 Cyg in 2010 emission was seen up to ∼5 GeV.

13.4.5 Particle Acceleration Driven by Supermassive Black Holes

The accretion of material onto supermassive (M ∼ 10⁴ M _sol − 10¹⁰ M _sol) black holes leads to the formation of oppositely-directed and highly-collimated jets of material. The mechanism for launching of these jets is still hotly debated, but magnetic fields in the accretion disc around the black hole look to be playing a crucial role [140, 141]. Radio emission associated with these jets has been know about for a long time, and is most dramatic in the case of Radio Galaxies where the jets are seen at a large angle to the observer and their true scale of (often) 100s of kiloparsecs can be seen, often dwarfing the host galaxy. Particle acceleration is clearly taking place in these objects, at several different locations, for example inside the inner (relativistic) jets, at the termination shocks of powerful jets and at the edges of the so-called radio “lobes” which result when jets are decelerated and spread out. Inverse Compton X-ray emission has been detected from several such systems, tracing the same population of electrons as seen in radio and allowing magnetic field strength and total energy densities to be estimated. X-ray Synchrotron emission, indicating the presence of very high energy electrons, is also seen in several places within systems powered by an active galactic nucleus (AGN). Despite the well established relativistic particle populations in these objects the nature of the acceleration mechanism is still not known. Diffusive shock acceleration does not seem to be the whole story in these objects, with a more distributed acceleration mechanism apparently needed to explain the X-ray synchrotron emission from the inner jets of nearby AGN [142].

Active galaxies are prime candidates for the acceleration of UHECRs, as can be seen from Fig. 13.8, with both the nucleus and the extended jets as possible acceleration sites for 10²⁰ eV particles. As discussed in Sect. 13.2.5 there are hints of UHECR anisotropy correlated with the distribution of matter in the nearby universe (within the GZK horizon) and in particular an excess in the direction of the very nearby active galaxy Cen A (and also the direction of the more distant Centaurus cluster of galaxies). Gamma-ray emission his been detected from Cen A on a wide range of spatial scales. Figure 13.17 shows emission from the giant (10^∘) lobes of Cen A in radio synchrotron emission and (very likely) inverse Compton gamma-ray emission in the Fermi band [143]. Non-thermal emission is also seen in Cen A from the nucleus, inner jets and inner lobes. The synchrotron X-ray emission seen from the termination shock of the inner lobe closely resembles the situation for supernova remnants, but on a very much larger scale [144]. TeV emission is seen from the inner parts of Cen A (see the right-hand panel of Fig. 13.17) with a position consistent with the inner parts of the jet or the nucleus itself [145]. The giant lobes, jets and nucleus are all candidate acceleration sites for UHECR [146,147,148].

The bulk of the ∼60 know extragalactic TeV gamma ray sources is of blazer type, as is the bulk of the extragalactic GeV sources. In blazers, jets are oriented close (within ∼10^∘) to the line-of-sight to the observer, presenting a dramatically different perspective compared to radio galaxies. Apparently super-luminal motions observed in very-long-baseline-interferometer (VLBI) images of the central regions of these objects indicate bulk relativistic motion. Particle acceleration is presumably powered by this bulk motion, related to inhomogenities and shocks arising in the flow. Blazers are characterised by rapidly variable emission and complete non-thermal dominance of their spectral energy distributions, with the peak energy output usually in the gamma-ray domain. Markarian 421 was the first extragalactic object to be discovered in TeV gamma-rays [150] and is a dramatic example of a high-energy-peaked blazar. The measured energy spectra of these objects are significantly influenced by gamma-ray absorption by pair production with infrared or optical extragalactic background light (EBL) (e.g. [151]); vice versa, with assumptions regarding the intrinsic blazar spectra the absorption features can be used to constrain the level of EBL (e.g. [152]), which traces the history of star formation in the Universe and which, in certain spectral ranges, is difficult to measure directly due to overwhelming foregrounds [153]. TeV Blazars exhibit extreme variability, down to minute time scale [154]. This extreme variability places tight constraints on the size r of the emission region, from causality arguments: r < δct _var, where δ is a Doppler boost factor reflecting the bulk motion of the particle acceleration region in the blazer jet. Blazars usually exhibit double-humped spectral energy distributions (Fig. 13.18), most likely reflecting a synchrotron component at radio and X-ray energies, and an IC component at GeV/TeV energies, hinting at electrons as the parent particles. Often, the synchrotron X-ray intensity is such that X-rays form the dominant target for IC scattering. The parameters of the system—the electron spectrum, size, boost factor and magnetic field—can be determined from the location of the peaks in the radiation spectra, the exact spectral shape, the variability timescale and the additional condition that the photon density in the source region must be low enough to allow gamma rays to escape without pair-producing. Combined with short variability timescales this approach usually enforces large Doppler factors well beyond δ = 10; how such bulk motions are achieved is not fully understood. While blazers obviously act as cosmic particle accelerators, it is unclear if they accelerate significant amounts of protons in addition to the electrons evident from their spectra, and most likely they have little impact on the cosmic rays detected on Earth.

13.5 Outlook

Significant progress has been achieved in the study of cosmic particle accelerators, in particular through the improved detection and imaging of high energy (GeV) and very high energy (TeV) gamma rays emitted in interactions of accelerated charged particles; also the first detection of very high energy cosmic neutrinos was reported. Particle acceleration is a ubiquitous feature in the Universe, associated especially with the evolution of massive stars and with black holes. Over 3000 multi-GeV accelerators are detected, and over 200 multi-TeV accelerators, with maximum energies well beyond 100 TeV. A variety of acceleration mechanisms seems to be realised in nature, including acceleration in non-relativistic SNR shocks and colliding-wind shocks, in relativistic pulsar wind shocks, in the unipolar inductors of pulsars, and in the compact and extended jets of AGN. In many systems, the acceleration process is highly efficient in converting bulk kinetic energy. The observed rapid variability in systems such as AGN or in the Crab Nebula represent a challenge to models and may require additional acceleration schemes. Despite this significant progress, a quantitative confirmation that SNR represent the sources of the bulk of nucleonic cosmic rays in our own galaxy and a first-principle calculation of their yield and spectrum is still lacking; other open questions concern the details of diffusive propagation of cosmic rays and of the resulting cosmic-ray anisotropies, the origin of the high-energy cosmic-ray positrons, and the origin of the highest-energy cosmic rays. A variety of new instruments aim to address these issues, including next-generation air-Cherenkov instruments such as CTA [155], ground-based cosmic-ray detectors like LHAASO [20], ultra-high-energy cosmic ray detectors such as JEM-EUSO [156] and a larger version of the Pierre Auger detector, or the very-high-energy neutrino detectors KM3Net [98] and the planned IceCube Gen2 instrument [157].

Notes

1.
1 kpc = 1000 pc ≈ 3300 light years; the distance from the Sun to the centre of the Galaxy is about 8 kpc.
2.
AU = Astronomical Unit, the mean Sun-Earth distance of ≈ 1.5 × 10¹¹ m.

References

V.F. Hess: Phys. Z. 21 (1912) 1084.
Google Scholar
A.W. Strong, I.V. Moskalenko, V.S. Ptuskin: Annu. Rev. Nucl. Part. Sci. 57 (2007) 285.
ADS Google Scholar
A.M. Hillas: J. Phys. G 31 (2005) 95.
ADS Google Scholar
S.P. Reynolds: Annu. Rev. Astron. Astrophys. 46 (2008) 89.
ADS Google Scholar
J. Blümer, R. Engel, J.R. Hörandel: Prog. Part. Nucl. Phys. 63 (2009) 293.
ADS Google Scholar
K. Kotera, A.V. Olinto: Annu. Rev. Astron. Astrophys. 49 (2011) 119.
ADS Google Scholar
A.M. Hillas: Annu. Rev. Astron. Astrophys. 22 (1984) 425.
ADS Google Scholar
J.A. Hinton, W. Hofmann: Annu. Rev. Astron. Astrophys. 47 (2009) 523.
ADS Google Scholar
F.A. Aharonian, et al.: Rep. Prog. Phys. 71 (2008) 096901.
ADS Google Scholar
P. Picozza, et al.: Astropart. Phys. 27 (2007) 296.
ADS Google Scholar
M. Aguilar, et al. (AMS Coll.): Phys. Rep. 366 (2002) 331.
Google Scholar
S. Wissel, et al.: arXiv:1107.3272 (2011).
Google Scholar
O. Adriani et al.: Phys. Rev. Lett. 119 (2017) 181101.
ADS Google Scholar
G. Ambrosi et al.: Nature 552 (2017) 63.
ADS Google Scholar
I. Allekotte, et al. (Pierre Auger Coll.): Nucl. Instrum. Meth. A 586 (2008) 409.
Google Scholar
J. Abraham, et al. (Pierre Auger Coll.): Nucl. Instrum. Meth. A 620 (2010) 227.
Google Scholar
U. Abbasi et al.: Astropart. Phys. 80 (2016) 131.
ADS Google Scholar
K.H. Kampert, et al.: Nucl. Phys. B Proc. Suppl. 136 (2004) 273.
ADS Google Scholar
M. Amenomori, et al.: Astrophys. J. 678 (2008) 1165.
ADS Google Scholar
G. Di Sciascio: Nucl. Part. Phys. Proc. 279–281 (2016) 166.
Google Scholar
O. Adriani, et al.: Science 332 (2011) 69.
ADS Google Scholar
M. Aguilar et al.: Phys. Rev. Lett. 114 (2015) 171103.
ADS Google Scholar
M. Aguilar et al.: Phys. Rev. Lett. 115 (2015) 211101.
ADS Google Scholar
D. Allard, E. Parizot, A. V. Olinto: Astropart. Phys. 27 (2007) 61.
ADS Google Scholar
K. Greisen: Phys. Rev. Lett. 16 (1066) 747.
Google Scholar
G.T. Zatsepin, V.A. Kuz’min: JETP Lett. 4 (1966) 78.
ADS Google Scholar
V. Berezinsky, A.Z. Gazizov, S.I. Grigorieva: Phys. Rev. D 74 (2006) 043005.
ADS Google Scholar
J. Abraham et al.: Phys. Lett. B685 (2010) 239.
ADS Google Scholar
A. Aab et al.: arXiv:1708.06592 and Proceedings, 35th International Cosmic Ray Conference (ICRC 2017): Bexco, Busan, Korea, July 12–20, 2017.
ADS Google Scholar
A. Aab et al.: JCAP 1704 (2017) 038.
ADS Google Scholar
K.H. Kampert, M. Unger: Astropart.Phys. 35 (2012) 660.
ADS Google Scholar
J.A. Simpson: Annu. Rev. Nucl. Part. Sci. 33 (1983) 323.
ADS Google Scholar
M. Simon, A. Molnar, S. Roesler: Astrophys. J. 499 (1998) 250.
ADS Google Scholar
V.L. Ginzburg, V.S. Ptuskin: Rev. Mod. Phys. 48 (1976) 161, (Erratum) Rev. Mod. Phys. 48 (1976) 675.
Google Scholar
R. Jansson, G.R. Farrar: Astrophys. J. 761 (2012) L11.
ADS Google Scholar
L.O’C. Drury, D.C. Ellisson, J.-P. Meyer: Nucl. Phys. A 663 (2000) 843–843.
Google Scholar
B.D. Fields, et al.: Astron. Astrophys. 370 (2001) 623.
ADS Google Scholar
A.W. Strong, et al.: Astrophys. J. Lett. 722 (2010) L58.
ADS Google Scholar
A. Aab et al.: Phys. Rev. Lett. 117 (2016) 192001
ADS Google Scholar
J. Abraham, et al.: Phys. Rev. Lett. 104 (2010) 091101.
ADS Google Scholar
A.Aab et al: Phys. Rev. D90 (2014) 122006.
ADS Google Scholar
R.U. Abbasi, et al.: Astropart. Phys. 64 (2015) 49.
ADS Google Scholar
J.R. Hörandel: Adv. Space Res. 41 (2008) 442.
ADS Google Scholar
M. Amenomori, et al.: Astrophys. J. 626 (2005) L29.
ADS Google Scholar
A.H. Compton, I.A. Getting: Phys. Rev. 47 (1935) 817.
ADS Google Scholar
P. Blasi, E. Amato: arXiv:1105.4529 (2011).
Google Scholar
M. Amenomori, et al.: Science 314 (2006) 439.
ADS Google Scholar
A.A. Abdo, et al.: Phys. Rev. Lett. 101 (2008) 221101.
ADS Google Scholar
R.U. Abbasi, et al.: Astrophys. J. 740 (2011) 16.
ADS Google Scholar
L.O’C. Drury, F.A. Aharonian: Astropart. Phys. 29 (2008) 420.
Google Scholar
G. Ciacinti, G. Sigl: arXiv:1111.2536 (2011).
Google Scholar
O. Adriani, et al.: Phys. Rev. Lett. 102 (2009) 051101.
ADS Google Scholar
M. Aguilar et al.: Phys. Rev. Lett. 113 (2014) 121102.
ADS Google Scholar
S. Abdollahi et al.: Phys. Rev. D95 (2017) 082007.
ADS Google Scholar
D. Kerszberg: 5th International Cosmic Ray Conference (ICRC 2017): Bexco, Busan, Korea, July 12–20, 2017.
Google Scholar
L. Accardo et al.: Phys. Rev. Lett. 113 (2014) 121101.
ADS Google Scholar
M. Pohl, et al.: Astron. Astrophys. 409 (2003) 581.
ADS Google Scholar
O. Adriani, et al.: Nature 458 (2009) 607.
ADS Google Scholar
M. Ackermann, et al.: arXiv:1109.0521.
Google Scholar
D. Grasso, et al.: Astroparticle Phys. 32 (2009) 140.
ADS Google Scholar
F.A. Aharonian, A. Atoyan, H.J. Völk: Astron. Astrophys. 294 (1995) L41.
ADS Google Scholar
A.U. Abeysekara et al.: Science 358 (2017) 911.
ADS Google Scholar
A. Aab et al.: Astrophys. J. 794 (2014) 172.
ADS Google Scholar
F. Zwicky: Phys. Rev. 55 (1939) 986.
ADS Google Scholar
R.D. Blandford, J.P. Ostriker: Astrophys. J. Lett. 221 (1978) L29; Astrophys. J. 237 (1980) 793.
Google Scholar
A.R. Bell: Mon. Not. R. Astron. Soc. 182 (178) 147; Mon. Not. R. Astron. Soc. 182 (1978) 443.
Google Scholar
J.K. Truelove, C.F. McKee: Astrophys. J. Suppl. 120 (1999) 299.
ADS Google Scholar
L.O’C. Drury, H.J. Völk: Astrophys. J. 248 (1981) 344.
Google Scholar
D.C. Ellison, A. Decourchelle, J. Ballet: Astron. Astrophys. 413 (2004) 189.
ADS Google Scholar
J. Vink: arXiv:1112.0576 (2011).
Google Scholar
V.S. Ptuskin, V.N. Zirakashvili: Astron. Astrophys. 429 (2005) 755.
ADS Google Scholar
M.A. Malkov et al.: Astrophys. J. 768 (2013) 73.
ADS Google Scholar
P. Blasi, E. Amato: arXiv:1105.4521 (2011).
Google Scholar
G. Pelletier, M. Lemoine, A. Marcowith: arXiv:0811.1506 (2008).
Google Scholar
A.K. Harding, arXiv:0710.3517 (2007).
Google Scholar
J. Arons: arXiv:0708.1050 (2007).
Google Scholar
Y. Lyubarsky, J.G. Kirk: Astrophys. J. 547 (2001) 437.
ADS Google Scholar
C.F. Kennel, F.V. Coroniti: Astrophys. J. 283 (1984) 694.
ADS Google Scholar
C.F. Kennel, F.V. Coroniti: Astrophys. J. 283 (1984) 710.
ADS Google Scholar
C.-Y. Ng, R.W. Romani: Astrophys. J. 601 (2004) 479; Astrophys. J. 673 (2008) 411.
Google Scholar
M.J. Rees, J.E. Gunn: Mon. Not. R. Astron. Soc. 167 (1974)1.
ADS Google Scholar
M. Nagano, A.A. Watson: Rev. Mod. Phys. 72 (2000) 689.
ADS Google Scholar
S.R. Kelner, F.A. Aharonian: Phys. Rev. D 78 (2008) 034013.
ADS Google Scholar
G.R. Blumenthal, R.J. Gould: Rev. Mod. Phys. 42 (1970) 237.
ADS Google Scholar
M.S. Longair: High Energy Astrophysics, Cambridge University Press.
Google Scholar
N.S. Kardashev: Sov. Astron. 6 (1962) 317.
ADS Google Scholar
A.M. Atoyan, F.A. Aharonian: Mon. Not. R. Astron. Soc. 287 (1996) 525.
ADS Google Scholar
A.A. Abdo, et al.: Astrophys. J. 708 (2010) 1254.
ADS Google Scholar
R. Bühler, et al.: arXiv:1112.1979 (2011).
Google Scholar
W.B. Atwood, et al.: Astrophys. J. 697 (2009) 1071.
ADS Google Scholar
W. Hofmann: arXiv:astro-ph/0603076 (2006).
Google Scholar
U. Abeysekara et al.: Astrophys. J. 843 (2017) 40.
ADS Google Scholar
F. Acero et al.: Astrophys. J. Suppl. 218 (2015) 23.
ADS Google Scholar
TeVCat, http://tevcat.uchicago.edu/
M.G. Aartsen et al.: Phys. Rev. Lett. 115 (2015) 081102
ADS Google Scholar
M.G. Aartsen et al., arXiv:1710.01191.
Google Scholar
M.G. Aartsen et al.: Astrophys. J. 835 (2017) 151
ADS Google Scholar
P. Bagley, et al.: KM3NeT Technical Design Report (ISBN 978-90-6488-033-9).
Google Scholar
M. Ackermann et al.: arXiv:1710.01207 and Proceedings, 35th International Cosmic Ray Conference (ICRC 2017): Bexco, Busan, Korea, July 12–20, 2017
ADS Google Scholar
https://fermi.gsfc.nasa.gov/ssc/observations/types/allsky/
M. Ackermann, et al.: Astrophys. J. 726 (2011) 81.
ADS MathSciNet Google Scholar
A.A. Abdo, et al.: Astrophys. J. 688 (2008) 1078.
ADS Google Scholar
A. Abramowski et al.: Nature 531 (2016) 476.
ADS Google Scholar
A.A. Abdo, et al.: Astrophys. J. Lett. 709 (2010) L152.
ADS Google Scholar
F. Acero, et al.: Science 326 (2009) 1080.
ADS Google Scholar
V.A. Acciari, et al.: Nature 462 (2009) 7274.
Google Scholar
G. Dobler, et al.: Astrophys. J. 717 (2010) 825.
ADS Google Scholar
M. Su, T.R. Slatyer, D.P. Finkbeiner: Astrophys. J. 724 (2010) 1044.
ADS Google Scholar
M. Ackermann et al.: Astrophys.J. 793 (2014) 64
ADS Google Scholar
R.M. Crocker, F.A. Aharonian: Phys. Rev. Lett. 106 (2011) 101102.
ADS Google Scholar
P. Mertsch, S. Sarkar: Phys. Rev. Lett. 107 (2011) 091101.
ADS Google Scholar
E.A. Helder, et al.: Science 325 (2009) 719.
ADS Google Scholar
S.G. Lucek, A.R. Bell: Mon. Not. R. Astron. Soc. 314 (2000) 65.
ADS Google Scholar
L.O’C. Drury, F.A. Aharonian, H.J. Völk: Astron. Astrophys. 287 (1994) 959.
Google Scholar
H.J. Völk, E.G. Berezhko, L.T. Ksenofontov: Astron. Astrophys. 483 (2008) 529.
ADS Google Scholar
S. Archambault et al.: Astrophys. J. 836 (2017) 23.
ADS Google Scholar
H. Abdalla et al.: Astron. Astrophys. 612 (2018)
Google Scholar
A.A. Abdo, et al.: Astrophys. J. 706 (2009) L1.
ADS Google Scholar
J. Aleksić, et al.: Astron. Astrophys. 541 (2012) 11.
Google Scholar
M. Ackermann et al.: Science 339 (2013) 807.
ADS Google Scholar
Y. Uchiyama, et al.: Astrophys. J. Lett. 723 (2010) L122.
ADS Google Scholar
T.C. Weekes, et al.: Astrophys. J. 342 (1989) 379.
ADS Google Scholar
A.A. Abdo, et al.: Science 331 (2011) 739.
ADS Google Scholar
M. Tavani, et al.: Science 331 (2011) 736.
ADS Google Scholar
P.M. Gaensler, P.O. Slane: Annu. Rev. Astron. Astrophys. 44 (2006) 17.
ADS Google Scholar
F. Mattana, et al.: Astrophys. J. 694 (2009) 12.
ADS Google Scholar
O. Kargaltsev, G. Pavlov: arXiv:1002.0885 (2010).
Google Scholar
J.M. Blondin, R.A. Chevalier, D.M. Frierson: Astrophys. J. 563 (2001) 806.
ADS Google Scholar
F.A. Aharonian, et al.: Astron. Astrophys. 460 (2006) 365.
ADS Google Scholar
S.W. Kong, et al.: Mon. Not. R. Astron. Soc. 416 (2011) 1067.
ADS Google Scholar
J.A. Hinton, et al.: Astrophys. J. Lett. 743 (2011) L7.
ADS Google Scholar
E. Aliu, et al.: Science 334 (2011) 69.
ADS Google Scholar
J. Aleksić, et al.: arXiv:1109.6124 (2011).
Google Scholar
J. Albert, et al.: Astrophys. J. 665 (2007) L51.
ADS Google Scholar
E.R. Parkin, et al.: Astrophys. J. 726 (2011) 105.
ADS Google Scholar
A.A. Abdo, et al.: Astrophys. J. 723 (2010) 649.
ADS Google Scholar
C. Farnier, R. Walter: Mem. Soc. Astron. Italiana 82 (2011) 796.
ADS Google Scholar
A. Abramowski, et al.: arXiv:1111.2043 (2011).
Google Scholar
A.A. Abdo, et al.: Science 329 (2010) 817.
ADS Google Scholar
R.D. Blandford, R.L. Znajek: Mon. Not. R. Astron. Soc. 179 (1977) 433.
ADS Google Scholar
R.D. Blandford, D.G. Payne: Mon. Not. R. Astron. Soc. 199 (1982) 883.
ADS Google Scholar
M.J. Hardcastle, et al.: Astrophys. J. 670 (2007) L81.
ADS Google Scholar
A.A. Abdo, et al.: Science 328 (2010) 725.
ADS Google Scholar
J.H. Croston, et al.: Mon. Not. R. Astron. Soc. 395 (2009) 1999.
ADS Google Scholar
F.A. Aharonian, et al.: Astrophys. J. Lett. 695 (2009) L44.
ADS Google Scholar
M.J. Hardcastle, et al.: Mon. Not. R. Astron. Soc. 393 (2009) 1041.
ADS Google Scholar
M. Honda, Astrophys. J. 706 (2009) 1517.
ADS Google Scholar
F.M. Rieger, F.A. Aharonian: Astron. Astrophys. 506 (2009) L41.
ADS Google Scholar
A.A. Abdo, et al.: Astrophys. J. 736 (2011) 131.
ADS Google Scholar
M. Punch, et al.: Nature 358 (1992) 477.
ADS Google Scholar
A. Franceschini, G. Rodighiero, M. Vaccari: Astron. Astrophys. 487 (2008) 837.
ADS Google Scholar
D. Mazin, M. Raue: Astron. Astrophys. 471 (2007) 439.
ADS Google Scholar
M.G. Hauser, E. Dwek: Annu. Rev. Astron. Astrophys. 39 (2001) 249.
ADS Google Scholar
F.A. Aharonian, et al.: Astrophys. J. 664 (2007) L71.
ADS Google Scholar
M. Actis, et al.: Exp. Astron. 32 (2011) 193.
ADS Google Scholar
T. Ebisuzaki, et al.: AIP Conf. Proc. 1367 (2011) 120–125.
Google Scholar
M. Ackermann, et al.: Intern. Cosmic Ray Conf. 2017, arXiv:1710.01207
Google Scholar

Download references

Author information

Authors and Affiliations

Max-Planck-Institut für Kernphysik, Heidelberg, Germany
W. Hofmann & J. A. Hinton

Authors

W. Hofmann
View author publications
You can also search for this author in PubMed Google Scholar
J. A. Hinton
View author publications
You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to W. Hofmann or J. A. Hinton .

Editor information

Editors and Affiliations

ADAM SA, Geneva, Switzerland
Stephen Myers
CERN, Geneva, Switzerland
Herwig Schopper

Rights and permissions

Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.

The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.

Reprints and permissions

Copyright information

About this chapter

Cite this chapter

Hofmann, W., Hinton, J.A. (2020). Cosmic Particle Accelerators. In: Myers, S., Schopper, H. (eds) Particle Physics Reference Library . Springer, Cham. https://doi.org/10.1007/978-3-030-34245-6_13

Download citation

DOI: https://doi.org/10.1007/978-3-030-34245-6_13
Published: 28 May 2020
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-34244-9
Online ISBN: 978-3-030-34245-6
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)

Publish with us

Policies and ethics

Cosmic Particle Accelerators

Abstract