14.1 A Forwards Run of Fifty Years

In 1905 two Dutch mathematics teachers, F. J. Vaes and C. A. Cikot, argued strongly in favour of the introduction of differential and integral calculus in the curriculum of Dutch secondary schools. The principal argument for introducing calculus was that in the subjects physics and mechanics calculus was applied in a disguised way in only one context, which limited understanding of the underlying process. The idea of introducing calculus at secondary school was discussed seriously, but in the end rejected by the association of secondary school teachers. Nevertheless, there were some teachers in that period who were experimenting with teaching calculus, and at least two calculus textbooks were issued.

The textbook by Van de Vooren (1919) was titled Grenswaarden. Eene inleiding tot de differentiaal-en integraalrekening, or in English: Limits. An introduction to the differential and integral calculus. According to me, this book is one of the best Dutch calculus textbooks for secondary education ever written. It starts with an introductory chapter on constant and variable quantities. This was in fact a short and informal way to teach the concept of function with real-world examples like the weight of a person dependent on his age, or the length of an iron bar as a function of its temperature. These examples were combined with graphical representations. This kind of introduction was very modern at that time, but nevertheless the implementation of so-called ‘functional thinking’ in mathematics would take almost the whole twentieth century.

In Van de Vooren’s book, after the introduction, a paragraph about limits of infinite sequences followed. As an example of a geometric limit the author considers the slope of the tangent in the point P(1, 1) of the parabola with equation y = x2 as a limit of chords. He uses the sequence \( 1,\,\frac{1}{2},\frac{1}{4},\frac{1}{8},\frac{1}{16}, \ldots \) of changes in the x-coordinate of a variable point Q on the parabola tending to P. The slope of the chord PQ in the general case that Q has an x-coordinate \( 1 + \left( {\frac{ 1}{ 2}} \right)^{n} \) is equal to \( 2 + \left( {\frac{ 1}{ 2}} \right)^{n} \), and this tends to 2 for \( n \to \infty \), which may be called the local slope of the curve in P. This is an example of ‘the road from discrete to continuous’ which in my eyes could be—or should be—an important principle in the teaching of elementary calculus.

Another remarkable point in Van de Vooren’s book is the inclusion of many practical applications, like Newton’s law of cooling, atmospheric pressure related to altitude, the working of a windlass, the refraction law of Snell, current intensity related to resistance, the harmonic movement. In short, one may conclude that this book was a real treasure for a good teacher. But how many teachers would have used this book or similar teaching resources for calculus? I am quite sure that there was only a very small minority of teachers who would spend a number of lessons on tackling these first principles of calculus.

Anyway, pioneers like Vaes, Cikot and Van de Vooren initiated and promoted thinking about curriculum reform, and, as a result of this, in 1926 a report about a new curriculum was published in Euclides, the Dutch magazine for mathematics teachers. The committee responsible for this report consisted of four people of which the president and secretary, H. J. E. Beth and E. J. Dijksterhuis, were highly qualified teachers in mathematics. Both had published a number of scientific books. Beth wrote a history-based book about non-Euclidean geometry. Dijksterhuis wrote a book about the mechanisation of the world view, which is his most famous book and for which he received the prestigious P. C. Hooft Award. A typical quote from the Beth-Dijksterhuis report is:

… the aim of placing mathematics education in the service of functional thinking with the aid of graphic representation to display a realistic view of how a quantity changes in relation to a variable quantity, leads inevitably to the teaching of the basic elements of calculus. (Beth, Van Andel, Cramer, & Dijksterhuis, 1925, p. 125) (translated from Dutch by the author)

The report proposed explicitly to include elements of differential and integral calculus (with applications in kinematics and in solid geometry) in the new curriculum. This proposal led to a great deal of discussion between supporters and opponents. Some professors at the Technical University in Delft were not in favour of including calculus in the mathematics curriculum in secondary school. One argument was the impossibility of teaching the limit concept in a concise way, and consequently future students in exact sciences would be spoiled in secondary school.

Finally, in 1937 the existing curriculum was adapted and then confirmed by the Ministry of Education. Calculus appeared in the formal curriculum, but the topic was not supposed to be a part of the Centraal Schriftelijk Eindexamen (CSE), which is the national written final examination at the end of secondary school. In the Netherlands, this examination has a strong influence on educational practice. Therefore, calculus became an optional subject, which meant that only a few mathematics teachers made time for calculus in their lessons. This situation would continue until 1958!

14.2 After 50 Years of Discussion, Calculus Entered the National Written Final Examination

In November 1948, a historical event took place: the first two-day conference about the didactics of mathematics was organised. One of the initiators was Hans Freudenthal who was also the chairman of the conference. At this conference Van Hiele gave a lecture, titled “An Attempt to Frame Guidelines for Didactics of Mathematics”, in which he quoted a known author of textbooks for physics who had asserted that in Grade 10 the concept of limit, the derivative and the definite integral should be taught for the convenience of the physics teacher. Van Hiele agreed with this assertion and underlined that kinematics, which is taught in physics, is the most adequate entrance to differential calculus.

In January 1954, a committee was appointed to report on the subject of mathematics as a whole and the examination programme, and in February 1955, the committee’s report was published. In the introduction section of the report it was stated that in science education the mathematics component had arrived at an impasse, particularly concerning differential and integral calculus. They posited that it should be possible to teach calculus in a didactically sound way, with no less rigour than for other subjects and yet according to the capacity of the students. To prevent an unwanted development in the future, the committee proposed to stop the calculus curriculum just before the introduction of the number e and the differentiation of exponential and logarithmic functions. The calculus part of the report was received positively.

The first new national written final examinations in 1961 and 1962 included only one calculus problem. In 1963, two calculus problems were part of the examination; including one very nice one (see Fig. 14.1).

Fig. 14.1
figure 1

An example of a calculus problem in the national written final examination of 1963 (translated from Dutch by the author)

Full size image

At the same time, early in the 1960s, a new and international movement arose: New Math. In June 1961, the Commissie Modernisering Leerplan Wiskunde (CMLW)Footnote 1 was appointed by the Dutch State Secretary of Education. The committee consisted of 18 members—four secondary teachers, twelve university professors, and two school inspectors—, and had a threefold task: (1) to give advice about new subjects in the curriculum which could be first piloted in schools; (2) to produce ideas for in-service courses for senior teachers to update their mathematical knowledge; (3) to investigate whether a special program could be made for mathematically gifted students.

14.3 The Influence of New Math

The first activity of the CMLW was to organise courses for teachers about ‘modern mathematics’ giving a mathematical background to intended new subjects in the mathematics curriculum for schools. Most of the topics of these courses were influenced by the international New Math movement. The first concern of the CMLW was to raise mathematical competence in line with the demands created by New Math. In the second phase, didactical meetings were organised about how to teach New Math at school. In Euclides and during meetings with mathematics teachers, there was much discussion about the pros and cons of New Math. Not everyone was convinced about its blessings. For example, the logician and university professor E. W. BethFootnote 2 was very sceptical about teaching topics like set theory to 12-year-old students. Freudenthal was also sceptical about the New Math movement, but the majority of the CMLW members kept up with the spirit of the times.

From 1965 on four experiments with New Math were started in a small number of secondary schools. New subjects like parametrised curves (in New Math terms: images of functions from IR to IR2) and differential equations were proposed. Much attention was given to limit and continuity. In traditional textbooks, the continuity of a function f in a was defined from the concept of limit, but now the main idea was to start with continuous function (for example defined in a topological style with open environments) and then introduce the limit, say of

$$ \Delta_{a} (x) = \frac{f(x) - f(a)}{x - a}\,\,\,{\text{for}}\,\,\,x \to a $$

as the value that makes the function Δa continuous in a.

A textbook that appeared in the years after the introduction of a new curriculum for calculus in 1968, started with the limit concept for infinite sequences which led to the definition: If for every sequence (x0, x1, x2,…)Footnote 3 in a reduced open interval around a with \( \mathop {\lim }\limits_{n \to \infty } x_{n} = a \) we have \( \mathop {\lim }\limits_{n \to \infty } f(x_{n} ) = b \), then we say \( \mathop {\lim }\limits_{x \to a} f(x) = b \). And in this book, this then led to the ‘old-fashioned’ definition of ‘f is continuous in a’.

Fortunately, there were also positive experiences. The most spectacular extension of the calculus program, the teaching of elementary differential equations together with slope fields turned out, beyond all expectations, to be attainable in the classroom.

A didactical point of discussion in those days was the introduction of more-or-less autonomous differentials. The language as introduced by Leibniz was and is still very effective, but did not fit well in the style of New Math. Some purists wanted to skip the use of differentials, but for example Freudenthal posed that teaching calculus without making students familiar with differentials is unacceptable. Another university professor, A. C. M. van Rooij wrote:

The learning of differentials in school is a tricky question. The calculations with them is easy, but to understand what they really are, the student must have a rather high level of abstraction. (Van Rooij, 1982, p. 81) (translated from Dutch by the author)

The dilemma of using differentials in calculus is that it may lead to a mechanistic style of working.

It makes no difference what meaning we attach to the differentials, or where we attach any meaning whatever to them. If we define appropriate rules of operation for them and if we employ these rules properly, it is certain that something reasonable and correct will result. (Klein, 2004, p. 215)

If we say that instead of \( \frac{\text{d}}{{{\text{d}}x}}f(x) = f'(x) \) we may write \( {\text{d}}f(x) = f'(x){\text{d}}x \) and reduce the question of differentials to a grammatical one, a real understanding of differentials is not necessary. For example, to treat (in)definite integrals without the use of differentials is needlessly ineffective.

In the Netherlands, in 1967 the first steps were set towards a reform of mathematics in the higher grades of secondary school. The initial plans included two mathematics strands for Grade 11 and 12 of the pre-university level, which were Mathematics I (calculus and statistics) and Mathematics II (geometry and linear algebra). Mathematics I became compulsory for students who wanted to study exact sciences (including econometrics), agricultural sciences and medical sciences. Mathematics II aimed at students who were interested in a wider scope of mathematics. The calculus part of Mathematics I turned out to be much more extensive than the programme of 1958. Logarithmic, exponential and cyclometric functions were added, as well as parametric curves.

The results in the first new examinations in 1974 were dramatic. The main cause was not the curriculum, but the fact that many more disciplines at university level, like economics, psychology, sociology and even history, required students to follow Mathematics I in secondary school, which was never meant to be a preparation for students in these disciplines. So, in the late 1970s the conclusion was drawn that two new programs were needed for the pre-university level in secondary education: Mathematics A for students who were going to study economic and social sciences and Mathematics B for students who were going to study exact and technical sciences.

14.4 The HEWET Project: A Small Revolution in Pre-University Secondary Education

The Dutch Ministry of Education commissioned the development of two new mathematics programmes for pre-university secondary education and started the HEWET project.Footnote 4 In fact, this development was meant to be only a simple reallocation: statistics and probability (which were in Mathematics I), some parts of linear algebra (which were in Mathematics II) and some parts of differential calculus (which were in Mathematics I) would move to Mathematics A. Analytical geometry (which was in Mathematics II) and the more advanced parts of calculus, including integral calculus and differential equations (which were in Mathematics I), would move to Mathematics B. To work on these ideas the HEWET working group was set up. This group existed of two secondary school inspectors, four university professors (two of them representing the exact and technical sciences, the other two representing economic and social sciences), one didactician and two secondary school teachers. The group was advised by three members of the IOWO (Institute for the Development of Mathematics Education), the predecessor of the Freudenthal Institute, M. Kindt, J. de Lange, and G. A. Vonk, the first two of whom would later be responsible for developing new materials for classroom experiments with the new topics and new didactical approaches. A concept version of the HEWET report appeared in 1979 and after a nationwide consultation of the secondary and higher educational sector the final report appeared in 1980. With respect to calculus, the report proposed for Mathematics A to include applied differential calculus (no integrals), and for Mathematics B it was proposed to include calculus as it was within Mathematics I.

The need for careful experiments was clear, since the proposed programme for Mathematics A was rather revolutionary because of the applied character preparing students for being able to use mathematics in economic and social sciences. In 1981 two pioneer schools started, with an experimental written final examination in 1983. From that year on, ten new schools joined the project, one year later the next forty schools started and in 1985 the remaining (circa 430) schools followed. The first national written final examination was in 1987.

The following elements of calculus were expected to be meaningful, relevant and within reach of Mathematics A students:

  • Trigonometric functions as models for periodic phenomena and trends

  • Exponential and logarithmic functions as models for types of growth

  • The derivative of a function as a rate of change in a variation of contexts.

Generally spoken, the intended approach was contextual and informal.

As an introduction to this program, three units for Grade 10 were designed at the IOWO, meant as a preparation for both Mathematics A and B. The (translated) titles were respectively: “Logarithms and Exponentials”, “Functions of Two Variables” (both designed by J. de Lange) and “Differentiation 1” (designed by M. Kindt). The last unit was an introduction of the concept of the derivative of a function and had as its subtitle “A Way to Track Changes”.

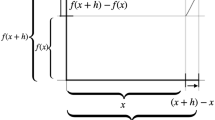
This last unit consisted of eight chapters: A Changes; B Time, distance, speed; C Measuring slopes; D Slope functions; E Free fall; F Differentiation; G Polynomials; H Maximums and minimums. In one of the meetings for teachers, one participant said that you could skip the first five chapters, because in the F chapter the ‘real stuff’ began. For this teacher differentiation was merely a type of algebraic trick. And so it was for many students at that time. The idea behind the unit was just to give a broadly oriented entrance to differential calculus. The unit was translated in German and after some adaption used in a number of schools in Berlin. The students there, like those in the Netherlands, gave the course a very positive evaluation. A student wrote: “We have never had so much fun with mathematics before.”Footnote 5 In the unit (see Kindt, 1982, p. B7), a text about the fastest animal in the world (Fig. 14.2) was used.

Fig. 14.2
figure 2

The fastest animal

Full size image

This text was followed by only one question:

A cheetah is woken up from his afternoon nap by the sound of horse’s hooves. He decides to pursue the horse at the moment that the horse has a lead of 200 meters. Does the cheetah overtake the horse?

In addition, the following hint was given:

You may assume that the cheetah reaches his top speed after 300 m.

This was followed by a figure of empty graph paper, which suggested tackling the problem by drawing a graph. Most of the students tried to draw a time-distance graph for both animals. The cheetah graph had to be inferred from the brief data in the text and by realising that a variable velocity induces a curved graph. There were also students (and teachers) who started with a time-velocity graph.

In an article that Freudenthal (1979) wrote about this problem, he focused on the hint that the cheetah reaches his top speed after 300 m and compared three models for the initial phase of the cheetah’s run (Fig. 14.3).

Fig. 14.3
figure 3

Three graphs of the initial phase of the cheetah’s run

Full size image

Each of the areas of the three squares represent a distance of roughly 520 m. The first diagram shows a velocity which grows slowly to then rise rapidly. The start-up distance may be estimated as 65 m (area below the graph is about \( \frac{1}{8} \) of the square). The second diagram shows a spectacular acceleration in the beginning, but it takes a relatively long time to reach top speed. The corresponding distance is about \( \frac{7}{8} \) of the square, so 455 m. The third model (uniform acceleration) gives a distance of 260 m. The hint of 300 m is not so strange, because the acceleration will not be zero at once in the last second. So, the time-velocity graph will be like the third one, but branch off more smoothly to the highest point. In his article Freudenthal proposed to delete the hint, to make the task even more open.

The examples used in the teaching units developed in the HEWET project (18 in total) inspired the authors of commercial textbooks. So did the cheetah problem. But contrary to the idea of Freudenthal, the authors extended the data and designed many sub-questions or introduced formulas for the time-distance function. One may say that this was a general trend: the textbooks which appeared after the nationwide introduction of Mathematics A were much more structured and less challenging than the units which were successfully used in the experimental phase.

The general conclusion about the content of Mathematics A was positive (De Lange & Kindt, 1984; De Lange, 1987). The strand of applied algebra was judged as the most adequate part, because of the relative simplicity of the mathematical structures and the possibility for the students to model in an autonomous way. Moreover, the main part of this strand had to do with discrete mathematics, which is more concrete—not always easier—than the continuous mathematics. The strand of probability and statistics was undoubtedly very useful in a lot of disciplines and there were more than enough interesting and realistic contexts available to teach. The crown on the course was the strand of testing hypotheses and this strand turned out to be attainable for the majority of the students. The strand of applied calculus was seen as a less successful part. Especially differential calculus with its many rules demanded much more mathematical endurance of the Mathematics A student than the other two strands. Moreover, it seemed to be very difficult to design meaningful contexts for the Mathematics A level in which students could make analytic models by themselves. The common practice in the national written final examination was (and still is) that for the calculus part a mathematical model in the form of an algebraic formula is given, accompanied by a lot of (often simple) questions, but this is done without challenging the students to do a critical investigation of why this formula would be a good idea and without offering students opportunities to construct or adapt a formula.

All in all, one can say that the introduction of Mathematics A thoroughly influenced general ideas about mathematics education. Teachers who thought before that it would not be possible to design written final examinations in more-or-less real-world contexts, were now more-or-less convinced about the feasibility of the RME approach, and in the commercial textbooks for secondary education one tried to implement this approach increasingly.

14.5 Discrete Calculus in Secondary Pre-Higher-Vocational Education

After the introduction of Mathematics A and B in the Dutch mathematics curriculum for secondary pre-university education (VWO), the Ministry of Education decided that there should also be Mathematics A and B in the Grades 10 and 11 of secondary pre-higher-vocational education (HAVO) as well.

Calculus in HAVO Mathematics B would be in the same spirit as calculus in VWO Mathematics A, but in HAVO the applications would be particularly inspired by the exact sciences. For HAVO Mathematics A it was decided not to include differential calculus, but rather to choose for a discrete approach of studying change. The strand was called TGF (tables, graphs and formulas). In this strand, the so-called ‘difference diagram’ was introduced as a tool to study changes. The teaching experiments with this approach showed no conceptual problems with this idea. The difference diagram turned out to be a surprisingly powerful instrument. One particular good exercise was the following matching problem (Fig. 14.4).

Fig. 14.4
figure 4

Difference diagrams for studying change (Roodhardt, 1990, p. 23)

Full size image

In this exercise students have to relate patterns in graphs to patterns of growth (linear, progressive, degressive). Verbal exercises were also used to make this relation. The exercise was preceded by another activity (Fig. 14.5) that was inspired by a newspaper article.

Fig. 14.5
figure 5

Change in crime (Roodhardt, 1990, p. 17)

Full size image

An illustration of a problem in the experimental written final examination of 1989 for Mathematics A was cast in a realistic context and required conceptual reasoning about growth (Fig. 14.6).

Fig. 14.6
figure 6

A problem in the experimental written HAVO examination for Mathematics A (Translation from Dutch by the author)

Full size image

This example appeared in the final examination for the experimenting schools and many students could solve this problem correctly. One student even formulated his answer, using good arguments, in the form of a letter to the farmer! Here, we have to realise that this mathematics programme was not meant for the most gifted students. It appeared to be possible to study the behaviour of functions in connections with local change, with less sophisticated means than differential calculus through a discrete and contextual approach (see also, Doorman, 2005).

14.6 Calculus in Mathematics B for Secondary Pre-university Education

In 1998 upper secondary education was reorganised again. In the last two years of VWO and HAVO the students would now have to choose between four profiles: Culture & Society, Economics & Society, Nature & Health, and Nature & Technology. For the last two profiles the Mathematics B program had to be changed with more emphasis on abstraction, modelling and reasoning. The teaching of calculus was expected to emphasise conceptual understanding with numerical and discrete approaches to differential and integral calculus at the cost of extensive training in procedural fluency (Wiskunde, 1995, p. 70).

In the period 1996–1999, the team of the PROFI project of the Freudenthal Institute designed experimental units for calculus in Mathematics B for secondary pre-higher-vocational education. One of the main ideas learned from the experiences at this school level was to start with the discrete concepts difference (Δ) and sum (Σ) of functions or sequences. In his retrospective publication Historia et Origo Calculi Differentialis, Leibniz looked back to his first work De Arte Combinatoria and said that this was his source of inspiration to invent calculus (Edwards, 1979) (Fig. 14.7).

Fig. 14.7
figure 7

Leibniz’s inspiration

Full size image

One would call this theorem the fundamental theorem of discrete calculus that can also be visualised graphically (Fig. 14.8).

Fig. 14.8
figure 8

The fundamental theorem of discrete calculus

Full size image

In the experimental unit (Kindt, 1997), the operators Δ and Σ on sequences were introduced. And the theorem of Leibniz could then be formulated briefly as

$$ \sum\limits_{k = 0}^{n - 1} {\Delta F(k) = F(n) - F(0)} $$

which is the discrete counterpart of

$$ \int\limits_{0}^{a} {{\text{d}}F(x) = F(a) - F(0)} $$

As it is possible to calculate integrals by using one’s knowledge about the rules for differentiation, so one can find formulas for the partial sums of a sequence by calculating differences. By expanding \( \left( {k + { 1}} \right)^{n} - k^{n} {\text{ for }}n = { 2},{ 3},{ 4} \) one may deduce

$$ \sum\limits_{0}^{n} k \, = \,\frac{1}{2}n(n + 1)\,\,\,\sum\limits_{0}^{n} {k^{2} } \, = \,\frac{1}{3}n(n + \frac{1}{2})(n + 1)\,\,\,\,\sum\limits_{0}^{n} {k^{3} } = \frac{1}{4}n^{2} (n + 1)^{2} $$

and the last two formulas would then be used for a calculation by Riemann sums of the areas under the curves \( y = x^{ 2} {\text{ and }}y = x^{ 3} \).

A special example used in the experiment was the approximation of the area (A) under the graph of \( y = { 2}^{x} \) on the interval 0 ≤ x ≤ 1. The estimation

$$ \frac{1}{10}\sum\limits_{k = 0}^{9} {2^{{\frac{k}{10}}} < A < \frac{1}{10}\sum\limits_{k = 1}^{10} {2^{{\frac{k}{10}}} } } $$

corresponds to a division of the interval in ten equal parts. Using the formula for the partial sum of a geometric sequence, one may write

$$ \frac{1/10}{{2^{1/10} - 1}} < A < \frac{{1/10 \cdot 2^{1/10} }}{{2^{1/10} - 1}} $$

Then by step-by-step refinement—dividing the interval in 100, 1000, etcetera parts—and using a calculator, one gets better and better approximations:

Number of rectangles

Lower estimate

Upper estimate

10

1.393272617

1.493272617

100

1.437700817

1.447700817

1000

1.442195099

1.443195099

10000

1.442645041

1.442745041

100000

1.442690047

1.442700047

1000000

1.442694584

1.442694584

The convergence is visible and this is not an optical illusion. One can simply show that the differences between lower and upper estimate is 0.1, 0.01, 0.001, etcetera! This type of two-sided approximation is probably the best introduction to the mathematical concept of limit. In fact, this is in line with the development of calculus in history which starts with the exhaustion methods of Eudoxus and Archimedes (e.g., Toeplitz, 1963).

Later it was noticed, looking at a chord of the graph of y = 2x starting from the point (0, 1) and ending in a nearby point, say (0.1, 20.1), that the slope of this chord is equal to the reciprocal of the first underestimate in the column above. This already suggests a sort of inverse relationship between area and slope! Aside, we know from history that Barrow—master of Newton—was the first mathematician who discovered this remarkable relationship, but he used a geometric entrance.

Even later the slope function of y = 2x was found in a numerical way on the graphic calculator, for example using the input y2 = [y1(x + 0.001) −  y1(x)]/0.001, with the discovery that the slope function seems proportional with the original function (factor about 0.693). Of course, after this numerical notion, also valid for exponential functions with other bases, came the classical algebraic explanation:

$$ \frac{{a^{x + r} - a^{x} }}{r} = a^{x} \cdot \frac{{a^{r} - 1}}{r} $$

so, with \( \mathop {\lim }\limits_{r \to 0} \frac{{a^{r} - 1}}{r} = c{}_{a} \)

it was found that \( \frac{\text{d}}{{{\text{d}}x}}a^{x} = c_{a} \cdot a^{x} \).

But what to say about the mysterious constant ca? Using numerical approximations, one may produce a table of values in 9 decimals:

a

\( c_{a} \)

2

0.693147181

3

1.098612289

4

1.386294361

5

1.609437921

6

1.791759469

7

1.945910149

8

2.079441542

9

2.197224577

10

2.302585093

Guided by direct questions, the students could discover a number of relationships such as \( c_{4}\,=\,2 \cdot c_{2} \), \( c_{8} = 3 \cdot c_{2} \), \( c_{2} + c_{3} = c_{6} \) and \( c_{2} + c_{5} = c_{10} \). The verification of these equalities was a good exercise in the known rules for derivation, particularly the so-called product rule:

figure a

Looking at the table above one may conjecture that, somewhere between 2 and 3, there must be a base a of an exponential function, for which ca = 1, so a function identical with its derivative. The task for the students—Grade 11—then was to find this number in at least two decimals. Here are the solutions of two students.

Leonie came up with:

figure b

Linda started from discovering \( c_{4} = 2 \cdot c_{2} \) and \( c_{8} = 3 \cdot c_{2} \). The teacher had asked her for an explanation and had given the hint to use powers of 2. This inspired Linda to come up with:

figure c

This approximation (of e) was correct in 8 decimals! After these activities and using the discovered property \( c_{a} + c_{b} = c_{ab} \), the students could discover that \( c_{a} =\,^{e} { \log }a \). This is a nice example of the principle of guided reinvention.

The above examples show that the relation between differentiation and integration can be introduced and discussed with discrete and numerical methods. These methods allow teachers and students to calculate and approach specific solutions and characteristics of these solutions. Linda’s work showed that students were offered opportunities to approach the value of the number e and its role in the derivative of exponential functions. Seven calculus units for the Nature and Health profile at the pre-university level were designed.Footnote 6 These units stressed the importance of conceptual understanding and relationships in calculus and illustrated how that can be realised in education with students who are interested in science careers at pre-university level.

14.7 Back to the Future?

In the beginning of the 20th century ‘calculus’ was sometimes referred to as ‘higher mathematics’, probably because of its conceptual and technical complexity. Undoubtedly this was the main reason that the implementation of the calculus took so much time. The temptation in teaching calculus is to teach it in a mechanistic way. Interesting concepts are easily overshadowed by algebraic techniques, and the ability to apply calculus in more-or-less realistic situations will then be very low. To illustrate this dominance of algebra I give you now two examples of reactions from classroom.

Example 1. Teacher: “Last year you learned something about differential calculus, what do you still remember of this?” After a short silence one student reacted: “x squared became two times x.”

Example 2. Student: “Differential calculus, I do understand it well, but what does the product rule have to do with it?”

The first example shows that for many students their view on differential calculus is a series of algebraic tricks, not a way to study processes of change. In contrast, the second example shows that after a careful conceptual approach–the teacher was a really good one–the algebraic aspect was experienced as a foreign element. Balancing conceptual understanding and algebraic techniques was, is and will be the dilemma in teaching calculus, perhaps more so than in any other mathematical topic. In an RME approach, such as was realised in the HEWET project, a long conceptual introduction preceded the simplest algebraic rules. Activities involving finding slope functions by measuring slopes using a ruler anticipated the drawing of tangents and calculations with difference quotients. The students were offered the opportunity to discover that the slope function corresponding to a parabola was a straight line. At that time, there was no graphic calculator nor much educational software, but with the help of modern tools there are many more possibilities to build the concept of the derivative in a constructive way (e.g., Drijvers et al., 1996). We have to realise that a numerical approach combined with a geometrical one will give much more insight than the algebraic rules, which of course have their own purpose and utility.

Leibniz (1684), in his very first article about calculus, propagated what he called the ‘Nova Methodus’,Footnote 7 a means to find maximums and minimums in a great diversity of situations. As an illustration, he gave a new proof of Snell’s refraction law. This was a very strong argument to believe in the value of the new calculus. But nowadays, one may object that we have calculators and computers, which after the input of an algebraic model give us the desired result. So, one might say that the main activity in calculus education must be to model, to mathematise change. But on the other hand, algebra is very helpful in proving more general results, for example Snell’s law. Of course, one can also use a symbolic calculator–nowadays still not allowed in the Dutch national written final examination–but do we want our students to use rules they do not understand?

At the time of the PROFI project, three main and ideal activities were formulated for Mathematics B: modelling, abstracting and reasoning. Finding a good balance of these activities together with the use of modern technology is the greatest challenge for teaching calculus in a realistic way and as a human activity!