A Learning Analytics Study of the Effect of Group Size on Social Dynamics and Performance in Online Collaborative Learning

Abstract

Effective collaborative learning is rarely a spontaneous phenomenon. In fact, it requires that a set of conditions are met. Among these central conditions are group formation, size and interaction dynamics. While previous research has demonstrated that size might have detrimental effects on collaborative learning, few have examined how social dynamics develop depending on group size. This learning analytics paper reports on a study that asks: How is group size affecting social dynamics and performance of collaborating students? In contrast to previous research that was mainly qualitative and assessed a limited sample size, our study included 23,979 interactions from 20 courses, 114 groups and 974 students and the group size ranged from 7 to 15 in the context of online problem-based learning. To capture the social dynamics, we applied social network analysis for the study of how group size affects collaborative learning. In general, we conclude that larger groups are associated with decreased performance of individual students, poorer and less diverse social interactions. A high group size led to a less cohesive group, with less efficient communication and less information exchange among members. Large groups may facilitate isolation and inactivity of some students, which is contrary to what collaborative learning is about.

Keywords

1 Introduction

Over the past decades, a large number of studies have demonstrated that collaboration can benefit learning from various theoretical and methodological perspectives. In fact, findings from over 1,200 research studies have consolidated and refined theories of collaborative learning [1]. Against this background, a strong consensus is asserting the higher achievement effects of collaborative learning on individual cognitive development as compared to individualistic learning and traditional instructional methods [2, 3]. Along with previous and ongoing research, collaborative learning has also increasingly gained momentum in educational systems [1]. Since the foundation of the field of Computer supported collaborative learning (CSCL), a substantial body of research has also provided evidence on the positive effects of introducing technology into collaborative learning tasks. Several large meta-analyses indicate that participants who collaborate making use of information technology show greater increases in motivation, elaboration, dialogue and debate, higher-order thinking, self-regulation, meta- cognitive processes, and divergent thinking [4, 5].

However, effective collaboration is rarely a spontaneous phenomenon, and not always the result of putting students together for collaborative work, but rather the result of orchestration and scaffolding of productive interactions [6]. That is, successful collaborative learning requires that necessary conditions are met. As one of the goals of collaborative learning is to maximize the learning performance of all participating students, group composition and size become a central aspect [7].

2 Related Work

So far research has shed light on several factors that needs to be considered when forming collaborative groups, such as students learning achievement, engagement, and interpersonal relationships [7,8,9]. However, there is little quantitative research that have investigated how group size affect the nature of collaboration and the social dynamics in groups. Furthermore, most of the research conducted have investigated smaller groups, such as dyads and triples with relatively small sample size (comparing 8–12 groups of students) [10], or as in the study of Cen et al. (2016), groups of 3 to 6 students with an analytical focus on how group size affect performance [11]. Akyol et al. used the concept community of inquiry (CoI) to find out that there was more effective communication in an online course than in a blended learning course. Furthermore, their results indicate that group cohesion in an online course developed throughout the course. Students’ use of inclusive pronouns was low at the beginning but increased towards the end of the course. The students in the online course indicated that the class size was too big for effective development of social presence, whereas students in the other blended learning setting group with approximately same size were pleased with the class size [12].

In a meta-study by Lou et al. (2001), it was concluded that small group size is a significant indicator towards individual’s achievement when learning with computing technologies: the students learn better in small groups [13]. This finding is also verified in the context of problem-based learning (PBL) by Lohman and Finkelstein [14]. Their results show that small and medium sized PBL groups (3–6 students) rated the value of the small group discussions higher than those in larger groups [14]. Tu and McIsaac in turn, suggest that especially in real-time online collaboration settings the group size should be limited to three participants. Otherwise, a strategy providing equal turn-taking need to be applied to ensure equal opportunities for all participants. Obviously, this issue is not equally relevant in asynchronous communication, for example in discussion forums in a learning management system [15].

While indications have been put forward that larger group sizes might decrease participation in collaborative learning and for instance magnify the “free rider” effect (the most able members make most effort) and the “sucker effect” (the most able members expend less mental effort because of a perceived free rider situation)[16], few are the studies that in detail have investigated how social dynamics and social networks develop depending on group size. That is, that have scrutinized how the nature of intra-group collaboration changes with group size.

In this paper, we report a study that asks: How is group size affecting social dynamics, social networks, and performance of collaborating students? In contrast to previous research, in this learning analytics study, we examine group sizes of 7 to 15 students in the context of problem-based learning in online environments in medical education. The sample studied consist of 20 courses, 114 groups of students, and a total of 974 students. To capture the social dynamics and the social networks, we applied social network analysis, which we argue is a novel approach for the study of how group size affects collaborative learning.

2.1 Social Network Analysis

Social network analysis (SNA) is a group of analytical methods and tools that are used to examine the social structures. A social structure is a collection of entities that are networked through a relationship; examples include a group of people, employees in an organization, animals in a forest, or a group of websites etc. The entities are always referred to as actors, nodes or vertices and the relationships are always referred to as links or edges [17]. SNA methods enable the study of the interactions and the relationships among the members of the structure through an established set of visual and mathematical methods. SNA visualization is a powerful graphical method of conveying the complexity of the relations among participants in an intuitive and easy to interpret way [17,18,19]. The structural properties of the actors and the structure may be more accurately captured through SNA quantitate analysis. Quantitative analysis may be performed on the structure level by computing metrics that describe the properties of the structure, such as size, interactivity or connectedness; or on the individual level by calculating the actor importance or influence in the social structure or what is known as centrality. Since importance varies in different contexts, a group of centrality measures were developed that quantify different importance concepts. Examples include popularity (degree centrality), connectedness to powerful actors (Eigen centrality), or eccentricity (isolation) [18, 20,21,22].

SNA has been used to study interactivity of online collaborative and face-to-face learning. The most common topic was the mapping the interactivity among collaborators in online computer supported collaborative learning (CSCL) [23, 24]. Researchers were able to map the interactions among students and identify the active, the inactive and the isolated students [25]. The role of teachers or moderating tutors have also been examined and how their interactions might help or otherwise hinder collaboration. SNA has also been used to diagnose and improve gaps in collaborative learning by examining the structure of networks and creating an appropriate intervention [26]. Researchers have used SNA centrality measures to identify roles such as leaders, collaborators, and influential students in online forums. In the same vein, centrality measures have also been used as a proxy for students’ online activity to predict performance using learning analytics methods [10, 27, 28]. SNA has been used to study semantic and epistemic networks, by examining the content of interactions and finding insights in how knowledge is constructed and exchanged among collaborators [29, 30].

Although the breadth of applications of SNA in collaborative learning are quite extensive, the small group dynamics have received little attention. The previous examples have studies diverse types of social structures however, limited in size. In other words, most of the research so far have examined whole course networks, or few groups in a course. The small group as a unit have also garnered a considerable attention in the realm of qualitative research. However, the dynamic complex and unique structure of small group have not received the due attention with a reasonable sample size. The small group as a unit could be considered as a complex adaptive system, in which independent participants interact, self-organize and contribute to a shared understanding of a common learning objectives [30,31,32]. We therefore, set our research to study the group dynamics using network analysis technique as a main method for studying interactions in collaborative learning, and complex systems as well. Our study offers a window into the dynamics of interactions in the group, how number of students affects it and how that affects enrolled students.

3 Methodology

3.1 The Context

Students in the University of Qassim study a problem based medical curriculum. The guiding philosophy of the curriculum is a constructivist collaborative small group teaching and learning. In each course, students are divided randomly into small groups and each group is assigned a weekly patient problem as a stimulant for discussions. Students are expected to follow the seven jump PBL approach where they start with clarifying the terms, identify the problem, brainstorm using their previous knowledge, and then formulate their learning objectives. Throughout the week, they share information online, discuss the learning issues, and by the end of the week they are supposed to reach a shared understanding of the assigned problem and the learning objectives. The PBL process is mostly online where each group discusses the assigned problem with the help of a tutor. The online discussions are based on Moodle learning management system fora. The fora are organized one thread per each weekly problem discussion, and each group is separate and can’t see the other group work until the end of the week. The seven jump approach is detailed in references like [33].

3.2 Methods

Interactions of the PBL groups were extracted from Moodle learning management system using a custom script that extracted the time stamp of each post, the subject of the post, the author, the group ID, the course ID, and the content of the post, the replies to the post and the target of each interaction. Users’ metadata were also extracted such as username, email, grade, course enrollment, and completion. Data were compiled and analyzed using R programming language version 3.52. The libraries Igraph and Centiserve were used to compute the centrality measures and network parameters [34,35,36,37]. Statistical analysis was also performed with R, correlations were calculated using spearman correlation coefficient since most of the parameters violated the normality assumption [37]. SNA visualization was done using Gephi version 9.2, using a force directed layout [18, 38]. The layout algorithm is a simulation of a physical system in which “Nodes repulse each other like charged particles, while edges attract their nodes, like springs. These forces create a movement that converges to a balanced state”. The final visualization places each node according to relationships with other nodes, so well connected nodes will be central and isolated nodes will be peripheral [38].

SNA Analysis.

Mathematical SNA analysis was performed to calculate two levels of parameters: a group level and individual students’ level. Since each group was separate and users were not allowed to enroll in other group discussions, all the centrality and SNA parameters reported here were done per group basis. In other words, the 114 student groups were separately analyzed as individual networks, all then all results were combined.

Network Level Parameters.

For each network, we calculated the following parameters: Group size (number of participants in the group); edge count (number of interactions in the group); and average distance (average shortest path among participants in the group), which corresponds to the average reachability of all nodes in the network and indicate the efficiency of the network to transfer information; network density (the number of interactions in the group as a ratio to the maximum possible), which reflects the relative interactivity, cohesion and inclusion of every group member in the interactions. Other cohesion parameters calculated were the cluster coefficient which measures the tendency of the group members to cluster together; reciprocity which measures how many of the interactions were reciprocated among the same users (replied to each other’s post); efficiency which reflect the efficiency of the network to act as an information exchange medium and is calculated as the inverse path length among all nodes; we also calculated group cohesion which is the minimum number of nodes to be removed that makes the graph disconnected and as such inefficient. Centralization parameters were also calculated to reflect how interactions are dominated around a central participants who acts as a hub (a dominant actor). A score of 1 means that all interactions are targeting a single person and it decreases when the interactions are distributed among participants. We also calculated the average centralities of group members (indegree, outdegree, degree, betweenness, closeness centrality and Eigen centralities) [20,21,22, 39, 40]. A description of these terms will follow in the next section.

Individual Level Parameters.

For each individual participant, we calculated the centrality measures most relevant to a collaborative learning context and commonly used for educational contexts. There are: the indegree (number of received interactions by a participant), which represent number of replies to the content posted by a student, and signifies that the user has posted a content that is relevant or worth to argue, add or compliment it; the outdegree (outdegree is the number of interactions posted by the student) to reflect activity and effort; degree is the sum of indegree and outdegree. We also calculated the closeness centrality which is a measure of how close is a participant to all other participants in the group and is calculated as the reciprocal average shortest path to all others. Betweenness centrality reflects how many times a person connected unconnected others (lied between them) and reflects the bridging role of a collaborator. Eigen and page rank centralities both reflect not just the number of connections but how strong their connections are and how the nodes a user connected to are important, a reflection of the worth of connections. Efficiency and clustering have been reflected upon above. While we have tried to give an account on all used indices and parameters, an elaborated discussion about these parameters is beyond the scope of this paper [20,21,22, 40]. Rich description of the concepts and their mathematical background is presented in other papers [20,21,22].

4 Results

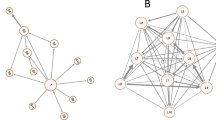
The study included 20 courses, 974 students, 114 tutors. Forty-one students in all courses were assigned to groups but did not attend the course and their data were removed. The number of students per course ranged from 45 to 54, the mean number of interactions per course was 1,198.95 (range 420 to 3,134) totaling 23,979 interactions. Twelve courses had 5 groups, six courses had 7 groups and two courses had six groups with a total of 114 groups. The number of students per group ranged from 7 to 15 with 11 being the mode (the most frequent). Since the courses were organized into small groups and each group was separate, we report the properties of the groups in details in Table 1. The mean density of interactions was 0.42, a fairly high density indicating the high reactivity of most groups. The mean degree per course was 33.44 which is also relatively high, indicating that the groups were mostly active. The average mean distance was 1.57, which indicates that students were reasonably connected. The average Eigen centrality was 0.46, an indication of high connectedness. In summary, the general properties of the groups are of dense interactive groups with participation of most students. Of course, some groups were not active as others as shown in Fig. 1. Eight groups had a mean degree less than 4, and seven groups had a density of interactions below 0.1. A visual plot of all groups is shown in Fig. 1. A closer visualization of two groups presented in Fig. 2 shows an example of the difference between a small group and a large group. In Fig. 2, the larger group is almost divided into two almost isolated subgroups. An efficient group would have all members engaged in a mutual discussion, inclusive of all members and not divided.

Table 1. Descriptive statistics

Fig. 1.

A visualization of 114 groups’ interactions plotted in graphs. The figure shows that small groups seem to be cohesive and dense, while large groups tend to have isolated students as pointed with the blue arrows. It also shows some isolated nodes, which represent course organizers who visited the groups to announce or comment (examples are pointed at with green arrows). (Color figure online)

Fig. 2.

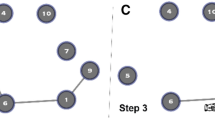
A visualization of two groups, a large group (left) and small group (right): the figure presents two groups, Group “A” on the left, which is a large group of 14 students, where there are two interacting subgroups, a small of subgroup of five, and a larger subgroup of 9 students. The overall interactions in group A were low, density of interactions (density = 0.34), with less cohesive structure, and the collaborators were distanced by longer path (Average path = 2.1). Furthermore, the group A shows lower clustering (0.46) and lower efficiency of information exchange (efficiency = 0.69). On the right, group B shows with more interactions and cohesion (Density = 0.89, Average path = 1.1, Clustering 0.96, efficiency = 0.98). Legend: each circle represents a node, arrows represents direction of interactions, the size of the nodes correspond to number of interactions (degree), color represents closeness centrality. (Color figure online)

4.1 Correlation with Grade

There was a statistically significant negative correlation between the size of the group and the performance of the group members (r = 0.22, p < 0.001). To have a deeper look into the group dynamics and how interactions influence participants, we investigate four groups of parameters worth studying in relation to group size, namely: group effort and productivity, group connectivity and cohesion, efficiency of interactions as well as centralization.

4.2 Group and Size Dynamics

Regarding group effort and interactivity, there was a positive correlation between the number of interactions and group size (r = 0.225*, p = 0.016), however, using the mean degree and its variants (in and outdegree), which control for the group size showed that they were not significantly positively correlated (r = 0.028, p < 0.764), which means that the average number of interactions per a member is comparable in small and large groups. Groups with larger sizes did not motivate members to participate more than in small groups. Similarly, the mean reciprocity was not correlated with size of the group (r = −0.032, p = 0.736). As such, members of all groups would receive comparable number of replies. These findings indicate that larger groups did not result in more productive members or more replies. Regarding connectivity, expectedly, the larger was the group size, the more it was associated with higher levels of mean betweenness centralities (r = 0.405, p < 0.001), as more participants play the bridging role among group members.

With larger group members there was more chances of connecting and bridging the distant others. The mean closeness centrality was negatively and strongly correlated with group size (r = −0.725, p < 0.001). This is an indication of how large group size would facilitate the isolation of some students and may also create isolated subgroups as shown in Fig. 2. Furthermore, isolated students may go unnoticed by the moderators or rely on others who do the work. In the mean vein, the average distance was positively correlated with group size (r = 0.268, p < 0.001), confirming the closeness and reachability difficulties in larger groups. The mean Eigen centrality were also negatively correlated with group size (r = −0.343, p < 0.001). This is an interesting result, as one would expect the opposite, that is, with a larger group it would be easier to make connections to influential people.

Regarding the cohesion parameters, we measured four parameters. Density of interactions was negatively correlated with the group size (r = −0.294, p < 0.001). This is an indication that an increasing group size negatively impacts the cohesion of the group. Efficiency – a measure of communicability – was also negatively correlated with group size (r = −0.34, p < 0.001), as well as vertex cohesion (r = −0.236, p < 0.001), and clustering coefficient (r = −0.209, p < 0.001), indicating that a larger group tends to be less cohesive, and members tend not to cluster together. These results confirm the previous ones that larger groups tend to have less reachability, therefore act as a good medium for isolated and inactive students, which is contrary to what collaborative learning is about. The last group of parameters that we examined, was the emergence of hubs or leader participants who would drive or motivate the interactions in larger groups. However, the results showed that group size is not correlated with the likelihood of having such leaders (Table 2).

Table 2. Correlation between group parameters and size

4.3 Individuals Students’ Level

On the individual students’ level, there were some interesting results. Being in a small or larger group did not affect the average level of interactions (as measured by the quantity of indegree or outdegree centralities). Larger groups however had, as mentioned before, a longer path distance and less closeness centrality, which was manifested as a negative correlation coefficient between group size and student performance. That was also demonstrated through a positive correlation between eccentricity and performance. Students in larger groups tended to have fewer valuable connections to connected students (lower Eigen centrality and page rank). Also, it’s worth noting that the efficiency (role in exchange of information) was negatively correlated with the group size. In summary, the results of individual students corroborate those of the groups; that larger groups tend to have negative influence on interacting students. Full details are shown in Table 3.

Table 3. Correlation of individual centrality measures with group size

5 Discussion

Today collaborative learning is a quite common pedagogical method in higher education and we see that many educational institutions enact this method in online environments. However, from previous research we have learned that effective collaborative learning rarely is a spontaneous phenomenon and that several factors needs to be considered for achieving successful collaboration [6]. One such factor relates to group size. While previous research has demonstrated that larger group sizes might have detrimental effects on collaborative learning (for example [14, 15, 28]), few are the studies that in detail have examined how social dynamics develop depending on group size, especially when the group size is in the range of 7–15 students which is common in for instance medical education where students work in teams in problem-solving scenarios. Thus, in this learning analytics study, we used social network analysis to understand the effect of group size on performance and in particular on the social dynamics in the collaborative groups. The analysis conducted resulted in the following conclusions:

In general, we conclude that larger groups are negatively correlated with individual students’ performance. While this result might be expected also in the light of the previous research [12,13,14], the social network analysis shed light on the “why” by describing how specific aspects of collaboration, and how the nature of the social dynamics, changes with increasing group size. Firstly, the findings demonstrated that there was a positive correlation between the number of interactions and group size, however, the mean degree and its variants (in and out degree) were not significant. This means that a group size increases the total number of interactions but does not motivate members to participate more or less than in small groups. In our study, the closeness centrality, the average distance, and the mean Eigen centrality measures rendered negative correlations with group size. Based on this, we conclude that students in larger groups have more difficulties to make connections to influential peers. Looking at these results from a theoretical perspective, one could make the interpretation that larger groups create less opportunities for students to work in their proximal development zones with more competent peers [41], as the distance to the competent peers is larger (captured by the average distance, closeness and Eigen centrality measures).

Furthermore, the findings also showed that density of interactions was negatively correlated with group size, an indication that an increasing group size, negatively impacts the cohesion of the group. Group efficiency and communicability were also negatively correlated with group size, as well as cohesion and clustering coefficient, indicating that a larger group tends to be less cohesive, and members tend not to socially cluster together. These findings are in line with the results by Akyol et al. [12], where it was concluded that development of social presence in a big group was more difficult in an online course than it was in a blended learning setting. Thus, we can conclude that a larger group does not lead to more interactions, but to a less cohesive group, with less efficient communication and information exchange among members. That is, as the group size increases it likely becomes more difficult to achieve the fundamental characteristics of productive collaborative learning, namely: “a coordinated, synchronous activity that is the result of a continued attempt to construct and maintain a shared conception of a problem” [42].

Generally speaking, this quantitative social network analysis of group size corroborates and extend Lohman & Finkelstein’s who provided a student perspective on group size, showing that students in small and medium sized PBL groups (3–6 students) rated the value of the small group discussions higher than those in larger groups [14]. This study corroborates and extends Lohman & Finkelstein’s in the sense that we quantitatively have shown that the nature of social dynamics in larger groups indeed are different from small group dynamics, and at the same time, we extend their work by providing detailed quantitative and visual descriptions for how social dynamics change as group size increases, using the lens of social network analysis. As far as we are aware, this is the first study that have used social network analysis to study group size effects on social dynamics in the context of collaborative learning, which is one of the novel contributions of this paper [14].

Overall, the results of this study encourage us to rethink the group sizes that are used in collaborative learning scenarios in education. Although it might be practical because of limited teacher resources and economy, larger groups seem to perform less well and we risk that students that need learning with more competent peers but don’t have the conditions to do so, risk to underachieve and dropout, which has severe consequences for individuals, institutions and societies. For future work, we recommend the use of social network analysis to study how social dynamics are shaped in smaller groups than the ones focused on in this paper.