Spherical Elementary Current Systems Applied to Swarm Data

Abstract

This chapter describes how the Spherical Elementary Current Systems (SECS) are applied to analyze the magnetic and electric field measurements provided by the Swarm spacecraft. The Swarm/SECS method produces two-dimensional (latitude–longitude) maps of the ionospheric horizontal and field-aligned currents around the satellite paths. If also electric field data are available, similar maps of the electric field and conductances can be obtained.

3.1 Introduction

The Spherical Elementary Current Systems (SECS) described in the previous Chap. 2 have been applied to the Swarm mission by Amm et al. (2015). Naturally, the SECS methods had been used to analyze magnetic measurements from other satellite missions before that. However, with the previous single satellite missions, one had to either use the 1D assumption of vanishing gradients in one direction (often either cross-track or zonal direction), or statistically average the data before analysis. These approaches were used for example by Juusola et al. (2007) and Juusola et al. (2014), when they estimated the ionospheric horizontal current $\mathbf {J}$ and field-aligned current $j_\parallel$ from Champ magnetic field data.

With data from the multi-satellite Swarm mission, it becomes possible to estimate $\mathbf {J}$ and $j_\parallel$ from individual passes of two or three satellites, without any simplifying assumptions apart from stationarity during the pass. The goal of the Swarm/SECS analysis method introduced by Amm et al. (2015) is to derive two-dimensional (latitude/longitude) maps of the current in a limited region around the satellite paths. As the amount and spatial coverage of the data is still quite limited (usually two, sometimes three, parallel satellite tracks), Amm et al. (2015) decided to use a hybrid 1D/2D technique, where 1D SECS are fitted to the magnetic data first in order to capture the large-scale electrojet currents, and 2D SECS are only fitted to the residual, which cannot be explained by the 1D systems.

SECS can be applied to any vector field on a sphere, and a similar analysis of the plasma drift measured by Swarm can be carried out, effectively interpolating and also slightly extrapolating the measurements into a 2D map of the electric field $\mathbf {E}$. A straightforward combination of the sheet current and electric field maps then gives the height-integrated Pedersen and Hall conductances ($\varSigma _P$ and $\varSigma _H$, respectively).

The Swarm/SECS analysis method was largely developed before the Swarm spacecraft were launched in November 2014. Therefore, initial testing was performed with synthetic datasets taken from data-based models of typical ionospheric current systems, as well as from global MHD simulations. After Swarm data became available, Juusola et al. (2016b) made an extensive comparison of the currents estimated from Swarm and the ground-based MIRACLE magnetometer network. Due to the lack of good electric field data from the Swarm satellites, the electric field analysis and estimation of the Hall and Pedersen conductances has only been carried out in one limited case study by Juusola et al. (2016a).

This chapter first describes the Swarm/SECS analysis method and the various tests that were performed by Amm et al. (2015). It continues with some examples of selected event studies, and summarizes the statistical comparisons of Swarm- and MIRACLE-based currents. Finally, some ongoing work and future prospects are discussed. This includes a dataset of ionospheric current maps derived with the Swarm/SECS method that has been calculated and published by the Finnish Meteorological Institute.¹

3.2 The Swarm/SECS Analysis Method

The SECS method, in general, and the curl-free (CF) and divergence-free (DF) basis functions are described in Chap. 2. It also includes a brief summary of ionospheric electrodynamics.

3.2.1 Current from Magnetic Field Analysis

A novel combination of the 1D and 2D SECS techniques is employed to make maximal use of the Swarm measurements. The default setting is to use data from the two lower satellites, but measurements from the upper satellite can also be included, when the three satellites are in close conjunction.

Necessary inputs are the positions ($\mathbf {r}_{sat}$) and the magnetic ($\mathbf {B}_{sat}$) measurements of the Swarm satellites. The Earth’s main field, lithospheric field and magnetospheric contributions need to be subtracted from the Swarm magnetic field data using for example the CHAOS or POMME models (Finlay et al. 2016; Maus et al. 2006, respectively). Output parameters are the height-integrated horizontal current and FAC along a strip around the ionospheric projection of the satellite tracks.

Fig. 3.1

From Amm et al. (2015)

Sketch of geometry for Swarm data analysis. Black lines show the ionospheric projection of the lower Swarm satellites orbits, blue circles the output grid, and red stars the positions of the 2D SECS poles. The 1D SECS are not shown, but they are placed at same latitudes as the 2D SECS.

The input data can be in any spherical coordinate system $(r,\theta ,\phi )$, where $\theta$ is the colatitude and $\phi$ is the longitude. The most typical choices are the geographic or geomagnetic systems. The analysis grid and output grid are generated around the ionospheric footpoints of the two lower Swarm satellites. Typically altitude for the ionospheric sheet current is about 110 km. The default analysis grid has the following parameters:

• Latitudinal separation is $0.5^\circ$ and longitudinal spacing is half of the satellite separation for both the 2D SECS grid and the output grid.

• The 2D SECS grid has 15 points in the longitudinal direction and it is extended 3 latitude points outside the output data area. 1D SECS are placed at the same latitudes as the 2D SECS.

• The output grid has 7 points in the longitudinal direction.

All these parameters can be changed by the user, but these were found to be a reasonable choice in the various test cases described in Sect. 3.3. An example of the default grids is shown in Fig. 3.1.

The four different current systems (1D/2D and CF/DF SECS) are fit one by one to the measured magnetic variation field. The analysis steps are as follows:

• (1) Fit 1D divergence-free SECS using only the parallel magnetic component $B_\parallel$,

• (2) fit 2D divergence-free SECS using the residual $B_\parallel$,

• (3) fit 1D curl-free SECS using the residual eastward component $B_\phi$, and

• (4) fit 2D curl-free SECS using the residual southward and eastward components, $B_\theta$ and $B_\phi$, respectively.

Ordering of the above analysis steps is a result of two factors. First, 1D SECS are used to fit the large-scale electrojet-type current systems whenever possible, as the amount of input data is limited to two satellite tracks. Second, $B_\parallel$ is mostly produced by the divergence-free ionospheric currents, whereas the perpendicular disturbances are dominated by FAC connected to the curl-free ionospheric current. Naturally, it would be possible to combine all these four steps into one large fitting problem, but keeping them separate gives better control over the analysis.

Each of the above steps results in a matrix equation between the measured field components and the unknown SECS scaling factors. For example, in the first step, it is necessary to form and solve relation

$$\begin{aligned} \mathbf {\mathscr {B}}_{\parallel } = \overline{\mathrm T} \cdot \mathbf {\mathscr {S}}_J^{1D,DF}, \end{aligned}$$

(3.1)

where the vector $\mathbf {\mathscr {B}}_{\parallel }$ contains the field-aligned magnetic disturbance components measured by the Swarm satellites at locations $\mathbf {r}_n=(r_n,\theta _n,\phi _n)$,

$$\begin{aligned} \mathbf {\mathscr {B}}_{\parallel } = [B_\parallel (\mathbf {r}_1) ,\,\,\,\,B_\parallel (\mathbf {r}_2) ,\,\,\,\,B_\parallel (\mathbf {r}_3) ,\,\,\,\,\ldots ]^T, \end{aligned}$$

(3.2)

and the vector $\mathbf {\mathscr {S}}_J^{1D,DF}$ contains scaling factors of the 1D DF SECS located at $\mathbf {r}^{el}_k=(R_I,\theta ^{el}_k,\phi ^{el}_k)$,

$$\begin{aligned} \mathbf {\mathscr {S}}_J^{1D,DF} = [S(\mathbf {r}^{el}_1) ,\,\,\,\,S(\mathbf {r}^{el}_2) ,\,\,\,\,S(\mathbf {r}^{el}_3) ,\,\,\,\,\ldots ]^T. \end{aligned}$$

(3.3)

The components of the transfer matrix $\overline{\mathrm T}$ give the parallel magnetic field components caused by each individual unit SECS at the measurement points. The transfer matrix depends only on the geometry, i.e., locations of the measurement points and the SECS poles. Detailed formulas for calculating the matrix elements and possible ways to invert the linear equation for the unknown scaling factors are presented in Sect. 4–8 of Chap. 2.

In the second step, the magnetic field explained by the 1D DF SECS is removed from the measured magnetic disturbance, and the fitting is repeated using 2D DF SECS. In a similar fashion the 1D and 2D CF SECS are fitted in steps 3 and 4, respectively.

Fig. 3.2

From left to right: Ionospheric horizontal current from the MHD simulation (moderate activity), current calculated from virtual Swarm measurements with the Swarm/SECS analysis method, and the difference between the two. Note the different scales. Tracks of the two satellites used in the analysis are also shown. Corresponding results for the electric field and Hall conductance are shown in Figs. 3.3 and 3.4, respectively

Once all the scaling factors of the different SECSs have been determined, the ionospheric horizontal current can be calculated as a sum of the individual elementary systems. An example of the output current map calculated using data from the lower pair of the Swarm satellites is shown in Fig. 3.2. This is one of the synthetic test cases further discussed in Sect. 3.3 and by Amm et al. (2015). In this test, the ionospheric current system and corresponding Swarm measurements are taken from a global magnetosphere–ionosphere simulation. The FAC can be calculated either directly from the scaling factors of the CF SECS, which describe the divergence of the current within the grid cells, or by numerically estimating $\nabla \cdot \mathbf {J}$ with finite differences.

3.2.2 Fitting the Electric Field with CF SECS

Electric field data from the Swarm satellites can be analyzed in a similar fashion. In this case only CF 1D and 2D elementary systems are needed, as the curl of $\mathbf {E}$ is assumed to vanish. The analysis is carried out in three steps:

• (1) Map the electric field measurements down to the ionospheric current layer,

• (2) fit 1D curl-free systems using the $\theta$-component of electric field, and

• (3) fit 2D curl-free systems using the residual $E_\theta$ and $E_\phi$.

In this case, the Swarm data already gives the electric field along the satellite tracks, so the purpose of fitting the CF elementary systems is to interpolate and extrapolate the measurements to an extended latitude–longitude maps. This is in contrast to the magnetic field analysis, where there is a need to estimate the ionospheric currents from the measured magnetic field.

Fig. 3.3

Same as Fig. 3.2, but for the electric field analysis

One practical way to map the electric field data from the satellite altitude down to the E-region current sheet is to use the apex coordinates, with readily available conversion library (see Laundal and Richmond 2016, and references therein). Once that has been done, the data can be fitted with the CF elementary systems. This is analogous to representing a given vector field with SECS, a topic which was discussed in Sect. 6 of Chap. 2. Also in this case there are matrix equations for the scaling factors of 1D and 2D CF SECS. For example, when fitting the 2D CF SECS in the third step, there is equation

$$\begin{aligned} \mathbf {\mathscr {\delta E}}_{\perp } = \overline{\mathrm M} \cdot \mathbf {\mathscr {S}}_E^{2D,CF}, \end{aligned}$$

(3.4)

where the vector $\mathbf {\mathscr {\delta E}}_{\perp }$ contains the residual of the downward mapped horizontal electric field after fitting the 1D CF SECS,

$$\begin{aligned} \mathbf {\mathscr {\delta E}}_{\perp } = [E_\theta ^{map}(\mathbf {r}_1) ,\,\,\,\,E_\phi ^{map}(\mathbf {r}_1) ,\,\,\,\,E_\theta ^{map}(\mathbf {r}_2) ,\,\,\,\,\ldots ]^T, \end{aligned}$$

(3.5)

and the vector $\mathbf {\mathscr {S}}_E^{2D,CF}$ contains scaling factors of the 2D CF SECS,

$$\begin{aligned} \mathbf {\mathscr {S}}_E^{2D,CF} = [S(\mathbf {r}^{el}_1) ,\,\,\,\,S(\mathbf {r}^{el}_2) ,\,\,\,\,S(\mathbf {r}^{el}_3) ,\,\,\,\,\ldots ]^T. \end{aligned}$$

(3.6)

Also in this case, the transfer matrix $\overline{\mathrm M}$ depends only on the geometry, and it can be inverted using similar methods as with the magnetic field analysis.

An example of the output electric field map is shown in Fig. 3.3. It is from the same synthetic test case as the current map in Fig. 3.2.

3.2.3 Conductances from Ohm’s Law

Once the ionospheric electric field and horizontal current have been determined, the height-integrated Pedersen and Hall conductances can be solved from Ohm’s law,

$$\begin{aligned} \varSigma _P = \frac{ \mathbf {J}_\perp \cdot \mathbf {E}_\perp }{ |\mathbf {E}_\perp |^2 }, \qquad \varSigma _H = \frac{ \mathbf {J}_\perp \times \mathbf {E}_\perp }{ |\mathbf {E}_\perp |^2 } \end{aligned}$$

(3.7)

An example of the output Hall conductance map is shown in Fig. 3.4. It has been calculated from the current and electric field shown in Figs. 3.2 and 3.3, respectively. It should be noted that the MHD model used in this test is completely self-consistent: The model electric field and conductance distribution produce the horizontal and field-aligned currents, which in turn were used to calculate the magnetic disturbance. However, in the Swarm/SECS analysis, the electric and magnetic data have been analyzed completely independently from each other, so the inevitable analysis errors accumulate in the conductance estimation. In fact, nothing guarantees that the conductances produced by the Swarm/SECS method are even positive. Nevertheless, the Swarm analysis result shown in the middle panel is in good qualitative agreement with the model, and especially between the satellite tracks the errors are small. This is quite an impressive result, when one takes into account the fact that there is measured data only along the two tracks.

Fig. 3.4

Same as Figs. 3.2 and 3.3, but showing the Hall conductance calculated from the current and electric field

In order to improve the conductance estimation and to mitigate effects of the unexpectedly large noise in the Swarm electric field measurements, Vanhamäki and Amm (2014) developed an alternative analysis scheme that guarantees positive Hall and Pedersen conductances. In this “positive definite” approach the current map is taken as is, but the Hall and Pedersen conductances are represented with positive definite functions, such as exp(x). A 2D map of the positivity parameter x is then obtained by fitting the Swarm electric field measurements, with possible additional constraints on spatial smoothness. This results in a nonlinear minimization problem that can be solved with standard techniques. However, the positive definite method has not really been applied in practice.

An alternative approach has been suggested by Marghitu et al. (2017). They also take the current map as given, but try to modify the measured electric field by linear transformations of the form

$$\begin{aligned} E'_x = a E_x + b, \qquad E'_y = c E_y + d. \end{aligned}$$

(3.8)

Their goal is to find such coefficients a, b, c, d that the conductances calculated from Ohm’s law match the conductances calculated from Robinson’s formulas (Robinson et al. 1987). The average energy of precipitating electrons and the total energy flux needed in the Robinson’s formulas are taken from the upward FAC and the conductance ratio estimated from Ohm’s law. This proposed method is essentially an attempt to validate and, if necessary, recalibrate the Swarm electric field measurements.

3.3 Tests with Synthetic Data

Amm et al. (2015) created three simple but still realistic test cases for the Swarm/SECS analysis tool. These test cases were (1) a one-dimensional electrojet where ionospheric electric field and conductances are independent of longitude, (2) a two-dimensional electrojet whose strength varies along the jet, and (3) a fully two-dimensional current vortex. Additionally, Amm et al. (2015) took three different test cases from a self-consistent, coupled magnetosphere–ionosphere MHD simulation. These cases correspond to low, moderate and high activity in the simulated magnetosphere. More details of the test cases and the simulation setup are given by Amm et al. (2015). Moreover, Juusola et al. (2016b) considered an additional $\varOmega$-band test case constructed from direct observational data, which will be further discussed in Sect. 3.5.1.

Table 3.1 RMS errors in the solution for the horizontal current ($\mathbf {J}_\perp$), field-aligned current (FAC), electric field ($\mathbf {E}$), Pedersen conductance ($\varSigma _P$), and Hall conductance ($\varSigma _H$) in the synthetic test cases. See Eq. (3.9) for definition of the RMS error

As an overview of the standard analysis results obtained using the two lower satellites, Table 3.1 shows the RMS errors of the output parameters (horizontal current, FAC, electric field, Pedersen conductance and Hall conductance) in the three synthetic and three simulated test cases. In general, the electric field, horizontal current, and Hall conductance seem to be reproduced most reliably. The Pedersen conductance results exhibit a slightly larger error than the Hall conductance results, but in each case FAC is the most difficult parameter to reproduce accurately.

The RMS error is calculated as

$$\begin{aligned} RMSerror = 100 * \frac{\sqrt{<|model - result|^2>}}{\sqrt{<|model|^2>}}. \end{aligned}$$

(3.9)

Here, $<>$ means spatial average over the output area. The RMS errors for the horizontal current, electric field and Hall conductance given in the “Moderate” row of Table 3.1 correspond to Figs. 3.2, 3.3 and 3.4. According to the above equation, the RMS error is obtained by dividing the square root of the averaged and squared analysis error shown in the rightmost panels, by the similarly averaged model field shown in the left panels. Thus, the RMS error provides a single number characterizing the overall relative error in the analysis results. While the RMS error is a useful parameter, it is also important to pay attention to the general structure and spatial pattern of the solution, as shown in Figs. 3.2, 3.3 and 3.4.

3.4 Examples of Event Studies

Auroral oval crossings in the early phase of the mission allow Swarm/SECS analyses both with AC and AB satellite pairs. The first example in Fig. 3.5 shows some results from such an exercise. This oval crossing took place in the dawn sector of the oval (MLT $\sim$ 0430) during a period of relatively weak global geomagnetic activity, with the Kp-index (Siebert and Meyer 1996) having value $2+$. The currents in the Fennoscandian sector of the auroral oval were anyway rather strong, being larger than 500 A/km. Main features in both horizontal and field-aligned currents are similar for the AC (right panel in Fig. 3.5) and AB (left panel in Fig. 3.5) pairings. A closer look reveals some small differences in the horizontal currents along the northern parts of the Swarm-A trajectory (at latitudes poleward of 76$^\circ$), where the AC pair yields currents with larger east components than in the results from the AB pair. The latter results are considered to be more reliable, because Swarm/SECS as applied to the AC pair tends to underestimate the north component of DF currents (c.f. Sect. 3.5.1).

Fig. 3.5

From Marghitu et al. (2017)

Swarm-A, B, and C passing over the MIRACLE network, 30 July 2014, 02:08:49-02:13:48 UT. The left panel shows Swarm/SECS analysis results for the AB satellite pair, the right panel for the AC pair.

Figure 3.6 shows the second example. It is from an event study by Juusola et al. (2016b), who applied Swarm/SECS for an overflight above the MIRACLE network² (Amm et al. 2001) of magnetometers and auroral cameras. The overflight took place in the dawn sector of the auroral oval (MLT $\sim$ 0530) during slightly stronger geomagnetic activity ($Kp = 3$) and pulsating auroras. The DF and CF currents by Swarm/SECS are shown in the panels (a) and (b) of Fig. 3.6, respectively. Panel (c) shows the DF currents (equivalent currents) as derived from MIRACLE data. An estimate of telluric currents (derived with a layer of SECSs at the ground surface) has been subtracted from the equivalent currents.

Fig. 3.6

From Juusola et al. (2016b)

Swarm-A and C flying over the MIRACLE network, 14 December 2014, 03:15:20-03:20:49 UT. Horizontal and field-aligned currents derived from Swarm data with the Swarm/SECS method are shown in panels a and b, while panel c shows the equivalent current derived from the ground-based MIRACLE magnetometers and the auroral intensity from Kilpisjärvi all-sky camera.

The satellite-based DF and ground-based equivalent current distributions are not completely identical. This is discussed in more detail in Sect. 3.5.1. In the case of Fig. 3.6 the Swarm/SECS method yields a westward DF current at magnetic latitudes $65^\circ - 72^\circ$, which is roughly consistent with the average oval location for $Kp=3$ according to statistics by Juusola et al. (2009). Also, the ground- based equivalent currents are westward, but the electrojet is tilted approximately along constant geomagnetic latitude direction and it is weaker and slightly narrower than the currents estimated with the Swarm/SECS method. Concerning the strength and width of the electrojet, the picture by Swarm/SECS method is most likely more reliable than that of MIRACLE, because the electrojet is above the Arctic Sea where the coverage of ground-based magnetometers is very limited. Concerning the tilt, however, the ground-based equivalent currents yield a more reasonable result, which is consistent with the pattern of CF currents in panel (b): The bands of radial currents have the same tilt as the equivalent currents and horizontal CF currents flow in the perpendicular direction to the equivalent currents.

In the field of view of the all-sky camera (ASC) at Kilpisjärvi (magnetic latitude $\sim 66^\circ$), the distribution of auroras have a sharp equatorward boundary, which is roughly colocated with the equatorward boundary of the electrojet (c.f. panel (c) in Fig. 3.6). Also DF and CF currents by the Swarm/SECS method are weak southward of this boundary. In this context, it is good to note that in Swarm/SECS analysis the coordinates of the Swarm magnetic field measurements have to be replaced with those corresponding to their ionospheric magnetic conjugacy points, in order to avoid obvious mismatches with spatial distributions in the auroras (for further discussion, see Juusola et al. 2016b). As electron precipitation causing auroras is also known to enhance ionospheric Hall conductances, the colocation of equivalent, and DF current and auroral equatorward boundaries is not surprising. Interpreting the distribution of CF currents and FAC in Fig. 3.6, however, is more complicated. In large scales the direction of FAC are in accordance with the standard R1/R2 pattern in the morning sector (downward current poleward of upward current), but the R2-currents are split into two bands. Swarm/SECS results show hints of a R2 band at the equatorward boundary of the electrojet, as anticipated, but another band of R2 appears poleward of the Kilpisjärvi ASC’s field of view. With the available observations it is difficult to judge whether this structure is associated with an auroral structure or with a zone of enhanced electric field (Archer et al. 2017).

The third and last example is taken from Juusola et al. (2016a), who demonstrated how the Swarm/SECS method can be used to derive latitude profiles of Hall and Pedersen conductances across the auroral oval, when both the $\mathbf {E}$- and $\mathbf {B}$-field data are available. Figure 3.7 shows conductance estimates and the electric field in the vicinity of a post-midnight auroral arc (MLT $\sim$ 02) with $Kp = 4-$. These results have been derived with the 1D Swarm/SECS analysis method applied to the $\mathbf {E}$- and $\mathbf {B}$-measurements from the Swarm-A satellite. The 1D approach assumes that longitudinal gradients and the east component of $\mathbf {E}$ are insignificant when compared to latitudinal gradients and the north component of $\mathbf {E}$, respectively. The assumption of small longitudinal gradients in currents and conductances is supported in this case by equivalent current maps and auroral camera data from the MIRACLE network. In 1D cases, the DF and CF horizontal currents can be interpreted as Hall and Pedersen currents, respectively, and can be combined separately with electric field to produce Hall and Pedersen conductance profiles in different latitudinal resolutions. The resolutions of Hall conductance and the conductance ratio $\alpha$ in Fig. 3.7 are limited by that of the DF component (2$^\circ$, c.f. discussion in Sect. 3.5.1). For consistency, the Pedersen conductance is shown in the same resolution, although it could be estimated with a better latitude resolution up to about 0.5$^\circ$. The electric field values shown in Fig. 3.7 are somewhat higher than reported in some previous studies on auroral arcs (for example Opgenoorth et al. 1990; Aikio et al. 2002). However, the latitudinal distributions of $\mathbf {E}$, currents and conductances follow closely the previously found pattern for morning sector arcs: Conductances are high at the arc location while $\mathbf {E}$ is high in a broader latitude range and particularly on the poleward side of the auroral arc. The westward directed Hall currents are strong in a latitudinal band, where currents in the poleward part are controlled by the strong $\mathbf {E}$ and in the equatorward part by enhanced conductances. These findings lead Juusola et al. (2016a) to suggest that this particular electrojet is in the transition zone between two different types of westward currents, conductance dominated (midnight sector) and electric field dominated (morning sector) electrojets, which are introduced in the substorm scenario by Kamide and Kobun (1996).

Fig. 3.7

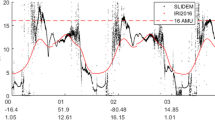
From Juusola et al. (2016a)

1D fit to the electric field (blue, left axis) measured by Swarm-A on August 31, 2014 between 23:08:29 and 23:13:59 UT. The electric field has been mapped down to 110 km altitude along the Earths main field. Pedersen ($\varSigma _P$, red) and Hall ($\varSigma _H$, green) conductances and their ratio $\alpha =\varSigma _H/\varSigma _P$ (magenta, right axis), calculated from the horizontal current density and electric field. The gray shading is the auroral intensity in arbitrary units from the Sodankylä all-sky camera, projected to 110 km altitude.

3.5 Statistical Studies

3.5.1 Swarm-MIRACLE Comparisons

It is possible to do a limited comparison between the ionospheric currents derived from Swarm magnetic field measurements using the Swarm/SECS method with those derived from ground magnetic field measurements. Such an analysis has been carried out for Swarm crossing of the MIRACLE network in 2013–2014 by Juusola et al. (2016b). A similar exercise was done previously by Ritter et al. (2004), who compared divergence-free currents estimated from CHAMP data with ground-based equivalent currents from the MIRACLE network. However, with the single CHAMP satellite only the east/west (or cross-track) electrojet current could be determined.

MIRACLE includes 38 magnetometers that form an irregular 2D network in Northern Europe between $58^\circ$ and $79^\circ$ geographic latitude and $5^\circ$ and $36^\circ$ longitude. The latitude range covers the auroral oval at most times. From the ground-based MIRACLE data, it is possible to derive 2D maps of the ionospheric equivalent current, as discussed in Sect. 7 of Chap. 2.

There are several issues that need to be taken into account when comparing currents derived from Swarm and MIRACLE. First, the comparison is limited to the DF component, as the equivalent current obtained from ground measurements should be identical to the DF part of the total current. Second, it takes Swarm approximately 6 min to cross the MIRACLE network, during which time the currents should remain stationary for the Swarm/SECS analysis. With MIRACLE data it is possible to analyze the instantaneous distribution every 10 s. Juusola et al. (2016b) resolved this discrepancy by averaging the MIRACLE currents over the Swarm crossing time. Third, the spatial resolutions of the DF currents derived from Swarm and the equivalent current from MIRACLE are not the same. Both the distance between the measurement and source current as well as the spatial resolution of the measurements play a role. Juusola et al. (2016b) concluded that the best spatial resolution for the MIRACLE currents is $\sim$50 km and for the DF currents derived from Swarm $\sim$200 km. The fourth issue in the Swarm-MIRACLE comparison has to do with the telluric currents. Juusola et al. (2016b) showed that accounting for these currents is important when analyzing ground-based magnetic data. In Swarm analysis, they can mostly be ignored, except for the most active events. For those cases, the mirror current method (Olsen 1996) works well, but it is not a good approach for quiet or only moderately active events.

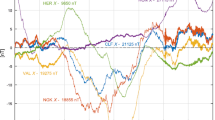
Comparison has revealed that although the east component of the DF current density derived from Swarm agrees very well with that from MIRACLE (see Fig. 3.8), the south component given by Swarm is generally much weaker than that given by MIRACLE. The explanation suggested by Juusola et al. (2016b) is that the longitudinal distance between the AC satellite pair ($\sim$60 km at MIRACLE latitudes) is too small compared to the distance to the E-region current layer ($\sim$350 km) to provide sufficient gradient information in this direction, effectively rendering the measurements equivalent to those of a single satellite and imposing the 1D limitation.

Fig. 3.8

From Juusola et al. (2016b)

Comparison of the DF current derived from Swarm and MIRACLE using the SECS analysis methods. Panel a is for the eastward component, and b for the northward component.

Although proper comparison of the CF component derived from Swarm is not possible with ground measurements, it was noted that unlike the DF component, the CF component showed 2D features compatible with those resolved by MIRACLE (for example tilt of an electrojet). Application of the Swarm analysis to a synthetic model of an $\varOmega$-band further confirmed that while the full CF current and the zonal component of the DF current are well resolved, the meridional DF component is too weak. However, as the full DF component can be obtained from ground measurements, a combined SECS analysis of MIRACLE and Swarm measurements, with telluric currents taken into account, could produce the total horizontal ionospheric current density around the Swarm-AC footprints. An added benefit would an improved spatial resolution: as the CF component is directly connected to Swarm altitude through FACs, the spatial resolution of the resolved currents is only limited by the density of the measurement points. Thus, the combined analysis could increase the spatial resolution of the total current density from the $\sim$200 km imposed by the DF part of Swarm/SECS analysis to the $\sim$50 km of the MIRACLE analysis.

3.5.2 Global Current Systems with the Swarm/SECS Method

The Swarm mission offers a possibility to study statistical properties of the global ionospheric and field-aligned current systems without many of the simplifying assumptions employed in previous works that relied on data from single satellites. With the side-by-side AC pair, for the first time, it is possible to get reliable estimates of the current also in those regions and situations where the current geometry is far from the ideal 1D electrojet.

Fig. 3.9

The average pattern of the FAC and horizontal ionospheric current in the northern hemisphere as determined from 8.5 months of Swarm magnetic field data. Each pass is analyzed with the Swarm/SECS method and the results are averaged into a $1^\circ$ times 0.5 MLT hour grid

Figure 3.9 shows a statistical picture of the northern hemispheric FAC and horizontal currents, based on Swarm/SECS analysis of about 8.5 month of data from the AC pair. Their orbital planes precess about 2.7 h of (solar) local time in one month, giving a complete local time coverage in about 4.4 months. Thus the magnetic local time coverage shown in the left panel of Fig. 3.9 is rather uniform.

The middle and right panels of Fig. 3.9 show the median FAC and $\mathbf {J}$, respectively. Each orbit was divided into 4 segments, consisting of ascending/descending auroral oval crossings in the northern/southern hemispheres. The passes are analyzed separately using the Swarm/SECS method, and the results were binned to a regular grid in magnetic latitude and local time (AACGM system, Shepherd 2014). The median FAC shows the familiar R1/R2 pattern, while the eastward and westward electrojets are clearly visible in the horizontal current.

Fig. 3.10

The top row shows the difference in medians of the current densities obtained with a 1D (single satellite) and the 1D+2D Swarm/SECS (dual satellite) methods. $J_\theta$ is southward and $J_\phi$ is eastward. The bottom row shows in different colors the bins with matching and opposing signs between the two analysis methods

As mentioned above, using the AC satellite pair, it is possible to reliably estimate currents also in those situations where single satellite methods do not work well due to complicated current geometry. Figure 3.10 shows the differences in the statistical results obtained using a single satellite method and the Swarm/SECS analysis. In both cases data from the A and C satellites was used, but in the single satellite analysis, the were analyzed using only 1D SECS, assuming vanishing gradients in the magnetic zonal direction. In order to get a feeling of relative magnitudes, the differences shown in Fig. 3.10 can be compared with the median currents shown in Fig. 3.9.

Both the 1D and Swarm/SECS methods give very similar pattern for the median currents, but the difference plots shown in the upper row of Fig. 3.10 reveal some systematic dissimilarities between the two methods. The dual satellite Swarm/SECS method gives slightly stronger R1 currents in both dawn and dusk sides, and also slightly stronger downward R2 currents around noon. These differences are also reflected in the southward current ($J_\theta$), which is mostly curl-free closure current associated with the FAC. For the east/west electrojet current $J_\phi$, the dual satellite method gives stronger eastward currents in the early afternoon, but weaker westward current in the early morning (03–07 MLT). In the Harang discontinuity region (22–24 MLT) the dual satellite method gives stronger westward current at high latitudes.

Nevertheless, plots in the bottom row of Fig. 3.10 show that while there are differences, the two methods generally give the same direction for the current components. Different directions (yellow and dark blue) are mostly encountered only in regions with small median current amplitudes. However, the differences between the single and dual satellite techniques get larger in the upper and lower quartiles and higher percentiles. This indicates that the stronger currents that dominate the tails of the distributions exhibit more complicated spatial structures, which are not captured so well in the single satellite analysis.

3.6 Conclusions, Discussion, and Future

This chapter describes how the Spherical Elementary Current Systems, discussed in detail in Chap. 2, can be used to analyze data from the multi-satellite Swarm mission. By fitting 1D/2D and CF/DF SECS to the magnetic data from the AC satellite pair, both the field-aligned and ionospheric horizontal currents can be estimated. This way the Swarm/SECS method gives a two-dimensional latitude–longitude picture of the currents around the satellite paths. In contrast to ground-based magnetic measurements, which give only the ionospheric equivalent currents, the Swarm/SECS method gives an estimate of the actual current. Data of the third Swarm satellite can also be used in the fitting.

If electric field data were available, a similar estimate of the two-dimensional distribution of the ionospheric electric field could be obtained. By combining the estimated horizontal current and electric field, the ionospheric Pedersen and Hall conductances could also be estimated.

A large number of the 2D current maps have been calculated and released to the community. The analysis has been carried out at the Finnish Meteorological Institute, and the results are available at http://space.fmi.fi/MIRACLE/Swarm_SECS/. This dataset forms an excellent basis for event studies and statistical investigations of auroral current systems, as discussed in Sects. 3.4 and 3.5 above.

As polar orbiting spacecraft, Swarm regularly pass over various ground-based instrument networks, such as the MIRACLE and other instruments located in northern Europe. These passes offer excellent opportunities for combining different datasets, both in event studies and statistical efforts. For example, in the case of currents, satellite magnetic measurements can reveal the FAC and curl-free part of the ionospheric horizontal currents, whereas ground-based measurements, due to their smaller distance from the ionospheric currents, give a better view of the divergence-free (or equivalent) currents. In fact, there is no reasons why both ground- and satellite-based magnetic data could not be used simultaneously in the Swarm/SECS analysis, which might further improve the results over magnetometer networks.

Combined with other data from the Swarm satellites and ground-based instruments, like electric field data and auroral images, such precise estimates of ionospheric horizontal currents and FAC can reveal the details of ionospheric electrodynamics and magnetosphere–ionosphere coupling.