Abstract
This chapter deals with flow, transport and reaction processes in porous and heterogeneous media characterised by multiple spatial scales. Although the governing equations, at the micro-scale, are simple (and often linear), complex upscaled (effective macro-scale) phenomena can emerge, due to the averaging process. After introducing some general concepts related to multiscale porous media, we present the Darcy’s equation and its assumptions and extensions. A more detailed analysis of dispersion theories for pore-scale and continuum-scale (with Darcy’s flow) solute transport is then carried out, presenting the classical results as well as the most recent research in the field. We then focus on the interaction between dispersion and reaction, through mixing, as well as more complex processes like particle deposition and multiphase flows.
You have full access to this open access chapter, Download chapter PDF
Similar content being viewed by others
Keywords
5.1 Introduction
Countless environmental, industrial and biological applications involve fluids flowing through complex media or heterogeneous environments. These can be soil, sand and rocks in aquifers and reservoirs, industrial separation and filtration devices, biological membranes and tissues, composite materials. Although all the fundamental laws and modelling approaches of fluid dynamics still apply, a completely different perspective has to be taken to deal with geometrical and physical complexity and multiscale structure of the underlying media. This is generally done by means of upscaling or averaging techniques, not different than the ones used to deal with the multiscale structure of turbulence. The main difference between flows through porous media and turbulent flows lies in the fact that the latter is an emerging phenomena purely due to the nonlinearity of the Navier–Stokes equations, while the former inherits its multiscale complexity directly from the geometrical and physical properties of the material. This means that, even starting from linearised or simplified flow regimes (e.g., Stokes), interesting emergent macro-scale dynamics can appear due to these properties. The ultimate scientific challenge is to develop a quantitative link between the properties of the media and the upscaled parameters in the macroscopic dynamics. Although a wide range of these emerging dynamics are more easily observed and studied than the turbulent structures (which, by nature, are hardly reproducible),Footnote 1 the high dimensionality of the set of all possible geometrical structures makes a systematic research and a predictive model development (e.g., closures, parameter estimation, etc.) particularly challenging. As turbulence models are naturally first developed and tested on clearly defined scenarios (such as the periodic isotropic turbulence or wall-bounded flows), similarly upscaled porous media models have traditionally been derived from simple granular materials, such as sphere packings. While the former usually assume the existence of a continuum of length scales, as dictated by the classical turbulence theory, the latter typically rely on clearly defined and well-separated scales (usually two or possibly more). These assumptions, however, are only very crude approximations of the actual natural and engineered media, and can lead to significantly misrepresent the overall transport processes.
In this chapter, while presenting the fundamentals of flow and transport through porous media (intended in the classical sense) and some of the specific methodologies and challenges, we take a more general point of view, focused on the underlying upscaling procedures and their assumptions, to help smooth out the still existent barrier between porous media and fluid dynamics research.
5.2 Flow Through Porous and Heterogeneous Media
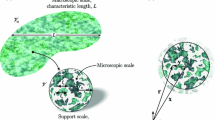
As already mentioned, although the concept of upscaling and averaging is present in many fluid dynamics problems, particularly relevant to many applications is the understanding of the emerging dynamics of fluid flowing through multiscale (porous) materials. As we will discuss in Sect. 5.2.1, the peculiarity of this problem is due to the presence of large surface areas where no-slip conditions generate, in the first approximation, linear damping in the momentum equation, proportional to an effective parameter known as permeability of the media. However, natural porous materials, such as soil and rocks, can have a highly irregular and heterogeneous structure, causing this emerging effect to be significantly space-dependent. Due to the limited a priori knowledge of the exact geology, this space heterogeneity is often modelled as a random field. This gives rise to another important upscaling problem, namely understanding the effect of meso- and macro-scale heterogeneities in the permeability. This is discussed in Sect. 5.2.3.
In both cases, crucial to the upscaling process is the solution of a closure problem, solved on a representative elementary volume (REV). This can be understood at different levels. The first simple definition of REV can be based solely based on geometrical information such as the porosity of the material, ϕ, i.e., the volume fraction of void space available for the fluid. This, being a very simple averaging process, can be computed on different length scales ℓ, i.e., ϕ = ϕ(ℓ). For increasing ℓ, if the media has only finite-size heterogeneities (or well-separated scales) and no fractal structure, this converges to a finite number 0 < ϕ 0 < 1. This implicitly defines a minimal REV of size ℓ ϕ. Even assuming the existence of this well-defined REV, the actual upscaling of transport and flow processes involves the average of fluctuating quantities (or closure variables), which are solutions of a differential model. This might require a much larger size to converge to a constant. For periodic structures, in the assumption of stationary (fully developed) profiles and local equilibrium (imposed through the pseudo-periodicity of the variables), the periodic cell represents not only the geometric REV but also the right REV for all processes. Relaxing these periodicity assumptions means allowing random “perturbation” in the material that results in a larger geometrical REV, and, possibly, in perturbation in the solution persisting over bigger scales. This means that, to obtain well-defined (e.g., space-independent) macroscopic effective parameters, the existence and size of the REV cannot be known a priori and could be significantly larger than the one obtained from purely geometrical considerations. This consideration applies not only to the upscaling of the flow discussed below (which could indeed need a REV much larger than the geometrical one) but also to the upscaling of transport and reaction processes (discussed in Sect. 5.3), and, more significantly to all non-linear and more complex models (such as multiphase flows).
5.2.1 Darcy’s Law
The earliest approaches to the study of flow in porous media were directed to the derivation of simple linear relation between pressure drop and superficial velocity, and implicitly made use of a macroscopic description of a continuous (pseudo-homogeneous) fluid–solid domain. Henry Darcy, who investigated the sand filter system employed in the delivery of freshwater to the city of Dijon, first proposed this relation, now known as Darcy’s law:
where δP is the integral pressure drop (or the so-called pressure head, including hydrostatic pressure) across the porous medium, L is its length and thus characterises flow in saturated porous media via its permeability, K, and the fluid superficial velocity q. This law, originally derived on purely phenomenological and experimental grounds, can be intuitively extended in three dimensions, as a force balance between pressure gradient and linear wall stresses, neglecting the transient and inertial term in an upscaled form of the Navier–Stokes equation:
where K can now be more generally a symmetric tensor, not necessarily isotropic, i.e., pressure gradients in one direction can possibly cause flow to happen in an arbitrary direction, due to non-symmetric porous structures. This result can also be rigorously derived using the tools of homogenisation or volume-averaging [1, 2], upscaling the incompressible Stokes’ law to obtain Darcy’s law. Equation (5.1), while still being useful in many porous media systems, has been found to have its limitations. The first is related to the relative magnitude of the superficial velocity q. More appropriately, and by analogy with the usual analysis of the laminar–turbulent flow transition, it can be expressed in terms of the Reynolds number where the system’s characteristic length is the average grain diameter or pore width. As such, in the vast majority of cases, Darcy’s law will find an upper range of validity at Re ranging from one to ten [3]. Other cases, where a more complex equation has to be used, include the already mentioned fractal porous media (where the permeability is no more a constant but a non-local kernel), multiphase flows, non-Newtonian fluids, non-equilibrium flows.
5.2.2 Extensions of Darcy’s Law
For high Reynolds numbers, the linear relationship expressed in Eq. (5.1) between superficial velocity and the hydraulic gradient (δP∕L) ceases to be valid, making Darcy’s law unsuitable for describing the nonlinearities arising under these conditions. Although there has been some controversies [4, 5] about the correct extension of Darcy’s law to transitional and turbulent flows, the most commonly used equation that can be used to that end is the Darcy–Forchheimer equation:
where β is the so-called inertial flow parameter and, like K, is independent of fluid properties and only depends on the microstructure of the porous medium. Various attempts at an explanation of this phenomenon have been made: the most intuitive of which would be to ascribe this nonlinearity to the onset of turbulence, by immediate analogy with the relationship between head loss and fluid velocity for the flow in pipes, which becomes non-linear right after the transition to the turbulent region corresponding to higher Reynolds numbers. The problem with this approach is that, while for the flow in pipes the laminar and turbulent zones are clearly identifiable, the transition in the case of flow in porous media is much smoother, with no clear separation between the two: this can be related to what is known for flow around spheres, where the same behaviour is found. A number of experiments were conducted in the past to identify the critical Reynolds number associated with the transition to the turbulent zone in porous media, and found it to be several orders of magnitude higher than the Re at which the nonlinearities begin to become apparent [6].
Beyond these difficulties caused by non-trivial changes in the fluid dynamic structure at the pore-scale when transitioning to high Reynolds numbers, there are also a number of other notable extensions, for which, brief pointers follow.
Multiphase and Unsteady Flows
While single-phase flow in porous media (also known as saturated) are generally steady, a trivial extension is to add a time derivative term to model unsteadiness caused, for example, by time-dependent pressure boundary conditions. However, when dealing with multiphase flows, the time-dependence naturally appears. While density-driven miscible Darcy’s flows are easily obtained, immiscible multiphase extensions of the Darcy’s equation rely on much stronger assumptions (see also the discussion in Sect. 5.5). The simplest form of multiphase flow is the Richards’ equation that describes a water plume travelling through a steady Darcian flow field.
Brinkman
One early and well-known approach to bridge the gap between the free flow and the Darcy’s descriptions was put forward by Brinkman, whose eponymous equation adds a viscous term to the Darcy’s equation (usually with an effective viscosity which is not necessarily equivalent to the viscosity of the fluid). Rigorous derivations of the Brinkman equation with homogenisation have been proposed [1], with the contemporary presence of the Darcy and Brinkman terms, under a specific scaling for the geometrical properties of the porous structure. Furthermore, the Brinkman equation has found interesting applications as a unified numerical approximation (e.g., penalisation approaches [7]) that, for limiting cases, can recover both Stokes and Darcy equations.
Non-Newtonian
When considering non-Newtonian fluids, the Darcy’s law for low fluid velocities is still used, with a modified “porous medium viscosity” comprising the non-Newtonian effects. In the higher velocities ranges, the interplay between shear-thickening effects and turbulent nonlinearities becomes more difficult to understand: both formal attempts of upscaling via volume-averaging [8] and accurate computational pore-scale simulations in reconstructed geometries [9] have been presented.
Knudsen
Finally, the constant assumption of all the theory presented up until this point (and henceforth, excluding this paragraph) has been that of considering the fluid as a continuum and as such, to employ the mentioned no-slip condition on the solid matrix boundary. In practice, many real-world systems (e.g., rarefied gases, shale gas) are characterised by Knudsen flow, and are not treatable within the usual framework, leading to non-trivial additions of slip-flow corrections to effective permeability.
5.2.3 Heterogeneous Media
As described in the previous section, the (space) averaged flow behaviour on the scale of a REV is described by the Darcy’s equation. Here we consider the transition from the Darcy to larger scales of heterogeneity. For geological porous media, this means an order of metres or hundreds of metres. Here, spatial or ensemble (considering random realisations of geological structures) averaging, or a combination of both, can be used to study emerging macroscopic dynamics. We denote here both averaging operation with the bracket notation \(\left <{\cdot }\right >\) and we limit our discussion to the steady state Darcy flow equation with heterogeneous medium properties
which is equivalent to a Laplacian equation for the pressure. This description implies that the flow field is helicity-free, i.e., q(x) ⋅∇×q(x) = 0. This means that there are no closed streamlines in d = 2 dimensional Darcy flow. For d = 3 dimensions, zero helicity implies that streamlines are either closed or organised on two-dimensional toruses [10]. These topological properties prohibit chaotic flow and thus have an impact on the stretching of material lines and surfaces.
The systematic upscaling of flow and transport upscaling in heterogeneous porous media has been performed with stochastic approaches in order to model the spatial variability of permeability [11,12,13]. This is motivated, on the one hand, by the incomplete knowledge of the small scale fluctuations of K(x), and on the other hand by the desire to identify the large scale behaviour due to “typical” spatial random fluctuations and quantify it in terms of only a few geo-statistical characteristics. This requires certain assumptions such as statistical stationarity and ergodicity. In this framework, the log-permeability \(f(\mathbf x) = \ln [K(\mathbf x)]\) has been modelled as a multi-Gaussian random field, which implies that K(x) is a multi-lognormal random field. This can be understood as follows. Consider a set of f(x) values evaluated at positions x i (i = 1, …, n) in the medium. The set \(\{f(\mathbf x_i)\}_{i=1}^{n}\) is modelled now as a spatial stochastic process, which is characterised by a joint Gaussian PDF characterised by the covariance matrix \(C_{ij} = \mathcal C(\mathbf x_i-\mathbf x_j)\),
The variance of f(x) is given by \(\sigma _{ff}^2 = \mathcal C(\mathbf 0)\). The covariance \(\mathcal C(\mathbf x)\) is typically modelled as a short-ranged function that decays on characteristic length scales, the correlation lengths. For an overview of common covariance models, see Refs. [11,12,13]. A statistically isotropic medium is characterised by a single correlation scale ℓ. For anisotropic media, the correlation scale depends on the spatial direction.
In this framework flow is upscaled in terms of an effective permeability K e tensor [14, 15], which is defined by
Here we focus on statistically isotropic media, for which \(K^e_{ij} = K^e \delta _{ij}\). Note that K e is in general not equal to the arithmetic average 〈K(x)〉.
In the following, we first report on some exact results for the effective permeability for flow in layered media and two-dimensional multi-Gaussian permeability fields. Then we discuss briefly perturbation theory results and conjectures for three-dimensional media.
Exact Solutions
For layered porous media, permeability is constant along one of the coordinate axis and variable in the other directions. This means the correlation length is infinite along one coordinate axis. For simplicity, we consider the case of 2 spatial dimensions. For a pressure gradient parallel or perpendicular to the layering exact solutions for the effective permeability exist. The direction of the mean pressure gradient in the following is aligned with the x-direction.
For flow aligned with the direction of stratification, the flow problem has an exact solution, which is
In this case, K e = K A = 〈K(y)〉, the effective permeability is equal to the arithmetic mean permeability. For flow perpendicular to stratification, the exact solution is
where L is the length of the flow domain. Here the effective permeability is given by the harmonic mean K e = K H = 1∕〈K(x)−1〉.
For flow in isotropic two-dimensional multi-lognormal permeability fields with finite correlation length, the effective permeability is exactly given by the geometric mean [16, 17],
This result can be derived based on a duality between stream function and flow potential using the fact that both K(x) and 1∕K(x) are lognormal distributed.
Perturbation Theory
For three-dimensional heterogeneous porous media, the duality argument invoked for two dimensions does not hold. Thus, the effective permeability has been determined using perturbation theory in the fluctuations of log-permeability about its mean value, f′(x) = f(x) −〈f(x)〉, which gives [18,19,20]
which is strictly valid only for \(\sigma _{ff}^2 \ll 1\). For larger values of \(\sigma _{ff}^2\) and d spatial dimensions, Matheron [18] conjectured the expression
which for d = 2 gives the exact result K e = K G and in d = 3 and small \(\sigma _{ff}^2 \ll 1\) is consistent with the perturbation theory result Eq. (5.10). The effective permeability is bounded between the harmonic and arithmetic mean, K H ≤ K e ≤ K A.
5.3 Macroscopic Transport Models
Transport in heterogeneous media can be described by the advection–dispersion equation
At the pore-scale, the velocity field v(x) is obtained from the Stokes equation and the dispersion tensor reduces to D = D m I, where D m is the molecular diffusion coefficient and I the identity matrix. At the Darcy scale, a similar equation can be derived by homogenisation or volume-averaging [1, 2], with the flow velocity given by v(x) = q(x)∕ϕ, where ϕ is porosity, which here is assumed to be constant, and the dispersion tensor D(x) given by the solution of a closure problem. Alternatively, dimensional and phenomenological arguments can lead to the following parameterisation [21, 22]:
where α 0 D m is the effective diffusivity (see Sect. I), and α ijkl are geometrical dispersivities. For an isotropic medium, the α ijkl are given by
This description of dispersion is valid at high Péclet numbers. The Péclet number compares the relative strength of diffusive and advective transport mechanisms and is here defined as Pe = V L∕D, where L is a characteristic heterogeneity length scale and V a characteristic velocity.
The advection–dispersion Eq. (5.12) is equivalent to a Ito’s stochastic differential equation [23, 24] for the position x(t) of a solute particle
where ξ(t) is a Gaussian white noise of zero mean, 〈ξ(t)〉 = 0 and covariance 〈ξ i(t)ξ j(t′)〉 = δ ij δ(t − t′). Equation (5.15) is the starting point for random walk particle tracking simulations for the solution of advective–dispersive transport in heterogeneous porous media.
A key issue for transport in heterogeneous media is to quantify the transport behaviours on a scale larger than the characteristic heterogeneity scale. For the transition from pore to Darcy scale, the observation scale is larger than the characteristic pore length, for the transition from Darcy to regional scale, it is larger than the correlation scale of permeability. In the following, we briefly report on upscaling efforts in terms of Fickian transport formulations, the occurrence of anomalous dispersion and modelling approaches to account for non-Fickian transport.
5.3.1 Fickian Dispersion
Before discussing Fickian large scale transport formulations, we briefly summarise some signatures of Fickian transport for one-dimensional transport at constant velocity v 0 and diffusion coefficient D 0. Firstly, for a point-like solute injection, the concentration distribution is Gaussian shaped as
The first and second centred moments of c(x, t), denoted by m(t) and κ(t) evolve linearly in time as m(t) = v 0 t and κ(t) = 2D 0 t. Solute breakthrough, i.e., the distribution of solute arrival times at a control plane located at the distance x from the plane at which solute is injected, is given by the inverse Gaussian distribution
Hydrodynamic Dispersion
As already mentioned, the upscaling of transport from the pore to the Darcy scale can be approached by stochastic approaches [25], spatial averaging and homogenisation. Under the assumption of local physical equilibrium, these approaches derive for the (homogeneous) Darcy scale the advection–dispersion Eq. (5.12). The hydrodynamic dispersion tensor D accounts for the impact of molecular diffusion and pore-scale velocity fluctuations on Darcy-scale solute transport. It is in general a function of the Péclet number. This has been observed both for the longitudinal, i.e., the mean flow direction, and the transverse dispersion coefficients D L and D T. For Pe ≪ 1, D L∕D ∼ 1, for 1 < Pe < Pec, it behaves as D L∕D ∼Peγ, with 1 < γ < 1.5, and for Pe > Pec it scales as D L∕D ∼Pe. The critical Péclet number is Pec ≈ 400 − 500 [26, 27]. These behaviours can be described by the expression [22]
where α accounts for the effect of the tortuous pore geometry on molecular diffusion in the bulk and δ is a parameter that characterises the shape of the pore channels and \(\overline v\) is the average pore velocity. The second term on the right-hand side of Eq. (5.18) is termed mechanical dispersion. It quantifies solute spreading due to the tortuous streamlines and velocity variability of the pore-scale flow field. Bear [22] proposes to use expression Eq. (5.18) also for the transverse dispersion coefficients D T. Experimental data suggest that D T∕D ∼Pe0.95 for 1 < Pe < Pec [28].
Macro-Dispersion
For transport upscaling from the Darcy to the regional scale, stochastic perturbation theory gives for macro-scale transport the advection–dispersion equation [20]
where the x-axis of the coordinate system is aligned with the mean hydraulic gradient. The Péclet number here is defined as Pe = 〈q〉ℓ∕D L. For a statistically isotropic heterogeneous porous medium, the macro-dispersion tensor D ∗ is diagonal. For Pe ≫ 1, the longitudinal macro-dispersion coefficient D L is given by
where the dots denote contributions of the order of D L and of order \(\sigma _{ff}^2\). This remarkable result relates the macroscopic dispersion effect due to local scale velocity fluctuations to the statistical medium properties in terms of the variance \(\sigma _{ff}^2\) and correlation length ℓ of log-permeability and the geometric mean permeability. Perturbation theory in \(\sigma _{ff}^2\) predicts that \(D^\ast _T\) is of the order of D T, this means local scale dispersion. While this is exact for two dimensions [29], observations and numerical simulations suggest that it is not valid for three dimensions [30, 31]. In fact, numerical results suggest that \(D_T^\ast \propto \sigma _{ff}^4\) in the advection-dominated limit of Pe →∞. The reader is referred to the textbooks by [11,12,13] for a thorough account of the macro-dispersion approach and stochastic perturbation theory for macro-scale transport in heterogeneous porous media.
5.3.2 Anomalous Dispersion
Fickian dispersion predicts that the first and second centred moments of a solute plume increase linearly with time that the solute distribution is Gaussian shaped, and solute breakthrough can be described inverse Gaussian distributions. Furthermore, within the Fickian dispersion paradigm, mixing is fully characterised by the constant dispersion coefficients. For heterogeneous porous media, and heterogeneous media in general, however, transport does not generally follow Fickian dynamics. Breakthrough curves are characterised by strong tailing, dispersion evolves in general non-linearly in time and spatial plumes do not show Gaussian shapes and are in general characterised by forward or backward tails. Such behaviours are closely related to the notion of incomplete mixing on the support scale. If the support scale is not fully mixed, for example, due to mass transfer between sub-scale mobile and immobile regions, or velocity variability, transport dynamics are history-dependent. Non-Fickian and anomalous transport behaviours have been observed both on the pore [32,33,34] and Darcy scales [35, 36].
The mechanism that mixes the support scale is diffusion (pore-scale) and hydrodynamic dispersion (Darcy scale). Note that ultimately the mechanism that attenuates concentration contrasts is diffusion. Mechanical dispersion quantifies the spread of a solute distribution due to advective heterogeneity and the formation of filaments, which facilitates the action of diffusion to homogenise concentration, and is discussed further in Sect. 5.3.3. Thus, for high Péclet numbers, the characteristic mixing time scales over the support scale may be significantly larger than the time scale of interest. The prediction of transport in heterogeneous media requires approaches that allow to quantify non-Fickian transport dynamics.
The moment equations and projector formalism approaches [37, 38] are obtained from the stochastic averaging of the local scale heterogeneous transport problem, Eq. (5.12), which yields space- and time-non-local integro-differential equations, whose memory kernels are related to the heterogeneity statistic. Closed-form expressions for the memory kernels are in general difficult to obtain. Fractional advection–dispersion equations [39, 40] are characterised by spatio-temporal kernel function with an asymptotic power-law scaling. This approach can be related to continuous time random walks and Levy flights [41]. In the following, we provide a summary of the continuous time random walk (CTRW) and multi-rate mass transfer (MRMT) frameworks to describe anomalous dispersion in porous media. The CTRW [42,43,44], and related time domain random walk (TDRW) [45, 46] frameworks, as well as the MRMT approach [47, 48] have been used for transport upscaling in highly heterogeneous porous and fractured media. These approaches account for the heterogeneity-induced distribution of advective and diffusive mass transfer rates and residence times.
5.3.2.1 Continuous Time Random Walks
The continuous time random walk (CTRW) [49, 50] models particle motion as a random walk in space and time. The concentration distribution, or equivalently, the particle density c(x, t) is given by
where R(x, t)dxdt is the average number of times a particle is in [x, x + dx] × [t, t + dt]; ψ(x, t) is the joint PDF of transition length and time. Thus, the right-hand side of Eq. (5.21) denotes the frequency by which a particle arrives at a position x at time t′ times the probability that it stays (waits) there for a time smaller that t. R(x, t) satisfies the Chapman–Kolmogorov type equation
The first term on the right-hand side denotes the initial particle distribution at time t = 0. Combining Eqs. (5.21) and (5.22) gives the generalised master equation [51]
where the memory kernel \(\mathcal K(x,t)\) is defined by its Laplace transform [52] as
Laplace transformed quantities are denoted by an asterisk, the Laplace variable is denoted by λ. For short-ranged spatial transitions, Eq. (5.23) can be localised in space such that
where the advection and dispersion kernels are defined by
The fluctuating micro-scale transport dynamics are encoded in the joint PDF ψ(x, t). For purely advective solute transport, for example, the transition length is of the order of the correlation scale ℓ c of the velocity magnitude v, and the transition time is given kinematically by ℓ c∕v. The distribution p s(v) of the particle speed sampled equidistantly along a streamline is related to the Eulerian velocity PDF by flux-weighting as [53]
Thus, the joint PDF of transition length and time is
For transport at an average velocity v 0 over the characteristic length ℓ 0 combined with mass transfer into immobile zones, the transition time distribution is given in Laplace space by Margolin et al. [54]
where τ 0 = ℓ 0∕v is the advective transition time, γ t the trapping rate and p f(t) the distribution of residence times in the immobile regions.
We briefly summarise the transport characteristics for an uncoupled CTRW, this means ψ(x, t) = Λ(x)ψ(t), characterised by a power-law long-time scaling of the transition time distribution as ψ(t) ∼ t −1−β with 0 < β < 2. Such heavy tailed transition distributions imply strong particle retention and thus memory effects. The power-law in ψ(t) directly relates to the solute breakthrough curves. Note that the breakthrough time at a control plane is the sum of n transition times τ i, where n may be approximated by the average number of spatial steps needed to arrive at the control plane. Thus, the generalised central limit theorem implies that the breakthrough curve scales as f(t, x) ∼ t −1−β. The first and second centred moments of the solute distribution scale asymptotically as m(t) ∼ t β and κ 2(t) ∼ t 2β for 0 < β < 1 and as m(t) ∼ t and κ 2(t) ∼ t 3−β.
For advective transport upscaling, the CTRW framework has been used together with Markov models for series of velocity magnitudes along streamlines [55,56,57], which allow for the evolution of the transition time distribution with increasing step number and for the conditioning of transport on initial particle velocities [53]. The CTRW framework has been employed for transport modelling in a wide range of fluctuating environments ranging from the diffusion of charge carriers in impure semi-conductors [50] to diffusion in living cells [58], see also [41, 59].
5.3.2.2 Multi-Rate Mass Transfer
The multi-rate mass transfer (MRMT) approach [47, 48] separates the support scale into a mobile continuum and a suite of immobile continua, which communicate through linear mass transfer. At each point, the immobile concentration c im(x, t) is related to the mobile concentration c m(x, t) through the linear relation [48]
The evolution of the mobile concentration is given by the advection–dispersion equation [47]
where ϕ im and ϕ m are the immobile and mobile volume fractions. The memory function φ(t) encodes the mass transfer mechanisms between the mobile and immobile continua. For diffusive mass transfer into slab shaped immobile regions, the memory function is defined by its Laplace transform as [48, 60]
where τ D is the characteristic diffusion time across the slab. For spherical inclusions, the memory function is
For purely diffusive mass transfer the MRMT approach is equivalent to transport under matrix diffusion [61], which describes transport in fractured media under diffusive mass transfer between the fracture and the rock matrix. In general for diffusive mass transfer, the memory function is obtained from the solution of a diffusion problem in a heterogeneous immobile domain [62].
For first-order mass transfer at a single rate ω the memory is given by
Oftentimes, the mass transfer processes and the geometries of immobile regions are not known in detail. The memory has then been modelled by a superposition of multiple first-order memory functions as [35, 47, 48]
where \(\mathcal P(\omega )\) is the rate distribution, which may be related to the volume fractions of the immobile zones, for example. Other approaches use parametric forms for the memory function, such as truncated power-laws [63].
In this framework, the behaviour of solute breakthrough at asymptotic times follows the time derivative of the memory function
This means, for a memory function, which asymptotically behaves as a power-law φ(t) ∼ t −β, the breakthrough curve scales as f(t, x) ∼ t −1−β [35, 64]. For matrix diffusion into a semi-infinite slab, the memory function scales as φ(t) ∼ t −1∕2 and consequently the breakthrough curve as f(t, x) ∼ t −3∕2, which is a signature of matrix diffusion.
Both the CTRW and MRMT frameworks share similar phenomenology in that they account for memory effects due to a distribution of characteristic mass transfer time scales. The correspondence between the two pictures was discussed in [64,65,66,67]. The time behaviour of the spatial moments of the concentration distribution is similar to the ones described by an uncoupled CTRW [64].
5.3.3 Mixing and Chemical Reactions
In this section, we are concerned with mixing and reactions in heterogeneous porous media. As chemical reactions are contact processes, mixing and dispersion are key processes for the sound quantification of chemical reactions in heterogeneous media. This refers both to homogeneous, i.e., fluid–fluid, reactions, and to heterogeneous, i.e., fluid–solid, reactions, as outlined in the following. We will first discuss the notions of mixing and dispersion, and specifically the difference between these two processes. Then, we discuss chemical reactions under spatial heterogeneity.
5.3.3.1 Mixing, Diffusion and Dispersion
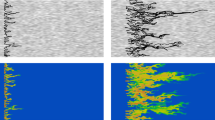
In Fickian transport descriptions, the process that leads to the mixing of initially segregated solutes or the mixing of an initially concentrated solute into the ambient fluid is mass transfer due to diffusion or dispersion. From expression Eq. (5.16) we obtain directly that the maximum concentration c m(t) in one dimension decays as \(c_m(t) = 1/\sqrt {4 \pi D t}\). In d spatial dimensions one finds that c m(t) = 1∕(4πDt)d∕2. Mixing due to molecular diffusion on mesoscopic length scales L is in general slow. The characteristic mixing time is given by τ m = L 2∕D. For a free fluid, stirring or chaotic flow accelerates the mixing process in that it generates laminar structures [68] whose size l(t) increases exponentially fast with time, \(l(t) = l_0 \exp (\lambda t)\), where λ here is the Lyapunov exponent. The width of the lamellar structures is limited by stretching and diffusion to the Batchelor scale \(s_B = \sqrt {D/\lambda }\) [69]. The number of lamellae in a closed area of size A = L 2 increases exponentially fast as n(t) ∼ ℓ(t)∕L, while each lamella occupies an area of A ℓ ∼ s B L. Complete mixing is achieved when n(t)A ℓ ∼ L 2. This gives a mixing time \(\tau _m = \lambda ^{-1} \ln (L^2/\ell _0 s_B)\) which is in general much shorter than the mixing time by diffusion only.
Mixing and Spreading in Porous Media
Here we are concerned with mixing in flows through heterogeneous porous media. We have seen above that solute transport has been quantified in terms of hydrodynamic dispersion (pore to Darcy scale) and macro-dispersion (Darcy to regional scale), which simulates that the support scale is well-mixed. This Fickian paradigm, however, breaks down for transport in heterogeneous media, for which anomalous or non-Fickian transport behaviours are observed. These involve history-dependence, which implies that the support scale cannot be considered well-mixed. Unlike for stirring in a free fluid, for porous media flows, the “stirring” is done by the medium itself, whose structure leads to tortuous path-lines and velocity heterogeneity. Chaotic flow patterns are in general prohibited topologically for steady two-dimensional flows. In three dimensions, steady pore-scale flow is chaotic [70], which may lead to similar mixing as in chaotic flow in a free fluid [71]. The existence of low velocity regions, stagnant zones in the wake of solute grains, velocity variability between pores and intra-grain mass transfer, however, leads to incomplete mixing on the REV scale and thus history-dependent transport [72, 73].
The topological properties of Darcy-scale flow through porous media prohibit chaotic flow [74], see also Sect. 5.2.3. Thus, while the action of the spatially variable flow velocity leads to the creation of lamellar structures [75], their lengths cannot increase exponentially fast [76]. In fact, the extension of a solute distribution due to such advection-induced spreading can be measured by the concept of macro-dispersion. When lamellae form along the mean flow direction, the separation distance between them is given by the characteristic transverse heterogeneity length scale ℓ. Thus, the time scale to mix the heterogeneous concentration distribution is given by the time for transverse dispersion over the distance ℓ, τ D = ℓ 2∕D T. These mechanisms are accounted for by effective dispersion coefficients [77, 78]. Unlike macro-dispersion, the concept of effective dispersion does not account for the effect of purely advective spreading [79, 80], but quantifies the combined effect of local scale dispersion and advective heterogeneity, which eventually leads to mixing.
Scalar Dissipation and Concentration Statistics
In order to illustrate the relative role of local scale dispersion and spreading as quantified by macro-dispersion in solute mixing, we consider the evolution of the variance of the concentration fluctuation about its ensemble mean value, c′(x, t) = c(x, t) −〈c(x, t)〉, defined here by
From the Darcy-scale advection–dispersion Eq. (5.12) one can derive [81]
The first term on the right-hand side is denoted as scalar dissipation rate. It quantifies the destruction of concentration variance due to local dispersive mass transfer. The second term on the right-hand side quantifies the creation of concentration variance due to spreading as quantified by macro-dispersion.
The mixing process can also be described in terms of the evolution of the PDF of concentration values c(x, t) in the heterogeneous mixture, which can be defined by
Based on the advection–dispersion Eq. (5.12) one can derive the following evolution equation for the PDF [82]:
The term on the right-hand side is the average over the local dispersive flux terms conditional to concentration, which represents a closure problem. The celebrated interaction by exchange with the mean (IEM) closure [83] approximates this expression as
where γ IEM is a rate constant that may be related to local scale dispersion and the local dissipation scales. This closure implies for the scalar dissipation rate
This closure approximation has been applied to predict mixing in heterogeneous porous media, but is not able to match the numerically observed evolution of the scalar dissipation rate [84]. The IEM closure has several shortcomings for porous media mixing. Firstly it implicitly assumes that the concentration PDF is Gaussian shaped or approximately Gaussian, while in porous media they are typically highly non-Gaussian [75]. Secondly, it assumes a constant local mixing scale, while the mixing scale in porous media evolves with time [85]. Alternative approaches employ parametric forms for the concentration PDF, such as beta-distributions, which can be parameterised by the concentration mean and variance [86], mapping approaches [87] and stochastic mixing models for the evolution of concentration [88].
Lamellar Mixing
Recently, the problem of mixing in porous media has been addressed using a lamellar mixing approach [75, 89]. The mixing process can be roughly separated in two regimes. In an early time regime, the initial solute distribution spreads out and advective heterogeneity generates a lamellar organisation of the concentration field. In the late time regime, the lamellar organisation is destroyed due to coalescence of adjacent lamellae. In both regimes, the concentration PDF can be constructed in terms of the concentration contents of individual lamellae and their interactions.
In the early time regime, lamellae are non-interacting and the evolution of the concentration content of the mixture can be understood by the superposition of the concentration contents of isolated lamellae, which is fully determined by fluid stretching and local scale dispersion [69, 90]. The concentration across a stretched lamella is Gaussian shaped and given by [75]
where z is the coordinate across the lamella, ℓ(t) = l(t)∕l(0) the relative strip elongation and s 0 the initial strip width. Note that the concentration here depends on the elongation ℓ(t). The PDF of concentration values across a strip is then given by
where 𝜖 is a lower concentration cut-off and c m(t) = c(z = 0, t) is the maximum strip concentration, which again depends on elongation ℓ(t). For heterogeneous media, the strip elongation ℓ(t) is the result of the random deformations a strip experiences as it is transported through the medium. For heterogeneous porous media, elongation is dominated by intermittent shear events along a trajectory [76]. The mean elongation may follow power-law behaviours 〈ℓ(t)〉∼ t α with 1∕2 < α < 2. The maximum concentration can be approximated by \(c_m(t) \approx 1/\ell (t) \sqrt {Dt}\) [75], because it decays at the same rate as the area of the lamella increases. Thus, the PDF of elongation can be mapped onto the PDF p m(c m, t) of maximum concentrations, and the global concentration PDF is obtained through superposition of the local laminar PDFs as
The decisive step here is to recognise that the concentration field at early times is organised in a lamellar structure and that the concentration content of a lamella depends explicitly on the strip elongation. This allows obtaining the concentration PDF by mapping from the PDF of strip elongations.
With increasing time, the length of the lamellae becomes larger than the mixing support, which increases slower than the lamella elongation (\(\sim \sqrt {t}\) for dispersive growth), or is constant in the case of a confined domain. Thus, the lamellae need to fold back to each other, which in the late time regime leads to diffusive overlap and the formation of lamella aggregates through a random aggregation process. The PDF of maximum concentrations of lamella aggregates after n aggregations is given by the gamma distribution [69]
In the centre of the plume, the number n(t) of lamellae in the aggregate is related to the average maximum concentration as \(n(t) \langle c_m(t) \rangle \sim 1/\sqrt {\kappa ^\ast (t)}\), where κ ∗(t) is the spatial variance of the average solute concentration, which can be described by macro-dispersion. This sets the concentration PDF at the plume centre as a result of random aggregation of lamellae. The evolution equation for the PDF p(c, t) of the concentration content in the mixture as a result of random aggregation is discussed in [69].
5.3.3.2 Chemical Reactions
In this section, we will briefly discuss the upscaling of chemical reactions in heterogeneous porous media and the influence of mixing on the reaction efficiency. Chemical reactions are contact processes and thus depend on the availability of reacting species and on the mechanisms that bring them into contact. In a well-mixed reactor, in which stirring-induced mixing is exponential as described above, mass transfer is not a limiting process. For a heterogeneous porous medium, in which mixing is much slower, reactions may be limited by the transport rate, i.e., the efficiency by which they are brought into contact. In the former case, the chemical reaction is rate limited, in the latter transport limited. These situations are distinguished by the Damköhler number
where k r is a reaction rate and τ m a characteristic mass transfer time scale. For Da < 1, the chemical reaction is rate limited, for Da ≫ 1 it is mixing, or transport limited.
Incomplete Mixing
A key issue for reaction upscaling in porous media is the notion of a well-mixed support scale. We have seen in the previous sections that mixing in porous media is slow because the “stirring” by the porous medium is much less efficient than stirring-induced chaotic advection in a free fluid. Spatial heterogeneity and consequently slow mass transfer between different compartments of a heterogeneous porous medium leads to reactant segregation and thus to a reduction of the reaction rate compared to a well-mixed system. We have seen in Sect. 5.3.2 that incomplete mixing on the support scale leads to non-Fickian transport and history-dependent transport phenomena. The same mechanisms lead to reaction behaviours that are different from the ones measured in well-mixed laboratory environments [91, 92]. However, traditional Darcy-scale reactive transport modelling is based on the advection–dispersion equation for the species concentration c i combined with a kinetic rate law determined for a well-mixed environment,
where ν ij are stoichiometric coefficient, r j is the reaction rate of the jth reaction and c(x, t) is the vector of concentrations of the reacting species. This formulation assumes that the support scale is a well-mixed environment. This means that the time scale by which the concentration on the support scale homogenises after a concentration perturbation due to mass transfer is smaller than the reaction time scale. Only under these conditions can the reaction rate on the right-hand side be identified with the one obtained in a well-mixed environment. The upscaling of reactive transport from the pore to the Darcy scale can be formally studied, for example, using volume-averaging [93, 94] or homogenisation theory [95]. The validity of Darcy-scale reaction–dispersion models such as Eq. (5.48) have been investigated in detail by Kechagia et al. [96] and Meile and Tuncay [97]. These studies systematically show discrepancies between the average reaction rates and reaction rates predicted by the advection–dispersion reaction equation. Similar observations have been made for the upscaling from Darcy to regional scale [98,99,100,101]. Incomplete mixing on the support scale leads in general to the reduction of the mixing efficiency compared to equivalent Fickian large scale models. The segregation of reactants on the support scale can be addressed using multi-continuum approaches [102, 103], which resolve concentration variability on the support scale due to subregions of slow and fast mass transfer.
An illustrative example for the impact of chemical heterogeneity on reactivity is diffusion in a medium characterised by a spatial distribution of specific reactive surfaces σ r(x) at which species A reacts to C. The concentration c A of A evolves according to the reaction–diffusion equation
We consider σ r(x) = 0, 1 randomly distributed in space with a characteristic distance ℓ c and Da = kL 2∕D ≫ 1, this means fast chemical reactions. Thus one would assume that the effective reaction rate is given by the mean diffusion time between reactive spots, k e = 1∕τ D, where \(\tau _D = \ell _c^2/D\) is the average diffusion time between reaction spots. However, the total mass of A decays at long times as a stretched exponential [104],
with β being a constant. It decays slower than the exponential decay predicted by τ D. This is due to the fact that the space between reaction spots has a finite probability to be arbitrarily large. Thus, segregation due to spatial heterogeneity leads to a slower decay than what would be predicted by mean field theory.
Mixing-Limited Reactions
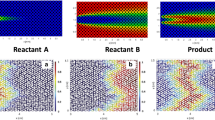
For mixing-limited chemical reactions, i.e., for high Da, the “stirring” action of the heterogeneous porous medium enhances the mixing efficiency compared to purely diffusive mass transfer and may lead to the formation of localised mixing and reaction hotspots [105, 106]. At high Da, the reaction rate is directly proportional to the mixing rate and the reactive transport problem can be mapped onto a conservative transport problem plus a speciation relation [107]. We illustrate this briefly for a fast reversible bimolecular reaction \(A + B \rightleftharpoons C \downarrow \) on the Darcy scale. Chemical equilibrium is described by the mass action law
where c A and c B are the concentrations of species A and B and K is the equilibrium constant. The reactive transport problem is described by Eq. (5.48) for each species (i = A, B), which for a heterogeneous medium reads as
where we have assumed the same dispersivity for both species, and where r(x, t) denotes the “equilibrium” reaction rate. It is determined by observing that ξ = c A − c B is a conserved variable (sometimes called mixture fraction) and obeys the conservative advection–dispersion equation
Secondly, both c A and c B depend only on u through the mass action law, Eq. (5.51),
and analogously for c B. Using this relation Eq. (5.52) together with Eq. (5.53) gives the following equation for the reaction rate:
The expression in the square brackets is identical to the scalar dissipation rate, see Eq. (5.38), which measures the rate of mixing of dissolved substances. This expression illustrates the direct dependence of the reaction rate at high Da with the mixing rate as quantified by the scalar dissipation rate. The impact of medium heterogeneity on the reaction rate has been investigated using the PDF of the conserved components ξ(x, t), which can be mapped directly on the PDF of the species concentrations via Eq. (5.54) [108, 109].
5.4 Multiphase and Surface Processes
In the previous sections, we presented the challenges related to the dispersion and the upscaling of bulk reactions in the fluid. These, when the Fickian assumption is not valid, can be conveniently approximated with multi-continuum models. This is not dissimilar from what is obtained in proper multiphase systems. For example, conjugate heat transfer problems, that would require the coupled solution of heat transfer in the fluid and solid region, can be averaged to obtain two-phase formulations with appropriate transfer terms. However, these transfer terms are local (in time and space) and linear only under local equilibrium conditions in both phases. An alternative approach is to perform the upscaling in two steps. First the phase which relaxes faster to equilibrium is approximated macroscopically with an equivalent heat transfer coefficient (possibly non-constant) at the solid boundary. This first upscaling reduces the dimensionality of the fast dynamics in a sub-domain, effectively representing it as a surface process, leaving us with the task of averaging transport in one phase only with complex boundary conditions.
Among these surface processes we can identify the following three categories:
-
Dynamic conditions: One of the most general surface process is the one encountered in adsorption–desorption processes that can be modelled with the following boundary conditions:
$$\displaystyle \begin{aligned} \mathbf j\cdot{\mathbf n} = \left({\mathbf u} - D_m\nabla\right)c\cdot{\mathbf n} = b\left(c,s\right), \end{aligned}$$where j is the flux, b represents the adsorption/desorption/transfer processes, r is a source/sink describing chemical reactions and s = s(x, t) is the adsorbed concentration on the surface. This has been solved separately with a surface ordinary differential equation

-
Mixed conditions: When the time scale defined by b is fast enough, one can explicitly find s = s(c) such that b(c, s) = 0. This means that the above conditions simplify to a, possibly non-linear, mixed boundary condition of the type
$$\displaystyle \begin{aligned} \mathbf j\cdot{\mathbf n} = \left({\mathbf u} - D_m\nabla\right)c\cdot{\mathbf n} = b\left(c,s\left(c\right)\right) = f(c). \end{aligned}$$Linearising f we obtain a mixed (Robin) boundary condition
$$\displaystyle \begin{aligned} \mathbf j\cdot{\mathbf n} = f_0 + f'c. \end{aligned} $$(5.56) -
Simple conditions: Assuming infinitely slow adsorption/reaction process f, the condition above reduces to a fixed flux (Neumann) condition
$$\displaystyle \begin{aligned} \mathbf j \cdot {\mathbf n} = f_0, \end{aligned}$$while, in the opposite case of infinitely fast surface process, we can retrieve a simple fixed concentration (Dirichlet) condition.
Clearly, the validity of these increasingly simplifying assumptions has to be verified case by case, and we consider this as part of the upscaling process. In all three cases, however, standard upscaling techniques (such as volume-averaging and homogenisation) can be applied only when the surface process is slow compared to advection and diffusion. When instead this is not the case, more advanced techniques have to be used [110, 111]. This is similar to the case of diffusion-limited bulk reactions (see above) that generally results in upscaled dispersion and velocity coefficients significantly different from the non-reactive case.
5.4.1 Mass and Heat Transfer
The transport and deposition of particles in porous media are fundamental multiscale phenomena present in a number of natural and engineered processes. Although we refer here to the transport of physical particles, the discussion below conceptually applies, with minor modifications, also to heat transfer mechanisms.
The classical theoretical framework typically used is the colloid filtration theory but, more in general, advances in this field generally belong to the so-called soft matter physics. Several complex physical mechanism, in fact, can arise due to the complex particle–particle and particle–wall interaction. In this chapter, however, we focus on a simple advection–diffusion description, in the dilute limit, with negligible Stokes and Reynolds numbers. Therefore most hydrodynamical interactions (sometimes called hydrodynamic retardation effects) between the particles and the surface of the solid grains, and the DLVO interactions happen at a very small scale and are therefore taken into account only at the boundaries, by modified boundary conditions. This is known as the Smoluchowski–Levich approximation that results in the molecular diffusion coefficient D m being constant, obtained, for example, via the Stokes–Einstein relation for diffusion of spheres in liquids. For larger particles instead, one should consider many other effects that act possibly also far from the wall, such as modified suspension viscosity, lift forces arising in small Reynolds number flows, the Faxen correction, due to the perturbed flow around the particles, and possibly also particle rotation, particle collisions, etc. Although some of these additional physics can easily be included in the upscaling, we limit ourselves to the effect of a surface process in the upscaling, namely in the equivalent macroscopic dispersion and reaction coefficients.
In the dimensional analysis of mass transfer phenomena, the most used dimensionless quantity is the Sherwood number, describing the ratio between convective mass transfer and diffusive transport, which is the analogue of the Nusselt number used in heat transfer. It is defined as:
where L is a characteristic length (in porous media application generally taken to be equal to the pore or grain size), and D m is the molecular diffusion coefficient. The mass transfer coefficient h is defined as the molar flux through the surface per unit surface, normalised by ΔC the concentration driving force. This representation implicitly considers the mass transfer as an equivalent diffusion process through the surface. If this is more often true at the micro-scale, after the upscaling, this effective transfer coefficient scaled by the diffusion strongly depends on the other transport mechanisms, such as advection, gravity and all the other external forces.
In the earlier studies of filtration, the most common upscaling approach was to determine a single parameter describing the filter effectiveness: this is obtained from its features and the operating conditions under investigation, and is defined the collector efficiency η D [112]. This efficiency coefficient is then assumed to be the product of two separated effects: the so-called attachment efficiency α, describing the probability of a particle that has reached the solid grain to be adsorbed, and the purely fluid-dynamical term η 0 to model the transport the bulk of the fluid to the surface of the grains. The latter is the often decomposed as a sum of different contributions due to, for example, Brownian diffusion, steric interception and inertial (and gravitational) effects. Some early works [113] analytically obtained, for Sh in idealised geometries, expressions such as
where As is a parameter depending on the porous medium porosity ϕ. Many other such relationships are available connecting the system features, in terms of geometrical features and fluid dynamic conditions, to an approximate particle deposition efficiency η D [114]. There are a number of issues facing these models; first of all they are most often based on a single idealised geometrical model representing the porous medium, thus failing to grasp the pore-scale complexities and heterogeneity and its effect on particle filtration. Another conceptual hurdle in the application of these models is the difficult translation of the obtained efficiency parameter η D into an effective macro-scale reaction term employable in a macroscopic transport equation [115], and to understand its dependence on the flow parameters and its inseparable connection with the effective dispersion and velocity.
5.4.1.1 From Surface Processes to Averaged Reaction Rates
We follow here [115], showing how to obtain a stationary effective reaction rate for a periodic geometry and its dependence on the (reactive) boundary condition and flow parameters, for arbitrary reaction/deposition regimes. To this aim, we consider Eq. (5.12) and we assume that the detailed surface processes can be averaged in a small boundary layer around the solid matrix and approximated with a generic effective linearised mixed boundary condition (see Eq. (5.56)) of the type:
where α is the deposition/attachment efficiency, Γ is the porous matrix surface area, r is the surface transfer coefficient and r 0 is a constant surface flux. When α = 1, Eq. (5.58) is equivalent to a Dirichlet conditions c = 0 on the solid grains (perfect sink). In a particle-based Lagrangian framework, such as the one considered when performing random walk simulations, this efficiency α can be interpreted as related to the probability of a single colloidal particle of attaching to the collector surface upon collision [116].
Applying a simple volume-average over a fixed REV Ω, defined as \(\overline { \cdot } = \frac {1}{V} \int \cdot \,\mathrm{d}v \) (with V being the total volume), the divergence theorem and the boundary condition, Eq. (5.58), we obtain

Considering a box with periodic boundary conditions on y − and z −directions, and no accumulation (stationary, local equilibrium hypothesis), it is possible to identify the second surface integral on the LHS of Eq. (5.59) with the total flux F through the x −boundaries of the domain (inlet and outlet in this case). Being the starting equation linear, it is reasonable to assume the above quantity (the average mass flux) to be a linear function of the average concentration, with a macroscopic effective reaction rate R defined as:
This quantity is simply computable from a micro-scale simulation on the periodic cell, simply looking at inlet–outlet fluxes and averaged volume concentration, even in the case of perfect sink (r →∞) condition. Assuming a Fickian macroscopic dispersion (see sections above), we can therefore postulate a closed-form for the one-dimensional macroscopic advection–diffusion–reaction equation for \(c=(\overline {c}/c_{\infty })\), in dimensionless form

where X represents the (dimensionless) macroscopic space variable and we have defined \(t_{\mathrm{diff}}=\frac {t D_m}{L^{2}}\), and the Damköhler numbers as \( \mathrm {Da}=\frac {R_s \ L^{2}}{D_m} \), and \(\mathrm {Da}_{0}=\frac {r_{0} \ L}{q}\).
For a periodic FCC packing [115] we obtain the following qualitative upscaling law for the long-time effective macroscopic reaction rate, as a function of the microscopic Damköhler number \(\mathrm {Da}_{m}=\frac {rL^{2}}{D}\):
with constants K i. This qualitative behaviour is universal, although the exponent 0.15 and the constants could possibly depend on the specific geometry. The dependence of Da with respect to Dam, on the other hand, is linear (independent of Pe) for slow surface processes while, for infinitely fast processes, it saturates to a constant (that depends on Pe). This is the typical behaviour for reactions happening on a localised lower-dimensional manifold where mixing can totally control the reaction.
5.5 Conclusions
In the previous sections we highlighted the most important physical models and macroscopic equations that can be relevant in porous and heterogeneous materials. We identified several assumptions and limitations of the upscaling processes.
Non-Equilibrium and Lack of Scale Separation
When no upscaling is available that can decouple the physical scales or when transition out-of-equilibrium effects are important at the micro-scale, alternative techniques can be used such as numerical multiscale approaches such as multiscale FEM, variational, heterogeneous or hybrid multiscale methods. These methods allow for a generic system to be solved efficiently explicitly accounting for some micro-scale information. They usually rely on a pre-processing offline step (similarly to the cell-problems in classical upscaling) or on an online dual-resolution computational approach.
Suspensions and Interfacial Flows
Multiphase flows such as suspensions and interfacial flows can be upscaled with the approaches described above, only under local equilibrium, and when the forces acting on each phase are relatively small. The presence of complex momentum transfer (in the case of suspensions) and strong localised forces, such as surface tension (in the case of interfacial flows), makes the standard upscaling inadequate. An intuitive interpretation of this inadequacy is the fact that volumetric/ensemble averages cannot properly represent interfacial forces and configuration-dependent forces. Time-dependent, non-linear, non-local and memory effects can arise at the macro-scale.
Notes
- 1.
For example, with the recent development of 3D printing, a wide range of porous media structures can be synthetically recreated and tested.
- 2.
With a total of three equations for three lowest powers of 𝜖, in the case second-order PDEs.
- 3.
Traditionally, homogenisation is performed on continuous domains with space-dependent oscillating diffusion coefficient. However, the case studied here, more relevant to porous media applications, can be interpreted as a limiting case in which the diffusion coefficient tends to a patch-wise constant. This is what is done practically when solving porous media problems with immersed boundaries, penalisation or diffuse domain methods.
- 4.
Which, in this case, is a unique and exact decomposition since this equation is defined up to an additive constant, \(\overline {c_1}\), and a multiplicative constant, \(\nabla _{{\mathbf x}_0}c_0\).
- 5.
Also a source term on the right-hand side would appear to counterbalance advection or faster reaction and obtain a periodic solution.
- 6.
Here is where the hypotheses on the porous media structure are introduced, through estimates of the (tensorial) spatial moments \(\overline {{\mathbf n}{\mathbf y}^j}^\Gamma \) with j = 0, 1, 2, … denoting the order of the tensorial product and y being the spatial coordinate.
References
U. Hornung, Homogenization and Porous Media, vol. 6 (Springer Science & Business Media, Berlin, 2012)
S. Whitaker, The Method of Volume Averaging, vol. 13 (Springer Science & Business Media, Berlin, 1998)
S.M. Hassanizadeh, W. Gray, High velocity flow in porous media. Transp. Porous Media 2(6), 521 (1987)
D. Lasseux, A.A. Abbasian Arani, A. Ahmadi, On the stationary macroscopic inertial effects for one phase flow in ordered and disordered porous media. Phys. Fluids 23(7), 73103 (2011)
E. Skjetne, J.L. Auriault, High-velocity laminar and turbulent flow in porous media, Transp. Porous Media 36(2), 131 (1999)
C.R. Dudgeon, An experimental study of the flow of water through coarse granular media. La Houille Blanche 7, 785 (1966)
P. Angot, C.H. Bruneau, P. Fabrie, A penalization method to take into account obstacles in incompressible viscous flows. Numer. Math. 81(4), 497 (1999)
R.E. Hayes, A. Afacan, B. Boulanger, A.V. Shenoy, Modelling the flow of power law fluids in a packed bed using a volume-averaged equation of motion. Transp. Porous Media 23(2), 175 (1996)
T. Tosco, D. Marchisio, F. Lince, R. Sethi, Extension of the Darcy-Forchheimer law for shear-thinning fluids and validation via pore-scale flow simulations. Transp. Porous Media 96(1), 1 (2013)
V.I. Arnol’d, On the topology of three-dimensional steady flows of an ideal fluid. J. Appl. Math. Mech. 30, 223 (1966)
L.W. Gelhar, Stochastic Subsurface Hydrology (Prentice-Hall, Upper Saddle River, 1993)
G. Dagan, Flow and Transport in Porous Formations (Springer Science & Business Media, Berlin, 2012)
Y. Rubin, Applied Stochastic Hydrogeology (Oxford University Press, New York, 2003)
P. Renard, G. de Marsily, Calculating equivalent permeability: a review. Adv. Water Resour. 20, 253 (1997)
X. Sanchez-Vila, A. Guadagnini, J. Carrera, Representative hydraulic conductivities in saturated groundwater flows. Rev. Geophys. 44, RG3002 (2006)
J.B. Keller, A theorem on the conductivity of a composite medium. J. Math. Phys. 5, 548 (1964)
D.S. Dean, I.T. Drummond, R.R. Horgan, Effective transport properties for diffusion in random media. J. Stat. Mech. 7, P07013 (2007)
G. Matheron, Composition des perméabilités en milieu poreux héterogène. Méthode de Schwydler et règles de pondération, Rev. l’Institute Français du Pet. Mars, 443 (1967)
A.L. Gutjahr, L.W. Gelhar, A.A. Bakr, J.R. MacMillan, Stochastic analysis of spatial variability in subsurface flows 2. Evaluation and applications. Water Resour. Res. 14, 953 (1978)
L.W. Gelhar, C.L. Axness, Three-dimensional stochastic analysis of macrodispersion in aquifers. Water Resour. Res. 19(1), 161 (1983)
A.E. Scheidegger, General theory of dispersion in porous media. J. Geophys. Res. 66, 3273 (1961)
J. Bear, Dynamics of Fluids in Porous Media (American Elsevier, New York, 1972)
H. Risken, The Fokker-Planck Equation (Springer, Heidelberg, 1996)
B. Noetinger, D. Roubinet, A. Russian, T. Le Borgne, F. Delay, M. Dentz, J.R. De Dreuzy, P. Gouze, Random walk methods for modeling hydrodynamic transport in porous and fractured media from pore to reservoir scale. Transp. Porous Media, 1–41 (2016)
P.G. Saffman, A theory of dispersion in a porous medium. J. Fluid Mech. 6(03), 321 (1959)
B. Bijeljic, M.J. Blunt, Pore-scale modeling and continuous time random walk analysis of dispersion in porous media. Water Resour. Res. 42, W01202 (2006)
M. Icardi, G. Boccardo, D.L. Marchisio, T. Tosco, R. Sethi, Pore-scale simulation of fluid flow and solute dispersion in three-dimensional porous media. Phys. Rev. E 90(1), 13032 (2014)
B. Bijeljic, M.J. Blunt, Pore-scale modeling of transverse dispersion in porous media. Water Resour. Res. 43, W12S11 (2007)
S. Attinger, M. Dentz, W. Kinzelbach, Exact transverse macro dispersion coefficient for transport in heterogeneous media. Stoch. Env. Res. Risk A. 18, 9 (2004)
L.W. Gelhar, C. Welty, K.R. Rehfeldt, A critical review of data on field-scale dispersion in aquifers. Water Resour. Res. 28(7), 1955 (1992)
A. Beaudoin, J.R. Dreuzy, Numerical assessment of 3-D macrodispersion in heterogeneous porous media. Water Resour. Res. 49, 2489 (2013)
B. Bijeljic, P. Mostaghimi, M.J. Blunt, Signature of non-Fickian solute transport in complex heterogeneous porous media. Phys. Rev. Lett. 107(20), 204502 (2011)
V.L. Morales, M. Dentz, M. Willmann, M. Holzner, Stochastic dynamics of intermittent pore-scale particle motion in three-dimensional porous media: Experiments and theory. Geophys. Res. Lett. 44, 9361 (2017)
E. Crevacore, T. Tosco, R. Sethi, G. Boccardo, D.L. Marchisio, Recirculation zones induce non-Fickian transport in three-dimensional periodic porous media. Phys. Rev. E 94(5) (2016)
R. Haggerty, S.A. McKenna, L.C. Meigs, On the late time behavior of tracer test breakthrough curves. Water Resour. Res. 36(12), 3467 (2000)
P.K. Kang, T. Le Borgne, M. Dentz, O. Bour, R. Juanes, Impact of velocity correlation and distribution on transport in fractured media: field evidence and theoretical model. Water Resour. Res. 51, 940 (2015)
S.P. Neuman, Eulerian-Lagrangian theory of transport in space-time nonstationary velocity fields: exact nonlocal formalism by conditional moments and weak approximation. Water Resour. Res. 29(3), 633 (1993)
J.H. Cushman, X. Hu, T.R. Ginn, Nonequilibrium statistical mechanics of preasymptotic dispersion. J. Stat. Phys. 75(5/6), 859 (1994)
D.A. Benson, S.W. Wheatcrat, M.M. Meerschaert, Application of a fractional advection-dispersion equation. Water Resour. Res. 36, 1403 (2000)
J.H. Cushman, T.R. Ginn, Fractional advection-dispersion equation: A classical mass balance with convolution–Fickian flux. Water Resour. Res. 36, 3763 (2000)
R. Metzler, J. Klafter, The random walk’s guide to anomalous diffusion: a fractional dynamics approach. Phys. Rep. 339(1), 1 (2000)
B. Berkowitz, H. Scher, Anomalous transport in random fracture networks. Phys. Rev. Lett. 79(20), 4038 (1997)
M. Dentz, A. Cortis, H. Scher, B. Berkowitz, Time behavior of solute transport in heterogeneous media: transition from anomalous to normal transport. Adv. Water Resour. 27(2), 155 (2004)
B. Berkowitz, A. Cortis, M. Dentz, H. Scher, Modeling non-Fickian transport in geological formations as a continuous time random walk. Rev. Geophys. 44, RG2003 (2006)
V. Cvetkovic, H. Cheng, X.H. Wen, Analysis of nonlinear effects on tracer migration in heterogeneous aquifers using Lagrangian travel time statistics. Water Resour. Res. 32(6), 1671 (1996)
F. Delay, J. Bodin, Time domain random walk method to simulate transport by advection-diffusion and matrix diffusion in fracture networks. Geophys. Res. Lett. 28, 4051 (2001)
R. Haggerty, S.M. Gorelick, Multiple-rate mass transfer for modeling diffusion and surface reactions in media with pore-scale heterogeneity. Water Resour. Res. 31(10), 2383 (1995)
J. Carrera, X. Sánchez-Vila, I. Benet, A. Medina, G. Galarza, J. Guimerà, On matrix diffusion: formulations, solution methods, and qualitative effects. Hydrogeol. J. 6, 178 (1998)
E.W. Montroll, G.H. Weiss, Random walks on lattices, 2. J. Math. Phys. 6(2), 167 (1965)
H. Scher, M. Lax, Stochastic transport in a disordered solid. I. Theory. Phys. Rev. B 7(1), 4491 (1973)
V.M. Kenkre, E.W. Montroll, M.F. Shlesinger, Generalized master equations for continuous-time random walks. J. Stat. Phys. 9(1), 45 (1973)
M. Abramowitz, I.A. Stegun, Handbook of Mathematical Functions (Dover, Mineola, 1972)
M. Dentz, P.K. Kang, A. Comolli, T. Le Borgne, D.R. Lester, Continuous time random walks for the evolution of Lagrangian velocities. Phys. Rev. Fluids 1, 74004 (2016)
G. Margolin, M. Dentz, B. Berkowitz, Continuous time random walk and multirate mass transfer modeling of sorption. Chem. Phys. 295, 71 (2003)
T. Le Borgne, M. Dentz, J. Carrera, Spatial Markov processes for modeling Lagrangian particle dynamics in heterogeneous porous media. Phys. Rev. E 78, 41110 (2008)
P.K. Kang, M. Dentz, T. Le Borgne, R. Juanes, Spatial Markov model of anomalous transport through random lattice networks. Phys. Rev. Lett. 107, 180602 (2011)
P. De Anna, T. Le Borgne, M. Dentz, A.M. Tartakovsky, D. Bolster, P. Davy, Flow intermittency, dispersion, and correlated continuous time random walks in porous media. Phys. Rev. Lett. 110(18), 184502 (2013)
E. Barkai, Y. Garini, R. Metzler, Strange kinetics of single molecules in living cells. Phys. Today 8, 29 (2012)
J. Klafter, I. Sokolov, Anomalous diffusion spreads its wings. Phys. World 18(8), 29 (2005)
C.F. Harvey, S.M. Gorelick, Temporal moment-generating equations: Modeling transport and mass transfer in heterogeneous aquifers. Water Resour. Res. 31(8), 1895 (1995)
P. Maloszewski, A. Zuber, On the theory of tracer experiments in fissured rocks with a porous matrix. J. Hydrol. 79, 333 (1985)
P. Gouze, Z. Melean, T. Le Borgne, M. Dentz, J. Carrera, Non-Fickian dispersion in porous media explained by heterogeneous microscale matrix diffusion. Water Resour. Res. 44, W11416 (2008)
M. Willmann, J. Carrera, X. Sanchez-Vila, Transport upscaling in heterogeneous aquifers: What physical parameters control memory functions? Water Resour. Res. 44, W12437 (2008)
M. Dentz, B. Berkowitz, Transport behavior of a passive solute in continuous time random walks and multirate mass transfer. Water Resour. Res. 39(5), 1111 (2003)
R. Schumer, D.A. Benson, M.M. Meerschaert, B. Bauemer, Fractal mobile/immobile solute transport. Water Resour. Res. 39(10), 1296 (2003)
D.A. Benson, M.M. Meerschaert, A simple and efficient random walk solution of multi-rate mobile/immobile mass transport equations. Adv. Water Resour. 32(4), 532 (2009)
A. Comolli, J.J. Hidalgo, C. Moussey, M. Dentz, Non-Fickian transport under heterogeneous advection and mobile-immobile mass transfer. Transp. Porous Media 115(2), 265 (2016)
E. Villermaux, J. Duplat, Mixing as an aggregation process. Phys. Rev. Lett. 91, 18 (2003)
J. Duplat, E. Villermaux, Mixing by random stirring in confined mixtures. J. Fluid Mech. 617, 51 (2008)
D.R. Lester, G. Metcalfe, M.G. Trefry, Is chaotic advection inherent to porous media flow? Phys. Rev. Lett. 111(17), 174101 (2013)
M. Kree, E. Villermaux, Scalar mixtures in porous media. Phys. Rev. Fluids 2, 104502 (2017)
F. Gjetvaj, A. Russian, P. Gouze, M. Dentz, Dual control of flow field heterogeneity and immobile porosity on non-Fickian transport in Berea sandstone. Water Resour. Res. 51, 8273 (2015)
M. Dentz, M. Icardi, J.J. Hidalgo, Mechanisms of dispersion in a porous medium. J. Fluid Mech. 841, 851 (2018)
G. Sposito, Steady groundwater flow as a dynamical system. Water Resour. Res. 30(8), 2395 (1994)
T. Le Borgne, M. Dentz, E. Villermaux, The lamellar description of mixing in porous media. J. Fluid Mech. 770, 458 (2015)
M. Dentz, D.R. Lester, T.L. Borgne, F.P.J. de Barros, Coupled continuous time random walks for fluid stretching in two-dimensional heterogeneous media. Phys. Rev. E 94(6-1), 061102 (2016)
M. Dentz, H. Kinzelbach, S. Attinger, W. Kinzelbach, Temporal behavior of a solute cloud in a heterogeneous porous medium, 1, Point-like injection. Water Resour. Res. 36(12), 3591 (2000)
M. Dentz, F.P.J. de Barros, Mixing-scale dependent dispersion for transport in heterogeneous flows. J. Fluid Mech. 777, 178 (2015)
P.K. Kitanidis, Prediction by the method of moments of transport in heterogeneous formations. J. Hydrol. 102, 453 (1988)
G. Dagan, Transport in heterogeneous porous formations: spatial moments, ergodicity, and effective dispersion. Water Resour. Res. 26, 1287 (1990)
V. Kapoor, P.K. Kitanidis, Concentration fluctuations and dilution in aquifers. Water Resour. Res. 34, 1181 (1998)
S.B. Pope. Turbulent flows. Meas. Sci. Technol. 12(11) (2001)
J. Villermaux, J.C. Devillon, in Proceedings of the 2nd International Symposium on Chemical Reaction Engineering (Elsevier, New York, 1972)
J.R. De Dreuzy, J. Carrera, M. Dentz, T. Le Borgne, Time evolution of mixing in heterogeneous porous media. Water Resour. Res. 48, W06511 (2012)
T. Le Borgne, M. Dentz, P. Davy, D. Bolster, J. Carrera, J.R. de Dreuzy, O. Bour, Persistence of incomplete mixing: A key to anomalous transport. Phys. Rev. E 84, 015301(R) (2011)
E. Caroni, V. Fiorotto, Analysis of concentration as sampled in natural aquifers. Transp. Porous Media 59(1), 19 (2005)
D.M. Tartakovsky, P.C. Lichtner, R.J. Pawar, PDF methods for reactive transport in porous media. Acta Univ. Carol. Geol. 46, 113 (2002)
A. Bellin, D. Tonina, Probability density function of non-reactive solute concentration in heterogeneous porous formations. J. Contam. Hydrol. 94, 109 (2007)
E. Villermaux, Mixing by porous media. C. R. Mécanique 340, 933 (2012)
W.E. Ranz, Application of a stretch model to mixing, diffusion and reaction in laminar and turbulent flows. AIChE J. 25(1), 41 (1979)
C.I. Steefel, D.J. DePaolo, P.C. Lichtner, Reactive transport modeling: An essential tool and a new research approach for the Earth sciences. Earth Planet. Sci. Lett. 240, 539 (2005)
M. Dentz, T. LeBorgne, A. Englert, B. Bijeljic, Mixing, spreading and reaction in heterogeneous media: A brief review. J. Contam. Hydrol. 120–121, 1 (2011)
D.A. Edwards, M. Shapiro, H. Brenner, Dispersion and reaction in two-dimensional model porous media. Phys. Fluids A 5, 837 (1993)
M. Quintard, S. Whitaker, Convection, dispersion and interfacial transport of contaminants: Homogeneous media. Adv. Water Resour. 17, 221 (1994)
A. Mikelic, V. Devigne, C.J. Van Duijn, Rigorous upscaling of the reactive flow through a pore, under dominant Peclet and Damkohler number. Siam J. Math. Anal. 38, 1262 (2006)
P.E. Kechagia, I.N. Tsimpanogiannis, Y.C. Yortsos, P.C. Lichtner, On the upscaling of reaction-transport processes in porous media with fast or finite kinetics. Chem. Eng. Sci. 57(13), 2565 (2002)
C. Meile, K. Tuncay, Scale dependence of reaction rates in porous media. Adv. Water Resour. 29, 62 (2006)
F.J. Molz, M.A. Widdowson, Internal inconsistencies in dispersion-dominated models that incorporate chemical and microbial kinetics. Water Resour. Res. 24(4), 615 (1988)
T.R. Ginn, C.S. Simmons, B.D. Wood, Stochastic-convective transport with nonlinear reaction: biodegradation with microbial growth. Water Resour. Res. 31(11), 2689 (1995)
V. Kapoor, L. Gelhar, F. Miralles-Wilhelm, Bimolecular second-order reactions in spatially varying flows: segregation induced scale-dependent transformation rates. Water Resour. Res. 33, 527 (1997)
C.M. Gramling, C.F. Harvey, L.C. Meigs, Reactive transport in porous media: A comparison of model prediction with laboratory visualization. Environ. Sci. Technol. 36, 2508 (2002)
P.C. Lichtner, Q. Kang, Upscaling pore-scale reactive transport equations using a multiscale continuum formulation. Water Resour. Res. 43, W12S15 (2007)
M. Dentz, P. Gouze, J. Carrera, Effective non-local reaction kinetics for transport in physically and chemically heterogeneous media. J. Contam. Hydrol. 120–121, 222 (2011)
D. Ben-Avraham, S. Havlin, Diffusion and Reactions in Fractals and Disordered Systems (Cambridge University Press, Cambridge, 2004)
J.J. Hidalgo, M. Dentz, Y. Cabeza, J. Carrera, Dissolution patterns and mixing dynamics in unstable reactive flow. Geophys. Res. Lett. 42, 6357 (2015)
M. Pool, M. Dentz, Effects of heterogeneity, connectivity and density variations on mixing and chemical reactions under temporally fluctuating flow conditions and the formation of reaction patterns. Water Resour. Res. 54 (2018). https://doi.org/10.1002/2017WR021820
M. De Simoni, J. Carrera, X. Sánchez-Vila, A. Guadagnini, A procedure for the solution of multicomponent reactive transport problems. Water Resour. Res. 41(11) (2005). https://doi.org/10.1029/2005WR004056
O.A. Cirpka, R.L. Schwede, J. Luo, D. M., Concentration statistics for mixing-controlled reactive transport in random heterogeneous media. J. Contam. Hydrol. 98, 61 (2008)
A. Bellin, G. Severino, A. Fiori, On the local concentration probability density function of solutes reacting upon mixing. Water Resour. Res. 47, W01514 (2010)
G. Allaire, A.L. Raphael, Homogenization of a convection–diffusion model with reaction in a porous medium. Comptes Rendus Math. 344(8), 523 (2007)
R. Mauri, Dispersion, convection, and reaction in porous media. Phys. Fluids A Fluid Dyn. 3(5), 743 (1991)
K.M. Yao, Influence of Suspended Particle Size on the Transport Aspect of Water Filtration. Ph.D. thesis, University of North Carolina (Chapel Hill, North Carolina, 1968)
R. Pfeffer, J. Happel, An analytical study of heat and mass transfer in multiparticle systems at low Reynolds numbers. AIChE J. 10(5), 605 (1964)
G. Boccardo, R. Sethi, D.L. Marchisio, Fine and ultrafine particle deposition in packed-bed catalytic reactors. Chem. Eng. Sci. 198, 290–304 (2019)
G. Boccardo, E. Crevacore, R. Sethi, M. Icardi, A robust upscaling of the effective particle deposition rate in porous media. J. Contam. Hydrol. 212, 3–13 (2017)
G. Boccardo, I.M. Sokolov, A. Paster, An improved scheme for a robin boundary condition in discrete-time random walk algorithms. J. Comput. Phys. 374, 1152 (2018)
I. Babuška, in Proceedings of the Third Symposium on the Numerical Solution of Partial Differential Equations–III (Elsevier, Amsterdam, 1976), pp. 89–116
S.M. Kozlov, Averaging of random operators. Mat. Sb. 151(2), 188 (1979)
E. Sánchez-Palencia, Non-homogeneous media and vibration theory. Lect. Notes Phys. 127 (1980)
L. Tartar, in North-Holland Mathematics Studies, vol. 30 (Elsevier, Amsterdam, 1978), pp. 472–484
J.L. Lions, G. Papanicolaou, A. Bensoussan, Asymptotic Analysis for Periodic Structures (North-Holland, Amsterdam, 1978)
A. Gloria, F. Otto, in ESAIM Proc., CEMRACS 2013 – Modelling and Simulation of Complex Systems: Stochastic and Deterministic Approaches, vol. 48 (EDP Sciences, Les Ulis, 2015), pp. 80–97
X. Blanc, C. Le Bris, F. Legoll, Some variance reduction methods for numerical stochastic homogenization. Phil. Trans. R. Soc. A 374(2066), 20150168 (2016)
S. Armstrong, T. Kuusi, J.C. Mourrat, Quantitative stochastic homogenization and large-scale regularity, arXiv Prepr. arXiv1705.05300 (2017)
G. Allaire, Homogenization and two-scale convergence. SIAM J. Math. Anal. 23(6), 1482 (1992)
P. Haynes, J. Vanneste, Dispersion in the large-deviation regime. Part 1: shear flows and periodic flows. J. Fluid Mech. 745, 321 (2014)
M. Icardi, Multiscale model reduction for advection diffusion problems in periodic media. Internal report
B.D. Wood, F. Cherblanc, M. Quintard, S. Whitaker, Volume averaging for determining the effective dispersion tensor: closure using periodic unit cells and comparison with ensemble averaging. Water Resour. Res. 39(8) (2003)
M. Quintard, S. Whitaker, Transport in ordered and disordered porous media II: generalized volume averaging. Transp. Porous Media 14(2), 179 (1994)
W.G. Gray, C.T. Miller, Thermodynamically constrained averaging theory approach for modeling flow and transport phenomena in porous medium systems: 1. Motivation and overview. Adv. Water Resour. 28(2), 161 (2005)
D.A. Drew, S.L. Passman, Theory of Multicomponent Fluids, vol. 135 (Springer Science & Business Media, Berlin, 2006)
R.O. Fox, Computational Models for Turbulent Reacting Flows (Cambridge University Press, Cambridge, 2003)
S.P. Neuman, Eulerian-Lagrangian theory of transport in space-time nonstationary velocity fields: exact nonlocal formalism by conditional moments and weak approximation. Water Resour. Res. 29(3), 633 (1993)
D.M. Tartakovsky, S.P. Neuman, Transient flow in bounded randomly heterogeneous domains: 1. Exact conditional moment equations and recursive approximations. Water Resour. Res. 34(1), 1 (1998)
J.H. Cushman, L.S. Bennethum, B.X. Hu, A primer on upscaling tools for porous media. Adv. Water Resour. 25(8–12), 1043 (2002)
W.G. Gray, P.C.Y. Lee, On the theorems for local volume averaging of multiphase systems. Int. J. Multiphas. Flow 3(4), 333 (1977)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
Appendix A: Homogenisation and Two-Scale Expansions
In this section we briefly sketch the main ideas and steps in the formal derivation of macroscopic equations using the method of periodic homogenisation with two-scale asymptotic expansion. The method has been initially proposed in theoretical mechanics for the study of composite materials and subsequently extensively studied in mathematical analysis, for elliptic (diffusion) operators and variational problems [117,118,119,120,121]. Quite interestingly, the first results in the area were developed in parallel both for periodic and random (stationary ergodic) media. Being the underlying mathematical techniques significantly different, the latter is also called stochastic homogenisation and has lately seen important developments [122,123,124], making it, in some cases, a more realistic and conceptually deeper alternative to the former. While the formal steps of periodic homogenisation are easily accessible with a basic background of asymptotic methods and PDEs, the mathematical proofs concerning the existence of a macroscopic limit (and the convergence towards it, [125]) require extensive knowledge of functional analysis and PDE theory and a much more complex notation, clearly beyond the scope of this chapter. For porous media applications we refer to [1] for a comprehensive, yet accessible, treatise.
We can identify the following steps that are usually needed to perform the two-scale expansion and derive a homogenised equation:
-
1.
Define the scale separation parameter \(\epsilon =\frac {\ell }{L}\), where L is a characteristic macroscopic length (e.g., the total domain size) and ℓ is a microscopic length (e.g., the size of the pores). While mathematical homogenisation theory deals with the existence, uniqueness, form and convergence rate of the problem when 𝜖 → 0, the more applied approach is to guess such a limit exist and constructively find its form and validity (measured in terms of corrections of the order of 𝜖).
-
2.
Put the (microscopic) equations in dimensionless form, to highlight and recognise the scaling, which is the crucial assumption for the validity of what follows. This is not strictly necessary but one of the advantages of homogenisation theory is, in fact, the clear identification of validity regimes of the macroscopic equation.
-
3.
Write down spatial (and possibly temporal) coordinates, derivatives and fields as an asymptotic expansion in terms of 𝜖. Neglecting time, given a spatial coordinate x ∈ Ω∈ [0, L]d and a field c = c(x), a two-scale expansion is performed as follows:
$$\displaystyle \begin{aligned} &{\mathbf x}={\mathbf x}_0+\epsilon{\mathbf x}_1 \end{aligned} $$(5.62a)$$\displaystyle \begin{aligned} &c({\mathbf x}) \approx c_0({\mathbf x})+\epsilon c_1({\mathbf x})+\epsilon^2 c_2({\mathbf x}) = c_0({\mathbf x}_0,{\mathbf x}_1)+\epsilon c_1({\mathbf x}_0,{\mathbf x}_1)+\epsilon^2 c_2({\mathbf x}_0,{\mathbf x}_1) \end{aligned} $$(5.62b)$$\displaystyle \begin{aligned} &\nabla{c}=\left(\nabla_{{\mathbf x}_0}+\frac{1}{\epsilon}\nabla_{{\mathbf x}_1}\right)c \approx \frac{1}{\epsilon}\nabla_{{\mathbf x}_1}c_0+\left(\nabla_{{\mathbf x}_0}c_0+\nabla_{{\mathbf x}_1}c_1\right) +\epsilon\left(\nabla_{{\mathbf x}_0}c_1+\nabla_{{\mathbf x}_1}c_2\right), \end{aligned} $$(5.62c)where x 0 ∈ Ω∈ [0, L]d defines the macro-scale and x 1 the (periodic with period [0, ℓ]d) micro-scale. While this expansion is formally always valid, its usefulness, as we will further explain below, relies on a wide separation of scales in the domain which is not always satisfied in real porous media.
-
4.
Starting from the lowest power of 𝜖, hierarchically define and solve (when a solution is trivially found) the cascade of equations for c 0, c 1, …. Usually it is enough to solve for the first two termsFootnote 2 to get a closed-form and computable parameters of the macroscopic limit (c 0). However, to achieve that, additional assumptions have to be made to close the system of equations. In particular, a simplified dependence of c 1 on the macro-scale c 0 has to be assumed (when it is not obtained formally), guessing a separable structure of the type:
$$\displaystyle \begin{aligned} c_1({\mathbf x}_0,{\mathbf x}_1)={\mathbf w}\cdot\nabla_{{\mathbf x}_0}c_0+\overline{c_1}, \end{aligned} $$(5.63)where the vectorial field w = w(x 1), periodic and with zero average, \(\overline {{\mathbf w}}=\mathbf {0}\), is also called corrector and can be found by solving the so-called cell-problem, usually derived, after some manipulation, from the first correction equation for c 1. This decomposition c 1 well represents the scale-separation hypothesis.
-
5.
Depending on the problem, also an average on c 0 (or, when c 0 is constant on the micro-scale, on c 0 + 𝜖c 1) might be defined to get rid of the micro-scale dependence, defining a new macroscopic field
$$\displaystyle \begin{aligned} \overline{c_0}({\mathbf x}_0)=\overline{c_0({\mathbf x}_0,{\mathbf x}_1)}=\int_{[0,\ell]^d}c_0({\mathbf x}_0,{\mathbf x}_1) d {\mathbf x}_1 \end{aligned}$$and a macroscopic evolution equation for \(\overline {c_0}\) (or \(\overline {c_{0}+\epsilon c_{1}}\)) can be derived from the terms of order 𝜖 0.
Example: Reaction–Diffusion in a Perforated Domain
It is important to notice that the steps outlined above are a constructive formal approach for homogenisation that is attractive (at least as a first approach) for new problems but does not cover the large number of possible problems for which a homogenised limit exists. This is much less general than, for example, variational approaches in which a given macroscopic limit is guessed and proven to be the correct limit. As an example, we illustrate the steps above for the simple case of pure diffusion with slow superficial reaction (or equivalently, heat transfer with a prescribed heat flux at the boundary), i.e.,
with constant diffusionFootnote 3 coefficient D, and a generic space-dependent source/sink term f. The equation is defined on a perforated (porous) domain Ω ∈ [0, L]d in d-dimensions, with periodic microstructure (cell) Ω𝜖 ∈ [0, ℓ]d. For simplicity we assume also periodicity in Ω but this can be easily replaced with any other simple (macroscopic) boundary conditions. On the internal boundaries (the porous matrix) we impose a linear mixed (normal flux) condition:
where k is a superficial reaction term (or heat transfer coefficient), and r is a constant superficial source (or sink) term. Despite its simplicity, this includes already important applications such as linear isotherm adsorption or heat transfer. The extension to the mass or heat transfer through an interface within two domain or two phases, instead of a boundary condition, is a possible extension which is discussed in Sect. 5.4.
Inserting the expansions Eq. (5.62) into Eq. (5.64), yields
while the expansion of the boundary condition can be rewritten as
At this point, since we have not put the equation in dimensionless form, it is important to identify the regime of interest. We will focus here on the simplest regime for which the homogenisation approach outlined above works seamlessly. This is the case when all coefficients (D, f) are of the same order, namely of order one, and the boundary coefficients (k = 𝜖k 1, r = 𝜖r 1) are of order 𝜖 1.
Collecting now terms with equal power of 𝜖, and taking into account the assumptions on the coefficients, the only term of order 𝜖 −2 leads to the linear homogeneous equation
that turns out to be a simple (linear homogeneous) equation for the variable c 0 at the micro-scale, i.e., in each periodic cell Ω𝜖 (since only derivatives with respect to x 1 appear). The largest terms in the boundary condition, i.e., a simple no-flux (homogeneous Neumann) condition, are \( {\mathbf n}\cdot \nabla _{{\mathbf x}_1}c_0=0 \) on the internal solid boundaries, with periodic boundary conditions on the external boundaries. This equation is trivially satisfied by a constant, i.e., a function c 0 = c 0(x 0) which is a function of x 0 only.
For the terms of order 𝜖 1, we obtain the following equation:
Given the conclusion above, i.e., c 0 constant at the micro-scale, the first term disappears and, replacing the assumption Eq. (5.63),Footnote 4 we obtain the equation
or, since this has to hold for an arbitrary \(\nabla _{{\mathbf x}_0}c_0\), equivalently written as a vectorial cell-problem for the corrector w
with I being the identity matrix, with boundary condition
or, equivalently, in vectorial form,
The next scale, 𝜖 0, reads
that, by using Eq. (5.63), the conclusions obtained above and the boundary conditions
can be averaged over the periodic cell to obtain the effective equation
where α is the specific surface area, ϕ is the porosity of the porous material, D is the (tensorial anisotropic) effective diffusion coefficient \({\mathbf D}=\overline {D I+\nabla _{{\mathbf x}_1}{\mathbf w}}\) that is computed from the cell-problem defined above. This gives us a macroscopic governing equation for \(\overline {c_0+\epsilon c_{1}}\) (which, in this case, is equivalent to c 0, being it constant over x 1, and c 1 with mean zero), where surface terms integrated over the surface (\(\overline {c_0}^\Gamma \) is, in fact, a surface average which, in this case, is again equivalent to c 0) appear in the right-hand side, together with f 0, as bulk reaction terms.
Physical Interpretation and Limitations
With respect to other upscaling techniques, the steps performed above do not to have a direct physical motivation and, therefore, it might be hard to understand and assess the validity of the underlying assumptions. However there are a few considerations that can be made:
-
Despite the apparent complexity, the cell-problem Eqs. (5.66) and (5.67) has a clear physical interpretation, being each component of w a harmonic function (i.e., a solution of the Laplace equation, while in other cases it would be the solution of the underlying microscopic physics), with periodic boundary conditions and a fixed gradient at the boundary.Footnote 5 These periodic cell-problems can often be shown to be equivalent to more intuitive closure problem, similar to the ones obtained in volume-averaging, where a concentration gradient is imposed at the external boundaries, respectively, in the x-, y- or z-direction. The periodicity, however, enforces also that a fully developed concentration profile (and not just a constant) is obtained while, as we will discuss in the next section, more general closure problems can be obtained by volume-averaging, with arbitrary boundary conditions.
-
Two often overlooked assumptions for homogenisation, possibly more important than the separation of scales or the periodicity of the geometry (which can be simply assumed as a first-order approximation) are the local equilibrium and stationarity conditions, implicitly assumed when imposing periodicity of all fields. This is particularly relevant for processes with long pre-asymptotic transition times (lengths) to equilibrium. In those cases, homogenisation is only able to retrieve the asymptotic stationary macroscopic model which might be significantly inaccurate for studying the initial times of processes like mixing. Even if, in principle, homogenisation can include explicitly the time-dependence both in the macro- and microscales, the periodic assumption implicitly defines steady closure (cell) problems. Generalisations of the homogenisation techniques to overcome these assumptions have been recently proposed [126, 127].
-
Another limitation is the particular scaling chosen which, on the one hand, clearly states the validity of the model, but, on the other hand, can be very restrictive. This aspect is also often overlooked when, for example, non-linear models, multiphase or fast reactions are considered. In those cases, additional terms arise in the leading orders that, only in some cases, can be tamed by ad hoc homogenisation techniques.
-
Homogenisation should be thought of as a rigorous and robust analysis of the multiscale features of the model (convergence properties to the macroscopic solution, identification of validity regimes and approximation errors) and not only as generic way of discovering emerging macroscopic equations. For more complex models, it is usually advisable to first tackle the problem with more phenomenological macroscopic models based, for example, on mixture theory and variation principles, using conservation laws and the second law of thermodynamics. Complementarily, volume-averaged computational results can be used to compute the parameters of these models, while homogenisation gives directly explicit formulas for upscaled parameters. From the practical point of view, both approaches require the solution a microscopic cell/closure problem.
Appendix B: Volume/Ensemble Averaging
An upscaling approach, developed extensively for porous media in the last 30 years [2, 128,129,130], is the theory of volume-averaging with its many variants. This is conceptually equivalent to the techniques more commonly used in fluid dynamics, turbulence, combustion and multiphase flows [82, 131, 132], such as the large eddy simulation. Closer instead to the Reynolds averaging in the RANS equations is instead the concept of ensemble averaging used predominantly in a surprisingly abundant amount of theoretical work in stochastic hydrology [11, 12, 133, 134]. These approaches have been separately developed by the porous media and fluid dynamics communities without significant connections. While it is out of the scope of this chapter to explain any of these approaches in detail, we offer here a very brief introduction and some general comments about the applicability, similarities, differences and meaning of these methodologies. The interested reader is referred to the previously cited works and to the review [135].
Both spatial averaging and ensemble/perturbation methods rely on the following steps:
-
Write the heterogeneous coefficients of the governing equation (e.g., velocity field, diffusion/dispersion coefficient) with a simple decomposition into a mean and fluctuating term, which for a generic quantity g reads
$$\displaystyle \begin{aligned} g({\mathbf x})=\int_{\Omega}{w({\mathbf y})g({\mathbf x}+{\mathbf y})\mathrm{d}{\mathbf y}}+\tilde{g}({\mathbf x})=\overline{g}({\mathbf x})+\tilde{g}({\mathbf x}) \end{aligned}$$for volume-averaging (better denoted, in this formulation, as generalised volume-averaging or space convolution filter), where w(x) is function with a compact and localised support such that ∫Ω w(y)dy = 1. The size of the support, ℓ, which defines the averaging length scale, should be related to the REV size (when the REV exists). Alternatively, for ensemble averaging, assuming that now g is a random field, we can similarly define
$$\displaystyle \begin{aligned} g({\mathbf x},\omega)=\int_\omega g({\mathbf x},\omega) \mathrm{d} \mu({\mathbf x},\omega) + g'({\mathbf x})= \left<g\right>({\mathbf x})+g'({\mathbf x}), \end{aligned}$$where μ(x, ω) is the probability associated with the random field measure, ω is a random event. While the first averaging is well-defined both for pore-scale (i.e., perforated) and macro-scale (i.e., continuous) domains, the second one strictly applies only to macro-scale (e.g., permeability) heterogeneities, although extensions are possible.
-
Applying the averaging operator to a generic transport equation for the field c, an unclosed equation for the mean (which we denote here generally with \(\overline {c}\) for both averages) is found, where the unclosed terms are either non-linear terms (for both volume and ensemble averages) or boundary terms (for volume-averaging). In fact, while in standard single-phase turbulence modelling, the averaging volume only contains fluid, in porous media the so-called spatial averaging theorem applies
$$\displaystyle \begin{aligned} \overline{\nabla c}=\nabla\overline{c}+\frac{\alpha}{\varepsilon}\overline{c{\mathbf n}}^\Gamma, \end{aligned}$$where, as discussed in the homogenisation section, \(\overline {\cdot }^\Gamma \) denotes an average over the fluid–solid interface, and n the normal to the surface. A generalisation is possible when dealing with generic multiphase systems whose interfaces between phases can be mobile. In that case, a more complex treatment has been used to derive upscaled equations for all phases [2, 131, 136].
-
To obtain a first-order upscaled model, the unclosed equation for \(\overline {c}\) is closed with a combination of geometricalFootnote 6 and physical/phenomenological arguments, and by the solution of the closure problem for the fluctuations \(\tilde {g}\). The latter can be easily obtained by subtracting the equation for \(\overline {g}\) from the initial equation. This, however, often contains other unclosed terms that could be written in terms of higher order moments of coefficients, e.g., g, and variables, e.g., c.
-
Higher order approximations can be obtained either by defining new problems for the higher order moments or, exploiting the linearity (or linearisation) of the transport equation, in defining a new sequence of problems to find an approximation for c of the type:
$$\displaystyle \begin{aligned} c=c_0+c_1+c_2+\dots, \end{aligned}$$where, for example, c 0 is obtained by neglecting all unclosed terms in the equation for \(\overline {c}\).
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this chapter
Cite this chapter
Icardi, M., Boccardo, G., Dentz, M. (2019). Upscaling Flow and Transport Processes. In: Toschi, F., Sega, M. (eds) Flowing Matter. Soft and Biological Matter. Springer, Cham. https://doi.org/10.1007/978-3-030-23370-9_5
Download citation
DOI: https://doi.org/10.1007/978-3-030-23370-9_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-23369-3
Online ISBN: 978-3-030-23370-9
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)